R.Rempała . Materiały dydaktyczne.
301
Wykłady 3-4. a) c.d. Wykładu 2, funkcja użyteczności,
krańcowa stopa substytucji, użyteczność krańcowa,
optymalne wybory.
Ad. a)
1. Zajmowaliśmy się relacją słabej preferencji ( ). Jest to
relacja określona w zbiorze konsumpcyjnym Z, która ma
trzy własności, jest zwrotna, przechodnia i zupełna.
Ekonomiści uważają, że taka relacja dobrze opisuje
upodobania konsumentów w odniesieniu do koszyków ze
zbioru Z. Przechodniośd i zwrotnośd oznaczają
niesprzecznośd gustów konsument ,
(tzn. (x
y y z)
( x z), oraz, że x ). Zupełność oznacza, iż dla
dowolnej pary koszyków (x,y) Z, konsument potrafi wyrazić
swoje upodobanie (x
y y x) .
2.
Relacja słabej preferencji (dla uproszczenia wygodnie jest
słabą preferencję nazywać krótko preferencją), w naturalny
sposób wyznacza dwie inne relację: indyferencji (
x ~ y
x
y y x)
i ścisłej (silnej) preferencji. (
x
y
x y
y
x)
;
y
x
oznacza: nie prawda, że
y
x.
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
302
3. Można pokazać, że relacja indyferencji jest relacją
równoważności (tzn. jest zwrotna symetryczna i
przechodnia). Z zasady abstrakcji (znana w matematyce
własność relacji równoważności) wynika, że zbiór Z rozpada
się na rozłączne podzbiory. Podzbiorami są klasy
równoważności relacji indyferencji).
W przypadku 2-
wymiarowych koszyków podzbiory te nazywają
się krzywymi obojętności. Uzasadnialiśmy, że dwie różne
krzywe obojętności nie mogą się przecinać. Między koszykami
na różnych krzywych mamy zatem ścisłe relacje. Można
powiedzieć, że krzywe prezentują różne poziomy
preferencji.
lub
4. Wprowadzili
śmy pojęcie wypukłości relacji ścisłej wypukłości
oraz monotoniczności. Dla relacji monotonicznych i ściśle
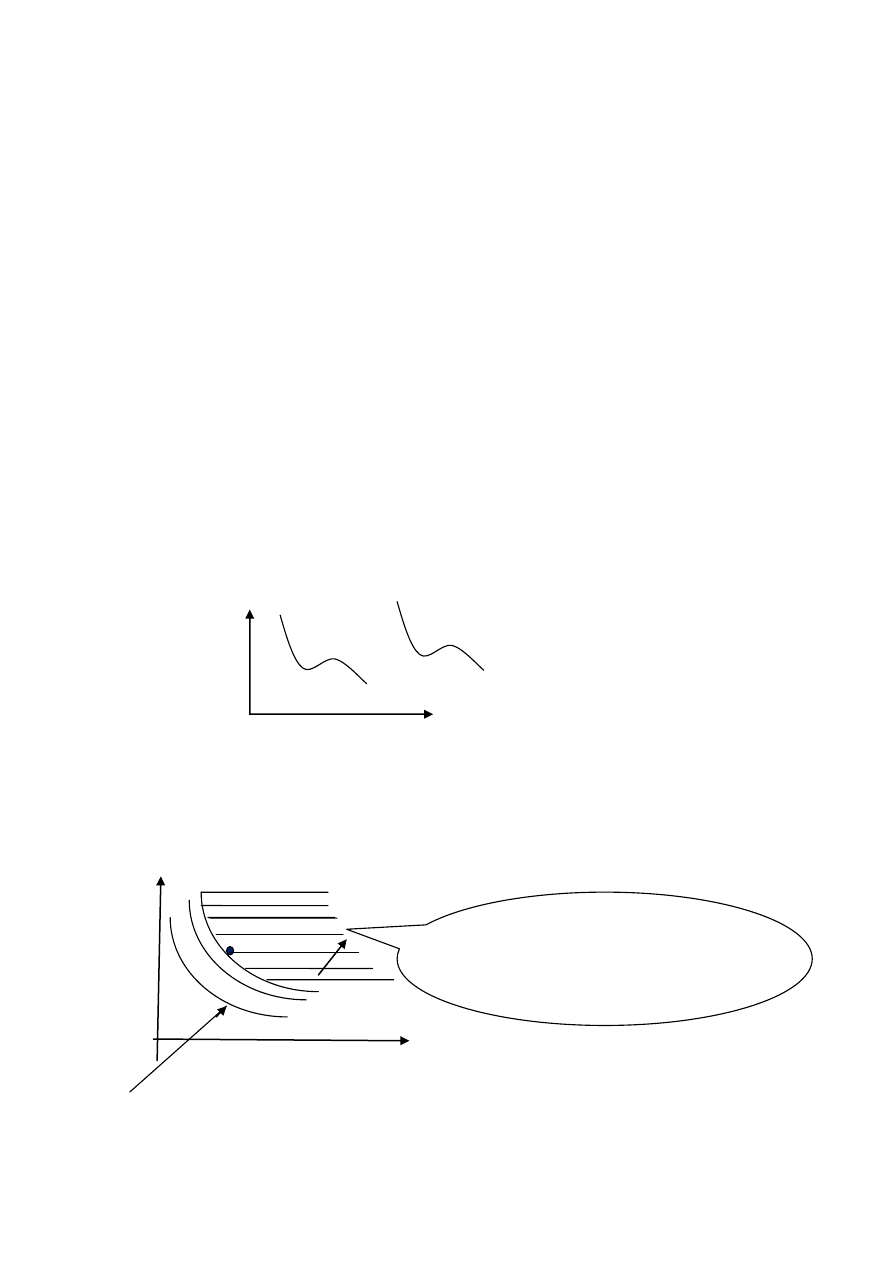
wypukłych mamy następujący” rysunkowy” opis relacji
a
Krzywe obojętności
Koszyki lepsze niż a. Zbiór F(a)={x; x }
jest wypukły. Krzywe indyferencji nie
mogą mieć „płaskich miejsc” .
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
303
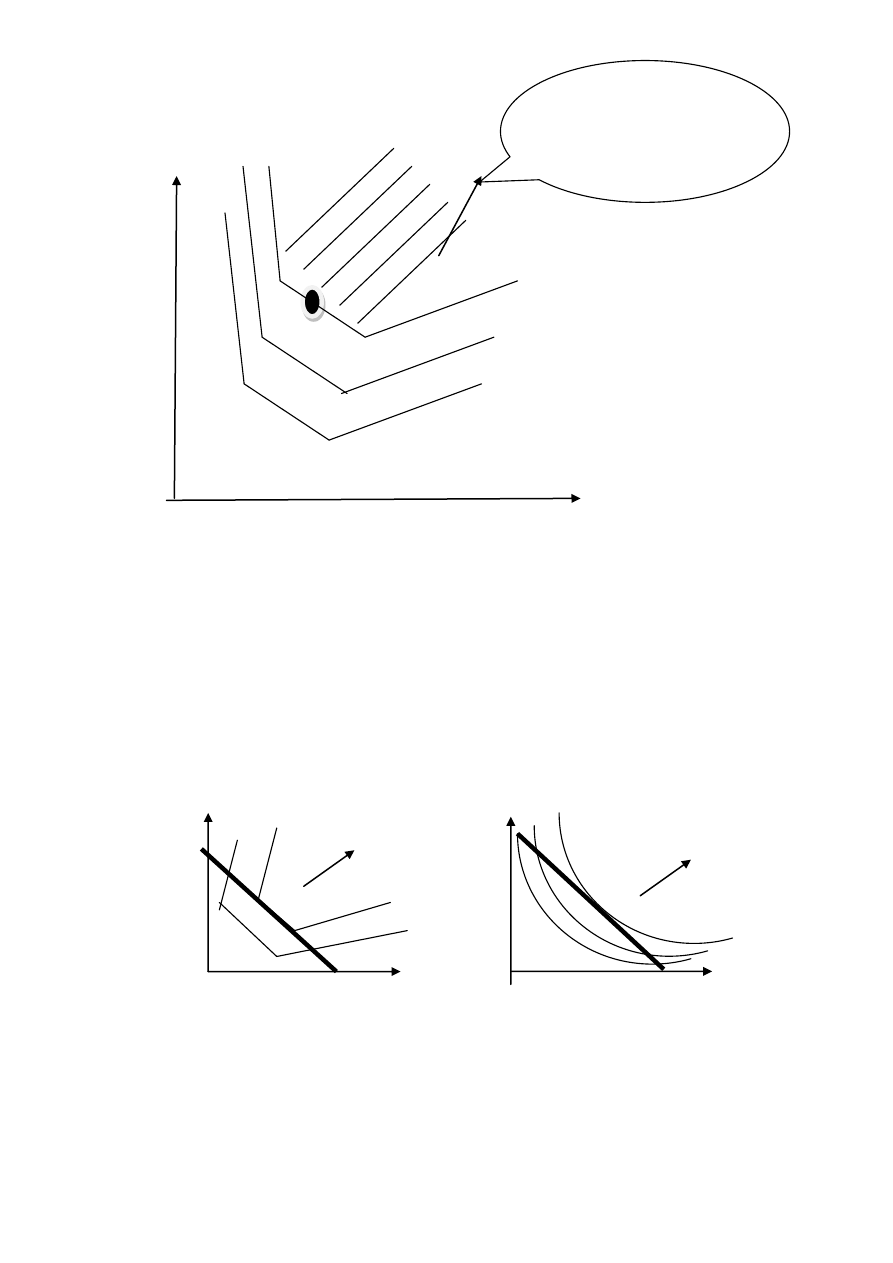
a
Rys.
Rysunek przedstawia relację, która jest wypukła, ale nie jest ściśle
wypukła. Krzywe obojętności mogą mieć płaskie fragmenty.
Koszyki optymalne
Zauważmy, że w przypadku relacji zaznaczonych na rysunku
koszyk optymalny
znajduje się w zbiorze budżetowym na
„najwyższej” krzywej obojętności.
Rys. Przykłady wyznaczania koszyków optymalnych.
Koszyki lepsze niż a. Zbiór
F(a)={x; x
} jest wypukły.
Relacja jest wypukła ale nie
jest ściśle wypukła.
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
304
Przykład rachunkowy.
Zb={x=(x
1
,x
2
)
2
R : x
1
+ x
2
d
}, p
1
=p
2
=1.
Zbiór konsumpcyjny Z =
2
R
Relacja preferencji jest
określona następująco:
x
y
def
a
1
x
1
+a
2
x
2
a
1
y
1
+a
2
y
2
, a
1
,a
2
– stałe dodatnie
Zadanie.
1) Wyznaczyć rodzinę krzywych obojętności. 2) Czy relacja jest
monotoniczna? 3) Czy relacja jest wypukła? 4) Czy relacja jest ściśle wypukła?
5) Wyznaczyć koszyki optymalne w Zb.
x ~ y
gdy x
y i y x
a
1
x
1
+a
2
x
2
= a
1
y
1
+a
2
y
2
Ad 1
.
Krzywe obojętności
: {x=(x
1
,x
2
): a
1
x
1
+a
2
x
2
= s}, s>0.
x
2
s/a
2
s/a
1
x
1
Rys. Dobra są substytutami. Konsument skłonny jest zamienić jedno na drugie
według stałej stopy.
Zauważmy, że preferencje rosną przy oddalaniu koszyków od początku układu.
Ad 2)-
4). Relacja jest monotoniczna i wypukła. Nie jest ściśle wypukła.
Ad 5) Koszyki optymalne leżą na tej krzywej obojętności, która jest
najbardziej odległej od środka układu i ma niepuste przecięcie ze
zbiorem budżetowym Zb.
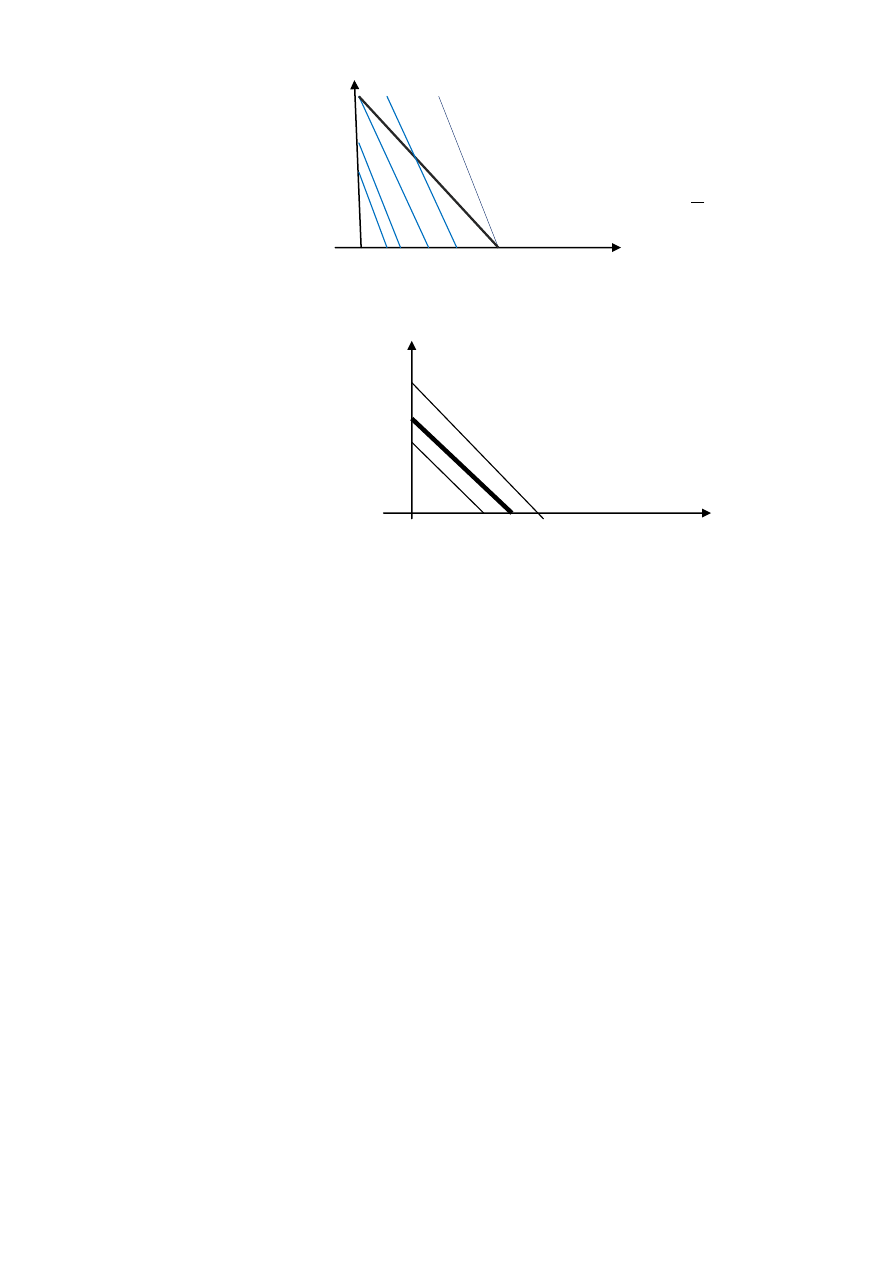
Rys.I
a
1
/a
2
<1
x
2
optimum
x
=
(0,d)
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
305
Rys.II
.
..
a
1
/a
2
> 1
x
2
optimum
x
=
(d,0)
x
1
x
2
optimum
RysIII
. a
1
/a
2
= 1
d
x
1
Optymalne są wszystkie koszyki z odcinka łączącego (0,d) z (d,0).
Założenie. W dalszych rozważaniach będziemy przyjmowali, że zbiór
konsumpcyjny Z=
m
R
Uwaga .
W przypadku relacji monotonicznej koszyki optymalne znajdują
się na hiperpłaszczyźnie budżetowej. ( Dla m=2 na linii budżetowej.)
Zadania. Zestaw 2 podany jest na ostatniej stronie.
UŻYTECZNOŚĆ
Funkcja użyteczności jest liczbową charakterystyką
relacji preferencji.
Def.
R
R
u
m
:
jest funkcją użyteczności jeśli dla
dowolnej pary koszyków x,y
m
R
spełnia warunki:
1. u(x) > u(y)
x
y
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
306
2. u(x) = u(y)
x ~ y
Wniosek. Ponieważ x y
x~ y lub x
y, to z definicji
wynika, że u(x)
u(y)
x
y.
Wartość u(x) nazywa się użytecznością koszyka x.
{y: u(y)=u(x)}
– koszyki obojętne względem x,
{y: u(y)>u(x)}
– koszyki lepsze niż x,
{y: u(y)
u(x)}
– koszyki nie gorsze niż x.
Funkcja u oddaje kierunek wzrostu preferencji.- inna
nazwa
– użyteczność porządkowa.
Użyteczność porządkową można opisać na wiele
sposobów, np.:
x
y
z
u
1
: 1 2 3
u
2
: 7 8 9
u
3 :
-2 -1 0
Def.
Niech R
~
R
Funkcja (transformacja)
R
R
f
~
:
nazywa się monotonicznie rosnąca na R
~
jeśli spełnia
warunek:
(u
1
, u
2
, R
~
, u
1
> u
2
)
f(u
1
) > f(u
2
)
Ważna własność użyteczności.
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
307
Jeśli funkcja u jest użytecznością, a funkcja f jest
monotonicznie rosnąca na zbiorze wartości u to nowa
funkcja v(x)= f(u(x)) jest
też funkcją użytecznością
opisującą tę samą relację preferencji, którą opisywała u.
Innymi słowy: monotonicznie rosnąca transformacja funkcji
użyteczności jest znowu funkcją użyteczności.
Konstrukcja funkcji użyteczności, m=2.
Wykorzystuje się następujące własności:
Funkcja użyteczności na krzywych obojętności jest
stała.
Różnym krzywym przypisuje różne wartości.
Krzywe bardziej preferowane otrzymują większe
wartości.
Przypadek preferencji monotonicznych
x
1
=x
2
a
a
Rys.Krzywe obojętności przecinają prostą : x
2
=x
1
.
Z monotoniczności relacji wynika, że punkt przecięcia jest jedyny.
Niech
K
a
={x=(x
1
,x
2
) : (x
1
,
x
2
) ~ (a,a)}, a>0.u(x)
def
a 2 dla x
K
a
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
308
Wyznaczanie krzywych obojętności przy znanej
użyteczności u(x)
Krzywa obojętności = {x : u(x)= const.}
Przykład: u(x
1
,x
2
)=x
1
x
2
Rodzina krzywych obojętności {x: x
1
x
2
= s} s 0
.
Uwaga. Funkcja v(x
1
,x
2
) = x
1
2
x
2
2
opisuje tę samą relację bo
v(x)=(u(x))
2
. Funkcja kwadratowa na R
+
jest ściśle rosnąca (
).
Optymalny wybór
W języku funkcji użyteczności: optymalny wybór to koszyk
x
o maksymalnej użyteczności w zbiorze budżetowym;
Innymi słowy: optymalny wybór to taki koszyk, którego
użyteczność jest nie mniejsza niż użyteczność każdego innego
koszyka ze zbioru budżetowego (tzn. u(
x
)
u(x)).
Poszukiwanie
x
Problem: Znaleźć koszyk
x
rozwiązujący następujący problem
optymalizacyjny
u(x)
max
Zb
x
Innymi słowy:
u(x)
max
przy warunkach ograniczających
d
x
p
x
p
x
p
m
m
2
2
1
1
...
,
x
1
,
0
x
2
,
0
. ...
, x
m
,
0
gdzie p
1
, p
2
, ...,p
m
– ceny, d – dochód.
Terminologia
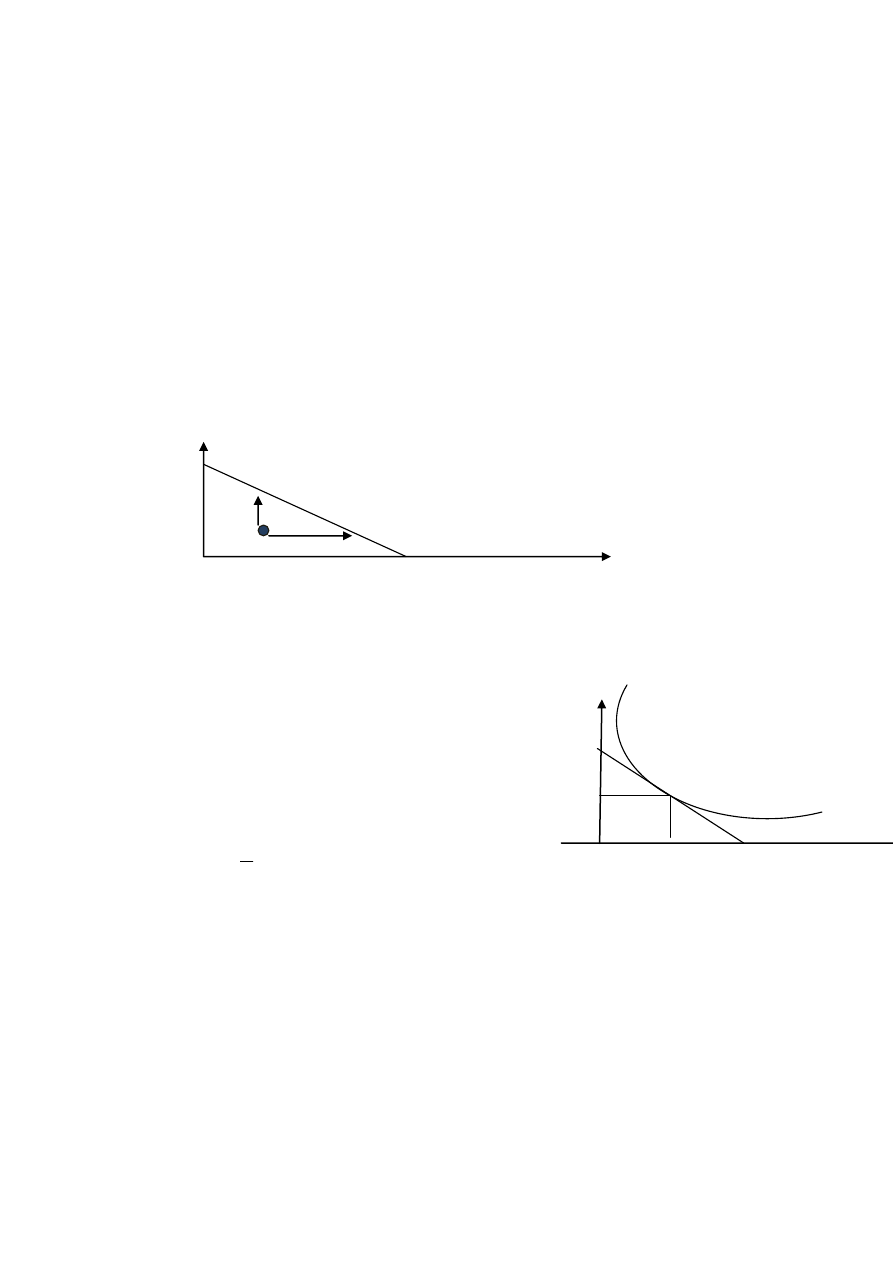
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
309
u(x)
– funkcja celu,
zbiór rozwiązań dopuszczalnych - zbiór koszyków
spełniających warunki ograniczające,
w zbiorze rozwiązań dopuszczalnych poszukujemy
koszyka, który maksymalizuje funkcję celu.
Uwaga. a) W przypadku relacji monotonicznej koszyki optymalne
znajdują się na hiperpłaszczyźnie budżetowej. ( Dla m=2 na linii
budżetowej; por. Rys. )
x
.
Wniosek. w przypadku relacji monotonicznych zbiór rozwiązań
dopuszczalnych wystarczy ograniczyć do tych koszyków, które spełniają
warunki:
d
x
p
x
p
x
p
m
m
2
2
1
1
...
,
x
1
,
0
x
2
,
0
. ...
, x
m
0
.
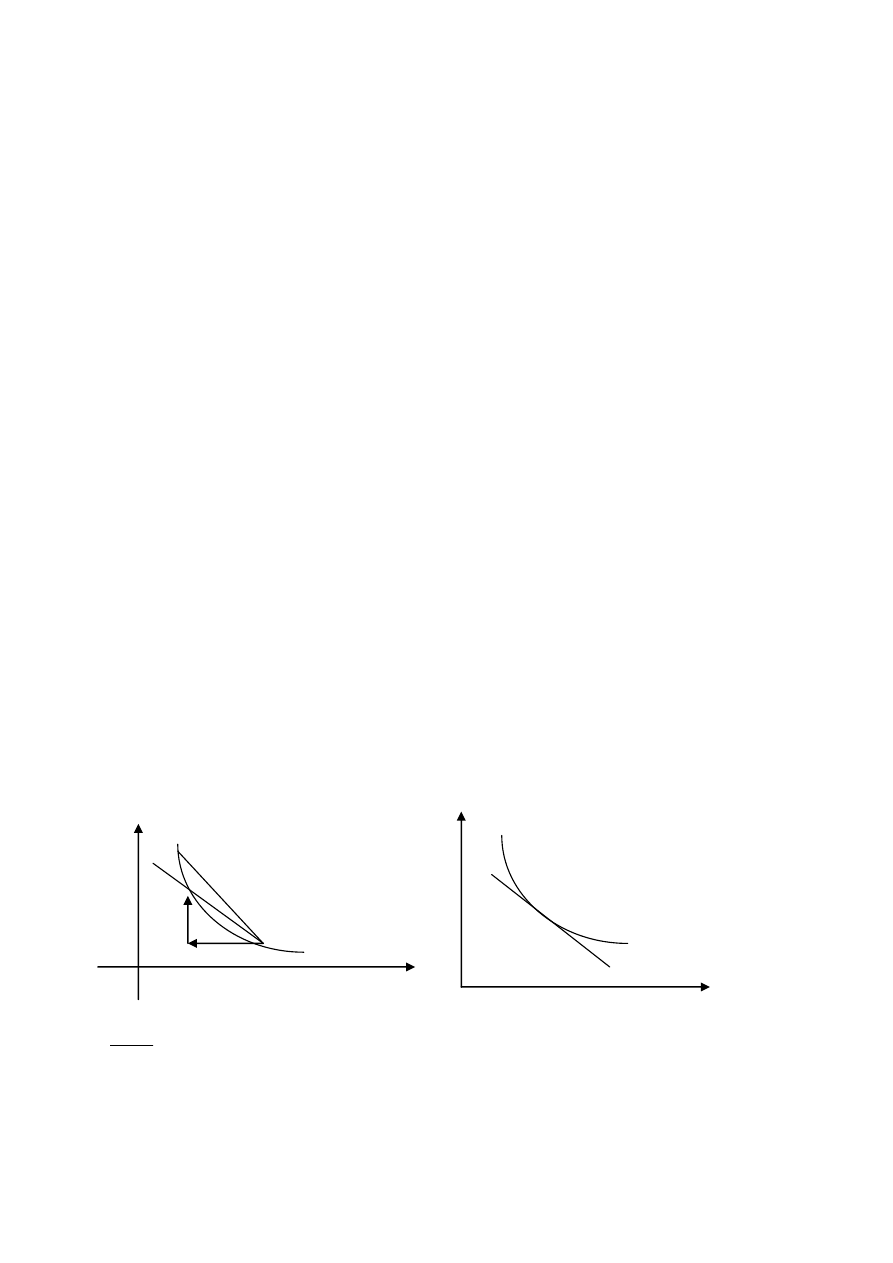
Przykład. u(x
1
,x
2
)=x
1
x
2
max,
.
x
1
+ x
2
= 2, 1
x
1
,
0
x
2
,
0
Rozwiązanie:
x
=(1,1)
1
Rys. W punkcie optymalnego wyboru krzywa obojętności jest styczna
do linii budżetu. Innymi słowy: nachylenie stycznej = nachylenie linii
budżetu.
Warunek konieczny optymalnego wyboru
.
J
eśli koszyk
optymalny jest punktem wewnętrznym linii budżetu ( tzn. obie współrzędne są
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
310
dodatnie), to w przypadku relacji monotonicznej ( i przy krzywych
obojętności opisanych funkcją różniczkowalną) w punkcie tym nachylenie
krzywej obojętności = nachyleniu linii budżetu.
Wynika to z faktu,
że krzywa obojętności, w punkcie optymalnego wyboru, nie
mo
że przecinać linii budżetu.
Uwaga
. a) Warunek ten nie musi być spełniony w przypadku optimum
brzegowego oraz w przy
braku regularności krzywych obojętności.
b) Warunek ten nie jest warunkiem wystarcz
ającym.
c) W dalszym toku wykładu będziemy badali dokładniej warunki
konieczne i dostateczne optymalnego wyboru koszyka.
Krańcowa stopa substytucji (KSS) przy m=2
Rozważmy przypadek, w którym krzywa obojętności daje się
zapisać za pomocą różniczkowalnej funkcji x
2
=g(x
1
).
Krańcowa
stopa substytucji dobra pierwszego przez drugie w punkcie
(x
1
,x
2
) (KSS)
1,2
(x
1
,x
2
) w przypadku m=2 jest poch
odną funkcji
g(x
1
).
X
2
.
x
1
1
2
x
x
-
wyraża nachylenie siecznej.
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
311
0
1
x
lim
1
2
x
x
-
wyraża nachylenie stycznej w punkcie (x
1
,x
2
).
KSS
1,2
opisuje krańcową stopę według, której konsument
zamieni dobro 1 na dobro 2.
Z
a marginalną ilość
1
x
„ jesteśmy skłonni płacić drugim
dobrem
” -
1
2
1
2
x
KSS
x
,
Nie mylić z ceną! Cena – to co musimy zapłacić. Ile mamy ochotę
zapłacić zależy od preferencji.
Wniosek. Warunek konieczny optymalnego wyboru oznacza,
że w punkcie optymalnego wyboru ( przy optimum wewnętrzny i
przy r
egularnych krzywych obojętności) KSS
1,2
=-p
1
/p
2
Przykład. Wyznaczanie KSS
Niech u(x
1
,x
2
) = x
1
x
2
Krzywa obojętności (KO) = {x
: x
1
x
2
=s}, s
– stała.
x
2
= s/x
1
. , g(x
1
)=s/x
1
,
1
2
x
x
=
'
g
(x
1
) = -s/
2
1
x
= KSS
1,2
(x
1
,x
2
) na krzywej z
parametrem s.
Zadanie.
Znaleźć KSS
1,2
dobra pierwszego przez drugie w koszyku
(x
1
,x
2
) = (1,2).
Rozwiązanie. Koszyk (1,2) znajduje się na krzywej z
parametrem s = 2
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
312
KSS
1,2
= -s/
2
1
x
=- 2/1=-2.
Użyteczne pojęcia matematyczne.
1.
Ciągłość funkcji.
Funkcja u:
R
R
m
jest ciągła w punkcie x=(x
1
,x
2
,...,x
m
) jeżeli dla
każdego ciągu {x
n
}, x
n
m
R
jeśli x
n
x to u(x
n
)
u(x)
(Przypominamy x
n
x
d(x
n
,x)
0, d oznacza odległość.)
Funkcja u:
R
R
m
jest ciągła na
m
R
jeśli jest ciągła w każdym
punkcie x
m
R
.
2.
Funkcje wklęsłe.
Funkcję u:
R
R
m
nazywamy wklęsłą na
m
R
jeśli dla każdego
]
1
,
0
[
i każdej pary punktów x,y
m
R
spełniony jest warunek (*)
(*) u(
x + (1-
)y)
u(x) +(1-
)u(y)
3.
Funkcje silnie (ściśle) wklęsłe
Jeżeli w poprzedniej definicji warunek (*) spełniony jest z ostrą
nierównością dla
)
1
,
0
(
,
to funkcję nazywamy ściśle wklęsłą.
(Por. Rysunek dla u:
R
R
).
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
313
4
Rosnące użyteczności.
Funkcja użyteczności nazywa się rosnąca na R
m
jeśli dla dowolnej pary
koszyków x,y prawdziwy jest warunek:
x
y
x
y
u(x) > u(y),
co
oznacza, że : jeśli x
1
y
1
,...,x
m
y
m
i co najmniej jedna z
nierówności jest ostra to u(x) > u(y)
Związek rosnących funkcji użyteczności z relacjami
monotonicznymi.
Wniosek z definicji.
Jeżeli funkcja użyteczności jest rosnąca to
relacja użyteczności, którą ta funkcja opisuje jest monotoniczna.
Związek wklęsłych użyteczności z relacjami wypukłymi.
Twierdzenie1.
Jeżeli funkcja użyteczności u:
R
R
m
jest
wklęsła (silnie wklęsła) na
m
R
to relacja preferencji, którą ta
funkcja opisuje jest wypukła ( silnie wypukła).
Dowód. Rozważmy taką parę takich koszyków x,y , że
x
y.
Należy wykazać, że
(**)
x + (1-
)y
y
Z założenia wiadomo, że
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
314
1. x
y
u(x)
u(y), ( z definicji u)
2. u(
x + (1-
)y)
u(x) +(1-
)u(y)
(z wklęsłości u)
Zatem z 1 i 2 wynika, że
u(
x + (1-
)y)
u(x) +(1-
)u(y)
u(y) +(1-
)u(y) = u(y).
Z definicji funkcji użyteczności mamy więc
x + (1-
)y
y, co
oznacza wypukłość relacji
”
.
Użyteczność krańcowa
Rozważmy koszyk x = (x
1
,x
2
,...,x
m
). Załóżmy, że zmieniamy ilość i-tego
towaru o
i
x
. Pozostałe zawartości nie zmieniają się. Wywołuje to
zmianę użyteczności: u(x
1
,x
2
,. x
i
+
i
x
...,x
m
) - u(x
1
,x
2
,...,x
m
).
Definicja użyteczności krańcowej
Krańcową użytecznością i-tego towaru w koszyku x nazywamy
pochodną cząstkową
i
x
x
u
)
(
=
0
i
x
lim
i
m
2
1
m
i
i
2
1
x
)
x
,...,
x
,
x
(
u
)
x
,...,
x
x
,...
x
,
x
(
u
Uwaga. Można wykazać, że jeżeli u:
jest rosnąca i silnie wklęsła,
to, dla każdego x>0
i
x
)
x
(
u
>0, i=1,2,…,n
Komentarz.
Krańcową użytecznością i-tego towaru w koszyku x
informuje o ile , w przybliżeniu, zmieni się użyteczność koszyka
x jeśli ilość i-tego towaru zmieni się o jednostkę, a ilości
pozostałych towarów nie ulegnie zmianie.
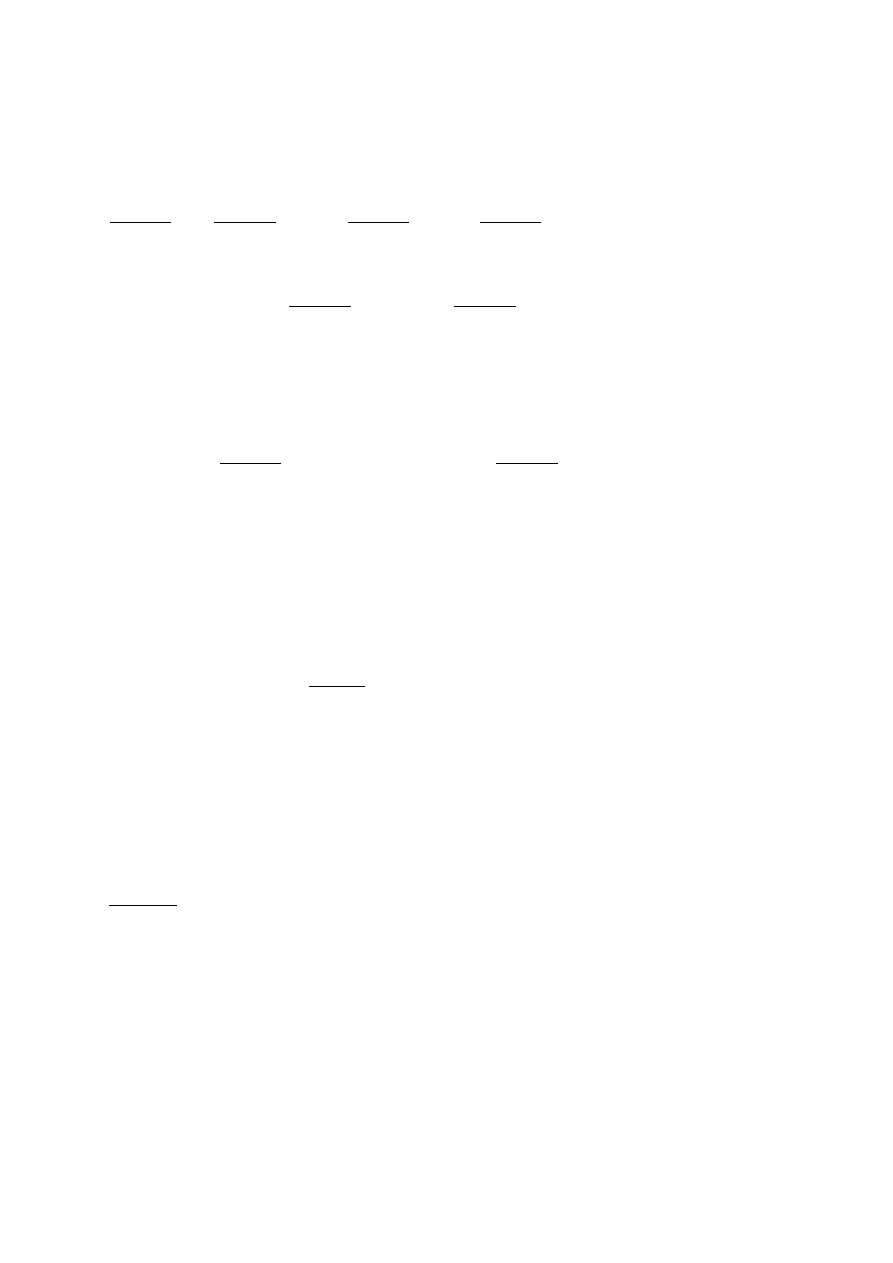
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
315
Przykłady.
1. u(x
1
,x
2
,...,x
m
) = x
1
+2x
2
+...+mx
m
1
x
x
u
)
(
=1,
2
x
x
u
)
(
=2, ,
i
x
x
u
)
(
=i,......
m
x
x
u
)
(
=m
2. u(x
1
,x
2
)=
3
2
2
1
x
x
,
1
x
x
u
)
(
=
3
2
1
x
x
2
;
2
x
x
u
)
(
=
2
2
2
1
x
3
x
Zadanie. Wyznaczyć użyteczność krańcową drugiego dobra w koszyku
x = (1,3)
Przykład 1.
2
x
x
u
)
(
|
(1,3)
= 2 Przykład 2.
2
x
x
u
)
(
|
(1,3)
= 1
3
3
2
= 27
Użyteczność krańcowa i-tego dobra informuje w przybliżeniu jak zmienia się
użyteczność koszyka x jeśli ilość i-tego dobra w koszyku x zmieni się o jednostkę.
Użyteczności różniczkowalne
Definicja. a)
Funkcję u:
m
R
R nazywamy różniczkowalną jeśli istnieją
wszystkie pochodne
i
x
)
x
(
u
i=1,2,...,m i pochodne te są funkcjami
ciągłymi na
m
R
.
b) Funkcję u:
m
R
R nazywamy dwukrotnie różniczkowalną jeżli
istnieją wszystkie pochodne czastkowe drugiego rzędu
j
i
2
x
x
)
x
(
u
(i,j=1,2,...,m) i pochodne te są funkcjami ciągłymi na
m
R
.
W dalszym ciągu będziemy zakładać, że u
(
m
R
R).
Przypominamy. a) Macierz drugich pochodnych nazywamy hesjanem
(H(x)).
b) Z t
wierdzenia Schwarza wynika, że hesjan jest macierzą symetryczną.
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
316
c) Mowimy, że hesjan jest niedodatnio (ujemnie ) określony jeśli dla
każdej pary koszyków x,y
m
R
, y
mamy
(*)
d) Twierdzenie
Sylvestera podaje warunki na spełnienie (*).
e)
Funkcja użyteczności u
(
m
R
R) jest wklęsła na
m
R
wtedy i
tylko wtedy gdy jej hesja H(x
) jest niedodatnio określony na
m
R
.
f) Jeżeli funkcja użyteczności u
(
m
R
R) i jej hesjan H(x) jest
ujemnie określony na określony na
m
R
, to jest ona silnie wklęsła na
m
R
.
( W przypadku funkcji silnie wklęsłych dla pewnych izolowanych
punktów hesja nie musi być ujemnie określony).
Twierdzenie 2. ( Prawo Gossena)
Jeżeli funkcja użyteczności u
(
m
R
R) i jej hesjan jest ujemnie
określony na
m
R
,
to dla każdego x
m
R
,
m
,...,
2
,
1
i
,
0
x
)
x
(
u
2
i
2
.
Dowód. Niech
= [0,…,0,1,0, będzie i-tym wersolem
.
R
m
Z
ujemnej określoności hesjanu wynika, że
H(x)
Komentarz.
Zauważmy, że własność ta oznacza , że użyteczność
krańcowa i-tego towaru maleje wraz ze wzrostem ilości i-tego towaru w
koszyku x przy ustalonych
ilościach pozostałych towarów.
W ekonomii własność ta nazywa się prawem Gossena.
Prawo to dotyczy realnych sytuacji życiowych. (Ekonomiści w tym
kontekście dają taki przykład:” im więcej zjedliśmy szynki ,to każdy
dodatkowy plasterek smakuje mniej
”).
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
317
W dalszych rozważaniach przyjmiemy następujące założenia o funkcji
u
żyteczności
Założenia o funkcji użyteczności (ZoFU)
Funkcja użyteczności u
(
m
R
R)
jest rosnąca i silnie
wklęsła a jej hesjan h(x) jest ujemnie określony przynajmniej na
int
m
R
.
Do
rozważanej klasy funkcji użyteczności dołączamy też funkcje
u
określone na int
m
R
i spełniające powyższe założenia, tzn.
u
(int
m
R
R)
, u jest rosnąca, a jej hesjan jest ujemnie
określony.
Związek krańcowej stopy substytucji z użytecznościami
krańcowymi.
P
rzykład.
u(x
1
,x
2
) = x
2
+
2
1
x
. Oblicz KSS pierwszego dobra
przez drugie w koszyku (1,1).
x
2
+
2
1
x
= s, s > 0
-
rodzina krzywych obojętności.
Interesuje nas krzywa obojętności z parametrem s=2.
x
2
= 2-
2
1
x
, x
2
= g(x
1
) = 2 -
2
1
x
,
'
g
(x
1
) = -2x
1
,
KSS
1,2
=
'
g
(1) = -2.
Inny sposób wyznaczania KSS, gdy x
2
traktujemy jak
funkcją uwikłaną zmiennej x
1
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
318
u(x
1
,x
2
)= u(x
1
,g(x
1
))=2. Zatem
1
x
x
u
)
(
+
2
x
x
u
)
(
'
g
(x
1
)=0.
Stąd
'
g
(x
1
)= -
1
x
x
u
)
(
/
2
x
x
u
)
(
,
1
x
x
u
)
(
=2x
1
,
2
x
x
u
)
(
=1,
a więc
'
g
(x
1
) = -
1
x
2
1
, KSS
1,2
=
'
g
(1) = -2.
Mamy następujące ogólne twierdzenie
Twierdzenie 3.
Jeśli funkcja użyteczności u spełnia założenia
ZoFU
, to dla każdego x
int
m
R
spe
łniona jest równość
KSS
i,j
(x)= -
i
x
x
u
)
(
/
j
x
x
u
)
(
W przykładzie dla x=(1,1) mamy:
1
x
x
u
)
(
|
(1,1)
=
2
,
2
x
x
u
)
(
|
(1,1)
=
1.
Zatem KSS
1,2
(1,1) = - 2.
Komentarz.
Definicj
ę KSS dobra i przez j określamy tak jak w
przypadku m=2. Okazuje si
ę, że przy przyjętych założeniach ZoFU
istnieje takie otoczenie ka
żdego punktu int
m
R
że funkcja u(x)=c,
c=const. daje si
ę, w tym otoczeniu, rozwikłać względem j-tej zmiennej,
tzn. x
j
daje si
ę zapisać jako :
dla pewnej
r
óżniczkowalnej funkcji g. Krańcową stopę substytucji dobra i – tego
przez j-te w koszyku
x definiuje
się jako:
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
319
KSS
i,j
(x)
i
j
x
x
Twierdzenie 3 daje spos
ób wyznaczania KSS za pomocą
pochodnych cz
ąstkowych.
Optymalne wybory c.d.
Twierdzenie.4.(O je
dyności optymalnego wyboru) Jeżeli
funkcja użyteczności u:
m
R
R
jest ciągła i silnie wklęsła, to
dla każdego dochodu d i dla każdego wektora cen p=(p
1
, p
2
,
,
) > 0 istnieje dokładnie jeden koszyk spełniający warunek
u(
dla każdego x ze zbioru budżetowego
wyznaczonego przez d i p.
Dowód (Podręczniki pozycja [1]).
Wniosek
a)
Z Twierdzenia 4 wynika, że jest rozwiązaniem
następującego zadania maksymalizacji użytecznosci (ZMaxU):
u(x)
max
przy warunkach ograniczających
d
x
p
x
p
x
p
m
m
2
2
1
1
...
,
x
1
,
0
x
2
,
0
. ...
, x
m
.
0
b) W przypadku gdy dodatkowo u jest funkcja rosnącą , to
znajduje się na hiperpłaszczyźnie budżetowej.
d
x
p
...
x
p
x
p
m
m
2
2
1
1
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
320
x
1
,
0
x
2
,
0
. ...
, x
m
.
0
Twierdzenie 5. ( Warunek konieczny i dostateczny ZMaxU)
Jeżeli funkcja użyteczności u:
m
R
R
jest rosnąca,
różniczkowalna i silnie wklęsła na int
m
R
, to koszyk
>0 jest
rozwiązaniem ZMaxU wtedy i tylko wtedy gdy istnieje że
para (
spełnia układ n+1 równań:
(a)
i
x
)
x
(
u
=
i=1,2,…,m
(b)
d
x
p
...
x
p
x
p
m
m
2
2
1
1
Dowód wynika z Twierdzenia Kuhna-Tuckera (Literatura [2] str.
785).
Wnioski z Twierdzenia 5.
a)Z Twierdzenia 3 o KSS i warunku (a) Twierdzenia 5 wynika,
że KSS
i,j
(
= -
i
x
)
x
(
u
:
j
x
)
x
(
u
=
b)
Zauważmy, że wynik ten jest zaskakujący. Oznacza on, ze
przy różnych funkcjach użyteczności spełniających założenia
Tw.5
mogą być różne koszyki optymalne przy tych samych
cenach,
a krańcowa stopa substytucji pozostaje taka sama.
KSS
i,j
(
x
)=-p
i
/p
j
c) Stosunek
–p
i
/p
j
jest stopą wymiany oferowaną przez
rynek.
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
321
Ważny przykład. Funkcja użyteczności Cobba-Douglasa
u(x
1
,x
2
) = x
a
1
b
2
x
; a > 0, b > 0.
Rys.a=b=1/2
Równoważny opis preferencji:
1.
u(x
1
,x
2
) = ln(x
a
1
b
2
x
) = a ln x
1
+b ln x
2
2.
u(x
1
,x
2
) = (x
a
1
b
2
x
)
b
a
1
=
b
a
b
2
b
a
a
1
x
x
Preferencje opisane użytecznością C-D są silnie wypukłe i
monotoniczne. Funkcja s
pełnia też założenia Tw. 5.
Optymalny wybór jest optimum wewnętrznym.
Zadanie z użytecznością C-D
Znaleźć koszyk popytu w przypadku użyteczności C-D
a ln x
1
+b ln x
2
max
przy warunkach ograniczających
d
x
p
x
p
2
2
1
1
,
x
1
,
0
x
2
,
0
.
Wystarczy rozważyć koszyki dla których
(*) KSS
1,2
(x)= -p
1
/p
2
.
Liczymy KSS wy
korzystując użyteczności krańcowe
krzywe
obojętności
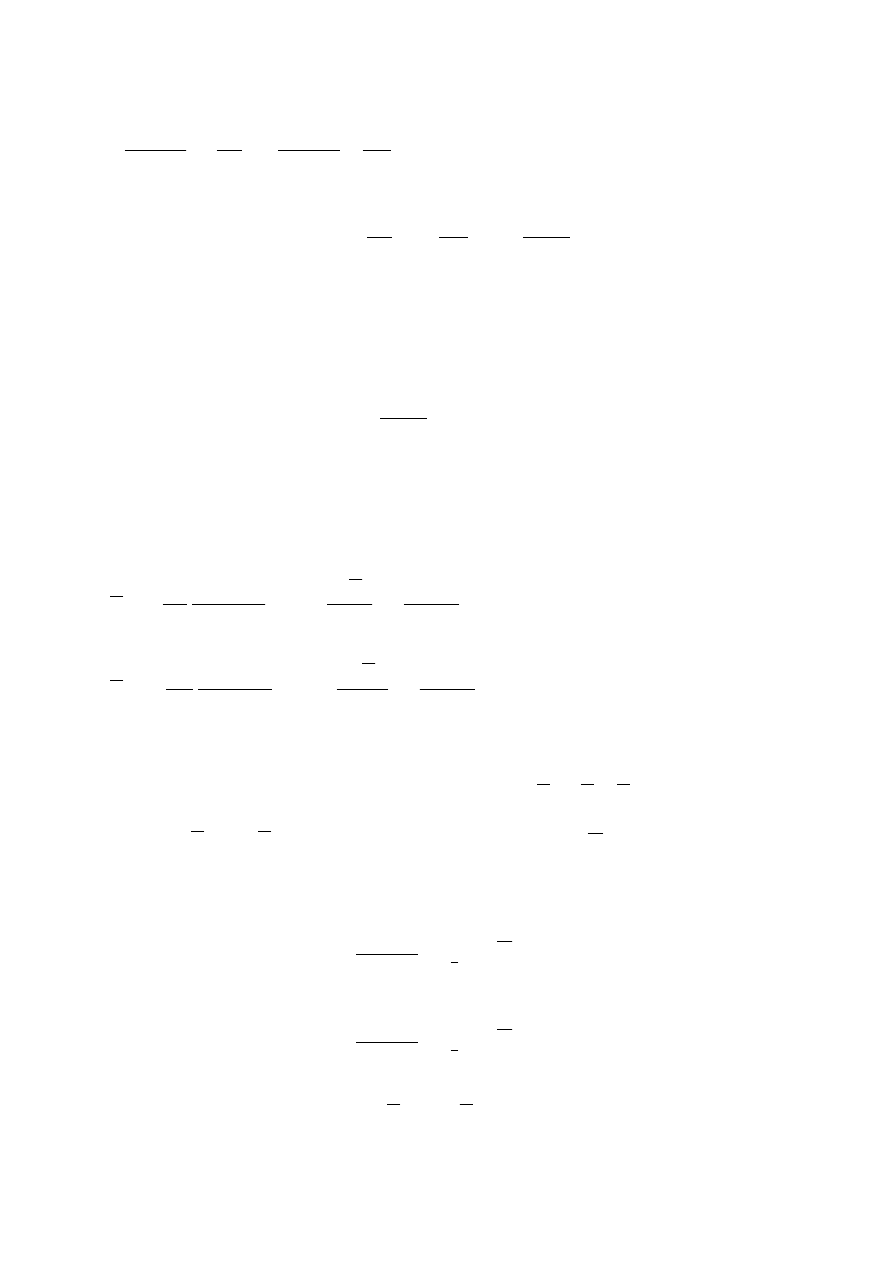
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
322
1
x
x
u
)
(
=
1
x
a
,
2
x
x
u
)
(
=
2
x
b
Zatem KSS
1,2
(x)= - (
1
x
a
) / (
2
x
b
)= -
1
2
x
b
x
a
.
Z
(*) i faktu, że poszukiwany koszyk znajduje się na linii
budżetowej wynika, że koszyk spełnia równania:
-
1
2
x
b
x
a
.=
-p
1
/p
2
d
x
p
x
p
2
2
1
1
Po rozwiązaniu układu otrzymujemy koszyk popytu :
)
(
b
a
a
p
d
x
1
1
b
a
a
d
x
p
1
1
udział wydatków na dobro 1
)
(
b
a
b
p
d
x
2
2
b
a
b
d
x
p
2
2
.
udział wydatków na dobro 2
Inny sposób rozwiązania zadania z użytecznością C-D
Pokażemy, że jeżeli pewien koszyk
x
=(
x
1
,
x
2
) > 0
(tzn.
x
1
>0,
x
2
>0) i pewna liczba
> 0 spełniają
następujący układ równości:
1
x
x
u
)
(
|
x
x
=
p
1
2
x
x
u
)
(
|
x
x
=
p
2
d
x
p
x
p
2
2
1
1
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
323
to
x
=(
x
1
,
x
2
) jest rozwiązaniem poprzedniego zadania z
użytecznością. C-D.
Uzasadnienie
.
1
x
a
=
p
1
2
x
b
=
p
2
1
2
x
b
x
a
.=
p
1
/p
2
d
x
p
x
p
2
2
1
1
d
x
p
x
p
2
2
1
1
Otrzymaliśmy ten sam układ równań, który wyznaczał
koszyk
x
w poprzednich rozważaniach.
Drugi sposób rozwiązywania nazywa się metodą mnożników Lagrange’a
Ćwiczenia. Zestaw 2
1.
Zbiór X składa się z czterech koszyków. X= {a,b,c,d}. Sprawdź czy
następująca relacja:
r
def
{(a,a), (a,b), (a,d), (b,b), (b,c), (c,a), (c,c), (d,b), (d,c), (d,d)}
a) jest zwrotna, b)czy jest symetryczna c) czy jest
b)
przechodnia, d) czy jest zupełna?
2.
Sprawdź czy koszyk z= (11, 32) należy do odcinka łączącego
koszyki x=(5,20) i y=(20,50).
3. Czy relacja x
y
def
x
1
+2x
2
y
1
+ 2y
2
jest
a)
monotoniczna b) wypukła c) ściśle wypukła.
Jaką funkcją użyteczności można opisać tę relację?
Podaj równania krzywej obojętności przechodzącej przez
(x
1
,x
2
)=(1,1). Podaj wartość krańcowej stopy substytucji dobra 1
R.Rempała. Materiały dydaktyczne( 2015. Wykłady 3-4).
324
przez 2 w punkcie (1,1). Wyznacz koszyk optymalny przy
cenach (p
1
,p
2
)=(1,1) i dochodzie d=10.
4. Czy funkcje: u(x
1
, x
2
) = 2 (x
1
+2x
2
), u(x
1
, x
2
) =log (2 x
1
+4x
2
) dla
(x
1
,x
2
)
(0,0) są funkcjami użyteczności opisującymi relację z
punktu 3.
5. Niech u(x
1
, x
2
) = x
1
+2x
2
. Wyznacz użyteczności krańcowe dobra 1 i
2 w punk
cie (2,1). Wykorzystując wynik podaj KSS
1,2
w punkcie
(2,1).
6. Rozwa
żmy funkcję użyteczności u(x
1
, x
2
) = lnx
1
+2 lnx
2
. Rozwi
ąż
ZMaxU traktuj
ąc ceny i dochód jako parametry.
7. Rozwi
ąż zadanie 6 przy u(x
1
, x
2
) = x
1
+2 lnx
2
.