IiE. Mat. Statystyka.Wykład 4. R. Rempała Materiały Dydaktyczne

1

Wykład 4. Próba losowa c.d., rozkład empiryczny, model statystyczny,
statystyka, najważniejsze statystyki w modelu normalnym, rozkład Chi-kwadrat,
rozkład t-Studenta, rozkład F Snedecora.

Próba losowa c.d.



Niech

n

2

1

X

,

,

X

,

X



będzie próbą losową pochodzącą z

pewnego rozkładu (czasami nazywanego rozkładem
teoretycznym).



Przypominamy: oznacza to, że zm. los są niezależne i mają takie

same rozkłady jak ten rozkład, z którego pochodzą.



Przyjęliśmy, że zmienne tworzące próbę określone są na tej

samej przestrzeni mierzalnej (

,



F)



Można przyjąć np, że jest to tzw. przestrzeń kanoniczna.

Oznacza to, że za zbiór



bierze się przestrzeń obserwacji, a

więc zbiór wartości próbek {x

1

,x

2

,…,x

n

}. Przyjmuje się, że

wartości poszczególnych obserwacji należą do pewnego zbioru

borelowskiego B

R



. Zatem



=

n

B

B

B

B











.

Zauważmy, że mamy wtedy
X

i

(



) =X

i

(x

1

,x

2

,…,x

n

) = x

i

. Za zdarzenia losowe wektora

losowego (

n

2

1

X

,

,

X

,

X



) przyjmuje się podzbiory

borelowskie z R

n

ograniczone do zbioru

.

B

n



Zaznaczyliśmy wcześniej, że rozkład prawdopodobieństwa

każdej zmiennej X

i

należącej do próby losowej, jest taki jak

rozkład, z którego pochodzi próba. W statystyce rozkład, z
którego

pochodzi

próba

nazywany

jest

rozkładem

teoretycznym.

Rozkład empiryczny

W poprzednim wykładzie definiowaliśmy dystrybuantę empiryczną.













n

1

i

)

x

)

(

X

(

n

i

1

n

1

)

,

x

(

F

ˆ

ustalamy x



R.

IiE. Mat. Statystyka.Wykład 4. R. Rempała Materiały Dydaktyczne

2



Dystrybuanta empiryczna przy ustalonym x jest zmienną losową

]

1

,

0

[

:

)

x

(

F

ˆ





Wniosek z MPWL dla schematu Bernoulliego.

Ponieważ

n

1

1

1

)

x

(

F

ˆ

x

X

x

X

x

X

n

n

2

1















, p = F(x). Mamy

następujące twierdzenie.

Twierdzenie 1.3 (O zbieżności dystrybuant empirycznych) Jeżeli
ciąg X

1

, X

2

, ...,X

n

jest prostą próbą losową z rozkładu o dystrybuancie

F, to dla każdego x

R



)

x

(

F

)

x

(

F

ˆ

n

.

p

n



przy n





.

Uwaga. Prawdziwy jest mocniejszy wynik (podstawowy w statystyce).
Wyraża go następujące twierdzenie.

Twierdzenie 2.3 Gliwienki – Cantellego. ( por. R.Zielioski’’ Siedem
wykładów...,PWN, 1990). Jeżeli ciąg X

1

, X

2

, ...,X

n

jest prostą próbą

losową z rozkładu o dystrybuancie F, to



















n

przy

0

|

)

x

(

F

)

x

(

F

ˆ

|

sup

n

.

p

n

x

Wniosek. Jeżeli próba może byd dowolnie liczna to dystrybuantę z
rozkładu, z którego pochodzi, można przybliżad z dowolną
dokładnością.

IiE. Mat. Statystyka.Wykład 4. R. Rempała Materiały Dydaktyczne

3

Prawdopodobieostwo empiryczne

Podobnie jak w przypadku dystrybuanty można zdefiniowad
prawdopodobieostwo empiryczne. Rozważmy zbiór borelowski
B

R



i próbę losową prostą X

1

, X

2

, ...,X

n

~ F(x). Przybliżeniem

nieznanej wartości P(B) jest częstośd obserwacji wpadających do
zbioru B tzn.









n

1

i

)

B

X

(

i

1

n

1

)

B

(

P

ˆ

Zauważmy, że

)

a

(

F

ˆ

]

a

,

(

P

ˆ





Wniosek. Przy wzroście próby prawdopodobieostwo empiryczne
(dystrybuanta empiryczna) przybliżają to prawdopodobieostwo
(dystrybuantę) z którego pochodzą.

Model statystyczny

W praktycznych zagadnieniach rozkład, z którego pochodzą zmienne
obserwowalne, nie jest dokładnie znany. Efektem tego jest
niedokładna znajomość rozkładu zmiennych X

i

.

W pewnych przypadkach, już z samej natury zjawiska losowego,
mamy pewne częściowe informacje o rozkładzie teoretycznym.
Znany jest np. typ rozkładu teoretycznego, lecz nie są znane jego
parametry (np. rozkład wykładniczy z nieznanym parametrem



).

Zakładamy, że nieznany rozkład teoretyczny, który „rządzi”
zachowaniem obserwacji (a więc ich rozkładem) zależy od parametru,
i jest indeksowany przez







. (Zbiór



może oznaczać zarówno

możliwe parametry liczbowe konkretnego rozkładu, jak i całe rodziny
rozkładów).

IiE. Mat. Statystyka.Wykład 4. R. Rempała Materiały Dydaktyczne

4

Modelem statystycznym nazywamy rodzinę ( ,



F,



P )







wraz z ciągiem zmiennych losowych

n

2

1

X

,

,

X

,

X



określanych

na ,



i nazywanych obserwacjami.

Uwaga Rozkłady, którymi „rządzi” rodzina rozkładów



P w naturalny

sposób dziedziczą parametr



.

Np.

)

x

X

(

P

)

x

(

F









,



f jest gęstością, jeśli













a

dx

)

x

(

f

)

a

(

F

.

Statystyka

Niech

n

2

1

X

,

,

X

,

X



będą obserwacjami w ustalonym modelu

statystycznym. Statystyką nazywamy dowolną funkcję obserwacji

T = T(

n

2

1

X

,

,

X

,

X



)

Przykłady statystyk:

a

) R = max (X

1

, X

2

, ..., X

n

) - min(X

1

, X

2

, ..., X

n

)

b) Z =

)

X

X

(

2

1

n

1



c)







n

1

i

i

X

n

1

X

---- średnia arytmetyczna z próby

d)









n

1

i

2

i

2

)

X

X

(

n

1

S

ˆ

---- wariancja z próby ( z daszkiem)

e)









n

1

i

2

i

)

X

X

(

n

1

S

ˆ

---- odchylenie standardowe z próby

f)











n

1

i

2

i

2

)

X

X

(

1

n

1

S

---- wariancja z próby

IiE. Mat. Statystyka.Wykład 4. R. Rempała Materiały Dydaktyczne

5

g)











n

1

i

2

i

)

X

X

(

)

1

n

(

1

S

---- odchylenie standardowe z próby



Zauważmy, że

2

2

S

)

1

n

(

S

ˆ

n





, stąd

2

2

S

]

n

/

)

1

n

[(

S

ˆ





.

h)

k

aˆ

=





n

1

i

k

i

X

n

1

---- k-ty moment zwykły z próby

i)

k

m

ˆ

=

k

)

X

X

(

n

1

n

1

i

i







---- k-ty moment centralny z próby

Momenty z próby są odpowiednikami momentów zwykłych i
centralnych z rozkładu. Mamy:

a

k

= E(X

k

) ---- k-ty moment zwykły z rozkładu,

k



= E(X-E(X))

k

---- k-ty moment centralny z rozkładu.

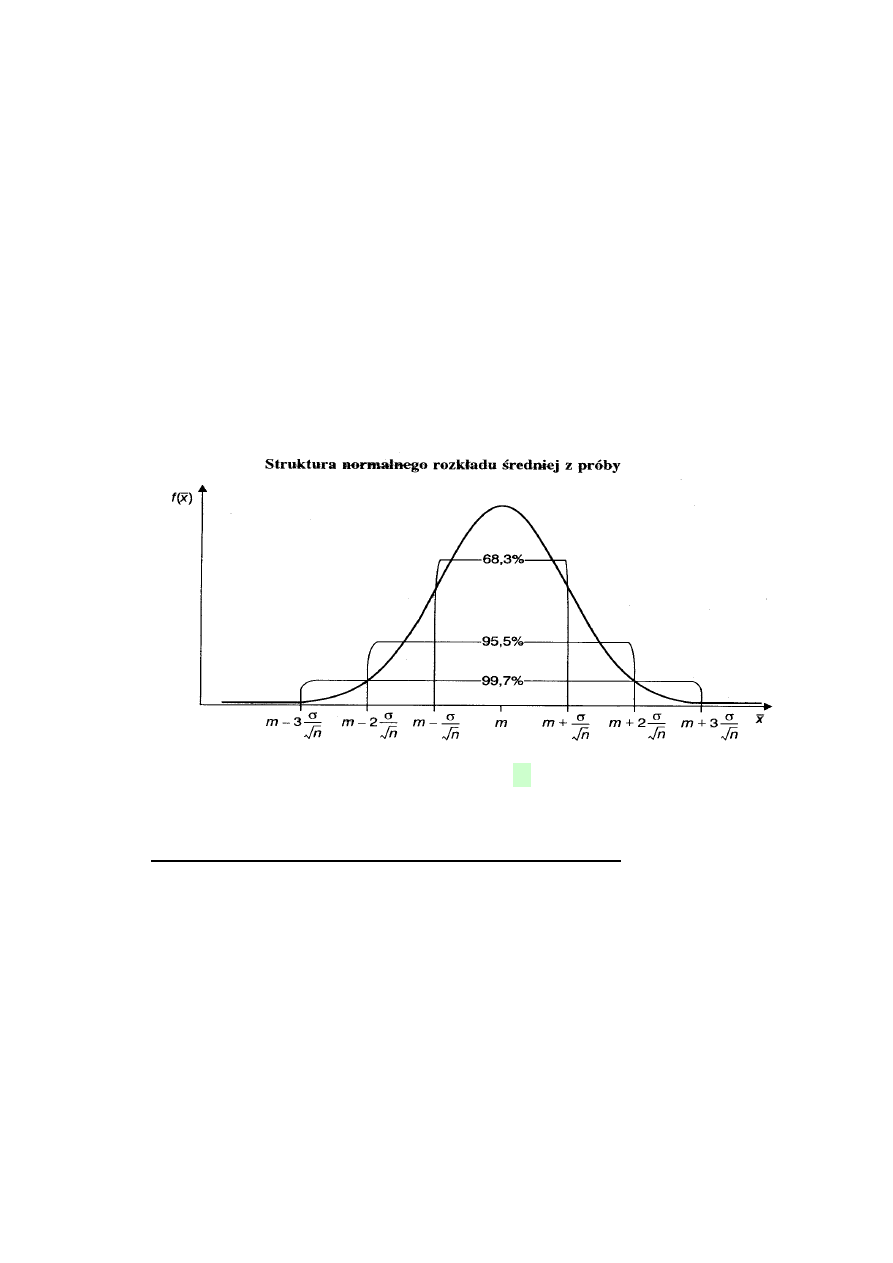
Najważniejsze Statystyki w modelu normalnym

Niech

n

2

1

X

,

,

X

,

X



będzie próbą prostą pochodzącą z rozkładu

N(





,

)

a)

Rozkład średniej: X

Przy założeniach normalności średnia arytmetyczna







n

1

i

i

X

n

1

X

ma rozkład normalny

)

n

,

(

N





Standaryzacja prowadzi do zmiennej

n

X

U









, która ma rozkład

)

1

,

0

(

N

.

Wykorzystaliśmy fakt, znany z rachunku prawdopodobieostwa, że
suma niezależnych zmiennych losowych o rozkładzie normalnym ma
rozkład normalny.

IiE. Mat. Statystyka.Wykład 4. R. Rempała Materiały Dydaktyczne

6



Parametry rozkładu łatwo wyliczyd wykorzystując następujące

własności wartości oczekiwanej i wariancji.

a) E(X

1

+…+X

n

)=E(X

1

)+…+E(X

n

) jeśli wartośd

E(X

i

) jest skooczona.

b) E(aX+b)= aEX+b, a,b



R.

c) Var (aX) = a

2

Var (X).

d) Jeżeli zm. los. są niezależne (wystarczy nieskorelowane) to

Var (X

1

+…+X

n

) = Var(X

1

)+…+Var(X

n

).

Na rysunku m =



.

b)

Rozkład Chi-kwadrat, z k-stopniami swobody

Jest to rozkład zmiennej losowej







k

1

i

2

i

Z

Y

gdzie

k

,

,

2

,

1

i

Z

i





są niezależnymi zmiennymi losowymi o

rozkładzie N(0,1). (Oznaczenie: Y

~

2



(k), k jest liczbą stopni

swobody).

IiE. Mat. Statystyka.Wykład 4. R. Rempała Materiały Dydaktyczne

7

Twierdzenie. 4.1. Rozkład

2



(k) jest rozkładem Gamma (

)

,





dla

2

/

1

,

2

/

k









.

Dowód pomijamy.



Gęstość prawdopodobieństwa dla rozkładu Gamma (

)

,





:

f(y)=

;

0

y

,

e

y

)

(

y

1



















0

r

,

e

x

)

r

(

0

x

1

r















. Parametry: E(Y) =





/

, Var (Y)=

2

/





.



Zatem dla rozkładu

2



(k): E(Y)= k, Var (Y)=2k.

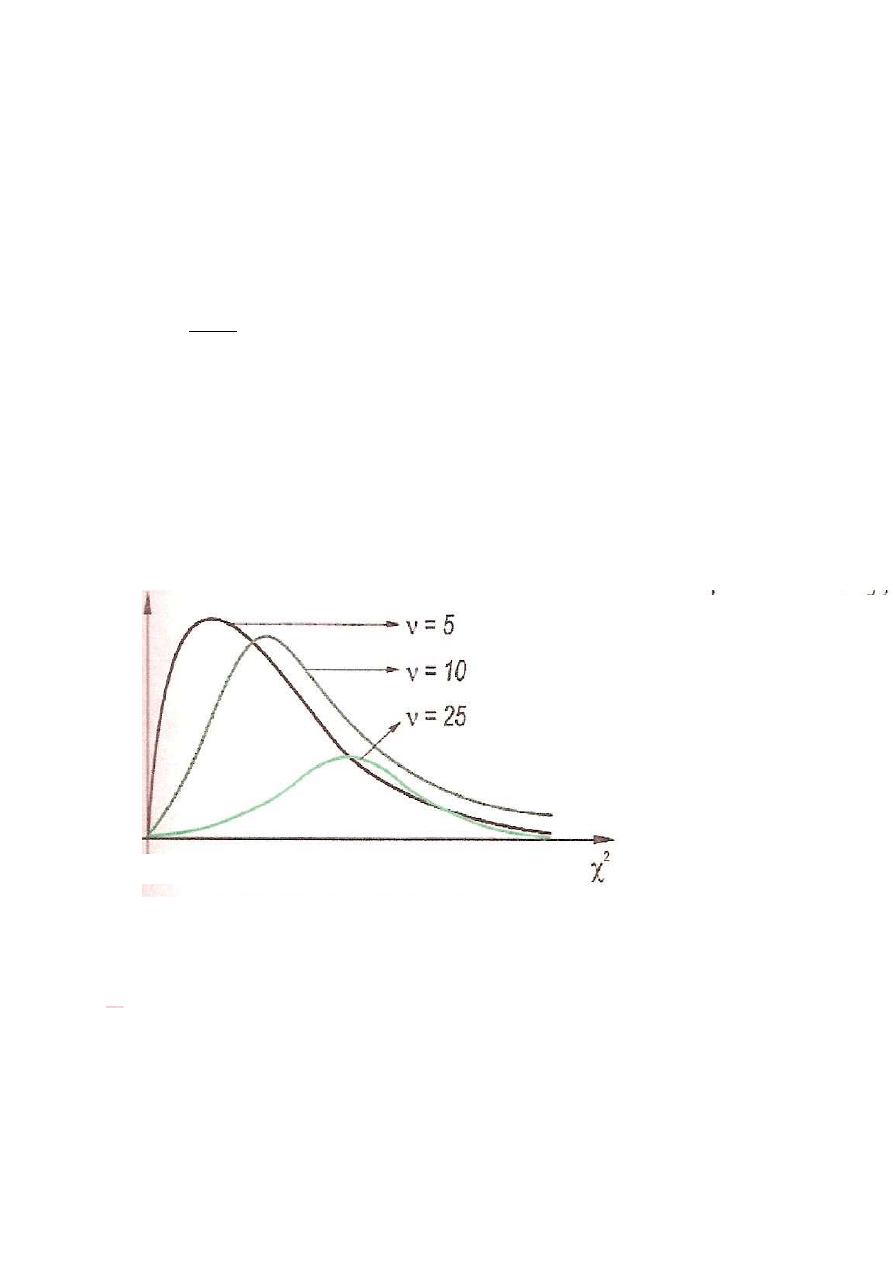
Rys. Rozklady

)

(

2





.

Rozkłady asymetryczne.

Kształt gęstości zależy od
liczby stopni swobody.

Przy dużej liczbie stopni
swobody, rozkłady zbliżają się
do rozkładu normalnego.

IiE. Mat. Statystyka.Wykład 4. R. Rempała Materiały Dydaktyczne

8

Twierdzenie4.2 W modelu normalnym

X

i

2

S

są niezależnymi

zmiennymi losowymi oraz

X

~

)

n

,

(

N





2

2

S

1

n





~

2



(n-1)

Dowód pomijamy.
Uwaga.



Zauważmy, że zarówno

X

jak i

2

S

są wyznaczone przez tę samą

próbę losową. Fakt, że są niezależne nie jest oczywisty. Okazuje się,
iż istotne jest tu założenie, że próba pochodzi z rozkładu normalnego.

Parametry statystyki S

2

Stwierdzenie 4.1:

2

2

)

S

(

E





,

Var

(

2

S

)=

1

n

2

4





.

Ponieważ E(

2

2

S

1

n





)=

1

n

)

S

(

E

1

n

2

2









(Na mocy Tw. 4.2 jest to

rozkład

2



(n-1). Zatem wartość oczekiwana = liczbie stopni

swobody). Z ostatniej równości mamy więc:

2

2

)

S

(

E





.

Rozumując podobnie otrzymujemy:

Var (

2

2

S

1

n





) =

)

1

n

(

2

)

S

(

Var

)

1

n

(

2

4

2









) zatem Var (

2

S

)=

1

n

2

4





.

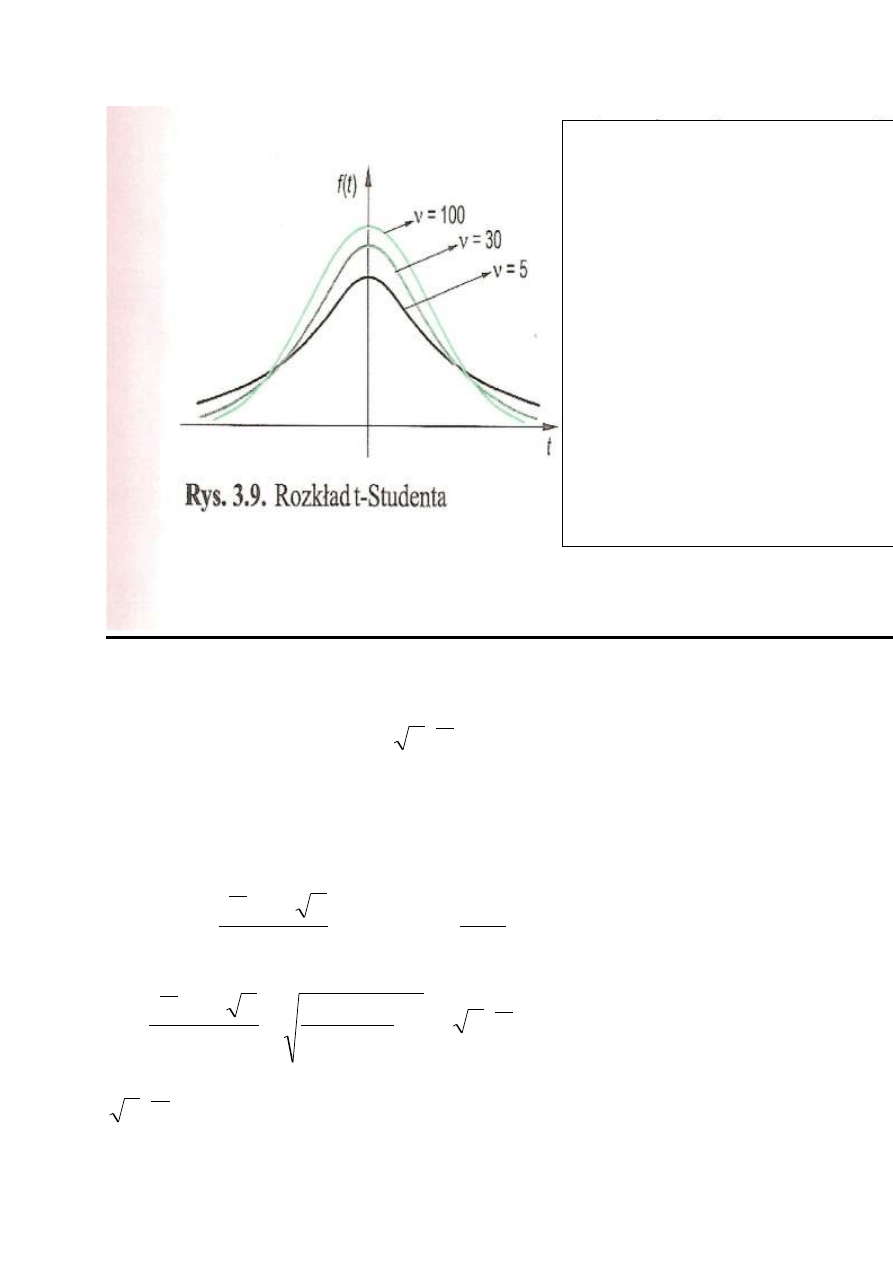
c) Rozkład t-Studenta

Rozkład t-Studenta z k stopniami swobody jest to z definicji rozkład
zmiennej losowej

T =

k

/

Y

Z

,

gdzie Z i Y są niezależnymi zmiennymi losowymi , Z o rozkładzie
N(0,1), Y o rozkładzie Chi-kwadrat, z k-stopniami swobody.
Zapis T

~t(k) .

IiE. Mat. Statystyka.Wykład 4. R. Rempała Materiały Dydaktyczne

9

Stwierdzenie 4.2. Statystyka

S

/

)

X

(

n





ma rozkład t-Studenta z

(n-1) stopniami swobody.

Dowód jest wniosekiem z Twierdzenia 4.2 i definicji statystyki
t-Studenta.

Niech Z =





n

)

X

(



i niech Y=

2

2

S

1

n





. Mamy więc

T =





n

)

X

(



:

S

/

)

X

(

n

S

)

1

n

(

1

n

2

2













.

Oznacza to, że statystyka

S

/

)

X

(

n





ma rozkład t-Studenta z (n-1) stopniami swobody.

Rozkłady t-Studenta są
indeksowane liczbą stopni
swobody

.



Są

symetryczne względem

prostej t = 0.

Zwyczajowo wartości
oznacza się literą „t”.

Każdy rozkład ma gestość
podobną do krzywej
Gaussa ze średnią zero.
E(T) = 0,
Var(T) =

)

2

/(







.

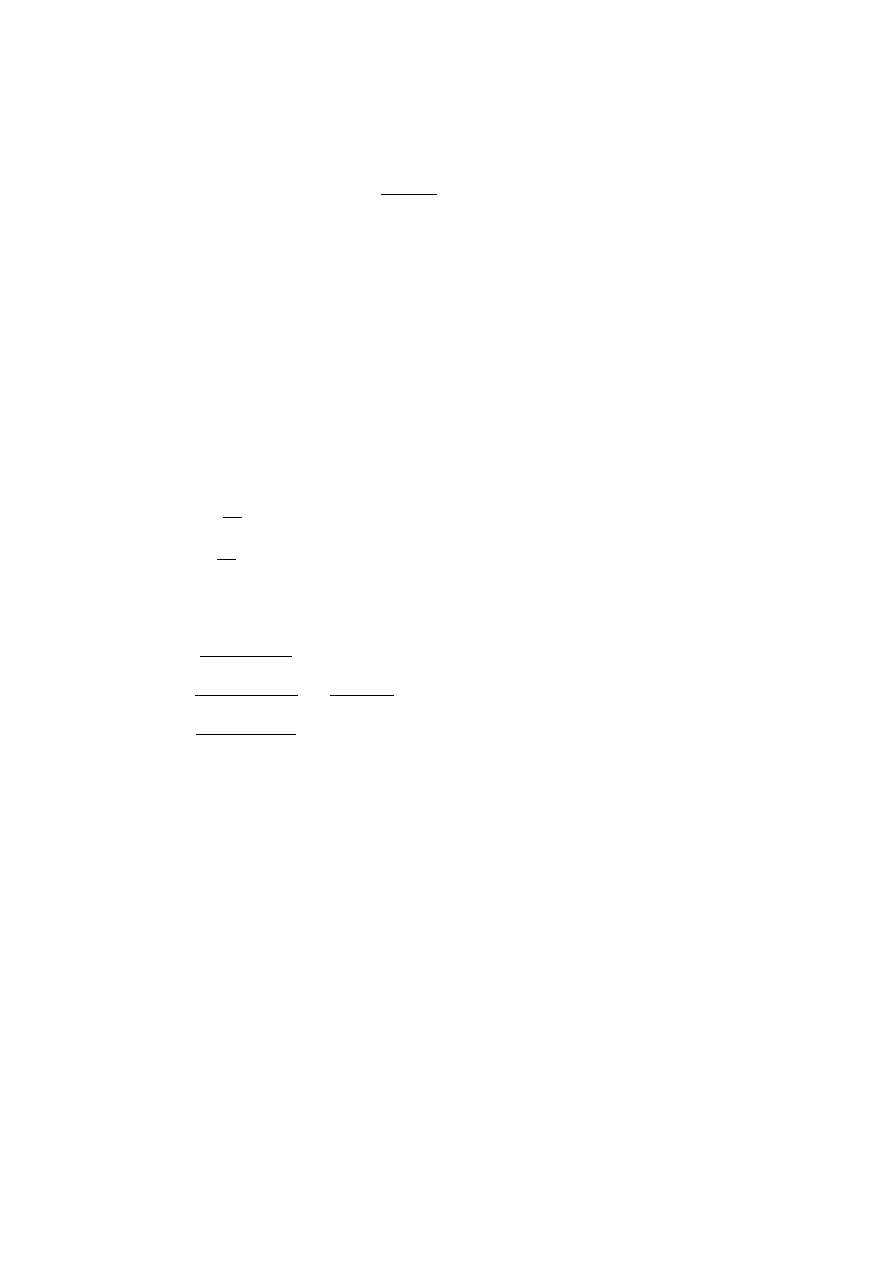
IiE. Mat. Statystyka.Wykład 4. R. Rempała Materiały Dydaktyczne

10

d) Rozkład F Snedecora z k i m stopniami swobody

Jest to rozkład zm. los.

m

/

U

k

/

Y

R



, gdzie Y i U są niezależne

Y

~

2



(k) i U

~

2



(m)

Zapis R

~ F(k,m).

e) Model dwu próbek

Załóżmy, że mamy dwie niezależne próby losowe

n

2

1

X

,

,

X

,

X



i

m

2

1

Y

,

,

Y

,

Y



gdzie X

i

~ N(

)

,

X

X





Y

i

~ N(

)

,

Y

Y





Statystyki

2

X

S

i

,

X

określone dla próby

n

2

1

X

,

,

X

,

X



oraz

2

Y

S

i

,

Y

określone dla próby

m

2

1

Y

,

,

Y

,

Y



Zatem





2

X

2

Y

2

Y

2

X

2

Y

2

Y

2

X

2

X

S

S

)

1

m

(

S

)

1

m

(

1

n

S

)

1

n

(



















~F(n-1,m-1) .

Jeśli założymy, że

2

Y

2

X



 

to

2

Y

2

X

S

/

S

~F(n-1,m-1) co jest pomocne przy testach weryfikujących

równość wariancji w rozkładach, z których pochodzą próby.