WYKŁAD 8 16.12.2006

PRZYKŁAD 1

produkt	1996		1997		q0p0	qtpt	q0pt	qtp0
		q0	p0	qt					pt
chleb	6,93	1,09	6,61	1,14	7,55	7,54	7,90	7,20
makaron	0,26	1,40	0,27	1,55	0,36	0,42	0,40	0,38
ziemniaki	7,01	0,47	6,51	0,56	3,29	3,65	3,93	3,06
mleko	5,16	0,88	4,88	0,98	4,54	4,78	5,06	4,29
ser	0,70	6,41	0,79	6,96	4,49	5,50	4,87	5,06
jaja	13,2	0,33	12,60	0,38	4,36	4,79	5,02	4,16
∑					24,59	26,68	27,18	24,15

INDEKS WARTOŚCI

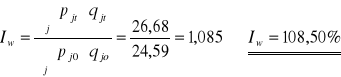
Wartość badanej grupy towarów w roku 1997 w stosunku do roku 1996 wzrosła o 8,5% z powodu zmiany ceny i ilości

INDEKSY CEN

Laspeyresa

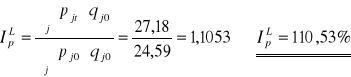
Wartość towarów wzrosłaby o 10,53% z powodu zmiany ceny gdyby ilość była stabilizowana na poziomie roku 1996

Paaschego

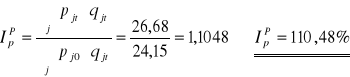
Wartość towarów wzrosłaby o 10,48% z powodu zmiany ceny gdyby ilość była stabilizowana na poziomie roku 1997

Fishera

Ceny powodowały przeciętnie 10,50% wzrost wartości.

INDEKSY WARTOŚCI

Laspeyresa

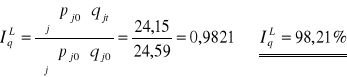
Wartość towarów zmniejszyłaby się o 1,79% z powodu zmiany ilości gdyby cena była stabilizowana na poziomie roku 1996

Paaschego

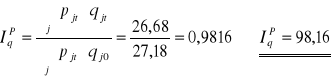
Wartość towarów zmniejszyłaby się o 1,84% z powodu zmiany ilości gdyby cena była stabilizowana na poziomie roku 1997

Fishera

Ilość spowodowała przeciętnie zmniejszenie wartości o 1,82%

PRZYKŁAD 2

Badano grupę towarów:

towar	2000r	indywidualne indeksy cen
			qtpt
A	10 000	110,2%
B	15 000	101,2%
C	5 000	90,0%
∑	30 000

Zanalizować wartość badanych towarów w roku badanym w stosunku do roku podstawowego.

INDEKS WARTOŚCI

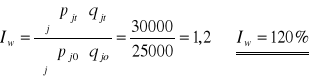
Wartość badanej grupy towarów w roku 2000 w stosunku do roku 1995 wzrosła o 20% z powodu zmiany ceny i ilości

DEKOMPOZYCJA SZEREGÓW DYNAMICZNYCH

Przyczyny dekompozycji:

• przyczyna główna

• przyczyny pozostałe, inne

Elementy szeregów dynamicznych:

1. trend / tendencja rozwojowa

2. wahania sezonowe - na skutek działań w sezonach zjawisko się powiększa lub zmniejsza; wahania w mniejszych okresach czasu (1/2 roku, kwartał, miesiąc)

3. wahania losowe / przypadkowe - występują gdy na zjawisko w czasie działa nieprzewidywalna przyczyna

4. wahania cykliczne - występują tylko przy szeregach badanych w bardzo długim okresie czasu; 20lat i >

• tendencja rozwojowa/trend może być prostoliniowa lub krzywoliniowa

• w szeregu może wystąpić jednocześnie trend i sezonowość

Sezonowość

Addytywna
amplitudy wahań są takie same

Multiplikatywna
amplitudy wahań są różne

ANALIZA TENDENCJI ROZWOJOWEJ (TRENDU)

Metody wyodrębniania trendu z szeregu:

• metoda mechaniczna

• metoda analityczna

metody mechaniczne

1. wykres

2. metoda średnich półokresów (szereg dzielimy na dwie części, liczymy średnią z pierwszego okresu i z drugiego okresu i porównujemy)

3. średnia ruchoma - nieparzysta i parzysta

• gdy okres badany jest w latach - średnia nieparzysta

• gdy lata i kwartały lub miesiące - średnia parzysta

• średnia ruchoma nieparzysta - 3-, 5-, 7- okresowa - zależy od ilości lat w szeregu

• średnia ruchoma 3-okresowa:

Np.

mamy do czynienia z szeregiem od 1994r do 2000r, liczymy średnią ruchomą 3-okresową; otrzymujemy:

średnia	lata z których liczona	rok któremu zostanie przypisana wartość średniej
	[94, 95, 96]	1995
	[95, 96, 97]	1996
	[96, 97, 98]	1997
	[97, 98, 99]	1998
	[98, 99, 2000]	1999
		1994 i 2000 - brak średniej

• średnia ruchoma wyrzuca działanie składnika losowego - pozostawia czystą tendencję rozwojową

• średnia ruchoma skraca szereg

metoda analityczna

• polega na zapisie tendencji rozwojowej przy pomocy f-cji matematycznej (identycznie jak przy regresji; wzory też te same)

• trend - regresja w czasie (x = t)

• trend liniowy, wykładniczy, potęgowy - parametr a oznacza wartość y dla roku przyjętego za zero

• zawsze w szeregu dynamicznym czas zamieniany jest na kolejne liczby naturalne; numeracja może być dowolna; w zależności od numeracji a będzie różne ale b zawsze takie same

Np.

b =13,285 a =64,557

INTERPRETACJA:

b - z roku na rok badana cecha rośnie przeciętnie o 13,285 [j]

a - w roku „0” badana cecha była na poziomie 64,557 [j]

---