Wykład XXII
Całki podwójne. Interpretacja geometryczna.
1. Definicja całki podwójnej po prostokącie
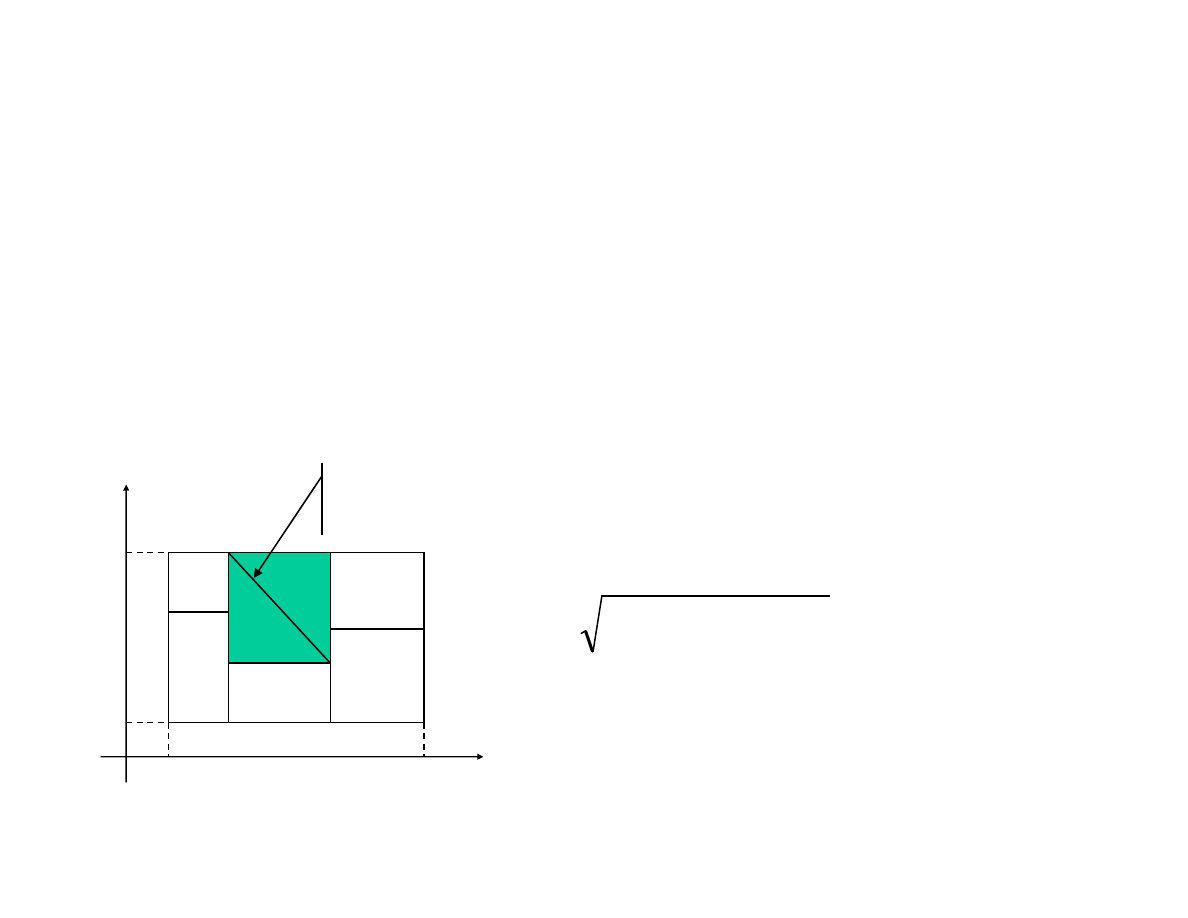
Podziałem prostokąta R = {(x, y) : a
≤
x
≤
b, c
≤
y
≤
d
}
(inaczej: R = [a, b] × [c, d]) nazywamy zbiór P złożony z
prostokątów: R
1
,R
2
, . . . ,R
n
,
które całkowicie go wypełniają
i mają parami rozłączne wnętrza.
a
b
d
c
Niech
∆x
k
,
∆y
k
będą długościami
boków prostokąta R
k
(k=1,…n),
jego przekątną.
(
)
(
)
2
2
k
k
k
y
x
d
∆
+
∆
=
R
k
∆y
k
∆x
k
d
k
Średnicą podziału
P nazywamy
liczbę:
δ(P) = max {d
k
: 1
≤ k ≤ n}.

2
Niech funkcja f(x,y) będzie ograniczona na prostokącie R
oraz niech P będzie podziałem tego prostokąta.
Oznaczmy przez
(
η
k
,
ξ
k
)
dowolny punkt należący do
R
k
.
Sumą całkowitą funkcji f(x,y) ograniczoną na R nazywamy
liczbę
(
)
k
k
n
k
k
k
y
x
f
∆
⋅
∆
⋅
ξ
η
∑
=1
,
Pojedyncze składniki powyższej sumy są objętościami
prostopadłościanów, których podstawami są prostokąty
R
k
,
natomiast wysokościami
f
(
η
k
,
ξ
k
)
.
Rozpatrując ciąg podziałów (P
n
) i przechodząc do granicy
przy n→
∞
,
dochodzimy do pojęcia całki podwójnej.
3
Definicja całki podwójnej z funkcji po prostokącie
Niech funkcja f(x,y) będzie ograniczona na prostokącie R.
Całkę podwójną z funkcji f(x,y) po prostokącie R określamy
wzorem:
(
)
( )
(
)
k
k
n
k
k
k
R
P
y
x
f
dxdy
y
x
f
∆
⋅
∆
⋅
ξ
η
=
∑
∫∫
=
→
δ
1
0
,
lim
,
o ile ta granica jest właściwa i nie zależy od sposobu
podziału prostokąta R oraz wyboru punktów
(
ξ
k
,
η
k
)
.
Jeżeli całka istnieje, to mówimy, że funkcja jest
całkowalna.
UWAGA: Każda funkcja ciągła na R jest całkowalna.

4
2. Interpretacja geometryczna.
Składnik
sumy całkowej
(
)
k
k
k
k
y
x
f
∆
∆
ξ
η ,
można interpretować jako objętość prostopadłościanu
krzywopowierzchniowego, którego podstawą jest prostokąt
o wymiarach
∆x
k
,
∆y
k
a przeciwległą ścianę tworzy
fragment powierzchni z = f(x,y).
(
)
∑
=
∆
∆
ξ
η
n
k
k
k
k
k
y
x
f
1
,
Suma całkowa jest zatem przybliżeniem objętości bryły
ograniczonej prostokątem R, powierzchnią z = f(x,y) oraz
ś
cianami bocznymi prostopadłymi do płaszczyzny OXY.
Całka, jako granica sum, jest objętością tej bryły.

5
2. Własności całki podwójnej
(
)
(
)
0
,
0
,
.
1
.
2
=
⇒
=
∫∫
R
dxdy
y
x
f
y
x
f
Jeśli
(
)
(
)
[
]
(
)
(
)
∫∫
∫∫
∫∫
+
=
+
R
R
R
dxdy
y
x
g
dxdy
y
x
f
dxdy
y
x
g
y
x
f
,
,
,
,
.
2
.
2
(
)
(
)
(
)
∫∫
∫∫
∫∫
+
=
2
1
,
,
,
R
R
R
dxdy
y
x
f
dxdy
y
x
f
dxdy
y
x
f
0
.
3
.
2
2
1
2
1
/
=
∩
∪
=
R
R
oraz
R
R
R
Jeżeli
(
)
(
)
∫∫
∫∫
=
R
R
dxdy
y
x
f
c
dxdy
y
x
cf
,
,
.
4
.
2
[ ] [
]
d
c
b
a
R
,
,
.
5
.
2
×
=
Jeżeli
(
)
(
)
∫ ∫
∫ ∫
=
d
c
b
a
b
a
d
c
dy
dx
y
x
f
dx
dy
y
x
f
,
,
6
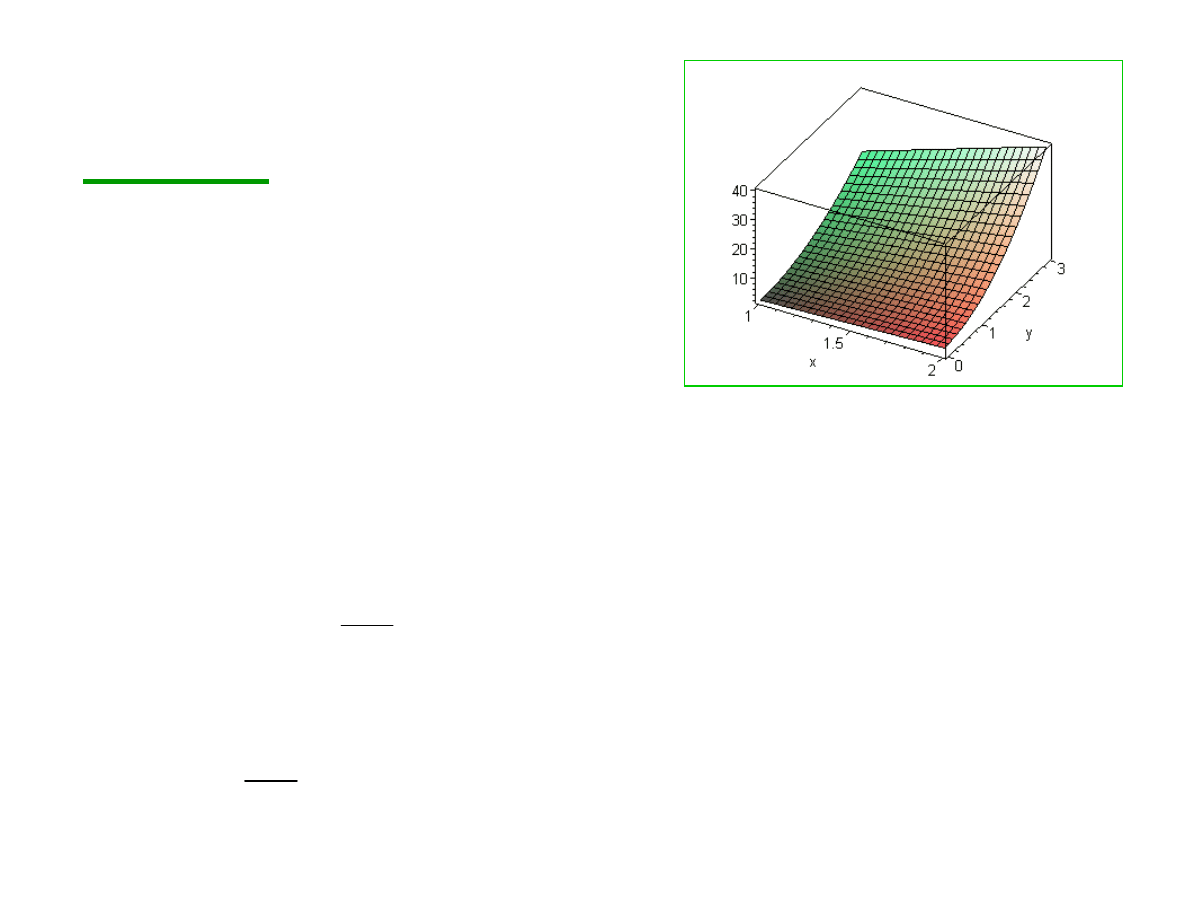
Przykład 1: Obliczyć całkę z
funkcji z=2x(1+y
2
) na
prostokącie [1,2]x[0,3]
(
)
(
)
∫
∫
∫ ∫
=
+
=
+
3
0
2
1
2
3
0
2
1
2
2
1
1
2
dy
xdx
y
dy
dx
y
x
(
)
(
)
∫
∫
=
+
=
+
=
=
=
3
0
2
3
0
2
1
2
2
1
3
2
2
1
dy
y
dy
x
y
x
x
(
)
.
36
9
3
3
3
3
3
0
3
=
+
=
+
=
=
=
y
y
y
y
7
Całkę moglibyśmy rozwiązać inną metodą
(własność 2.5), mianowicie:
(
)
(
)
∫
∫
∫ ∫
=
+
=
+
2
1
3
0
2
2
1
3
0
2
1
2
1
2
dx
dy
y
x
dx
dy
y
x
36
12
48
12
2
12
3
2
2
1
2
2
1
2
1
3
0
3
=
−
=
=
=
+
=
∫
∫
x
xdx
dx
y
y
x
8
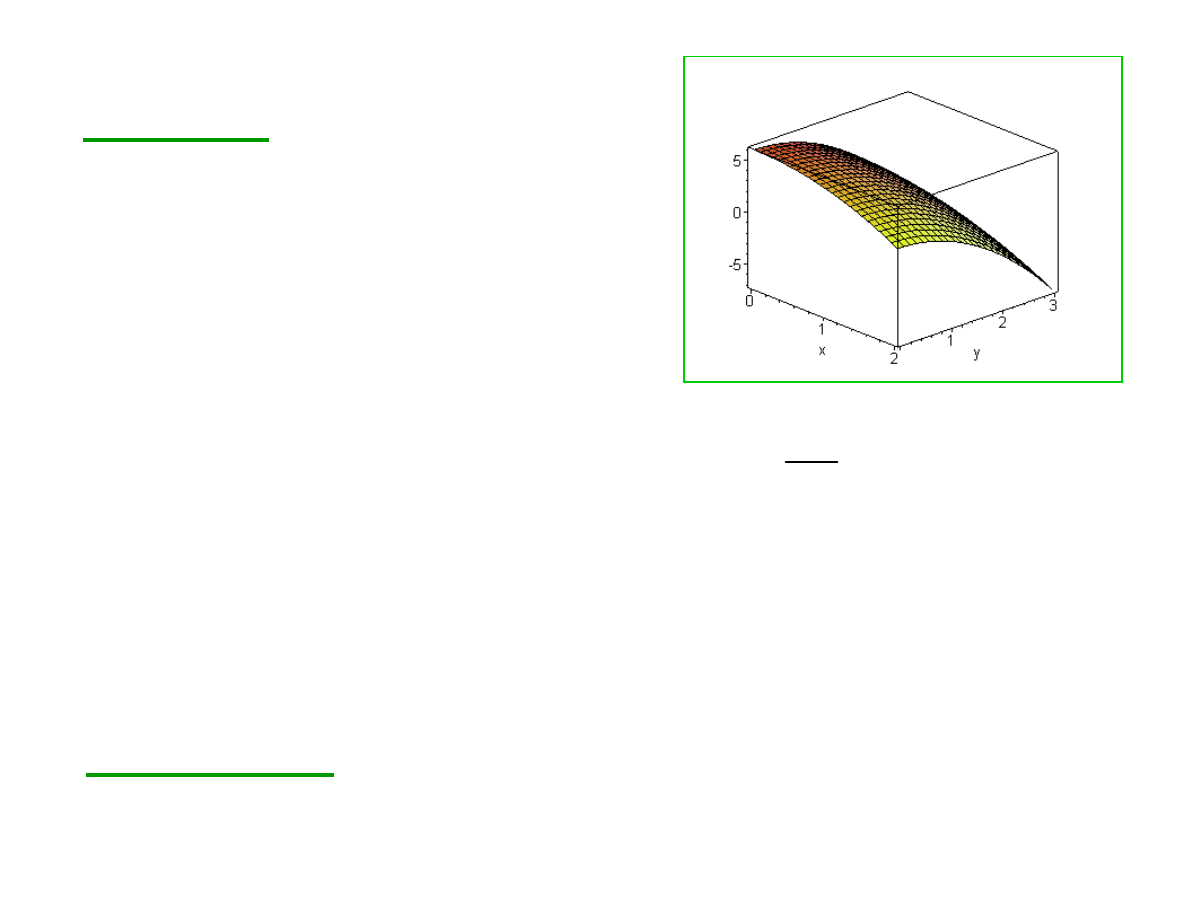
Przykład 2: Obliczyć objętość
prostopadłościanu opartego na
prostokącie [0,2]x[0,3]
ograniczonego powierzchnią
z
=6-x
2
-y
2
(
)
∫
∫ ∫
=
−
−
=
−
−
=
=
2
0
3
0
3
2
2
0
3
0
2
2
3
6
6
dx
y
y
x
y
dx
dy
y
x
y
y
(
)
(
)
[
]
2
0
3
2
0
2
2
0
2
9
3
9
9
3
18
=
=
−
=
−
=
−
−
=
∫
∫
x
x
x
x
dx
x
dx
x
10
8
18
=
−
=
Odpowiedź: Objętość tego prostopadłościanu
wynosi 10 (jednostek^3).
Wyszukiwarka
Podobne podstrony:
Mat WIP Wyk ad23
Mat WIP Wyk ad25
Mat WIP Wyk ad19
Mat WIP Wyk ad26
IiE, Mat Statystyka,Wyk 4
Mat Bud wyk 07
Mat Bud wyk 09
Mat Stat Wyk 8 PrzedziaĹ y(2013L)
Mat Bud wyk 03
Mat WIP Wykład21
Mat Bud wyk 02
mat konstr wyk, PKM egzamin kolosy ( łukasik, Salwiński )
Mat WIP Wykład16
więcej podobnych podstron