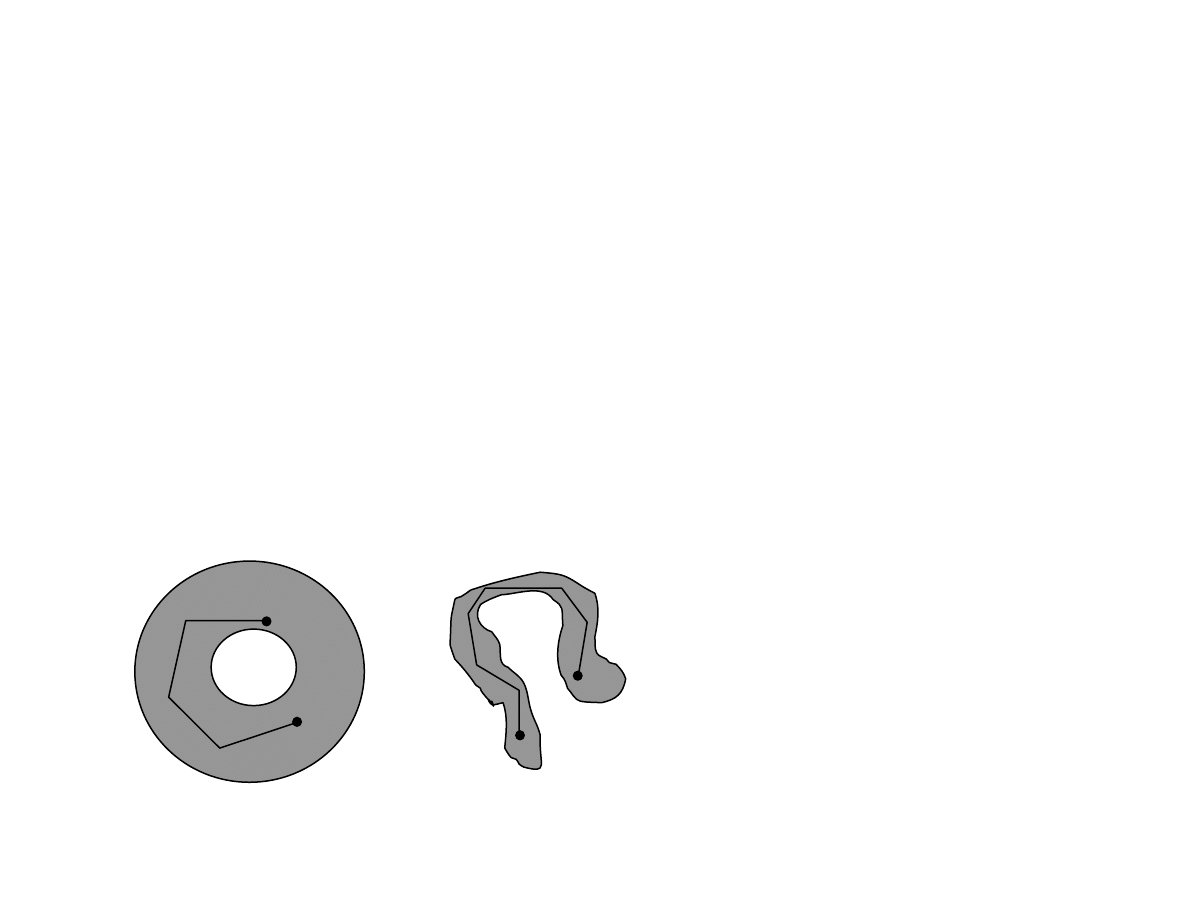
D
Wykład XXIII
Całki podwójne po obszarze normalnym
Definicja obszaru
Obszarem D nazywamy zbiór o niepustym wnętrzu, taki że
dowolne dwa punkty z wnętrza obszaru można połączyć
łamaną zawartą w tym wnętrzu.
Przykłady obszarów:
D
2
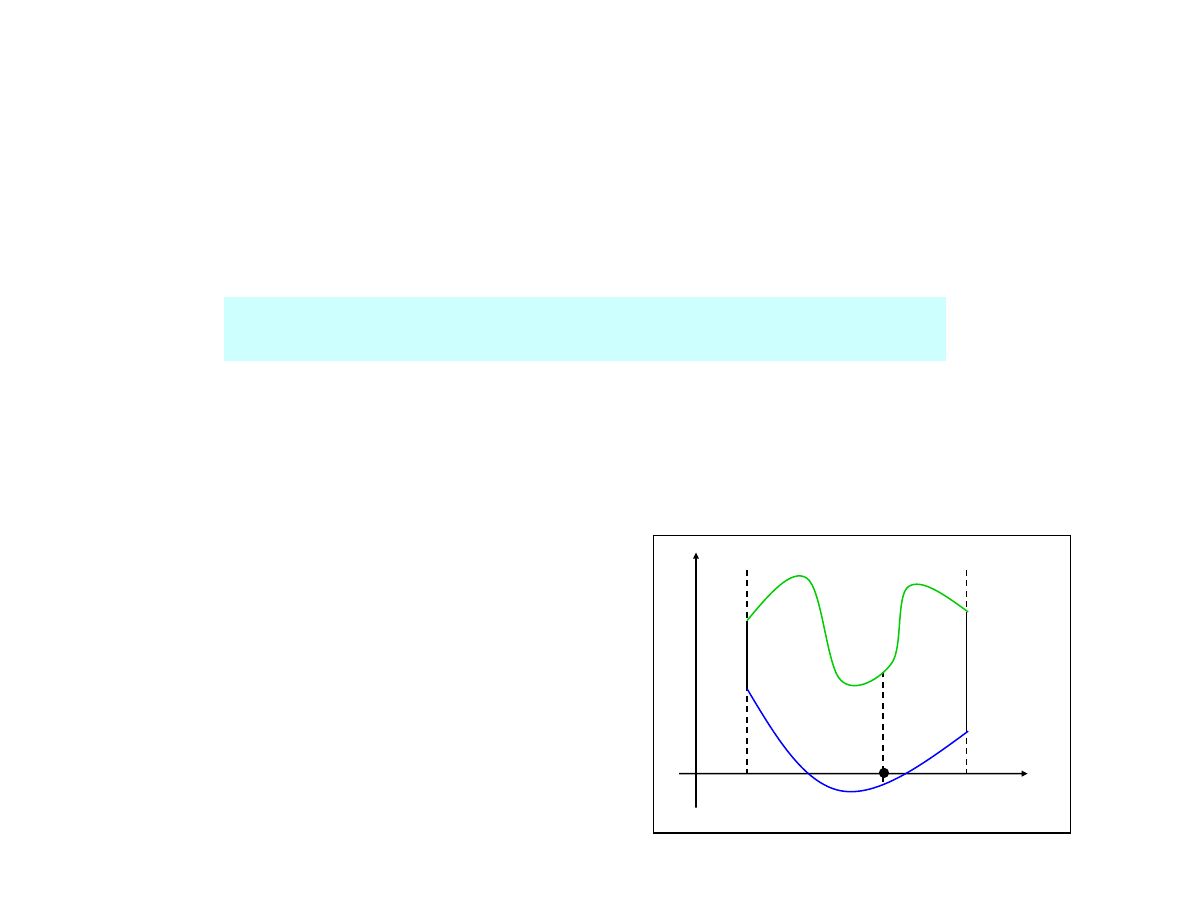
Obszarem normalnym względem osi OX nazywamy
obszar D postaci:
Obszar normalny względem osi OX
(
)
( )
( )
{
}
x
y
x
b
x
a
y
x
2
1
;
:
,
D
ϕ
≤
≤
ϕ
≤
≤
=
gdzie
ϕ
1
(x) i
ϕ
2
(x) są funkcjami ciągłymi na przedziale
[a,b] oraz
ϕ
1
(x) <
ϕ
2
(x) dla każdego x
∈[a,b]
Przykład obszaru normalnego
względem osi OX:
a
b
x
ϕ
2
(x)
ϕ
1
(x)
3
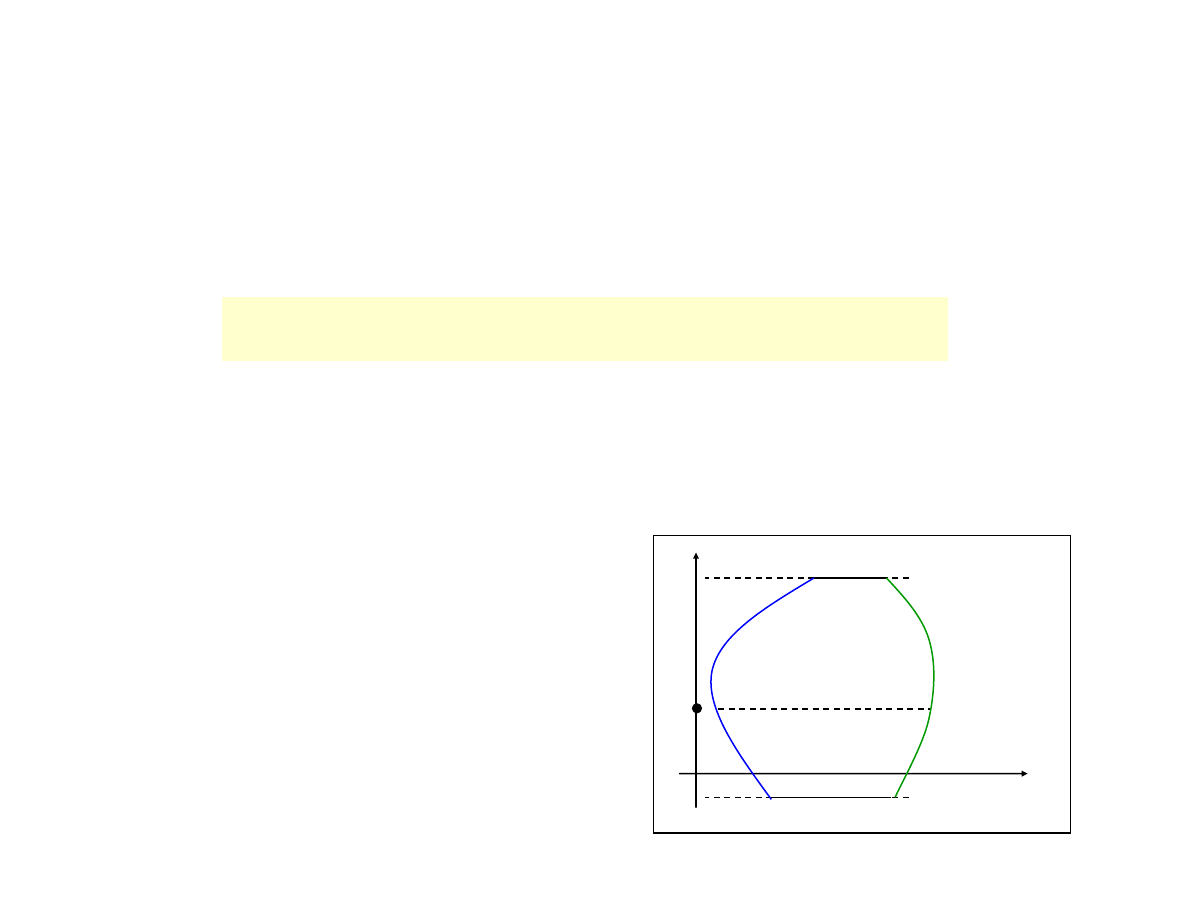
Obszarem normalnym względem osi OY nazywamy
obszar D postaci:
Obszar normalny względem osi OY
(
)
( )
( )
{
}
y
g
x
y
g
d
y
c
y
x
2
1
;
:
,
D
≤
≤
≤
≤
=
gdzie g
1
(y) i g
2
(y) są funkcjami ciągłymi na przedziale [c,d]
oraz g
1
(y) < g
2
(y) dla każdego y
∈[c,d]
Przykład obszaru normalnego
względem osi OY:
d
c
y
g
1
(y)
g
2
(y)
4
Całki podwójne z funkcji po obszarach normalnych
Jeśli funkcja f(x,y) jest ciągła na obszarze normalnym D
względem osi OX, wówczas całkę podwójną z funkcji
f
(x,y) określamy wzorem:
(
)
(
)
( )
( )
∫ ∫
∫∫
=
ϕ
ϕ
b
a
x
x
D
dx
dy
y
x
f
dxdy
y
x
f
2
1
,
,
Jeśli funkcja f(x,y) jest ciągła na obszarze normalnym D
względem osi OY, wówczas całkę podwójną z funkcji f(x,y)
określamy wzorem:
(
)
(
)
( )
( )
∫ ∫
∫∫
=
d
c
y
g
y
g
D
dy
dx
y
x
f
dxdy
y
x
f
2
1
,
,
5
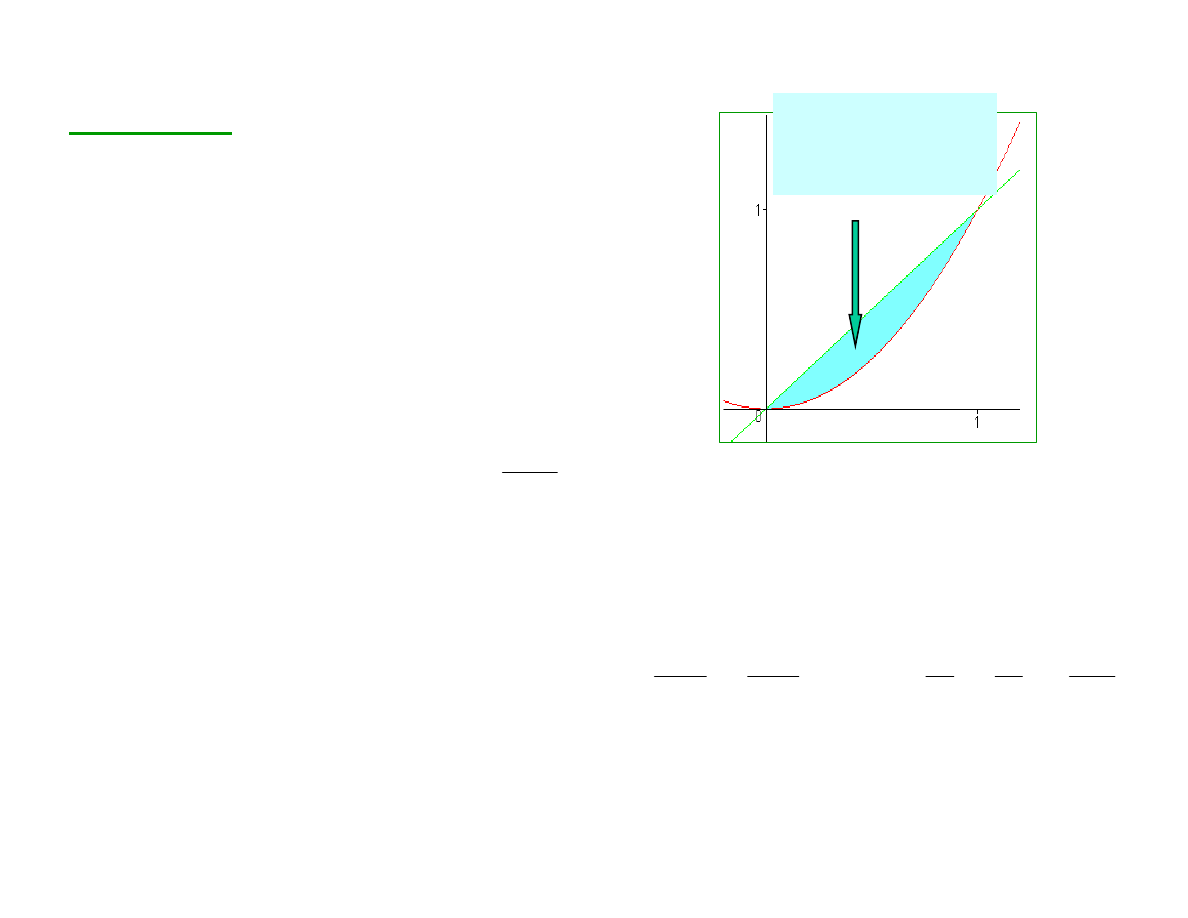
Przykład 1:
Obliczyć całkę z funkcji z=2xy
po obszarze D ograniczonym
y
=x
2
i y=x.
(
)
∫
∫ ∫
=
=
=
=
1
0
2
1
0
2
2
2
2
2
dx
y
x
dx
dy
xy
x
y
x
y
x
x
[ ]
[
]
12
1
6
1
4
1
6
4
1
0
6
4
1
0
1
0
5
3
2
2
=
−
=
−
=
−
=
=
=
=
=
=
∫
∫
x
x
x
y
x
y
x
x
dx
x
x
dx
xy
≤
≤
≤
≤
x
y
x
x
D
2
1
0
:
6
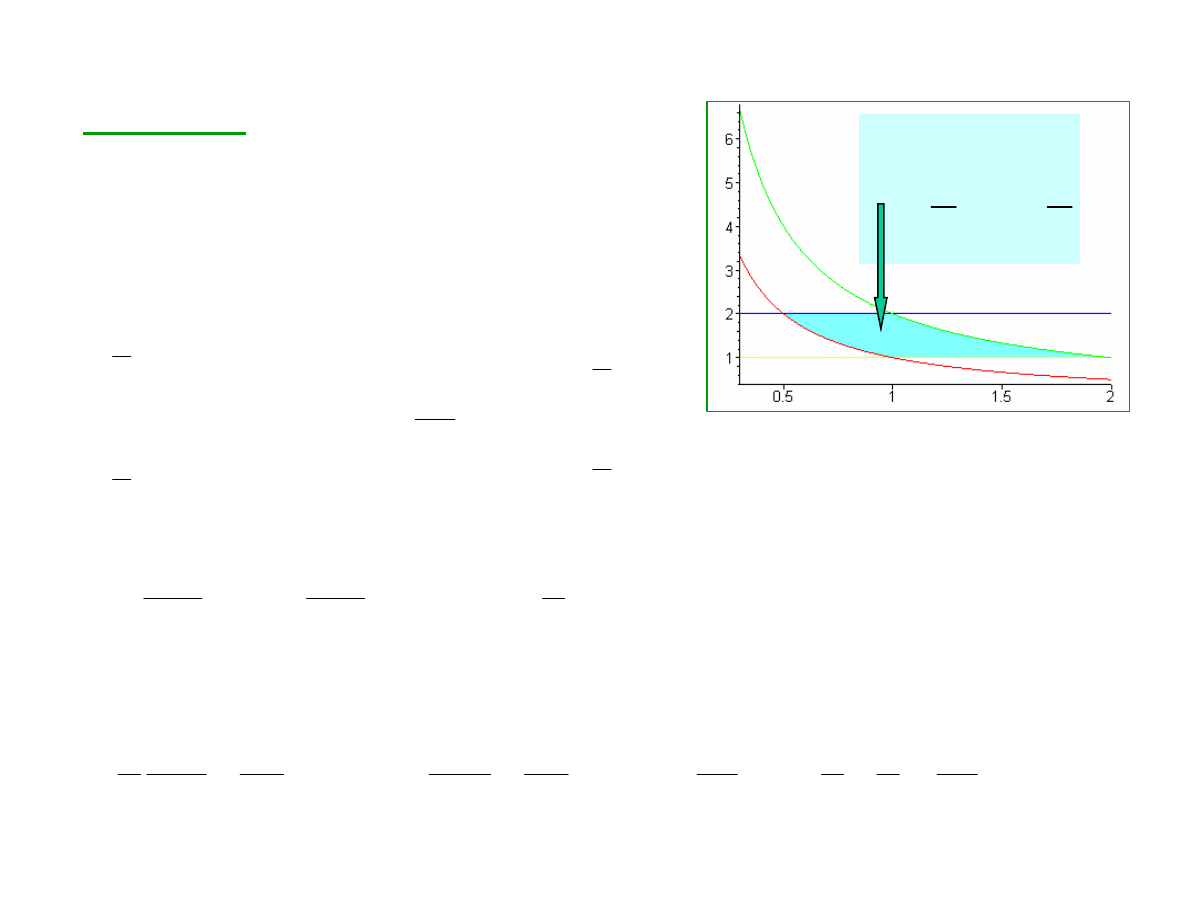
Przykład 2:
Obliczyć całkę z funkcji z=x
2
+y
2
po obszarze D ograniczonym:
xy
=1, xy=2 y=1, y=2.
(
)
∫
∫ ∫
=
+
=
+
=
=
2
1
2
1
2
3
2
1
2
1
2
2
3
dy
x
y
x
dy
dx
y
x
y
x
y
x
y
y
∫
∫
=
+
=
−
−
+
=
−
2
1
2
1
3
3
3
3
7
3
1
2
3
8
dy
y
y
dy
y
y
y
y
24
57
2
1
6
7
2
24
7
2
6
7
2
2
3
7
2
1
2
2
2
1
2
2
=
−
+
+
−
=
+
−
=
+
−
=
=
=
=
=
−
y
y
y
y
y
y
y
y
≤
≤
≤
≤
y
x
y
y
D
2
1
2
1
:
7
Uwaga: Całkę po dowolnym obszarze obliczamy
dzieląc ten obszar na obszary normalne.
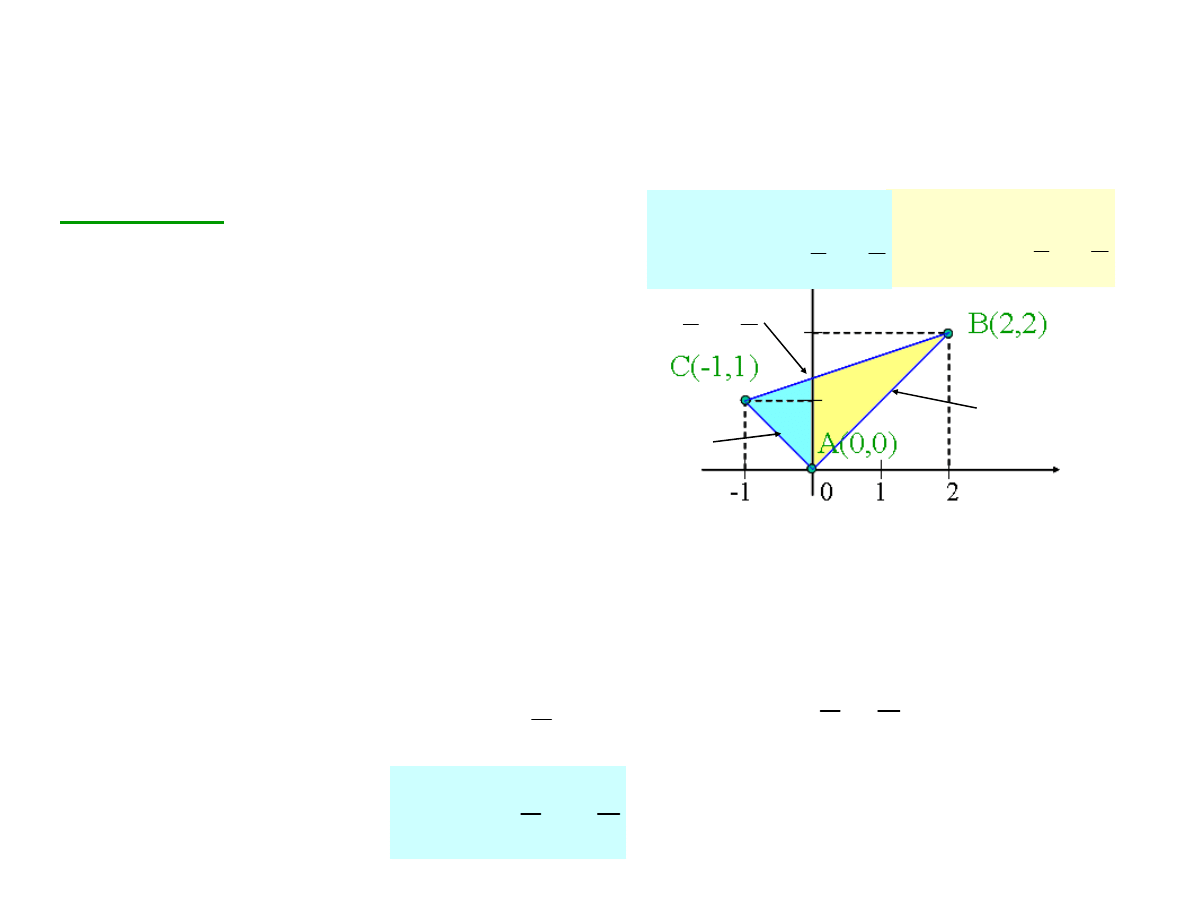
Przykład 3:
Obliczyć całkę z funkcji z=x+2y
po trójkącie o wierzchołkach:
A(0,0), B(2,2), C(-1,1).
3
4
3
1
1
1
=
+
=
+
=
a
b
Wyznaczamy proste przechodzące przez odpowiednie
wierzchołki: AB: y=x; AC: y=-x; BC: y=ax+b. Wstawiając
punkty B i C dostajemy układ:
;
3
1
3
1
1
2
2
=
⇔
=
⇔
+
−
=
+
=
−
a
a
b
a
b
a
+
≤
≤
≤
≤
3
4
3
1
2
0
:
2
x
y
x
x
D
+
≤
≤
−
≤
≤
−
3
4
3
1
0
1
:
1
x
y
x
x
D
y=x
y=-x
3
4
3
1
+
=
x
y
3
4
3
1
:
BC
+
=
x
y

8
Obliczamy sumę całek:
(
)
(
)
∫ ∫
∫ ∫
=
+
+
+
+
−
+
−
2
0
3
4
3
1
0
1
3
4
3
1
2
2
dx
dy
y
x
dx
dy
y
x
x
x
x
x
[
]
[
]
∫
∫
=
+
+
+
=
+
=
=
−
+
=
−
=
2
0
3
4
3
1
2
0
1
3
4
3
1
2
dx
y
xy
dx
y
xy
x
y
x
y
x
y
x
y
+
−
+
+
+
+
=
∫
−
0
1
2
2
2
2
3
4
3
1
3
4
3
1
dx
x
x
x
x
x
=
−
−
+
+
+
+
∫
2
0
2
2
2
2
3
4
3
1
3
4
3
1
dx
x
x
x
x
x
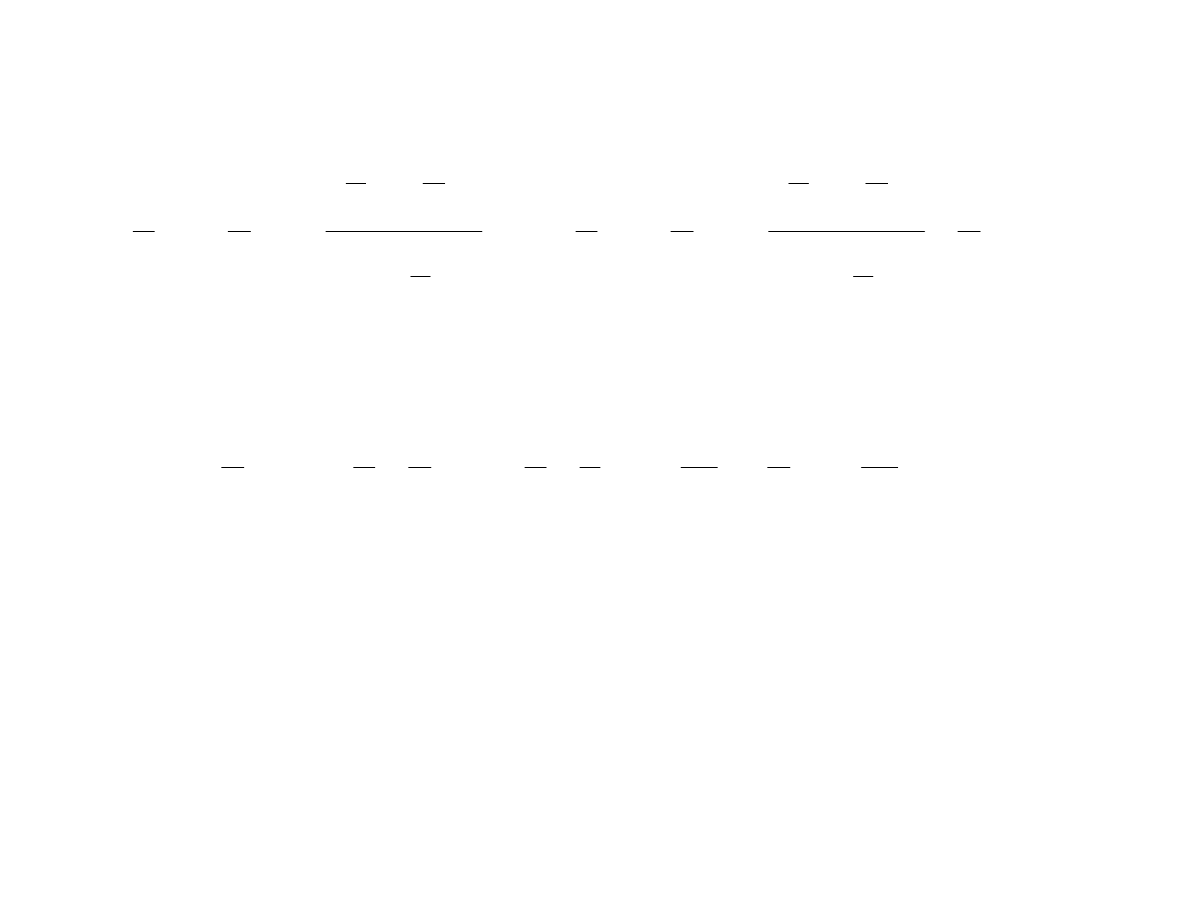
9
=
−
⋅
+
+
+
+
⋅
+
+
+
=
−
2
0
3
3
2
3
0
1
3
2
3
3
2
3
1
3
3
4
3
1
3
2
9
1
3
1
3
3
4
3
1
3
2
9
1
x
x
x
x
x
x
x
3
14
3
4
3
16
8
3
8
9
8
1
3
2
9
1
3
4
3
3
=
−
−
+
+
+
+
+
−
−
=
10
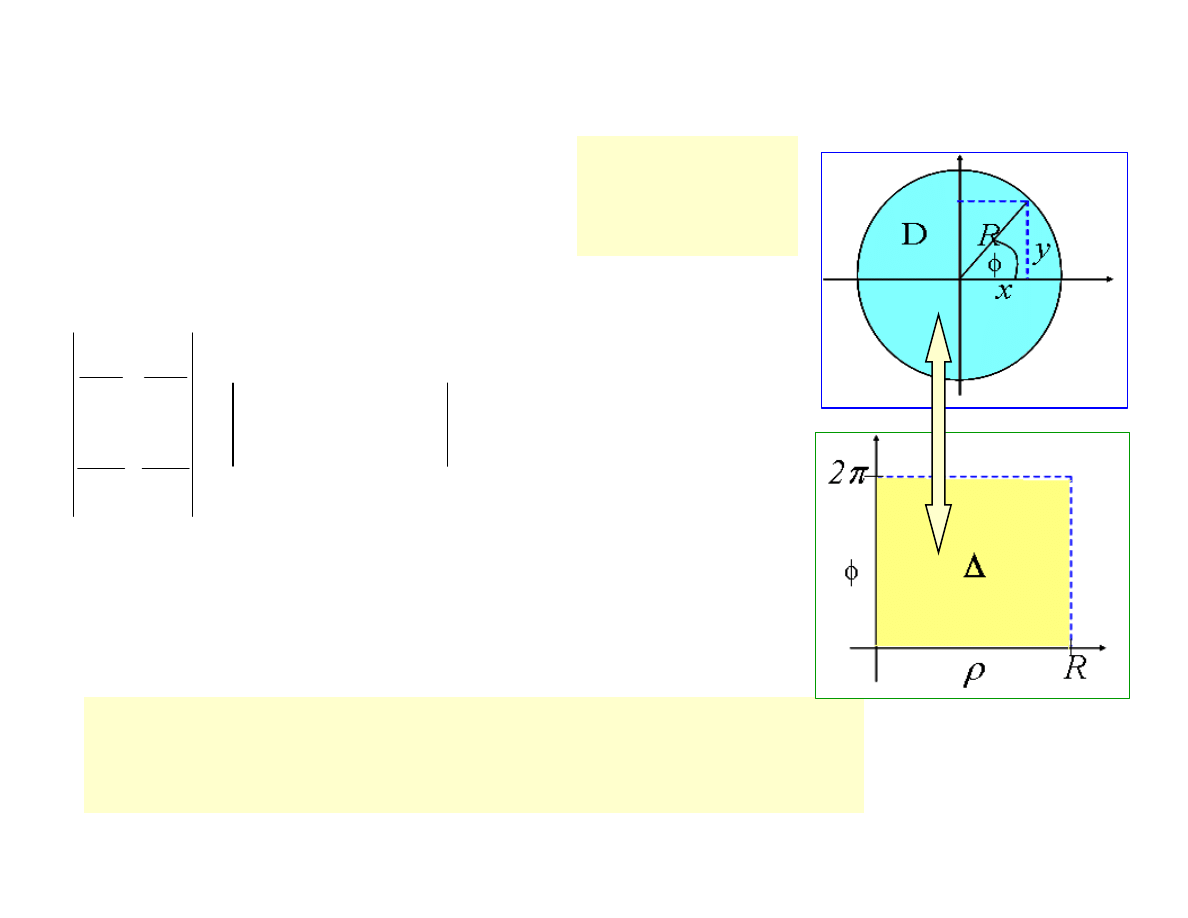
Zamiana zmiennych w całce podwójnej
0
≠
∂
ψ
∂
∂
ψ
∂
∂
ϕ
∂
∂
ϕ
∂
v
u
v
u
które odwzorowuje obszar domknięty
∆ (w płaszczyźnie
zmiennych u, v) na obszar regularny D (w płaszczyźnie
zmiennych x i y). Jeżeli ponadto
1. Funkcje
ϕ i ψ są ciągłe w obszarze ∆
2. Funkcja f(x,y) jest ciągła w obszarze D
3. Odwzorowanie wnętrza obszaru
∆ we wnętrze obszaru D
jest wzajemnie jednoznaczne
4. Wewnątrz obszaru
∆ jakobian
(
)
(
)
ψ
=
ϕ
=
v
u
y
v
u
x
,
,
Rozważmy przekształcenie:
11
ρ
=
φ
ρ
+
φ
ρ
=
φ
ρ
φ
φ
ρ
−
φ
=
φ
∂
ψ
∂
ρ
∂
ψ
∂
φ
∂
ϕ
∂
ρ
∂
ϕ
∂
2
2
sin
cos
cos
,
sin
sin
,
cos
Jakobian takiego przekształcenia wynosi:
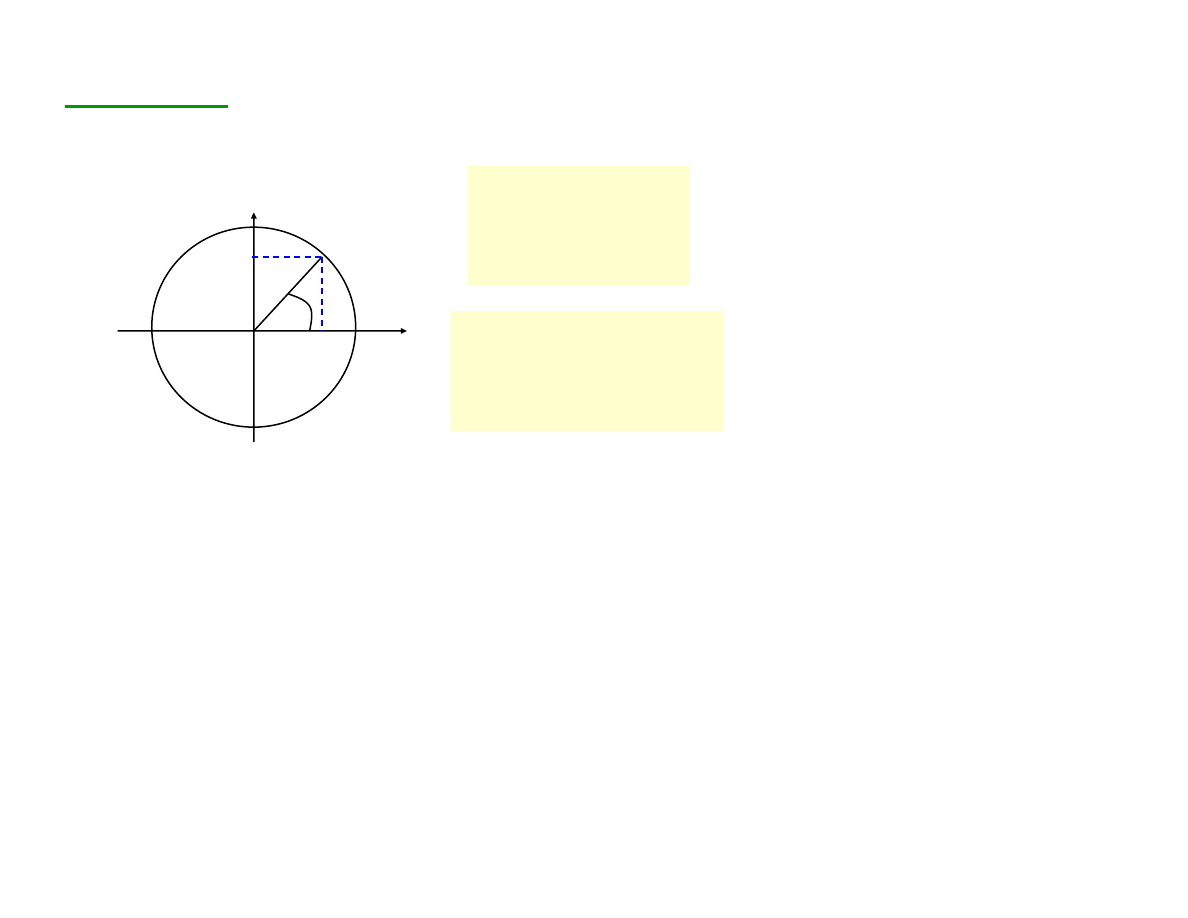
Szczególnym przekształceniem jest wprowadzenie
współrzędnych biegunowych:
Wówczas
(
)
(
)
φ
ρ
ρ
φ
ρ
φ
ρ
=
∫∫
∫∫
∆
d
d
f
dxdy
y
x
f
D
sin
,
cos
,
φ
ρ
=
φ
ρ
=
sin
cos
y
x
12
Przykład 4:
Obliczyć całkę z funkcji z=10-x-y po kole: x
2
+y
2
≤4.
x
R=2
y
α
φ
ρ
=
φ
ρ
=
sin
cos
y
x
π
≤
φ
≤
≤
ρ
≤
∆
2
0
2
0
:
(
)
(
)
=
ρ
φ
φ
ρ
−
φ
ρ
−
ρ
=
−
−
∫ ∫
∫∫
π
≤
+
2
0
2
0
4
sin
cos
10
10
2
2
d
d
dxdy
y
x
y
x
(
)
[
]
(
)
∫
∫
=
ρ
ρ
−
ρ
+
π
ρ
=
ρ
φ
ρ
+
φ
ρ
−
φ
ρ
=
π
=
φ
=
φ
2
0
2
0
2
0
20
cos
sin
10
d
d
[ ]
π
=
ρ
π
=
40
10
2
0
2
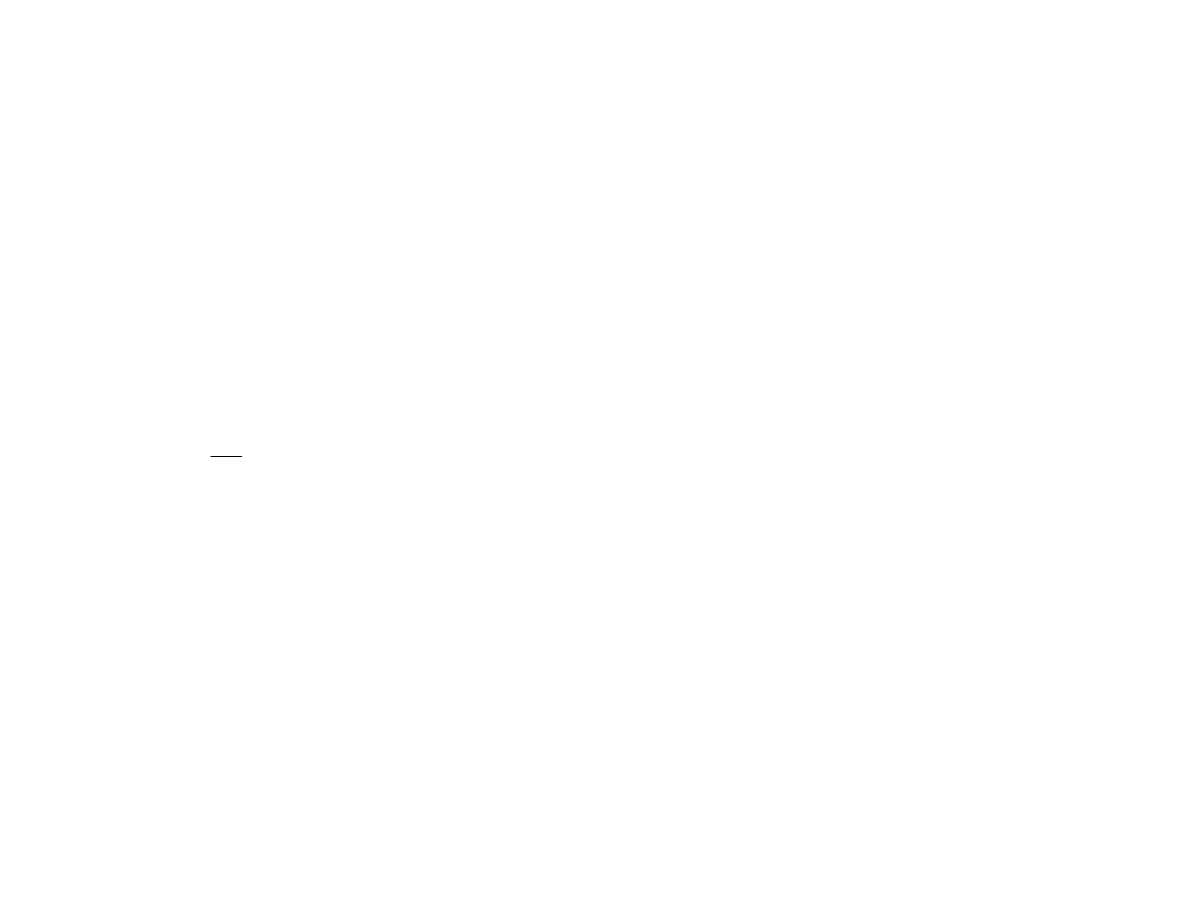
13
Zadania na ćwiczenia z całek podwójnych:
1. Obliczyć całkę podwójną:
1.1.
dy
xydx
∫ ∫
4
0
5
2
.
1.2.
∫∫
D
xydxdy
4
, gdzie
<
<
<
<
3
1
2
0
:
y
x
D
.
1.3.
∫∫
D
dxdy
y
x
4
, gdzie
{
4
2
1
0
:
<
<
<
<
y
x
D
.
1.4.
(
)
∫∫
+
D
dxdy
y
x
2
, gdzie D jest obszarem pomiędzy prostymi:
+
−
=
=
=
4
0
x
y
x
y
x
.
1.5.
(
)
∫∫
+
D
dxdy
y
x
2
4
, gdzie D jest obszarem pomiędzy prostymi:
+
−
=
=
=
2
0
x
y
x
y
y
.
1.6. Obliczyć objętość bryły ograniczonej powierzchniami:
y
x
z
+
+
= 1
,
0
=
x
,
0
=
y
,
0
=
z
oraz
1
=
+ y
x
.
Wyszukiwarka
Podobne podstrony:
Mat WIP Wyk ad22
Mat WIP Wyk ad25
Mat WIP Wyk ad19
Mat WIP Wyk ad26
IiE, Mat Statystyka,Wyk 4
Mat Bud wyk 07
Mat Bud wyk 09
Mat Stat Wyk 8 PrzedziaĹ y(2013L)
Mat Bud wyk 03
Mat WIP Wykład21
Mat Bud wyk 02
mat konstr wyk, PKM egzamin kolosy ( łukasik, Salwiński )
Mat WIP Wykład16
więcej podobnych podstron