Wykład XVI
Temat: Całki nieoznaczone
Funkcję F(x) spełniającą warunek F
’(x)=f(x) nazywamy
funkcją pierwotną
. Poszukiwanie funkcji pierwotnej
nazywa się całkowaniem. Całkowanie jest działaniem
odwrotnym do różniczkowania.
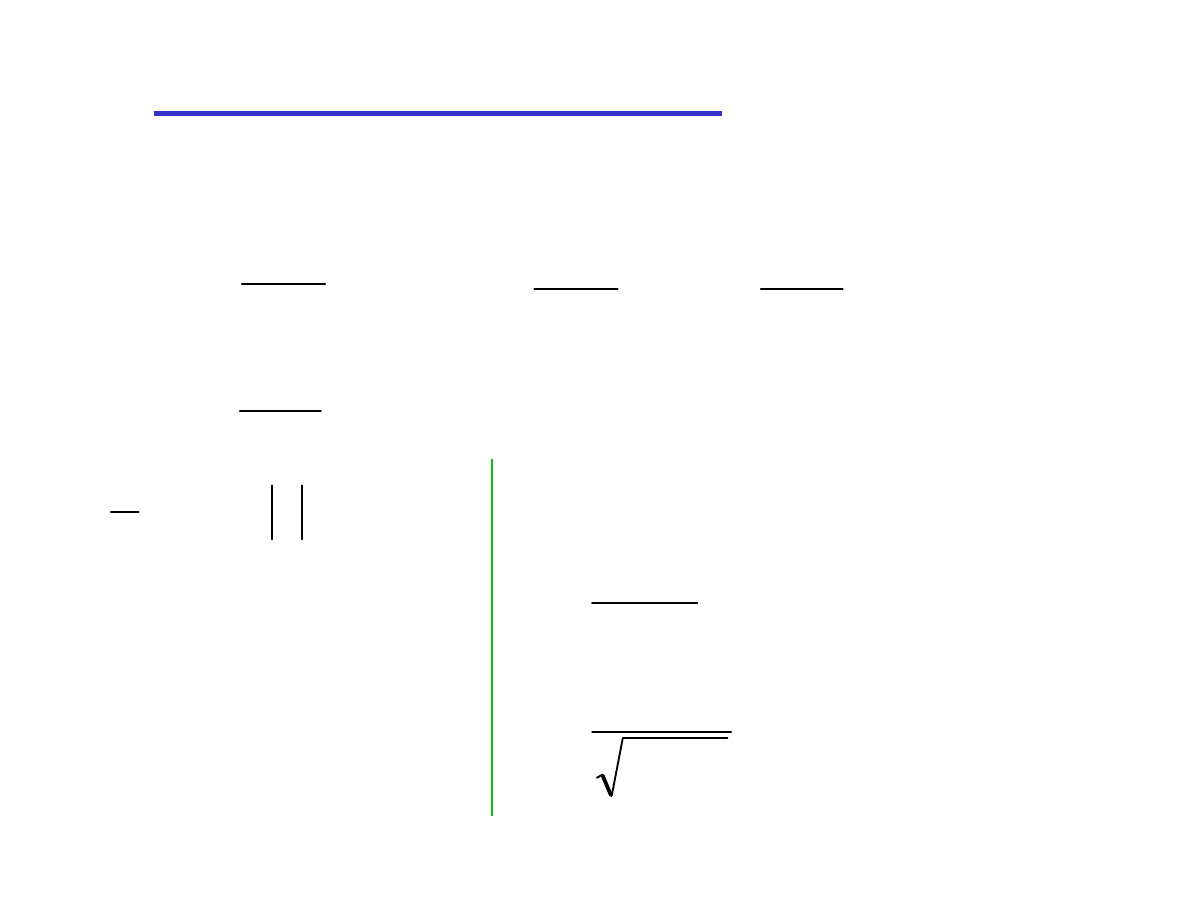
( )
( )
( )
(
)
( )
x
f
c
x
F
c
x
F
dx
x
f
=
′
+
⇔
+
=
∫
symbol
całki
stała
funkcja
pierwotna
funkcja
podcałkowa
2
Własności całki nieoznaczonej
Własność 1.
Czynnik stały można wynieść przed znak całki:
( )
( )
dx
x
f
c
dx
x
f
c
∫
∫
=
Własność 2.
Całka z sumy (różnicy) dwóch funkcji jest
równa sumie (różnicy) całek z tych funkcji:
( )
( )
[
]
( )
( )
dx
x
g
dx
x
f
dx
x
g
x
f
∫
∫
∫
±
=
±
3
Podstawowe wzory całkowe
∫
+
=
+
c
tgx
arc
dx
x
2
1
1
∫
+
=
−
c
sinx
arc
dx
x
2
1
1
∫
+
=
c
x
dx
1
ponieważ
(
)
1
=
′
+ c
x
∫
+
+
=
+
c
n
x
dx
x
n
n
1
1
(
)
n
n
n
x
x
n
n
c
n
x
=
+
⋅
+
=
′
+
+
+
1
1
1
1
1
gdyż
1
1
1
−
≠
+
+
=
∫
+
r
dla
c
r
x
dx
x
r
r
∫
+
=
c
x
ln
dx
x
1
∫
+
−
=
c
cosx
sindx
∫
+
=
c
sinx
cosdx
∫
+
=
c
e
dx
e
x
x
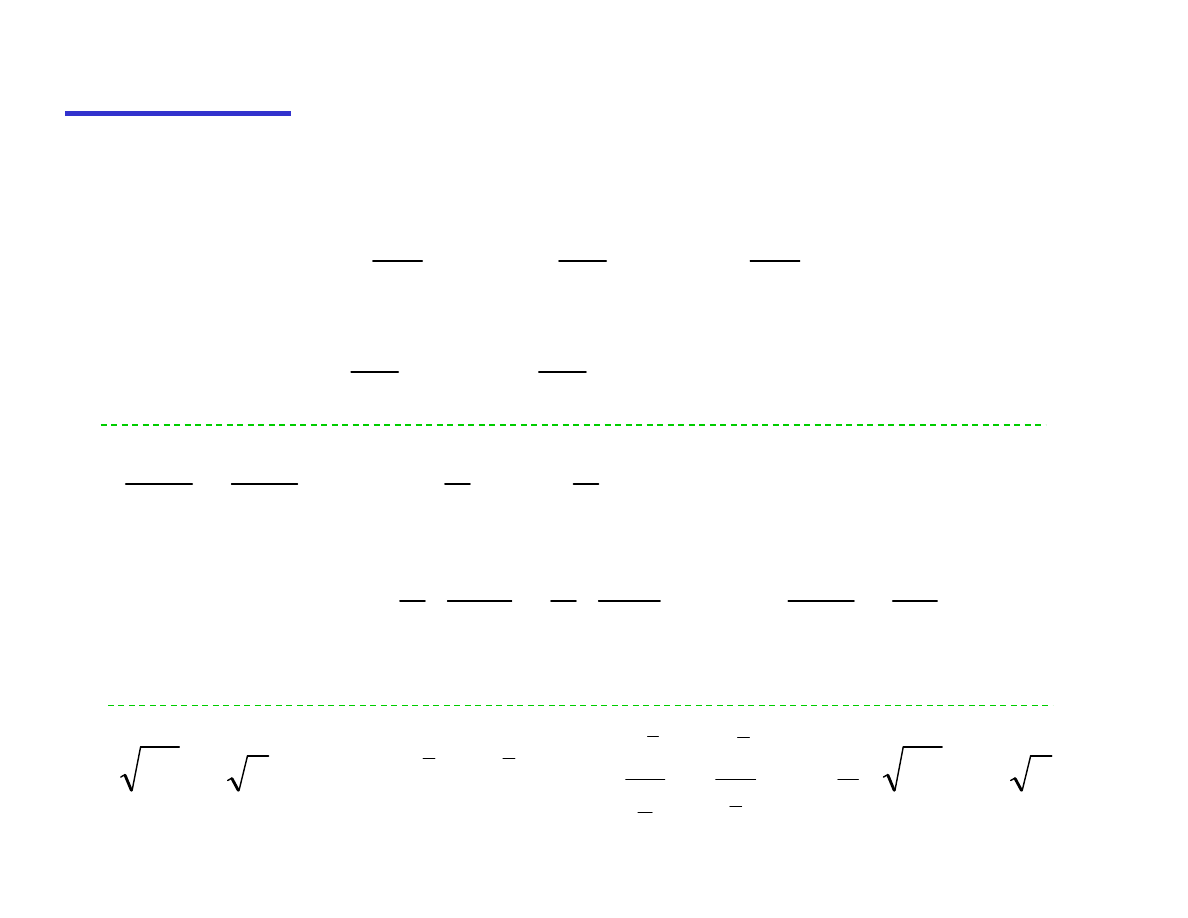
4
Przykłady:
(
)
=
−
+
−
=
−
+
−
∫
∫
∫
∫
∫
dx
xdx
dx
x
dx
x
dx
x
x
x
1
7
5
3
2
7
5
3
2
2
3
2
3
∫
∫
=
+
=
+
−
−
dx
x
x
dx
x
x
2
3
2
3
3
4
4
1
3
4
4
1
c
x
x
x
x
c
x
x
dx
x
x
dx
x
x
+
−
=
+
−
=
−
=
−
∫
∫
2
5
6
3
2
3
2
3
2
3
2
3
5
3
2
2
3
2
3
3
5
2
1
3
2
=
+
−
+
+
+
−
+
=
4
3
2
2
3
1
4
7
2
5
3
3
4
2
c
x
c
x
c
x
c
x
c
x
x
x
x
+
−
+
−
=
7
2
5
2
2
3
4
c
x
x
c
x
x
+
−
−
=
+
−
⋅
+
−
⋅
=
−
−
3
4
8
1
1
3
4
2
4
1
2
1
2
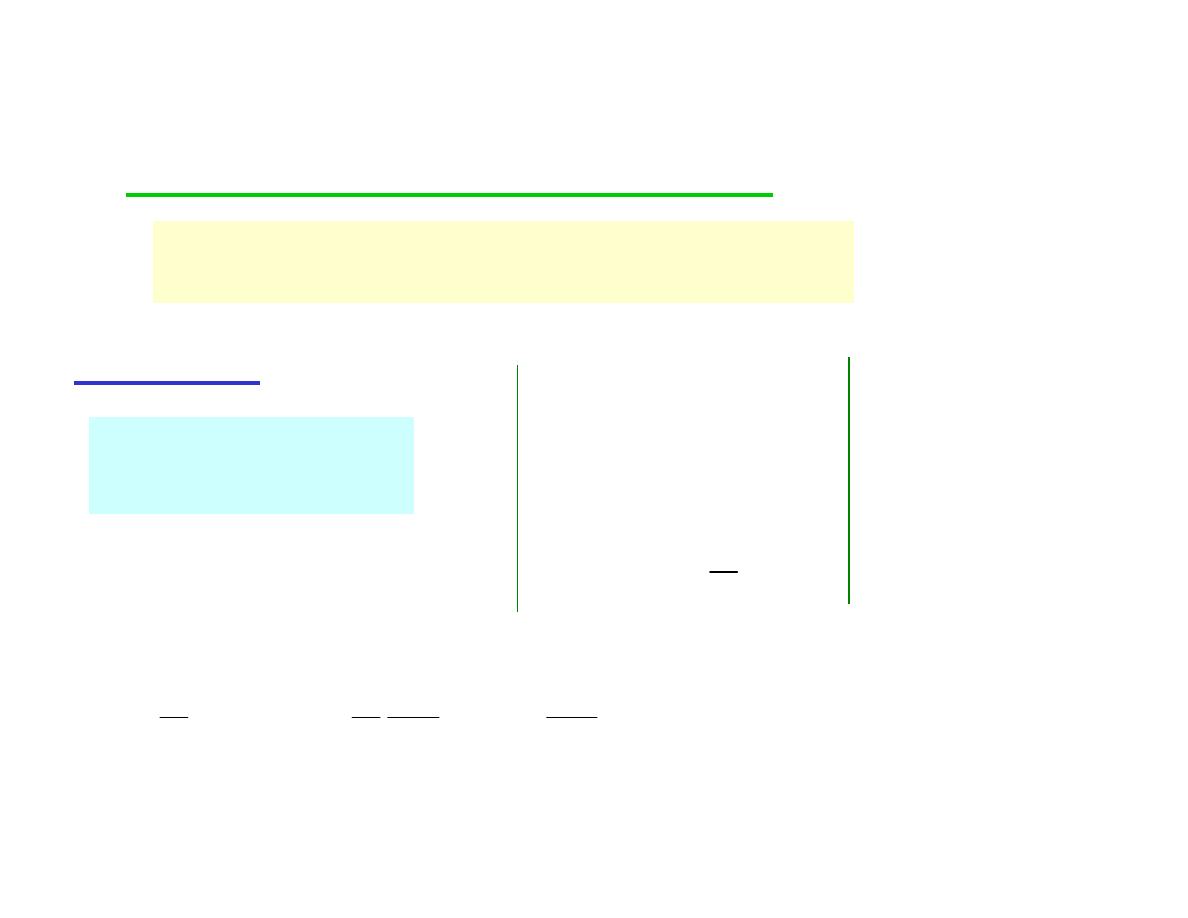
5
Metody całkowania:
I. Całkowanie przez podstawianie
( )
(
) ( )
( )
( )
c
u
F
du
u
f
dx
x
u
x
u
f
+
=
=
′
∫
∫
Przykład
(
)
∫
=
+
dx
x
x
5
2
7
2
podstawiamy
:
(
)
c
x
c
u
du
u
+
+
=
+
=
=
∫
6
2
6
5
7
2
24
1
6
4
1
4
1
u
x
=
+ 7
2
2
du
xdx =
4
du
xdx
4
1
=
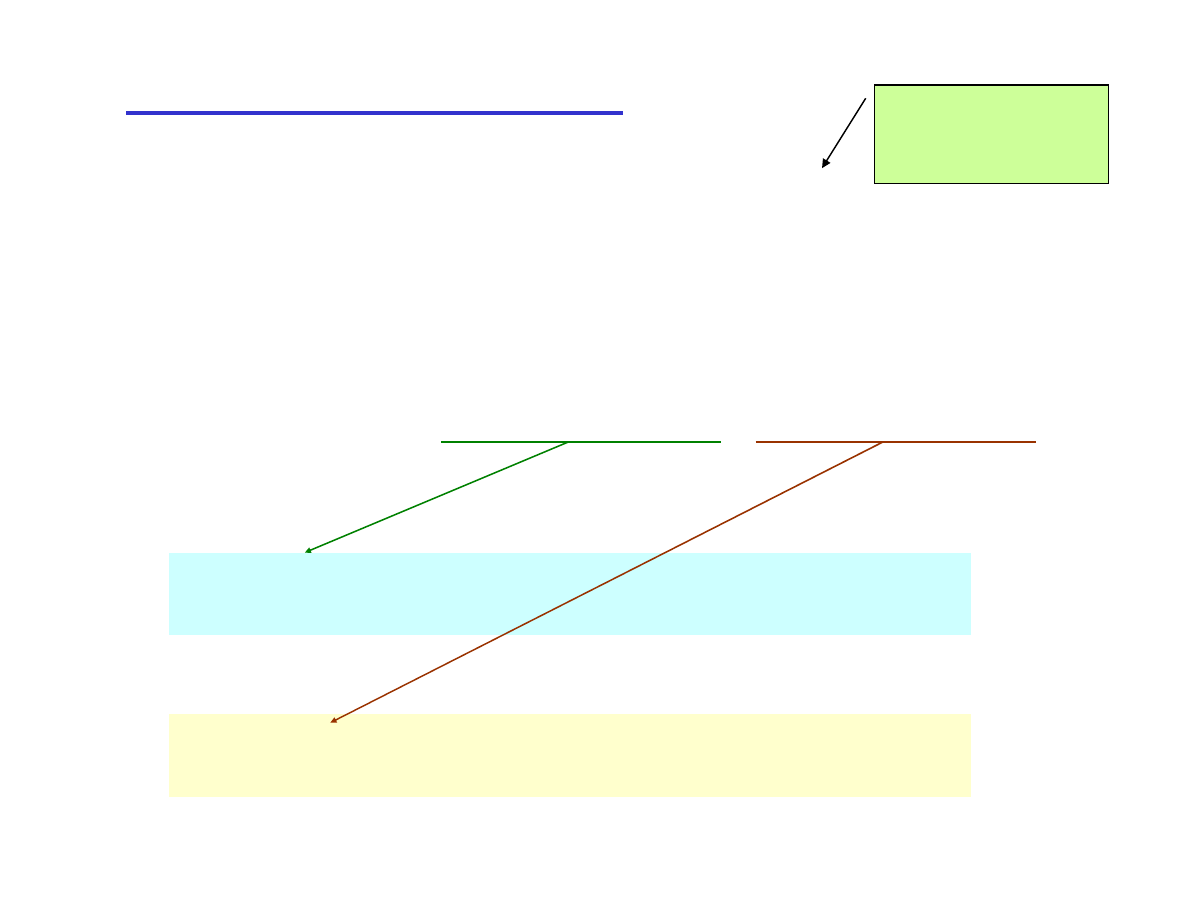
6
II. Całkowanie przez części
( ) ( )
[
]
( ) ( )
( )
( )
x
g
x
f
x
g
x
f
x
g
x
f
′
⋅
+
⋅
′
=
′
⋅
co daje nam wzór na całkowanie przez części:
( ) ( )
( ) ( )
( )
( )
dx
x
g
x
f
x
g
x
f
dx
x
g
x
f
∫
∫
′
⋅
−
⋅
=
⋅
′
( ) ( )
[
]
( ) ( )
( )
( )
dx
x
g
x
f
dx
x
g
x
f
dx
x
g
x
f
∫
∫
∫
′
⋅
+
⋅
′
=
′
⋅
( ) ( )
( ) ( )
( )
( )
dx
x
g
x
f
dx
x
g
x
f
x
g
x
f
∫
∫
′
⋅
+
⋅
′
=
⋅
( )
( )
( ) ( )
( ) ( )
dx
x
g
x
f
x
g
x
f
dx
x
g
x
f
∫
∫
⋅
′
−
⋅
=
′
⋅
lub
Pochodna
iloczynu
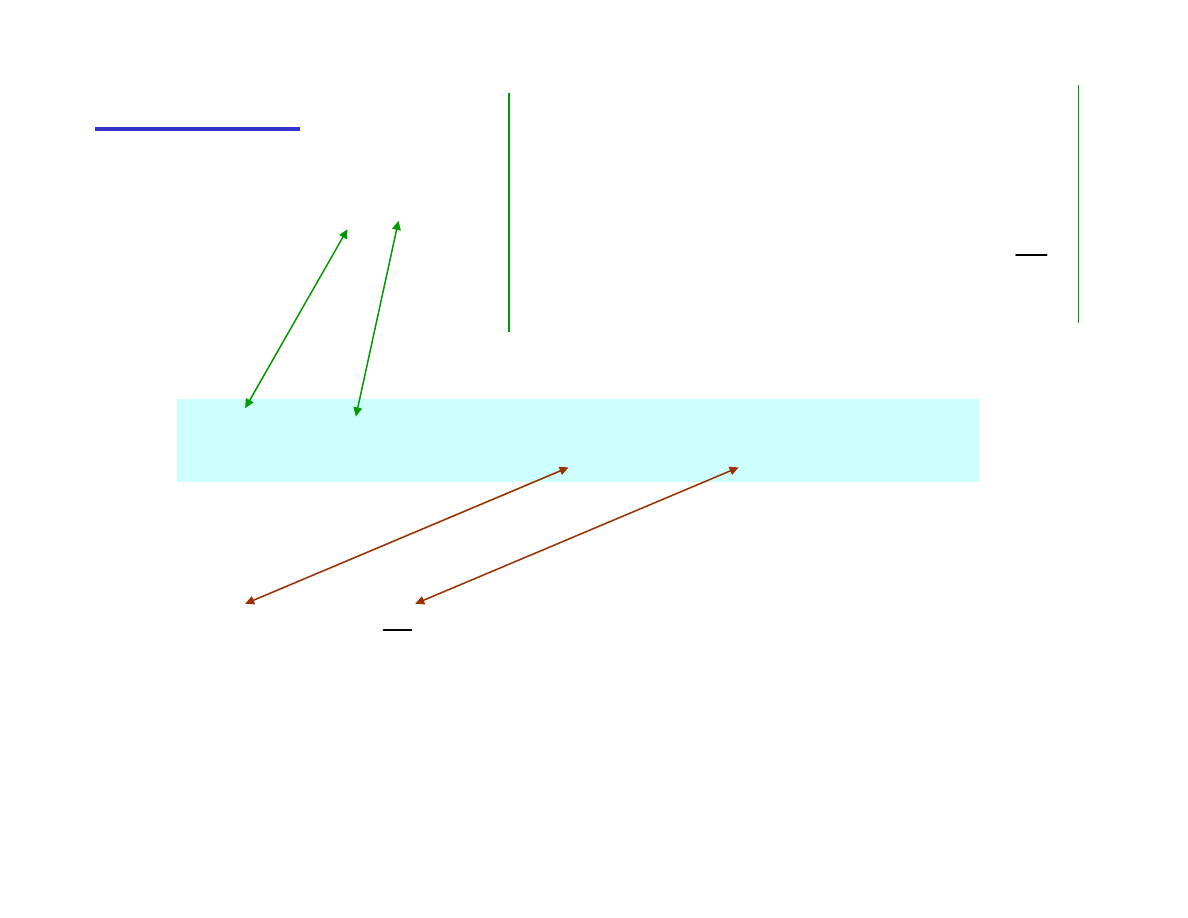
7
Przykład 1.
=
⋅
=
∫
∫
lnxdx
lnxdx
1
( )
( )
lnx
x
g
x
f
=
=
′
1
c
x
xlnx
dx
xlnx
dx
x
x
xlnx
+
−
=
−
=
⋅
−
=
∫
∫
1
1
( )
( )
x
x
g
x
dx
x
f
1
1
=
′
=
=
∫
( ) ( )
( ) ( )
( )
( )
dx
x
g
x
f
x
g
x
f
dx
x
g
x
f
∫
∫
′
⋅
−
⋅
=
⋅
′
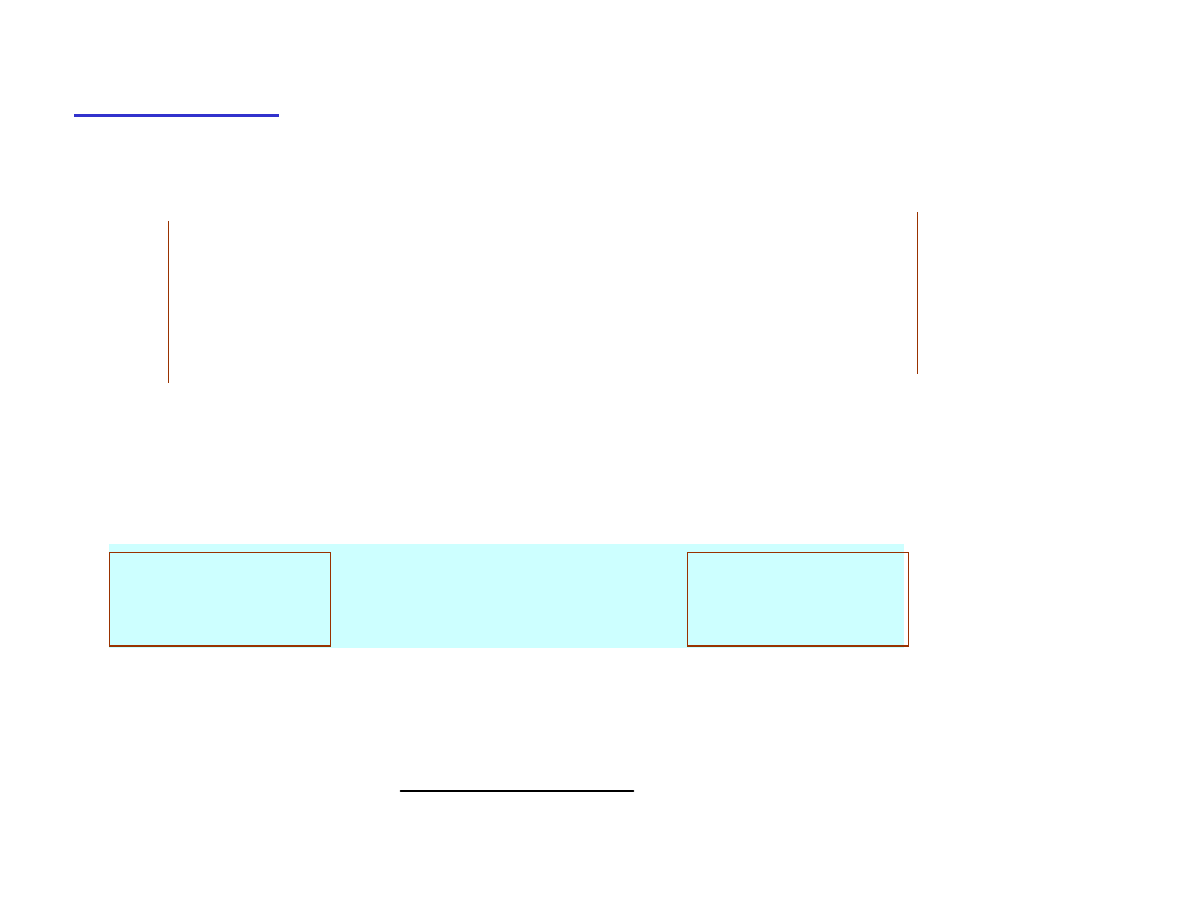
8
Przykład 2.
=
⋅
=
∫
∫
xdx
x
xdx
cos
cos
cos
2
( )
( )
cosx
x
g
cosx
x
f
=
′
=
(
)
∫
∫
−
+
=
⋅
+
⋅
=
dx
x
cos
sinxcosx
sinxdx
sinx
sinx
cosx
2
1
ostatecznie otrzymujemy:
∫
∫
−
+
=
xdx
cos
x
sinxcosx
xdx
cos
2
2
∫
+
=
x
x
sinx
xdx
cos
cos
2
2
( )
( )
sinx
cosxdx
x
g
sinx
x
f
∫
=
=
−
=
′
c
x
cosx
sinx
xdx
cos
+
+
=
∫
2
2
9
dx
x
x
x
x
x
∫
+
−
−
+
−
3
2
3
2
8
6
1
5
4
3
.
1
dx
x
x
x
x
x
x
∫
+
+
−
−
+
−
5
8
6
2
5
3
5
.
2
4
3
2
2
4
dx
x
x
∫
+ 5
3
2
.
4
2
(
)
dx
x
x
∫
+ 3
2
3
.
3
3
2
dx
xe
x
∫
+3
2
2
2
.
5
(
)
dx
x
x
3
cos
8
.
6
4
3
+
∫
dx
xe
x
∫
2
.
10
dx
x
x
∫
cos
5
.
7
dx
x
x
∫
sin
7
.
8
dx
x
x
∫
ln
5
.
9
4
Zadania na
Zadania na
ć
ć
wiczenia
wiczenia
Metoda przez podstawienie:
Metoda przez części:
Wyszukiwarka
Podobne podstrony:
Mat WIP Wykład21
Analiza mat I semstr wykłady
MAT BUD WYKŁAD 3 ceramika
MAT BUD WYKŁAD 4 ocena zgodności
PYTANIA metodologia, MAT.OD WYKŁADOWCÓW, METODOLOGIA I
Mat WIP Wyk ad22
Mat met Wykład 1, Studia, ZiIP, SEMESTR II, Materiały metalowe
Mat WIP Wyk ad23
MAT BUD WYKŁAD 4 drewno
TEST NIEDOKOĹCZONYCH ZDAĹ, MAT.OD WYKŁADOWCÓW, DIAGNOZA INTELIGENCJI OSOBY DOROSŁEJ, DIAGNOZA OSOB
MAT BUD WYKŁAD 4 termoizolacje
MAT BUD WYKLAD 1
Mat WIP Wyk ad25
Inne materiały, mat-funkcja wykładnicza, a >1
MAT BUD WYKŁAD 5 spoiwa
Mat WIP Wyk ad19
więcej podobnych podstron