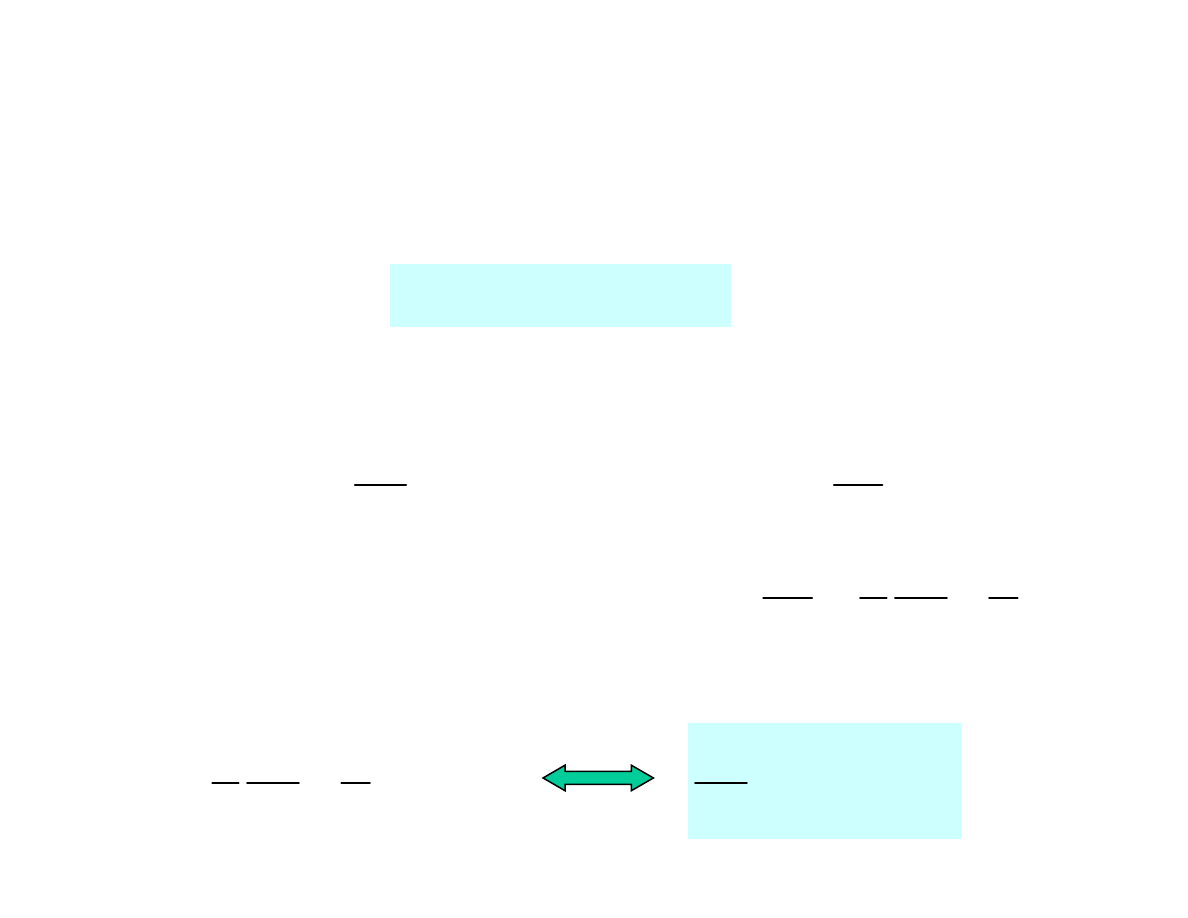
(
)
c
by
ax
f
y
+
+
=
′
c
by
ax
u
+
+
=
Wykład XXV
Równania różniczkowe zwyczajne (c.d.)
1. Równanie różniczkowe zwyczajne postaci:
Po wstawieniu nowej zmiennej u oraz
W celu rozwiązania równania dokonujemy podstawienia:
Obliczamy
(
)
dx
dy
b
a
c
by
ax
dx
du
x
+
=
′
+
+
=
b
a
dx
du
b
dx
dy
−
=
1
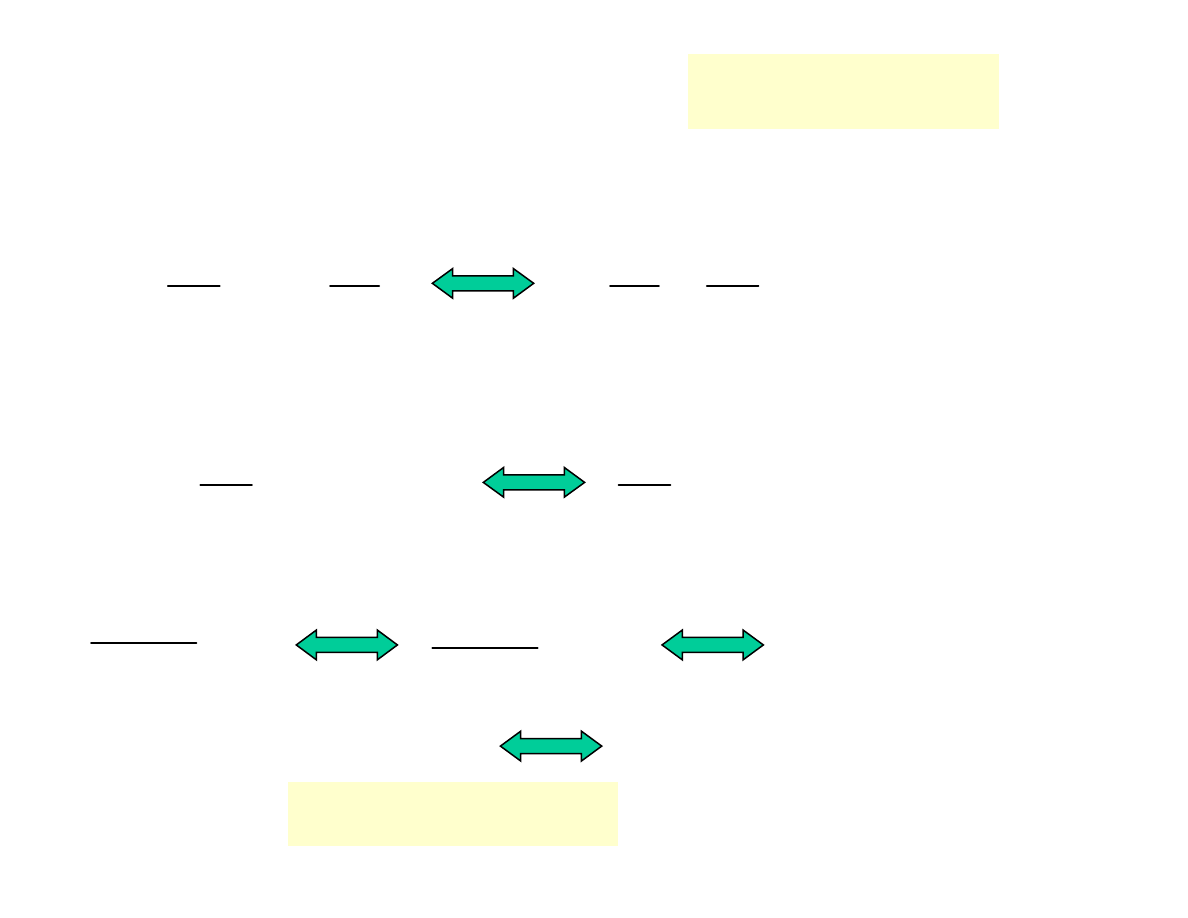
równanie przyjmie ostateczną postać:
( )
a
u
bf
dx
du
+
=
( )
u
f
b
a
dx
du
b
=
−
1
2
Przykład 1. Rozwiązać równanie
Rozwiązanie: Dokonujemy podstawienia:
(
)
1
2
2
−
+
=
′
y
x
y
.
2
y
x
u
+
=
Liczymy pochodną po x:
dx
dy
dx
du
+
= 2
2
−
=
dx
du
dx
dy
Po wstawieniu do równania otrzymujemy nowe
równanie różniczkowe:
1
2
2
−
=
−
u
dx
du
1
2
+
= u
dx
du
Rozwiązując równanie dostajemy:
dx
u
du
=
+1
2
∫
∫
=
+
dx
u
du
1
2
C
x
arctgu
+
=
(
)
C
x
y
x
arctg
+
=
+
2
(
)
C
x
tg
y
x
+
=
+
2
(
)
x
C
x
tg
y
2
−
+
=
Ostatecznie
3
=
′
x
y
f
y
x
y
u =
2. Równanie różniczkowe postaci:
Po wstawieniu nowej zmiennej u oraz
Rozwiązując równanie dokonujemy podstawienia:
Obliczamy
u
dx
du
x
u
x
dx
du
dx
dy
+
=
⋅
+
⋅
=
1
u
dx
du
x
dx
dy
+
=
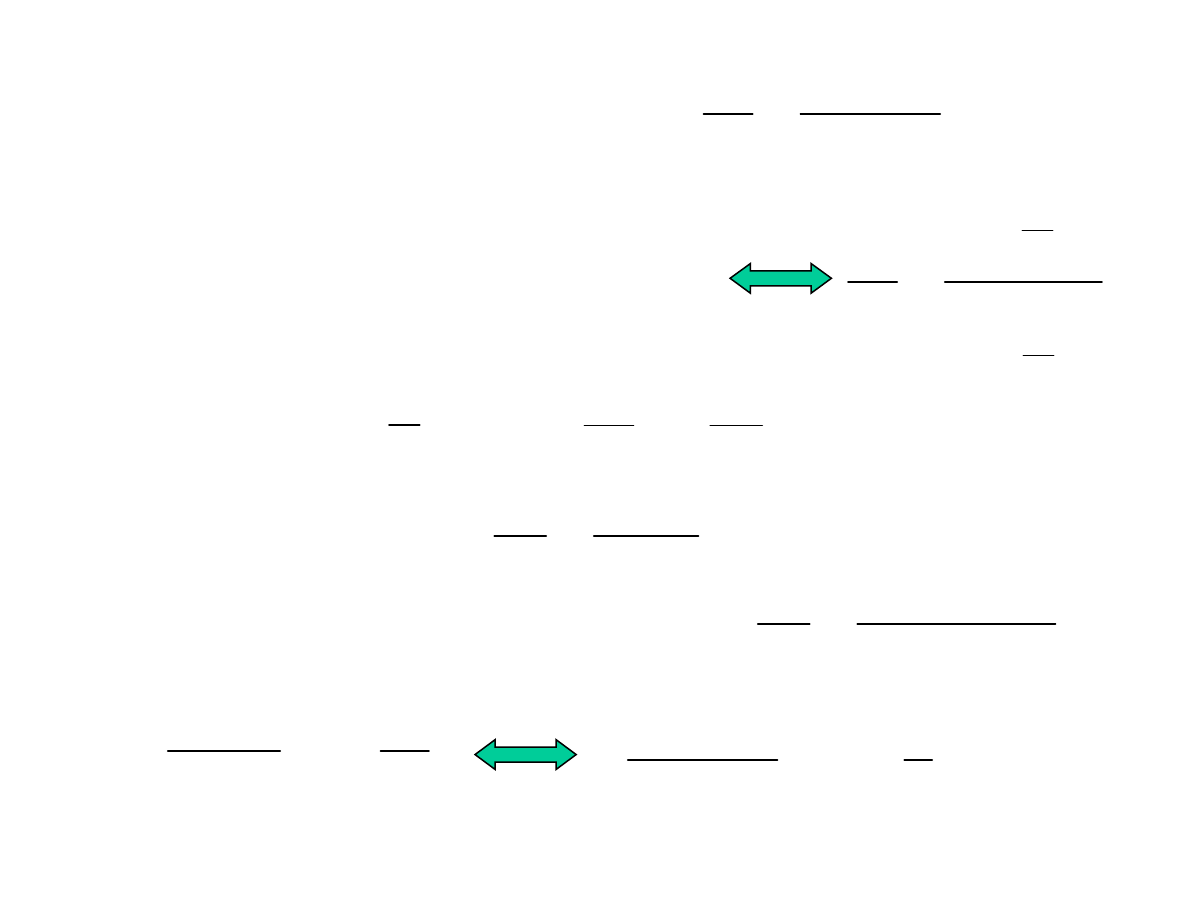
Otrzymujemy równanie różniczkowe postaci:
( )
u
u
f
dx
du
x
−
=
czyli
ux
y =
4
Przykład 2. Rozwiązać równanie
(dotyczące pęku prostych z
poprzedniego wykładu)
Rozwiązanie: Podzielimy licznik i
mianownik po prawej stronie przez x
2
:
Przekształcając prawą stronę mamy:
Dostajemy równanie:
x
dx
du
u
u
u
=
+
−
3
2
1
2
2
2
y
x
xy
dx
dy
−
=
2
1
2
−
=
x
y
x
y
dx
dy
x
y
u =
Wstawiamy
oraz
u
dx
du
x
dx
dy
+
=
u
u
u
dx
du
x
−
−
=
2
1
2
2
3
1
2
u
u
u
u
dx
du
x
−
+
−
=
(
)
∫
∫
=
+
−
dx
x
du
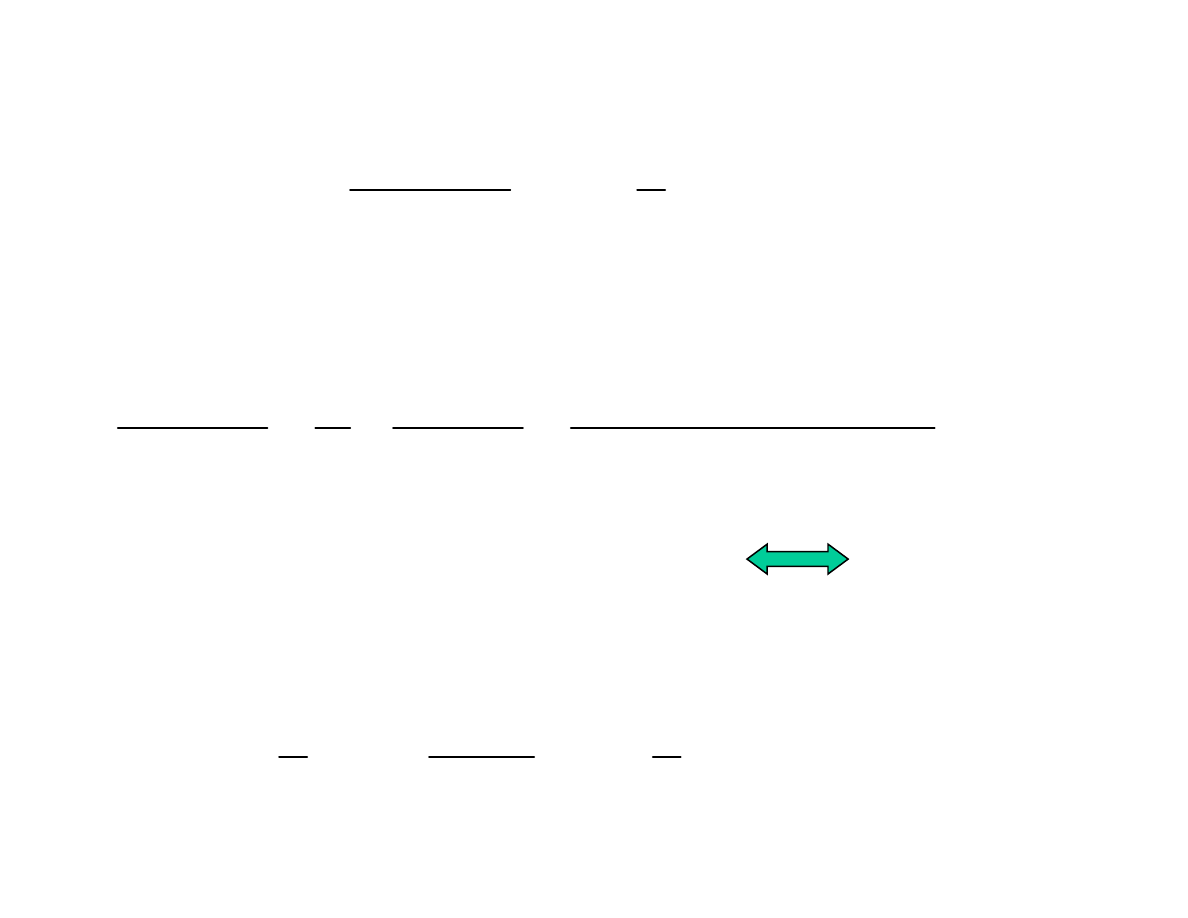
u
u
u
1
1
1
2
2
5
W celu obliczenia całki po lewej stronie dokonujemy
rozbicia funkcji wymiernej na ułamki proste:
∫
∫
=
+
−
dx
x
du
u
u
u
1
)
1
(
1
2
2
Po wstawieniu symbolu całki dostajemy:
(
)
(
)
2
2
2
2
2
2
1
1
1
1
u
u
Cu
Bu
Au
A
u
C
Bu
u
A
u
u
u
+
+
+
+
=
+
+
+
=
+
−
Rozwiązujemy układ:
=
=
−
=
+
1
0
1
A
C
B
A
−
=
=
=
2
1
0
B
A
C
∫
∫
∫
=
+
−
+
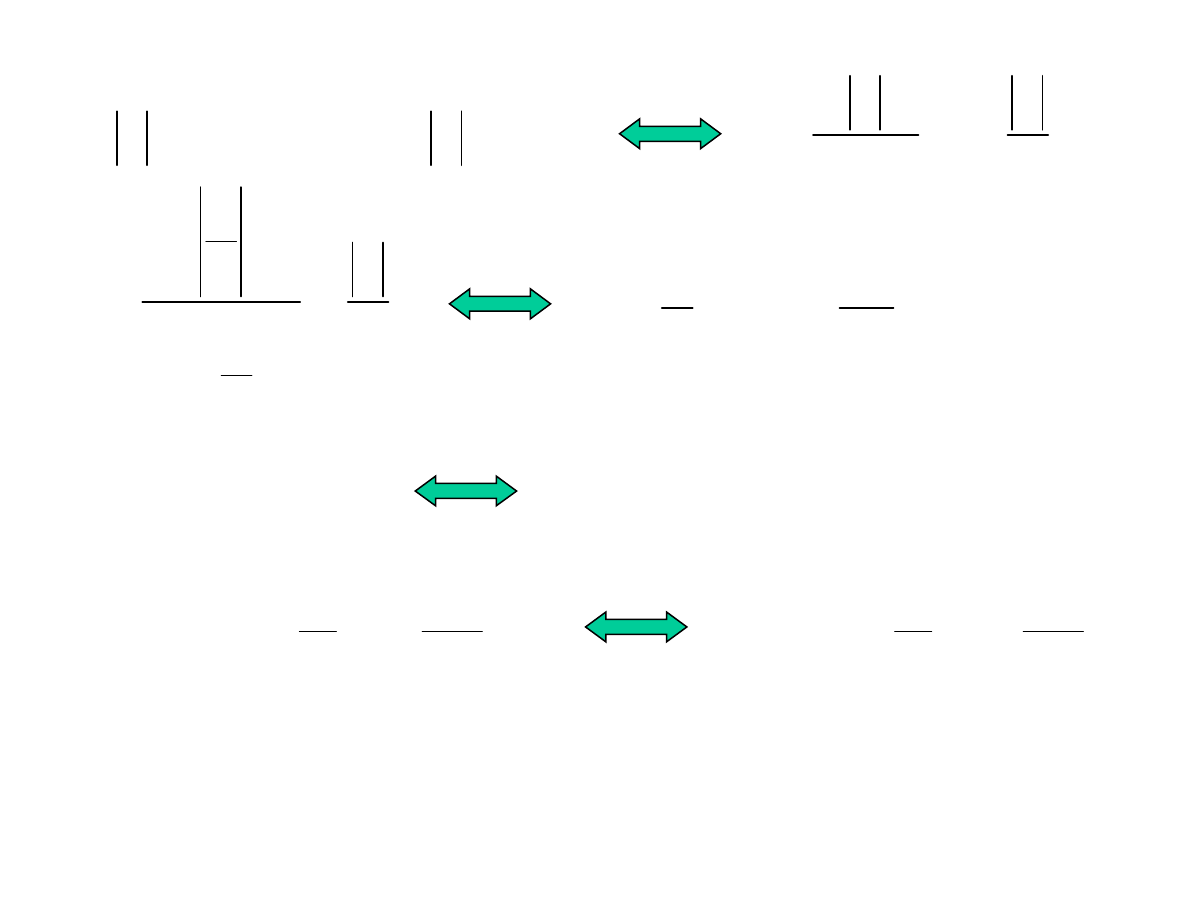
dx
x
du
u
u
du
u
1
1
2
1
2
6
(
)
C
x
u
u
ln
ln
1
ln
ln
2
−
=
+
−
C
x
u
u
ln
1
ln
2
=
+
C
x
x
y
x
y
=
+
2
1
x
x
y
x
x
y
C
⋅
+
=
±
/
1
2
2
2
2
y
x
Cy
+
=
±
0
2
2
=
+
Cy
y
x
m
0
4
2
2
2
2
=
−
+
C
C
y
x
m
4
2
2
2
2
C
C
y
x
=
+
m
Jeśli wstawimy r=C/2, otrzymamy równanie okręgu o
ś
rodku w punkcie (0,±r) i promieniu r, są więc styczne do
osi OX w punkcie (0,0).
7
Jeżeli q(x)=0 wówczas równanie różniczkowe nazywamy
jednorodnym. Jeżeli q(x)≠0 równanie różniczkowe nazywane
jest niejednorodnym.
gdzie p(x) i q(x) są ciągłe w pewnym przedziale, natomiast
y
jest pewną funkcją zależną od x.
Równaniem różniczkowym liniowym I rzędu nazywamy
równanie postaci:
Metoda rozwiązywania równania liniowego rzędu
pierwszego
( )
( )
x
q
y
x
p
y
=
+
′
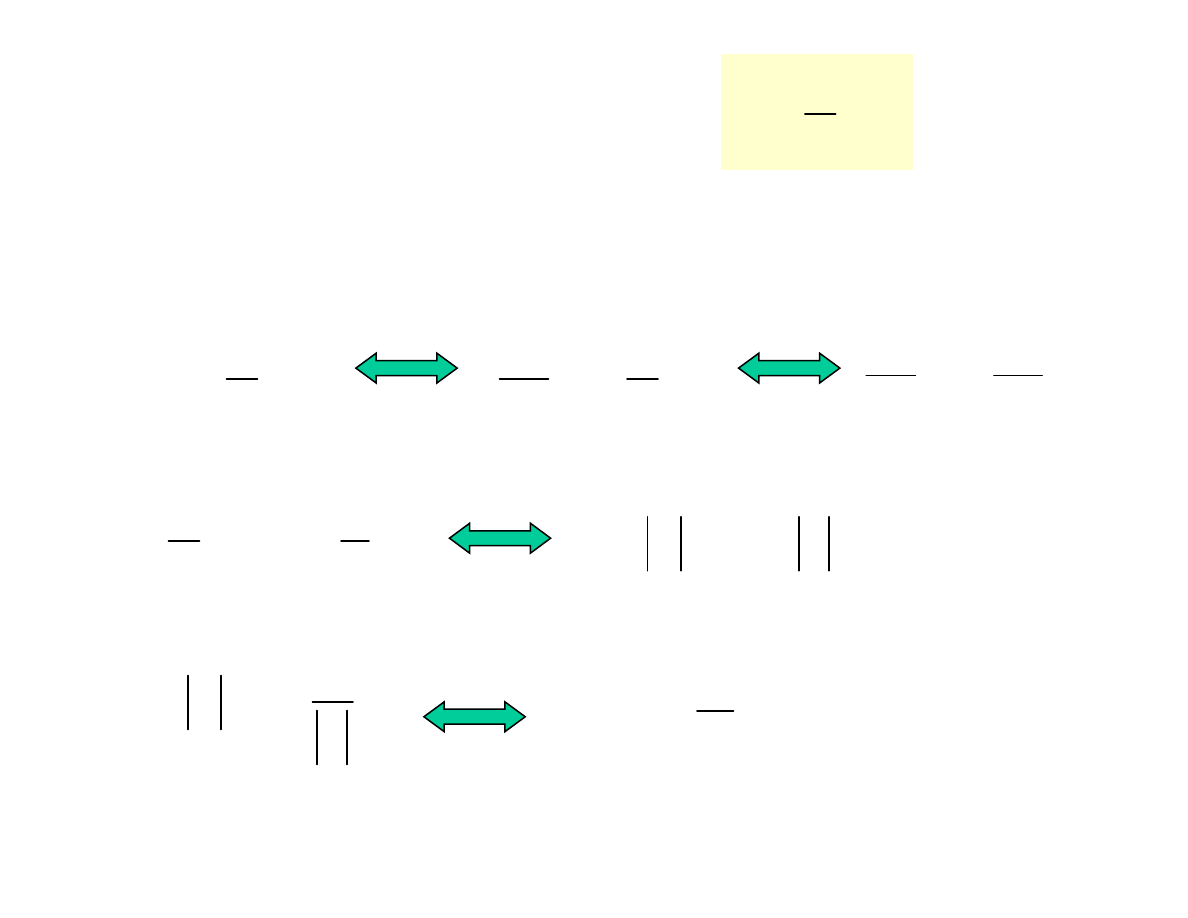
3. Równania różniczkowe liniowe rzędu pierwszego
a) Rozwiązujemy równanie jednorodne y'+p(x)y=0
(równanie różniczkowe o zmiennych rozdzielonych)
b) Uzmienniamy stałą w rozwiązaniu równania
jednorodnego.
8
Przykład 3. Rozwiązać równanie
Rozwiązanie:
a) Rozwiązujemy równanie jednorodne
x
x
y
y
=
+
′
0
=
+
′
x
y
y
x
y
dx
dy
−
=
x
dx
y
dy
−
=
dx
x
dy
y
∫
∫
−
=
1
1
C
x
y
ln
ln
ln
+
−
=
x
C
y
ln
ln
=
( )
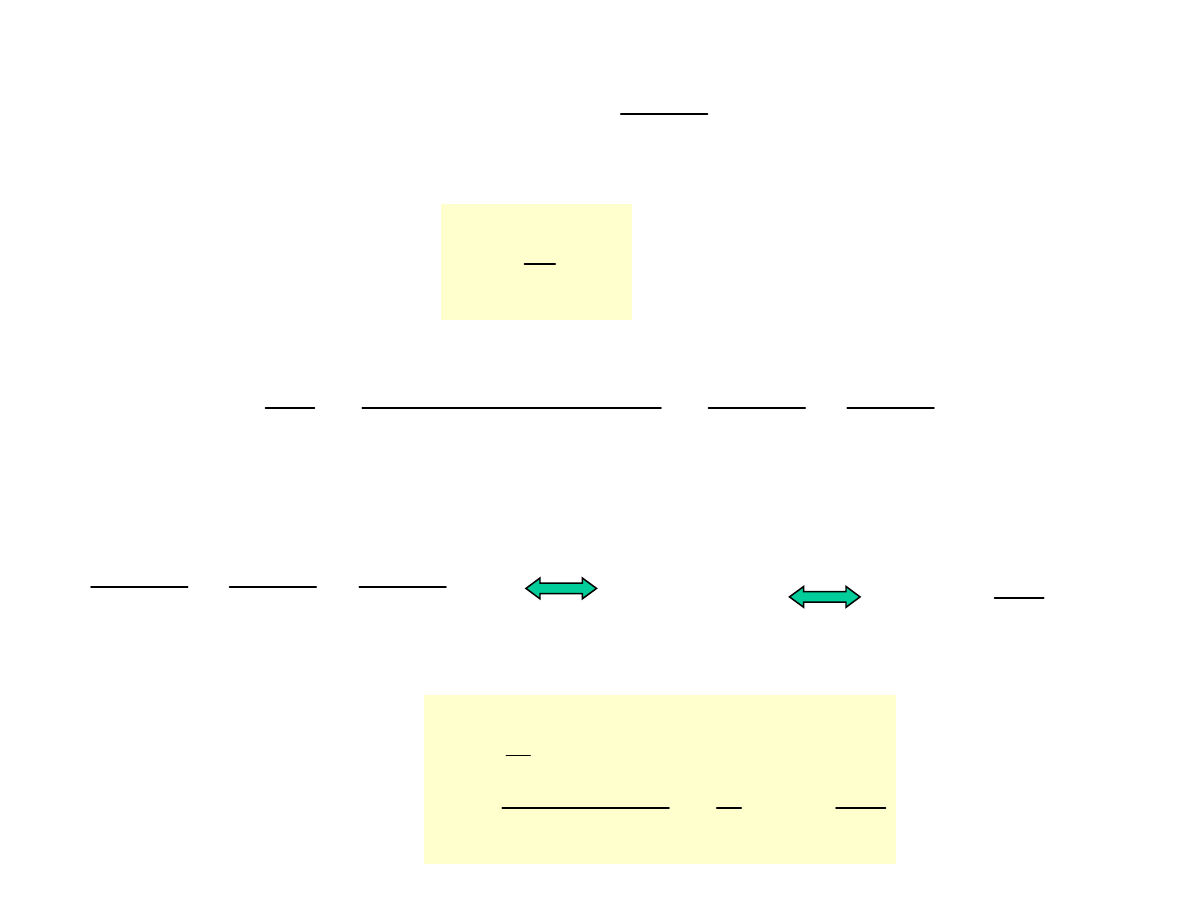
x
C
x
y
=
9
b) Uzmienniamy stałą:
( )
( )
x
x
C
x
y
=
Ponieważ funkcja musi spełniać równanie różniczkowe:
x
x
y
y
=
+
′
obliczamy pochodną (
pochodna ilorazu
):
( )
( )
( )
( )
2
2
1
x
x
C
x
x
C
x
x
C
x
x
C
dx
dy
y
−
′
=
⋅
−
⋅
′
=
=
′
i wstawiamy ją do równania uzyskując:
( )
( )
( )
x
x
x
C
x
x
C
x
x
C
=
+
−
′
2
2
( )
2
x
x
C
=
′
( )
1
3
3
C
x
x
C
+
=
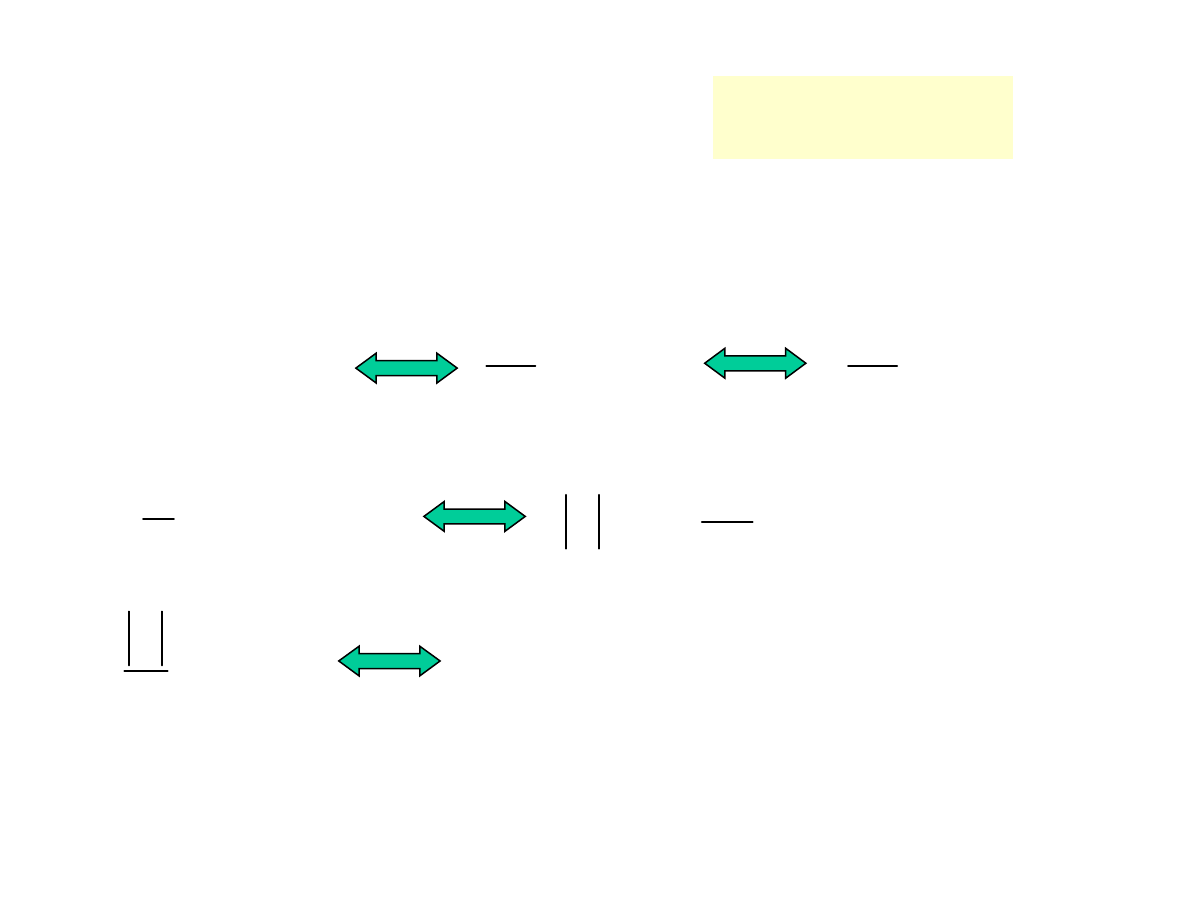
Ostatecznie otrzymujemy rozwiązanie:
x
C
x
x
C
x
y
1
2
1
3
3
1
3
1
+
=
+
=
10
Przykład 4. Rozwiązać równanie
Rozwiązanie:
a) Rozwiązujemy równanie jednorodne
xy
dx
dy
2
−
=
xdx
y
dy
2
−
=
∫
∫
−
=
xdx
dy
y
2
1
2
x
e
C
y
−
=
0
2
=
+
′
xy
y
C
x
C
x
y
ln
ln
2
2
ln
2
2
+
−
=
+
−
=
2
x
Ce
y
−
=
2
2
x
xe
xy
y
−
=
+
′
11
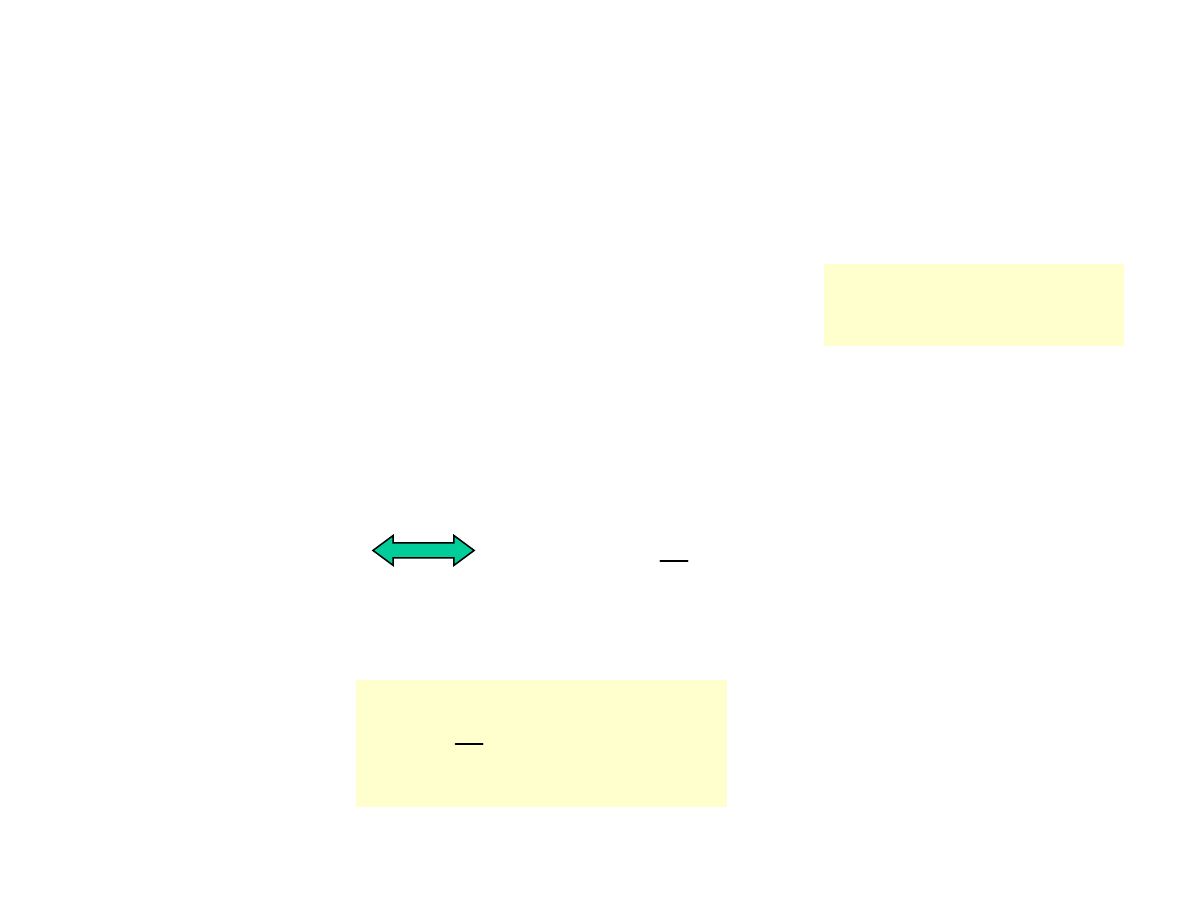
b) Uzmienniamy stałą:
( )
( )
2
x
e
x
C
x
y
−
=
Obliczamy pochodną (
pochodna iloczynu
):
( )
x
x
C
=
′
Ostatecznie otrzymujemy rozwiązanie:
2
1
2
2
1
x
e
C
x
y
−
+
=
Wstawiamy pochodną i funkcję do równania
uzyskując:
2
2
x
xe
xy
y
−
=
+
′
( )
( )
( )
2
2
2
2
2
2
x
x
x
x
xe
e
x
xC
e
x
xC
e
x
C
−
−
−
−
=
+
−
′
( )
( )
( )
(
)
x
e
x
C
e
x
C
x
y
x
x
2
2
2
−
⋅
+
′
=
′
−
−
( )
1
2
2
1
C
x
x
C
+
=
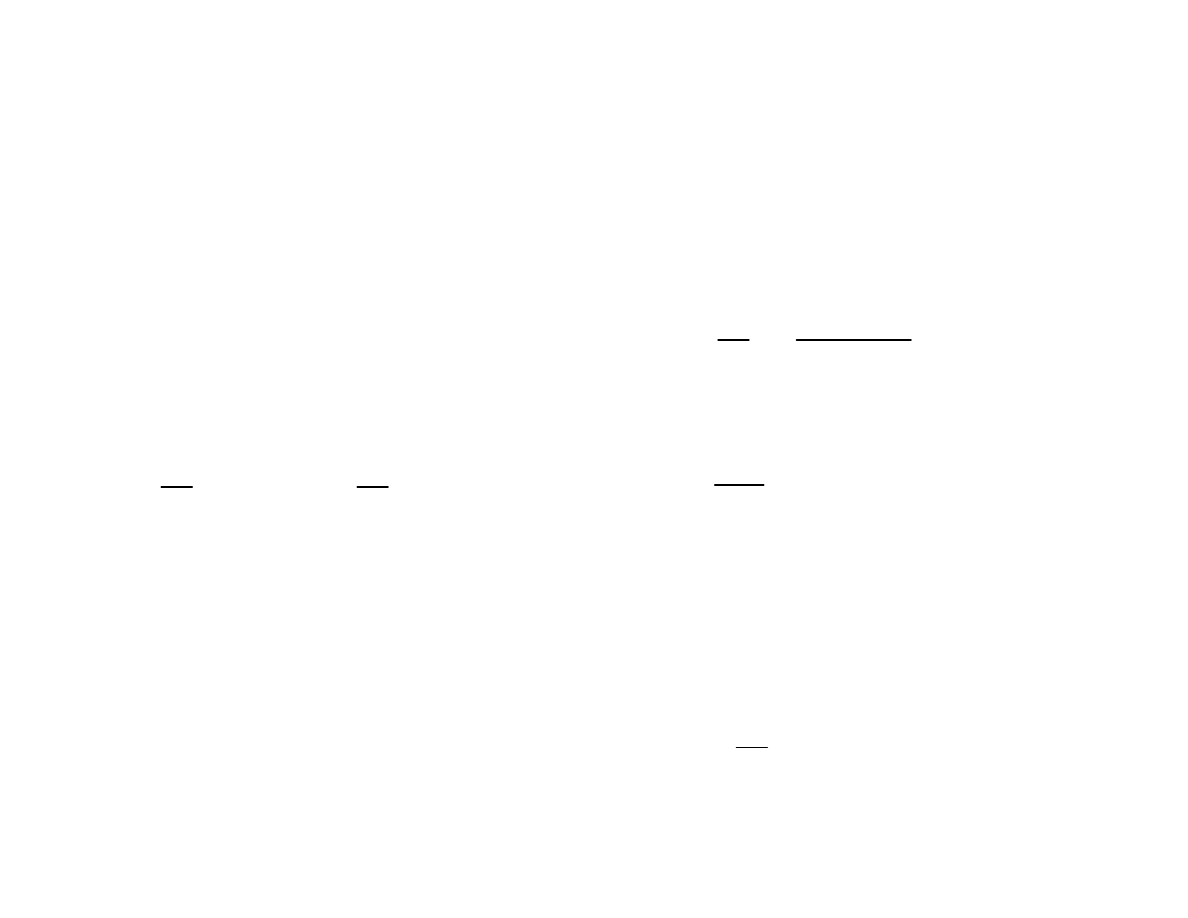
12
Zadania na ćwiczenia:
Rozwiązać równania różniczkowe
(
)
1
.
1
2
+
−
=
′
y
x
y
y
x
x
x
y
y
+
=
−
′
3
.
4
1
3
2
.
2
+
+
=
′
y
x
y
2
2
2
2
.
6
y
x
dx
dy
xy
−
=
2
3
2
.
3
+
=
+
′
x
y
y
0
5
.
5
2
=
+
−
′
−
x
y
y
x
y
x
e
y
y
5
3
5
.
7
=
+
′
x
y
y
3
sin
5
.
8
=
+
′
1
4
3
.
9
+
=
+
′
x
y
y
3
2
.
10
x
x
y
y
=
+
′