1
Wykład XIX:
Całki oznaczone
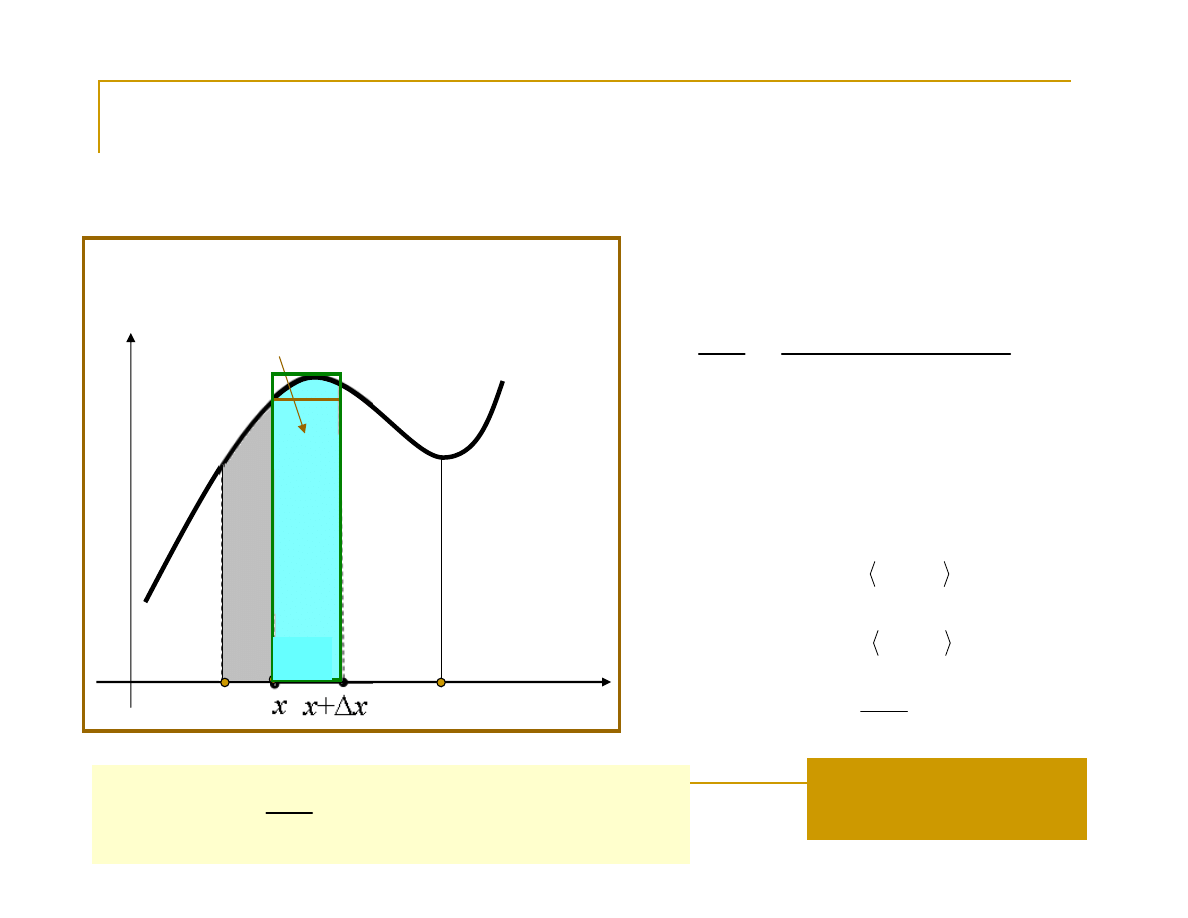
Związek całki oznaczonej z polem
(
)
( )
x
S
x
x
S
S
−
∆
+
=
∆
(
)
( )
x
x
S
x
x
S
x
S
∆
−
∆
+
=
∆
∆
x
M
S
x
m
∆
⋅
≤
∆
≤
∆
⋅
Zauważmy, że
( )
x
f
min
m
x
x
x
∆
+
=
,
gdzie
( )
x
f
M
x
x
x
max
,
∆
+
=
M
x
S
m
≤
∆
∆
≤
( )
( )
( )
( )
x
f
x
S
x
f
x
S
x
f
lim
x
=
′
⇔
≤
∆
∆
≤
→
∆
0
( )
( )
∫
=
dx
x
f
x
S
czyli
x
∆
x
+∆x
y=f
(x)
∆S
S(x)
a
b
x
m
M
∆x
2
( )
( )
c
x
F
x
S
+
=
( )
( )
c
a
F
a
S
+
=
( )
( )
a
F
c
c
a
F
−
=
⇒
+
=
0
( )
( )
( )
( )
( )
.
a
F
b
F
b
S
c
b
F
b
S
−
=
⇒
+
=
( )
( )
( )
( )
a
F
b
F
x
F
dx
x
f
b
a
b
a
−
=
=
∫
Ponadto
Ostatecznie
3
(
)
62
6
68
2
4
2
4
4
4
4
1
4
4
4
2
4
4
2
3
=
−
=
+
−
+
=
+
=
+
∫
x
x
dx
x
(
)
=
+
∫
1
0
5
4 dx
x
=
=
+
du
dx
u
x
4
5
1
4
0
=
⇒
=
=
⇒
=
u
x
u
x
6
4
6
5
6
6
6
5
4
6
5
4
5
−
=
=
=
∫
u
du
u
Przykłady:
{dokonujemy podstawienia}
Przy podstawieniu nowej zmiennej,
zmieniają się granice całkowania

4
Własności całki oznaczonej:
( )
( )
∫
∫
=
⋅
b
a
b
a
dx
x
f
c
dx
x
f
c
( )
( )
(
)
( )
( )
∫
∫
∫
±
=
±
b
a
b
a
b
a
dx
x
g
dx
x
f
dx
x
g
x
f
( )
( )
( )
(
)
b
a
c
dla
dx
x
f
dx
x
f
dx
x
f
b
c
c
a
b
a
,
∈
+
=
∫
∫
∫
( )
( )
∫
∫
−
=
a
b
b
a
dx
x
f
dx
x
f
5
Zastosowanie całek do liczenia pól
( )
0
≥
x
f
( )
∫
b
a
dx
x
f
Jeżeli
wówczas
jest równa polu zawartemu pomiędzy
funkcją
f
(x),
osią OX oraz prostymi
x=a
i
x=b
.
6
( )
( )
[
]
π
π
−
=
=
∫
0
0
x
cos
dx
x
sin
S
( )
( )
2
1
1
0
=
+
=
+
π
−
=
cos
cos
S
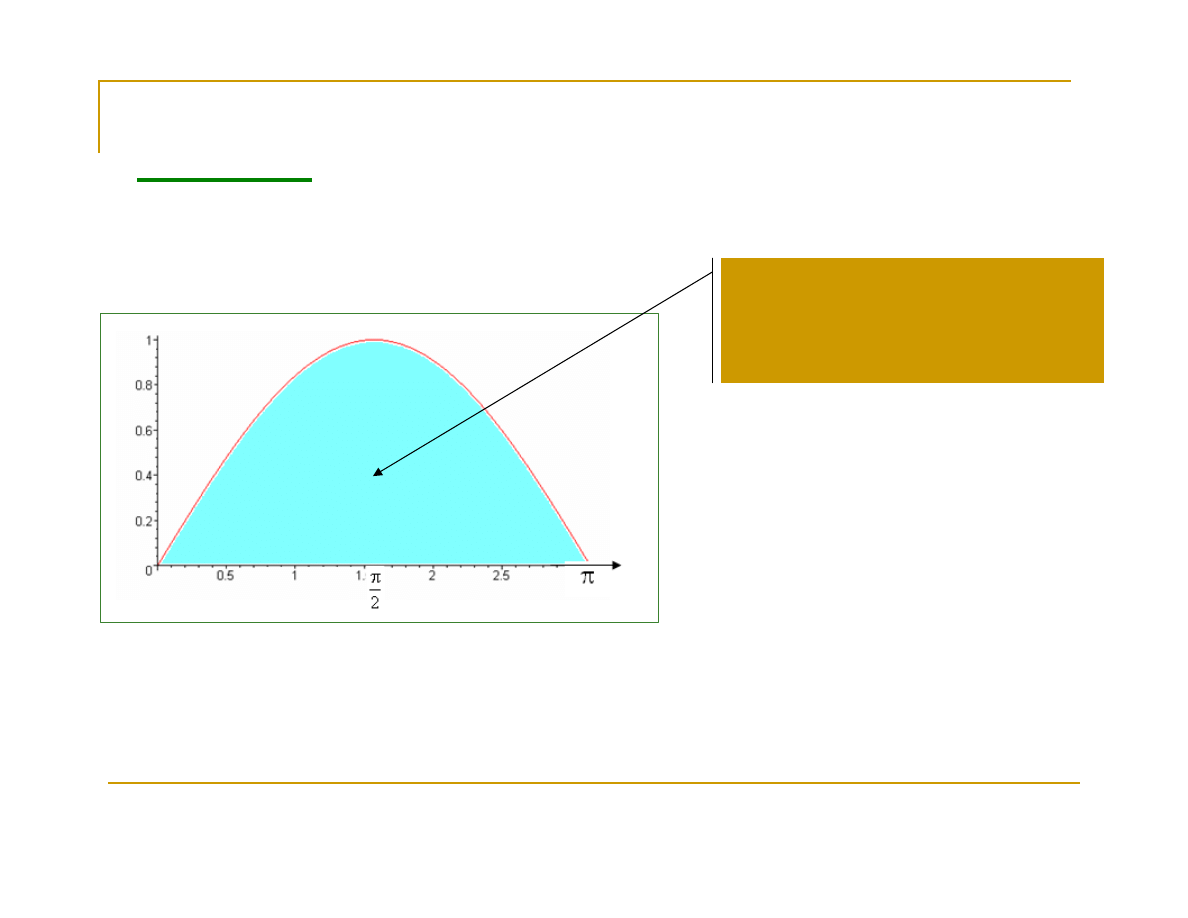
Przykład:
Obliczyć pole zawarte pomiędzy
sinusoidą i osią OX w przedziale (0,π).
Obliczamy
zamalowane pole
7
( )
[
]
( )
∫
∫
−
=
−
=
b
a
b
a
dx
x
f
dx
x
f
S
( )
0
≤
x
f
Jeżeli
wówczas pole zawarte pomiędzy funkcją f(x), osią OX
oraz prostymi x=a i x=b wynosi
4
5
2
+
−
=
x
x
y
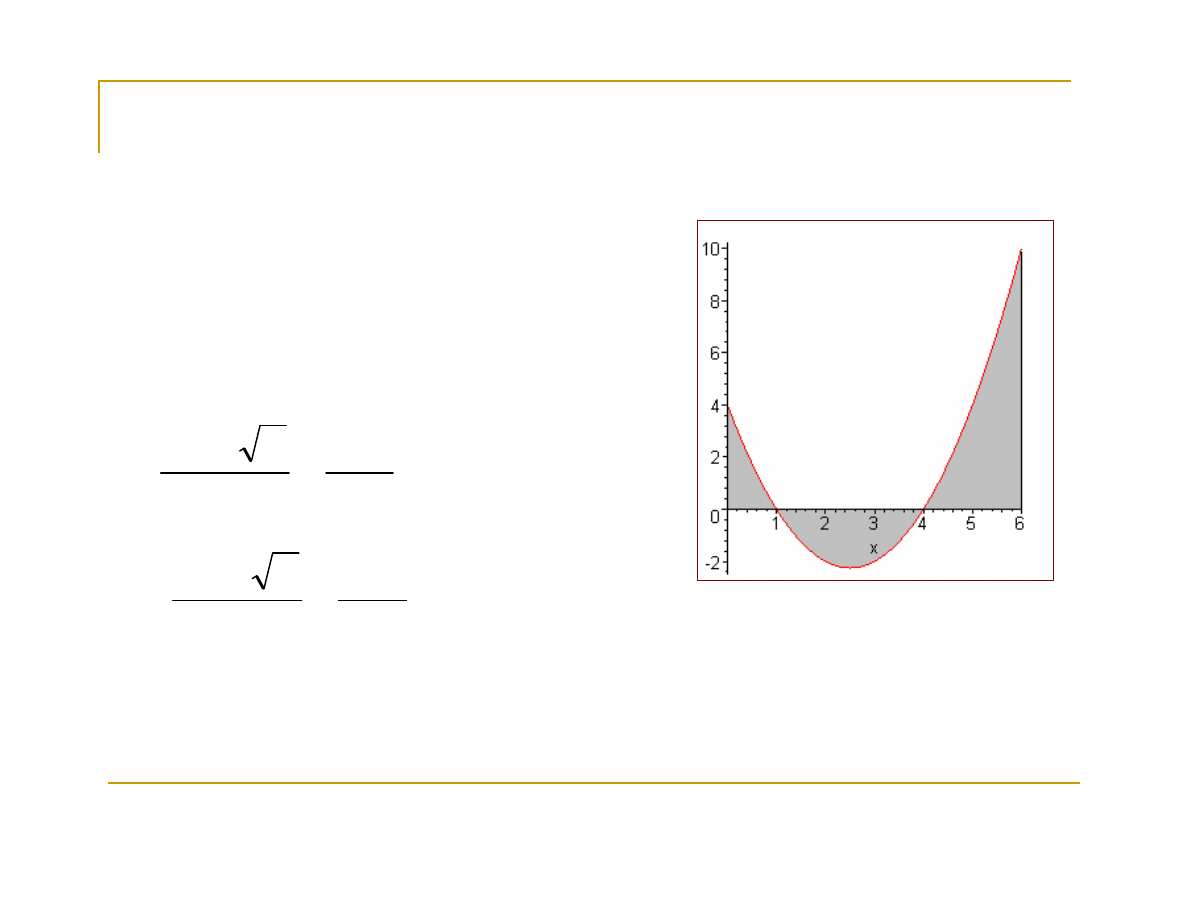
Przykład:
Obliczyć pole zawarte pomiędzy parabolą
i osią OX w przedziale (0,6).
8
Rozwiązanie:
0
4
5
2
=
+
− x
x
(
)
9
16
25
4
1
4
5
4
2
2
=
−
=
⋅
⋅
−
−
=
−
=
∆
ac
b
Szukamy punktów przecięcia paraboli z osią OX
1
2
3
5
2
1
=
−
=
∆
−
−
=
a
b
x
4
2
3
5
2
2
=
+
=
∆
+
−
=
a
b
x
(
)
(
)
(
)
∫
∫
∫
+
−
+
+
−
−
+
−
=
4
1
6
4
2
2
1
0
2
4
5
4
5
4
5
dx
x
x
dx
x
x
dx
x
x
S

9
+
−
−
+
−
+
16
2
4
5
3
4
24
2
6
5
3
6
2
3
2
3
+
+
⋅
−
−
+
−
−
−
+
⋅
−
=
4
2
1
5
3
1
16
2
4
5
3
4
0
4
2
1
5
3
1
2
3
S
6
4
2
3
4
1
2
3
1
0
2
3
4
2
5
3
4
2
5
3
4
2
5
3
+
−
+
+
−
−
+
−
=
x
x
x
x
x
x
x
x
x
S
6
26
6
36
32
22
6
144
540
432
6
96
240
128
2
6
24
15
2
2
=
=
+
−
+
−
+
+
−
⋅
−
+
−
⋅
=
S
10
( )
( )
( )
( )
[
]
∫
∫
∫
−
=
−
=
b
a
b
a
b
a
dx
x
g
x
f
dx
x
g
dx
x
f
S
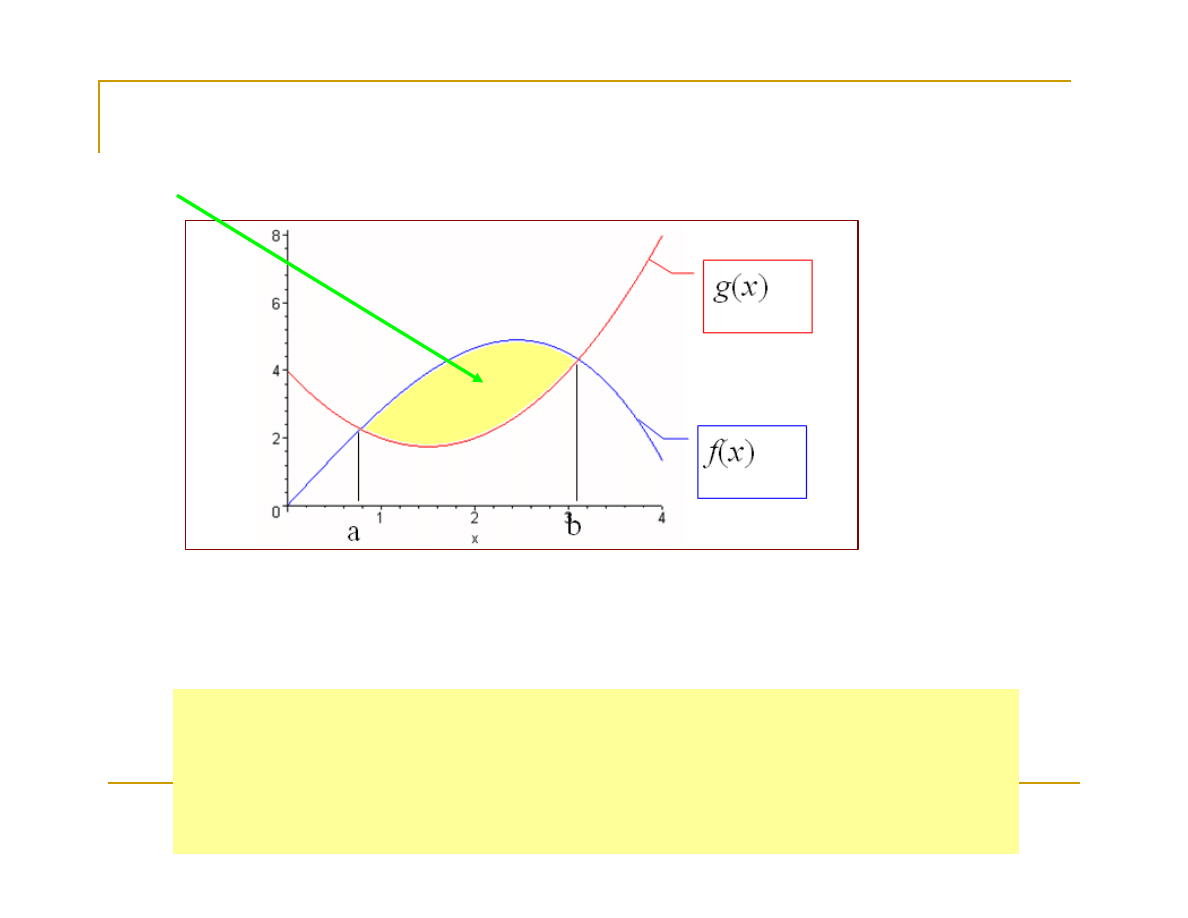
Uwaga.
Przy pomocy całki oznaczonej liczymy także
miarę pola
pomiędzy dowolnymi funkcjami y=f(x) i y=g(x).
W celu obliczenia pola pomiędzy funkcjami, musimy
wyznaczyć punkty przecięcia się wykresów a następnie
obliczyć:
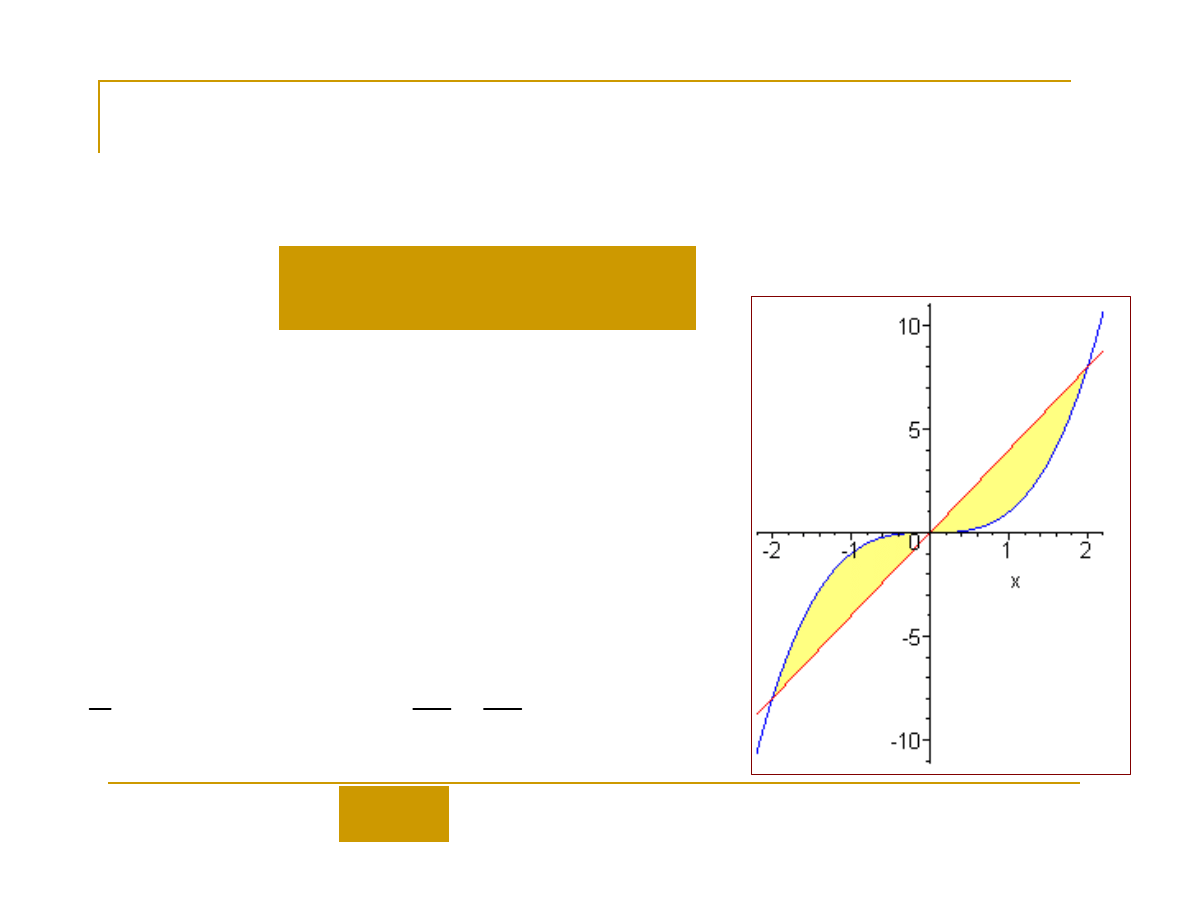
11
Przykład
3
4
x
y
i
x
y
=
=
Obliczyć pole zawarte pomiędzy funkcjami:
Rozwiązanie:
0
4
4
4
3
3
3
=
−
⇔
=
⇔
=
=
x
x
x
x
x
y
x
y
(
)
(
)(
)
0
2
2
0
4
2
=
+
−
⇔
=
−
x
x
x
x
x
2
2
0
−
=
∨
=
∨
=
x
x
x
(
)
4
4
8
4
2
4
4
2
1
2
0
4
2
2
0
3
=
−
=
−
=
−
=
∫
x
x
dx
x
x
S
8
=
S
Ostatecznie:

12
Zadania na ćwiczenia
(
)
∫
−
2
1
4
1
2
)
dx
x
b
∫
1
0
2
)
dx
xe
a
x
∫
e
dx
x
x
ln
c
1
4
)
1. Obliczyć wartości całek oznaczonych:
2. Obliczyć wartości pól zawartymi pomiędzy wykresami
funkcji:
2
)
2
2
+
−
=
=
x
y
i
x
y
a
OX
osią
i
x
y
x
x
y
b
=
−
=
;
2
)
2
2
2
)
2
+
−
=
+
−
=
x
y
i
x
x
y
c
4
1
;
)
=
=
=
x
i
x
y
x
y
d
6
5
)
+
−
=
=
x
y
i
x
y
e
Wyszukiwarka
Podobne podstrony:
Mat WIP Wyk ad22
Mat WIP Wyk ad23
Mat WIP Wyk ad25
Mat WIP Wyk ad26
IiE, Mat Statystyka,Wyk 4
Mat Bud wyk 07
Mat Bud wyk 09
Mat Stat Wyk 8 PrzedziaĹ y(2013L)
Mat Bud wyk 03
Mat WIP Wykład21
Mat Bud wyk 02
mat konstr wyk, PKM egzamin kolosy ( łukasik, Salwiński )
Mat WIP Wykład16
więcej podobnych podstron