
Mat. Statystyka.Wykład 8. (2013 L) R. Rempała. Materiały dydaktyczne
1
Przedziały ufności
Definicja przedziału ufności
Przykłady konstrukcji przedziałów ufności
Przedziały ufności dla wartości oczekiwanej
Przedziały ufności dla wariancji
Przedziały ufności dla ilorazu wariancji

Mat. Statystyka.Wykład 8. (2013 L) R. Rempała. Materiały dydaktyczne
2
Definicja przedziału ufności
Zajmowaliśmy się punktową estymacją nieznanego
parametru rozkładu. Obecnie zajmiemy się tzw. estymacją
przedziałową określając górną i dolną granicę oszacowania.
Niech
n
1
X
,
,
X
będzie próbą prostą pochodzącą z
populacji, w której cecha X ma rozkład typu ciągłego,
zależny od nieznanego parametru
. Niech
oznacza
małą liczbę z przedziału (0,1).
Definicja. Niech
)
(
g
będzie estymowana wielkością.
Rozważmy dwie statystyki g
1
(
n
1
X
,
,
X
) i g
2
(
n
1
X
,
,
X
).
Mówimy, że losowy przedział [g
1
(
n
1
X
,
,
X
), g
2
(
n
1
X
,
,
X
)]
jest przedziałem ufności dla wielkości
)
(
g
na poziomie
ufności
1
jeśli
1
)]
X
,
,
X
(
g
)
(
g
)
X
,
,
X
(
g
[
P
n
1
2
n
1
1
. (*)
Jako poziom ufności najczęściej przyjmuje się
1
= 0,95
lub
1
= 0,99.
Komentarz do definicji przedziału ufności
Krańce przedziału ufności są zmiennymi losowymi. Zależą od
obserwowalnych zmiennych losowych.
Zauważmy także, że
)
(
g
jest stałą wielkością. Zatem (*)
należy rozumieć tak: losowy przedział
[g
1
(X
1
,…X
n
), g
2
((X
1
,…X
n
)]
z prawdopodobieństwem
1
pokrywa nieznaną wielkość
)
(
g
.

Mat. Statystyka.Wykład 8. (2013 L) R. Rempała. Materiały dydaktyczne
3
Innymi słowy, biorąc pod uwagę częstościową definicję
prawdopodobieństwa, można powiedzieć tak: w dużej serii
próbek częstość zdarzenia polegającego na tym, że realizacje
przedziałów ufności pokrywają nieznaną wartość parametru
)
(
g
jest w przybliżaniu równa (
%.
100
)
1
Uwaga. Przy konkretnej realizacji próby losowej x
1
,x
2
,...,x
n
krańce przedziału ufności są dokładnie wyznaczonymi
konkretnymi wielkościami. Nie ma wtedy sensu stwierdzenie,
że wielkość
)
(
g
znajdzie się w takim przedziale z
prawdopodobieństwem
1
.
Ogólna metoda konstrukcji przedziału ufności. (por. A.
Plucińska…)
Przy konstrukcji przedziałów, postępuję się najczęściej
następująco.
Wybiera się taki estymator
)
X
,
…
,
X
(
gˆ
n
1
wielkości
)
(
g
,
którego rozkład asymptotyczny lub dokładny jest znany.
Dla danego poziomu ufności
1
poszukuje się takich
stałych
1
,
2
, dla których
P (
1
1
)
u
~
)
X
,...,
X
,
(X
gˆ
2
n
2
1
(*)
W przypadku, gdy nierówność
1
2
n
1
u
~
)
X
,...,
X
(
gˆ
daje
się zastąpić równoważną nierównością postaci
f
1
(
)
X
,...,
X
(
gˆ
n
1
)
)
(
g
f
2
(
)
X
,...,
X
(
gˆ
n
1
)
stąd po podstawieniu:
g
1
(X
1
,…X
n
) = f
1
(
)
X
,...,
X
(
gˆ
n
1
),
g
2
(X
1
,…X
n
) = f
2
(
)
X
,...,
X
(
gˆ
n
1
),

Mat. Statystyka.Wykład 8. (2013 L) R. Rempała. Materiały dydaktyczne
4
otrzymujemy przedział [g
1
(X
1
,…X
n
),g
2
((X
1
,…X
n
)], który jest
przedziałem ufności nieznanej wielkości
)
(
g
na poziomie
ufności
1
.
Ponieważ dla ustalonego poziomu ufności
1
, liczby
1
i
2
w równości (*) można wybierać na wiele
sposobów, zazwyczaj wybiera się je w taki sposób, aby
2
/
)
u
~
)
X
,...,
X
,
(X
gˆ
(
P
)
u
~
)
X
,...,
X
,
(X
gˆ
(
P
2
n
2
1
1
n
2
1
Przypadek cechy skokowej
Jeśli cecha badana X ma rozkład skokowy, to liczby
1
,
2
spełniające równość (*) mogą nie istnieć. Dlatego też w
sytuacji, gdy próba pochodzi z rozkładu skokowego
przedziałem ufności na poziomie
1
dla wielkości
)
(
g
nazywa się taki przedział losowy[g
1
(X
1
,..
,X
n
), g
2
(X
1
,..
,X
n
],
dla którego spełniona jest nierówność
1
)]
X
,
,
X
(
g
)
(
g
)
X
,
,
X
(
g
[
P
n
1
2
n
1
1
.
Zatem liczby
1
i
2
spełniają warunki:
2
/
)
u
~
)
X
,...,
X
,
(X
gˆ
(
P
1
n
2
1
2
/
)
u
~
)
X
,...,
X
,
(X
gˆ
(
P
2
n
2
1
Przykłady konstrukcji przedziałów ufności
1. Przedziały ufności dla wartości oczekiwanej
Przypadek a).
Niech
n
1
X
,
,
X
będzie próbą losową z rozkładu
N(
,
) o
nieznanym
, znanym
. Estymujemy
. Jako estymator
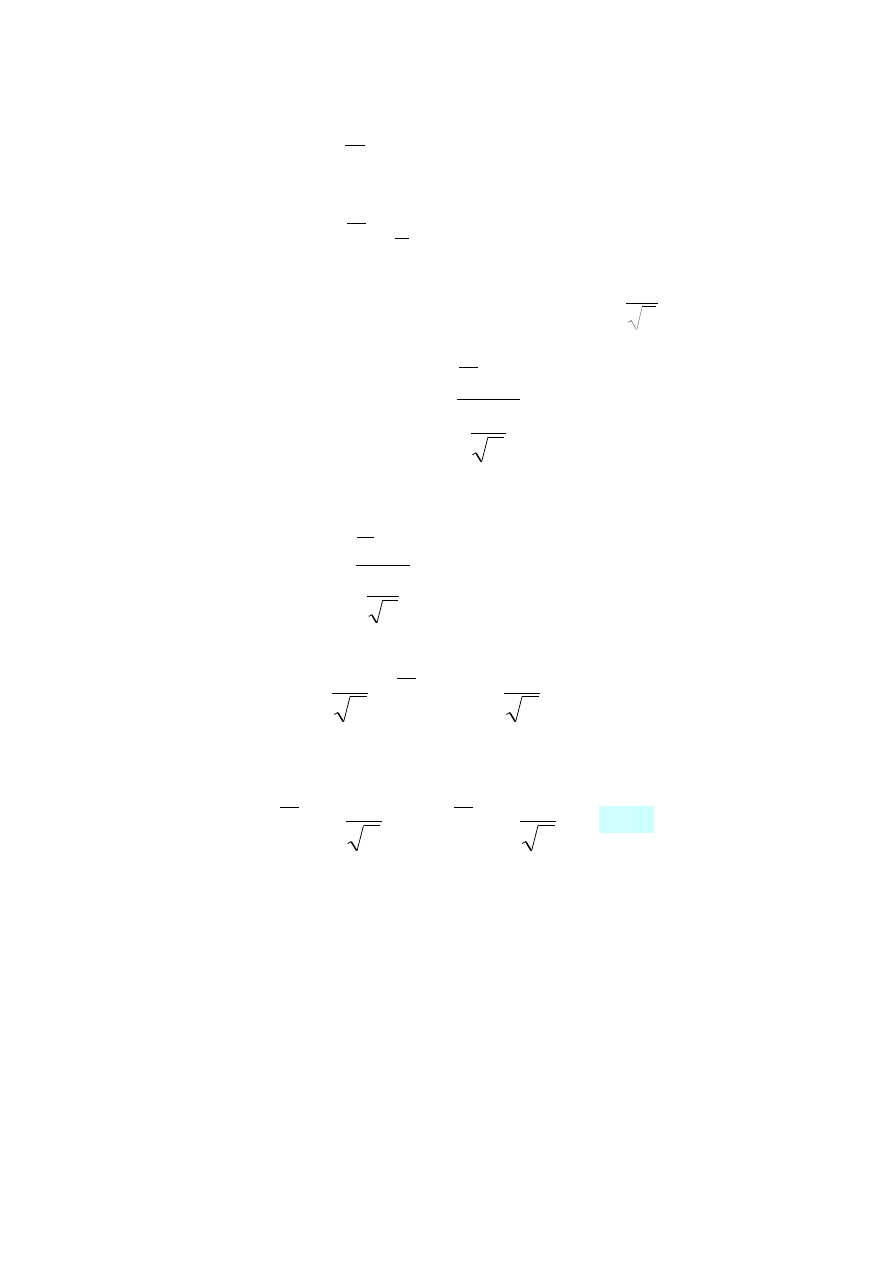
Mat. Statystyka.Wykład 8. (2013 L) R. Rempała. Materiały dydaktyczne
5
nieznanego
parametru
wybieramy
)
X
,...,
X
(
ˆ
n
1
(1/n)(X
1
+…+X
n
)=
X
Wiadomo, że średnia
X
n
1
i
i
X
n
1
z próby losowej pochodzącej
z rozkładu N(
,
) ma rozkład normalny N(
,
n
)
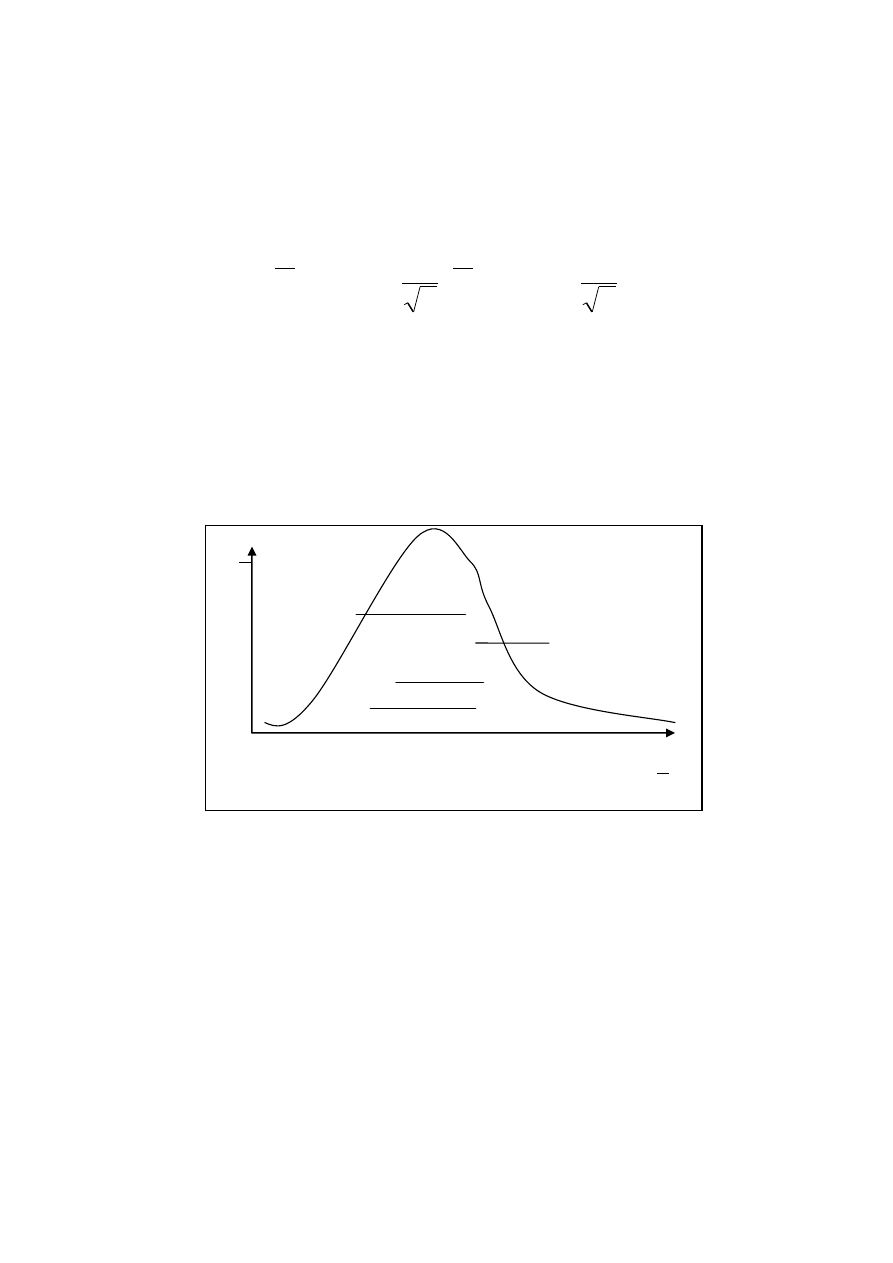
Zatem standaryzowana średnia
n
X
ma rozkład N(0,1).
Dla ustalonego poziomu ufności 1-
możemy więc
wyznaczyć taką wielkość u~ , że dla
1
=
u~ ,
2
=
u
~
1
)
u
~
n
X
u
~
(
P
(**)
co oznacza, że
.
1
)
n
u
~
X
n
u
~
(
P
Stąd otrzymujemy
}
n
u
~
X
n
u
~
X
{
P
=
1
Z zapisu (**) wynika, że u~ jest kwantylem rzędu 1
2
/
z
rozkładu N(0,1). Przyjmijmy wygodniejsze oznaczenie
u
~ =
2
/
1
u
.
Kwantyle rozkładu N(0,1) są podawane w tablicach
statystycznych.
(Przypominamy. Ogólnie: kwantylem rzędu p z rozkładu
Mat. Statystyka.Wykład 8. (2013 L) R. Rempała. Materiały dydaktyczne
6
o dystrybuancie ciągłej F nazywamy taką wartość
p
u
, że
F(
p
u
) = p, p
)).
1
,
0
(
Tak wiec przedział
]
n
u
X
,
n
u
X
[
2
/
1
2
/
1
jest przedziałem losowym, który z prawdopodobieństwem 1-
pokrywa nieznaną wartość oczekiwaną rozkładu. Zatem,
zgodnie z definicją, jest on przedziałem ufności dla wartości
oczekiwanej na poziomie ufności
1
.
Częstościowa interpretacja przedziałów ufności dla średniej
Rys. 1. Przykłady przedziałów dla
. Spodziewamy się, że około
(1-
)100% przedziałów pokrywa nieznaną wartość
(interpretacja
rysunku na wykładzie).
Przykład.1. Załóżmy, że waga proszku do prania w pudełku, które napełniane
jest automatycznie jest zmienną losową o rozkładzie normalnym.
Dokonano nowego ustawienia automatu dozującego proszek do prania, tak że
wartość oczekiwana wagi zawartości pudełka przy nowym ustawieniu nie jest
znana. W celu jej oszacowania pobrano próbę prostą -10 pudełek - uzyskując
następujące wyniki podane w gramach: 605, 601, 605, 599, 602, 597, 602, 603,
602, 600. Wyznacz realizację przedziału ufności dla średniej wagi w nowym
f
(
x
)
|
x
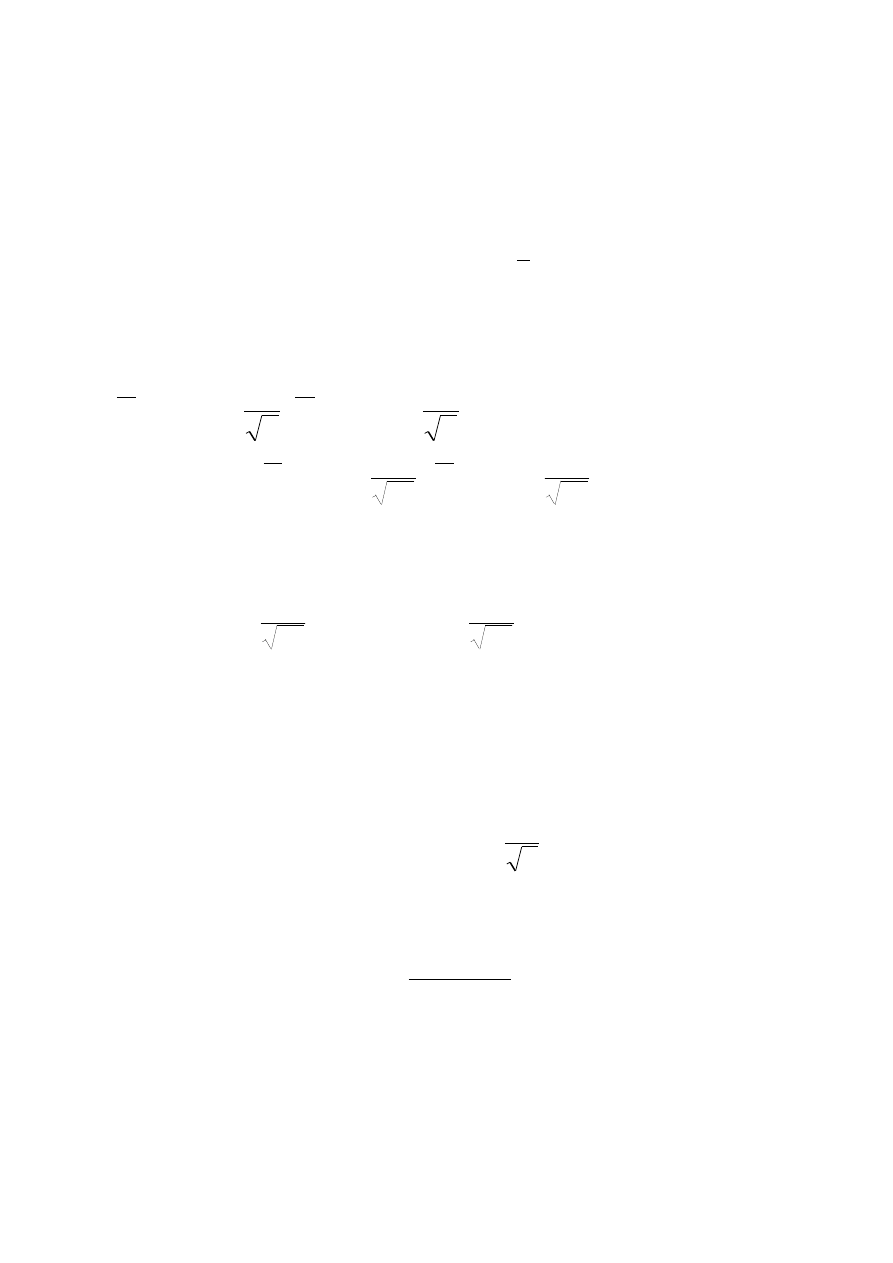
Mat. Statystyka.Wykład 8. (2013 L) R. Rempała. Materiały dydaktyczne
7
ustawieniu przy współczynniku ufności 0.95 przyjmując, że odchylenie
standardowe wagi proszku wynosi 2.4 g.
Dane: n=10,
= 2.4,
05
.
0
.
Założenia. Badana cecha ma rozkład normalny N(
,2.4).
Estymujemy parametr
.
Wyliczenia:
,
6
.
601
x
Odczyt z tablicy rozkłady normalnego N(0,1) :
96
.
1
u
025
.
0
1
Podstawiając dane do wzoru na przedział ufności dla
]
n
u
X
,
n
u
X
[
2
/
1
2
/
1
Otrzymujemy
[
X
– 1.96
10
4
.
2
,
X
+ 1.96
10
4
.
2
].
W tym przykładzie mamy następującą realizację przedziału ufności na
poziomie 0.95
[601.6 – 1.96
10
4
.
2
, 601.6 + 1.96
10
4
.
2
]
[600.11,603.09]
Estymacja z zadaną precyzją. Przypadek a)
Niech 2d oznacza długość przedziału ufności na poziomie
1
dla parametru
w rozważanym modelu.
Zatem
2d = 2
n
u
2
/
1
Stąd wynika, że
n
2
2
2
d
u
2
/
1
.
Jeśli badacz może ustalać rozmiary próby (wielkość n), to
dla otrzymania przedziału ufności o zadanej długości, która
nie przekracza 2d (zadanej precyzji ), wystarczy rozważać
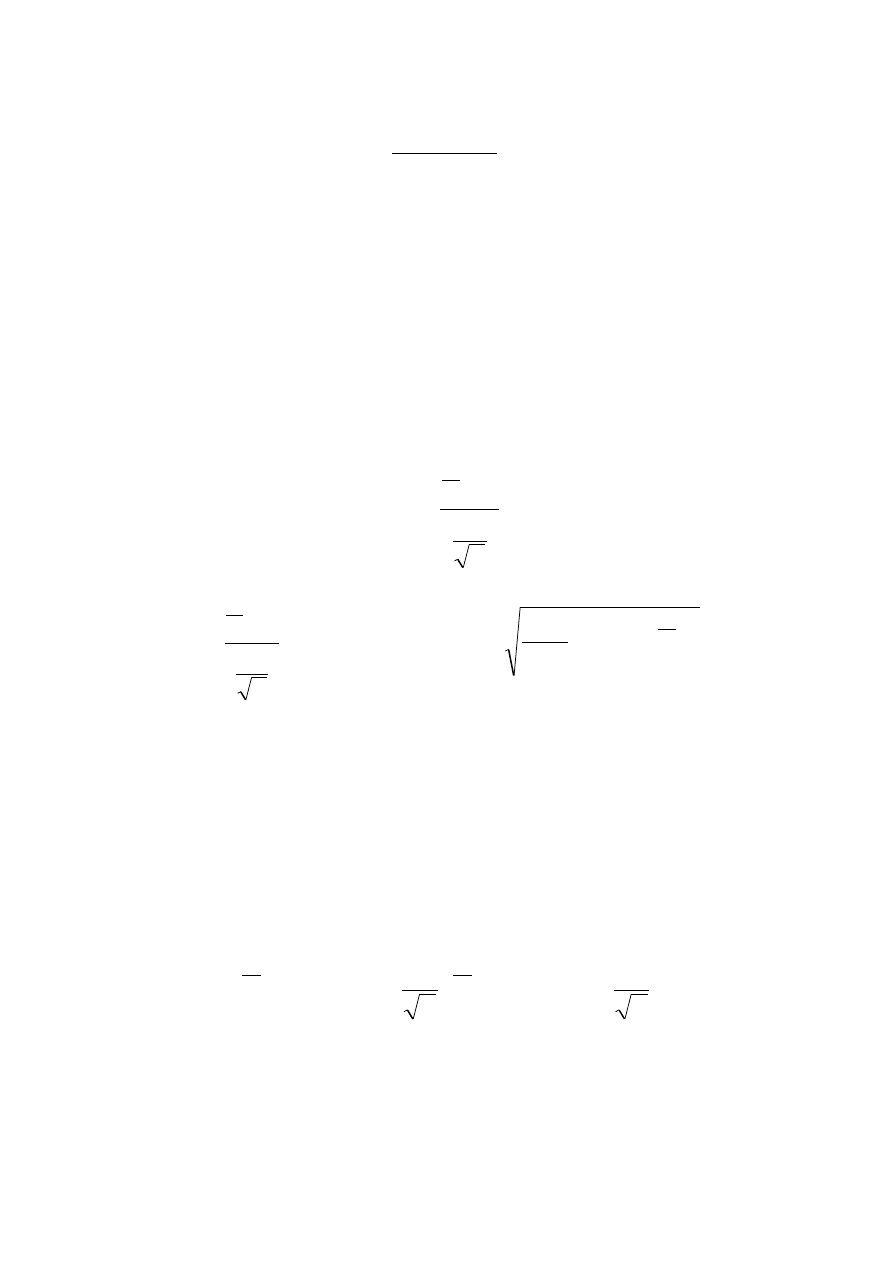
Mat. Statystyka.Wykład 8. (2013 L) R. Rempała. Materiały dydaktyczne
8
próby o rozmiarze n
2
2
2
d
u
2
/
1
. Mówimy wówczas o
estymacji z zadaną precyzją.
Przypadek 2. Populacja normalna N(
,
), nieznane
,
nieznane
Niech
n
1
X
,
,
X
będzie próbą losową z tego rozkładu.
Przy konstrukcji przedziału ufności zamiast statystyki
n
X
U
stosuje się statystykę
n
s
X
t
gdzie
2
n
1
i
i
)
X
X
(
1
n
1
S
Statystyka ta ma rozkład t-Studenta z (n-1) stopniami
swobody (por. definicji rozkładu t-Studenta). Postępując
podobnie jak w przypadku statystyki U, konstruujemy
przedział ufności dla średniej
na zadanym poziomie ufności
1
(dokładną konstrukcję zostawiamy jako ćwiczenie).
W tym przypadku otrzymujemy przedział
]
n
S
t
X
,
n
S
t
X
[
1
n
,
2
/
1
1
n
,
2
/
1
gdzie
1
n
,
2
/
1
t
jest kwantylem rzędu 1-
2
/
z rozkładu
t-Studenta o (n-1) stopniach swobody (kwantyle dla
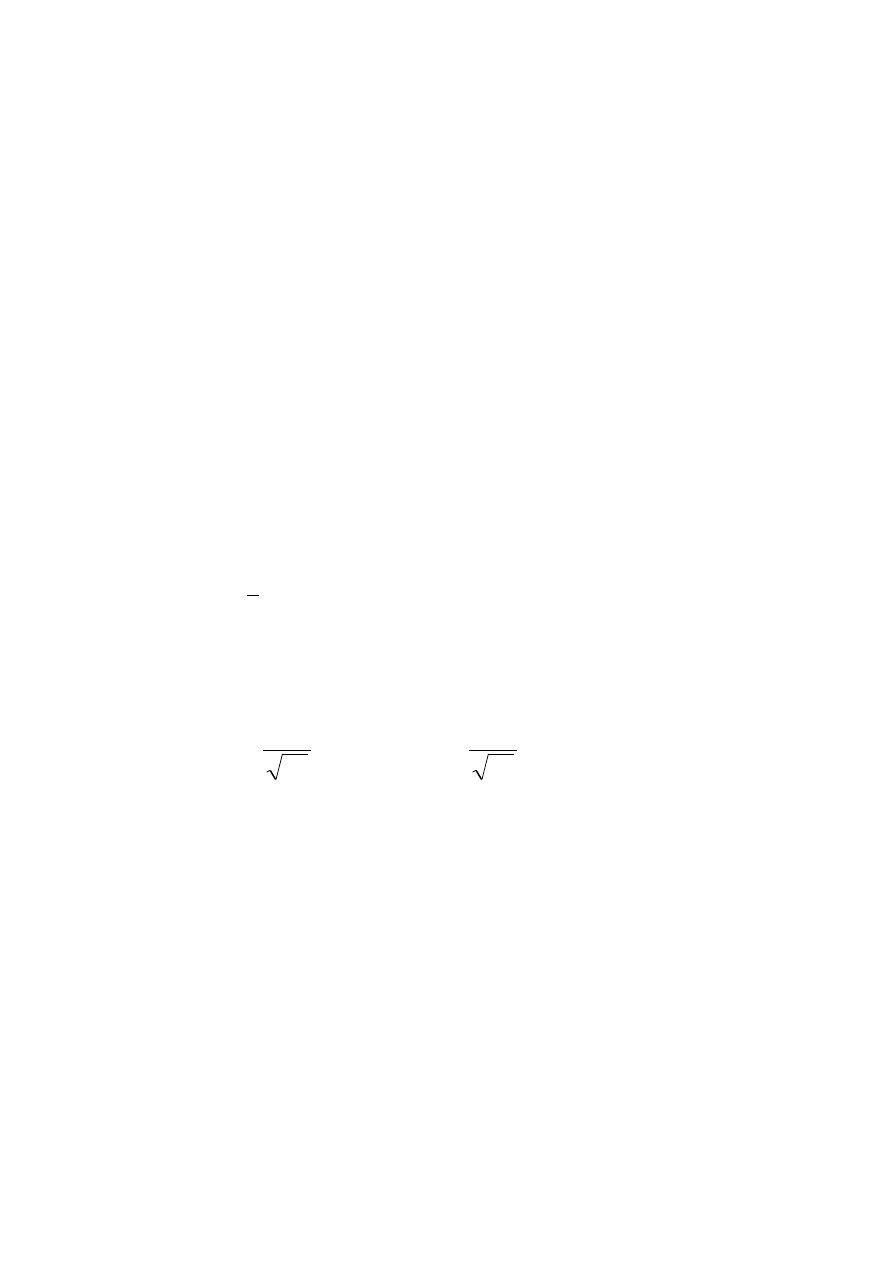
Mat. Statystyka.Wykład 8. (2013 L) R. Rempała. Materiały dydaktyczne
9
rozkładów t-Studenta podane są w tablicach statystycznych).
Przykład 2.
Zauważono, że waga ludzi dorosłych odwiedzających pewną
przychodnię rodzinną ma rozkład normalny.
Postanowiono ocenić, na podstawie 15-elementowej próby prostej,
średnią wagę dorosłych pacjentów odwiedzających przychodnię.
Posłużono się metodą opartą na przedziałach ufności, przy
współczynniku ufności 0.95 i przy nieznanym odchyleniu
standardowym populacji. Podać realizację przedziału ufności dla
wartości oczekiwanej znając wyniki próby (dane w kg): 76, 82, 67,
52, 79, 86, 77, 70, 68, 76, 80, 74, 66, 60, 73.
Dane zadania: n=15,
= 0,05, liczba stopni swobody =14.
Założenia. Cecha ma w populacji rozkład normalny o
nieznanych parametrach. Estymujemy wartość oczekiwaną
.
Wyliczenia:
4
.
72
x
,
s
= 8.84
Odczyt z tablic :
145
.
2
t
14
,
975
.
0
Podstawienie do wzoru
]
15
84
.
8
145
.
2
4
.
72
,
15
84
.
8
145
.
2
4
.
72
[
Wniosek. Przedział (67.5,77.3) jest realizacją takiego
przedziału ufności, który z prawdopodobieństwem 0.95
pokrywa nieznaną wartość średniej wagi pacjenta w badanej
przychodni.
2. Przedziały ufności dla wariancji
Rozważmy ten sam model, który opisuje Przypadek 2.
Badana zmienna ma rozkład N(
,
), nieznane
, nieznane
.
Estymujemy
2
.
Niech
n
1
X
,
,
X
będzie próbą losową z tego rozkładu.
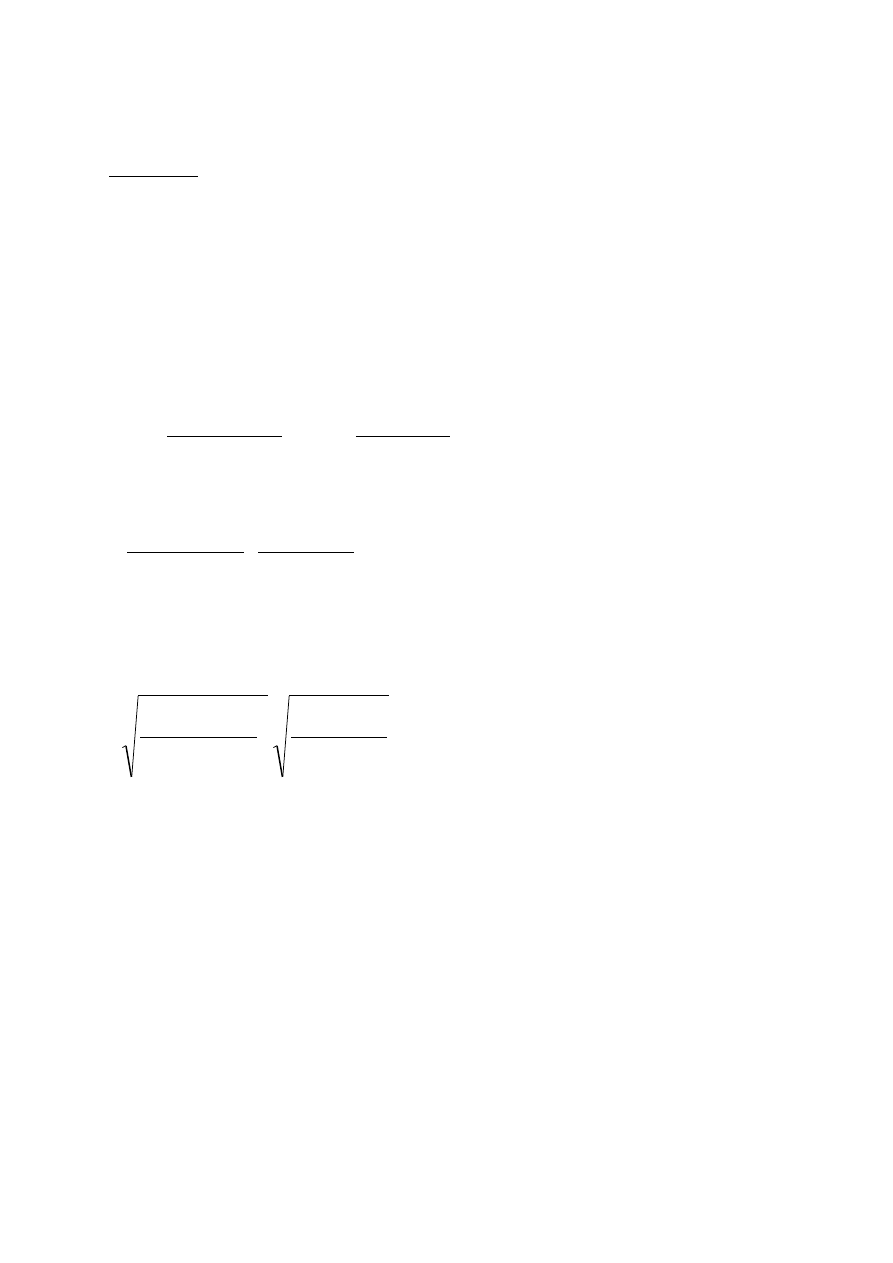
Mat. Statystyka.Wykład 8. (2013 L) R. Rempała. Materiały dydaktyczne
10
Przy budowie przedziału ufności posłużymy się statystyką
2
2
S
)
1
n
(
, która ma rozkład
)
1
n
(
2
(por. Wykład 3).
Niech
1
n
,
2
/
i
1
n
,
2
/
1
oznaczają odpowiednie kwantyle
z rozkładu
)
1
n
(
2
. Zatem
1
]
/
S
)
1
n
(
[
P
1
n
,
2
/
1
2
2
1
n
,
2
/
Stąd
1
S
)
1
n
(
S
)
1
n
(
P
1
n
,
2
/
2
2
1
n
,
2
/
1
2
Zatem przedziałem ufności dla
2
jest
1
n
,
2
/
2
1
n
,
2
/
1
2
S
)
1
n
(
,
S
)
1
n
(
Natomiast przedział ufności dla odchylenia standardowego
przyjmuje postać
1
n
,
2
/
2
1
n
,
2
/
1
2
S
)
1
n
(
,
S
)
1
n
(
Przykład 3. W celu zbadania zróżnicowania płac (brutto) w
pewnej firmie wybrano losowo 20 pracowników i zbadano ich
miesięczne zarobki. Podać realizację 95% przedziału ufności
dla wariancji i odchylenia standardowego całej populacji
pracowników firmy, jeżeli wariancja (s
2
) obliczona z próby
wynosiła 0.313.
Dane: n = 20,
= 0.05, s
2
= 0.313.
Wartości kwantyli wyznaczonych z tablic wynoszą:
852
.
32
,
907
.
8
1
n
,
2
/
1
1
n
,
2
/

Mat. Statystyka.Wykład 8. (2013 L) R. Rempała. Materiały dydaktyczne
11
Zatem realizacja 95% przedziału ufności dla wariancji
to przedział:
]
668
.
0
,
18
.
0
[
]
907
.
8
313
.
0
19
,
852
.
32
313
.
0
19
[
s
)
1
n
(
,
s
)
1
n
(
1
n
,
2
/
2
1
n
,
2
/
1
2
95% realizacją przedziału ufności dla odchylenia
standardowego jest przedział [0.424, 0.817].
3.Przedział ufności dla ilorazu wariancji
Rozważmy dwie niezależne próby
n
2
1
X
,
,
X
,
X
i
m
2
1
Y
,
,
Y
,
Y
gdzie X
i
N(
)
,
X
X
Y
i
N(
)
,
Y
Y
Załóżmy, że nieznane są parametry:
X
X
,
,
Y
Y
,
.
Zbudujemy przedział ufności dla ilorazu
2
X
2
Y
Zadanie takie pojawia się np. wówczas gdy chcemy porównać
dokładność pomiarów dokonanych dwoma przyrządami.
Statystyki
2
X
S
i
,
X
określone dla próby
n
2
1
X
,
,
X
,
X
oraz
2
Y
S
i
,
Y
określone dla próby
m
2
1
Y
,
,
Y
,
Y
Z wykładu 3 wiadomo, że
2
X
2
Y
2
Y
2
X
S
S
F(n-1,m-1) – rozkład F-Snedecora z
(n-1) –stopniami swobody licznika i (m-1)- stopniami
swobody mianownika.
Niech f
1
i f
2
oznaczają odpowiednio kwantyle rzędu
2
/
i 1-
2
/
z rozkładu F(n-1,m-1).
)
1
m
,
1
n
,
2
/
1
(
2
)
1
m
,
1
n
,
2
/
(
1
F
f
,
F
f
Z definicji kwantyli mamy więc

Mat. Statystyka.Wykład 8. (2013 L) R. Rempała. Materiały dydaktyczne
12
1
f
(
P
y
x
y
x
2
X
2
Y
2
Y
2
X
S
S
)
f
2
= 1
Stąd po przekształceniu otrzymujemy
2
X
2
Y
1
S
S
f
(
P
y
x
y
x
2
X
2
Y
)
S
S
f
2
X
2
Y
2
= 1
.
(Warto pamiętać (np. przy korzystaniu z tablic), że kwantyle
dowolnego ustalonego rozkładu F są związane zależnością
1/
,
.
Ostatecznie przedział ufności na poziomie 1- dla ilorazu
wariancji
2
X
2
Y
przybiera postać
]
S
S
f
,
S
S
f
[(
2
X
2
Y
2
2
X
2
Y
1
Przykład. Automat produkuje pewne detale, których długości
mają rozkład normalny. Dokonano nowego ustawienia
automatu. Zakładamy, że zmiana nie naruszyła typu rozkładu.
Zbudować 90% przedział ufności dla ilorazu wariancji
długości z ustawień po zmianie i przed zmianą , jeżeli w dwu
niezależnych próbkach o 10 pomiarach przed zmianą
ustawienia i 10 po zmianie, wariancje długości wynosiły
odpowiednio 4cm i 6cm.
Rozwiązanie. Niech
oznacza wariancje w próbce przed
zmianą,
po zmianie. Zatem
=4,

Mat. Statystyka.Wykład 8. (2013 L) R. Rempała. Materiały dydaktyczne
13
Odczyt z tablic kwantyla rzędu 0.95 z rozkładu F-Snedecora dla
rzędu (9,9) daje:
)
9
,
9
,
2
/
1
(
F
2.98 . Zatem
33
.
0
)
F
(
1
)
9
,
9
,
2
/
1
(
.
Realizacją 90% przedziału ufności dla ilorazu wariancji
2
X
2
Y
jest więc przedział [0.33 (6/4). 2.98 (6/4)]=[0.495, 4.47].
Wyszukiwarka
Podobne podstrony:
Mat Stat WykĹ ad 3 (2013L)(1)
Mat Stat WykĹ 6 7 Est c d (2013L)
Mat Stat WykĹ ad 2 ( 2013L)
Mat Stat WykĹ ad 3 (2013L)(1)
Mat Stat WykĹ 7b Es c d (2013L)
Mat Stat WykĹ ad 5 Ws Estym ( 2013L)
IiE, Mat Statystyka,Wyk 4
Mat Bud wyk 07
Met mat i stat w inz chem W 1
Mat Bud wyk 09
Mat Bud wyk 03
Met mat i stat w inz chem W 2
stat wyk zaocz4
Mat Stat WykĹ ad 4 5a 2013
Met mat i stat w inz chem W 5
Mat Bud wyk 02
mat konstr wyk, PKM egzamin kolosy ( łukasik, Salwiński )
więcej podobnych podstron