© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

MATEMATYKA STOSOWANA

W INŻYNIERII CHEMICZNEJ

Wykład – 2

Układy równań – metody analityczne

Metody numeryczne rozwiązywania

równań liczbowych

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

2

ROZWIĄZYWANIE UKŁADÓW

RÓWNAŃ

0

)

,...,

,

(

0

)

,...,

,

(

0

)

,...,

,

(

2

1

2

1

2

2

1

1

n

n

n

n

x

x

x

F

x

x

x

F

x

x

x

F

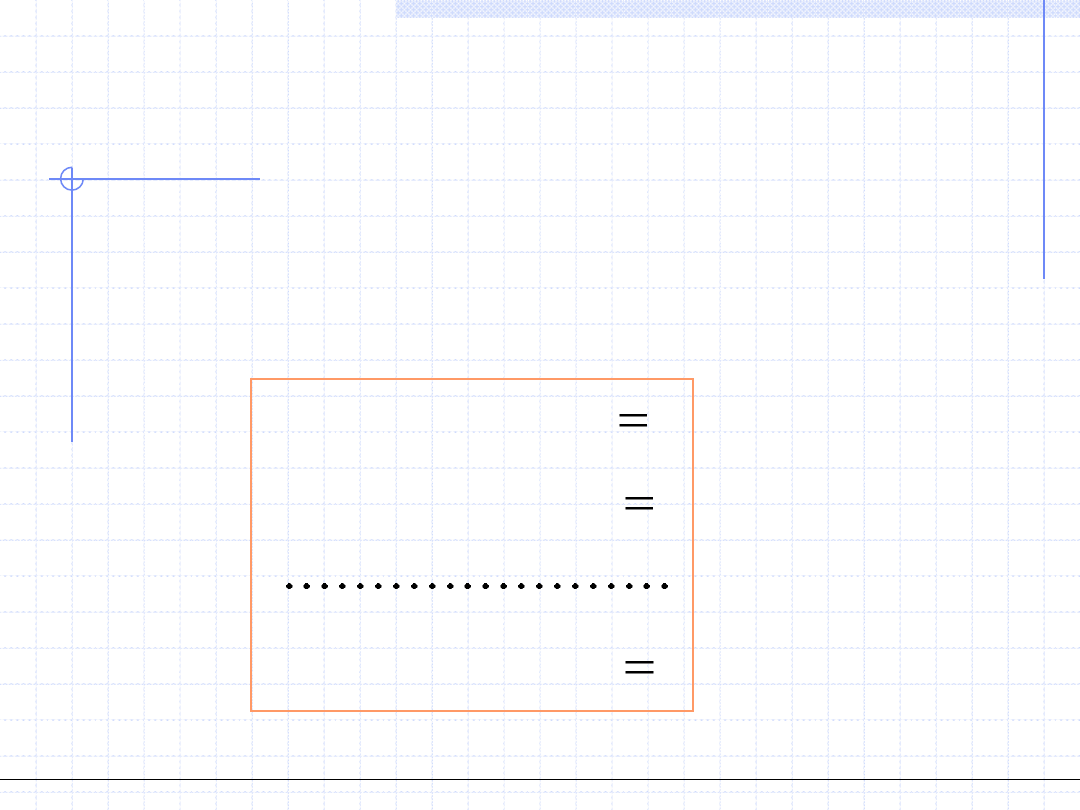
Układem równań nazywamy n równości, w których występuje na ogół

n niewiadomych.

Każdy układ równań daje się sprowadzić do postaci:

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

3

ROZWIĄZYWANIE UKŁADÓW

RÓWNAŃ

0

33904

.

1

)

,

,

(

0

989351

.

0

)

sin(

)

,

,

(

0

)

ln(

4411

.

61

)

,

,

(

3

2

1

3

2

1

3

3

2

1

3

2

1

2

3

2

1

3

3

2

2

1

3

2

1

1

2

1

x

x

x

e

x

x

x

F

x

x

x

x

x

x

F

x

x

x

x

x

x

x

x

x

F

x

x

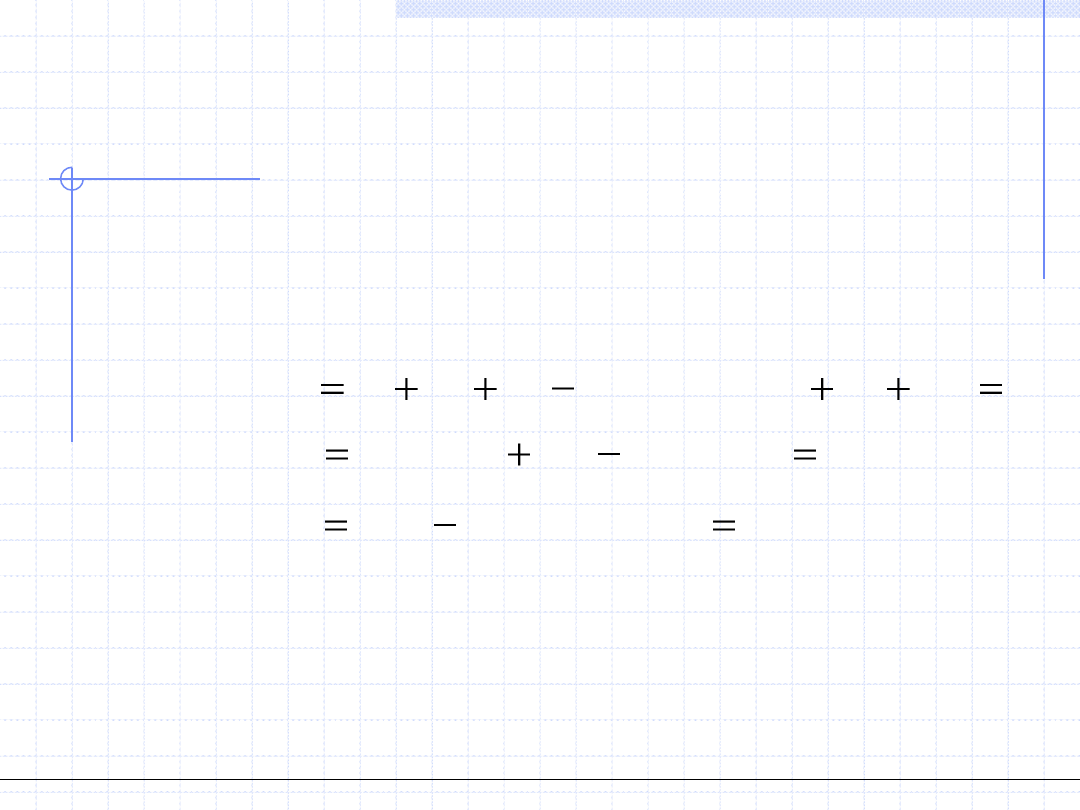
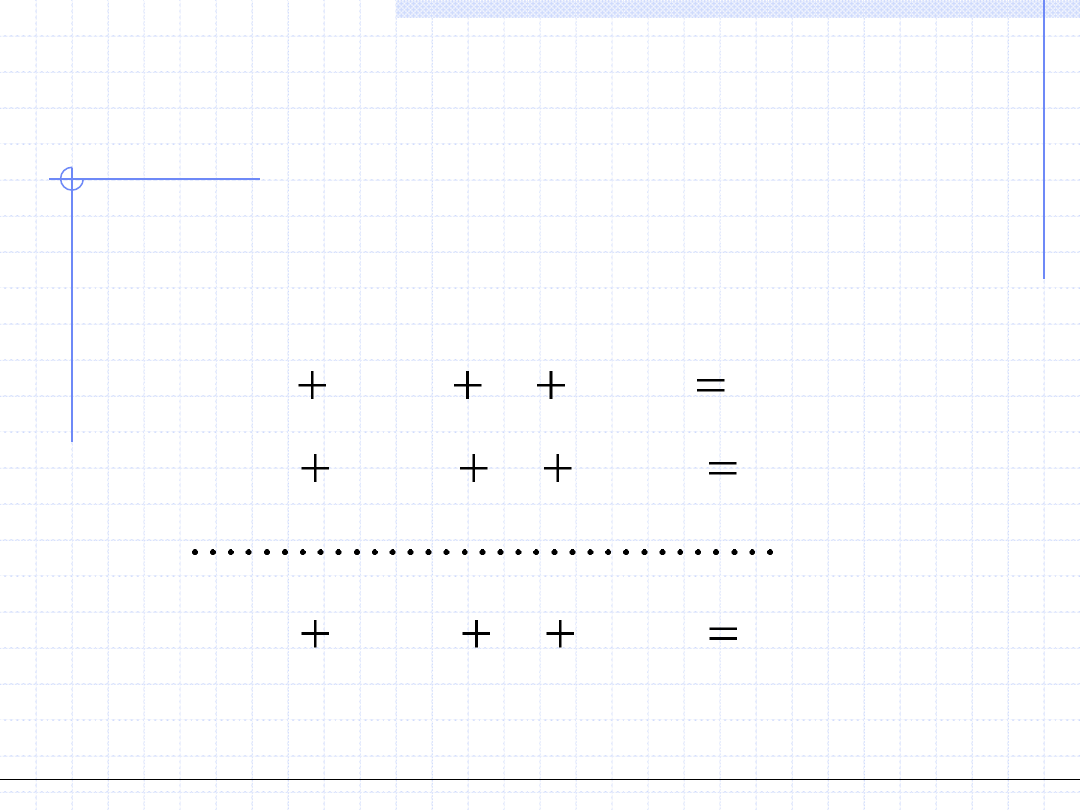
Przykładowy układ równań

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

4

ROZWIĄZYWANIE UKŁADÓW

RÓWNAŃ

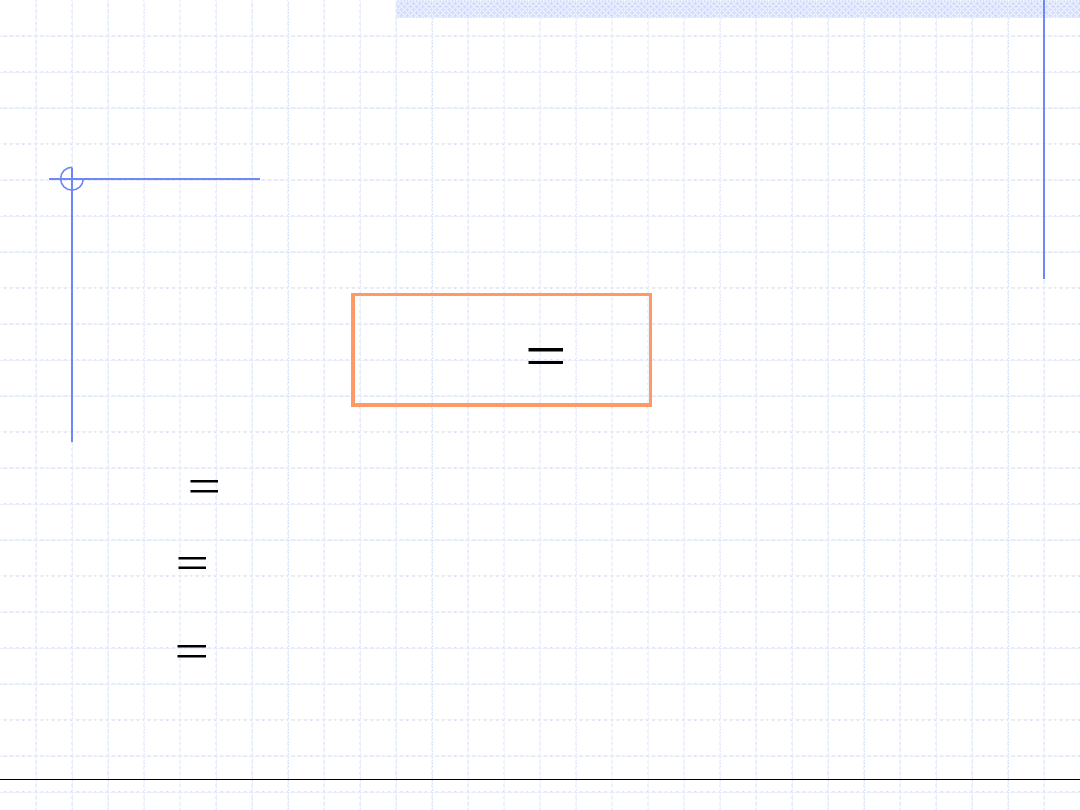
Układ równań możemy zapisać w postaci wektorowej:

wektorowa

funkcja

F

F

F

F

n

]

,...

,

[

2

1



0

)

(







x

F

ch

niewiadomy

wektor

x

x

x

x

n

]

,...

,

[

2

1



zerowy

wektor

]

0

,...

0

,

0

[

0



© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ANALITYCZNE ROZWIĄZYWANIE

UKŁADÓW RÓWNAŃ

Analityczne rozwiązanie układów jest możliwe w rzadkich przypadkach,

gdy za pomocą różnych przekształceń można układ sprowadzić do równania

algebraicznego stopnia co najwyżej 4.

Przykład:

2

2

1

2

2

1

1

2

13

2

3

x

x

x

x

x

Wyznaczając z drugiego równania x

2

i podstawiając do równania pierwszego

otrzymujemy równanie 4 – tego stopnia:

4

3

2

1

1

1

1

4

4

10

6

4

0

x

x

x

x

Równanie to ma dwa pierwiastki rzeczywiste: x

1,1

=2 x

1,2

=-1.537

Podstawienie tych wartości do drugiego równania daje x

2,1

=3 x

2,2

=3.2616

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ANALITYCZNE ROZWIĄZYWANIE

UKŁADÓW RÓWNAŃ LINIOWYCH

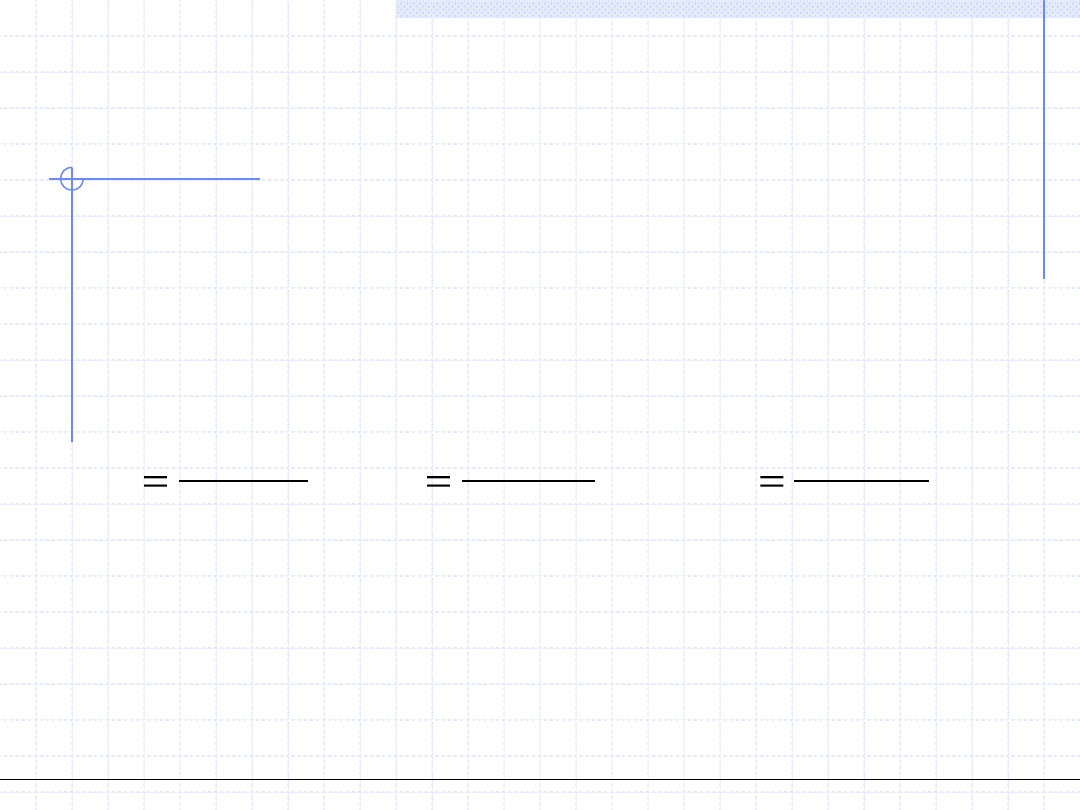
Stosunkowo często w wielu zastosowaniach występują układy równań liniowych.

Układy takie można rozwiązywać analitycznie za pomocą wielu metod.

Układ równań liniowych można zapisać następująco:

11 1

12

2

1

1

21 1

22

2

2

2

1 1

2

2

...

...

...

n

n

n

n

n

n

nn

n

n

a x

a x

a x

w

a x

a x

a x

w

a x

a x

a x

w

Współczynniki liczbowe występujące po lewej stronie tworzą tzw. macierz

główną układu. Liczby po prawej stronie tworzą tzw. wektor wyrazów wolnych.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ANALITYCZNE ROZWIĄZYWANIE

UKŁADÓW RÓWNAŃ LINIOWYCH

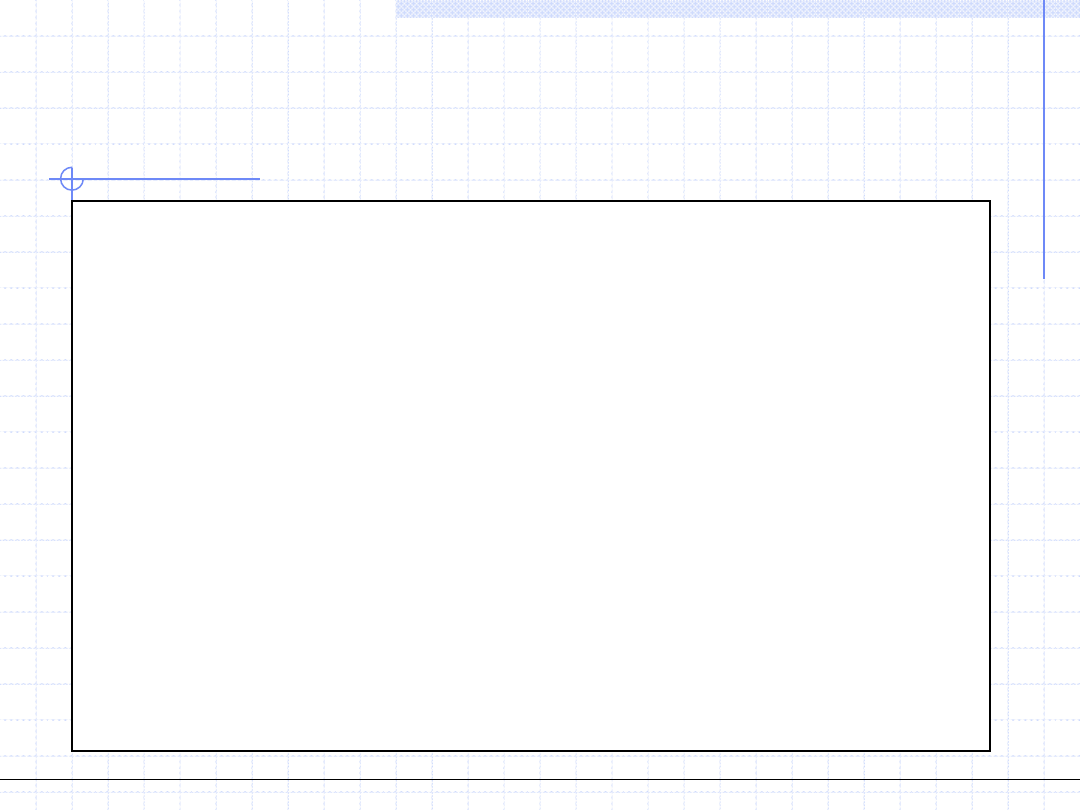
Układ równań liniowych ma jednoznaczne rozwiązanie wtedy, gdy wyznacznik

macierzy głównej jest różny od zera.

Spośród wielu metod analitycznych rozwiązywania układów liniowych

przypominam metodę wyznacznikową Cramera:

Zgodnie z tą metodą rozwiązanie liniowego układu równań jest dane

za pomocą wzorów:

1

2

1

2

det(

)

det(

)

det(

)

....

det( )

det( )

det( )

n

n

A

A

A

x

x

x

A

A

A

gdzie:

A – macierz główna układu

A

i

– macierz główna, w której i - tą kolumnę zastąpiono wektorem

wyrazów wolnych

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

Numeryczne metody rozwiązywania

równań liczbowych

1.

Uwagi ogólne

2.

Błąd pierwiastka i równania

3.

Metoda bisekcji

4.

Metoda „regula falsi”

5.

Metoda siecznej

6.

Metoda Newtona (stycznej)

7.

Metoda iteracji prostej

8.

Numeryczne rozwiązywanie układów

równań

© Wydział Chemiczny Politechniki Wrocławskiej, prof. Antoni Kozioł

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ

,...

,...,

,

}

{

)

(

)

2

(

)

1

(

)

(

i

i

x

x

x

x

Numeryczne rozwiązywanie tego równania polega na konstrukcji ciągu

liczbowego zbieżnego do szukanego pierwiastka:

Załóżmy że mamy do rozwiązania równanie:

)

(

)

(

x

G

x

F

x

x

i

i

)

(

)

(

lim

)

(

)

(

x

G

x

F

szukany pierwiastek równania.

© Wydział Chemiczny Politechniki Wrocławskiej, prof. Antoni Kozioł

10

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ

)

(

)

(

i

i

x

x

x

)

(

)

(

)

(

)

(

)

(

i

i

i

y

x

G

x

F

W związku z tym, że w praktyce zamiast granicy należy przyjąć konkretny,

skończony wyraz ciągu, w metodach numerycznych dużą rolę odgrywa

zagadnienie dokładności obliczeń lub też błędu pierwiastka lub równania.

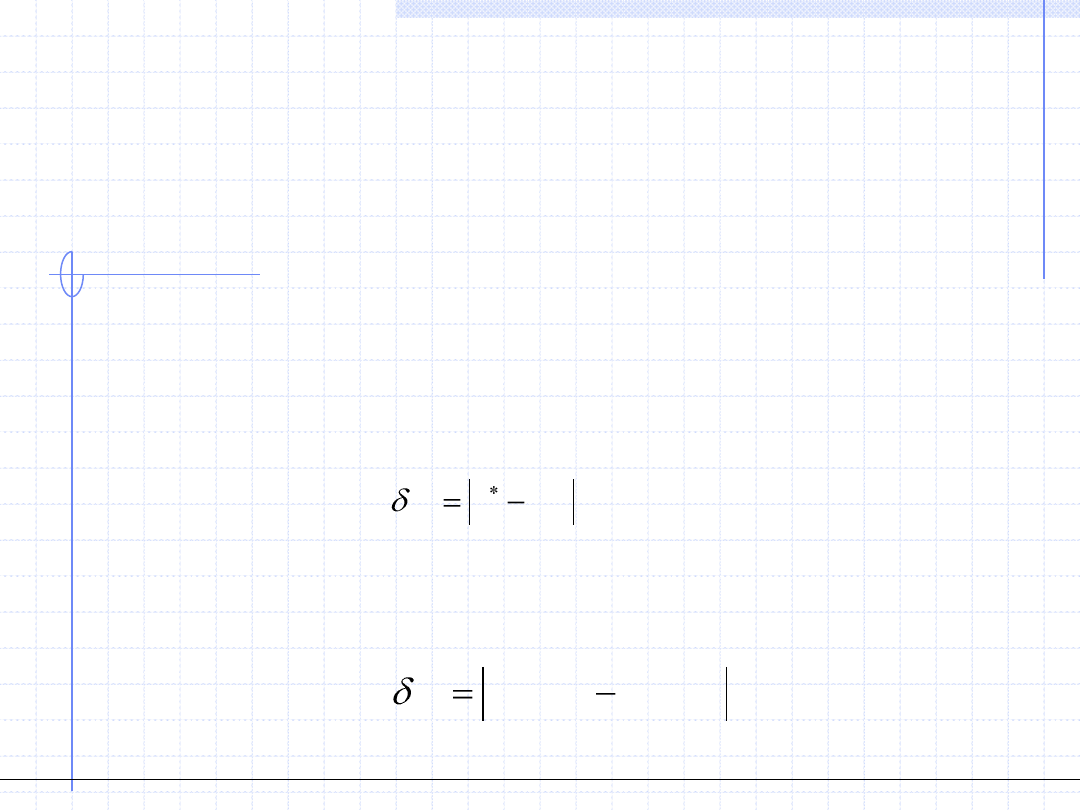
Błędem pierwiastka będziemy nazywać wartość absolutną różnicy

rzeczywistego pierwiastka x

*

a konkretnym wyrazem x

i

ciągu liczbowego

kończącym konstrukcję:

Błędem równania nazywamy wartość absolutną różnicy rzeczywistych

wartości funkcji F i G w punkcie x

i

:

© Wydział Chemiczny Politechniki Wrocławskiej, prof. Antoni Kozioł

11

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ

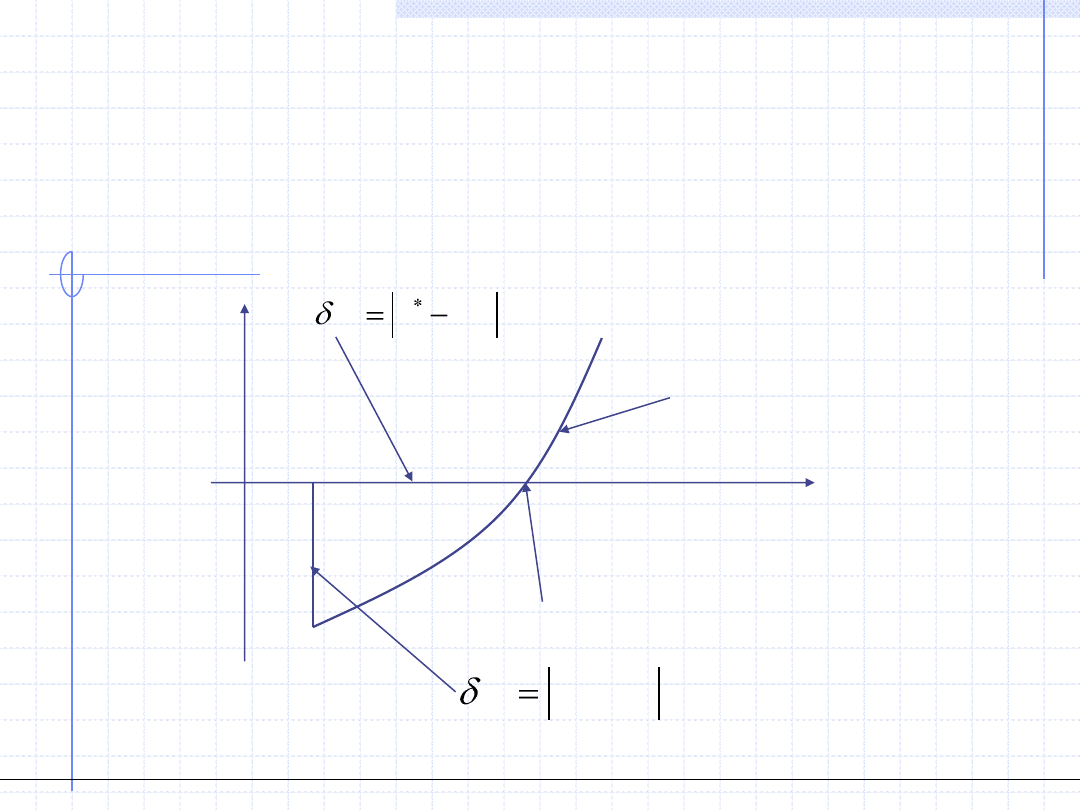
Pojęcia błędu pierwiastka i równania dla równania F(x)=0

można pokazać graficznie:

x

y

x

i

x*

F(x

i

)

y=F(x)

)

(

)

(

i

i

x

x

x

( )

( )

(

)

i

i

y

F x

© Wydział Chemiczny Politechniki Wrocławskiej, prof. Antoni Kozioł

12

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ

Konstrukcję ciągu {x

i

} kończy się gdy błąd pierwiastka lub błąd równania

(lub obydwu wartości) będzie mniejszy od z góry zadanej liczby dodatniej ε.

)

(i

x

)

(

lub

i

y

)

(

lub

)

(

)

(

i

y

i

x

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

13

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ

0

)

(x

F

0

)

(

)

(

0

0

b

F

a

F

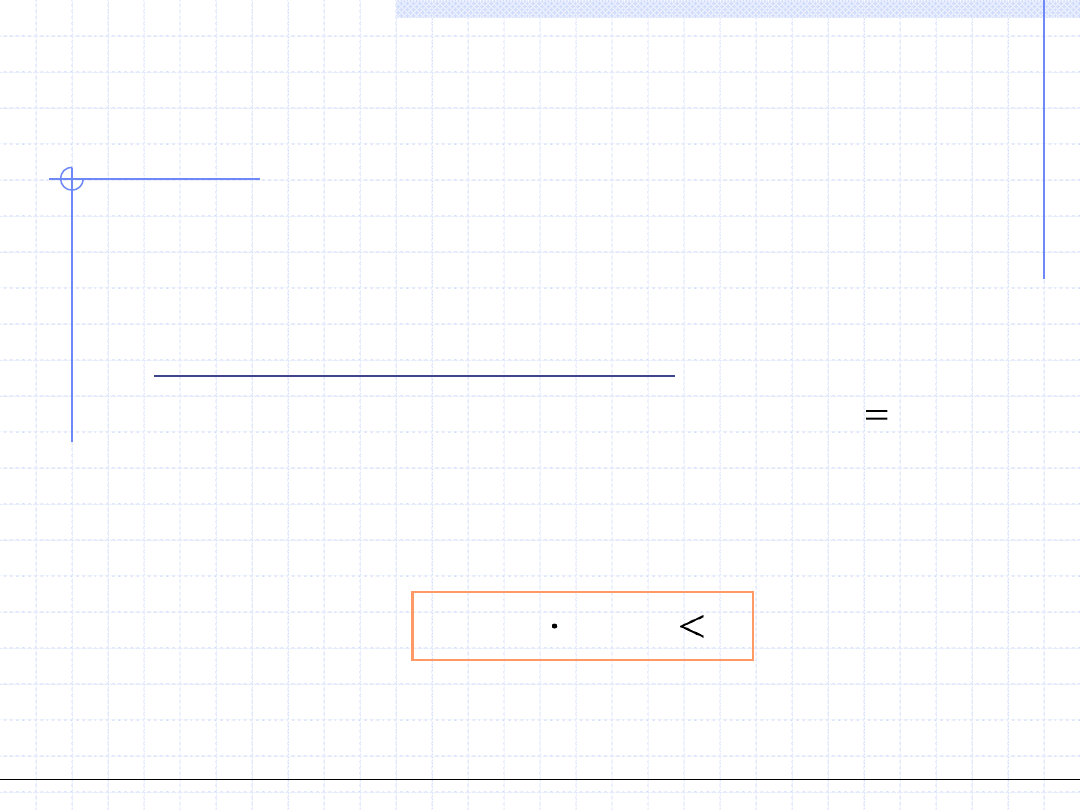
Istnieje kilka metod przybliżonego (numerycznego) rozwiązywania

równań z jedną niewiadomą. Tutaj zaprezentuję Państwu 5 takich metod.

Wszystkie metody zostaną przedstawione w postaci algorytmów

(przepisów) za pomocą kolejnych kroków.

1. Metoda połowienia przedziału (bisekcji)

Metodę stosujemy do równania postaci:

Krok 1 - Za pomocą dowolnej metody znajdujemy przedział [a

0

,b

0

],

w którym funkcja F(x) ma na brzegach przedziału różne

znaki czyli spełnia warunek:

Jeżeli funkcja F jest ciągła to wiemy wtedy że pierwiastek

znajduje się w przedziale [a

0

,b

0

].

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

14

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ

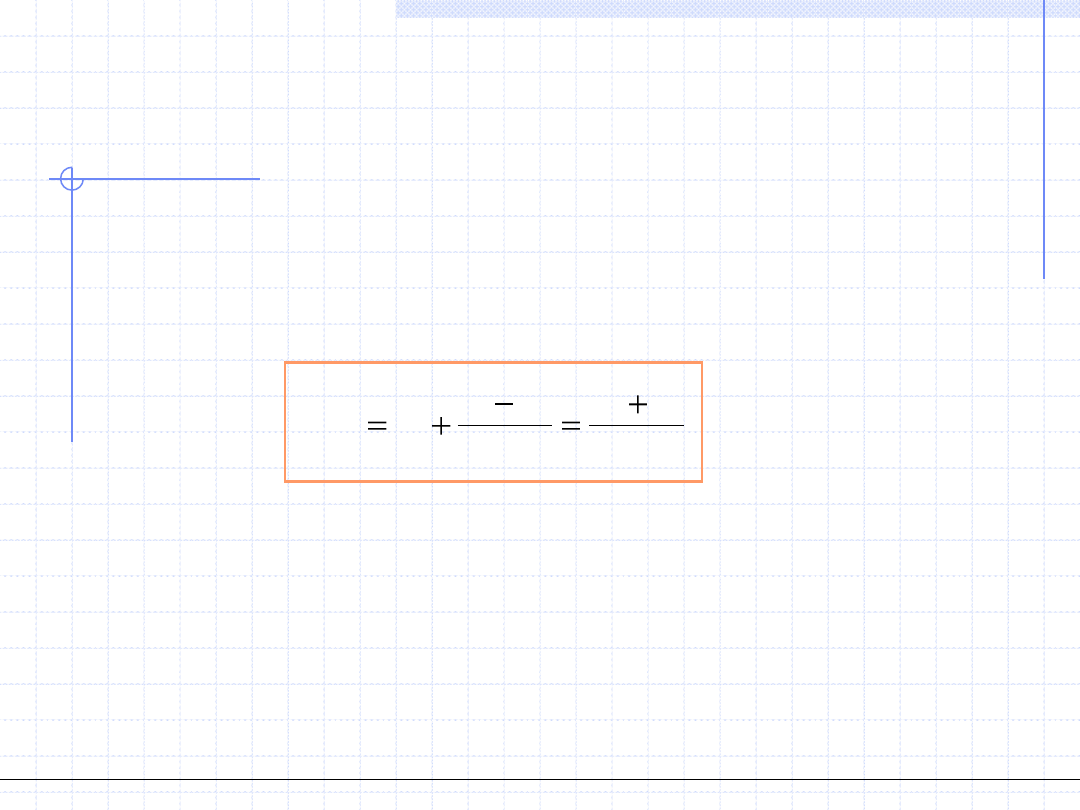
Krok 2 - Dzielimy przedział na pół tzn. zakładamy że pierwszym

przybliżeniem pierwiastka jest środek przedziału:

2

2

0

0

0

0

0

1

b

a

a

b

a

x

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ –Metoda bisekcji cd.

)

:

(

)

:

(

0

)

(

)

(

)

:

(

)

:

(

0

)

(

)

(

0

1

1

1

0

1

0

1

1

1

0

1

b

b

x

a

b

F

x

F

a

a

x

b

a

F

x

F

Krok 3 - Badamy znak funkcji F(x) w punkcie x

1

i porównujemy ze

znakami tej funkcji na brzegach przedziału. Porównanie to

daje nam informację, w której połówce znajduje się szukany

pierwiastek. Jest on zawsze tam gdzie znaki na brzegach są

różne. Po tej lokalizacji pierwiastka do dalszej procedury

bierzemy odpowiednią połówkę. W tym celu środek przedziału

podstawiamy jako brzeg b

1

lub a

1

.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

16

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ –Metoda bisekcji cd.

Krok 4 - Wracamy do kroku 2 tzn. nowy przedział dzielimy na pół

i znajdujemy drugie przybliżenie pierwiastka x

2

. Następnie

powtarzamy krok 3 itd.

Powstaję w ten sposób typowa pętla numeryczna,

którą przerywamy wtedy gdy osiągniemy żądaną dokładność

obliczeń. Żądaną dokładność obliczeń na ogół określa się

wybierają pewną dostatecznie małą dodatnią liczbę ε,
np. ε =10

-6

. Pętla kolejnych obliczeń zostaje przerwana, gdy

długość aktualnego przedziału będzie mniejsza od zadanej

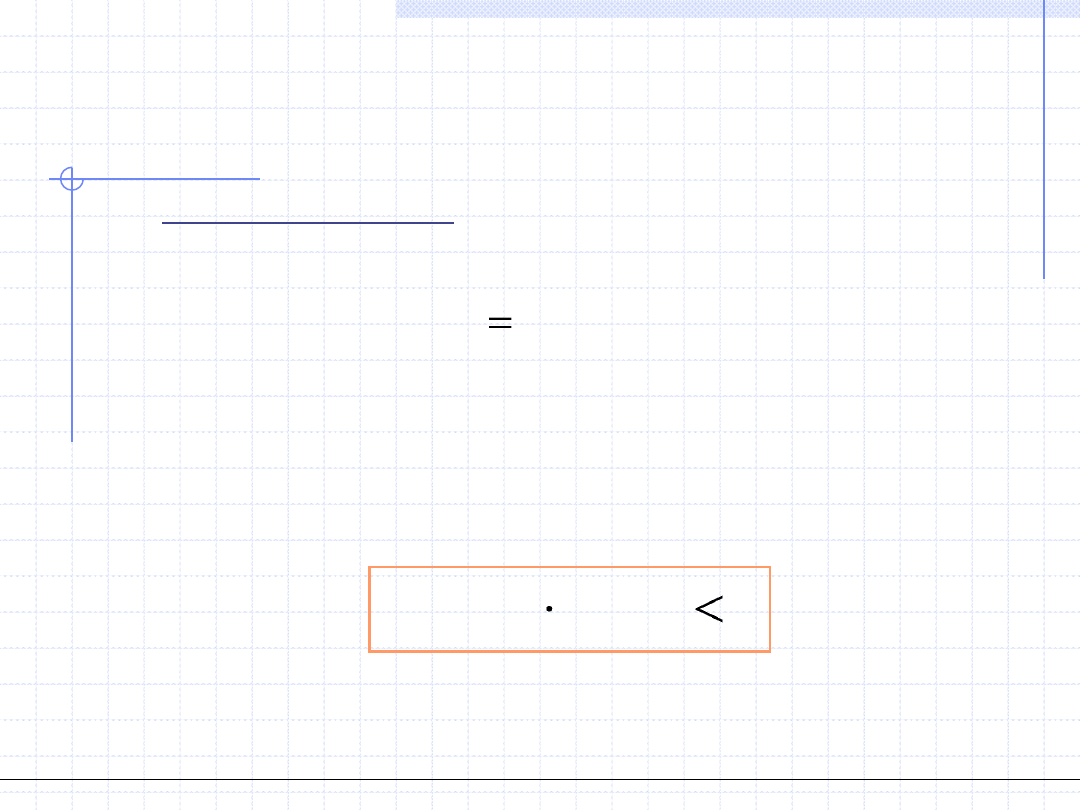
dokładności, tzn.:

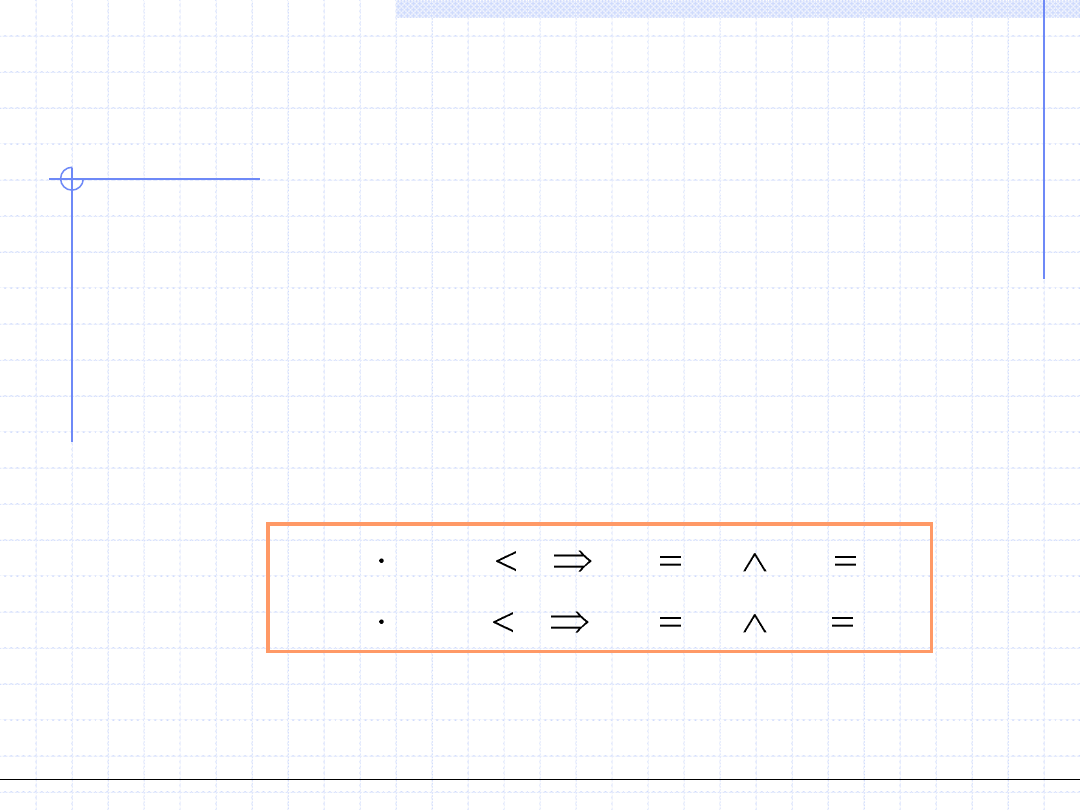
n

n

n

x

x

a

b

)

(

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ –Metoda bisekcji cd.

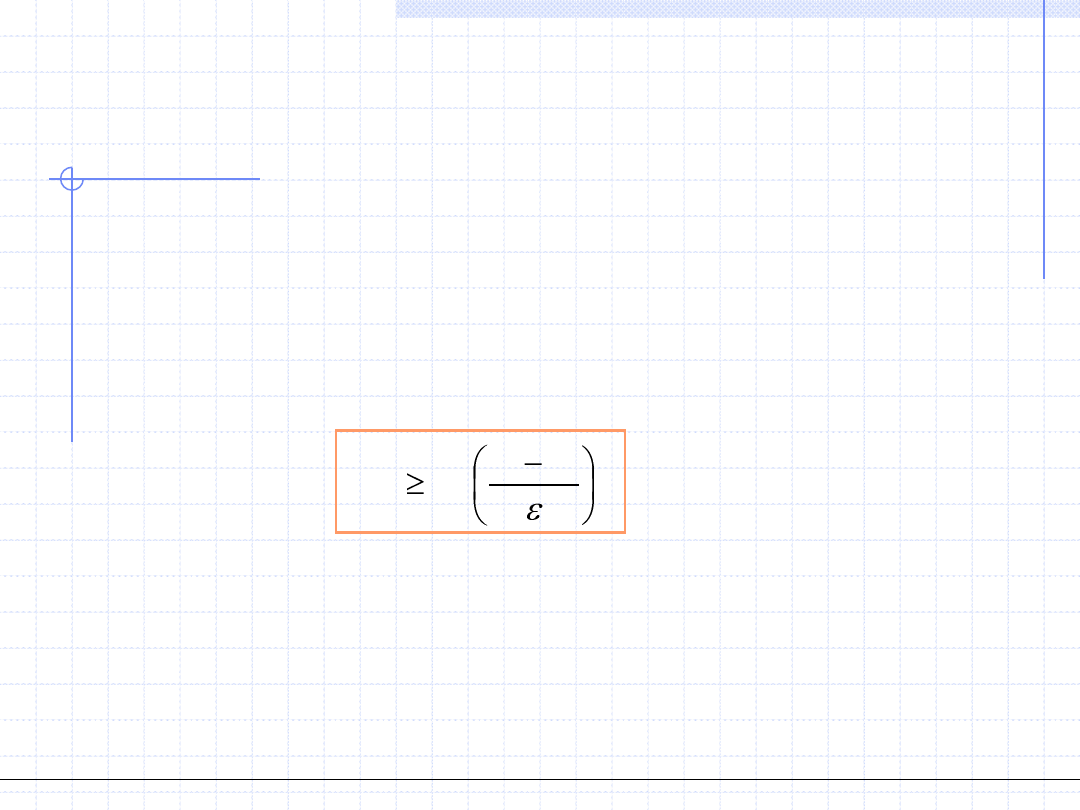
W przypadku metody bisekcji można z góry określić liczbę kroków

wymaganą do osiągnięcia żądanej dokładności. Konstrukcja metody

prowadzi do wzoru:

0

0

2

lg

a

b

n

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

18

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ –Metoda bisekcji cd.

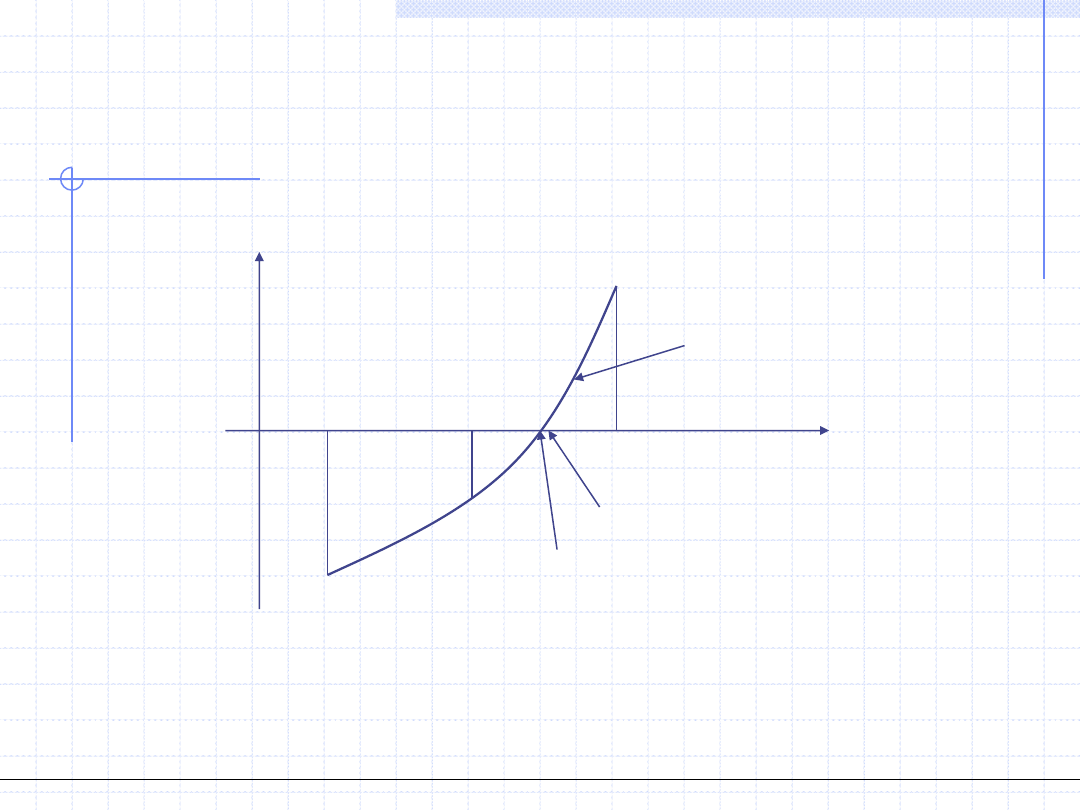
Graficzna ilustracja metody bisekcji:

x

y

a

0

b

0

x*

x

1

F(b

0

)

F(a

0

)

y=F(x)

Metoda bisekcji jest zawsze zbieżna, pod warunkiem znalezienia

przedziału [a

0

,b

0

]

x

2

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

19

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ –Metoda „regula falsi”

0

)

(x

F

0

)

(

)

(

0

0

b

F

a

F

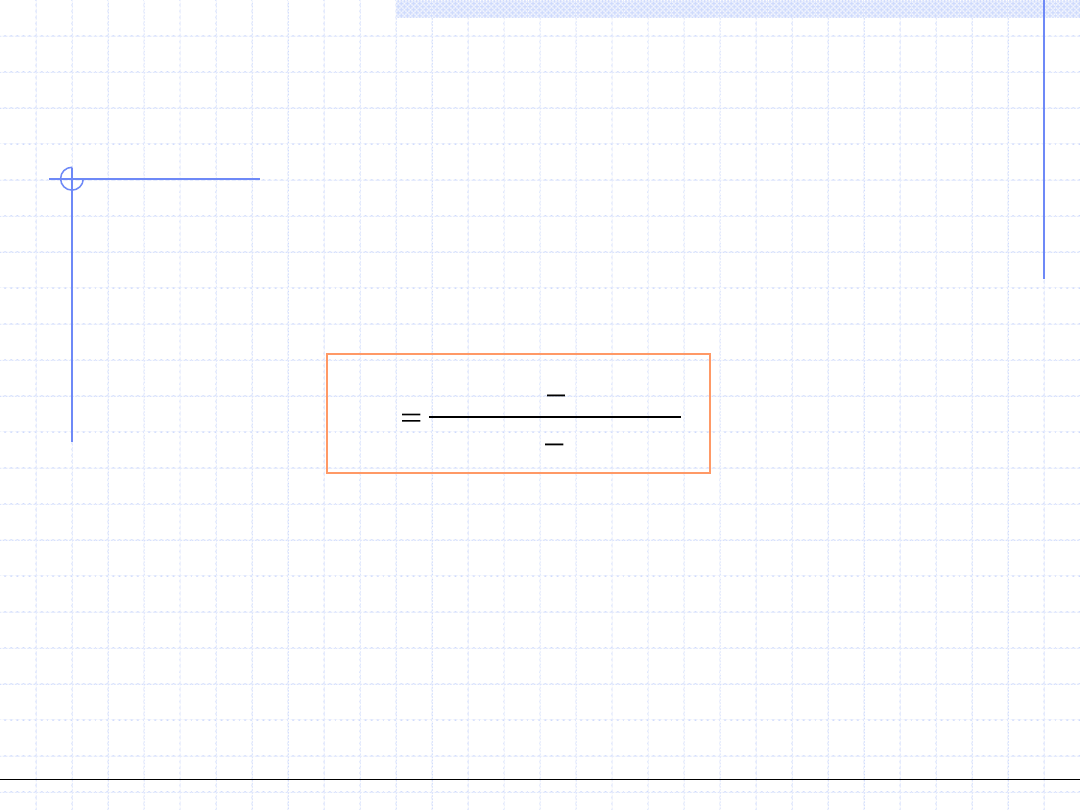
2. Metoda „regula falsi”

Metodę stosujemy do równania postaci:

Krok 1 - Za pomocą dowolnej metody znajdujemy przedział [a

0

,b

0

],

w którym znajduje się szukany pierwiastek x

*

.

Funkcja F(x) ma wtedy na brzegach przedziału różne znaki

czyli musi spełniać warunek:

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

20

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ –Metoda „regula falsi”

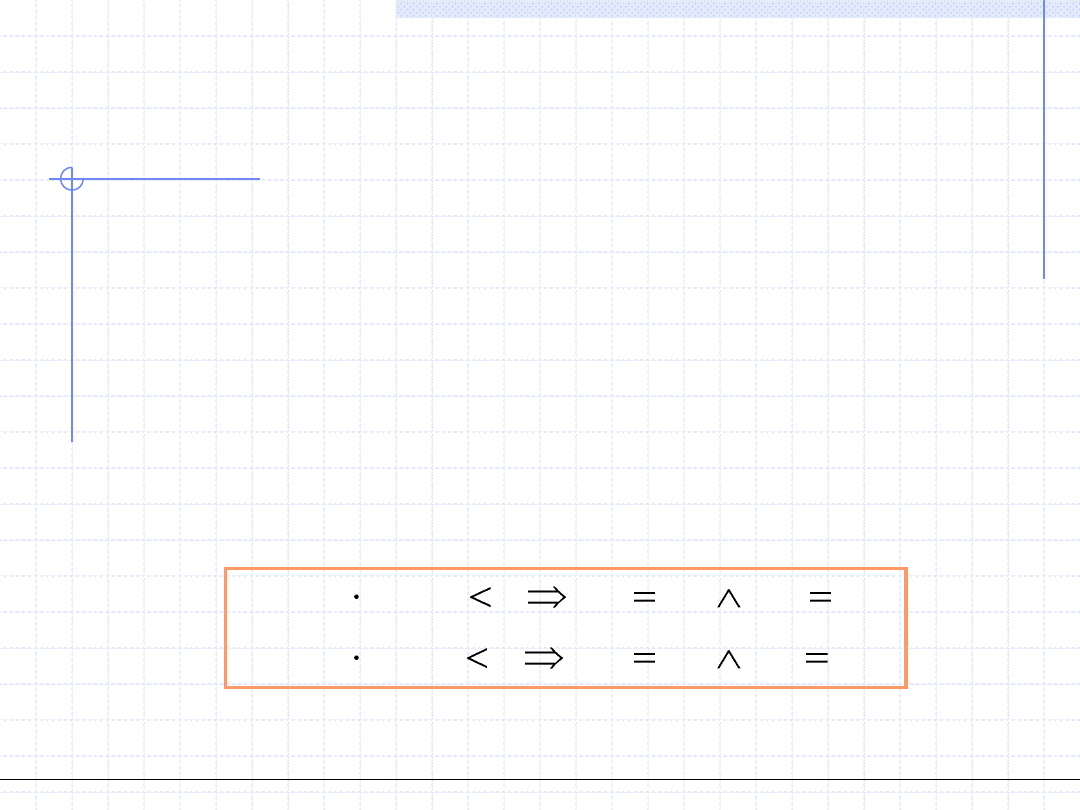
Krok 2 - Zakładamy, że w przedziale tym funkcja jest liniowa.

Prowadzi to do następującego wzoru określającego pierwsze

przybliżenie pierwiastka:

)

(

)

(

)

(

)

(

0

0

0

0

0

0

1

a

F

b

F

a

F

b

b

F

a

x

Otrzymany punkt x

1

dzieli pierwotny przedział na dwa na ogół

nierówne podprzedziały. W jednym z tych podprzedziałów będzie

się znajdował szukany pierwiastek.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ – metoda „regula falsi” cd.

)

:

(

)

:

(

0

)

(

)

(

)

:

(

)

:

(

0

)

(

)

(

0

1

1

1

0

1

0

1

1

1

0

1

b

b

x

a

b

F

x

F

a

a

x

b

a

F

x

F

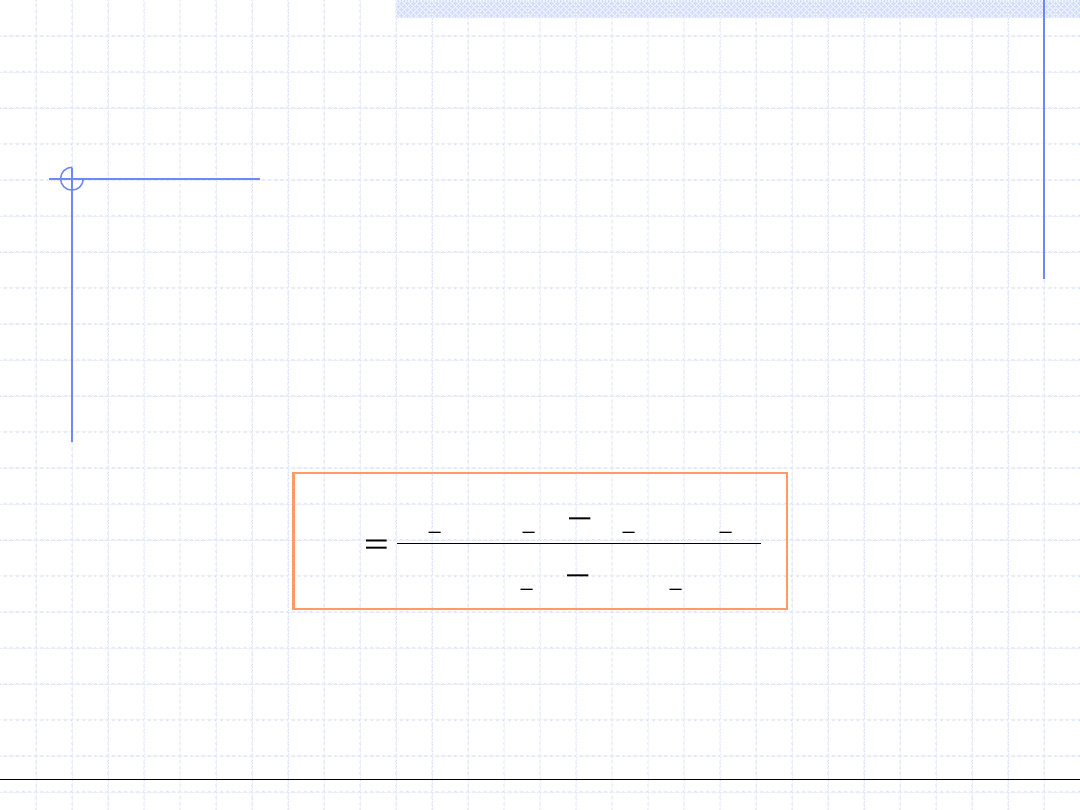
Krok 3 - Obliczamy wartość funkcji F(x) w punkcie x

1

a znak tej wartości

porównujemy ze znakami tej funkcji na brzegach przedziału.

Porównanie to daje nam informację, w którym podprzedziale

znajduje się szukany pierwiastek. Jest on zawsze tam gdzie

znaki na brzegach są różne.

Po tej lokalizacji pierwiastka do dalszej procedury wybieramy

odpowiedni podprzedział. W tym celu obliczony punkt x

1

podstawiamy jako brzeg b

1

lub a

1

.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

22

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ – metoda „regula falsi” cd.

Krok 4 - Wracamy do kroku 2 tzn. nowy przedział dzielimy na dwie

części za pomocą założenia liniowości i znajdujemy drugie

przybliżenie pierwiastka x

2

.

Wzór wynikający z tego założenia dla i – tego przybliżenia

jest następujący:

)

(

)

(

)

(

)

(

1

1

1

1

1

1

i

i

i

i

i

i

i

a

F

b

F

a

F

b

b

F

a

x

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ – metoda „regula falsi” cd.

Następnie powtarzamy krok 3° itd. Pętla kolejnych obliczeń zostaje

przerwana, gdy długość aktualnego przedziału będzie mniejsza od

zadanej dokładności, tzn.:

n

n

n

x

x

a

b

)

(

W przypadku metody „regula falsi” nie można z góry określić liczby

kroków koniecznych do osiągnięcia żądanej dokładności.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

24

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ – metoda „regula falsi” cd.

Graficzna ilustracja metody „regula falsi”:

x

y

a

0

b

0

x*

x

1

F(b

0

)

F(a

0

)

y=F(x)

Metoda „regula falsi” podobnie jak metoda bisekcji jest zawsze zbieżna,

pod warunkiem znalezienia przedziału [a

0

,b

0

]

x

2

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ –Metoda siecznej

0

)

(x

F

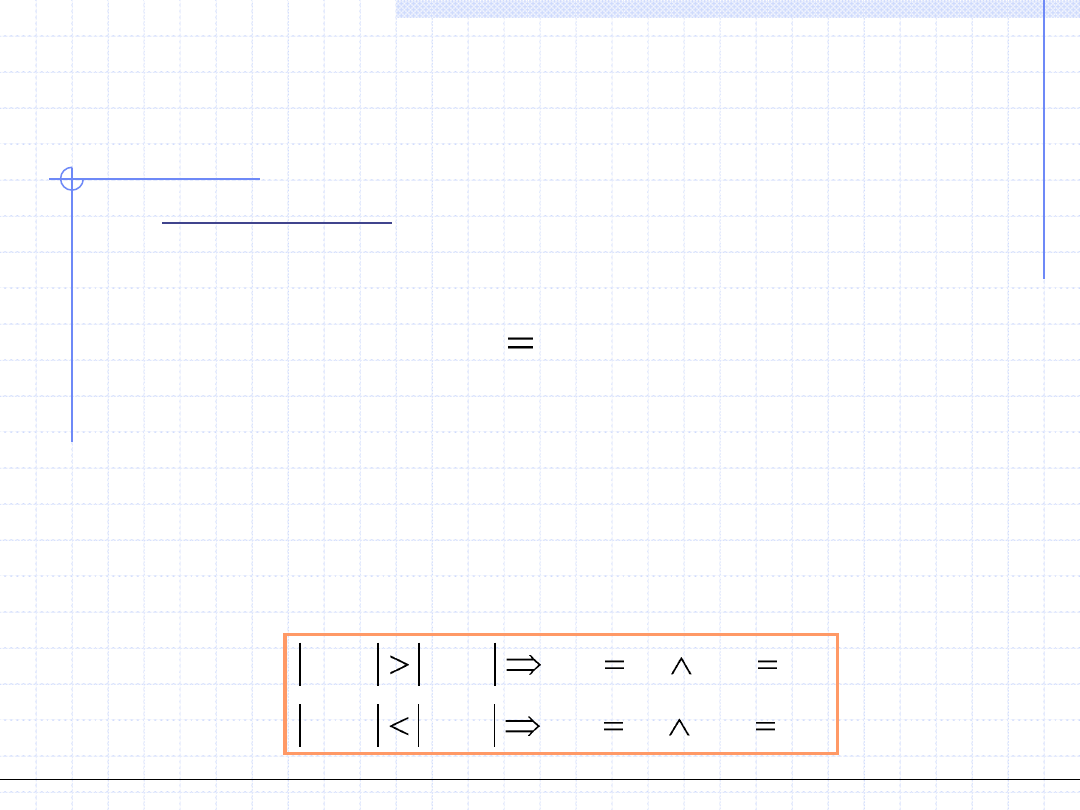
3. Metoda siecznej

Metodę stosujemy do równania postaci:

Krok 1 - Za pomocą dowolnej metody znajdujemy dwie różne

liczby a i b leżące w pobliżu szukanego pierwiastka x

*

.

Następnie obliczamy wartości funkcji F(a) i F(b).

W zależności od tych wartości określamy dwa pierwsze

przybliżenia x

1

i x

2

:

)

:

(

)

:

(

)

(

)

(

)

:

(

)

:

(

)

(

)

(

2

1

2

1

a

x

b

x

b

F

a

F

b

x

a

x

b

F

a

F

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

26

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ –Metoda siecznej

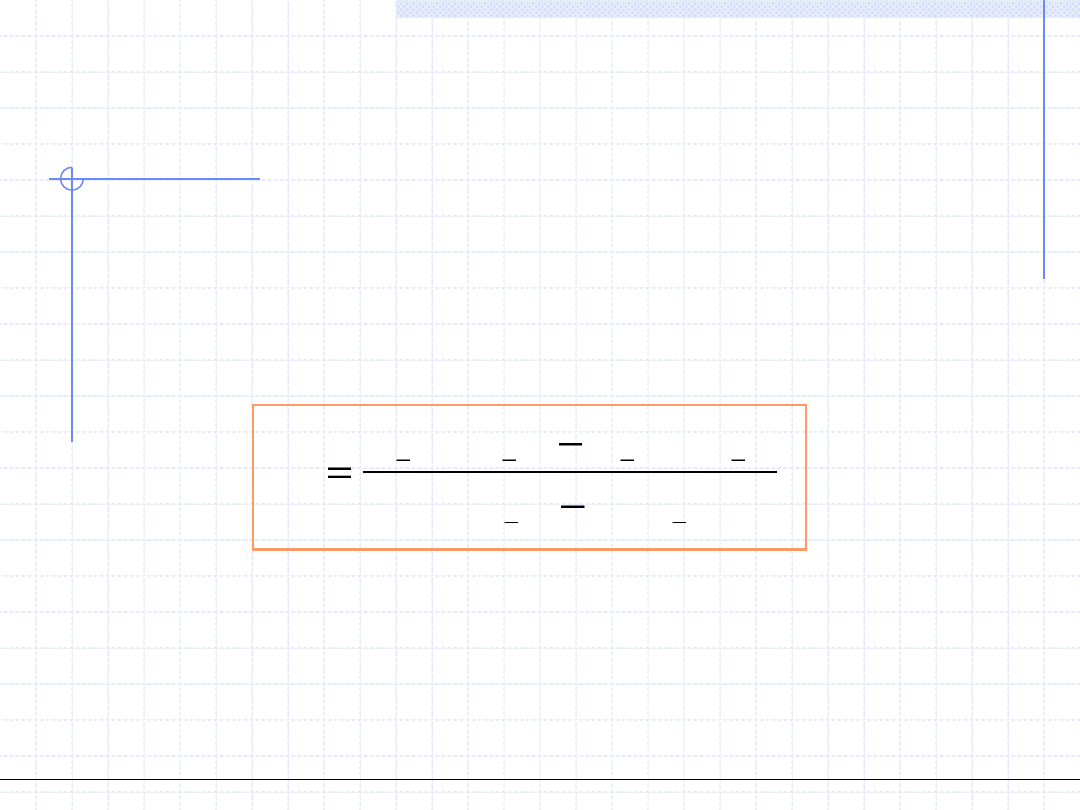
Krok 2 - Na podstawie znajomości wartości funkcji w dwu poprzednich

przybliżeniach obliczmy wartość kolejnego przybliżenia stosując

wzór zakładający liniową postać funkcji (prowadzimy sieczną

przez te punkty – stąd nazwa metody) :

)

(

)

(

)

(

)

(

1

2

1

2

2

1

i

i

i

i

i

i

i

x

F

x

F

x

F

x

x

F

x

x

Otrzymujemy w ten sposób ciąg kolejnych wartości pierwiastka

x

1

,x

2

,…x

i

,…

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

27

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ – metoda siecznej cd.

1

i

i

i

x

x

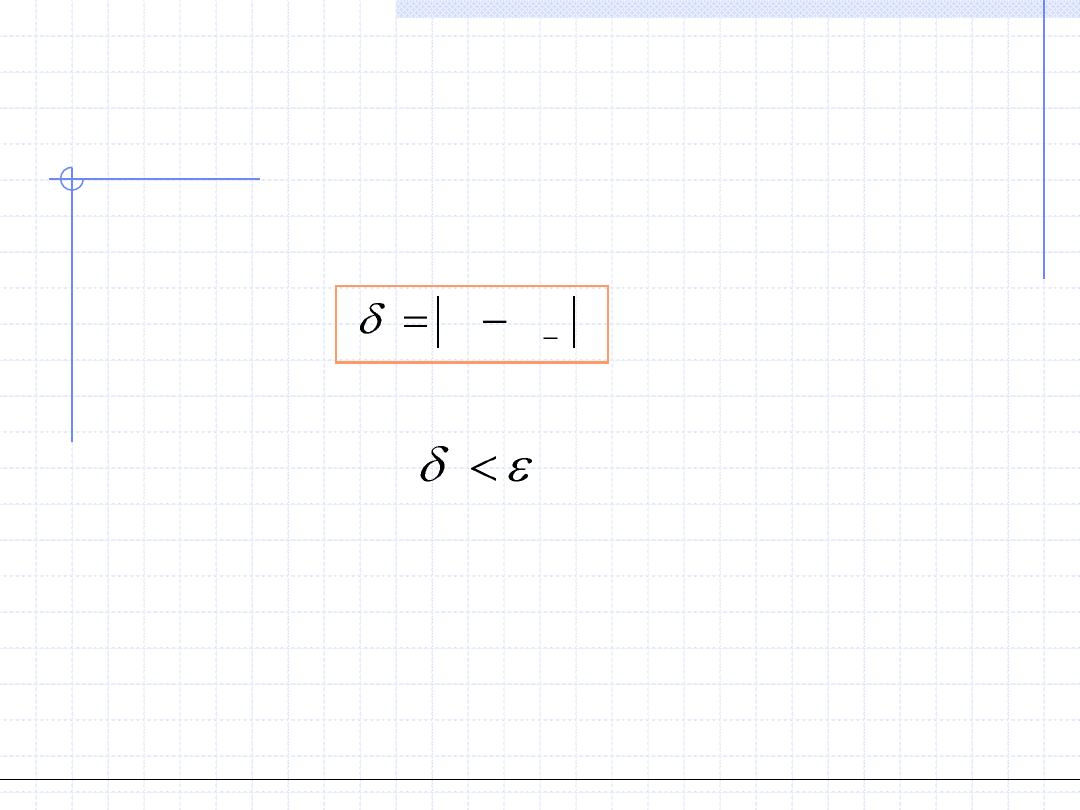
W celu oszacowania dokładności na każdym etapie obliczamy wartość

szacunkowego błędu :

Na ogół pętlę obliczeń przerywa się gdy:

i

Metoda siecznej może być rozbieżna tzn. kolejne błędy mogą

wzrastać. W takim przypadku należy zmienić punkty startowe

lub metodę.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

x

2

x

1

28

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ – metoda siecznej cd.

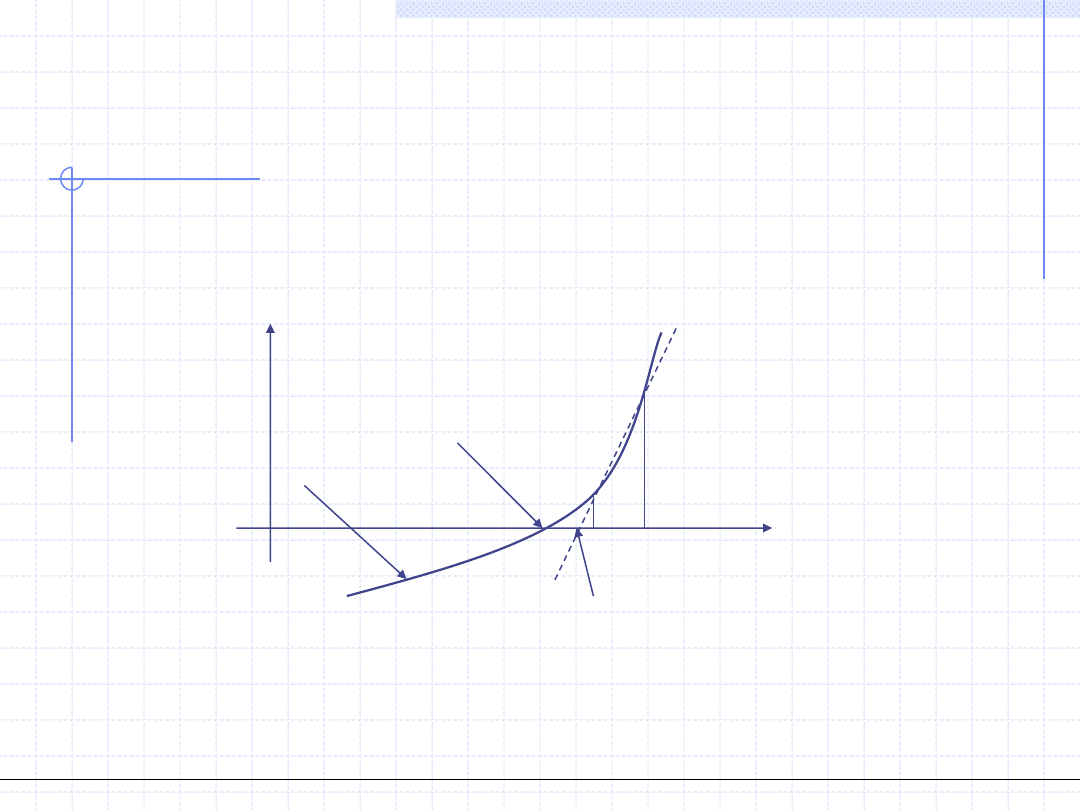
Graficzna ilustracja metody siecznej:

y

x

F(x

1

)

F(x

2

)

x

3

x

*

y=F(x)

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ

–

Metoda Newtona (stycznej)

0

)

(x

F

4. Metoda Newtona (stycznej)

Metoda ta jest bardzo znana i często stosowana.

Warunkiem stosowalności metody jest różniczkowalność

funkcji F w pobliżu pierwiastka.

Ponadto wartość pochodnej funkcji F musi być różna od zera.

Oznacza to, że metoda nie nadaje się do równań, w których

pierwiastek jest jednocześnie ekstremum lub punktem

przegięcia.

Metodę stosujemy do równań w postaci:

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ

–

Metoda Newtona (stycznej)

Krok 1 - Za pomocą dowolnej metody znajdujemy przybliżoną wartość

pierwiastka x

1

oraz przyjmujemy że i=1

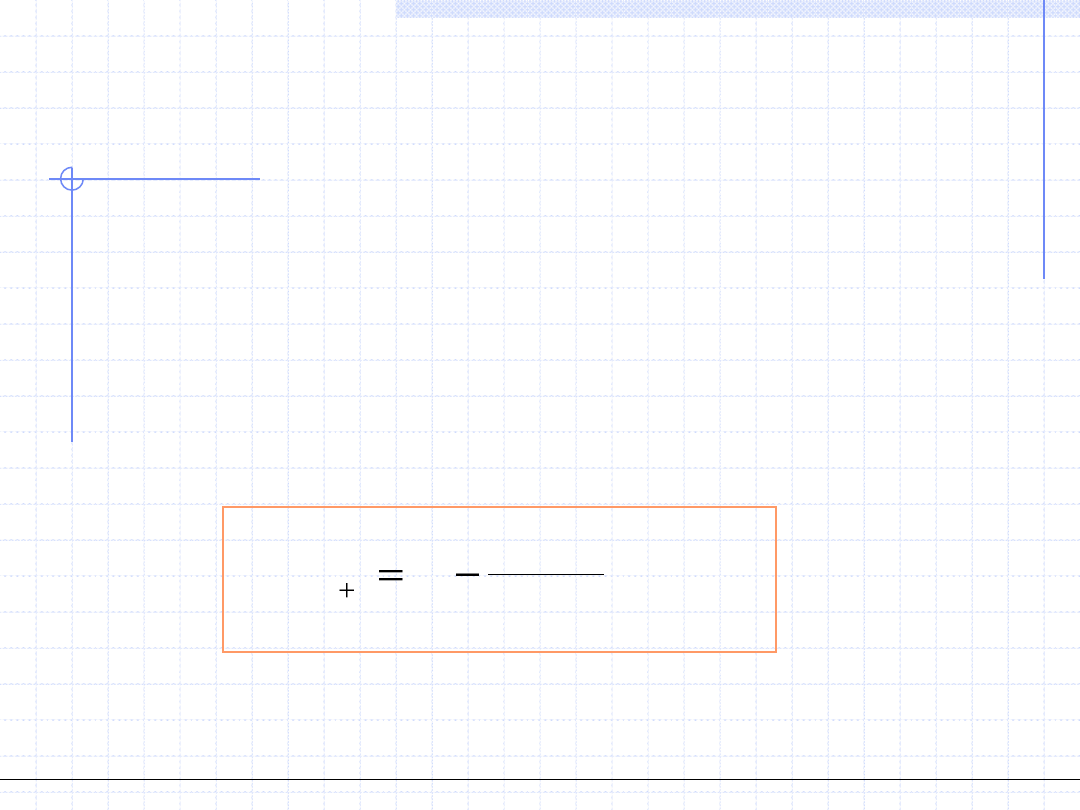
Krok 2 - Różniczkujemy funkcję F(x) i obliczamy pochodną F’(x

i

)

)

(

'

)

(

1

i

i

i

i

x

F

x

F

x

x

Krok 3 - Obliczamy przybliżenie następne x

i+1

za pomocą wzoru

iteracyjnego (na podstawie przybliżenia poprzedniego x

i

)

Istotą metody Newtona jest przyjęcie że funkcja ma w pobliżu

pierwiastka przebieg liniowy zbliżony do stycznej jej wykresu

w punkcie x

i

. Wzór powyższy wynika z tego założenia.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

31

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ

–

Metoda Newtona (stycznej)

Krok 4 - Obliczamy różnicę |x

i+1

-x

i

| i porównujemy ją z zadaną

dokładnością ε.

Krok 5 - Jeżeli aktualna dokładność jest mniejsza od założonej to

zwiększamy numer i o 1 i wracamy do kroku 3 .

Obliczenia przerywamy po uzyskaniu zadanej dokładności.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

32

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ – Metoda Newtona cd.

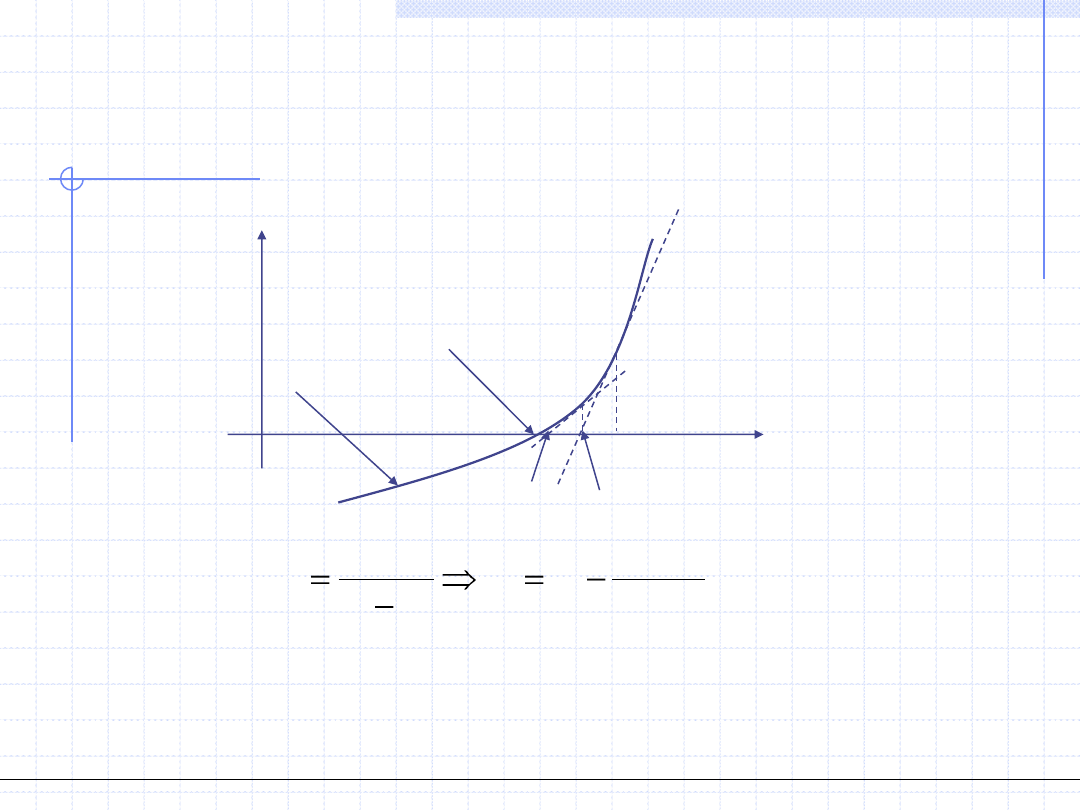
Graficzna ilustracja metody stycznej:

y

x

x

1

F(x

1

)

x

*

y=F(x)

)

(

'

)

(

)

(

)

(

'

1

1

1

2

2

1

1

1

x

F

x

F

x

x

x

x

x

F

x

F

Metoda Newtona może być rozbieżna. W takim przypadku należy albo

poszukać nowego przybliżenia początkowego albo przekształcić równanie

do innej postaci albo też zmienić metodę.

x

2

x

3

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ

–

Metoda iteracji prostej

)

(x

f

x

5. Metoda iteracji prostej Jest to najprostsza z istniejących metod

numerycznych.

Metodę stosujemy do równań postaci:

Krok 1 - Za pomocą dowolnej metody znajdujemy przybliżoną wartość

pierwiastka x

1

oraz przyjmujemy że i=1

)

(

1

i

i

x

f

x

Krok 2 - Obliczamy przybliżenie następne x

i+1

za pomocą wzoru

iteracyjnego (na podstawie przybliżenia poprzedniego x

i

)

będącego bezpośrednim zapisem równania:

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

34

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ

–

Metoda iteracji prostej

Krok 3 - Obliczamy różnicę |x

i+1

-x

i

| i porównujemy ją z zadaną

dokładnością ε.

Krok 4 - Jeżeli aktualna dokładność jest mniejsza od założonej to

zwiększamy numer i o 1 i wracamy do kroku 2 . Obliczenia

przerywamy po osiągnięciu zadanej dokładności.

Również metoda iteracji prostej dosyć często jest rozbieżna. W takim

przypadku zmiana przybliżenia początkowego nic nie daje. Należy albo

przekształcić równanie do innej postaci albo też zmienić metodę.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

x

2

35

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ –

Metoda iteracji prostej cd.

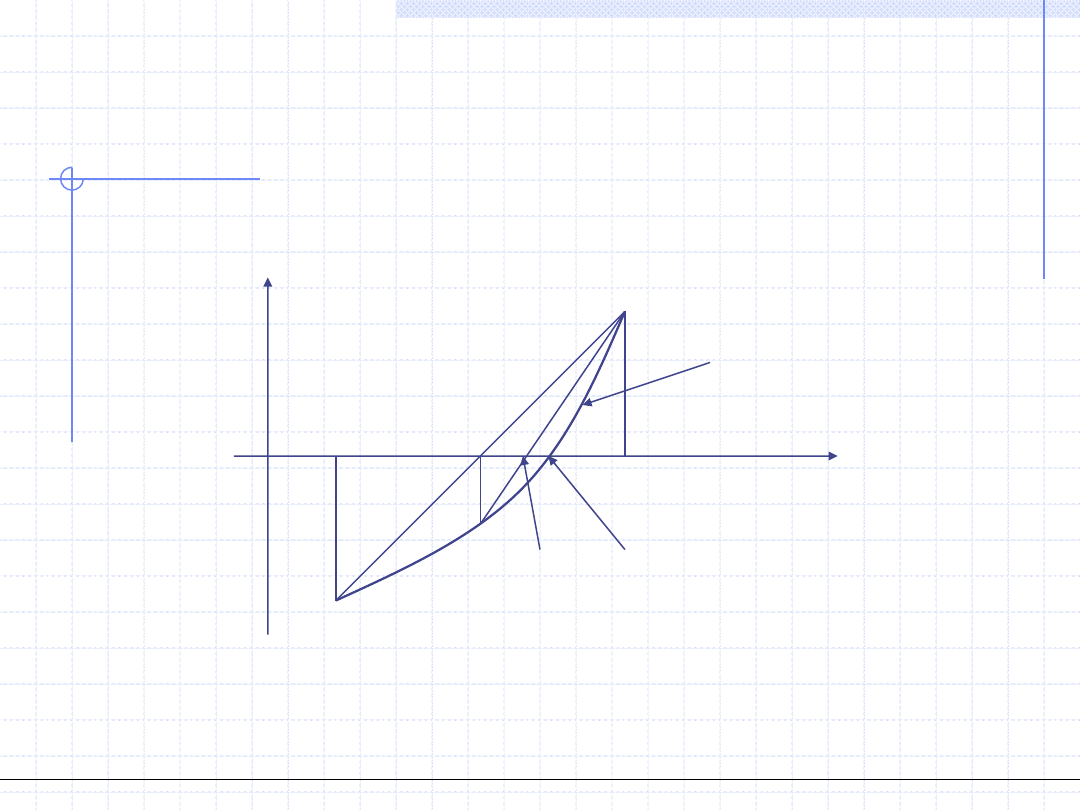
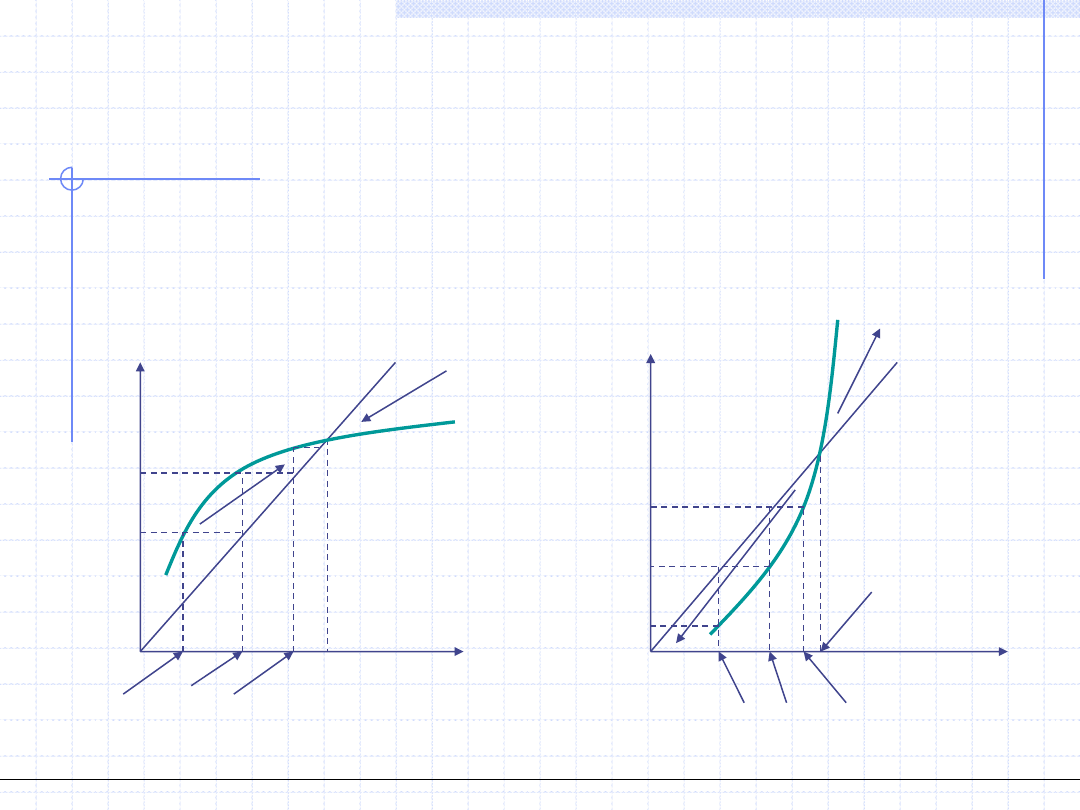
Za pomocą ilustracji graficznej można pokazać przypadki, w których

metoda ta jest zbieżna lub rozbieżna. Rozpatrzmy najpierw funkcje

rosnące.

x

y

y=f(x)

y=x

x

*

f(x

1

)

f(x

2

)

x

y

y=x

y=f(x)

f(x

1

)

f(x

2

)

Metoda zbieżna

Metoda rozbieżna

x*

x

1

x

2

x

3

x

1

x

3

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

36

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ –

Metoda iteracji prostej cd.

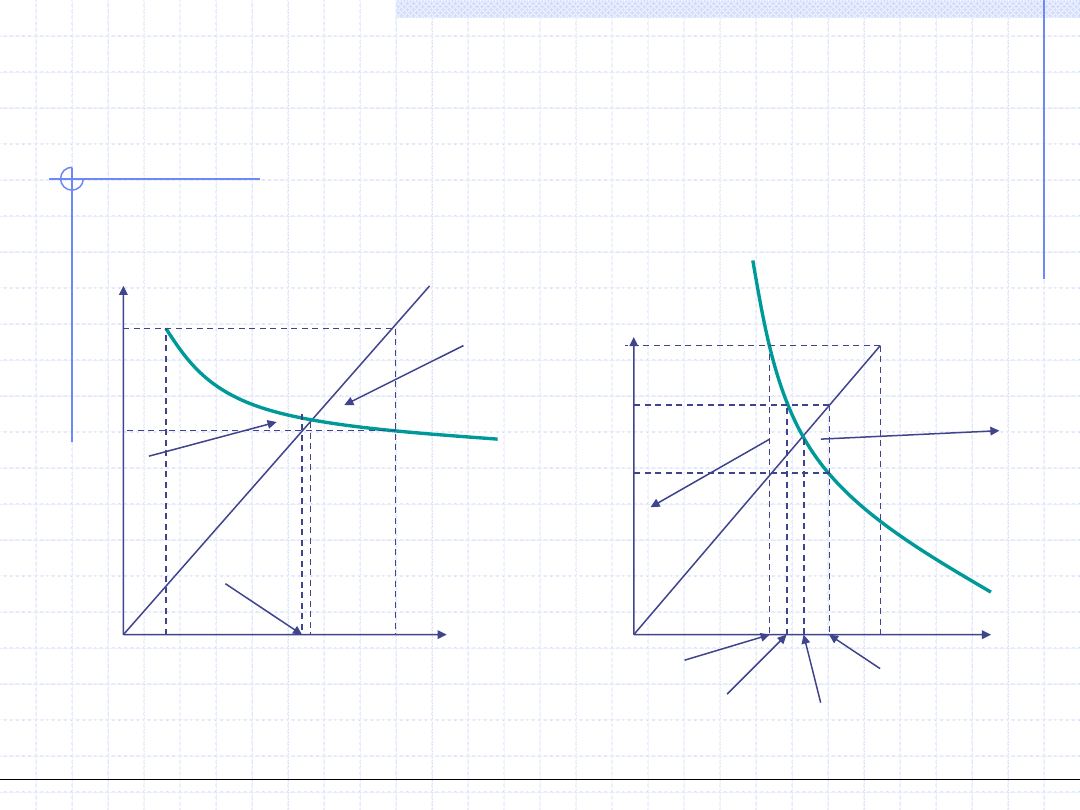
A teraz funkcje malejące.

x

y

y=f(x)

y=x

x

*

x

1

f(x

1

)

f(x

2

)

x

y

y=x

y=f(x)

f(x

1

)

f(x

2

)

Metoda zbieżna

x

2

Metoda rozbieżna

x

3

x

*

x

1

x

2

x

3

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

37

NUMERYCZNE ROZWIĄZYWANIE

RÓWNAŃ –

Metoda iteracji prostej cd.

1

)

(

'

1

x

f

Jeżeli funkcja f(x) jest różniczkowalna to można w prosty sposób określić

zbieżność metody iteracji prostej. O zbieżności metody decyduje

następujące twierdzenie:

Jeżeli w pobliżu pierwiastka równania x=f(x) pochodna funkcji f spełnia

warunek:

to metoda jest zbieżna. Jeżeli natomiast

1

)

(

' x

f

to metoda jest rozbieżna.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

38

ROZWIĄZYWANIE UKŁADÓW

RÓWNAŃ

0

)

,...,

,

(

0

)

,...,

,

(

0

)

,...,

,

(

2

1

2

1

2

2

1

1

n

n

n

n

x

x

x

F

x

x

x

F

x

x

x

F

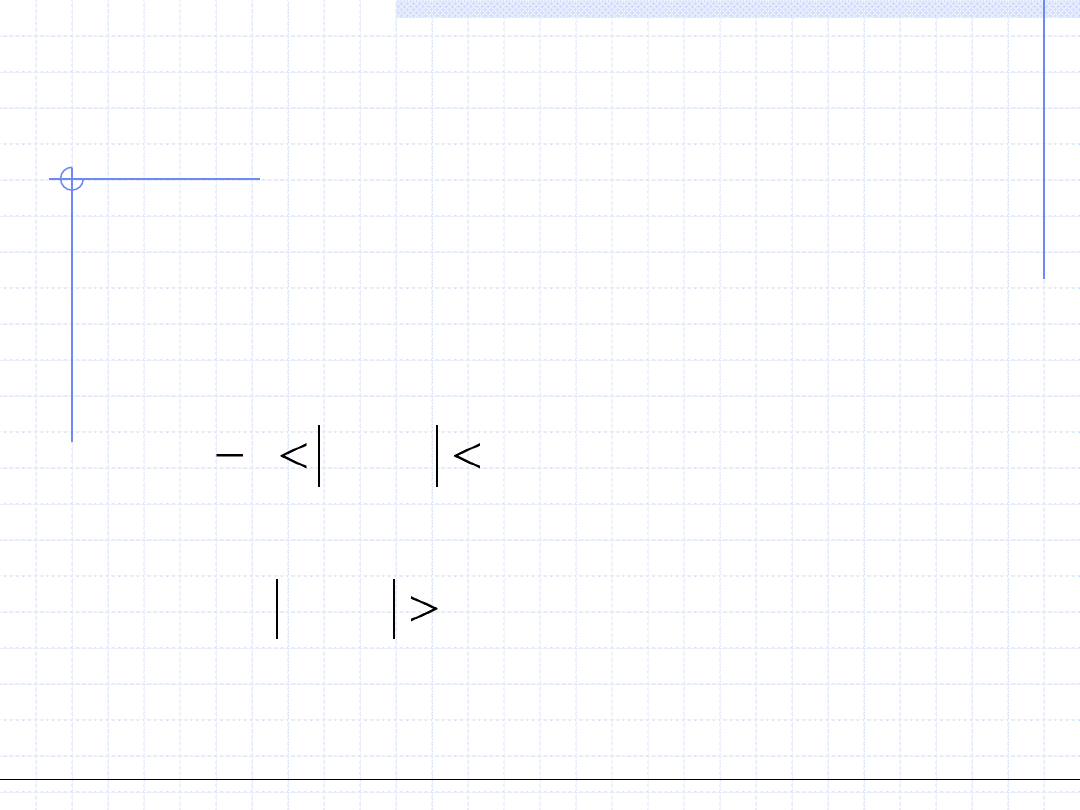
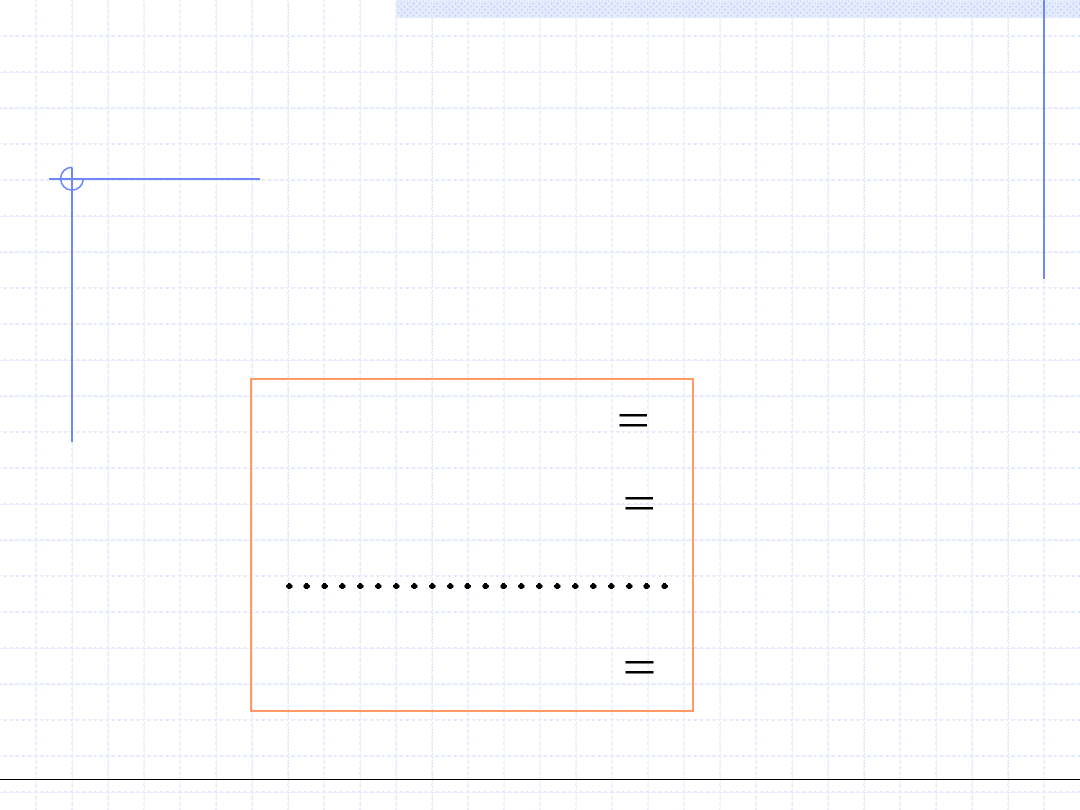
Układem równań nazywamy n równości, w których występuje na ogół

n niewiadomych.

Każdy układ równań daje się sprowadzić do postaci:

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

39

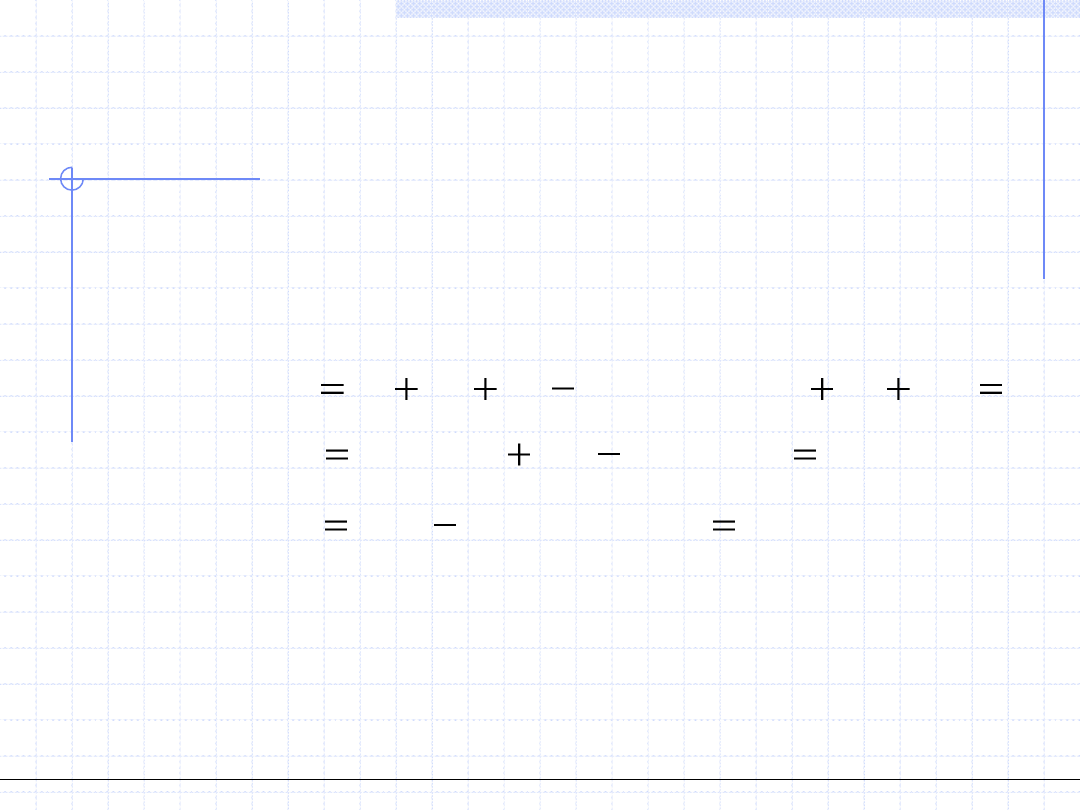
ROZWIĄZYWANIE UKŁADÓW

RÓWNAŃ

0

33904

.

1

)

,

,

(

0

989351

.

0

)

sin(

)

,

,

(

0

)

ln(

4411

.

61

)

,

,

(

3

2

1

3

2

1

3

3

2

1

3

2

1

2

3

2

1

3

3

2

2

1

3

2

1

1

2

1

x

x

x

e

x

x

x

F

x

x

x

x

x

x

F

x

x

x

x

x

x

x

x

x

F

x

x

Przykładowy układ równań

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

40

ROZWIĄZYWANIE UKŁADÓW

RÓWNAŃ

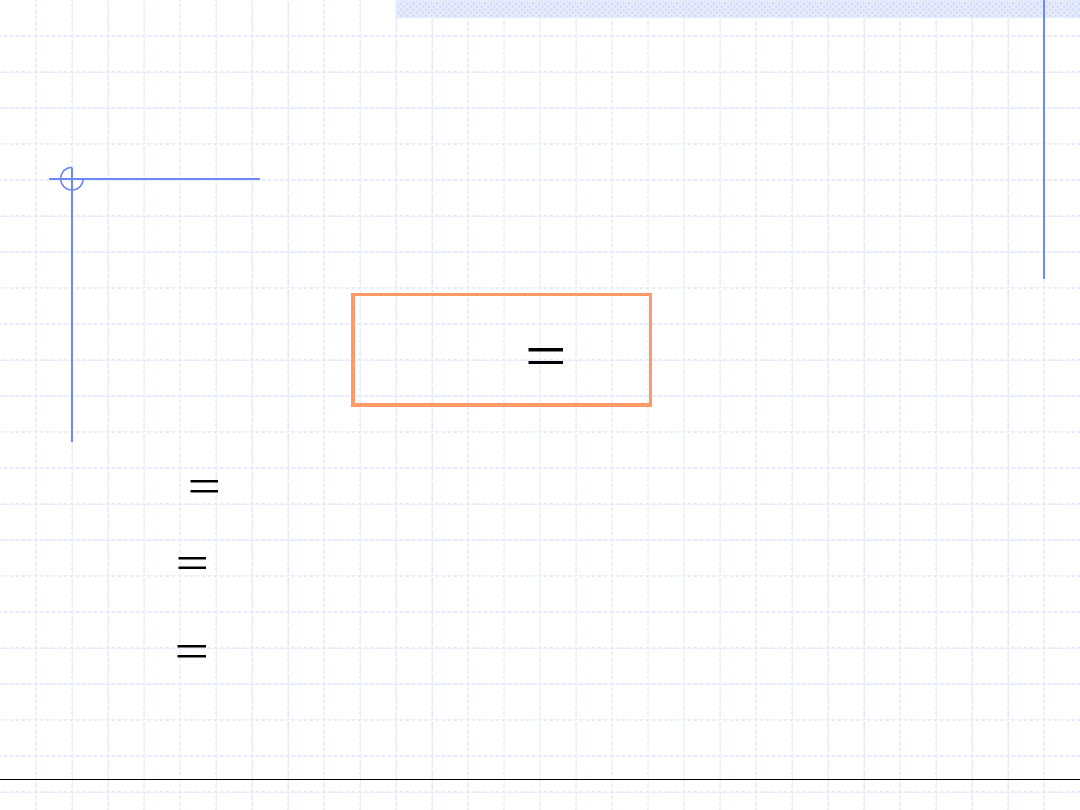
Układ równań możemy zapisać w postaci wektorowej:

wektorowa

funkcja

F

F

F

F

n

]

,...

,

[

2

1



0

)

(







x

F

ch

niewiadomy

wektor

x

x

x

x

n

]

,...

,

[

2

1



zerowy

wektor

]

0

,...

0

,

0

[

0



© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

41

ROZWIĄZYWANIE UKŁADÓW

RÓWNAŃ

Układy podobnie jak pojedyncze równania można rozwiązywać metodami

analitycznymi (dokładnymi) lub numerycznymi (przybliżonymi).

Analitycznie można rozwiązywać np. układy równań liniowych lub

niektóre proste układy nieliniowe.

W metodach numerycznych konstruuje się ciąg wektorów zbieżny do

wektora pierwiastków niewiadomych. W związku z tym, że jest to ciąg

wektorowy, charakter wektorowy ma również dokładność pierwiastka

i dokładność równań.

]

)

(

,...,

)

(

,

)

(

[

]

,...,

,

[

)

(

)

(

2

)

(

1

)

(

)

(

2

)

(

1

)

(

i

n

i

i

i

yn

i

y

i

y

i

y

x

F

x

F

x

F









]

,...,

,

[

]

,...,

,

[

)

(

)

(

2

2

)

(

1

1

)

(

)

(

2

)

(

1

)

(

i

n

n

i

i

i

xn

i

x

i

x

i

x

x

x

x

x

x

x



© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

42

ROZWIĄZYWANIE UKŁADÓW

RÓWNAŃ

W celu stwierdzenia kiedy należy zakończyć konstrukcję ciągu rozwiązań

konieczne jest znormalizowanie (czyli „zmierzenie”) powyższych wektorów.

Najczęściej stosowane są dwie normy: jednostajna i średniokwadratowa.

Stosowanie normy jednostajnej jest bardziej rygorystyczne niż normy

średniokwadratowej, tzn. że norma jednostajna zazwyczaj prowadzi do

dłuższych obliczeń.

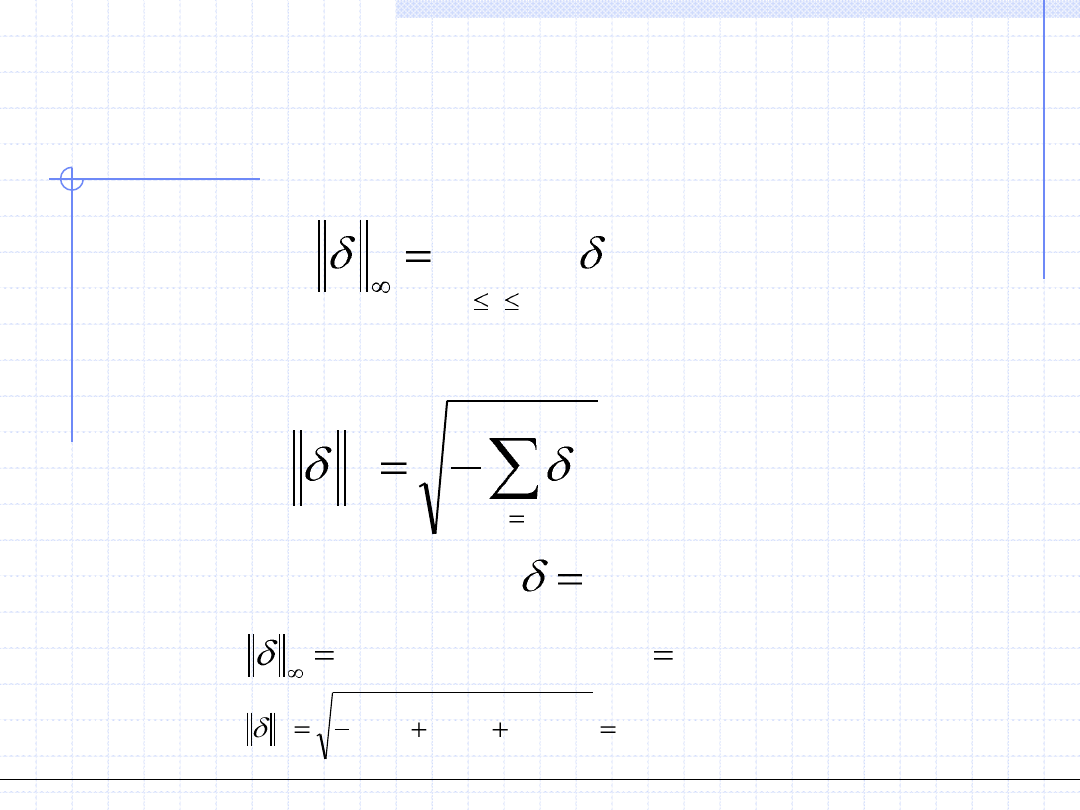
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

43

ROZWIĄZYWANIE UKŁADÓW

RÓWNAŃ

)

(

max

1

j

n

j



n

j

j

n

1

2

2

1



Norma jednostajna:

Norma średniokwadratowa:

Rozważmy przykładowy wektor:

1

.

0

)

001

.

0

,

01

.

0

,

1

.

0

max(

]

001

.

0

,

01

.

0

,

1

.

0

[

058026

.

0

)

001

.

0

01

.

0

1

.

0

(

3

1

2

2

2

2

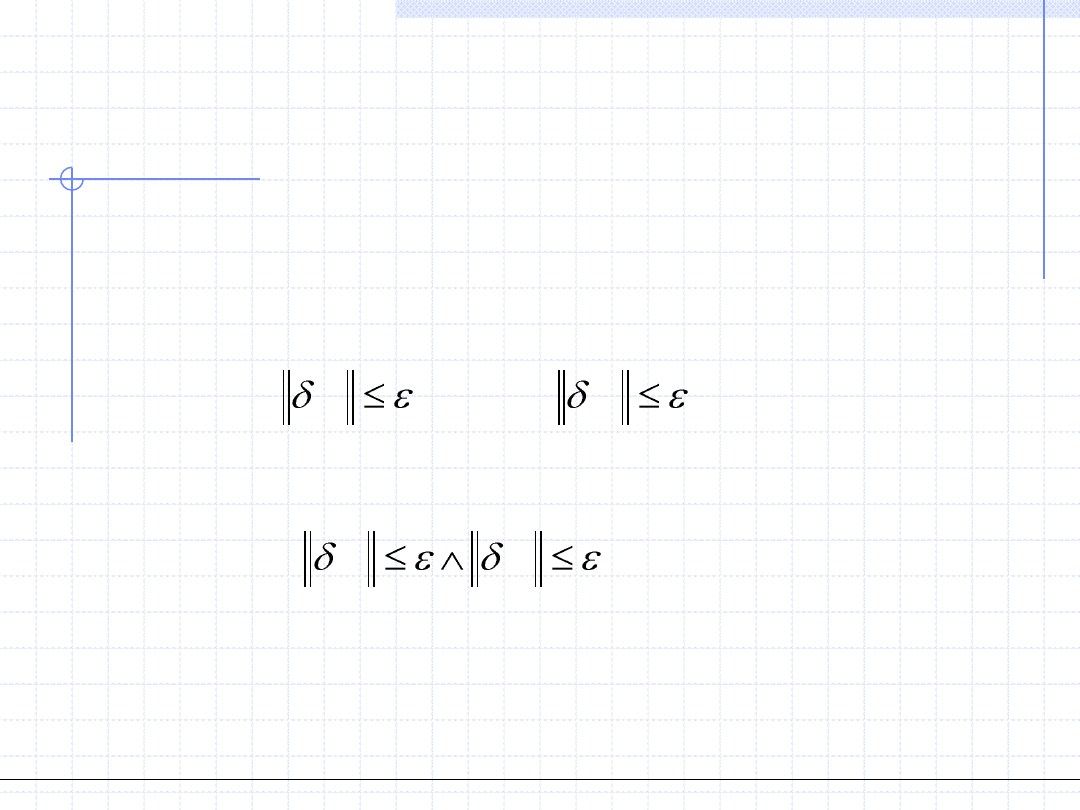
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

44

ROZWIĄZYWANIE UKŁADÓW

RÓWNAŃ

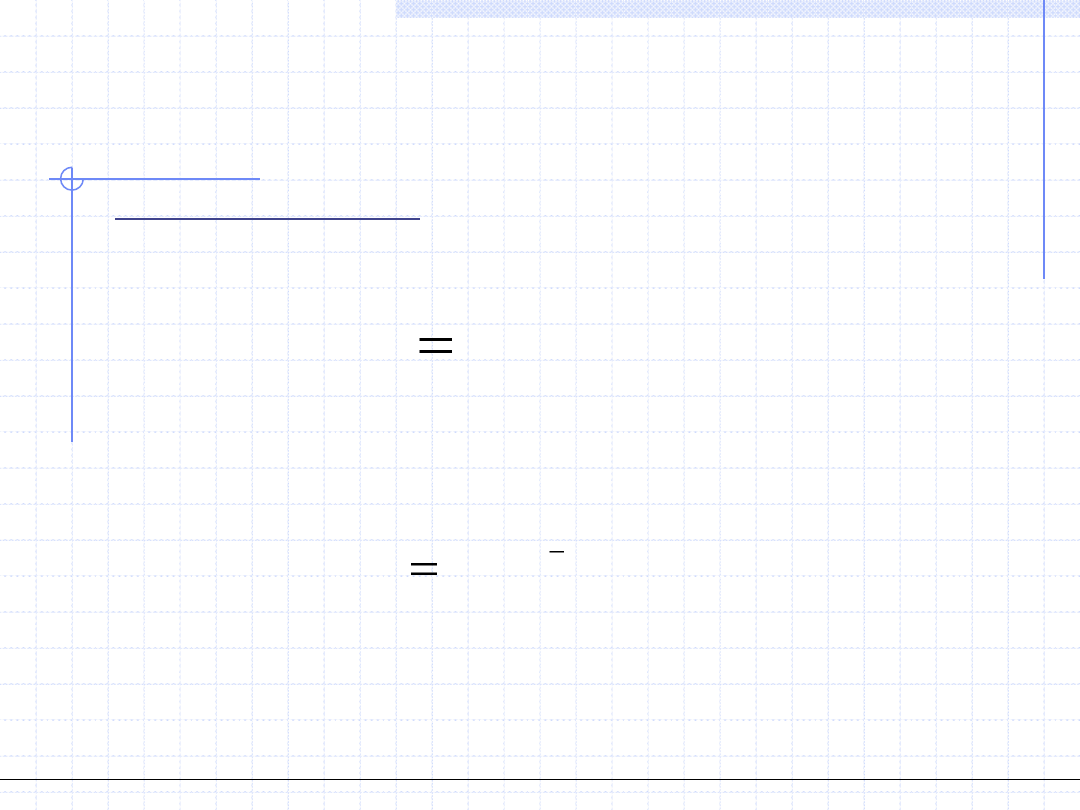
Konstrukcja ciągu rozwiązań jest przerywana gdy norma wybranej

dokładności (pierwiastka lub równania) staje się mniejsza lub równa

zadanej dokładności obliczeń ε czyli:

)

(

)

(

lub

i

y

i

x

)

(

)

(

)

(

i

y

i

x

albo

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

45

NUMERYCZNE ROZWIĄZYWANIE

UKŁADÓW RÓWNAŃ

)

(x

f

x







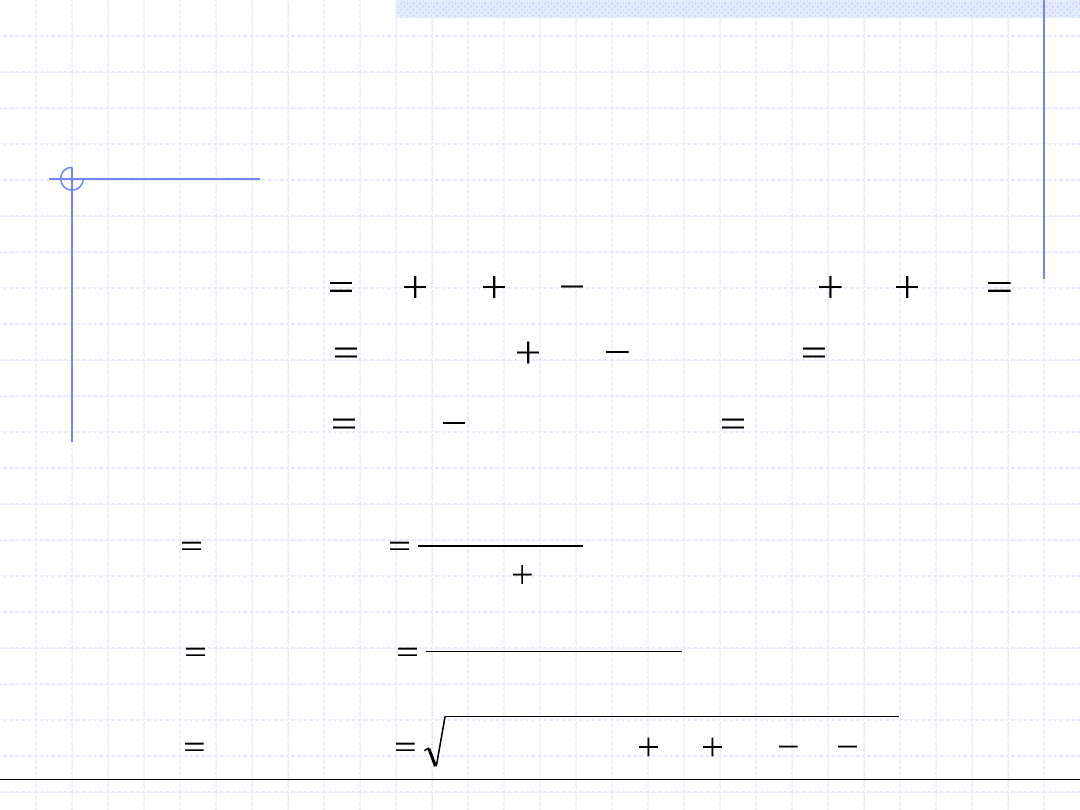
1. Metoda iteracji prostej.

Aby zastosować tę metodę układ równań należy przekształcić

do postaci:

W pierwszym kroku trzeba znaleźć pierwsze przybliżenie wektora

niewiadomych czyli startowe wartości wszystkich niewiadomych.

Kolejne wyrazy ciągu znajdujemy bezpośrednio za pomocą równania tzn.:

)

(

)

1

(

)

(

i

i

x

f

x







Metoda jest zbieżna gdy ciąg norm wektora dokładności jest zbieżny do zera.

Na ogół jednak metoda iteracji prostej nie jest zbieżna.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

46

NUMERYCZNE ROZWIĄZYWANIE

UKŁADÓW RÓWNAŃ

0

33904

.

1

)

,

,

(

0

989351

.

0

)

sin(

)

,

,

(

0

)

ln(

4411

.

61

)

,

,

(

3

2

1

3

2

1

3

3

2

1

3

2

1

2

3

2

1

3

3

2

2

1

3

2

1

1

2

1

x

x

x

e

x

x

x

F

x

x

x

x

x

x

F

x

x

x

x

x

x

x

x

x

F

x

x

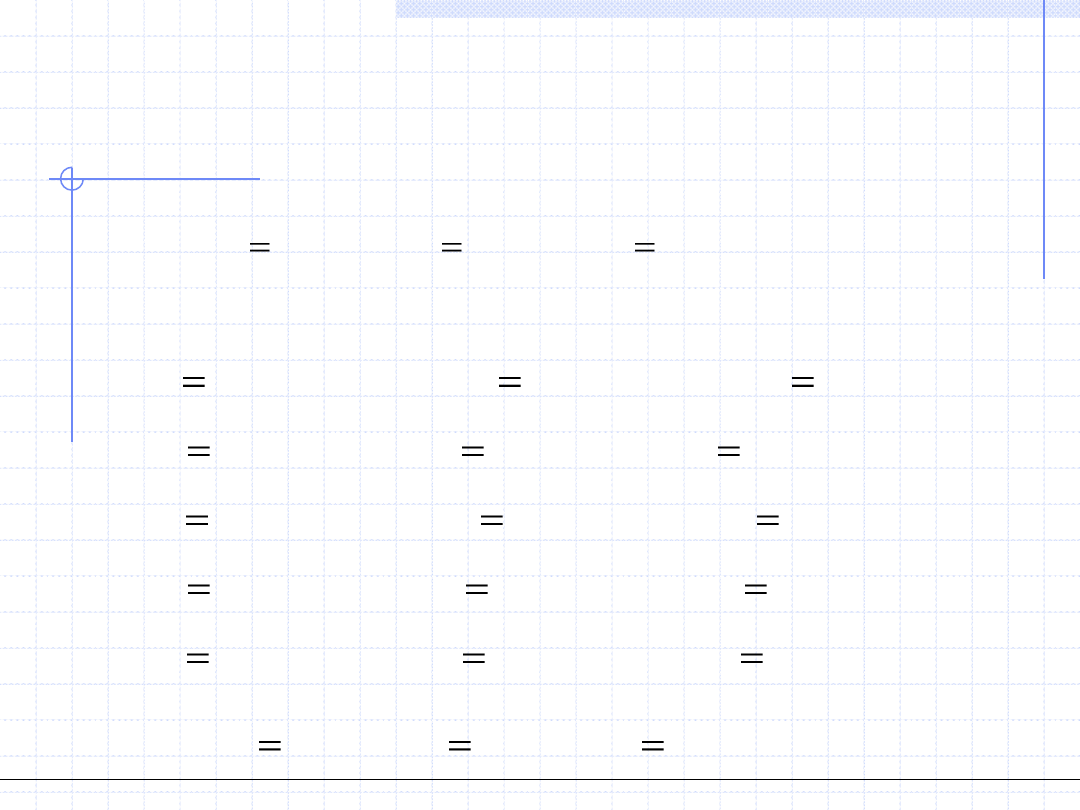
Spróbujmy rozwiązać metodą iteracji prostej nasz przykładowy

układ równań:

Za pomocą prostych przekształceń układ ten można doprowadzić do postaci:

3

2

2

1

3

2

1

3

2

1

3

3

1

3

2

1

3

2

1

2

2

3

2

3

2

1

1

1

)

ln(

4411

.

61

)

,

,

(

)

33904

.

1

ln(

)

,

,

(

)

sin(

989351

.

0

)

,

,

(

x

x

x

x

x

x

x

x

f

x

x

x

x

x

x

x

x

f

x

x

x

x

x

x

f

x

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

47

NUMERYCZNE ROZWIĄZYWANIE

UKŁADÓW RÓWNAŃ

9

.

4

9

.

2

9

.

0

)

0

(

3

)

0

(

2

)

0

(

1

x

x

x

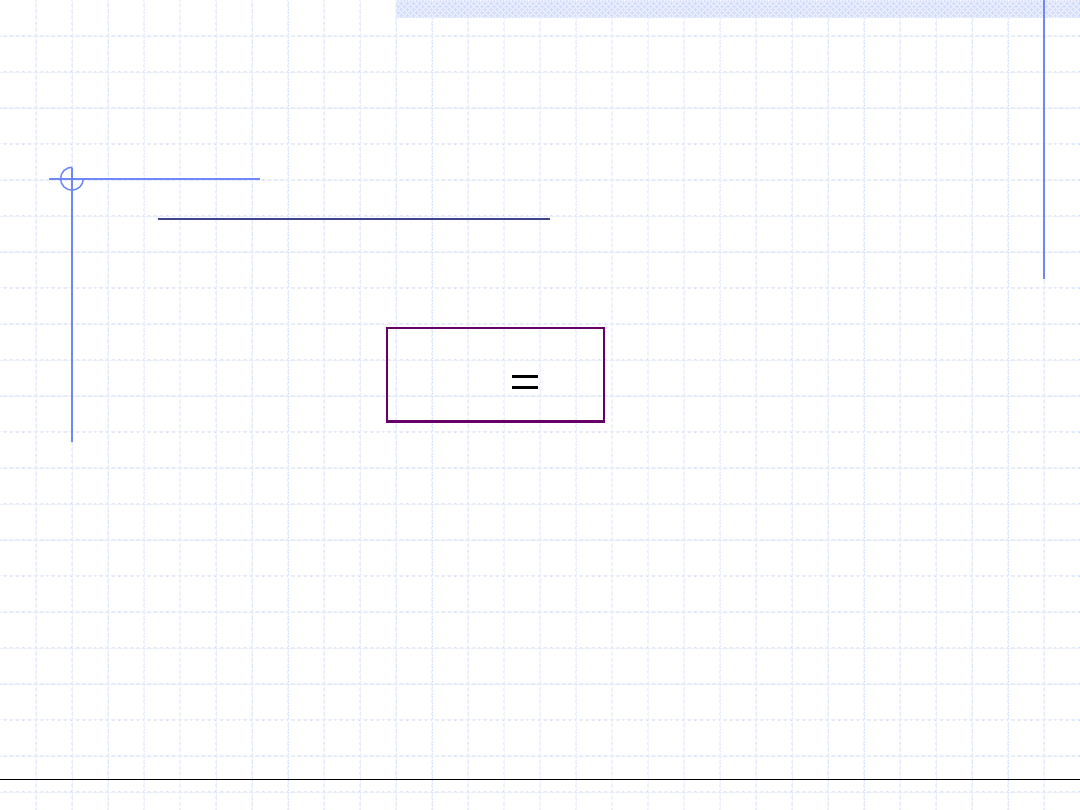
Załóżmy że początkowy wektor rozwiązań wynosi:

Za pomocą wzorów określających postać iteracyjną układu można obliczyć

kolejne wektory rozwiązania:

9993

.

4

9974

.

2

9955

.

0

0073

.

5

9644

.

2

9954

.

0

0029

.

5

9613

.

2

01177

.

1

9989

.

4

066

.

3

0305

.

1

8139

9

.

4

15615

.

3

990794

.

0

)

5

(

3

)

5

(

2

)

5

(

1

)

4

(

3

)

4

(

2

)

4

(

1

)

3

(

3

)

3

(

2

)

3

(

1

)

2

(

3

)

2

(

2

)

2

(

1

)

1

(

3

)

1

(

2

)

1

(

1

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

Widzimy że metoda jest zbieżna a wektor rozwiązań wynosi:

0

.

5

0

.

3

0

.

1

3

2

1

x

x

x

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

NUMERYCZNE ROZWIĄZYWANIE

UKŁADÓW RÓWNAŃ

0

)

(







x

F

2. Metoda Newtona - Raphsona.

Jest to adaptacja metody stycznej do układów równań.

Metodę stosuje się do układu w postaci:

W pierwszym kroku trzeba znaleźć pierwsze przybliżenie wektora

niewiadomych czyli startowe wartości wszystkich niewiadomych.

Kolejne wyrazy ciągu znajdujemy za pomocą następującej procedury:

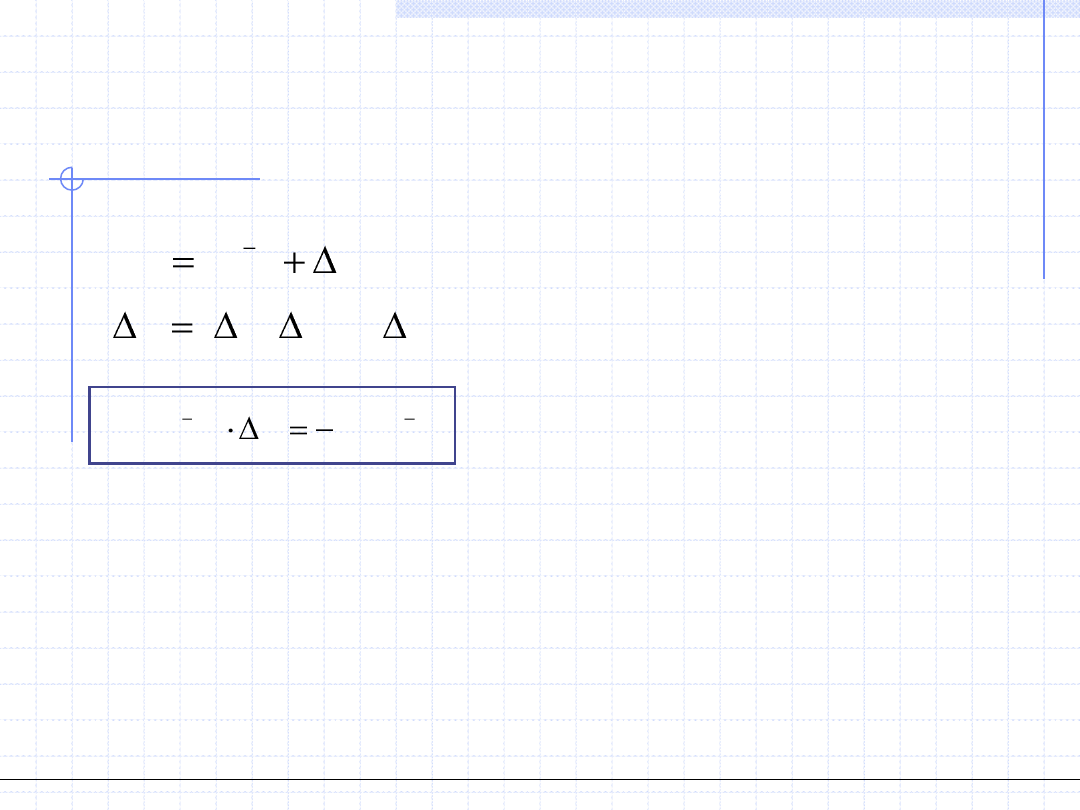
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

49

NUMERYCZNE ROZWIĄZYWANIE

UKŁADÓW RÓWNAŃ

]

,...,

,

[

)

(

)

(

2

)

(

1

)

(

)

(

)

1

(

)

(

i

n

i

i

i

i

i

i

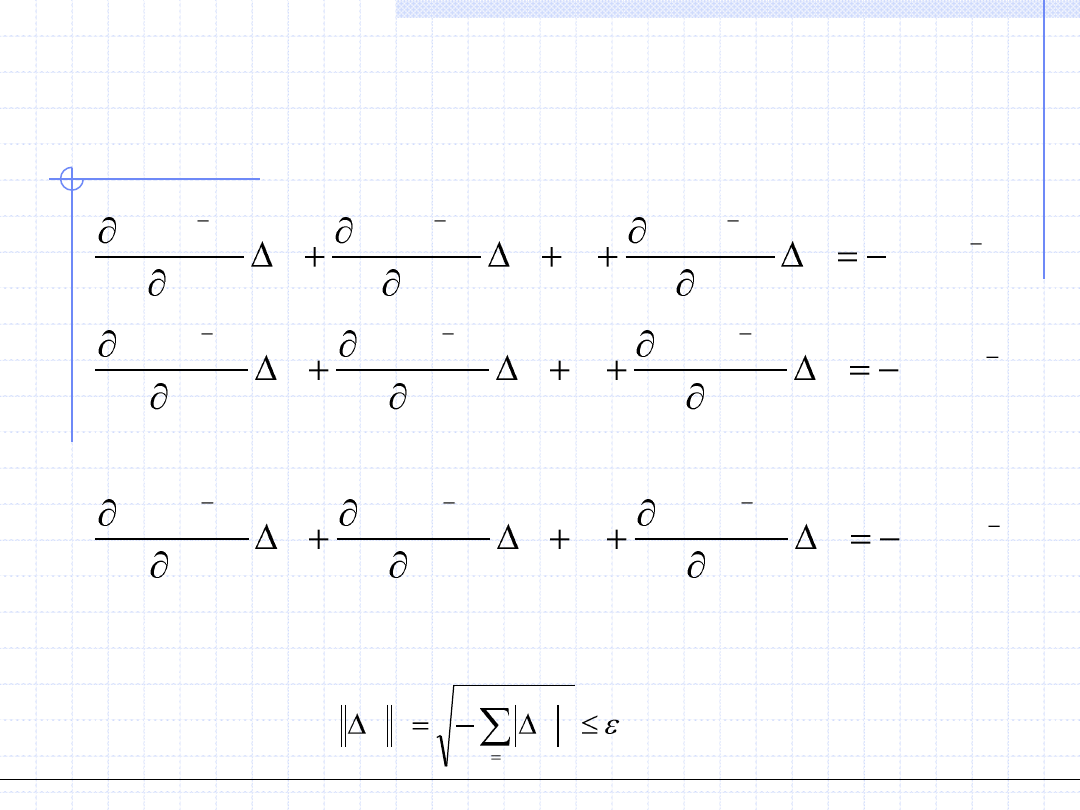
gdzie

x

x









- wektor przyrostów wyznaczany za

pomocą układu równań liniowych

w zapisie macierzowym:

)

(

)

(

'

)

1

(

)

(

)

1

(

i

i

i

x

F

x

F











F’ oznacza macierz kwadratową pochodnych cząstkowych funkcji

wektorowej F.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

50

NUMERYCZNE ROZWIĄZYWANIE

UKŁADÓW RÓWNAŃ

)

(

)

(

...

)

(

)

(

..

..........

..........

..........

..........

..........

..........

..........

..........

..........

..........

)

(

)

(

...

)

(

)

(

)

(

)

(

...

)

(

)

(

)

1

(

)

(

)

1

(

)

(

2

2

)

1

(

)

(

1

1

)

1

(

)

1

(

2

)

(

)

1

(

2

)

(

2

2

)

1

(

2

)

(

1

1

)

1

(

2

)

1

(

1

)

(

)

1

(

1

)

(

2

2

)

1

(

1

)

(

1

1

)

1

(

1

i

n

i

n

n

i

n

i

i

n

i

i

n

i

i

n

n

i

i

i

i

i

i

i

n

n

i

i

i

i

i

x

F

x

x

F

x

x

F

x

x

F

x

F

x

x

F

x

x

F

x

x

F

x

F

x

x

F

x

x

F

x

x

F

























Pełny zapis tego pomocniczego układu równań jest następujący:

Proces konstrukcji ciągu rozwiązań przerywamy gdy norma

(średniokwadratowa lub jednostajna) wektora przyrostów osiągnie zadaną

dokładność ε.

n

j

i

j

i

n

1

2

)

(

2

)

(

1

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

51

NUMERYCZNE ROZWIĄZYWANIE

UKŁADÓW RÓWNAŃ

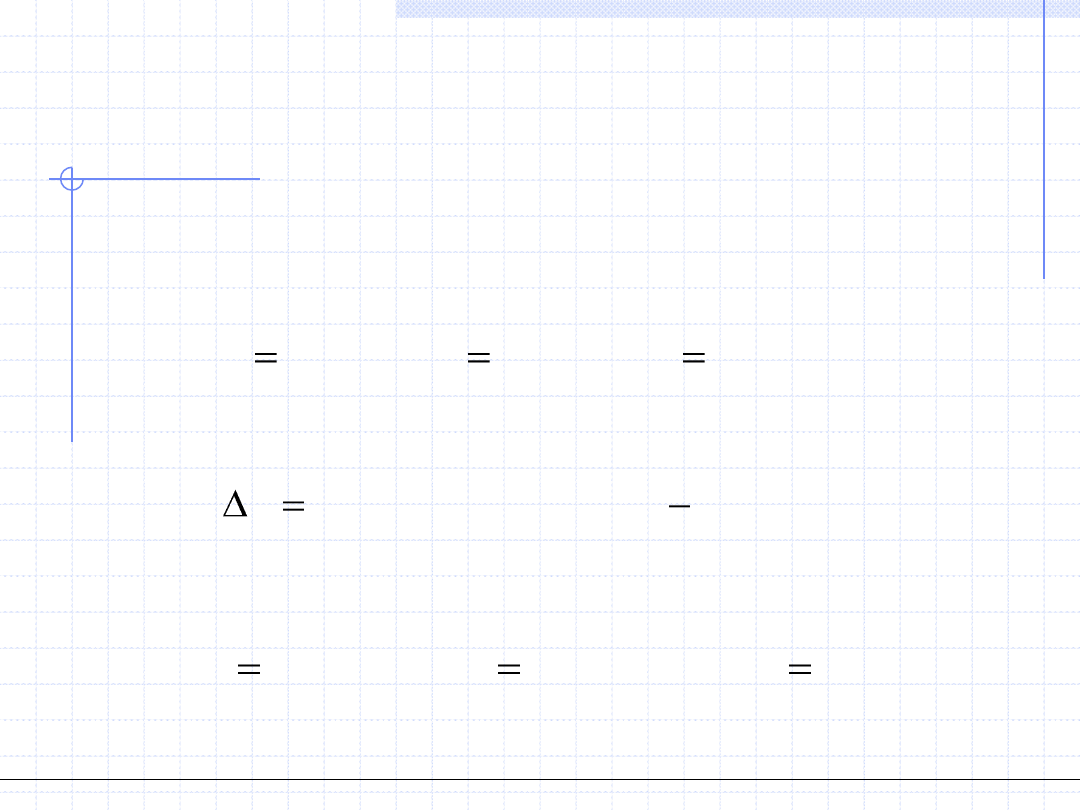
Rozwiążmy za pomocą metody Newtona – Raphsona nasz przykładowy

układ równań.

5

.

5

7

.

2

8

.

0

)

0

(

3

)

0

(

2

)

0

(

1

x

x

x

Załóżmy że początkowy wektor rozwiązań wynosi:

Podstawiając te wartości do zasadniczego układu równań liniowych

otrzymujemy wektor przyrostów Δ:

]

422735

.

0

,

671782

.

0

,

323508

.

0

[

)

1

(

Dodając odpowiednie przyrosty otrzymujemy poprawiony wektor

rozwiązań:

07724

.

5

37178

.

3

12351

.

1

)

1

(

3

)

1

(

2

)

1

(

1

x

x

x

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

52

NUMERYCZNE ROZWIĄZYWANIE

UKŁADÓW RÓWNAŃ

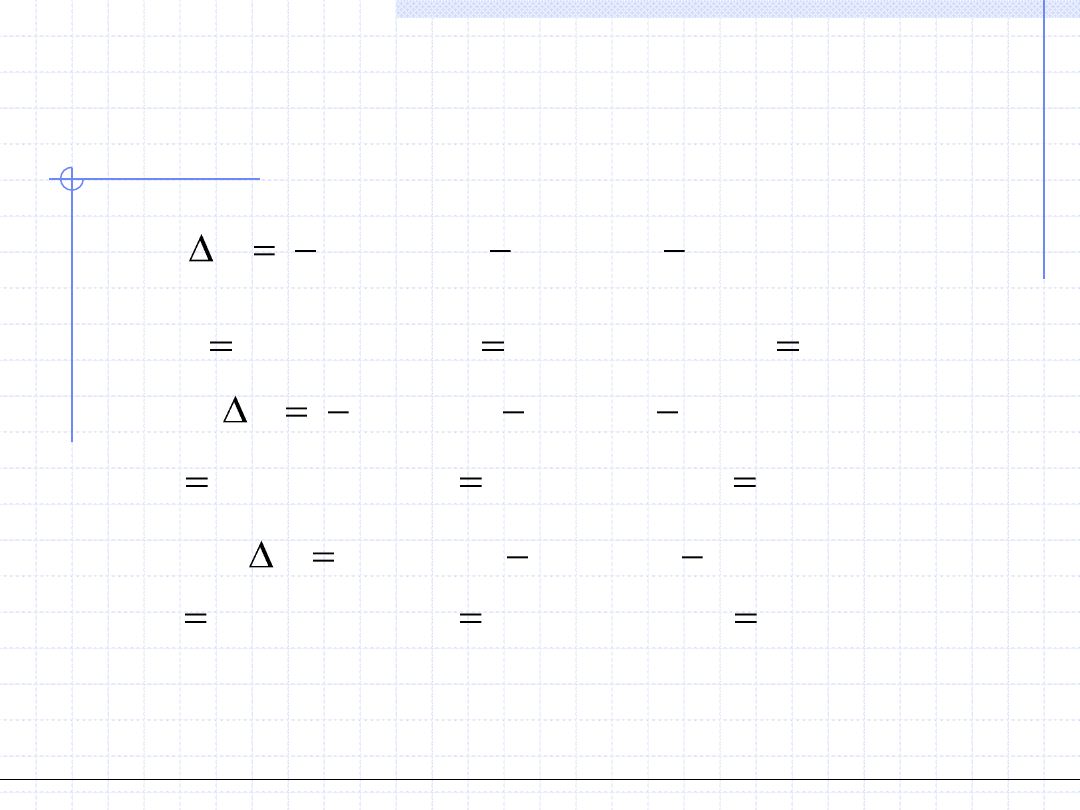
Podstawieniu nowych wartości prowadzi do drugiego wektora Δ:

]

073858

.

0

,

17273

.

0

,

116344

.

0

[

)

2

(

co daje kolejny wektor rozwiązań:

0034

.

5

19905

.

3

00716

.

1

)

2

(

3

)

2

(

2

)

2

(

1

x

x

x

i dalej:

]

002946

.

0

,

1583

.

0

,

01354

.

0

[

)

3

(

00044

.

5

0408

.

3

99362

.

0

)

3

(

3

)

3

(

2

)

3

(

1

x

x

x

]

00044

.

0

,

03925

.

0

,

00585

.

0

[

)

4

(

00000

.

5

0015

.

3

99948

.

0

)

4

(

3

)

4

(

2

)

4

(

1

x

x

x

Widzimy, że w czwartej iteracji otrzymaliśmy dokładność

rzędu jednej tysięcznej.