© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
1
METODY MATEMATYCZNE I
STATYSTYCZNE
W INŻYNIERII CHEMICZNEJ
Wykład 3
Elementy analizy pól skalarnych,
wektorowych i tensorowych
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
2
Analiza pól – Uwagi wstępne
Bardzo ważnym pojęciem w fizyce a także inżynierii chemicznej jest
pojęcie pola.
Polem nazywamy pewną funkcję wielu zmiennych, w której
argumentami są położenie i czas.
Za pomocą pól opisuje się różne procesy zachodzące w przestrzeni
i czasie.
pole
(po o enie, czas)
f
ł ż
W zależności od rodzaju wielkości jaką opisuje dane pole rozróżniamy
pola skalarne, wektorowe i tensorowe.
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
3
Analiza pól – Uwagi wstępne
Stosunkowo prostą zmienną jest czas, który często identyfikowany
jest ze zbiorem nieujemnych liczb rzeczywistych R
+
. Najczęściej czas
jest oznaczany literą t.
Zatem tєR+tzn. 0≤t<∞.
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
4
Analiza pól – Uwagi wstępne
Znacznie bardziej złożone jest zagadnienie opisu położenia.
Przyjmuje się, że procesy zachodzą w przestrzeni trójwymiarowej
a zatem do opisu położenia potrzebne są 3 składowe. W zależności
od geometrii opisywanego zjawiska stosowane mogą być różne
układy współrzędnych przestrzennych.
Najczęściej stosowane są trzy rodzaje układów współrzędnych
przestrzennych:
-
kartezjański układ prostokątny,
-
układ cylindryczny,
-
układ sferyczny.
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
5
Analiza pól – Układy
współrzędnych przestrzennych
1. Układ kartezjański.
Ustalenie położenia polega na wyborze w przestrzeni trzech
wzajemnie prostopadłych i przecinających się w jednym
punkcie prostych określanych tradycyjnie jako osie
współrzędnych x,y,z.
Położenie „u” danego punktu w przestrzeni określa trójka
liczb x,y,z będących rzutami punktu u na odpowiednie osie.
Możemy to zapisać: u=[u
x
,u
y
,u
z
]
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
6
Analiza pól – Układy
współrzędnych przestrzennych
x
y
z
u
u
xy
u
x
u
y
u
z
O
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
7
Analiza pól – Układy
współrzędnych przestrzennych
1. Układ kartezjański.
Współrzędne układu kartezjańskiego są dowolnymi liczbami
rzeczywistymi x,y,z:
-∞<x<∞
-∞<y<∞
-∞<z<∞
x
y
z
u
u
xy
u
x
u
y
u
z
O
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
8
Analiza pól – Układy
współrzędnych przestrzennych
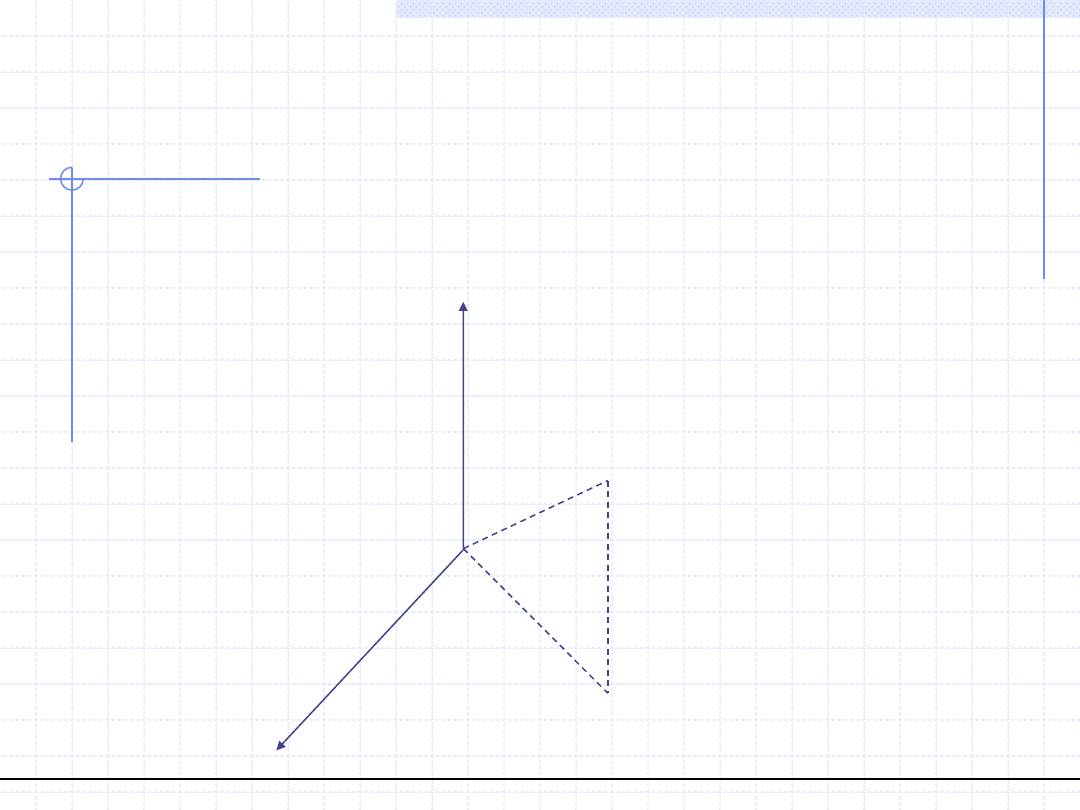
2. Układ cylindryczny.
Podstawową rolę w układzie cylindrycznym odgrywa płaszczyzna z wyróżnioną
półprostą Ox oraz prostopadła do tej płaszczyzny i przechodząca przez punkt O
oś z. Położenie punktu u określamy za pomocą trójki liczb rzeczywistych
u=[r
c
,φ,u
z
]=[r
c
,φ,z] gdzie:
x
z
u
u’
u
z
O
φ
r
c
r
c
– odległość punktu u’ będącego
rzutem punktu u na płaszczyznę
od punktu O, czyli długość
odcinka u’O. r
c
≥0
φ – kąt między półprostą Ox
a odcinkiem Ou’. 0≤φ<2π
u
z
=z – współrzędna rzutu punktu
u na oś z. -∞<z<∞
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
9
Analiza pól – Układy
współrzędnych przestrzennych
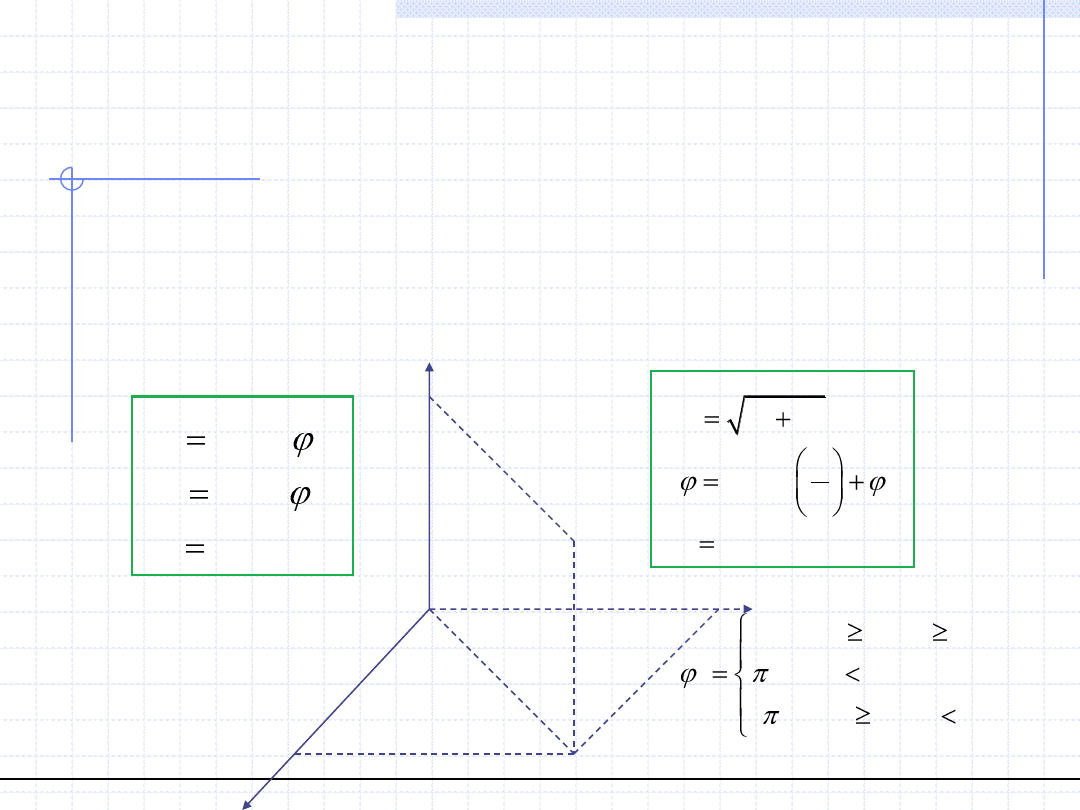
3. Układ sferyczny.
Podstawową rolę w układzie sferycznym odgrywa płaszczyzna z wyróżnioną
półprostą Ox oraz prostopadła do tej płaszczyzny i przechodząca przez punkt O
oś z. Położenie punktu u określamy za pomocą trójki liczb rzeczywistych
u=[r
s
,φ,θ] gdzie:
x
z
u
u’
O
φ
r
s
r
s
– odległość punktu u będącego
od punktu O, czyli długość
odcinka uO. r
s
≥0
φ – kąt między półprostą Ox
a odcinkiem Ou’. 0≤φ<2π
θ – kąt między dodatnim kierunkiem
osi z a odcinkiem Ou. 0≤θ≤π
θ
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
10
Analiza pól – Przeliczanie
współrzędnych
cos
sin
c
c
x
r
y
r
z
z
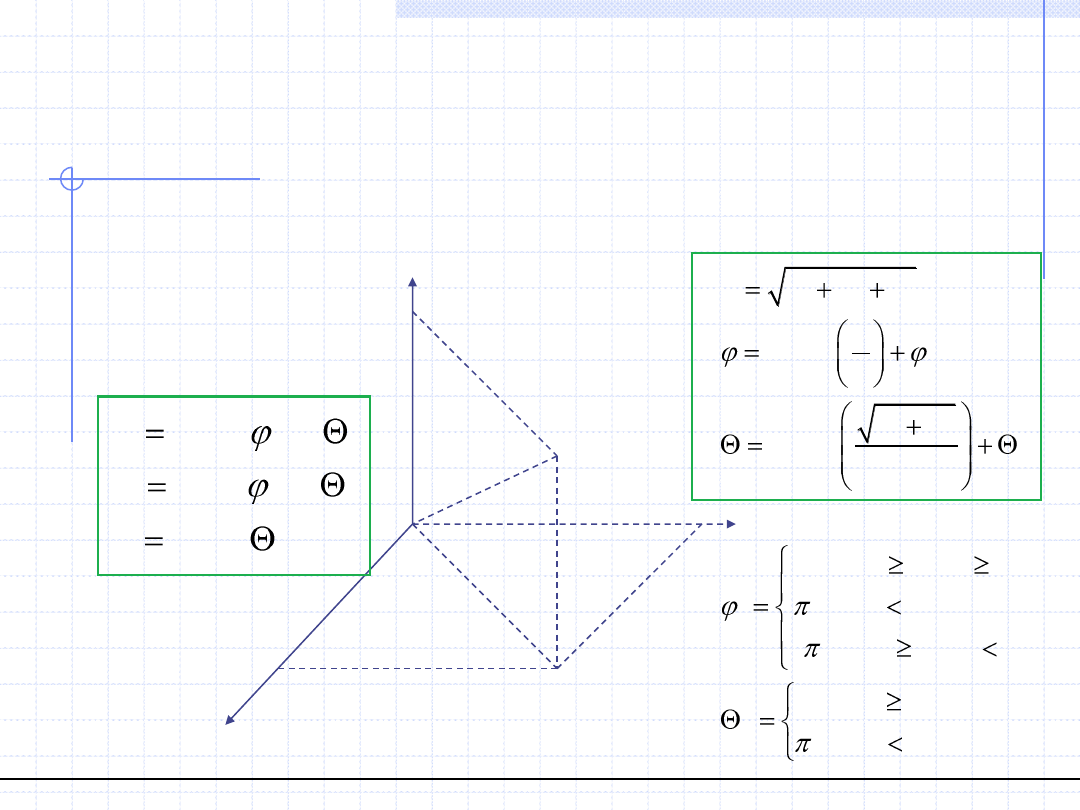
Współrzędne w różnych układach można wzajemnie przeliczać. Szczególnie ważne
są wzory przeliczeniowe między układem kartezjańskim a cylindrycznym i sferycznym.
Wzory te można otrzymać na podstawie elementarnych relacji geometryczno –
trygonometrycznych.
x
z
u
u’
u
z
O
φ
r
c
y
2
2
0
0
arctan
0
0
0
0
2
0
0
c
r
x
y
y
x
z
z
gdzie
dla x
i y
dla x
dla x
i y
Układ cylindryczny –> układ kartezjański:
.
Układ kartezjański –> układ cylindryczny:
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
11
Analiza pól – Przeliczanie
współrzędnych
cos sin
sin sin
cos
s
s
s
x
r
y
r
z
r
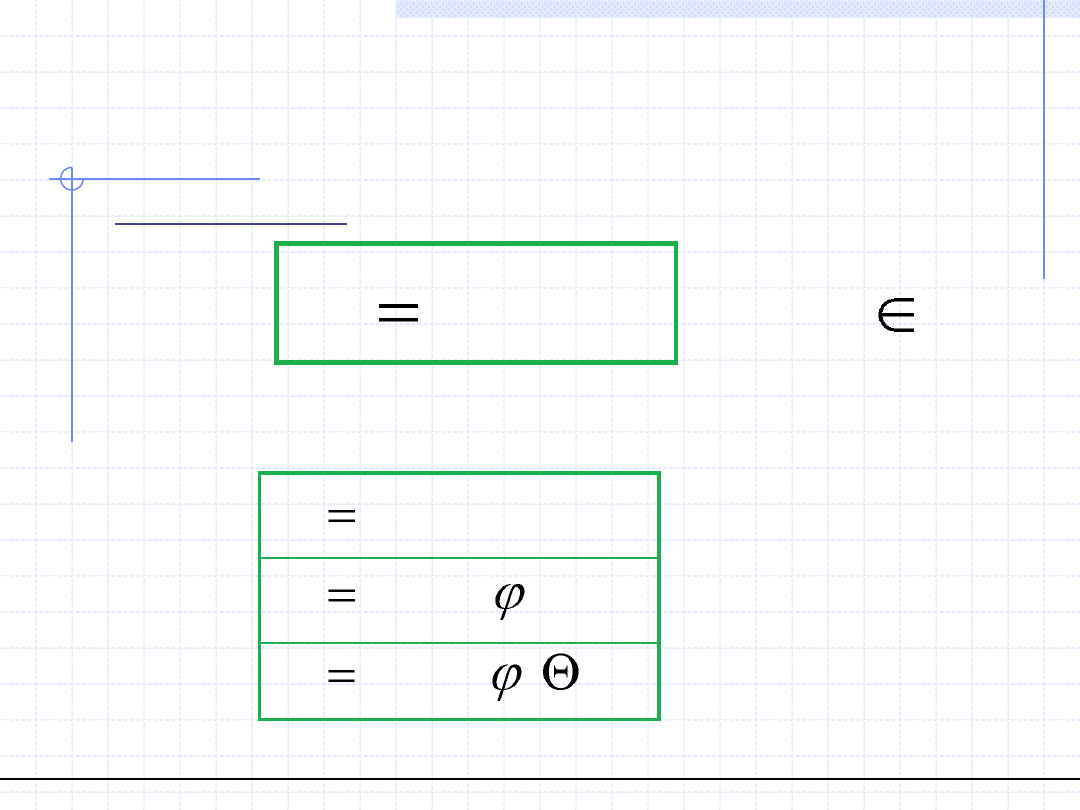
Układ sferyczny –> układ kartezjański:
x
z
u
u’
u
z
O
φ
r
s
y
2
2
2
0
2
2
0
0
0
arctan
arctan
0
0
0
0
2
0
0
0
0
0
s
r
x
y
z
y
x
x
y
z
gdzie
dla x
i y
dla x
dla x
i y
dla z
dla z
θ
r
s
’
.
.
Układ kartezjański –> układ sferyczny:
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
12
Analiza pól – Pole skalarne
R
s
t
u
f
s
)
,
(
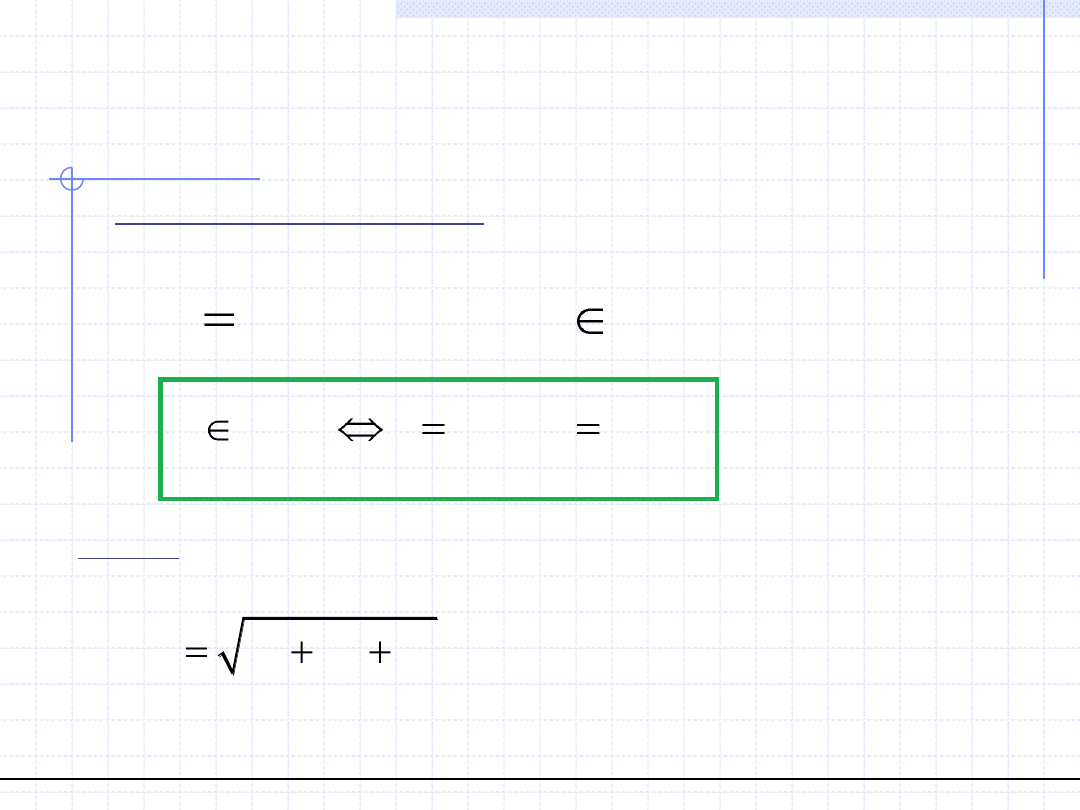
Polem skalarnym nazywamy funkcję rzeczywistą położenia i czasu.
Pole skalarne jest więc funkcją 4 zmiennych: 3 przestrzennych i czasu. Zmienne
przestrzenne zależą od stosowanego układu współrzędnych:
( , , , )
( , , , )
( , , , )
K
C
c
S
s
s
f
x y z t
s
f
r
z t
s
f r
t
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
13
Pole skalarne – powierzchnia
ekwiskalarna
R
s
t
u
f
s
)
,
(
Powierzchnią ekwiskalarną nazywamy zbiór punktów przestrzennych
dla których wartości funkcji s w określonym czasie są stałe.
Przykład
Niech s będzie polem określonym za pomocą wzoru:
( )
( , )
s
u
t
s
f u t
const
A
2
2
2
s
x
y
z
Powierzchniami ekwiskalarnymi dla tego pola są powłoki kuliste (sfery) dla których
odległości od początku układu są stałe.
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
14
Analiza pól – Pole wektorowe
3
)
,
(
R
w
t
u
f
w
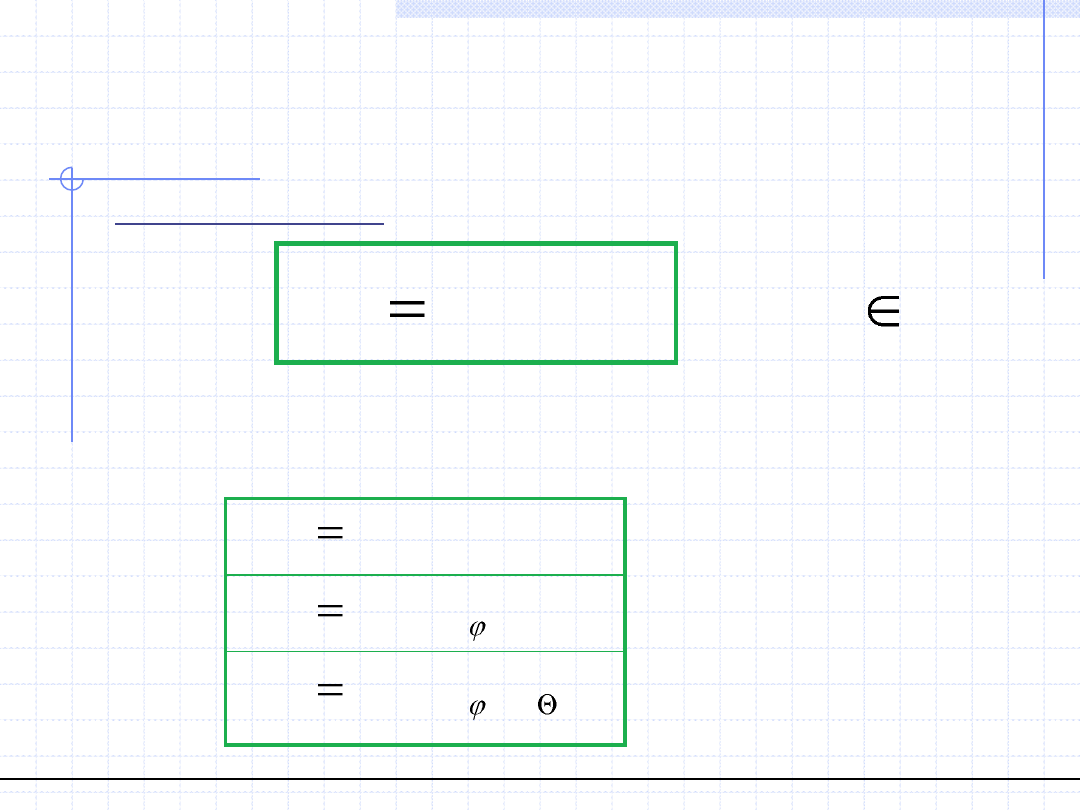
Polem wektorowym nazywamy funkcję wektorową położenia i czasu.
Ponieważ wektor w przestrzeni R
3
ma 3 składowe, więc funkcja f musi w sposób
niezależny określać te składowe. Rodzaj tych składowych zależy od rodzaju
stosowanego układu współrzędnych:
[
,
,
]
[
,
,
]
[
,
,
]
c
s
x
y
z
r
z
r
w
w w w
w
w w w
w
w w w
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
15
Analiza pól – Pole wektorowe
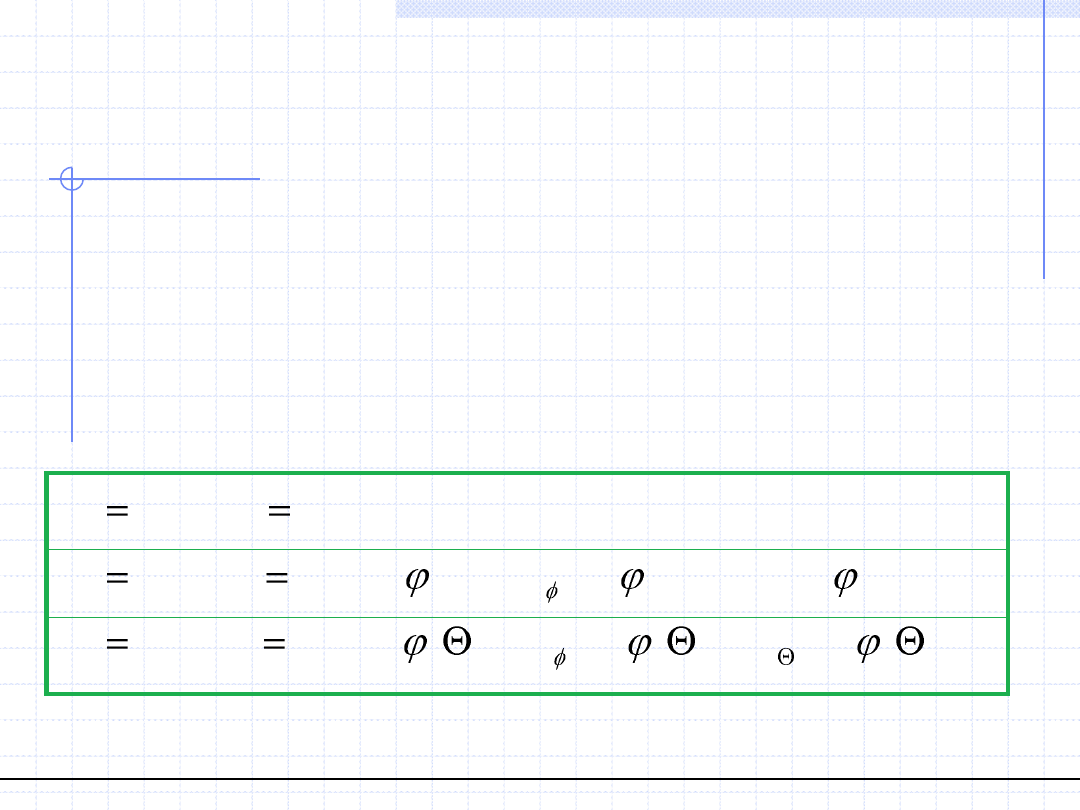
Pole wektorowe jest zatem równoważne trzem funkcjom rzeczywistym
czterech zmiennych.
W zależności od rodzaju układu funkcje te mają różne postacie:
( , )
[
( , , , ),
( , , , ),
( , , , )]
( , )
[
( , , , ),
( , , , ),
( , , , )]
( , )
[
( , , , ),
( , , , ),
( , , , )]
K
x
y
z
C
r
c
c
z
c
S
r
s
s
s
w
f
u t
w x y z t w x y z t w z y z t
w
f u t
w r
z t w r
z t w r
z t
w
f u t
w r
t w r
t w r
t
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
16
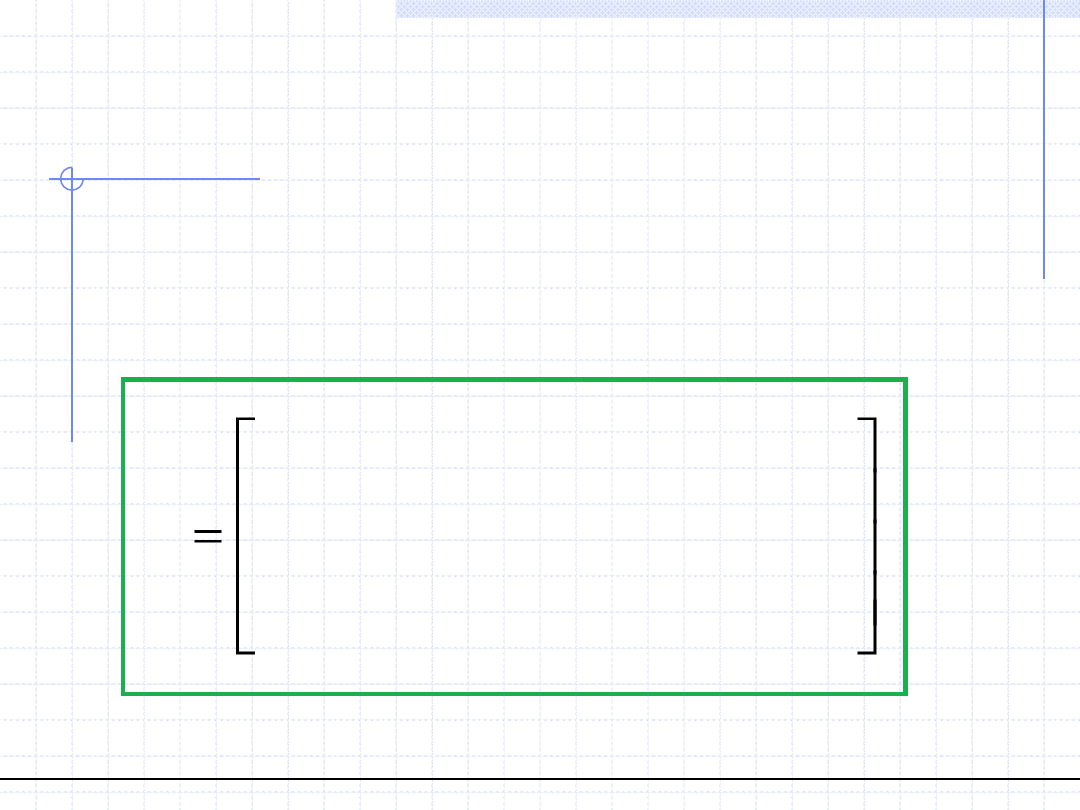
Analiza pól – Pole tensorowe
( , )
T
f u t
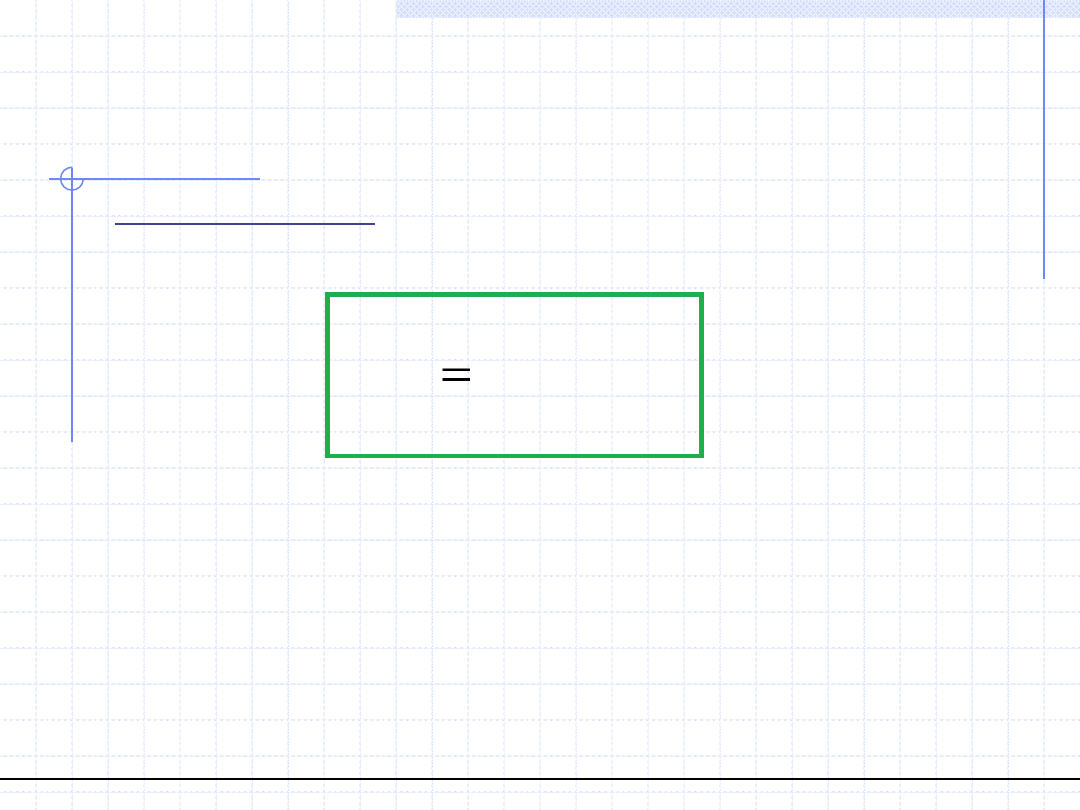
Polem tensorowym nazywamy funkcję tensorową położenia i czasu.
W przypadku tensorów drugiego rzędu określonych w przestrzeni trójwymiarowej
tensor ma 9 składowych, więc funkcja f musi w sposób niezależny określać te
składowe. Każda ze składowych jest funkcją 4 zmiennych.
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
17
Analiza pól – Pole tensorowe
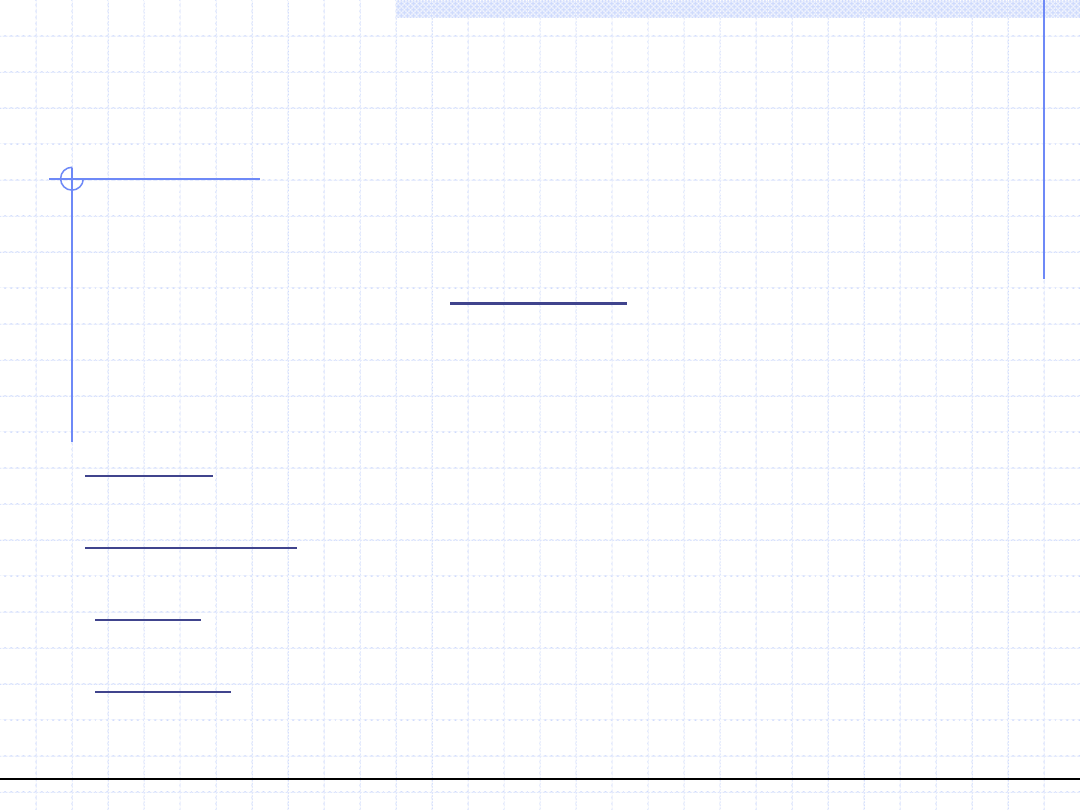
Pole tensorowe jest zatem równoważne 9 - ciu funkcjom rzeczywistym
czterech zmiennych.
W układzie kartezjańskim popularny jest macierzowy zapis tensorów:
( , )
( , )
( , )
( , )
( , )
( , )
( , )
( , )
( , )
xx
xy
xz
yx
yy
yz
zx
zy
zz
f
u t
f
u t
f
u t
T
f
u t
f
u t
f
u t
f
u t
f
u t
f
u t
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
18
Analiza pól – Różniczkowanie
Pola jako funkcje można różniczkować. Ponieważ jednak są to funkcje
dosyć złożone więc również różniczkowanie nie jest proste.
Ogólnie różniczkowanie jest operatorem.
Istnieją różne operatory różniczkowania pól noszące różne nazwy.
Najważniejsze z nich to:
-gradient pola skalarnego
- dywergencja pola wektorowego
- rotacja pola wektorowego
- laplasjan (operator Laplace’a – nie mylić z transformatą Laplace’a)
pola skalarnego
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
19
Analiza pól – Różniczkowanie
Formalne definicje poszczególnych operatorów są niezależne od rodzaju
układu współrzędnych przestrzennych, jednakże nie nadają się one do
obliczeń praktycznych (podobnie jak formalna definicja zwykłej pochodnej
czy całki).
W praktyce stosuje się wzory, których postać zależy od rodzaju układu
współrzędnych. Z reguły najprostsze są wzory dla układu kartezjańskiego
i te wzory przedstawię poniżej.
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
20
Analiza pól – Gradient pola
skalarnego
Operację gradientu wykonuje się na polu skalarnym.
Wynikiem jest pole wektorowe. Dla układu kartezjańskiego mamy:
z
f
y
f
x
f
s
grad
t
z
y
x
f
s
,
,
)
(
)
,
,
,
(
Odpowiednie wzory określające gradient w innych układach
współrzędnych można znaleźć w podręcznikach lub poradnikach
matematycznych.
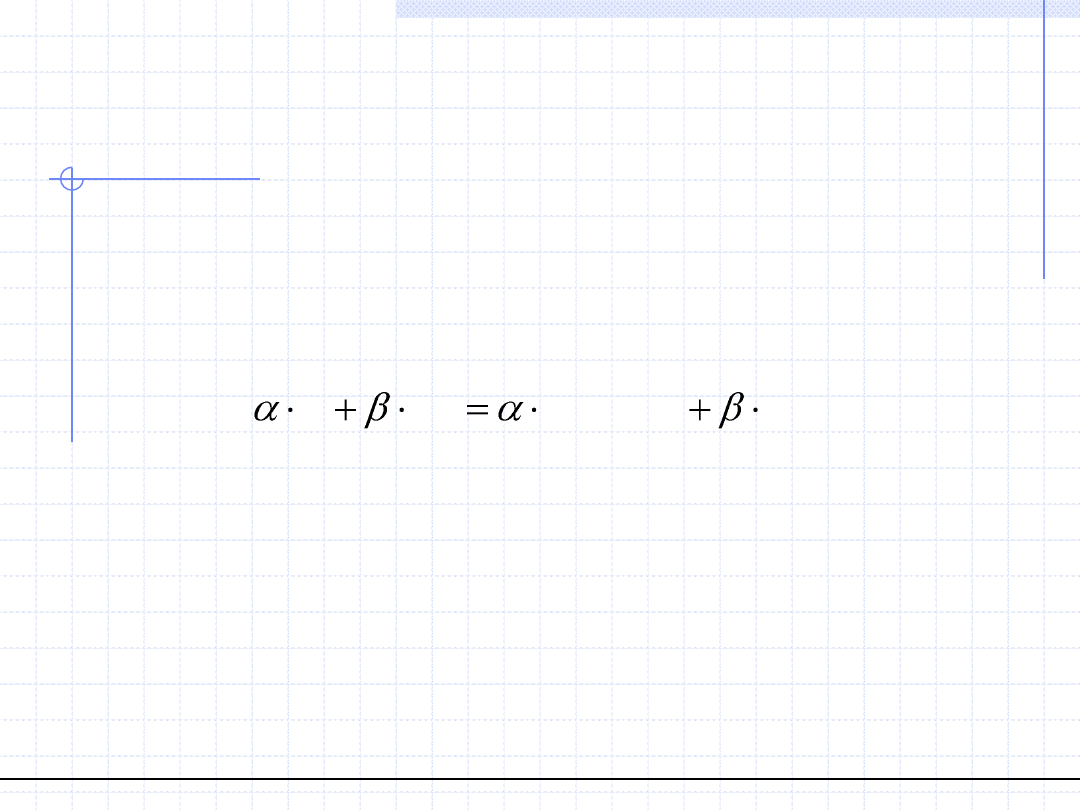
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
21
Właściwości gradientu pola
skalarnego
Można wykazać że:
1. Operator gradientu jest liniowy tzn. obowiązuje wzór
gdzie – α i β dowolne liczby rzeczywiste, s
1
i s
2
dowolne pola skalarne
2. Wektor gradientu wskazuje kierunek, w którym wartość pola
rośnie najszybciej.
3. Wektor gradientu jest prostopadły do powierzchni ekwiskalarnej.
1
2
1
2
(
)
( )
( )
grad
s
s
grad s
grad s
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
22
Analiza pól – Dywergencja pola
wektorowego
Operację dywergencji wykonuje się na polu wektorowym.
Wynikiem jest pole skalarne. Inne określenie tego operatora
to rozbieżność.
[
( , , , ),
( , , , ),
( , , , )]
( )
x
y
z
y
x
z
w
w x y z t w x y z t w x y z t
f
f
f
div w
x
y
z
Odpowiednie wzory określające dywergencję w innych układach
współrzędnych można znaleźć w podręcznikach lub poradnikach
matematycznych.
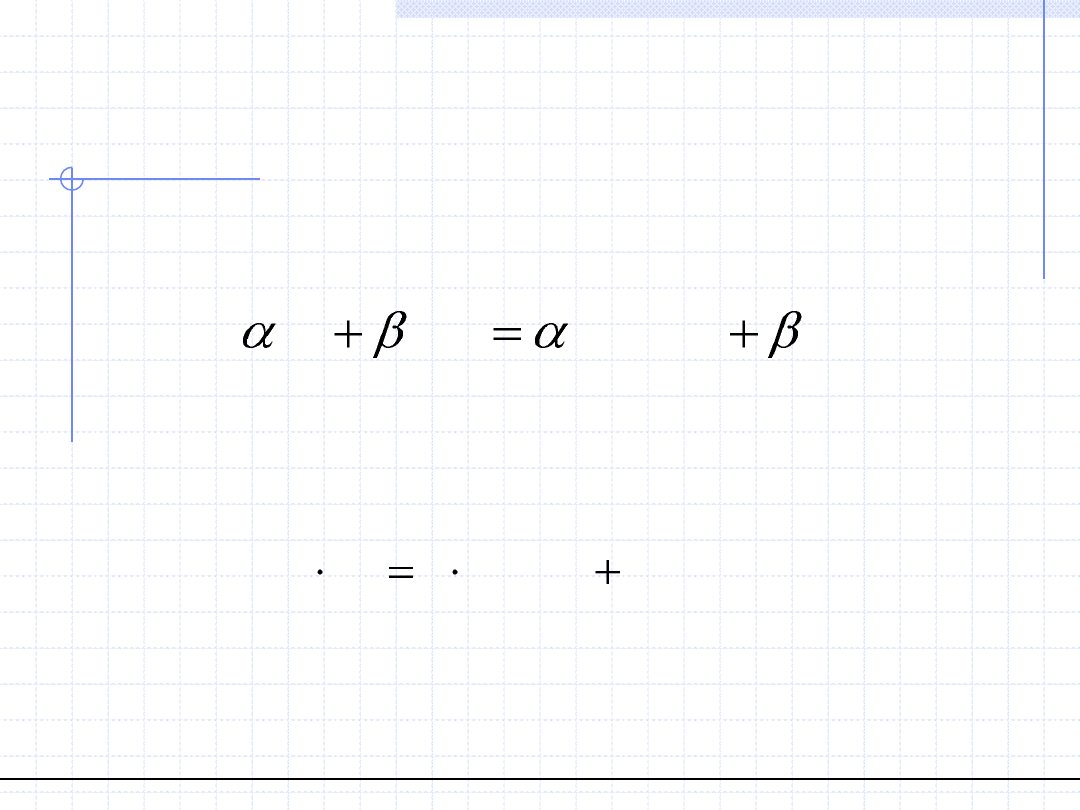
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
23
Niektóre właściwości operatora
dywergencji pola wektorowego
Można wykazać że:
1
2
1
2
(
)
(
)
(
)
div
w
w
div w
div w
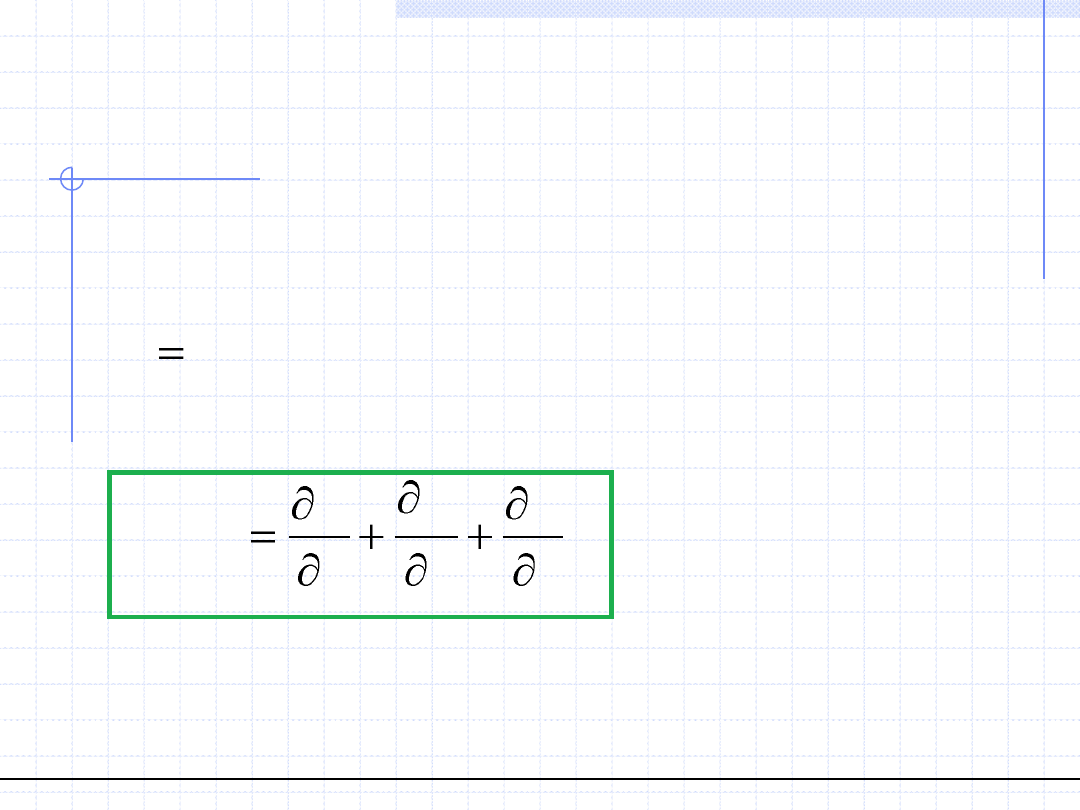
1. Dywergencja jest operatorem liniowym tzn.
2. Zachodzi wzór:
(
)
( )
( )
div s w
s div w
grad s
w
gdzie α i β – dowolne liczby rzeczywiste,
w
1
i w
2
dowolne pola wektorowe
gdzie s – dowolne pole skalarne,
w - dowolne pole wektorowe
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
24
Analiza pól – Rotacja pola
wektorowego
Operację rotacji wykonuje się na polu wektorowym. Wynikiem jest pole
wektorowe. Polskie określenie tego operatora to wirowość.
[
( , , , ),
( , , , ),
( , , , )]
( )
[ , , ]
x
y
z
x
y
z
y
z
x
x
z
y
y
x
z
w
w x y z t w x y z t w x y z t
rot w
r r r
gdzie
w
w
r
y
z
w
w
r
z
x
w
w
r
x
y
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
25
Analiza pól – Laplasjan pola
skalarnego
( , , , )
( )
[
( )]
s
f x y z t
s
div grad s
Laplasjan jest operatorem złożonym składającym się z operatorów gradientu
i diwergencji.
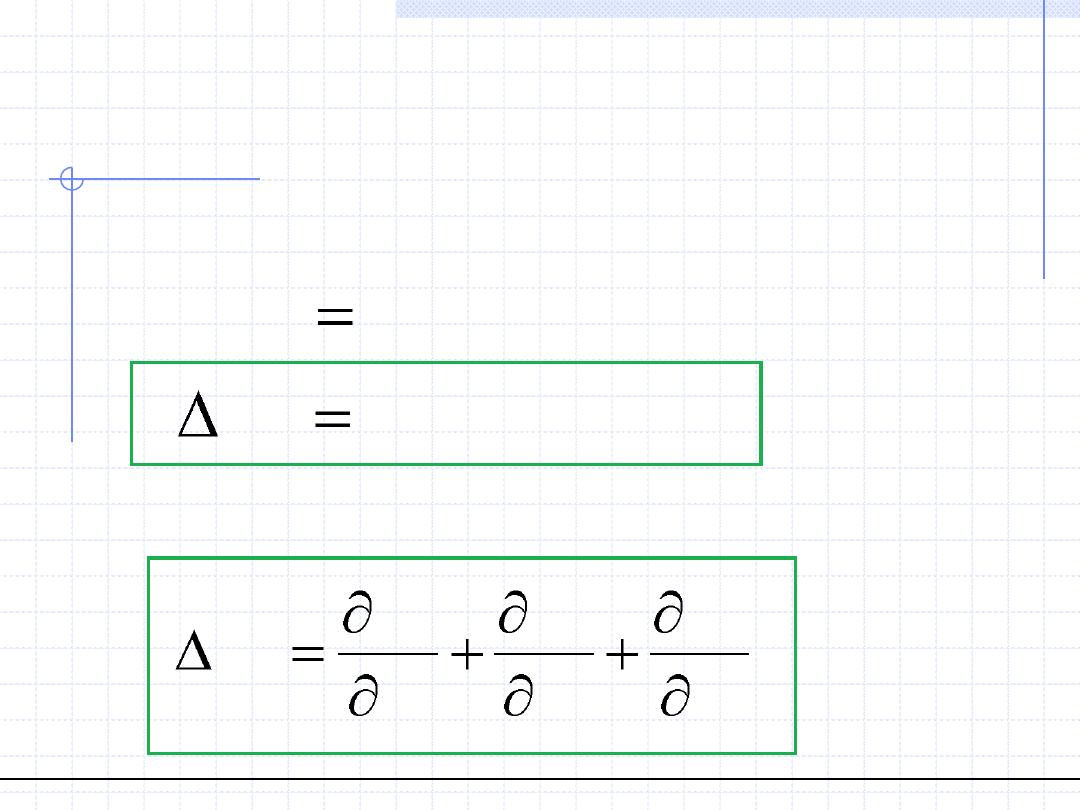
Laplasjanem działamy na pole skalarne w wyniku otrzymując inne pole skalarne:
Dla układu kartezjańskiego operator Laplace’a jest sumą drugich pochodnych
cząstkowych pola skalarnego względem współrzędnych przestrzennych:
2
2
2
2
2
2
)
(
z
f
y
f
x
f
s
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
26
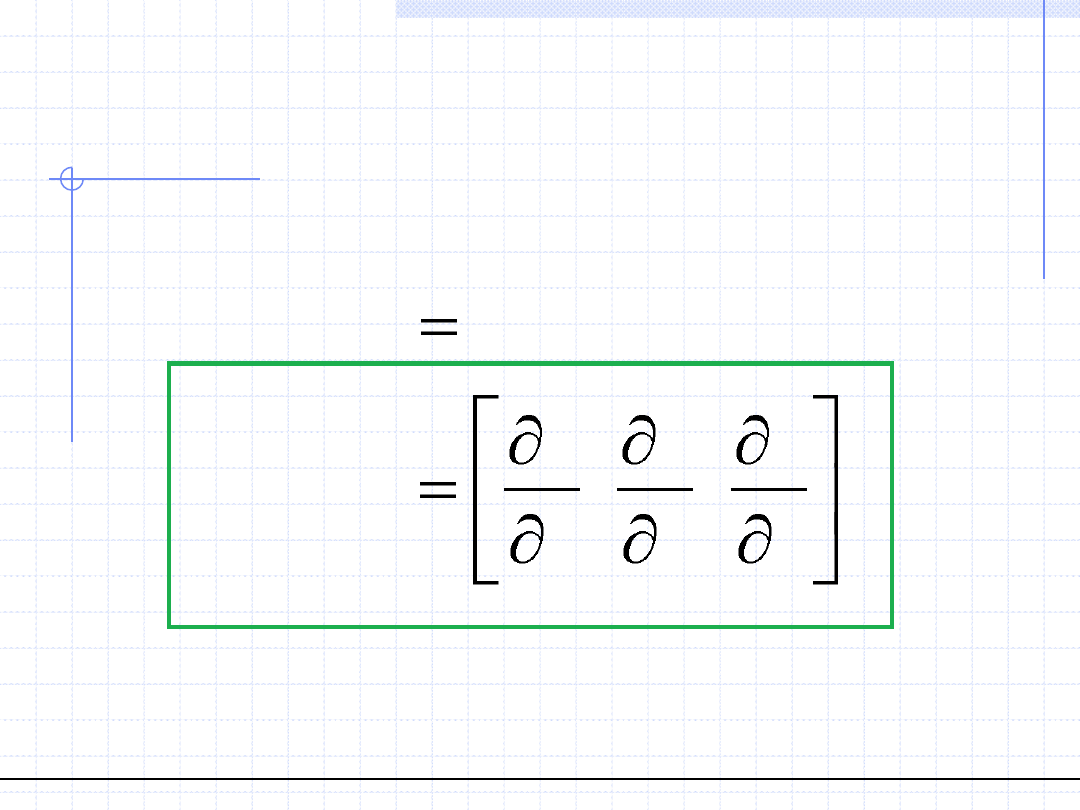
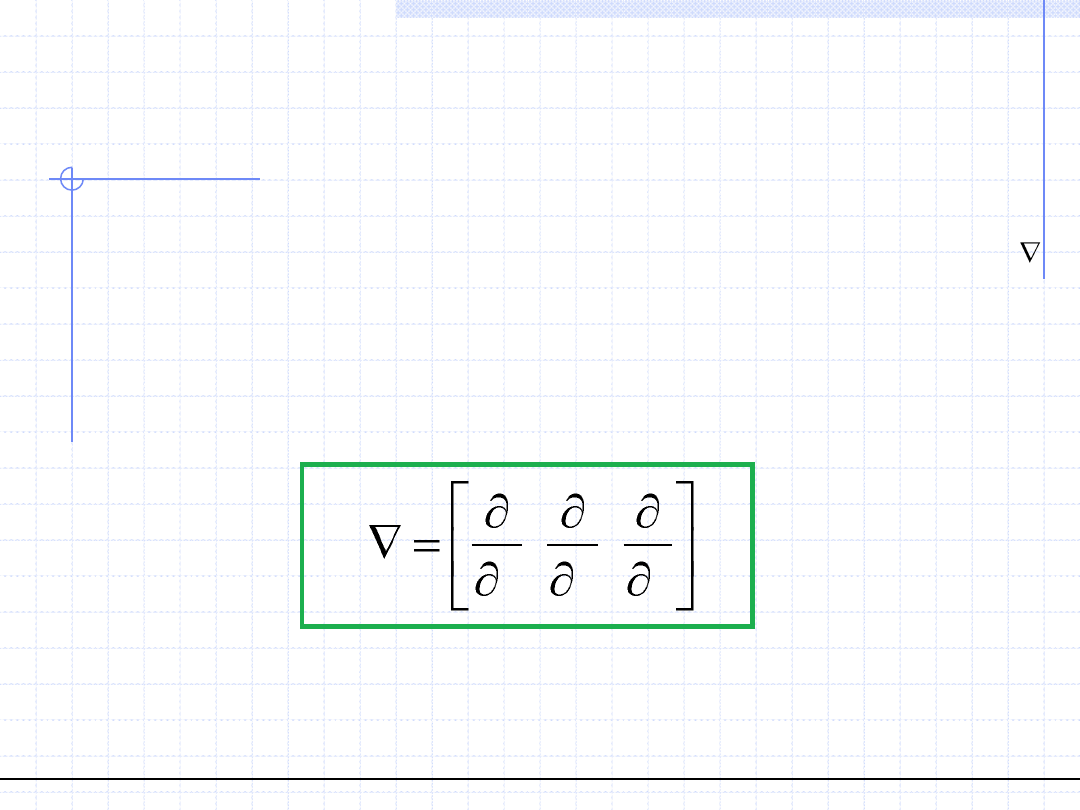
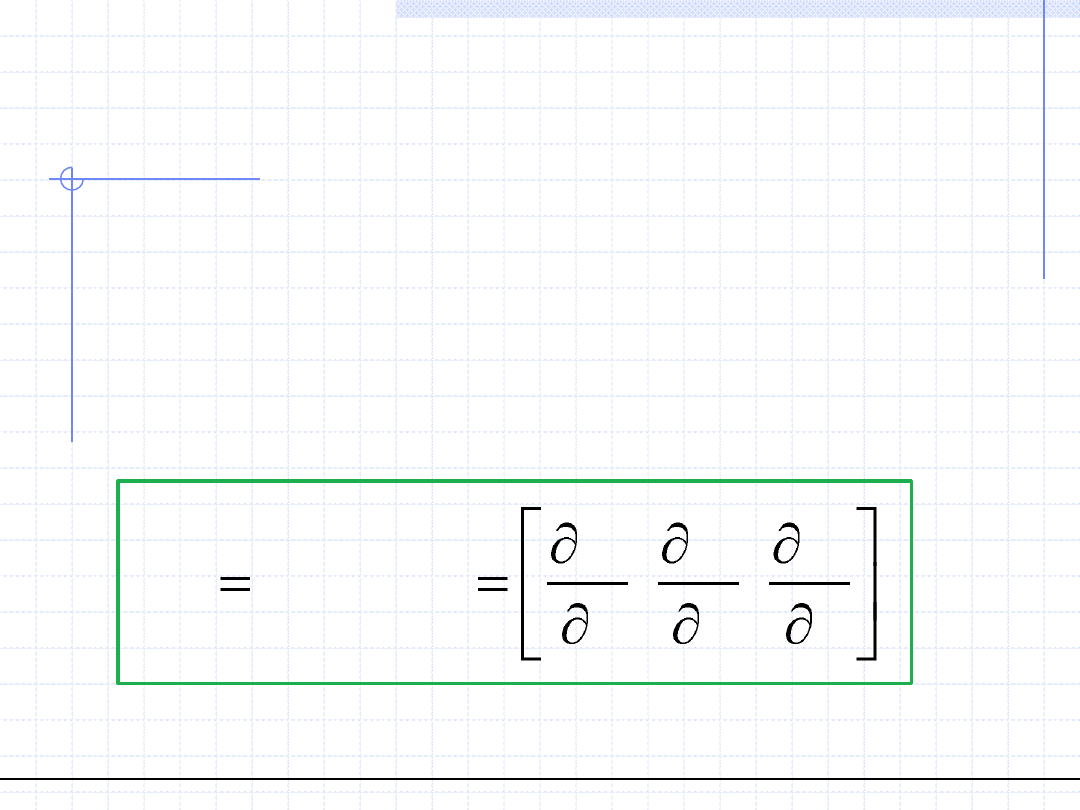
Analiza pól – Operator Hamiltona
z
y
x
,
,
W układzie kartezjańskim jest to symboliczny wektor, którego składowymi
są operatory różniczkowania względem zmiennych przestrzennych:
W celu uporządkowania i łatwego zapisu powyższych pojęć czasami
jest stosowany tzw. operator Hamiltona oznaczony symbolem „nabla”.
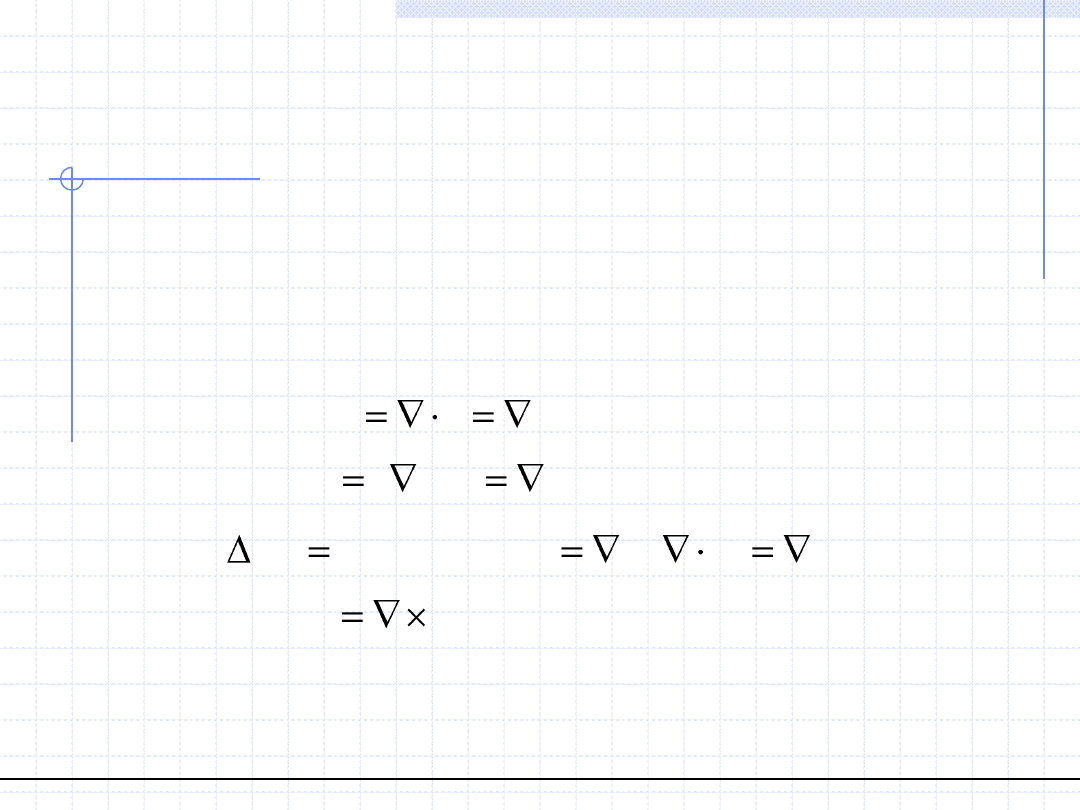
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
27
Analiza pól – Operator Hamiltona
Za pomocą operatora „nabla” można otrzymać wszystkie do tej pory
zdefiniowane pojęcia:
2
( )
( )
,
( )
( )
(
)
( )
grad s
s
s
div w
w
w
s
div grad s
s
s
rot w
w
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
28
Analiza pól – Pola potencjalne
Operacją odwrotną do różniczkowania jest całkowanie. W przypadku pola
wektorowego odpowiednikiem całki nieoznaczonej (czyli tzw. funkcji
pierwotnej) może być pojęcie potencjału. Pojęcie to można definiować
tylko dla tzw. pól potencjalnych.
Dane pole wektorowe w nazywamy polem potencjalnym, jeżeli istnieje
pole skalarne U, którego gradientem jest dane pole w. Czyli
( )
,
,
U
U
U
w
grad U
x
y
z
Potencjał danego pola (podobnie jak całka nieoznaczona) jest określony
z dokładnością do pewnej stałej addytywnej.
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
29
Analiza pól – Pola potencjalne
Warunkiem koniecznym i wystarczającym aby dane pole wektorowe w
było polem potencjalnym jest jego bezwirowość tzn. że jego rotacja
musi być równa 0:
( )
[
( )]
0
rot w
rot grad U
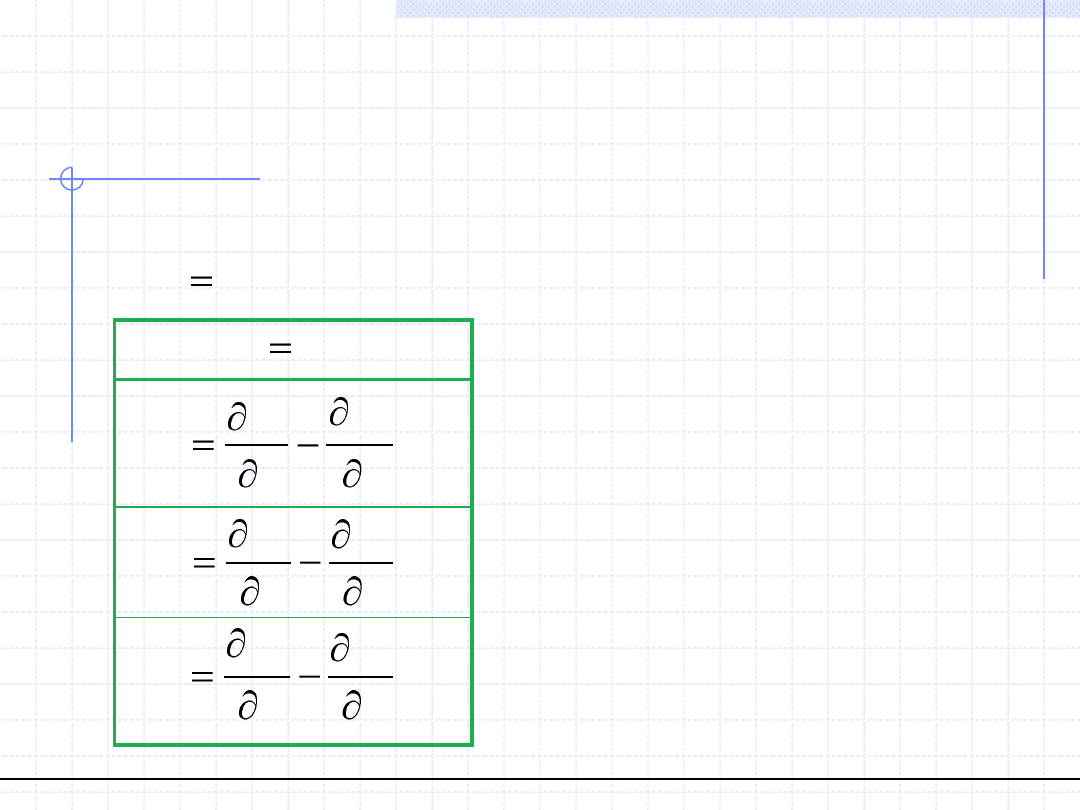
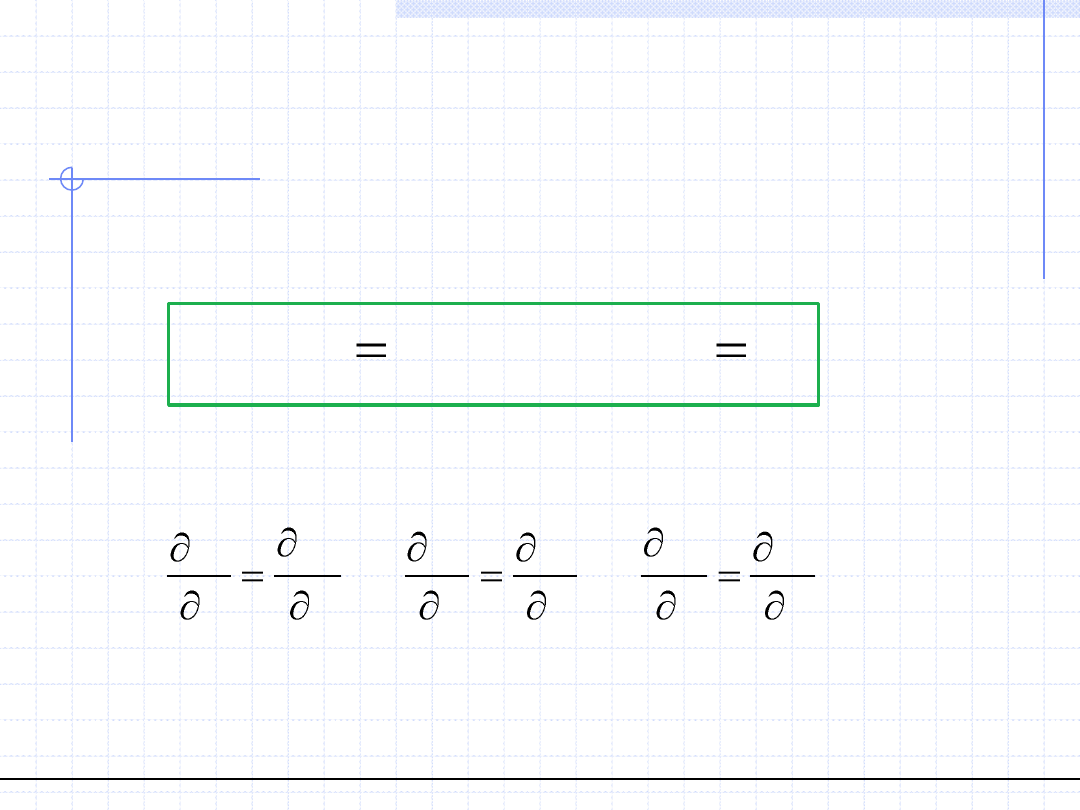
Warunek ten w układzie kartezjańskim można zapisać za pomocą 3 równań:
y
y
x
x
z
z
w
w
w
w
w
w
y
z
z
x
x
y
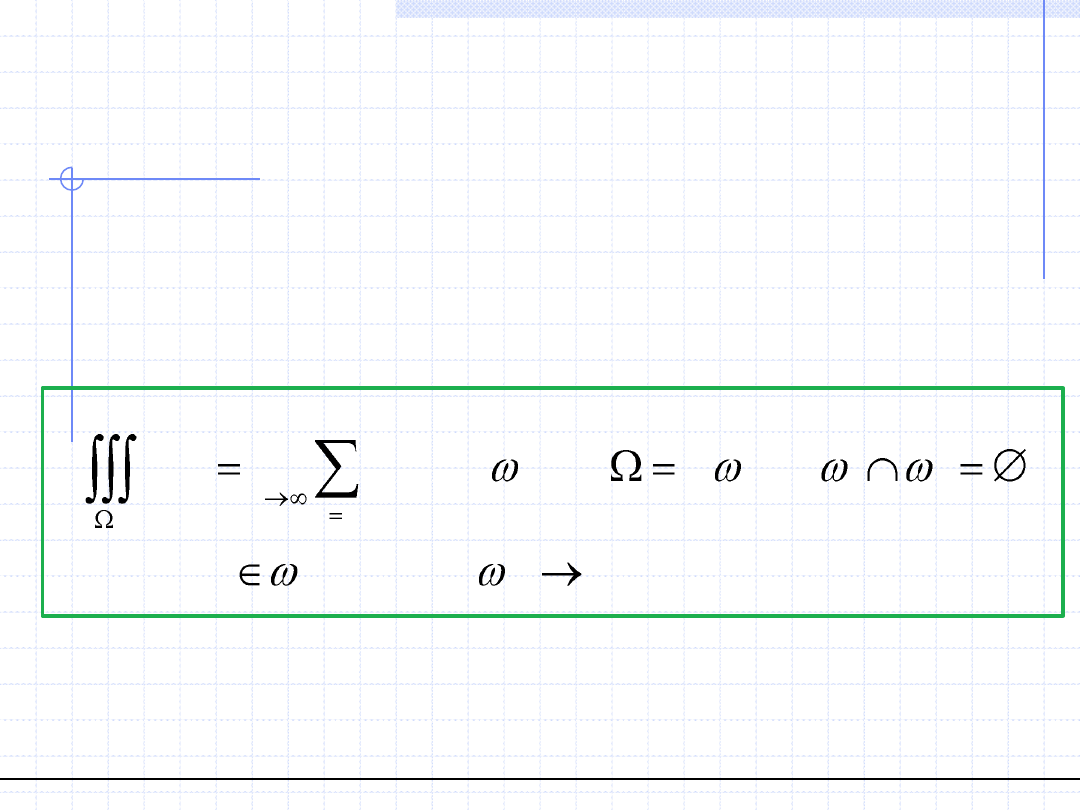
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
30
Analiza pól – Całkowanie
W analizie pól rozpatruje się również operacje analogiczne do całki
oznaczonej. Najważniejsze są tzw. całki objętościowe i całki
powierzchniowe.
Dla pola skalarnego s w zamkniętym obszarze przestrzennym Ω
definiuje się całkę objętościową jako granicę:
1
lim
( ) ( )
( )
0
n
i
i
i
j
i
n
i
i
i
i
sdV
s u V
u
V
W dowolnym układzie przestrzennym dla odpowiednio zdefiniowanego
zbioru Ω można całkę objętościową zapisać za pomocą całki potrójnej
W odpowiednich granicach.
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
31
Analiza pól – Całkowanie
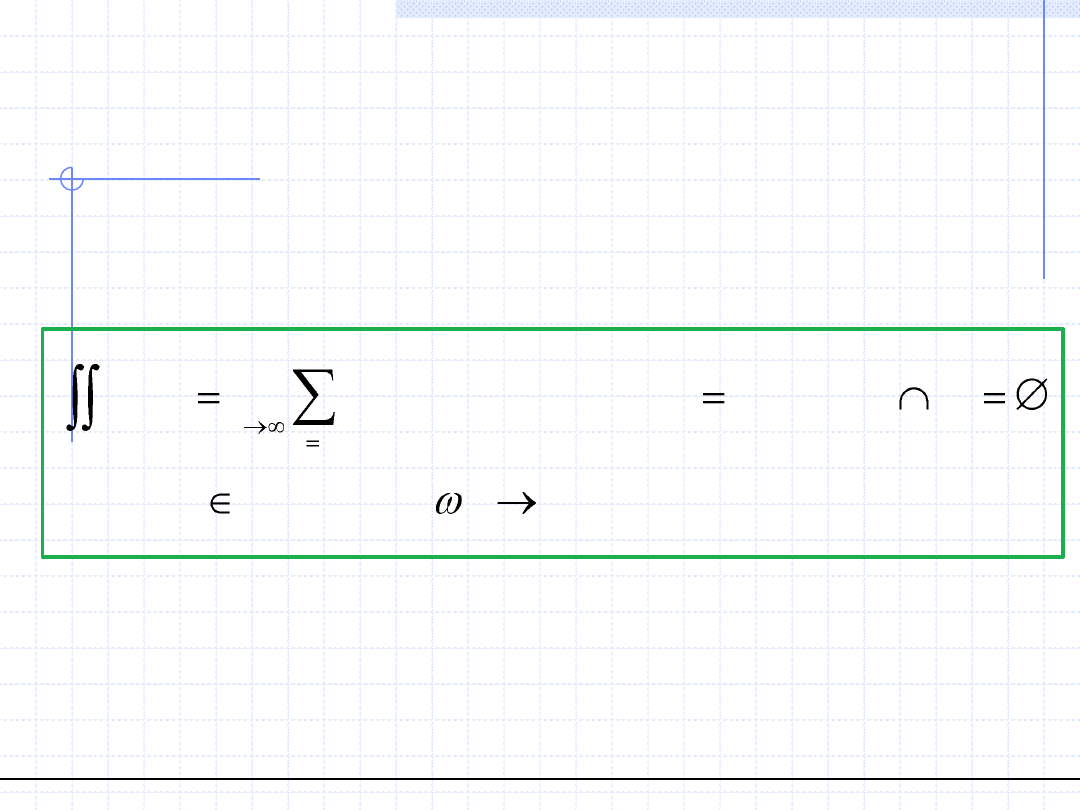
Dla pola wektorowego w i ograniczonej powierzchni zorientowanej A
definiuje się całkę powierzchniową drugiego rodzaju jako granicę:
1
lim
( ( )
) ( )
( )
0
n
i
i
i
j
i
n
i
i
i
i
wd
w u
n A a
a
a
a
u
a
A
A
A
A
W dowolnym układzie przestrzennym dla odpowiednio zdefiniowanej
powierzchni A można całkę powierzchniową zapisać za pomocą całki
podwójnej w odpowiednich granicach.
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej
32
Analiza pól – Twierdzenie
Gaussa
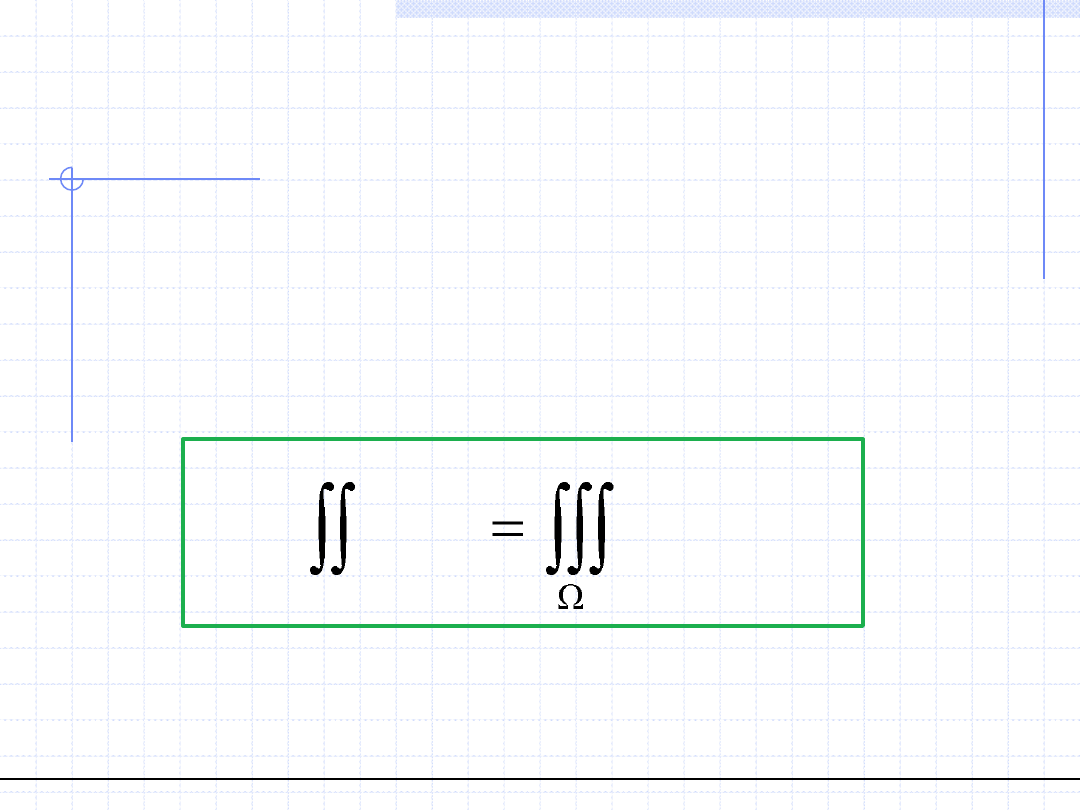
W szczególnym przypadku, gdy mamy dane pole wektorowe w
zdefiniowane w zamkniętym obszarze Ω, którego brzegiem jest
powierzchnia zorientowana na zewnątrz A całkę powierzchniową tego
pola po tej powierzchni można wyrazić za pomocą całki objętościowej.
Umożliwia to tzw. twierdzenie Gaussa:
( )
wd
div w dV
A
A
Wyszukiwarka
Podobne podstrony:
Met mat i stat w inz chem W 1
Met mat i stat w inz chem W 2
Met mat i stat w inz chem W 5
Met mat i stat w inz chem W 6
Met mat i stat w inz chem W 4
Mat Stat WykĹ ad 3 (2013L)(1)
Wyniki egzamin IIIrok-inż.chem., III rok semestr letni, inżynieria chemiczna
opracowania inż chem egzamin
Inz chem LAB, sprawozdanie-2831
inz chem profil kołowy
inz chem sciaga egz, podstawy inżynierii chemicznej
Mat Stat WykĹ ad 1 ( 2013L)
Mat Stat Wyk 8 PrzedziaĹ y(2013L)
ICh S Inz chem wstep
Mat Stat WykĹ 6 7 Est c d (2013L)
Mat Stat WykĹ ad 4 5a 2013
Technologia chemiczna-Inż.Chem-2011-2012, technologia chemiczna
inz chem zagadnienia, podstawy inżynierii chemicznej
więcej podobnych podstron