© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

MATEMATYKA STOSOWANA W

INŻYNIERII CHEMICZNEJ

Wykład – 5

Elementy algebry i analizy zespolonej

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

2

ALGEBRA ZESPOLONA

)

,

(

y

x

iy

x

z







Liczby zespolone pod względem algebraicznym tworzą tzw. ciało algebraiczne.

Ciało jest to zbiór elementów, w którym możliwe są następujące działania:

• dodawanie

• odejmowanie

• mnożenie

• dzielenie (z wyjątkiem elementu zerowego)

Liczby zespolone mają dwie interpretacje: algebraiczną i geometryczną.

W interpretacji algebraicznej liczbą zespoloną nazywamy uporządkowaną

parę liczb rzeczywistych. Tradycyjny zapis liczb zespolonych wykorzystuje

tzw. jednostkę urojoną oznaczaną literą „i”:

Pierwszy element pary – liczba x nazywana jest częścią rzeczywistą,

natomiast drugi element – liczba y nazywany jest częścią urojoną.

Odpowiednie oznaczenia:

Re( )

Im( )

(0,1)

x

z

y

z

i







© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

3

ALGEBRA ZESPOLONA – INTERPRETACJA

GEOMETRYCZNA

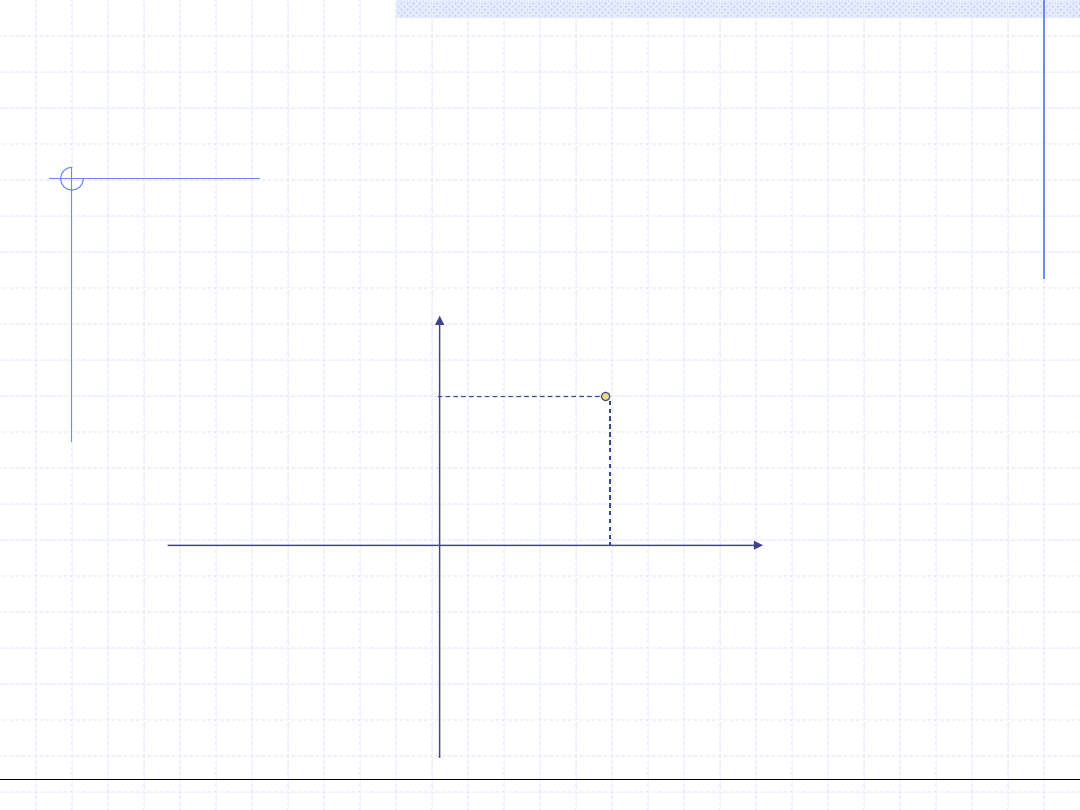
W interpretacji geometrycznej liczby zespolone traktowane są jako

punkty na płaszczyźnie z prostokątnym kartezjańskim układem

współrzędnych.

x=Re(z)

y=Im(z)

z=(x,y)=x+iy

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

4

ALGEBRA ZESPOLONA - DZIAŁANIA

)

,

(

)

,

(

)

,

(

2

1

2

1

2

2

1

1

2

1

y

y

x

x

y

x

y

x

z

z













)

,

(

)

,

(

)

,

(

1

2

2

1

2

1

2

1

2

2

1

1

2

1

y

x

y

x

y

y

x

x

y

x

y

x

z

z













)

0

,

1

(

)

1

0

1

0

,

1

1

0

0

(

)

1

,

0

(

)

1

,

0

(





















Dodawanie i odejmowanie liczb zespolonych polega na dodawaniu i odejmowaniu

odpowiednich elementów tych liczb:

Mnożenie liczb zespolonych jest bardziej złożone i wyraża się wzorem:

Obliczmy zgodnie z tą definicją kwadrat jednostki urojonej czyli liczby i=(0,1):

Jeżeli liczby zespolone, których część urojona jest równa zero utożsamimy

z liczbami rzeczywistymi (z=x+i∙0=x) to możemy napisać:

1

1

)

1

,

0

(

)

1

,

0

(

2















i

i

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

5

ALGEBRA ZESPOLONA - DZIAŁANIA

)

,

(

)

(

)

(

)

(

1

2

2

1

2

1

2

1

1

2

2

1

2

1

2

1

2

1

1

2

2

1

2

1

2

2

1

1

2

1

y

x

y

x

y

y

x

x

y

x

y

x

i

y

y

x

x

y

y

y

ix

y

ix

x

x

iy

x

iy

x

z

z

































)

0

,

0

(

2

3

2

1

3

2

1











z

z

z

z

z

z

z

Własność powyższa pozwala na mnożenie liczb zespolonych zapisanych

w tradycyjnej formie jako dwumianów algebraicznych:

Dzielenie liczb zespolonych jest działaniem odwrotnym do mnożenia tzn:

Jeżeli dzielnik jest liczbą rzeczywistą (jego część urojona jest równa zero)

to dzielenie jest proste i sprowadza się do zwykłego dzielenia obydwu części

przez dzielnik:

















2

1

2

1

2

1

1

2

1

,

)

0

,

(

)

,

(

x

y

x

x

x

y

x

z

z

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

6

ALGEBRA ZESPOLONA - DZIAŁANIA

iy

x

z

iy

x

z











W przypadku gdy dzielnik nie jest liczbą rzeczywistą należy albo wykorzystać

definicję dzielenia i rozwiązać odpowiedni układ równań liniowych albo też

wykorzystać pojęcie tzw. liczby sprzężonej: Liczbą sprzężoną nazywamy liczbę

zespoloną mającą taką samą część rzeczywistą oraz część urojoną przeciwnego

znaku czyli:

Można zauważyć, że iloczyn danej liczby zespolonej oraz liczby do niej sprzężonej

zawsze jest liczbą rzeczywistą gdyż:

2

2

2

2

)

(

)

)(

(

y

x

iy

x

iy

x

iy

x













Dzielenie liczb zespolonych za pomocą liczb sprzężonych polega na pomnożeniu

dzielnej i dzielnika przez liczbę sprzężoną do dzielnika. W taki sposób dzielnik

staje się liczbą rzeczywistą a dzielenie jest dalej proste.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

7

ALGEBRA ZESPOLONA –

TRYGONOMETRYCZNY ZAPIS LICZB

ZESPOLONYCH – MODUŁ I ARGUMENT

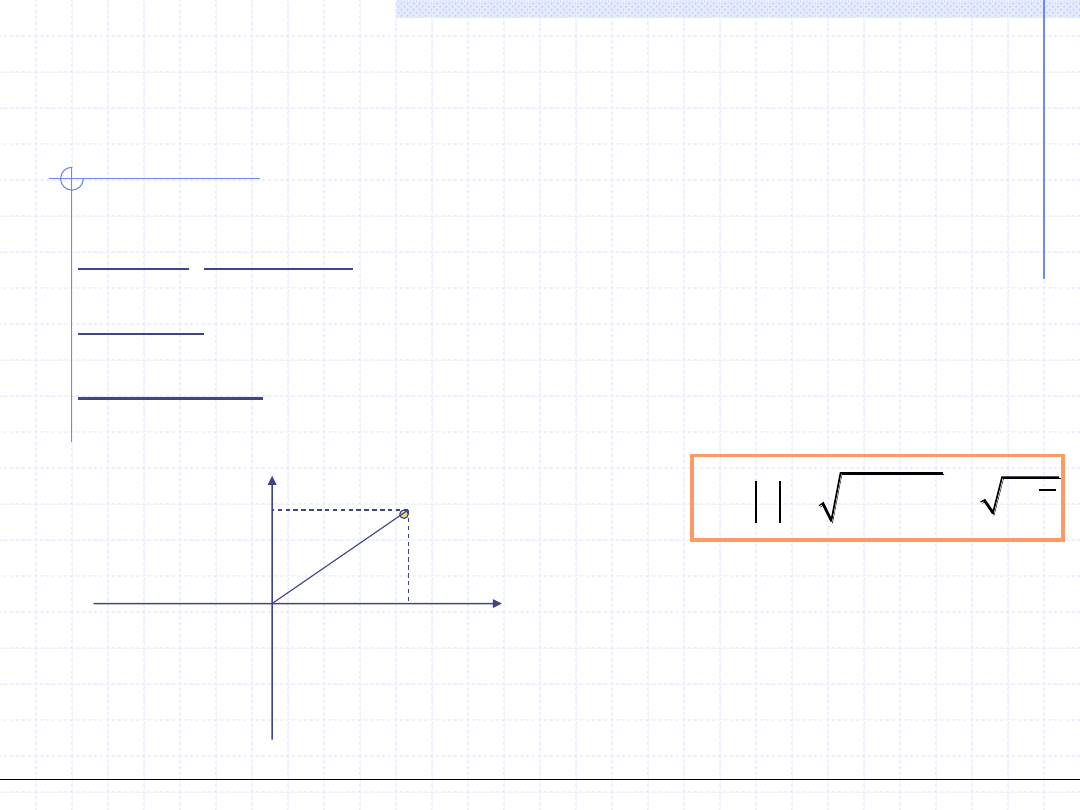
Geometryczna interpretacja liczb zespolonych umożliwia zupełnie inny sposób

zapisu liczb zespolonych. Podstawowymi narzędziami tego zapisu są pojęcia

modułu i argumentu.

Modułem danej liczby zespolonej z nazywamy odległość punktu reprezentującego

tą liczbę od początku układu współrzędnych.

Argumentem danej liczby zespolonej nazywamy kąt między dodatnią osią x

a prostą łączącą dany punkt z początkiem układu.

z=x+iy

x

y

O

A

r

φ

2

2

r

z

x

y

z z











( )

Arg z





© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

8

TRYGONOMETRYCZNY ZAPIS LICZB

ZESPOLONYCH – MODUŁ I ARGUMENT

Moduł liczby zespolonej jest zawsze liczbą nieujemną. Jedyną liczbą, której moduł

wynosi 0 jest liczba (0,0).

Argument liczby zespolonej jako kąt jest wyrażany w mierze łukowej (w radianach)

i mieści się w zakresie: [0,2π). Ścisłe wyznaczenie argumentu wymaga uwzględnienia
w której ćwiartce leży punkt reprezentujący daną liczbę zespoloną. Podstawowe
zależności trygonometryczne prowadzą do wzoru:

0

0

0,

0 (

.)

0 (

.)

2

0,

0 (

.)

dla x

y

I ćw

dla x

II i III ćw

dla y

x

IV ćw





























0

( )

arctan

y

Arg z

x





 

 



 

 

gdzie:

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

9

ALGEBRA ZESPOLONA –

TRYGONOMETRYCZNY ZAPIS LICZB

ZESPOLONYCH

Uwzględniając podstawowe zależności trygonometryczne między modułem,

argumentem i składowymi liczby zespolonej możemy napisać:

cos

sin

cos

sin

cos

sin

(cos

sin )

(cos

sin )

x

y

r

r

x

r

y

r

z

x iy

r

ir

r

i

z

r

i

































  













Zapis ten nazywamy trygonometryczną postacią liczb zespolonych. Postać ta

bardzo ułatwia mnożenie i dzielenie oraz potęgowanie i pierwiastkowanie

w dziedzinie liczb zespolonych.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

10

ALGEBRA ZESPOLONA – MNOŻENIE

Trygonometryczna postać liczb zespolonych pozwala na stosunkowo prostą

interpretację mnożenia i dzielenia liczb zespolonych. Niech z

1

i z

2

oznaczają

dwie dowolne liczby zespolone:





1

1

1

1

2

2

2

2

1

2

1

1

1

2

2

2

1 2

1

2

1

2

1

2

2

1

(cos

sin

)

(cos

sin

)

(cos

sin

) (cos

sin

)

cos

cos

sin

sin

(cos

sin

cos

sin

z

r

i

z

r

i

z z

r

i

r

i

r r

i









































 















Mnożenie liczb zespolonych jest jednoznaczne z mnożeniem modułów

i dodawaniem argumentów.





1

2

1 2

1

2

1

2

cos(

)

sin(

)

z z

r r

i

 

 

 







© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

11

ALGEBRA ZESPOLONA – DZIELENIE

W podobny sposób można wyprowadzić odpowiedni wzór określający

dzielenie liczb zespolonych:





1

1

1

2

1

2

2

2

cos(

)

sin(

)

z

r

i

z

r

 

 









Zgodnie z tym wzorem dzielenie jest równoznaczne z dzieleniem modułów

i odejmowaniem argumentów.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

12

ALGEBRA ZESPOLONA - POTĘGOWANIE

[cos(

)

sin(

)]

n

n

z

r

n

i

n









Stosując własność określającą mnożenie do tego samego elementu

n razy otrzymujemy tzw. wzór de Moivre’a pozwalający potęgować

liczby zespolone:

Potęgowanie liczb zespolonych jest równoznaczne z potęgowaniem

modułu i mnożeniem argumentu przez potęgę n.

Wzór ten obowiązuje dla całkowitych wartości n.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

13

ALGEBRA ZESPOLONA - PIERWIASTKOWANIE

W przypadku pierwiastkowania stopnia n otrzymuje się n różnych

pierwiastków dla których wzór de Moivre’a ma postać:

1

,...,

2

,

1

,

0

2

sin

2

cos



























 













 



n

k

n

k

i

n

k

r

z

n

n









© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

14

ANALIZA ZESPOLONA – Ciągi i szeregi

,...

,...,

,

}

{

2

1

n

n

z

z

z

z



















1

2

1

...

...

n

n

n

z

z

z

z

Podobnie jak w zbiorze liczb rzeczywistych , w zbiorze liczb zespolonych

możemy rozpatrywać pojęcia ciągu oraz szeregu.

Ciągiem zespolonym nazywamy nieskończony uporządkowany układ liczb

zespolonych:

Szeregiem zespolonym nazywamy nieskończoną uporządkowaną sumę

liczb zespolonych:

Ciąg zespolony jest zbieżny wtedy i tylko wtedy gdy zbieżne są odpowiednie

ciągi rzeczywiste części rzeczywistych i części urojonych tzn.:

.

}

{

}

{

.

}

{

}

{

zbież

są

y

i

x

zbież

jest

iy

x

z

n

n

n

n

n







© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

15

ANALIZA ZESPOLONA – Ciągi i szeregi





























n

i

i

n

n

n

z

z

1

1

lim

Mówimy że dany szereg liczb zespolonych jest zbieżny jeżeli zbieżny jest

ciąg jego sum częściowych:

Jeżeli dany szereg zespolony jest zbieżny to zbieżne są również odpowiednie

szeregi rzeczywiste składowych i ważny jest wzór:



































1

1

1

n

n

n

n

n

n

y

i

x

z

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

16

ANALIZA ZESPOLONA – Funkcje

Y

D

C

Y

C

D

z

f







)

(

Y

z

f



)

(

D

z



Zbiór wszystkich liczb zespolonych oznaczamy literą C. Niech D i Y będą

podzbiorami C.

Funkcją zespoloną zmiennej zespolonej nazywamy jednoznaczne

przyporządkowanie elementów zbioru Y elementom zbioru D.

)

(z

f

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

17

ANALIZA ZESPOLONA – Funkcje

)

,

(

)

(

)

(

)

,

(

)

(

)

(

)

(

)

(

)

(

)

(

y

x

f

iy

x

f

z

f

y

x

f

iy

x

f

z

f

z

f

i

z

f

iy

x

f

z

f

y

y

y

x

x

x

y

x





















Zbiór D nazywamy dziedziną funkcji, natomiast zbiór Y jest to zbiór wartości

funkcji. Zbiory D i Y mogą być rozłączne, mogą się pokrywać częściowo lub

całkowicie, mogą też pokrywać się ze zbiorem C.

Elementy zbiory Y czyli wartości funkcji są oczywiście liczbami zespolonymi

tzn. można je zapisać za pomocą części rzeczywistej i urojonej:

Funkcje rzeczywiste f

x

i f

y

nazywamy częścią rzeczywistą i urojoną danej funkcji f(z).

Z powyższego zapisu wynika, że każda funkcja zespolona jest równoznaczna

z układem dwu funkcji rzeczywistych dwu zmiennych.

)}

,

(

),

,

(

{

)

(

y

x

f

y

x

f

z

f

y

x



© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

18

ANALIZA ZESPOLONA – Sposoby

definiowania funkcji zespolonych

Mamy 3 zasadnicze sposoby definiowania funkcji zespolonych:

1. Bezpośrednio za pomocą działań algebraicznych tzn. dodawania, odejmowania,

mnożenia, dzielenia, potęgowania i pierwiastkowania. W przypadku użycia

pierwiastków konieczne jest zapewnienie jednoznaczności przez wybór jednego

z wyników pierwiastka.

Przykłady:

3

2

3

2

)

(

)

(

5

)

(

)

(

i

z

i

z

z

f

i

z

z

z

i

z

z

f

z

z

f



















© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

19

ANALIZA ZESPOLONA – Sposoby

definiowania funkcji zespolonych

)

,

(

)

,

(

)

(

y

x

f

i

y

x

f

z

f

y

x





2. Za pomocą jawnych postaci części rzeczywistej i urojonej.

Przykłady:

0

)

,

(

,

)

,

(

)

(

)

,

(

,

)

,

(

)

(

)

(

)

,

(

,

)

,

(

)

(

)

,

(

,

)

,

(

)

(

)

(

)

(

2

2

2

2

3

2

3

2



























































































y

x

f

y

x

y

x

f

y

x

z

z

f

y

y

x

f

x

y

x

f

y

i

x

z

z

f

y

x

y

y

x

f

y

x

x

y

x

f

y

x

y

i

y

x

x

z

f

y

x

y

x

f

y

x

y

x

f

y

x

i

y

x

z

f

y

x

y

x

y

x

y

x

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ANALIZA ZESPOLONA – Sposoby

definiowania funkcji zespolonych

0

( )

[

( )]

n

n

n

f z

a z z









3. Za pomocą szeregów potęgowych.

Wiele ciekawych funkcji można zdefiniować przy użyciu zbieżnych

szeregów potęgowych. Funkcja taka ma postać:

Warunkiem prawidłowej definicji jest tzw. zbieżność jednostajna powyższego

szeregu. Współczynniki szeregu a

n

(z) są w ogólnym przypadku funkcjami

zespolonymi zdefiniowanymi w inny sposób. W praktyce najczęściej są to

stałe liczby rzeczywiste (zależne od n).

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

21

ANALIZA ZESPOLONA – Sposoby

definiowania funkcji zespolonych

Rozważmy prosty ale ważny przykład tzw. funkcji ekspotencjalnej.

Niech:

























0

3

2

!

1

...

!

1

...

!

3

1

!

2

1

1

)

(

!

1

n

n

n

n

z

n

z

n

z

z

z

z

f

n

a

Jeżeli zmienna z ograniczymy tylko do części rzeczywistej tzn. przyjmiemy,

że część urojona z jest równa zero, wtedy z=x, szereg powyższy pokrywa

się z szeregiem rzeczywistym określającym zwykłą funkcję

ekspotencjalną e

x

.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

Elementy analizy zespolonej cd.

Różniczkowanie i całkowanie

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ANALIZA ZESPOLONA – Funkcja

ekspotencjalna











0

!

)

(

n

n

def

z

n

z

e

z

f

W związku z tym funkcję zespoloną określoną za pomocą tego szeregu

również nazywamy funkcją ekspotencjalną i oznaczamy ją jako e

z

.

Ponieważ szereg jest zbieżny jednostajnie dla dowolnej liczby zespolonej,

zatem dziedziną funkcji ekspotencjalnej jest cały zbiór liczb zespolonych.

Metodami analizy matematycznej można wykazać, że szereg powyżej

zdefiniowany jest jednostajnie zbieżny dla dowolnej liczby zespolonej z.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ANALIZA ZESPOLONA – Funkcja

ekspotencjalna

Rozważmy teraz funkcję e

z

dla osi urojonej tzn. przyjmijmy z=iy.

W celu zbadania funkcji obliczmy kolejne potęgi z=iy:

0

0

1

1

2

2

2

3

3

3

4

4

4

5

5

5

6

6

6

( )

1

( )

( )

( )

( )

( )

( )

z

iy

z

iy

iy

z

iy

y

z

iy

iy

z

iy

y

z

iy

iy

z

iy

y











 



 











 

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ANALIZA ZESPOLONA – Funkcja

ekspotencjalna

















































...

!

5

!

3

...

!

6

!

4

!

2

1

...

!

6

!

5

!

4

!

3

!

2

1

5

3

6

4

2

6

5

4

3

2

y

y

y

i

y

y

y

y

iy

y

iy

y

iy

e

iy

Podstawiając otrzymane wyrażenia do szeregu otrzymujemy:

Po rozłożeniu szeregu na część rzeczywistą i urojoną stwierdzamy, że części te

są równoznaczne z szeregowym zapisem prostych funkcji trygonometrycznych

kosinus i sinus:

y

y

y

y

y

y

y

y

sin

...

!

5

!

3

cos

...

!

6

!

4

!

2

1

5

3

6

4

2



















© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ANALIZA ZESPOLONA – Funkcja

ekspotencjalna

y

i

y

e

iy

sin

cos





2

1

2

1

z

z

z

z

e

e

e





Podstawiając otrzymane zapisy do wyrażenia na funkcję ekspotencjalną osi
urojonej otrzymujemy słynny

wzór Eulera

wiążący funkcję ekspotencjalną

z funkcjami trygonometrycznymi:

Można wykazać, że funkcja ekspotencjalna zmiennej zespolonej spełnia większość

własności funkcji e

x

a w szczególności że:

W związku z tym:

)

sin

(cos

y

i

y

e

e

e

e

e

e

x

z

iy

x

iy

x

z













© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ANALIZA ZESPOLONA – Funkcja

ekspotencjalna





[(cos

)

(sin

)]

cos

sin

( )

z

z

z

z

x

e

e

z

x

z

e

e

i

e

y i

y

e

e

Arg e

y



















Jeżeli otrzymany wzór porównamy z tzw. trygonometryczną postacią liczb

zespolonych to otrzymamy pewne własności zespolonej funkcji ekspotencjalnej:

Oraz:

y

e

y

x

f

e

y

e

y

x

f

e

x

y

z

x

x

z

sin

)

,

(

)

Im(

cos

)

,

(

)

Re(









© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ANALIZA ZESPOLONA – Funkcja

ekspotencjalna









 

 

0

0

0

0

0

0

0

0

0

(2

)

0

0

0

0

(2

)

(2

)

(

2

)

0, 1, 2,...

[cos

2

sin

2

]

[cos

sin

]

z

i

k

x

z

x

z

z

z

i

k

x

iy

i

k

x

i y

k

k

e

e

e

y

k

i

y

k

e

y

i

y

e































  



















Niech:

0

0

)

2

(

z

i

k

z

e

e







Funkcja e

z

jest funkcją okresową (!!!) o okresie 2πi.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ANALIZA ZESPOLONA – Funkcje

trygonometryczne

Za pomocą szeregów potęgowych można oprócz funkcji ekspotencjalnej definiować

również funkcje trygonometryczne zmiennej zespolonej. Odpowiednie definicje są

uogólnieniem wzorów określających rozwinięcia szeregowe funkcji trygonometrycznych

zmiennej rzeczywistej:

z

z

z

z

z

z

n

z

z

z

z

z

n

z

z

z

z

z

z

n

n

n

n

n

n

sin

cos

cot

cos

sin

tan

)!

2

(

)

1

(

...

!

6

!

4

!

2

1

cos

)!

1

2

(

)

1

(

...

!

7

!

5

!

3

sin

0

2

6

4

2

0

1

2

7

5

3

















































Funkcje sin(z) i cos(z) są określone dla dowolnych liczb zespolonych. Z zapisu szeregowego

wynika, że funkcja sin(z) jest nieparzysta natomiast cos(z) jest parzysta.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ANALIZA ZESPOLONA – Funkcje

trygonometryczne

z

i

z

e

iz

sin

cos





Można wykazać, że funkcje trygonometryczne zmiennej zespolonej są ściśle

związane z funkcją ekspotencjalną za pomocą ogólnego wzoru Eulera:

Napiszmy powyższy wzór dla z oraz –z.

z

i

z

z

i

z

e

z

i

z

e

iz

iz

sin

cos

)

sin(

)

cos(

sin

cos



















© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ANALIZA ZESPOLONA – Funkcje

trygonometryczne

2 cos

cos

2

iz

iz

iz

iz

e

e

z

e

e

z















Dodając i odejmując stronami otrzymane równania dostajemy wzory wiążące

funkcje trygonometryczne zmiennej zespolonej z funkcją ekspotencjalną:

2 sin

sin

2

iz

iz

iz

iz

e

e

i

z

e

e

z

i















© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

r

z

0

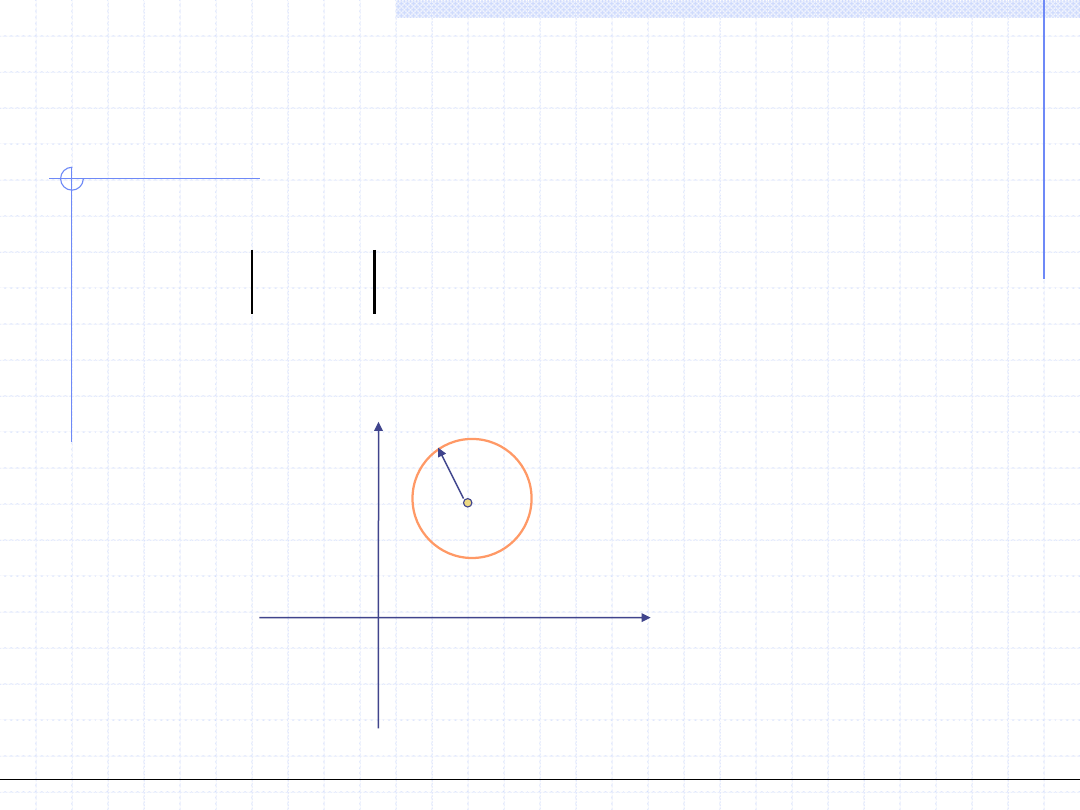
ANALIZA ZESPOLONA – Otoczenie

punktu zespolonego

Otoczeniem punktu z

0

=x

0

+iy

0

o promieniu r nazywamy zbiór wszystkich liczb

zespolonych spełniających nierówność:

0

0







r

r

z

z

x

y

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

r

z

0

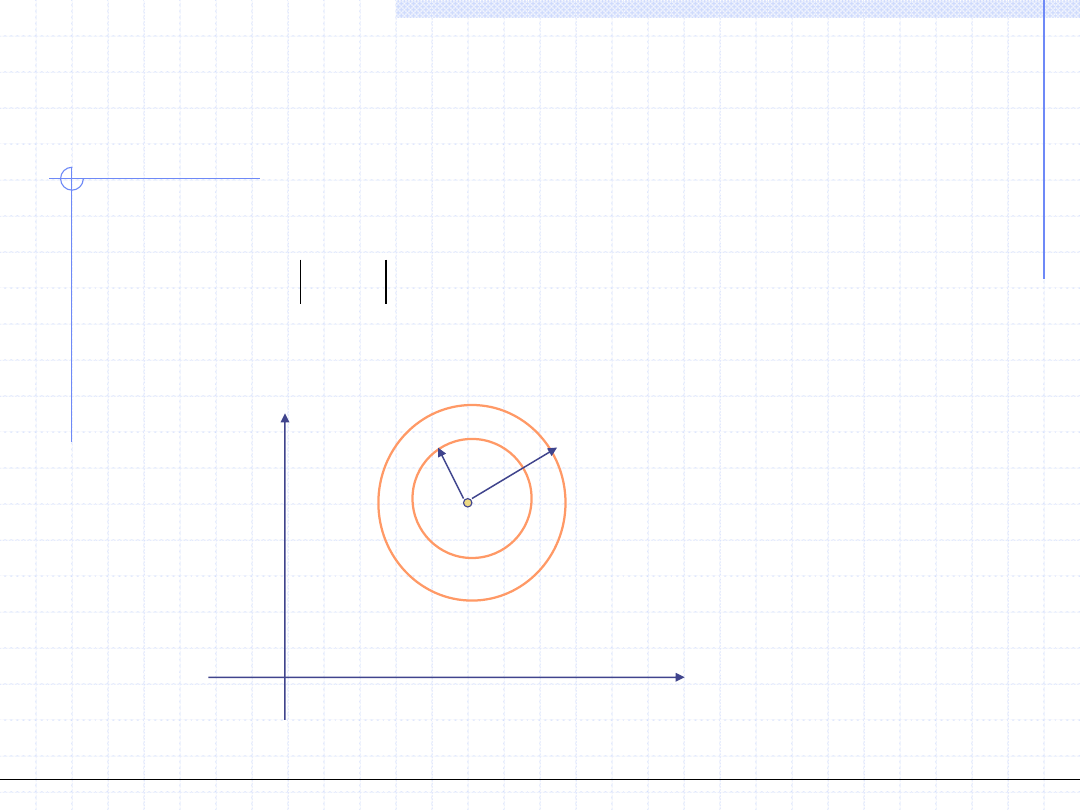
ANALIZA ZESPOLONA – Otoczenie

pierścieniowe

Otoczeniem pierścieniowym punktu z

0

=x

0

+iy

0

o promieniach r i R nazywamy zbiór

wszystkich liczb zespolonych spełniających podwójną nierówność:

0

0











r

R

R

z

z

r

x

y

R

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ANALIZA ZESPOLONA – Pochodna

funkcji zespolonej

Jeżeli dla danego punktu z

0

i danej funkcji zespolonej f(z) istnieje otoczenie tego

punktu o promieniu r>0 takie, ze dla dowolnego ciągu z

n

−>z

0

zawartego w tym

otoczeniu istnieje granica:

)

(

'

)

(

)

(

0

0

0

lim

0

z

f

z

z

z

f

z

f

n

n

z

z

n





















to mówimy że funkcja jest różniczkowalna w z

0

a liczbę f’(z) nazywamy pochodną

funkcji z. Ponieważ z jest zmienną więc otrzymana w wyniku różniczkowania pochodna

również jest nową funkcją zespoloną.

Funkcje zespolone, które są różniczkowalne nazywamy funkcjami analitycznymi.

Różniczkowanie za pomocą powyższej definicji jest bardzo uciążliwe i w praktyce

nie stosowane.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ANALIZA ZESPOLONA –

Różniczkowanie funkcji zespolonych

W praktyce technika różniczkowania zespolonego zależy od sposobu zdefiniowania

funkcji. Dla funkcji zdefiniowanych za pomocą wzorów zawierających operatory

algebraiczne i proste funkcje elementarne stosuje się wszystkie metody analogiczne

do różniczkowania funkcji rzeczywistych. Prawie wszystkie stosowane tam

twierdzenia (o różniczkowaniu sumy, iloczynu, ilorazu itd.) można przenieść

bezpośrednio na różniczkowanie zespolone. W szczególności wielomiany zespolone

oraz zespolone funkcje wymierne różniczkuje się tak samo jak funkcje rzeczywiste.

Proste funkcje zespolone zdefiniowane za pomocą szeregów takie jak funkcja

ekspotencjalna i funkcje trygonometryczne różniczkuje się identycznie jak odpowiednie

funkcje rzeczywiste. Mamy więc:

z

z

z

z

e

e

z

z

sin

)'

(cos

cos

)'

(sin

)'

(









© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ANALIZA ZESPOLONA –

Różniczkowanie funkcji zespolonych

o

y

x

iy

x

z

y

x

f

i

y

x

f

z

f

Niech









0

0

)

,

(

)

,

(

)

(

Istotna różnica między różniczkowaniem zespolonym a rzeczywistym zachodzi

dla funkcji zdefiniowanych za pomocą części rzeczywistej i urojonej. Dla tego

przypadku obowiązuje tzw. twierdzenie Cauchy – Riemanna:

1. Jeżeli funkcja f(z) jest różniczkowalna w z

0

to istnieją pochodne cząstkowe

funkcji f

x

i f

y

oraz spełniają one tzw. równania Cauchy – Riemanna:

x

f

y

f

y

f

x

f

y

x

y

x























© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ANALIZA ZESPOLONA –

Różniczkowanie funkcji zespolonych

2. Jeżeli funkcje f

x

(x,y) oraz f

y

(x,y) określające daną funkcję zespoloną spełniają

powyższe równania Cauchy – Riemanna a wszystkie pochodne cząstkowe

występujące w tych równaniach są ciągłe w punkcie (x

0

,y

0

) to funkcja zespolona

f(z)=f

x

(x,y)+if

y

(x,y) jest różniczkowalna a jej pochodna wyraża się wzorem:

y

f

i

y

f

x

f

i

x

f

z

f

x

y

y

x

























)

(

'

Technika różniczkowania za pomocą twierdzenia Cauchy – Riemanna polega

na znajdowaniu odpowiednich pochodnych cząstkowych funkcji składowych.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ANALIZA ZESPOLONA –

Różniczkowanie funkcji zespolonych

Przykład:

( )

(

)

cos( )

sin( )

x

x

f z

f x iy

e

y

i e

y









Mamy zatem:

( , )

cos( )

( , )

sin( )

x

x

x

y

f x y

e

y

f x y

e

y





W celu zróżniczkowania tej funkcji należy najpierw sprawdzić jej różniczkowalność

za pomocą równań Cauchy – Riemanna. Musimy zatem wyznaczyć 4 pochodne cząstkowe:

( , )

( , )

cos( )

cos( )

( , )

( , )

sin( )

sin( )

y

x

x

x

y

x

x

x

f x y

f x y

e

y

e

y

x

y

f x y

f x y

e

y

e

y

y

x

















 







Widzimy że równania Cauchy – Riemanna są spełnione.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ANALIZA ZESPOLONA –

Różniczkowanie funkcji zespolonych

Zatem zgodne ze wzorem Cauchy – Riemanna możemy wyznaczyć pochodną:

'( )

cos( )

sin( )

( )

!!!

y

x

x

x

f

f

f z

i

e

y

i e

y

f z

x

x



















( , )

( , )

cos( )

cos( )

( , )

( , )

sin( )

sin( )

y

x

x

x

y

x

x

x

f x y

f x y

e

y

e

y

x

y

f x y

f x y

e

y

e

y

y

x

















 







Czyli pochodna tej funkcji jest tożsama z tą funkcją. Ale można sprawdzić, że

funkcja ta jest równoznaczna z funkcją ekspotencjalną więc własność ta jest

oczywista.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ANALIZA ZESPOLONA –

Różniczkowanie funkcji zespolonych

W przypadku funkcji zdefiniowanych za pomocą szeregu, możemy skorzystać

z jednostajnej zbieżności tego szeregu i różniczkować szereg wyraz po wyrazie.

Przykładowo zróżniczkujmy funkcję ekspotencjalną zdefiniowaną za pomocą szeregu:

2

3

0

1

1

1

1

( )

1

...

...

!

2!

3!

!

n

n

n

f z

z

z

z

z

z

n

n







  



 





1

2

1

0

2

1

1

2

3

'( )

0 1

...

...

!

2!

3!

!

1

1

1

....

....

2!

(

1)!

n

n

n

n

z

n

n

f z

z

z

z

z

n

n

z

z

z

e

n















  



 

 

 











Otrzymaliśmy oczywistą postać pochodnej funkcji ekspotencjalnej.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

z

n-1

z

2

z

1

ANALIZA ZESPOLONA – Całkowanie

funkcji zespolonych

W przypadku funkcji zespolonych podstawową operacją odwrotną do różniczkowania

jest tzw. całkowanie krzywoliniowe. Teraz zdefiniujemy pojęcie całki funkcji

zespolonej po pewnej linii leżącej w płaszczyźnie zespolonej.

Niech f(z) będzie daną funkcją zespoloną a K pewną linią regularną (gładką) leżącą

w dziedzinie funkcji zaczynającą się w punkcie z

p

i kończącą się w z

k

.

x

y

z

p

=z

0

z

k

=z

n

K

Podzielmy linię K na skończoną liczbę n części za pomocą punktów:

k

n

i

i

p

z

z

z

z

z

z

z

z







,...,

,

,...,

,

,

1

2

1

0

z

i-1

z

i

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ANALIZA ZESPOLONA – Całkowanie

funkcji zespolonych

]

,

[

1

i

i

i

z

z







1









i

i

i

z

z

z

Z każdej części wybierzmy dowolny punkt

Dla każdej części możemy obliczyć różnicę

Utwórzmy teraz sumę











n

i

i

i

i

n

z

f

S

1

)

(



Jeżeli teraz będziemy zwiększać liczbę n i dla każdego nowego podziału linii będziemy

powtarzać powyższą operację to otrzymamy ciąg liczb zespolonych S

n

. Jeżeli ciąg ten ma

granicę to funkcja jest całkowalna a granicę nazywamy całką krzywoliniową funkcji f(z) po

krzywej K i oznaczamy wzorem:

z

n-1

z

2

z

1

x

y

z

p

=z

0

z

k

=z

n

K

z

i-1

z

i

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

ANALIZA ZESPOLONA – Całkowanie

funkcji zespolonych

0

(

)

( )

lim

i

n

n

K

z

S

f z dz



 





Z pojęciem całki krzywoliniowej związane jest pojęcie funkcji pierwotnej.

Mówimy, że funkcja F(z) jest funkcją pierwotną do funkcji f(z) w obszarze D

jeżeli w każdym punkcie tego obszaru zachodzi równość F’(z)=f(z).

Funkcję pierwotną oraz całkę krzywoliniową łączy następujące twierdzenie:

Jeżeli funkcja f(z) jest ciągła w obszarze D i ma w tym obszarze funkcję pierwotną F(z)

to całka krzywoliniowa po dowolnej linii regularnej zawartej w D o początku z

p

i końcu z

k

wyraża się prostym wzorem:

)

(

)

(

)

(

p

k

K

z

F

z

F

dz

z

f







© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

Na tym kończymy dzisiejszy wykład.

Dziękuję bardzo Państwu za uwagę.