© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

MATEMATYKA STOSOWANA W 

INŻYNIERII CHEMICZNEJ

Wykład – 4

Matematyczne opracowywanie wyników 

eksperymentalnych

Cz. I. Metoda najmniejszych kwadratów

Cz. II. Metody statystyczne

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Eksperymenty wykonywane w nauce można podzielić na dwie kategorie:

UWAGI OGÓLNE



eksperymenty jakościowe, których wynikiem jest potwierdzenie lub zaprzeczenie

określonej tezy



eksperymenty ilościowe, których wynikiem jest szereg liczb wyznaczonych

dla określonych parametrów. Liczby te najczęściej dają wartości pewnych

funkcji na ogół niewiadomych.

Wyniki eksperymentów jakościowych są opracowywane metodami statystyki

matematycznej. W inżynierii chemicznej eksperymenty jakościowe są 

przeprowadzane rzadko i dlatego w dalszym ciągu nie będziemy się zajmować

ich opracowywaniem.

Większość eksperymentów ma charakter ilościowy. Odpowiednie opracowanie

takich ilościowych wyników pozwala zarówno na ilościowy opis badanego procesu,

jak i na pewne jakościowe wnioski dotyczące naukowego wyjaśnienia 

różnych zjawisk.

W toku opracowywania wyników ilościowych bardzo ważną rolę odgrywa fakt,

że nie są one dokładne ale są zawsze obarczone pewnym błędem. 

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

W przypadku badania przebiegu jakiejś funkcji możliwe jest jej 

doświadczalne wyznaczenie tylko w określonych punktach. 

Badanie najczęściej polega na tym, że po ustaleniu wartości zmiennej 

niezależnej w punkcie  x

i

dokonuje się pomiaru wartości funkcji a wynik 

zapisuje się jako y

i

. Aby dobrze uchwycić przebieg funkcji wykonuje się 

szereg pomiarów w różnych punktach. 

Wynikiem eksperymentu jest zatem zbiór par {x

i

,y

i

}. 

Taki zbiór jest to doświadczalnie wyznaczona funkcja y=f(x) 

w postaci dyskretnej. 

UWAGI OGÓLNE

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

UWAGI OGÓLNE

Opis jednak funkcji w postaci dyskretnej jest na ogół mało przydatny. 

W zastosowaniach bardziej użyteczne są funkcje ciągłe określone dla

dowolnych argumentów x. 

Zagadnienie zastępowania funkcji dyskretnej otrzymanej doświadczalnie, 

pewną funkcją ciągłą mającą na ogół podstawę teoretyczną, nazywamy 

aproksymacją.   

Jedną z metod aproksymacji bardzo szeroko stosowaną w inżynierii

jest tzw. metoda najmniejszych kwadratów.

W dalszym ciągu omówię tę metodę dla przypadku funkcji jednej zmiennej.

W łatwy sposób można rozważania uogólnić na funkcje wielu zmiennych.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

APROKSYMACJA FUNKCJI ZA POMOCĄ 

METODY NAJMNIEJSZYCH KWADRATÓW

)

,...,

,...,

,

,

(

2

1

k

j

a

a

a

a

x

f

y

]

,...,

,...,

,

[

]

,...,

,...,

,

[

2

1

2

1

n

i

t

eksperymen

n

i

y

y

y

y

y

x

x

x

x

x





Zakładamy, że w danym problemie występuje funkcja jednej zmiennej x, 

która jest określona za pomocą k stałych parametrów a

j

:

W celu wyznaczenia wartości parametrów przeprowadza się 

n eksperymentów dla pewnego zbioru wartości zmiennej x 

mierząc odpowiednie wartości y:

]

,...

,

[

2

1

k

ja

aproksymac

a

a

a

y

x





© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

APROKSYMACJA FUNKCJI ZA POMOCĄ 

METODY NAJMNIEJSZYCH KWADRATÓW

Rozważmy wzajemne relacje między k i n tzn. między liczbą niewiadomych

parametrów a liczbą niezależnych eksperymentów.

Przypadek I      n<k    

(liczba eksperymentów jest mniejsza niż liczba parametrów).

W takim przypadku na ogół proces aproksymacji nie będzie jednoznaczny.

Przypadek II     n=k    

(liczba eksperymentów jest równa liczbie parametrów)

Dla każdego niezależnego eksperymentu można napisać równanie, 

w którym prawa strona jest wynikiem eksperymentu. 

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

APROKSYMACJA FUNKCJI ZA POMOCĄ 

METODY NAJMNIEJSZYCH KWADRATÓW

W rezultacie otrzymujemy układ równań:

n

n

n

n

n

y

a

a

x

f

y

a

a

x

f

y

a

a

x

f

)

,...,

,

(

..........

..........

..........

)

,...,

,

(

)

,...,

,

(

1

2

1

2

1

1

1

Tak można postąpić pod warunkiem, że pomiary są absolutnie dokładne czyli 

obarczone zerowym błędem. W rzeczywistości błędy pomiarowe mogą być 

dosyć duże. Aby uniknąć przenoszenia się tych błędów na wyznaczane 

parametry, wykonuje się zazwyczaj znacznie więcej pomiarów niż wynosi 

liczba parametrów.

Rozwiązanie tego układu równań 

daje nam niewiadomy wektor 

parametrów a=[a1,a2,…,ak].

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

APROKSYMACJA FUNKCJI ZA POMOCĄ 

METODY NAJMNIEJSZYCH KWADRATÓW

Przypadek III      n>k    

(liczba eksperymentów jest większa niż liczba parametrów).

Do tego właśnie przypadku stosowana jest metoda najmniejszych kwadratów.

Podobne postępowanie jak w przypadku II prowadzi do układu równań, 

w którym jest więcej równań niż niewiadomych. Takie układy równań są 

z reguły sprzeczne tzn. nie mają dokładnych rozwiązań. 

Możemy jednak poszukiwać rozwiązań przybliżonych tzn. takich dla których 

funkcja będzie opisywać wyniki doświadczeń z pewnym błędem. 

Minimalizację tych błędów zapewnia właśnie metoda najmniejszych kwadratów. 

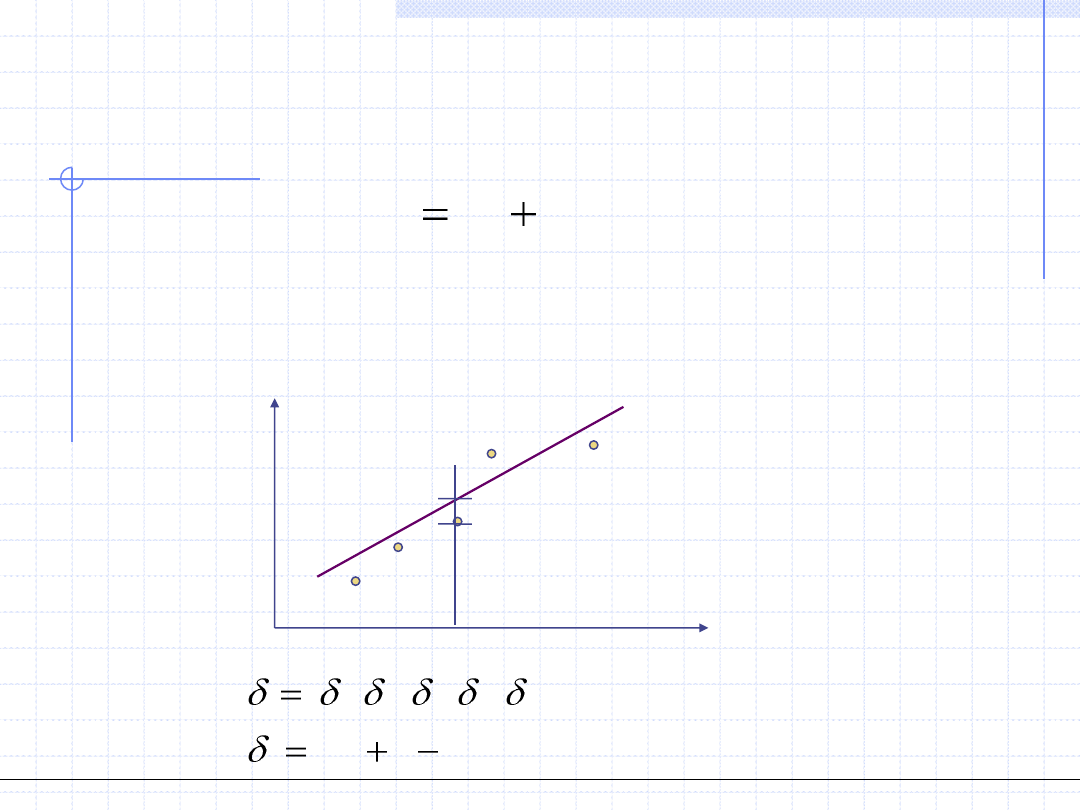
Rozważmy prosty przykład funkcji liniowej o dwu parametrach:

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

APROKSYMACJA FUNKCJI ZA POMOCĄ 

METODY NAJMNIEJSZYCH KWADRATÓW

b

ax

y

Wykonajmy 5 eksperymentów dla [x

1

,x

2

,x

3

,x

4

,x

5

] otrzymując wyniki

[y

1

,y

2

,y

3

,y

4

,y

5

]. Arbitralne przeprowadzenie linii prostej daje wektor

odchyleń (błędów bezwzględnych):

x

y

i

i

i

y

b

ax

gdzie

]

,

,

,

,

[

5

4

3

2

1



x

i

δ

i

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

APROKSYMACJA FUNKCJI ZA POMOCĄ 

METODY NAJMNIEJSZYCH KWADRATÓW

Rozważmy teraz szczegółowo przypadek aproksymacji funkcji 

z k parametrami za pomocą wyników n eksperymentów, przy czym n>k. 

Ponieważ poszczególne eksperymenty mogą mieć różną dokładność, 

fakt ten uwzględnia się za pomocą tzw. wag. 

Mamy więc: 

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

APROKSYMACJA FUNKCJI ZA POMOCĄ 

METODY NAJMNIEJSZYCH KWADRATÓW

i

k

i

i

n

i

n

n

n

k

y

a

a

x

f

w

w

w

w

w

y

y

y

y

k

n

x

x

x

x

a

a

x

f

y

)

,...,

,

(

]

,...,

,

[

0

]

,...,

,

[

]

,...,

,

[

]

,...,

,

[

)

,...,

,

(

1

2

1

2

1

2

1

2

1

1









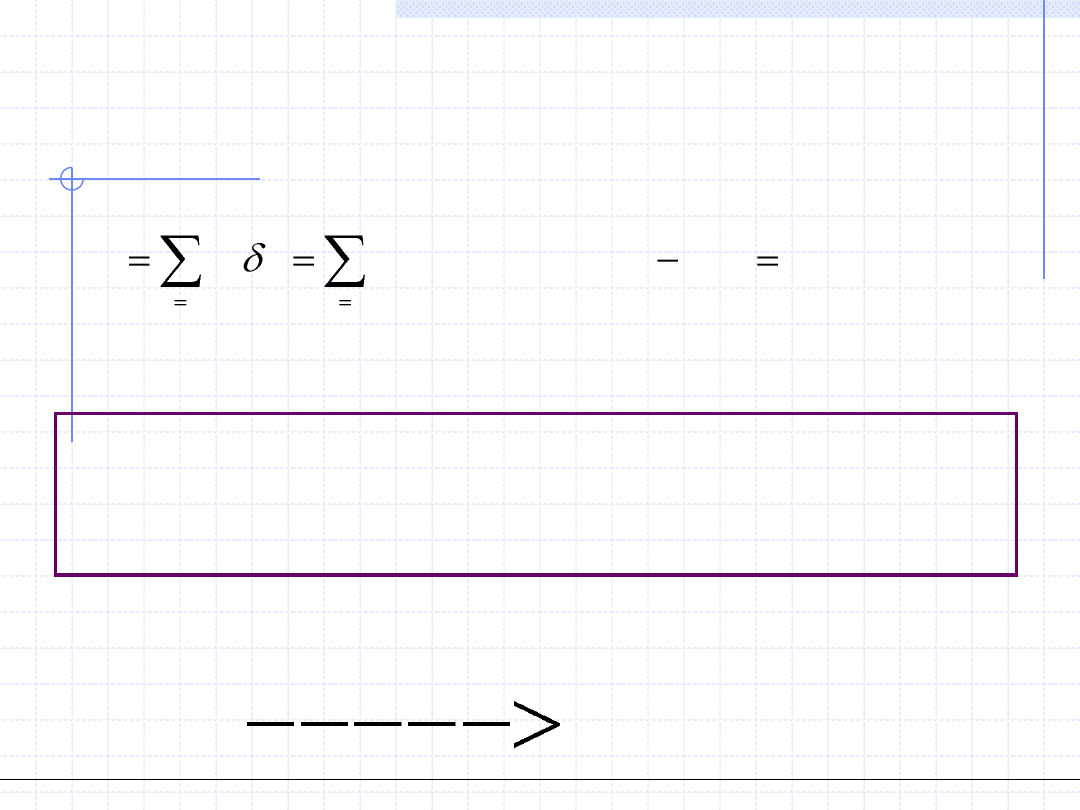
W celu minimalizacji wektora błędów wprowadźmy funkcję S zdefiniowaną 

jako ważoną sumę kwadratów błędów poszczególnych pomiarów:

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

APROKSYMACJA FUNKCJI ZA POMOCĄ 

METODY NAJMNIEJSZYCH KWADRATÓW

2

2

1

1

2

1

1

[ ( ,

,...,

)

]

( ,

,...,

)

n

n

i

i

i

i

k

i

k

i

i

S

w

w f x a

a

y

S a a

a

Funkcja S ma swoje głębokie uzasadnienie w rachunku prawdopodobieństwa. 

Jest ona ściśle związana z tzw. rozkładem normalnym Gaussa.

Istotą metody najmniejszych kwadratów jest 

poszukiwanie takich wartości parametrów 

a

1

,a

2

,…,a

k

, przy których wartość S jest najmniejsza.

]

,...,

,

[

2

1

minimum

k

a

a

a

S

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

APROKSYMACJA FUNKCJI ZA POMOCĄ 

METODY NAJMNIEJSZYCH KWADRATÓW

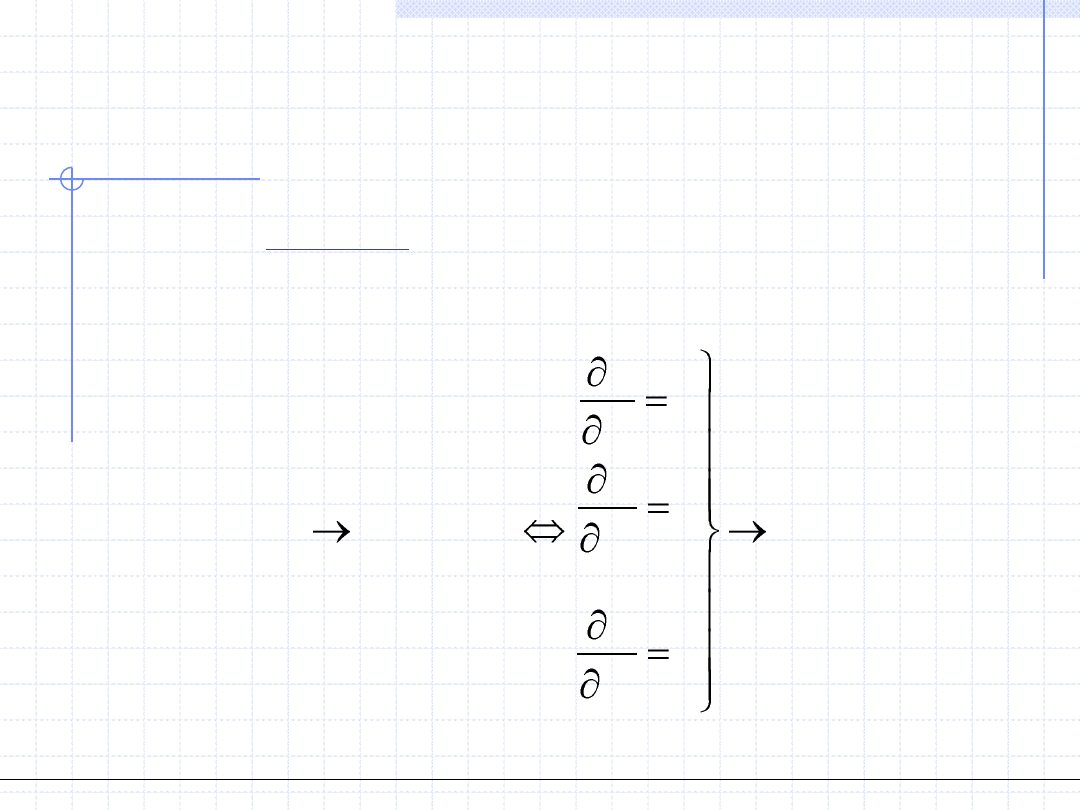
Poszukiwaniem ekstremalnych punktów różnych funkcji zajmuje się osobny dział 

matematyki – optymalizacja. W przypadku różniczkowanych funkcji wielu zmiennych

najprostszą metodą optymalizacji jest porównanie do zera wszystkich pochodnych 

cząstkowych. W naszym przypadku należy przyrównać do zera pochodne cząstkowe 

funkcji S względem szukanych parametrów. W rezultacie otrzymujemy układ k równań

z k niewiadomymi:

]

,...,

,

[

0

...

..........

0

0

minimum

)

,...,

,

(

2

1

2

1

2

1

k

k

k

a

a

a

a

S

a

S

a

S

a

a

a

S

W ogólnym przypadku rozwiązanie analityczne tego układu nie jest możliwe. 

Jednak dla szerokiej klasy funkcji układ ten jest liniowy i teraz zajmiemy się 

tym przypadkiem. 

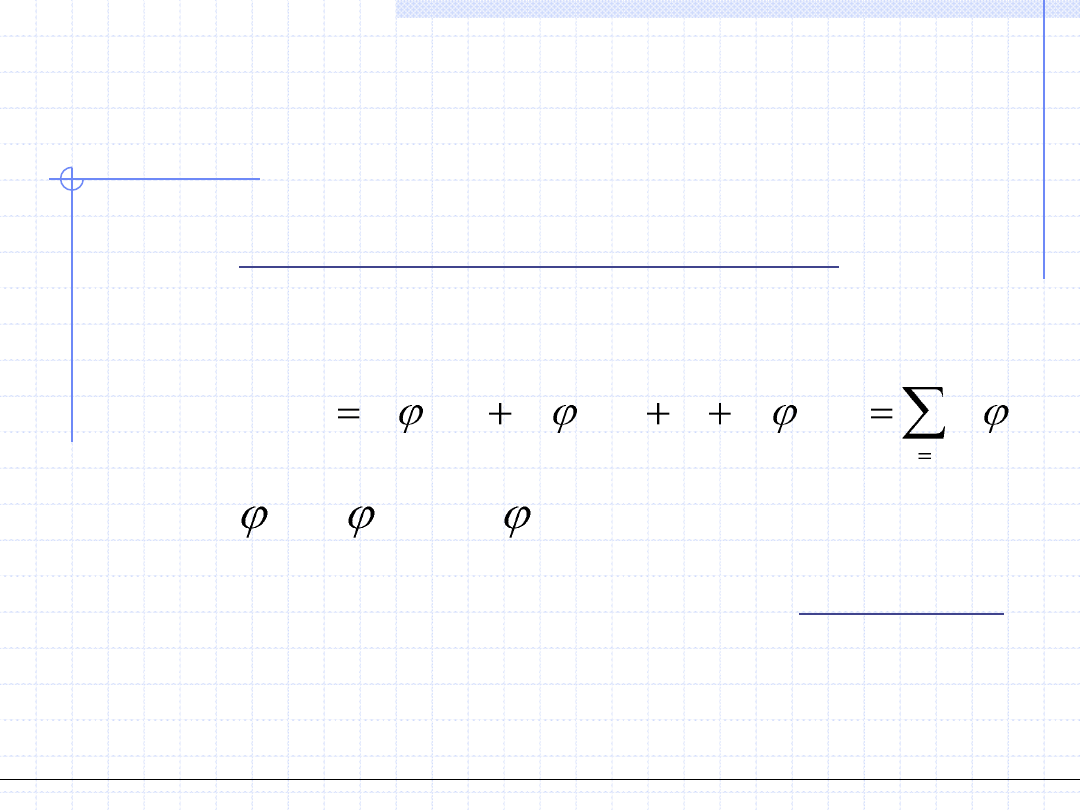
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

METODY NAJMNIEJSZYCH KWADRATÓW

DLA FUNKCJI LINIOWYCH ZE WZGLĘDU 

NA PARAMETRY 

k

j

j

j

k

k

k

x

a

x

a

x

a

x

a

a

a

a

x

f

1

2

2

1

1

2

1

)

(

)

(

...

)

(

)

(

)

,...,

,

,

(

)

(

),...,

(

),

(

2

1

x

x

x

k

Funkcje, w których parametry a

1

,a

2

,…,a

k

występują w postaci liniowej 

nazywamy funkcjami liniowymi ze względu na parametry. 

Funkcje takie można zapisać w postaci:

gdzie

są to stosunkowo proste ale liniowo niezależne tzw. funkcje bazowe.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

METODY NAJMNIEJSZYCH KWADRATÓW

DLA FUNKCJI LINIOWYCH ZE WZGLĘDU 

NA PARAMETRY 

Przykłady funkcji bazowych:

2

0

1

2

0

1

2

0

( ,

, ,

,...,

)

( )

...

k

j

k

k

j

k

j

f x a a a

a

a x

a

a x a x

a x

2

0

1

2

0

1

2

0

( ,

, ,

,...,

)

...

k

jx

x

x

kx

k

j

k

j

f x a a a

a

a e

a

a e

a e

a e

0

1

2

0

0

1

2

( ,

, ,

,...,

)

sin(

)

sin( )

sin(2 ) ...

sin(

)

k

k

j

j

k

f x a a a

a

a

jx

a

a

x

a

x

a

kx

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

METODY NAJMNIEJSZYCH KWADRATÓW

DLA FUNKCJI LINIOWYCH ZE WZGLĘDU 

NA PARAMETRY 

Załóżmy teraz że nasza funkcja, której parametrów poszukujemy ma 

postać funkcji liniowej ze względu na parametry.

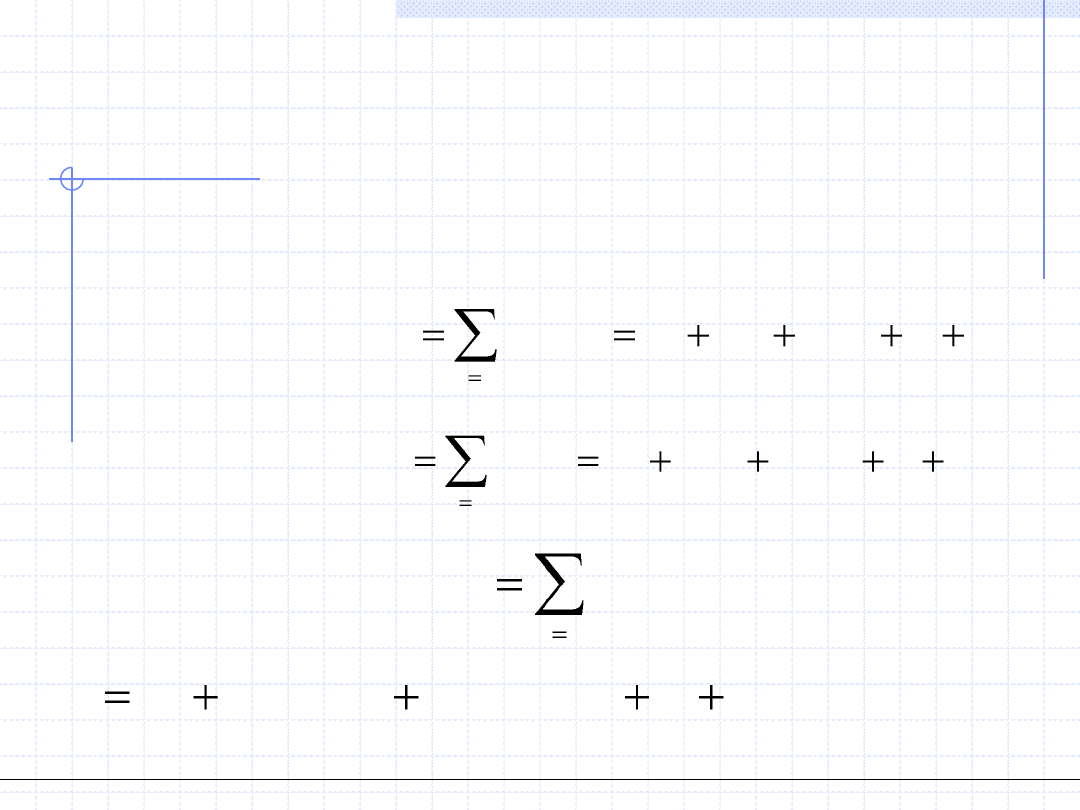
W celu znalezienia parametrów należy wyznaczyć pochodne cząstkowe 

funkcji S względem kolejnych parametrów i skonstruować odpowiedni 

układ równań. 

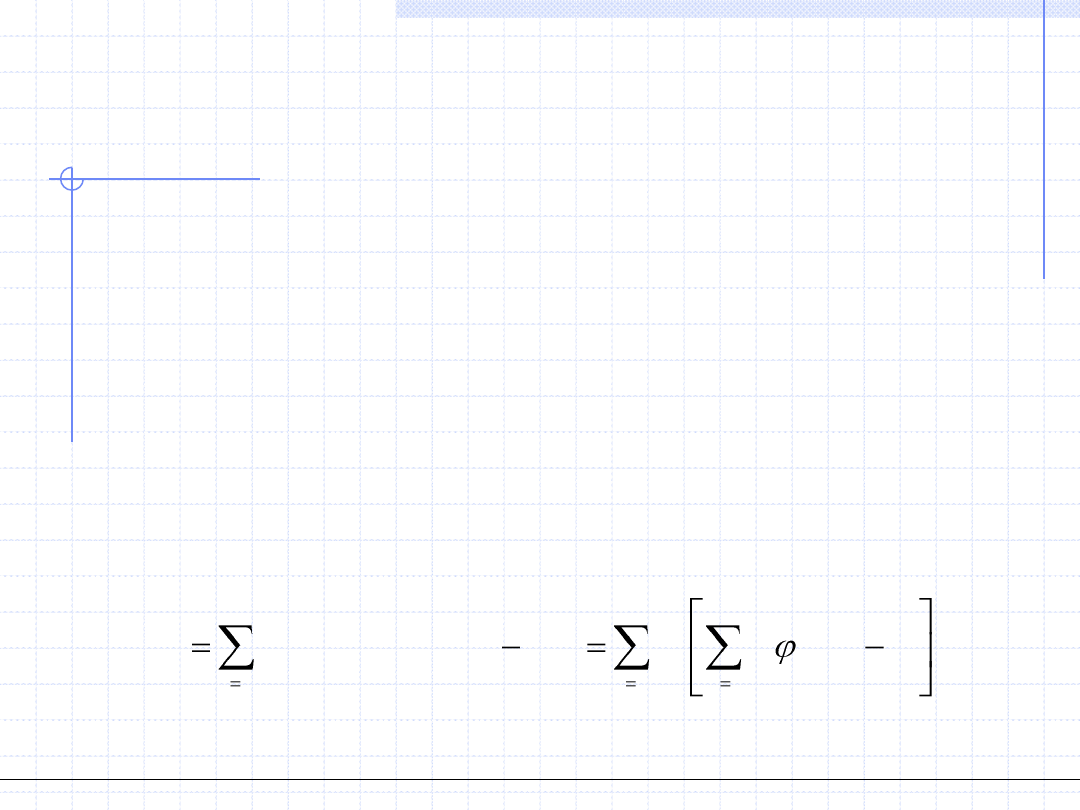
Funkcja S będzie miała postać:

2

2

1

1

1

1

[ ( , ,...,

)

]

( )

n

n

k

i

i

k

i

i

j

j

i

i

i

i

j

S

w f x a

a

y

w

a

x

y

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

METODY NAJMNIEJSZYCH KWADRATÓW

DLA FUNKCJI LINIOWYCH ZE WZGLĘDU 

NA PARAMETRY 

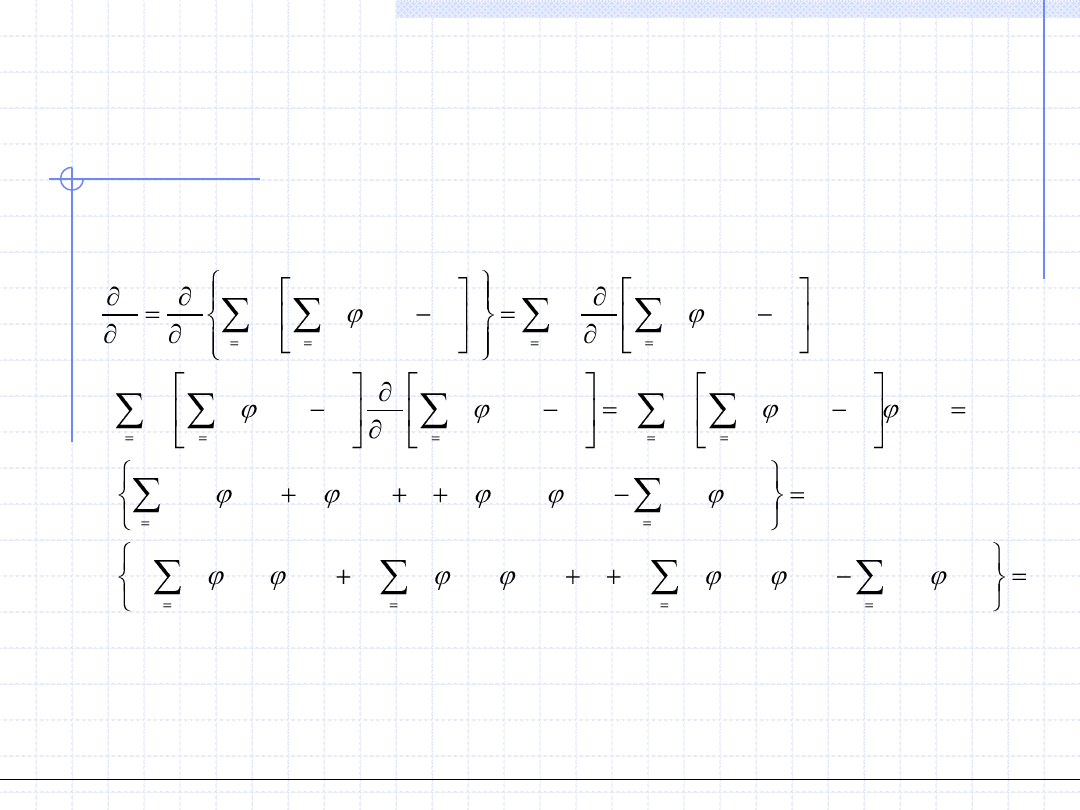
Pochodna ze względu na parametr a

1

będzie miała postać:

2

2

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1 1

2

2

( )

( )

2

( )

( )

2

( )

( )

2

[

( )

( )

n

k

n

k

i

j

j

i

i

i

j

j

i

i

i

j

i

j

n

k

k

n

k

i

j

j

i

i

j

j

i

i

i

j

j

i

i

i

i

j

j

i

j

i

i

i

S

w

a

x

y

w

a

x

y

a

a

a

w

a

x

y

a

x

y

w

a

x

y

x

a

w a

x

a

x

1

1

1

1

1

1

1

2

2

1

1

1

1

1

1

1

...

( )] ( )

( )

2

( ) ( )

( ) ( ) ...

( ) ( )

( )

0

n

n

k

k

i

i

i

i

i

i

i

n

n

n

n

i

i

i

i

i

i

k

i

k

i

i

i

i

i

i

i

i

i

a

x

x

w y

x

a

w

x

x

a

w

x

x

a

w

x

x

w y

x

Porównanie tej pochodnej do zera daje nam pierwsze równanie z układu równań.

Możemy łatwo zauważyć, że jest to równanie liniowe ze względu na szukane

niewiadome a

1

,a

2

,…,a

k

. W sposób analogiczny otrzymujemy kolejne równania.

Cały układ będzie miał postać:

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

METODY NAJMNIEJSZYCH KWADRATÓW

DLA FUNKCJI LINIOWYCH ZE WZGLĘDU 

NA PARAMETRY 

n

i

i

k

i

i

n

i

n

i

n

i

i

k

i

k

i

k

i

k

i

i

i

k

i

i

n

i

i

i

i

n

i

n

i

n

i

i

i

k

i

k

i

i

i

i

i

i

n

i

i

i

i

n

i

n

i

n

i

i

i

k

i

k

i

i

i

i

i

i

x

y

w

x

x

w

a

x

x

w

a

x

x

w

a

x

y

w

x

x

w

a

x

x

w

a

x

x

w

a

x

y

w

x

x

w

a

x

x

w

a

x

x

w

a

1

1

1

1

2

2

1

1

1

2

1

1

1

2

2

2

2

2

1

1

1

1

1

1

1

1

1

2

2

1

1

1

)

(

)

(

)

(

...

)

(

)

(

)

(

)

(

......

..........

..........

..........

..........

..........

..........

..........

..........

..........

..........

..........

..........

..........

)

(

)

(

)

(

...

)

(

)

(

)

(

)

(

)

(

)

(

)

(

...

)

(

)

(

)

(

)

(

Wprowadzenie oznaczeń:

1

1

( )

( )

( )

n

i

j

i

r

i

rj

i

n

i

i

r

i

r

i

w

x

x

b

w y

x

c

gdzie j oznacza numer kolumny a r numer równania

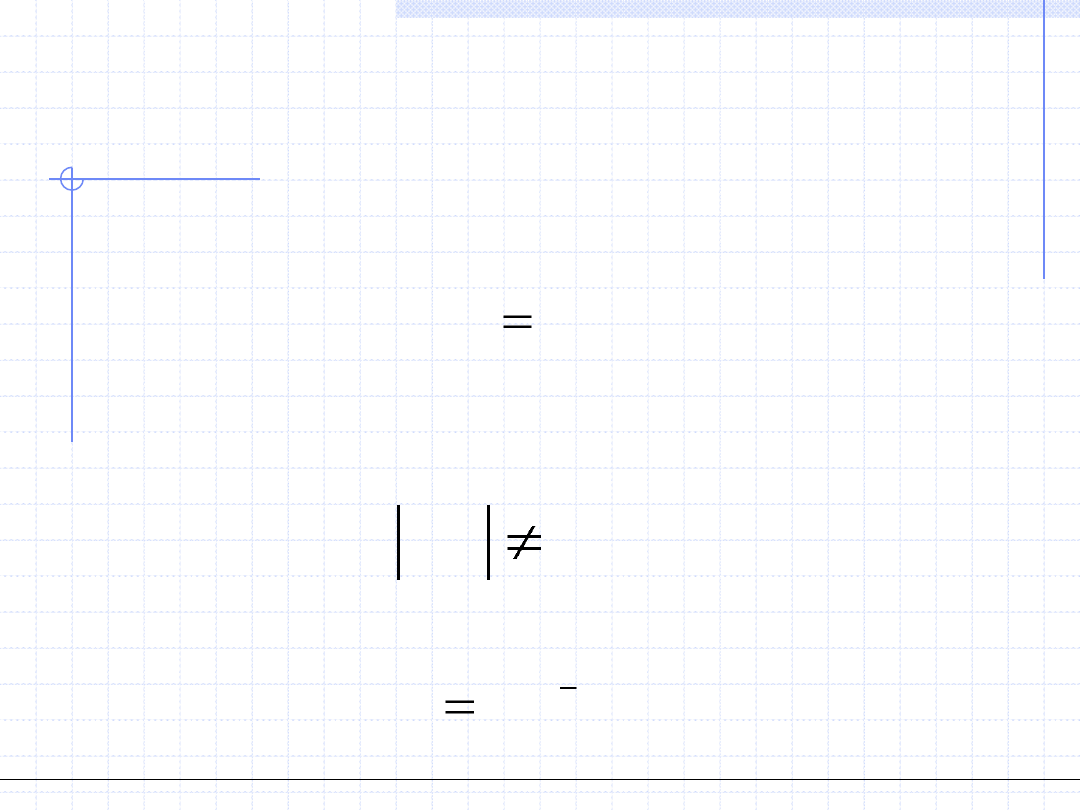
otrzymujemy układ równań w postaci:

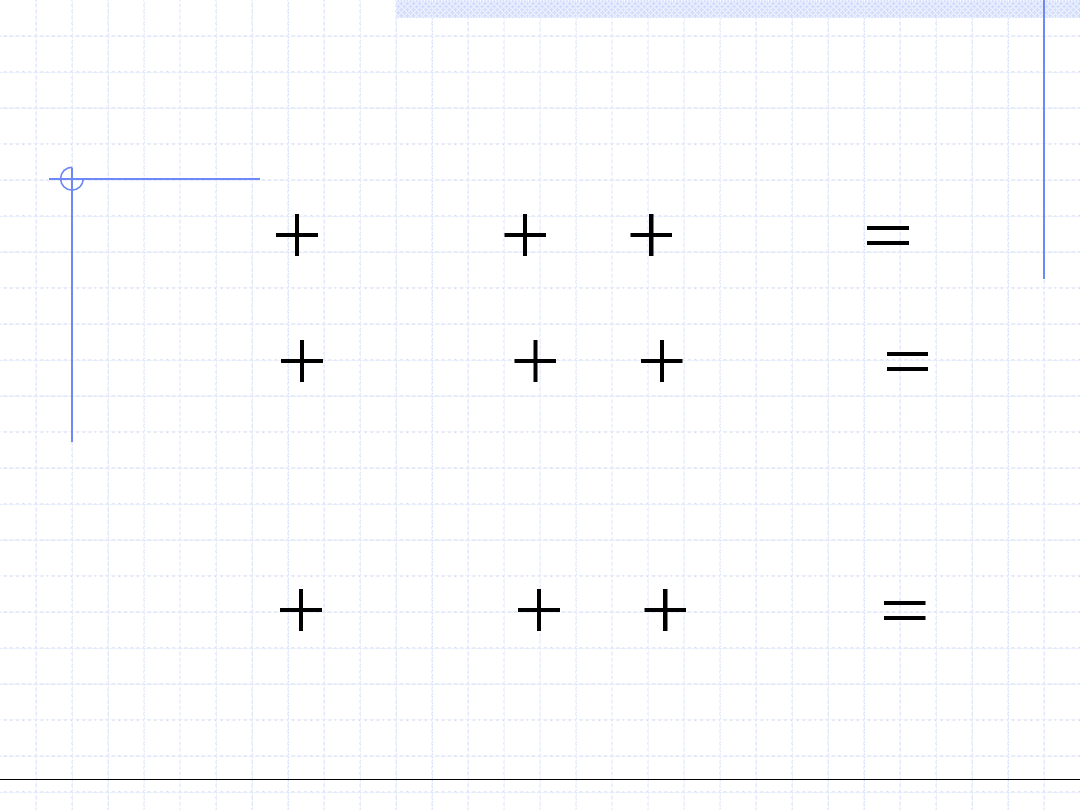
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

METODY NAJMNIEJSZYCH KWADRATÓW

DLA FUNKCJI LINIOWYCH ZE WZGLĘDU 

NA PARAMETRY 

1 11

2 12

1

1

1 21

2 22

2

2

1

1

2

2

...

...

...........................................

...

k

k

k

k

k

k

k kk

k

a b

a b

a b

c

a b

a b

a b

c

a b

a b

a b

c

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Układ równań liniowych ma jednoznaczne rozwiązanie wtedy gdy 

wyznacznik macierzy głównej układu jest różny od zera tzn. 

METODY NAJMNIEJSZYCH KWADRATÓW

DLA FUNKCJI LINIOWYCH ZE WZGLĘDU 

NA PARAMETRY 

[ ] [ ] [ ]

B

a

c



[ ]

0

B

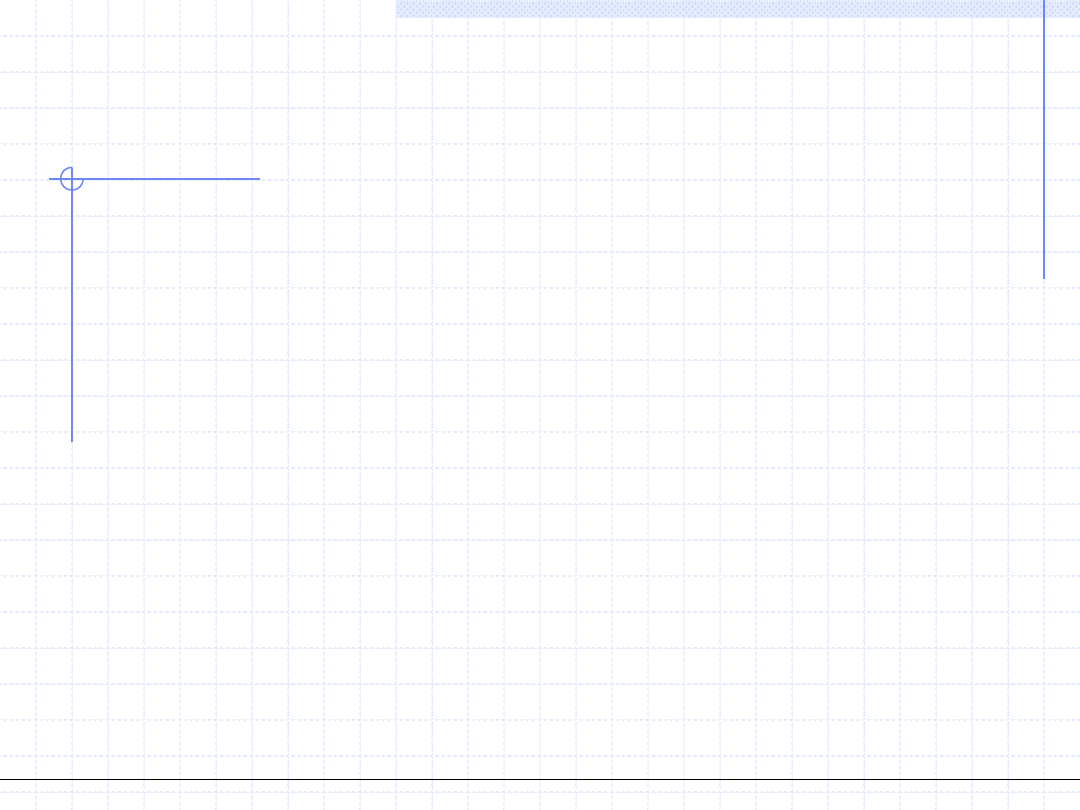
Układ ten ma bardzo prostą postać macierzową:

W takim przypadku rozwiązanie możemy zapisać macierzowo:

1

[ ] [ ]

[ ]

a

B

c



© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

METODY NAJMNIEJSZYCH KWADRATÓW

DLA FUNKCJI LINIOWYCH ZE WZGLĘDU 

NA PARAMETRY 

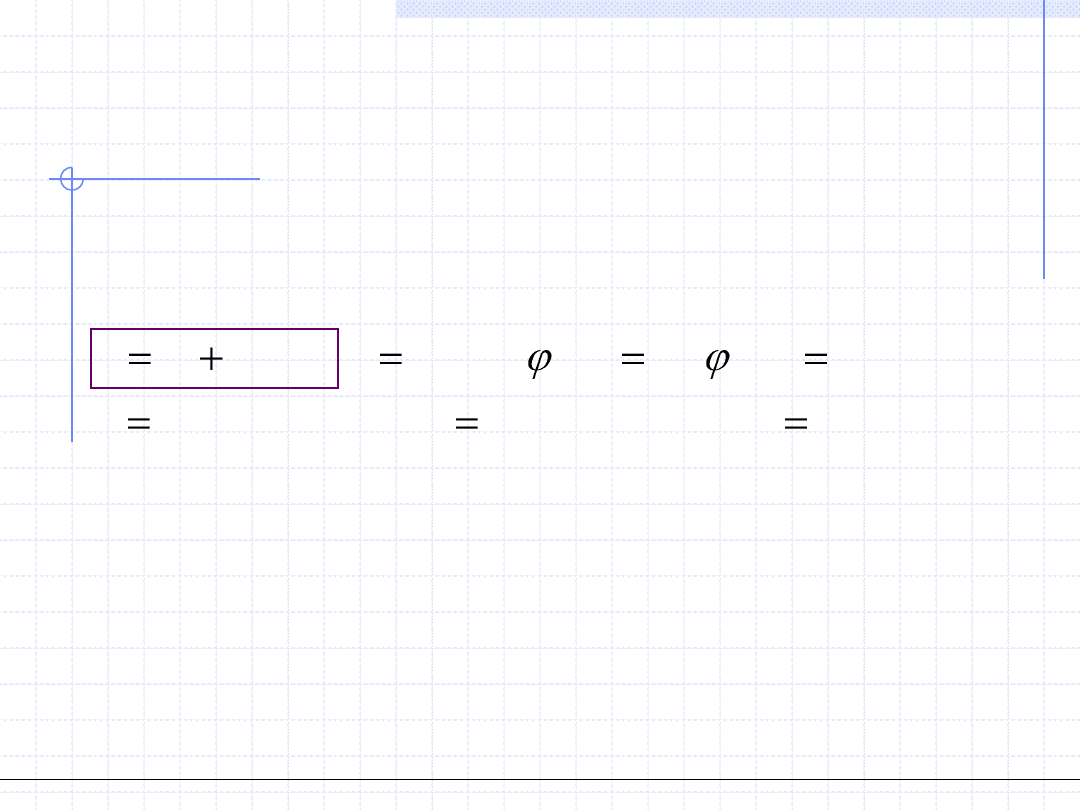
W naszym przypadku można wykazać że jeżeli:

a) układ funkcji φ

1

,φ

2

,…,φ

k

jest liniowo niezależny

b) punkty x

i

dla których były wykonywane doświadczenia są różne 

(nie powtarzają się) to wyznacznik macierzy [B] jest różny od zera 

i układ ma jednoznaczne rozwiązanie.

W praktyce układy równań liniowych rozwiązujemy albo metodami 

analitycznymi (np. metodą Cramera) albo przybliżonymi (np. Gaussa).

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

METODY NAJMNIEJSZYCH KWADRATÓW

DLA FUNKCJI LINIOWYCH ZE WZGLĘDU 

NA PARAMETRY 

Jako szczególny przypadek powyższej metody wyprowadzimy wzory 

określające współczynniki w równaniu linii prostej:

]

,...,

,

[

]

,...,

[

]

,...,

,

[

)

(

1

)

(

2

2

1

2

,

1

2

1

2

1

2

1

n

n

n

w

w

w

w

y

y

y

y

x

x

x

x

x

x

x

k

x

a

a

y







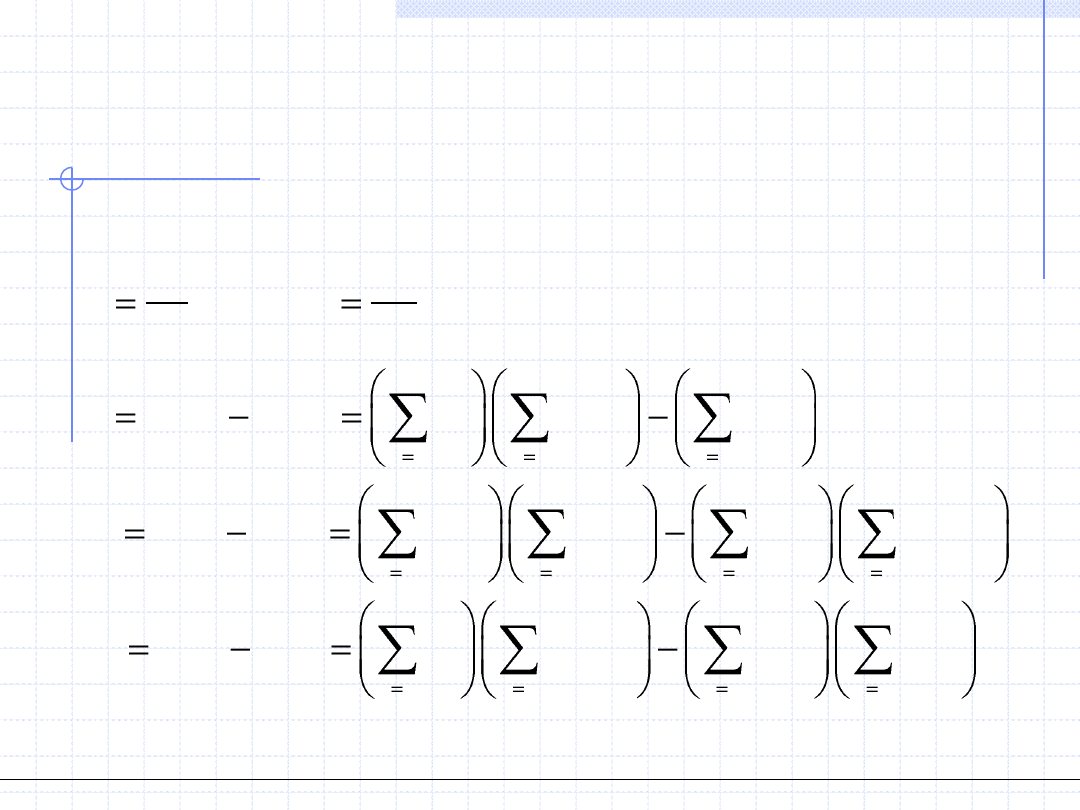
Ponieważ mamy 2 parametry, układ równań liniowych będzie układem 

dwu równań z dwoma niewiadomymi. 

Poszczególne współczynniki w tym układzie będą miały postać:

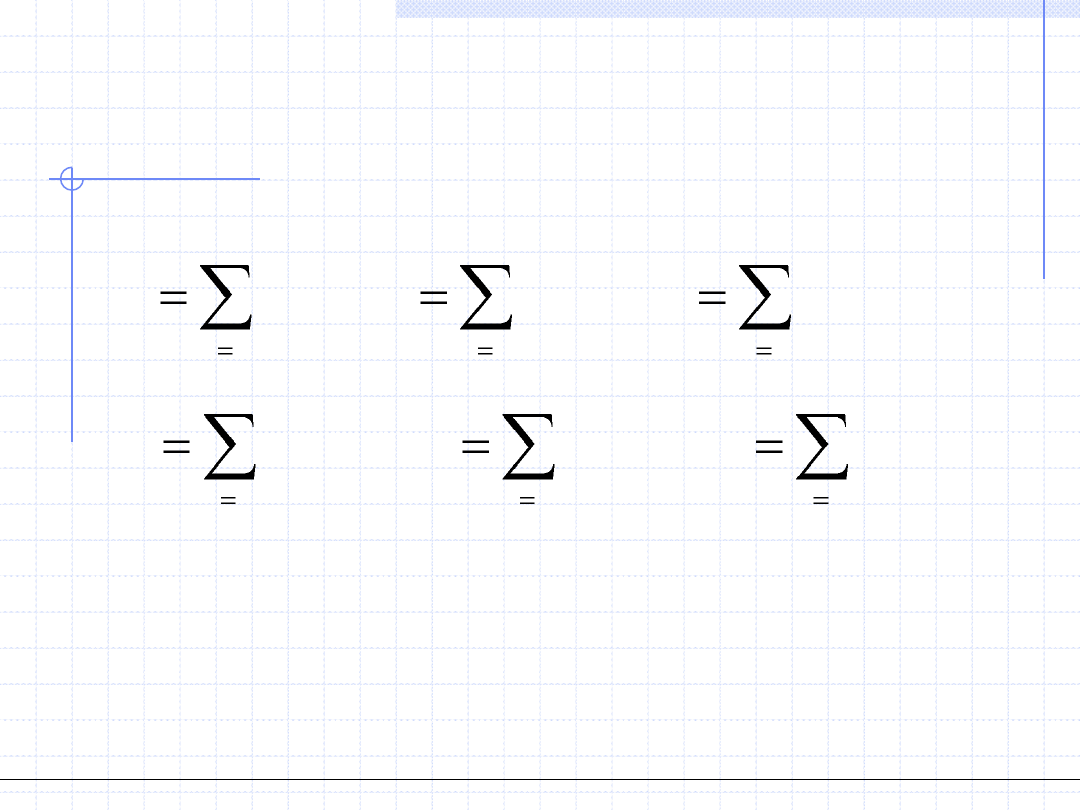
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

METODY NAJMNIEJSZYCH KWADRATÓW

DLA FUNKCJI LINIOWYCH ZE WZGLĘDU 

NA PARAMETRY 

11

12

1

1

1

1

2

21

22

2

1

1

1

n

n

n

i

i

i

i

i

i

i

i

n

n

n

i

i

i

i

i

i

i

i

i

i

b

w

b

w x

c

w y

b

w x

b

w x

c

w x y

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

METODY NAJMNIEJSZYCH KWADRATÓW

DLA FUNKCJI LINIOWYCH ZE WZGLĘDU 

NA PARAMETRY 

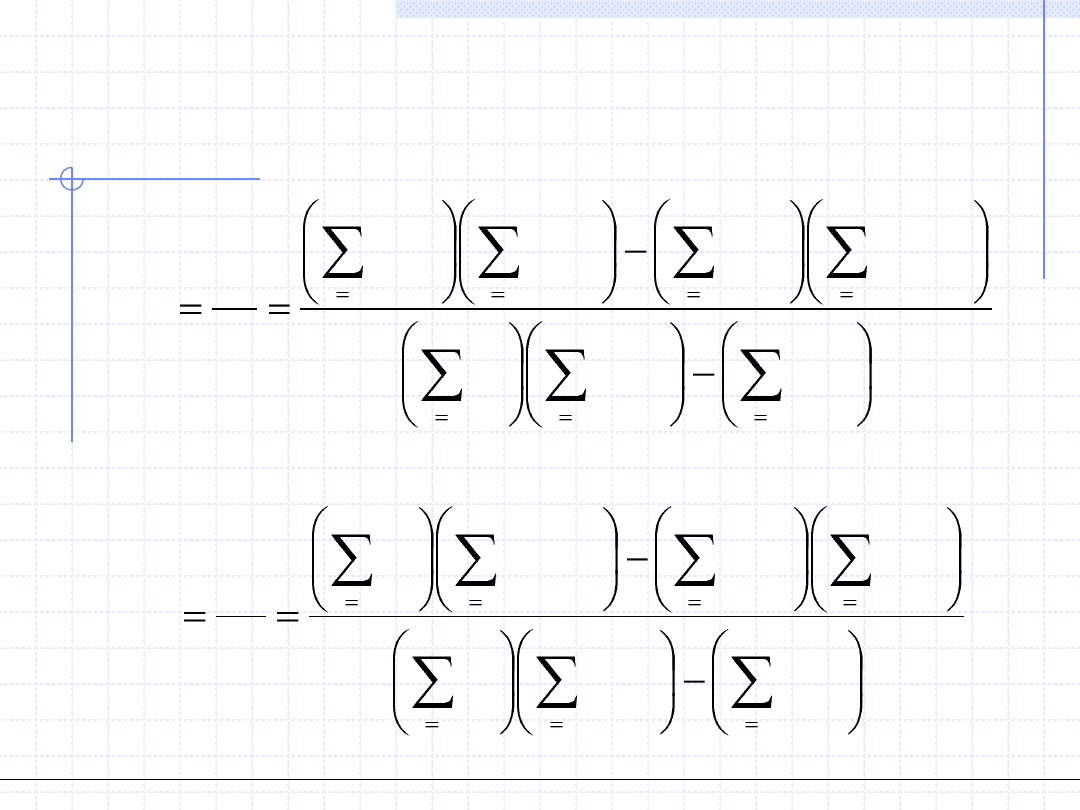
Rozwiążmy ten układ metodą Cramera tzn. za pomocą wyznaczników:

1

2

1

2

2

2

11 22

21 12

1

1

1

2

1

1 22

12 2

1

1

1

1

2

11 2

1 21

1

1

n

n

n

i

i

i

i

i

i

i

i

n

n

n

n

i

i

i

i

i

i

i

i

i

i

i

i

i

n

n

i

i

i

i

i

i

D

D

a

a

gdzie

D

D

D

b b

b b

w

w x

w x

D

c b

b c

w y

w x

w x

w x y

D

b c

c b

w

w x y

1

1

n

n

i

i

i

i

i

i

w y

w x

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

METODY NAJMNIEJSZYCH KWADRATÓW

DLA FUNKCJI LINIOWYCH ZE WZGLĘDU 

NA PARAMETRY 

2

1

1

2

1

1

1

1

1

2

2

2

1

1

2

1

1

1

1

2

1

1

1

n

i

i

i

n

i

i

i

n

i

i

n

i

i

i

n

i

i

i

i

n

i

i

i

n

i

i

n

i

i

i

n

i

i

i

n

i

i

i

n

i

i

i

n

i

i

i

n

i

i

i

n

i

i

i

x

w

x

w

w

x

w

y

w

y

x

w

w

D

D

a

x

w

x

w

w

y

x

w

x

w

x

w

y

w

D

D

a

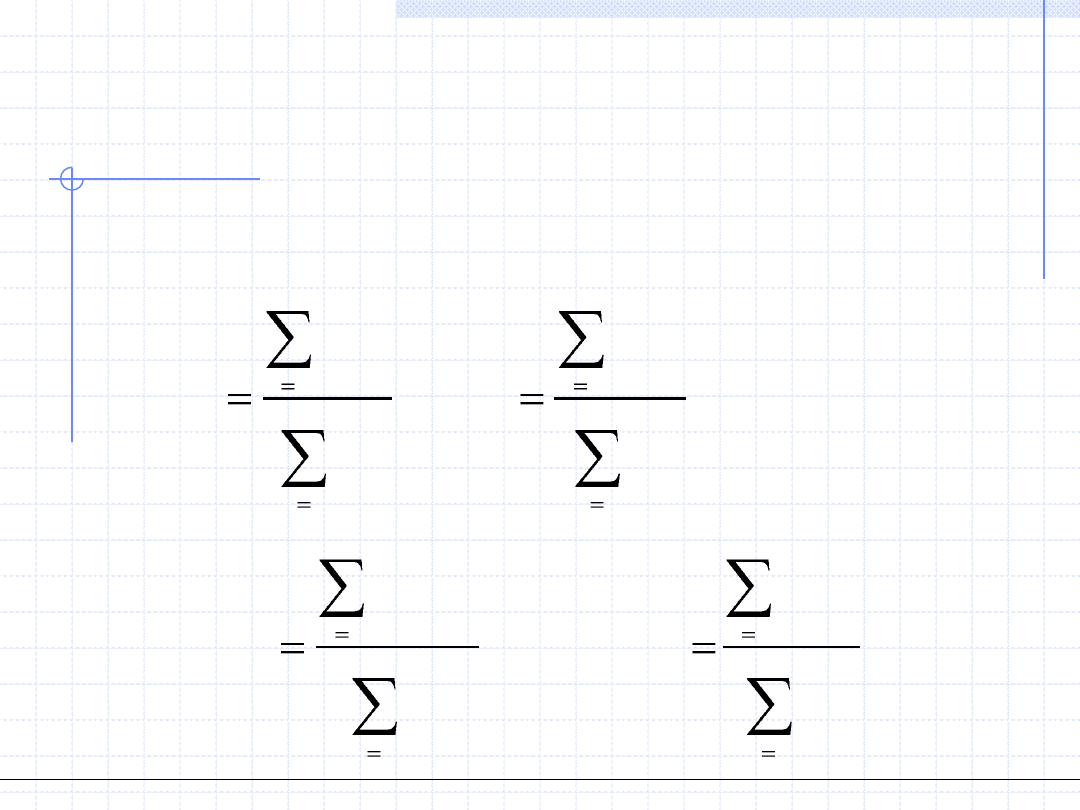
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

METODY NAJMNIEJSZYCH KWADRATÓW

DLA FUNKCJI LINIOWYCH ZE WZGLĘDU 

NA PARAMETRY 

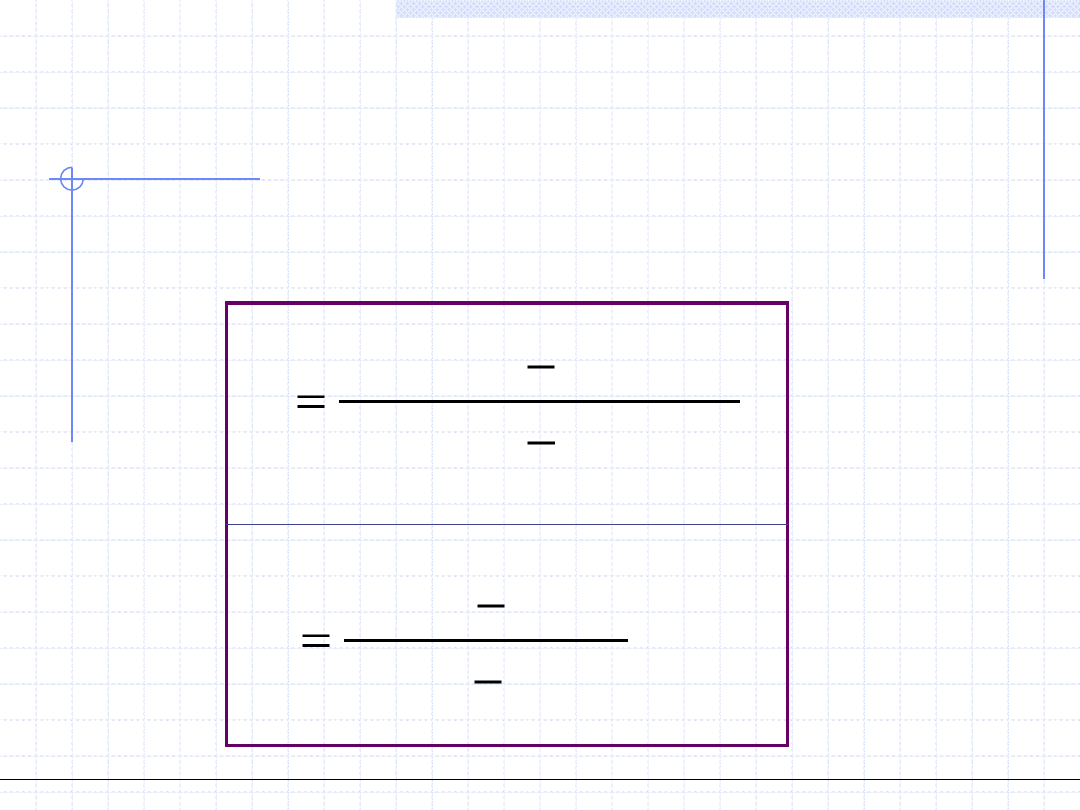
Wprowadźmy jako oznaczenia tzw. średnie ważone:

1

1

1

1

2

2

1

1

1

1

(

)

(

)

n

n

i

i

i

i

i

i

m

m

n

n

i

i

i

i

n

n

i

i

i

i

i

i

i

m

m

n

n

i

i

i

i

w x

w y

x

y

w

w

w x y

w x

xy

x

w

w

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

METODY NAJMNIEJSZYCH KWADRATÓW

DLA FUNKCJI LINIOWYCH ZE WZGLĘDU 

NA PARAMETRY 

2

1

2

2

2

2

2

(

)

(

)

(

)

(

)

(

)

(

)

(

)

m

m

m

m

m

m

m

m

m

m

m

y

x

x

xy

a

x

x

xy

x y

a

x

x

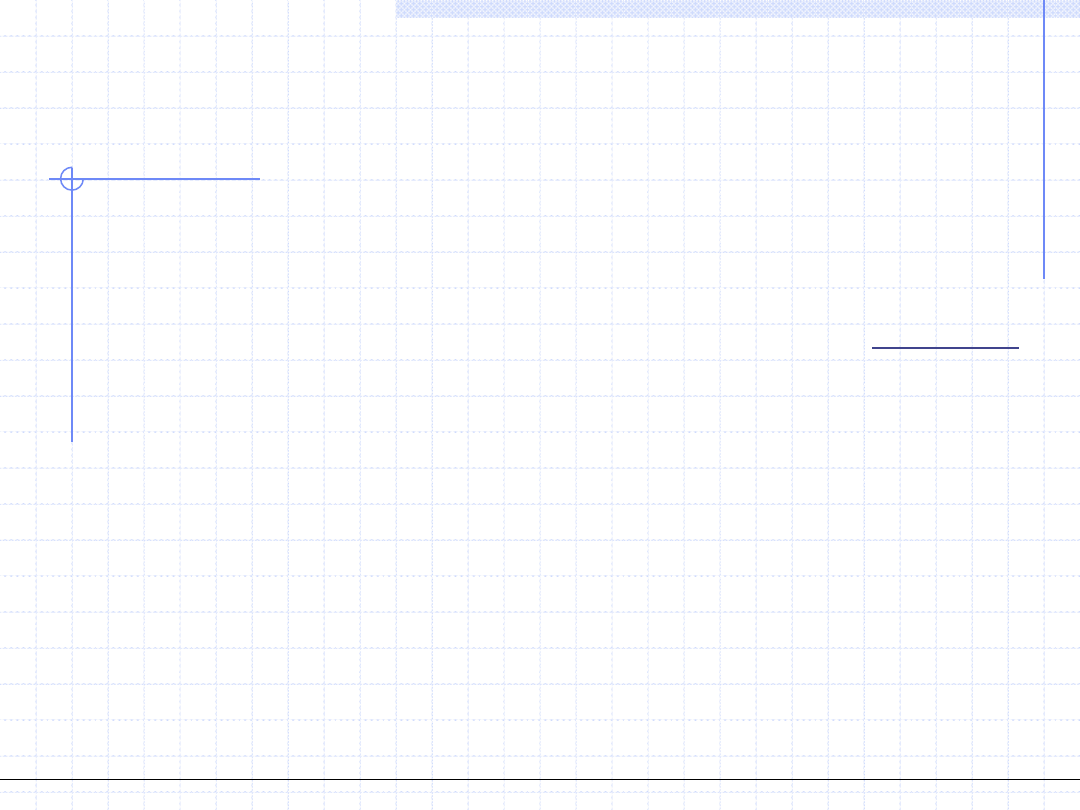
Wprowadzenie średnich ważonych pozwala na zapisanie otrzymanych

wcześniej wzorów w postaci łatwej do stosowania i zapamiętania:

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

METODY NAJMNIEJSZYCH KWADRATÓW

FUNKCJE NIELINIOWE ZE WZGLĘDU NA 

PARAMETRY

W praktyce inżynierskiej często parametry wchodzą do funkcji w sposób 

nieliniowy. W takim przypadku układ równań wynikający z przyrównania 

pochodnych do zera też jest nieliniowy. Można ten układ rozwiązywać 

numerycznie. W praktyce jednak często stosuje się metodę linearyzacji. 

Metodyka postępowania jest następująca:

Zasadnicze zmienne x i y zastępujemy nowymi zmiennymi X i Y w taki 

sposób, aby po podstawieniu i przekształceniu otrzymać funkcję liniową 

ze względu na parametry.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

METODY NAJMNIEJSZYCH KWADRATÓW

FUNKCJE NIELINIOWE ZE WZGLĘDU NA 

PARAMETRY

1

2

1

2

1

1

2

1

2

1

2

1

2

1

2

( , ,

,...,

)

( ,

,

,...,

)

( )

[ ,

,...,

]

[

,

,...,

]

[ ,

,...,

]

[ ,

,...,

]

[ ,

,...,

]

k

linearyzacja

k

k

j

j

j

linearyzacja

n

n

linearyzacja

n

n

linearyzac

n

y

f x a a

a

Y

F X A A

A

A

X

x

x x

x

X

X X

X

y

y y

y

Y

Y Y

Y

a

a a

a











1

2

2

1

1

1

2

1

2

[

,

,...,

]

(

)

[

,

,...,

]

[ ,

,...,

]

ja

n

n

k

minimalizacja

i

j

j

i

i

i

j

n

n

A

A A

A

S

w

A

X

Y

A

A A

A

a

a a

a







© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

METODY NAJMNIEJSZYCH KWADRATÓW

FUNKCJE NIELINIOWE ZE WZGLĘDU NA 

PARAMETRY

2

1

i

i

y y

w

Y

y

Należy zwrócić uwagę, że linearyzacja co prawda ułatwia rozwiązanie

problemu, ale wprowadza pewien dodatkowy błąd związany

z przekształceniem funkcji. Minimalizuje się tutaj nie odchylenia

badanej funkcji ale odchylenia funkcji przekształconej. Na ogół ten

dodatkowy błąd jest niewielki i pomijalny. Można go jednak skorygować

wprowadzając odpowiednią wagę:

W przypadku gdy funkcja linearyzacyjna Y(y) jest funkcją logarytmiczną

linearyzacja prowadzi do minimalizacji błędów względnych funkcji y.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

METODY NAJMNIEJSZYCH KWADRATÓW

FUNKCJE NIELINIOWE ZE WZGLĘDU NA 

PARAMETRY

1

2

1

( )

1 ln(

)

x

y

f x

a e

a

Przykład

Załóżmy, że funkcja aproksymowana ma postać:

Funkcję tę można łatwo zlinearyzować za pomocą następujących

przekształceń: 

1

2

1

1

ln(

)

1

2

1

2

x

x

a e

a

x

y

X

e

Y

e

e

a e

a

a X

a

Korekta błędów linearyzacji za pomocą wag będzie miała postać:

4

2

2

2

2

1/

1

2

1

1

1

1

i

i

i

i

y

i

i

i

y y

y y

y

w

Y

Y

e

Y

y

y

y

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej

Cz. – II

Matematyczne opracowywanie 

wyników eksperymentalnych

Metody statystyczne

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

W II części wykładu chciałbym Państwu przedstawić podstawowe 

wiadomości związane z analizą błędów eksperymentalnych za pomocą

metod statystycznych. 

UWAGI OGÓLNE

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

BŁĘDY POMIAROWE

Podstawowe informacje o błędach pomiarowych.

Najczęściej używanymi pojęciami określającymi niepewność wyników 

pomiarowych są: błąd bezwzględny (absolutny) oraz błąd 

względny (procentowy). 

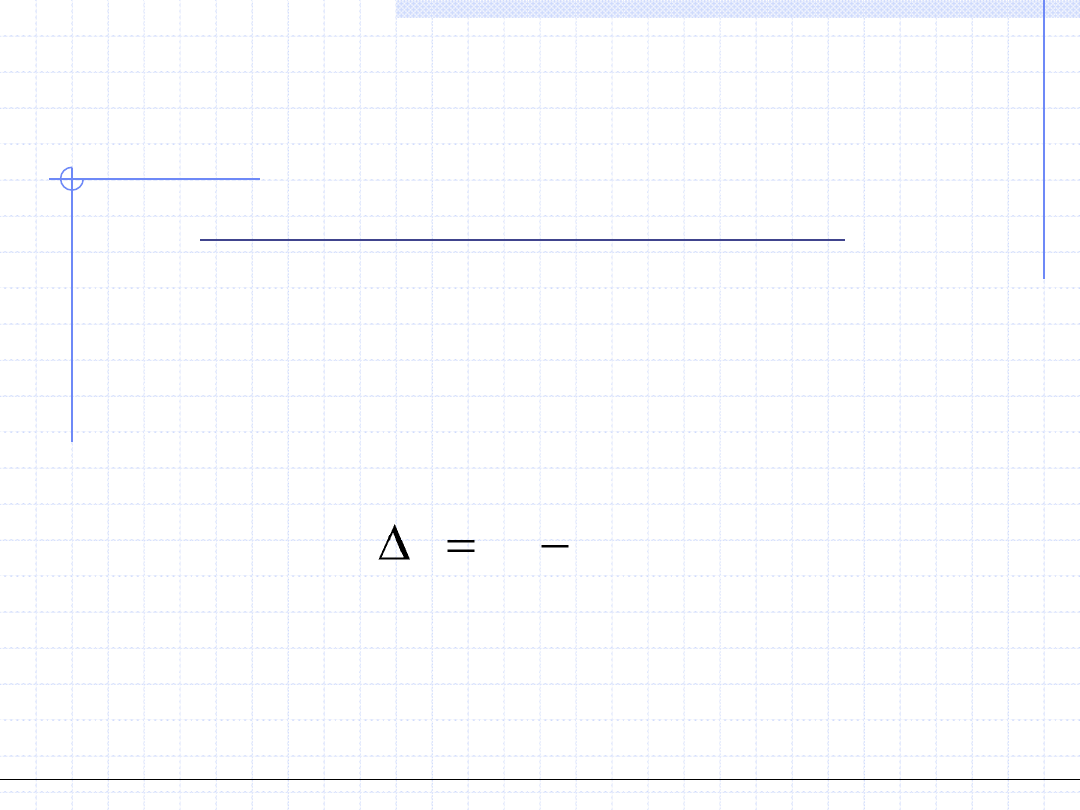
Błąd bezwzględny jest to po prostu różnica między uzyskaną wartością 

zmierzoną a wartością rzeczywistą.

y

y

y

i

Dokładna wartość mierzonej wielkości 

y

na ogół nie jest znana 

(jej wyznaczenie jest celem pomiaru). 

Błąd bezwzględny ma ten sam wymiar, co wielkość mierzona 

i może być dodatni lub ujemny. 

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

BŁĘDY POMIAROWE

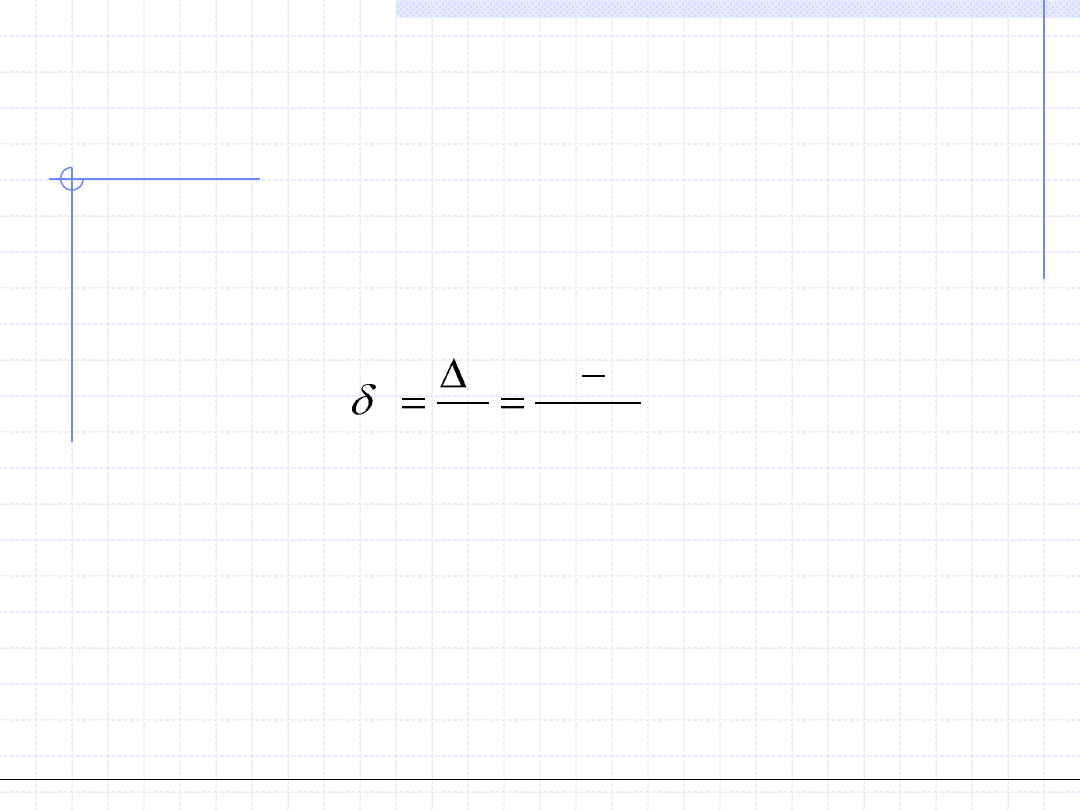
Błąd względny jest to stosunek błędu bezwzględnego do wartości 

rzeczywistej:

y

y

y

y

y

i

y

Błąd względny jest bezwymiarowy i może być dodatni lub ujemny. 

W popularnym zastosowaniu jest jego wartość pomnożona przez 100 

nazywana względnym błędem procentowym. 

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

BŁĘDY POMIAROWE

Bardzo istotne z punktu widzenia statystyki są pojęcia błędu 

systematycznego i przypadkowego. 

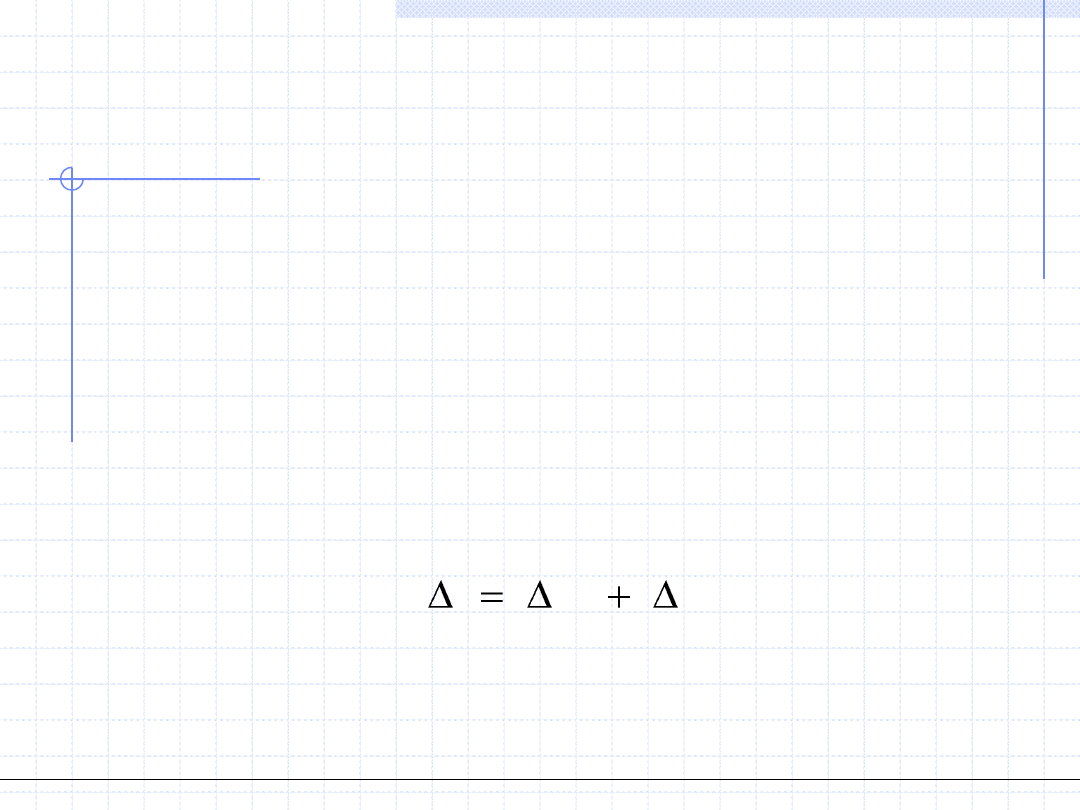
Błędem systematycznym – nazywamy część błędu bezwzględnego, 

która pojawia się w każdym pomiarze i której nie można wyeliminować 

za pomocą powtarzania pomiarów. Przyczyną błędów systematycznych 

na ogół jest ukryta wada przyrządów pomiarowych lub niewłaściwa 

procedura pomiarowa. 

Błąd przypadkowy – jest to natomiast ta część błędu bezwzględnego, 

która powstaje na skutek wielu przyczyn pojawiających się losowo 

podczas określonego pomiaru. 

p

s

y

y

y

)

(

)

(

W związku z tym, że błędów systematycznych nie można zmniejszyć za 

pomocą powtarzania pomiarów w dalszych rozważaniach nie będziemy 

się tymi błędami zajmować tzn. będziemy przyjmować, że cały błąd ma 

charakter losowy. 

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Rozkłady prawdopodobieństwa

Rozkłady prawdopodobieństwa stosowane w analizie statystycznej 

eksperymentu fizykochemicznego.

Powtarzanie danego pomiaru daje różne wyniki, dlatego zarówno wynik 

pomiaru, błąd bezwzględny jak i względny można traktować jako 

zmienne losowe o pewnym rozkładzie prawdopodobieństwa. Spośród 

wielu rozkładów prawdopodobieństwa stosowanych w statystyce 

matematycznej fundamentalne znaczenia ma tzw. 

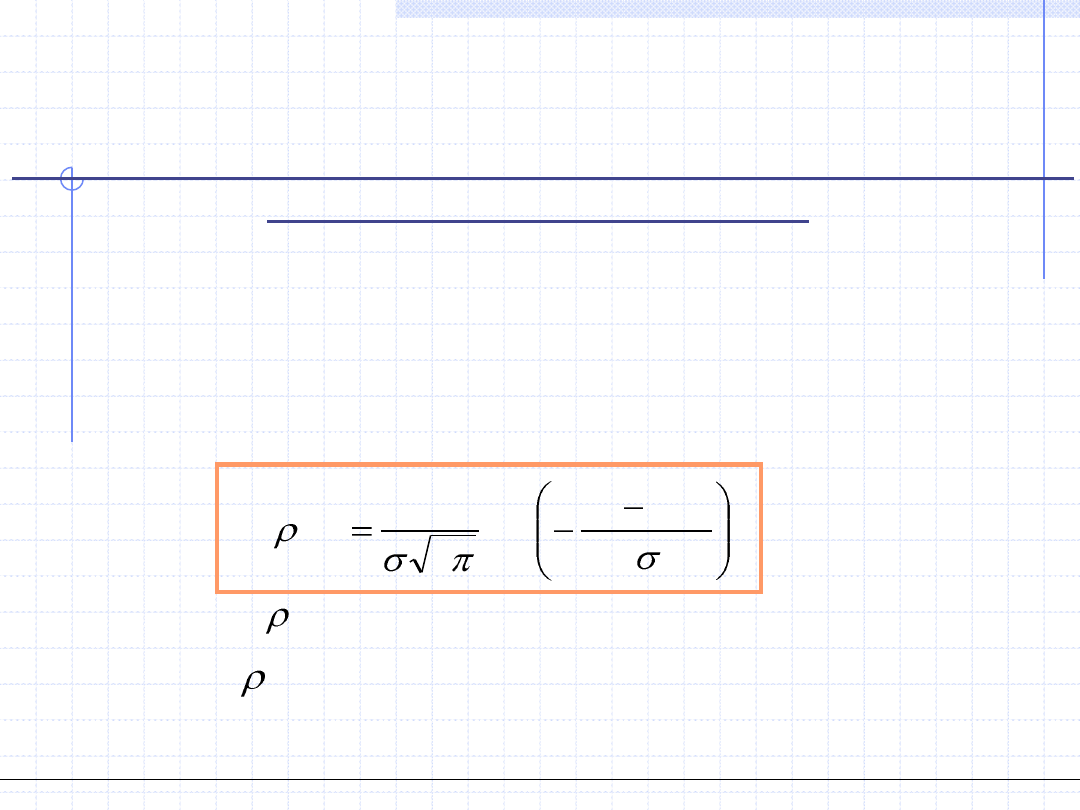
rozkład normalny Gaussa, którego postać analityczna jest następująca:

2

2

0

2

)

(

exp

2

1

)

(

y

y

y

Wielkość 

)

( y

jest to tzw. gęstość rozkładu zmiennej losowej 

y

.  

Iloczyn

dy

y)

(

oznacza prawdopodobieństwo, że wartość zmiennej 

losowej 

y

znajdować się będzie między 

y

a 

y+dy

. 

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Rozkłady prawdopodobieństwa

Rozkład normalny jest określony za pomocą dwu parametrów:

y

0

– oznacza środek rozkładu, 

- oznacza szerokość rozkładu. 

Można wykazać, że środek rozkładu normalnego  jest jednocześnie 

wartością oczekiwaną (w znaczeniu teorii prawdopodobieństwa) 

zmiennej losowej 

y

, natomiast szerokość rozkładu σ jest jednocześnie 

odchyleniem standardowym zmiennej losowej 

y

. 

Kwadrat odchylenia standardowego σ

2

nazywany jest wariancją 

rozkładu zmiennej losowej.  

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

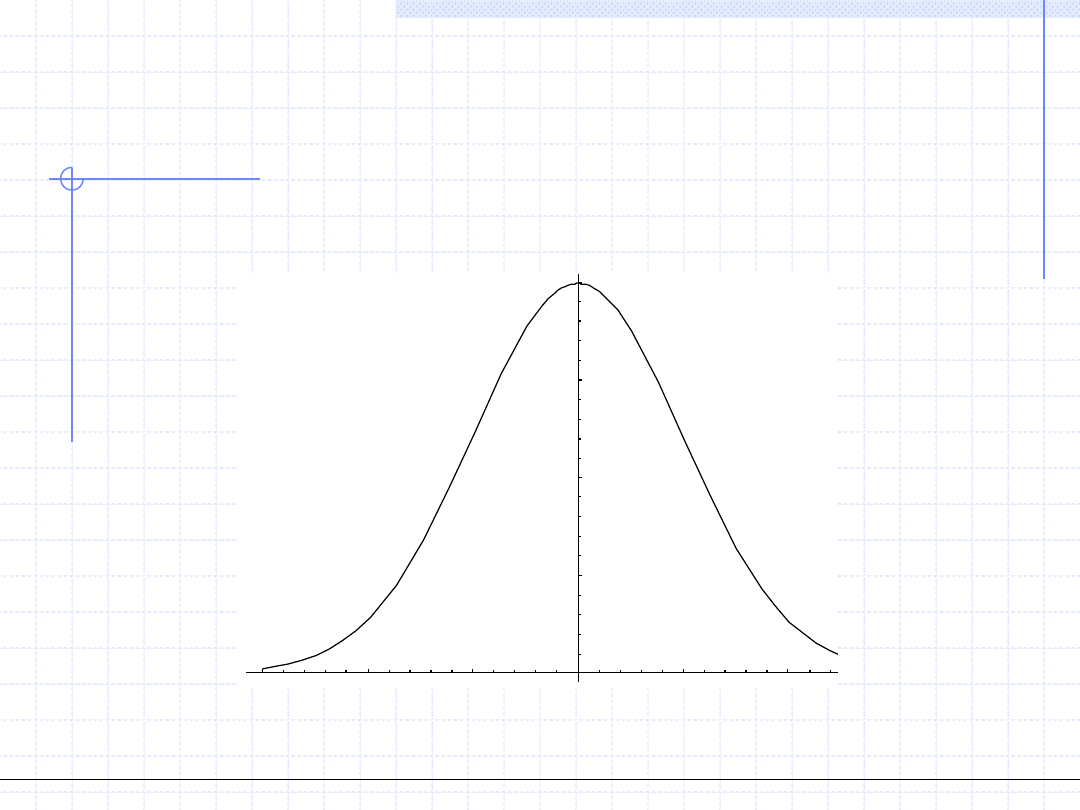
Rozkłady prawdopodobieństwa

Przykładowy wykres rozkładu normalnego: 

-3

-2

-1

1

2

3

0.1

0.2

0.3

0.4

y

ρ(y)

Przedstawiony rozkład ma parametry: y

0

=0,   σ=1

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Rozkłady prawdopodobieństwa

Odchylenie standardowe wskazuje, że prawdopodobieństwo tego że 

wynik pomiaru  będzie zawierał się w granicach:  

0

0

y

y

y

wynosi 68,26 %. 

Wartość ta określa tzw.  poziom ufności często stosowany 

w statystyce. Podwyższenie poziomu ufności skutkuje dopuszczeniem, 

że błąd będzie większy niż wartość σ. Np. przedział  

2

0

y

posiada poziom ufności 95,45 %. 

Zależność między poziomem ufności a dopuszczalnym zakresem błądu 

określa tzw. funkcja błędu będąca całką rozkładu normalnego:

dz

z

t

y

y

y

y

y

P

t

t

2

exp

2

1

)

(

erf

)

(

2

0

0

gdzie 

t

y

Wyrażenie po lewej stronie (3.45) oznacza 

prawdopodobieństwo (poziom ufności) otrzymania 

wyniku w zakresie 

y

y

0

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Analiza statystyczna pomiarów

Analiza statystyczna pomiaru jednej wielkości.

W niektórych eksperymentach fizykochemicznych wyznacza się jedną 

wielkość 

y

za pomocą 

n

pomiarów prowadzonych w podobnych warunkach. 

Zakładając, że błędy wpływające na wynik pomiaru mają charakter losowy 

można wykazać, że rozkład zmiennej losowej będącej wynikiem pomiarów 

jest rozkładem normalnym, którego środek jest dobrą miarą wielkości 

mierzonej, a odchylenie standardowe jest dobrą miarą wartości 

bezwzględnej średniego błędu bezwzględnego.

Załóżmy, że wykonaliśmy 

n

pomiarów, których wyniki tworzą dyskretny zbiór

}

,...,

,

{

}

{

2

1

n

i

y

y

y

y

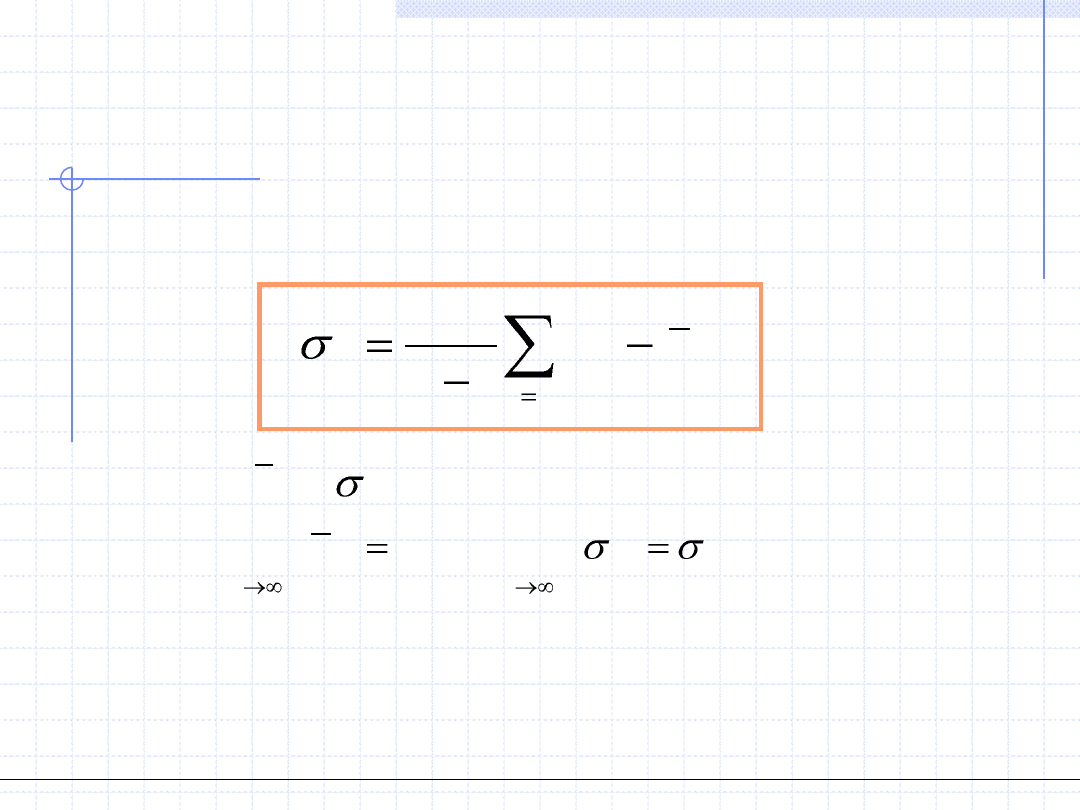
Założenie o normalnym rozkładzie wyników prowadzi do wniosku, że 

najlepszą miarą środka rozkładu, czyli rzeczywistej wartości 

y 

jest średnia 

arytmetyczna

y

n

i

i

n

i

n

y

n

n

y

y

y

y

y

1

2

1

1

...

...

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Analiza statystyczna pomiarów

Znajomość zbioru pomiarowego 

}

{

i

y

pozwala również na obliczenie dobrego oszacowania wariancji 

rozkładu normalnego σ

n

2

:

n

i

i

n

y

y

n

1

2

2

)

(

1

1

Wielkości 

n

y

i

2

n

mają ważne własności graniczne:

2

2

0

(

)

(

)

lim

lim

n

n

n

n

y

y

Oznacza to, że rozkład normalny jest rozkładem granicznym przy 

nieskończonej liczbie pomiarów. W rzeczywistości zazwyczaj 

wystarczająca liczba pomiarów to kilka lub kilkanaście. 

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Analiza statystyczna pomiarów

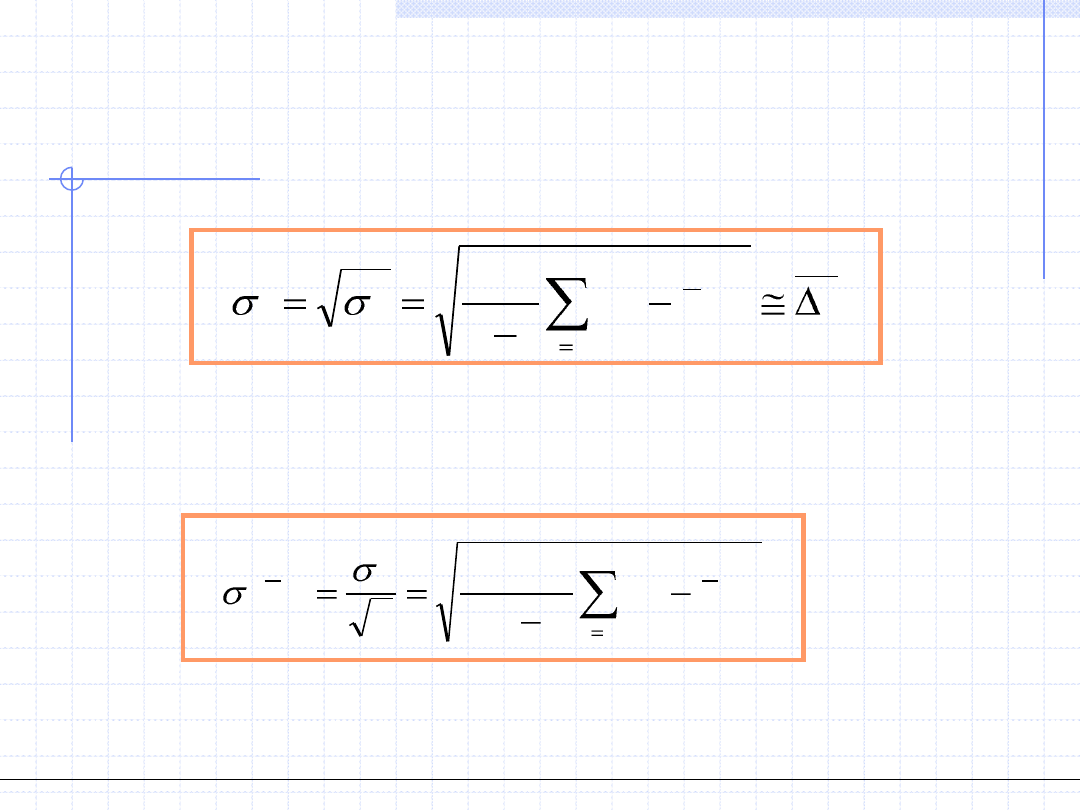
W praktyce bardzo istotne jest oszacowanie wariancji. 

Pozwala ono na obliczenie odchylenia standardowego będącego miarą 

niepewności (czyli błędu) wyznaczanej wielkości: 

i

n

i

n

i

n

n

y

y

y

n

1

2

2

)

(

1

1

Wzór powyższy określa oszacowanie odchylenia standardowego pojedynczego 

pomiaru w serii pomiarowej. 

Średnia arytmetyczna wszystkich pomiarów jest oczywiście dokładniejsza 

a oszacowane dla niej odchylenie standardowe dane jest wzorem:

n

i

n

i

n

n

y

y

n

n

n

y

1

2

)

(

)

1

(

1

)

(

Zauważmy, że pojawiają się tutaj sumy kwadratów różnicy wartości mierzonej 

i średniej arytmetycznej. Zatem zastosowanie metody najmniejszych kwadratów 

prowadzi do minimalizacji odchylenia standardowego mierzonej wielkości.

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Analiza statystyczna pomiarów

Zasady przenoszenia i kumulacji błędów.

W wielu przypadkach ostateczny wynik eksperymentu powstaje na 

skutek pewnego przekształcenia wyniku pomiarowego. Przykładowo, 

objętość kuli otrzymamy po zmierzeniu jej średnicy i zastosowaniu 

odpowiedniego wzoru. W takim przypadku zmianie ulegnie również błąd. 

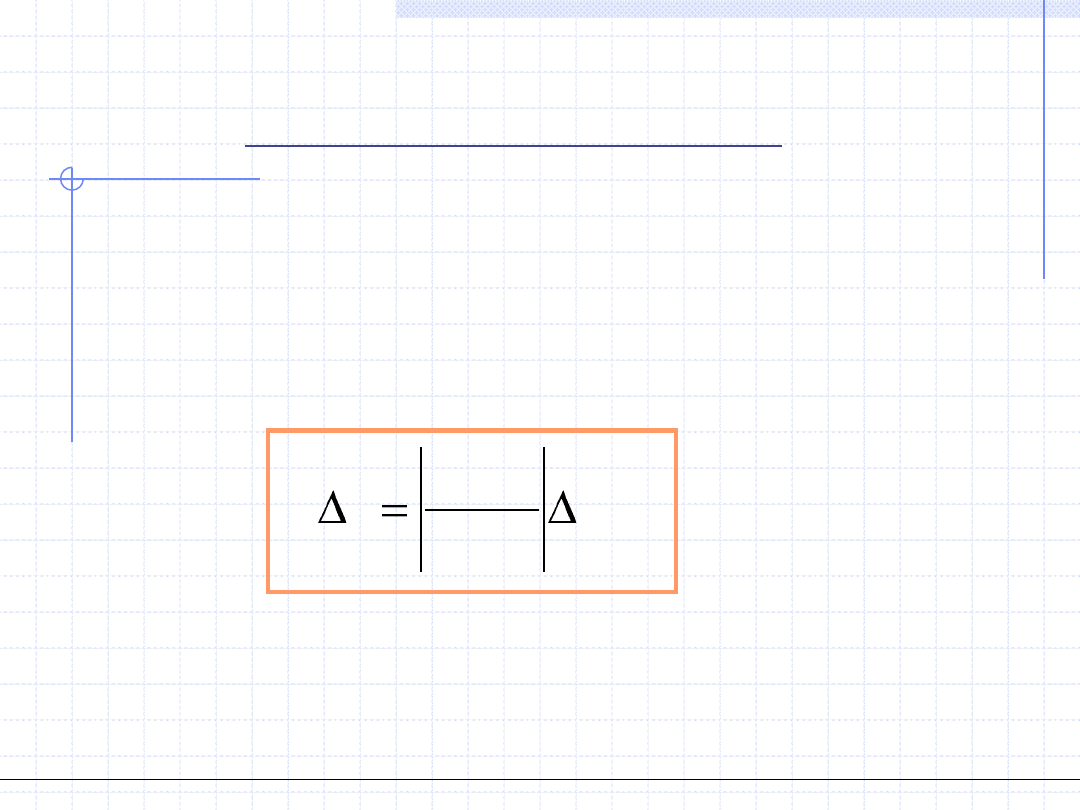
Zasada przenoszenia błędu, w przypadku przekształcenia jednej 

wielkości polega na zastosowaniu wzoru: 

y

dy

y

dq

q

)

(

gdzie mierzoną wielkością jest 

y

, a końcowy wynik 

q

otrzymujemy 

na podstawie funkcji 

)

( y

q

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Analiza statystyczna pomiarów

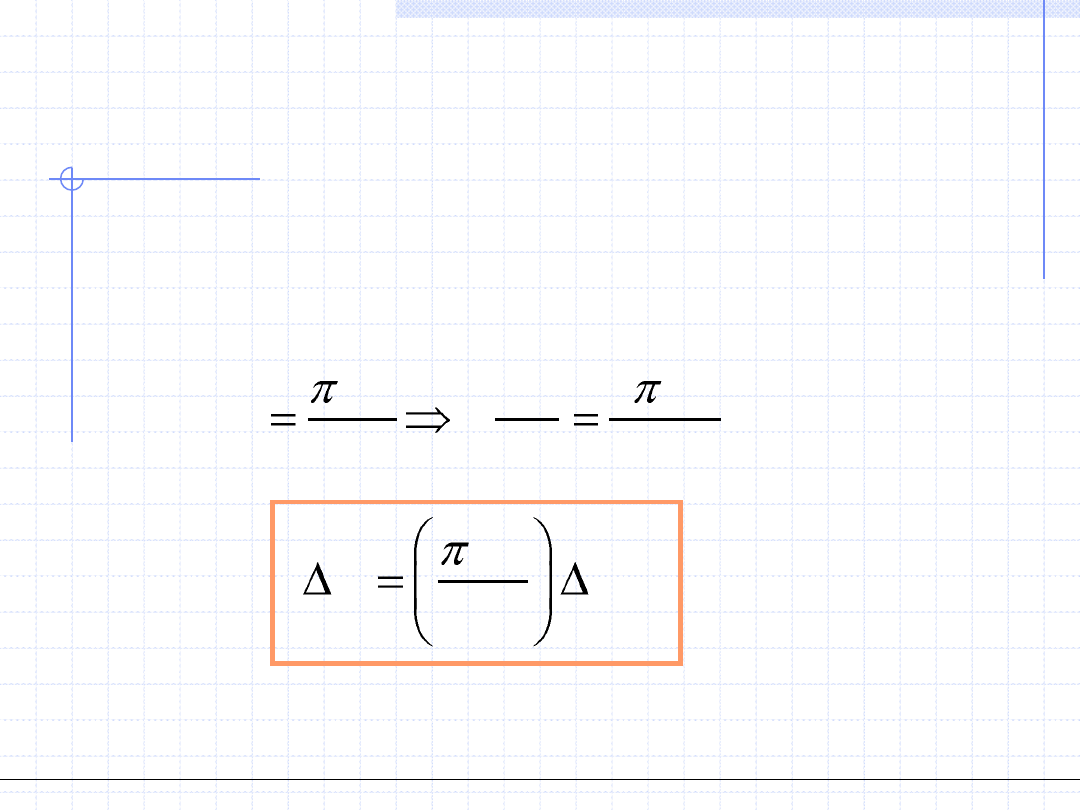
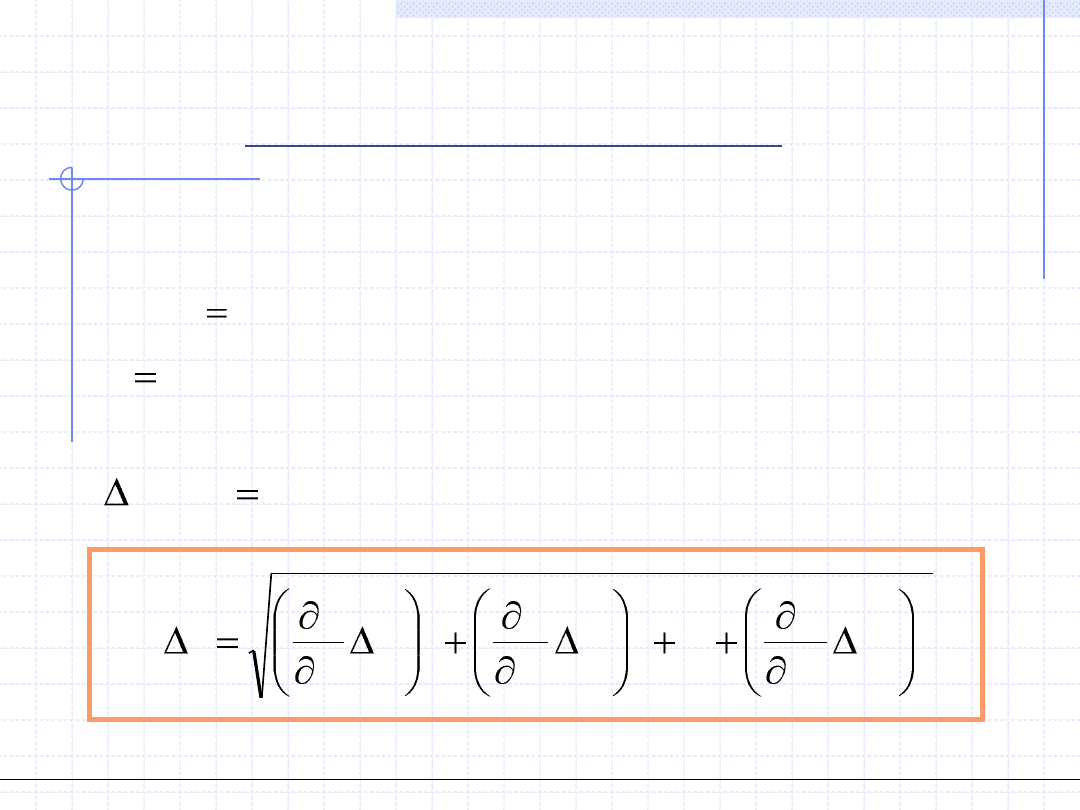
Jako przykład rozpatrzymy zagadnienie wyznaczenia objętości kuli za 

pomocą pomiaru jej średnicy. Aby otrzymać objętość należy

zastosować wzór 

2

2

D

V

D

3

2

3

6

6

D

dV

D

V

dD

stąd

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Analiza statystyczna pomiarów

Zasady przenoszenia i kumulacji błędów.

Dosyć często, końcowy wynik 

q

jest rezultatem  niezależnych pomiarów 

różnych wielkości 

N

i

y

i

,...,

2

,

1

oraz funkcji wielu zmiennych: 

)

,...,

,

(

2

1

N

y

y

y

q

q

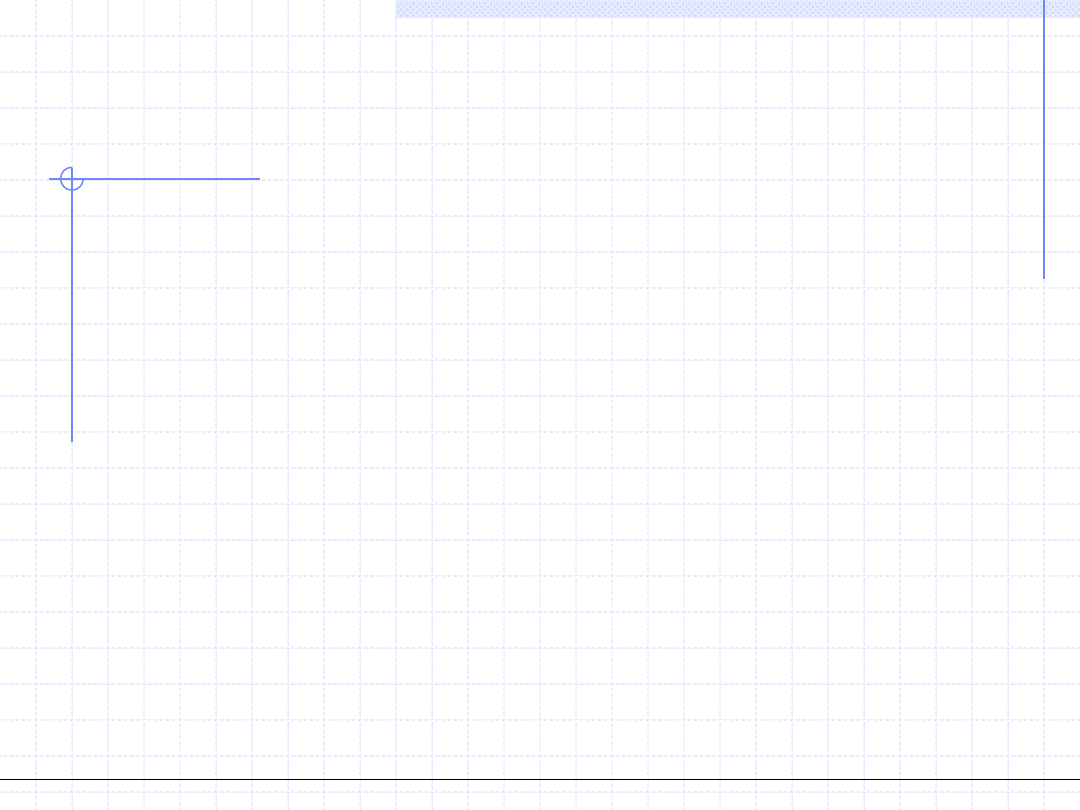
Załóżmy, że  znamy oszacowania błędów pomiarów poszczególnych 

zmiennych: 

N

i

y

i

,...,

2

,

1

Oszacowanie błędu końcowej wielkości  jest 

dane wzorem:

2

2

2

2

2

1

1

...

N

N

y

y

q

y

y

q

y

y

q

q

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Analiza statystyczna pomiarów

Przykładowo rozpatrzymy błąd popełniony podczas wyznaczania 

gęstości pewnego materiału za pomocą pomiaru masy próbki 

w kształcie sześcianu. 

Mamy tutaj dwa niezależne pomiary: masy „m” a pomocą wagi 

i długości boku „a” za pomocą np. suwmiarki. 

Te dwa pomiary mają określone błędy: ∆m i ∆a. 

Błąd bezwzględny gęstości ∆ρ obliczymy stosując powyższy wzór 

z uwzględnieniem wzoru określającego gęstość:    

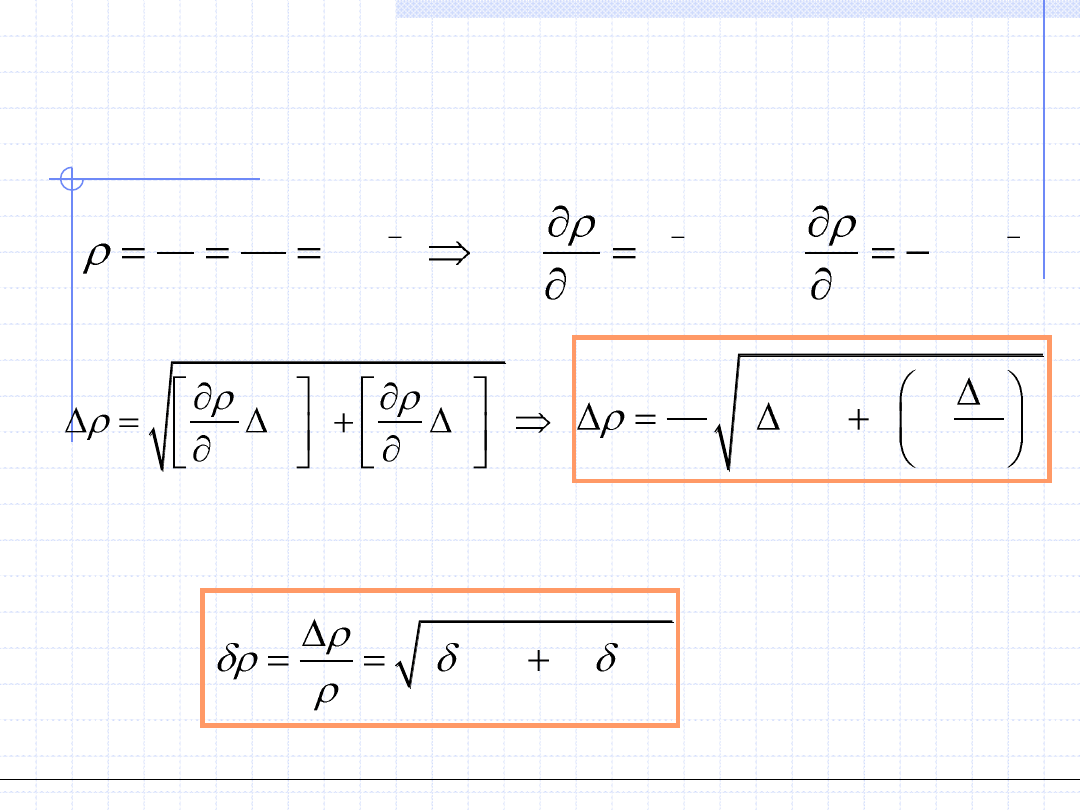
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Analiza statystyczna pomiarów

2

2

m

a

m

a

3

3

4

3

3

m

m

ma

a

ma

V

a

m

a

2

2

3

1

9

a

m

m

a

a

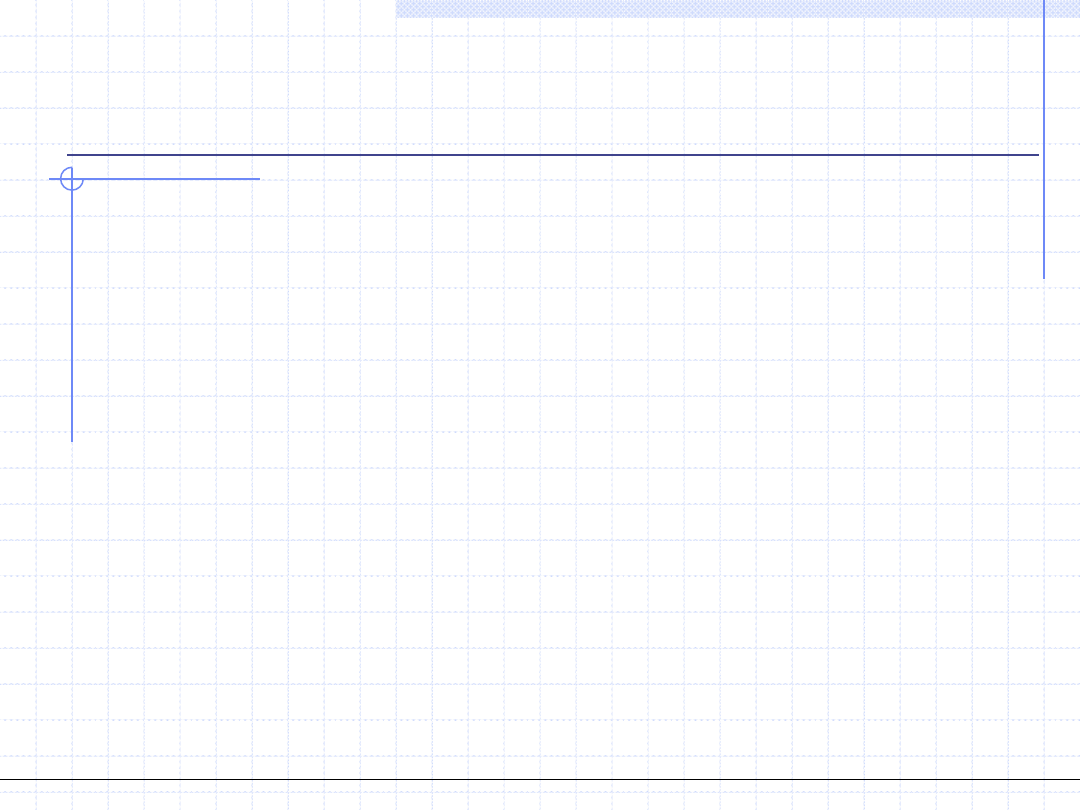
Dzieląc obustronnie przez gęstość można otrzymać wzór określający błąd

względny pomiaru gęstości:

2

2

9

m

a

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Analiza statystyczna pomiarów

Analiza statystyczna eksperymentu wyznaczającego zależność funkcyjną. 

W ogromnej większości, eksperymenty polegają na doświadczalnym 

wyznaczaniu wartości pewnej funkcji jednej lub wielu zmiennych.  

Celem eksperymentu jest albo sama funkcja (np. zależność 

prężności pary nasyconej od temperatury), albo jej parametry 

(np. wartość energii aktywacji w zależności Arrheniusa).

Funkcję (lub jej parametry) wyznacza się prowadząc szereg pomiarów 

w wybranych z dziedziny funkcji punktach. Pomiary w różnych punktach, 

ściśle rzecz biorąc, są pojedynczymi eksperymentami opisanymi przez 

pojedyncze zmienne losowe (różne dla różnych pomiarów). Aby 

przeprowadzić analizę statystyczną takich pomiarów, zakłada się że 

prowadzone są one z taką samą dokładnością a zmienna losowa opisująca 

ich błędy bezwzględne ma rozkład normalny o środku 0 i pewnej 

szerokości równej średniemu odchyleniu standardowemu. 

Na podstawie tego założenia można przeprowadzić aproksymację funkcji 

metodą najmniejszych kwadratów oraz oszacować średnie błędy wartości 

funkcji i jej parametrów. 

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Błędy parametrów wyznaczonych metodą 

najmniejszych kwadratów

Załóżmy, że wykonano 

n

pomiarów w różnych punktach 

x

i

. 

Punkty te tworzą dyskretny zbiór {

x

i

}. 

Wagi poszczególnych pomiarów są określone przez nieujemne liczby 

w

i

. 

Wyniki pomiarów dają dyskretny zbiór {

y

i

}. 

W przypadkach, kiedy dokładności poszczególnych pomiarów są istotnie 

różne, słuszność powyższego założenia można zachować, wprowadzając 

odpowiednie wagi sprowadzające różne rozkłady losowe do jednego 

rozkładu ważonego. 

Następnie za pomocą metody najmniejszych kwadratów aproksymujemy 

dyskretną funkcję eksperymentalną, otrzymując ciągłą funkcję modelową: 

1

1

( , , ,...,

)

k

y

f x a a

a

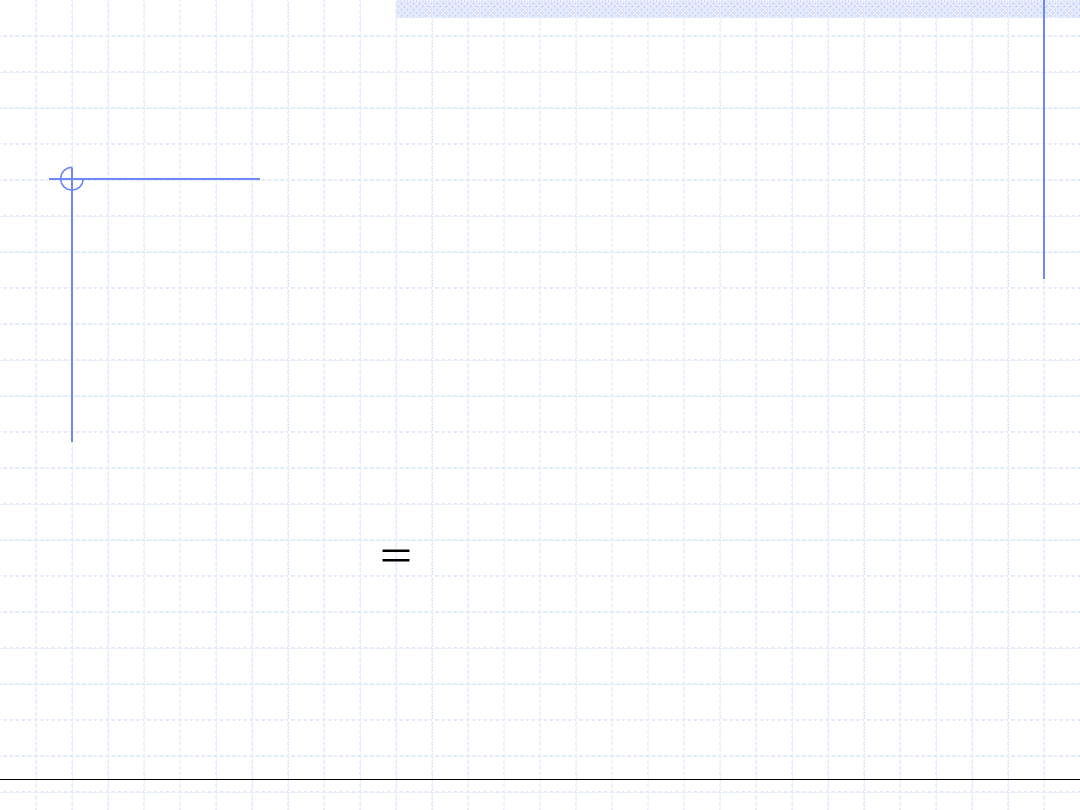
Znajomość tej funkcji pozwala na oszacowanie średnich wartości wariancji 

i odchylenia standardowego pojedynczego pomiaru wielkości 

y

:

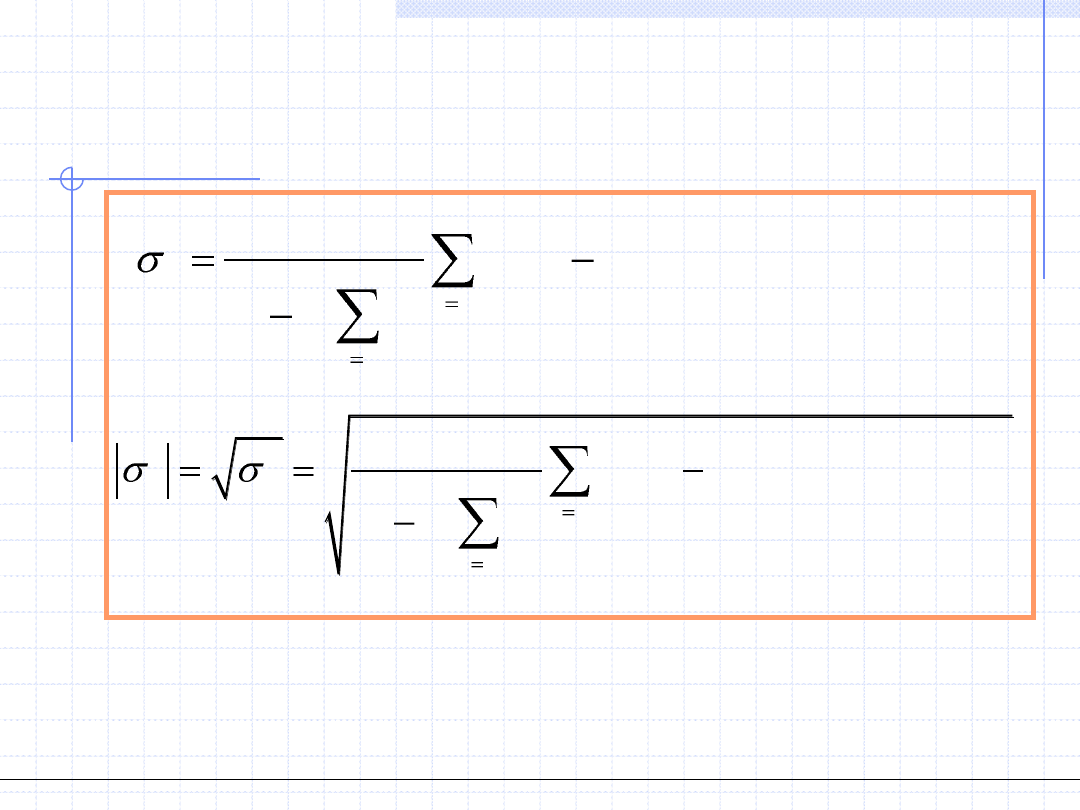
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Błędy parametrów wyznaczonych metodą 

najmniejszych kwadratów

2

2

1

2

1

1

[

( , ,

,...,

)]

(

)

n

y

i

i

i

k

n

i

i

i

n

w y

f x a a

a

n k

w

2

2

1

2

1

1

[

( , ,

,...,

)]

(

)

n

y

y

i

i

i

k

n

i

i

i

n

w y

f x a a

a

n k

w

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Błędy parametrów wyznaczonych metodą 

najmniejszych kwadratów

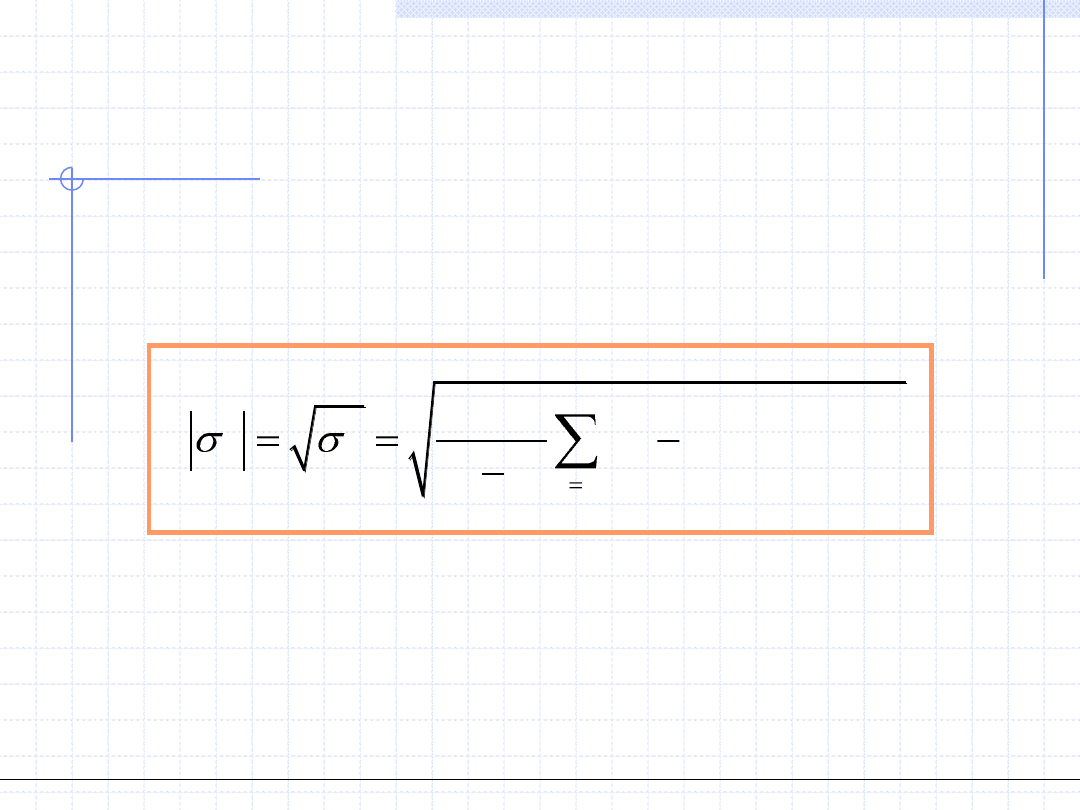
W częstym przypadku, gdy pomiary są jednakowo ważne a liczba 

parametrów wynosi 2, wzór określający odchylenie standardowe

przyjmuje postać:

2

2

1

2

1

1

[

( , ,

)]

(

2)

n

y

y

i

i

i

y

f x a a

n

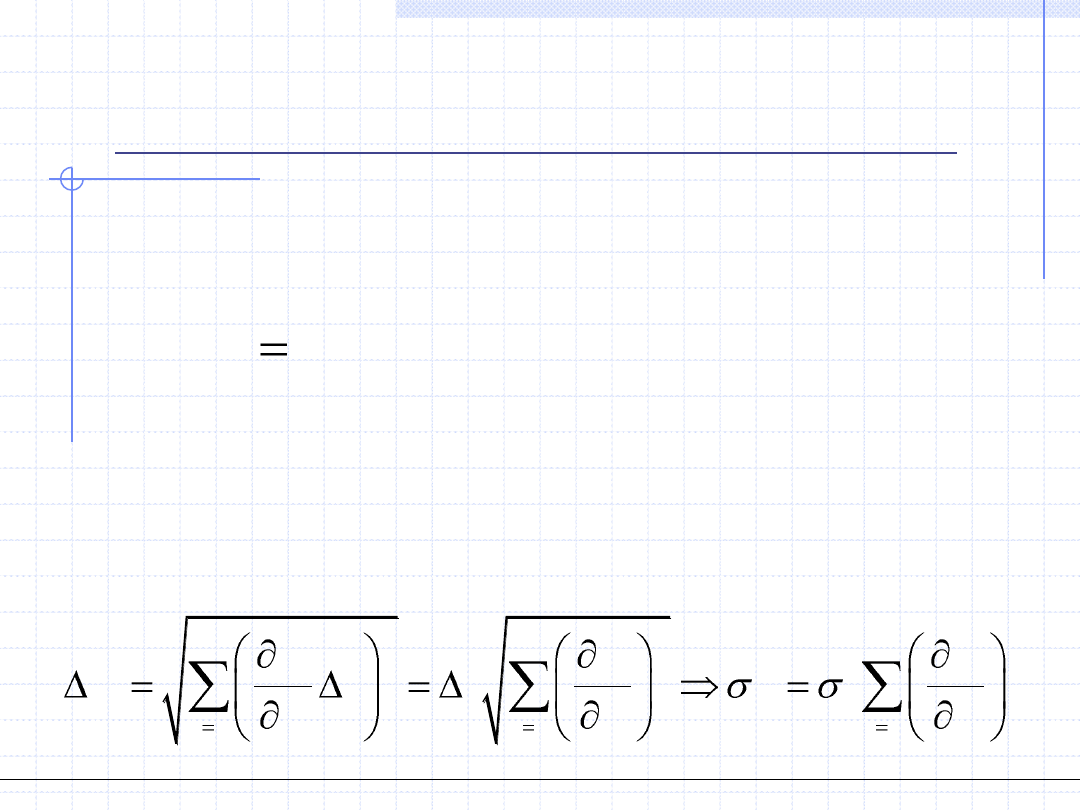
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Błędy parametrów wyznaczonych metodą 

najmniejszych kwadratów

Wyznaczone metodą najmniejszych kwadratów parametry a

1

,a

2

,…,a

k

funkcji aproksymującej f(x) są również obarczone niepewnością. 

Zakładając, że punkty x

i

są ustalone dokładnie można napisać

Niepewności parametrów w metodzie najmniejszych kwadratów

1

2

( ,

,...,

,...,

)

j

i

n

a

f y y

y

y

Postać powyższej funkcji f wynika z zastosowanej procedury najmniejszych

kwadratów wyznaczającej wartości parametrów. Każdy pomiar jest 

wykonany z określoną dokładnością, którą można oszacować za pomocą

wzorów na  σ

y

. Błędy poszczególnych pomiarów przenoszą się na wartości

parametrów. Trzeba zatem zastosować wzór określający to przenoszenie 

2

2

2

2

2

1

1

1

j

n

n

n

j

j

j

j

a

y

i

i

i

i

i

i

a

a

a

a

y

y

y

y

y

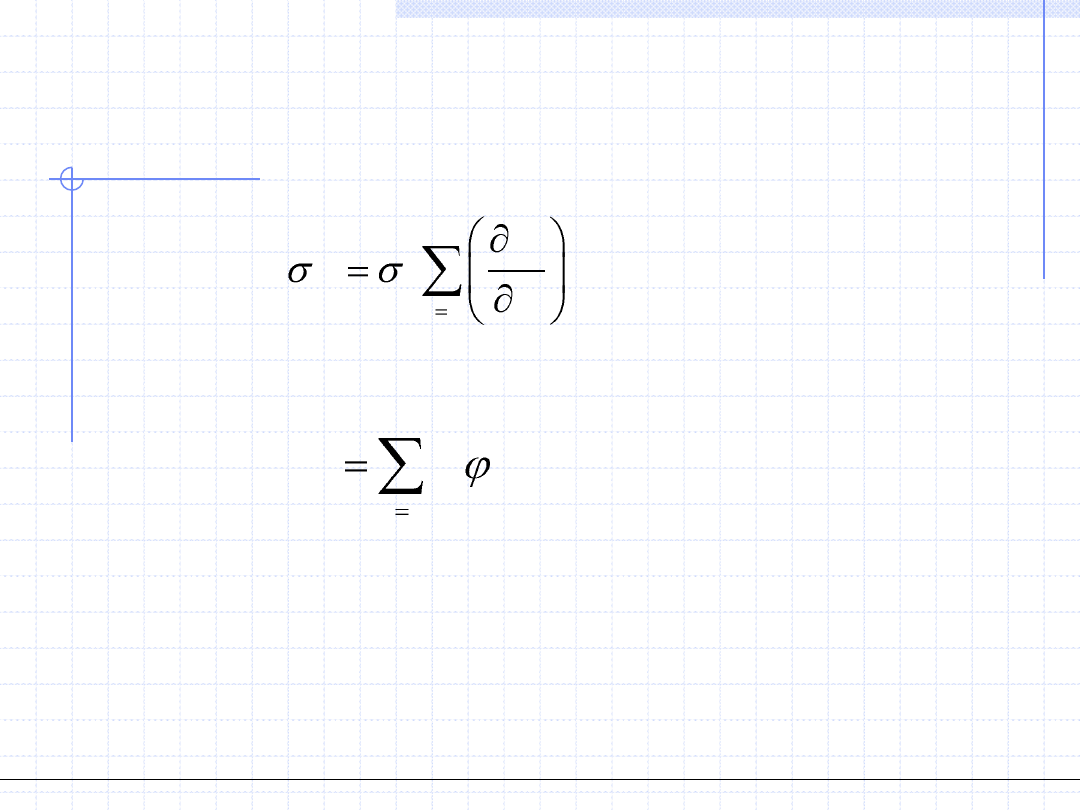
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Błędy parametrów wyznaczonych metodą 

najmniejszych kwadratów

Mamy zatem wzór uzależniający niepewności parametrów z wariancją

zmiennej y:

1

( )

k

j

j

j

y

a

x

2

2

2

1

j

n

j

a

y

i

i

a

y

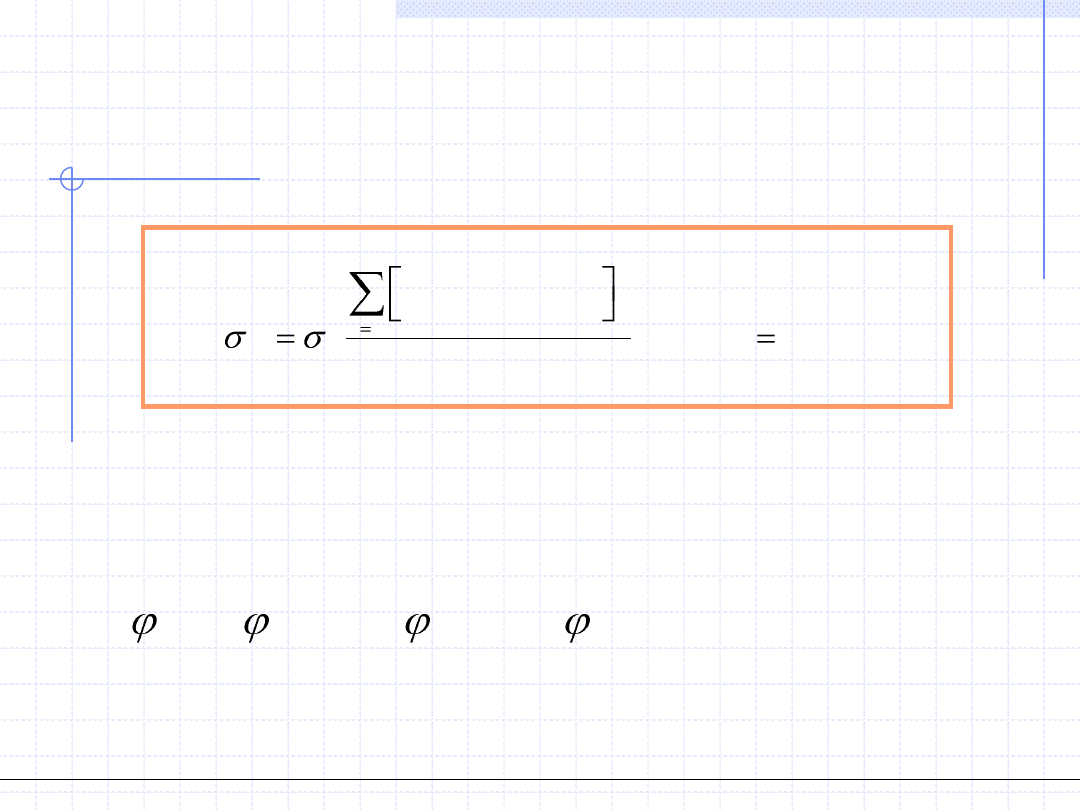
Dla funkcji liniowej ze względu na parametry

postać funkcji określającej dany parametr można określić za pomocą

metody Cramera rozwiązującej układ równań metody najmniejszych

kwadratów. Odpowiednie podstawienia i przekształcenia prowadzą

do wzorów:

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Błędy parametrów wyznaczonych metodą 

najmniejszych kwadratów

2

2

2

1

2

det

( )

1, 2,...,

det

j

n

i

j

i

i

a

y

w

x

j

k

B

B

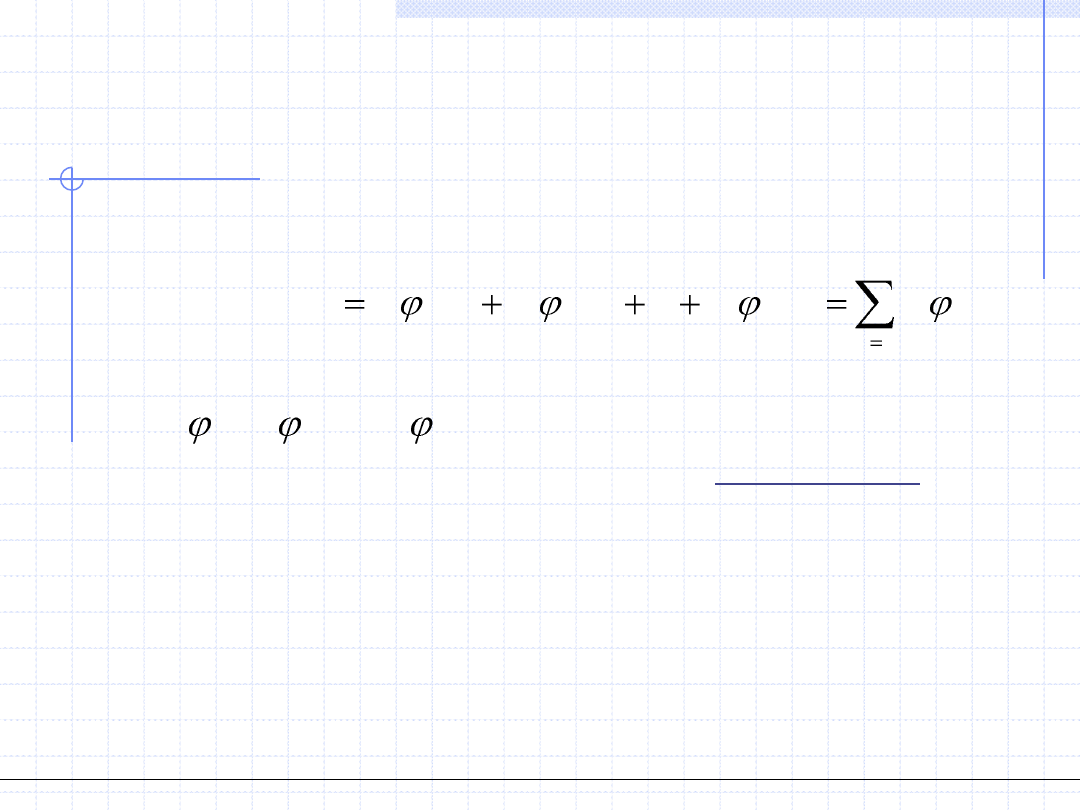
gdzie B jest macierzą główną układu równań opisujących współczynniki

natomiast 

( )

j

i

x

B

jest macierzą kwadratową rzędu k, powstałą przez 

zastąpienie j – tej kolumny w macierzy B wektorem: 

1

2

[ ( ),

( ),...,

( ),...,

( )]

i

i

r

i

k

i

x

x

x

x

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Błędy parametrów wyznaczonych metodą 

najmniejszych kwadratów

Przypominam, że funkcja liniowa ze względu na parametry ma postać:

k

j

j

j

k

k

k

x

a

x

a

x

a

x

a

a

a

a

x

f

1

2

2

1

1

2

1

)

(

)

(

...

)

(

)

(

)

,...,

,

,

(

)

(

),...,

(

),

(

2

1

x

x

x

k

gdzie

są to stosunkowo proste ale liniowo 

niezależne tzw. funkcje bazowe.

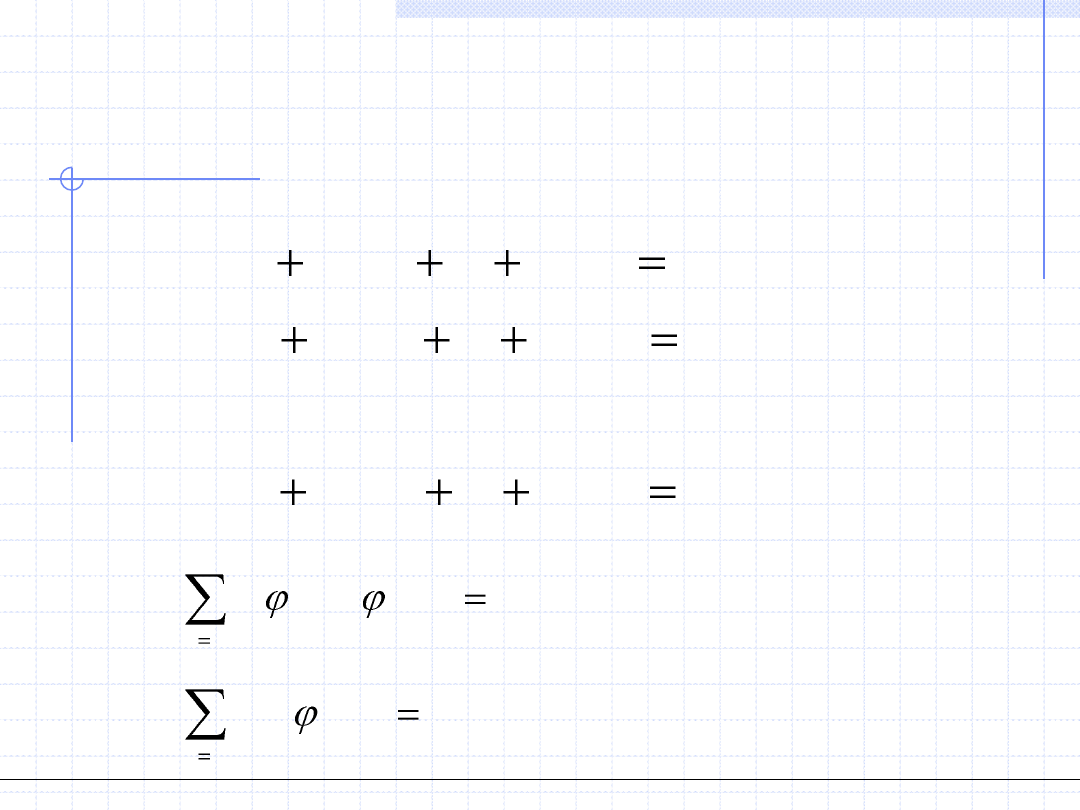
© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Błędy parametrów wyznaczonych metodą 

najmniejszych kwadratów

Natomiast liniowy układ równań określający współczynniki ma postać:

1 11

2 12

1

1

1 21

2 22

2

2

1

1

2

2

...

...

...........................................

...

k

k

k

k

k

k

k kk

k

a b

a b

a b

c

a b

a b

a b

c

a b

a b

a b

c

gdzie:

1

1

( )

( )

( )

n

i

j

i

r

i

rj

i

n

i

i

r

i

r

i

w

x

x

b

w y

x

c

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Błędy parametrów wyznaczonych metodą 

najmniejszych kwadratów

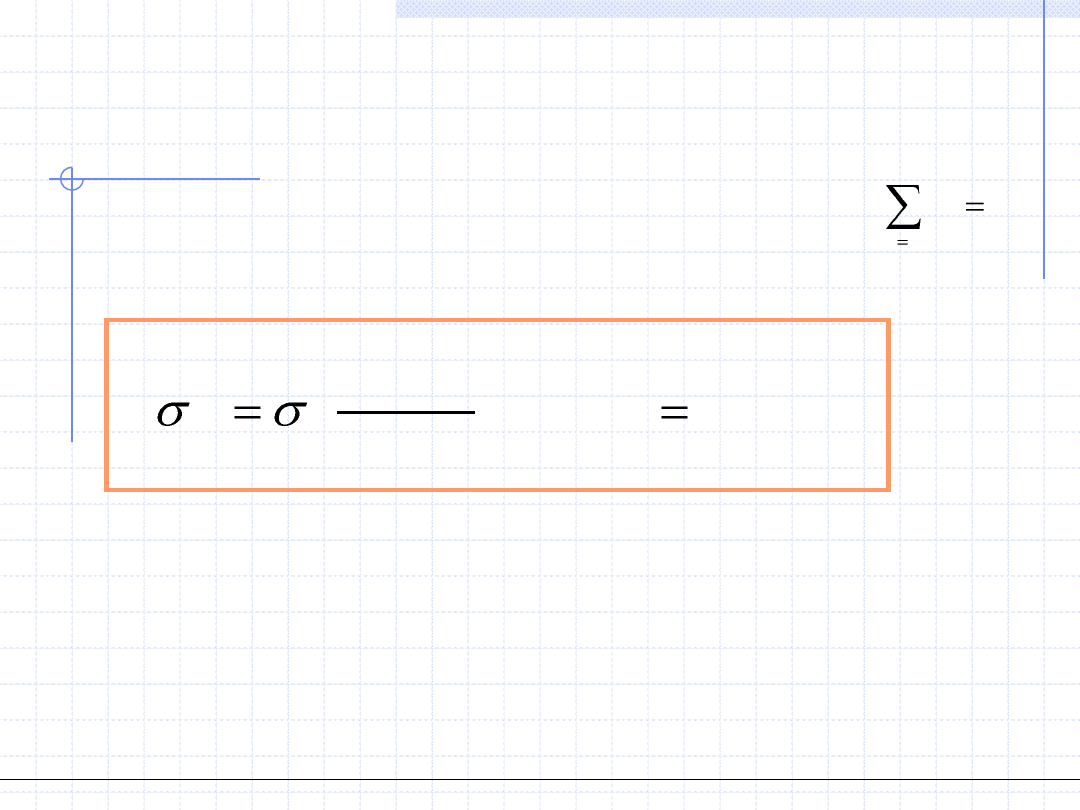
W przypadku pomiarów jednakowo ważnych gdy 

w

i

=1 oraz

1

n

i

i

w

n

wzór powyższy można uprościć do wyrażenia:

2

2

det

1, 2,...,

det

j

jj

a

y

j

k

B

B

gdzie:

jj

B

oznacza macierz k-1 rzędu powstałą przez skreślenie 

w macierzy B j – tej kolumny oraz j – tego wiersza. 

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

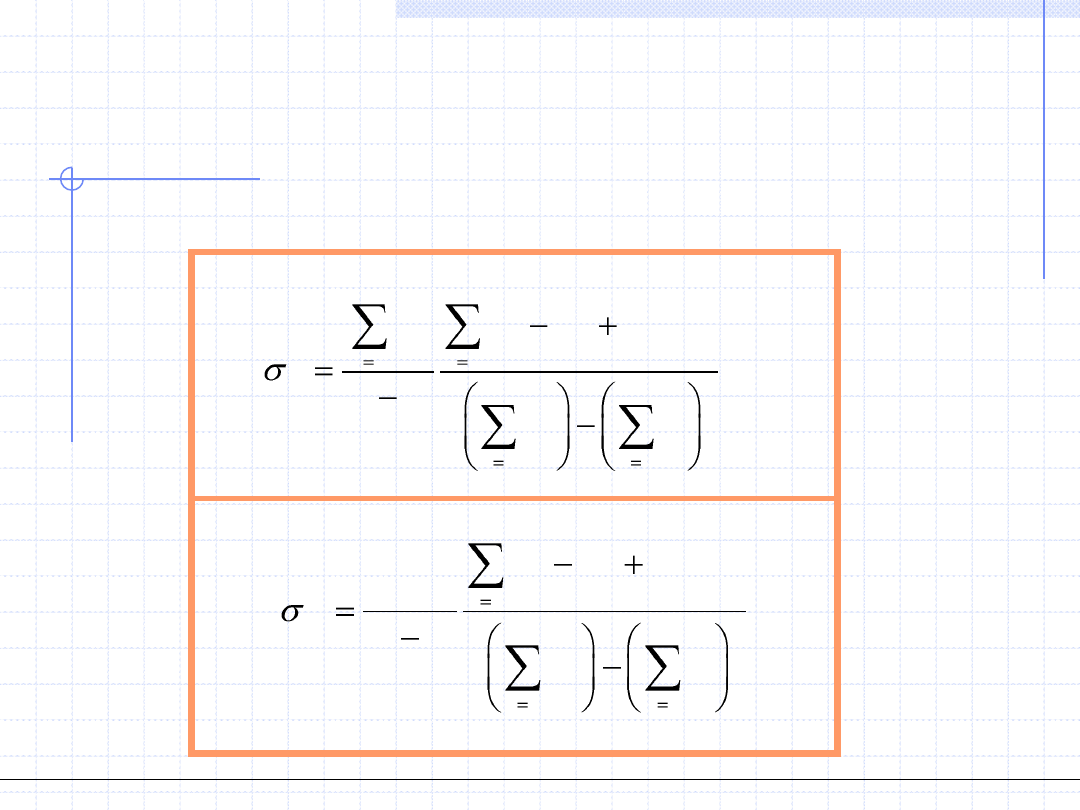
Błędy parametrów wyznaczonych metodą 

najmniejszych kwadratów

Dla funkcji liniowej postaci f(x)=a

1

+a

2

x w przypadku pomiarów 

jednakowo ważnych wyrażenia określające wariancje parametrów 

przyjmują następującą postać:

1

2

2

1

2

2

1

1

2

2

1

1

[

(

)]

(

2)

n

n

i

i

i

i

i

a

n

n

i

i

i

i

x

y

a

a x

n

n

x

x

2

2

1

2

2

1

2

2

1

1

[

(

)]

(

2)

n

i

i

i

a

n

n

i

i

i

i

y

a

a x

n

n

n

x

x

© Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 

Na tym kończymy dzisiejszy wykład

Dziękuję bardzo Państwu za uwagę