Wykład 12. Ekonomia matematyczna.   R.Rempała .          Materiały dydaktyczne         

 

22 

Duopol i oligopol 

Teorię  duopolu  sformułował  i  rozwinął  francuski 

matematyk  i  ekonomista  Antoine  Cournot  (1801-1877), 

który  przez  wielu  uważany  jest  za  ojca  matematycznej 

ekonomii. 

Dwaj producenci produkują i dostarczają na rynek pewien 

towar. Zakładamy, że producenci tak opanowali rynek, iż 

cena rynkowa produktu zależy od łącznej ilości dostarczonej 

na rynek przez obu producentów. 

Producenci nie mają trudności ze zbytem towaru i z 

nabywaniem czynników produkcji. Koszt produkcji 

poszczególnych producentów zależy od wielkości własnej 

produkcji. 

Oznaczenia 

y

i

 - 

ilość towaru wyprodukowana przez i-tego duopolistę, i=1,2  

k

i

(y

i

) 

– funkcja kosztów produkcji i-tego producenta 

p

i

(y

1

+y

2

) 

–  funkcja  określająca  cenę  rynkową  produktu  i-tego 

producenta; y

1

+y

2

 

– jest łączną produkcją duopolistów 



i

(y

1

,y

2

) 

– funkcja wyrażająca zysk i-tgo producenta 

Zauważmy, że 



i

(y

1

,y

2

) = y

i

 p

i

(y

1

+y

2

) 

– k

i

(y

i

),  i=1,2 

 

                             



 

      



 

  



 

                               zysk  = przy

chód – koszt 

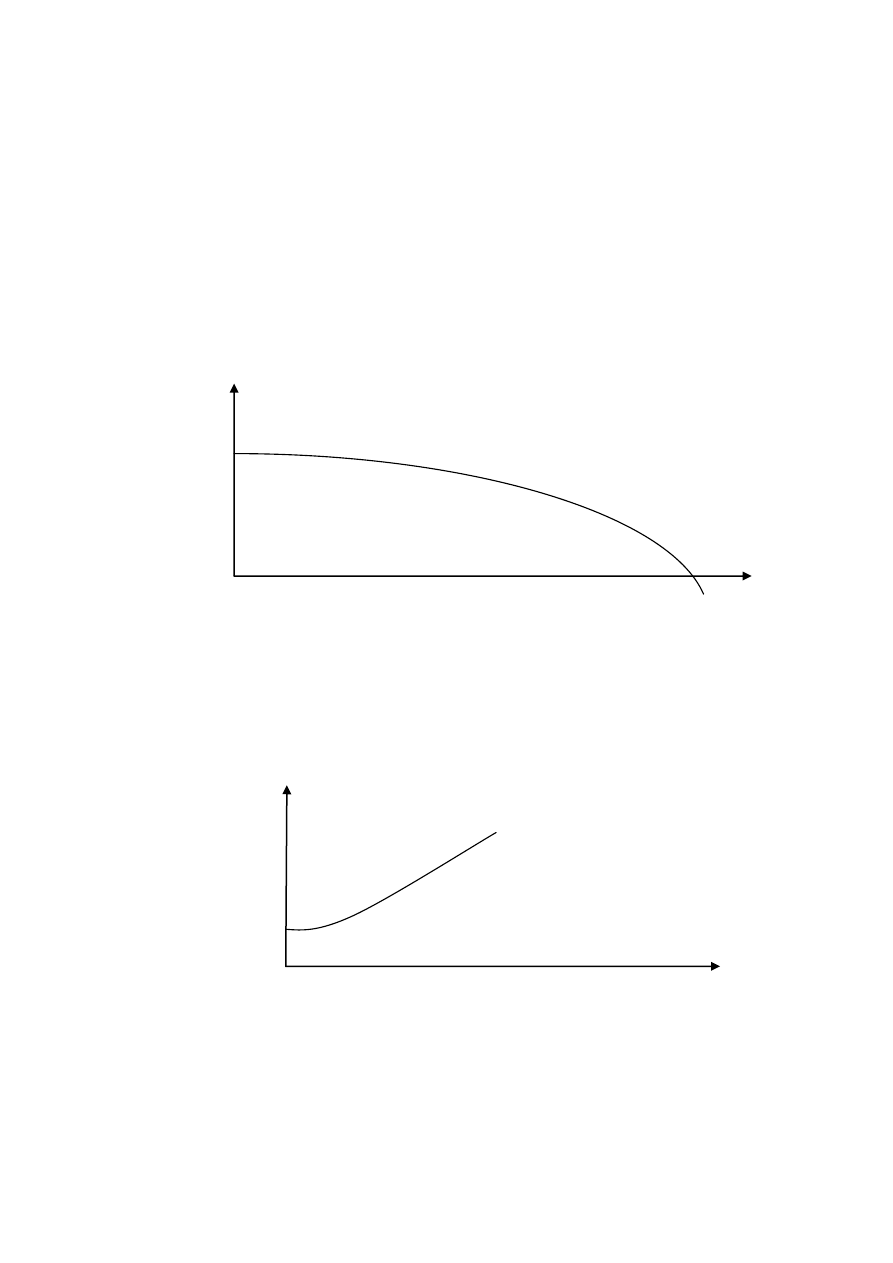
Wykład 12. Ekonomia matematyczna.   R.Rempała .          Materiały dydaktyczne         

 

23 

Założenia modelu 

Dla każdego i 

(a) 

p

i

  i  k

i

 

są  funkcjami  określonymi  na  [0,

)



  przy 

czym:funkcja  p

i

 

jest  malejąca  od  pewnego  a

i

=p

i

(0)>0  i 

p

i

(b

i

)=  0  dla  pewnego  b

i

>0;  ponadto  jest  ona 

różniczkowalna i ma ciągłą malejącą pochodną ( zatem 

jest wklęsła, por. Rys 3.1) 

     p

i

(s) 

           a        

            

 

            0                                                                        

                                                                                   b

i

     

Rys.3.1 p

i

(s),  s = y

1

+y

2

 

(b) 

funkcja  kosztów  k

i

 

jest  rosnąca,  różniczkowalna  i  ma 

ciagłą  rosnącą  pochodną.(zatem  jest  wypukła,  por. 

Rys.3.2) 

   k

i

(y

i

) 

 

 

 

              Rys. 3.2  k

i

 (y

i

)

                                                                  

 y

i 

Przypominamy problem monopolisty (PM) 

W  przypadku  monopolu  mieliśmy  do  czynienia  z  jednym 

producentem.  Chodziło  o  wyznaczenie  takiego  poziomu 

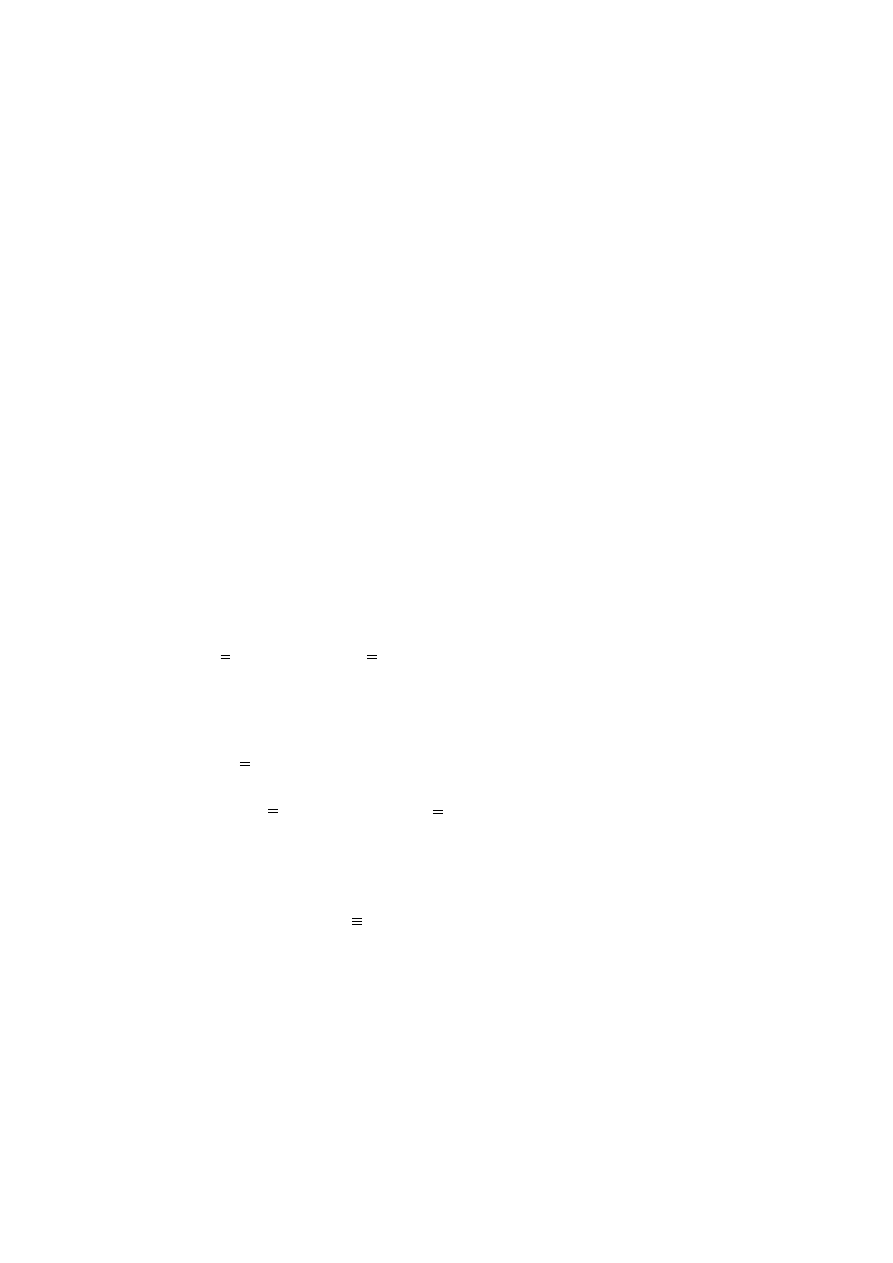
Wykład 12. Ekonomia matematyczna.   R.Rempała .          Materiały dydaktyczne         

 

24 

produkcji  y*,  który  maksymalizuje  zysk  przedsiębiorstwa. 

Przypominamy,  że  problem  optymalizacyjny  przybierał 

postać. 

(PM) :                   



(y) = yp(y) 

– k(y)         

max



 

                                       x

0



 

 

Podobnie  jest  w  duopolu.  Każdy  z  producentów  chciałby 

maksymalizować  zysk.  Rzecz  jednak  w  tym,  że  tym  razem 

zysk  zależy  nie  tylko  od  wielkości  własnej  produkcji  ale 

(poprzez  cenę  rynkową  )  od  wielkości  produkcji  drugiego 

duopolisty. 

 

Zatem  jeśli  pierwszy  wyprodukuje 

1

y

~

  to  drugi  wybierze  taki 

poziom 

2

y

, że  



2

(

2

1

y

,

y

~

) = 

)

y

,

y

~

(

max

2

1

2

0

2

y





 

Podobnie  zachowuje  się  pierwszy  producent.  Na  wielkość 

produkcji 

2

y

 zareaguje takim wyborem poziomu produkcji 

1

y

~

~

, 

żeby  



2

(

2

1

y

,

y

~

~

) = 

)

y

,

y

(

max

2

1

1

0

1

y





 

Na  wybór  pierwszego  producenta 

1

y

~

~

  drugi  producent 

zareaguje wyborem 

2

y

itp. 

Zauważmy,  że  mamy  tu  do  czynienia  z  pewną  grą. Wypłatą 

są funkcje zysków a decyzją - wielkość produkcji. 

 

Wykład 12. Ekonomia matematyczna.   R.Rempała .          Materiały dydaktyczne         

 

25 

Pojawia się  pytanie: czy istnieją takie poziomy produkcji 



1

y

,



2

y

,  że  każdy  z  producentów  maksymalizuje  swój  zysk  i  nie 

potrzebuje przy tym zmieniać swojego wyboru? 

Innymi słowy 

czy istnieje taka para 



1

y

,



2

y

, że  

(a) 



1

(



1

y

,



2

y

) = 

)

y

,

y

(

max

2

1

1

0

1

y







 

(b) 



2

(



1

y

,



2

y

) = 

)

y

,

y

(

max

2

1

2

0

2

y







 

Para  decyzji  spełniająca  warunki  (a)-(b)  nazywa  się 

równowagą duopolu.  



1

y

 jest poziomem produkcji pierwszego 

duopolisty  w  stanie  równowagi,  a 



2

y

  jest  poziomem  produkcji 

drugiego duopolisty w stanie równowagi. 

 

W  jezyku  teorii  gier  para  (



1

y

,



2

y

)  nazywana  jest  punktem 

ekwilibrium Nasha lub punktem równowagi Nasha. 

 

Twierdzenie3.1. 

Przy  przyjętych  założeniach  duopol  posiada 

punkt równowagi i jest to punkt jedyny.(por. ref [5]) 

 

Powstaje  pytanie:  czy  można  podać  warunki  konieczne  i 

dostateczne na to, aby para 



1

y

,



2

y

 

była punktem równowagi. 

Odpowiedzią jest następujące twierdzenie. 

 

Wykład 12. Ekonomia matematyczna.   R.Rempała .          Materiały dydaktyczne         

 

26 

Twierdzenie3.2  Na  to,  aby  para  (



1

y

,



2

y

)  była  punktem 

równowagi rozważanego modelu duopolu potrzeba i wystarcza, 

aby  dla i=1,2 

(c)  

0

y

2

1

2

1

y

y

y

y

i

i















)

,

(

)

,

(

|

 

jeśli 

0

y

i





, 

(d)  p

i

(



1

y

+



2

y

)

)

(0

k

i





   

jeśli 

0

y

i





. 

Ekonomiczna interpretacja warunków (c) – (d) 

 

Ad (d)  

i

k



(y

i

)  oznacza koszt krańcowy. Z założenia koszt 

krańcowy jest rosnący. Zatem z warunku (d) wynika, że jeśli w 

punkcie równowagi duopolista nie produkuje towaru to oznacza, 

że cena rynkowa jest tak niska, iż nie przekracza jego 

najniższego kosztu krańcowego. 

Ad (c)  

Warunek ten przyjmuje postać 























i

i

2

1

2

1

y

y

i

i

i

y

y

y

y

i

2

1

i

i

y

y

k

y

y

y

p

y

|

)

(

|

)

(

(

)

,

(

)

,

(

 

Oznacza to, że w punkcie równowagi  

krańcowy przychód = krańcowemu kosztowi 

 

Przykład numeryczny 

Niech 

p

1

(y

1

+y

2

) = 16 

– (y

1

+y

2

)

2

,         k

1

(y

1

) = 

2

1

y

 

p

2

(y

1

+y

2

) = 32 

– 2(y

1

+y

2

)

2

,       k

2

(y

2

) = 

2
2

y

2

 

W przykładzie tym cena produktu i koszt wytwarzania drugiego producenta są dwa 

razy wyższa niż odpowiednio cena i koszt pierwszego producenta 

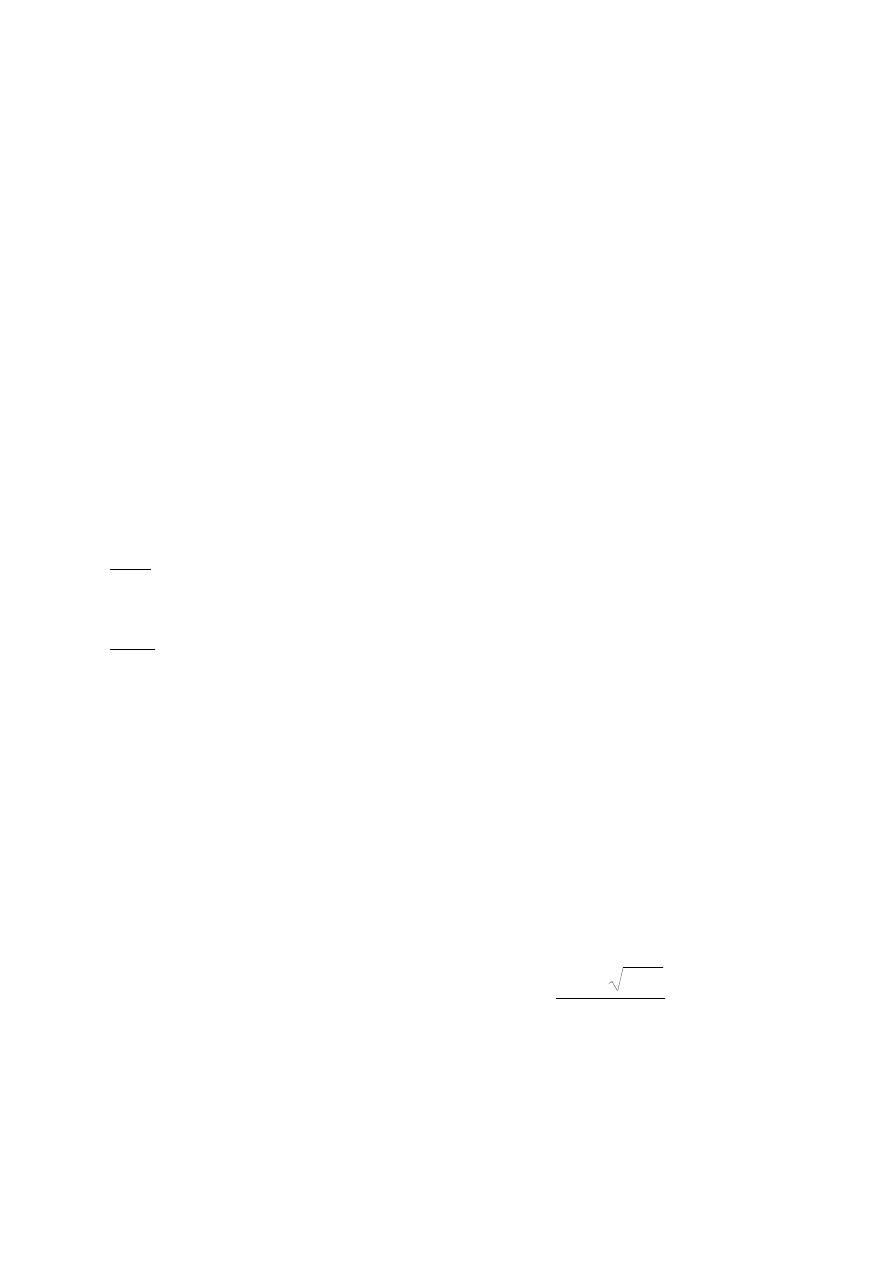
Wykład 12. Ekonomia matematyczna.   R.Rempała .          Materiały dydaktyczne         

 

27 

Zauważmy, że p

i,

 k

i 

spełniają założenia modelu. 

Stałe wymienione w założeniach wynoszą: a

1

=16, b

1

=4; a

2

=32, 

b

2

=4. Funkcje p

1

, p

2 

 

sa malejące  o malejących pochodnych. 

Funkcje kosztów k

1

, k

2 

są rosnące i ich pochodne także. 

Dla wyznaczenia punktu równowagi stosujemy Twierdzenie 3.2. 

Pokażemy, że  tym przypadku wystarczy wykorzystać warunek 

(c) Twierdzenia. 











)

(

)

(

)

,

(

1

1

1

2

1

1

2

1

1

y

k

y

y

y

p

y

y

 16y

1

 

– (y

1

 + y

2

)

2

y

1

 - 

2

1

y

 











)

(

)

(

)

,

(

2

2

2

2

1

2

2

1

2

y

k

y

y

y

p

y

y

 32y

2

 

– 2(y

1

 + y

2

)

2

y

2

 - 2

2
2

y

 

Mamy więc 

,

)

(

)

(

0

y

2

y

y

y

y

y

2

16

y

1

2

2

1

1

2

1

1

1





















 

.

)

(

)

(

0

y

4

y

y

2

y

y

y

4

32

y

2

2

2

1

2

2

1

1

2





















 

Dzieląc obie strony drugiego równania przez dwa mamy układ: 

(*)

,

)

(

)

(

0

y

2

y

y

y

y

y

2

16

1

2

2

1

1

2

1













 

    

.

)

(

)

(

0

y

2

y

y

y

y

y

2

16

2

2

2

1

2

2

1













 

Dodając równości stronami i podstawiając s=y

1

+y

2

 otrzymujemy 

32 

– 4 s

2 

– 2s = 0 a więc 2 s

2

 +s 

–16 = 0. Równanie 

kwadratowe rozwiązuje się standardowo. 

129

2

16

4

1













  

 

Dodatni pierwiastek równania wynosi s = 

589

2

4

129

1

.







4 

Podstawiając s do równania (*) łatwo wyznaczyć y

1

. Mamy 

więc: 

Wykład 12. Ekonomia matematyczna.   R.Rempała .          Materiały dydaktyczne         

 

28 

294

1

2

s

2

16

s

y

2

1

.

*











7.  Zatem 

*
2

y

=s-

*

1

y

 

= 2.5894 

– 1.2947 



1.2947. 

Punktami równowagi są 

2947

1

y

y

2

1

.

*

*





. Przy takim wyborze 

wielkości produkcji obaj producenci są usatysfakcjonowani. 

Oligopol 

Z oligopolem mamy do czynien

ia wtedy gdy większa liczba 

producentów opanowała rynek i „n” (n 2



) producentów 

produkuje i dostarcza na rynek pewien towar. Zakładamy, że 

cena towaru zależy od łącznej ilości towaru dostarczonej na 

rynek przez wspomnianych producentów. 

 

Podobnie jak poprzednio producenci nie mają trudności ze 

zbytem towaru i z nabywaniem czynników produkcji. Koszt 

produkcji poszczególnych producentów zależy od wielkości 

własnej produkcji. 

Zauważmy, że model oligopolu jest prostym uogólnieniem 

duopolu. Zatem opis modelu jest podobny. Tym razem 

i=1,2,...,n. 

y

i

  - 

ilość  towaru  wyprodukowana  przez  i-tego  producenta, 

i=1,2,...n 

k

i

(y

i

) 

– funkcja kosztów produkcji i-tego producenta 

p

i

(y

1

+y

2

+   +y

n

) 

– funkcja określająca cenę rynkową produktu i-

tego producenta. Wygodnie jest oznaczyć  

s = y

1

+y

2

+....+y

n

 

– jako łączną produkcję oligopolistów. 



i

(s) 

– funkcja wyrażająca zysk i-tgo producenta, 

Wykład 12. Ekonomia matematyczna.   R.Rempała .          Materiały dydaktyczne         

 

29 

Funkcje k

i

(y

i

), p

i

(s) 

– spełniają takie założenia  jak w duopolu. 

Zau

ważmy, że 



i

(s) = y

i

 p(s) 

– k

i

(y

i

),  i=1,2,   ,n 

Pytanie o punkt równowagi przybiera teraz formę: czy istnieje 

taki wybór wielkości produkcji (



1

y

,



2

y

,...,

*

n

y

)  że  

(1) 



1

(



1

y

,



2

y

,...,



n

y

) = 

)

,...,

,

,

(

max

*

*

n

3

2

1

1

0

y

y

y

y

y

1







 

(2) 



2

(



1

y

,



2

y

,...,



n

y

) = 

)

,...,

,

,

(

max

*

*

n

3

2

1

2

0

y

y

y

y

y

2







 

 

 

(n) 



n

(



1

y

,



2

y

,...,



n

y

) = 

)

,...,

,

,

(

max

*

*

n

3

2

1

1

0

y

y

y

y

y

n







 

Układ decyzji (



1

y

,



2

y

,...,



n

y

) spełniająca  warunki (1)-(n) nazywa 

się  równowagą  oligopolu.   



1

y

  jest  poziomem  produkcji 

pierwszego  producenta  w  stanie  równowagi,  a 



2

y

  jest 

poziomem produkcji drugiego itd. 

 

W języku teorii gier układ (



1

y

,



2

y

,...,



n

y

) nazywana jest punktem 

ekwilibrium Nasha lub punktem równowagi Nasha. 

 

Twierdzenie3.3. 

Przy  przyjętych  założeniach  oligopol  posiada 

punkt równowagi i jest to punkt jedyny.(por. ref [5]) 

 

Wykład 12. Ekonomia matematyczna.   R.Rempała .          Materiały dydaktyczne         

 

30 

Pytanie  jest  takie  j

ak  w  duopolu:  czy  można  podać  warunki 

konieczne  i  dostateczne  na  to,  aby  układ  (



1

y

,



2

y

,...,y

*

n

)  był 

punktem równowagi oligopolu? 

Odpowiedzią jest następujące twierdzenie. 

 

Twierdzenie3.3  Na  to,  aby 

układ  (



1

y

,



2

y

,...,

*

n

y

)  był  punktem 

równowagi  rozważanego  modelu  oligopolu  potrzeba  i 

wystarcza, aby  dla i=1,2,...,n 

(I)  

0

y

n

2

1

n

2

1

y

y

y

y

y

y

i

i















)

,...,

,

(

)

,...,

,

(

*

|

 

jeśli 

0

y

i





, 

(II)  p

i

(



1

y

+



2

y

+...+y

*

n

)

)

(0

k

i





   

jeśli 

0

y

i





. 

Ekonomiczna interpretacja warunków (I) – (II) jest dokładnie taka jak w 

duopolu. 

Ćwiczenia. Zestaw 2 

1.Co to jest oligopol? 

2. Czym różni się duopol od oligopolu? 

3

. Określ funkcje krańcowych przychodów producentów 

duopolu w przypadku gdy p

1

(y

1

+y

2

) = 9- (y

1

+y

2

-2)

2

,  

 p

2

(y

1

+y

2

) = 25 - (y

1

+y

2

-1)

2 

4. 

Przy założeniu, że punkt równowagi duopolu ma obie współrzędne 

dodatnie, funkcje kosztów producentów są postaci k

1

(y

1

)= 

2

1

y

,  k

2

(y

2

)= 

2
2

y

 

, a funkcje cen takie jak  w punkcie 4 podaj równania  określające j  

 j

ednoznacznie równowagę duopolu.