Ekonomia matematyczna. Wykład14b R. Rempała. Materiały dydaktyczne

39

Model von Neumanna c.d.

Ćwiczenia + uwagi o modelu dynamicznym.

Rozważamy m procesów technologicznych nazywanych

bazowymi. Procesy numerujemy liczbami: 1,2,...,m.

j-

ty bazowy proces technologiczny jest opisany parą n -

wymiarowych wektorów.

a

j

= (a

j1

,a

j2

,...,a

jn

)----

wektor nakładów, a

ji



0

b

j

= (b

j1

,b

j2

,...,b

jn

)----

wektor wyników b

ji



0.

Przy intensywności x= (0,0,...,0,1,0,...,0) - jedynka na j-tym

miejscu -

zużycie opisane jest wektorem (a

j1

,a

j2

,...,a

jn

) a

produkcja wektorem (b

j1

,b

j2

,...,b

jn

).

Wygodnie jest opisać wszystkie procesy bazowe za pomocą pary

macierzy:





































































mn

2

m

1

m

n

2

22

21

n

1

12

11

m

2

1

a

a

a

a

a

a

a

a

a

a

a

a

A

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

-

macierz nakładów





































































mn

2

m

1

m

n

2

22

21

n

1

12

11

m

2

1

b

b

b

b

b

b

b

b

b

b

b

b

B

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

-

macierz wyników (produkcji)

Ekonomia matematyczna. Wykład14b R. Rempała. Materiały dydaktyczne

40

W macierzach może występować wiele zer.

Zakłada się, że:

Każdy wiersz macierzy nakładów (A) zawiera element dodatni

Każda kolumna macierzy wyników (B) zawiera element dodatni.

Przypuśćmy teraz, że poszczególne bazowe technologie

zostały użyte z intensywnościami odpowiednio x

1

,x

2

,...x

m

.

Wektor x = (x

1

,x

2

,...,x

m

) jest wektorem -

wierszem opisującym

intensywności. Przy intensywnościach wyrażonych przez x

mamy następujące łączne nakłady czynników:

(*) (x

1

a

11

+...+ x

m

a

m1,

x

1

a

12

+...+ x

m

a

m2

,..., x

1

a

1n

+...+ x

m

a

mn

)= x A,



nakład 1 czynnika,



nakład 2 czynnika,

,



nakład n-tego czynnika



inny zapis

natomiast łączne wyniki produkcji wynoszą:

(**) (x

1

b

11

+...+ x

m

b

m1,

x

1

b

12

+...+ x

m

b

m2

,..., x

1

b

1n

+...+ x

m

b

mn

)= x B



1 produkt,



2 produkt,



n-ty produkt,



inny zapis

Przykład 1.

A=













5

1

2

1

75

0

.

.

, B=













2

2

1

1

.

xA=(0.75x

1

+2x

2

, x

1

+1.5x

2

) = wektor nakładów,

xB=(x

1

+2x

2

, x

1

+2x

2

) = wektor produkcji.

Przypominamy.

Wskaźnikiem technologicznej efektywności

wytwarzania i-tego

towaru

przy intensywności produkcji x=(x

1

,x

2

,...,x

m

) nazywamy liczbę

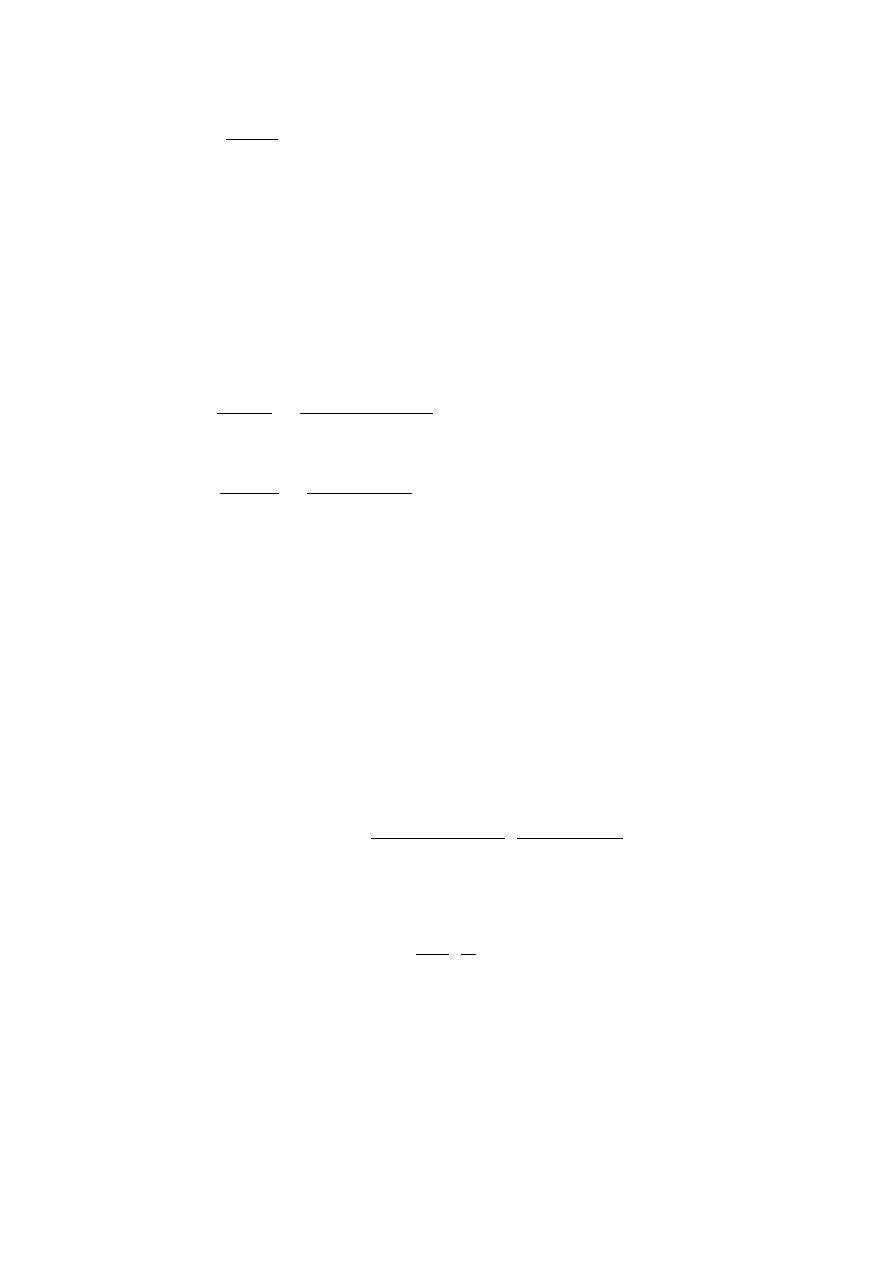
Ekonomia matematyczna. Wykład14b R. Rempała. Materiały dydaktyczne

41



































0

xB

xA

gdy

na

nieokre

śie

0

xB

0

xA

gdy

0

xA

gdy

xA

xB

x

i

i

i

i

i

i

i

i

)

(

)

(

,

,

)

(

,

)

(

,

,

)

(

,

)

(

)

(

)

(

W Przykładzie 1 przy wektorze intensywności x 0, x

mamy:

2

1

2

1

1

1

1

x

2

x

75

0

x

2

x

xA

xB

x











.

)

(

)

(

)

(

,

2

1

2

1

2

2

2

x

5

1

x

x

2

x

xA

xB

x

.

)

(

)

(

)

(











(II) Wska

źnikiem technologicznej efektywności procesu

wytwarzania (stopą produkcji) przy intensywności

produkcji x=(x

1

,x

2

,...,x

m

) nazywamy liczbę

)

(

min

)

(

x

x

i

i







Innymi słowy przy

x

0

}

:

max{

)

(

xB

xA

x











W Przykładzie 1 przy x 0, x mamy:

)

(

min

)

(

x

x

i

i







=

)

.

,

.

(

min

2

1

2

1

2

1

2

1

x

5

1

x

x

2

x

x

2

x

75

0

x

2

x









;

Niech x=(2,0)

1

2

2

5

1

2

0

2

0

2

i

i











)

,

.

min(

)

,

(

min

)

,

(

Zauważmy, że













































2

2

2

5

1

1

0

2

.

:

max

)

,

(

Ekonomia matematyczna. Wykład14b R. Rempała. Materiały dydaktyczne

42

(III)

Optymalnym

wskaźnikiem

technologicznej

efektywności w modelu (optymalną stopą produkcji)

nazywamy liczbę

)

(

max

x

0

x

opt









.

Wektor intensywności

x

dla którego

)

(x

opt







nazywa się

optymalnym wektorem intensywności w modelu. Optymalny wektor

intensywności jest określony z dokładnością do struktury ( z

dokładnością do mnożenia przez stałą dodatnią).

Zauważmy, że w Przykładzie 1,





opt

5

3

4

1

2

.

)

,

(





Efektywność ekonomiczna.

Niech p

i

oznacza ce

nę rynkową i-tego towaru.

(x B)

1

p

1

+ (x B)

2

p

2

+...+(x B)

n

p

n

=

wartość produkcji przy intensywności

x=

(x

1

,x

2

,...,x

m

). W zapisie macierzowym przy traktowaniu

wektora cen jako kolumnę wartość tę wyraża się krótko: xBp.

(xA)

1

p

1

+ (xA)

2

p

2

+...+(x A)

n

p

n

=

wartość nakładu przy intensywności

x=

(x

1

,x

2

,...,x

m

). W zapisie macierzowym przy traktowaniu

wektora cen jak kolumnę wartość tę wyraża się krótko: xAp.

Powrót do Przykładu 1.

xA=(0.75x

1

+2x

2

, x

1

+1.5x

2

) = wektor nakładów,

xB=(x

1

+2x

2

, x

1

+2x

2

) = wektor produkcji.

Zatem

(x B)

1

p

1

+ (x B)

2

p

2

=

(x

1

+2x

2

)p

1

+ (x

1

+2x

2

)p

2

=

wartość produkcji

przy intensywności x=

(x

1

,x

2

); xBp = (x

1

+2x

2

)p

1

+ (x

1

+2x

2

)p

2

Ekonomia matematyczna. Wykład14b R. Rempała. Materiały dydaktyczne

43

(xA)

1

p

1

+ (xA)

2

p

2

=

(0.75x

1

+2x

2

)p

1

+ (x

1

+1.5x

2

)p

2

wartość

nakładu przy intensywności x=

(x

1

,x

2

); xAp = (0.75x

1

+2x

2

)p

1

+

(x

1

+1.5x

2

)p

2

Wskaźnikiem ekonomicznej efektywności (stopą dochodu )

przy intensywnościach x i cenach p nazywamy liczbę

































.

,

.

,

,

,

)

,

(

0

xBp

0

xAp

gdy

nieokr

0

xBp

0

xAp

gdy

0

xAp

gdy

xAp

xBp

p

x

W

Przykładzie 1 wskaźnik efektywności ekonomicznej dla x= (2,1) i

p

T

=(1,1) wynosi :

7

8

5

3

5

3

4

4

1

1

1

2











.

.

))

,

(

),

,

((

Warunki równowagi w modelu von Neumanna.

Definicja.

O wektorze intensywności x~ 0, x~ , i wektorze

cen

p

~

0,

p

~

oraz liczbie

0





mówimy, że charakteryzuje

gospodarkę w równowadze von Neumanna, jeżeli spełniają

następujące warunki:

(I)

,

~

~

B

x

A

x





(II)

dla każdego x

0



,

p

xA

p

xB

~

~





,

(III)

0

p

B

x



~

~

.



Ekonomia matematyczna. Wykład14b R. Rempała. Materiały dydaktyczne

44

Wektor

x

~

nazywamy

wektorem

intensywności

procesów

technologicznych w równowadze, wektor cen

p

~

nazywa się wektorem

cen w równowadze. Warunek (II) jest równoważny (II)’

p

A

p

B

~

~





W Przykładzie 1. warunki równowagi opisane są układem

nierówności:

2

1

2

1

2

1

2

1

x

2

x

x

5

1

x

x

2

x

x

2

x

75

0

















)

.

(

)

.

(

)

.

(

)

.

(

2

1

2

1

2

1

2

1

p

5

1

p

2

p

2

p

2

p

p

75

0

p

p

















xBp = (x

1

+2x

2

)p

1

+ (x

1

+2x

2

)p

2

> 0.

Zauważmy, że :

1

p

x

1

p

2

x

5

3

4

2

2

1

1













~

~

,

~

,

~

,

.

-

spełniają

ten układ. Zauważmy także, iż - zgodnie z wnioskami

wynikającymi z definicji równowagi - w stanie równowagi









)

,

( 1

2

7

8

5

3

4

1

1

1

2







.

))

,

(

),

,

((

.

tzn. wskaźnik technicznej efektywności = wskaźnikowi

ekonomicznej efektywności = poziomowi równowagi.

Model dynamiczny

Załóżmy, że w kolejnych okresach t=0,1,2, ,t

1

produkcja

odbywa się z intensywnościami opisanymi ciągiem wektorów

x(t)=(x

1

(t),x

2

(t),...,x

n

(t)). W poszczególnych okresach ceny

opisane są ciągiem wektorów kolumnowych p(t)= (p

1

(t),...,p

n

(t))

T

Ekonomia matematyczna. Wykład14b R. Rempała. Materiały dydaktyczne

45

Zakładamy, że w żadnym okresie wektor nakładów nie może

być większy od wektora wyników z poprzedniego okresu.

Oznacza to, że

a) x(t+1)A

B

t

x

)

(



, t=0,1,...,t

1

-1

a ponadto zakładamy, że

b) x(t)

0



, t=0,1,...,t

1

c) x(0)=x

0

0, x

0

- stan początkowy

Ciąg intensywności {x(t)

1

t

0

t



}

spełniający warunki a) – c) nazywa

się dopuszczalną trajektorią intensywności a odpowiednie ciągi

{x(t)A} i {x(t)B} dopuszczalnymi ciągami nakładów i wyników.

Trajektorie równomiernego wzrostu (stacjonarne)

Dopuszczalną trajektorię intensywności {x(t)

1

t

0

t



}

nazywamy

stacjonarną jeśli ma następującą postać:

x(t) =

1

0

t

t

2

1

0

t

x

,...,

,

,

,





. gdzie

.

0





Współczynnik



nazywa się współczynnikiem wzrostu

gospodarczego.

Wniosek z warunku a)

. Stacjonarna trajektoria intensywności z

tempem wzrostu



istnieje wtedy i tylko wtedy gdy spełniony jest

warunek:

B

x

A

x

0

0





Ekonomia matematyczna. Wykład14b R. Rempała. Materiały dydaktyczne

46

Trajektorie nakładów i wyników odpowiadające stacjonarnej

trajektorii x(t) =

1

0

t

t

2

1

0

t

x

,...,

,

,

,





mają postać

,

A

x

0

t



1

t

2

1

0

t

,...,

,

,



.

,

B

x

0

t



1

t

,...,

2

,

1

,

0

t

1





.

Zauważmy, że



=1 charakteryzuje stagnację,

1





równomierny wzrost gospodarczy a

1





zamieranie

działalności gospodarczej.

Pytanie. Czy istnieje stacjonarna trajektoria z maksymalnym

tempem wzrostu?

Twierdzenie.

W modelu von Neumana istnieją stacjonarne

trajektorie z tempem wzrostu

opt







, które jest najwyższym

możliwym wzrostem tej gospodarki.

Stacjonarną trajektorię intensywności z tempem

opt







nazywamy optymalną stacjonarną trajektorią

intensywności.

Ważna uwaga. Jeżeli x~ (t)=

0

t

opt

x

~

)

(



jest optymalna to dla

każdego

0





, trajektoria

)

(

~

~

)

(

~

)

(

)

(

~

~

t

x

x

x

t

x

0

t

opt

o

t

opt

















jest także optymalna.

Półprostą

N = {

0

x







:

~

}

gdzie x

~ jest dowolnym wektorem intensywności w optymalnym

stacjonarnym procesie wzrostu , nazywamy magistralą

intensywności w modelu von Neumanna.