BŁĘDY

POMIARÓW

GEODEZYJNYCH

rodzaje, źródła, zasady i metody

poprawnych technik pomiarów wielkości

kątowych i liniowych

Źródła błędów (przyczyny ich

powstawania):

-     niedoskonałość zmysłów obserwatora,
-     niedoskonałość narzędzi pomiarowych,
-     zmiany zachodzące w środowisku zewnętrznym lub

trudności terenowe

(temperatura, wiatr, deszcz, mgła, teren górzysty

lub

zadrzewiony).

Rodzaje błędów pomiarów:

   

  błędy grube (omyłki),

    błędy systematyczne,

  błędy przypadkowe.

Błędy grube

Są to poważne odchylenia wyników pomiarów od

wartości rzeczywistej mierzonej wielkości. Omyłki
powstają na skutek nieuwagi, pośpiechu, zmęczenia lub
braku staranności obserwatora. Omyłki wykrywamy i
eliminujemy z pomiarów przez kilkakrotne obserwacje tej
samej wielkości.

Błędy systematyczne

Towarzyszą wszystkim pomiarom, są więc nie do

uniknięcia. Błędy te mają stałe znaki, plus lub minus, a
czasem i stałe wartości. Często wzrastają proporcjonalnie
do mierzonej wielkości, niemniej są małe co do
bezwzględnej wartości

Są one powodowane wszystkimi trzema źródłami,

ale najczęściej niedoskonałością narzędzi pomiarowych.

Błędy systematyczne można ująć wzorami

matematycznymi, w związku z czym powinny być
eliminowane z obserwacji przez wprowadzanie do
wyników pomiarów odpowiedniej poprawki lub przez
zastosowanie odpowiedniej metody pomiarowej.

Błędy przypadkowe

Występują także przy wszystkich pomiarach, są też

niewielkie. Są one najczęściej powodowane przez
niedoskonałość zmysłów obserwatora.

Na podstawie wielkiej liczby doświadczeń stwierdzono następujące
właściwości błędów przypadkowych:

-prawdopodobieństwo popełnienia błędu małego jest większe od
prawdo
podobieństwa popełnienia błędu dużego,

-liczba błędów ze znakami dodatnimi równa się w przybliżeniu
liczbie błędów ze znakami ujemnymi,

-wystąpienie błędów o tych samych wartościach, lecz o znakach
przeciwnych,
jest równie prawdopodobne,

-wartość błędów nigdy nie przekracza pewnej wartości granicznej
będącej
funkcją precyzji użytego narzędzia i doskonałości metody pomiaru.

Zatem, błędy przypadkowe są niewielkie, nieuchwytne i z różnymi
znakami.

Wśród błędów przypadkowych wyróżniamy

-

błędy prawdziwe

-

pozorne.

Błąd prawdziwy jest to różnica między prawdziwą

wartością X mierzonej wielkości a wartością spostrzeganą
1, zatem:

E = X-1

Wielkość prawdziwa jest czasami znana (np. suma kątów w

trójkącie), jednak najczęściej z braku jej znajomości poprzestajemy
na wyznaczeniu najbardziej prawdopodobnej wartości x na
podstawie n-krotnej liczby obserwacji.

W wyniku tego możemy obliczyć błędy pozorne zamiast

błędów prawdziwych, czyli:

v = x – 1

Znając wartość najbardziej prawdopodobną możemy obliczyć,

z jaką dokładnością dokonano pomiarów i z jaką dokładnością
określono wartość najbardziej prawdopodobną:

[ vv ] = min gdy obserwacje są wykonane z tą samą
dokładnością

[ pvv ] = min gdy obserwacje mają rożne
dokładności

Na podstawie teorii rachunku prawdopodobieństwa błędy

przypadkowe podlegają następującym prawom:

1. prawdopodobieństwo popełnienia błędu małego jest większe,

aniżeli prawdopodobieństwo pojawienia się błędu dużego:

2. prawdopodobieństwo popełnienia błędu o tej samej wartości, ale

o różnych znakach, jest jednakowe;

3. największe prawdopodobieństwo pojawienia się w szeregu

spostrzeżeń ma błąd równy zero

4. błąd maksymalny nigdy nie przekracza określonej granicy.

Z tych naturalnych założeń wywodzi się prawo rozkładu błędów,
wyrażone wzorem Gaussa-Laplace’a o postaci

gdzie:
e = 2.7182 - podstawą logarytmów naturalnych,
h - stalą charakteryzująca precyzję, z jaką wykonano pomiary.
Wzór określa, z jakim prawdopodobieństwem () występuje błąd

przypadkowy s..

Prawdopodobieństwo popełnienia błędu przypadkowego s w
określonym Przedziale zależy od przyjętej funkcji P(s) rozkładu
błędów oraz interwału Jeżeli przyjmujemy, że s - de = a oraz s + de
= b. otrzymamy:

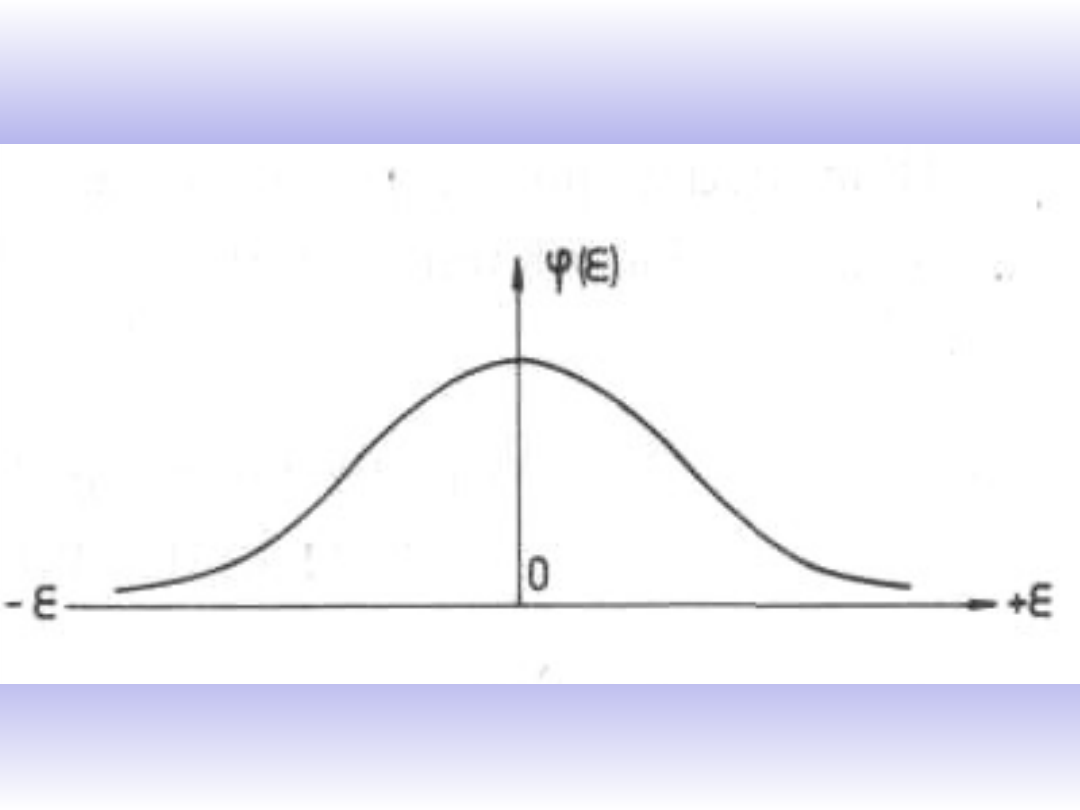
Krzywa rozkładu Gaussa

POMIARY KĄTÓW

POZIOMYCH I

PIONOWYCH

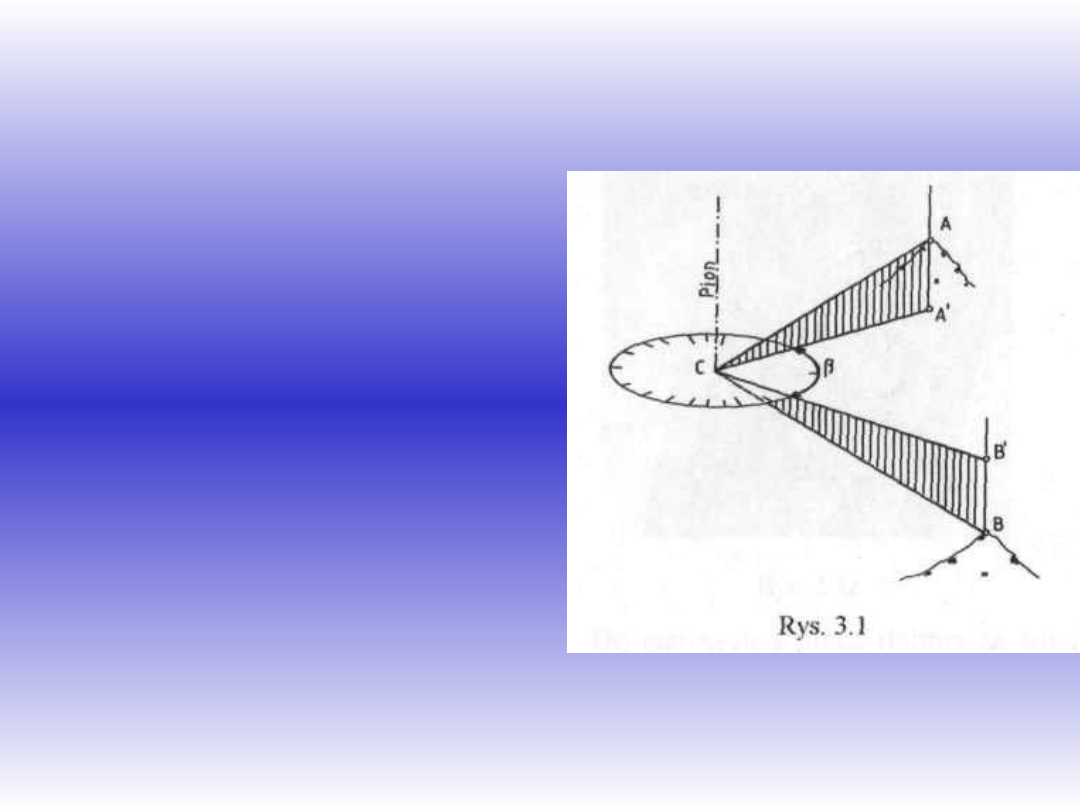
Kątem poziomym  -

nazywamy kąt dwuścienny
utworzony

przez

dwie

płaszczyzny

pionowe

przechodzące przez dwa
kierunki

wychodzące

z

jednego punktu

Miarą

kąta

dwuściennego jest kąt płaski
między rzutami kierunków
na płaszczyznę poziomą.

Definicje kątów:

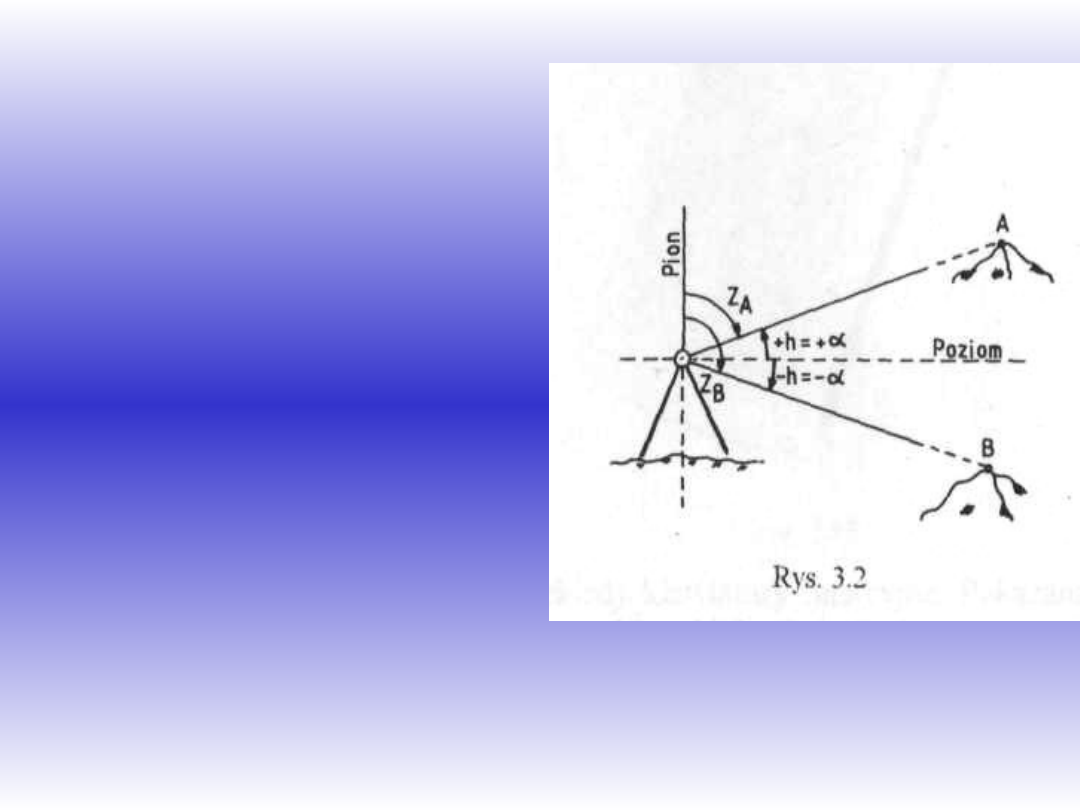
Kątem pionowym



-

będziemy nazywali kąt
zawarty między danym
kierunkiem a jego rzutem
na płaszczyznę poziomą
zwaną horyzontem
instrumentu.

Kąt pionowy jest

dodatni, gdy dany kierunek
znajduje się nad
płaszczyzną poziomą, a
ujemny, gdy leży poniżej
płaszczyzny poziomej.

Warunki geometryczne które powinien
spełniać instrument przed rozpoczęciem
pomiarów:

1. Oś libelli alidadowej powinna być prosto
padła do osi obrotu instrumentu (warunek

libelli).

2. Oś celowa powinna być prostopadła do osi
obrotu lunety (warunek kolimacji).

3. Oś obrotu lunety powinna być prostopadła
do osi obrotu instrumentu (warunek inklinacji).

4. Przy poziomej osi celowej odczyty na kole
pionowym powinny wynosić 0° i 180° (0

g

i 200

g

)

lub 90° i 270° (100

g

i300

g

).

Przygotowanie teodolitu do
pomiaru

Kąty poziome mierzy się pomiędzy kierunkami trwale oznaczonymi w
terenie.Należy zasygnalizować końce obu ramion kąta za pomocą tyczek
mierniczych bądź za pomocą tarcz celowniczych ustawionych na statywach.
Nad wierzchołkowym punktem kąta ustawia się teodolit na statywie.

•       

 

ustawiamy instrument w przybliżeniu nad punktem za pomocą

pionu sznurkowego.

•       za pomocą trzech śrub nastawczych naprowadzamy znaczek pionu

optycznego na centr

znaku naziemnego,

•         wbijając nogi statywu w ziemię lub zmieniając ich długość,

doprowadzamy libellę

okrągłą do górowania,

•         wykonujemy dokładne poziomowanie libelli rurkowej za pomocą

trzech śrub

nastawczych.

•         sprawdzamy, czy znaczek pionu optycznego nie zszedł z punktu,

jeżeli tak.

to po odkręceniu śruby sprzęgającej przesuwani)' teodolit na głowicy

statywu do

momentu, aż znaczek pionu optycznego znajdzie się nad punktem.

• sprawdzamy i ewentualnie korygujemy spoziomowanie instrumentu.

Pomiar pojedynczego kąta poziomego :

•

Po wycelowaniu w I położeniu lunety na cel lewy sprzęgamy

alidadę z kołem poziomym i naprowadzamy nitkę pionową dokładnie
na cel za pomocą leniwki.

Jeżeli celujemy na tyczkę, staramy się ustawić krzyż nitek jak

najniżej, u dołu tyczki!

•

Wykonujemy odczyt O‘l1 i zapisujemy go w formularzu.

Wykonując pól obrotu leniwką, wyprowadzamy krzyż nitek z celu i
ponownie go naprowadzamy oraz dokonujemy odczytu O”

ll

.

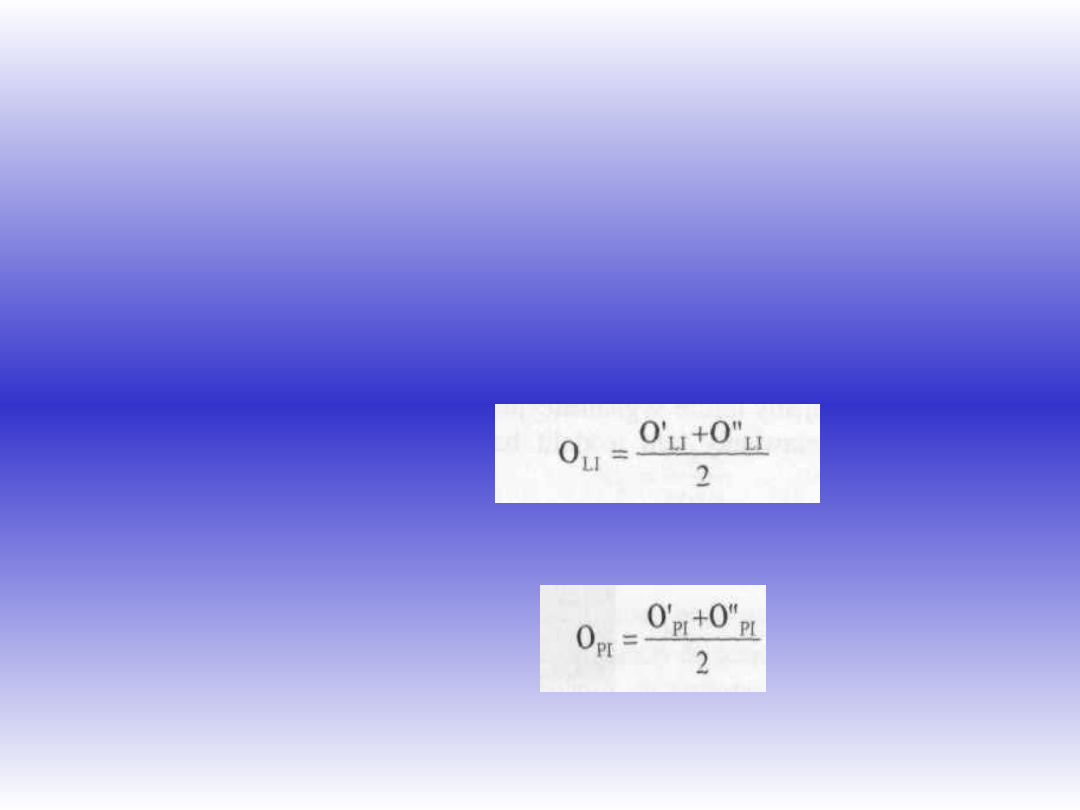
Obliczamy średnia wartość odczytu:

•

Następnie celujemy na punkt prawy, ustawiamy jego ostrość

i postępując tak

samo jak przy punkcie lewym, odczytujemy O”

ll

.Stąd

średni odczyt:

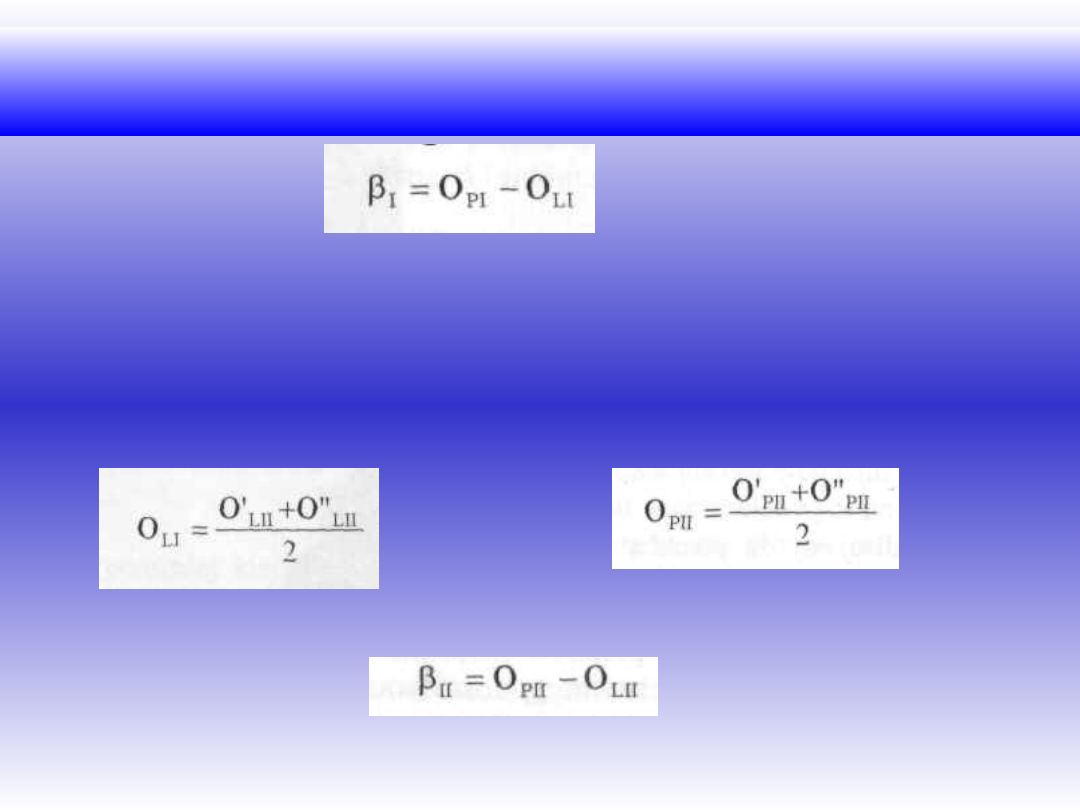
4. Obliczamy wartość kąta w I położeniu lunety. Z uwagi na to, że podział
kątowy rośnie zgodnie z ruchem wskazówek zegara

5. Przerzucamy lunetę przez zenit rozpoczynamy pomiar w drugim
położeniu od wycelowania do punktu lewego. Wykonujemy i zapisujemy
dwa odczyty O‘

LII

i O„pII i obliczamy odczyt średni:

oraz

Ten kąt jest wolny od wpływu błędów instrumentalnych,

w szczególności kolimacji i inklinacji.

czyli
:

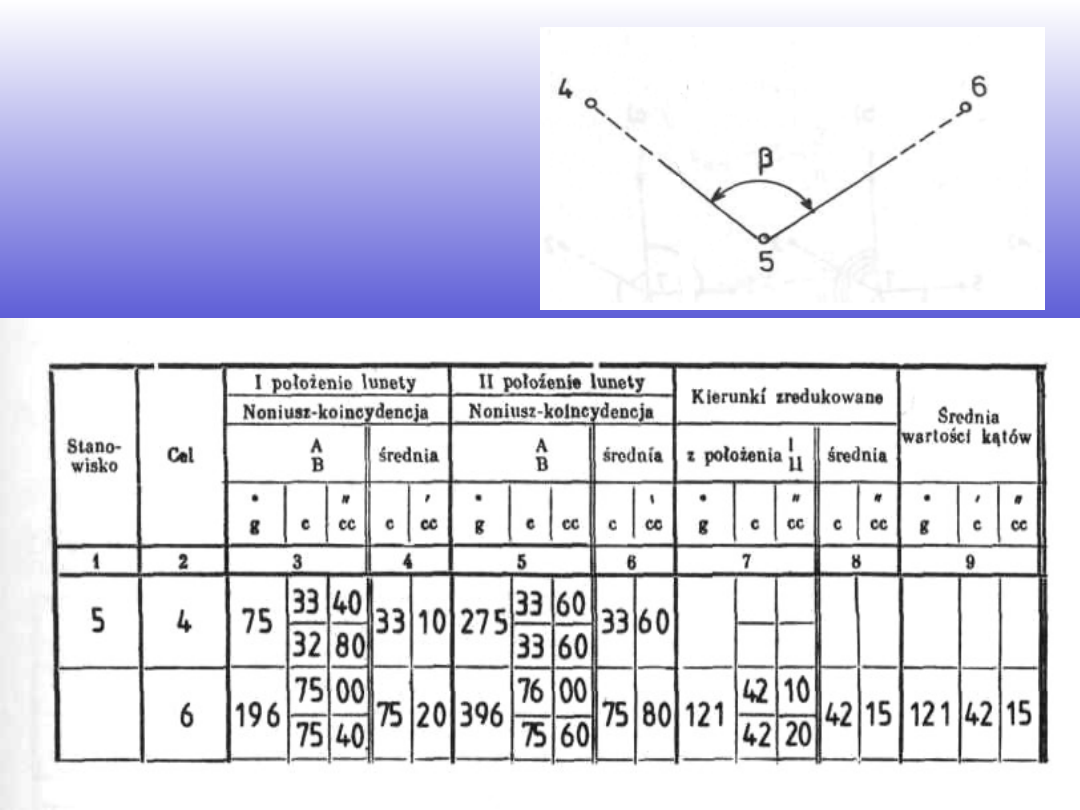
Przykład pomiaru pojedynczego kąta:

Zapis i obliczenia:

Pomiar kilku kątów metodą

kierunkową:

Metodę kierunkową stosujemy wówczas, gdy z

wierzchołka kąta wychodzi pęk promieni i należy określić
kąty między nimi.

W pierwszej kolejności dokonuje się pomiaru

kierunków, a następnie stosownie do potrzeb oblicza się
kąty między kierunkami

.

1. Jako początkowy kierunek wybieramy daleki punkt, najlepiej
leżący w północnej części widnokręgu.

2. Pomiar rozpoczynamy w I położeniu lunety od punktu 1,
następnie poprzez punkty 2, 3, 4,5, po czym powtórnie celujemy
na punkt 1.

Różnica odczytów początkowego i końcowego na punkcie
pierwszym powinna się mieścić w granicach dopuszczalnych dla
danego instrumentu, tzn. w granicach błędów celowania i
odczytywania. Różnica ta nosi nazwę odchyłki zamknięcia
horyzontu.
Stanowi ona kontrolę, czy w czasie pomiarów instrument nie
został poruszony lub czy nie oddziaływały na niego czynniki
atmosferyczne (np. skręty statywu pod wpływem słońca).

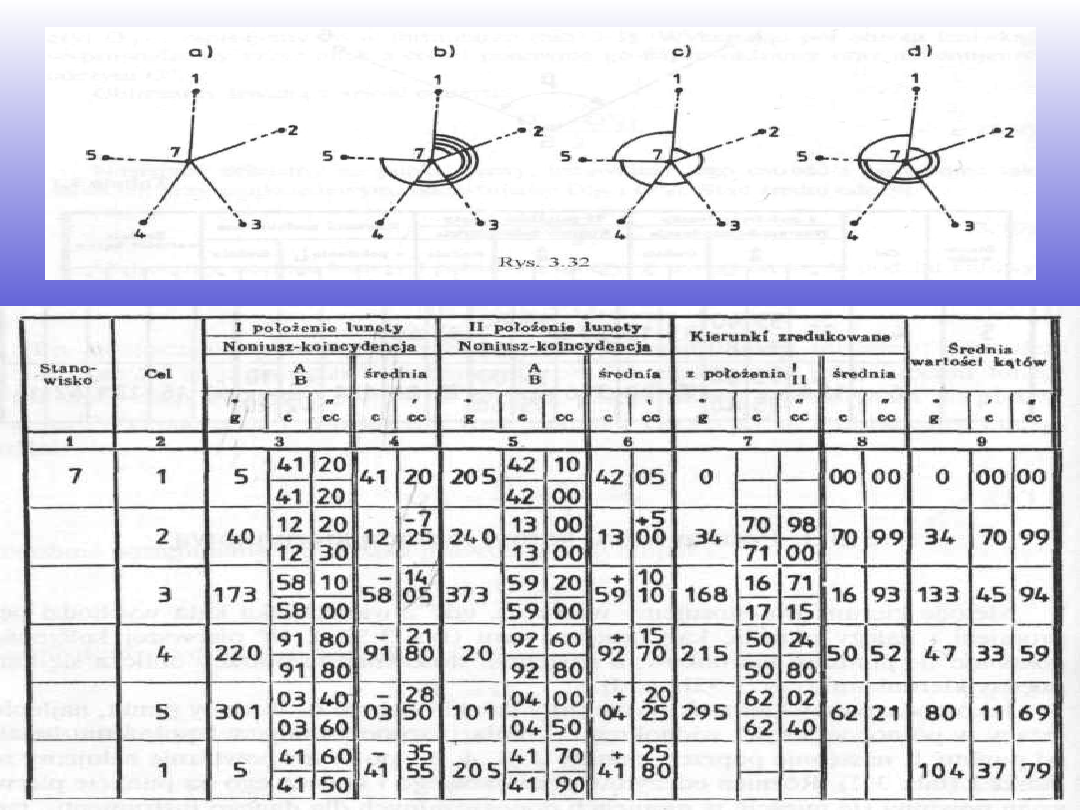
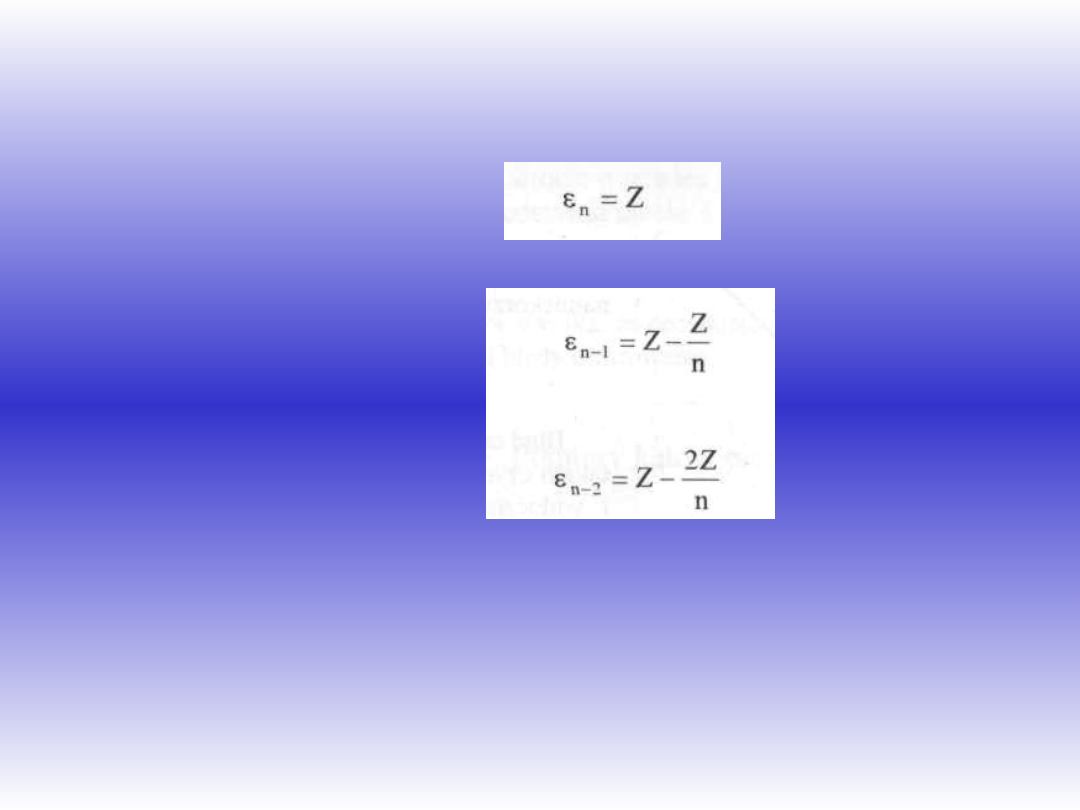
Odchyłkę zamknięcia horyzontu Z

r

o ile nie przekroczy podwójnego

nominalne go błędu różnicy kierunków (dla Theo 020 mamy: m

k

« 15

CC

, czyli

Z

max

= 42

CC

, patrz rozdz. 3.5). rozrzucamy proporcjonalnie do numerów

kierunków. Kierunek zamyka-

kierunek przedostatni:

itd. przy czym n jest liczbą kierunków

Pierwszy kierunek nie otrzymuje żadnej poprawki. Jeżeli odchyłka
zamknięcia horyzontu przekracza wartość Z

max

, pomiar należy powtórzyć.

Po wykonaniu pomiaru w I położeniu lunety w podobny sposób postępuje się
przy II położeniu lunety. Między I i II położeniem, a także między seriami,
można poprawić poziomowanie i centrowanie instrumentu oraz sygnałów.
Kąty poziome oblicza się najczęściej względem pierwszego kierunku, dla
którego przyjmuje się wartość 0

9

00

c

00

tc

. Można również obliczać kąt}'

poziome między kierunkami, za leżnie od potrzeb, w innych kombinacjach.

ANALIZA BŁĘDÓW WYSTĘPUJĄCYCH PRZY POMIARZE
KĄTÓW POZIOMYCH

Błędy można podzielić na trzy grupy:

1. Błędy instrumentalne:

a)      błąd poziomowania instrumentu,
b)     kolimacja i inklinacja,
c)      mimośrody alidady i osi celowej,
d)     błąd podziału limbusa.

2. Błędy ustawcze instrumentu i sygnałów:

a)        błąd centrowania instrumentu,
b)       błąd niecentrycznego ustawienia tyczek

(sygnałów).

3. Błędy wykonania samego pomiaru:

a)       błąd celowania,
b)      błąd odczytu limbusa.

Błąd poziomowania instrumentu jest istotny tylko przy stromych

celowych. Właściwie dobrana przewaga libeli alidadowej i dokładne
poziomowanie gwarantują uzyskanie odpowiedniej dokładności

Wpływ błędów instrumentalnych l b i c eliminujemy przez

podwójny pomiar kąta w dwóch położeniach lunety. Inne błędy
instrumentalne są mało znaczące w teodolitach o małej lub średniej
dokładności

Natomiast, błędy centrowania instrumentu i niecentrycznego

ustawienia sygnałów znacznie zmniejszają dokładność pomiaru
kątów.

Błąd odczytu limbusa jest także przypadkowy i zależy w teodolicie z

mikroskopem odczytowym od podziału skali naniesionej na płytkę ogniskową
mikroskopu - w mikroskopach skalowych - lub od podziału limbusa -w
mikroskopach kreskowych.

Błąd średni odczytu przy pomiarze kierunku w jednym położeniu lunety

jest dość znaczny i waha się na ogół w granicach od 0,1 do 0,15
elementarnej działki skali lub limbusa.

Z analizy poszczególnych błędów występujących przy pomiarze

kątów wynika, że największy wpływ na dokładność pomiarów
wywierają:

-     błąd centrowania instrumentu,
-     błąd niecentrycznego ustawienia tyczek,
-     błąd odczytu limbusa.

W teodolitach o dużej dokładności odczytów - ok. 10" - przy

pomiarze kątów poziomych należy uwzględniać także błąd celowania.

POMIARY LINIOWE

ZAKRES POMIARÓW LINIOWYCH

Dziedzina pomiarów liniowych
obejmuje metody wyznaczania
odległości między punktami w
terenie. W zależności od
konkretnego zastosowania celem
pomiaru jest określenie odległości
poziomej lub ukośnej

PODZIAŁ POMIARÓW LINIOWYCH

METODY

• Bezpośrednie
• Pośrednie
• Metody wykorzystujące dalmierze

METODY POŚREDNIE POMIARÓW LINIOWYCH

• obejmują metody pozwalające na

określenie długości danego odcinka
na podstawie wyznaczenia innych
wielkości liniowych

• wykonywane za pomocą innych

wielkości,
które z szukaną długością pozostają
w związku funkcyjnym

METODY BEZPOŚREDNIE POMIARÓW LINIOWYCH

•

pomiar taśmą lub innymi

przymiarami bezpośrednio w
terenie - wzdłuż odcinka, między
mierzonymi punktami

• przez kolejne przykładanie

przymiaru na wytyczonej prostej

METODY WYKORZYSTUJĄCE DALMIERZE

• Obejmują dużą gamę urządzeń i

sposobów zdalnego pomiaru
odległości

• System pomiarowy składa się z

dalmierza i urządzenia
retransmitującego emitowaną falę

Odległość wyznaczana jest na podstawie
wzoru:

L = v · t

v -

prędkość przebiegu fali

elektromagnetycznej między końcami
mierzonego odcinka

t -

czas przebiegu fali

elektromagnetycznej między końcami

mierzonego odcinka

TYPOWE SPOSOBY POMIARÓW ODLEGŁOŚCI I ICH

DOKŁADNOŚCI

METODA POMIARÓW
DŁUGOŚCI

BŁĄD WZGLĘDNY

ZMIERZONEJ DŁUGOŚCI

BŁAD PRZYPADAJĄCY NA

JEDNOSTKĘ DŁUGOŚCI

BEZPOŚREDNIA
Taśmą stalową o długości
20m lub 50m

Od 1/2000 do 1/5000

Od 5 do 2 cm / 100
metrów

Łatami poligonowymi o
długości 5m lub 3m

Od 1/5000 do 1/10000

Od 2 do 1 cm / 100
metrów

Drutami inwarowymi

Od 1/30000 do

1/1000000

Od 3 do 1 mm / 1km

POŚREDNIA
Optycznym dalmierzem
jednoobrazowym z łatą
pionową

Od 1/200 do 1/500

Od 50 do 20 cm / 100m

Optycznym dalmierzem
dwuobrazowym z łatą
poziomą

Od 1\2000 do 1\5000

Od 5 do 2 cm / 100m

Dalmierzem
elektooptycznym

Od 1\50000 do

1\1000000

Od 2 cm do 1mm / 1km

TECHNIKA WYKONANIA POMIARU

BEZPOŚREDNIEGO

Wymaga stosowania określonych zasad,
których spełnienia wymagają
geodezyjne instrukcje techniczne.
Najważniejsze z nich to odpowiedni
przebieg pomiaru i obliczeń. Należy
wykonać obliczenia obejmujące korektę
błędów (poprawki komparacyjna i
termiczna) oraz redukcję do poziomu i
ewentualną poprawkę odwzorowawczą.

ZASADY WYKONYWANIA POMIARÓW

BEZPOŚREDNICH

• Istotą pomiaru bezpośredniego jest wyznaczenie odległości za

pomocą urządzenia stanowiącego wzorzec odległości. Przed
przystąpieniem do zasadniczego pomiaru mierzoną linię należy
przetyczyć, czyli oznakować tyczkami wzdłuż prostej łączącej
jej końce.

• Stosuje się metody tyczenia: w przód, wstecz i ze środka.

Tyczenie wstecz stanowi specyficzną formę omawianej metody,
gdzie tyczkę ustawia się na przedłużeniu odcinka AB.
Tyczenie ze środka stosuje się wówczas, gdy warunki
terenowe uniemożliwiają wzajemną widoczność tyczek na
końcach odcinka. W takim przypadku dwie lub trzy osoby
ustawiają się w okolicach środka tyczonej linii i wprowadzają
się naprzemiennie wzdłuż osi wyznaczonej przez własną
tyczkę i jedną z tyczek końcowych.

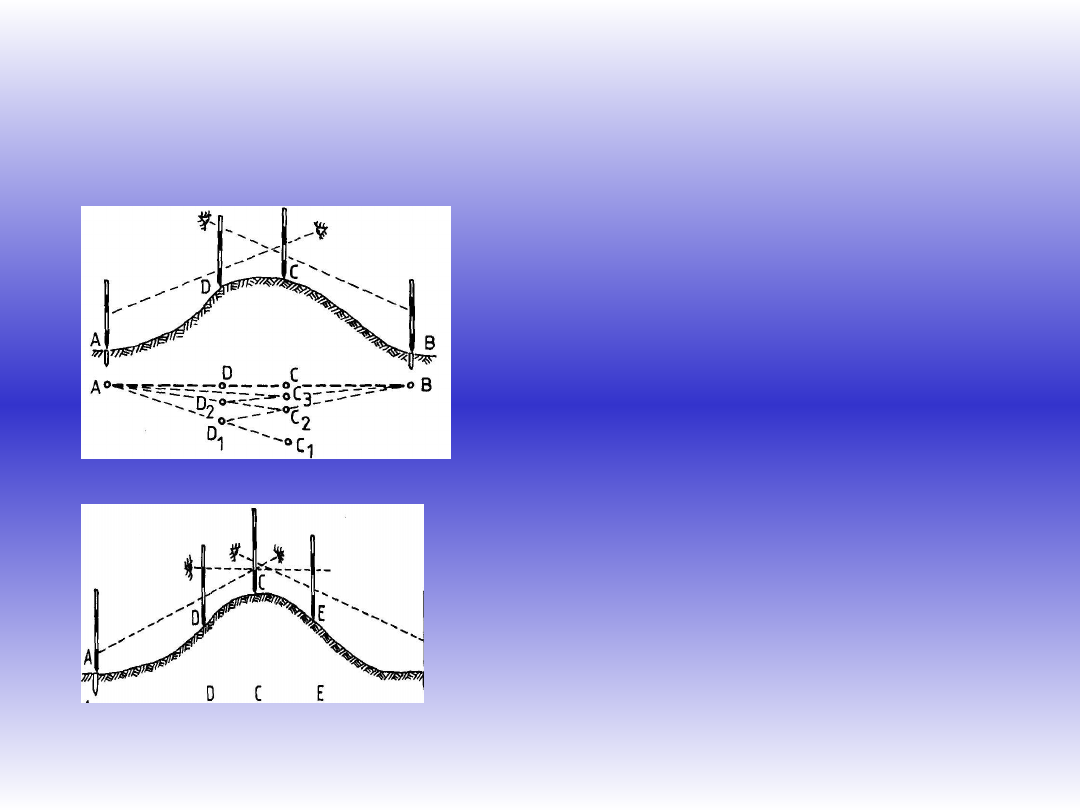
TYCZENIE ZE ŚRODKA

Może być wykonywane:

• Przez 2 osoby

• Przez 3 osoby

POMIAR ODLEGŁOŚCI TAŚMĄ STALOWĄ

Najczęściej do pomiaru długości używane są

taśmy stalowe 20-metrowe, rzadziej 50-metrowe.
Do taśmy należy komplet 11 stalowych szpilek o

długości 30-40 cm służących do zaznaczania

liczby odłożeń taśmy w terenie. Taśma jest

podzielona na metry i decymetry, co pozwala

szacować odczyty końcowe do 1 cm.
Po skończonym pomiarze nawija się taśmę na

metalową obręcz. Do sprzętu pomocniczego

należy ruletka stalowa służąca do pomiaru

domiarów prostokątnych.

ZASADY PRZEPROWADZANIA POMIARU

Przy pomiarze długości w terenie nierównym

każdorazowo sprowadzamy taśmę do poziomu,

zgodnie z zasadą, że każda długość ma być rzutem

na Płaszczyznę poziomą.
Pomiar długości w terenie nachylonym możemy w

związku z tym wykonać w dwojaki sposób:

1. Najczęściej każdorazowo sprowadzamy taśmę

do poziomu, rzutując jej koniec na teren za pomocą

pionu, jest to tzw. pomiar „schodkami”,

dokonywany zawsze z góry.

2. W terenie jednostajnie nachylonym mierzymy

długość wprost po terenie, wyznaczając przy tym

kąt nachylenia terenu za pomocą pochylnika lub na

kole pionowym teodolitu. Następnie obliczamy rzut

poziomy zmierzonego po pochyłości odcinka

Każda długość powinna być pomierzona

dwukrotnie, w terenie płaskim „tam” i „z
powrotem”, zaś w przypadku silniejszego
spadku terenu - zawsze w kierunku nachylenia
stoku. Różnica Δ d dwukrotnego pomiaru
długości przy użyciu szpilek nie powinna
przekraczać 1/2000 całej mierzonej długości

W wyniku dwukrotnego pomiaru długości

taśmą ze szpilkami w terenie dość trudnym
powinno się uzyskać dokładność rzędu 1/2 000
mierzonej długości (5 cm dla 100 m) terenie
łatwym 1/3 000 mierzonej długości (ok. 3 cm
na 100 m).

Wartość liniowa taśmy określona napisem i

kreskami na jej końcach nazywa się
długością nominalną taśmy. Jest to wartość
dla danej taśmy stała i wynosi np. 20 m.
Natomiast długość rzeczywista taśmy
wynika z porównania jej ze wzorcem w
określonej temperaturze, przy czym długość
ta zmienia się nieznacznie w zależności od
zmian temperatury otoczenia.

Każda taśma stalowa przed użyciem do

pomiaru powinna być skomparowana, czyli jej
długość porównana z wzorcem w ściśle
określonych warunkach w temperaturze

komparacji.

BŁĘDY WYSTĘPUJĄCE PRZY POMIARZE TAŚMĄ 20

METROWĄ ZE SZPILKAMI

• Nieuwzględnienie komparacji
• Zmiany temperatury
• Zwis taśmy
• Niewłaściwy naciąg taśmy
• Niedokładne układanie taśmy w linii
• Nierówności terenu
• Niedokładne przyłożenie taśmy do punktu

początkowego oraz do szpilek kolejno

wbijanych w teren

• Niedokładny odczyt
• Niedokładne odpionowanie końca taśmy w

terenie nierównym

• Niedokładne wbijanie szpilek w teren

CHARAKTERYSTYKA BŁEDÓW POMIARU TAŚMĄ

Jak wynika z przeglądu błędów występujących przy
pomiarze taśmą ze szpilkami uwzględniamy jedynie
błędy dotyczące poprawki komparacji, zmian
temperatury i nachylenia terenu, ale tylko w
niekorzystnych warunkach pomiaru a mianowicie
gdy:
( Δl

o

+ Δl

t

) > 5 mm albo gdy kąt nachylenia α >

1°.

Błędów przypadkowych nie możemy wyeliminować
z wyników pomiarów jedynie możemy osłabić ich
wpływ przez starannie wykonane kilkakrotne
pomiary.

POMIAR DŁUGOŚCI DALMIERZEM

ELEKTROOPTYCZNYM

W ostatnich latach, w pomiarach geodezyjnych
znalazły powszechne zastosowanie dalmierze
elektrooptyczne, które zastąpiły dotychczasowy
pracochłonny i żmudny pomiar długości, szczególnie
w trudnym terenie, szybkim pomiarem o dużej
dokładności. W dalmierzach tych zostały zastosowane
fale elektromagnetyczne, ściślej fale świetlne
widzialne o długościach ułamka mikrometru.
Dalmierz elektrooptyczny składa się z nadajnika,
urządzenia odbijającego, odbiornika i urządzenia
pomiarowego. Przy pomiarze odległości na jednym
końcu mierzonego boku ustawia się dalmierz
wyposażony w nadajnik - źródło modulowanego
światła - oraz odbiornik z urządzeniem odczytowym, a
na drugim końcu - system zwierciadeł odbijających.

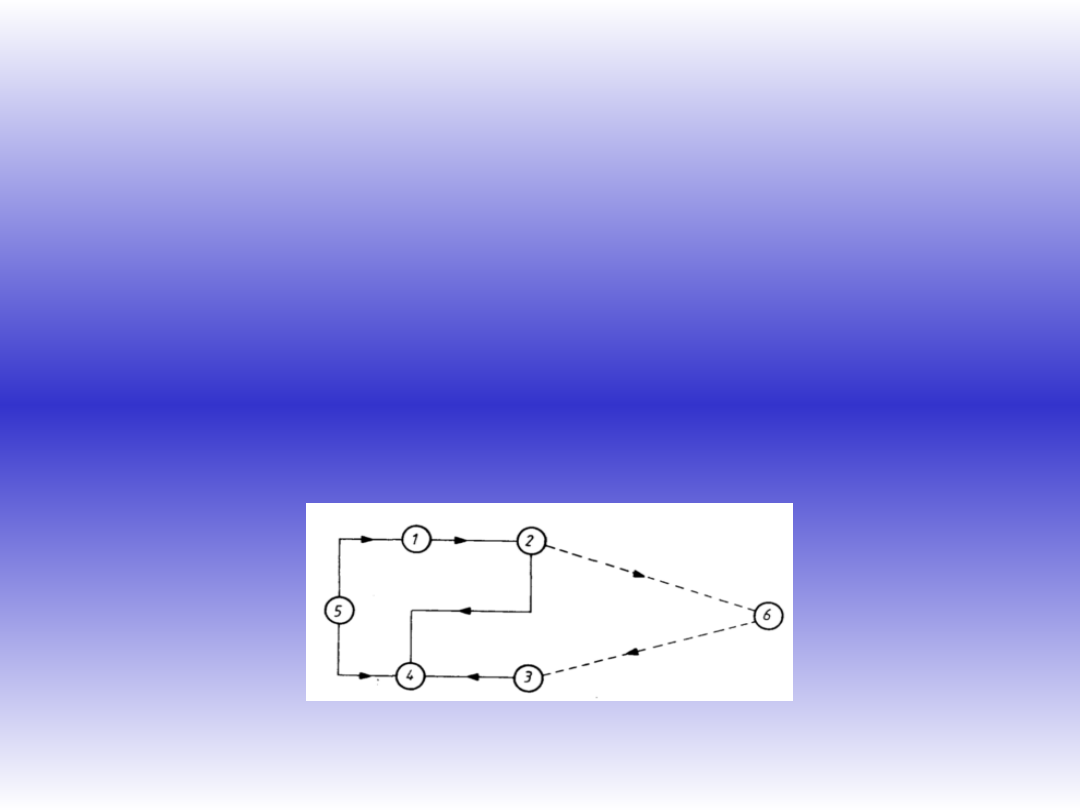
SCHEMAT DZIAŁANIA DALMIERZA

ELEKTROOPTYCZNEGO

Wychodząca ze źródła światła 1 wiązka promieni
świetlnych zostaje zmodulowana w aparaturze 2 i
przesłana w kierunku reflektora (układu zwierciadeł
lub pryzmatów) umieszczonego na końcu mierzonego
odcinka. Po odbiciu od układu pryzmatów 6 sygnał
falowy powraca do układu odbiorczego 3. Długość
boku określa się na podstawie przesunięcia fazowego
fali (różnicy faz fali wychodzącej i powrotnej)
następującego w urządzeniu pomiarowym 4, do
którego dochodzi fala wysyłana i odbita. Aparaturę
dalmierza zasila bateria lub akumulator 5.

OBLICZANIE DŁUGOŚCI FALI

Mierzona długość wynosi:

D = nl + r

gdzie:
l – długość fali w m
n – liczba pełnych ułożeń fali wzdłuż mierzonego

odcinka

r – długość odpowiadająca ostatniemu niepełnemu

ułożeniu fali

 

Wartość przesunięcia fazowego pozwala tylko
na określenie długości r. Całkowitą długość
odcinka otrzymuje się na podstawie pomiarów
przeprowadzonych na kilku częstotliwościach
fali.
Przesunięcie fazowe w tradycyjnych
dalmierzach określa obserwator, a w nowszych
jest ono określane automatycznie. Nowsze
dalmierze redukują mierzone odległości do
poziomu, a także wyświetlają wynik pomiaru
określonego boku na ekranie systemu
odczytowego. W większości dalmierzy istnieje
możliwość pomiaru kątów na stanowisku.