str. 1

P O L I T E CH N I K A P O Z N A Ń S K A

Wydział Technologii Chemicznej

Instytut Technologii i Inżynierii Chemicznej

Zakład Inżynierii i Aparatury Chemicznej

PROJEKT Z ELEMENTÓW AUTOMATYKI I POMIARÓW W

TECHNOLOGII CHEMICZNEJ

Rok akademicki

2012/2013

Rok studiów

IV

Nr referatu

1

Data oddania

15.11.2012

Wykonał

Sprawdził

Zwrot

Ocena

Marta Martyła

Joanna Lewandowska

mgr inż.

K. Stachurska

TEMAT REFERATU

METROLOGIA, BŁĘDY POMIARÓW I METODY POMIAROWE

UWAGI

str. 2

1. METROLOGIA

Metrologia i inżynieria pomiarowa obejmują obszary wiedzy i działalności człowieka,

odnoszące się do teorii i praktyki pomiarów, niezależne od stosowanych technik i

wymaganej dokładności. Zajmuje się sposobami dokonywania pomiarów oraz zasadami

interpretacji uzyskanych wyników. W przeciwieństwie do obserwacji zjawisk lub ciał

fizycznych prowadzących do subiektywnych wniosków jakościowych, wynikiem pomiaru

jest przeważnie ocena ilościowa.

Do intensywnego rozwoju współczesnej metrologii przyczyniły się rewolucyjne

przemiany w sferze technologii. Komputerowo wspomagane systemy pomiarowe,

wyspecjalizowane czujniki wielkości elektrycznych i nieelektrycznych, na bazie

mikromechaniki krzemowej (w tym tzw. czujniki inteligentne) znamionują charakter

obecnych prac w zakresie teorii i praktyki pomiarów.

W różnych gałęziach nauki i przemysłu, ochrony zdrowia i życia codziennego istnieje

zapotrzebowanie na zaawansowane i komercyjne zastosowania technik pomiarowych,

obejmujące:

- pomiary wielkości elektrycznych i nieelektrycznych

- tradycyjne i najnowsze metody i sposoby przetwarzania sygnałów

- wykorzystanie technik telekomunikacyjnych i informacyjnych oraz Internetu

- zintegrowane i inteligentne czujniki pomiarowe

- projektowanie, konstruowanie, uruchamianie oraz badania analogowych i cyfrowych

urządzeń pomiarowych

- właściwą eksploatację aparatury pomiarowej

- tworzenie struktur i organizację skupionych oraz rozproszonych systemów

pomiarowych.

Można wyróżnić następujące rodzaje metrologii:

a) Ogólną – obejmuje zagadnienia wspólne dla wszystkich dziedzin zastosowań

pomiarów (np. błędy pomiarowe, układy jednostek miar)

b) Stosowaną – zajmuje się praktycznym zastosowaniem pomiarów (np. w handlu:

ważenie, określenie objętości cieczy)

c) Naukową - zajmuje się teoretycznymi zagadnieniami pomiarów (np. ogólna teoria

pomiarów, teoria wielkości)

str. 3

d) Prawną – zajmuje się zagadnieniami odnoszącymi się do jednostek miar, metod

pomiarów i narządzi pomiarowych z punktu widzenia urzędowo ustalonych

wymagań technicznych i prawnych.

Podstawą metrologii są jednostki miar. Jednostki grupowane są w układy. Obecnie

najpowszechniej używanym standardem jest układ SI.

Jednostką nazywamy określoną miarę danej wielkości służącą za miarę

podstawową, czyli wzorzec ilościowego wyrażania innych miar danej wielkości

metodą porównania tych miar za pomocą liczb. Wartość liczbowa takiej miary

podstawowej wynosi jeden, stąd jej nazwa – jednostka miary. Konkretne wartości

wielkości można przedstawić zarówno wielokrotnościami, jak i ułamkami jednostek, a

same wartości, o ile to możliwe, mogą być zarówno dodatnie i ujemne.

2. BŁĘDY POMIAROWE

Pojęcie pomiaru przechodziło dość długą ewolucję. Wstępnie przyjmuje się, że

pomiar jest procesem doświadczalnym prowadzącym do znalezienia wartości

wielkości mierzonej, a ogólna definicja pomiaru brzmi:

Pomiar jest procesem doświadczalnym, prowadzącym do otrzymania

informacji o wartości wielkości mierzonej w formie najwygodniejszej do

wykorzystania, z punktu widzenia celu, jakiemu ma służyć.

Współcześnie w pojęciu pomiaru uwzględniono przyjmowane jako pewnik

stwierdzenie, że w czasie pomiaru występują błędy.

Błędem pomiaru nazywamy algebraiczną różnicę między wynikiem pomiaru, a

wartością prawdziwą wielkości mierzonej. W praktyce zamiast nieznanej wartości

stosuje się znaną wartość umownie prawdziwą.

Aby pojęcie błędu miało dla nas praktyczne znaczenie konieczne jest

wyrażenie go liczbą. Liczbowo błąd określamy jako różnicę pomiędzy otrzymanym

wynikiem, a wartościa stanowiącą wystarczające dla danego celu przybliżenie

wartości rzeczywistej. Tę wartość przybliżoną nazywamy wartością poprawną.

Wartość poprawna równa jest wartości rzeczywistej wówczas, gdy dotyczy wzorca

przyjętego za jednostkę miary.

str. 4

Wzór na obliczanie błędu ma postać:

e = V

i

- V

c

gdzie:

V

i

– wynik pomiaru o rzeczywistej wartości V

V

c

– wartość poprawna równa wartości rzeczywistej V lub stanowiąca

dostateczne jej przybliżenie.

Obliczony wg powyższego wzoru błąd ma jednostkę (miano) odpowiadającą

jednostce wielkości mierzonej i nosi nazwę błędu bezwzględnego.

Pod względem natury i zachowania się przy powtarzaniu pomiarów błędy

podzielono na trzy rodzaje

a) Systematyczne – błąd który przy wielu pomiarach tej samej wartości

pewnej wielkości, wykonany w tych samych warunkach, pozostaje stały

zarówno co do wartości bezwzględnej, jak i co do znaku lub zmienia się

według określonego prawa wraz ze zmianą warunków. Określony błąd

systematyczny obliczony lub wyznaczony doświadczalnie można

wyeliminować przez wyznaczenie odpowiedniej poprawki, tj. wartości,

którą należy algebraicznie dodać do surowego wyniku pomiaru w celu

otrzymania wyniku poprawionego. Natomiast błędy systematyczne,

których nie można wyznaczyć, a których wartość w porównaniu z

niedokładnością pomiaru jest uważana za dostatecznie małą, należy

traktować, jako błędy przypadkowe.

b) Przypadkowe – błąd zmieniający się w sposób nieprzewidziany, zarówno

co do wartości bezwzględnej, jak i znaku, przy wykonaniu dużej liczby

pomiarów, pewnej wielkości w warunkach praktycznie niezmiennych.

Błędu przypadkowego nie można uwzględnić jako poprawki, można tylko

na podstawie serii pomiarów, wykonywanych w tych samych warunkach,

ustalić z określonym prawdopodobieństwem granicę, których ten błąd nie

przekroczy.

c) Nadmierne (grube) – są to wszelakiego rodzaju omyłki popełnione podczas

pomiarów. A więc należeć tu będą pomyłki w odczytywaniu wskazań

narzędzi pomiarowych (np. przesunięcie wyniku o jedną działkę), omyłki

rachunkowe, itp.

str. 5

Model matematyczny procedury pomiarowej, który transformuje zbiór

powtórzonych obserwacji wyniku pomiaru, ma szczególne znaczenie, ponieważ

zwykle, oprócz wyników obserwacji, zawiera także różne wielkości wpływające, które

nie są dokładnie znane. Ten brak informacji, wraz ze zmiennością powtarzalnych

informacji i niepewnością związaną z jako takim modelem matematycznym wpływa

na niepewność pomiaru.

Niepewność pomiarowa to parametr związany z wynikiem pomiaru,

charakteryzujący rozrzut wielkości, które można w uzasadniony sposób przypisać

wielkości mierzonej. Takim parametrem może być np. wielokrotność odchylenia

standardowego.

Wyróżniamy różne rodzaje niepewności pomiaru:

a) Standardowa – niepewność wyniku pomiaru wyrażona w formie

odchylenia standardowego

b) Standardowa złożona – niepewność standardowa wyniku pomiaru

określona, gdy wynik ten jest otrzymany z wartości pewnej liczby innych

wielkości. Jest ona równa pierwiastkowi kwadratowemu z sumy wyrazów

będących wariancjami lub kowariancjami tych innych wielkości, z wagami

zależnymi od tego jak wynik pomiaru zmienia się wraz ze zmianami tych

wielkości

c) Rozszerzona – wielkość określająca przedział wokół wyniku pomiaru,

obejmujący dużą część rozkładu wartości, który w uzasadniony sposób

można przypisać wielkości mierzonej. Ułamek określający tę część można

traktować jako prawdopodobieństwo objęcia lub poziom ufności tego

przedziału.

str. 6

3. METODY POMIAROWE

Logiczny ciąg (algorytm) wykonywanych podczas pomiaru operacji, opisanych

w sposób ogólny nosi nazwę metody pomiarowej.

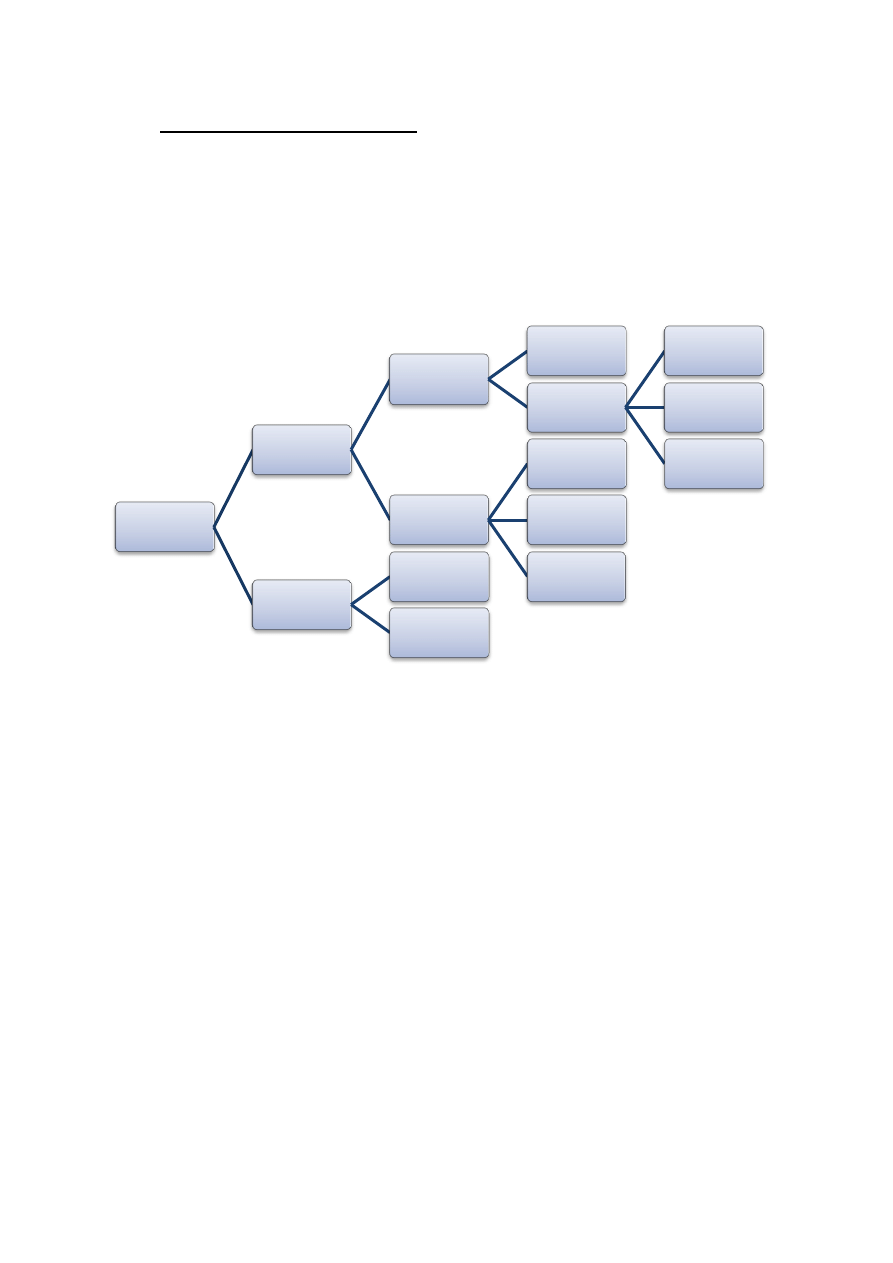
W ramach pierwszego podstawowego podziału rozróżnia się metody

pomiarowe pośrednie i bezpośrednie (schemat 1).

Schemat 1. Podział metod pomiarowych.

3.1.

Metody pośrednie

Metoda pośrednia polega na bezpośrednim pomiarze innej wielkości,

związanej z wielkością szukaną znaną zależnością. Z zależności tej wyznacza się

wartość X mierzonej wielkości:

X = f(A, B, C, …)

gdzie: A, B, C, … - to wielkości mierzone bezpośrednio.

Metody pośrednie są powszechnie stosowane w praktyce pomiarowej, a

zwłaszcza w pomiarach długości i kąta.

Metody pośrednie są najczęściej stosowane w postaci klasycznej zdefiniowanej

powyżej. Przykładem wykorzystanie tej metody może być pomiar natężenia

METODY

POMIAROWE

BEZPOŚREDNIE

PORÓWNAWCZE

WYCHYLENIOWA

RÓŻNICOWA

KLASYCZNA

ZEROWA

KOICYDENCYJNA

BEZPOŚREDNIEGO

PORÓWNANIA

KLASYCZNA

PRZEZ

PODSTAWIENIE

PRZEZ

PRZESTAWIENIE

POŚREDNIE

KLASYCZNA

PODSTAWOWA

str. 7

przepływu cieczy, który odbywa się na podstawie pomiaru objętości przepływającej

cieczy i czasu.

Szczególnym przypadkiem metody pomiarowej pośredniej jest metoda

podstawowa (bezwzględna). Polega ona na pomiarach wielkości podstawowych,

zawartych w definicji tej wielkości. Przykładem wykorzystania omawianej metody

może być pomiar pola trójkąta ABC zdefiniowanego, jako iloczyn długości dwóch

boków i sinusa kąta między nimi zawartego, na podstawie ustalenia wartości długości

tych boków i kąta.

3.2.

Metody bezpośrednie

Metody bezpośrednie, najczęściej stosowane w metrologii, dzielą się na dwie

grupy:

a) Metody porównawcze – polegają na porównaniu wartości wielkości mierzonej z

inną wartością tej samej wielkości lub ze znaną wartością innej wielkości, jako

funkcji wielkości mierzonej. Przykładem jej zastosowania jest pomiar

chropowatości powierzchni za pomocą przyrządu pneumatycznego polegający na

porównaniu wskazań przyrządu na powierzchni mierzonej i wzorcowej. Rodzaje:



Wychyleniowa – polega na określeniu wartości wielkości mierzonej, przez

wychylenie urządzenia wskazującego. Z definicji wynika, że tą metodą

najczęściej wykonuje się pomiary, gdyż zdecydowana większość narzędzi

pomiarowych jest wyposażona w analogowe, bądź cyfrowe urządzenia

wskazujące



Różnicowa – oparta na porównaniu wartości wielkości mierzonej z

niewiele różniącą się od niej znaną wartością tej samej wielkości i

pomiarze różnicy tych wartości. Dzieli się na:

 Zerowa – polega na sprowadzeniu do zera różnicy między

wartością wielkości mierzonej X, a wartością znaną X

p

, tej samej

wielkości z nią porównywaną według zależności

X – X

p

= α

jeżeli α = 0, to X = X

p

Przykładem tej metody jest pomiar masy materiałów sypkich za

pomocą wagi uchylnej oraz odważnika o znanej masie.

str. 8

 Koincydencyjna – polega na wyznaczeniu przez obserwację

koincydencji i pewnych wskazów lub sygnałów małej różnicy

między wartością wielkości mierzonej i z nią porównywanej

wartości znanej tej samej wielkości. Przykład: pomiar długości

przedmiotu za pomocą suwmiarki z noniuszem.

b) Metody bezpośredniego porównywania – polegają na porównywaniu całkowitej

wartości wielkości mierzonej z wartością znaną tej samej wielkości, która w

postaci wzorca wchodzi bezpośrednio do pomiarów. Wśród tych metod (oprócz

metody klasycznej) wyróżniamy:



Metoda pomiarowa przez podstawienie – polega na zastąpieniu wartości

wielkości mierzonej wartością znaną tej samej wielkości, wybraną w ten

sposób, aby skutki wywołane przez te dwie wartości były takie same.

Przykład: wyznaczenie masy za pomocą wagi i odważników.



Metoda pomiarowa przez przestawienie – polega na zróżnicowaniu

wartości wielkości mierzonej, najpierw ze znaną wartością A, tej samej

wielkości, następnie na podstawieniu wielkości mierzonej na miejsce A i

ponownym zrównoważeniu jej ze znana wartością B tej samej wielkości.

Przykład: pomiar długości za pomocą przyrządu z podziałką, pomiar

objętości cieczy za pomocą menzurki.

4.

LITERATURA:

 Senczyk D., Podstawy teorii pomiarów, Wydawnictwo PP, Poznań 2003.

 Cysewska-Sobusiak A., Podstawy metrologii i inżynierii pomiarowej,

Wydawnictwo PP, Poznań 2010.

 Rakowiecki J., Podstawy metrologii, Państwowe Wydawnictwo Szkolnictwa

Zawodowego, Katowice 1972.

 Adamczuk S., Makieła Wł., Podstawy metrologii i inżynierii jakości dla

mechaników, Wydawnictwa Naukowo-Techniczne, Warszawa 2010.