Materiał pomocniczy cz. 1 (poprawkowa)

1.Minimalizacja DAS

Opis postępowania:
a)Eliminujemy stany do których nie możemy dotrzeć ze stanu
początkowego (jeśli takie istnieją)
b)Identyfikujemy zbiory (bloki) stanów równoważnych (poprzez
tablicę rozróżnialności) a następnie budujemy nowy DAS w oparciu o
te bloki (każdy blok/zbiór traktujemy jako jeden stan)

Konstrukcja tablicy rozróżnialności:
I.Każda para stanów (p,q) gdzie p jest stanem akceptującym a q jest
nieakceptującym jest rozróżnialna.
II.Indukcyjnie: jeżeli p i q są rozróżnialną parą stanów, oraz p=(r,a) i

q= (s,a) (gdzie a – dodolwny symbol z alfabetu minializowanego

DAS; r,s – inne stany) wówczas para (r,s) jest rozróżnialna.
przykład:
rozważmy następujący DAS:

stan

pobierane

symbole / nowy

stan

0

1

A

B

A

B

A

C

C

D

B

*D

D

A

E

D

F

F

G

E

G

F

G

H

G

D

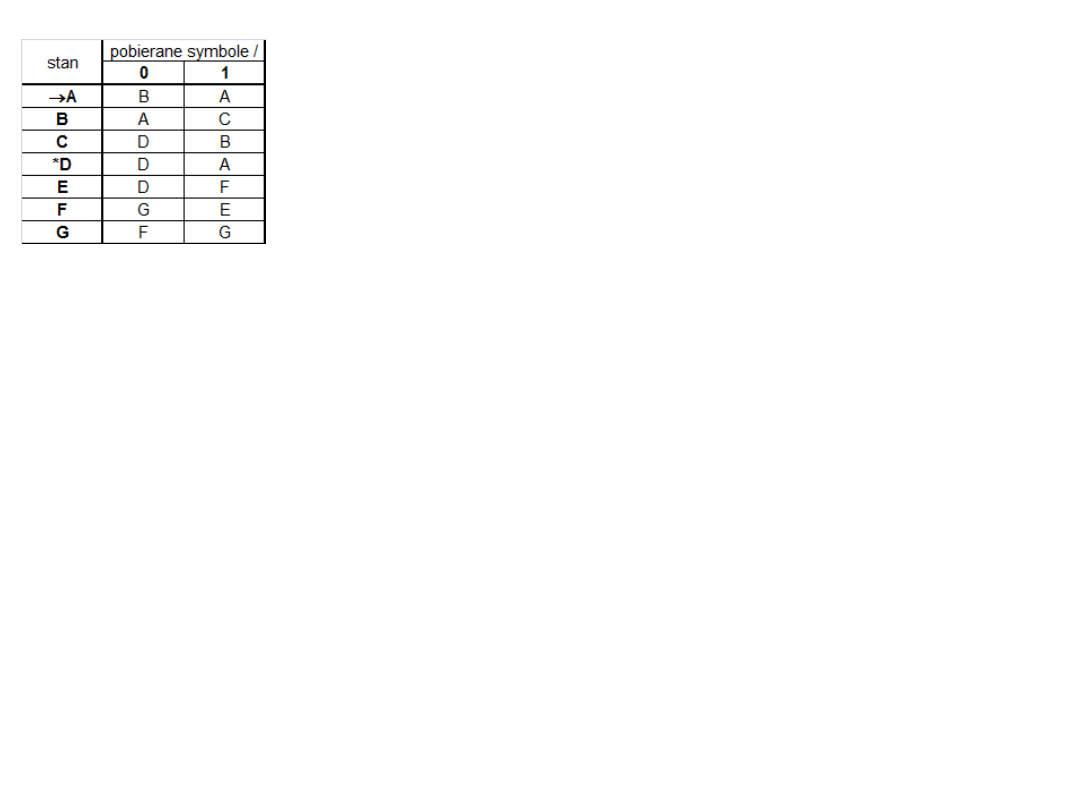
ponieważ macierz rozróżnialności jest symetryczna,
będziemy zajmowali się tylko jej dolną częścią.
Stosując wyżej opisany algorytm (zamiast symbolu „”

pojawi się symbol „ƒƒƒf”) dla wspomnianego przykładu
otrzymujemy (napisałem dla Państwa funkcję w
matlabie która dla wejścia w pliku excelowym pokazuje
kolejne kroki):

Ponieważ stan H jest nieosiągalny, możemy go od razu usunąć z naszych
rozważań:

>> tablica_rozroznialnosci('przyklad1.xls')
po zidentyfikowaniu par: (stan akceptujący, stan_nieakceptujący) nasza tablica rozróżnialności wygląda tak:

tablica teraz wyglada tak:
' ' 'A' 'B' 'C' 'D' 'E' 'F' 'G'
'A' ' ' ' ' ' ' ' ' ' ' ' ' ' '
'B' '[ ]' ' ' ' ' ' ' ' ' ' ' ' '
'C' '[ ]' '[ ]' ' ' ' ' ' ' ' ' ' '
'D' '[x]' '[x]' '[x]' ' ' ' ' ' ' ' '
'E' '[ ]' '[ ]' '[ ]' '[x]' ' ' ' ' ' '
'F' '[ ]' '[ ]' '[ ]' '[x]' '[ ]' ' ' ' '
'G' '[ ]' '[ ]' '[ ]' '[x]' '[ ]' '[ ]' ' '

poniewaz stany D i A sa rozroznialne oraz f(C,0)=D i f(B,0)=A wiec stany: C i B sa rozroznialne
poniewaz stany D i A sa rozroznialne oraz f(E,0)=D i f(B,0)=A wiec stany: E i B sa rozroznialne
poniewaz stany D i B sa rozroznialne oraz f(C,0)=D i f(A,0)=B wiec stany: C i A sa rozroznialne
poniewaz stany D i B sa rozroznialne oraz f(E,0)=D i f(A,0)=B wiec stany: E i A sa rozroznialne
poniewaz stany F i D sa rozroznialne oraz f(G,0)=F i f(C,0)=D wiec stany: G i C sa rozroznialne
poniewaz stany F i D sa rozroznialne oraz f(G,0)=F i f(E,0)=D wiec stany: G i E sa rozroznialne
poniewaz stany G i D sa rozroznialne oraz f(F,0)=G i f(C,0)=D wiec stany: F i C sa rozroznialne
poniewaz stany G i D sa rozroznialne oraz f(F,0)=G i f(E,0)=D wiec stany: F i E sa rozroznialne

tablica teraz wyglada tak:
' ' 'A' 'B' 'C' 'D' 'E' 'F' 'G'
'A' ' ' ' ' ' ' ' ' ' ' ' ' ' '
'B' '[ ]' ' ' ' ' ' ' ' ' ' ' ' '
'C' '[x]' '[x]' ' ' ' ' ' ' ' ' ' '
'D' '[x]' '[x]' '[x]' ' ' ' ' ' ' ' '
'E' '[x]' '[x]' '[ ]' '[x]' ' ' ' ' ' '
'F' '[ ]' '[ ]' '[x]' '[x]' '[x]' ' ' ' '
'G' '[ ]' '[ ]' '[x]' '[x]' '[x]' '[ ]' ' '

poniewaz stany C i A sa rozroznialne oraz f(B,1)=C i f(A,1)=A wiec stany: B i A sa rozroznialne
poniewaz stany E i A sa rozroznialne oraz f(F,1)=E i f(A,1)=A wiec stany: F i A sa rozroznialne
poniewaz stany G i C sa rozroznialne oraz f(G,1)=G i f(B,1)=C wiec stany: G i B sa rozroznialne
poniewaz stany G i E sa rozroznialne oraz f(G,1)=G i f(F,1)=E wiec stany: G i F sa rozroznialne

tablica teraz wyglada tak:
' ' 'A' 'B' 'C' 'D' 'E' 'F' 'G'
'A' ' ' ' ' ' ' ' ' ' ' ' ' ' '
'B' '[x]' ' ' ' ' ' ' ' ' ' ' ' '
'C' '[x]' '[x]' ' ' ' ' ' ' ' ' ' '
'D' '[x]' '[x]' '[x]' ' ' ' ' ' ' ' '
'E' '[x]' '[x]' '[ ]' '[x]' ' ' ' ' ' '
'F' '[x]' '[ ]' '[x]' '[x]' '[x]' ' ' ' '
'G' '[ ]' '[x]' '[x]' '[x]' '[x]' '[x]' ' '

wiecej par rozroznialnych nie jestesmy juz w stanie zidentyfikowac

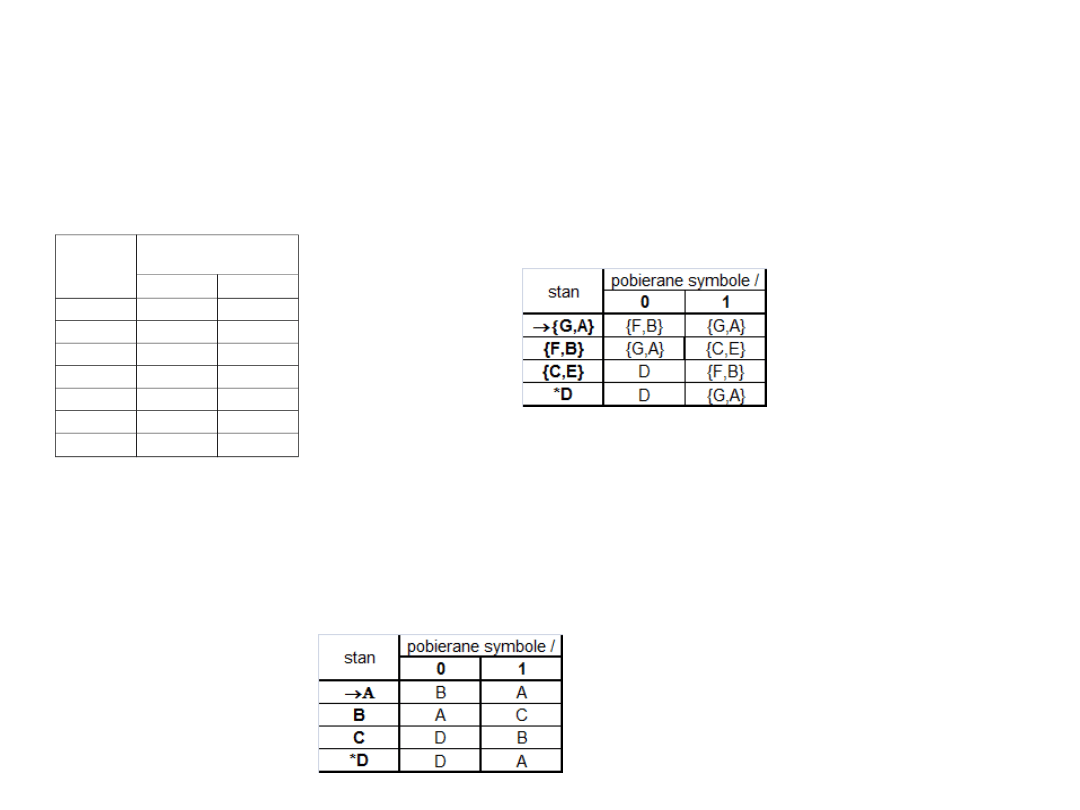
wiemy zatem, że bloki {G,A}, {F,B} , {C,E}, {D} są blokami stanów
równoważnych (możemy zatem traktować ja jako jeden stan (ogólnie
bloki mogą zawierać oczywiście większą liczbę stanów niż 2) ).
Teraz pozostała już najłatwiejsza część przedstawienia DASu w
oparciu o wyznaczone wcześniej bloki czyli:

albo lepiej
rozpisując od
razu w oparciu
o bloki: ->

w ogólności pamiętajmy, że blok który zawiera stan początkowy jest
teraz stanem początkowym, wszystkie bloki, które zawierają choć
jeden stan końcowy są stanami końcowymi

teraz możemy jeszcze ładniej zaetykietować nowe stany (A:={G,A,}
B:={F,B}, C:={C,E}, D:=D) i otrzymamy:

i to jest
ostateczna odpowiedź.

stan

pobierane symbole

/ nowy stan

0

1

G,A}

{F,B}

{G,A}

{F,B}

{G,A}

{C,E}

{C,E}

D

{F,B}

*D

D

{G,A}

{C,E}

D

{F,B}

{F,B}

{G,A}

{C,E}

G,A}

{F,B}

{G,A}

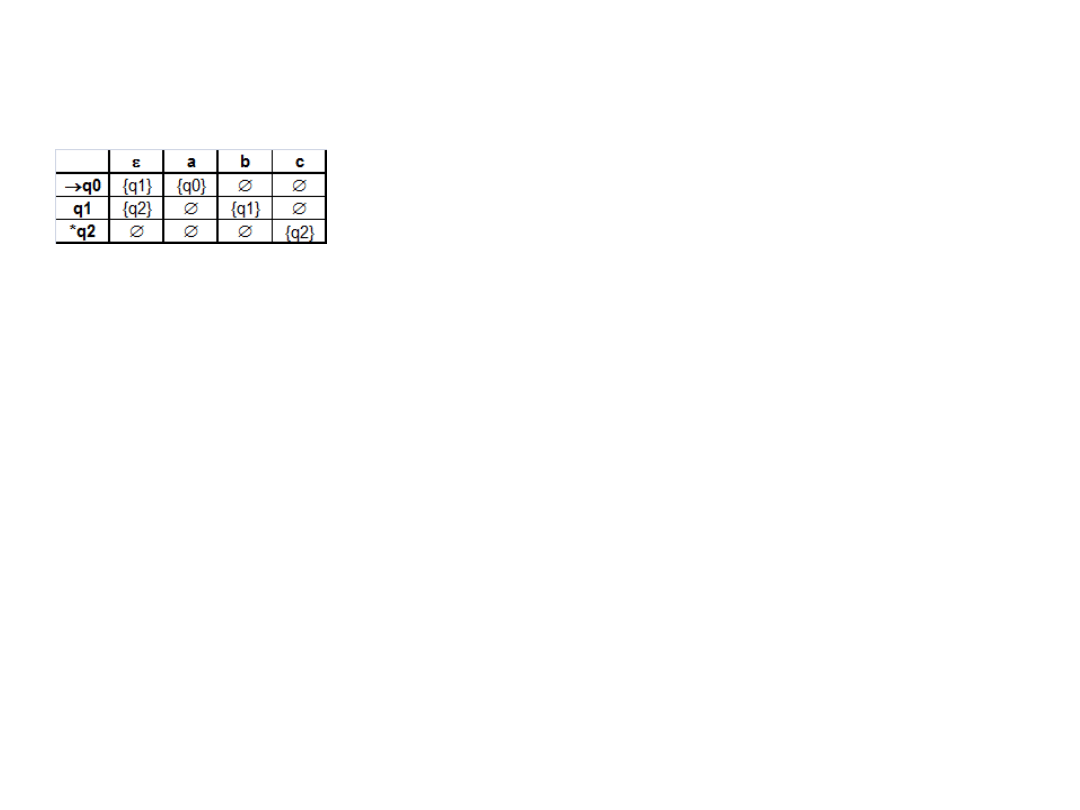
2. Przekształcenia ENAS na DAS

Omawiając postępowanie równolegle posłużmy się przykładem ENASu

E=(Q

E

, , 

E

, q

oE

,F

E

),

gdzie: Q

E

={q

o

,q

1

,q

2

},  ={a,b,c}, q

0E

=q

0

, F

E

={q

2

}, zaś 

E

jest określona

następująco:

Rozważania zawężamy tylko do stanów osiągalnych, wszystkie stany

nieosiągalne możemy wykreślić.

a) Obliczamy -Domknięcia dla każdego stanu q (zbiór stanów jakich

możemy dość od q nie połykając żadnego symbolu (różnego od ) ).

W ogólności dla każdego stanu q , qEDOMK(q)

Jeżeli p  EDOMK(q) oraz r  

E

(p, ) to r  EDOMK(q)

w naszym przykładzie:
EDOMK(q

0

)={q

0

,q

1

,q

2

}, zauważmy, że możemy przejść połykając  od q

0

do q

1

, a z q

1

do q

2

EDOMK(q

1

)={q

1

,q

2

}

EDOMK(q

2

)={q

2

}

Następnie konstruujemy tablicę dla EDOMKnięć naszych stanów i

obliczamy przejścia. Pamiętajmy, że EDOMK to zbiór stanów. Stanem
początkowym DASu D (q

0D

)

będzie EDOMK(q

0E

), gdzie q

0E i

q

0D

to stany

początkowe w ENASie i DASie odpowiednio.

Zbiór stanów akceptujących naszego DASu będzie składał się z kazdego

zbioru stanów (w naszej budowanej tabelce) który zawiera choć jeden z
stanów akceptujących pierwotnego ENASu.

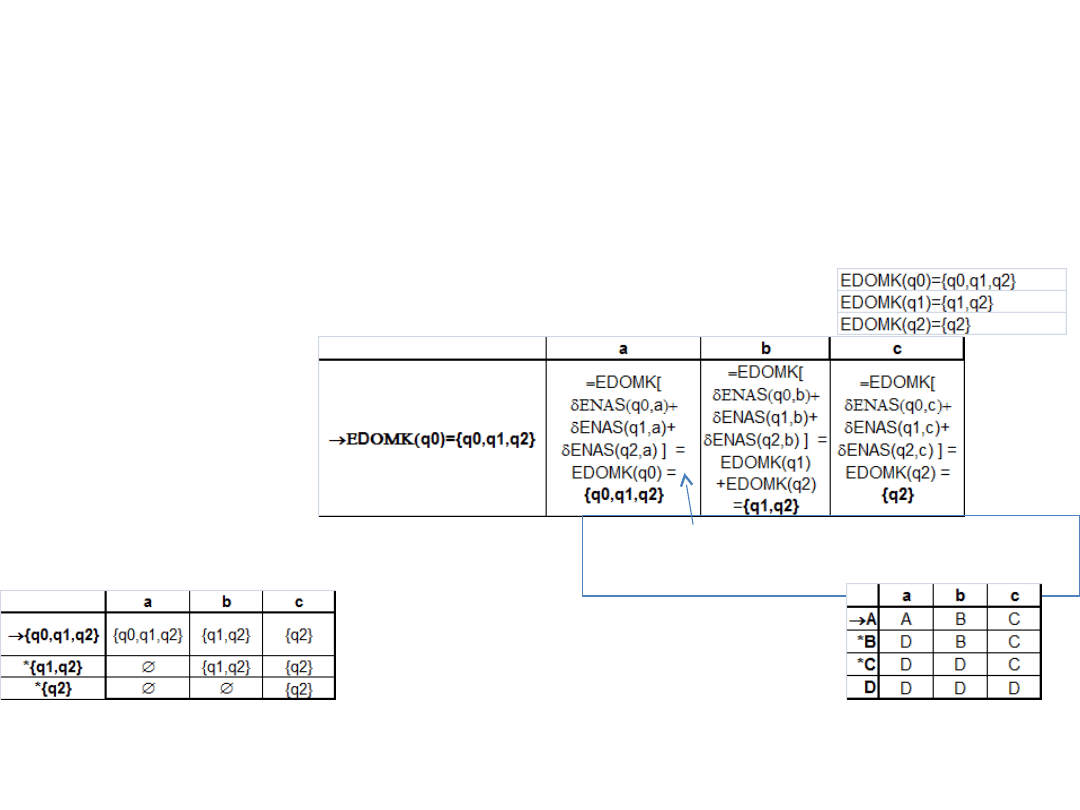
Funkcja przejście w DASie (dla stanu q i połykanego symbolu „a”) będzie
określona następująco: jeżeli mamy stan q DASowy (reprezentowany przez
pewien zbiór stanów ENASu) tj. q={p

1

,p

2

,…,p

k

} , obliczamy zbiór do jakiego

możemy dość po połknięciu symbolu a w ENASie czyli:

załóżmy, że zbiór ten jest równy: {r

1

,r

2

,…,r

m

}

finalnie bierzemy sumę domknięć r

i

tj:

Wracając do przykładu:

zauważmy, że pojawiły nam
się nowy stany {q1,q2} i {q1}
Musimy zatem dla niej również rozpisać funkcję przejścia. Itd. Otrzymując:

albo po reetykietowaniu stanów:

Przy okazji zauważmy, że rozważaliśmy język postaci a*b*c*, stan D jest
stanem z którego nie ma już możliwości wyjścia i jest on stanem
nieakceptującym



k

i

i

E

a

p

1

)

,

(







m

i

i

D

r

EDOMK

a

q

1

)

(

)

,

(







bo 

E

(q

1

,a)+

E

(q

1

,a)+

E

(q

2

,a)={q0}

+  +

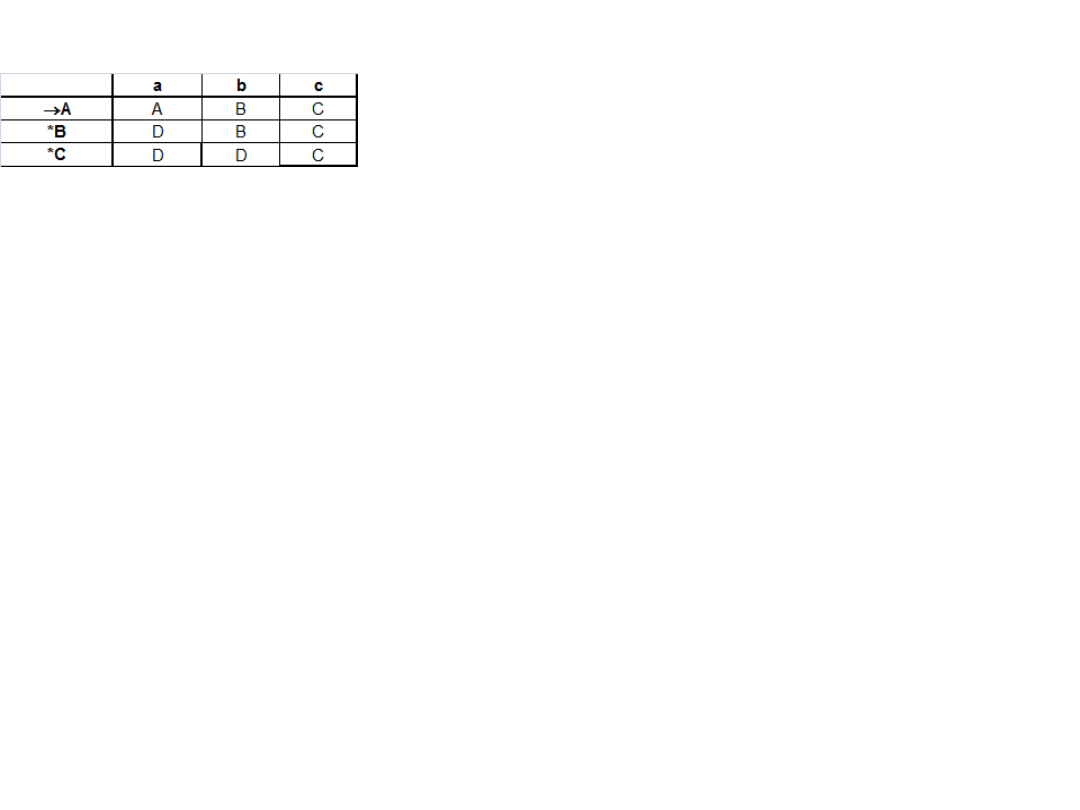
Końcowo zatem DAS D=({A,B,C,D},{a,c,d},

D

, q

0D

, {B,C}) ,gdzie 

D

jest

określona następująco:

------------------------------------------------------------------------------------------------------------
----------------

3. Przekształcenia do postaci PNC

Poruszamy się teraz wśród gramatyk bezkontekstowych, czyli

G=(V

N

, V

T

, P, S), gdzie każde prawo ze zbioru P ma postać

A →

β

,

A

V

N

,

β

(V

N



V

T

)

*

. Czyli po lewej stronie reguły jest pojedynczy

nieterminal, po prawej zaś dowolne słowo (być może puste).

V

N

– zbiór nieterminali, V

T

– zbiór terminali.

Postać Normalna Chomsky’ego to postać gramatyki, gdzie wszystkie

produkcje mają postać:

A  BC lub Aa (duże litery oznaczają nieterminale, małe terminale)

oraz gramatyka taka nie zawiera symboli bezużytecznych.

Zgodnie z teorią kroki są następujące:

a)eliminacja -produkcji

b)elimacja produkcji jednostkowych

c)eliminacja symboli bezużytecznych

d)reorganizacja zapisu/nazw zmiennych do postaci PNC („zwijanie” produkcji)

W praktyce eliminację symboli bezużytecznych możemy robić kiedykolwiek

(ale pamiętając, że na końcu i tak musimy ją ponownie przeprowadzić – punkt

„c” ). Często wygodnie jest na początku zastanowić nad gramatyką się czy

nie ma w niej symboli bezużytecznych i wstępnie już ją z nich oczyścić.

Zacznijmy od eliminacji symboli bezużytecznych. Eliminujemy najpierw
symbole symbole niegenerujące, później nieosiągalne.

Eliminacji symboli niegenerujących można dokonać poprzez zidentyfikowanie
wszystkich symboli generujących , pozostały zbiór będzie zbiorem symboli
(nieterminali) niegenerujących.
każdy symbol A, dla którego istnieje produkcja:
Aw, wV

T

* (nieterminal łańcuch terminali) jest symbolem generującym,

również każdy terminal jest symbolem generującym.
podobnie każdy symbol dla którego istnieje produkcja:
AA

1

A

2

…A

k

, gdzie A

1

, A

2

, …, A

k

są symbolami generującymi, jest symbolem

generującym.

Eliminacji symboli nieosiągalnych można dokonać poprzez zidentyfikowanie
wszystkich symboli osiągalnych , pozostały zbiór będzie zbiorem symboli
nieosiągalnych.
każdy symbol A, dla którego istnieje produkcja:
Sw

1

Aw

2

, w

1

,w

2

(V

T

V

N

)* jest symbolem osiągalnym

podobnie każdy symbol dla którego istnieje produkcja:
B w

1

Aw

2

, gdzie B jest symbolem osiągalnym, jest symbolem osiągalnym.

Rozważmy gramatykę: G=({S,A,B,C,D,E}, {a,b}, P, S), gdzie zbiór produkcji P
ma postać:
(1)S  aAa | bBb | aBbABa 

(2)A  C | aA |a

(3)B  C | b | A

(4)C  CDE | 

(5)D  A | B | ab

Zauważmy, że: E jest symbolem niegenerującym (nie wyprowadzimy z niego
żadnego łańcucha złożonego z samych terminali) ,zatem bezużytecznym,
możemy więc wykreślić produkcję: C  CDE, otrzymując:

(1)S  aAa | bBb | aBbABa 

(2)A  C | aA |a

(3)B  C | b | A

(4)C  

(5)D  A | B | ab

Zauważmy, że: D jest symbolem nieosiągalnym (nie możemy do niego dojść z
S), zatem bezużytecznym, możemy więc wykreślić produkcje: D  A | B | ab,

otrzymując:
(1)S  aAa | bBb | aBbABa 

(2)A  C | aA |a

(3)B  C | b | A

(4)C  

(1)S  aAa | bBb | aBbABa | 

(2)A  C | aA |a

(3)B  C | b | A

(4)C  

teraz przystępujemy do eliminacji -produkcji . Inaczej mówiąc dążymy do

usunięcia wszelkich produkcji typu: A (powiemy, wówczas, że A jest -

zmienną).
podobnie, jeśli istnieje produkcja która ma postać
AA

1

A

2

…A

k

, gdzie wszystkie A

i

(i=1,2,…k) zmienne są -zmiennymi

(„zerowalnymi”), wówczas A jest także jest -zmienną.

Proces usuwania -produkcji rozpoczynamy od zidentyfikowania -zmiennych.

Dla powyższej gramatyki są nimi:
S,C (w jednym kroku)
B, A (ponieważ AC i BC).

[// gdyby istniała produkcja Z  BC wówczas Z byłaby też zerowalna)]

Zatem finalnie zbiór zmiennych {S,A,B,C} jest zbiorem zmiennych
zerowalnych.

Teraz musi rozważyć co by się stała gdyby dowolny podzbiór zmiennych
zerowalnych przyjął wartości równe . Czyli np. w produkcja

S  aBbABa

mogłaby przyjąć postacie:
S  aBbABa | abABa | aBbBa | aBbAa | aBba | abBa | abAa | aba

Rozpisując zgodnie z powyższym postepowaniem otrzymamy:
(1)S  aAa | bBb | aBbABa | 

(2)A  C | aA |a

(3)B  C | b | A

(4)C  

(1) S  aAa | bBb | aBbABa |  | abABa | aBbBa | aBbAa | aBba | abBa | abAa |

aba
(2)A  C | aA |a | 

[//gdyby w powyższej produkcji było np. aaA to dodalibyśmy jeszcze aa]

(3)B  C | b | A | 

(4)C  

Zauważmy, że do tej pory nasza przekształcona gramatyka generuje język
taki sam jak gramatyka pierwotna.
Teraz usuwamy już produkcje w których po prawej stronie występuje tylko :

(1) S  aAa | bBb | aBbABa | abABa | aBbBa | aBbAa | aBba | abBa | abAa |

aba
(2)A  C | aA |a

(3)B  C | b | A

Zauważmy, że teraz nasza gramatyka nie jest równoważna poprzedniej z
dokładnością do  (gramatyka nie generuje już ).

Zauważmy, też że symbol C stał się symbolem niegenerującym, możemy
zatem usunąć wszystkie produkcje gdzie po prawej stronie występuje C.

Mamy zatem
(1) S  aAa | bBb | aBbABa | abABa | aBbBa | aBbAa | aBba | abBa | abAa |

aba
(2)A  aA |a

(3)B  b | A

Teraz eliminujemy produkcje jednostkowe. Produkcją jednostkową
nazywamy produkcję typu:
A*B gdzie A i B są terminalami. W pierwszym kroku identyfikujemy wszelkie

pary jednostkowe.
Dla każdej zmiennej A para (A,A) jest parą jednostkową.
Jeżeli (A,B) jest parą jednostkową oraz istnieje produkcja BC to (B,C) jest

produkcją jednoskową.
Wypisujemy wszytskie pary jednostkowe
(S , S)

[// gdyby istniała produkcja SB to również (S,B) i (S,A) ponieważ BA byłyby parami jednostkowymi]

(A , A)
(B , B)
(B , A)
Przepisujemy wszelkie niejednostkowe produkcje odpowiadające param
jednostkowym.
(S , S) : S  aAa | bBb | aBbABa | abABa | aBbBa | aBbAa | aBba | abBa |

abAa | aba
(A , A) : A  aA |a

(B , B) : B  b

(

B

,

A

) :

B



aA |a

czyli głowa produkcji jest w pierwszej zmiennej z pary

jednostkowej, ciała produkcji jest ciałem produkcji od drugiej zmiennej z pary
jednostkowej.
Zauważmy, że nie przepisaliśmy produkcji B  A (gdyż była to produkcja

jednostkowa)

Mamy zatem
S  aAa | bBb | aBbABa | abABa | aBbBa | aBbAa | aBba | abBa | abAa | aba

A  aA |a

B  b

B  aA |a

Teraz jeszcze musi nastąpić rzut oka na gramatykę i eliminacja symboli
bezużytecznych. Ponieważ nasza gramatyka nie zawiera symboli
bezużytecznych przystępujęmy do dalszego etapu.

Teraz dążymy już do uformowania gramatyki zgodnej ze strukturą PNC.
W tym etapie terminale które występują w obecności innych symboli
(terminalnych bądź nieterminalnych) zastępujemy poprzez odpowiadające im
nieterminale:
S  A

1

AA

1

| B

1

BB

1

| A

1

BB

1

AB A

1

| A

1

B

1

ABA

1

| A

1

BB

1

BA

1

| A

1

BB

1

AA

1

| A

1

BB

1

A

1

|

A

1

B

1

BA

1

|

A

1

B

1

AA

1

| A

1

B

1

A

1

A  A

1

A |a

[// ponieważ „a” w produkcji A a wystepuje samo więc je pozostawiamy]

B  b

B  A

1

A |a

A

1

 a

B

1

 b

Następnie „zwijamy” produkcje. Tzn. jeżeli mamy produkcję postaci:
AB

1

B

2

…B

k

, gdzie k3 to zastępujemy ją poprzez zbiór produkcji

(wprowadzając nowe symbole C

i

,i=1,2,..k-2) :

AB

1

C

1

C

1

B

2

C

2

.
.
.
C

k-3

B

k-2

C

k-2

C

k-2

B

k-1

B

k

Wracając do przykładu:
S 

A

1

AA

1

|

B

1

BB

1

|

A

1

BB

1

AB A

1

|

A

1

B

1

ABA

1

|

A

1

BB

1

BA

1

|

A

1

BB

1

AA

1

|

A

1

BB

1

A

1

|

A

1

B

1

BA

1

|

A

1

B

1

AA

1

|

A

1

B

1

A

1

A  A

1

A |a

B  b

B  A

1

A |a

A

1

 a

B

1

 b

rozpisujemy:

SA

1

C

1

C

1

AA

1

S B

1

C

2

C

2

BB

1

S A

1

C

3

C

3

 BC

4

C

4

 B

1

C

5

C

5

 AC

6

C

6

 BA

1

S A

1

C

7

C

7

B

1

C

4

S A

1

C

8

C

8

BC

9

C

9

 B

1

C

6

S  A

1

C

10

C

10

 BC

11

C

11

B

1

C

1

S  A

1

C

12

C

12

BC

13

C

13

B

1

A

1

S

A

1

C

9

S  A

1

C

11

S A

1

C

13

1

pozostałe produkcją są już w
PNC:
A  A

1

A |a

B  b

B  A

1

A |a

A

1

 a

B

1

 b

Zatem finalnie gramatyka ma postać:
G=({S, A, B, C, D, E, A

1

, A

2

, C

1

,C

2

, …, C

13

}, {a,b}, P’, S) , gdzie zbiór produkcji

P’ ma postać:

SA

1

C

1

C

1

AA

1

S B

1

C

2

C

2

BB

1

S  A

1

C

3

C

3

 BC

4

C

4

 B

1

C

5

C

5

 AC

6

C

6

 BA

1

S A

1

C

7

C

7

B

1

C

4

S A

1

C

8

C

8

BC

9

C

9

 B

1

C

6

Koniec 

S  A

1

C

10

C

10

 BC

11

C

11

B

1

C

1

S  A

1

C

12

C

12

BC

13

C

13

B

1

A

1

S A

1

C

9

S  A

1

C

11

S A

1

C

13

A  A

1

A |a

B  b

B  A

1

A |a

A

1

 a

B

1

 b

1