Materiał pomocniczy cz. 1 (poprawkowa)

1.Minimalizacja DAS
Opis postępowania:
a)Eliminujemy stany do których nie możemy dotrzeć ze stanu
początkowego (jeśli takie istnieją)
b)Identyfikujemy zbiory (bloki) stanów równoważnych (poprzez
tablicę rozróżnialności) a następnie budujemy nowy DAS w oparciu o
te bloki (każdy blok/zbiór traktujemy jako jeden stan)

Konstrukcja tablicy rozróżnialności:
I.Każda para stanów (p,q) gdzie p jest stanem akceptującym a q jest
nieakceptującym jest rozróżnialna.
II.Indukcyjnie: jeżeli p i q są rozróżnialną parą stanów, oraz p=(r,a) i

q= (s,a) (gdzie a – dodolwny symbol z alfabetu minializowanego

DAS; r,s – inne stany) wówczas para (r,s) jest rozróżnialna.
przykład:
rozważmy następujący DAS:

stan

pobierane

symbole / nowy

stan

0

1

A

B

A

B

A

C

C

D

B

*D

D

A

E

D

F

F

G

E

G

F

G

H

G

D

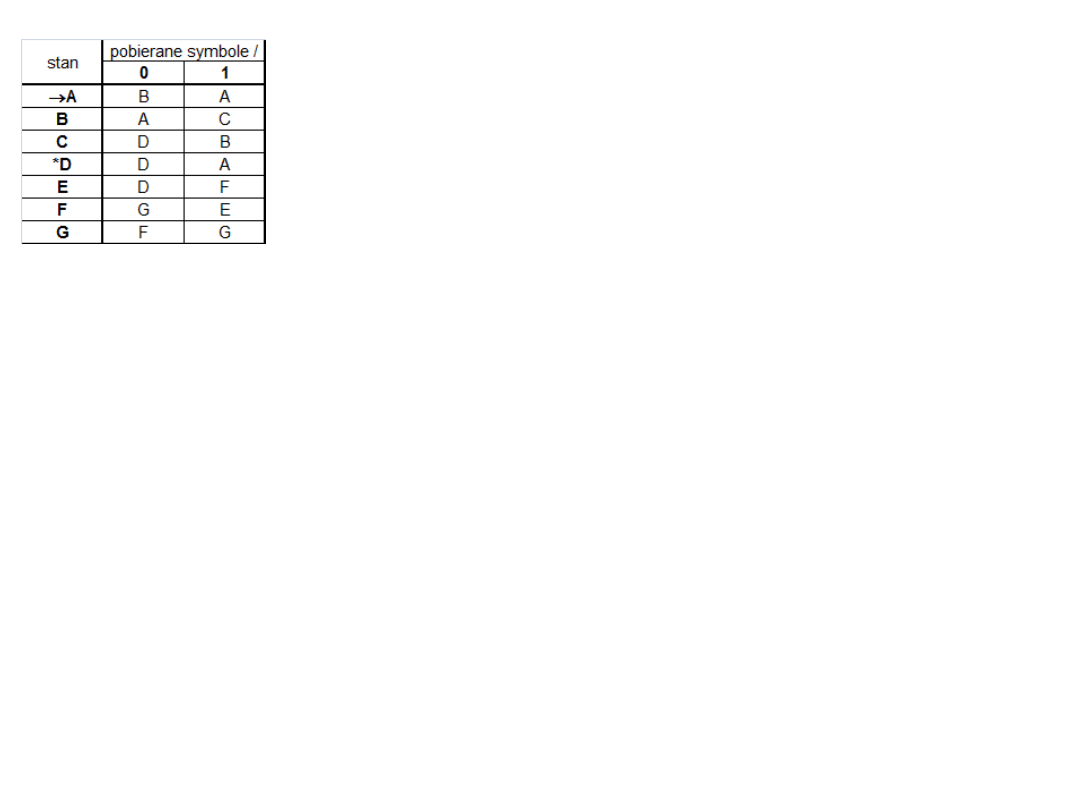
ponieważ macierz rozróżnialności jest symetryczna,
będziemy zajmowali się tylko jej dolną częścią.
Stosując wyżej opisany algorytm (zamiast symbolu „”

pojawi się symbol „ƒƒƒf”) dla wspomnianego przykładu
otrzymujemy (napisałem dla Państwa funkcję w
matlabie która dla wejścia w pliku excelowym pokazuje
kolejne kroki):

Ponieważ stan H jest nieosiągalny, możemy go od razu usunąć z naszych
rozważań:

>> tablica_rozroznialnosci('przyklad1.xls')
po zidentyfikowaniu par: (stan akceptujący, stan_nieakceptujący) nasza tablica rozróżnialności wygląda tak:

tablica teraz wyglada tak:
' ' 'A' 'B' 'C' 'D' 'E' 'F' 'G'
'A' ' ' ' ' ' ' ' ' ' ' ' ' ' '
'B' '[ ]' ' ' ' ' ' ' ' ' ' ' ' '
'C' '[ ]' '[ ]' ' ' ' ' ' ' ' ' ' '
'D' '[x]' '[x]' '[x]' ' ' ' ' ' ' ' '
'E' '[ ]' '[ ]' '[ ]' '[x]' ' ' ' ' ' '
'F' '[ ]' '[ ]' '[ ]' '[x]' '[ ]' ' ' ' '
'G' '[ ]' '[ ]' '[ ]' '[x]' '[ ]' '[ ]' ' '

poniewaz stany D i A sa rozroznialne oraz f(C,0)=D i f(B,0)=A wiec stany: C i B sa rozroznialne
poniewaz stany D i A sa rozroznialne oraz f(E,0)=D i f(B,0)=A wiec stany: E i B sa rozroznialne
poniewaz stany D i B sa rozroznialne oraz f(C,0)=D i f(A,0)=B wiec stany: C i A sa rozroznialne
poniewaz stany D i B sa rozroznialne oraz f(E,0)=D i f(A,0)=B wiec stany: E i A sa rozroznialne
poniewaz stany F i D sa rozroznialne oraz f(G,0)=F i f(C,0)=D wiec stany: G i C sa rozroznialne
poniewaz stany F i D sa rozroznialne oraz f(G,0)=F i f(E,0)=D wiec stany: G i E sa rozroznialne
poniewaz stany G i D sa rozroznialne oraz f(F,0)=G i f(C,0)=D wiec stany: F i C sa rozroznialne
poniewaz stany G i D sa rozroznialne oraz f(F,0)=G i f(E,0)=D wiec stany: F i E sa rozroznialne

tablica teraz wyglada tak:
' ' 'A' 'B' 'C' 'D' 'E' 'F' 'G'
'A' ' ' ' ' ' ' ' ' ' ' ' ' ' '
'B' '[ ]' ' ' ' ' ' ' ' ' ' ' ' '
'C' '[x]' '[x]' ' ' ' ' ' ' ' ' ' '
'D' '[x]' '[x]' '[x]' ' ' ' ' ' ' ' '
'E' '[x]' '[x]' '[ ]' '[x]' ' ' ' ' ' '
'F' '[ ]' '[ ]' '[x]' '[x]' '[x]' ' ' ' '
'G' '[ ]' '[ ]' '[x]' '[x]' '[x]' '[ ]' ' '

poniewaz stany C i A sa rozroznialne oraz f(B,1)=C i f(A,1)=A wiec stany: B i A sa rozroznialne
poniewaz stany E i A sa rozroznialne oraz f(F,1)=E i f(A,1)=A wiec stany: F i A sa rozroznialne
poniewaz stany G i C sa rozroznialne oraz f(G,1)=G i f(B,1)=C wiec stany: G i B sa rozroznialne
poniewaz stany G i E sa rozroznialne oraz f(G,1)=G i f(F,1)=E wiec stany: G i F sa rozroznialne

tablica teraz wyglada tak:
' ' 'A' 'B' 'C' 'D' 'E' 'F' 'G'
'A' ' ' ' ' ' ' ' ' ' ' ' ' ' '
'B' '[x]' ' ' ' ' ' ' ' ' ' ' ' '
'C' '[x]' '[x]' ' ' ' ' ' ' ' ' ' '
'D' '[x]' '[x]' '[x]' ' ' ' ' ' ' ' '
'E' '[x]' '[x]' '[ ]' '[x]' ' ' ' ' ' '
'F' '[x]' '[ ]' '[x]' '[x]' '[x]' ' ' ' '
'G' '[ ]' '[x]' '[x]' '[x]' '[x]' '[x]' ' '

wiecej par rozroznialnych nie jestesmy juz w stanie zidentyfikowac

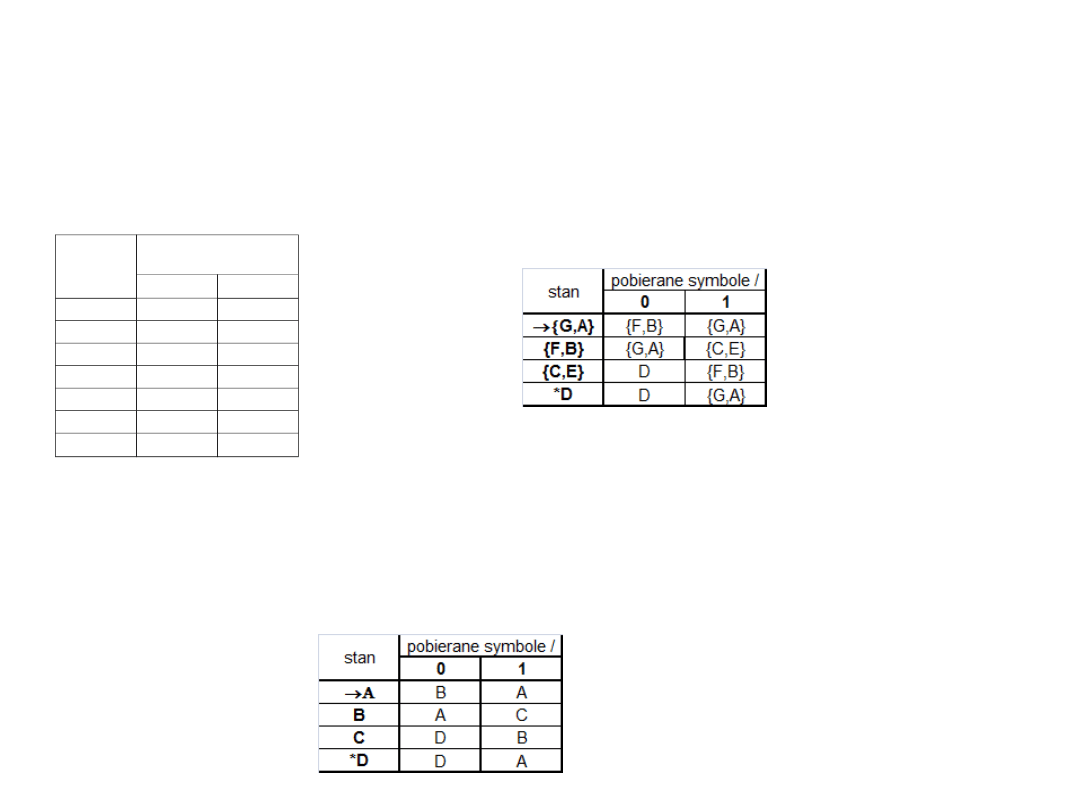
wiemy zatem, że bloki {G,A}, {F,B} , {C,E}, {D} są blokami stanów
równoważnych (możemy zatem traktować ja jako jeden stan (ogólnie
bloki mogą zawierać oczywiście większą liczbę stanów niż 2) ).
Teraz pozostała już najłatwiejsza część przedstawienia DASu w
oparciu o wyznaczone wcześniej bloki czyli:

albo lepiej
rozpisując od
razu w oparciu
o bloki: ->

w ogólności pamiętajmy, że blok który zawiera stan początkowy jest
teraz stanem początkowym, wszystkie bloki, które zawierają choć
jeden stan końcowy są stanami końcowymi

teraz możemy jeszcze ładniej zaetykietować nowe stany (A:={G,A,}
B:={F,B}, C:={C,E}, D:=D) i otrzymamy:

i to jest
ostateczna odpowiedź.

stan

pobierane symbole

/ nowy stan

0

1

G,A}

{F,B}

{G,A}

{F,B}

{G,A}

{C,E}

{C,E}

D

{F,B}

*D

D

{G,A}

{C,E}

D

{F,B}

{F,B}

{G,A}

{C,E}

G,A}

{F,B}

{G,A}