1-54

PROCESY UTLENIANIA I REDUKCJI

DEFINICJE PODSTAWOWE I TEORETYCZNE ZAŁOŻENIA METOD

POMIAROWYCH

W Y K Ł A D 1 (2008)

HENRYK SCHOLL®

Katedra Chemii Ogólnej i Nieorganicznej

Wydział Chemii

Uniwersytetu Łódzkiego

e mail: [e-mail]

1.

Podział i podstawowe definicje procesów utleniania i redukcji

a)

Procesy utleniania i redukcji (procesy redox) zachodzące w roztworach
są procesami homofazowymi zachodzącymi pomiędzy jonami lub
cząsteczkami różniącymi się wartościami standardowych potencjałów
elektrochemicznych (E

0

) oraz zmieniającymi się wartościami stężeń

reagujących substancji

ELEKTROCHEMIA STOSOWANA

1-54

b) Reakcje utleniania i redukcji zachodzące na granicy faz elektroda/
roztwór elektrolitu z międzyfazową wymianą elektronów jest zatem
procesem heterofazowym.

 

c) Procesy redukcji

1.

Redukcja jonów lub kompleksów do niższych stopni utlenienia,
redukcja cząsteczek nieorganicznych lub organicznych - postać
zredukowana pozostaje w roztworze po zmianie stopnia utlenienia.

2.

Wydzielanie z roztworów lub na elektrodzie gazów, fazy metalicznej
lub amalgamatowej powstałych na drodze redukcji jonów lub
kompleksów.

3.

Redukcja nierozpuszczalnych związków lub warstw
powierzchniowych związana z utworzeniem fazy metalicznej lub
amalgamatu - jest to zwykle faza również nierozpuszczalna, ale o
układzie innym niż wyjściowy.

d) Procesy utleniania.

 1. Utlenianie jonów, kompleksów lub innych cząstek do postaci
rozpuszczalnych o wyższym stopniu utlenienia.

2. Utlenianie metalu, ich tlenków lub soli, czy też ogólnie ujmując -
materiału elektrody prowadzące do utworzenia rozpuszczalnych jonów
lub kompleksów.

3. Utlenianie ich tlenków lub soli, czy też ogólnie ujmując materiału
elektrody z wytworzeniem nierozpuszczalnych warstewek tlenkowych lub
o składzie soli tego metalu.

Oczywiste jest, że mamy do czynienia ze sprzężeniem dwóch spośród
wyżej wymienionych reakcji zachodzących w układzie reduktor –
utleniacz lub katoda – anoda

2

1-54

2. KILKA POJĘĆ ELEMENTARNYCH O POTENCJAŁACH FAZY

Siła elektromotoryczna ogniwa (SEM) składa się z różnic potencjałów
występujących na wszystkich granicach faz, które z reguły (oprócz granicy
faz ciecz ciecz) znajdują się w warunkach równowagowych.

Równowaga podziału naładowanych cząstek między dwie fazy jest
uwarunkowana równością ich potencjałów chemicznych w obydwu fazach.

Wartość ujemna potencjału chemicznego jest miarą pracy, która musi być
wykonana w stałych warunkach, w celu przeprowadzenia jednego mola
nienaładowanych cząstek z wnętrza fazy w stan gazowy o nieskończenie
wielkim

rozcieńczeniu,

odpowiadającemu

umownemu

zeru

skali

potencjałów chemicznych (

i

=0).

Wydobycie mola naładowanych cząstek z wnętrza fazy wymaga nie tylko
pracy rozerwania wiązań chemicznych, lecz również pokonania sił
elektrycznych. Miarą tej pracy jest potencjał elektrochemiczny o zapisie:

3

1-54



e

=  + zF

(1)

Drugi człon formalny strony powyższego równania jest pracą
elektrostatyczną

nieskończenie

powolnego

przeniesienia

niema-

terialnego ładunku zF z nieskończenie wielkiej odległości w próżni do
wnętrza rozważanej fazy - tj. do punktu o potencjale  .
Stosunek wartości tej pracy do przeniesionego ładunku nosi nazwę
wewnętrznego potencjału elektrycznego fazy ( ) lub inaczej - potencjału

Galvaniego

Rys.1. Ilustracja do rozważań o potencjałach fazowych.

 

Wewnętrzny potencjał elektryczny może się składać z dwóch udziałów:

•

potencjału zewnętrznego fazy (

) - potencjału Volty, 2) potencjału powierzchniowego

fazy (

).

4

1-54

Zewnętrzny potencjał elektryczny przewodnika definiuje się jako wartość

graniczną stosunku w/q dla q

  0.

Jest to praca przeniesienia ładunku w pobliże przewodnika i zbliżenie do

punktu C leżącego poza działaniem "sił obrazu", pochodzących od

fikcyjnych ładunków wyindukowanych na powierzchni metalu przez

zbliżającą się cząstkę.

Odległość tę określa się wartością rzędu 10

-4

cm. Ładunek przenoszony z

tego punktu do wnętrza rozważanej fazy (punkt A) musi pokonać spadek

potencjału warstwy elektrochemicznej znajdującej się na powierzchni fazy.

Ta składowa potencjału wewnętrznego jest równa powierzchniowemu

potencjałowi elektrycznemu . Wobec tego:

  =  + 

(2)

5

1-54

co w połączeniu z równaniem (1) daje:

 



e

=  + zF + zF (3)

 

Należy również pamiętać, że to formalne ujęcie pomija składowe

elektryczne wchodzące w skład potencjału chemicznego, występującego np.

przy oddziaływaniu chmury jonowej na cząstkę.

Zmierzenie bezwzględnych wartości potencjałów wewnętrznych

nie jest

możliwe

w przypadku rozpatrywania dwóch sąsiadujących ze sobą faz.

Dołączając badany układ do jakiegokolwiek przyrządu pomiarowego
tworzy się dodatkową granicę faz i mierzy się sumę algebraiczną
istniejących różnic potencjałów na powierzchniach granicznych.

REASUMUJĄC

:

mierzy się zawsze różnicę potencjałów wewnętrznych na

końcach dwóch doprowadzeń - jednakowych chemicznie.

Niemierzalne są natomiast różnice potencjałów zewnętrznych i różnice tzw.
potencjałów rzeczywistych pomiędzy dwoma fazami:

  = + zF

(4)

gdzie (-) jest pracą wyjścia elektronu z metalu.

 

6

1-54

2. Zdefiniowanie i sens fizyczny pojęcia „potencjał standardowy”

Reakcja przebiegająca w ogniwie jest sumą reakcji zachodzących na

obydwu elektrodach. Przepływ ładunku uwarunkowany jest przez:

•

siły chemiczne zależne od powinowactwa reakcji (suma iloczynów
potencjałów

chemicznych

i

odpowiednich

współczynników

stechiometrycznych) równego zmniejszeniu entalpii swobodnej
układu (-G),

2) przepływ ładunku proporcjonalny do całkowitej wielokrotności stałej

Faraday’a.

Dla warunków równowagi mamy:

 - 

i



i

= -G - -nFE (5)

 

Przeprowadźmy analizę różnic potencjałowych wewnątrz ogniwa o

budowie:

 Pt  H

2

  HCl

c

  AgCl

(s)

  Ag   Pt

7

1-54

Oznaczmy i ponumerujmy poszczególne fazy z zaznaczonymi granicami ich

podziału:

Pt(e) H

2

r-r (H

+

, Cl

-

, Ag

+

AgCl (Ag

+

, Cl

-

) Ag (Ag

+

, e  Pt’ (e)

1

2

3

4

5

1’

Siła elektromotoryczna ogniwa będzie równa sumie różnic wewnętrznych
potencjałów elektrycznych poszczególnych faz:

E = (

1’

- 

5

) + (

5

- 

4

) + (

4

- 

3

) + (

3

- 

2

) + (

2

- 

1

) (5)

co w efekcie daje:

E = (

1’

- 

1

) (6)

Oznacza to, że mierzymy wartość różnicy potencjałów wewnętrznych

ogniwa, które pracuje w warunkach bez poboru prądu ( I = 0)

W rozpatrywanym ogniwie zachodzi samorzutna reakcja odwracalna:

½ H

2

(2) + AgCl(4)  H

+

(3) + Cl

-

(3) + Ag(5) (6)

8

1-54

Równowagi fazowe cząstek zdolnych do przechodzenia z jednej fazy do

drugiej są określone równaniami:



e

Cl

-

,

3

= 

e

Cl

-

,

4

; 

e

Ag

+

,

5

= 

e

Ag+;4

; 

e

e,1’

= 

e

e,1

;

(7)

Wprowadzając formalne zależności:



e

AgCl,4

= 

e

Ag+,

+ 

e

Cl-;4

; 

e

Ag,5

= 

e

e,1’

+ 

e

Ag+, 5

(8)

Wówczas dla reakcji elektrodowej:

2H

+

(3) + 2e  H

2

(2)

(9)

mamy:

2

H

+

,3

+ 2 

e

e,1

= 

e

H2,2

(10)

9

1-54

Przechodząc do potencjałów chemicznych i uwzględniając definicję

termodynamiczną SEM ( E = -zF

i

lub w innej formie: E = -zF G)

otrzymamy:

FE = -



H+,3

-



Cl-, 3

-



Ag,5

-



AgCl,4

+

1/2



H2, 2 (11)

Dla stanu podstawowego (standardowego) mamy:

p

H2

= 1013 hPa, Ag jest w stanie metalicznym (a

Ag

= 1)

Wobec tego słuszne są zależności:



H2

,

2

=



H2

;



Ag,5

=



Ag

;



AgCl,4

=



AgCl

(12)

Ponieważ podstawowa formuła termodynamiczna opisująca wartość
potencjału chemicznego (potencjału Gibbsa, energii swobodnej), ma
postać:



H+ =



H+

0

+

RT ln a

H+

(13)

a równocześnie średni współczynnik roztworu elektrolitu typu 1 – 1 (tutaj:
kwasu solnego)oblicza się korzystając z równania :

a

HCl

= (a

H+

* a

Cl-

)

1/2

(14)

10

1-54

Równanie (11) przyjmie postać:

FE =

-



0

H+

-



0

Cl-

-



0

AgCl

+ ½



0

H2

– 2RT a



HCl

(15)

Suma wartości chemicznych potencjałów standardowych jest nową stałą

wielkością standardową

:

E

0

= -

 G

0

/ zF

(15)

Tym samym otrzymaliśmy równanie Nernsta:

E = E

0

 [(0,059/ zF ] lg a



(16)

11

1-54

3. Elektrody odwracalne. Elektrody odniesienia

Konieczne jest zdefiniowanie powszechnie stosowanego pojęcia

elektrody odwracalnej.

Elektrodą taką nazywamy elektrodę, na której ustala się równowaga

odpowiedniego odwracalnego procesu elektrodowego z szybkością

wystarczającą dla celów praktycznych. Równowaga ta jest w istocie

równowagą podziału między metalem i roztworem cząstek naładowanych i

wspólnych dla obu faz. Pojęcie elektrody odwracalnej nie obejmuje

przypadku granicznego, gdy w jednej z faz stężenie cząstek określających

potencjał elektrody jest równe zeru.

12

1-54

I.

Elektrody pierwszego rodzaju

 a) Odwracalne względem kationu

M

+

/M

.

Potencjał takiej elektrody jest określony zależnością:
 

 

(17)

W tym miejscu można mówić, że

dwie elektrody pierwszego rodzaju

tworzące ogniwo, np.:
 

Ag   AgNO

3

(m

1

)     AgNO

3

(m

2

)   Ag

 
tworzą w istocie

ogniwo stężeniowe

, którego SEM określona jest

wzorem:
 

 

(18)

Jeśli w ogniwie tym występuje dodatkowo potencjał dyfuzyjny, to
ogniwo takie nazywa się ogniwem stężeniowym z przenoszeniem,
gdzie t

+

i t

-

są odpowiednio liczbami przenoszenia kationów i anionów

 

 







M

a

zF

RT

E

E

ln

0



































2

,

1

,

2

,

1

,

ln

ln

a

a

F

RT

t

F

RT

t

a

a

F

RT

E

13

1-54

b)

Elektrody amalgamatowe: M

+

/M(Hg) o potencjale określonym

wzorem:

 

  (19)

c) Elektrody gazowe typu H

+

/H

2

lub Cl

2

/Cl

-

o potencjałach

określonych równaniami:

 

(20)

)

(

ln

0

Hg

a

a

F

z

RT

E

E

M



















H

H

H

H

a

F

RT

p

F

RT

E

ln

ln

2

2

,

14

1-54

II.

Elektrody drugiego rodzaju

.

 
Zbudowane są z metalu pokrytego trudno rozpuszczalną solą tego metalu i

układ ten zanurzony jest w roztworze elektrolitu o wspólnym anionie z

solą trudno rozpuszczalną. Należą do nich często stosowane i wygodne w

użyciu elektrody: kalomelowa Hg/Hg

2

Cl

2

/Cl

-

, siarczanowo-rtęciowa

Hg/Hg

2

SO

4

/SO

4

2-

, czy też chlorosrebrowa Ag/AgCl/Cl

-

. Potencjał tej

ostatniej elektrody jest np. określony wzorem:

(21) 

gdzie E

0

AgCl/Ag

jest standardowym potencjałem elektrody chlorosrebrnej

wynikającym wprost ze wzoru Nernsta.









Cl

Ag

AgCl

Ag

AgCl

a

F

z

RT

E

E

ln

/

0

/

15

1-54

III.

Elektrody redox

 
Są to elektrody oparte na reakcji podstawowej:
 

Ox + ne  n

Red

Red

(22) 

Budowa takiej elektrody zwykle sprowadza się do zanurzenia do roztworu
zawierającego substancję na dwóch różnych i trwałych stopniach utlenienia i
nie reagującego z nią "metalu obojętnego", np. Au lub Pt. Wartość potencjału
elektrody redox zależy od aktywności form utlenionej i zredukowanej, co
opisuje równanie podstawowe:
 

(23)

 

W przypadku reakcji jednoelektronowej w temperaturze 298K,to po wstawieniu
odpowiednich wartości stałych fizycznych i po przeliczeniu wartości
logarytmów o podstawie naturalnej na wartości logarytmów o podstawie
dziesiętnej, wzór ten przyjmuje postać końcową:
 

(24)













n

n

n

n

M

M

M

M

a

a

zF

RT

E

E

1

1

ln

/

0









n

N

M

M

a

a

E

E

1

lg

059

,

0

0

1
6

1-54

Wartości potencjałów standardowych układów redox wyznacza się

korzystając z wartości zmian standardowych entalpii tworzenia będącej

wartością SEM odpowiedniego ogniwa:

zF

G

E

0

0







Warunki standardowe: ciśnienie gazów

p = 1013 hPa

temperatura

T = 298,15 K

aktywność jonów

a = 1

aktywność fazy stałej a = 1

stała Faraday’a F = 96 484 coul/mol

Symbol „z” oznacza liczbę elektronów przenoszonych w procesie
jednostkowym

17

1-54

Układem odniesienia potencjałów standardowych w roztworach

wodnych jest tzw.

Standardowa elektroda wodorowa

(angielski

skrót: she) tworząca półogniwo:

Pt  H

2

 H

+

a = 1

Potencjał standardowy tej elektrody zdefiniowany jako równy zero:

E

0

 0,000 V

Wartość ta stanowi punkt odniesienia dla tzw. skali potencjałów

elektrodowych utworzonej poprzez pomiary (lub obliczenia) różnicy

potencjałów elektrycznych ogniw, w których jednym z półogniw stanowi

właśnie standardowa elektroda wodorowa

Praktyczne zastosowanie elektrody wodorowej jest ograniczone ze

względu na następujące trudności:

1)

stabilizacji wartości ciśnienia jednostkowego gazowego wodoru,

2)

korygowanie ciśnienia atmosferycznego i wilgotności otoczenia,

3)

jon wodorowy, wprawdzie najmniejszy rozmiarami wśród pozostałych
jonów, jest hydratowany otoczką sześciu cząsteczek wody,

4) nie można elektrody wodorowej stosować w rozpuszczalnikach

aprotycznych ze względu na chemiczne reakcje ich protonowania.

18

1-54

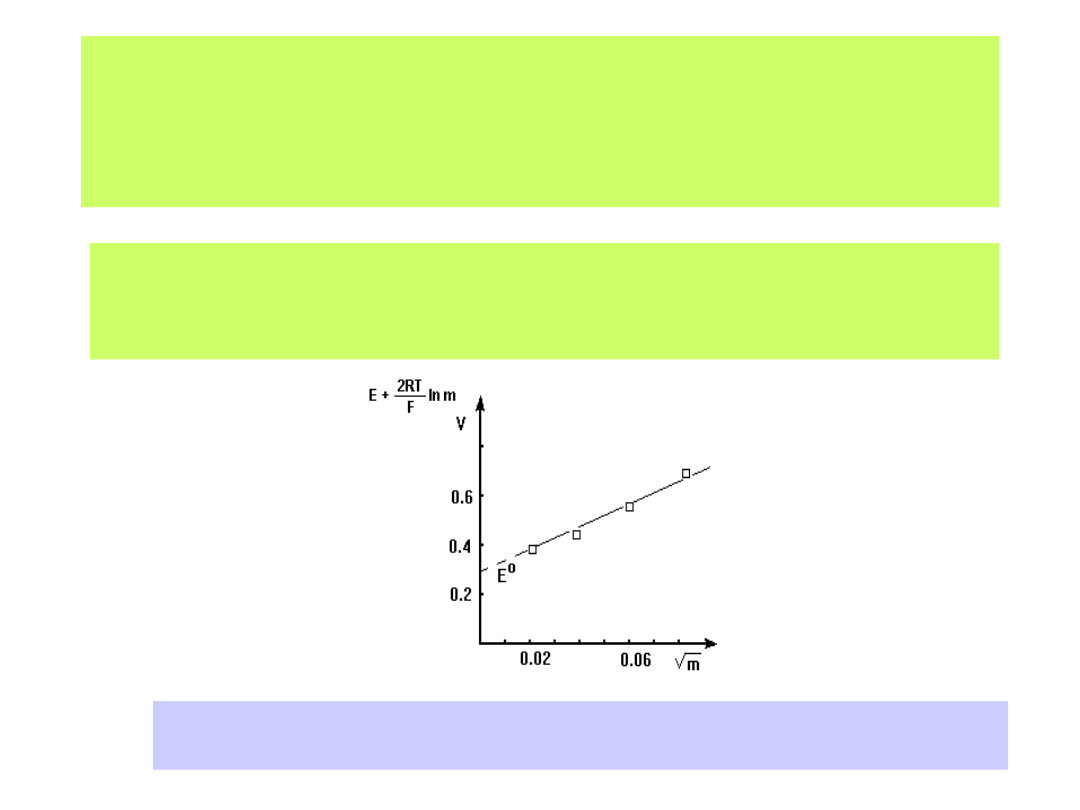
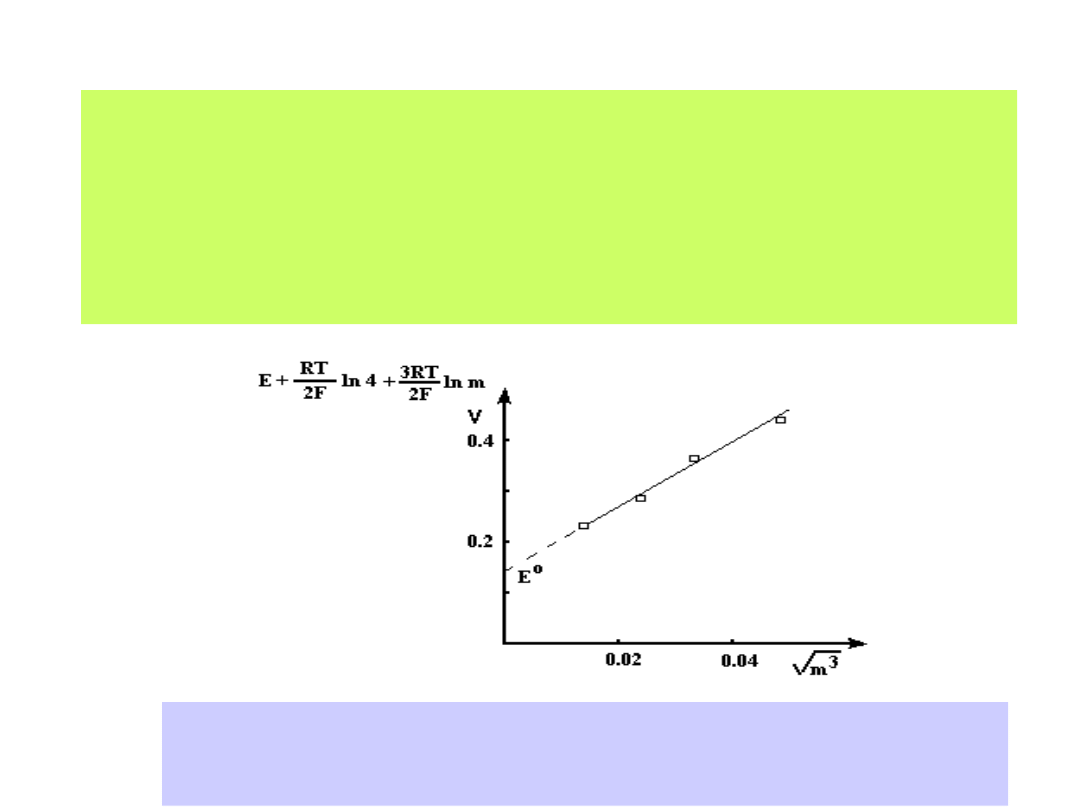
Wartość potencjału standardowego układów redox również wyznacza się
doświadczalnie budując odpowiednio zestawione ogniwo i mierząc
wartości SEM dla różnych stężeń roztworów elektrolitów. Graficzny zapis
zmierzonych SEM-ów ekstrapolujemy do wartości c

 0:

Dla ogniwa:

Pt H

2

  HCl  AgCl   Ag

otrzymamy wykres:

Ekstrapolacja graficzna wyników pomiarów SEM ogniwa Pt/H

2

/ HX/ AgX/Ag

pozwala na wyznaczenie wartości potencjału E

0

(m

1/2

 0)

19

1-54

Natomiast dla ogniwa o układzie półogniw:

Zn ZnCl

2

(m)    Hg

2

Cl

2

  Hg 

o reakcji podstawowej:

 

Zn +Hg

2

Cl

2

  Zn

2+

 +2Cl

-

 + 2Hg 

mamy zależność graficzną w postaci:

Ekstrapolacja wyników pomiarów SEM ogniwa zawierającego elektrolit

typu 2 : 1 pozwala na wyznaczenie wartości potencjału standardowego

dla

m

 0

20

1-54

WARTOŚCI STANDARDOWYCH POTENCJAŁÓW WYBRANYCH

(spośród ok. 900) UKŁADÓW REDOX

UKŁAD REDOX

REAKCJA REDOX

E

0

she

/V

Li

+

/ Li

H

2

(g) / OH

-

Na

+

/ Na

Mg(OH)

2

/ Mg

Mg

2+

/ M

Ti

2+

/ Ti

CdS /Cd

Si /H

2

O

Fe

2+

/ Fe

H

+

/ H

2

Cu

2+

/ Cu

Ag

2+

/Ag

Cl

2

/Cl

-

Li

+

+ e  Li

H

2

(g) + OH

-

 H

2

O + e

Na

+

+ e  Na

Mg(OH)

2

+2e 

Mg+2OH

-

Mg

2+

+ 2e  Mg

Ti

2+

+ 2e  Ti

CdS + 2e  Cd + S

-2+

Si+H

2

O SiO

2

+4H

+

+4e

Fe

2+

+ 2e  Fe

H

+

+ e  ½ H

2

Cu

2+

+ 2e  Cu

Ag

+

+ e  Ag

Cl

2

+ 2e  2 Cl

-

-3,045
-2,930

- 2,714

-2,682

-2,404

-1,752

- 1,233

-0,842
-0,440

0,000 (def.)

+0,344
+0,800
+1,359

21

1-54

3. INFORMACJE O OGÓLNEJ CHARAKTERYSTYCE WARSTWY

ELEKTROCHEMICZNEJ

 

Pojęcia przedstawione w tej informacji są wprowadzeniem do

zagadnień o kluczowym znaczeniu dla elektrochemii. Ich rozwinięcie

przedstawić można jedynie zostanie w ramach wykładu specjalizacyj-

nego.

Na granicy rozdziału dwóch faz powstaje obszar, w którym natężenie pola

elektrycznego ma wartość różną od zera. Źródłem tego pola jest

nadmiarowy ładunek elektrycznie naładowanych cząstek - tj. jonów,

elektronów, zorientowanych dipoli itd.

22

1-54

Obszar ten, o nadmiarowym ładunku elektrycznym, nosi nazwę

warstwy

elektrochemicznej

,

dawniej zwaną - podwójną warstwą elektryczną.

Powstawanie warstwy elektrochemicznej jest zjawiskiem o charakterze

powszechnie spotykanym. Mamy więc do czynienia z warstwą

elektrochemiczną na granicach faz:

-ciecz / ciecz (dla niemieszających się cieczy)

-ciecz / powietrze (zwana swobodną powierzchnią roztworu)

-elektroda / gaz (w znikomym stopniu dotyczy elektrochemii)

-elektroda / roztwór (zasadnicza grupa zagadnień).

23

1-54

Pojęcie i propozycje modelu elektrycznego warstwy elektrochemicznej

datują się już z XIX wieku ( Helmholtz, Gouy, Chapman, Stern, Parsons i

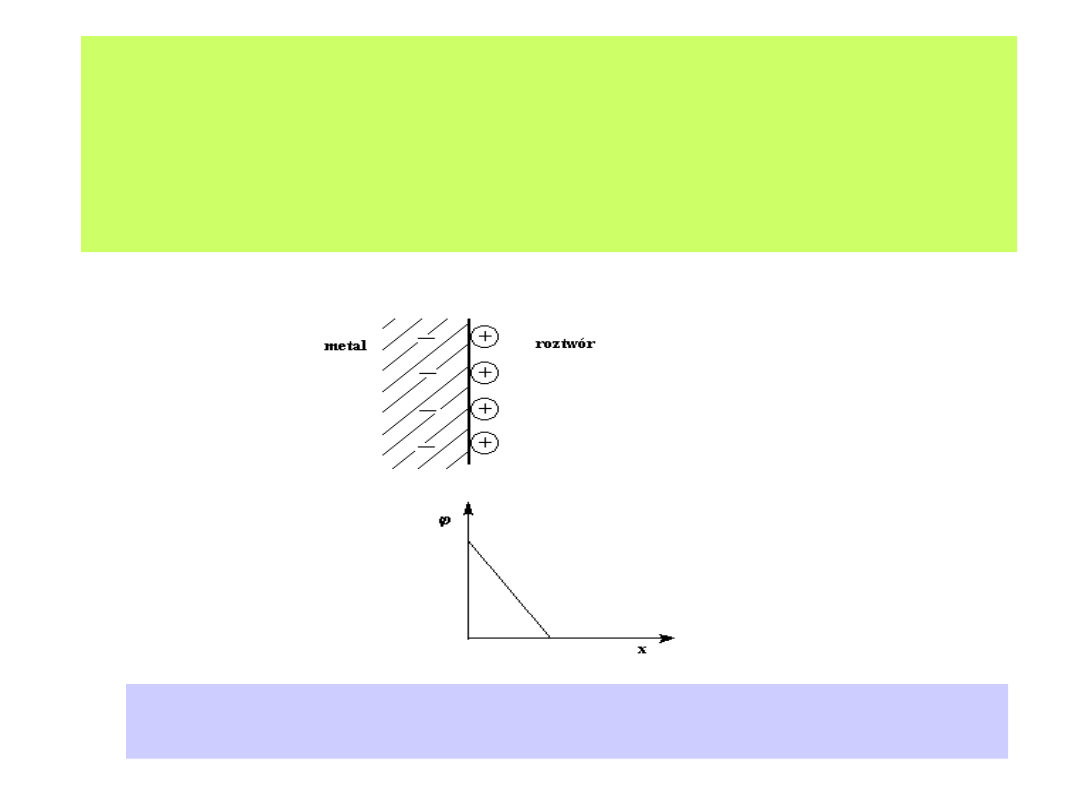
inni). Początek prostym modelem warstwy elektrochemicznej dał

Helmholtz:

Model warstwy elektrochemicznej według propozycji Helmholtza.

Zwraca uwagę liniowy spadek potencjału wraz ze wzrostem odległości od elektrody.

24

1-54

Zgodnie z dzisiejszymi poglądami złożona warstwa elektrochemiczna może

być zilustrowana w następujący sposób:

Model warstwy elektrochemicznej w roztworze zawierającym powierzchniowo

czynne cząsteczki organiczne: a) - dipole wody, b) - zaadsorbowane molekuły

organiczne, c) - specyficznie zaadsorbowane aniony, d) - hydratowane jony

tworzące warstwę OHP

1

w odległości wynikającej z oddziaływań dipoli wody w

IHP, e) - OHP

2

odległa od elektrody w zależności od oddziaływań molekuł

organicznych, f) - hydratowane jony w warstwie dyfuzyjnej

25

1-54

Taka budowa warstwy elektrochemicznej daje się w zastępczym obwodzie

elektrycznym zapisać jako szeregowe połączenie kondensatorów:

Metal IHP OHP

1

OHP

2

Opisuje to równanie

pojemności warstwy:

2

1

1

1

1

1

OHP

OHP

IHP

C

C

C

C







(26)

Wartości pojemności różniczkowej warstwy elektrochemicznej wyznacza

się doświadczalnie, a obecnie stosowane systemy aparatury pomiarowej

pozwalają na szybkie obliczanie jej wartości zgodnie z zastosowanymi

metodami pomiaru i oprogramowania komputerowego.

Gdzie z kolei pojemność różniczkowa opisana jest jako:

C

E

i

T

p

p



























,

,

2

2

(26 a)

lub

C

E

T

p

p

m



























,

,

)

(

(26 b)

26

1-54

4. PODSTAWY KINETYKI PROCESÓW ELEKTRODOWYCH

Jeżeli wynikiem procesu na rozważanej elektrodzie jest

przejście elektronu z elektrody do elektrolitu lub ładunku

dodatniego z elektrolitu do elektrody, to związany z tym prąd

elektryczny nazywa się

prądem katodowym

(I

k

). Prąd ten ma

znak ujemny.

Reakcja zachodząca jest

reakcją katodową lub reakcją

elektroredukcji.

Przypadek przeciwny - przejście ładunku dodatniego z elektrody

do elektrolitu lub odwrotne przejście elektronu z elektrolitu

charakteryzuje

prąd anodowy (I

a

)

o znaku dodatnim. Reakcja

zachodząca na tej elektrodzie jest

reakcją anodową lub

elektroutleniania.

27

1-54

Stosowana powszechnie gęstość prądu (i

a

, i

k

) dotyczy przeliczenia wartości

prądu na jednostkę powierzchni geometrycznej. Przeliczenie go na

rzeczywistą gęstość prądu (j

a

, j

k

) wymaga znajomości współczynnika

rozwinięcia powierzchni, co zwykle jest pomiarem dość skomplikowanym.

Głównym etapem elektrochemicznego procesu elektrodowego

jest bezpośrednia wymiana cząstek naładowanych między elektrodą a

roztworem. Kinetykę i mechanizm procesu elektrodowego rozpatruje się

w oparciu o

reakcję przejścia

(zwaną też reakcją przeniesienia ładunku

czy też wprost reakcją elektrodową).

28

1-54

Dokładniejsza

klasyfikacja

procesów

elektrodowych

uwzględnia

charakter przejścia ładunku pomiędzy elektrodą a substancją
elektroaktywną:

1. Przejście elektronu lub dziury między elektrodą a substancją
elektroaktywną.

2. Przejście jonu metalu z roztworu do elektrody lub odwrotnie.

3. Emisja elektronów z elektrody do roztworu z utworzeniem
solwatowanych elektronów, a następnie reakcja między solwatowanym
elektronem i obecnym

w roztworze "zmiataczem" elektronów (ang. scavenger), tj.
rozpuszczalnikiem lub

akceptorem elektronów.

Podstawowym warunkiem przejścia elektronu lub dziury z elektrody do
substancji elektroaktywnej (akceptora elektronów) jest jej obecność na
zewnętrznej płaszczyźnie Helmholtza (OHP) i obecność nieobsadzonego
termu zdolnego do przyjęcia elektronu.

Odpowiedni donorowy stan kwantowy elektronu w elektrodzie musi mieć
energię w przybliżeniu taką, jak nieobsadzony term w substancji „Ox”.
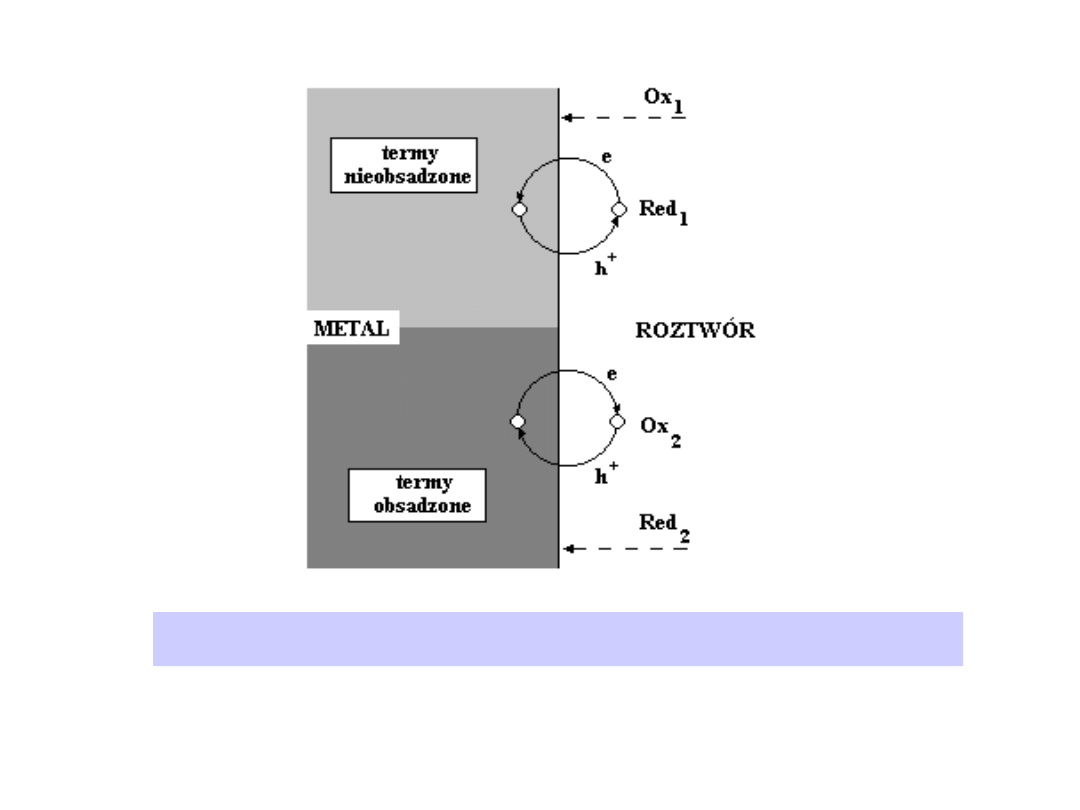
Podobnie jest w przypadku, gdy redukcja przebiega według mechanizmu
dziurowego, tj. wskutek przejścia dziury z substancji elektroaktywnej do
elektrody (Rys.)

Odwrotnie rzecz się ma w przypadku reakcji elektroredukcji - postać
„Red” musi mieć charakter elektronodonorowy i musi zawierać
obsadzony term o energii odpowiadającej nieobsadzonemu stanowi
kwantowemu w elektrodzie.

29

1-54

Przypomnijmy, że energia poziomu Fermiego (F) jest identyczna z
elektrochemicznym potencjałem elektronu w metalu. Zmieniając potencjał
wewnętrzny fazy (polaryzacja elektrody E =  ) można przesunąć



F

w

kierunku większych lub mniejszych energii odpowiednio ułatwiając lub
utrudniając proces elektrodowy.Ogólnie rzecz ujmując - schemat reakcji
elektrodowej wygląda nastąpująco:

 Ox+ + [term obsadzony]    Red + [term nieobsadzony]

 

Substancje elektroaktywne wchodzą z reguły w reakcję przejścia
elektronu, gdy zbliżają się na odległość zewnętrznej warstwy Helmholtza
(oznakowanej skrótem OHP). Niekiedy konieczna jest ich uprzednia
adsorpcja. Często na reakcję przejścia hamująco (inhibitująco) lub
przyspieszająco (stymulująco) działa adsorpcja produktów lub innych
cząstek z roztworu. Zmienia się wówczas struktura warstwy
elektrochemicznej i w konsekwencji obserwuje się zmianę szybkości
procesu elektrodowego.

Należy

pamiętać,

że

rzeczywisty

mechanizm

procesu

elektrodowego należy odróżnić od sumarycznej reakcji
zachodzącej na elektrodzie.

Występowanie gradientów stężenia reagentów elektroaktywnych w
otoczeniu elektrody (przestrzeni przyelektrodowej), obecność pola
elektrycznego i działanie sił mechanicznych uruchamiają procesy
transportu.

30

1-54

Ilustracja do rozważań o mechanizmie reakcji elektrodowej. Przejście

elektronu i przejście dziury

31

1-54

Substancje elektroaktywne wchodzą z reguły w reakcję

przejścia, gdy zbliżają się na odległość OHP.

Niekiedy konieczna jest ich uprzednia adsorpcja. Często na

reakcję przejścia hamująco (inhibitująco) lub przyspieszająco

(stymulująco) działa adsorpcja produktów lub innych cząstek z

roztworu. Zmienia się wówczas struktura warstwy

elektrochemicznej i w konsekwencji obserwuje się zmianę

szybkości procesu elektrodowego.

32

1-54

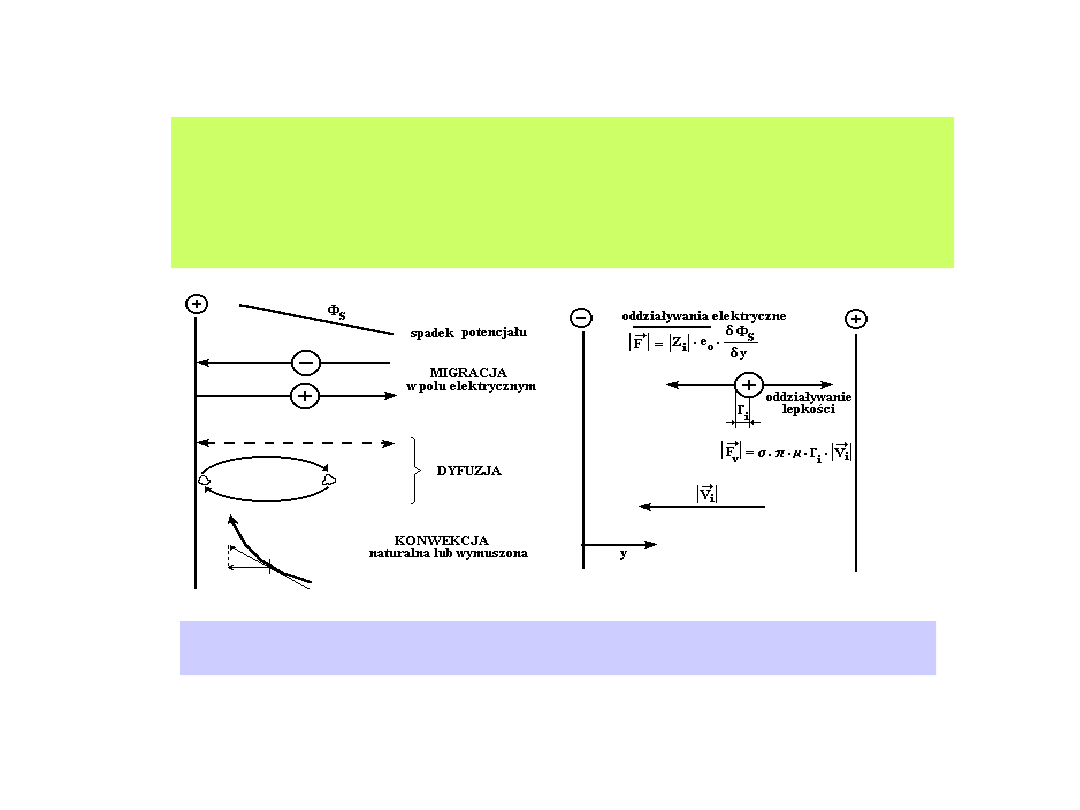
Występowanie gradientów stężenia reagentów

elektroaktywnych w otoczeniu elektrody (przestrzeni

przyelektrodowej), obecność pola elektrycznego i działanie sił

mechanicznych uruchamiają procesy transportu.

Transport jonowy w roztworze. a) - mechanizmy transportu substancji

jonowych, b) - siły działające na substancje jonowe.

33

1-54

Reakcja elektrodowa zwykle przebiega w potencjale innym niż potencjał

równowagowym. Charakteryzuje ją wówczas wartość

nadpotencjału

reakcji:

















































ox

red

c

RT

E

E

zF

c

RT

E

E

zF

zFk

j

)

(

exp

(

)

1

(

exp

0

0

0





gdzie k

0

– stała szybkości reakcji opisująca proces redox

 - współczynnik przejścia elektronów. Jeśli  = 0.5, to reakcja

elektrodowa jest reakcją doskonale odwracalną. Jest to też
prawdopodobieństwo energetycznie barierowego i

bezbarierowego przejścia elektronu

0

Re

0

0

ln

d

ox

c

c

zF

RT

E

E









Uwzględniając stężenia form Ox i Red wraz z potencjałem E

0

odnosimy

nadpotencjał do potencjału równowagowego reakcji poprzez wyrażenie
prądu wymiany:

(27)

(28)

34

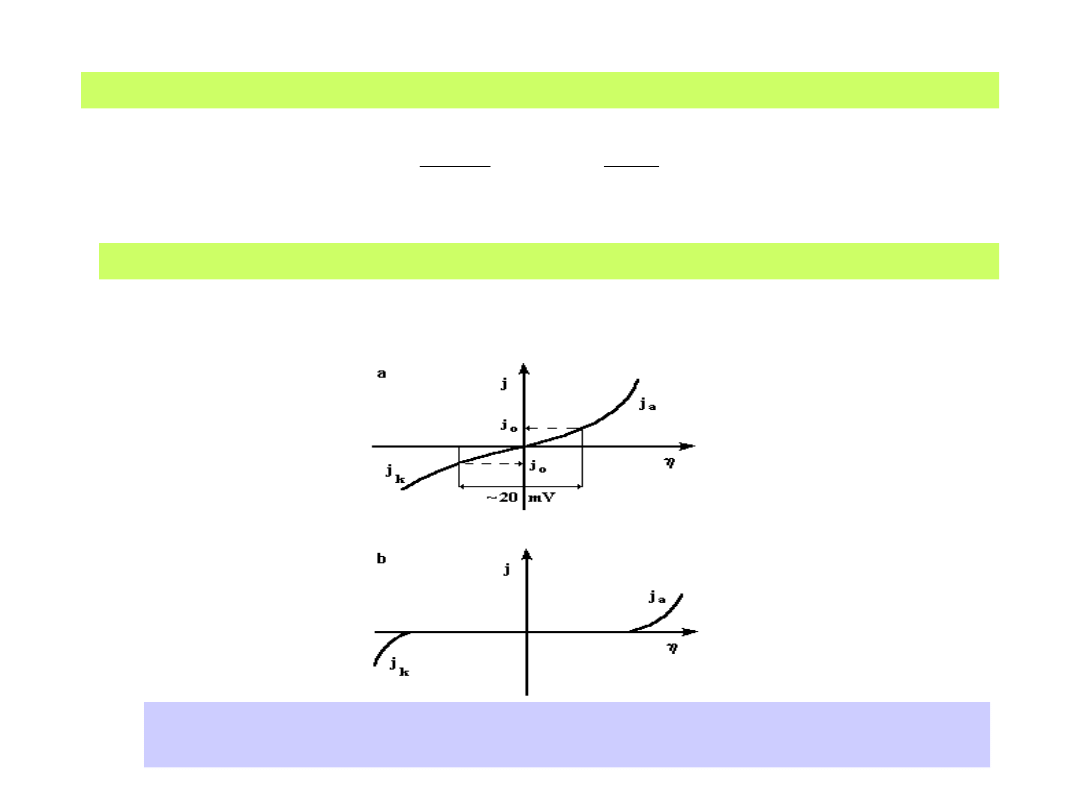
1-54

Równanie (28) można przekształcić i otrzymać je w postaci:

 





























zF

RT

zF

RT

j

j

exp

)

1

(

exp

0

(29)

gdzie z kolei:





d

Ox

c

c

zFk

j

Re

1

0

0







(30)

Podstawowe krzywe polaryzacji elektrodowej: a) dla <<(RT/zF)

b) dla  (RT/zF)

35

1-54

 

2. Jeśli nadpotencjał ma dużą wartość w porównaniu z RT/zF ,

wówczas równanie

(30)

 

po zlogarytmowaniu prowadzi do równania Tafela:

 

(31)

 lub prościej je zapisując w postaci równania liniowego:

(32)

Omówione przypadki odnoszą się do odwracalnych (1) i

nieodwracalnych lub quasi-odwracalnych (2) reakcji pierwszego

rzędu. Oczywiste jest, że jak w klasycznej kinetyce chemicznej,

podobne rozważania obejmują także reakcje wyższych rzędów.















RT

zF

j

j



exp

0

j

zF

RT

j

zF

RT

lg

303

,

2

lg

303

,

2

0











j

b

a

lg







36

1-54

Równanie Tafela, opisujące kinetykę reakcji

zachodzącą w warunkach zewnętrznego źródła

elektronów (a głównie występujący w nim

współczynnik n



) jest klasycznym przykładem

ilustrującym fakt, że:

proces elektrochemiczny nie jest procesem
czysto chemicznym i klasyczna
termodynamika reakcji chemicznych nie
może być stosowana.

Równanie to ponadto opisuje w swoisty sposób

istnienie bariery potencjału wynikającej z teorii

absolutnej szybkości reakcji chemicznych.

37

1-54

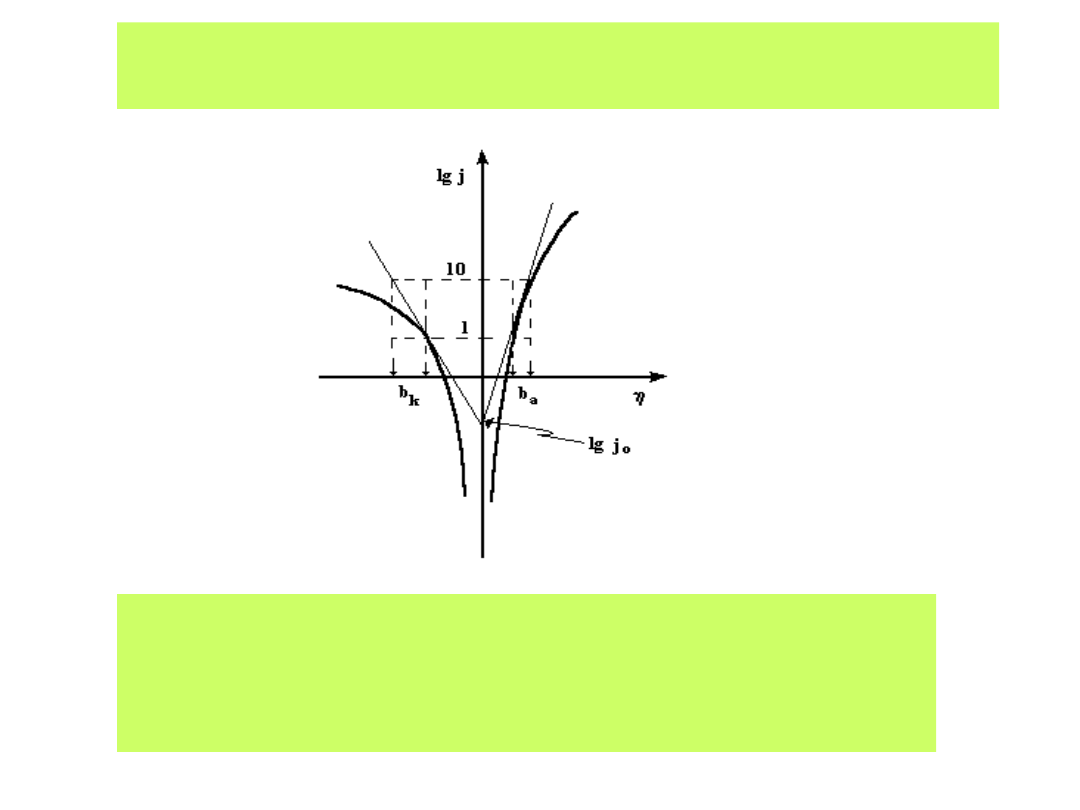
Zależności Tafela ilustruje wykres półlogarytmiczny, w którym albo
znajdujemy odcinki prostoliniowe, albo prowadzimy styczne ( jest to
mniej dokładne:

Z którego wyznacza się wartość prądu wymiany j

0

oraz

współczynniki Tafela b

a

i b

k

charakteryzujące odwracalność reakcji

i liczby elektronów przenoszonych w procesach anodowych

i katodowych

38

1-54

Składnik

 

 

Rola składnika w procesie

elektroosadzania metalu

 

1) Sól metalu (ML

m

n+

)

2) Czynnik redukujący (Red)
3) Bufor pH
4) Ligand kompleksujący (L)
5) Dodatki
 
 

Źródło jonów metalu osadzanego
Redukcja jonu metalu z jonu ML

n+

m

Regulacja wartości pH roztworu
Tworzenie jonu kompleksowego (ML

n+

m

)

stabilizuje skład kąpieli lub reguluje wielkość
osadzanych ziaren metalu
 
 

 

39

5.KATODOWE ELEKTROSADZANIE METALI

Elektrodowe osadzanie metali jest określeniem pochodzącym z lat 40 ubiegłego
stulecia, wywodzącym się z autokatalitycznego osadzania niklu przy
nieobecności zewnętrznego źródła prądu.
Obecnie określenie to jest powszechnie stosowane. Obejmuje różnorodne
procesy elektroosadzania metali i stopów metali na dowolnym podłożu z innego
materiału przewodzącego.

Proces osadzania metalu powinien uwzględniać warunki zawarte w tabeli:

1-54

Ogólny schemat reakcji redukcji kompleksu do metalu można opisać

równaniem:

 

ML

m

n+

+ Red  M + mL + Ox

n+

na którą składają się procesy cząstkowe:

redukcji:

M L

m

n+

+ ne  M + mL

i utleniania:

Red +

 ne + Ox

n+

Konieczna jest znajomość tzw. potencjału elektroosadzania, który

wyznaczamy na podstawie wykresów:

40

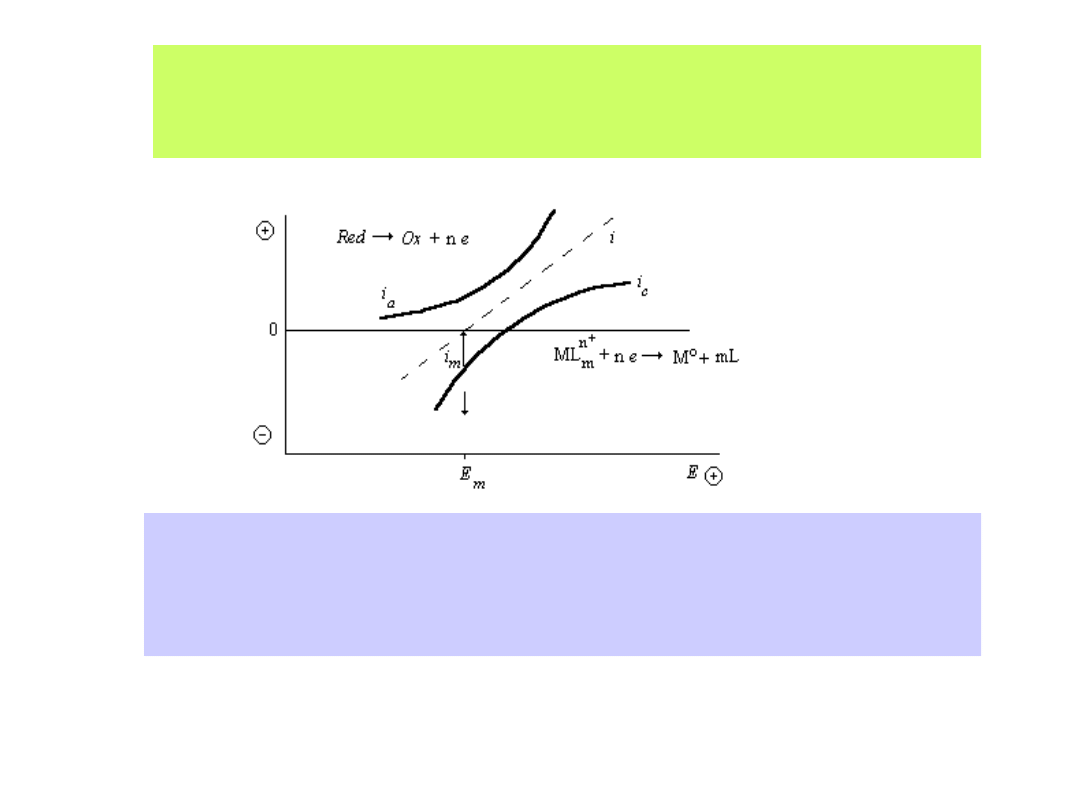
1-54

Konieczna jest też znajomość tzw. mieszanego potencjału

elektroosadzania metalu,

który wyznaczany jest na podstawie wykresu:

Wyznaczanie mieszanego potencjału elektroosadzania (E

m

):

i - sumaryczny prąd reakcji, i

a

- cząstkowy anodowy prąd reakcji,

i

k

- cząstkowy katodowy prąd reakcji, i

m

- prąd elektroosadzania w mieszanym

potencjale E

m

41

1-54

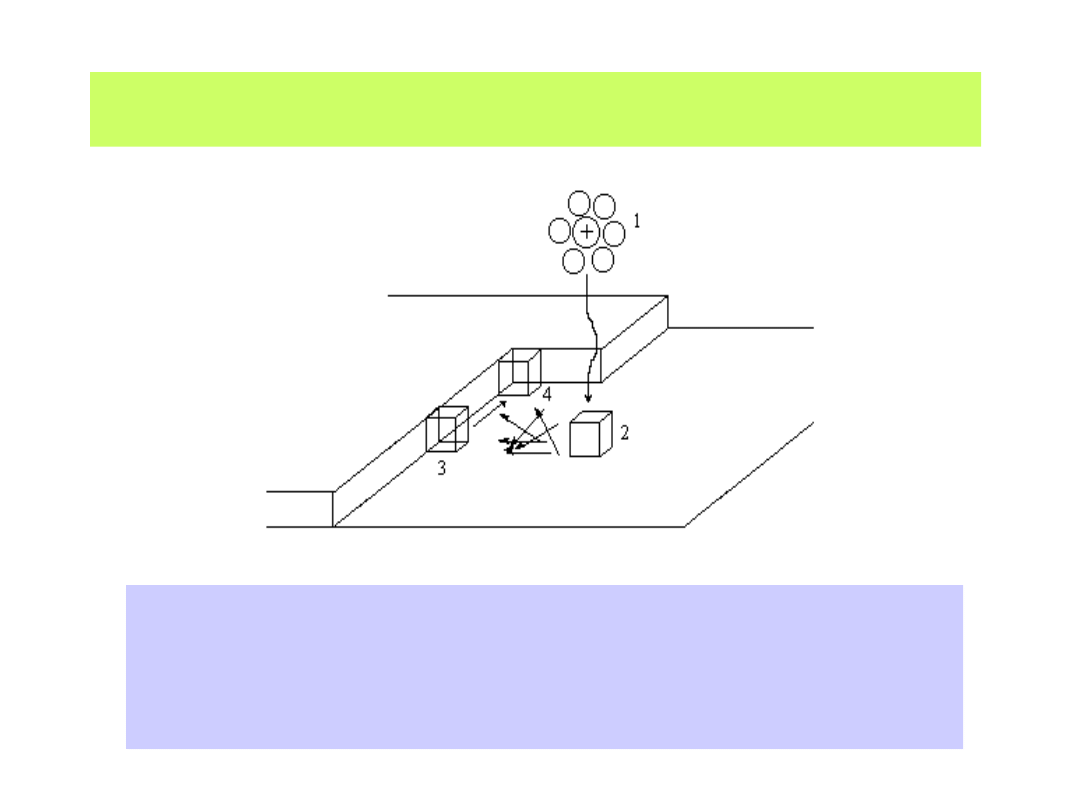
Kation zbliżający się do katody rozładowuje się i umieszcza się na niej

w sposób podany na poniższym schemacie

1 - jon zbliżający się do powierzchni traci otoczkę solwatacyjną, wymienia

elektron i w położeniu 2 tworzy tzw. adatom (atom zaadsorbowany);

3 - poprzez powierzchniową migrację dyfuzyjną atom wbudowuje się w sieć

krystaliczną, by przesunąć się w położenie 4 - o najmniejszej energii sieciowej

42

43

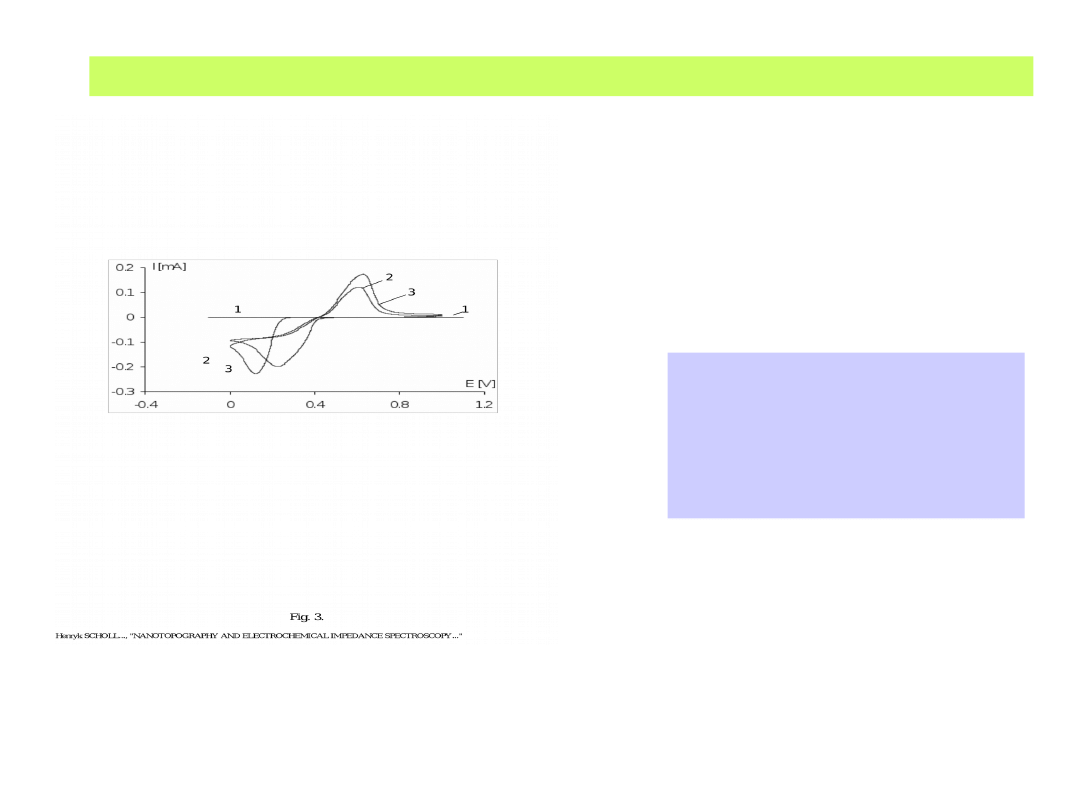
A jak to wygląda w rzeczywistości ?

Krzywa polaryzacyjna

osadzania katodowego i

roztwarzania anodowego

palladu z roztworu PdCl

6

2-

na podłożu złotym i na

graficie HOPG

1-54

44

2 m

Pd 0.96%
C 99%

Pd 0.00%
C 99.99%

Pd 0.78%
C 99%

0

5

10

15

Energy (keV)

0

2

4

6

8

10

cps

C

O

Pd

Pd

Pd Pd

2 m

Pd 0.00%
C 99.99%

Pd 1.01%
C 98%

Pd 1.28%
C 98%

Pd 0.07%
C 99.9%

0

5

10

15

Energy (keV)

0

20

40

60

80

100

cps

C

O

Pd

Pd

Pd

Pd

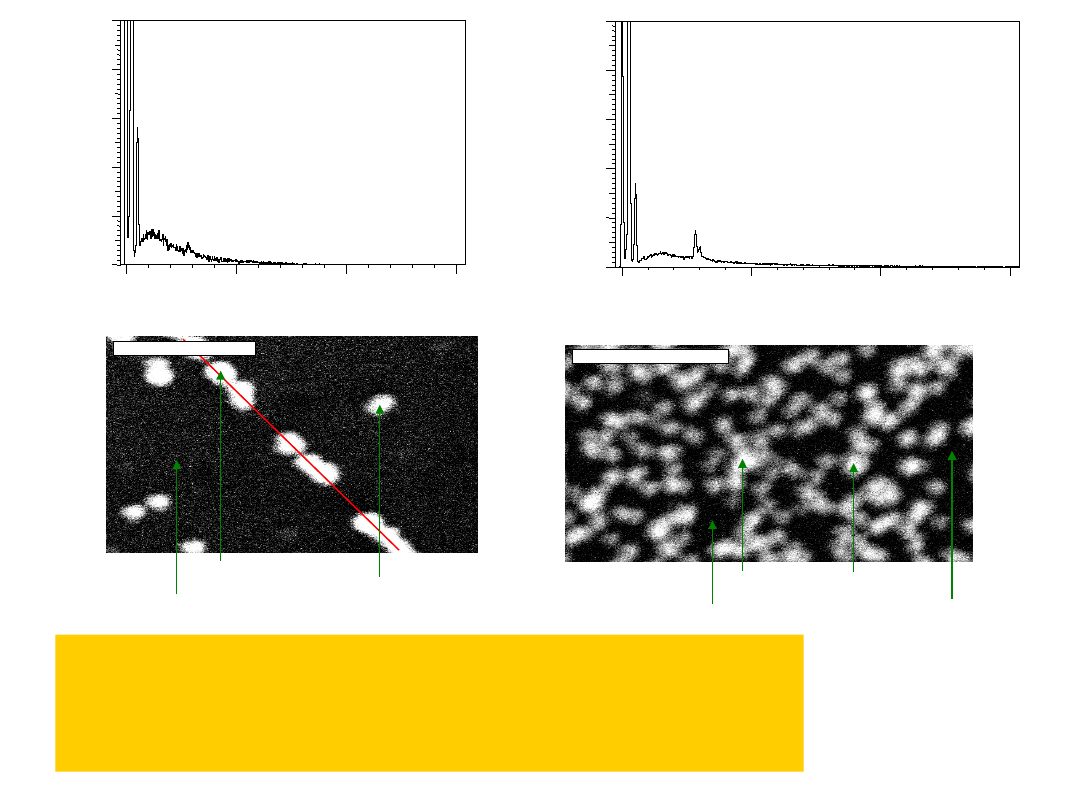
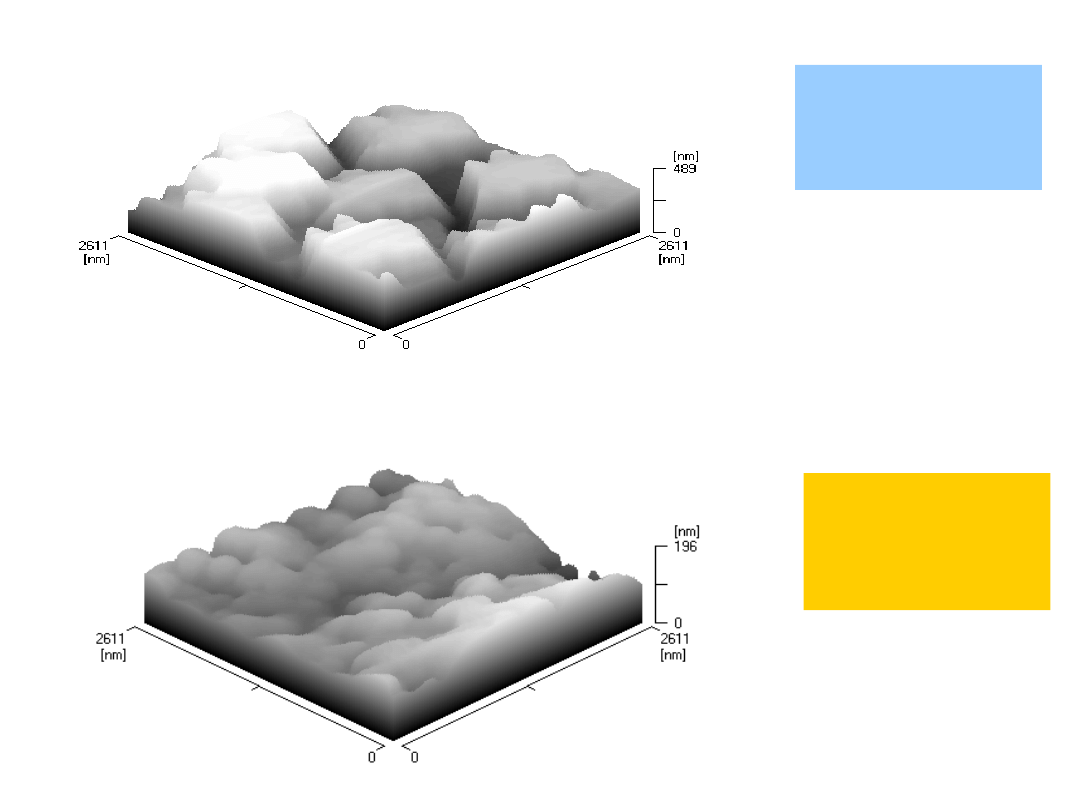
Widma i struktury analizy SEM-EDX (ex situ) elektrody

HOPG: a) po samorzutnym osadzaniu palladu t = 15 min. i b)

po elektrochemicznym osadzaniu palladu

(1 krzywa elektroosadzania) w roztworze zawierającym 0.01

mol/dm3 (NH4)2PdCl4

1-54

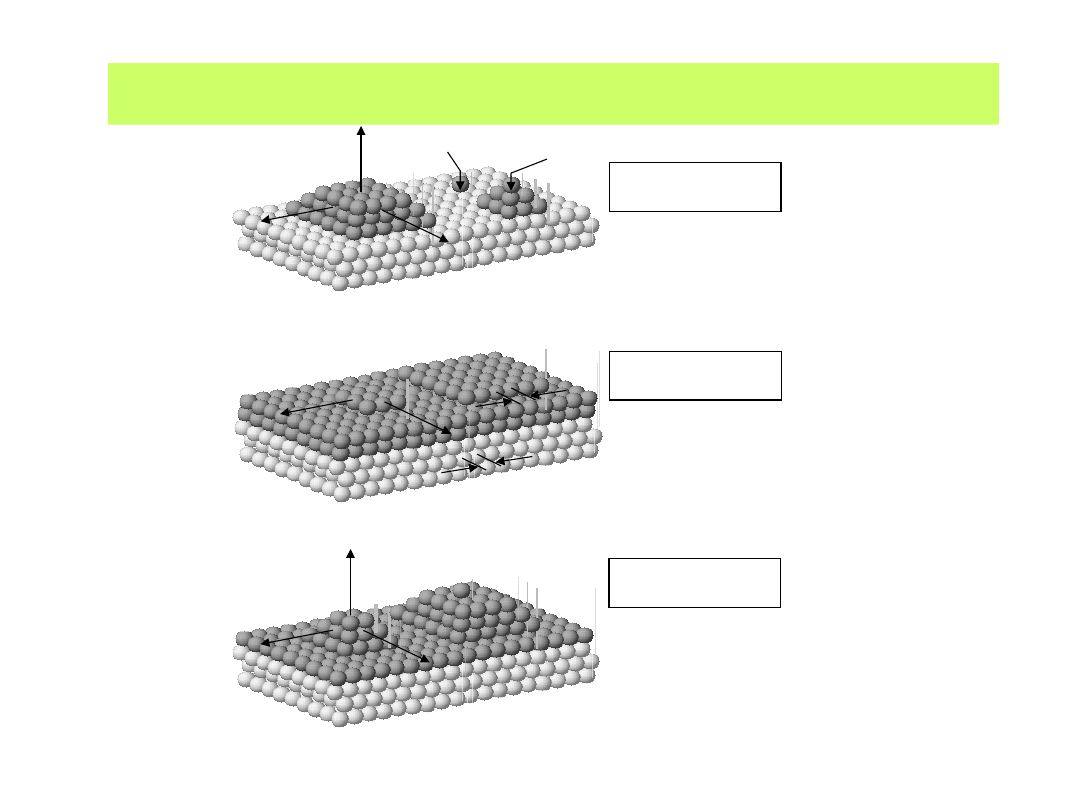
45

b)

Krystality

rozbudowują się.

Obraz po 10

cyklach

a)

Po wielokrotnym

elektroosadzaniu

warstwa palladu

rośnie i tworzy

stabilną warstwę

1-54

46

Dalszy przyrost warstw atomów metalu znalazł swój obraz w kilku

propozycjach modelowych:

Ψ

Me-Me

Ψ

Me-S

Ψ

Me-S

<< Ψ

Me-Me

model wzrostu "Volmer-Weber"

(wzrost 3D wysp)

a)

d

0

Me

d

0

S

Ψ

Me-S

>> Ψ

Me-Me

d

0

Me

≈ d

0

S

model wzrostu "Frank-van der

Merwe"

(wzrost warstwa na warstwie)

b
)

Ψ

Me-S

>> Ψ

Me-Me

d

0

Me

≠ d

0

S

model wzrostu "Stranski-

Krastanov"

(wzrost 3D wysp na wcześniej

osadzonej monowarstwie)

c)

1-54

47

Rzeczywiste obrazy powierzchni w skali atomowej (w

rozmiarach nanometrowych; 1 nm =10

-9

m, czyli 10

-6

mm można

obecnie doświadczalnie obserwować za pomocą systemów

pomiarowych wyposażonych w Elektrochemiczny Skaningowy

Mikroskop Tunelowy (ESTM) dla powierzchni przewodzących

prąd elektryczny lub w Mikroskop Sił Atomowych (AFM) dla

powierzchni nie przewodzących prądu.

Wyniki naszych prac można zobaczyć na posterach

prezentowanych na korytarzach Katedry

1-54

48

6. KATODOWE WYDZIELANIE WODORU

 

Katodowe wydzielanie wodoru opisuje sumaryczne równanie:

H

+

+ e  ½ H

2

(33)

W rzeczywistości proces ten przebiega dwuetapowo, według

mechanizmu Volmera-Tafela lub według mechanizmu Volmera-

Heyrovskiego. W przypadku kwaśnego roztworu elektrolitu reakcje

Volmera, Tafela i Heyrovskiego opisują równania:

a) reakcja wydzielania wodoru jest

reakcją przeniesienia elektronu

,

zwana reakcją Volmera:

H

3

O

+

+ e  H

ads

+ H

2

O

(34)

b) następuje reakcja rekombinacji zaadsorbowanych atomów wodoru,
zwana reakcją Tafela:

2 H

ads

 H

2

(35)

c) następuje elektrochemiczna desorpcja zaadsorbowanego wodoru
(pochodzącego np. z reakcji Volmera) połączona z równoczesną
wymianą ładunku, zwana reakcją Heyrovsky'ego.

H

ads

+ H

3

O

+

+ e  H

2

+ H

2

O(36)

1-54

49

Zależnie od rodzaju metalu zmienia się trwałość wiązań M - H,

odzwierciedlona w wartości entalpii swobodnej adsorpcji atomów

wodoru. Zatem natura metalu wywiera duży wpływ zarówno na

kinetykę, jak i na mechanizm procesu wydzielania wodoru na danej

elektrodzie. Eksperymentalnie uwidacznia się to w wartości prądu

wymiany i współczynnika przejścia elektronu .

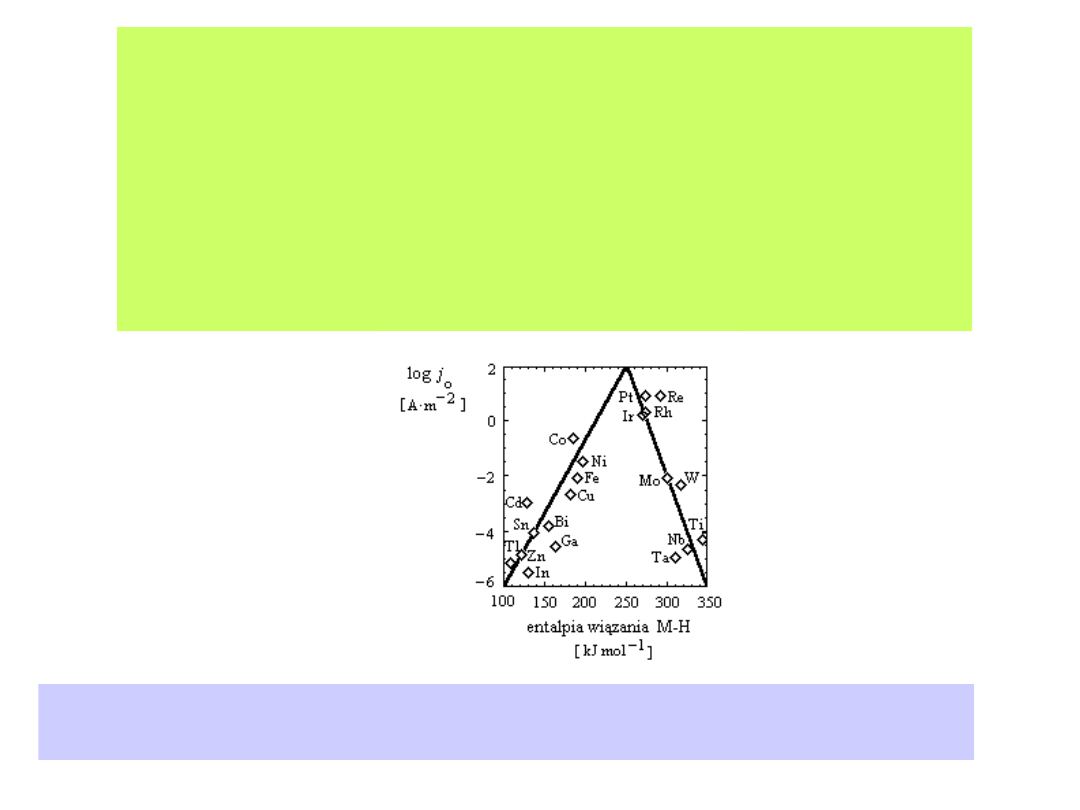
Ilustrują to tzw. krzywe wulkaniczne zaproponowane przez

Trasattiego

Wartości gęstości prądu wydzielania wodoru na różnych metalach z wodnych roztworów

elektrolitów w zależności od entalpii wiązania metal - wodór (kJ mol-1). Wykres wykonany

na podstawie pracy J. Trasatti, J. Electroanal. Chem., 39 (1972), 163

1-54

50

W przypadku metali o niskiej energii adsorpcji wodoru, jak Pb, Ag, Hg,

proces wydzielania wodoru jest limitowany przez reakcję Volmera.

Metale te charakteryzuje wysoki nadpotencjał wydzielania wodoru,

oczywiście z wodnych roztworów elektrolitów.

Im silniej wodór jest adsorbowany na powierzchni elektrody (np. Pt,

Ir, Rh, W), tym szybciej przebiega reakcja Volmera, a szybkość

wydzielania wodoru jest limitowana przez przebieg reakcji

Heyrovskiego lub reakcji Tafela. Elektrody takie charakteryzują się

niskim nadpotencjałem wydzielania wodoru.

We współczesnej technologii i w poszukiwaniach alternatywnych

źródeł energii stosowanie metali, ich stopów i tzw. kompozytów ma

wielkie znaczenie dla otrzymywania, magazynowania lub przesyłania

gazowego wodoru. Omawiane jest to w wykładzie o alternatywnych

źródłach energii.

1-54

51

7. ANODOWE WYDZIELANIE TLENU

 

Powróćmy do wielokrotnie sygnalizowanego procesu elektrodowego

wydzielania tlenu. Anodowe wydzielanie tlenu jest - mimo pozorów –

procesem wysoce złożonym.

Najlepiej został zbadany ten proces przebiegający na elektrodach z

metali szlachetnych Au, Pt, Rh). Reakcja przebiega z dużym

nadpotencjałem, spełniając równanie Tafela w zakresie potencjałów od

1,2 do 2,0 V

she

.

Etapem limitującym szybkość reakcji wydzielania tlenu jest

prawdopodobnie adsorpcja jonu hydroksylowego lub cząsteczki wody na

powierzchni metalu pokrytej tlenkami:

OH

-

ads

rds OH

ads

+ e (35)

lub H

2

O

ads

rds OH

ads

+ H

+

+ e (36)

Po nich następują szybkie reakcje: 2 OH

ads

 O

ads

+ H

2

O (37)

2 O

ads

 O

2

(38)

1-54

52

8. ANODOWE ROZTWARZANIE METALI

Anodowe utlenianie metali następuje w wyniku:

a)

samorzutnego utleniania (roztwarzania) metalu stanowiącego w

układzie elektrolizera elektrodę dodatnią, znajdującą się

w roztworze elektrolitu;

b) samorzutnego lub kontrolowanego roztwarzania metalu z

wytworzeniem trwałej warstewki pasywnej,

c) korozyjnego roztwarzania metali stanowiących materiał anodowy i

pod wpływem czynników zewnętrznych;

Korozji

, jej rodzajom i sposobom zapobiegania poświęcony jest inny

wykład;

d) kontrolowanego roztwarzania metalu przy niewielkich wartościach

gęstości prądu anodowego (elektropolerowanie), szczególnie

w nowoczesnych

nanotechnologiach i w elektronice;

e) kontrolowanego roztwarzania metalu w warunkach wymuszonego

anodowego prądu o wysokiej gęstości (rzędu kilkuset A /m

2

) i przy

turbulentnej wymianie elektrolitu (zwanego inaczej anodową obróbką

metali - ang. Electromachining.

1-54

53

9. REDUKCJA I UTLENIANIE ZWIĄZKÓW ORGANICZNYCH

ELEKTROSYNTEZA ORGANICZNYCH POŁĄCZEŃ

Pierwszą reakcję elektrodową związku organicznego wykonał

Faraday w XVIII wieku prowadząc elektrolizę roztworu kwasu octowego

dla udowodnienia, że i produkty gazowe (tutaj CO

2

) również są objęte

prawem zachowania masy.

Pierwszą elektrosyntezę przedłużania łańcucha alifatycznego

wykonał Kolbe w XIX wieku.

Dzisiaj metody elektroanalizy, elektroredukcji, elektroutleniania i

elektropolimeryzacji związków organicznych stosowane są powszechnie

ze względu na:

1)

selektywność reakcji wybranej grupy funkcyjnej;

2)

czystość produktów elektrosyntezy ze względu na brak produktów

reakcji reduktorów lub utleniaczy chemicznych (oczyszczanie

produktów końcowych);

3)

możliwość prowadzenia procesów elektrodowych w odpowiednio

4)

dobranych rozpuszczalnikach i na dowolnie wybranej elektrodzie.

1-54

K O N I E C

DZIĘKUJĘ ZA UWAGĘ

51