Wykład 6: Testy zgodności

dopasowania

Biometria i

Biostatystyka

Testy zgodności



Te metody znajdują zastosowanie
przy analizie danych w skali
nominalnej, pozwalają sprawdzić czy
obserwowany rozkład

zliczeń

(nigdy

częstotliwości lub proporcji) zgadza
się z rozkładem hipotetycznym.



Najbardziej znaną techniką analizy
jest test zgodności chi-kwadrat (χ

2

).

Wprowadzenie



Załóżmy, że genetyk w ramach
eksperymentu skrzyżował
mieszaną populację F

1

i otrzymał

potomstwo F

2

z 90-oma

potomkami, z których n

1

=80 ma

fenotyp typu wild-type, a u n

2

=10

zaobserwowano mutacje.

Wprowadzenie



Genetyk, zgodnie z prawem
dziedziczenia (model recesywny), założył
stosunek fenotypów 3:1, ale rzeczywisty
stosunek wyniósł 80/10 = 8:1.



Spodziewane wartości p i q wynoszą

odpowiednio dla wild-type i mutantów.

25

.

0

q

ˆ

75

.

0

p

ˆ





and

Wprowadzenie



Używamy symbolu „daszek” żeby
zaznaczyć hipotetyczne lub
oczekiwane wartości proporcji.



Obserwowane proporcje tych
dwóch klas wynoszą odpowiednio

11

.

0

q

89

.

0

p

90

10

90

80









and

Wprowadzenie



Innym sposobem pokazania różnic
między wartościami oczekiwanymi
a obserwowanymi to wyrazić je w
zliczeniach (niektórzy nazywają je
częstościami).

Wprowadzenie



Obserwowana liczba zliczeń to

n

1

=80 i n

2

=10 dla dwóch fenotypów.



Oczekiwana liczba zliczeń to

gdzie N to liczność próby - liczba

potomków.

5

.

22

90

25

.

0

N

qˆ

n

ˆ

5

.

67

90

75

.

0

N

p

ˆ

n

ˆ

2

1





















Wprowadzenie



Czy obserwowane odchylenie od hipotezy

3:1 jest tak wielkie, że praktycznie

nieprawdopodobne?



Innymi słowy, czy zaobserwowane dane

wystarczająco różnią się od wartości

oczekiwanych, żeby odrzucić hipotezę

zerową? – Jakie jest prawdopodobieństwo,

że przy powtórzeniu eksperymentu

zaobserwujemy sytuację taką jak ta albo

jeszcze „gorszą”?

Wykorzystanie funkcji
gęstości
prawdopodobieństwa



Rozkład, w którym p jest
prawdopodobieństwem naturalnego
fenotypu, a q zmutowanego, jest
rozkładem dwumianowym.



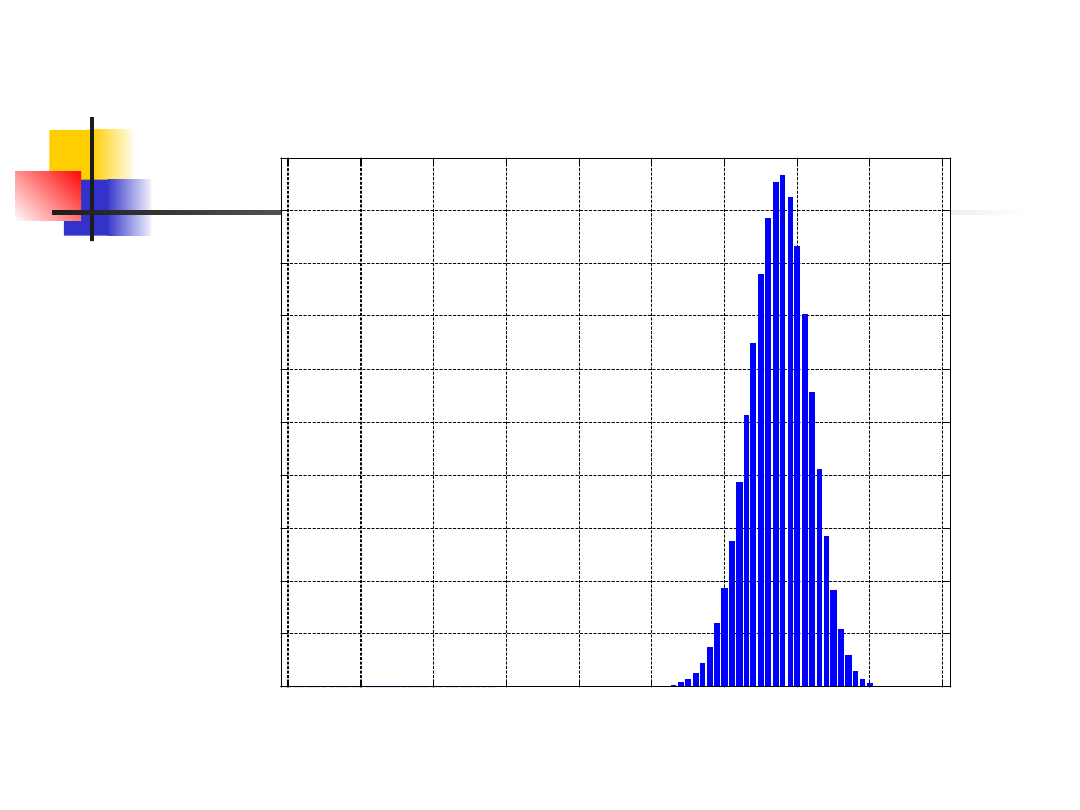
Możemy wyliczyć prawdopodobieństwo
otrzymania wyniku 80 naturalnych i 10
zmutowanych fenotypów, podobnie jak dla
wszystkich „gorszych” przypadków w
próbie 90 potomków dla

25

.

0

q

ˆ

75

.

0

p

ˆ





and

0

10

20

30

40

50

60

70

80

90

0

0.01

0.02

0.03

0.04

0.05

0.06

0.07

0.08

0.09

0.1

k

p

(k

)

Binomial pdf, N=90, p=0.75

Wykorzystanie funkcji
gęstości
prawdopodobieństwa

jest równe dopełnieniu do jedności
wartości dystrybuanty.





























90

80

k

k

N

k

90

80

k

k

N

k

q

ˆ

p

ˆ

)!

k

N

(

!

k

!

N

q

ˆ

p

ˆ

k

N

Wykorzystanie funkcji
gęstości
prawdopodobieństwa



Wyliczona wartość jest
prawdopodobieństwem 0.00084895
uzyskania wyniku co najmniej tak
odległego od hipotezy jak obserwowany.



Zauważ, że jest to test jednostronny;
alternatywna hipoteza mówi, że jest
więcej potomków z fenotypem typu wild-
type, niż liczba określona przez prawo
Mendla.

Wykorzystanie funkcji
gęstości
prawdopodobieństwa



Zaobserwowana próba jest dość
rzadkim wynikiem i możemy
wnioskować, że to jest istotne
odchylenie od oczekiwań.

Zastosowanie przedziałów
ufności



Jest to łatwiejsze podejście,
wymagające obliczenia
przedziałów ufności dla
dwumianowych proporcji i
przeprowadzenia wnioskowania
statystycznego w oparciu o
uzyskane wyniki.

Test zgodności



Opracujemy trzecie podejście do
oceny hipotezy zerowej - poprzez
testy zgodności dopasowania.



Tabela przedstawia dotychczasowe
wyniki.

Test G

Fenot

ypy

Obserwow

ane

zliczenia

Obserwowa

ne

proporcje

Oczekiw

ane

proporcj

e

Oczekiw

ane

zliczenia

Wild-

type

80

0.89

0.75

67.5

Mutan

t

10

0.11

0.25

22.5

Suma

90

1.0

1.0

90.0



Test G



Test G może być skonstruowany
następująco:
Prawdopodobieństwo zaobserwowania
wyniku zgodnego z próbą, przy
założeniu, że parametry p i q rozkładu
są równe proporcjom w próbie, wynosi

1326838

.

0

90

10

90

80

80

90

10

80







































Test G

Prawdopodobieństwo zaobserwowania
wyniku zgodnego z próbą, przy
założeniu proporcji Mendla, jest równe

0005518

.

0

4

1

4

3

80

90

10

80







































Test G

Jeśli obserwowane proporcje są zgodne

z proporcjami z hipotezy zerowej,

obydwa obliczone wcześniej

prawdopodobieństwa będą równe, a ich

stosunek L równy 1.
Im większa różnica między proporcjami,

tym większe odchylenie L od 1.

Test G

Stosunek tych dwóch prawdopodobieństw
lub wiarygodności może być użyty w formie
statystyki do zmierzenia zgodności między
zliczeniami w próbie a oczekiwanymi.

Test G (logarytmiczny test ilorazu
wiarygodności)

to test oparty właśnie na

takim stosunku.

Test G

Zostało dowiedzione, że rozkład

G = 2 ln L

może być przybliżony przez rozkład χ

2

z jednym stopniem swobody.

Test G

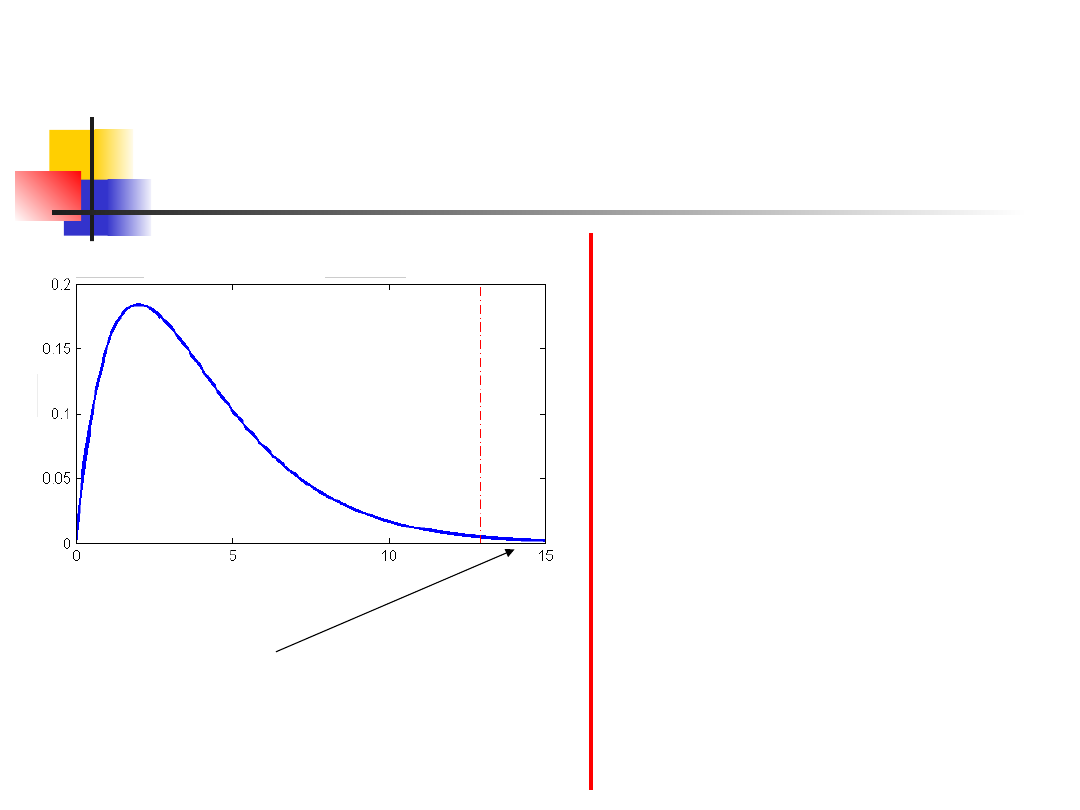
W naszym wypadku

G = 2 ln L = 10.96524

Jeśli porównamy tę wartość z rozkładem

χ

2

o jednym stopniu swobody (df),

otrzymujemy że wynik jest istotny
statystycznie

(p-wartość = 0.000928 < 0.001)

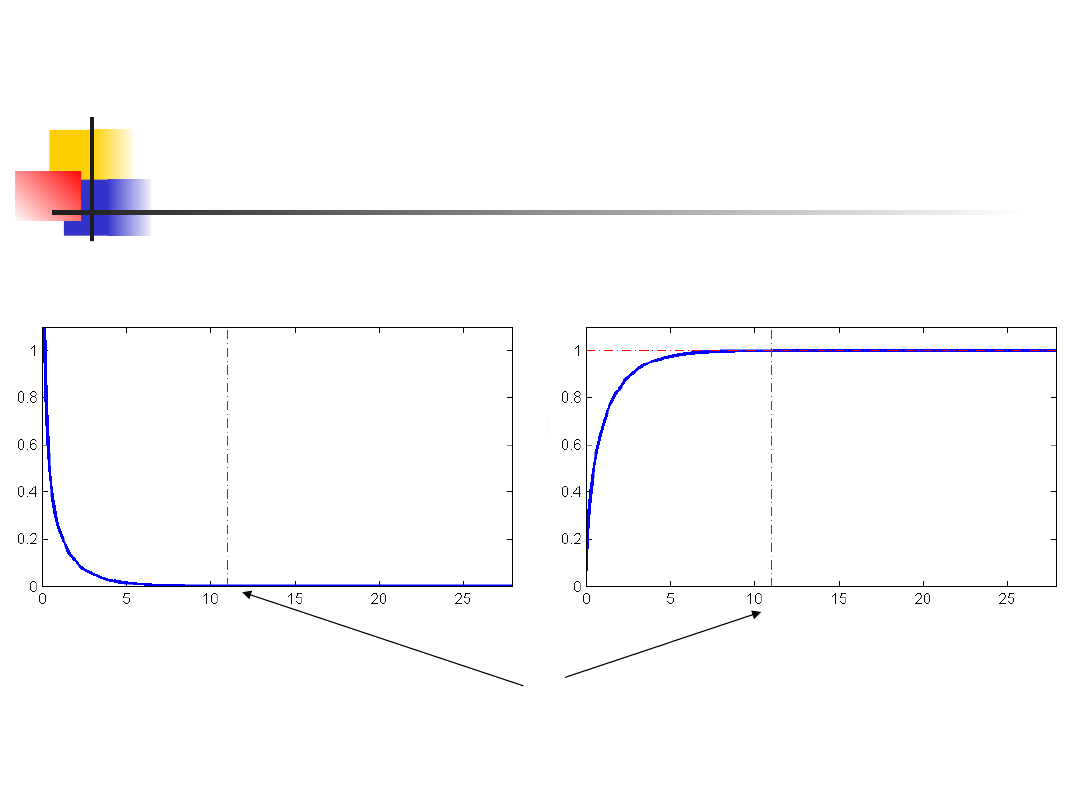
Rozkład chi-kwadrat, 1df

10.96524

Wzór obliczeniowy

2

1

2

1

2

1

n

n

n

n

1

n

n

1

q

ˆ

q

p

ˆ

p

q

ˆ

p

ˆ

n

n

q

p

n

n

L





















































Ponieważ

q

ˆ

n

n

ˆ

nq

n

p

ˆ

n

n

ˆ

np

n

2

2

1

1









2

1

n

2

2

n

1

1

n

ˆ

n

n

ˆ

n

L



























to





























2

2

2

1

1

1

n

ˆ

n

ln

n

n

ˆ

n

ln

n

L

ln

i

Test G

Fenot

ypy

Obserwow

ane

zliczenia

Obserwowa

ne

proporcje

Oczekiw

ane

proporcj

e

Oczekiw

ane

zliczenia

Stosunek

zliczeń

obserwowa

nych do

oczekiwany

ch

Wild-

type

80

0.89

0.75

67.5

1.185185

13.59192

Mutan

t

10

0.11

0.25

22.5

0.444444

-8.10930

Suma

90

1.0

1.0

90.0

Ln L =

5.48262













i

i

i

n

ˆ

n

ln

n



Test G dla więcej niż dwóch
klas



Test zgodności można zastosować do

rozkładu z większą liczbą klas niż dwie.



Obliczamy stosunki obserwowanych

zliczeń do oczekiwanych, logarytmujemy

i mnożymy przez liczność obserwowaną.



Suma daje ln L, podczas gdy rozkład G =

2 ln L w przybliżeniu pokrywa się z

rozkładem chi-kwadrat z a-1 stopniami

swobody, gdzie a to liczba klas.

Przykład 1



Badanie miejsc powrotu łososi na tarło
– strumień macierzysty versus
sąsiednie.

N = 200

ryb

Strumie

ń

macierz

ysty

Strumie

ń 1

Strumie

ń 2

Strumie

ń 3

Strumie

ń 4

Obserwowan

e

zliczenia

135

15

17

10

23

Przykład 1

Hipoteza:

H

0

: Łososie wybierają strumień

macierzysty w 75% przypadków;

pozostałe w 25% przypadków

(6.25% na każdy z czterech).

H

a

: nie H

o

Przykład 1



Można sformułować hipotezę
zerową w inny sposób
H

0

: próba pochodzi z populacji

łososi z proporcjami 12:1:1:1:1
wyboru strumienia macierzystego i
alternatywnych.
H

a

: nie H

0

.

Przykład 1

Obserwowan

e zliczenia

Oczekiwan

e zliczenia

Stosune

k

Strumień
domowy

135

150

0.90

-

14.223
7

Strumień
1

15

12.5

1.20

2.7348

Strumień
2

17

12.5

1.36

5.2272

Strumień

3

10

12.5

0.80

-2.2314

Strumień

4

23

12.5

1.84

14.024
6

Suma

200

200

ln L =

5.5315

i

n

ˆ

i

n

i

i

n

ˆ

/

n













i

i

n

ˆ

n

i

ln

n

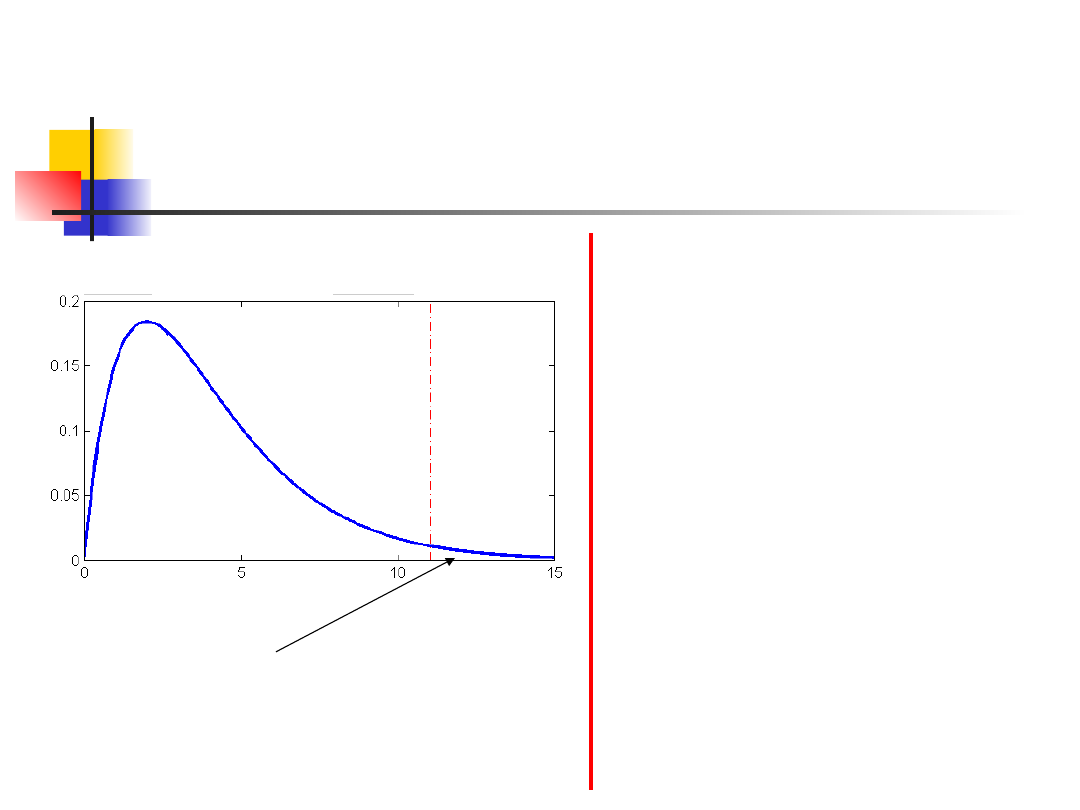
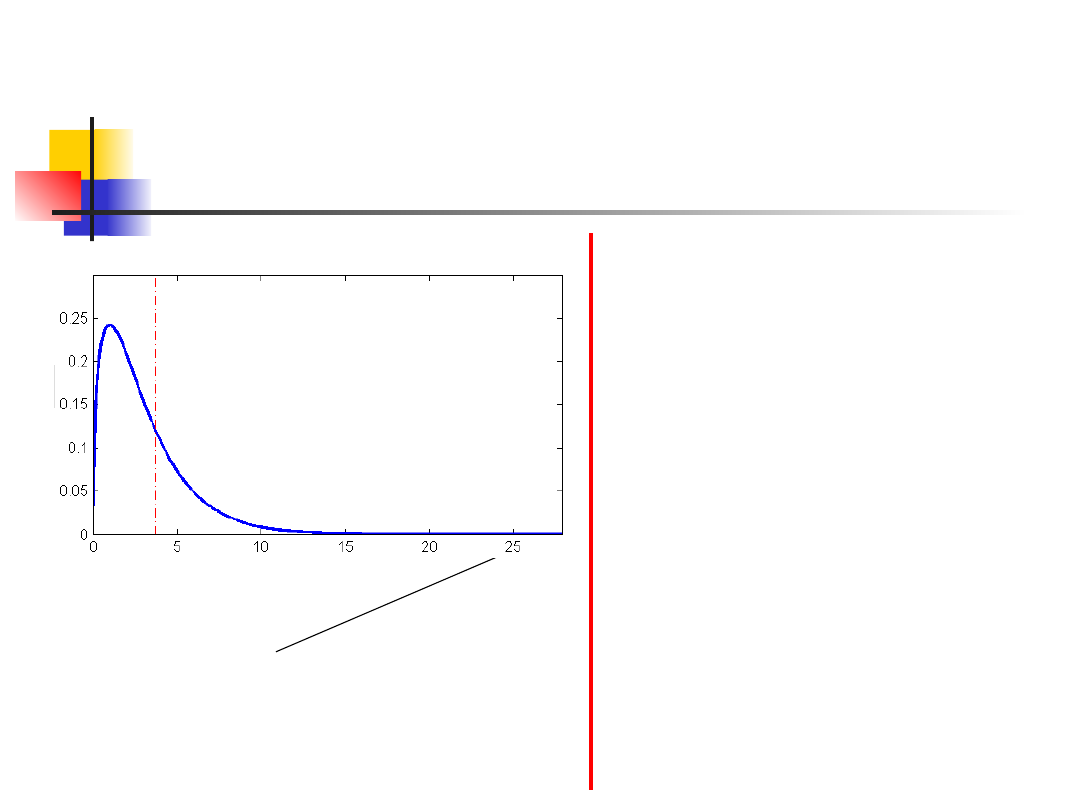
Przykład 1

0259

.

0

}

063

.

11

{

:

2

]

4

[









P

value

p

0.05

z

H

odrzucamy

G

poniewa

ż

4877

.

9

063

.

11

ln

2

0

2

]

4

[

05

.

0

2

]

4

[

05

.

0



















crit

G

L

G

Test chi-kwadrat zgodności
dopasowania



To tradycyjne podejście, stosowane
w znacznej liczbie publikacji
naukowych.



Jeszcze raz spójrzmy na
eksperyment genetyka z wynikiem
80 potomków wild-type i 10
mutantów.

Test chi-kwadrat zgodności
dopasowania



Najpierw obliczamy odchylenia

zliczeń obserwowanych od zliczeń

oczekiwanych i podnosimy je do

kwadratu.



Następnie obliczamy względne

kwadraty odchyleń - dzielimy je

przez liczbę zliczeń oczekiwanych.



Ostatecznie sumujemy otrzymane

wartości.

Test chi-kwadrat zgodności
dopasowania



Otrzymana statystyka jest nazywana

statystyką chi-kwadrat X

2

, ale ma

ona jedynie

rozkład przybliżony do

rozkładu X

2

z jednym stopniem

swobody

.



Niektórzy nazywają statystykę X

2

statystyką Pearsona.



Test chi-kwadrat jest zawsze

jednostronny!!

Test chi-kwadrat zgodności
dopasowania

Fenotyp

y

Obserwo

wane

zliczenia

Oczekiwa

ne

stosunki

Oczekiwa

ne

zliczenia

Odchylen

ia do

kwadratu

Względn

e

kwadraty

odchyleń

Wild-

type

80

0.75

67.5

156.25

2.3148

Mutant

10

0.25

22.5

156.25

6.9444

Suma

90

1.0

90.0

X

2

=

9.2592

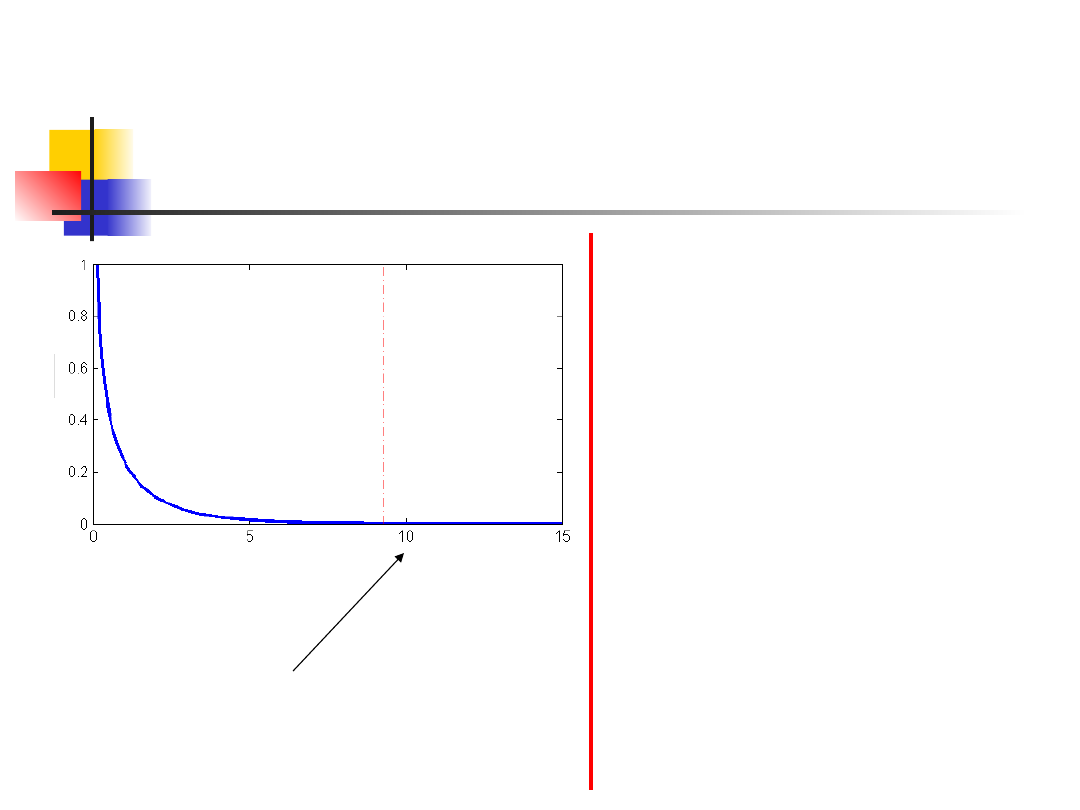
Test chi-kwadrat zgodności
dopasowania

0023

.

0

}

2592

.

9

{

P

:

value

p

1

]

1

[









0.05

z

H

odrzucamy

X

poniewa

ż

8415

.

3

2592

.

9

0

2

]

1

[

05

.

0

2

2

]

1

[

05

.

0

2















X

Test chi-kwadrat zgodności
dopasowania dla więcej niż
dwóch klas



Test dopasowania chi-kwadrat można

zastosować dla więcej niż dwóch klas.



Oblicz:



Statystyka X

2

ma w przybliżeniu

rozkład

chi-kwadrat z a-1 stopniami swobody,

gdzie a to liczba klas.











a

i

2

i

i

2

n

ˆ

n

ˆ

n

X

Przykład 1 - cd.

Obserwowan
e zliczenia

Oczekiwan
e zliczenia

Odchylenie Względne

odchylenia

Strumień

macierzyst
y

135

150

225

1.50

Strumień 1

15

12.5

6.25

0.50

Strumień 2

17

12.5

20.25

1.62

Strumień 3

10

12.5

6.25

0.50

Strumień 4

23

12.5

110.25

8.82

Suma

200

200

X

2

=12.94

i

n

ˆ

i

n





2

i

i

n

ˆ

n 

Przykład 1 - cd.

0116

.

0

}

94

.

12

{

P

:

value

p

2

]

4

[









0.05

z

H

odrzucamy

X

poniewa

ż

4877

.

9

94

.

12

0

2

]

4

[

05

.

0

2

2

]

4

[

05

.

0

2















X

Testowanie cząstkowe



W naszym przykładzie o łososiach,
wygląda na to, że liczba ryb płynąca do
strumienia 4 spowodowała odrzucenie
H

0

.



Dlatego stosujemy analizę cząstkową.



Przetestujmy H

0

: Próbka pochodzi z

populacji z proporcjami 12:1:1:1 wyboru
strumienia macierzystego i
alternatywnych 1-3.

Przykład 1 - testowanie
cząstkowe

Obserwowa

ne zliczenia

Oczekiwan

e zliczenia

Odchylen

ie

Względne

odchylenie

Strumień

macierzyst
y

135

177*12/15

=141.6

43.56

0.3076

Strumień 1

15

177*1/15=

11.8

10.24

0.8678

Strumień 2

17

11.8

27.04

2.2915

Strumień 3

10

11.8

3.24

0.2746

Suma

177

X

2

=3.7415

i

n

ˆ

i

n





2

i

i

n

ˆ

n 

Przykład 1 - testowanie
cząstkowe

2908

.

0

}

7415

.

3

{

P

:

value

p

2

]

3

[









0.05

z

H

odrzucamy

nie

X

poniewa

ż

8174

.

7

7415

.

3

0

2

]

3

[

05

.

0

2

2

]

3

[

05

.

0

2















X

Korekty na nieciągłość



Wartości statystyk G lub X

2

liczone na

podstawie danych mają rozkład
dyskretny.



Jednak teoretyczny rozkład chi-kwadrat
jest ciągły.



Z wartościami nieskorygowanymi można
łatwiej fałszywie odrzucić H

0

(błąd I-

szego rodzaju jest większy niż
zamierzony).

Korekty na nieciągłość



W przypadku dwóch klas jest to

poważny problem. Jeśli N<200

musimy stosować korekty na

nieciągłość.



Test G – korekta Williams’a



Test X

2

– korekta Yates’a

q

G

G

,

N

2

1

1

q

adj



















2

i

2

i

i

2

adj

n

ˆ

5

.

0

n

ˆ

n

X

Testowanie dla innych
rozkładów



Możemy zastosować przedstawione
testy zgodności do weryfikacji hipotez o
rozkładach innych niż dwumianowy.



Jeśli szacujemy parametry rozkładu na
podstawie danych, musimy poprawnie
ustalić liczbę stopni swobody.

Testowanie dla innych
rozkładów

Rozkład

Parametry

szacowane

na podstawie

próby

Liczba df

Dwumianow

y

p

a-2

Normalny

μ,σ

a-3

Poissona

μ

a-2

Przykład 2



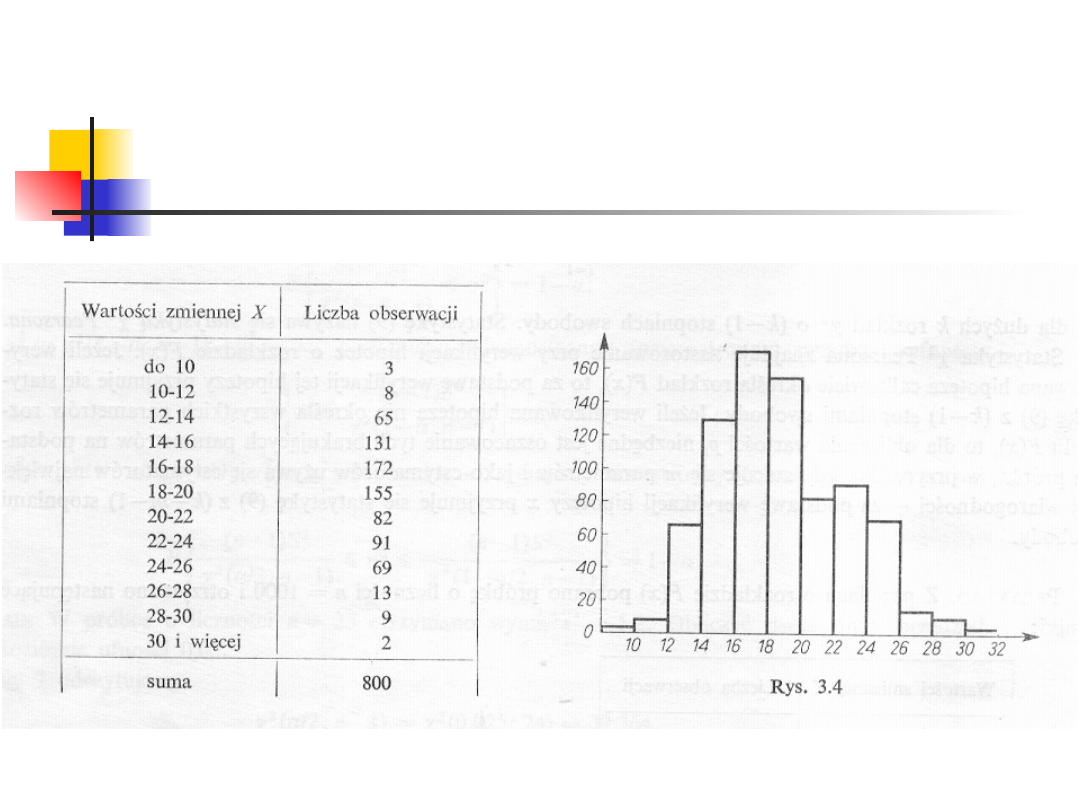
Z populacji o rozkładzie F(x)
pobrano próbę o liczności n=800 i
otrzymano następujące wyniki.



Czy wyniki te przeczą na poziomie
istotności 0.01 hipotezie H: F(x)
jest rozkładem normalnym?

Ryszard Zieliński: Tablice statystyczne. PWN 1972

Przykład 2

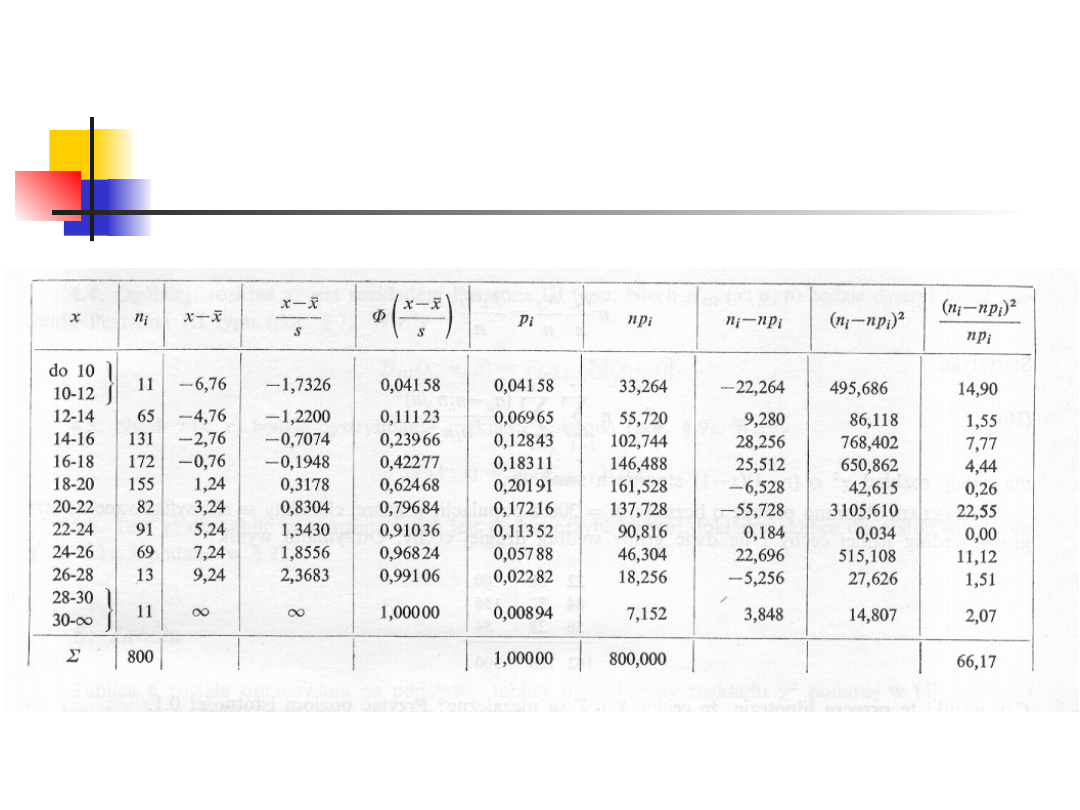
Przykład 2



Ponieważ hipoteza H nie określa
parametrów F(x), μ oraz σ należy
oszacować na podstawie próby.



Parametry te wynoszą odpowiednio
x

sr

=18.76 oraz s=3.9016.



Prawdopodobieństwo p

i

obliczamy

według wzoru:

)

9016

.

3

76

.

18

x

(

)

9016

.

3

76

.

18

x

(

p

1

i

i

i















Przykład 2

Przykład 2



Ponieważ liczba przedziałów (po
zredukowaniu) równa jest 10 oraz
ponieważ oszacowaliśmy dwa
parametry na podstawie danych,
liczba stopni swobody równa jest
10-2-1=7.



Z tablicy odczytujemy wartość
krytyczną.

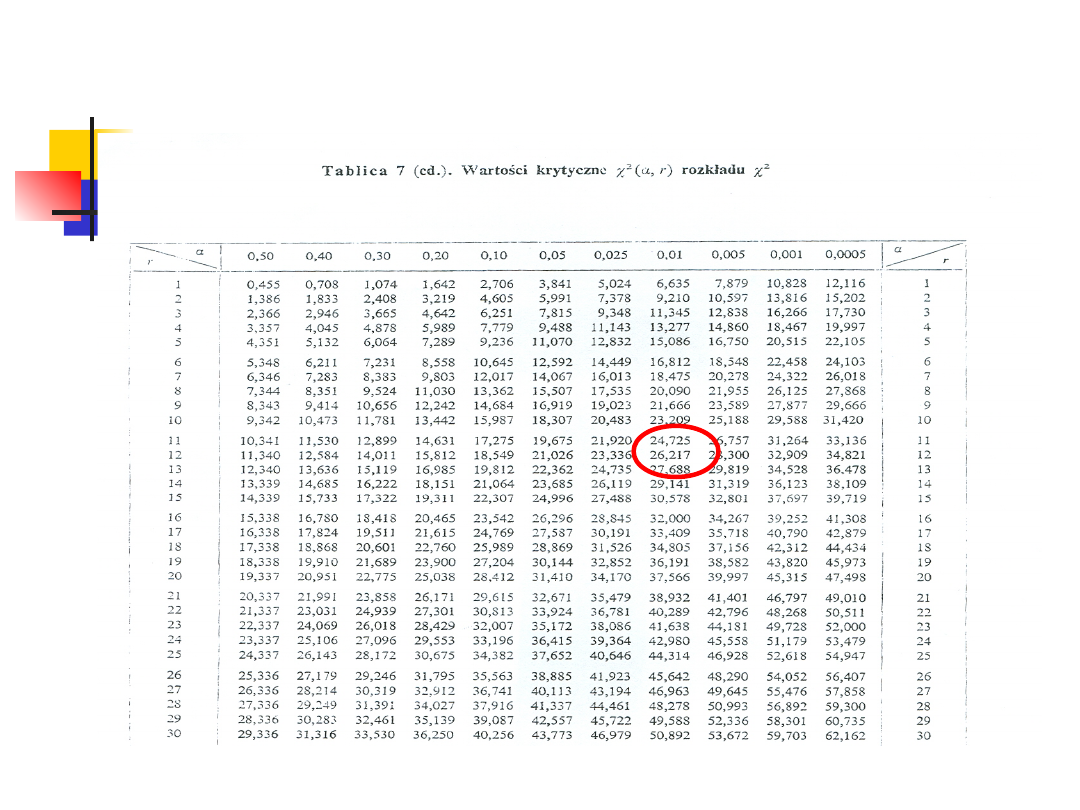
Przykład 2



Odczytana wartość krytyczna
wynosi 18.475.



Ponieważ otrzymana wartość
statystyki testowej 66.17 jest
większa od wartości krytycznej,
weryfikowaną hipotezę H

0

odrzucamy na poziomie alfa 0.01

.

Test Kołmogorowa-
Smirnowa



Nieparametryczny test, stosowany do analizy
zmiennych o ciągłych i dyskretnych
rozkładach częstości, mający większą moc niż
testy zgodności G i X

2

, jest nazywany testem

Kołmogorowa-Smirnowa (KS).



Test KS jest szczególnie przydatny dla małych
prób, nie jest wskazane grupowanie klas.



Jest to test jednostronny!!!

Test Kołmogorowa-
Smirnowa



Buduje się dystrybuantę empiryczną F

n

(x)



Oblicza się wartość statystyki mierzącej
odległość tej dystrybuanty empirycznej od
dystrybuanty teoretycznej F(x)



Obliczoną wartość statystyki porównuje się z
wartością krytyczną dla zadanego poziomu
istotności alfa. Jeżeli obliczona wartość
statystyki jest większa od wartości krytycznej
– odrzuca się weryfikowaną hipotezę.

)

x

(

F

)

x

(

F

sup

D

n

x

n















Test Kołmogorowa-
Smirnowa



Często zamiast statystyki Smirnowa-
Kołmogorowa (typu supremum) D

n

wyznaczamy statystykę Smirnowa D

n+

definiowaną jako:



Wartość krytyczną dla statystyki Smirnowa
znajdujemy z zależności:

)

(

)

(

max

x

F

x

F

D

n

n

n







)

2

(

)

(





n

n

D

D





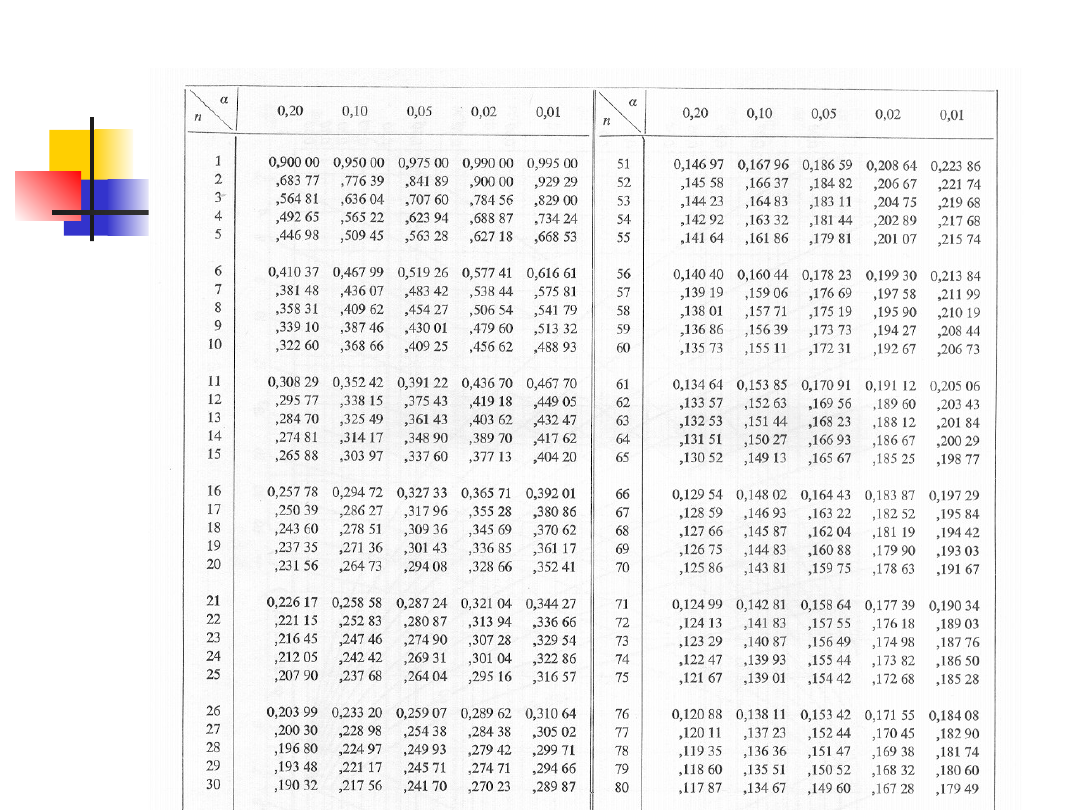
Wartości krytyczne
D

n

(α)

Test Kołmogorowa-
Smirnowa



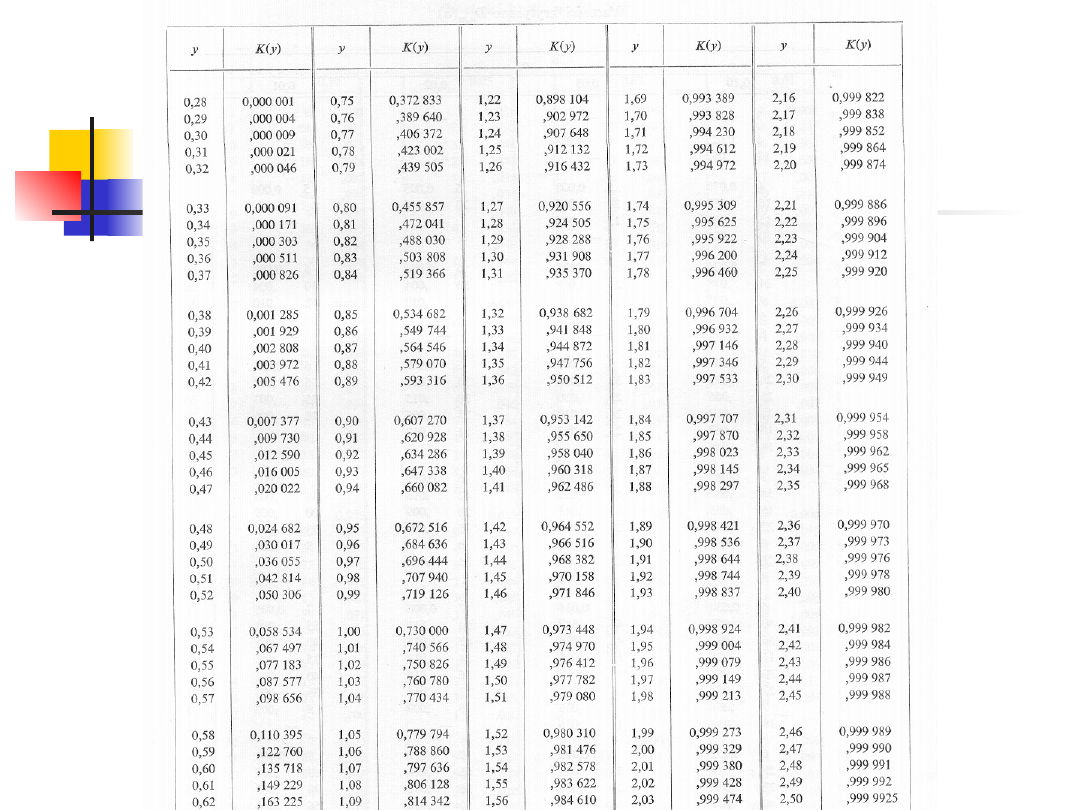
Dla dużych n statystyka D

n

√n ma rozkład

Kołmogorowa K(y)

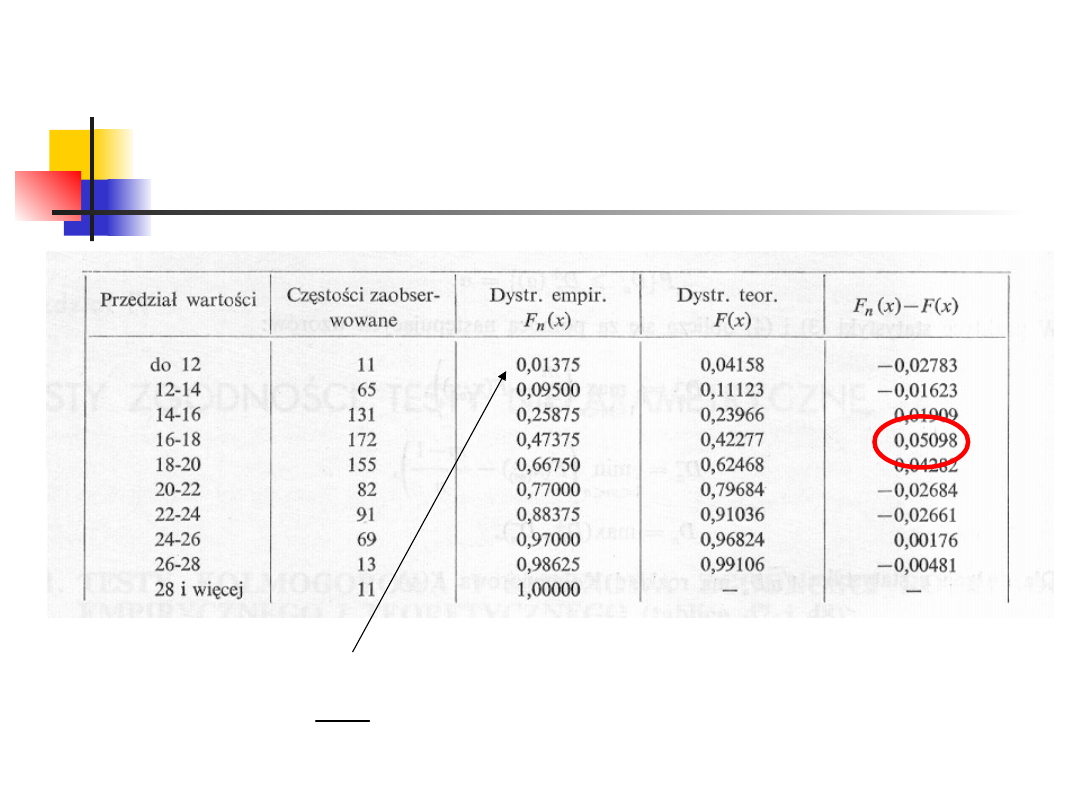
Przykład 2 - kontynuacja



Powtórzmy obliczenia korzystając z
testu Kołmogorowa - Smirnowa.



Przyjmujemy α=0.01



Wyniki obliczeń przedstawia
tabelka.

800

11

Przykład 2



Otrzymujemy D

n+

=0.05098,

zatem D

n+

√n =1.442.



Wartość krytyczna dla D

n+

(0.01)

jest równoważna wartości
krytycznej D

n

(0.02) znajdowanej

na podstawie rozkładu K(y) dla
y=0.98 i wynosi y

kryt

≈1.52.



1.442<1.52 więc nie mamy
podstaw do odrzucenia H

0

na

poziomie istotności 0.01.

Test Kołmogorowa-
Smirnowa



Test dla dyskretnych danych analizuje
skumulowane zliczenia obserwowane i
oczekiwane oraz przyjmuje za statystykę

największą różnicę między nimi

:

Ta wartość jest porównywana z wartością
krytyczną:

i

d

d

max

max



)

(



n

kryt

D

n

d





Przykład 3 - dane
dyskretne



Chcemy sprawdzić czy insekty mają
preferencje związane z natężeniem
oświetlenia – czy ich liczność jest
równomiernie rozłożona wzdłuż gradientu
światła.



Nie można zmierzyć w skali liniowej różnic
gradientu światła, ale można określić, że
mniejsze liczby odpowiadają mniejszemu
natężeniu światła niż większe liczby.

Przykład 3



H

0

: Liczba insektów jest

równomiernie rozłożona wzdłuż
gradientu światła



H

a

: nie H

0



Ustalamy α = 0.05

Przykład 3

N=65

Ciemno -

1

2

3

4

Jasno - 5

Obserwowan

e zliczenia

0

7

6

38

14

Oczekiwane

zliczenia

13

13

13

13

13

Obserwowan

e

kumulatywne

zliczenia

0

7

13

51

65

Oczekiwane

kumulatywne

zliczenia

13

26

39

52

65

|d

i

|

13

19

26

1

0

Przykład 3



Statystyka testowa

d

max

= 26



Wartość krytyczna

D

65

(0.05) =

0.16567 więc d

kryt

=65·0.16567≈10.77



Zasada decydowania

:



odrzucenie H

0

jeśli d

max

≥10.77; w

przeciwnym razie przyjęcie H

0

.



Ponieważ 26>10.77, odrzucamy H

0

.

Przykład 3



Wniosek:

Zaobserwowane dane nie mają
rozkładu równomiernego wzdłuż
uporządkowanych poziomów
natężenia światła (p<0.05).