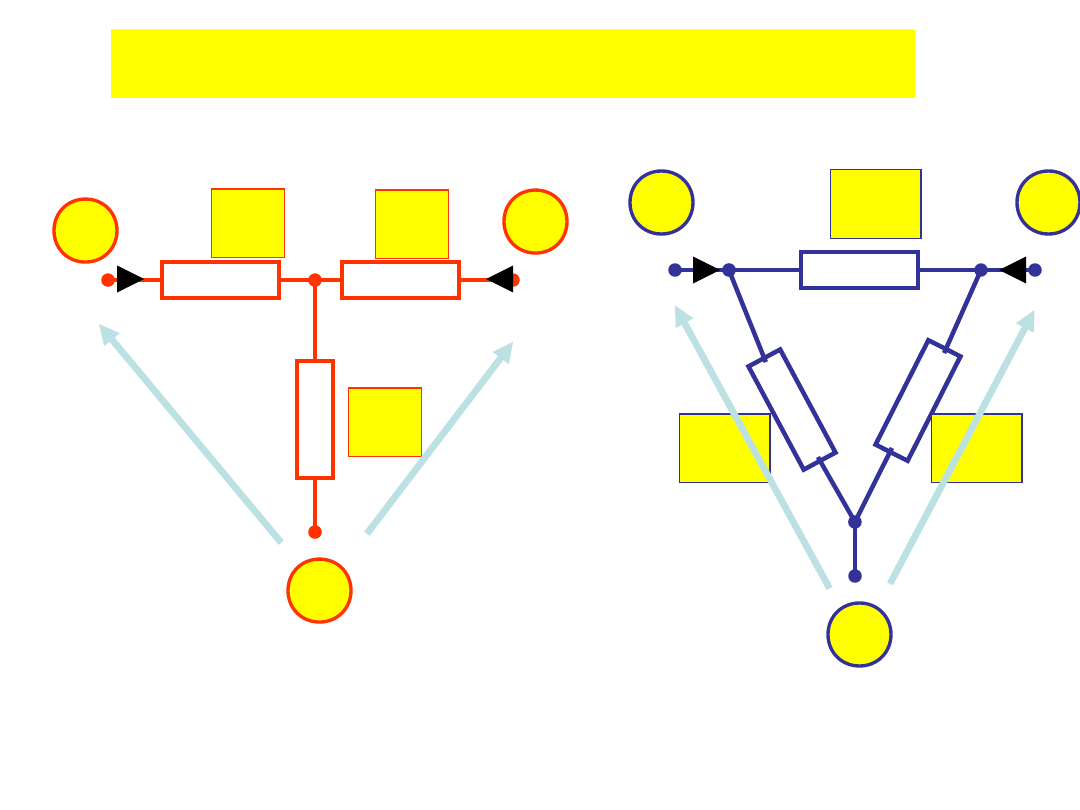
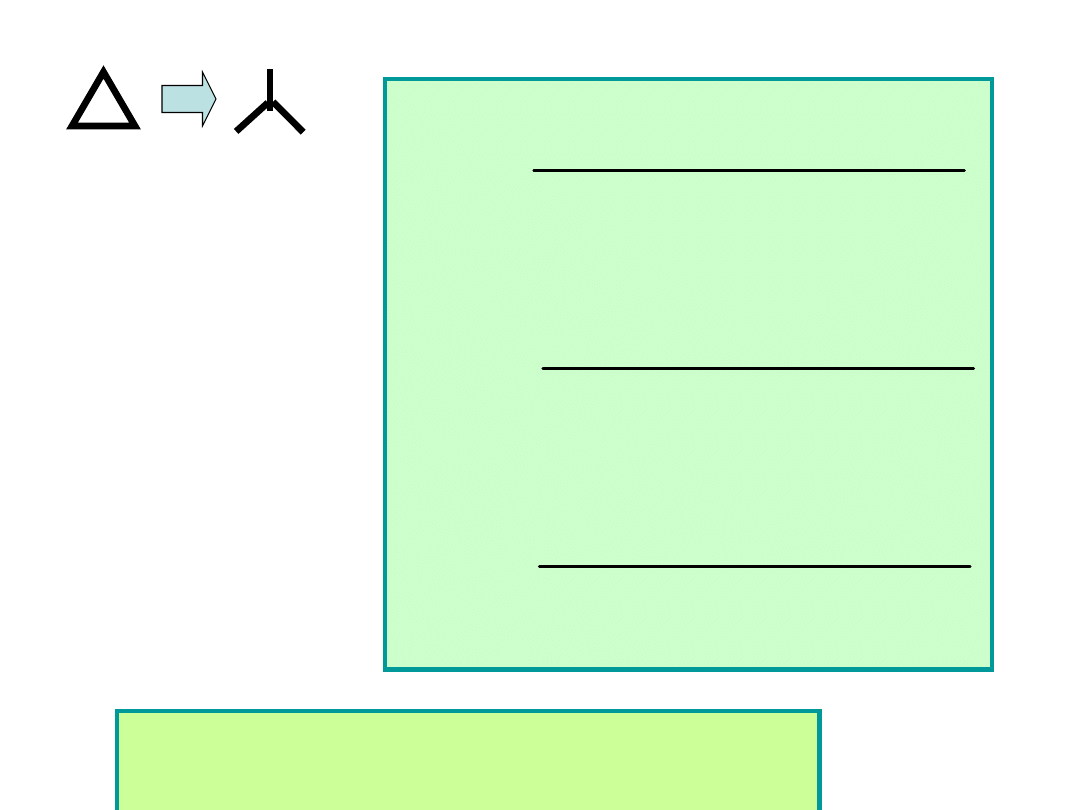
Zamiana GWIAZDA-TRÓJKĄT

R

1

R

2

R

3

1

2

3

2

1

3

R

12

R

31

R

23

u

1

V

1

u

2

V

2

i

1

j

1

i

2

j

2

R

1

R

2

R

3

1

2

3

u

1

u

2

i

1

i

2



 











2

3

2

1

3

2

1

3

2

2

2

2

3

1

3

1

2

1

3

1

1

1

i

R

R

i

R

i

i

R

i

R

u

i

R

i

R

R

i

i

R

i

R

u

























i

1

+i

2

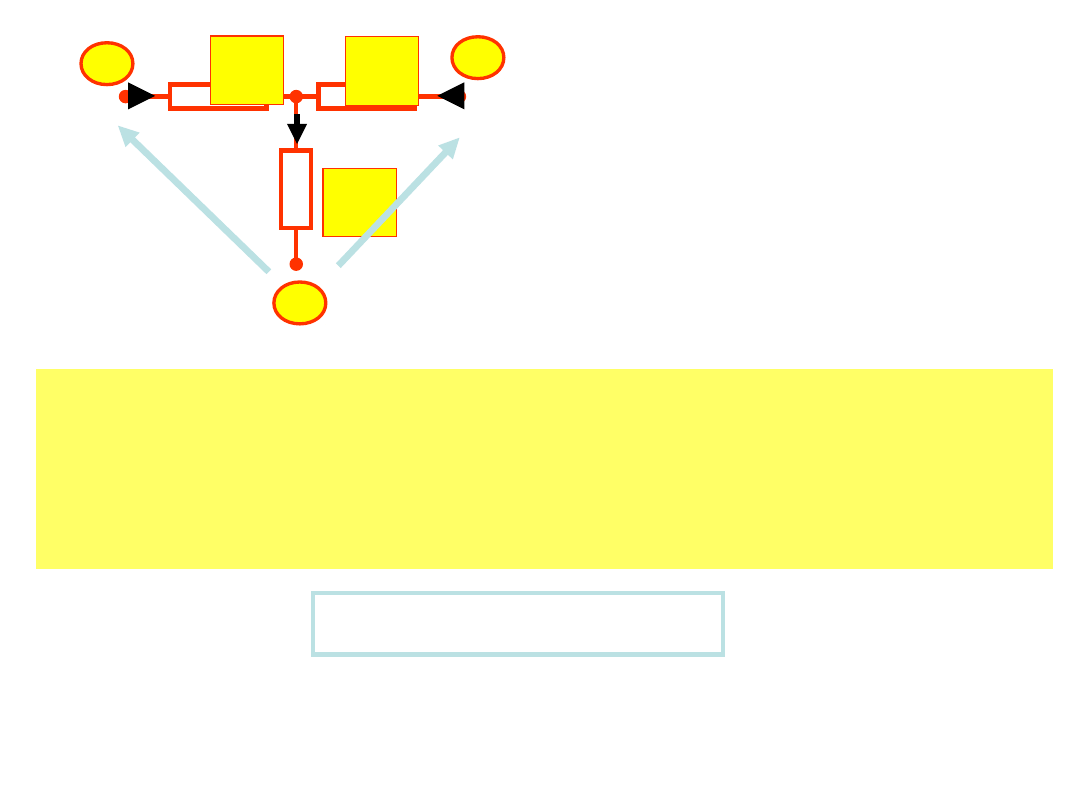
Są to równania (*)

2

1

3

R

12

R

31

R

23

V

1

V

2

j

1

j

2









2

31

23

12

31

12

23

1

31

23

12

23

31

1

2

31

23

12

31

23

1

31

23

12

23

12

31

1

j

R

R

R

R

R

R

j

R

R

R

R

R

v

j

R

R

R

R

R

j

R

R

R

R

R

R

v





























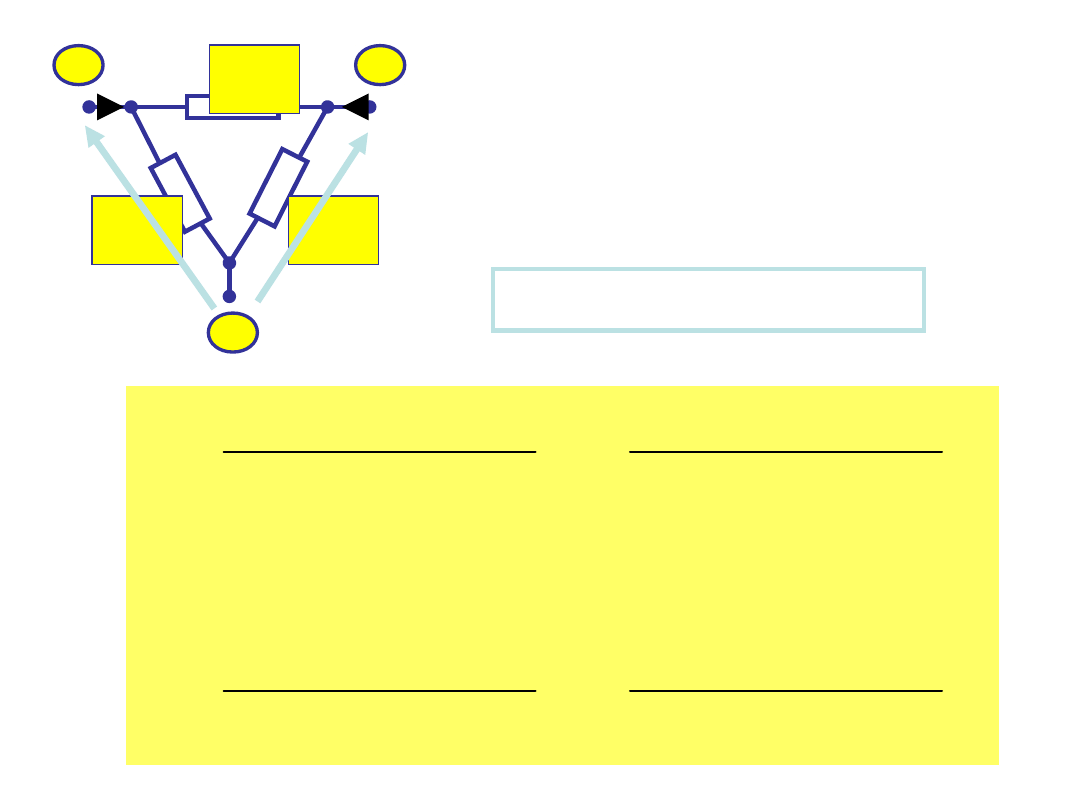
Są to równania (**)

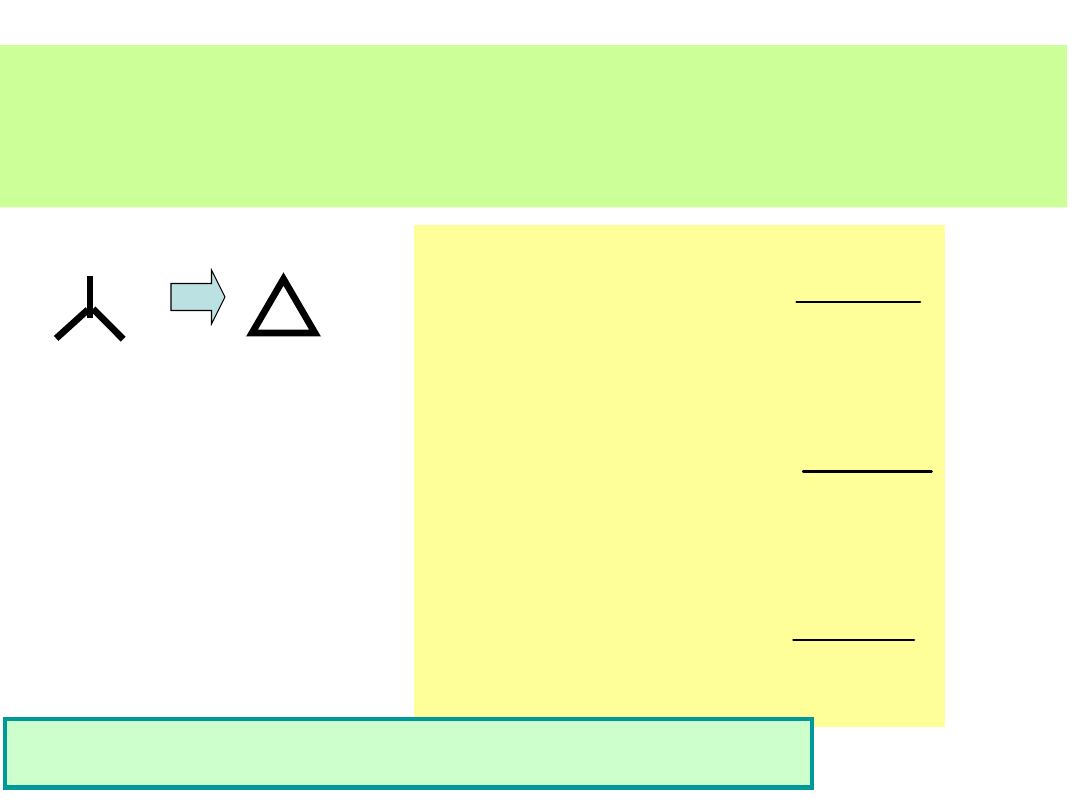
Z definicji równoważności układów
wynika równość odpowiednich współczynników
w równaniach (*) i (**). Wynikają stąd wzory:

2

1

3

1

3

31

1

3

2

3

2

23

3

2

1

2

1

12

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R



















Gdy R

1

=R

2

=R

3

=R

Y

R

Δ

=3R

Y

31

23

12

31

23

3

31

23

12

23

12

2

31

23

12

31

12

1

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R



















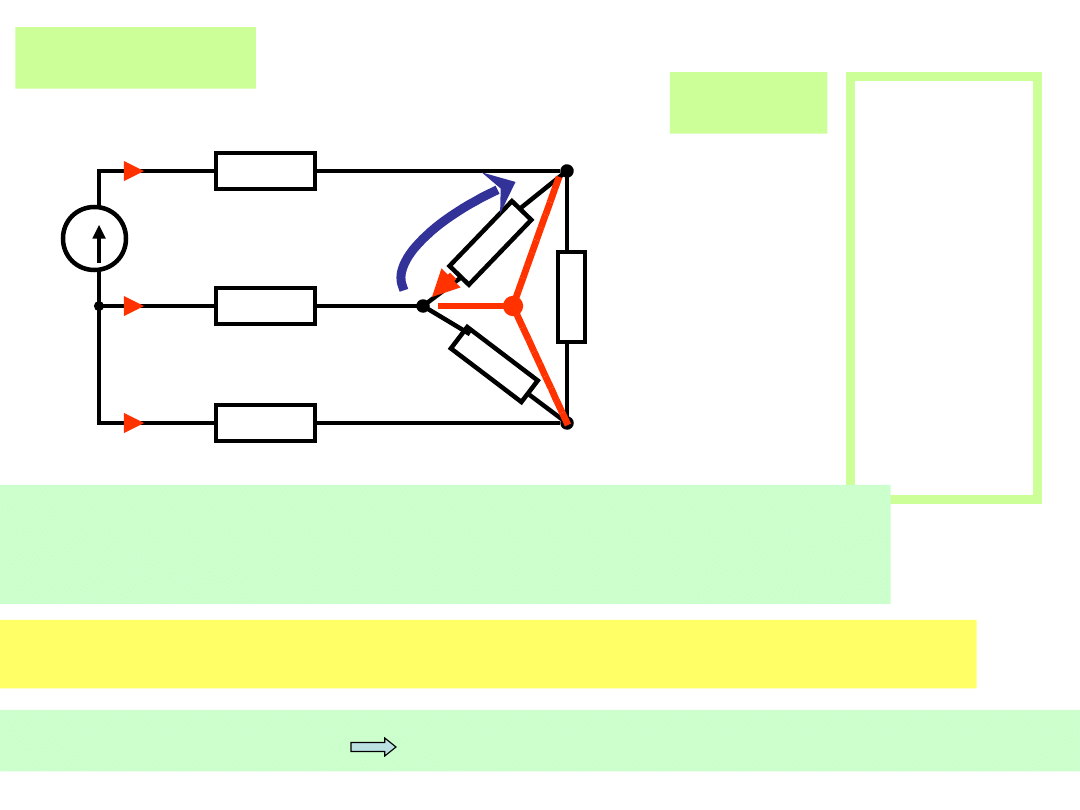
Gdy R

12

=R

23

=R

34

=R

Δ

R

Y

=1/3R

Δ

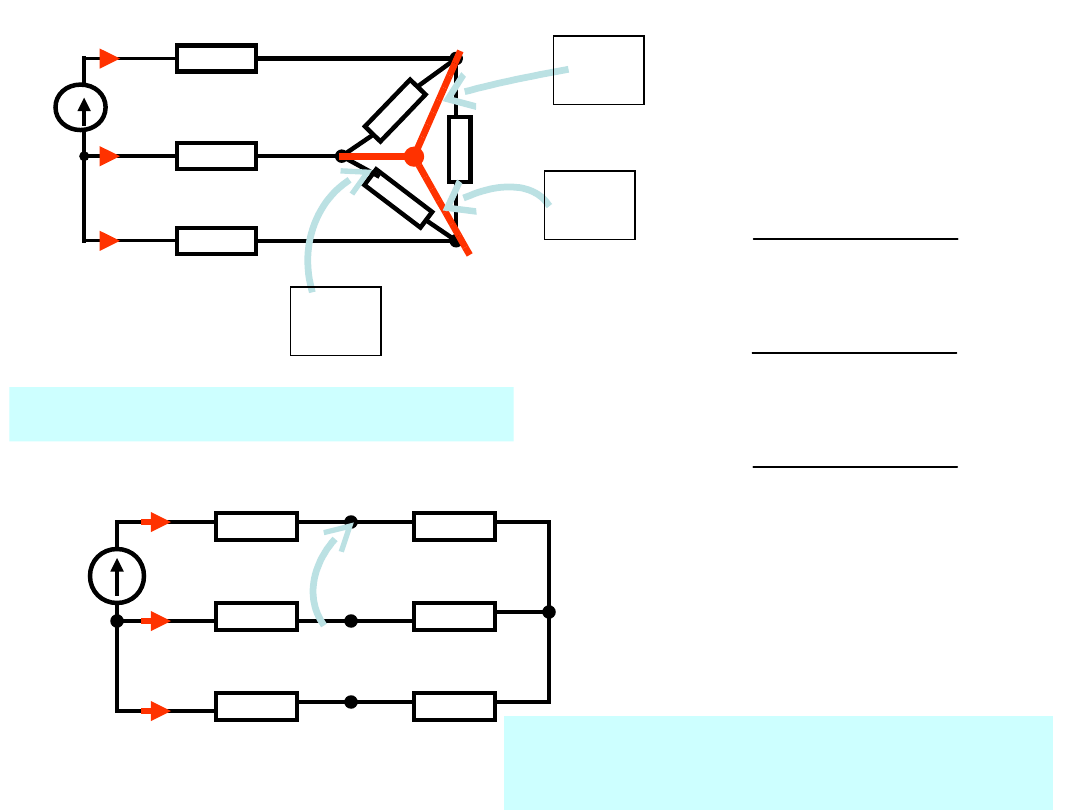
Przykład:

R

1

R

2

R

3

i

1

i

2

i

3

A

B

C

R

4

R

5

R

6

u

Dane:

V

u

R

R

R

R

R

R

6

2

3

5

4

,

1

5

,

0

1

6

5

4

3

2

1



























Celem jest obliczenie prądu
w jednej z gałęzi trójkąta, np. prądu i

4

i

4

Aby obliczyć ten prąd musimy znaleźć u

AC

u

AC

Po zamianie Δ Y nie możemy zgubić punktów AC

R

1

R

2

R

3

i

1

i

2

i

3

A

B

C

R

4

R

5

R

6

u

R

46

R

65

R

54































5

,

1

6

,

0

1

6

5

4

4

5

54

6

5

4

5

6

65

6

5

4

6

4

46

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

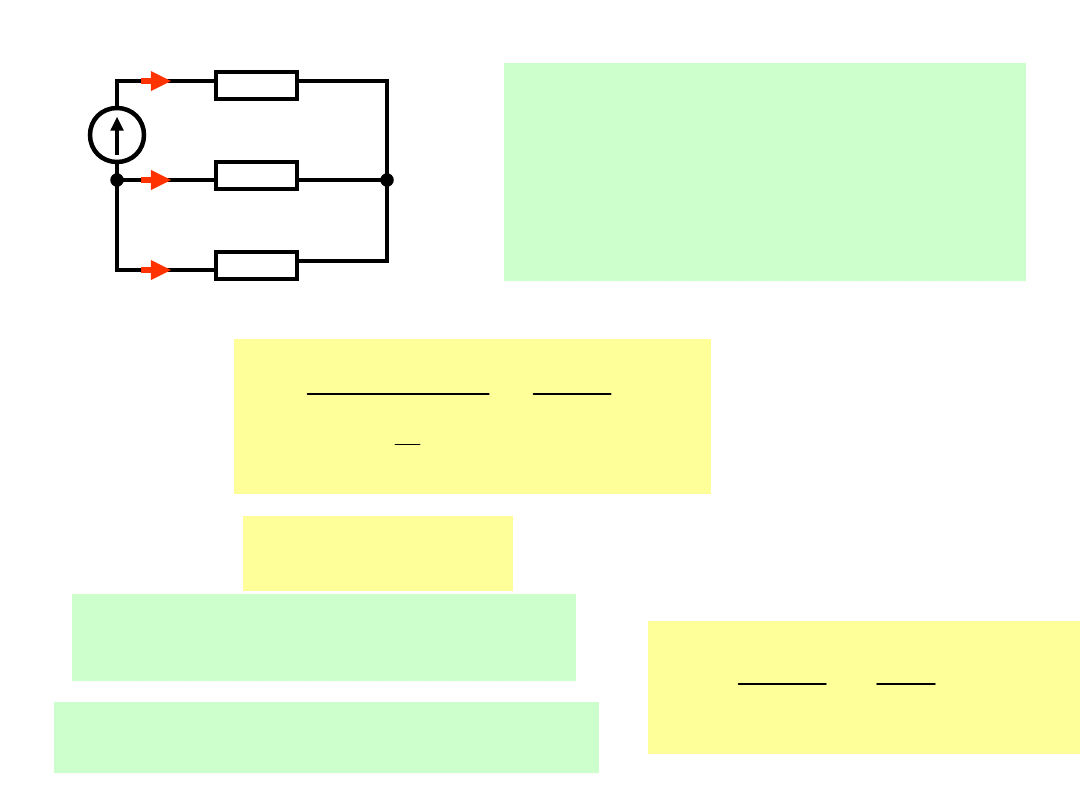
Obwód ma teraz postać:

R

1

R

2

R

3

A

B

C

O

R

46

R

54

R

65

i

1

i

2

i

3

u

AC

1

46

2

54

i

R

i

R

u

AC







u

*

R

*

*

R

*

*

*

R

i

1

i

2

i

3

0





































2

6

,

0

4

,

1

2

5

,

1

5

,

0

2

1

1

65

3

*

*

*

54

2

*

*

46

1

*

R

R

R

R

R

R

R

R

R

A

R

R

u

i

2

1

2

6

2

1

*

*

*

1











A

i

i

1

3

2







1

46

2

54

i

R

i

R

u

AC







A

R

u

i

AC

7

,

0

5

5

,

3

4

4







 

V

u

AC

5

,

3

2

1

1

5

,

1











