Rozszerzalność liniowa ciał
(przyczyny, wydłużenie
liniowe)
Rozszerzalność termiczna ciał związana jest z dostarczaniem do ciała
energii, dzięki której atomy, pozostające w stanie związanym z
otaczającymi je atomami, poruszają się bardziej dynamicznie. W efekcie
tego sąsiadujące atomy nieco oddalają się od siebie. Skutkiem
dostarczenia energii do ciała może być także przemiana fazowa, np. ciało
stałe-ciecz lub przebudowa sieci krystalicznej, a także wzrost liczby
defektów punktowych (wakansów). W związku z przemianami fazowymi
nie zawsze mamy do czynienia ze wzrostem rozmiarów ciał przy wzroście
temperatury. Osobliwie zachowanie można zaobserwować przy
przemianie z lodu w wodę, czemu towarzyszy zmniejszenie objętości.
Zastanawiające jest także, że woda największą gęstość osiąga nie przy 0
0
C a przy 4
0
C.
Na podstawie eksperymentów wykonanych dla długich prętów
(wydłużenia liniowe) ustalono proporcjonalność wydłużeń (Δl) do długości
początkowej prętów (l
0
) i zmiany temperatury (ΔT). Alfa we wzorze (70)
jest współczynnikiem rozszerzalności liniowej ciała i odzwierciedla skalę
jego podatności na rozszerzanie.
(70).
T
Δ
α
l
=
l
Δ
0
Rozszerzalność objętościowa
Skutkiem dostarczonej energii do ciała jest nie tylko wzrost jego długości.
Zwiększają się wszystkie wymiary ciała, a w efekcie także objętość.
Wzrost obiętości (ΔV) jest również proporcjonalny do przyrostu
temperatury (ΔT), a także do objętości początkowej (V
0
). Beta we wzorze
(71) pełni rolę współczynnika objętościowej rozszerzalności cieplnej.
(71).
T
Δ
β
V
=
V
Δ
0
Na podstawie wzorów (70) i (71) można określić odpowiednio długość (l) i
objętość (V) w danej temperaturze (T).
(
)
(72).
T
Δ
α
+
1
l
=
l
T
Δ
α
l
+
l
=
l
T
Δ
α
l
=
l
-
l
T
Δ
α
l
=
l
Δ
0
0
0
0
0
0
(
)
(73).
T
Δ
β
+
1
V
=
V
T
Δ
β
V
+
V
=
V
T
Δ
β
V
=
V
-
V
T
Δ
β
V
=
V
Δ
0
0
0
0
0
0
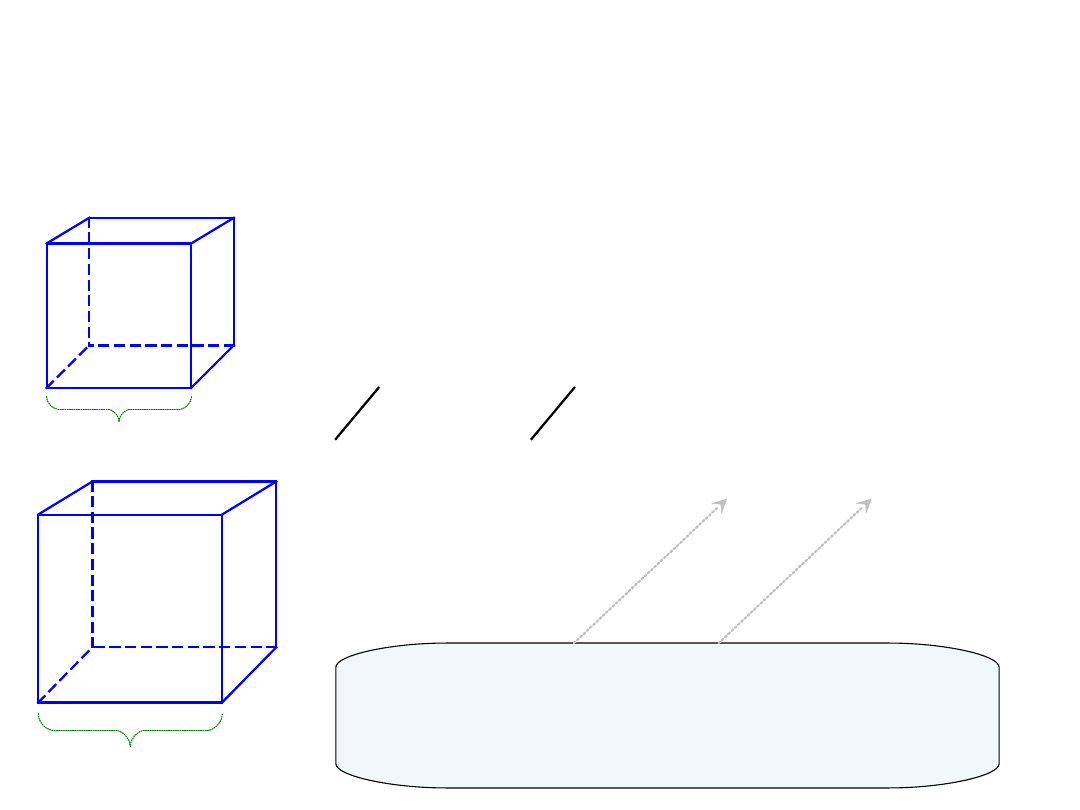
Związek i β
Związek pomiędzy współczynnikami rozszerzalności liniowej () i
objętościowej (β) można ustalić na podstawie analizy dla ciała
sześciennego.
(
)
(
) (
) (
)
(
)
(
)(
)(
)
(
)
(
)
(
)
(
)
(
)
(74).
α
3
β
T
Δ
α
3
+
1
T
Δ
β
+
1
)
T
Δ
(
α
+
)
T
Δ
(
α
3
+
T
Δ
α
3
+
1
=
T
Δ
β
+
1
T
Δ
α
+
1
)
T
Δ
(
α
+
T
Δ
α
2
+
1
V
=
T
Δ
β
+
1
V
T
Δ
α
+
1
T
Δ
α
+
1
T
Δ
α
+
1
l
=
T
Δ
β
+
1
V
T
Δ
α
+
1
l
T
Δ
α
+
1
l
T
Δ
α
+
1
l
=
T
Δ
β
+
1
V
l
=
V
3
3
2
2
2
2
0
0
3
0
0
0
0
0
0
3
≈
⇒
≈
l
0
,
T
0
l, T
Wskazane składniki ze względu na bardzo
małe wartości i z racji podnoszenia do
kwadratu i do sześcianu dają bardzo mały
wkład w sumę i dlatego można je pominąć.
Konsekwencje rozszerzalności
Zjawisko rozszerzalności termicznej
nie
zawsze
jest
pożądane.
Konsekwencje projektowania budowli,
mostów,
trakcji
jezdnych
bez
uwzględnienia
rozszerzalności
termicznej mogą być brzemienne w
skutkach, co ilustruje przykładowe
zdjęcie.
Przykrych
konsekwencji
można jednak uniknąć wyposażając
konstrukcje w szczeliny dylatacyjne
oraz dobierając spojone materiały
konstrukcyjne tak aby miały takie
same
wartości
współczynników
rozszerzalności
termicznej,
np.
plomby
dentystyczne
i
szkliwo
zębów, czy pręty zbrojeniowe i beton.
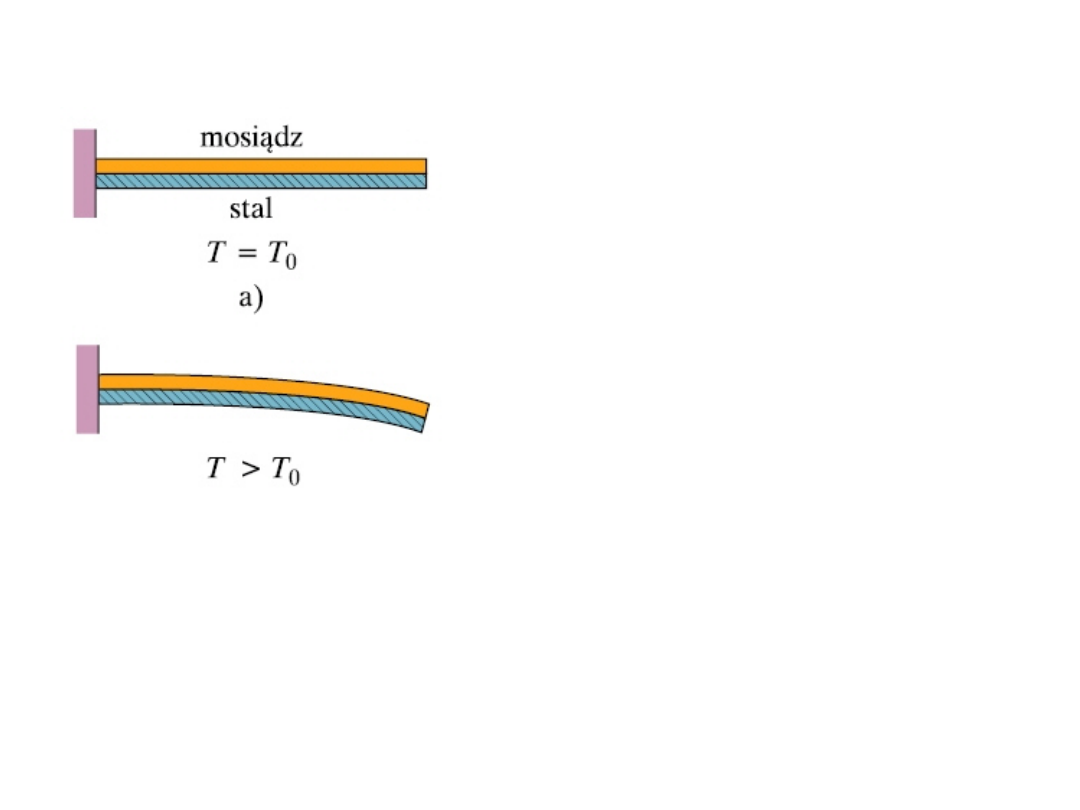
Wykorzystanie zjawiska rozszerzalności
Zjawisko rozszerzalności termicznej
znalazło także szereg praktycznych
zastosowań. Przykładem mogą być
wszelkiego rodzaju czujniki termiczne
wykorzystujące
bimetal.
Bimetal
składa się z dwóch połączonych
materiałów o różnych współczynnikach
rozszerzal-ności, np. mosiądzu i stali.
W efekcie zmian temperatury bimetal
wykrzywia się bądź prostuje zwykle
załączając lub przerywając obwód
elektryczny.
Innym przykładem zastosowań zjawiska rozszerzalności termicznej są
termometry gazowe i cieczowe. Warto dodać, że w termometrach
rtęciowych oprócz rtęci rozszerza się także szklana obudowa i aby
uzyskać przejrzysty efekt zmian wysokości słupka rtęci w dolnej części
termometrów znajduje się zasobnik gromadzący sporą ilość rtęci.
Wartości współczynników rozszerzalności
liniowej wybranych substancji
Posługując się wartościami współczynników rozszerzalności termicznej
trzeba mieć na uwadze, że są one, choć w nieznacznym stopniu,
zależne od temperatury. Wszystkie dane (oprócz lodu) w przedstawionej
poniżej tabeli podano dla temperatury pokojowej.
Substancja
(10
-6
/
0
C)
Substancja
(10
-6
/
0
C)
Łód (0
0
C)
51
Stal
11
Ołów
29
Szkło (zwykłe)
9
Aluminium
23
Szkło (pyrex)
3,2
Mosiądz
19
Diament
1,2
Miedź
17
Inwar
0,7
Beton
12
Kwarc
0,5
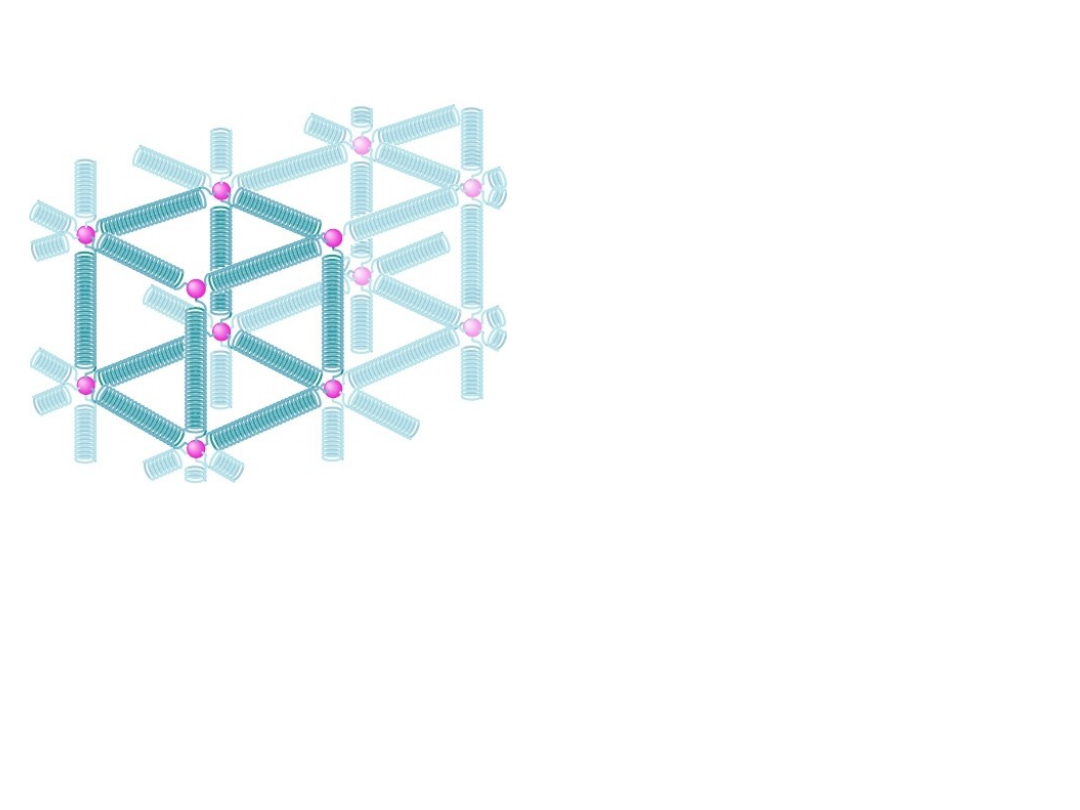
Sprężystość
Ze względu na atomowe siły
wiązania ciała stałe a także i ciecze
stanowią
układ
skupiony.
W
oddziaływaniach międzyatomowych
przeważają zatem siły przyciągania.
W ciałach stałych obowiązuje pewien
wzór ułożenia atomów, co ilustruje
rysunek. Działanie siłą na ciało stałe,
czyli np. ściskanie, rozciąganie bądź
skręcanie zaburza układ położeń
atomów i w konsekwencji możliwe są
pewne zmiany rozmiarów ciał.
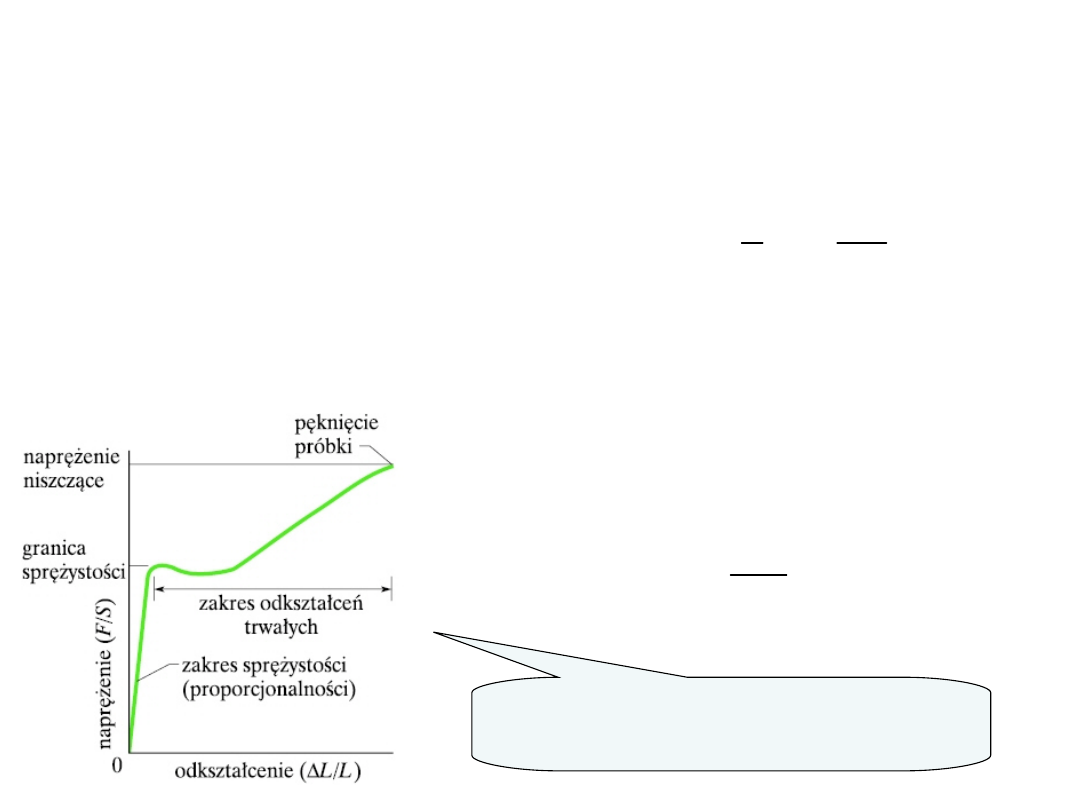
Przy czym, np. dla stalowego pręta rozciąganie go do 0,05 % długości nie
powoduje trwałych odkształceń. W zakresie wydłużeń od 0,05% do 0,2%
pręt taki odkształca się plastycznie. Zadziałanie naprężeniem powodującym
przekroczenie wydłużenia o 0,2% powoduje zerwanie pręta.
Zakres wydłużeń nie powodujący trwałych odkształceń nazywa się
zakresem sprężystości.
Proporcjonalność odkształcenia do
naprężenia
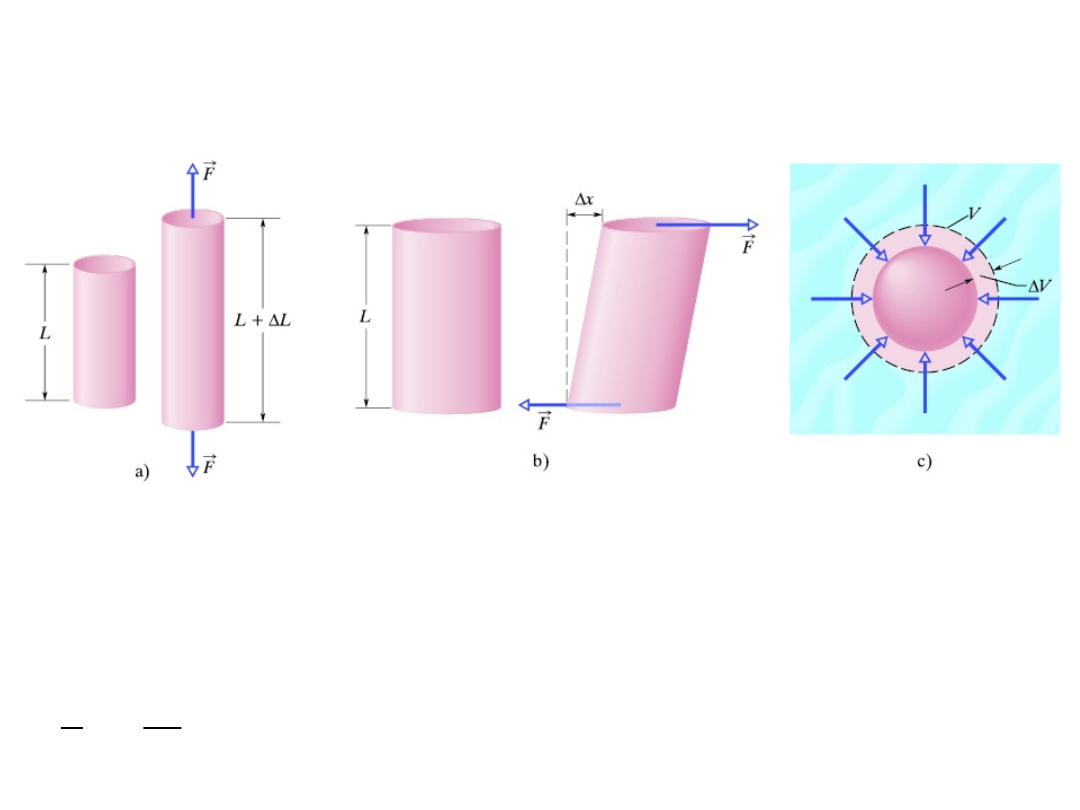
Na przedstawionym rysunku na poszczególne ciała działa naprężenie
rozciągające (a), naprężenie ścinające (b), oraz naprężenie objętościowe
(c).
We
wszystkich
przedstawionych
przypadkach
odkształcenie
reprezentowane przez Δl, Δx, oraz przez ΔV jest proporcjonalne do
naprężenia. Ilustracją tej proporcjonalności jest następujące równanie:
(75),
l
l
Δ
E
=
S
F
gdzie, E jest modułem sprężystości
zwanym modułem Younga.
Proporcjonalność odkształcenia do
naprężenia
Wzór (75) obowiązuje przy rozciąganiu bądź
ściskaniu.
Przy
naprężeniach
ścinających
(poprzecznych) naprężenie mierzy się także za
pomocą siły na jednostkę pola powierzchni, ale
siła działa tu nie prostopadle do tej powierzchni,
lecz równolegle do niej. Moduł sprężystości nosi
tu nazwę modułu ścinania i oznaczany jest literą
(G).
(76).
l
x
Δ
G
=
S
F
Przy naprężeniach objętościowych odpowiedni
moduł nazywa się modułem sprężystości
objętościowej, czyli modułem ściśliwości (K).
Rolę naprężenia pełni ciśnienie.
(77).
Vl
V
Δ
K
=
p
Zależność odkształcenia od
naprężenia dla próbki ze stali
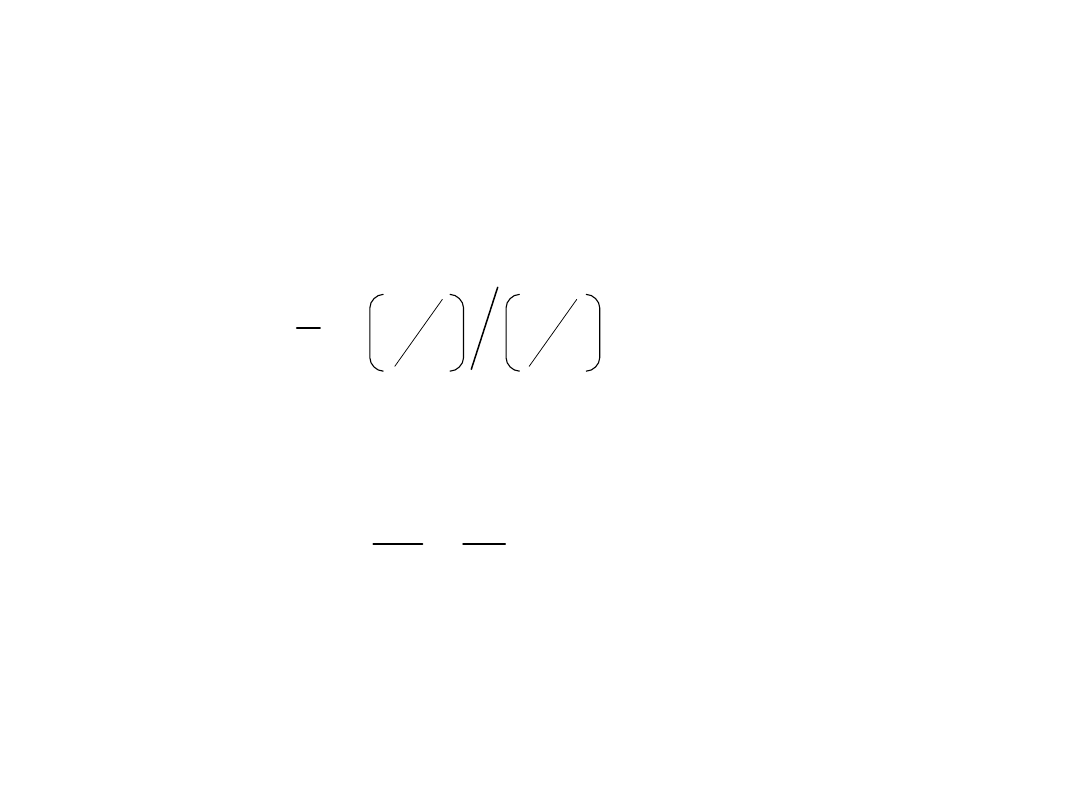
Współczynnik Poissona i Gęstość energii
potencjalnej deformacji
Współczynnik Poissona (μ) jest określony jako stosunek względnego
skrócenia (ε’) w kierunku prostopadłym do działającej siły do względnego
wydłużenia (ε) w kierunku działającej siły.
(78).
l
l
Δ
r
r
Δ
=
ε
'
ε
=
μ
0
0
Gęstość energii potencjalnej deformacji (U) określona jest jako funkcja
naprężenia (δ) lub wydłużenia względnego (ε):
(79).
2E
δ
=
2
ε
E
=
U
2
2
Odkształcenie mierzy się często tensometrem. Jest to prosty i użyteczny
czujnik, który przykleja się do badanego przedmiotu, dzięki czemu
odkształca się on tak samo jak badany przedmiot. W wyniku odkształcenia
zmienia się opór elektryczny czujnika, co umożliwia pomiar odkształceń.
Niektóre cechy sprężyste wybranych
materiałów
Materiał
Gęstość
Moduł Younga
Naprężenie
niszczące
Granica
sprężystośc
i
(kg/m
3
)
(10
9
N/m
2
)
(10
6
N/m
2
)
(10
6
N/m
2
)
Stal (ASTM A36)
7860
200
400
250
Aluminium
2710
70
110
95
Szkło
2190
65
50*
___
Beton
(o dużej
wytrzymałości)
2320
30
40*
___
Drewno
(Daglezja)
525
13
50*
___
Kość
1900
9*
170*
___
Polistyren
1050
3
48
___
* Przy ściskaniu
Document Outline