POMIARY 

W ENERGETYCE

TECHNIKA POMIAROWA

Andrzej Wawszczak

42 631 25 97

andrzej.wawszczak@p.lodz.pl

Poprawną  jakość  eksploatacji

  obiektów  energetycznych  można  osiągnąć 

między innymi dzięki zastosowaniu nowoczesnych systemów informatyki i 
sterowania, zarówno w sfe-rze 

użytkowania

, jak i 

zarządzania

. 

Obiekt

 

energetyczny

  wyposażony  w  odpowiednią  aparaturę  pomiarową, 

informującą  użytkownika  o przebiegu  procesu  technologicznego  i  stanie 
eksploatowanego obiektu.
Ze wzrostem mocy urządzenia, wzrastają: 
•

gabaryty

, 

•

skomplikowanie budowy

, 

•

koszty

, 

•

wartości parametrów fizycznych

 procesu technologicznego: 

- zmniejszanie bezpiecznych (dopuszczalnych) zmian, 

    -wzrasta wymagana liczba punktów pomiarowych i dokładność pomiaru.
Znaczne 

wymiary  obiektów  energetycznych

  uniemożliwiają  obserwację 

zainstalowanych  bezpośrednio  na  obiekcie  przyrządów  pomiarowych. 
Wyniki pomiarów są 

zdalnie przesyłane

 do dyspozytorni, gdzie znajdują się 

przyrządy wskazujące i rejestrujące poszczególne parametry (temperaturę, 
ciśnienie,  strumienie  przepływów  itd.)  w  wybra-nych  punktach  procesów 
technologicznych.  Z  dyspozytorni,  np.  nastawni  elektrowni,  personel 
nadzoruje pracę urządzeń technologicznych.

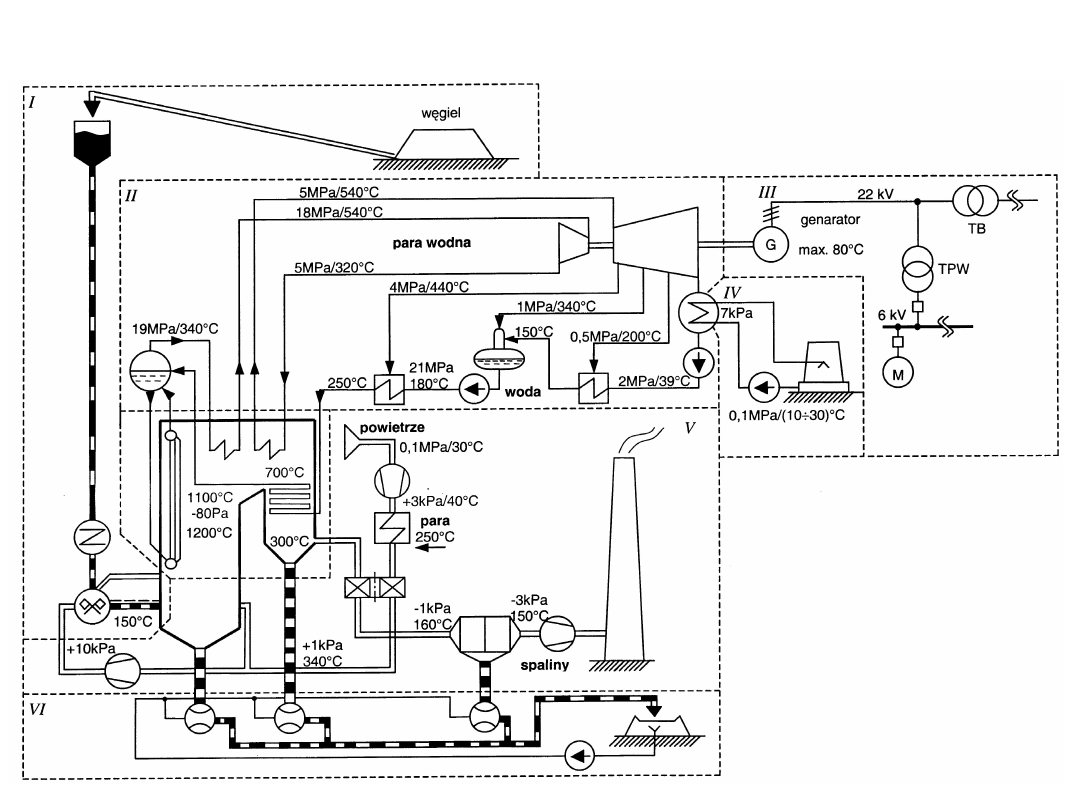
CIŚNIENIA I TEMPERATURY W ELEKTROWNI

I  – układ nawęglania,
II  – układ cieplny, 
III – układ elektryczny,
IV – układ chłodzący,
V – układ paliwo-

powietrze-

 

spaliny,

VI – układ 

odpopielania.

PODSTAWOWE POJĘCIA I DEFINICJE 

Pomiar

  to  proces  poznawczy  polegający  na  porównaniu  z  odpowiednią 

dokładnością

  wartości  wielkości  mierzonej  x  z  pewną  jej  wartością 

przyjętą  za 

jednostkę

  miary,  w  określonych  warunkach  za  pomocą 

odpowiednich środków technicznych. Na proces pomiaru składa się wiele 
kolejnych czynności, które stanowią kolejne zadania:

• zdefiniowanie wielkości mierzonej X,

• wybór zasady fizycznej i metody pomiaru,

• wykonanie pomiaru,

• opracowanie wyników pomiaru.

Wielkość fizyczna

 – jednoznacznie zdefiniowana właściwość materii.

Jednostka miary

 – wartość wielkości umownie przyjętej za liczbowo równą 

jedności, którą odtwarza się za pomocą wzorców.

Zasada  pomiaru

  –  wykorzystane 

zjawisko  fizyczne

,  stanowiące  podstawę 

pomiaru,  np.  zjawisko  termoelektryczne  wykorzystane  do  pomiaru 
temperatury.

Metoda  pomiaru

  – 

sposób  uzyskania  wyniku  pomiaru

  przez  wykorzystanie 

zasad  i środków  pomiarowych.  Metoda  pomiaru  mówi  o  obranym 
sposobie porównywania z wzorcem miary.

Sposób pomiaru

 – 

kolejność czynności

 niezbędnych do wykonania pomiaru.

Cel 

pomiaru

 

– 

uzyskanie 

informacji

 

o 

parametrach 

fizycznych 

charakteryzujących badany obiekt i o przebiegających w nim procesach i 
przemianach.  Zależnie  od  sposobu  uzyskiwania  i  wykorzystywania  tych 
informacji,  na  przykładzie  elektrowni  parowej,  można  wyróżnić 
następujące rodzaje pomiarów.

Pomiary  bieżące

  (ciągłe,  eksploatacyjne)  –  ciągły  pomiar  wielkości 

fizycznych  charakte-rystycznych  dla  procesu  eksploatacyjnego  i mające 
na celu:

• zapewnienie  prawidłowego  prowadzenia  procesu

  technologicznego  i 

bezpieczeństwa  pracy  urządzeń  (np.  poziomy  wody  w  zbiornikach, 
temperatury pary i metalu, ciśnienie pary, prędkości obrotowej itp.), przy 
czym  część  wyników  tych  pomiarów  jest  wyko-rzystywana  w  układach 
automatycznej regulacji procesu technologicznego,

• zapewnienie ekonomicznych warunków eksploatacji

 wszystkich urządzeń 

elektrowni (np. temperatura i skład chemiczny spalin na wylocie z kotła, 
analiza składu chemicznego wody itp.),

• dostarczenie  danych  do  oceny  wskaźników  techniczno-ekonomicznych

, 

charakteryzu-jących  poziom  eksploatacji  elektrowni  jako  całości  (np. 
wartość obciążenia).

Pomiary  kontrolne

  –  sprawdzenie  dokładności  przyrządów  do  pomiarów 

bieżących.

Pomiary gwarancyjne

 i 

zdawczo–odbiorcze

 – mają na celu ocenę 

zbudowanej instalacji, jej sprawność i możliwość otrzymania 
projektowanych parametrów (np. możliwość za-pewnienia znamionowej 
temperatury pary w określonym zakresie obciążeń kotła). Po-miary te są 
wykonane ściśle według norm odbiorczych przez odpowiednie instytucje.

Pomiary  badawcze

 

i

 

prototypów

  –  są  najczęściej  przeprowadzone  w 

laboratoriach  specjalistycznych,  a  ich  celem  jest  uzyskanie  informacji  o 
własnościach 

technicznych 

urządzeń 

nowo 

zbudowanych 

lub 

modernizowanych  oraz  urządzeń,  w  których  wykorzystuje  się  nowe 
zdobycze nauki.

Pomiar  miejscowy

  –  wynik  pomiaru  otrzymuje  się  w  miejscu  pobrania 

sygnału wielkości mierzonej.

Pomiar  zdalny

  –  sygnał  wielkości  mierzonej  jest  przenoszony  na  pewną 

odległość  do  miejsca,  gdzie  zainstalowany  jest  miernik  wielkości 
mierzonej  (przyrząd  pomiarowy).  Przenoszenie  to  może  być  realizowane 
na drodze: 

• mechanicznej, 

• hydraulicznej, 

• pneumatycznej, 

• optycznej, 

• elektrycznej.

 

Rozwój  techniki  cyfrowej  spowodował,  że  w  układach  pomiarowych 
sygnały  analogowe  są  przetwarzane  na  postać  cyfrową  i  dalej  są 
wykorzystywane w systemach pomiaro-wo-kontrolnych. Oprócz systemów 
cyfrowych, 

do 

transmisji 

danych 

pomiarowych, 

są 

jeszcze 

wykorzystywane 

sygnały 

elektryczne 

prądowe 

oraz 

niekiedy 

pneumatyczne.

Sygnał pomiarowy

 – wielkość fizyczna, zawierająca informację podstawową 

o wartości wielkości mierzonej. Sygnał pomiarowy ma dwa elementy: 

• nośnik  sygnału

  –  wielkość  fizyczna  opisująca  procesy  energetyczne 

przenoszące  informację  (prąd  lub  napięcie  elektryczne,  przesunięcie 
mechaniczne, ciśnienie itp.), 

• parametr informacji

 – wartość określonego parametru wielkości fizycznej, 

np.: I = 16,3 mA, U = 5 V, l = 2,5 mm, p = 68 kPa.

SYGNAŁY POMIAROWE

MIEJSCE POWSTANIA: 

pierwotne

–

powstające w 

czujniku 
i przetworniku 
pierwotnym, np. 
przesunięcie 
mechaniczne, 
rezystancja; 

wtórne

– 

powstające 

w następnych elementach 
przetwarzających;

FIZYCZNY CHARAKTER 

NOŚNIKA:

 

• elektryczne, 

• pneumatyczne, 

• mechaniczne, 

• optyczne.

 

CIĄGŁOŚĆ PRZESYŁANIA INFORMACJI W 

CZASIE:

 

• ciągłe

 

– analogowe, 

• dyskretne

 

– impulsowe, cyfrowe. 

ANALOGOWE SYGNAŁY ELEKTRYCZNE:

• stałoprądowe

  –  duża  odporność  na  zakłócenia  i  zmianę  parametrów  w 

linii przesyłowej;

• stałonapięciowe

  –  mała  odporność  na  zakłócenia  zewnętrzne,  trudne  do 

wzmacniania,  wrażliwe na zmiany parametrów linii przesyłowej; 

• amplitudowe

  –  nośnikiem  sygnału  jest  napięcie  sinusoidalne  lub 

okresowe  impulsowe  o  stałej  częstotliwości,  parametrem  informacji: 
amplituda  sinusoidy  lub  impulsu;  duża  odporność  na  zakłócenia,  łatwe 
wzmocnienie, wrażliwe na zmiany parametrów linii; 

• częstotliwościowe

  (czasowe,  fazowe)  –  nośnikiem  sygnału  jest  napięcie 

sinusoidalne  lub  okresowe  impulsowe  o  stałej  amplitudzie,  parametrem 
informacji  może  być:  częstotliwość,  czas  trwania  impulsu,  przesunięcie 
fazowe  między  przebiegami;  łatwe  do  przesyłania  i  wzmacniania,  przy 
doborze  odpowiedniej  częstotliwości  nośnej  odporne  na  zakłócenia 
zewnętrzne. 

Sygnały standaryzowane (zunifikowane):

 

stałoprądowe

: (0..5) mA, (0..20) mA i (4..20) mA; 

pneumatyczne

: (0,02..0,1) MPa; 

stałonapięciowe

: (0..10) V, (–10..+10) V –

jako sygnały wewnętrzne, 

do przesyłu informacji 

między elementami systemu 

pomiarowego.

PRZYRZĄDY POMIAROWE

• Przyrząd  pomiarowy

  –  narzędzie  służące  do  przetwarzania  wielkości 

mierzonej  lub  innej  (związanej  z  wielkością  mierzoną)  na  wskazanie  lub 
równoważną informację (np. rejestrację, zapis w pamięci); np.: manometr 
sprężysty,  przepływomierz,  termometry:  szklane,  termoelektryczne  i 
rezystancyjne (wraz z urządzeniem wskazującym) itp.

• Miernik

  –  przyrząd  pomiarowy  określający  tylko  za  pomocą  wskazania 

wartość wielkości mierzonej; np. miliwoltomierz.

• Wskaźnik

  –  przyrząd  lub  ciało  fizyczne  służące  do  stwierdzenia,  czy 

określone zjawisko lub określona wartość wielkości mierzonej występuje 
czy nie występuje; np.: stożki Segera jako wskaźnik temperatury.

• Aparatura  pomiarowa

  –  zespół  środków  technicznych  przeznaczony  do 

wykonania  zadania  pomiarowego  określoną  metodą  pomiarową, 
obejmujący  wszystkie  narzędzia  pomiarowe  i  osprzęt  pomocniczy 
połączone  ze  sobą  według  określonego  schematu;  np.:  aparatura  do 
pomiaru wartości ciepła spalania paliwa.

• Wyposażenie  pomiarowe

  –  zespół  przyrządów  i  aparatur  pomiarowych 

przeznaczonych  do  wykonania  pomiarów  wartości  wielkości  jednego  lub 
więcej  rodzajów;  np.:  wyposażenie  laboratorium  umożliwiającego 
pomiary różnych wielkości.

• Czujnik

  –  element  składowy  przyrządu  pomiarowego  (układ  fizyczny, 

fizyczno-chemiczny itp.), służący do odbierania i przetwarzania informacji 
o  wielkości  mierzonej  –  stanowi  przy  tym  pierwszy  element 
przetwornikowy, np. rurka sprężysta manometru, termoelement, rezystor 
termometryczny  itp.  Sygnał  wyjściowy  z  czujnika  nazywa  się  sygnałem 
pierwotnym.

• Przetwornik  pomiarowy

  –  narzędzie  służące  do  przetworzenia,  z 

określoną dokładnoś-cią i według określonego prawa, wartości wielkości 
mierzonej  (lub  wielkości  już  przetworzonej  z  wielkości  mierzonej)  na 
wartość innej wielkości lub inną wartość tej samej wielkości. Najczęściej 
sygnałem  wyjściowym  z  przetwornika  pomiarowego  jest  sygnał 
stosowany 

w 

standaryzowanych 

(zunifikowanych) 

systemach 

pomiarowych.

• Tor  pomiarowy

  –  ciąg  przetworników  i  części  łączących  narzędzia 

pomiarowe,  znajdujących  się  między  czujnikiem,  stanowiącym  pierwszy 
element toru, a urządzeniem wskazującym (rejestrującym), stanowiącym 
jego element końcowy.

• Układ  pomiarowy

  –  zestaw  sprzętu  pomiarowego,  którego  elementy 

(czujniki,  przetworniki,  przełączniki,  mierniki  itp.)  są  wzajemnie 
połączone w sposób umożliwiający wykonanie pomiaru.

• System  pomiarowy

  –  zbiór  środków  pomiarowych,  konieczny  i 

wystarczający 

do 

przeprowadzenia 

eksperymentu 

pomiarowego. 

Urządzenia  wejściowe  systemu  pomiarowego  realizują  sprzężenie 
badanego  obiektu  z  systemem  przetwarzania  (obróbki),  w  którym 
realizuje  się  algorytm  pomiaru.  Dla  dopasowania  charakterystyk 
sygnałów  wyjściowych  czujników  pomiarowych  do  wejścia  systemu 
przetwarzania  stosuje  się  pośrednie  wzmacniacze  (przetworniki) 
pomiarowe lub przetworniki analogowo-cyfrowe.

Ze względu na przeznaczenie przyrządy pomiarowe dzielą się na:

Przyrządy  użytkowe

  (techniczne,  ruchowe,  eksploatacyjne)  –  do 

użytkowych  (normal-nych)  pomiarów  (nie  do  sprawdzania  innych  narzędzi 
pomiarowych).  Wykorzystywane  do  kontroli  procesu  produkcyjnego. 
Przystosowane do trudnych warunków pracy, powinny być odporne na: pył, 
wilgoć, wstrząsy mechaniczne itp. 

Przyrządy  kontrolne

  –  do  sprawdzenia  przyrządów  użytkowych,  czasami 

również do pomiarów w pracach naukowo–badawczych. Przyrząd kontrolny 
powinien być dokład-niejszy od przyrządu kontrolowanego.

Przyrządy  wzorcowe

  –  używane  do  sprawdzania  i  wzorcowania  innych 

przyrządów 

pomiarowych. 

Błąd 

maksymalny 

wskazań 

przyrządu 

wzorcowego  powinien  być  co  najmniej  czterokrotnie  mniejszy  od 
dopuszczalnego  błędu  podstawowego  wskazań  przyrządu  badanego  (o 
dwie klasy lepszy od przyrządu badanego).

Wzorzec  miary

  (etalon)  –  narzędzie  pomiarowe  odtwarzające,  praktycznie 

niezmiennie  podczas  jego  użycia,  jedną  lub  kilka  znanych  wartości  danej 
wielkości,  np.  rezystor  wzorcowy,  tłokowy  wzorzec  ciśnienia,  definicyjne 
punkty stałe Międzynarodowej Skali Temperatur itp.
Ze  względu  na  sposób  przetwarzania  sygnału  pomiarowego  w  procesie 
pomiarowym przyrządy dzielą się na: 

analogowe

 oraz 

cyfrowe

.

Sprawdzanie

  –  porównanie  wskazań  przyrządu  pomiarowego  ze 

wskazaniem przyrządu wzorcowego w celu określenia jego dokładności lub 
wprowadzenia  odpowiednich  poprawek.  Sprawdzenie  należy  wykonać  w 
warunkach  odniesienia,  w  co  najmniej  5  punktach  wskazań,  przyczym 
punkty  te  powinny  być  równomiernie  rozłożone  w  zakresie  wskazań 
przyrządu  badanego  i  powinny  obejmować  górną  i  dolną  granicę  zakresu 
wskazań. Sprawdzenie należy wykonać najpierw dla wartości narastającej, 
aż  do  górnej  granicy  zakresu  wskazań,  a  następnie  dla  malejącej,  aż  do 
dolnej granicy zakresu wskazań.

Wzorcowanie

  –  ustalenie  położenia  wskazów  narzędzia  pomiarowego  (w 

przypadku  narzędzia  z  podziałką)  albo  wyznaczenie  wartości  wielkości  za 
pomocą  wzorców  odtwa-rzających  jedną  lub  kilka  różnych  wartości 
wielkości.

Skalowanie

  –  wykonanie  podziałki  narzędzia  pomiarowego  na  podstawie 

wskazów,  których  położenie  ustalono  na  podstawie  wzorcowania,  w  razie 
potrzeby dokonuje się interpolacji między głównymi wskazami.

Legalizacja

  –  zespół  czynności  wykonywanych  przez  Państwową  Służbę 

Miar, w celu stwierdzenia i zaświadczenia, że badane narzędzie pomiarowe 
spełnia  wymagania  techniczne  i  metrologiczne  określone  przepisami 
legalizacyjnymi.  Legalizacji  podlegają  narzędzia  stosowane  do  rozliczeń 
(liczniki  paliw, energii cieplnej i elektrycznej, odważni-ki, taksometry itp.) 
oraz  stosowane  przy  czynnościach  urzędowych  i  zawodowych  (ochrony 
zdrowia, bezpieczeństwa i higieny pracy itp.). 

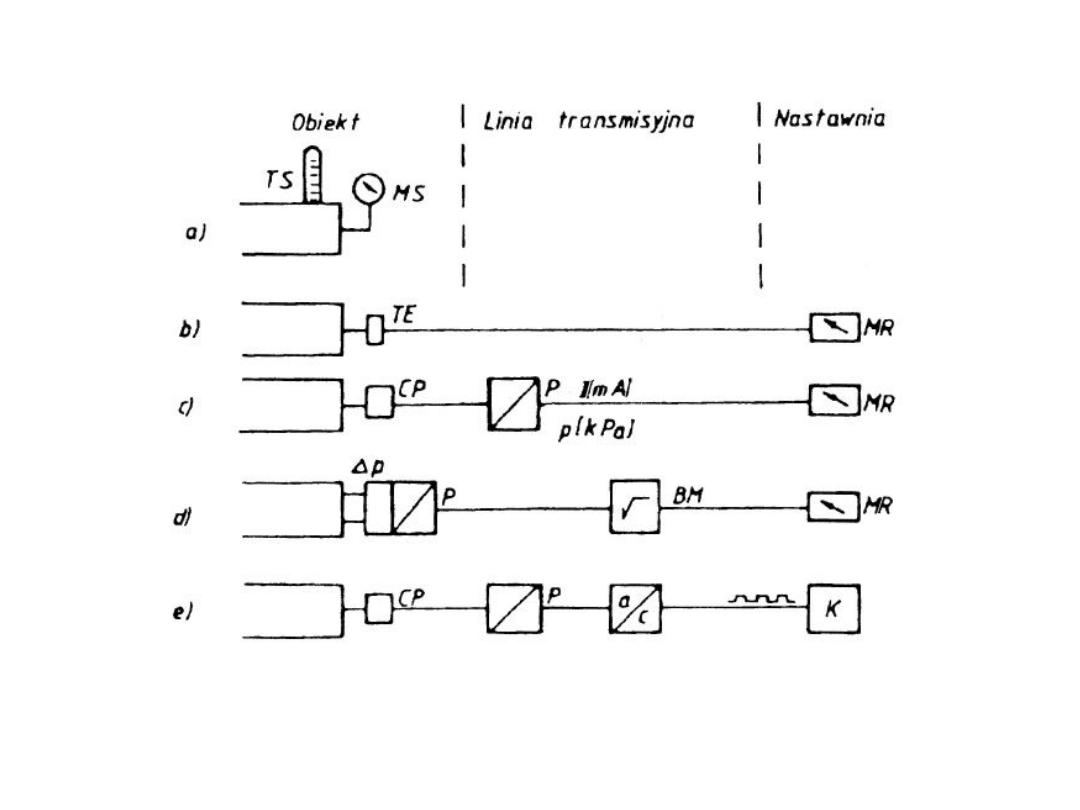
TORY POMIAROWE

CP – czujniki pomiarowe, p – czujnik pomiarowy różnicy, TS – termometr 

szklany, 
MS – ciśnieniomierz sprężysty, TE – termoelement, MR – miernik wskazujący, 
rejestrator, 
P – przetwornik pomiarowy, BM – blok arytmetyczny, a/c – przetwornik 
analogowo–cyfrowy, 
K – komputer. 

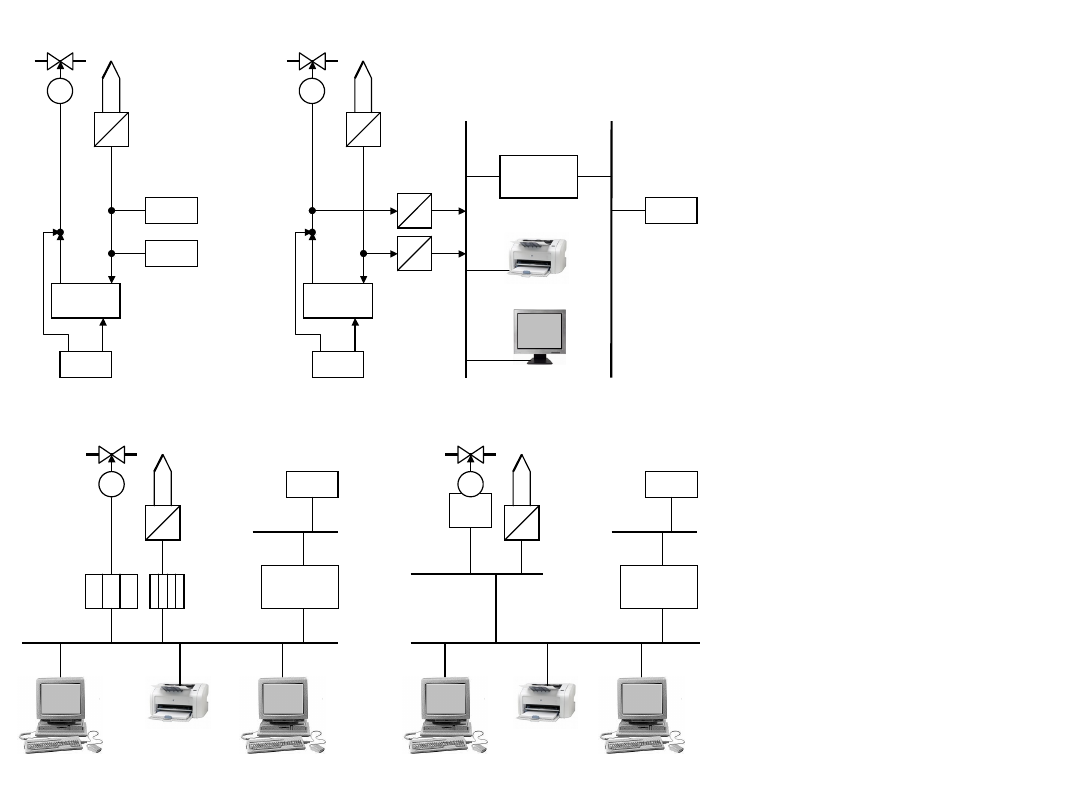
Porównanie prostych 
układów pomiarowych i 
regulacyjnych w różnych 
wersjach sprzętowych

 

t / I – przetwornik temperatura-
prąd
A / C – przetwornik 
analog./cyfrowy,
UAR – układ automatycznej 
regulacji,
RA – rejestrator analogowy,
WA – wskaźnik analogowy, 
R/A – przełączanie 
automat./ręcznie, 
DIRE – Dyżurny Inżynier Ruchu. .

a)

układ klasyczny, 

b)

układ klasyczny z 

wydzieloną 

częścią 

informatyczną 

w postaci cyfrowej, 

c)układ cyfrowy, 
d)

układ cyfrowy o 

dużym  rozproszeniu 
(decentralizacji). 

 

t 

I 

S 

UAR 

R/A 

WA 

RA 

t 

I 

S 

UAR 

R/A 

A 

C 

A 

C 

M 

SERWER 

DANYCH 

t 

I 

S 

SERWER 

DANYCH 

DIRE 

DIRE 

Stacja 

Inżynierska  

Stacja 

Operatorska  

Szafa 

wejść  

Szafa 

sterowników  

t 

C 

SERWER 

DANYCH 

DIRE 

Stacja 

Inżynierska  

Stacja 

Operatorska  

a) 

b) 

c) 

d) 

UAR 

S 

Sieć 

niskiego 

poziomu 

Sieć 

wysokiego 

poziomu 

Sieć 

lokalna 

Często  trudno  jest  wyróżnić  granicę  podziału  między  poszczególnymi 

elementami 
w torze pomiarowym: 

• termometr  szklany

  -  to  czujnik  (bańka  termometryczna),  przetwornik 

(kapilara) i przy-rząd wskazujący (podziałka na kapilarze); 

• manometr sprężysty

 - z wskazówką pomiarowa na osi, jeżeli z osią tego 

manometru  zostanie  sprzęgnięty  potencjometr  obrotowy,  wówczas  do 
toru  pomiarowego  wprowa-dza  się  dodatkowy  przetwornik  i  dodatkowy 
miernik, którym może być przetwornik (miernik) rezystancji;

• termoelement

  oraz 

rezystor  termoelektryczny

  –  są  zarazem  czujnikami 

jak i przetworni-kami pomiarowymi (pierwotnymi), ponieważ ich sygnały 
wyjściowe  mogą  być  bez  dalszego  przetwarzania  wykorzystane  w 
miernikach elektrycznych;

• układ  pomiarowy  ciśnienia  z  przetwornikiem  indukcyjnym  lub 

pojemnościowym

 

–  wielkość  mierzona  nie  oddziałuje  bezpośrednio  na  element  ruchomy 
przetwornika,  wymagany  jest  tu  czujnik  pomiarowy  ciśnienia,  którego 
element  ruchomy  zmienia  swoje  położenie  wraz  z  odkształceniem 
elementu sprężystego czujnika.

Poszczególne elementy toru pomiarowego spełniają funkcje:

• czujnik  pomiarowy

  –  uzyskanie  sygnału  pierwotnego,  związanego  z 

wielkością mierzo-ną poprzez określoną funkcją;

• przetwornik pomiarowy

 – przekształcenie sygnału pierwotnego na sygnał 

użyteczny 
o odpowiedniej postaci i mocy;

• układ  filtrujący

  –  usunięcie  (wytłumienie)  z  sygnału  pomiarowego 

zakłóceń i szumów; 

• blok  arytmetyczny  (obliczeniowy)

  -  przeprowadzenie  korekt  i  działań 

matematycznych;

• układ  wyjściowy

  –  doprowadzenie  sygnału  pomiarowego  do  postaci 

odpowiedniej dla użytkownika (postać analogowa lub cyfrowa).

METODY POMIAROWE

Metody  pomiarowe

  –  sposób  wykorzystania  zjawisk  fizycznych  i  środków 

pomiarowych,  realizowane  za  pomocą  różnych  układów,  w  których  mogą 
być  stosowane  różne  zasady  przetwarzania  i  porównywania  oraz  różne 
drogi otrzymywania poprawnego wyniku.
Metody  pomiaru  ze  względu  na  sposób  wyznaczenia  wartości  mierzonej 
dzielą się na: 

•

bezpośrednie

  (proste)  –  wartość  wielkości  mierzonej  jest  równoznaczna 

z odczytanymi 

wskazaniami, 

np. 

pomiar 

ciśnienia 

manometrem 

sprężystym, pomiar napięcia 

woltomierzem itp.;

•

pośrednie

  (złożone)  –  wartość  wielkości  mierzonej  jest  funkcją  innych 

wielkości 

fizycznych  i  na  podstawie  wyników  bezpośrednich 

pomiarów 

tych 

wielkości 

(po 

wykonaniu 

określonych 

działań 

matematycznych)  wyznacza  się  wartość  wielkości 

mierzonej,  np. 

sprawność  kotła  na  podstawie  pomiaru  strat  cząstkowych,  pomiar 
strumienia  masy  w  kanale  niekołowym  z  wykorzystaniem  rurek 
spiętrzających.
Metody  pomiaru  ze  względu  na  sposób  otrzymywania  wyniku  pomiaru 
wielkości mierzonej:

•

bezwzględne

  (podstawowe)  –  wartość  wielkości  mierzonej  jest 

wyznaczana  na  podstawie  definicji  tej  wielkości,  np.  ciśnienie  jako  siła 
działająca 

na 

jednostkę 

powierzchni, 

natężenie 

prądu 

elektrycznego  jako  siła  działająca  na  przewodniki, 

w których  płynie 

ten prąd;

•

porównawcze

  –  wartość  wielkości  mierzonej  otrzymuje  się  przez 

porównanie wyniku 

pomiaru ze znaną wartością tej wielkości lub też ze 

znaną wartością innej wielkości 

jako funkcji wielkości mierzonej.

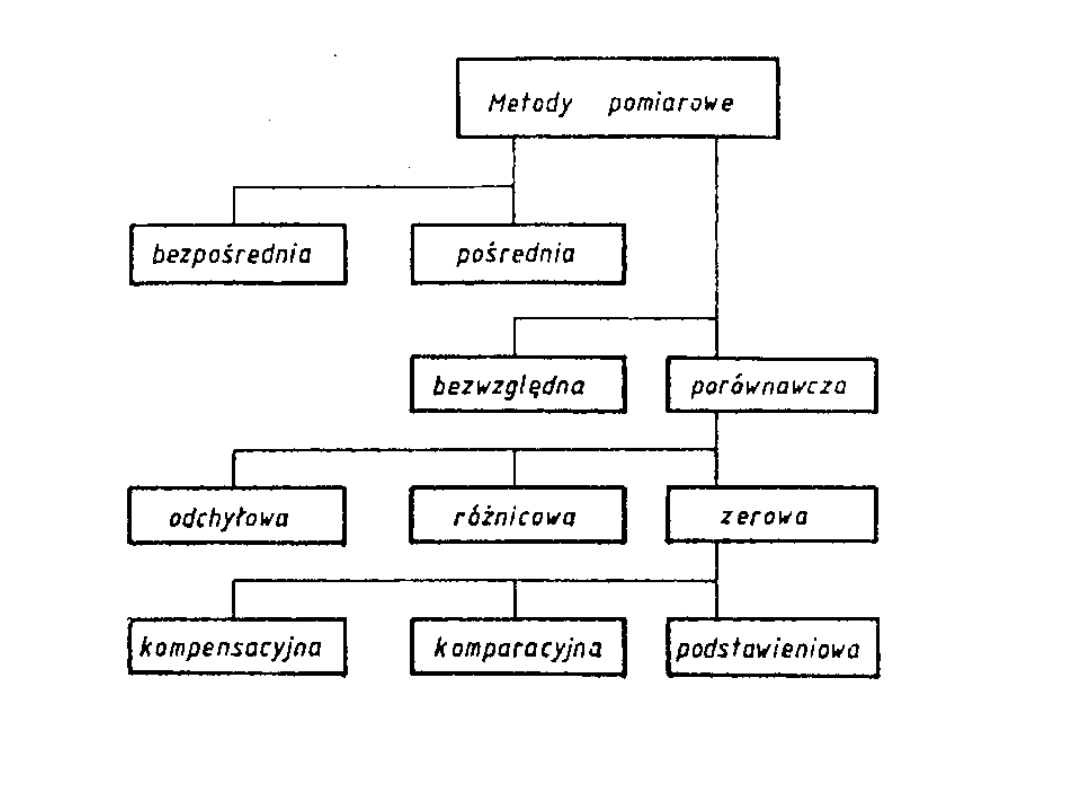
Schemat klasyfikacji metod pomiarowych 

Ze  względu  na  wykorzystane  charakterystyczne 

zjawiska  fizyczne

  można 

metody pomia-rowe podzielić na:

•

metody nieelektryczne

, 

•

metody elektryczne

.

Stosowane  układy  i  przyrządy  pomiarowe  wykorzystują  metody 
porównawcze – wielkość mierzoną porównuje się z odpowiednią wielkością 
wzorcową.  Ze  względu  na  sposób  porównania,  czyli  sposób  otrzymania 
wyniku, rozróżnia się:

metodę odchyłową

 – polegającą na określeniu wartości wielkości mierzonej 

x  przez  odchylenie  urządzenia  wskazującego  przyrządu  pomiarowego 
wyskalowanego w jednos-tkach wielkości mierzonej;

metodę różnicową

 – polegającą na porównaniu wartości wielkości 

mierzonej x

 

z niewiele różniącą się od niej znaną wartością tej samej 

wielkości x

0 

i następnie pomiarze różnicy: x

r

 = x – x

0

 tych wartości; 

metodę zerową

 – polegająca na sprowadzeniu do zera różnicy: x

r

 = x – x

0

 

między  war-tością  mierzoną  x,  a  znaną  wartością  wielkości  porównawczej 
x

0

.  Miarą  wartości  x  jest  w  tej  metodzie  wartość  x

0

.  Czynność  badania 

różnicy x

r

 i sprowadzenia jej do zera przez zmianę x

0

 nazywa się procesem 

równoważenia,  przy  czym  proces  ten  może  odbywać  się  ręcznie  lub 
automatycznie. 

WŁAŚCIWOŚCI METROLOGICZNE 

PRZYRZĄDÓW I UKŁADÓW POMIAROWYCH 

Właściwości metrologiczne:

• statyczne

:

 

• dynamiczne

:

gdzie: X – wielkość mierzona, y – sygnał pomiarowy, Z – wektor wielkości 

wpływowych, 

 – czas (zmienność w czasie).

W zależności od warunków, powstają: 

błędy statyczne

błędy dynamiczne

.

)

Z

,

X

(

f

y

1



))

(

Z

),

(

X

(

f

)

(

y

2









Pomiary  wielkości  fizycznych

  są  zawsze  operacjami  niedokładnymi. 

Otrzymany  na  drodze  pomiaru  (doświadczenia) 

wynik  pomiaru

  x  zawsze 

różni się  od rzeczywistej wartości wielkości mierzonej,  zwanej 

wartością 

prawdziwą

  x

0

.  Równość  wyniku  pomiaru  x  i wartości  prawdziwej  x

0

 

wielkości  mierzonej  X  jest  zdarzeniem  wyjątkowym,  i fakt  jego 
wystąpienia pozostaje zazwyczaj nieznany. Istotą pomiaru jest jednak to, 
że 

niedokładność wyniku pomiaru

 zawsze można 

oszacować

, czyli można 

określić  możliwie  mały  przedział  zmian  wartości  wielkości  mierzonej,  w 
którym  ze  znanym 

prawdopodobieństwem

  znajduje  się 

wartość  wyniku 

pomiaru

 x oraz nieznana

 wartość prawdziwa wielkości mierzonej

 x

0

. 

Mogą być różne przyczyny wystąpienia różnicy między 

wynikiem pomiaru

 

x, a 

wartością prawdziwą

 x

0

. Najczęściej są to: 

• błędy metody pomiarowej

, wynikające z przyjętych uproszczeń;

• błędy przetwarzania

 wielkości fizycznej na inną dogodniejszą do 

zmierzenia; 

• błędy operacji metrologicznych

, wynikające z niedoskonałości 

wzorcowania, odczytu, opracowania wyniku;

• błędy urządzeń pomiarowych

: 

podstawowe

 i 

dodatkowe

, których wartość 

jest najczęściej określona przez producenta i podana w 

dokumentacji 

techniczno-ruchowej

 (

DTR

) przyrządu.

OCENA JAKOŚCI POMIARU

Wynik  pomiaru

  –  wartość  wielkości  mierzonej  X  uzyskana  w  procesie 

pomiaru;  gdy  uwzględnimy  poprawki,  otrzymamy 

wynik  pomiaru 

poprawiony

.

Wartość  poprawna 

–  wartość  wielkości  mierzonej  X,  którą  uważa  się  w 

takim  stopniu  przybliżoną  do 

wartości  prawdziwej

  x

0

  tej  wielkości,  pod 

względem 

ilościowym 

i  jakościowym,  że  różnica  między  tymi  wartościami  może  być  pominięta  z 
punktu  widzenia  celu,  do  którego  wartość  poprawna  (przybliżona)  jest 
potrzebna.

Błąd pomiaru

 – różnica między wynikiem pomiaru x a wartością prawdziwą 

x

0

  lub  wartością  poprawną  wielkości  mierzonej  X.  Rozbieżność  ta  jest 

wyrażana  za  pomocą  liczby  w  takich  samych  jednostkach  jak  wartość 
wielkości mierzonej X.

Błąd  pomiaru

  definiowany  jako  różnica  między 

wynikiem  pomiaru

  x  i 

wartością prawdziwą

 x

0

 wielkości mierzonej X: 

x = x – x

0

nazywanego  niekiedy 

błędem  prawdziwym  pomiaru

,  nie  można  obliczyć  z 

tej  zależności,  ponieważ  nie  jest  znana 

wartość  prawdziwa 

x

0

 

wielkości 

mierzonej  X.  Można  go  oszacować  lub  obliczyć  jego  niektóre  składowe, 
przy  czym  sposób  postępowania  zależy  od  rozpoznania  rodzaju 
oddziaływań wielkości wpływających na wynik pomiaru. 

Zamiast  wartości  prawdziwej,  znana  jest 

wartość  poprawna

  x

p

,  np. wynik 

otrzymany przy-rządem wzorcowym, o którym wiemy, że jego błąd pomiaru 
jest  wielokrotnie  mniejszy  od  błędu  pomiaru  przyrządu  sprawdzanego. 
Wówczas  błąd  pomiaru,  nazywany  jest  niekiedy  błędem  poprawnym 
pomiaru. 

Błąd  poprawny  pomiaru

  x

p

  ze  zmienionym  znakiem  może  być 

określany  jako: 

poprawka

.  Po  dodaniu  poprawki  do  wyniku  pomiaru 

otrzymuje się 

wartość poprawną

. :

x + x

p

 = x

p

 . 

Często  w  praktyce  nie  jest  możliwe  wyznaczenie  błędu  poprawnego,  np. 
nie  ma  przyrzą-du  wzorcowego  lub  jego  wykorzystanie  jest  z  przyczyn 
technicznych  bardzo  trudne  lub  wręcz  niemożliwe,  a  można  jedynie 
oszacować jego wartość na podstawie 

błędu granicz-nego

 wykorzystanego 

przyrządu lub urządzenia pomiarowego. 

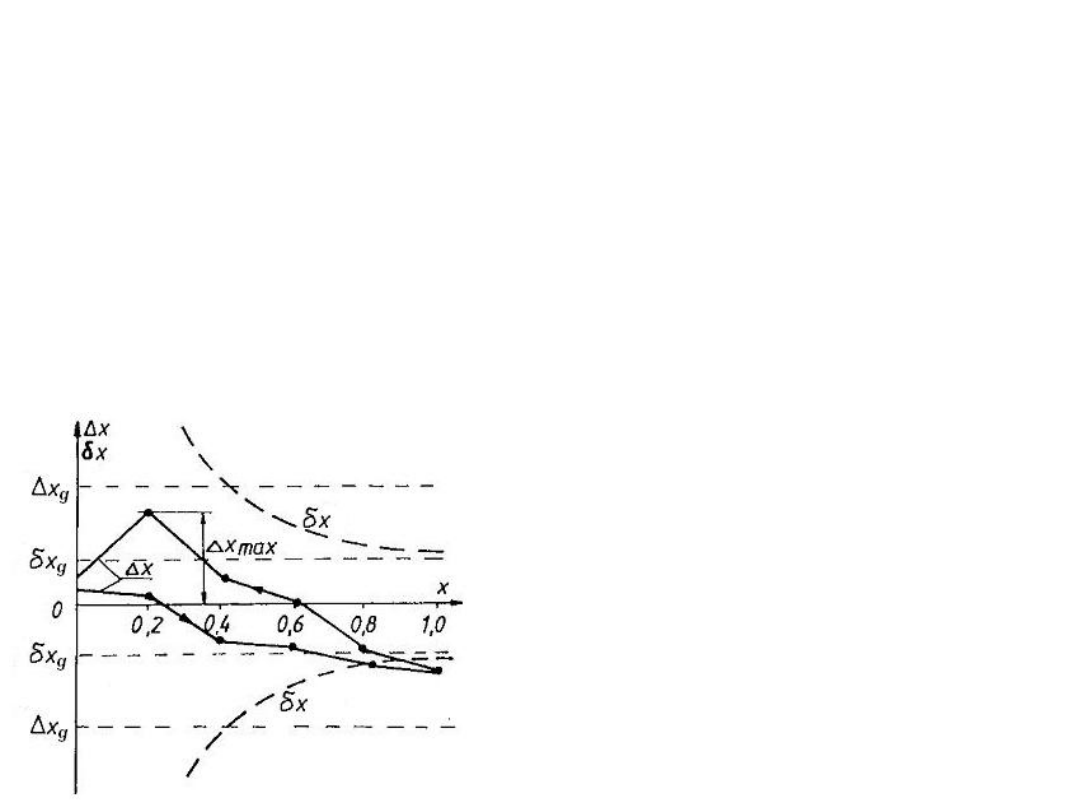
Błąd  graniczny  pomiaru

  x

g

  –  możliwie  najmniejszy  przedział  wokół 

wartości  wyniku  pomiaru  x,  wewnątrz  którego  znajduje  się 

wartość 

prawdziwa

 x

0

: 

x

0

  < x – x

g

 ; x + x

g

 >

Błąd poprawny

 x

p

 w stosunku do 

błędu granicznego

 x

g

 zachowuje relację: 

  x

p

  x

g

 .

Wartość błędu granicznego

 x

g

 określa się podczas wzorcowania przyrządu 

w odpowied-nio  wyposażonym  i  przystosowanym  do  tego  laboratorium 
pomiarowym. 

Najczęściej  dane  na  temat  błędu  granicznego  można  uzyskać  w  jego 

Dokumentacji  Tech-niczno-Ruchowej

  (DTR‑ce)  lub  też  na  podstawie  jego 

klasy  dokładności,  której  wartość  zwykle  jest  umieszczana  bezpośrednio 
na przyrządzie pomiarowym, np. na jego skali. 

Klasa  dokładności

  przyrządu  pomiarowego  podawana  jest,  jako  wyrażony 

w  [%] 

względny  błąd  graniczny

  odniesiony  do  zakresu  pomiarowego 

przyrządu: 

gdzie: x

m

 – zakres przyrządu pomiarowego.

%

100

x

x

x

m

g

g









U = a∙U

x

 +b∙U

n

. 

U -błąd pomiaru

U

x

  -wartość odczytana

U

n

. -zakres pomiaru 

a, b-

stałe 

współczynniki 

DOKUMENTACJA TECHNICZNO-RUCHOWA

URL – Upper Range Limit

DANE METROLOGICZNE …

Rosemont 3095MV

BŁĘDY POMIAROWE

Błędy pomiarowe można podzielić na trzy zasadnicze grupy:

• błędy systematyczne,

• błędy przypadkowe,

• błędy nadmierne i omyłki

. 

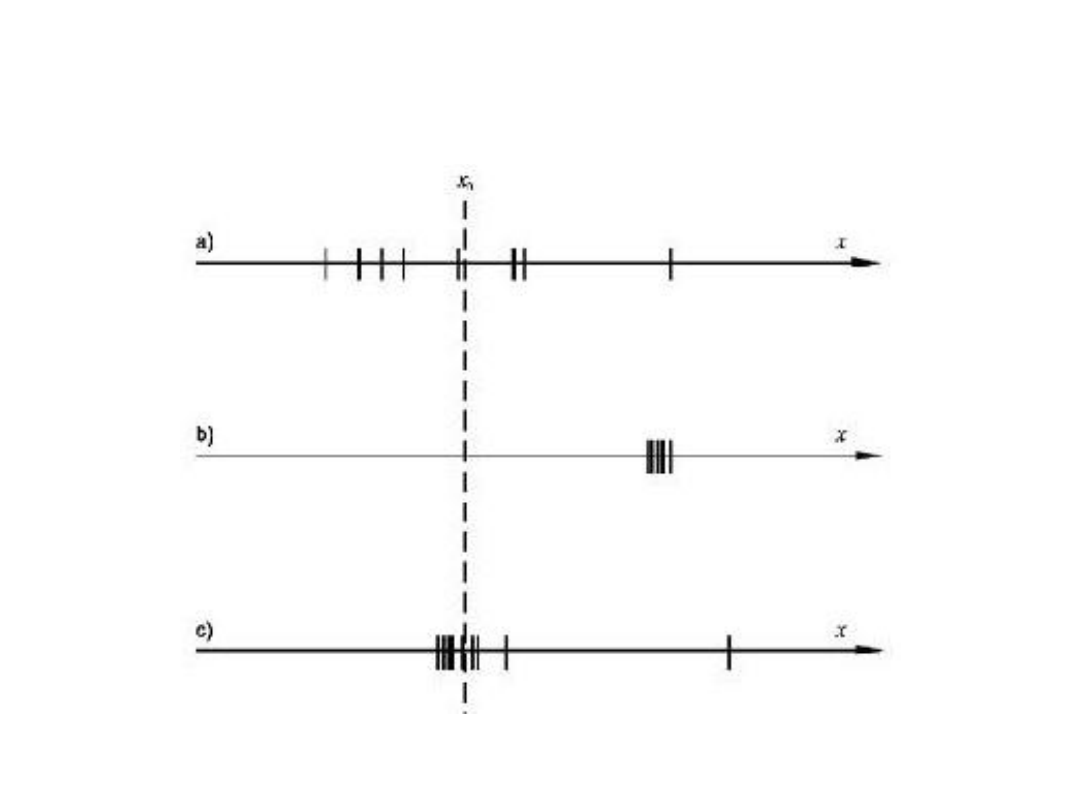
Wzajemna relacja wartości prawdziwej x

0

 i zbioru wyników pomiaru 

dla: 

a) błędu przypadkowego, b) błędu systematycznego, c) błędu grubego

Błędy  systematyczne

  –  przy  wielu  pomiarach  w  tych  samych  warunkach 

mają  wartości  będące  funkcją  wielkości  mierzonej  X.  Dla  określonej 
wartości wielkości mierzonej x można jednoznacznie określić wartość tego 
błędu. 
Często 

wartość  błędu  systematycznego  jest  stała

  w  całym  zakresie 

przyrządu  pomiarowego.  Błędy  systematyczne  to  np.:  błąd  pomiaru 
temperatury 

termoelementem 

o  temperaturze  zimnych  końców  termoelementu  innej  niż  znamionowa 
(przyjęta przy wzorcowaniu przyrządu), błąd zera wskaźnika wychyłowego, 
błąd  wskazania  miernika  analogowego  spowodowany  niepoprawnym 
wykreśleniem podziałki. 
Przyczyną  błędu  systematycznego  może  być  również 

błąd  metody 

pomiarowej

,  spowodo-wany  oddziaływaniem  przyrządu  pomiarowego  na 

wielkość  mierzoną  lub  zjawisko:  zbyt  duży  czujnik  (sonda)  pomiarowa, 
niewłaściwa  oporność  użytego woltomierza  (zbyt  mała) lub  amperomierza 
(zbyt duża), itp. 
Błędy  wynikające  ze  złego  lub 

niestarannego  zestawienia  przyrządów

 

i wzorców miar w łańcuchu pomiarowym lub zmian warunków pomiaru

Błędy subiektywne

 stale popełniane przez obserwatora, będące najczęściej 

wynikiem  jego:  złych  nawyków  przy  wykonywaniu  odczytów,  stałego 
przyspieszania  lub  opóźniania  czasu  rejestracji,  złej  interpolacji  wskazań 
(brak doświadczenia). 

Błędy  systematyczne  można  wyeliminować

  poprzez  właściwą 

regulację

 

przyrządu  pomiarowego  lub  wprowadzenie  odpowiednich 

poprawek

. 

Poprawki  te  mogą  być  podane  w metrykach  przyrządów  pomiarowych  lub 
mogą zostać określone poprzez wzorcowanie za pomocą dokładniejszego (o 
„wyższej  klasie”)  wzorcowego  przyrządu  pomiarowego,  często  również 
przy zastosowaniu dokładniejszej metody pomiarowej. 

Błędy  przypadkowe

  –  dla  których  nie  można  określić  funkcji,  która  by  w 

sposób jedno-znaczny wiązała ich wartość z wielkością mierzoną X. 

Błędy 

przypadkowe

 

zmieniają 

się 

w 

sposób 

nieprzewidziany

, 

stochastycznie

, zarówno co do wartości jak i znaku. 

Źródłem  błędów  przypadkowych 

może  być  niesprawne  działanie 

przyrządów,  np.:  przy-padkowe  zmiany  warunków  pomiaru,  zjawiska 
o charakterze  tzw.  szumów,  luzy,  tarcie,  histereza)  lub  obserwator,  gdy 
w pomiarach wymagana jest jego subiektywna ocena. 
Błędów  przypadkowych  nie  można  wyeliminować,  ani  ich  jednoznacznie 
określić drogą elementarnych operacji rachunkowych. Można jedynie przy 
użyciu metod rachunku prawdopodobieństwa i statystyki matematycznej 
oszacować ich absolutną wartość. 

Błędy  nadmierne

,  tzw.  błędy  grube,  spowodowane  są  najczęściej 

nieuwagą  obserwatora,  uszkodzeniem  przyrządu  lub  też  pomyłką 
rachunkową. 
Charakterystyczne  dla  błędów  nadmiernych  jest  to,  że  wśród  pomiarów 
występują wartości znacznie różniące się od pozostałych. 
Jeżeli  wykonujemy  tylko  jeden  pomiar,  wówczas  wykrycie  błędu 
nadmiernego jest niemożliwe. Tylko wykonanie serii pomiarów pozwala na 
ujawnienie tego typu błędów. 
Wynik pomiaru obarczony błędem nadmiernym jest niewiarygodny i musi 
być usunięty z serii pomiarów. Istnieją metody statystyczne pozwalające 
na ujawnienie, a tym samym na eliminację wyniku pomiaru obarczonego 
błędem  nadmiernym.  Wszystkie  one  bazują  na  przyjęciu  pewnego 
poziomu  prawdopodobieństwa,  że  wynik  pomiaru  mieści  się  w 
określonym  przedziale  wartości  i  odrzuceniu  tych  wyników  pomiarów, 
które  się  w  tym  zakresie  nie  mieszczą.  Najczęściej  przyjmuje  się  jego 
wartość równą 3∙ (gdzie  jest odchyleniem standardowym). 

BŁĄD W POMIARACH POŚREDNICH 

W  pomiarach  metodą  pośrednią  wielkość  mierzona  X  jest  związana  z 
wielkościami 
U, V i W równaniem definicyjnym: 

X = X(U, V, W)

Wartości wielkości mierzonych u, v i w mogą być obarczone bezwzględnymi 
błędami: u, v i w. Błąd wyznaczenia wartości x w metodzie pośredniej:

2

2

2

w

W

X

v

V

X

u

U

X

x





































































Błędy  wartości  wielkości  mierzonych  u,  v  i  w,  mogą  być  różnego  rodzaju, 
najczęściej są to błędy graniczne:

 u = u

g

,   v = v

g

    i     w = w

g

. 

ROZKŁADY PRAWDOPODOBIEŃSTWA

W procesie poznania rodzaju i wielkości przyczyn, które powodują różnicę 
między  wyni-kiem  pomiaru  x,  a  wartością  prawdziwą  x

0

  wielkości 

mierzonej,  istotnym  narzędziem  jest  analiza  statystyczna  wyników 
pomiaru. Wówczas wyniki pomiarów x są traktowane jako 

zmienne losowe

 

podlegające określonemu 

rozkładowi prawdopodobieństwa

. 

Rozkład  prawdopodobieństwa

  –  przyporządkowuje  wartości  zmiennej 

losowej  x  prawdopodobieństwo  przyjęcia  określonej  wartości  przez  tę 
zmienną. 
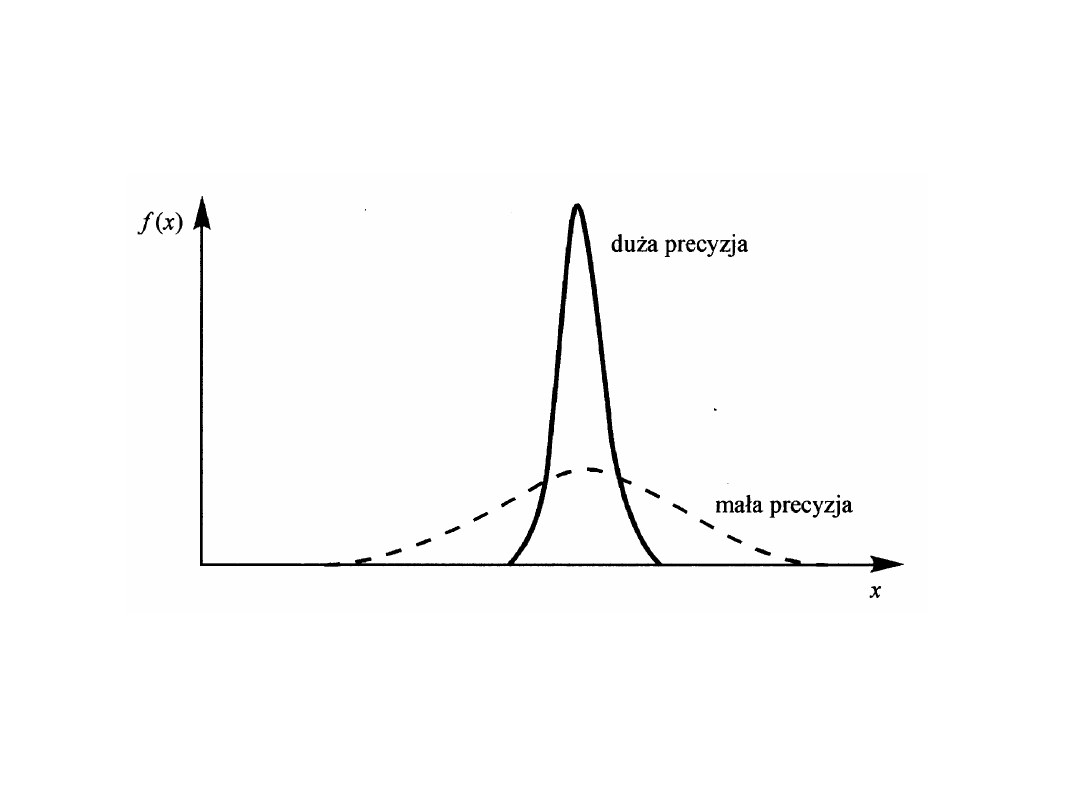
W  zagadnieniach  technicznych  i  praktyce  przemysłowej  przyjmuje  się 
najczęściej,  że  wynik  pomiaru,  jako  zmienna  losowa,  podlega  dwom 
rodzajom rozkładu prawdopodo-bieństwa: 

normalnemu

 i 

jednostajnemu

. 

Rozkład 

normalny

 

został 

opisany 

przez 

wybitnego 

matematyka 

niemieckiego  Carla  Friedricha  Gaussa  (1777-1855)  i  znany  jest  również 
jako 

rozkład Gaussa

. 

Dla  ilości  pomiarów  n      gęstość  prawdopodobieństwa  dla  rozkładu 

normalnego (krzy-wa graniczna rozkładu Gaussa) jest określona wzorem: 

2

2

0

2

)

x

x

(

e

2

1

)

x

(

f





















gdzie:

x

0 

– wartość prawdziwa wielkości mierzonej (środek rozkładu), 

 – odchylenie standardowe (szerokość rozkładu). 

prawdopodobieństwo wystąpienia wyników pomiarów: 





b

;

a

x







b

a

dx

)

x

(

f

1

dx

)

x

(

f













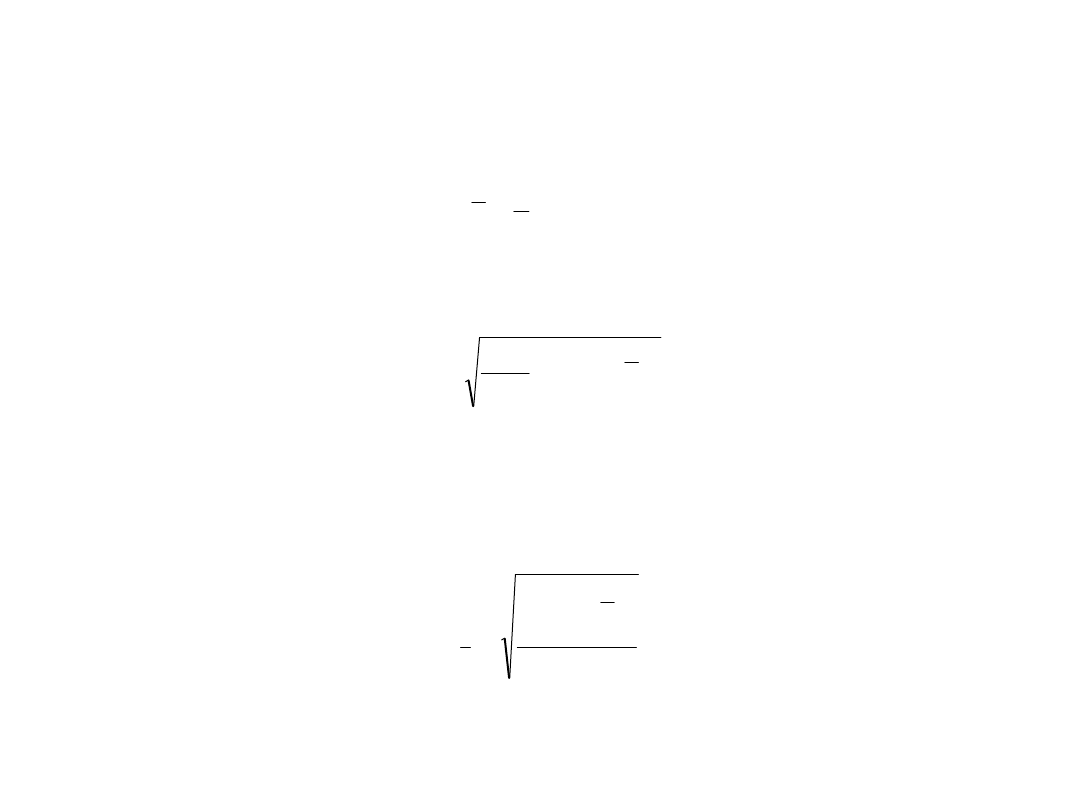
W  rzeczywistości  dysponujemy  skończoną  liczbą 

n

  pomiarów  wielkości 

fizycznej 

X

 

o wartościach: 

(x

1

, x

2

, x

3 

... x

i 

… x

n

).

 Traktując x jako zmienną losową, można 

udowodnić, że 

średnia arytmetyczna

 z n pomiarów: 

jest  wartością  najbardziej  zbliżoną  do  wartości  prawdziwej  x

0

,  jest  jej 

estymatą

,  najlepszym,  najbardziej  prawdopodobnym  przybliżeniem. 

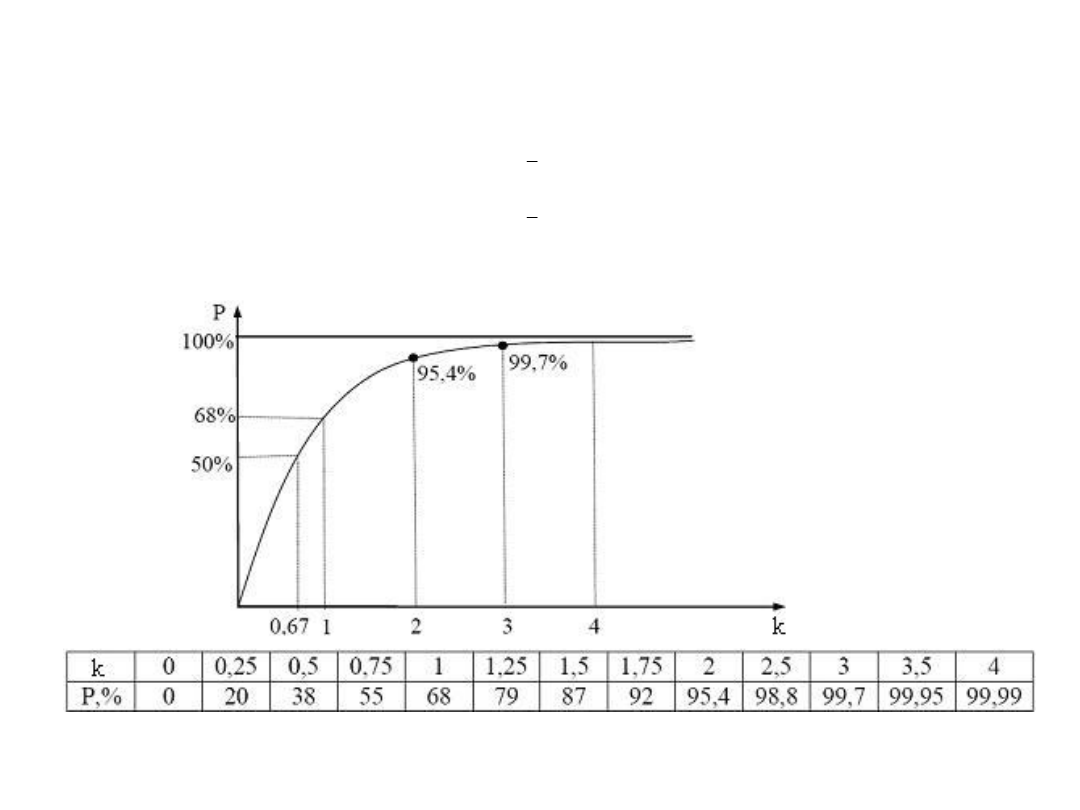
Natomiast 

estymatę odchylenia standardowego

 dla pojedynczego pomiaru 

można obliczyć z zależności: 

Wielkość  

x

  można  by  utożsamiać  z  błędem  pomiaru,  gdybyśmy  za  jego 

wynik  przyjęli  którąkolwiek  z  wartości  x

i

.  Przy  obliczaniu  średniej 

następuje jednak częściowa kompen-sacja odchyłek różnych znaków, dzięki 
czemu  jest  ona  prawdopodobnie  bliższa  wartości  prawdziwej  x

0

  niż  wynik 

pojedynczego  pomiaru.  Ilościowo, 

estymator  odchylenia  stan-dardowego 

średniej

  będzie mniejszy od estymatora 

x

 : 

 









n

1

i

i

x

n

1

x















n

1

i

2

i

x

)

x

x

(

1

n

1

)

1

n

(

n

)

x

x

(

n

1

i

2

i

x















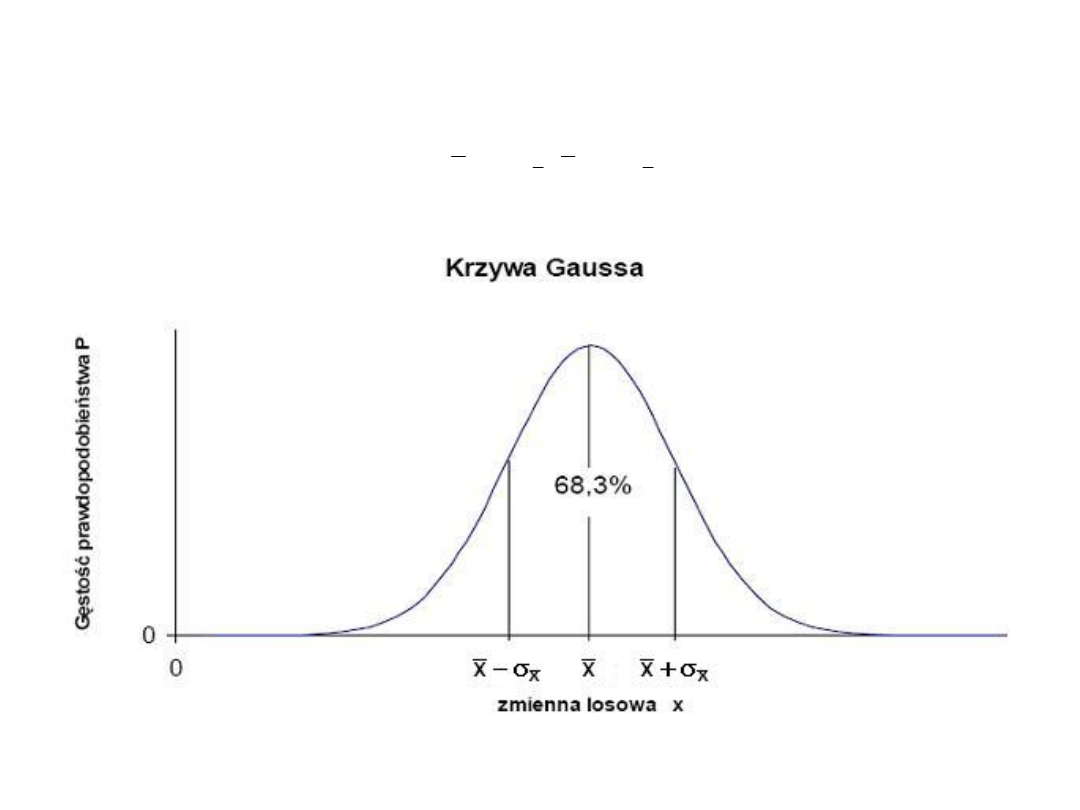
Prawdopodobieństwo 

P

,  że  wynik  pojedynczego  pomiaru  leży  w  zadanej, 

stanowiącej  krotność  odchylenia  standardowego 

(k)

,  odległości  od 

wartości  średniej  (estymaty  wartości  prawdziwej  x

0

),  można  otrzymać 

obliczając całkę: 























x

x

k

x

k

x

dx

)

x

(

f

)

k

(

P

Wartość średnia  jest estymatą wartości prawdziwej  x

0

, można przyjąć, że 

znajduje się ona z prawdopodobieństwem p (tabela i wykres) w przedziale: 

















x

x

0

k

x

;

k

x

x

Często  w  praktyce  liczba  n  pomiarów  mierzonej  wielkości  fizycznej  X  jest 
mała  (n << 30),  wówczas  do  wyznaczenia  błędu  przypadkowego  na 
określonym poziomie ufności należy stosować opracowany w 1908 r.  przez 
angielskiego  statystyka  W. S. Gosseta  (1876-1937),  pseudonim  Student, 

rozkład t-Studenta

.  

Funkcja  opisująca  gęstość  prawdopodobieństwa  dla  rozkładu  t-Studenta 
nie  zależy  od  odchylenia  standardowego,  zależy  natomiast  od  liczby  n 
wykonywanych 

pomiarów 

oraz 

poziomu 

ufności 

p, 

czyli 

prawdopodobieństwa, że: 

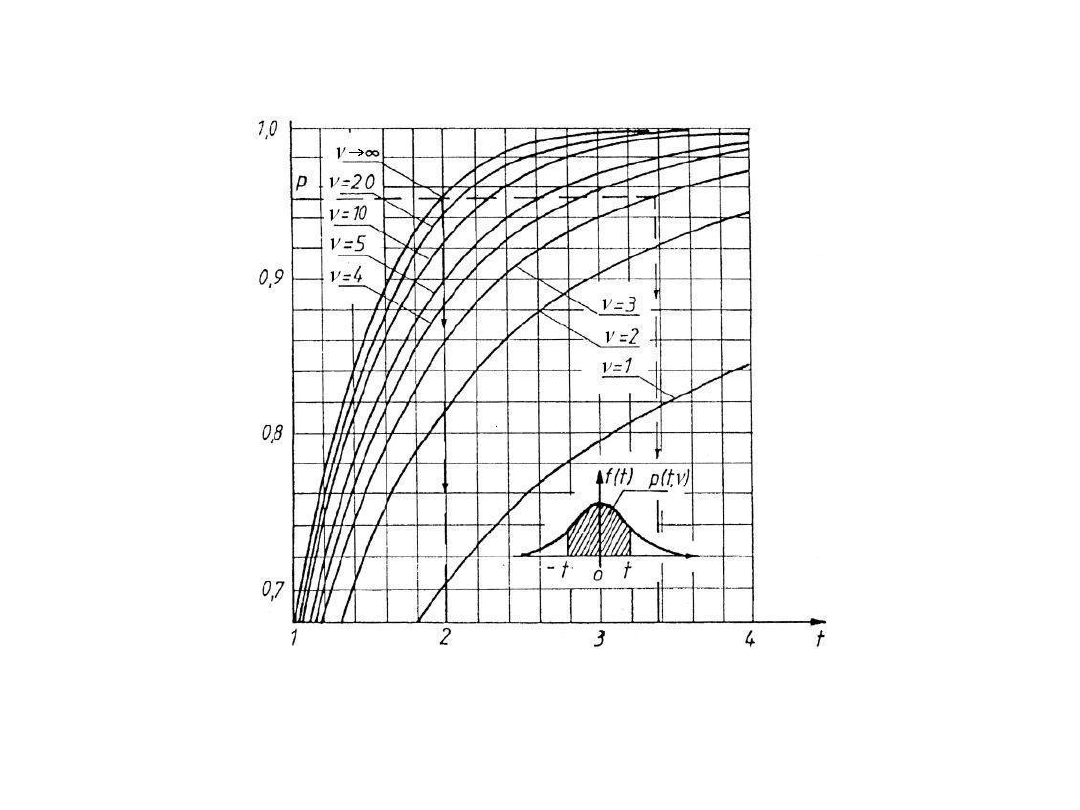
Funkcja  gęstości  prawdopodobieństwa  zmiennej  losowej  t  dla  n  punktów 
pomiarowych ((n-1) 

stopni swobody

) jest opisana zależnością:

















x

x

0

t

x

;

t

x

x

gdzie:  t – krotność odchylenia standardowego średniej      ,

      –  jest tzw. „funkcją gamma” Eulera.

 

Gdy n   wówczas rozkład t-Studenta dąży do rozkładu normalnego 

(Gaussa). 















2

n

x







2

n

2

1

n

t

1

1

-

n

π

2

1

n

2

n

)

t

(

f



































 



















Rozkład  t-Studenta

  jest  stabelaryzowany  lub  można  go  przedstawić  w 

formie  wykresu,  przy  czym  wartość  zmiennej  losowej 

t

  podawana  jest  dla 

wartości  prawdopodobieństwa  odpowiadającej  poziomowi  ufności 

p

  oraz   

liczby stopni swobody:     = n - 1. 

Przyjęcie  granic  tolerancji  słusznych  dla  dużej  liczby  pomiarów  (rozkład 
Gaussa),  w  przy-padku  niewielkiej  liczby  pomiarów,  prowadzi  do  mylnych 
wniosków  dotyczących  dokład-ności  pomiaru.  Dla  zadanego  poziomu 
ufności  p = 0,954,  wartości  współczynników  roz-szerzenia:  dla  rozkładu 
normalnego  (    )  t = 2  ,  natomiast  z  rozkładu  t-Studenta  dla  np. 

 = 3  t = 3,4. 

Rozkład  jednostajny

  (prostokątny,  równomierny)  najprawdopodobniej 

występuje  wów-czas,  gdy  w  kolejnych  n  pomiarach  nie  ma  zauważalnego 
rozrzutu wyników: 

x = x

1

 = x

2

 = ... = x

i

 = ... = x

n

 

Wówczas  za  główną  przyczynę  błędu  pomiaru  należy  uznać  błąd 
wzorcowania  przyrządu  pomiarowego 

a

,  który  może  być  traktowany  jako 

błąd  graniczny.  Jego  wartość  jest  najczęściej  podawana:  bezpośrednio  na 
przyrządzie  pomiarowym  (klasa  przyrządu),  w  DTR-ce  lub  w  protokole 
wzorcowania.  Gdy  nie  ma  takich  informacji,  wówczas  wykonujący  pomiar, 
wykorzystując  swoją  wiedzę  i  doświadczenie,  może  oszacować  wartość 

a

 

(najmniejsza  działka  skali,  ostatnia  cyfra  znacząca  itp.)  i  przyjąć  ją  jako 
najbardziej prawdopodobną. 

Dla  rozkładu  jednostajnego  funkcja  gęstości  prawdopodobieństwa  jest 
opisana: 

w przedziale :

< x – a ; x + a >

a poza tym przedziałem: 

f(x) = 0. 

Natomiast odchylenie standardowe: 

       .

a

2

1

)

x

(

f





3

a

dx

)

x

(

f

x

a

a

2















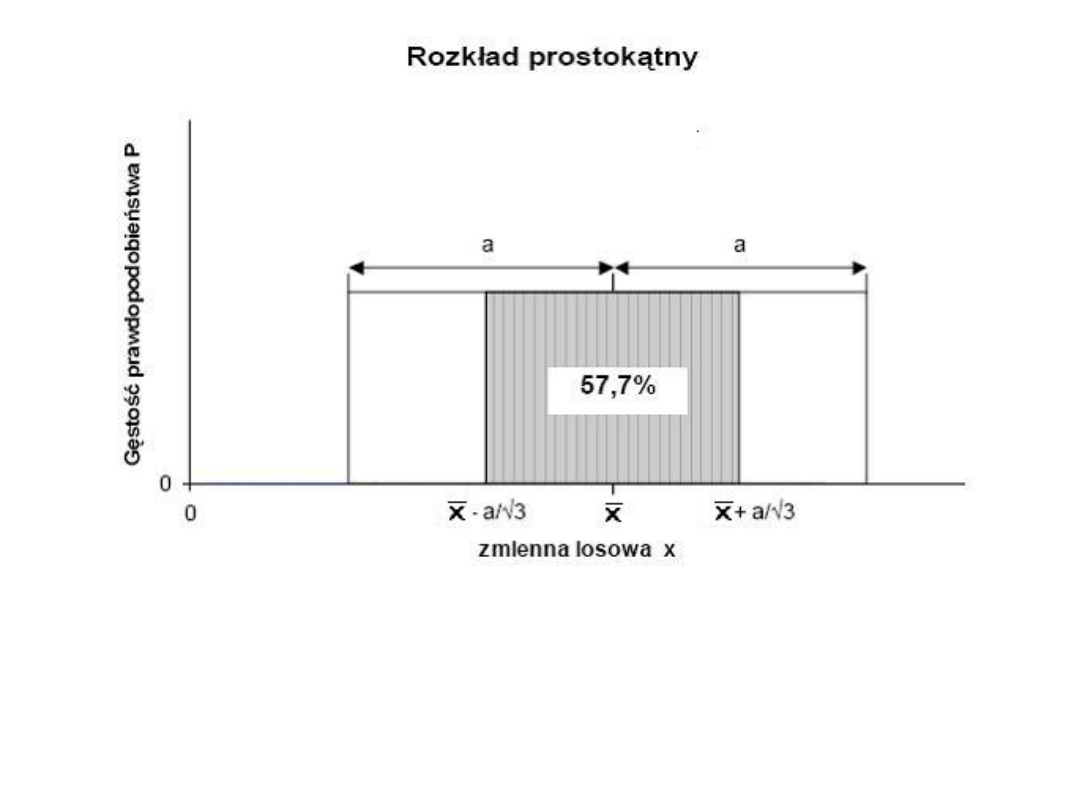
Dla 

rozkładu jednostajnego

 przyjmuje się, że wartość prawdziwa 

x

0

 

wielkości mierzonej 

X

 znajduje się w przedziale 

< x – a ; x + a >

 z 

prawdopodobieństwem 

p=1

. 

Często zdarza się, że dla dokładnych przyrządów pomiarowych błąd 
wzorcowania przyrządu pomiarowego a składa się z kilku składników i 
również może być funkcją (najczęściej liniową) wielkości mierzonej X: 

b

X

m

a







NIEPEWNOŚĆ POMIARU

Oceny  niedokładności  uzyskanych  w  procesie  pomiarowym  wyników, 
można  dokonać  przy  wykorzystaniu 

teorii  błędów

  lub 

teorii  niepewności

, 

przy  czym  zgodnie  z  zalecenia-mi  ISO  (International  Organization  for 
Standardization)  wprowadzonymi  w  1995 roku,  należy  wykorzystywać 

teorię niepewności

. 

Zaleca  się  unikać  określenia  „

błąd  pomiaru

”,  zastępując  go  określeniem 

„

niepewność  pomiaru

”.  Słowo  „błąd”  powinno  używać  się  wyłącznie  dla 

nazywania  pomyłek  ekspery-mentatora  (błędy  grube)  lub  błędów 
wywołanych  niewłaściwą  metodą  pomiarową.  Do  opisu  niepewności 
zmiennej  x  norma  zaleca  używanie  symbolu 

u(x)

  od  angielskiego  słowa 

uncertainty

 - 

niepewność

. 

Teoria  niepewności  stanowi  próbę  ujednolicenia  zasad  obliczania  i 
wyrażania 

niedokład-ności  pomiaru

  stosowanej  do  wszystkich  pomiarów  i 

do  wszystkich  rodzajów  wielkości  mierzonej.  Siedem  międzynarodowych 
organizacji  (BIPM,  IEC,  IFCC,  ISO,  IUPAC,  IUPAP  oraz  OIML)  opracowało 

teorię  niepewności

,  która  w  taki  sam  sposób  traktuje  wszystkie  źródła 

niedokładności pomiarowych. 
Zasady  określania  niepewności  pomiarowych  zostały  przyjęte  przez 
Międzynarodowy  Komitet  Miar  (CIPM)  i  stały  się  obowiązujące  dla 
wszystkich  organizacji  metrologicznych  i  laboratoriów  akredytowanych 
wszędzie tam gdzie wymagają tego przepisy prawa. 
Opracowano  i  wydało  w 1993 r.  przewodnik  pod  tytułem  „

Guide  to the 

Expression  of Uncertainty  in  Measurement

”,  a Główny  Urząd  Miar  (GUM) 

wydał w 1999 r. jego polskie tłumaczenie. 

Niedokładność  pomiaru

  charakteryzowana  jest  za  pomocą  parametru 

nazywanego  „

niepewnością

”  (

uncertainty

),  który  jest  definiowany  jako 

„

parametr  związany  z  wynikiem  pomiaru  charakteryzujący  rozrzut 

wartości,  który  można  w  uzasadniony  sposób  przypi-sać  wartości 
mierzonej

”.  Takim  parametrem  może  być  na  przykład 

odchylenie 

standardo-we

 



  (lub  jego  wielokrotność)  lub  też  połowa  szerokości 

przedziału odpowiadającego określonemu poziomowi ufności. 

Niepewność  pomiaru

  jest  pojęciem  samodzielnym,  której  w  żaden  sposób 

nie należy wiązać z pojęciem błędu - błąd może być zerowy, a niepewność 
duża.
W polskim  tłumaczeniu  przewodnika  pod  redakcją  prof. J. Jaworskiego, 
znajduje  się  uwaga,  iż  „

niepewność  w  ogólnym  znaczeniu  jest  cechą 

pomiaru,  a  ilościowe  miary  niepewności  powinny  być  nazywane 
parametrami niepewności

” 

Teoria  niepewności  pomiaru 

nie  jest  ścisłą  teorią  fizyczną,  lecz  raczej 

przybliżonym,  matematycznym  opisem  niedoskonałości  eksperymentu.  Jej 
metody  i  rezultaty  nie  ograniczają  się  tylko  do  zjawisk  fizycznych,  lecz  są 
takie same, lub bardzo podobne, dla wszystkich nauk doświadczalnych. 

Dla określenia 

niepewności pomiaru bezpośredniego

 wykorzystujemy dwie 

miary: 

• niepewność  standardowa

  u  (standard  uncertainty),  wyrażana  przez 

odchylenie standardowe średniej arytmetycznej serii pomiarów; 

• niepewność  rozszerzona

  U  (expanded  uncertainty)  określająca  przedział 

niepewności 

przy 

określonym 

prawdopodobieństwie 

p

, 

zwanym 

poziomem  ufności

  (coverage  propability),  który  może  przyjąć  dowolną 

wartości pomiędzy 0 a 1.

Pod względem sposobu otrzymania wyróżniamy:

niepewność typu A

 - u

A

 – wyznaczaną metodami statystycznymi,

niepewność typu B

 - u

B

 – wyznaczaną metodami innymi niż statystyczne.

Niepewność typu A

 – u

A

, obliczana metodami statystyki matematycznej na 

podstawie serii pomiarów. Ogólnie, 

rozrzut wartości 

x

 wielkości mierzonej

 

X może mieć rozkład inny niż normalny. 

Niepewność  typu  B

  -  u

B

,  szacowana  w  inny  sposób  niż  metodami  analizy 

statystycznej. Niepewność typu B można oceniać na podstawie: 

• właściwości przyrządu lub metody pomiarowej, 

• danych kalibracyjnych, 

• informacji podawanych przez producenta (DTR), 

• danych z wcześniejszych pomiarów itp. 
Przy  pomiarach  technicznych  może  wystąpić  przypadek  gdy 

niepewność 

typu  B

  jest  dużo  większa  niż 

niepewność  typu  A

  (u

A 

< 0,1∙u

B

).  Wtedy 

niepewność 

pomiaru 

wnoszona 

przez 

aparaturę 

pomiarową 

jest dominująca  wobec  niepewności  wnoszonej  przez  losowy  rozrzut 
wartości wielkości mierzonej x. 
Gdy 

niepewność  typu  A

  jest  dużo  większa  niż 

niepewność  typu  B

 

(u

B 

< 0,1∙u

A

),  oznacza  to,  że  niepewności  związane  z rozrzutem  wartości 

mierzonych  są większe  od  niepewnoś-ci  wnoszonych  przez  aparaturę 
pomiarową.

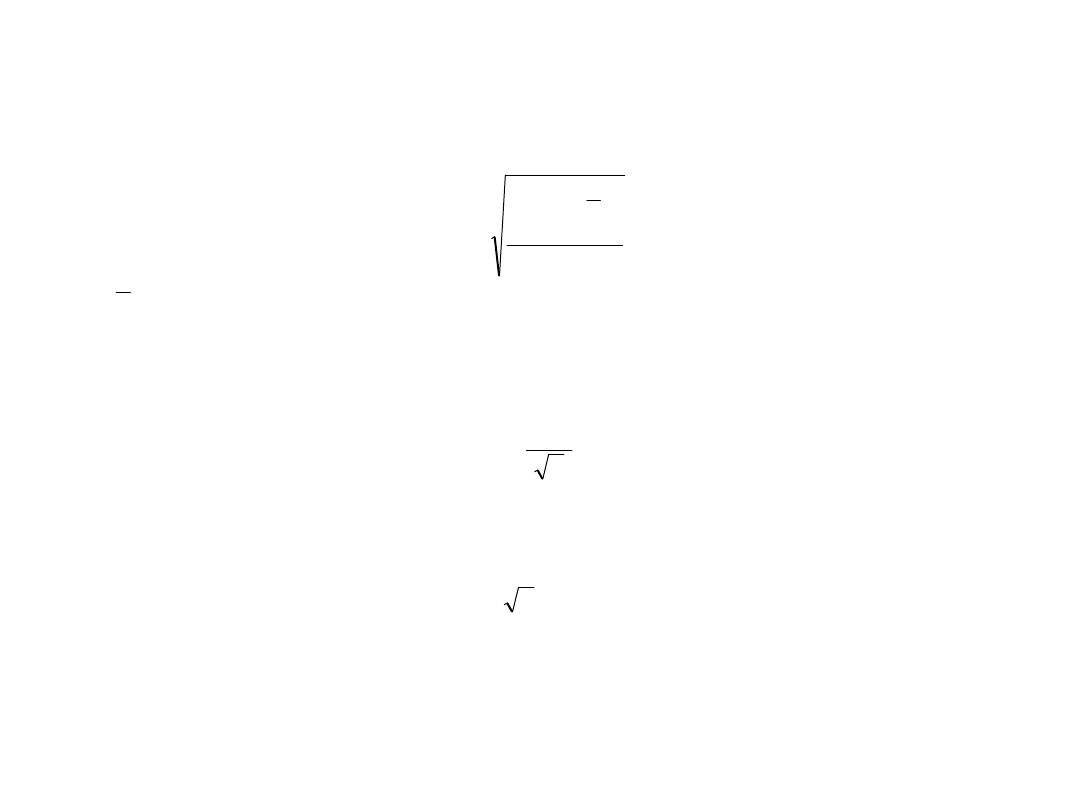
Niepewności  typu  A

  najczęściej  przypisuje  się  rozkład  Gaussa  lub  t-

Studenta  i  wówczas 

niepewność  standardową  typu  A

  można  wyznaczyć 

jako odchylenie standardowe średniej: 

gdzie: - średnia arytmetyczna n pomiarów.

Niepewności  typu  B

,  pochodzącej  od  aparatury  pomiarowej,  którą 

charakteryzuje  wartość  błędu  granicznego  x

g

  (klasa  przyrządu,  DTR), 

przypisywany jest rozkład prostokątny i wówczas niepewność standardową 
typu B można wyznaczyć, jako:

Gdy  uwzględnia  się  tylko 

niepewność  typu  B

  (u

B 

> 0,1u

A

),  to  niepewność 

rozszerzona jest opisana wzorem:

U = k  u

B

 ,

w  którym, 

współczynnik  rozszerzenia

  k,  zależy  od  przyjętego 

poziomu 

ufności

 p i wynosi, dla 

rozkładu jednostajnego

:

.

Dla p = 1, niepewność rozszerzona: U = x

g

 i jest to najczęściej spotykany 

przypadek w technice pomiarowej.

)

1

n

(

n

)

x

x

(

u

n

1

i

2

i

A













x

3

x

u

g

B





p

3

k





Znając 

niepewności typu A i B

 można wyznaczyć niepewność standardową 

złożoną, jako:

Niepewność rozszerzoną

 określa zależność:

U = k  u

C

 .

Współczynnik  rozszerzenia

 

k

  ma  wartość  zależną  od  przyjętego 

poziomu 

ufności

 

p 

oraz  rozkładu  wypadkowego,  wynikającego  ze  złożenia  rozkładu 

niepewności  typu A

  (najczęś-ciej 

normalnego

)  oraz  rozkładu 

niepewność 

typu  B

  (najczęściej 

jednostajnego

).  Dla  roz-kładów  o  zbliżonych 

wartościach  odchyleń  standardowych  ocena  niepewności  nie  jest 
jednoznaczna,  toteż  zaleca  się  przyjęcie  współczynnika  rozszerzenia 
odpowiadającego rozkładowi normalnemu lub określanie splotu rozkładów.

2

B

2

A

c

u

u

u





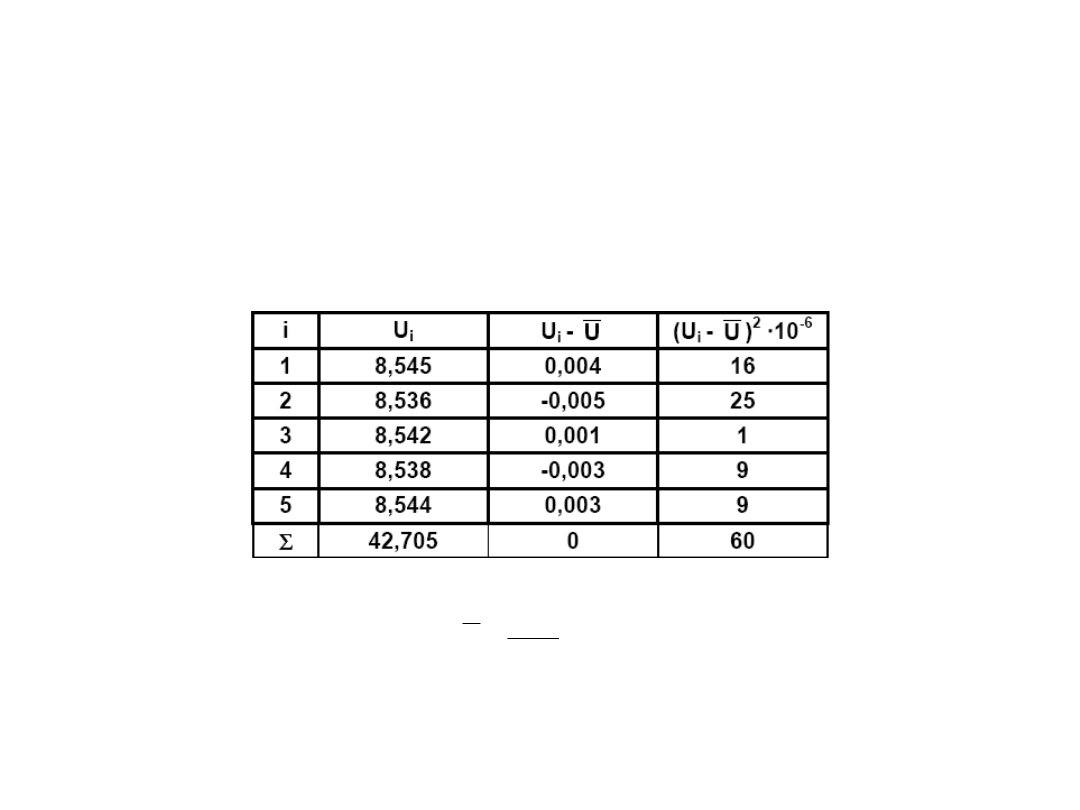
PRZYKŁAD 1

Aby wyznaczyć natężenie prądu w obwodzie zmierzono spadek napięcia na 
rezystorze  wzorcowym  R

n 

= 10   o  klasie  dokładności  kl. = 0,02.  Pomiar 

napięcia  przeprowadzono  pięciokrotnie  woltomierzem  cyfrowym  na 
zakresie  U

n 

= 10V  i  błędzie  określonym  przez  producenta  jako 

U = 0,02%∙U

x

 +0,01%∙U

n

. W wyniku pomiaru otrzymano wartości napięć U

i

 

(tabela).  Należy  wyznaczyć  przedział  niepewności  wyników  pomiaru  dla 
poziomu ufności p = 0,99.

(

na podstawie: Kalus-Jęcek B., Kuśmierek Z.: Wzorce wielkości elektrycznych i ocena 

niepewności pomiaru. Wyd. PŁ, 2006. ISBN 83-7283-183-1, przykład 5.7

) 

V

541

,

8

5

U

U

5

1

i

i









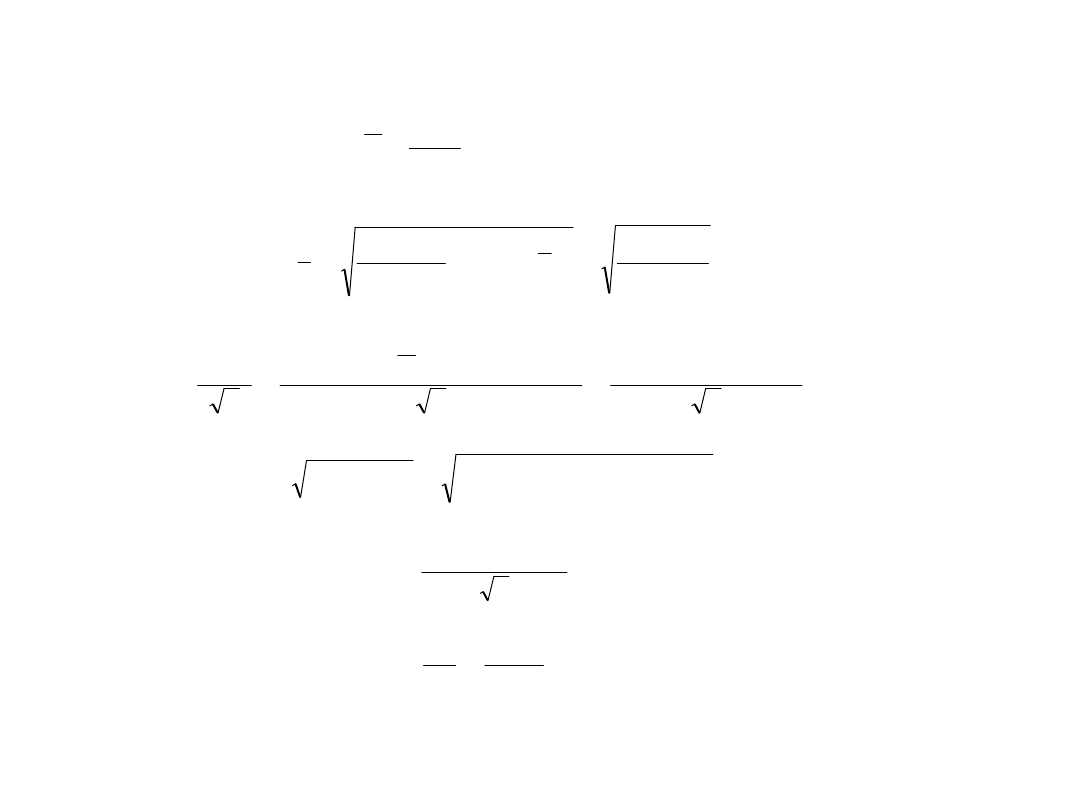
Wartość średnia napięcia:

Niepewność standardowa napięcia typu A: 

Niepewność standardowa typu B, przy założeniu jednostajnego rozkładu 
błędów:

Niepewność złożona pomiaru napięcia wynosi: 

Niepewność standardowa typu B wzorcowego rezystora, przy jednostajnym 
rozkładzie błędów:

Wartość natężenia prądu:













V

10

7

,

1

1

5

5

10

60

x

x

1

n

n

1

u

3

6

n

1

i

2

i

U

AU



































V

10

6

,

1

3

10

1

10

7

,

1

3

U

01

,

0

01

,

0

U

02

,

0

01

,

0

3

u

u

3

3

3

n

gr

BU





































 



V

10

3

,

2

10

6

,

1

10

7

,

1

u

u

u

3

2

3

2

3

2

BU

2

AU

cU



































 3

n

BR

10

2

,

1

3

R

02

,

0

01

,

0

u

A

8541

,

0

0

,

10

541

,

8

R

U

I

n







V

541

,

8

5

U

U

5

1

i

i









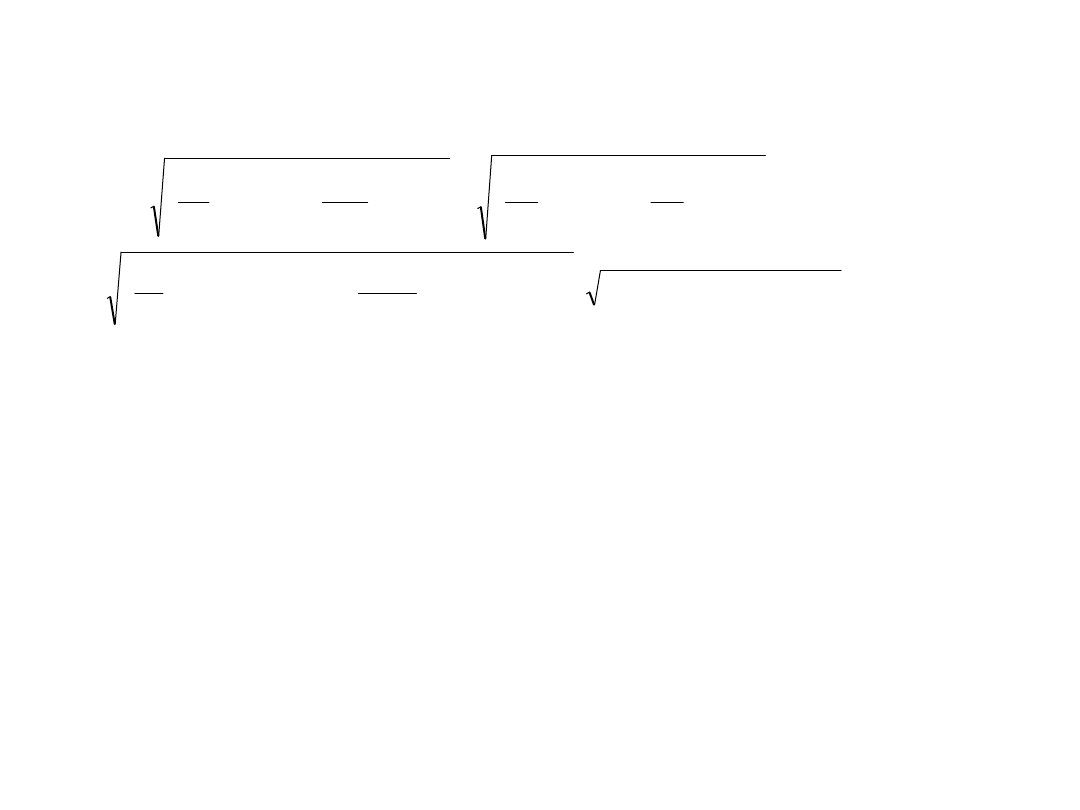
Niepewność złożona natężenia prądu:

Dla  poziomu  ufności  p = 0,99  z  tablic  rozkładu  normalnego  współczynnik 
rozszerzenia  k = 2,576.  Zatem  niepewność  rozszerzona  przy  założeniu 
rozkładu normalnego wynosi:

U

cI 

= k

 

∙u

cI 

= 2,576 ∙ 2,518∙10

-4

 A ≈ 6,5∙10

-4

 A

W  rozpatrywanym  przykładzie  wykonano  jednak  tylko  niewielką  liczbę 
pomiarów.  Zatem  współczynnik  rozszerzenia  powinien  być  obliczony  z 
rozkładu  t-Studenta,  dla  liczby  pomiarów  n  =  5  (  =  4),  poziomu  ufności 

p=0,99,  z  tablic  lub  wykresu  rozkładu  t-Studenta  można  otrzymać  t4,  a 

więc niepewność rozszerzona: 

U

cI 

= t ∙u

ci 

= 4 ∙2,518∙10

-4

  ≈ 10∙10

-4

 A.

Widać,  że  obliczona  niepewność  jest  większa  niż  w  przypadku  przyjęcia 
rozkładu normalnego. Tak więc ostatecznie:

I = (854 1) mA dla poziomu ufności p = 0,99.









A

10

518

,

2

10

05

,

1

10

29

,

5

10

2

,

1

10

541

,

8

10

3

,

2

10

1

u

R

U

u

R

1

u

R

I

u

U

I

u

4

8

8

2

3

2

2

2

3

2

2

BR

2

2

n

2

cU

2

n

2

BR

2

n

2

cU

2

cI







































































































































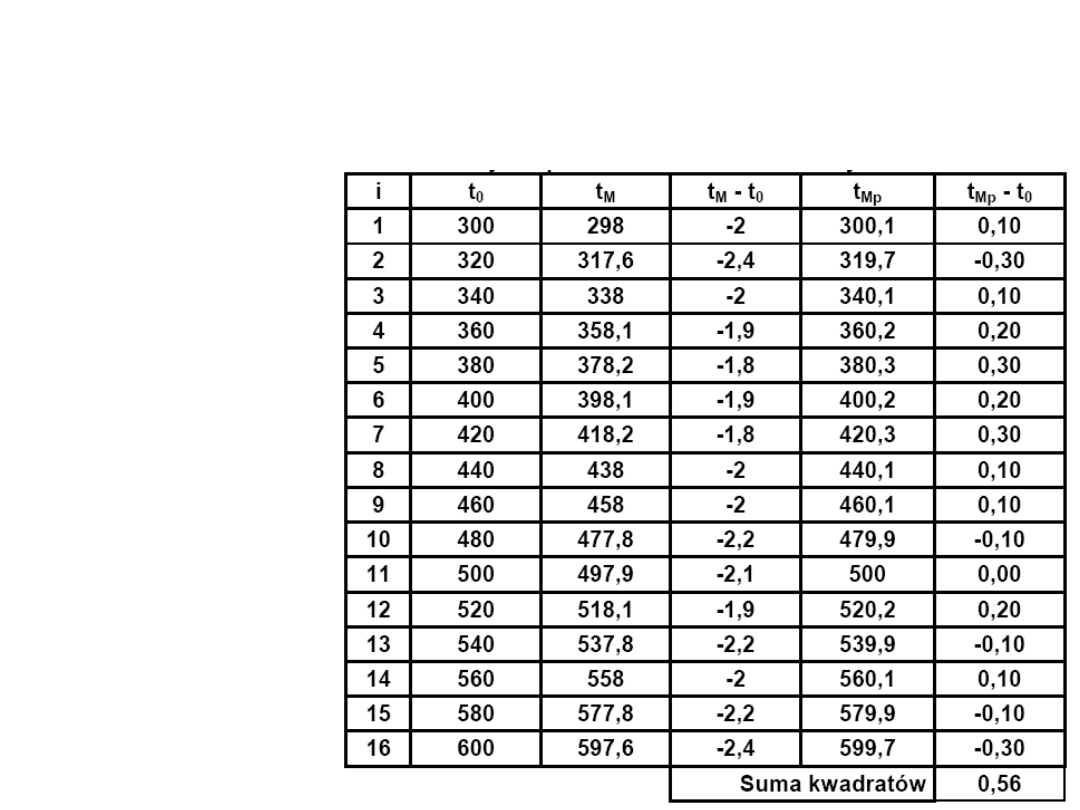
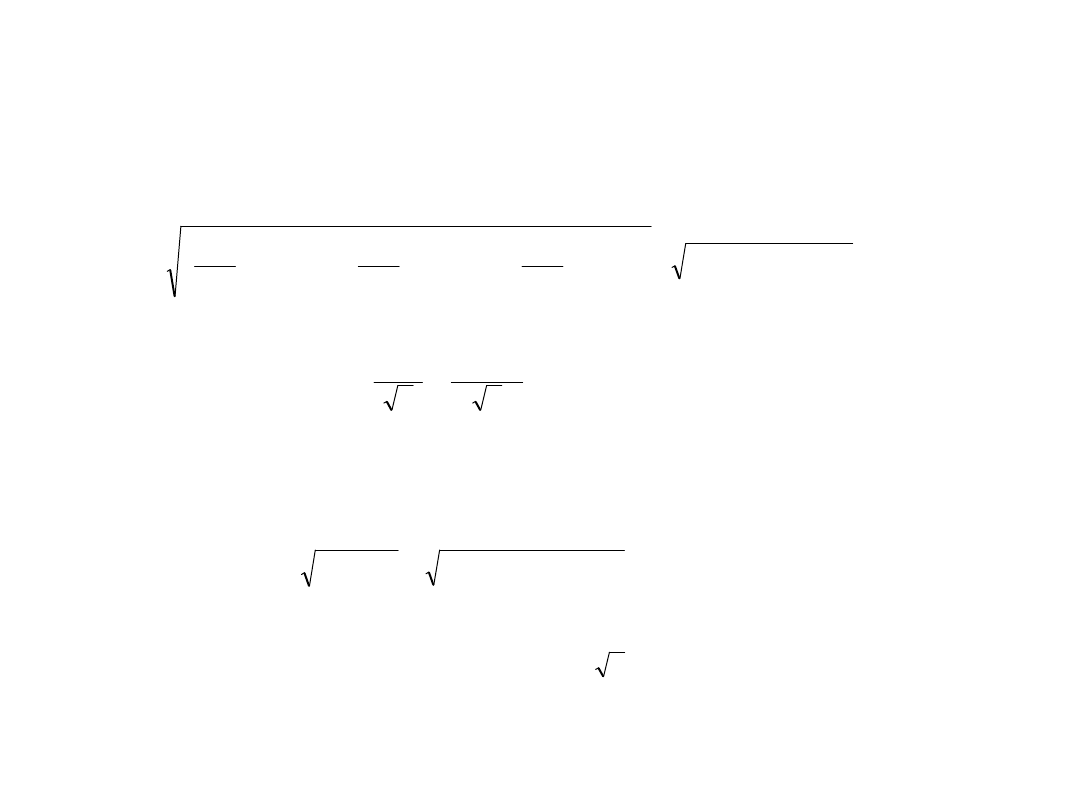
PRZYKŁAD 2

W  laboratorium  przeprowadzono  pomiary  kontrolne  miernika  tablicowego 
z wyświetla-czem  cyfrowym  (4 cyfry)  przeznaczonego  do  pomiaru 
temperatury  w zakresie  pomiarowym  (300600)C,  termoparą  typu  K. 

Wyniki pomiarów i obliczeń zostały umieszczone w tabeli. 

t

0

 – wartość temperatury 

jaka została zadana z 
kalibratora;
t

M

 – wartość temperatury 

odczytana z miernika 
tablicowego;
t

M

- t

0

 – różnica między 

temperaturą odczytaną z 
miernika tablicowego, 
a temperaturą zadaną 
z kalibratora;
t

Mp

 – wartość temperatury 

odczytana z miernika 
tablicowego po 
wprowadzeniu poprawki 
(przesunięcie zakresu 
pomiarowego miernika);
t

Mp

- t

0

 – różnica między 

temperaturą odczytaną z 
miernika tablicowego po 
wprowadzeniu poprawki, 
a temperaturą zadaną z 
kalibratora.

Wartość  różnicy  (t

M 

- t

0

)  wskazywała  na  występowanie  stałego  błędu 

systematycznego  wynoszącego  ok.  2°C.  W  badanym  mierniku  istnieje 
możliwość wyeliminowania tego typu błędu poprzez przesunięcie początku 
oraz  końca  zakresu  pomiarowego  (przeprogramo-wanie  miernika).  W  tym 
przypadku występuje konieczność znajomości wartości poprawki o jaką ma 
być  przesunięty  zakres.  Wartość  poprawki  t

p

  o  jaką  powinien  zostać 

przesu-nięty  początek  i  koniec  zakresu  pomiarowego  powinna  spełniać 
warunek:

Po  przeprowadzeniu  obliczeń  optymalizacyjnych  uzyskano  wynik:

t

p 

= 2,1C. 

O 

tę 

wartość 

został 

przesunięty 

początek 

i 

koniec 

zakresu. 

Przeprowadzono  ponowne  pomiary  i  ich  wynik  umieszczono  w  rubryce  t

Mp

 

tabeli.  Policzono  różnicę  (t

Mp 

- t

0

)  i wynik  umieszczono  w  kolejnej  rubryce 

tabeli.  Różnice  w  pomiarach  zdecydowanie  uległy  zmniejszeniu.  Na 
podstawie  otrzymanych  wyników  została  policzona  niepewność  pomia-
rowa miernika po korekcji.

Niepewność typu A wynosi:













16

1

i

2

p

i

0

Mpi

min

)

t

|

t

t

(|

C

048

,

0

)

1

16

(

16

56

,

0

)

1

n

(

n

)

t

t

(

u

n

1

i

2

i

0

Mpi

A























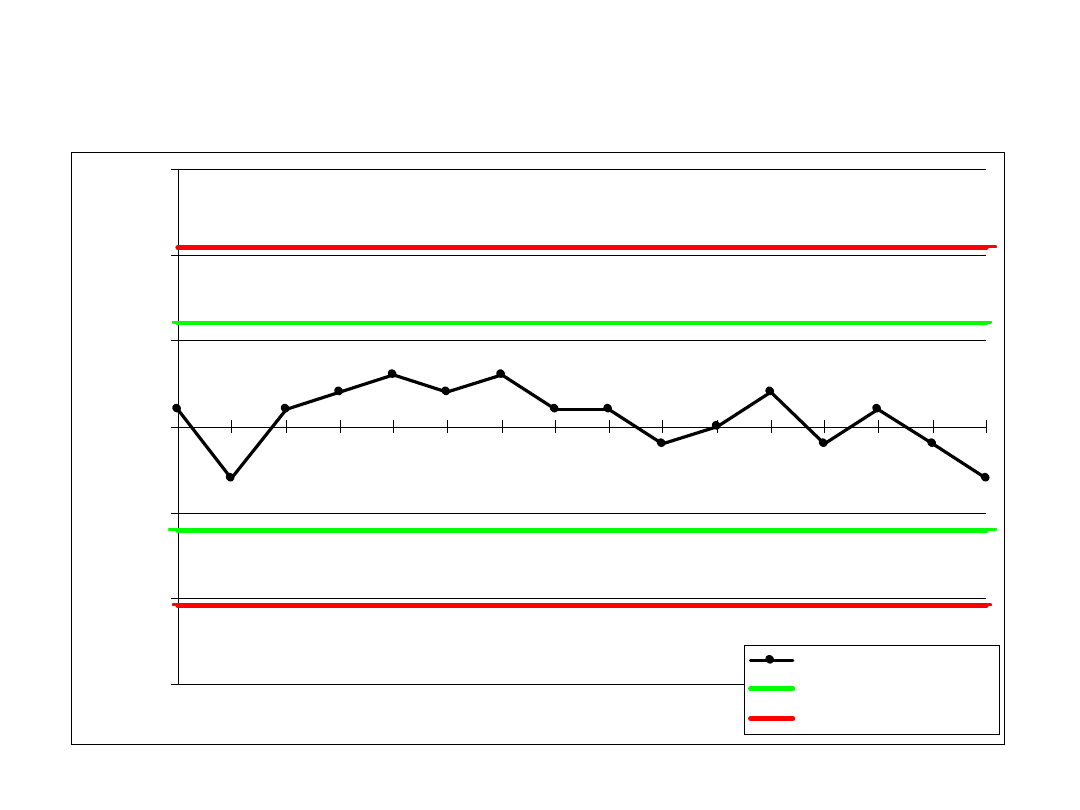
W przypadku niepewności typu B należy uwzględnić podane przez 
producenta miernika tablicowego wartości zgodnie z Dokumentacją 
Techniczno-Ruchową: 
błąd podstawowy:

±0,2% zakresu

kompensacja zmiany temperatury odniesienia: ±0,2% zakresu;
kompensacja zmiany rezystancji przewodów:

±0,2% zakresu.

Wartość błędu granicznego jest sumą kwadratów poszczególnych 
składników:

Zakładając w tym przypadku rozkład jednostajny (prostokątny), 
niepewność typu B można określić, jako:

Przy pomiarach technicznych, może wystąpić przypadek gdy niepewność 
typu B jest dużo większa niż niepewność typu A (w praktyce u

A 

< 0,1u

B

). 

Wtedy niepewność pomiaru wnoszona przez aparaturę pomiarową jest 
dominująca, wobec niepewności wnoszonej przez losowy rozrzut wartości 
mierzonej. Niepewność złożona miernika tablicowego:

Tak  więc  niepewność  złożona  u

c

=u

B

.  Ponieważ  niepewność  typu  B 

wnoszona  przez  aparaturę  pomiarową  jest  dominująca,  w  rozkładzie 
niepewności  dominuje  rozkład  jednostajny  o  współczynniku  rozszerzenia:

dla  poziomu  ufności  p=1.  Czyli  ostatecznie  niepewność 

rozszerzona miernika tablicowego: 

C

0392

,

1

)

300

002

,

0

(

3

ZAK

100

2

,

0

ZAK

100

2

,

0

ZAK

100

2

,

0

t

o

2

2

2

2

gr



























































C

60

,

0

59998

,

0

3

0392

,

1

3

t

u

gr

B













C

60

,

0

6019

,

0

)

60

,

0

(

)

048

,

0

(

u

u

u

o

2

2

2

B

2

A

C













3

k 

C

04

,

1

u

k

U

C









-1,50

-1,00

-0,50

0,00

0,50

1,00

1,50

300 320 340 360 380 400 420 440 460 480 500 520 540 560 580 600

Zakres pomiarowy [°C]

W

ar

to

ść

 o

d

ch

yl

en

ia

 [

°C

]

wartość pomierzona
niepewność złożona
niepewność rzoszerzona

Na  rysunku  przedstawiono  graficzną  interpretację  wyników  pomiarów 
i obliczeń poszcze-gólnych niepewności pomiarowych tablicowego miernika 
temperatury. 

ZAPIS WYNIKU POMIARU 

Wyniki pomiaru

 wielkości ciągłych są liczbami przybliżonymi. 

Sposób  prezentacji  wyników  powinien  umożliwiać  ocenę  dokładności  ich 
otrzymania. 
Dokładność  liczby  przybliżonej  określa  liczba  jej  cyfr  znaczących.  Cyfrą 
znaczącą jest każda cyfra, z wyjątkiem zer na początku liczby dziesiętnej, 
np.:
- liczba 328,01 ma 5 cyfr znaczących,
- liczba 0,023 ma 2 cyfry znaczące,
- liczba 2,30 ma 3 cyfry znaczące,
- licba 5000 ma 4 cyfry znaczące. 

Liczbę przybliżoną

 zaokrągla się tak, aby zawierała tyle cyfr znaczących, że 

tylko cyfra na ostatnim, najmniej znaczącym miejscu jest cyfrą niepewną, a 
błąd może wynosić nie wię-cej niż 5 jednostek następnego nieujawnionego 
miejsca. Jeżeli wartość rezystancji zapi-sano w postaci 628,1 , to można 

wnioskować, że błąd nie przekracza wartości 0,05 . 

W pierwszej  kolejności

  zaokrągla  się  liczbę  wyrażającą  granice  błędu  lub 

niepewność  pomiaru,  zawsze  w  górę  do  jednej  cyfry  znaczącej.  Tylko  w 
szczególnie uzasadnionych przypadkach stosuje się zaokrąglenie do dwóch 
cyfr znaczących. Jednym z takich przypadków jest zasada, wg. której liczbę 
wyrażającą  granice  błędu  należy  zaokrąglać  do  dwóch  cyfr  znaczących 
wtedy,  gdy  błąd  zaokrąglenia  przekracza  20%.  Prawidłowe  zaokrąglenie 
wartości błędów wygląda następująco: 


1 

= 1,06 ≈ 1,1; 

2 

= 0,821 ≈ 0,9;

 

3 

= 241 ≈ 3∙10

2

;



4 

= 0,0105 

≈ 0,011 .

W  drugiej  kolejności

  zaokrągla  się  liczbę  wyrażającą  wartość  mierzonej 

wielkości,  zostawiając  ostatnią  cyfrę  znaczącą  na  tym  miejscu,  na  którym 
występuje ostatnia cyfra znacząca oszcowanego błędu. Liczbę tę zaokrągla 
się w górę lub w dół, w zależności od wartości odrzucanej cyfry, wg. zasad:

• jeżeli  pierwsza  z  odrzucanych  cyfr  jest  większa  od  5,  to  ostatnią  cyfrę 
wyniku pomiaru 

należy zwiększyć o 1,

• jeżeli  pierwsza  z  odrzucanych  cyfr  jest  mniejsza  od  5,  to  ostatnią  cyfrę 
wyniku pomiaru 

pozostawia się bez zmian,

• jeżeli pierwsza z odrzucanych cyfr jest równa 5 i po niej następuje cyfra 
inna niż zero,  to ostatnią cyfrę wyniku pomiaru zaokrągla się w górę,

• jeżeli pierwsza cyfra z odrzucanych jest równa 5 i po niej następuje zero, 
to ostatnią 

cyfrę wyniku pomiaru zaokrągla się do liczby parzystej.

Końcowy  wynik  pomiaru

,  zgodnie  z  zasadami  zapisu  niepewności 

pomiarowej,  może  być  scharakteryzowany  przez  podanie  niepewności 
standardowej  złożonej  u

c 

lub niepewnoś-ci  rozszerzonej  U,  określającej 

przedział  niepewności  wyniku  pomiaru  wewnątrz  którego  leży  wartość 
prawdziwa. 
Gdy  miarą  niepewności  jest 

niepewność  rozszerzona

  U = k ∙ u

c

(x),  wynik 

pomiaru należy przedstawić w formie: 

• podać pełną definicję wielkości mierzonej X, 

• podać wynik pomiaru jako X = y ± U łącznie z jednostkami, 

• podać przyjętą do obliczenia U wartość współczynnika rozszerzenia k, 

• podać  przybliżoną  wartość  poziomu  ufności  związanego  z przyjętym 
przedziałem 

ufności x ± U oraz podać sposób jego wyznaczenia, 

• podać gdy zachodzi potrzeba względną niepewność rozszerzoną U/y. 

Przykładowo

:

„m

s 

=100,02147 ± 0,00047 g,  gdzie  liczba  za symbolem ± jest  wartością 

niepewności  roz-szerzonej  U = k ∙ u

c 

,  obliczonej  dla  u

c 

= 0,35 mg  i 

współczynnika rozszerzenia k = 2,26 wyznaczonego jako wartość krytyczna 
zmiennej  losowej  rozkładu  t Studenta  o  9  stop-niach  swobody  i  poziomie 
ufności 95%”.

OBLICZANIE I WYRAŻANIE NIEPEWNOŚCI

1.Wyrażenie związku między wielkością mierzoną Y i wielkościami X

i

 od 

których Y zależy, w postaci funkcji Y = f(X

1

, X

2

,..., X

N

). Funkcja f powinna 

zawierać wszystkie wielkości, włączając w to poprawki i współczynniki 
poprawkowe uwzględniające oddziaływania, które mogą wnosić znaczące 
składowe do niepewności wyniku pomiaru. 

2.Wyznaczenie estymat x

i

 wartości wielkości wejściowych X

i

  albo na 

podstawie  analizy statystycznej serii obserwacji, albo za pomocą innych 
metod. 

3.Obliczenie niepewności standardowych u(x

i

) estymat wartości wielkości 

wejściowych x

i

. Dla estymat x

i

 wyznaczonych: 

- na drodze statystycznej analizy serii obserwacji obliczanie niepewności 
metodą typu A 
- innymi metodami obliczanie niepewności metodą typu B.

4.Obliczenie kowariancji (wzajemnych zależności w pomiarach złożonych) 

związanych z estymatami wartości wielkości wejściowych skorelowanych. 

5.Obliczenie wyniku pomiaru, to jest estymaty y wielkości mierzonej Y z 

zależności funkcyjnej f, dla wartości wielkości wejściowych X

i

 równych 

estymatom x

i

, wyznaczonym w punkcie 2. 

6.Określenie złożonej niepewności standardowej u

c

(y) wyniku pomiaru y na 

podstawie niepewności standardowych i kowariancji związanych z 
estymatami wartości wielkości wejściowych. 

7.Określenie, jeżeli jest to konieczne, niepewności rozszerzonej U służącej 

do wyznaczania przedziału <y – U ; y + U>, który powinien obejmować 
dużą część rozkładu wartości, które można w sposób uzasadniony 
przypisać wielkości mierzonej Y. Niepewność rozszerzona U = ku

c

(y), 

gdzie k wybiera się na podstawie żądanego poziomu ufności p oraz 
przyjętego rozkładu prawdopodobieństwa.

8.Podanie wyniku pomiaru y wraz z jego złożoną niepewnością standardową 

u

c

 (y) lub niepewnością rozszerzoną U. Do wyniku pomiaru należy dołączyć 

opis sposobu wyznaczenia y i u

c

(y) lub U.

LITERATURA