WYTRZYMAŁOŚĆ

WYTRZYMAŁOŚĆ

MATERIAŁÓW

MATERIAŁÓW

prowadzący

prof. dr hab. inż. Kazimierz WÓJS

Wykład 8

Opracował

dr inż. Andrzej Sitka

POJĘCIA PODSTAWOWE,

OBCIĄŻENIA ZEWNĘTRZNE,

NAPRĘŻENIA I ODKSZTAŁCENIA

Literatura podstawowa

Literatura podstawowa

 

 

1.

1.

Żuchowski R., Wytrzymałość materiałów,

Żuchowski R., Wytrzymałość materiałów,

Oficyna Wydawnicza PWr., Wrocław 1998

Oficyna Wydawnicza PWr., Wrocław 1998

2.

2.

Niezgodziński M., Niezgodziński T., Zadania z

Niezgodziński M., Niezgodziński T., Zadania z

wytrzymałości materiałów, WNT, Warszawa 2000

wytrzymałości materiałów, WNT, Warszawa 2000

 

 

Literatura uzupełniająca

Literatura uzupełniająca

 

 

1.

1.

Misiak J., Mechanika Techniczna tom I,

Misiak J., Mechanika Techniczna tom I,

statyka i wytrzymałość materiałów, WNT,

statyka i wytrzymałość materiałów, WNT,

Warszawa 2003.

Warszawa 2003.

Wytrzymałość materiałów, opierając się na prawach

i zasadach mechaniki ogólnej, zajmuje się badaniem sił
wewnętrznych w ciałach, aby odpowiedzieć na pytanie
czy pod wpływem danych obciążeń w jakimś obszarze
ciała siły wewnętrzne nie osiągną zbyt dużych wartości.

Drugą,

równie

ważną

dziedziną

badań

wytrzymałości materiałów jest analiza odkształceń ciał i
konstrukcji. Dzięki uwzględnieniu odkształceń można
obliczyć układy nierozwiązalne na gruncie mechaniki
ogólnej, to jest układy statycznie niewyznaczalne.

Wprowadzen

Wprowadzen

ie

ie

Wprowadzen

Wprowadzen

ie

ie

Obliczanie

elementów

konstrukcyjnych

wymaga

uwzględnienia:

•

współczynnika bezpieczeństwa,

•

czynnik warunkujący sztywność elementu lub

konstrukcji,

•

czynnik ekonomiczny – minimalny koszt

wykonania, niskie zużycie materiału, lekkość
konstrukcji,

•

czynnik estetyczny.

r

0

=2,9Å=2,910

-

7

mm

0,05
mm

Powiększenie 10
000 000

Powiększenie 2
000

MODEL CIAŁA

MODEL CIAŁA

STAŁEGO

STAŁEGO

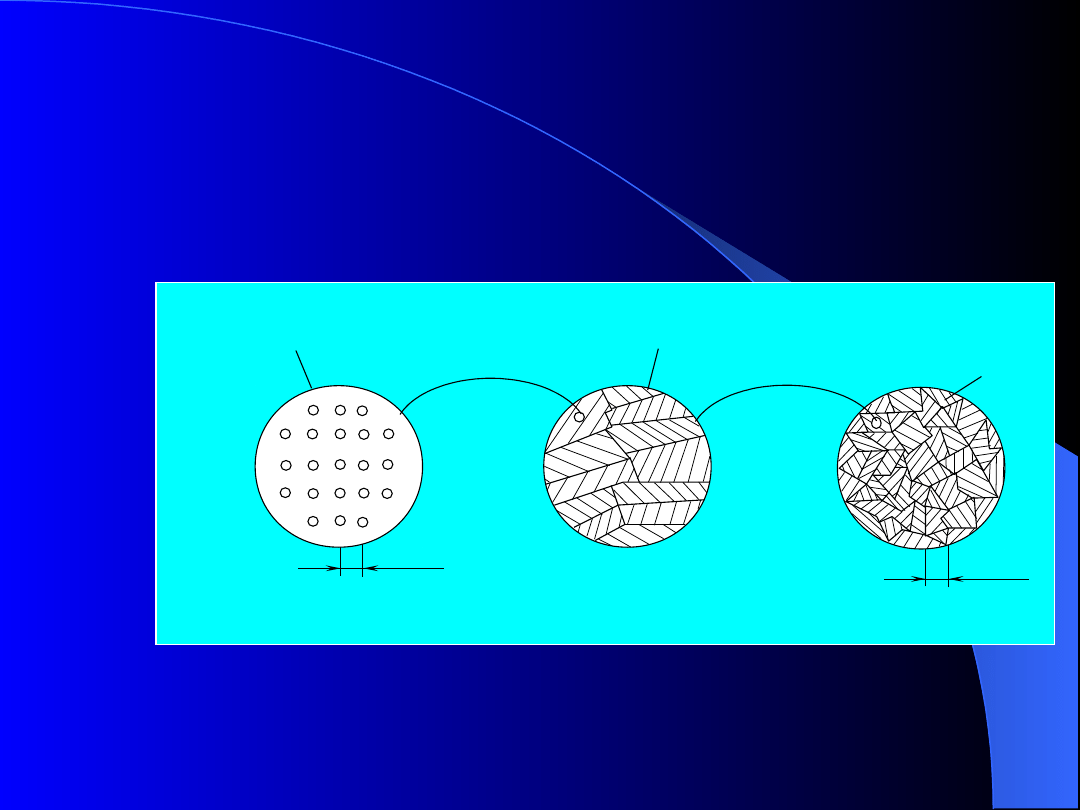
W wytrzymałości materiałów uproszczonym modelem

ciała jest ciało stałe odkształcalne, które pod wpływem
obciążeń zmienia swoje wymiary.

położenie
atomów

bloki

ziarna

a)

b)

c)

Rys. 1. Mikrostruktura
metali

Powiększenie
200

MODEL CIAŁA

MODEL CIAŁA

STAŁEGO

STAŁEGO

MODEL -

jednolite

continuum materialne

Materiał

izotropowy

–

jednakowe

własności

wytrzymałościowe we wszystkich kierunkach

Materiał

anizotropowym

–

różne

własności

wytrzymałościowe .......

Materiały izotropowe:

•

wszystkie metale,

•

beton,

•

niektóre tworzywa

sztuczne.

Materiały anizotropowe:

•

drewno (własności są inne w kierunku wzdłuż

włókien a inne w kierunku prostopadłym do
włókien),

•

beton zbrojny.

SIŁY I ICH PODZIAŁ

SIŁY I ICH PODZIAŁ

Siła

jest

wektorową

wielkością mechaniczną.

Siłą nazywamy mechaniczne oddziaływanie jednego ciała
na drugie. Oddziaływanie to może być bezpośrednie
(zachodzi przy zetknięciu ciał) lub pośrednie (objawiające
się na odległość).

C

A

B

C

s

1

F



2

F



3

F



4

F



3

R



2

R



1

R



G



Rys. 2. Siły

Do określenia siły należy

podać następujące jej cechy:

•

         jej wartość,

•

         kierunek, czyli linię

działania,

•

         zwrot działania,

•

         punkt zaczepienia.

 

SIŁY I ICH PODZIAŁ

SIŁY I ICH PODZIAŁ

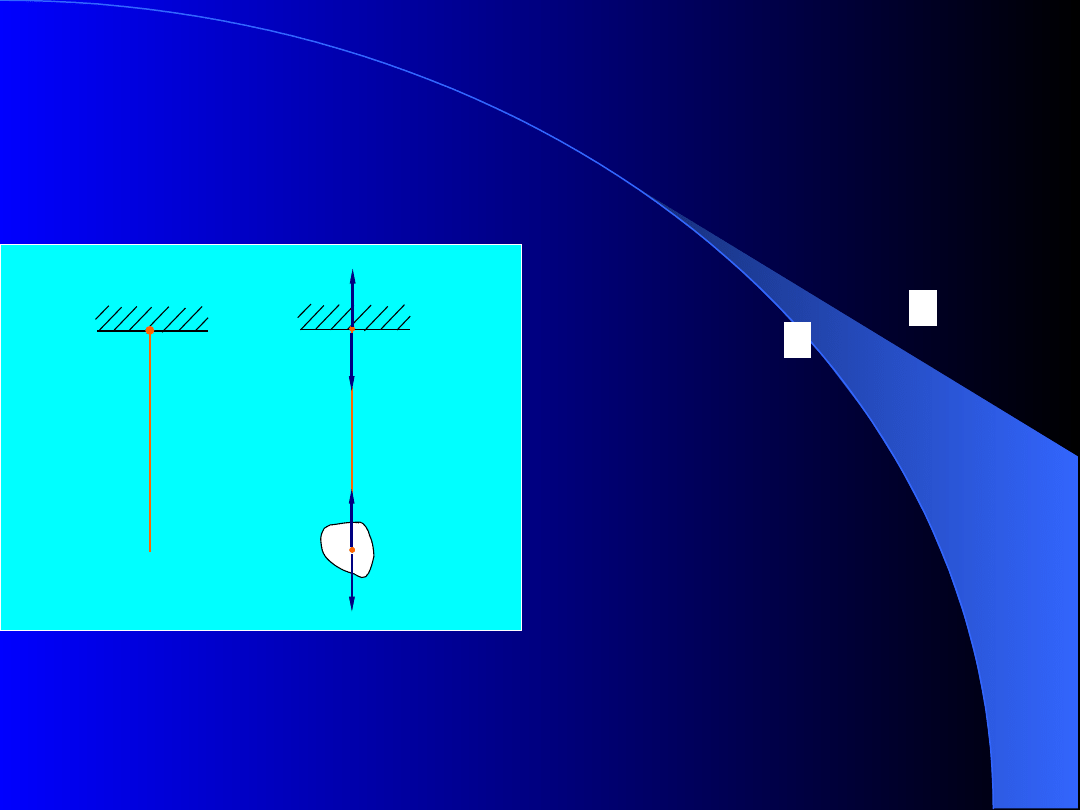
Jeżeli

na końcu nici

znajdować się będzie ciało o
ciężarze , to pod wpływem tej
siły wewnątrz tej nici
powstaje

dodatkowa

siła

wewnętrzna –

napięcie

.

Siły wewnętrzne

. Jeżeli w punkcie 0 zamocujemy nić

swobodnie wisząca i pominiemy jej ciężar jedynymi
siłami

wewnętrznymi

w

nici

będą

siły

międzycząsteczkowe.

Rys. 3. Siły

wewnętrzne

0

A

0

l

R



s

F



s

F



G



G



G



SIŁY I ICH PODZIAŁ

SIŁY I ICH PODZIAŁ

Siły to obciążenia działające na dane ciało,

które pochodzą z różnych źródeł takich jak:



        grawitacja (siły ciężkości),



        ciśnienie wody, wiatru lub innych mediów,



        zmiany temperatury,



        działanie pola elektromagnetycznego.

 

Podział sił ze względu na miejsce

występowania:

SIŁY I ICH PODZIAŁ

SIŁY I ICH PODZIAŁ

Siły

zewnętrzne

–

oddziaływanie

otoczenia

zewnętrznego na ciało.

Siły wewnętrzne – oddziaływanie międzycząsteczkowe
w ciele.

SIŁY

WEWNĘTRZN

E

ZEWNĘTRZN

E

Bezpośrednie

-grawitacja

-bezwładność

-pole
elektromag.

-temperatura

Pośrednie

-siły styku a
następnie
przez siły
wewnętrzne

Międzycząsteczk
owe

Napięcia

SIŁY

ZEWNĘTRZN

E

bierne

(reakcje)

czynne

SIŁY I ICH PODZIAŁ

SIŁY I ICH PODZIAŁ

Podział sił ze względu na czynniki je

wywołujące:

Siły czynne – oddziaływanie innych ciał na
dane ciało.

Siły bierne – reakcja ciała na obciążenie.

Reakcje nigdy nie mogą spowodować ruchu
ciała.

SIŁY WYSTĘPUJĄCE W MODELU

SIŁY WYSTĘPUJĄCE W MODELU

DWUATOMOWYM CIAŁA STAŁEGO

DWUATOMOWYM CIAŁA STAŁEGO

A

B

r

r

1

r

0

r

2

r

3

P

3

P

m

a

x

P

2

P

1

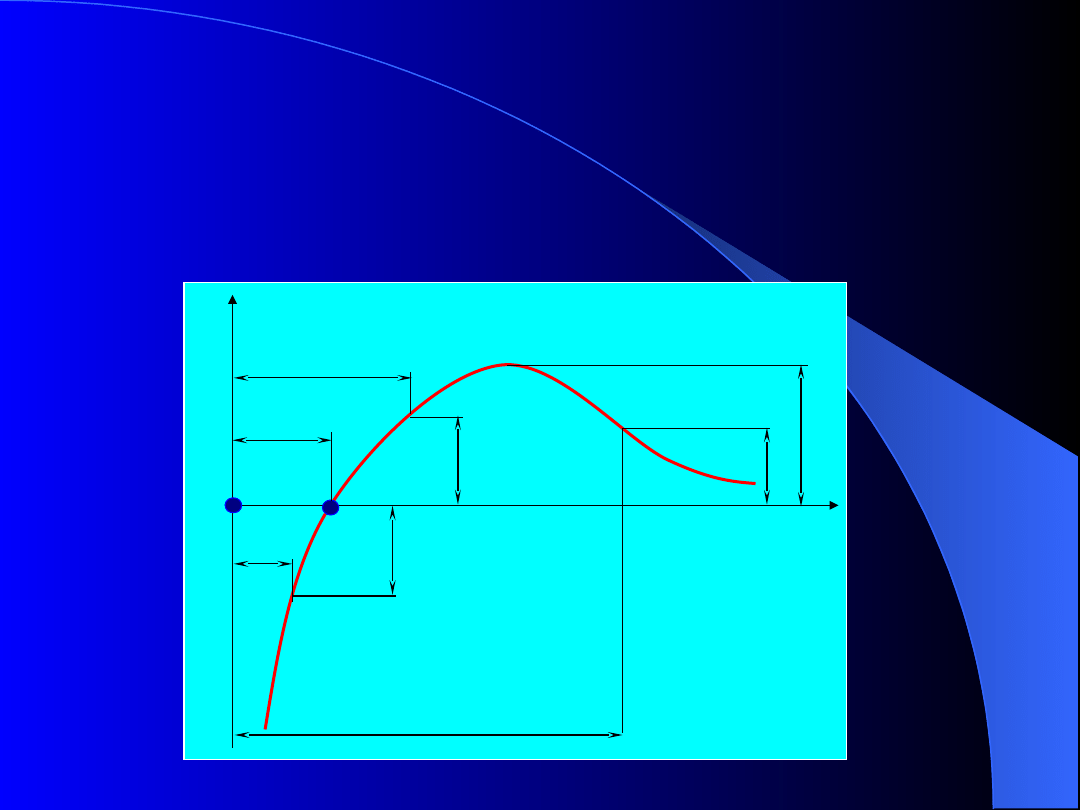
Średnie położenie atomów wypełniających przestrzeń
ciała stałego znajdują się w ustalonych dla danego
materiału

odległościach,

zwanych

odległością

międzyatomową - dla żelaza 2,9 10

-7

mm.

Rys.4. Wykres sił wzajemnego oddziaływania
dwóch atomów

P

SIŁA PRZEDSTAWIONA JAKO

SIŁA PRZEDSTAWIONA JAKO

WEKTOR

WEKTOR

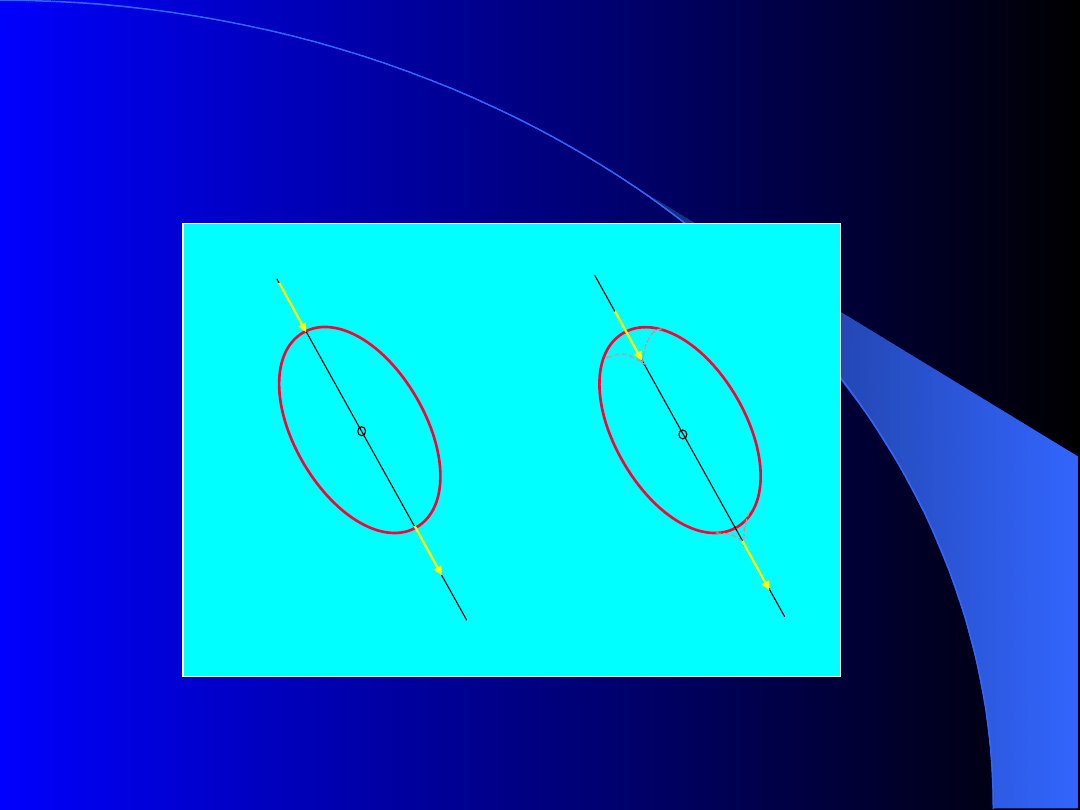
W statyce za model ciała przyjmuje się ciało

sztywne, a w wytrzymałości materiałów – ciało
odkształcalne.

F

F

F

F

S

S

a

b

Rys. 5. Dwa modele ciała pod działaniem siły: a) ciało sztywne –

siła jako wektor związany z prostą, b) ciało odkształcalne – siła

jako wektor związany z punktem

DZIAŁANIE SIŁ ZEWNĘTRZNYCH

DZIAŁANIE SIŁ ZEWNĘTRZNYCH

Skutkiem działania sił na ciało jest jego

przemieszczenie, a nawet utrata spójności.
Przemieszczenia mogą
występować jako:

PRZEMIESZCZE

NIA

JEDNAKOWE DLA

WSZYSTKICH

PUNKTÓW CIAŁA

WZGLĘDNE

- ODKSZTAŁCENIE
CIAŁA

SPRĘŻYST
E

PLASTYCZN
E

Utrata

spójności

mikroskopowa

makroskopowa

Skala utraty spójności ciała

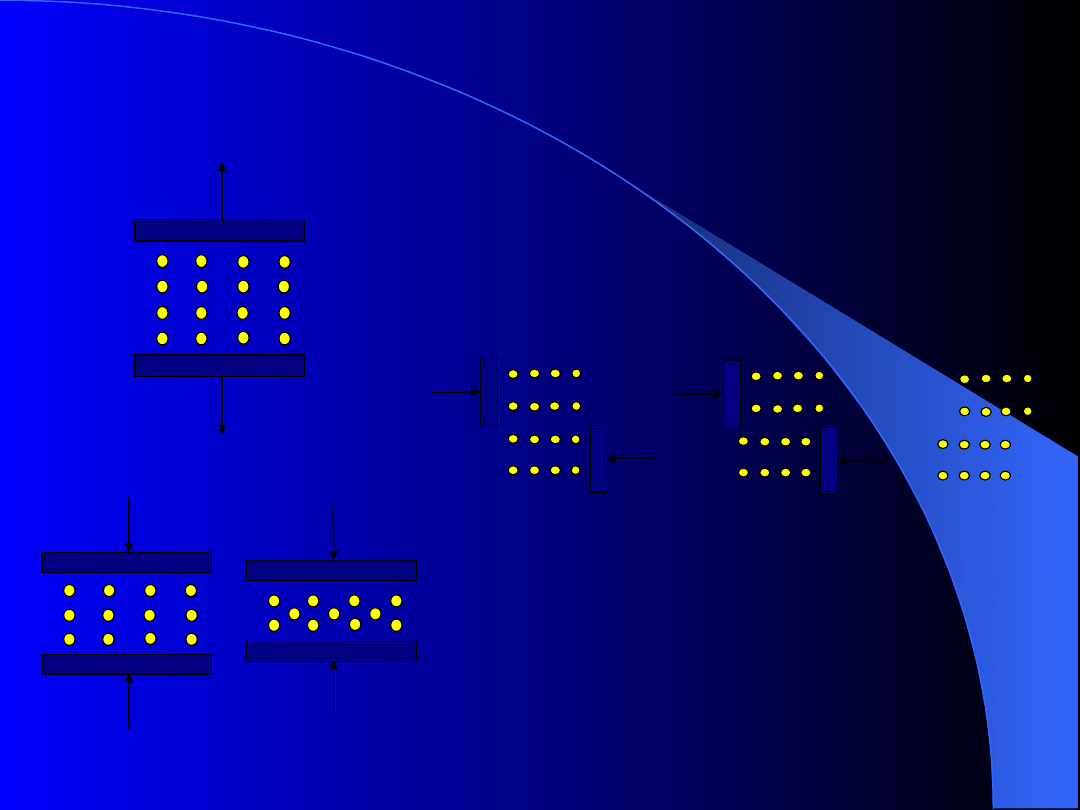
SIŁY SPÓJNOŚCI I MECHANIZM

SIŁY SPÓJNOŚCI I MECHANIZM

ODKSZTAŁCEŃ W CIELE STAŁYM

ODKSZTAŁCEŃ W CIELE STAŁYM

Rys. 6. Układ atomów w

modelu

poddanym rozciąganiu

N

N

N

N

a

b

Rys. 7. Układ atomów w

modelu poddanym

ściskaniu

T

T

T

1

T

1

Rys. 8. Schemat przebiegu

przemieszczeń atomów pod

działaniem sił poprzecznych T

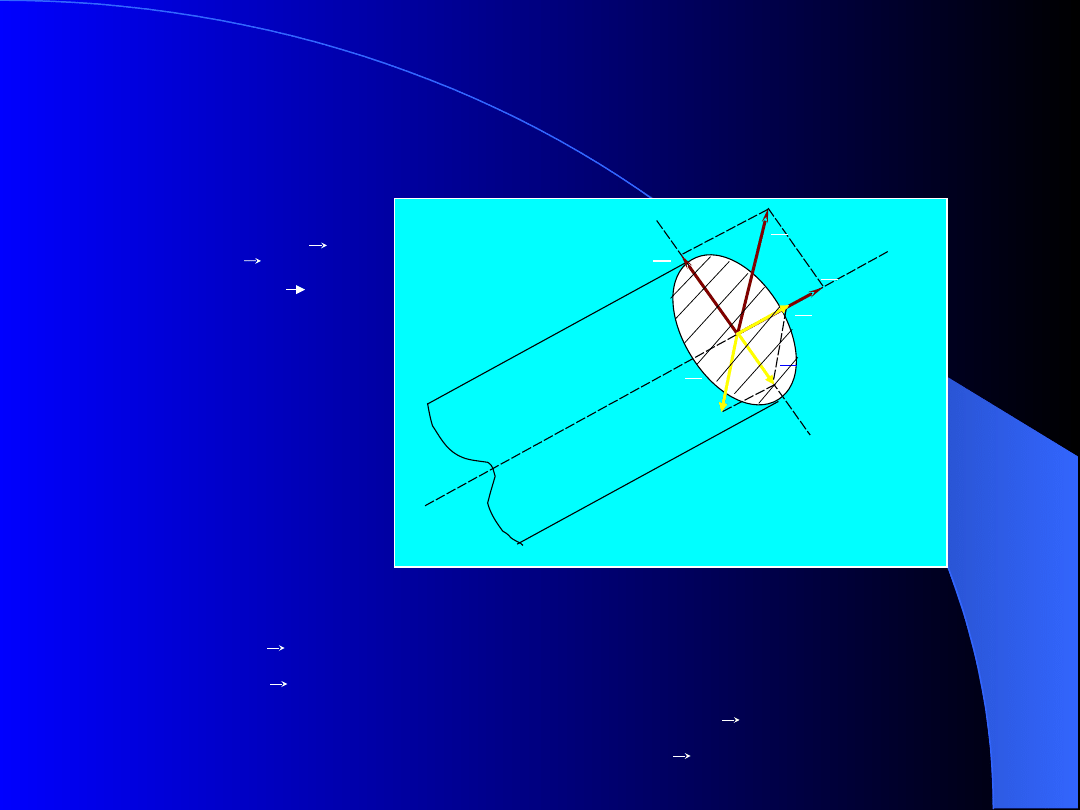
SIŁY WEWNĘTRZNE

SIŁY WEWNĘTRZNE

Mając obciążony pręt (rys.9) dokonujemy w myślach
przekroju poprzecznego pręta i po odrzuceniu jego
prawej części ujawnią się siły wewnętrzne.

• moment główny M,

• wektor główny S.

Po rozłożeniu momentu głównego i wektora głównego na

składowe normalne i styczne otrzyma się następujące składowe:
-         siła osiowa N – rozciąganie (ściskanie),
-         siła styczna T – ścinanie,
-         osiowa składowa momentu (moment skręcający) M

s

–

skręcanie,
-         styczna składowa momentu (moment gnący) M

g

– zginanie.

S

T

N

M

s

M

g

M

Rys. 9. Siły

wewnętrzne w

przekroju pręta

KLASYFIKACJA OBCIĄŻEŃ

KLASYFIKACJA OBCIĄŻEŃ

W zależności od sposobu przyłożenia sił

zewnętrznych rozróżniamy następujące proste
przypadki obciążeń:

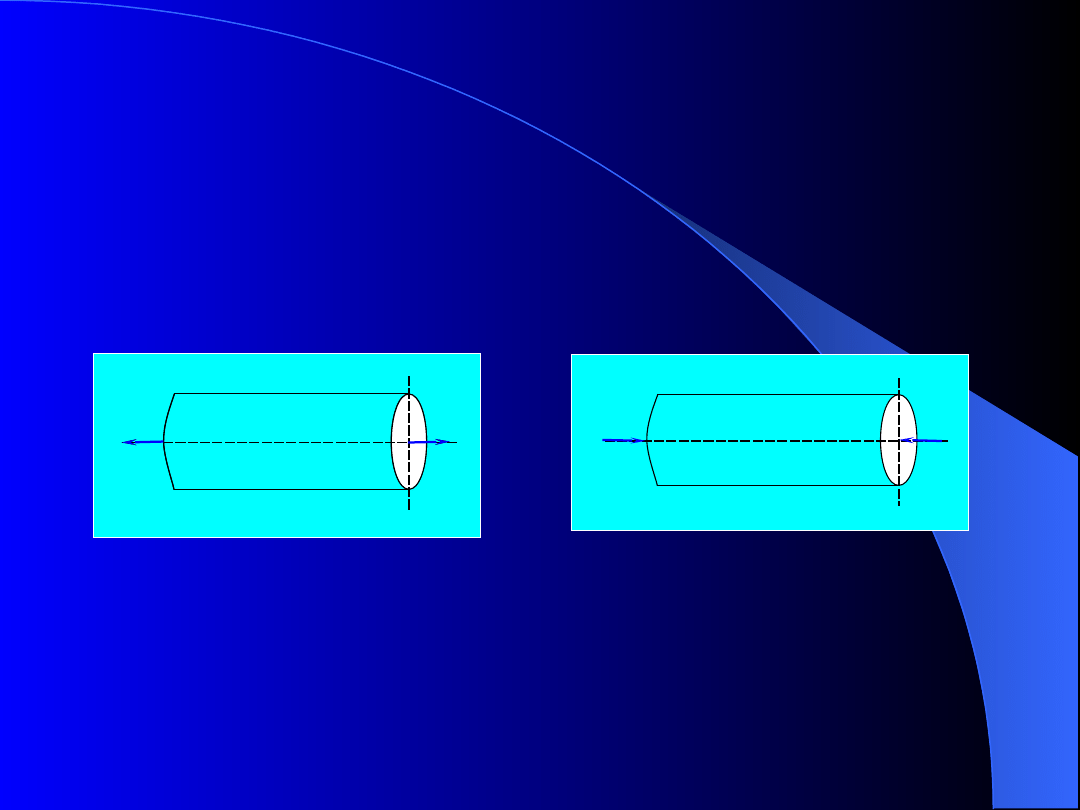
Rozciąganie lub ściskanie

powodują dwie siły

równe co do wartości, przeciwnie skierowane,
działające wzdłuż osi pręta.

N

N

N

N

Wszystkie elementy pracujące na rozciąganie

nazywamy prętami lub cięgnami. Przykładem
takich elementów są: liny, łańcuchy, niektóre pręty
kratownic, itp.

Rys.10. Rozciąganie

pręta

Rys.11. Ściskanie pręta

KLASYFIKACJA OBCIĄŻEŃ

KLASYFIKACJA OBCIĄŻEŃ

Zginanie

pręta powstaje wówczas, gdy siły obciążające

(lub ich składowe) są prostopadłe do osi pręta, a linie
działania sił znajdują się w pewnych odległościach od
siebie i leżą w jednej płaszczyźnie zawierającej oś pręta.

Elementy pracujące na zginanie nazywane są
belkami. Mogą to być belki mostowe,
stropowe, wały, itp.

P

R

1

R

2

Rys.12. Zginanie
pręta

KLASYFIKACJA OBCIĄŻEŃ

KLASYFIKACJA OBCIĄŻEŃ

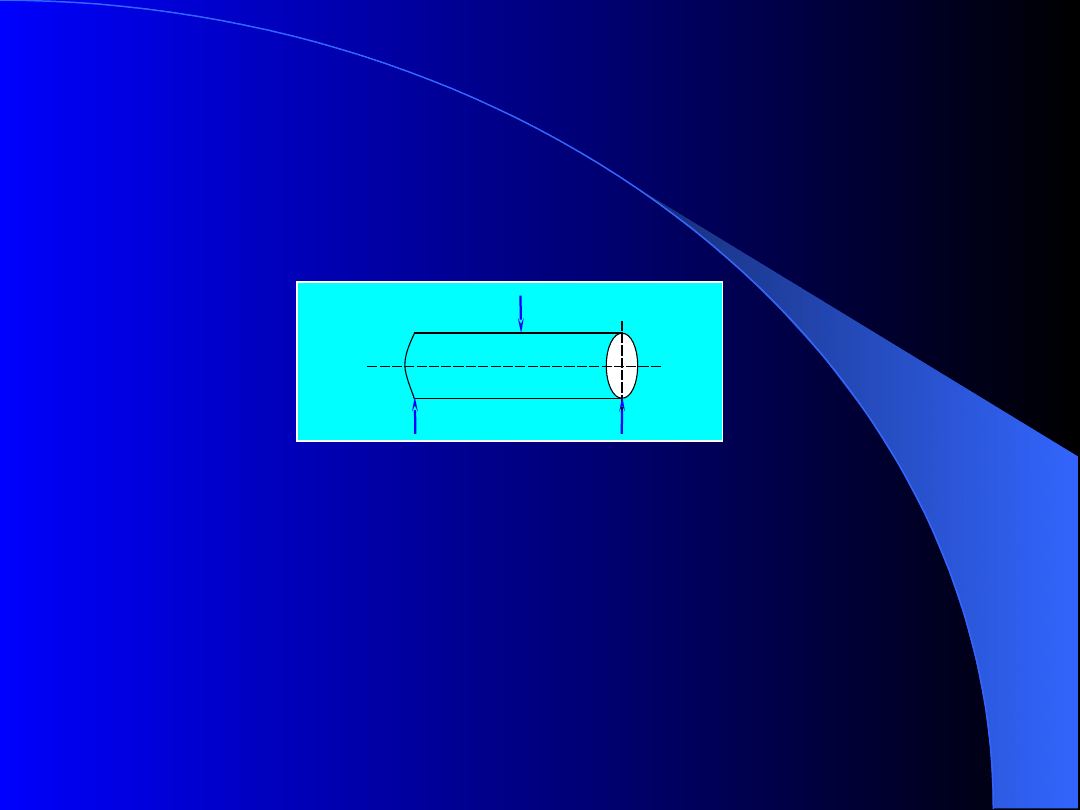
Skręcanie

pręta wywołują dwie pary sił działające

w dwóch różnych płaszczyznach prostopadłych do osi
pręta.

Odkształcenia przy skręcaniu polegają na obrocie
przekrojów elementów względem siebie, wokół osi
tego elementu.
Typowym przykładem elementów skręcanych są
wały maszyn.

Rys. 13. Skręcanie
pręta

P

P

P

P

KLASYFIKACJA OBCIĄŻEŃ

KLASYFIKACJA OBCIĄŻEŃ

Ścinanie

pręta powstaje wtedy, gdy działają dwie siły

tworzące parę o bardzo małym ramieniu (rys.14). Siły te
starają się przesunąć jedną część pręta względem
drugiej. Powiększając wartość siły można doprowadzić
do zniszczenia elementu (do jego ścięcia).

Rys. 14. Ścinanie
pręta

Na ścinanie pracują przede wszystkim nity, śruby,
sworznie, spoiny, itp

P

P

P

P

Podane powyżej przykłady obrazują przypadki obciążeń
prostych. Jeżeli kilka obciążeń prostych występuje
równocześnie, mówimy wówczas o wytrzymałości
złożonej.

NAPRĘŻENIE I ODKSZTAŁCENIE

NAPRĘŻENIE I ODKSZTAŁCENIE

Naprężenie

Rys.15. Rozkład siły S na

składowe

Naprężeniem p

w danym punkcie przekroju A

danego ciała stałego nazywamy granicę, do której
dąży iloraz siły wewnętrznej S przez elementarne

pole A tego przekroju, gdy to pole dąży do zera.

A

T



N

S

Rozpatrzymy działanie siły S przypadającej na

element powierzchni A

m

N

dA

S

d

A

S

p

A

2

,

lim

0



















(1)

NAPRĘŻENIE I ODKSZTAŁCENIE

NAPRĘŻENIE I ODKSZTAŁCENIE

Po rozłożeniu siły S na składową normalną

N i styczną T otrzymamy naprężenia

normalne  i styczne :

m

N

dA

N

d

A

N

A

2

,

lim

0





















(2)

m

N

dA

T

d

A

T

A

2

,

lim

0





















(3)

Odkształceni
e

Analiza odkształceń wymaga określenia ich miary.
Miarę taką uzyskuje się podczas badania zmiany
wybranego odcinka AB i przyjętego kąta CDE.

Średnie (względem długości odcinka l) wydłużenie tego
odcinka wyniesie:

Odcinek AB = l zmienił się po obciążeniu w odcinek
A’B’ = l+l.

NAPRĘŻENIE I ODKSZTAŁCENIE

NAPRĘŻENIE I ODKSZTAŁCENIE

P

1

P

2

A

B

A’

B’

l

l+l

C

D

E

C’

D’

E’

Rys. 16. Określenie wydłużenia względnego  i

odkształcenia postaciowego 

l

l

sr







(4)

NAPRĘŻENIE I ODKSZTAŁCENIE

NAPRĘŻENIE I ODKSZTAŁCENIE

Graniczną wartość stosunku wydłużenia l odcinka

AB do jego początkowej długości l nazywamy
wydłużeniem względnym w punkcie A w kierunku
AB, albo odkształceniem liniowym.

Określa się ją z
zależności:

l

l

l









lim

0



(5)

Miarą zmiany pierwotnie prostego kąta CDE w kąt
C’D’E’ jest kąt , który określa zmianę postaci – kąt

odkształcenia postaciowego:

)

'

'

'

(

lim

0

,

0

E

D

C

CDE

DE

CD















(6)

ZASADA DE SAINT VENATA

ZASADA DE SAINT VENATA

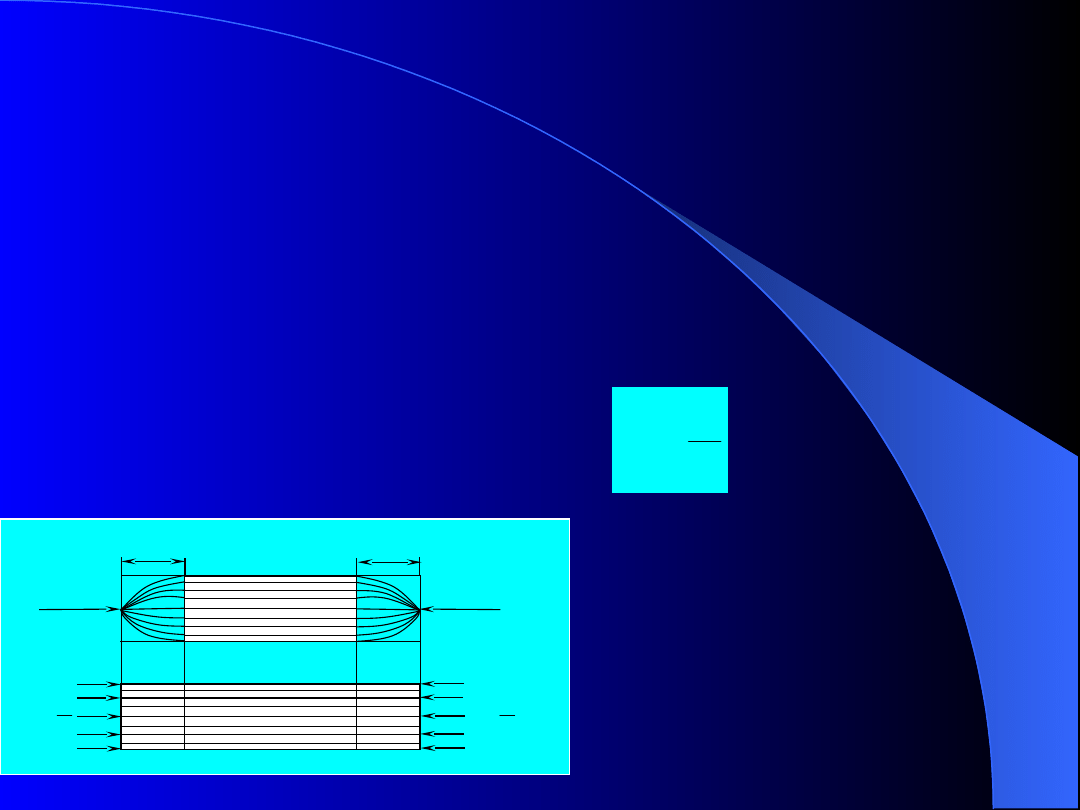
Rozpatrując dwa pręty o jednakowych przekrojach i
długościach i poddane działaniu takiemu samemu
obciążeniu. Jeden z prętów obciążony jest siłą skupioną
drugi natomiast obciążony jest równomiernie w całym
przekroju.
W pobliżu przyłożenia obciążenia rozkłady naprężeń będą
się znacznie różniły w obu przypadkach, lecz w dalszej
części każdego z prętów rozkłady naprężeń będą
jednakowe.

A

P





(7)

l

l

P

P

a

b

A

P





A

P





Rys.17. Schematyczna

interpretacja zasady de Saint

Venanta, a) pręt obciążony siłą

skupioną, b) pręt obciążony

obciążeniem równomiernie

rozłożonym na przekroju

ZASADA DE SAINT VENATA

ZASADA DE SAINT VENATA

Wnioski takie wyprowadził w 1855r. de Saint Venant na
podstawie analizy teoretycznej i sformułował je
następująco:
Jeżeli na pewien niewielki obszar ciała sprężystego
będącego w równowadze działają kolejno rozmaicie
rozmieszczone, ale statycznie równoważne obciążenia, to
w odległości przewyższającej wyraźnie rozmiary ciała
powstają praktycznie jednakowe stany naprężenia.

Odległości l, w których rozkłady naprężeń w obu prętach
są równoważne wynoszą:
l = 1.5d – dla przekroju kołowego o średnicy d,
l = 1.5d

z

– dla przekroju prostokątnego

Średnicę zastępczą wyznaczamy:

2

b

a

d

z





(8)

THE END

THE END