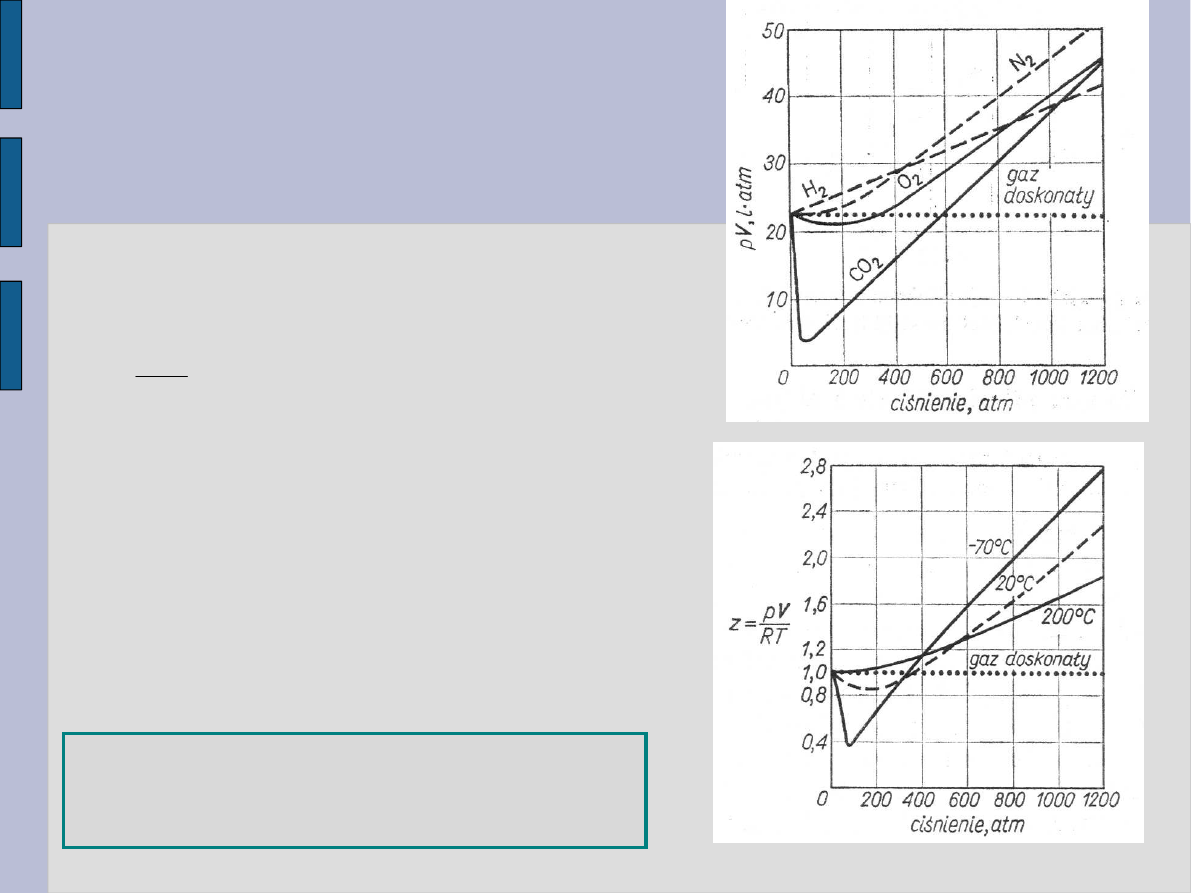
Gazy i pary
rzeczywiste
Zgodnie z równaniem Clapeyrona dla
gazów
doskonałych:
Stąd można zdefiniować współczynnik
ściśliwości dla gazu doskonałego
tj. z = f (p,T). Ogólnie obserwujemy
przy wysokich p i T:
z > 1.
Przyczyna:
Siły oddziaływania między
cząsteczkami.
.
0
RT
pV
.
1
0
RT
PV
z
(1)
(2)
(3)
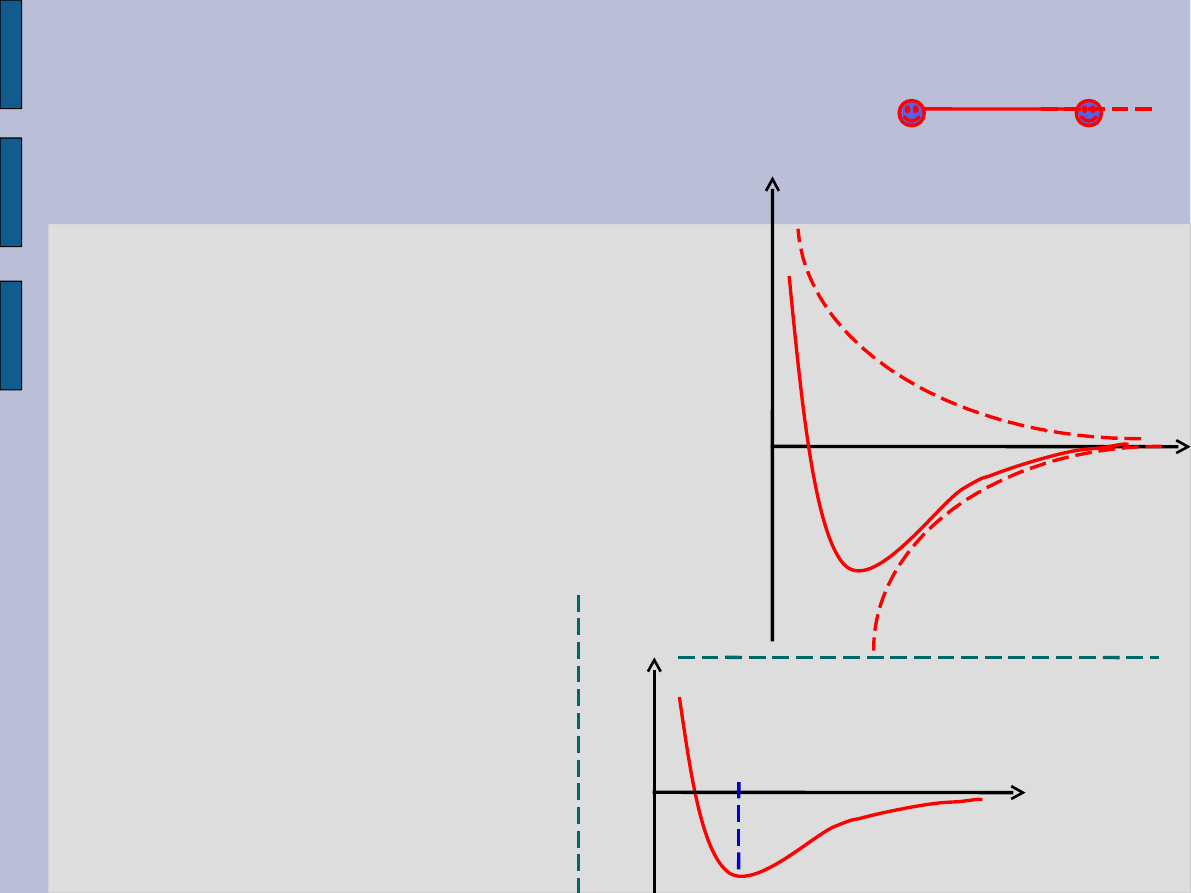
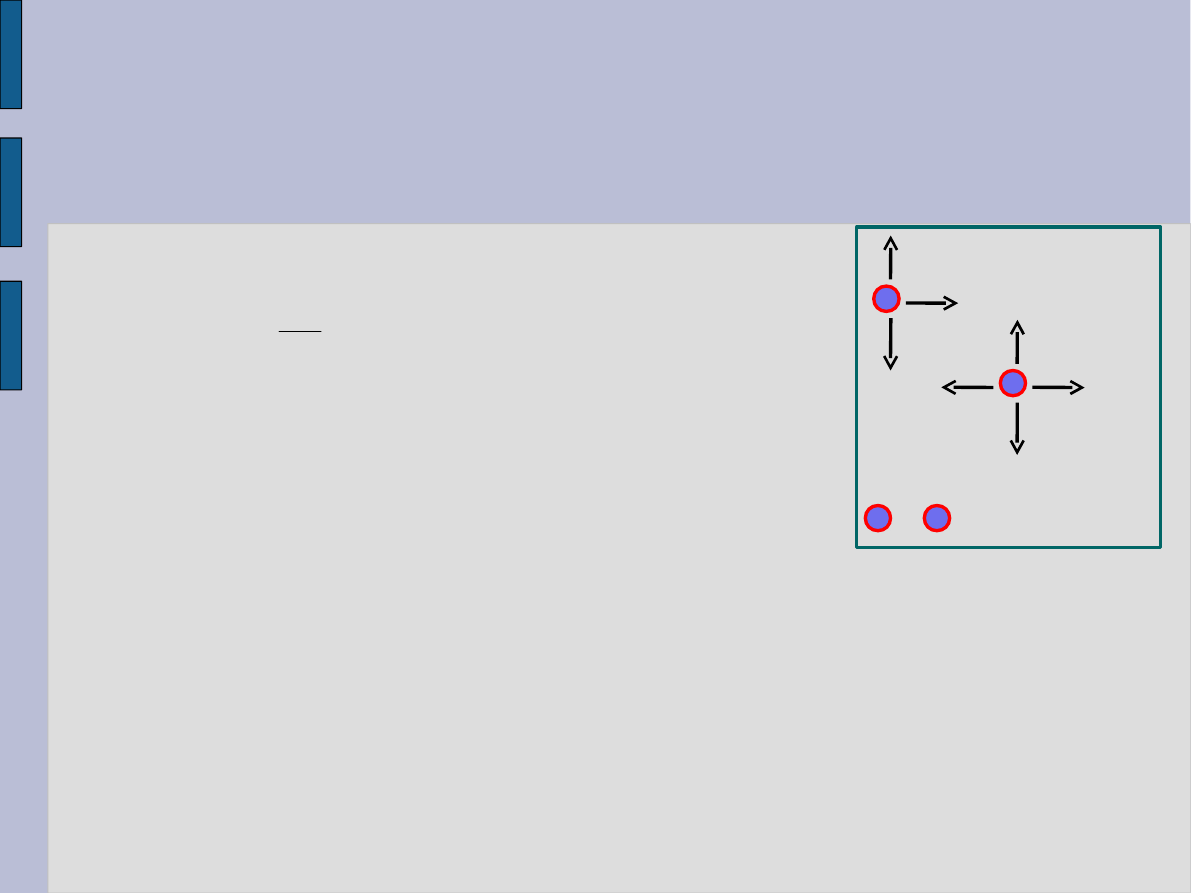
Siły
oddziaływania
.
2
1
F
F
F
1) Siła przyciągania
F1
2) Siła odpychania F2
Siła wypadkowa
(1
)
więc
,
d
d
p
p
E
E
r
p
r
F
E
(3
)
F
1
F
2
F
Gdy F = 0, tj. gdy r = r
0
.
2
1
F
F
(2
)
A
B
r
r
r
0
F
dr
B’
Siła oddziaływania obecna gdy:
r < 10
-9
m tj. rzędu 5-7 średnic atomowych.
Energia potencjalna układu
cząsteczek A i B:
.
d
r
p
p
p
r
F
E
E
E
(4
)
E
p
0
+
-
r
r
0
0
0
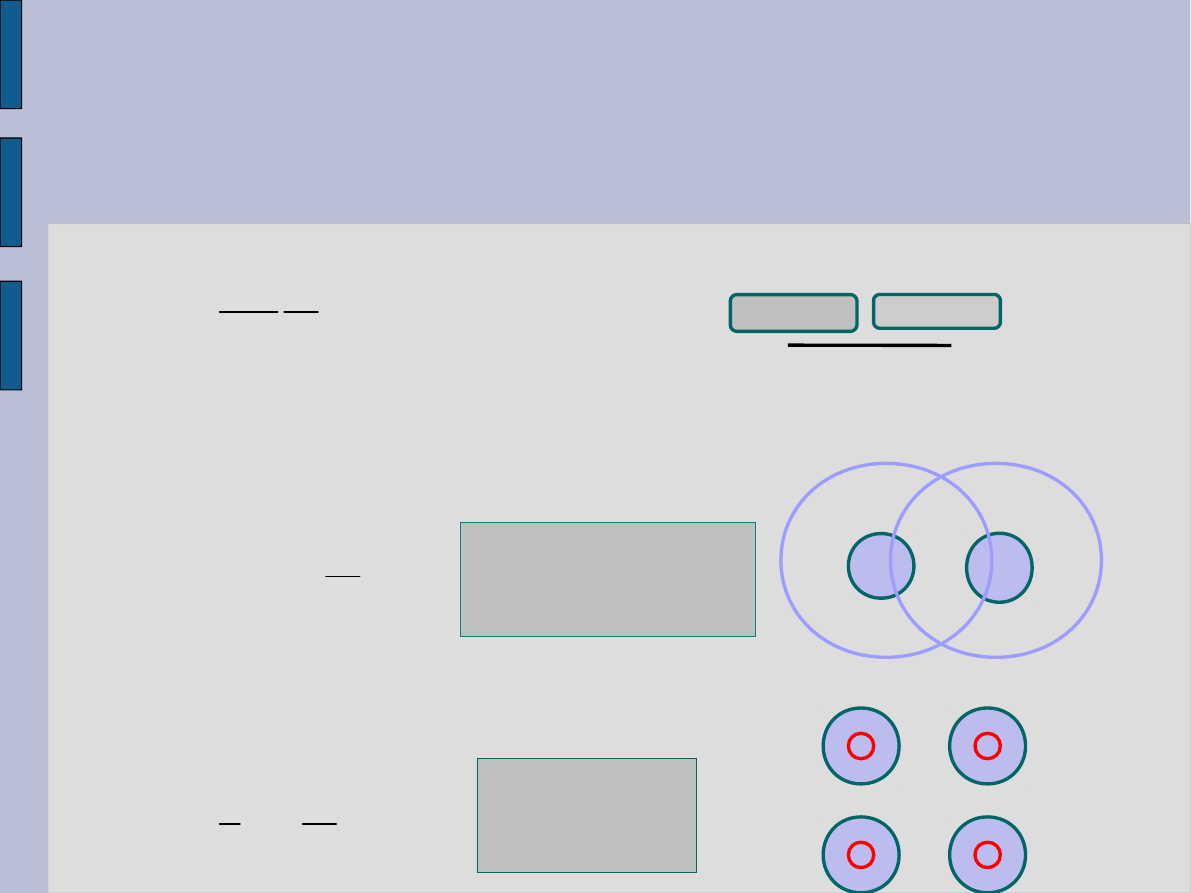
Siły van der Waalsa
Słabe siły przyciągania między dwiema cząsteczkami.
.
1
4
F
7
4
1
r
kT
p
e
1) Siły orientacyjne
Cząsteczki polarne – cząsteczki niesymetrycznej budowy.
Takie cząsteczki mają dipolowy moment elektryczny p
e.
A
B
(1)
(3)
(2)
Siła przyciągania
+
+ -
-
r
2) Siły indukowane
Cząsteczki niepolarne – cząsteczki symetrycznej
budowy.
Takie cząsteczki znajdują się w polu elektrycznym
wytworzonym przez niepolarną cząsteczkę
.
Siła przyciągania
.
1
12
F
7
2
1
r
p
e
3) Siły dyspersyjne
Rezonansowe siły przeciągania .
Drgania elektronów cząsteczki A powodują
wzbudzenie drgań elektronów cząsteczki B.
Siła
przyciągania
.
1
2
9
F
7
2
1
r
I
-
+
-
+
- +
-
+
I – pierwszy
potencjał
jonizacji.
α –
polaryzowalność
cząsteczki.
W cząsteczkach występują wszystkie 3 rodzaje
oddziaływania.
Orientacyjne i dyspersyjne siły silniejsze niż
indukowane.
Zakres działania:
,
nm
10
,
/
1
nm;
10
,
/
1
10
2
9
7
1
r
r
F
r
r
F
n
gdzie n 9.
F
2
– to kwantowe oddziaływania.
Siły Coulombowskie 1/r
2
– siły dłuższego
zasięgu;
Siły van der Waalsa 1/r
7
– krótszego
zasięgu.
Równanie van der
Waalsa
Cząsteczka ma wymiar tj. średnicę d i objętość v.
W równaniu Clapeyrona dla gazów
doskonałych
,
)
(
'
'
0
2
0
0
RT
b
V
V
a
p
V
p
(2)
Równanie (1) słuszne dla jednego kmola
gazu.
(1)
gdzie: a, b - stałe.
b – objętość wzbroniona (= 4vN
A
), a – stała
zależy od chemicznego składu gazu
(współczynnik van der Waalsa). a, b –
poprawki van der Waalsa.
RT
pV
0
Ciśnienie i objętość gazu rzeczywistego są inne niż
p i V
0
:
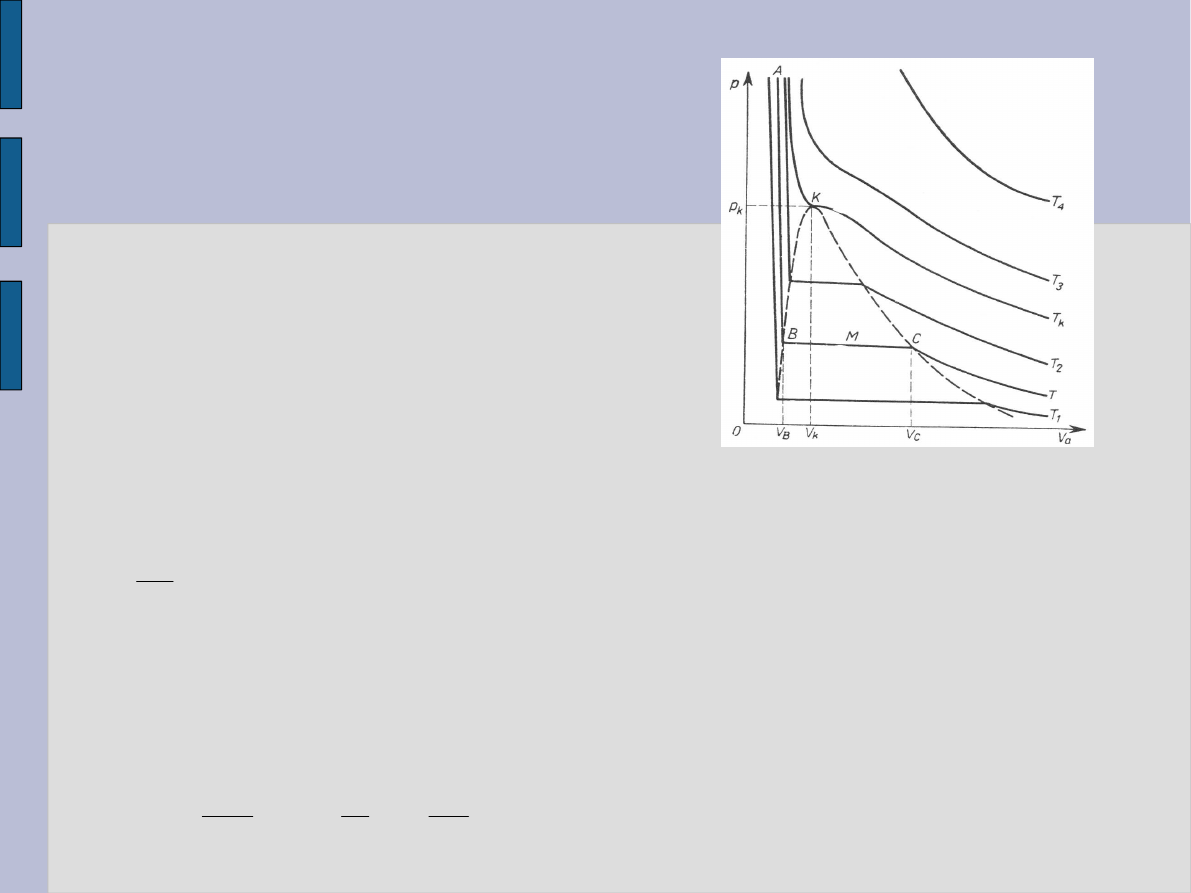
Izotermy gazów
rzeczywistych
Andrews badał zależność p od V
0
dla
CO
2
przy sprężaniu izotermicznym
.
1
2
3
4
T
T
T
T
T
T
k
T
k
– temperatura krytyczna.
Dla T < T
k
:
AB – ciecz,
CT – gaz,
CB - ciecz i gaz.
Takie zachowanie się gazów
przewiduje równania van der Waalsa.
,
)
(
2
RT
b
V
V
a
p
Równanie van der Waalsa dla 1 mola
gazu
(1)
(2
)
(3
)
można wyrazić w
postaci:
(4)
Stąd
.
0
)
(
2
3
ab
aV
V
RT
pb
pV
.
0
2
3
p
ab
V
p
a
V
p
RT
b
V
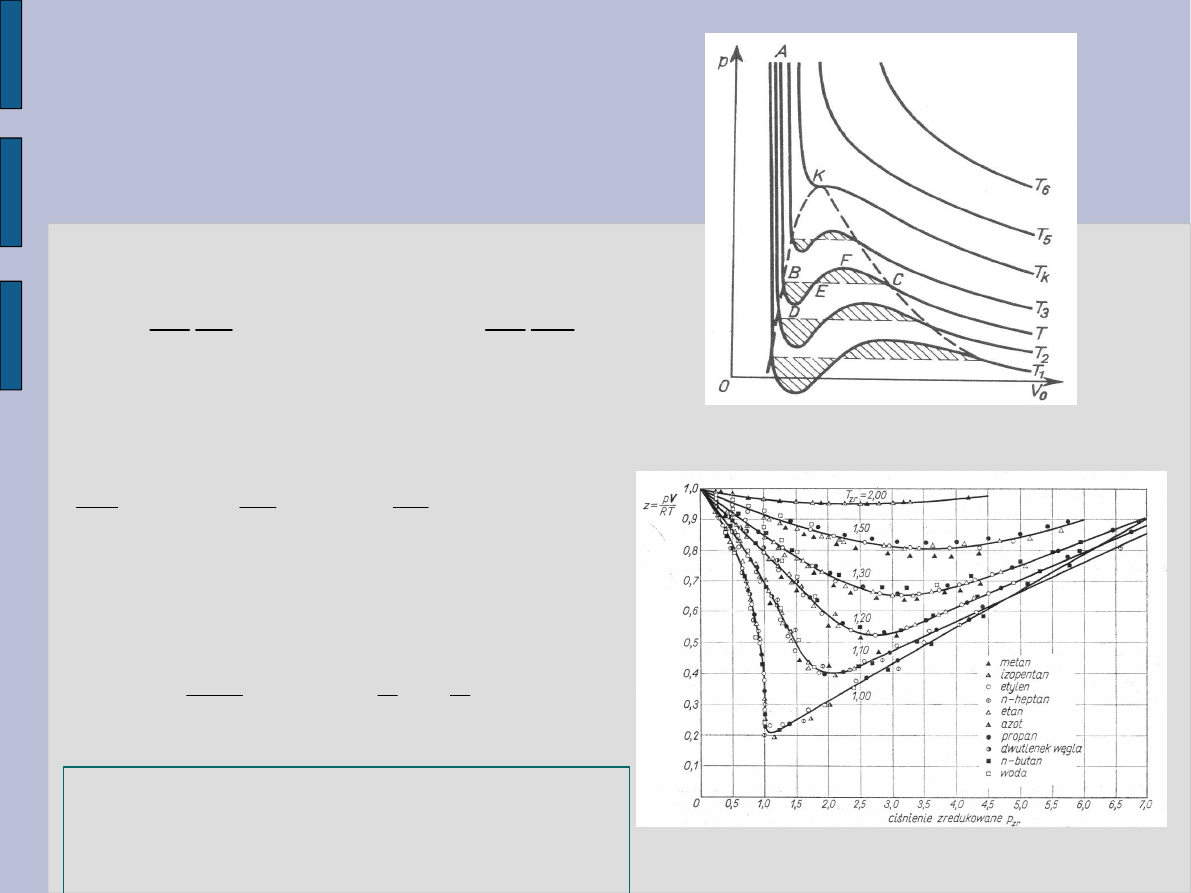
Równanie (4) ma 1-3 pierwiastki
rzeczywiste dla określonych p i T, które
można otrzymać po porównaniu z
równaniem
.
0
3
3
0
)
(
3
2
2
3
3
k
k
k
k
V
V
V
V
V
V
V
V
(5)
Wtedy otrzymujemy
.
27
8
,
3
,
27
1
2
bR
a
T
b
V
b
a
p
k
k
k
(6)
Jeżeli
.
3
8
3
1
3
2
zr
zr
zr
zr
T
V
V
p
,
,
,
zr
k
zr
k
zr
k
T
T
T
V
V
V
p
p
p
to mamy zredukowane
równanie van der Waalsa
Zredukowane równanie van der
Waalsa opisuje zachowanie się
różnych gazów rzeczywistych
identycznie.
(7)
(8)
