Gazy doskonałe i rzeczywiste. Lotność.
ZADANIA
Odgazowane naczynie zawiera resztki argonu pod ciśnieniem 10-3 Pa w temperaturze 320K. Obliczyć a) liczbę cząsteczek w jednostce objętości, b) średnią drogę swobodną, c) średni czas między zderzeniami. Średnica cząsteczki argonu d = 0,29 [nm], stała Boltzmanna k = 1,38⋅10-23 [kg⋅m2⋅s-2⋅K-1]. MAr = 39,9 [g/mol].
Rozwiązanie.
a) Liczbę cząsteczek w jednostce objętości (Ncz.) obliczamy dzieląc liczbę cząsteczek w jednym molu gazu doskonałego (NA - liczba Avogadra) przez jego objętość molową (Vm), którą można obliczyć dla danych warunków ciśnienia i temperatury z równania Clapeyrona
![]()
(1)
b) Średnią drogę swobodną obliczamy posługując się równaniem (2)
![]()
(2)
c) Średni czas między zderzeniami jest to czas, w którym cząsteczka poruszająca się ze średnią prędkością przebędzie średnią drogę swobodną
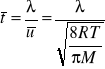
(3)
____________________________________
Ilu zderzeniom w temperaturze 25 [0C] w ciągu 1 [s] ulega pojedynczy atom argonu gdy ciśnienie wynosi a) 10 bar, b) 1 bar. Średnica atomu argonu wynosi 0,29 [nm]. Stała Boltzmanna kB = 1,38⋅10-23 [J ⋅ K-1], MAr = 39,9 [g/mol].
Rozwiązanie.
Liczbę zderzeń jednej cząsteczki w ciągu jednej sekundy przedstawia wyrażenie(3.3). Występującą tam liczbę cząsteczek zawartych w objętości jednostkowej można obliczyć za pomocą wyrażenia
![]()
(1a)
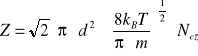
(4)
Wyniki wskazują że częstość zderzeń jest wprost proporcjonalna do ciśnienia gazu.
_____________________________________
Naczynie o objętości 4,157 dm3 zawiera 3,0115⋅1023 cząsteczek argonu przy czym ciśnienie w naczyniu wynosi 1 bar. Obliczyć jaka jest temperatura gazu i ile wynosi średnia prędkość kwadratowa cząsteczek. Obliczyć także jaka w tej temperaturze byłaby średnia prędkość kwadratowa cząsteczek helu. MHe = 4,003 [g/mol], MAr = 39,9 [g/mol].
Rozwiązanie.
Zakładając, że argon jest gazem doskonałym obliczamy temperaturę z równania Clapeyrona
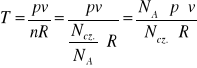
(5)
Średnią szybkość kwadratową argonu obliczamy za pomocą wyrażenia
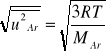
(6)
a średnią szybkość kwadratową helu podobnie
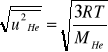
Wynika stąd, że stosunek średnich szybkości kwadratowych jest odwrotnie proporcjonalny do pierwiastków mas molowych poszczególnych gazów w danej temperaturze.
_____________________________________
Obliczyć ciśnienie 1 kmola wodoru zajmującego objętość 0,448 [m3] w temperaturze T = 273 [K]: a) przyjmując równanie stanu gazu doskonałego, b) równanie Van der Waalsa.
Rozwiązanie.
a) ![]()
b) ![]()
Uwaga: stałe równania Van der Waalsa należy wziąć z tablic fizykochemicznych.
________________________________
Etan (C2H6) zamknięty w butli o objętości 2 dm3 w temp. 57 oC ma gęstość 0,075 [g/cm3]. Obliczyć ciśnienie tego gazu stosując : a) równanie gazu doskonałego i b) równanie van der Waalsa, oraz porównać otrzymane wyniki. Stałe: R = 8,314 [J⋅mol-1⋅K-1], a = 5,562 [bar (dm3/mol)2]; b = 0,0638⋅[dm3/mol]
Rozwiązanie.
Zadania tego typu najwygodniej jest rozwiązywać obliczając najpierw objętość molową gazu w podanych warunkach. W tym przypadku jest ona równa stosunkowi masy molowej (M) do gęstości gazu (ρ):
a) z równania Clapeyrona
![]()
b) z równania van der Waalsa
![]()
Wyniki znacznie się różnią co związane jest głównie z dużą wartością stałej a.
__________________________________
32 g N2 zajmuje objętość 1, 12 dm3 w temp. 30 oC. Obliczyć ciśnienie tego gazu stosując: a) równanie gazu doskonałego, b) równanie van der Waalsa i porównać otrzymane wyniki.
Rozwiązanie.
![]()
______________________________________
Temperatura krytyczna i ciśnienie krytyczne argonu wynoszą odpowiednio Tkr = 151,0 [K], pkr = 4,86 [MPa]. Obliczyć stałe Van der Waalsa i promień cząsteczki argonu.
Rozwiązanie.
Temperatura krytyczna i ciśnienie krytyczne są współrzędnymi punktu przegięcia na izotermie Van der Waalsa. Wyliczając ciśnienie jednego mola gazu z równania Van der Waalsa, otrzymujemy:
![]()
Z właściwości punktu przegięcia wynika, że pierwsza i druga pochodna ciśnienia względem objętości są równe zeru:
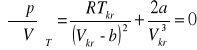
; 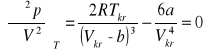
Z powyższych wyrażeń można wyznaczyć związki pomiędzy stałymi równania Van der Waalsa a parametrami krytycznymi.
Vk =3b Tk = 8a/27Rb pk = a/27b2
Znając wartości, parametrów krytycznych obliczamy wartości stałych Van der Waalsa:
a = 27R2T2/(64pk) b = RTk/8pk
a = 0,136 [N⋅m4/mol2] b = 3,22⋅10-5 [m3/mol]
Objętość własna cząsteczek 1 mola argonu jest równa wartości stałej b, a zatem objętość jednej cząsteczki
VAr = b/NA = 5,346⋅10-23 [cm3/cz.]
NA -liczba Avogadra.
Przyjmując, że jednoatomowa cząsteczka argonu jest kulą, obliczamy jej promień (4/3) π r3 = VAr stąd r = 2,337⋅10-8 [cm]
________________________________________
Dla wysokich temperatur i ciśnień równanie stanu gazu może przybrać postać: pV = RT + bp. Obliczyć lotność azotu w temperaturze 1000 [K] i pod ciśnieniem 100 [MPa] przyjmując, że b = 39 [cm3/mol].
Rozwiązanie.
Lotność czystego gazu przy T = const., oblicza się z zależności wynikającej z równań (3.14 - 3.16):
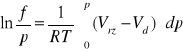
Vrz - oznacza objętość molową gazu rzeczywistego a Vd - objętość molową gazu doskonałego.
Z podanego równania wirialnego ![]()
; a z równania Clapeyrona ![]()
;
a więc Vrz - Vd = b . Stąd
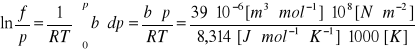
= 0,469
f/p = 1,598, f = 1,598* 100 [MPa] = 159,8 [MPa]
_____________________________________________
Obliczyć współczynnik lotności ditlenku węgla w temperaturze 40 oC i pod ciśnieniem 80 i 160 [bar] korzystając z równania Van der Waalsa i parametrów krytycznych pkr = 7,40 [MPa], Tkr = 304.2 [K].
Rozwiązanie.
Współczynnik lotności jest to stosunek lotności do ciśnienia, a więc
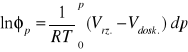
Objętość molową gazu doskonałego wyliczamy z równania Clapeyrona ![]()
, a objętość molową gazu rzeczywistego z równania Van der Waalsa
![]()
Ponieważ jest to równanie trzeciego stopnia względem V wymagające stosowania metod iteracyjnych, posługujemy się jego postacią uproszczoną powstałą przez podstawienie zamiast iloczynu pV iloczynu RT z równania stanu gazu doskonałego:
po podstawieniu do równania na współczynnik lotności i scałkowaniu otrzymujemy
Wykorzystując związki między parametrami krytycznymi a stałymi Van der Waalsa, można powyższe równanie przedstawić za pomocą parametrów zredukowanych pr, Tr i Vr :
![]()
![]()
Po obliczeniach otrzymujemy
Tr = 1,029 a) pr80 = 1,081 b) pr160 = 2,162
φ80 = 0,76 b) φ160 = 0,62
________________________________________________
Obliczyć współczynnik lotności amoniaku w temperaturze 473 [K] pod ciśnieniem 10 i 40 [MPa] korzystając z równania Berthelota i parametrów punktu krytycznego amoniaku : pk = 11,30 [MPa], Tk = 406 [K].
Rozwiązanie. -------SKRYPT
Równanie Berthelota jest pewnym ulepszeniem równania Van der Waalsa polegającym na uniezależnieniu stałej a od temperatury:
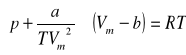
Równanie to można przedstawić w wygodnej uproszczonej postaci zawierającej parametry krytyczne:
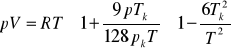
Współczynnik lotności można również obliczyć posługując się współczynnikiem kompresji (3.16):
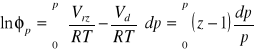
Wyszukiwarka
Podobne podstrony:
Konduktometria zad1, Technologia Chemiczna AGH, inne, Chemia fizyczna
INŻ K 3, Technologia Chemiczna AGH, inne, Inżynieria chemiczna i procesowa, Pęd
cwiczenie 34, Technologia chemiczna, Chemia fizyczna, Laboratorium, inne, chemia fizyczna
izomeria optyczna, Technologia chemiczna, Chemia fizyczna, Laboratorium, inne, chemia fizyczna
04 struktury ok, Technologia chemiczna pw, 1rok, chemia kolosy egz
02 rozkład ok, Technologia chemiczna pw, 1rok, chemia kolosy egz
07 reszta ok, Technologia chemiczna pw, 1rok, chemia kolosy egz
chemia nieorganiczna egzamin, Technologia chemiczna pw, 1rok, chemia kolosy egz
Elektrony w polu... - odp, Technologia chemiczna pw, 1rok, chemia kolosy egz
chemia1PRACA DOMOWA5, Technologia chemiczna pw, 1rok, chemia kolosy egz
redox, Technologia chemiczna pw, 1rok, chemia kolosy egz
06 reakcje2 ok, Technologia chemiczna pw, 1rok, chemia kolosy egz
REAKCJE, Technologia chemiczna pw, 1rok, chemia kolosy egz
otrzymywanie, Technologia chemiczna pw, 1rok, chemia kolosy egz
01 otrzymywanie ok, Technologia chemiczna pw, 1rok, chemia kolosy egz
gontarz I termin, Technologia chemiczna pw, 1rok, chemia kolosy egz
CAŁOŚĆ, Technologia chemiczna pw, 1rok, chemia kolosy egz
chemia1PRACA DOMOWA4, Technologia chemiczna pw, 1rok, chemia kolosy egz
rozkład, Technologia chemiczna pw, 1rok, chemia kolosy egz
więcej podobnych podstron