Przeliczanie jednostek

• Po za układem SI w USA i innych

krajach używane są jednostki
angielskie.

• Warto zapoznać się ze sposobem ich

przeliczania na jednostki SI.

• Przykłady
• 1 funt (lb) – 453,6 g
• 1 cal (in.) 2,54 cm

Reguły przeliczania – zasada

ogólna

• Właściwość fizyczna (np. długość)

pozostaje ta sama:wartość
przeliczona to po prostu inna
wielokrotność innej jednostki

• Procedura
• Gdy informacja jest podana w

jednostkach innych niż wymagane,
przeliczamy na jednostki wymagane

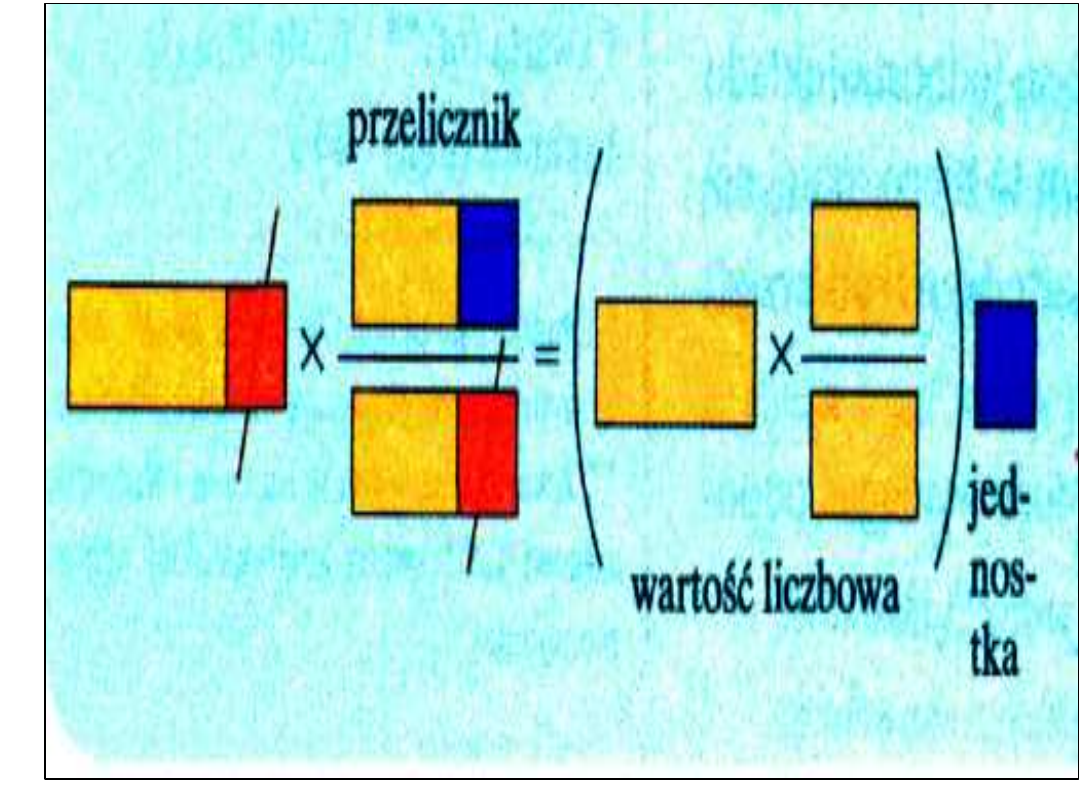
Procedura przeliczania

• Informacja wymagana =

informacja podana*przelicznik

• Przelicznik jest określony wzorem

podane

jednostki

wymagane

jednostki

k

przeliczni



Potęgowanie i przeliczanie

• Jeżeli jednostka jest podniesiona do

potęgi, zastosuj te samą procedurę w
każdym przypadku występowania
jednostki. Gdy więc jednostka
przeliczana występuje w n-tej potędze,
zastosuj n-tą potęgę przelicznika.

• Jeżeli jednostka znajduje się w

mianowniku, zastosuj odwrotność
przelicznika.

Przykład stosowania

przelicznika

• Chemik bada wartość odżywczą

nowego napoju owocowego i musi
wyrazić masę napoju w gramach.
Jaka jest masa jednej porcji (12
uncji) napoju w gramach?

Strategia

• Znajdź przelicznik w poradniku

(książce). Zastosuj procedurę
opisaną w przezroczu nr 39.

• Rozwiązanie
• Wiemy, że 1 uncja = 28,35 g

cd. rozwiązania

• A zatem

g

uncja

g

uncji

g

masa

340

)

1

35

,

28

(

*

)

12

(

)

(





Przeliczanie jednostek

występujących w

mianowniku

• Rtęć, którą stosuje się w różnych

przyrządach laboratoryjnych ze
względu na jej znaczną gęstość,
jest cieczą. Wyraź gęstość rtęci,
13,5 g/cm3, w kilogramach na
metr sześcienny(kg/m3).

Strategia postępowania

• Należy zastosować procedury opisane

w przezroczu 39, przeliczania
jednostek występujących w
mianowniku i jednostek podniesionych
do potęgi. Potrzebne są ty dwa
przeliczniki. Do przeliczenia gramów
(jednostki podane) na
kilogramy(jednostki wymagane)
zastosuj przelicznik 1 kg/10^3g.

Strategia postępowania

cd.

• Do przeliczenia centymetrów

(jednostki podane) na
metry(jednostki wymagane)
zastosujemy przelicznik 10^2
cm/1 m (gdyż centymetry
występują w mianowniku)

Rozwiązanie

• Każdy przelicznik podnosi się do

tej samej potęgo co przeliczoną
jednostkę





3

4

3

2

3

3

3

2

3

3

3

/

10

35

,

1

1

10

10

1

5

,

13

1

10

10

1

5

,

13

/

m

kg

m

cm

g

kg

cm

g

m

cm

g

kg

cm

g

m

kg

g





















































































cd. rozwiązania

• Przelicznik długości należy więc

podnieść do trzeciej potęgi, by
otrzymać przelicznik objętości.

• Każde przeliczenie można

wykonać oddzielnie, zwykle jednak
jednoczesne ich wykonywanie jest
szybsze.

Niepewność pomiarów

• Jednym z warunków wiarygodności

naukowców jest rzetelne
publikowanie przez nich wyników
pomiarów.

• Wyniki pomiarów zawierają liczby.
• Liczby te różnią się od liczb

spotykanych w matematyce w
dwóch aspektach:

Wyniki

• W pomiarach występuje zawsze proces

porównania. Np.. Kiedy powiemy , że

Zosia jest 1,8 m wysoka, oznacza to w

rzeczywistości, że jest ona 1,8 razy

wyższa aniżeli obiekt , którego

wysokość przyjęto za 1m. Metr jest w

tym wypadku jednostką, pomiar

wzrostu odbywa się przez porównanie

z innym obiektem, którego wysokość

jest znana.

Niepewność

• Drugą cechą charakterystyczna

pomiarów jest to, ze każdy pomiar
zawiera niepewność. Liczby w
matematyce są dokładne. Np.. W
słowie „rower” mamy dokładnie 5
znaków literowych.

• Pomiary są zawsze niedokładne.

Niepewność pomiarowa

• Pomiar zawsze zawiera w sobie

element oszacowania.

• Eksperymentator i przyrząd

pomiarowy wykazują fizyczne

ograniczenia.

• Wynika z tego, że z pomiarami zawsze

się łączy niepewność pomiarowa.

• Niepewność może być ograniczona

ale nie zlikwidowana.

cd. Niepewność

pomiarowa

• Jakakolwiek decyzja lub wniosek

oparte na pomiarach muszą
uwzględniać błąd zawarty w
pomiarach.

Niepewność pomiarowa

• Wiemy że pomiary są niedokładne.
• Różnica pomiędzy wartością mierzoną a

wartością prawdziwą nosi nazwę błędu.

• Przyczyny błędu:
• Ograniczenia w procedurze pomiarowej.
• Wynikają one z ograniczeń

aparaturowych i możliwości
eksperymentatora.

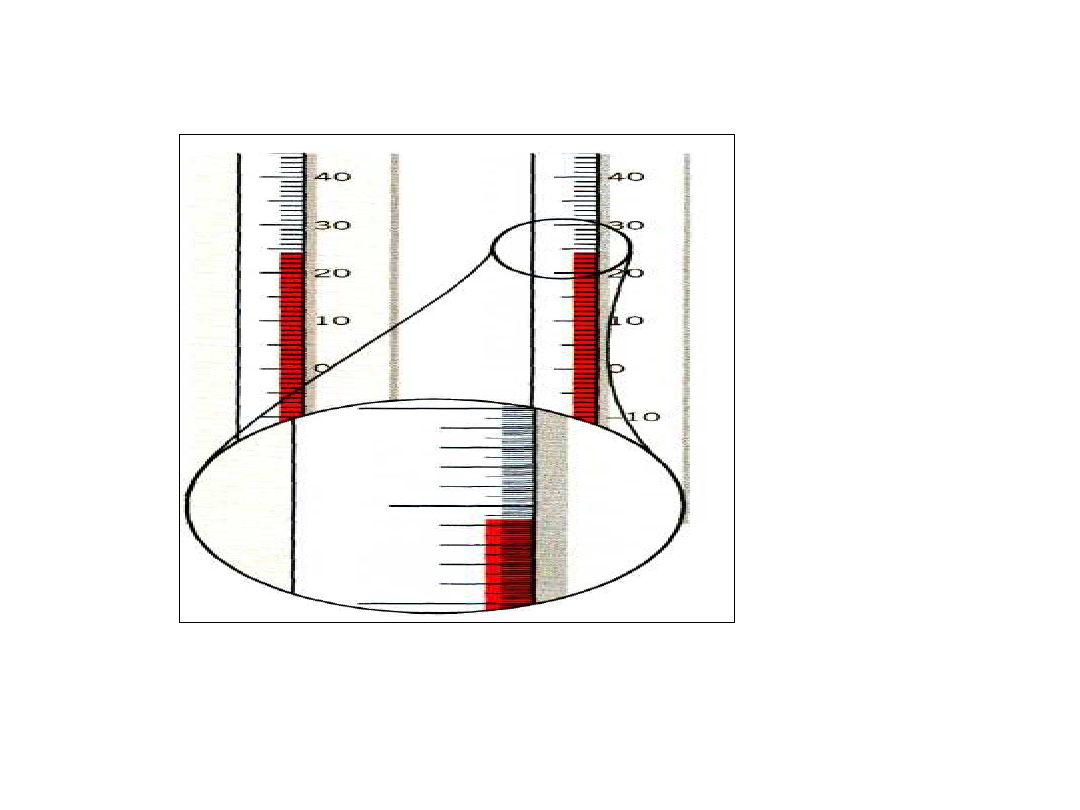
Skala -odczyt

• Rozpatrzmy dwa termometry różniące się

skalami.

• Na pierwszym termometrze kreski są

oddalone co jeden stopień. Możemy
oszacować i być pewni, że temperatura jest
powyżej 24C i poniżej 25C. Lepsze
przybliżenie uzyskamy podając cyfrę
określająca położenie pomiędzy zaznaczonymi
wskaźnikami. Zatem możemy podać 24,3 C.

• Ostatnia cyfra jest tylko oszacowaniem.

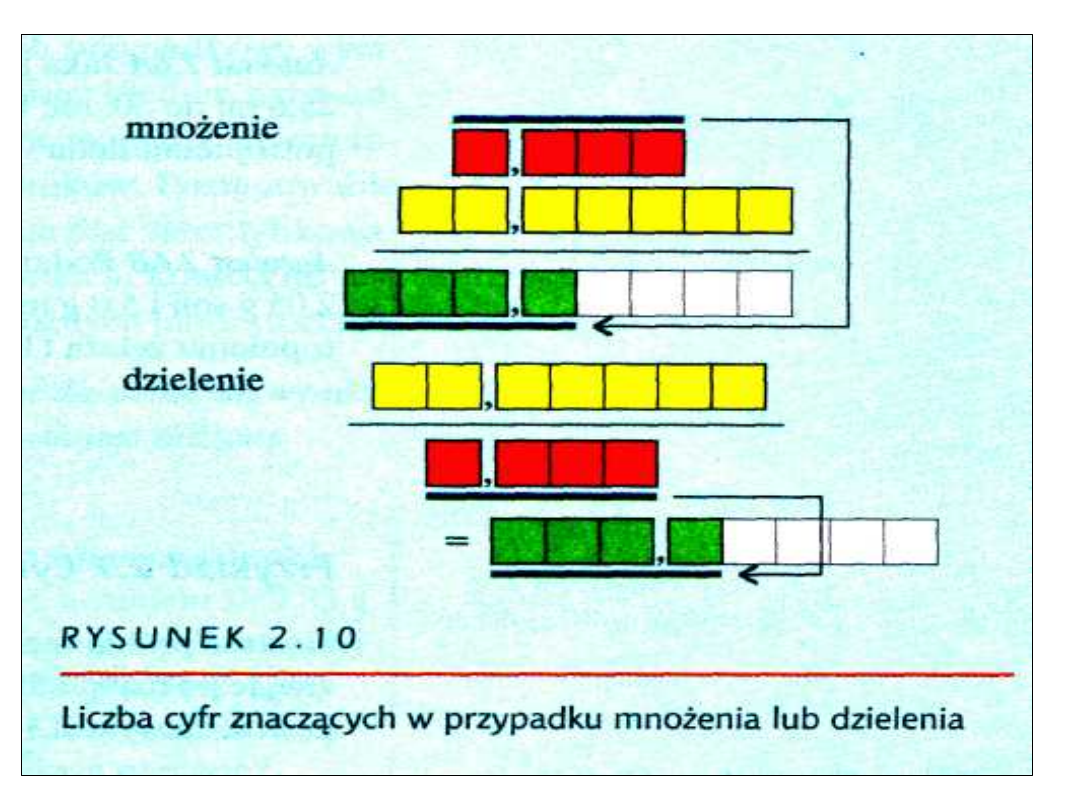
Cyfry znaczące

• Przyjmujemy zasadę: w pomiarach

zapisujemy wszystkie cyfry, do
cyfry niepewnej włącznie.
Zapisane cyfry noszą nazwę cyfr
znaczących.

• Kiedy odczytujemy ze skali,

ostatnia cyfra odpowiada 1/10
najmniejszej podziałki

Cyfry znaczące

• Termometr lewy: podziałka co

jeden stopień, zatem możemy
podawać wynik z dokładnością do
1/10 stopnia.

• Termometr prawy: podziałka co

1/10 stopnia.Zatem można
podawać z dokładnością do 1/100.

Cyfry znaczące

• Więcej mamy zaufania do odczytu

na termometrze prawym (24,32C)
ponieważ w wyniku mamy więcej
cyfr znaczących i mniejszą
niepewność.

• Zaufanie do wyników wynika z

liczby cyfr znaczących użytych do
ich zaprezentowania

Cyfry znaczące w

pomiarach

• Liczba cyfr znaczących w

wynikach pomiarów równa się
liczbie cyfr pewnych +1.

• Np.. 11,2 m
• Jedynki oznaczają cyfry pewne
• Dwójka oznacza cyfrę niepewną.

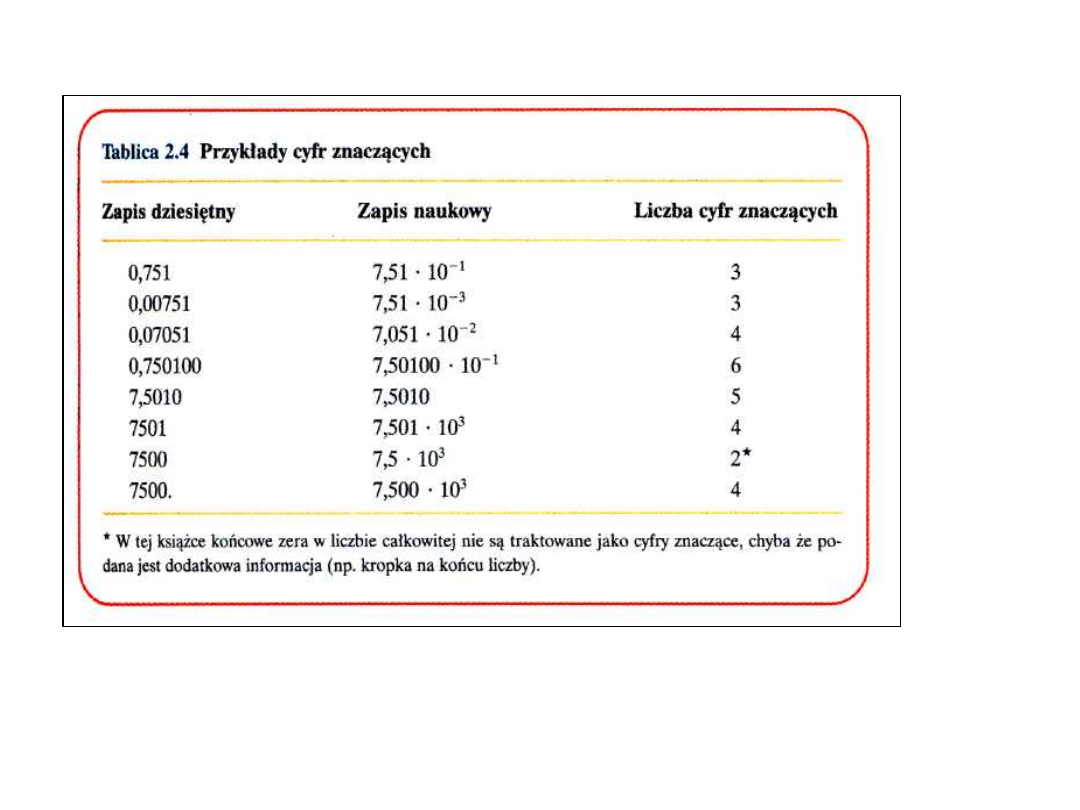
Wyznaczanie liczby cyfr

znaczących

• Niepewność danych warunkuje

niepewność wyników opartych na nich

obliczeniach.

• W celu wyznaczenia liczby cyfr

znaczących należy:

• Wyrazić wartość w notacji naukowej,

umieszczając przed przecinkiem

dziesiętnym cyfrę niezerową

• Określić liczbę cyfr mnożonych przez

potęgę dziesięciu

Cyfry znaczące w

obliczeniach

• Zasada ogólna
• Wynik obliczenia opartego na

danych pomiarowych zależy od
dokładności pomiarów.
Niedokładność pomiarów
powoduje niedokładność wyniku
obliczenia.

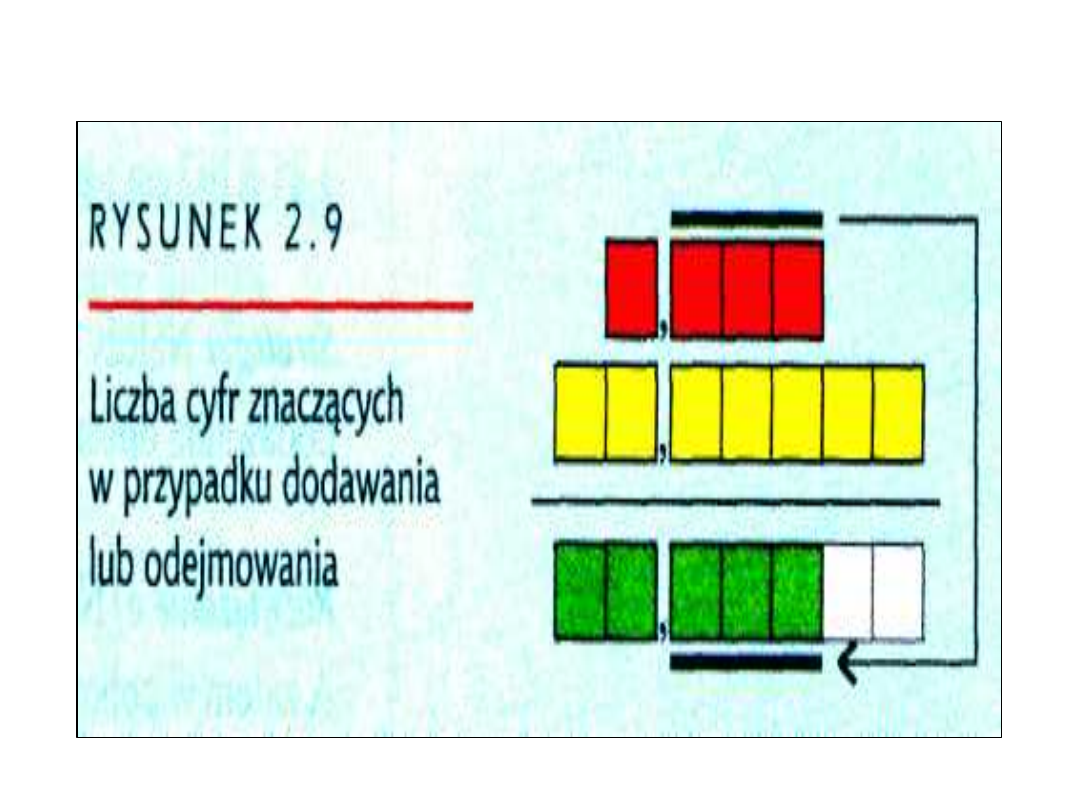
Zaokrąglanie

• Odmienne reguły dotyczą

dodawania (i jego odrowtności –
odejmowania) i mnożenia(i jego
odwrotności – dzielenia). W
obydwu przypadkach konieczne
jest zaokrąglanie wyników do
prawidłowej liczby cyfr
znaczących.

Zaokrąglanie

• Ostatnia cyfra > 5 w górę
• Ostatnia cyfra <5 w dół
• Jeżeli 5 to do najbliższej parzystej
• Zaokrąglanie prowadzimy

jednorazowo

• Zaokrąglanie prowadzimy w

końcowym etapie obliczeń

Warunki niekontrolowane

• Błędy powstają nie tylko przy

odczytach na skalach ale również
przy braku kontroli w czasie
pomiarów. Np.. Mierzymy długość
druta za pomocą linijki. Nie
zawsze drut będzie idealnie prosty,
lub koniec idealnie pokrywał się z
zerem.

Błędy wynikające z braku

dokładnego zdefiniowania

warunków pomiarów

• Pomiar ciężaru ciała na wadze

łazienkowej można przeprowadzić z

dokładnością do trzech cyfr znaczących

95,1kg. Natomiast sposób ważenia może

być bardzo różny: po kąpieli ale bez

dokładnego wytarcia się, w ubraniu lub

nago, na jednej nodze itp.. Zróżnicowanie

warunków może prowadzić do większych

błędów aniżeli wynikających z zapisu

czyli z dokładnością do 0,1 kg.

Powtarzanie pomiarów

• Wiele błędów nie zostałoby

wykrytych gdyby pomiary nie zostały
powtórzone, a tylko ograniczone do
pojedynczego pomiaru.

• Jeżeli wykonamy dużą liczbę

pomiarów to okazuje się, że wyniki
pomiarów skupiają się wokół

pewnej

wartości centralnej

.

Wartość średnia

• Np.. Temperatura została zmierzona przez

10 osób i uzyskano wyniki:24,1,
24,2;24,2;23,3;24,3;24,3;24,3;24,4;24,4;2
4,5

• Niepewność związana z pomiarem odnosi

się do dziesiątej części stopnia, pomiary
zawarte są w przedziale od 24.1 do 24.5.
Grupują się one wokół wartości 24,3.
Zatem tą wartością centralną jest średnia.

Obliczanie średniej

• Wzór do obliczenia średniej.

n

X

X

n

i

i







1

Liczba pomiarów

• Ile pomiarów należy wykonać?
• Odpowiedź na to pytanie będzie

zależała od stopnia ufności z jaką
chcemy przedstawić średnią.

• Im więcej pomiarów tym większa

pewność, że średnia z pomiarów
zbliża się do wartości centralnej.

Dokładność

• Powtórzenie pomiarów może pozwolić

na oszacowanie niepewności i dać
nam wiedzę na temat natury błędów.

• Oszacowanie błędów dokonujemy

odpowiadając na pytania:

• Jak dokładny jest pomiar tzn. jak

blisko jest wartości prawdziwej lub
poprawnej

Precyzja

• Jak precyzyjny jest pomiar tzn. jak

blisko jest do wartości średniej z
serii pomiarów.

• Dla uzyskania pomiarów

dokładnych przyrząd musi być
poprawnie skalibrowany