Rozdział 5

Metoda analizy

macierzy

współczynników

korelacji

Sld. 5.2. W

artość współczynnika

korelacji

Idea metody sprowadza się do wyboru takich zmiennych

objaśniających, które są silnie skorelowane ze zmienną

objaśnianą i jednocześnie słabo skorelowane między sobą.

Punktem wyjścia jest wektor R

o

i macierz R.

Dla zadanego poziomu istotności y oraz dla n–2 stopni

swobody wyznaczacie krytyczną wartość współczynnika

korelacji:

gdzie I jest wartością statystyki odczytanej z tablic

testu t Studenta dla danego y oraz n–2 stopni
swobody.

Krytyczna wartość współczynnika korelacji r*

może być także zadawana z góry przez badacza.

Sld. 5.3. Procedura doboru zmiennych

objaśniających

1. Ze zbioru potencjalnych zmiennych objaśniających eliminuje się te
wszystkie
zmienne, dla których zachodzi nierówność:

r r*.

Są to bowiem zmienne nieistotnie skorelowane ze zmienną
objaśnianą.

2. Spośród pozostałych zmiennych jako zmienną objaśniającą
powołuje się taką
zmienną X

h

, dla której:

|r

h

| = max{|r

j

|}.

Zmienna X

h

jest nośnikiem największego zasobu informacji o

zmiennej objaśnianej.

3. Ze zbioru potencjalnych zmiennych objaśniających eliminuje się te
wszystkie
zmienne, dla których:

|r

hi

|>r*.

Są to zmienne zbyt silnie skorelowane ze zmienną objaśniającą X

h

,

a więc powielające dostarczane przez nią informacje.

Postępowanie opisane w punktach 1, 2 i 3 kontynuuje się aż do
momentu wyczerpania zbioru potencjalnych zmiennych
objaśniających.

Sld. 5.4. Przyklad

W celu wyjaśnienia kształtowania się poziomu spożycia mięsa Y w wybranych krajach

zaproponowano wstępnie 8 potencjalnych zmiennych objaśniających; jest to spożycie innych
artykuіów żywnościowych: X

1

– artykułów zbożowych, X

2

- ziemniaków, X

3

- warzyw, X

4

–

owoców, X

5

– tłuszczów, X

6

- ryb, X

7

- mleka, X

s

-jaj.

Na podstawie danych statystycznych dotyczących spożycia tych artykółów w 28

krajach obliczono wektor współczynników korelacji zmiennej objaśnianej z potencjalnymi
zmiennymi objaśniającymi:

R

0T

= [-0,59 -0,06 0,08 0,13 -0,54 -0,15 -0,10 -0,72].

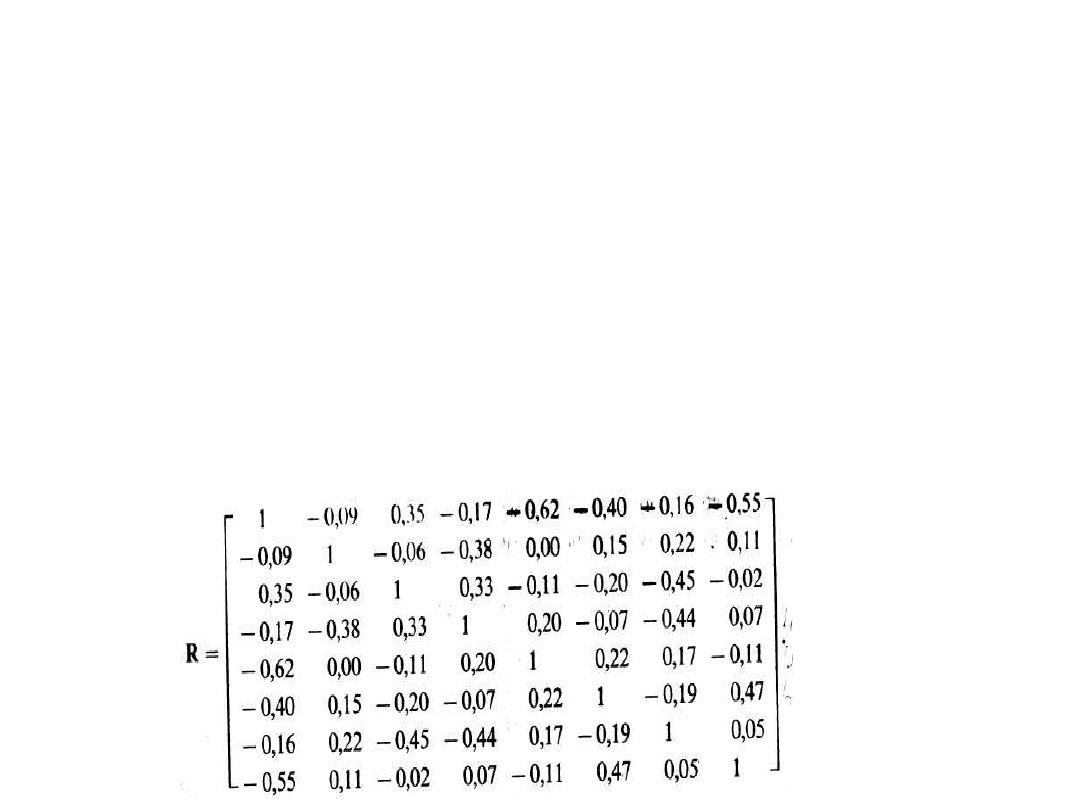
I macierz współczynników korelacji między potencjalnymi zmiennymi objaśniającymi:

Sld. 5.5. Przykład

 

Dobór zmiennych objaśniających przeprowadzimy dla poziomu
istotności y = 0,10. Z tablic testu t Studenta dla założonego
poziomu istotności oraz dla n - 2 = 26 stopni swobody
odczytujemy wartość statystyki teoretycznej I* = 1,706, a
następnie obliczamy krytyczną wartość współczynnika korelacji:

Eliminujemy wszystkie zmienne, które są słabiej skorelowane ze

zmienną objaśnianą niż 0,318. Są to zmienne X

2

, X

3

, X

4

, X

6

i X

7

dla

których:

r

2

= -0,06; r

3

= 0,08; r

4

= 0,13; r

6

= -0,15; r

7

= -0,10.

Spośród pozostałych zmiennych pierwotnych wybieramy zmienną

najsilniej skorelowaną ze zmienną objaśnianą. Jest nią X

8

: r

8

= 0,72.

Eliminujemy wszystkie zmienne, dla których zachodzi nierówność: |

r

8i

| > 0,318. Jest jedna taka zmienna, a mianowicie X

1

gdyż |r

81

| =

0,55. Zmienną X

6

wyeliminowano wcześniej.

Z

tak

zredukowanego

zbioru

potencjalnych

zmiennych

objaśniających wybieramy następną zmienną objaśniającą. Jest to
X

5

,.

Ostatecznie zbiór zmiennych objaśniających zawiera dwie zmienne:

X

5

i X

8

. Model spożycia:

Y = a

0

+ a

1

X

5

+ a

2

X

8

+ ε.

LITERATURA

1.E.Nowak. Zarys metod ekonometrii.

Warszawa 2002