Systemy

odniesień przestrzennych

Państwowe

układy współrzędnych

Układ "1992"

- utworzony w oparciu o jednostrefowe dla

obszaru Polski (w szerokim 10° pasie południkowym)
odwzorowanie Gaussa - Krügera elipsoidy GRS-80 z południkiem
osiowym (środkowym) Lo=19° i przy założeniu skali długości na
tym południku m

o

= 0.9993.

Współrzędne pełne w układzie 1992 oblicza się z formuł:
X

1992

= m

0

* X

GK

- 5300000

Y

1992

= m

0

* Y

GK

+ 500000

współrzędne Gaussa-Krugera:
X

GK

- względem obrazu równika

Y

GK

- względem obrazu południka środkowego

Układ "1992" jest przeznaczony dla map w skalach 1: 10000
i mniejszych. Jest stosowany również w obliczeniach państwowych
osnów geodezyjnych

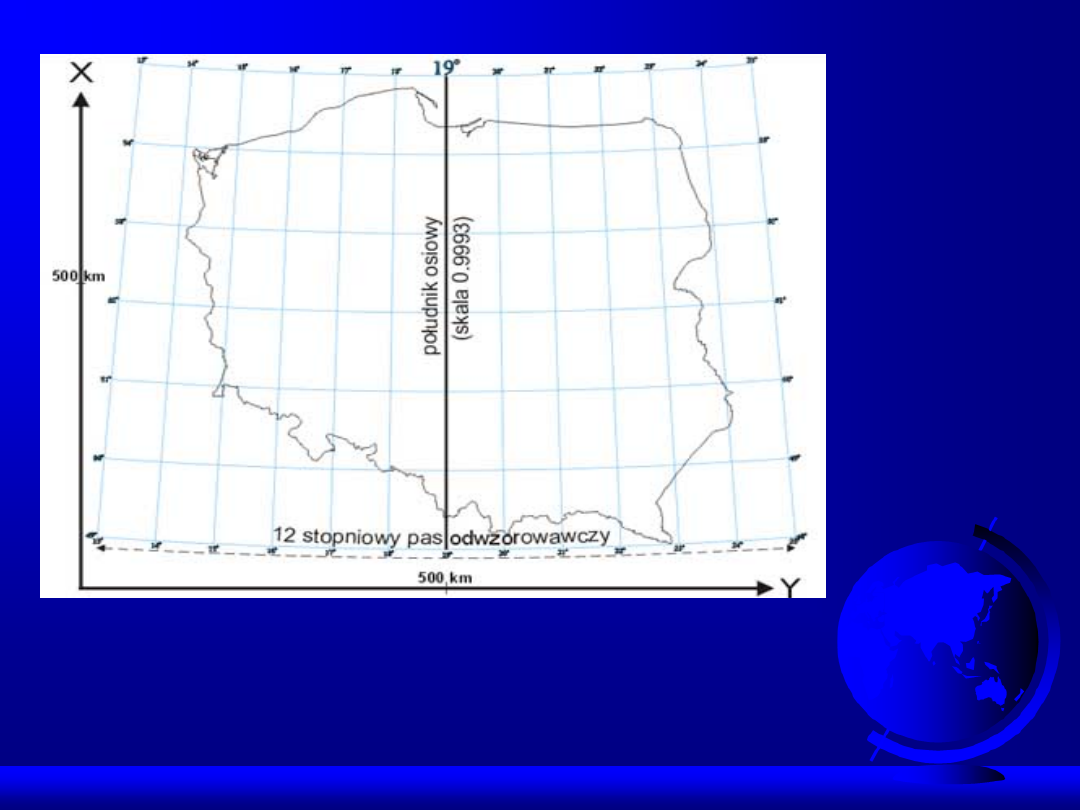
Układ 1992

Układ "2000"

jest złożony z czterech stref, z których każda

powstała jako odwzorowanie Gaussa - Krügera elipsoidy GRS-80 w
pasie południkowym 3° ze skalą kurczenia na południku osiowym
każdej strefy m

o

= 0.999923. Dla kolejnych stref przyjęto następujące

południki osiowe: 15°, 18°, 21°, 24°. Powstałe układy oznaczamy
odpowiednio:
2000/15, 2000/18, 2000/21, 2000/24

Współrzędne pełne w układzie 2000 wyznacza się z zależności:
X

2000

= m

0

* X

GK

Y

2000

= m

0

* X

GK

+ 500000 + c * 1000000

X

GK

, Y

GK

- współrzędne Gaussa-Krügera

m

0

= 0.999923

c = L

0

/ 3 - cecha strefy wynosząca dla kolejnych stref

odpowiednio: 5, 6 , 7, 8
L

0

- długość południka osiowego strefy w stopniach

Przyjęta skala na południku środkowym każdej strefy oznacza, że
zniekształcenia odwzorowawcze na tym południku wynoszą -7.7
cm/km. Na styku sąsiednich stref w obszarze Polski wynoszą one
maksymalnie ok. + 7 cm/km. Układ 2000 jest przeznaczony dla map
gospodarczych wielkoskalowych.

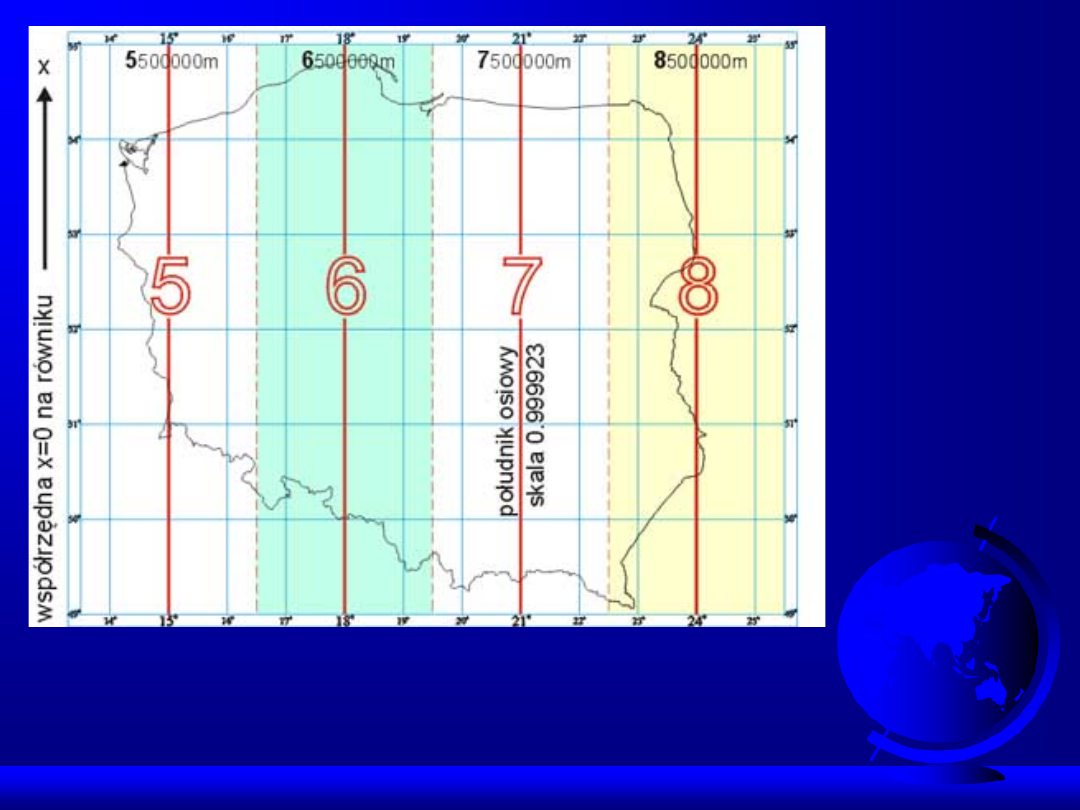
Układ 2000

PROJEKTOWANIE I GEODEZYJNE OPRACOWANIE

PROJEKTU INWESTYCJI

Zadaniem opracowania projektu i jego geodezyjnego opracowania
jest jednoznaczne określenie położenia jego elementów
w ustalonym układzie odniesienia.

Projekty inwestycji pod kątem ich geodezyjnego
opracowania możemy podzielić na dwie grupy:

- obejmujące zespoły obiektów

- plany zagospodarowania przestrzennego,
- plany realizacyjne osiedli mieszkaniowych,
- plany generalne zakładów przemysłowych,
- projekty szlaków komunikacyjnych.

- pojedynczych obiektów

- budynki,
- mosty wiadukty,

- wielkie maszyny.

Projektowanie i geodezyjne opracowanie inwestycji powinno
uwzględniać hierarchię elementów geometrycznych.

Analiza geometryczna projektu powinna obejmować;

- układ elementów głównych i podrzędnych,
- powiązania elementów projektowych z elementami

istniejącymi

- wymiary ustalone w projekcie i ich wzajemna zgodność,
- tolerancję wymiarów.

Z analizy powinny wynikać warunki:

- wzajemnej równoległości elementów,
- wzajemnej prostopadłości elementów,
- zachowania kątów,
- zachowania odległości,
- ustalone promienie krzywizny,
- normatywy budowlane (np. szerokość drogi).

Układy współrzędnych lokalnych stosowane
w geodezyjnym opracowaniu projektu

1. Układy bezwzględne

1. kartezjańskie
2. biegunowe
3. walcowe
4. sferyczne

2. Układy
względne

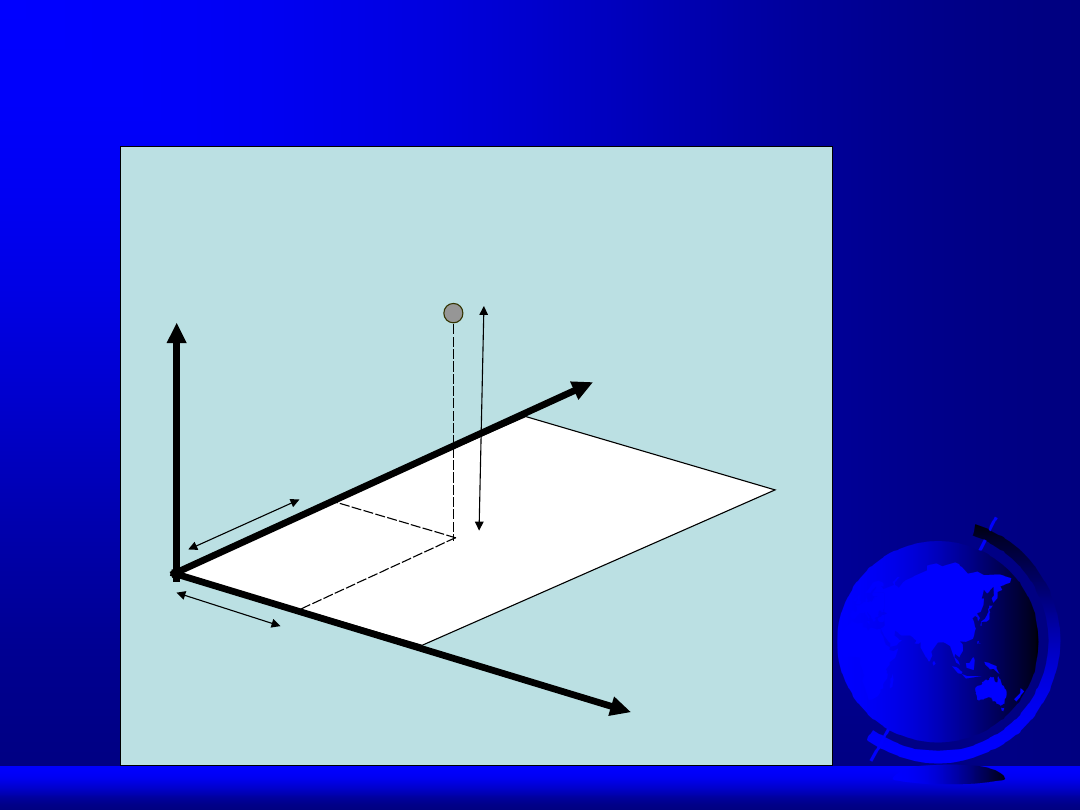
Układ kartezjański

Y

X

Z

z

x

y

P(x,y,z)

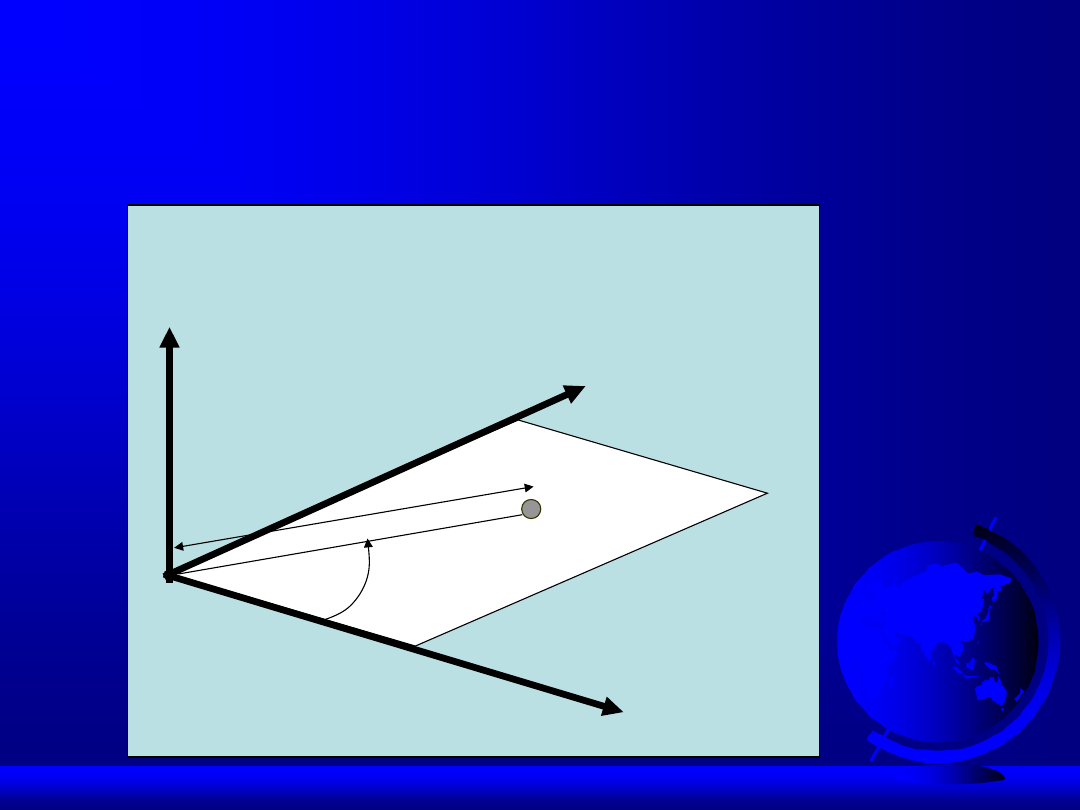
Układ biegunowy

Y

X

Z

P(d,φ)

d

φ

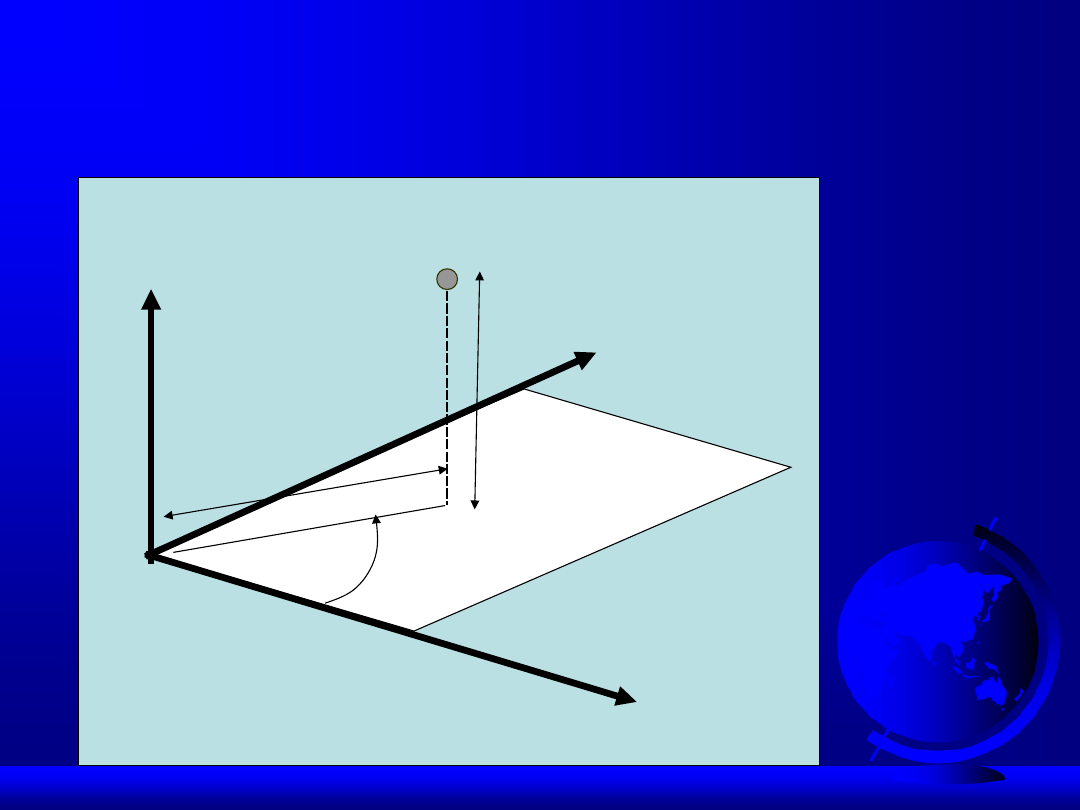
Układ walcowy

Y

X

Z

z

P(d,φ,z)

φ

d

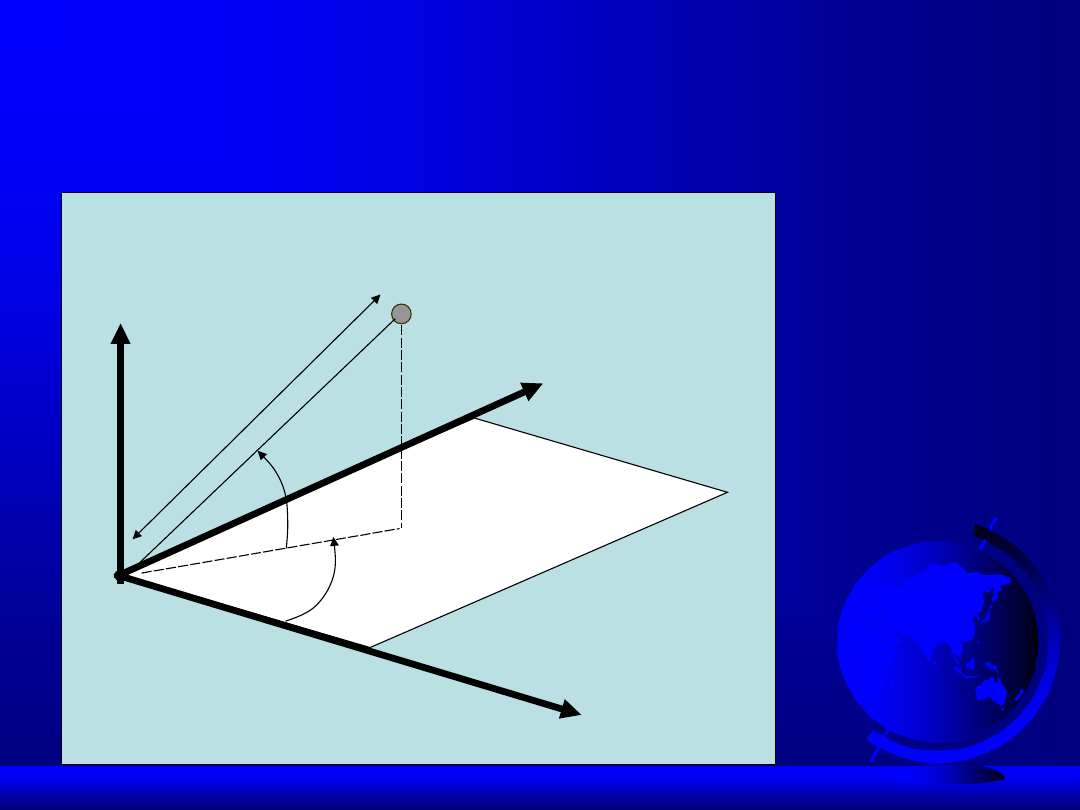
Układ sferyczny

Y

X

Z

P(d,φ,β)

φ

d

β

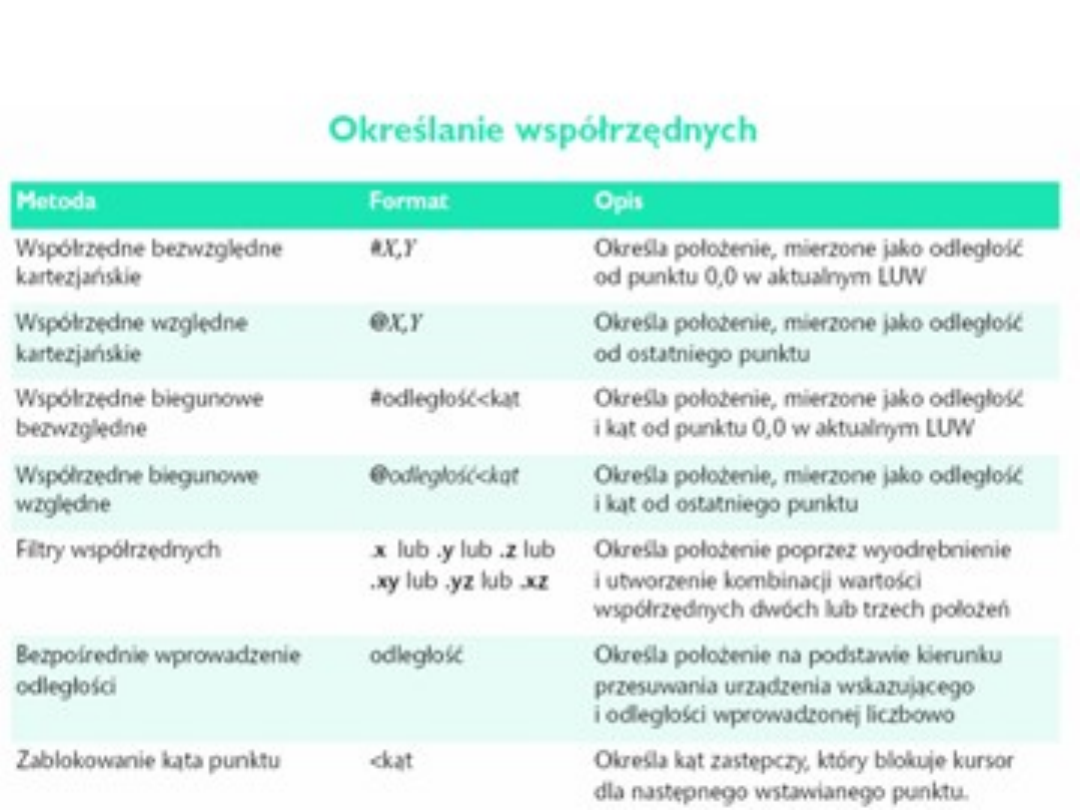
Lokalny układ współrzędnych

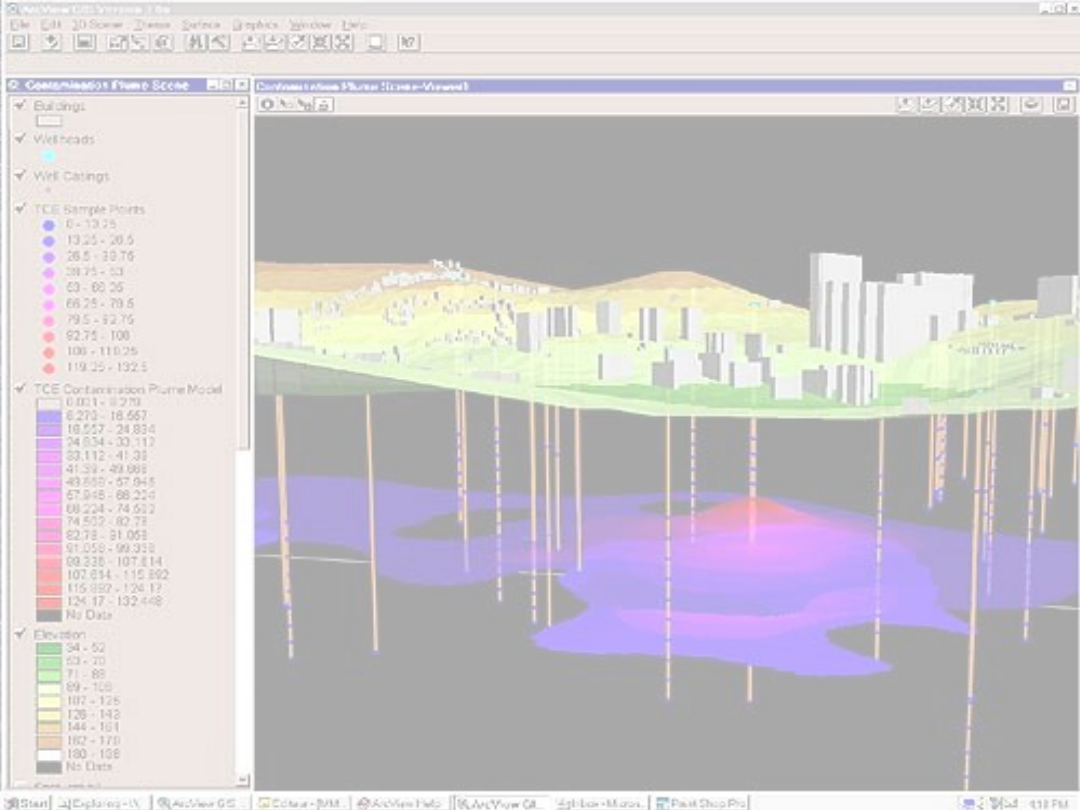
Numeryczne

modele przestrzenne

NUMERYCZNE MODELE

PRZESTRZENNE

1. wektorowy,

- prosty
- topologiczny

2. rastrowy,
3. hybrydowy.

SPOSOBY REPREZENTACJI

DANYCH PRZESTRZENNCYH

W MAPIE NUMERYCZNEJ

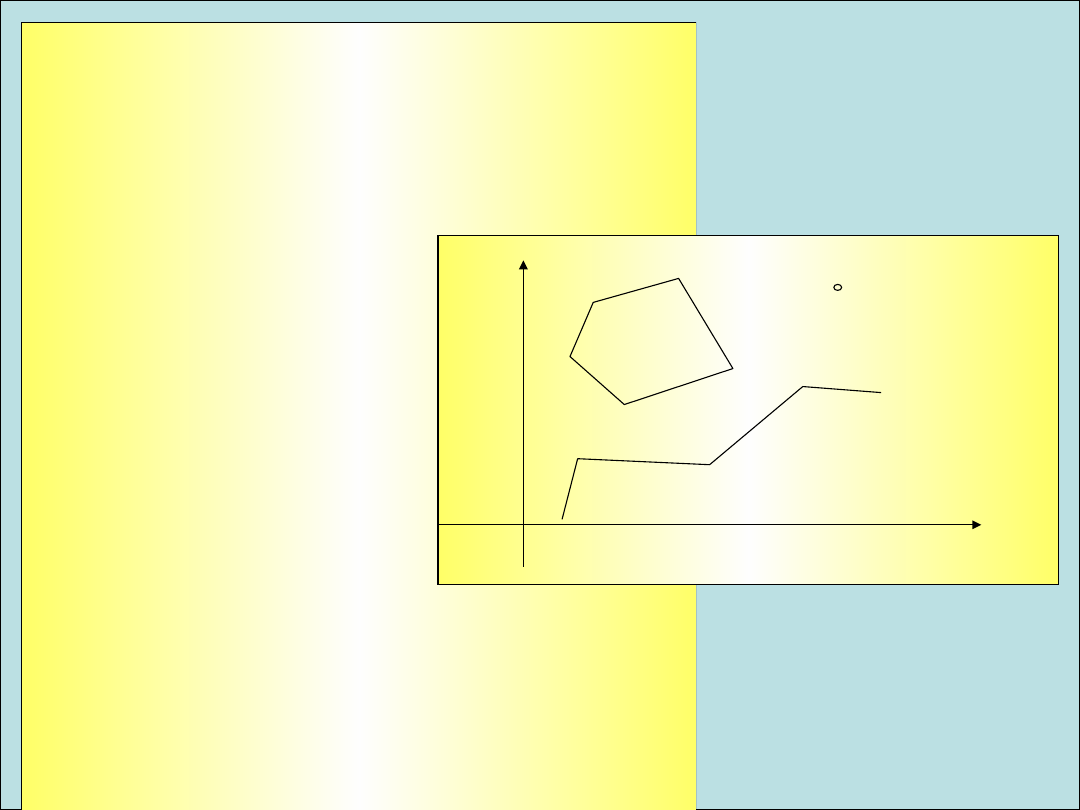
PROSTY MODEL WEKTOROWY

Model ten stanowi odtworzenie rysunku mapy,
traktowanej jako zbiór nie powiązanych ze sobą
obiektów punktowych, liniowych i
powierzchniowych.

ZALETY

- prostota,

- rozbudowane funkcje geometrii analitycznej.

WADY

- w obiektach mających elementy wspólne, część
wspólna musi
być zapisana niezależnie dla każdego obiektu,
- związki na mapie mogą być wykrywane jedynie
aparatem
geometrii analitycznej .

A(X

A

,Y

A

)

B (X

1

,Y

1

;X

2

,Y

2 .....

X

N

,Y

N

; X

1

,Y

1

)

C (X

1

,Y

1

;X

2

,Y

2

;X

3

,Y

3 .....

)

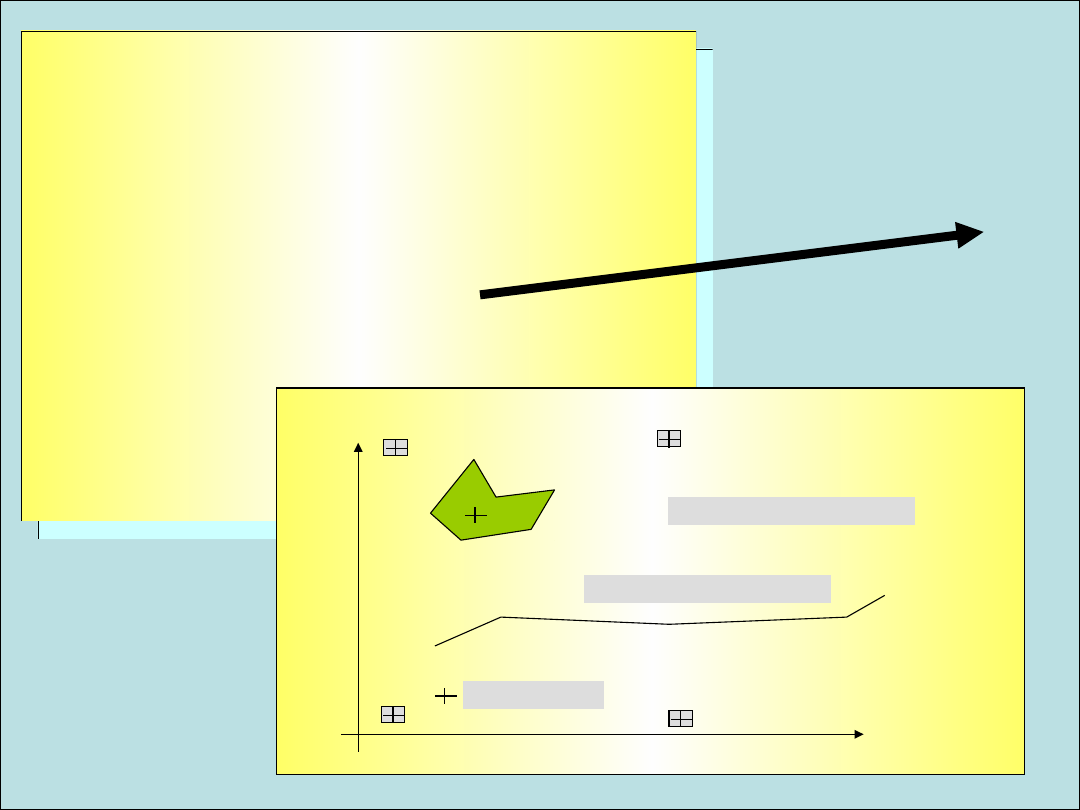
TOPOLOGICZNY MODEL

WEKTOROWY

W modelu topologicznym rozpatruje się
płaszczyznę x,y podzieloną liniami granicznymi
L

1

, L

2

, ... Na obszary P

1

,P

2

, ....

Linie graniczne nie mogą się przecinać i łączą
punkty zwane węzłami W1, W2, ...

ZALETY

- kontrola struktury rysunku,
- możliwość stosowania funkcji analiz
przestrzennych.

WADY

- duża złożoność.

TOPOLOGICZNY MODEL

WEKTOROWY

W modelu topologicznym rozpatruje się
płaszczyznę x,y podzieloną liniami granicznymi
L

1

, L

2

, ... Na obszary P

1

,P

2

, ....

Linie graniczne nie mogą się przecinać i łączą
punkty zwane węzłami W1, W2, ...

ZALETY

- kontrola struktury rysunku,

- możliwość stosowania funkcji analiz
przestrzennych.

WADY

- duża złożoność.

Poligon

Punkt

L1,WP,WK,PL,PP ....

X,Y

W

Linia

WP,WK,L1 WP, WK, L2.

L

i

P

L

P

p

W

p

W

k

Obraz rastrowy

Obraz zapisany w postaci rastrowej stanowi układ barwnych
(lub czarnych i białych) punktów — pikseli, wypełniających obszar,
zwykle o kształcie prostokąta.

 

Sposób numeracji zgodny z numeracją pól
macierzy.

Zapis w formie [X,Y] gdzie:
X - numer kolumny.
Y - numer wiersza.

Każda komórka macierzy przechowuje liczbę określającą wartość koloru.
Np.: Przyjmując paletę kolorów o 256 odcieniach szarości, numerowanych 0 - 255:

 

Przykładowe wartości

kolorów:

 

 

- 1 bitowe - 0 lub 1 (obrazy czarno-białe);
- 4 bitowe - 0 - 15 (16 kolorów lub odcieni szarości);
- 8 bitowe - 0 - 255 (256 kolorów lub odcieni szarości);
- 10 bitowe - 0 - 1023 (1024 kolorów lub odcieni
szarości);
- 12 bitowe - 0 - 4095 (4096 kolorów lub odcieni
szarości);
- 16 bitowe - …

 
 

Przekształcenia geometryczne

Przekształcenia geometryczne są często wykorzystywane w obróbce
obrazów cyfrowych szczególnie w przypadku wyeliminowania zniekształceń
geometrycznych oraz w przypadku dopasowania obrazu do układu
współrzędnych jaki został mu przyporządkowany

Przesuwanie obrazu
Najprostszym przekształceniem geometrycznym jest przesunięcie obrazu.
Przesunięcie to polega na zmianie współrzędnych każdego z pikseli obrazu
o określoną wartość zgodnie z zależnością:
X

W

=X

P

+WP

Y

W

=Y

P

+WP

Skalowanie obrazu
Innym, ważnym przekształceniem geometrycznym obrazu jest
skalowanie obrazu. Skalowanie odbywa się poprzez pomnożenie
współrzędnych obrazu przez współczynnik skalowania, zgodnie ze wzorem:
X

W

=X

P

*WS

Y

W

=Y

P

*WS

Obracanie obrazu
X

W

=X

P

*cos( ) - Yo*sin( )

Y

W

=X

P

*sin() + Yo*cos( )

 

Wpasowanie obrazu

Proces wpasowania obrazu przebiega kilkuetapowo.
- wybór układu współrzędnych docelowych
- zdefiniować odpowiednią ilość punktów dostosowania
- wybór odpowiedniej metody przekształcenia obrazu i przetestowanie jej
skorygowanego obrazu oraz jego przetestowanie według wybranej metody.

Jako wskaźnik dokładności transformacji przyjmuje się średni błąd kwadratowy
obliczany na podstawie rzeczywistych wartości wprowadzonych punktów
kontrolnych, oraz wartości tych samych punktów obliczonych poprzez
transformację. Błąd ten oblicza się według zależności:



 



2

2

w

o

w

o

w

y

y

x

x

m







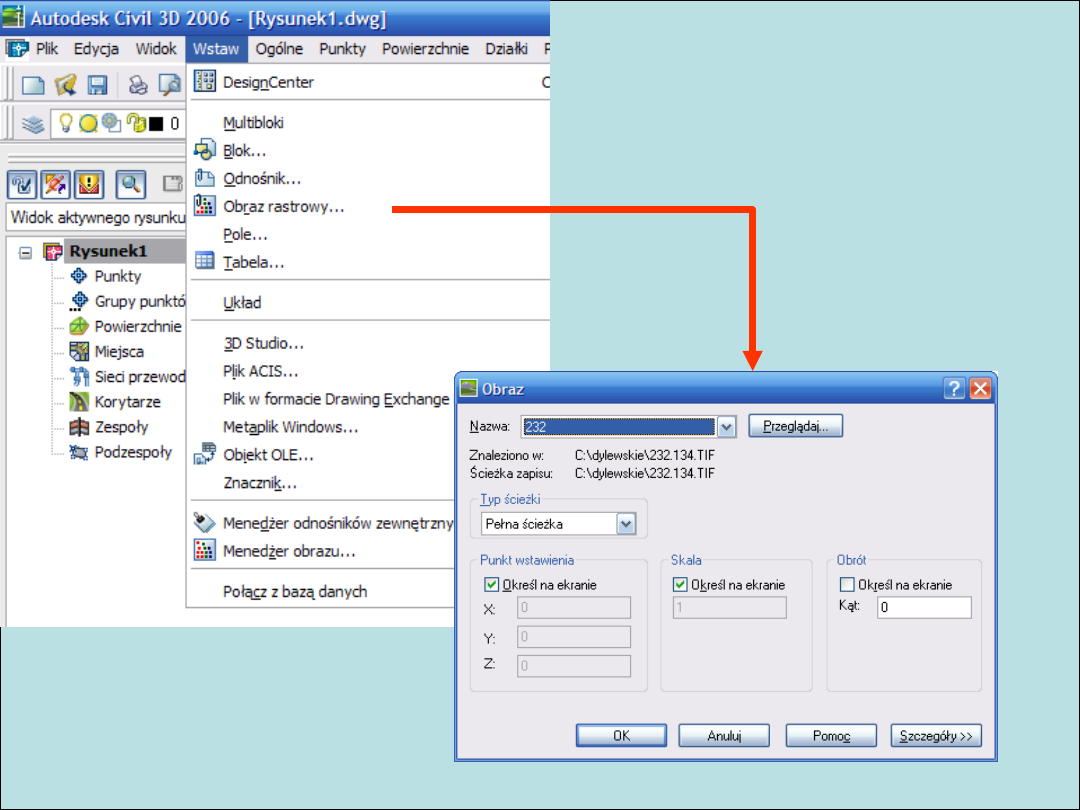
Wczytanie obrazu rastrowego

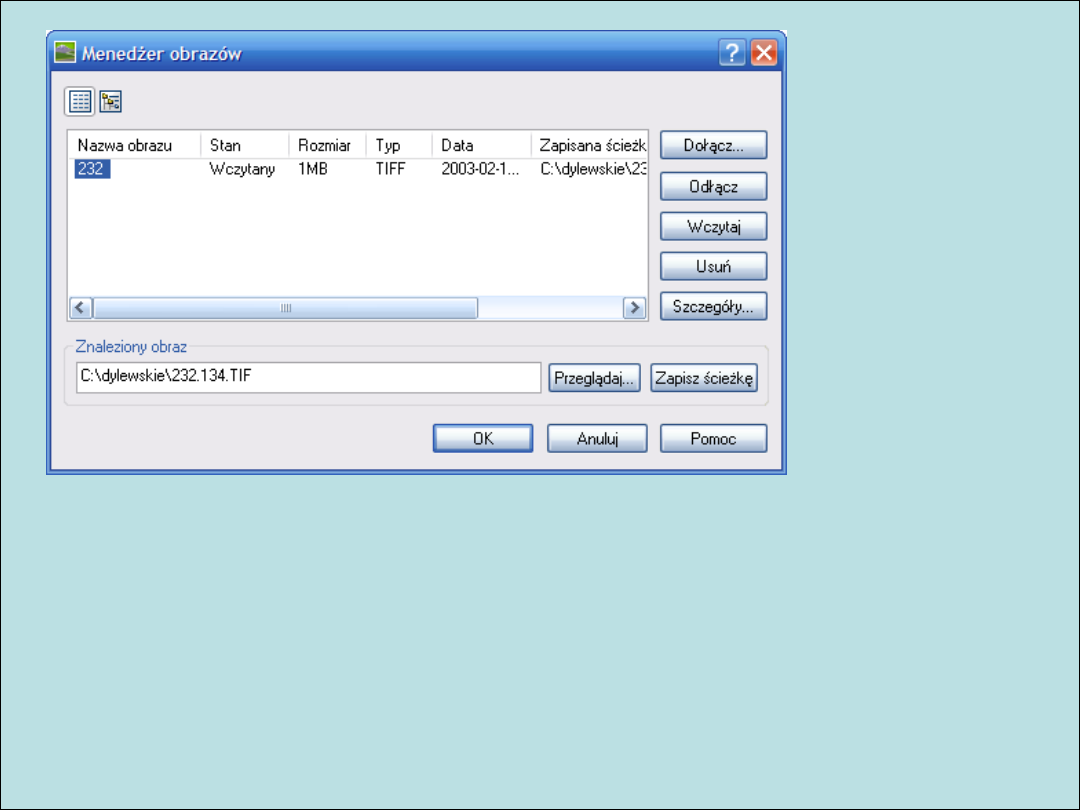
Menadżer obrazów rastrowych