POŁĄCZENIA GWINTOWE I
ŚRUBOWE
• Linia śrubowa i zarys gwintu
• Cechy geometryczne gwintu
• Rodzaje złączy gwintowych
• Połączenia śrubowe
• Zależność między siłą obciążającą nakrętkę
a siłą obracającą nakrętkę
• Sprawność gwintu (mechanizmu śrubowego)
• Warunek samohamowności gwintu
• Wytrzymałość gwintu
• Optymalny stan obciążenia śruby
• Wytrzymałość połączeń śrubowych
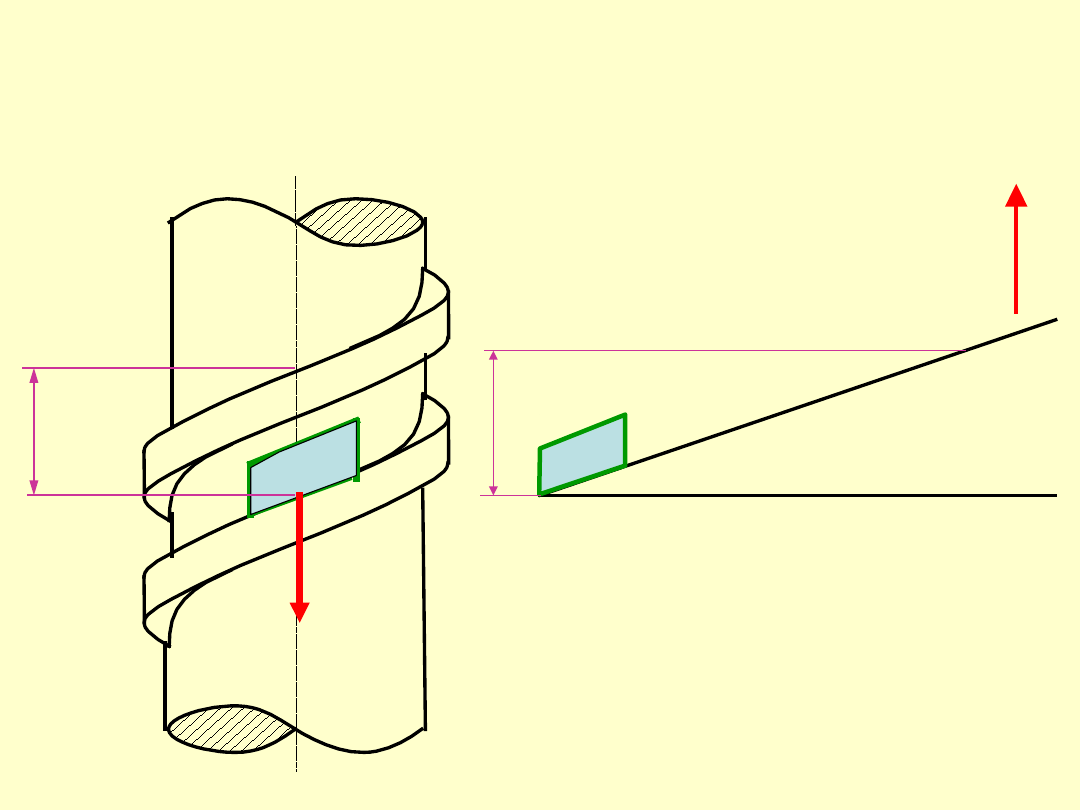
Linia śrubowa walcowa jest to tor punktu
wykonującego ruch obrotowy w
płaszczyźnie przesuwającej się w
kierunku prostopadłym do tej
płaszczyzny.
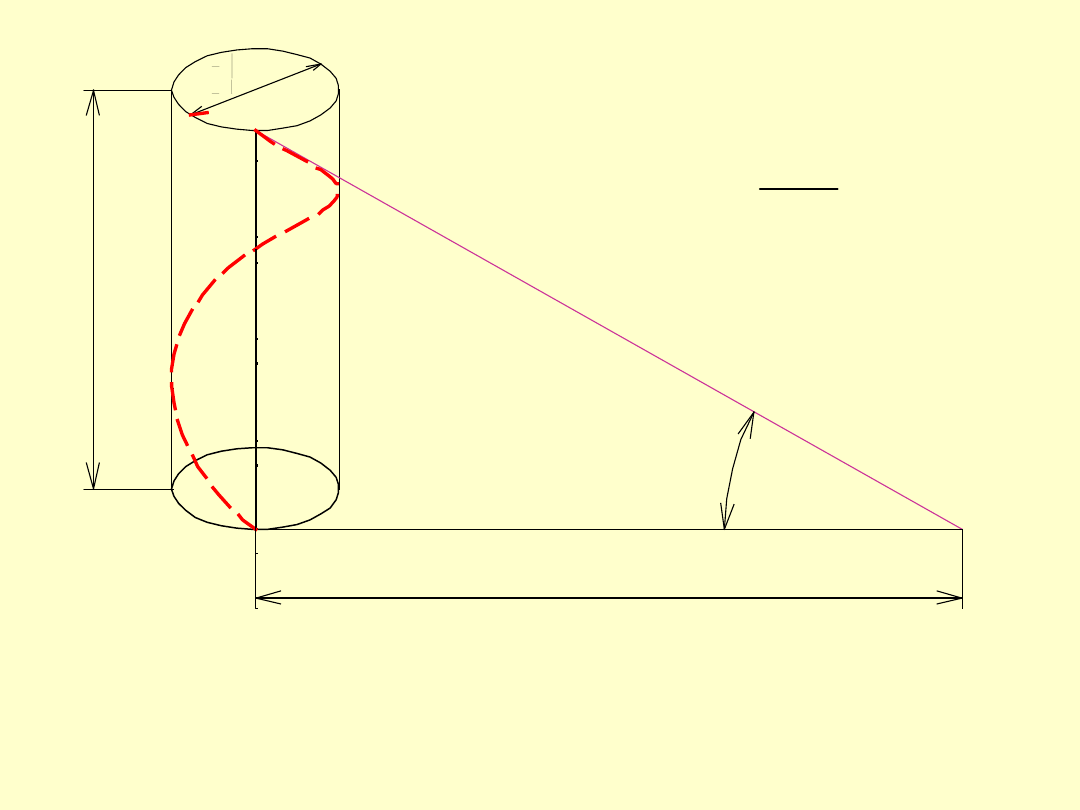
Linia śrubowa wynika z nawinięcia
trójkąta prostokątnego na
walec
.
h
d
d
d
h
tg
Zależnie od kierunku ruchu obrotowego
linia śrubowa może mieć gwint lewy lub
prawy.
Jeżeli podczas obrotu figury płaskiej
(trójkąta, prostokąta, trapezu, koła) jej
płaszczyzna stale przechodzi przez oś
obrotu, a jej punkty zakreślają walcowe
linie śrubowe to powstaje bryła zwana
gwintem.
Tworząca figura płaska nosi nazwę zarysu
gwintu.
Gwint jest ograniczony powierzchnią
śrubową powstałą przy ruchu jego zarysu
oraz powierzchnią walcową.
Jeżeli powierzchnia śrubowa ogranicza
gwint:
od zewnątrz to nazywamy go
zewnętrznym (śrubą),
od wewnątrz to nazywamy go
wewnętrznym (nakrętką).
Zależnie od kształtu zarysu rozróżnia się
gwinty:
trójkątne,
prostokątne,
trapezowe,
kołowe.
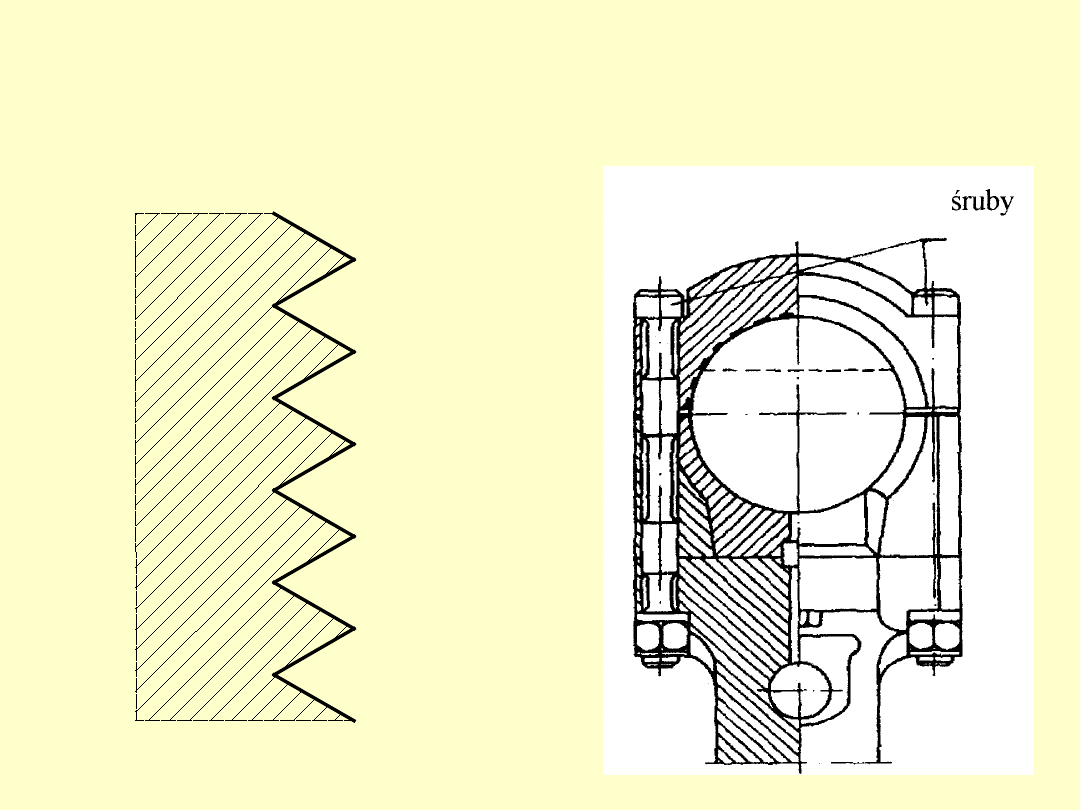
Zarys gwintu trójkątny najczęściej
stosowany jest w śrubach złącznych.
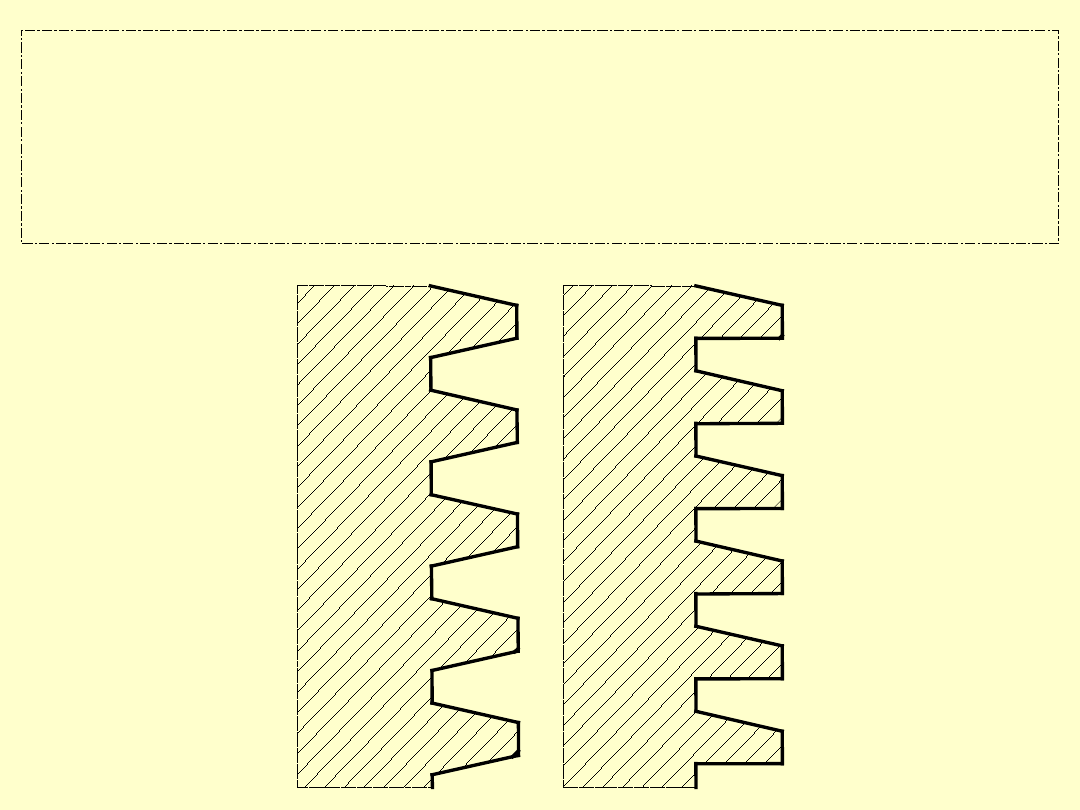
Rozróżnia się dwa rodzaje zarysów gwintu
trapezowego:
symetryczny,
niesymetryczny.
Zarys gwintu trapezowego symetrycznego
stosowany jest w mechanizmach śrubowych
przy działaniu dużych obciążeń dwustronnych,
np. ściągi śrubowe want.
Zarys gwintu trapezowego nie symetrycznego
stosowany jest w mechanizmach śrubowych
przy działaniu dużych obciążeń
jednostronnych, np. podnośniki.
Zarys gwintu prostokątny stosowany jest
w mechanizmach śrubowych do zamiany
ruchu obrotowego na posuwisty
przypadku, gdy wymagana jest duża
dokładność posuwu, np. napędu suportu
w tokarkach.
Gwint prostokątny ze
względu na trudności
wykonawcze i zmniejszoną
wytrzymałość, w porównaniu
do trapezowego, jest rzadko
stosowany.
Zarys gwintu kołowy stosowany jest w
urządzeniach poddanych obciążeniom
dynamicznym, np. złącza wagonów
kolejowych.
Podziałką gwintu h
z
nazywa się odległość
sąsiednich zarysów mierzoną wzdłuż osi
gwintu.
Skokiem gwintu
(zarysu) nazywa się
przesuniecie zarysu zwoju wzdłuż osi po
pełnym jego obrocie.
Skok może być równy podziałce
(
h = h
z
),
wtedy gwint jest jednokrotny, lub stanowi
jej krotność
(
h = zh
z
), wtedy gwint jest
wielokrotny.
.
Rozpatrując połączenie śruby ze
współpracującą z nią nakrętką rozróżnia
się następujące charakterystyczne
wielkości:
średnicę nominalną śruby
d
średnicę podziałową śruby
d
p
średnicę rdzenia
d
r
średnicę nominalną nakrętki
D
średnicę otworu
D
o
średnicę podziałową nakrętki
D
p
średnicę roboczą gwintu
d
s
przy czym
d
s.
=0,5(D
o
+d)
oraz
D
p
= d
p
śruba
nakrętk
a
d
d
p
d
r
t
n
D
D
p
D
o
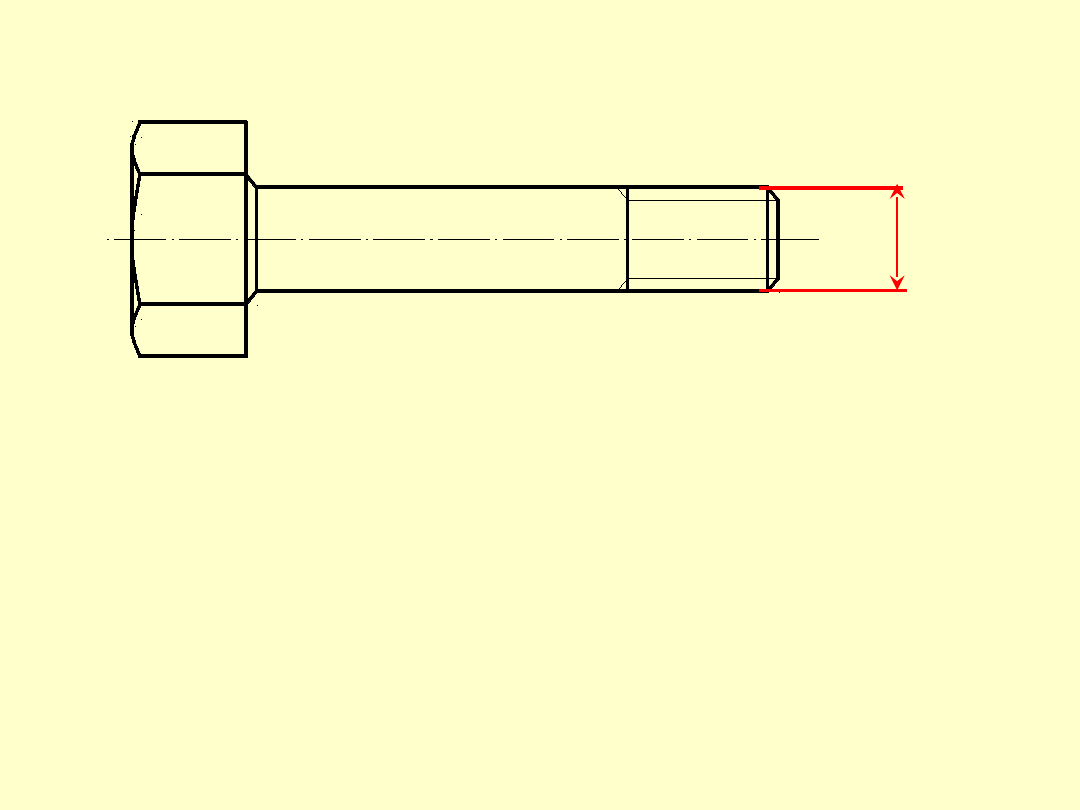
M16
Liczba podana przy oznaczeniu
gwintu zawsze oznacza średnicę
nominalną
d
śruby, tj. średnicę
zewnętrzną zarysu gwintu
Wszystkie gwinty poza prostokątnym są
znormalizowane, a więc znoramalizowane są
ich średnice nominalne d i podziałki h
z
.
Wszystkie inne wymiary zarysu gwintu są
uzależnione od podziałki.
W każdym rodzaju gwintów rozróżnia się
podstawowy szereg gwintów normalnych
zwykłych, w których średnica nominalna d jest
skojarzona z pewną podziałką.
W przypadku gdy z dana średnicą jest
skojarzona podziałka mniejsza niż w gwincie
zwykłym, to mamy do czynienia z gwintem
drobnozwojowym; w przypadku przeciwnym
grubozwojowym.
Rodzaje złączy gwintowych
bezpośrednio wkręcane, np.
smarowniczki w łożyskach
ślizgowych,
rurowe, np.. złączki rurowe,
złącza śrubowe.
Połączenia śrubowe
W zależności od postaci konstrukcyjnych
rozróżnia się połączenia :
śrubowe,
szpilkowe,
wkrętowe.
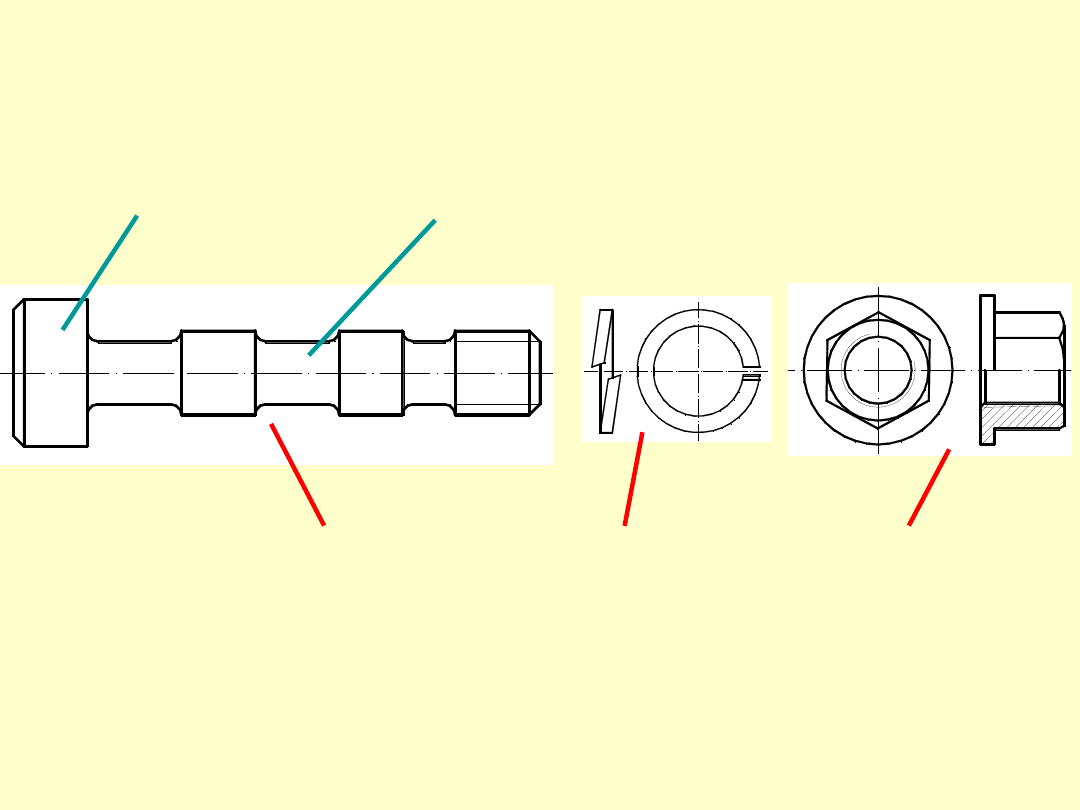
podkładka
nakrętka
śruba
łeb
śruby
trzpień
śruby
Elementy połączenia
śrubowego
szpilka
Zależność między siłą
obciążającą nakrętkę a siłą
obracającą nakrętkę
Wyznaczenie takiej zależności pozwala na:
obliczenie siły (momentu) niezbędnego
do dokręcenia nakrętki,
obliczenie siły (momentu) niezbędnego
do odkręcenia (poluzowania) nakrętki,
obliczenie strat tarcia na gwincie.
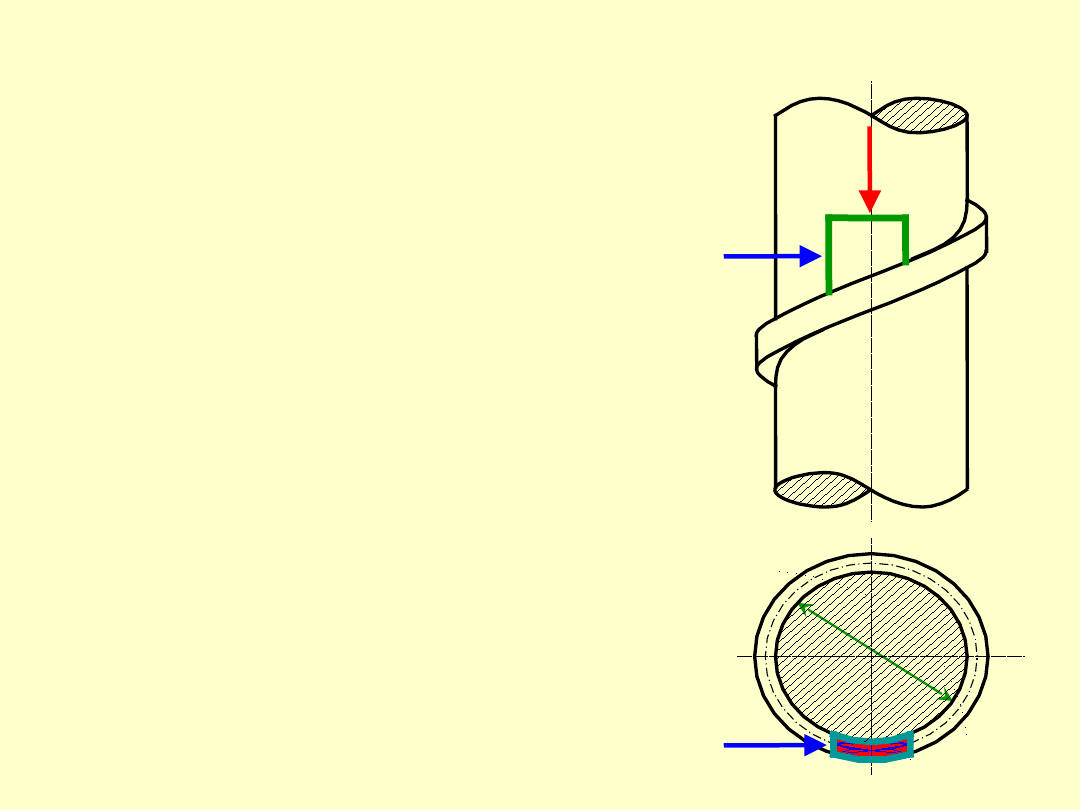
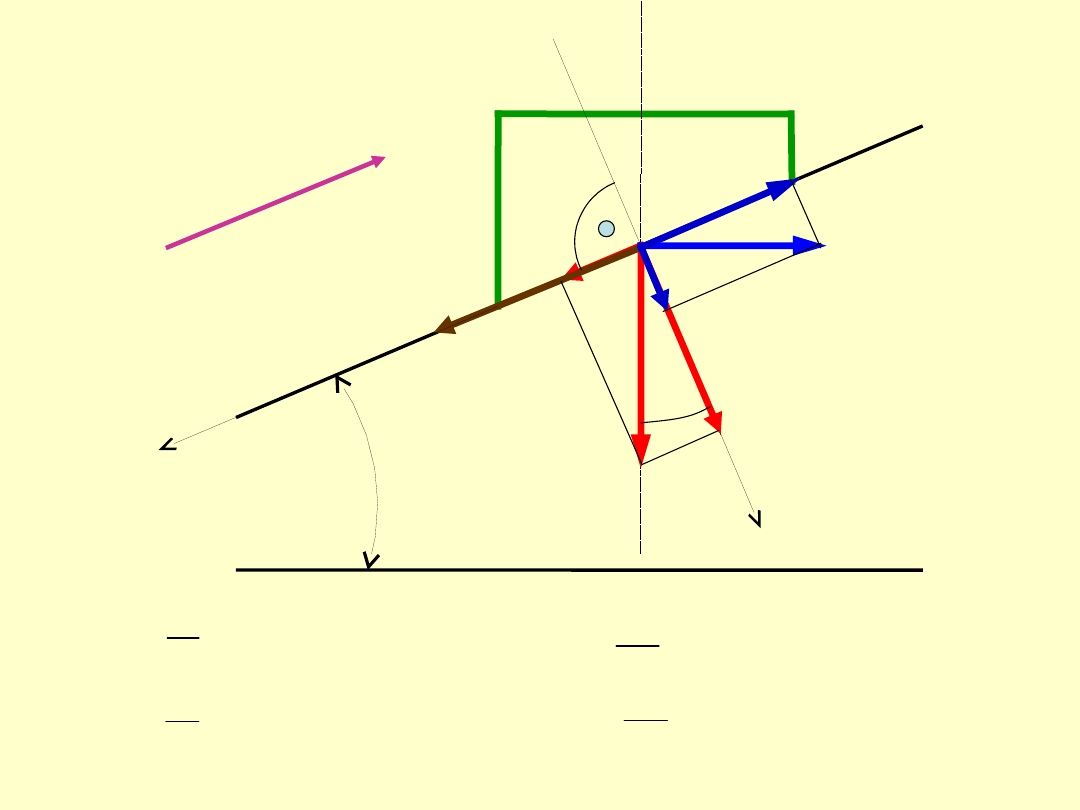
Zależność między siłą
obciążającą nakrętkę a
siłą obracającą nakrętkę
„wyznacza się analizując
wycinek nakrętki.
W tym celu rozważa się
ruch nakrętki jako ruch
klocka po równi pochyłej.
Klocek obciążony jest
siłami:
obciążającą nakrętkę
P
,
obracającą nakrętkę
H
.
P
H
H
P
H
y
x
P
x
P
y
H
x
H
y
ruc
h
kloc
ka
T
sin
sin
P
P
P
P
x
x
cos
cos
P
P
P
P
y
y
sin
sin
H
H
H
H
y
y
cos
cos
H
H
H
H
x
x
Warunek równowagi dla klocka
znajdującego się na równi pochyłej:
0
x
x
H
P
T
(1)
Wiemy jednak, że:
N
T
zaś
y
y
H
P
N
oraz
sin
P
P
x
cos
P
P
y
cos
H
H
x
sin
H
H
y
Wówczas warunek (1) można zapisać
następująco:
0
cos
sin
sin
cos
H
P
H
P
Przemnażając pierwszy człon równania
przez
:
0
cos
sin
sin
cos
H
P
H
P
oraz grupując człony z
P
i
H
, otrzymujemy:
sin
cos
sin
cos
P
P
H
H
Wyciągając
H
i
P
przed nawiasy,
otrzymujemy:
Po przekształceniu, uzyskuje się
zależność:
sin
cos
sin
cos
P
H
sin
cos
sin
cos
P
H
Dzieląc obie części ułamka przez
cos
,
otrzymuje się:
Z tematu dotyczącego kąta tarcia
wiemy, że:
tg
1
tg
cos
sin
cos
cos
sin
cos
P
P
H
tg
Wówczas:
Z trygonometrii szkoły średniej wiemy,
że:
tg
tg
1
tg
tg
P
H
tg
tg
1
tg
tg
tg
Ostatecznie otrzymujemy zależność
pomiędzy siłą obracającą nakrętkę
H
a
siłą ją obciążającą
P
:
Należy jednak pamiętać, że wywody te
dotyczyły ruchu klocka do góry czyli
dokręcania nakrętki siłą
H
:
tg
P
H
W przypadku luzowania nakrętki (ruch
klocka w dół po równi pochyłej
uzyskujemy zależność:
Ogólnie można zapisać zależność
między siłami
H
i
P
jako:
tg
P
H
tg
P
H
‘
+
’ dokręcanie nakrętki; ‘
’ odkręcanie
nakrętki:
Sprawność gwintu (mechanizmu
śrubowego)
Ogólnie sprawność dowolnego
mechanizmu (maszyny) można zapisać
jako stosunek pracy uzyskanej
L
u
do
pracy włożonej
L
w
:
w
u
L
L
Pracy uzyskana
L
u
:
P
h
h
P
Ph
L
u
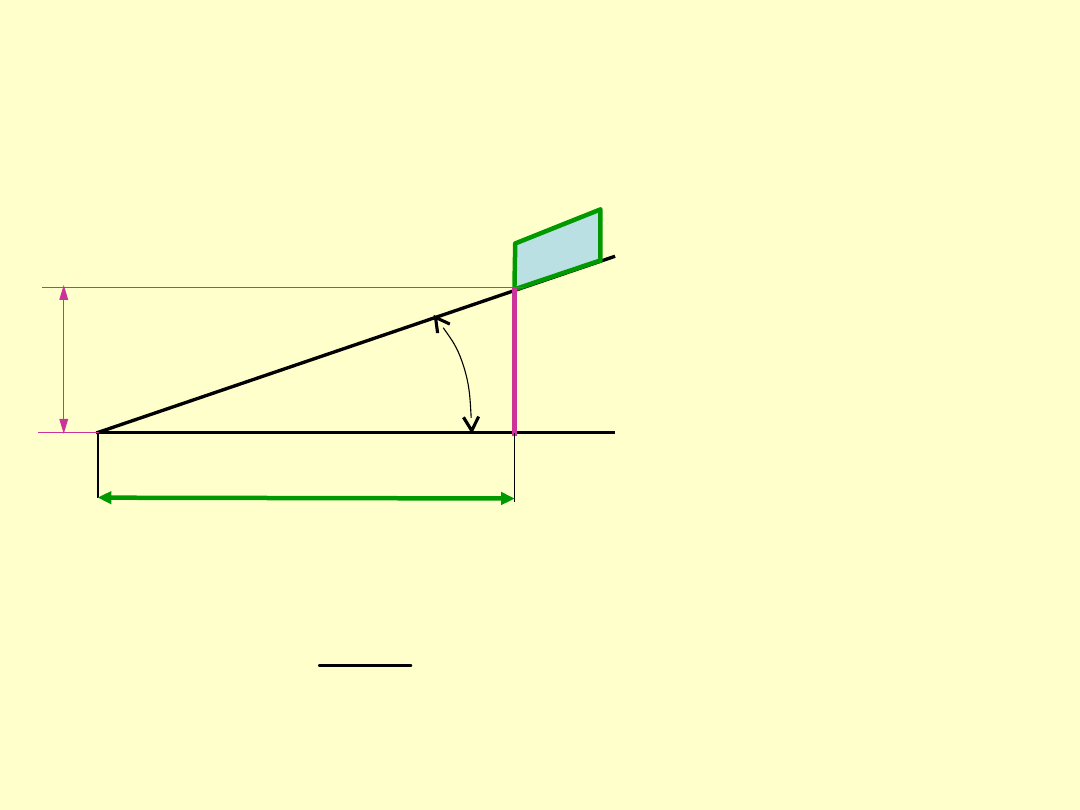
Z trójkąta prostokątnego uzyskamy
zależność:
h
d
s
tg
tg
s
s
d
h
d
h
Wówczas praca uzyskana
L
u
:
tg
s
u
d
P
L
Z mechaniki ogólnej wiemy, że pracę
włożoną
L
w
możemy wyznaczyć z
równania dynamicznego ruchu
obrotowego ciała sztywnego:
0
d
z
w
M
L
gdzie:
M
z
- moment główny sił zewnętrznych
względem osi obrotu ciała,
- kąt obrotu
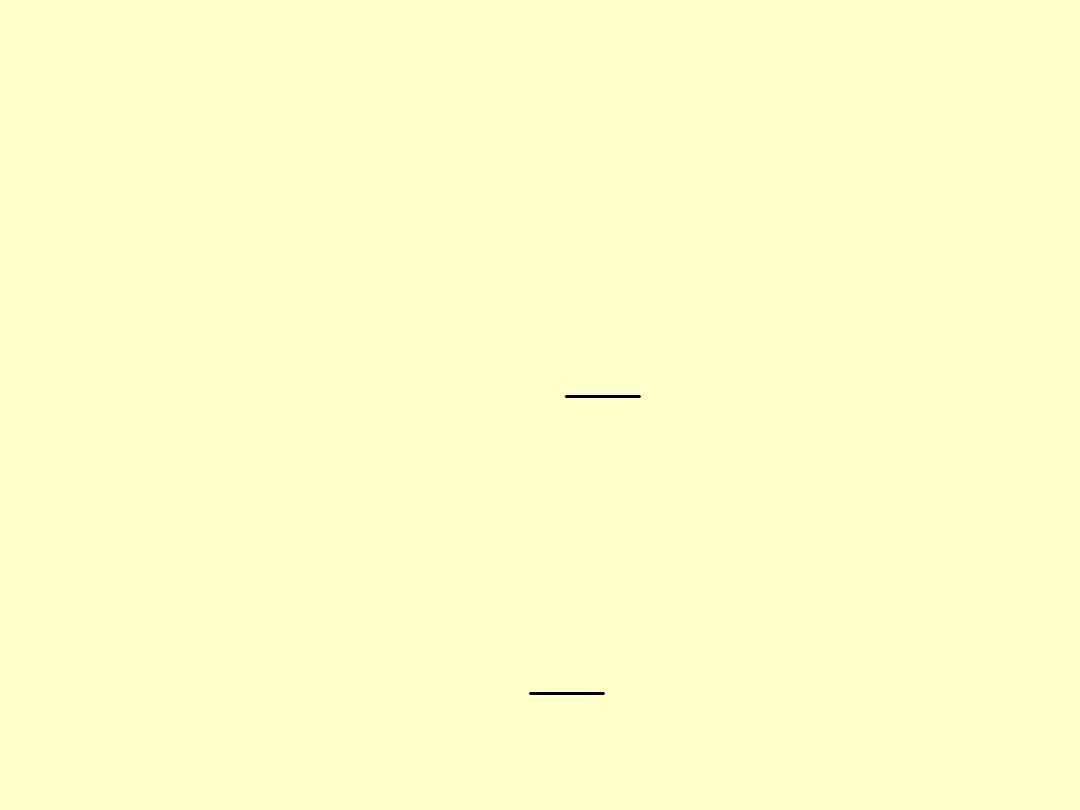
W rozważanym przypadku kąt obrotu
nakrętki wynosi
2
,
zaś moment główny sił zewnętrznych
względem osi obrotu ciała:
Po podstawieniu uzyskuje się zależność
na pracę włożoną
L
w
:
2
s
z
d
H
M
2
2
s
w
d
H
L
Z poprzednich rozważań wiemy jednak,
że:
Wówczas:
s
w
d
P
L
tg
tg
P
H
Ostatecznie uzyskujemy następującą
zależność na sprawność gwintu
:
s
s
w
u
d
P
d
P
L
L
tg
tg
tg
tg
Po uproszczeniu zaś:
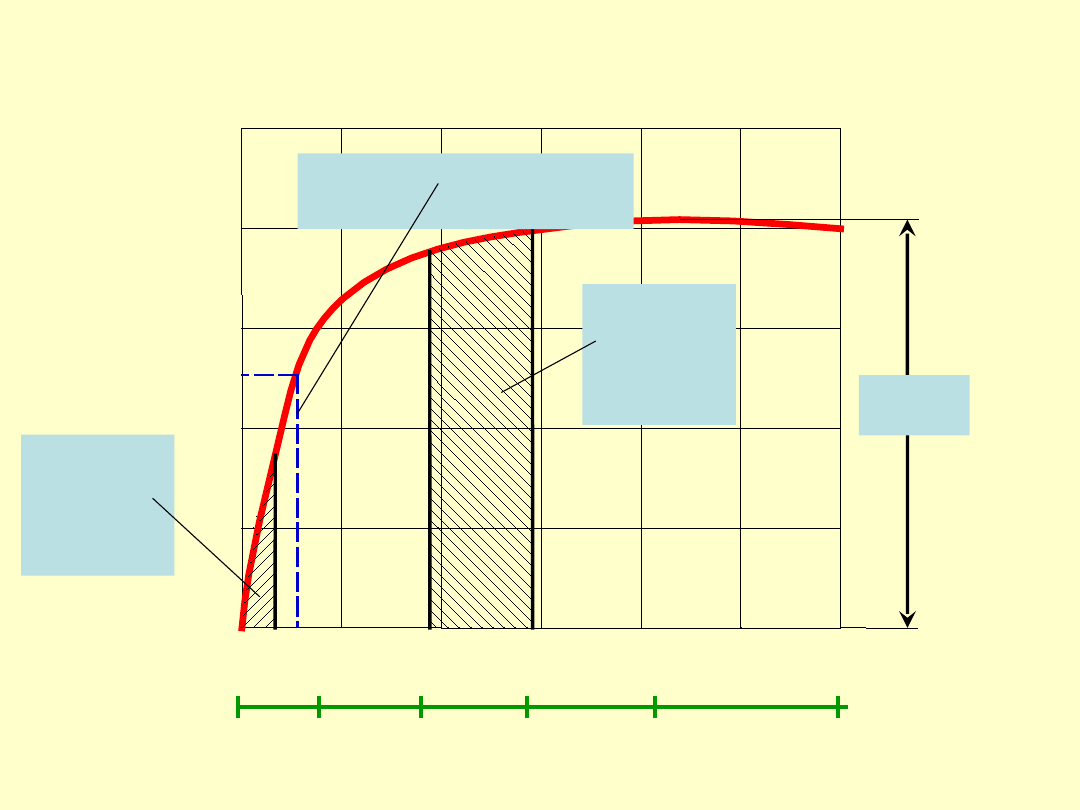
Kat przy którym sprawność
jest
największa można znaleźć z
warunku
:
0
d
d
Największą sprawność uzyskuję się dla
kąta:
2
45
opt
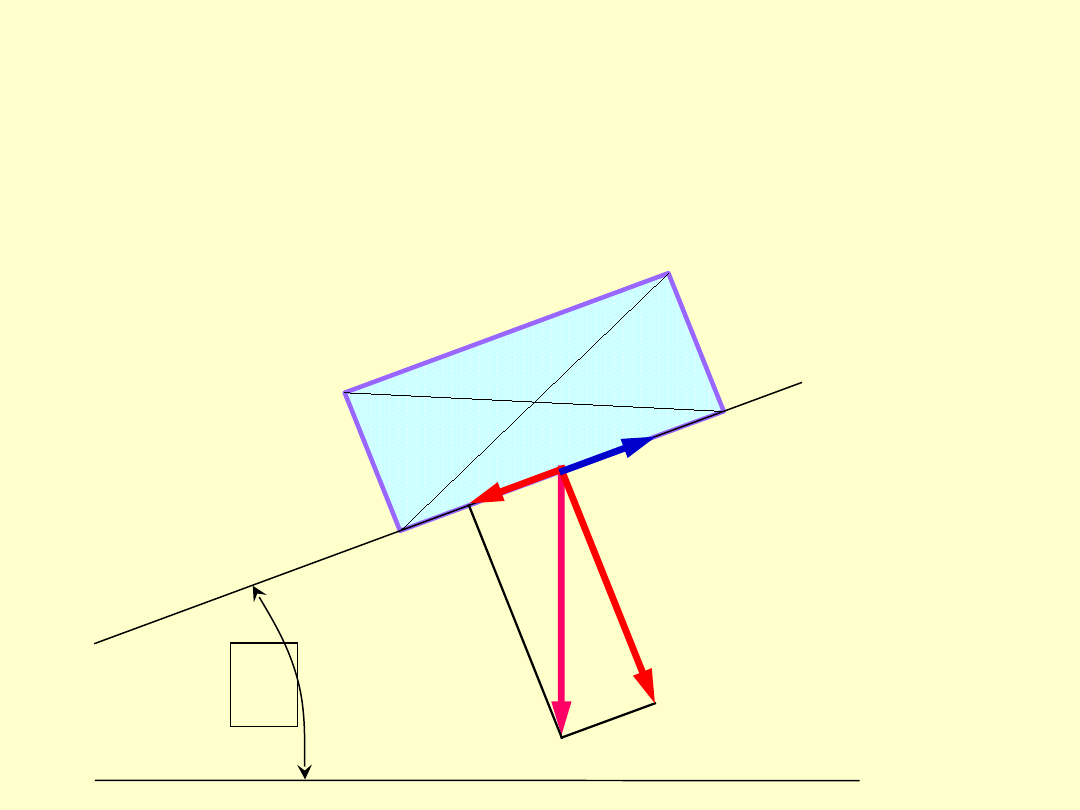
Warunek samohamowności gwintu
Rozpatrzmy przypadek zsuwania się
klocka po równi pod działaniem siły
P
:
P
P
y
P
x
T
Rozpatrzmy przy jakich warunkach siła
osiowa
P
będzie powodować zsuwanie
się klocka:
I.
If
>
then Psin>T and H>0
II. If
<
then Psin>T and H<0
Warunkiem samohamowności złącza
śrubowego jest nierówność:
Dla zrównoważenia składowej na równi
pochyłej wystarczy tylko siła tarcia
T
.
Oznacza to, że dowolnie duża siła
osiowa
P
nie jest w stanie przesunąć
klocka na równi pochyłej, czyli odkręcić
nakrętki.
Dla jej zluzowania należy odwrócić
kierunek siły
H
.
W połączeniach ze śrubami złącznymi
warunek samohamowności powinien być
spełniony, natomiast złącza ruchowe w
mechanizmach śrubowych powinny mieć
jak największą sprawność.
100
80
60
40
20
0
[%]
0,
2
0,
4
0,
6
0,
8
1,
0
1,
2
tg
max
0
10
º
20
º
30
º
40
º
50
º
kąt pochylenia gwintu
obszar
śrub
złącznyc
h
obszar
śrub
ruchowyc
h
50
granica
samohamowności
Wytrzymałość gwintu
W połączeniach gwintowych powinno się
dążyć do równomiernego rozkładu
nacisków na poszczególne zwoje gwintów.
Nie zawsze jest to możliwe do spełnienia i
przyczynami nierównomierności nacisków
mogą być:
różnice skoku w gwincie śruby i nakrętki
spowodowane niedokładnym wykonaniem,
różna sztywność (podatność) śruby i
nakrętki,
różnoimienne odkształcenia w śrubie i
nakrętce.
Równoimienność nacisków w śrubie i
nakrętce można uzyskać za pomocą
kształtowania postaci konstrukcyjnej
połączenia śrubowego.
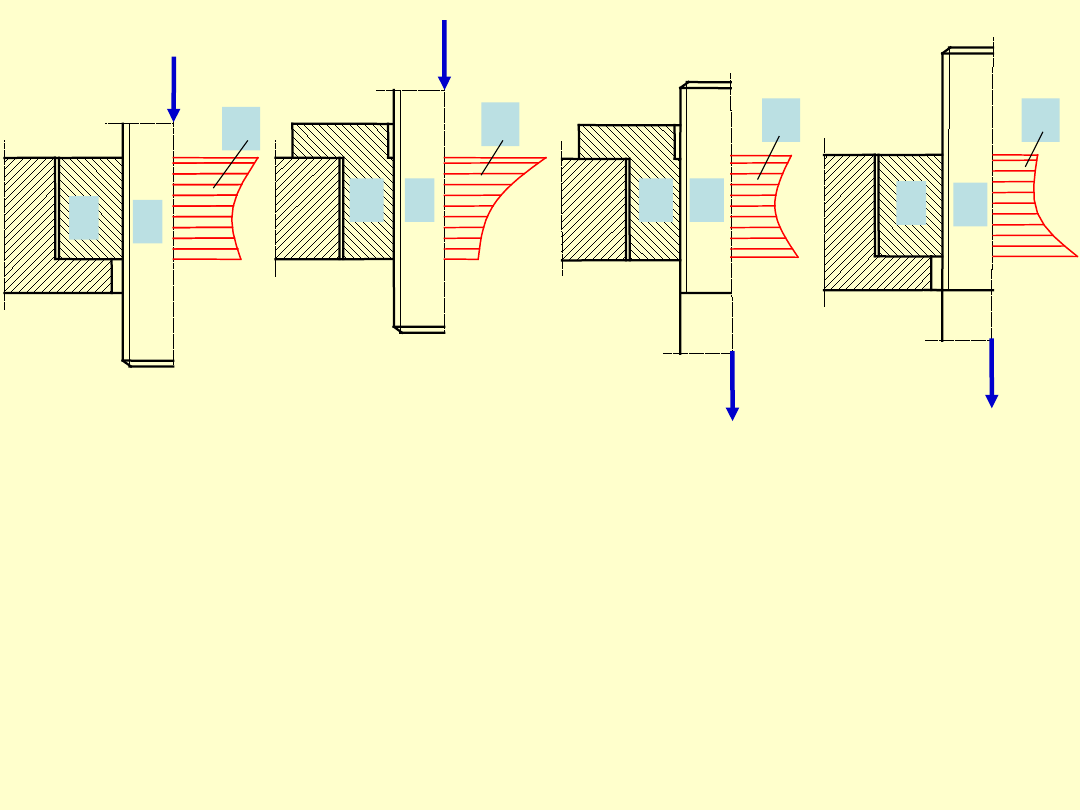
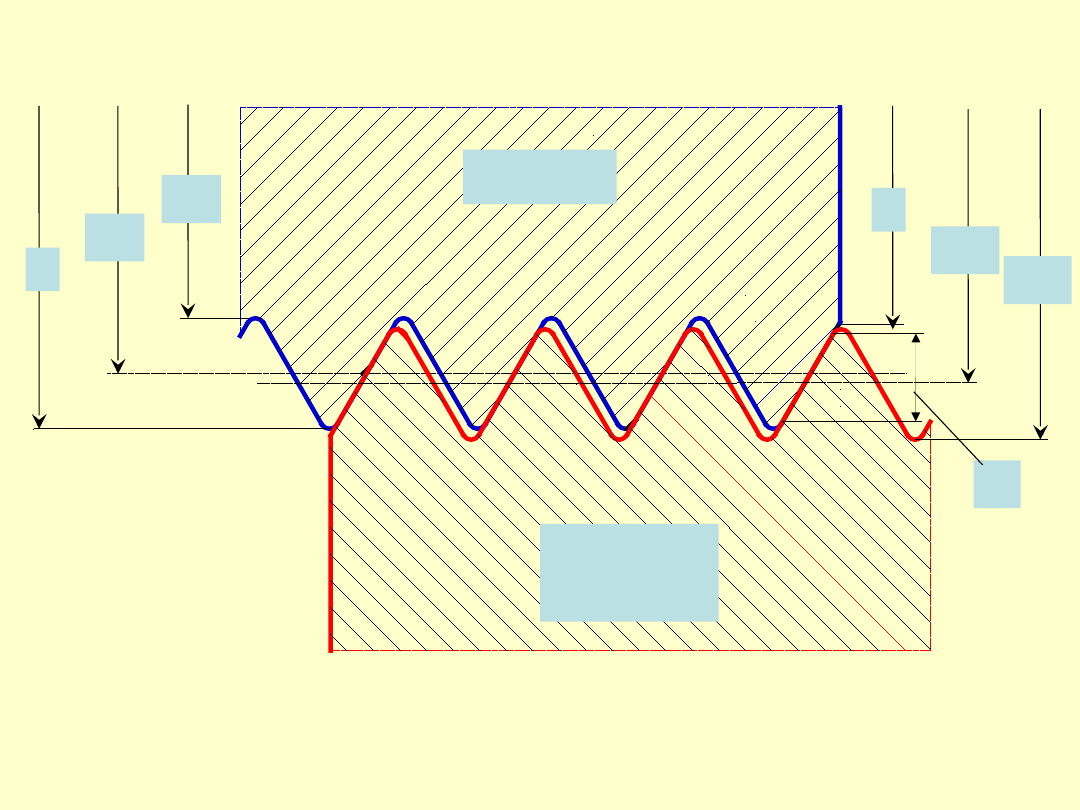
Jeżeli naprężenia w śrubie i nakrętce są
jednoimienne, a więc śruba i nakrętka są
rozciągane lub ściskane, rozkład nacisków jest
bardziej korzystny, przy czym minimum
wypada tym bliżej środka połączenia, im
bardziej zbliżone są do siebie odkształcenia obu
elementów.
P
-
-
p
p
-
+
P
P
p
+
+
P
p
+
-
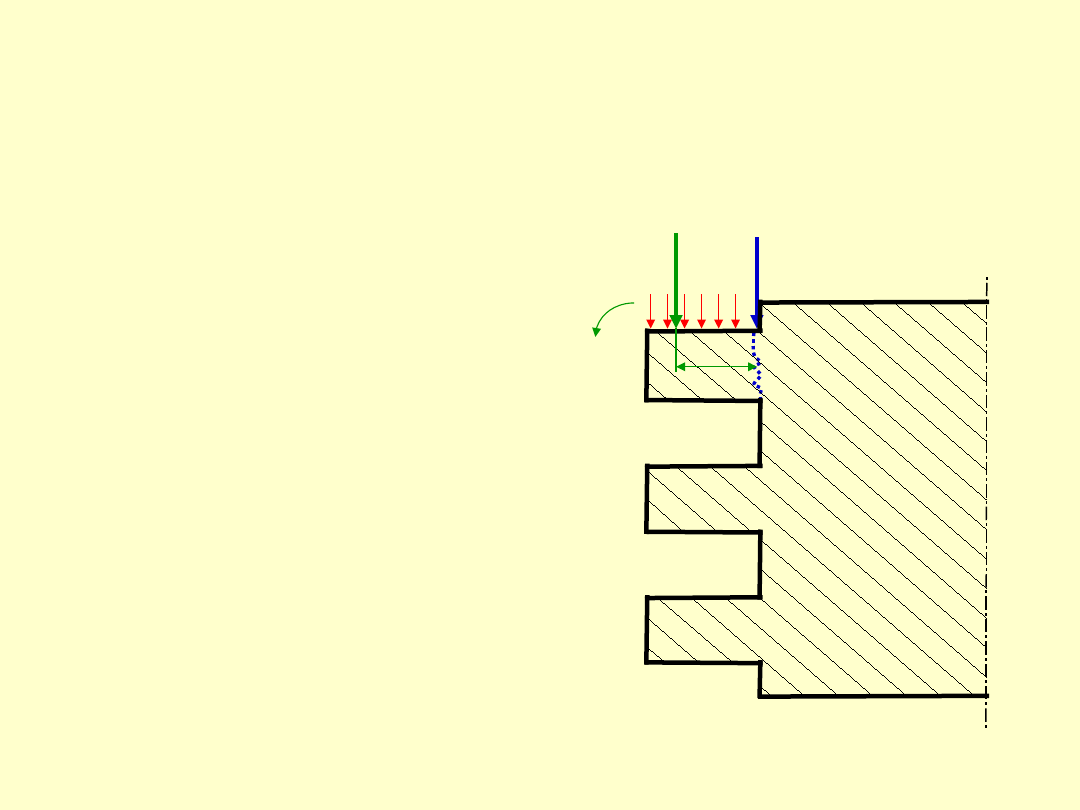
Gwint w połączeniu
śrubowym podlega
obciążeniom
złożonym, a
mianowicie jest on:
–
zginany,
–
ścinany,
–
zgniatany.
p
P
t
Wytrzymałość gwintu na naciski
powierzchniowe i ścinanie
P
g
r
M
g
Biorąc pod uwagę skomplikowany rozkład
obciążeń w połączeniu gwintowym, oblicza
się go w sposób uproszczony , zakładając
równomierność nacisków w obu
współpracujących elementach.
Z trzech rodzajów obciążeń działających na
gwint, najbardziej niebezpieczne jest
zgniatanie gwintu czyli obciążenie w postaci
nacisków powierzchniowych.
Zakłada się, że jeżeli gwint będzie
wystarczająco wytrzymały na naciski
powierzchniowe, to będzie on również
wytrzymały na pozostałe rodzaje obciążeń.
Jaka powinna być wysokość nakrętki
m
, aby przy
zadanej średnicy nominalnej śruby
d
zwoje nakrętki
były odporne na naciski powierzchniowe i nie ulegały
ścięciu.
Niech śruba będzie rozciągana siłą
P
.
W praktyce połączenie śrubowe projektuje się tak, aby
wytrzymałość gwintu na naciski powierzchniowe była
większa niż wytrzymałość rdzenia śruby na rozerwanie.
p
>
r
gdzie:
p
-
wytrzymałość gwintu na naciski powierzchniowe,
r
-
wytrzymałość rdzenia śruby na rozerwanie
Wytrzymałość
r
rdzenia śruby na rozerwanie:
r
r
k
F
P
4
2
r
d
F
Powierzchnia przekroju poprzecznego rdzenia śruby:
Stąd śruba może być obciążaną siłą:
2
4
1
r
r
d
k
P
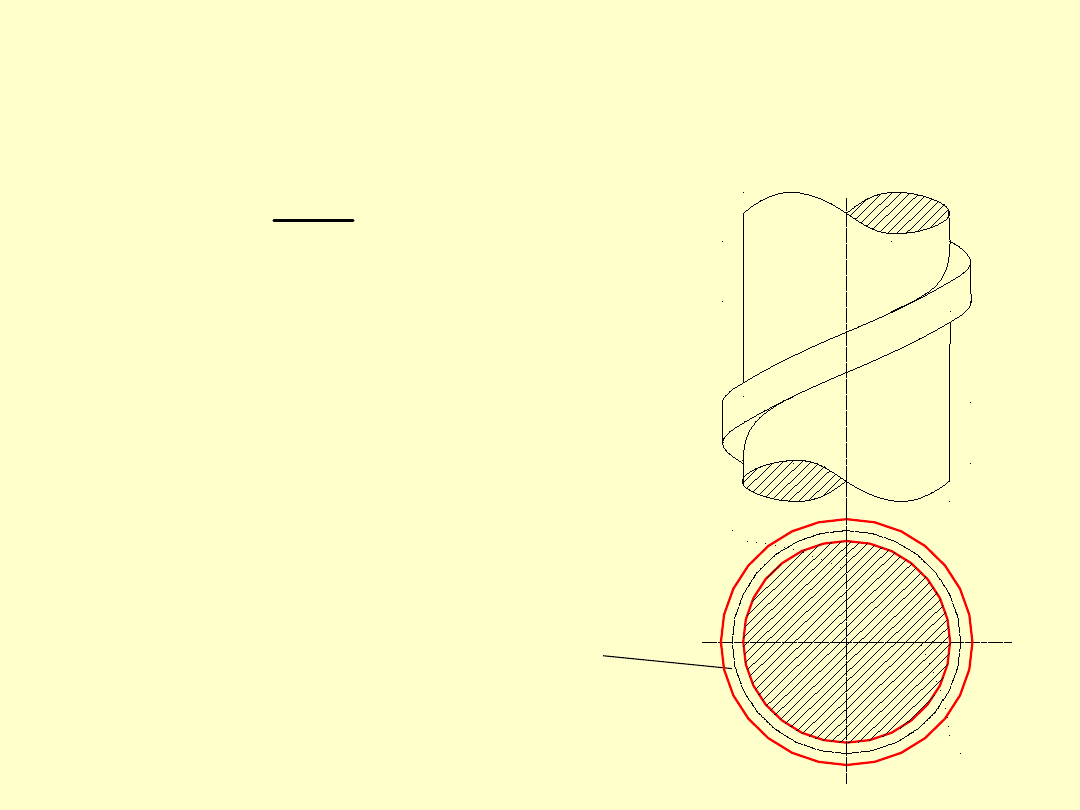
Dla tej siły powinien też być spełniony warunek na
naciski powierzchniowe:
gdzie:
F
p
- powierzchnia nacisku
jednego
zwoju
(rzut
powierzchni styku gwintu
na płaszczyznę prostopadłą
do osi śruby).
.
dop
p
p
F
P
p
F
p
Podstawiając siłę obciążającą śrubę
P
uzyskuje się:
p
dop
r
r
dop
p
r
r
F
p
d
k
p
F
d
k
2
2
4
1
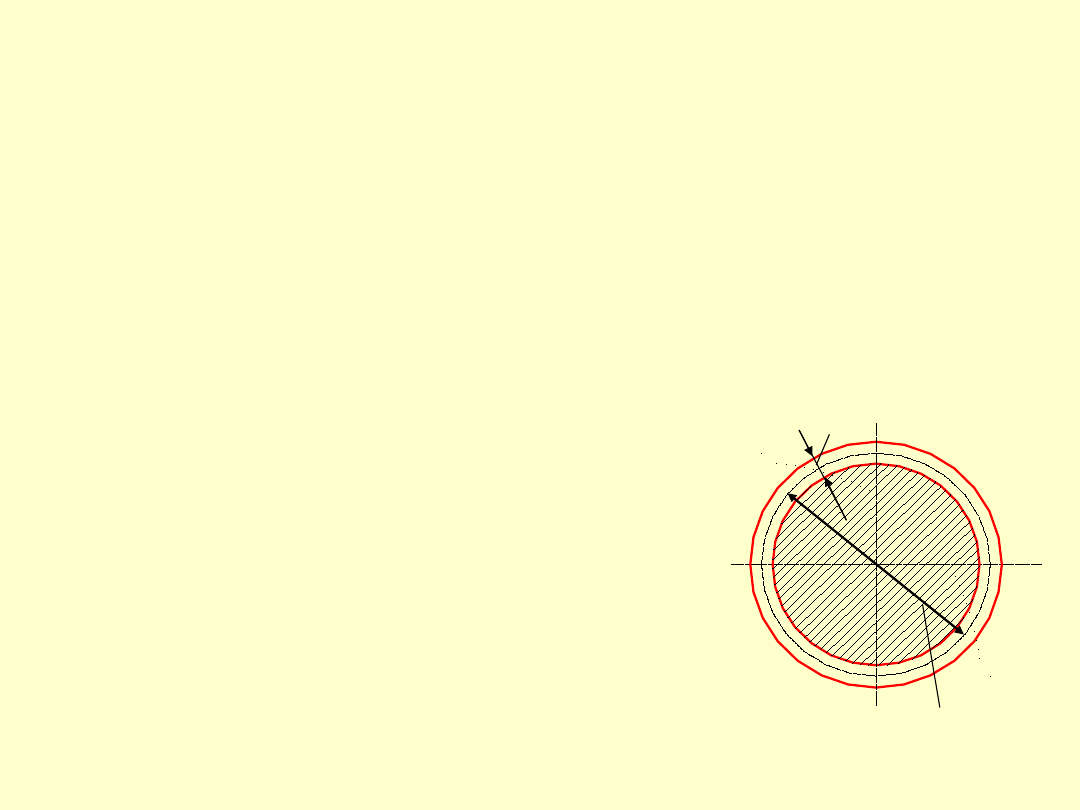
gdzie:
i
t
d
F
n
s
p
d
s
- średnia średnica
gwintu,
t
n
- nośna głębokość
gwintu, na jakiej śruba
styka się z nakrętką,
i
– liczba zwojów gwintu;
i = m/h
z
m
- wysokość nakrętki,
h
z
- podziałka zarysu
gwintu.
d
s
t
n
Po przekształceniach:
m
t
d
p
d
k
h
n
s
dop
r
r
z
4
2
otrzymuje się następującą zależność:
n
s
dop
r
z
r
r
t
d
p
d
h
d
k
m
4
Upraszczając i grupując otrzyma się:
r
n
z
s
r
dop
r
d
t
h
d
d
p
k
m
4
1
Wzór ten pozwala obliczyć wysokość
nakrętki
m
w mechanizmie śrubowym.
Dla zwykłych śrub złączowych z gwintem
metrycznym występują następujące
zależności:
d
,
d
,
t
h
,
d
d
r
n
z
s
r
8
0
54
1
88
0
Po podstawieniu uzyskuje się:
d
,
p
k
m
dop
r
27
0
W śrubach złącznych śruba i nakrętka są
stalowe, dla których:
5
2,
p
k
dop
r
Wówczas:
d
,
m
67
0
W rzeczywistości w zwykłych śrubach złączy
przyjmuje się
m
= 0,8
d
i taką nakrętkę nie
należy obliczać na naciski powierzchniowe.
Podobne rozważania można przeprowadzić
na wytrzymałość gwintu na ścinanie, przy
czym inna będzie powierzchnia ścinana.
Dla stalowych śrub złącznych uzyskuje się
warunek:
Oznacza to, że jeżeli gwint w nakrętce
spełnia warunek na naciski powierzchniowe
to tym bardziej spełnia warunek na ścinanie.
A zatem w normalnych śrubach złącznych
gdzie
m
= 0,8
d
gwintu nie trzeba obliczać.
d
,
m
47
0
Wpływ zginania gwintu (nie śruby) na
jego wytrzymałość jest nieznaczny i w
obliczeniach można pominąć.
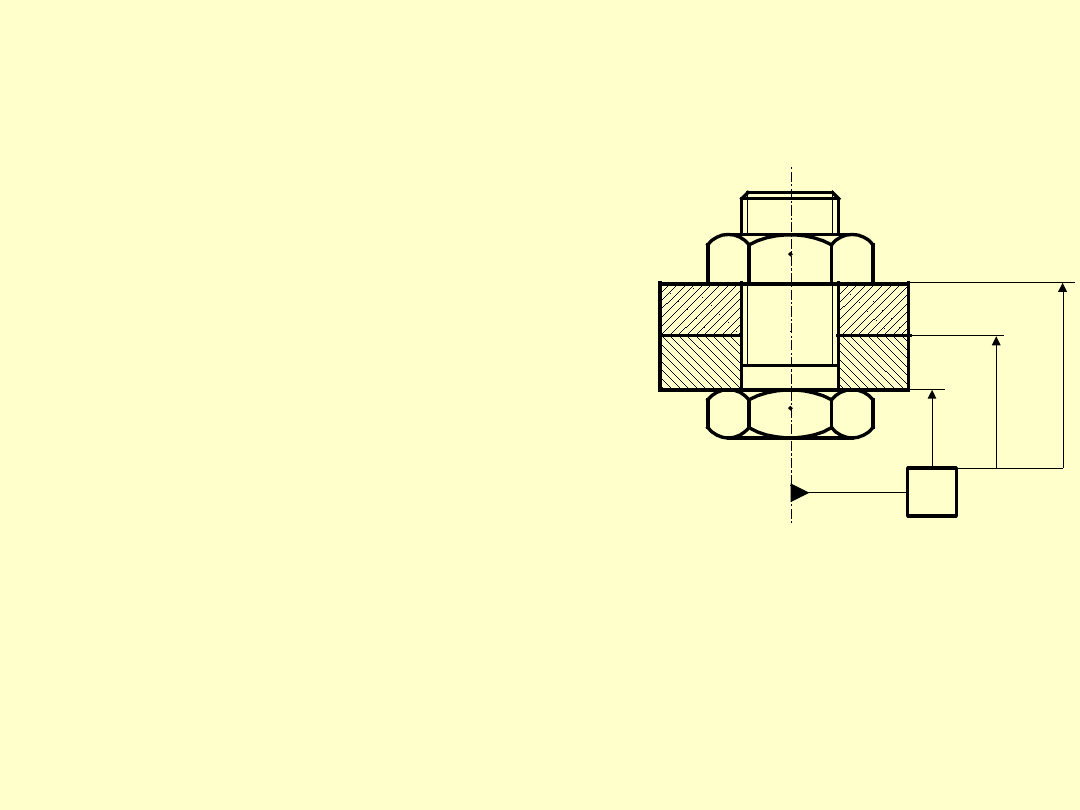
Optymalny stan obciążenia
śruby
Optymalnym stanem
obciążenia złącza śrubowego
jest jego obciążenie siłą
osiową.
Warunkiem tego jest
prostopadłość osi śruby do
powierzchni:
łba śruby,
oporowych nakrętki,
styku elementu
łączonych.
Jeżeli ten warunek nie zostanie spełniony
to pojawiają się dodatkowe naprężenia w
śrubie, wywołane działaniem momentu
gnącego.
Naprężenia te w połączeniu ze
zmiennymi naprężeniami roboczymi
mogą prowadzić do zniszczenia śruby.
W praktyce zawsze występują
nieprostopadłości wymienionych
powierzchni i osi śruby, wywołane np.
niedokładnym wykonaniem lub
występowaniem zanieczyszczeń.
Pojawia się przy tym pytanie:
czy można minimalizować konstrukcyjnie
wpływ tego rodzaju naprężeń gnących?
W celu określenia czynników
wpływających na zmniejszenie
dodatkowych naprężeń gnących
pojawiających się w wyniku
nieprostopadłości osi śruby i powierzchni
oporowych, rozpatruje się zginaną śrubę.
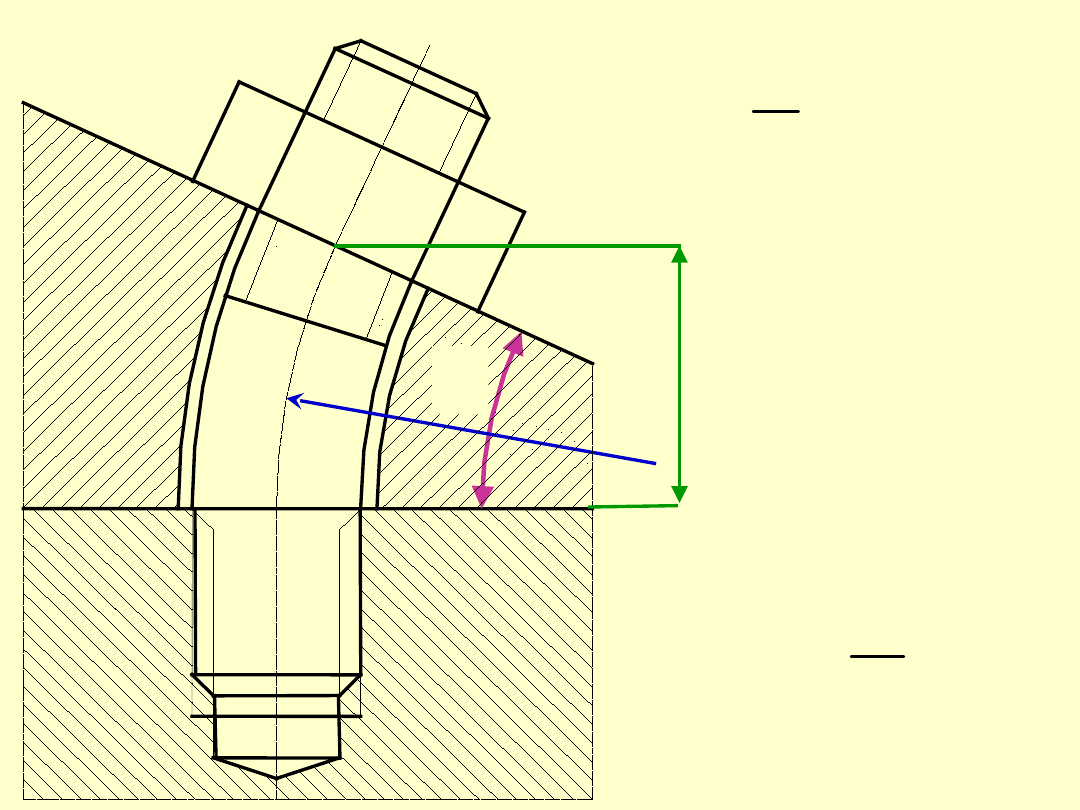
l
s
s
l
tg
(1)
s
l
(2)
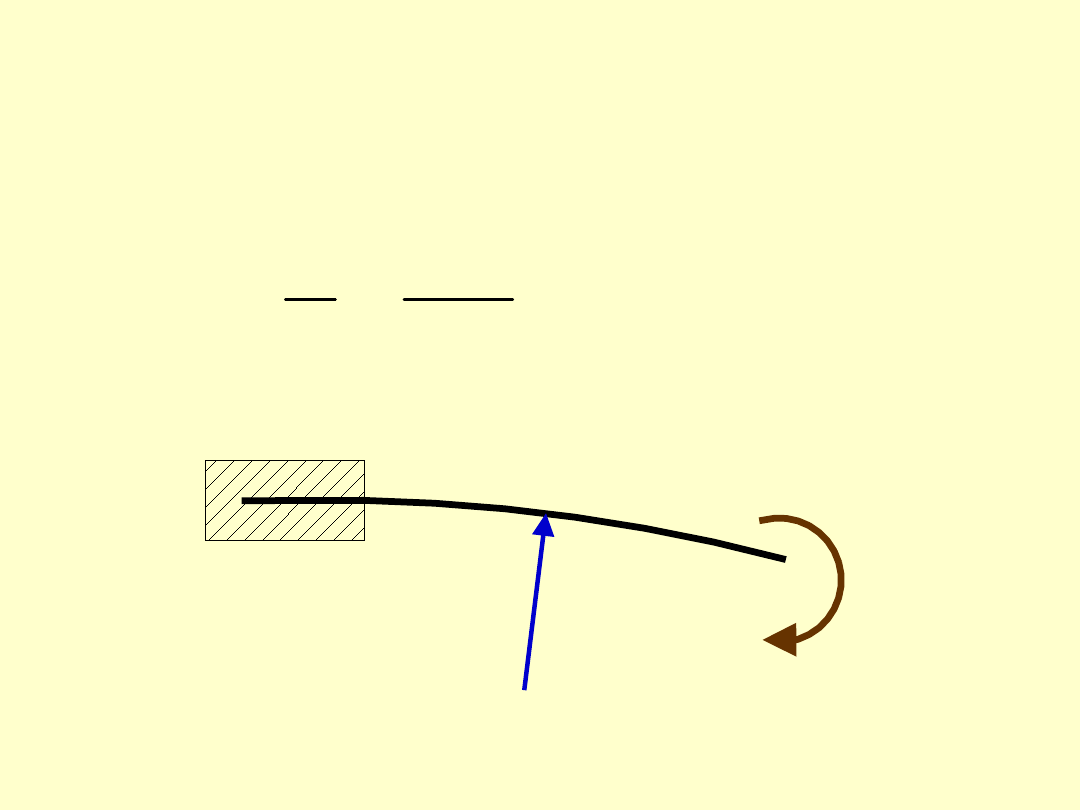
Z wytrzymałości materiałów wiemy, że dla
zginanej belki istnieje zależność:
EI
g
1
(3
)
M
g
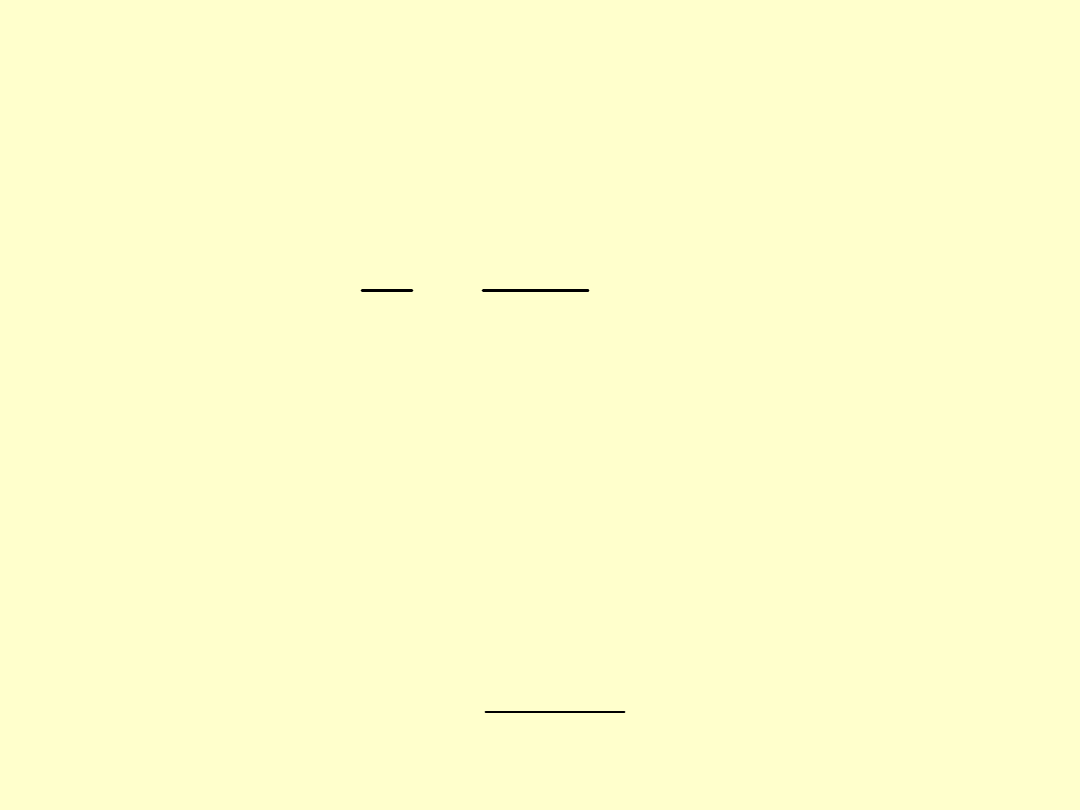
0
EI
l
g
s
Podstawiając zależność (2) do równania (3)
uzyskuje się:
Po przekształceniach zaś:
0
EI
l
M
s
g
i:
s
g
l
EI
M
0
(4
)
(5
)
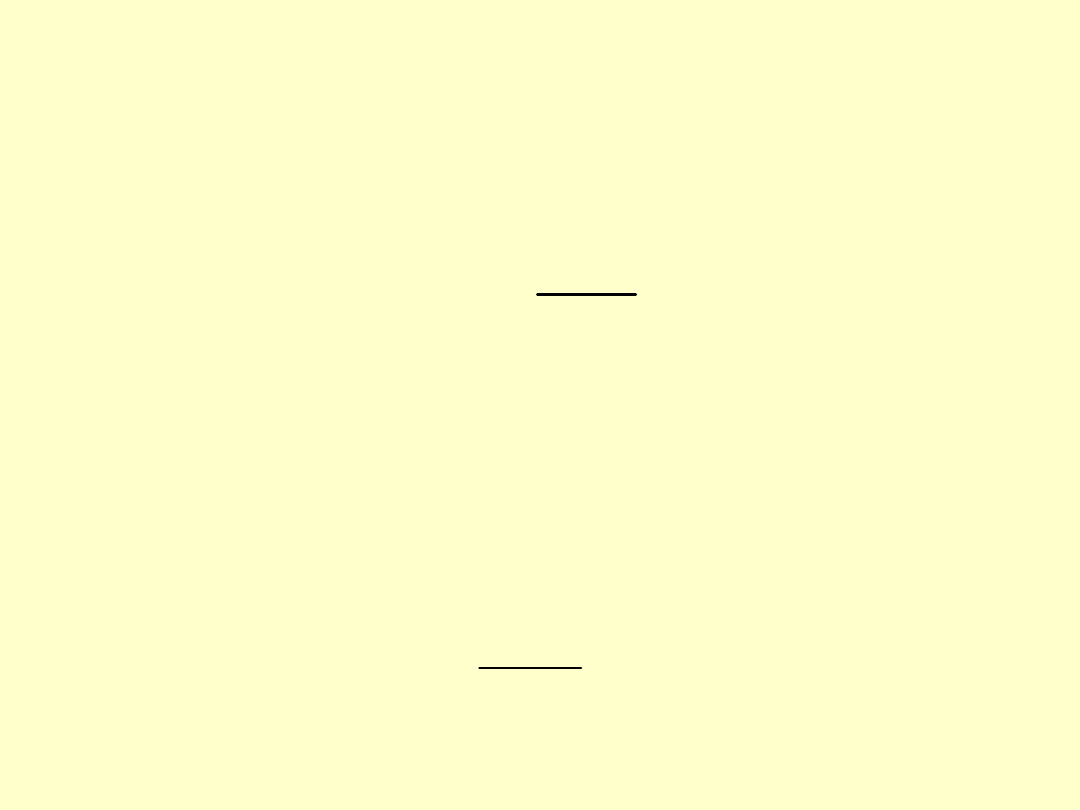
Z drugiej zaś strony wiemy, że naprężenia
gnące w przekroju rdzenia śruby wynoszą:
gdzie:
W
o
– wskaźnik przekroju kołowego rdzenia
śruby
d
r
na zginanie
0
W
M
g
g
32
3
0
r
d
W
(6
)
(7
)
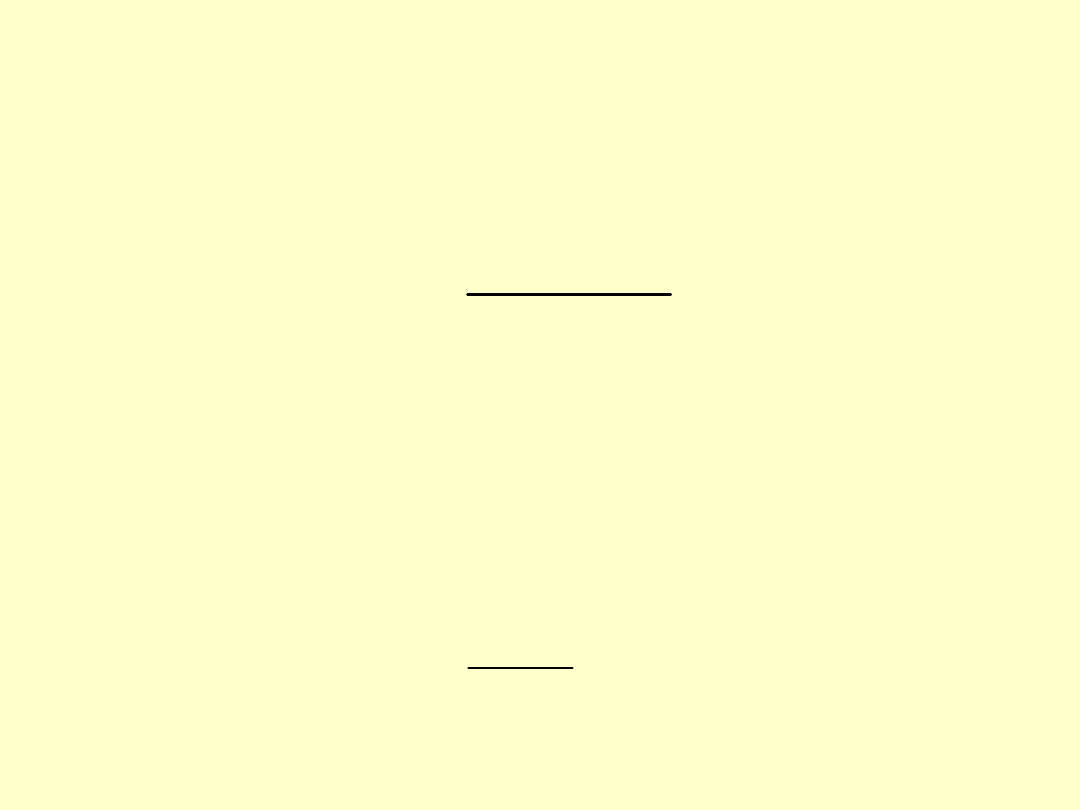
Po podstawieniu wartości
M
g
z równania (5)
do równania (7) uzyskuje się:
Podstawiając z kolei wartość momentu
I
0
bezwładności dla przekroju kołowego:
s
r
g
l
d
EI
3
0
32
64
4
0
r
d
I
(8
)
(9
)
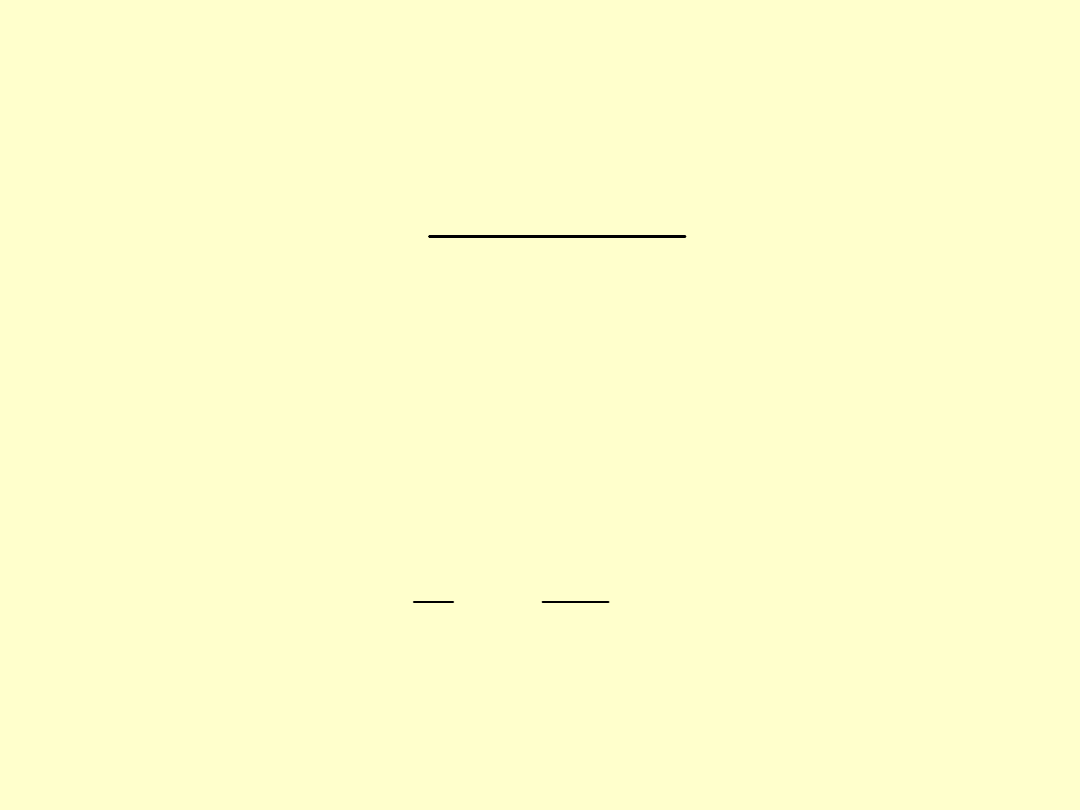
do równania (9) uzyskuje się:
Po uproszczeniu zaś ostatecznie:
s
r
r
g
l
d
E
d
3
4
64
32
(10)
s
r
g
l
d
E
2
1
Analiza wzoru (10) pokazuje, że dodatkowe
naprężenia gnące wywołane
nieprostopadłością powierzchni oporowej do
osi śruby (kąt
) są tym mniejsze im większy
jest stosunek czynnej długości śruby
l
s
do
średnicy jej rdzenia
d
r
, tzn. im bardziej jest
elastyczna śruba.
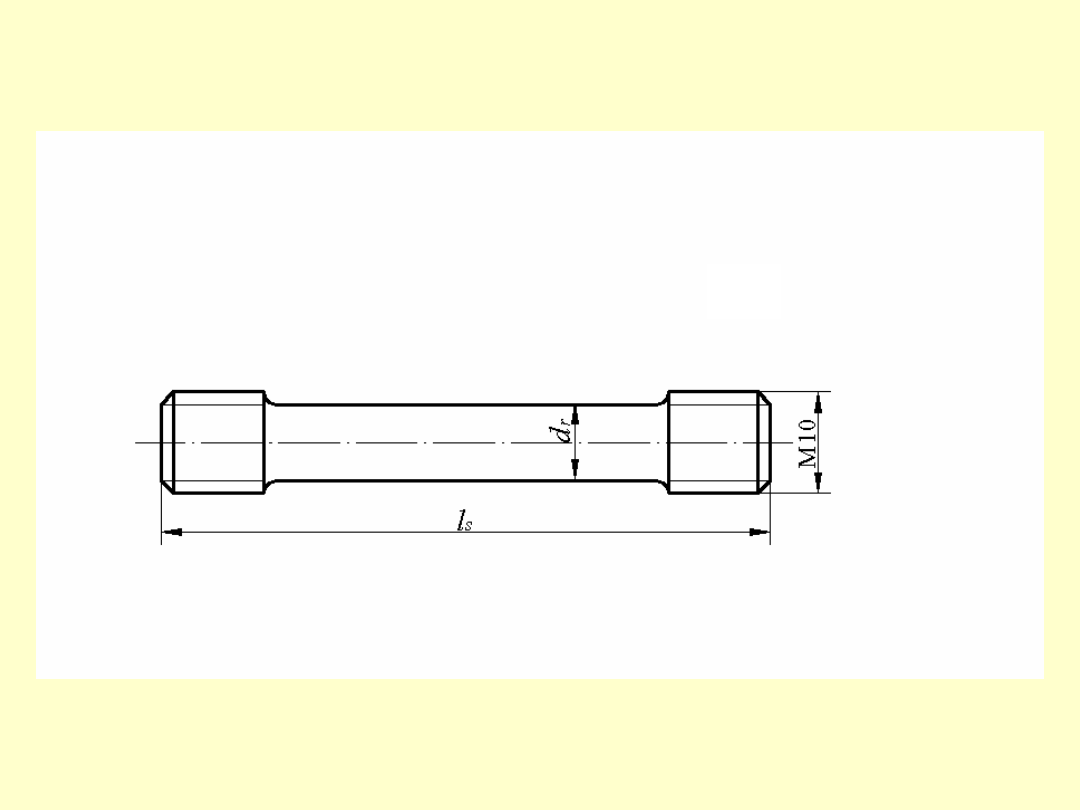
r
s
g
d
l
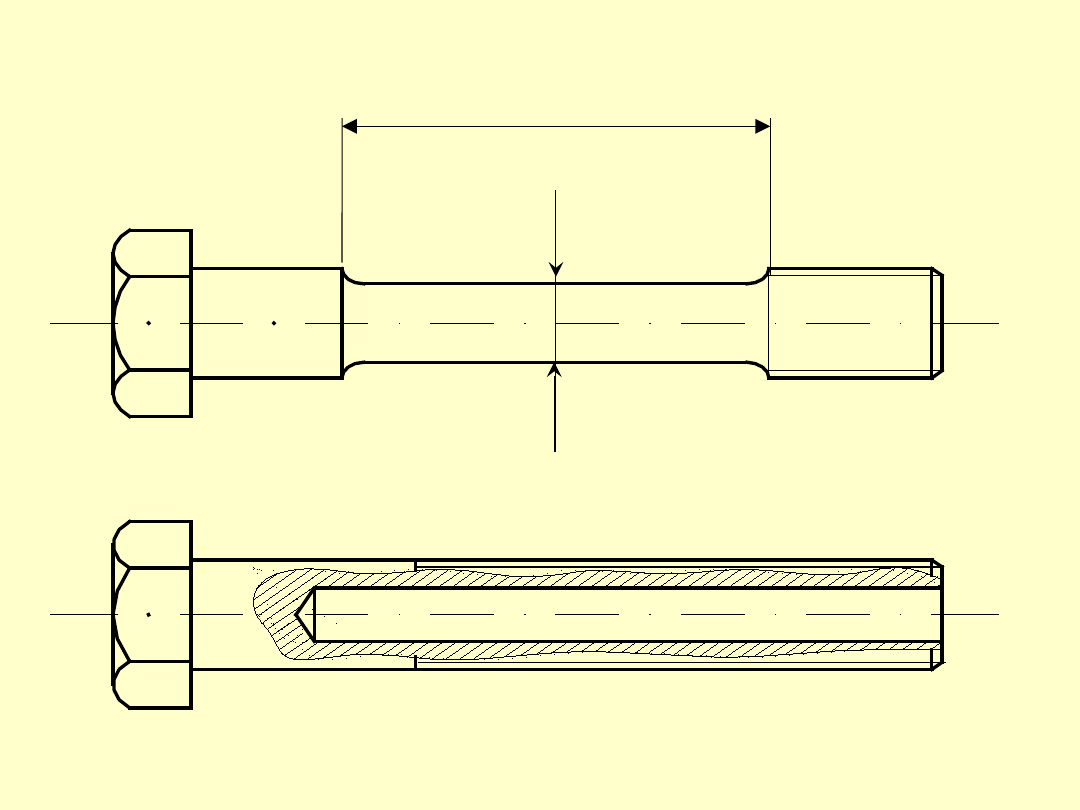
d
r
l
s
Śruby elastyczne
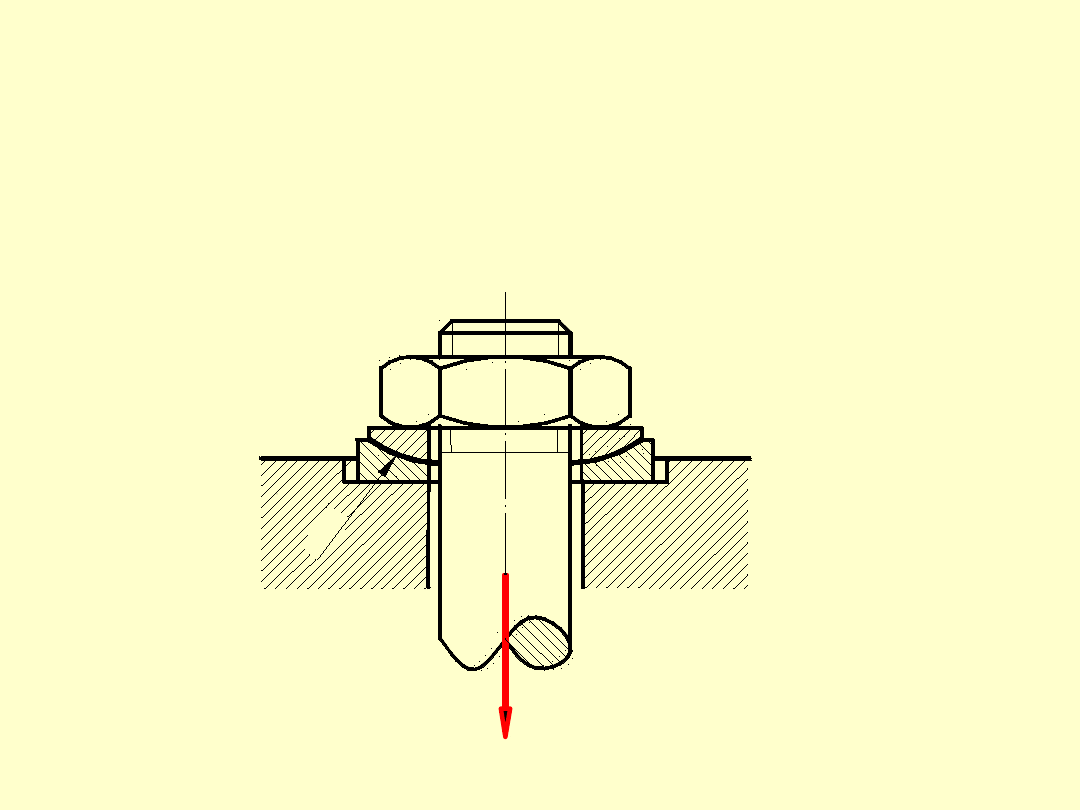
W celu wyeliminowania szkodliwych
naprężeń gnących dodatkowo stosuje się
specjalne podkładki zapewniające poprawę
prostopadłości powierzchni elementów
łączonych oraz powierzchni nakrętki (łba) do
osi śruby.
r
ku
li
P
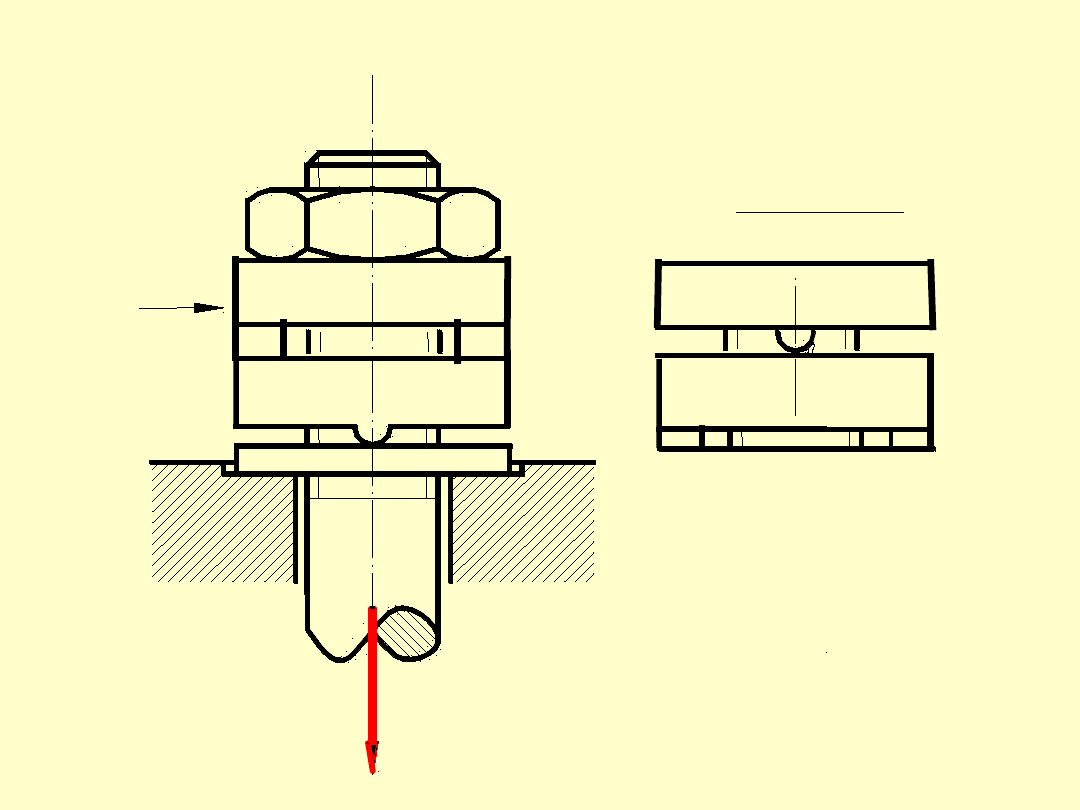
x
Widok x
P
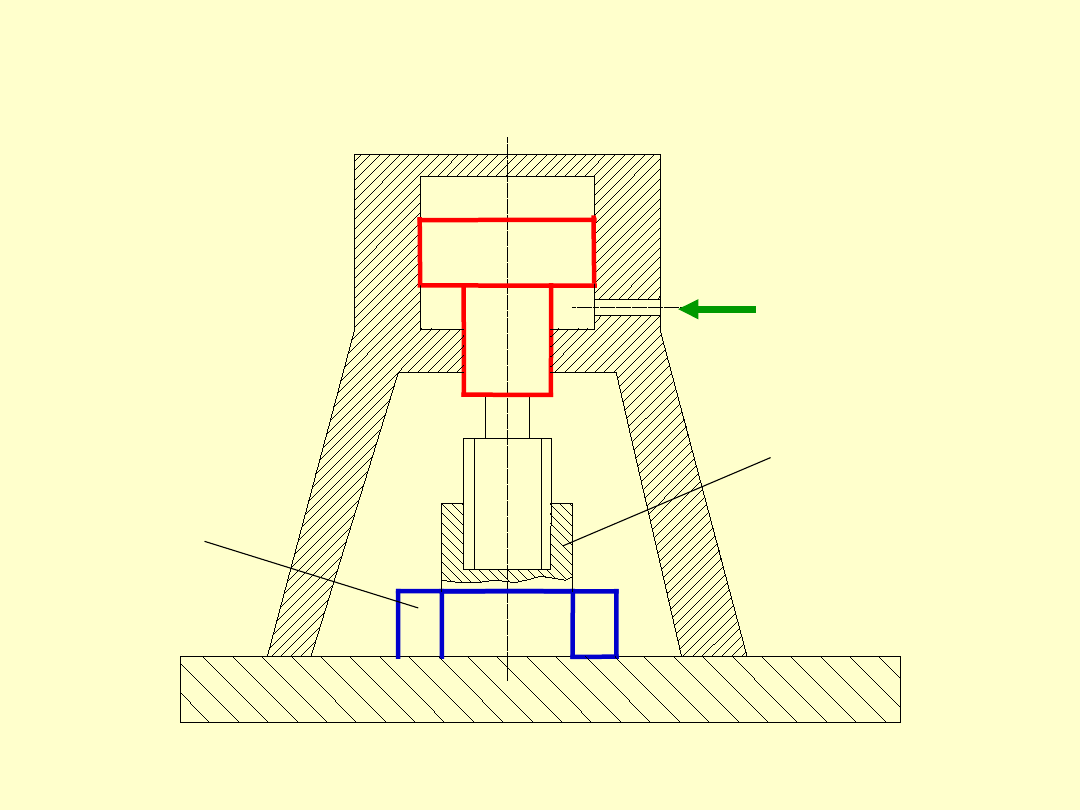
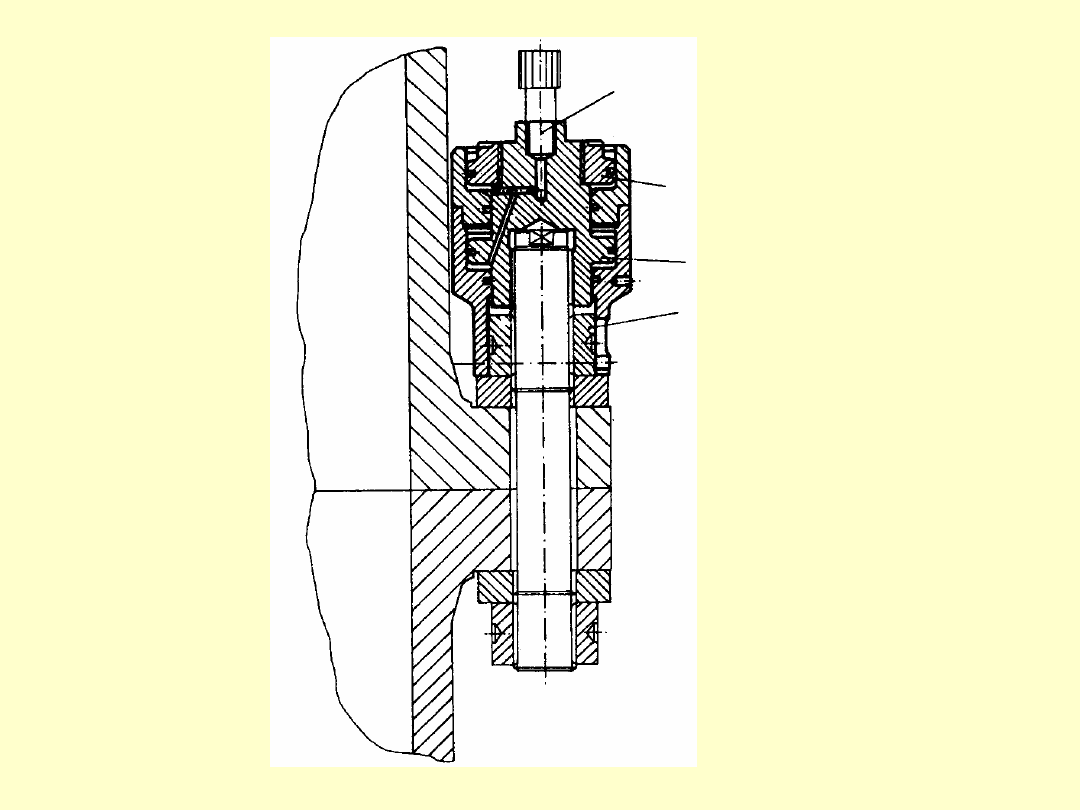
olej pod
ciśnienie
m
nakrętk
a
śruba
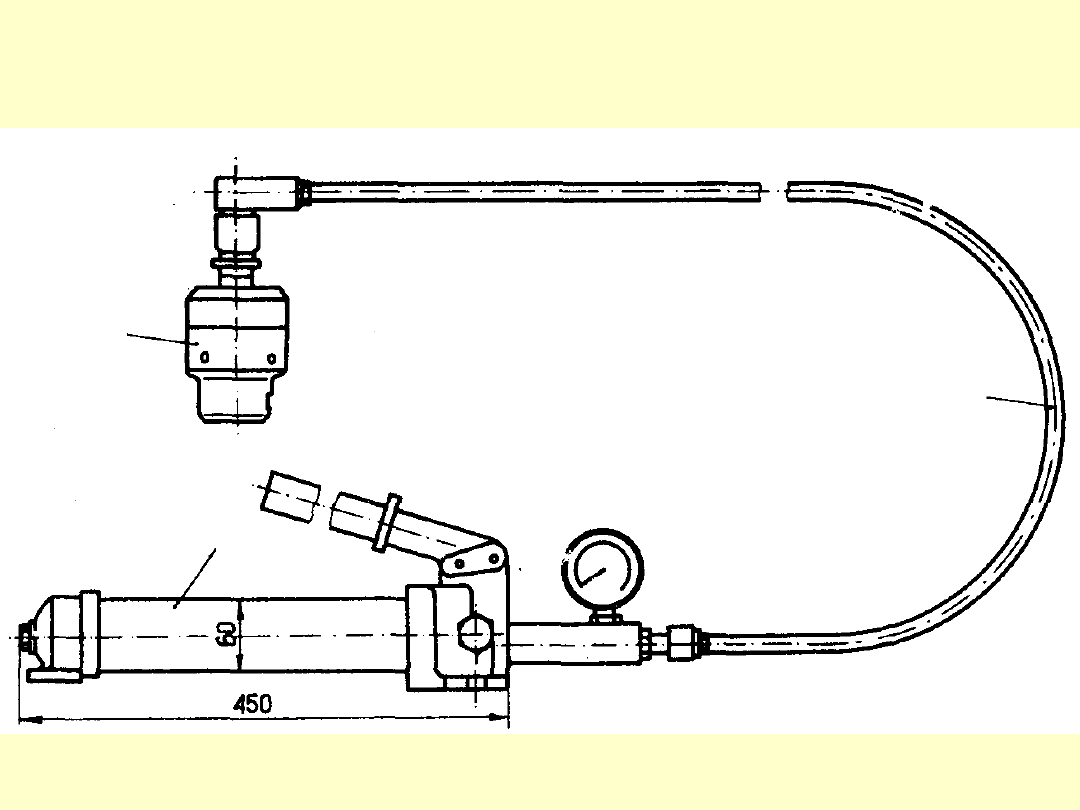
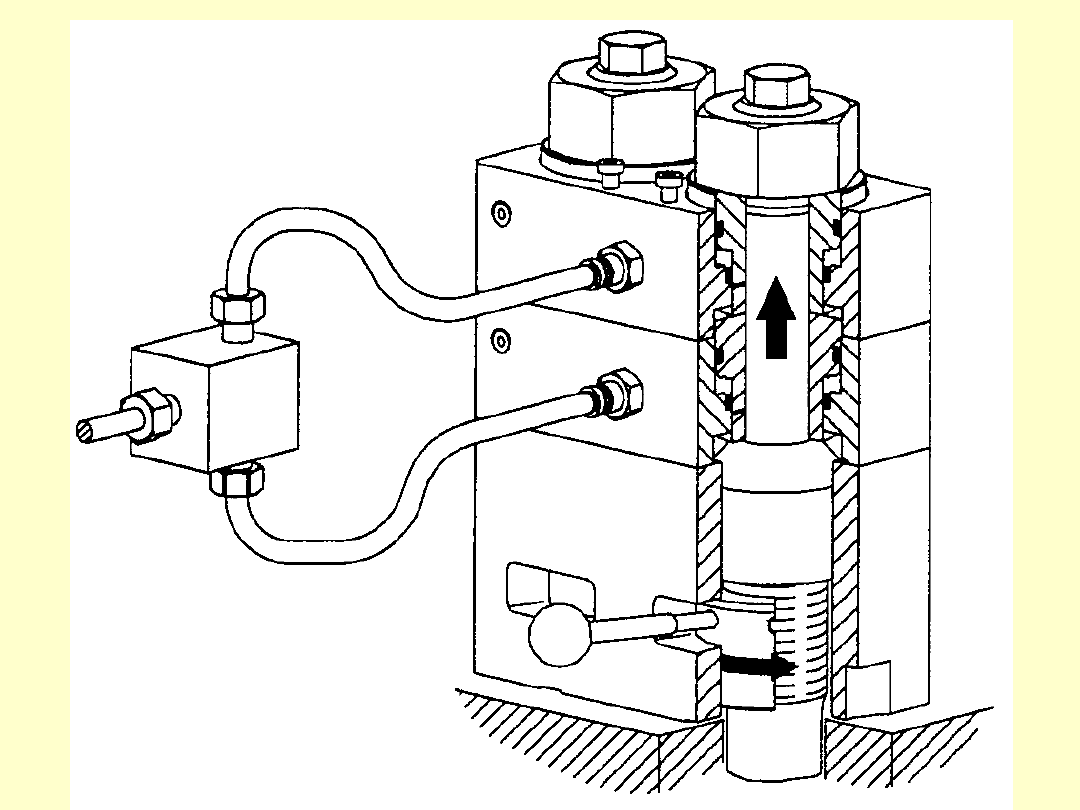
Zasada działania hydraulicznego urządzenia do
napinania
Wytrzymałość połączeń śrubowych
Rozróżnia się cztery podstawowe
przypadki obciążeń połączeń śrubowych:
I. Śruba obciążona siłą osiową
II. Śruba obciążona siłą osiową i momentem
skręcającym
III.Śruba napięta wstępnie i obciążona siłą
osiową
IV. Śruba obciążona siłą poprzeczną:
– śruba założona z luzem
– śruba pasowana
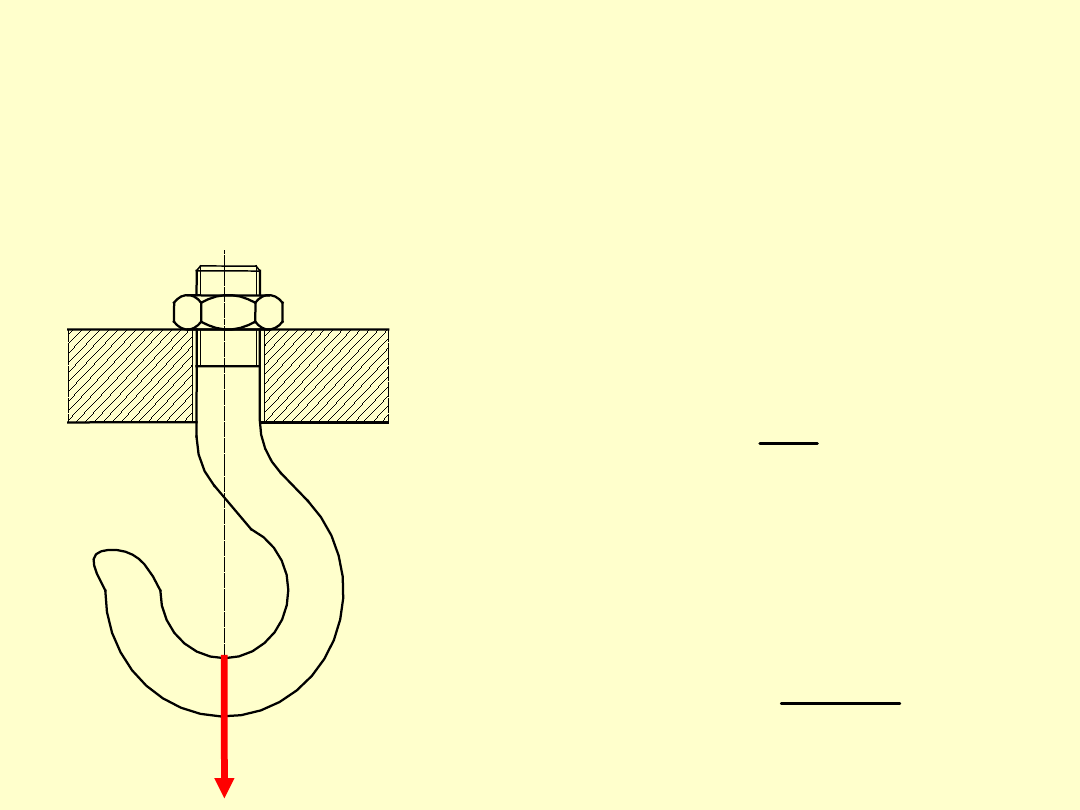
Przypadek I: Śruba obciążona siłą osiową
Przykładem takiego przypadku obciążenia może
być np. hak urządzenia dźwigowego.
r
r
k
F
P
P
Warunek
wytrzymałościowy:
4
2
r
d
F
gdzie
F
przekrój rdzenia
śruby:
r
r
k
d
P
2
4
Po podstawieniu uzyskuje się zależność:
Zależność ta pozwala rozwiązać trzy
podstawowe zadania:
Dane:
– obciążenie
P
,
– materiał
k
r
należy obliczyć:
– średnice rdzenia
śruby
d
r
Dane:
– średnica rdzenia
śruby
d
r
– materiał
k
r
należy obliczyć:
– obciążenie
P
Dane:
– obciążenie
P
,
– średnica rdzenia
śruby
d
r
należy obliczyć:
– materiał
k
r
2
4
r
r
d
P
k
r
r
k
P
d
4
4
2
r
r
k
d
P
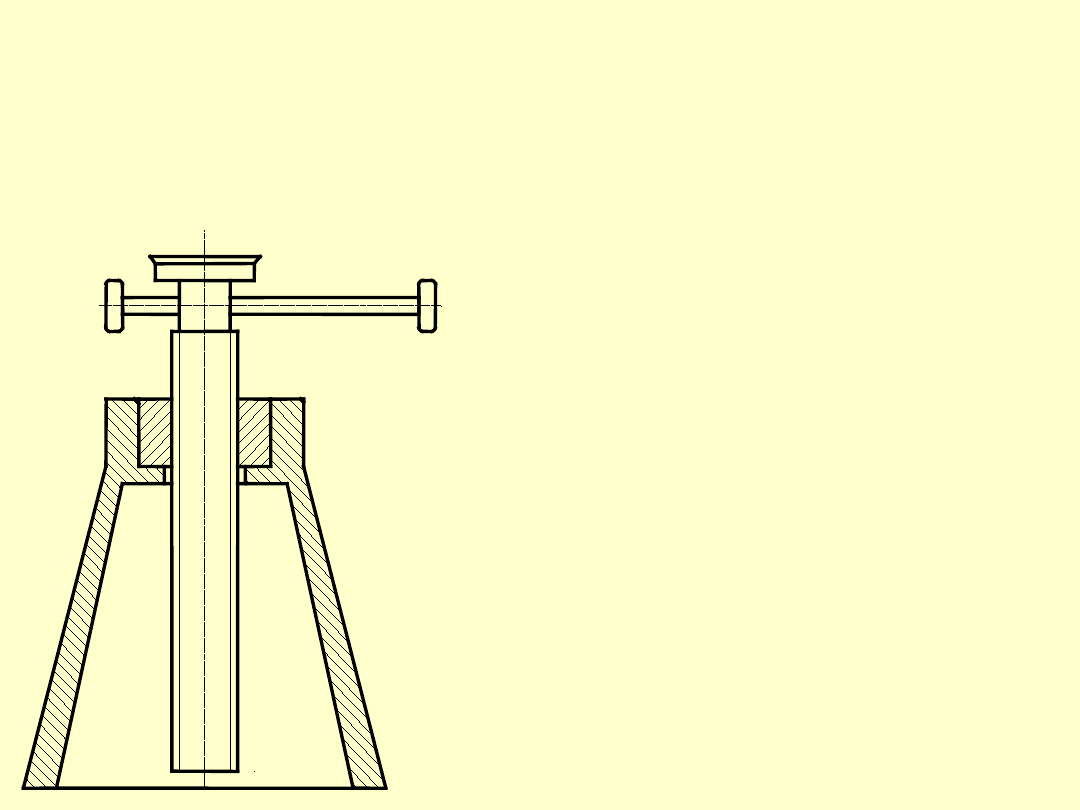
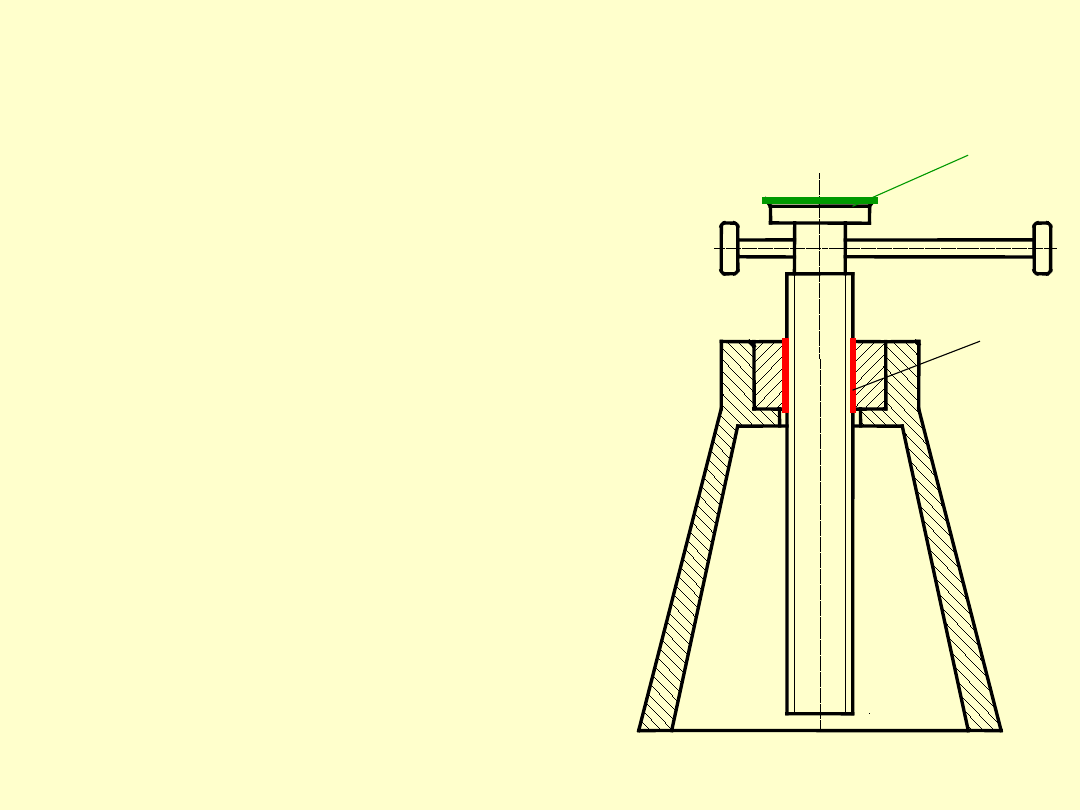
Przypadek II: Śruba obciążona siłą osiową
i momentem skręcającym
Przykładem takiego przypadku obciążenia może
być np. podnośnik.
W śrubie obciążonej
siłą osiową
P
i momentem
skręcającym
M
s
wystąpią
naprężenia rozciągające
względnie ściskające
oraz naprężenia
skręcające
F
P
r
Naprężenia rozciągające (ściskające):
Naprężenia skręcające:
s
s
W
M
gdzie:
M
s
– moment skręcający,
W
s
– wskaźnik przekroju kołowego na skręcanie
Moment skręcający:
Sumaryczny moment
tarcia:
gdzie:
M
TG
– moment tarcia na
gwincie,
M
TPO
– moment tarcia na
powierzchni oporowej
T
s
M
M
TPO
TG
T
M
M
M
M
TG
M
TPO
Moment tarcia
na gwincie
:
H
d
,
M
s
TG
5
0
Wiemy jednak że:
tg
P
H
Wówczas moment tarcia na gwincie :
tg
5
0
P
d
,
M
s
TG
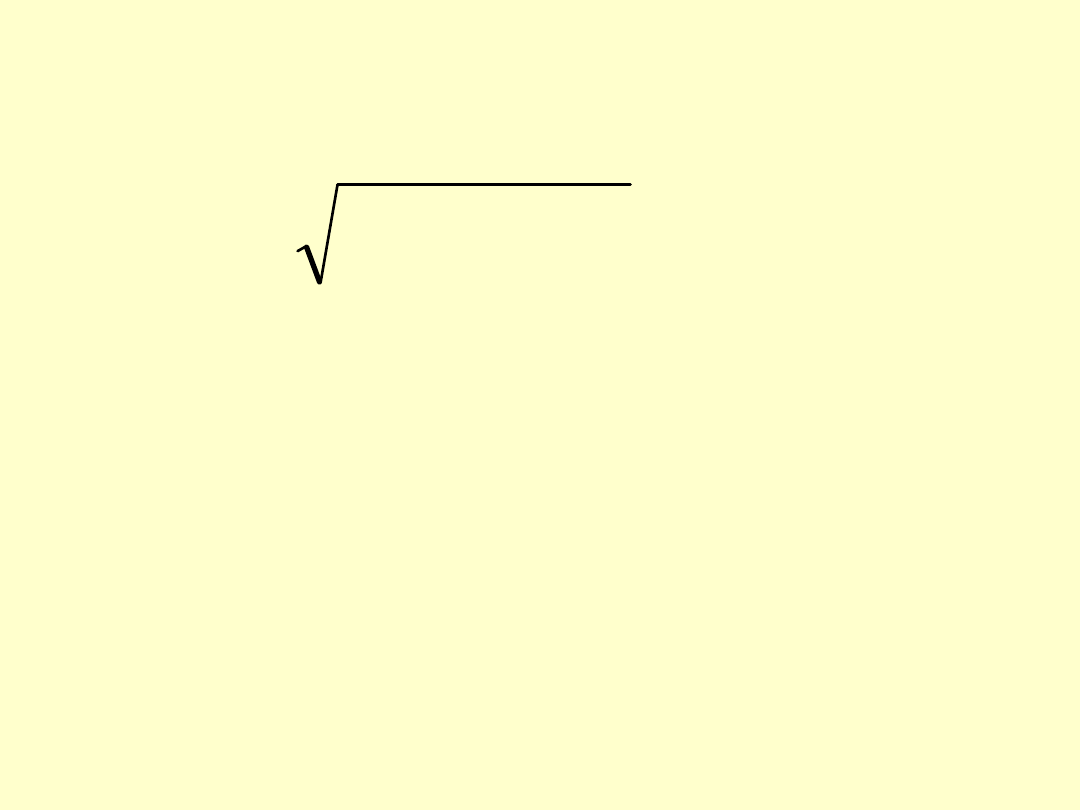
O wytężeniu materiału decydują naprężenia
zastępcze (np. według hipotezy Hubera):
gdzie:
- współczynnik przeliczeniowy,
k
r
– dopuszczalne naprężenia na rozciąganie
(ściskanie)
r
c
z
k
2
2
Z otrzymanej zależności z reguły oblicza się
średnicę rdzenia śruby.
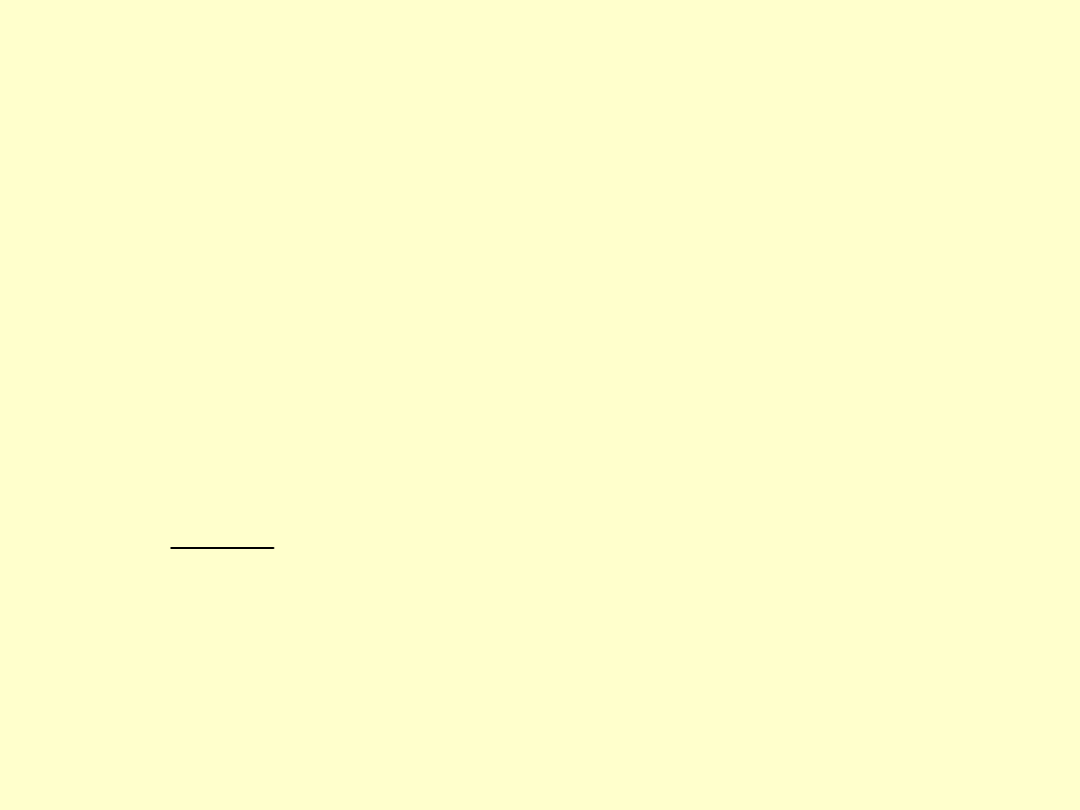
Przy obliczeniach wstępnych i obliczeniach nie
wymagających dużej dokładności, śruby
oblicza się jak gdyby były obciążone tylko siłą
osiową
P
mnożąc ją przez współczynnik
poprawkowy równy
1,251,3
.
Współczynnik ten uwzględnia naprężenia
skręcające, pojawiające się w gwincie wskutek
tarcia.
wstepnych
ch
obliczenia
w
k
F
P
,
r
3
1
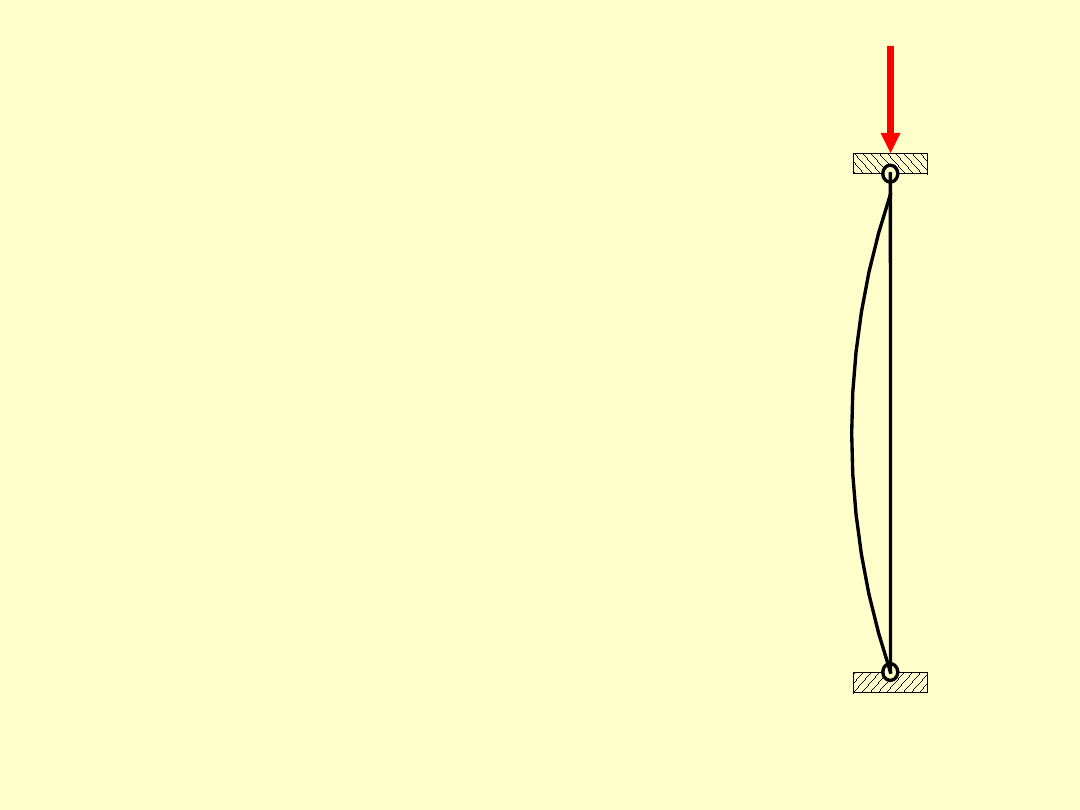
Śruby ściskane należy ponadto
sprawdzić na wyboczenie.
O charakterze wyboczenia
(sprężyste, niesprężyste) śrub
decyduje ich smukłość oraz
sposób zamocowania śruby.
P
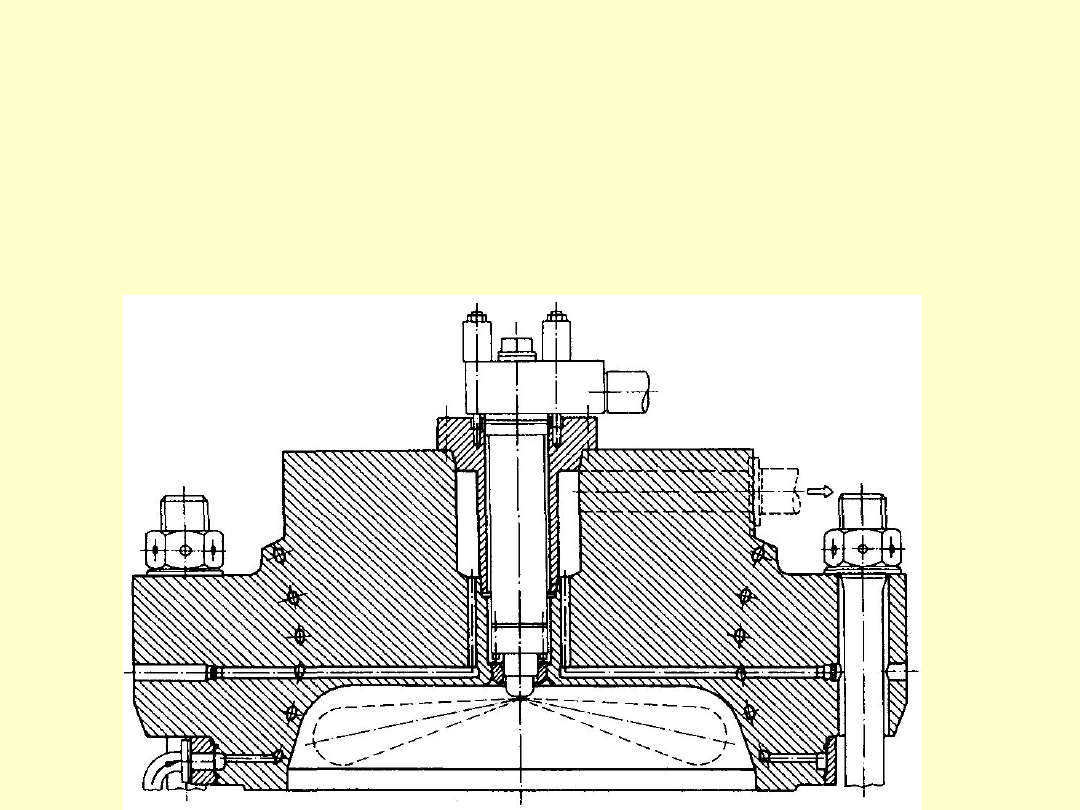
Przypadek III: Śruba napięta wstępnie i
obciążona siłą osiową
Przykładem takiego przypadku obciążenia może
być np. mocowanie głowicy cylindra w silniku.
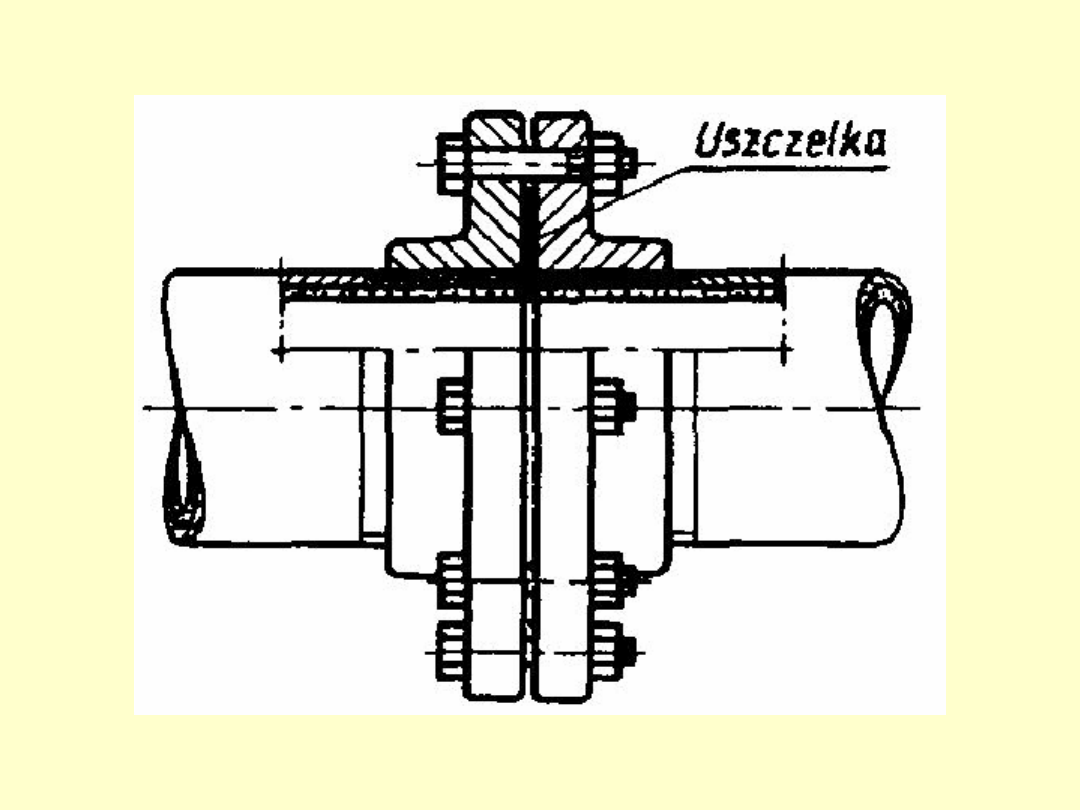
Napięcie wstępne połączeń śrubowych stosuje się w
przypadku działania obciążeń zmiennych oraz istnienia
wymagań w zakresie szczelności połączenia.
Doświadczenia zebrane podczas eksploatacji maszyn
pokazują, że niezawodna praca takich połączeń
śrubowych zależy w znacznej mierze od sposobu ich
wstępnego napinania.
Zbyt mała wartość siły napięcia wstępnego może
spowodować takie odkształcenie śrub, że nastąpi
utrata styku.
Natomiast zbyt duża wartość tej siły może doprowadzić
do przekroczenia granicy plastyczności materiału śrub,
co w konsekwencji spowoduje nadmierne wydłużanie
się śrub i utratę styku.
p
w
c
P
P
P
Całkowita siła
P
c
obciążająca śrubę
wynosi:
gdzie:
P
w
– siła napięcia wstępnego,
P
p
– siła zewnętrzna (obciążenie
podstawowe),
– współczynnik obciążenia
podstawowego.
Analiza wzoru (1) pokazuje , że całkowite
obciążenie śruby
P
c
napiętej wstępnie siłą
P
w
, a potem poddanej działaniu
obciążeniu zewnętrznemu
P
p
nie jest
arytmetyczną sumą tych sił i jest
mniejsze od sumy tych sił.
Oznacza to, że cześć obciążenia
zewnętrznego
P
p
przejmują elementy
łączone, przy czym wartość tego
przejęcia zależy od podatności śruby
K
s
i
elementów łączonych
K
c
.
Zagadnienie to jest omawiane w
ćwiczeniu laboratoryjnym.
Dużą rolę w prawidłowym doborze napięcia
wstępnego ma kolejność dokręcania śrub, np.
podczas montażu głowic.
Niewłaściwa kolejność mogłaby doprowadzić do
jej uszkodzenia lub spowodować w niedługim
czasie awarię (nieszczelność głowicy), co w
rezultacie może doprowadzić do poważnej
usterki silnika.
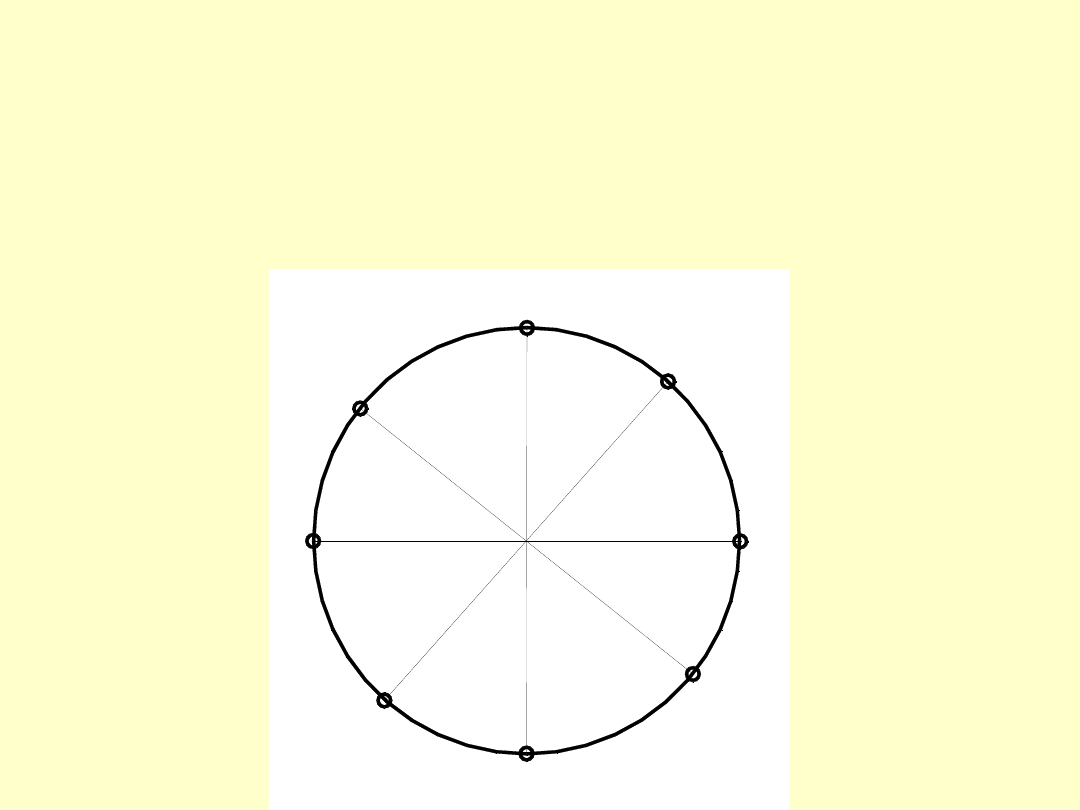
Metoda ta jest podzielona na cztery etapy „dociągania”
śrub:
pierwszy etap to dociąganie wstępne śrub na krzyż
w kolejności pokazanej na rysunku,
drugi etap dociągania śrub jest w tej samej
kolejności jak w etapie pierwszym, lecz ze
zwiększonym momentem siły dokręcającej nakrętki.
1
3
5
7
2
4
6
8
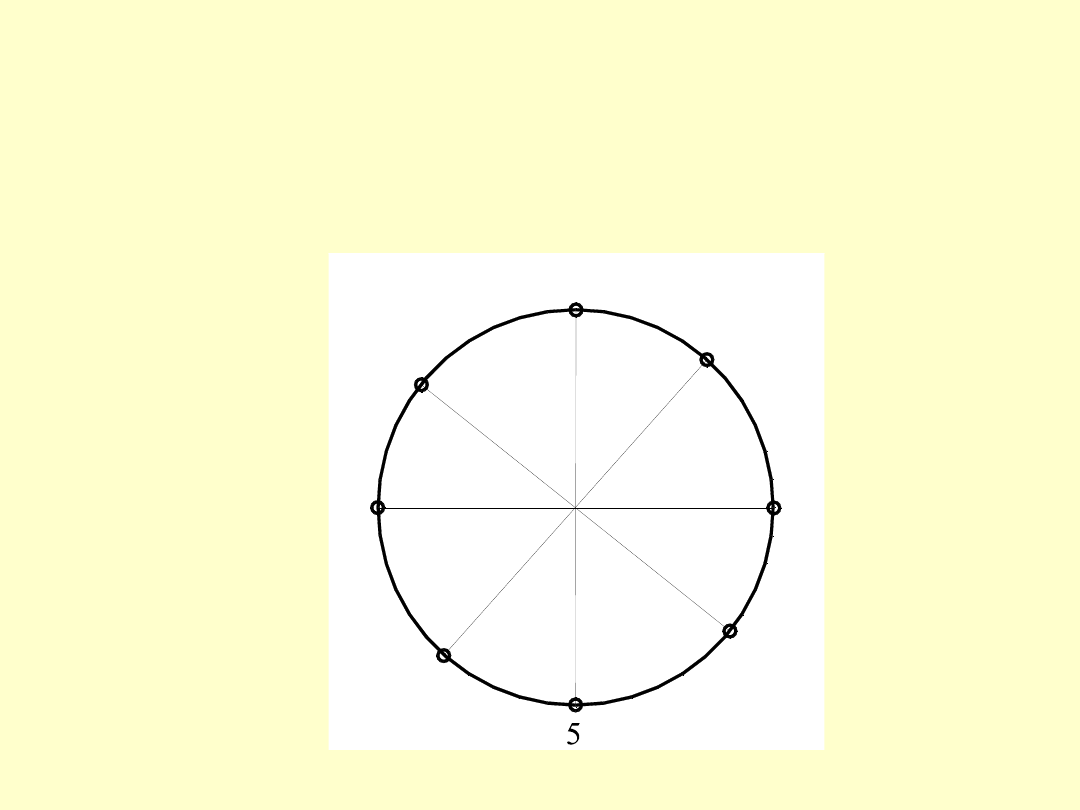
Etap trzeci i czwarty są końcowymi w których
śruby dociąga się „na gotowo”, kolejno jedną
śrubę po drugiej, zwiększając za każdym razem
moment siły dokręcającej nakrętki.
1
2
3
4
6
7
8
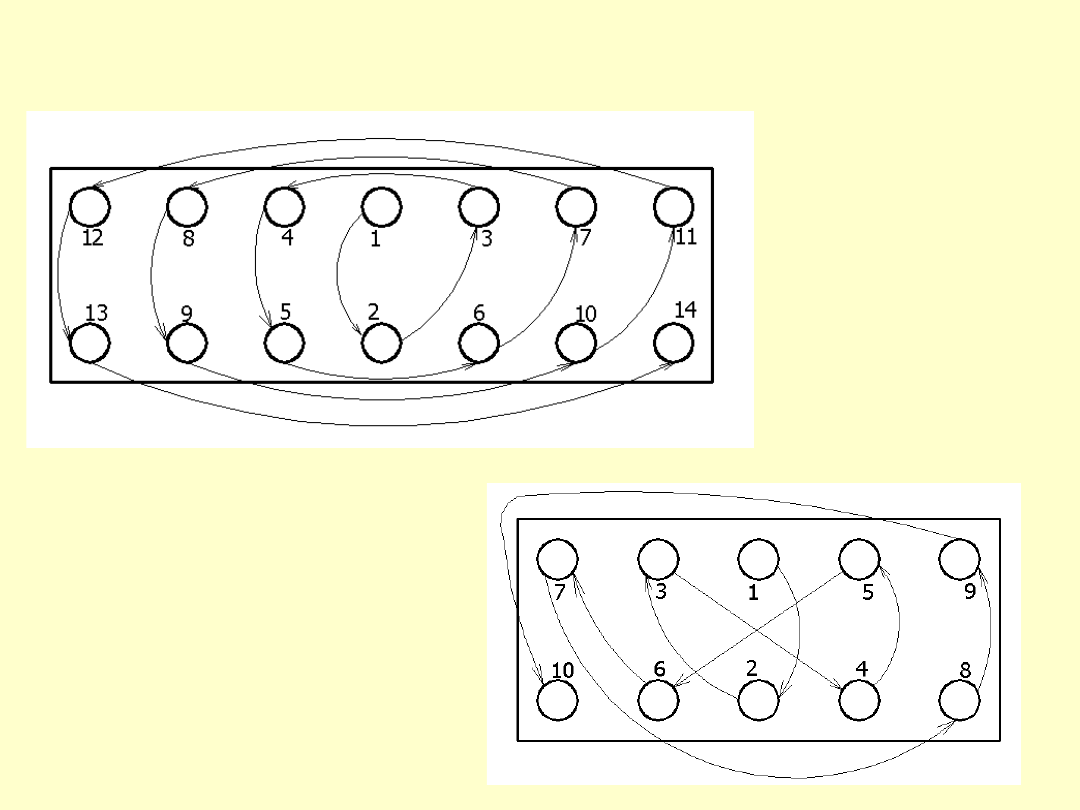
Podczas dokręcania głowic jednolitych stosuje
się dwa sposoby dokręcania:
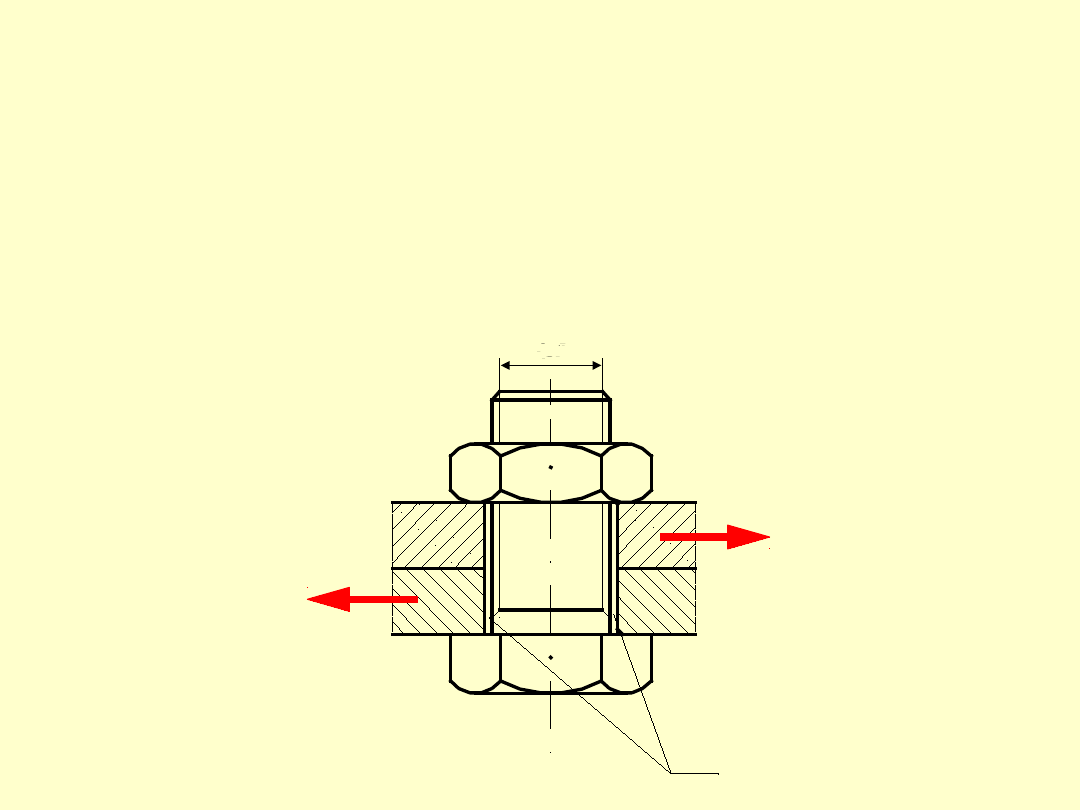
Przypadek IV: Śruba obciążona siłą
poprzeczną - śruba założona z luzem
Przykładem takiego przypadku obciążenia
może być np. kołnierz sprzęgła sztywnego.
luz
P
t
P
t
d
r
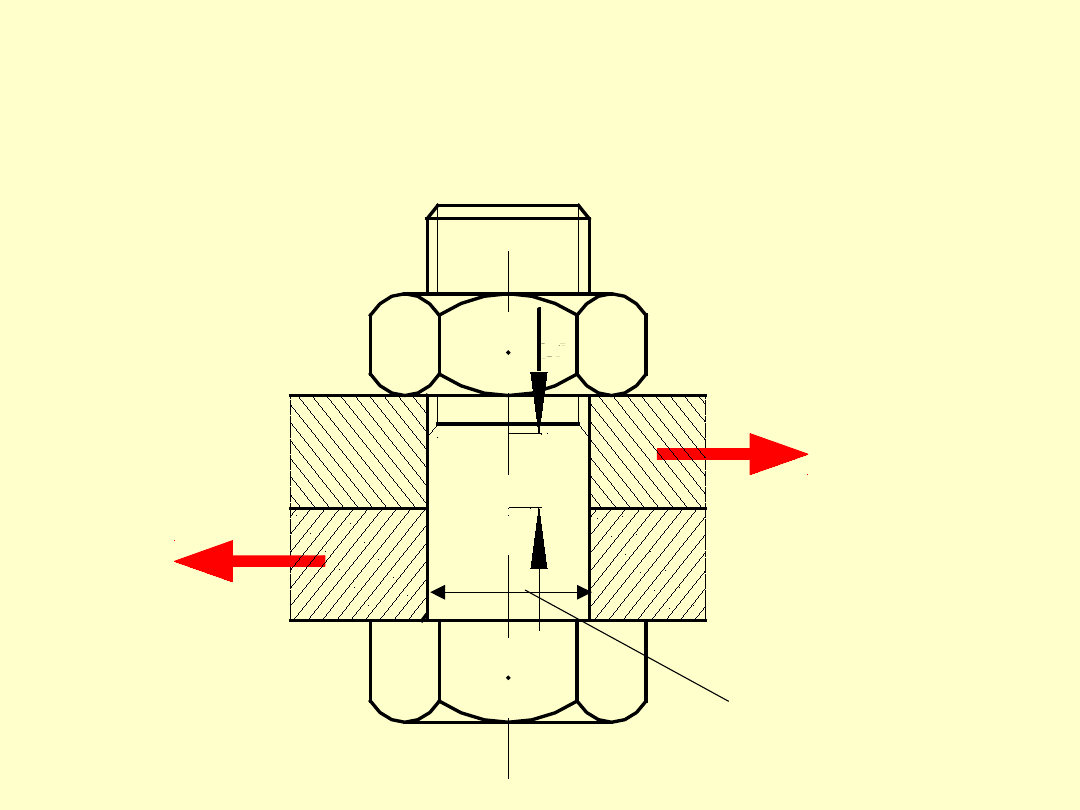
Tego rodzaju połączenie przenosi obciążenie
za pomocą sił tarcia:
w
T
P
N
T
P
r
w
r
k
F
P
Naprężenia rozciągające w rdzeniu śruby
wywołane siła napięcia wstępnego wynoszą:
Po przekształceniu otrzymuje się:
4
4
2
2
r
r
w
r
r
w
d
k
P
k
d
P
(1
)
(2
)
(3
)
Podstawiając zależność (3) do równania (1),
otrzymujemy zależność pozwalającą obliczyć
obciążalność złącza:
4
2
r
r
T
d
k
P
Przypadek IV: Śruba obciążona siłą
poprzeczną - śruba pasowana
d
t
P
t
g
min
P
t
W danym przypadku trzpień śruby będzie
ścinany:
t
t
T
k
d
P
2
4
Połączenie to należy sprawdzić również z
warunku na naciski powierzchniowe:
dop
min
t
T
p
g
d
P
p