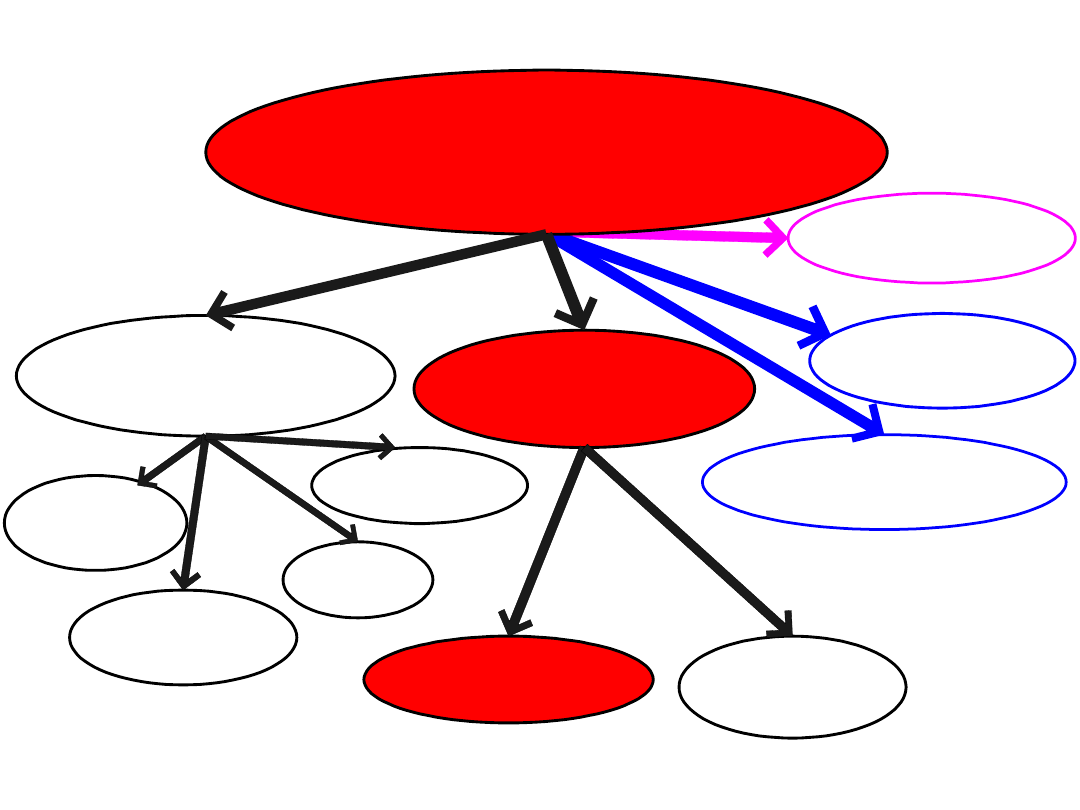
SPRĘŻYSTE
RUCHOWE
SPOCZYNKOWE
POŁĄCZENIA
NIEROZŁĄCZNE
ROZŁĄCZNE
spójnoś-
ciowe
cierno-
kształtowe
cierne
kształtowe
kształtowe
kształtowo
-cierne

Połączenia
śrubowe
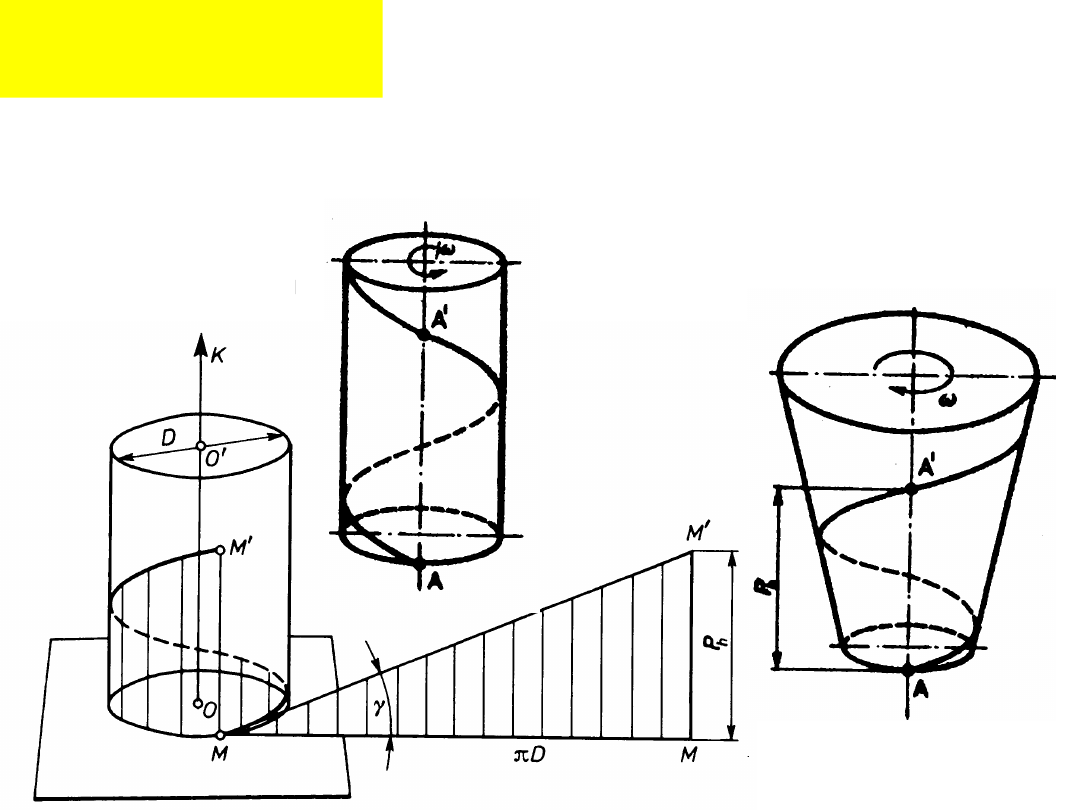
Linia śrubowa:
Zależnie od kierunku ruchu obrotowego
linia śrubowa może mieć gwint lewy lub
prawy.
Walcowa prawa
Walcowa lewa
Stożkowa prawa
Połączenia
śrubowe
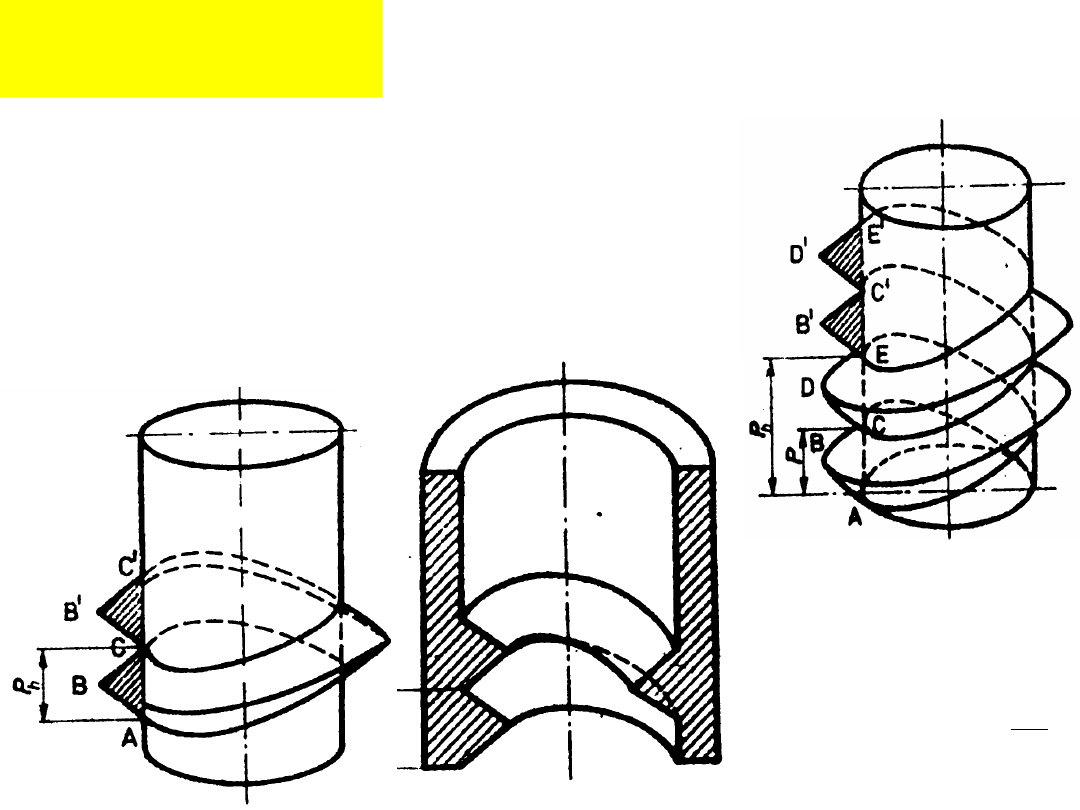
Gwint
y:
Dwukrotn
y
zewnętrzn
y
Jednokrot
ny
zewnętrzn
y
Jednokrot
ny
wewnętrz
ny
z
P
P
h
:
podziałka
Jeżeli podczas obrotu figury płaskiej (trójkąta, prostokąta,
trapezu, koła) jej płaszczyzna stale przechodzi przez oś
obrotu, a jej punkty zakreślają walcowe linie śrubowe to
powstaje bryła zwana gwintem. Tworząca figura płaska
nosi nazwę zarysu gwintu.
Połączenia
śrubowe
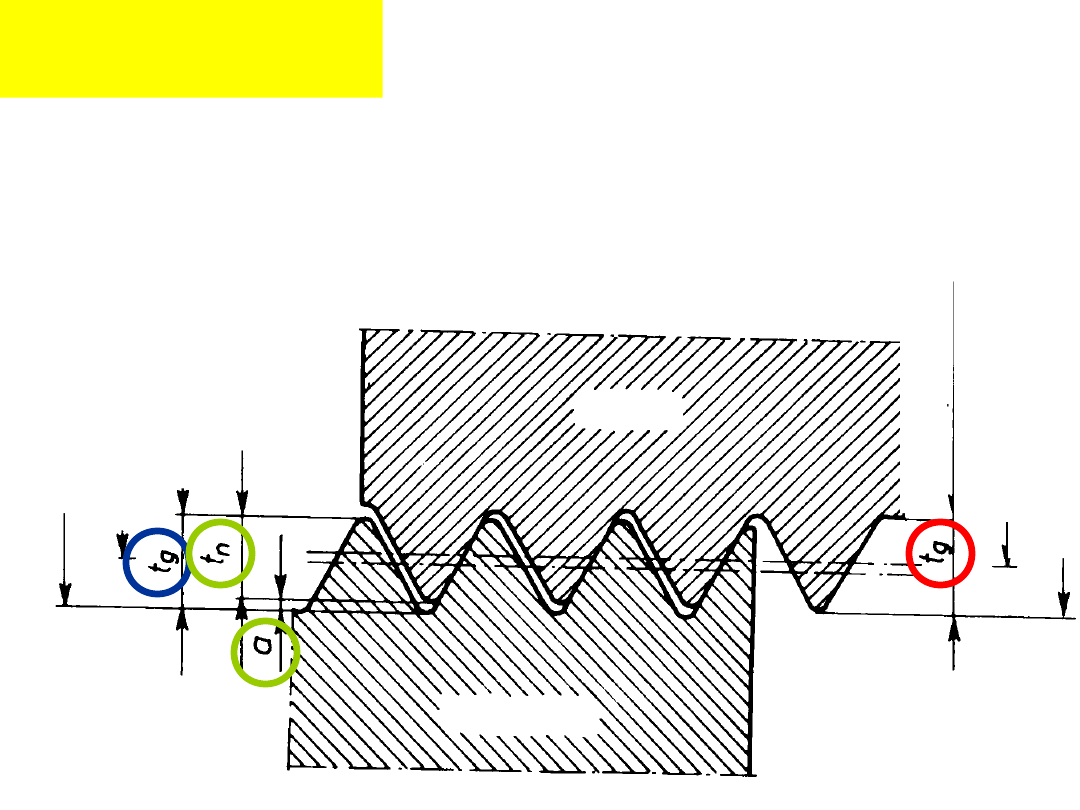
Podstawowe
wymiary:
Ś
re
d
n
ic
a
o
tw
o
ru
n
a
k
rę
tk
i
Ś
re
d
n
ic
a
p
o
d
z
ia
ło
w
a
n
a
k
rę
tk
i
Ś
re
d
n
ic
a
n
o
m
in
a
ln
a
n
a
k
rę
tk
i
Ś
re
d
n
ic
a
r
d
ze
n
ia
ś
ru
b
y
Ś
re
d
n
ic
a
p
o
d
z
ia
ło
w
a
ś
ru
b
y
Ś
re
d
n
ic
a
n
o
m
in
a
ln
a
ś
ru
b
y
śrub
a
nakrętka
Wysokoś
ć zarysu
gwintu
nakrętki
Wysokoś
ć zarysu
gwintu
śruby
robocza
wysokoś
ć zarysu
Luz
gwint
u
Połączenia
śrubowe
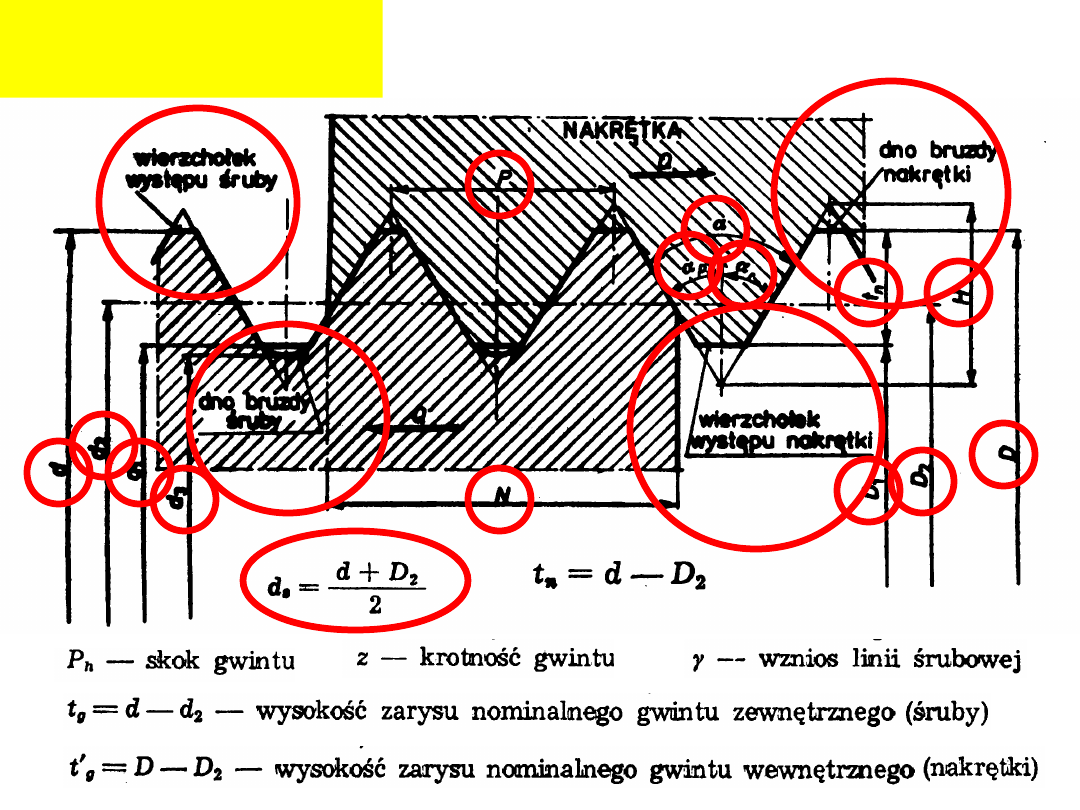
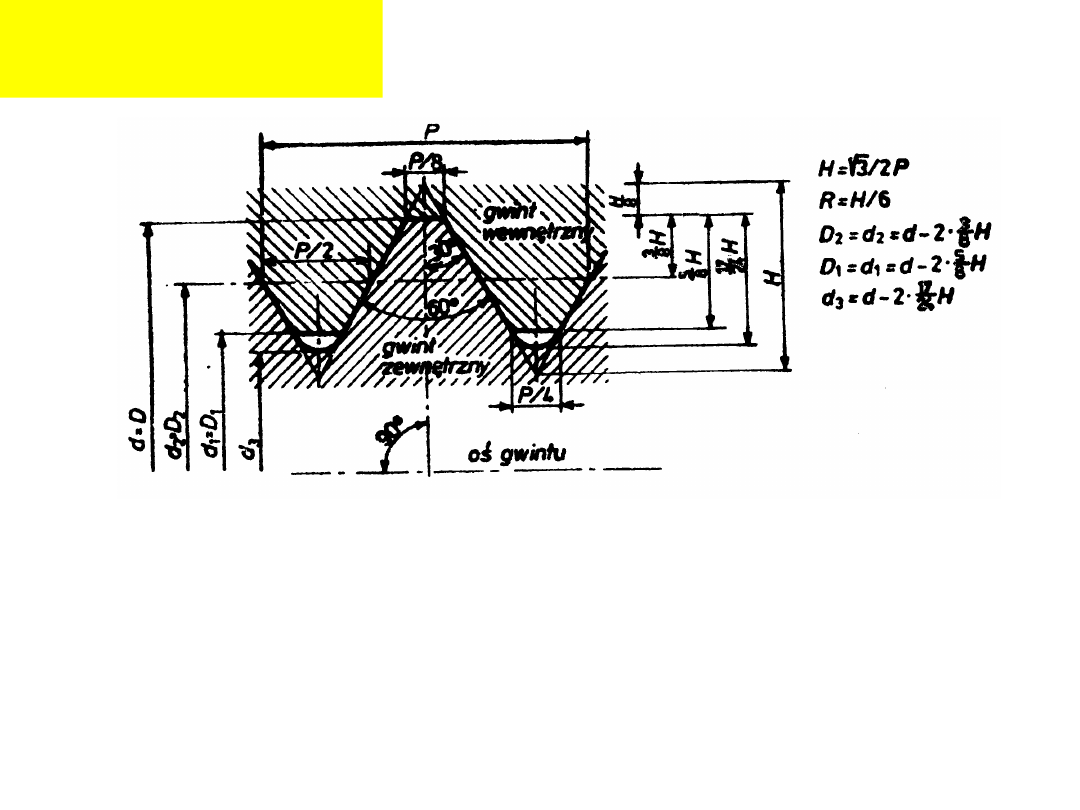
Podstawowe wymiary
(PN-85/M-02001):
Połączenia
śrubowe
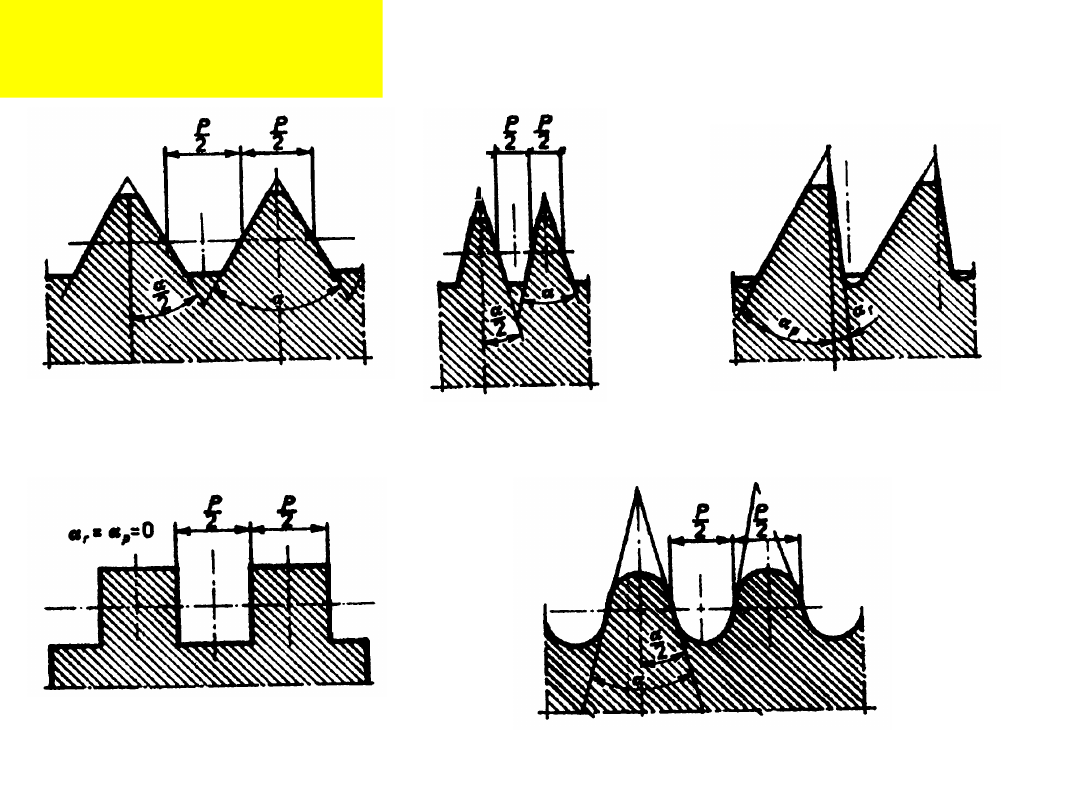
Rodzaje
zarysów:
Trójkątny
Prostoką
tny
Okrągł
y
Trapezowy
symetrycz
ny
Trapezowy
niesymetryc
zny
Połączenia
śrubowe
Zarys trójkątny
najczęściej stosowany
jest w śrubach złącznych.
Połączenia
śrubowe
Zarys gwintu trapezowego
symetrycznego stosowany
jest w mechanizmach
śrubowych przy działaniu
dużych obciążeń, np.
podnośniki, ściągi śrubowe
want, itp.
Połączenia
śrubowe
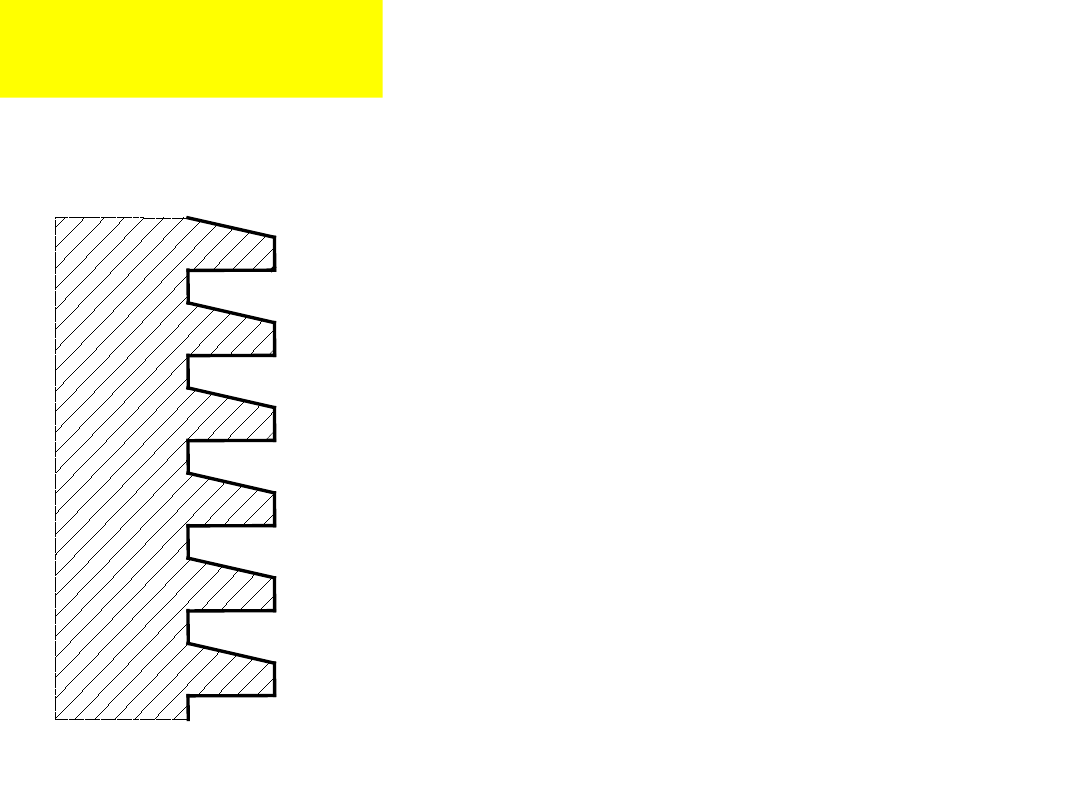
Zarys trapezowy
niesymetryczny stosowany
jest w mechanizmach
śrubowych przy działaniu
dużych obciążeń
jednostronnych i pożądanej
wyższej sprawności, np.
tłocznie.
Połączenia
śrubowe
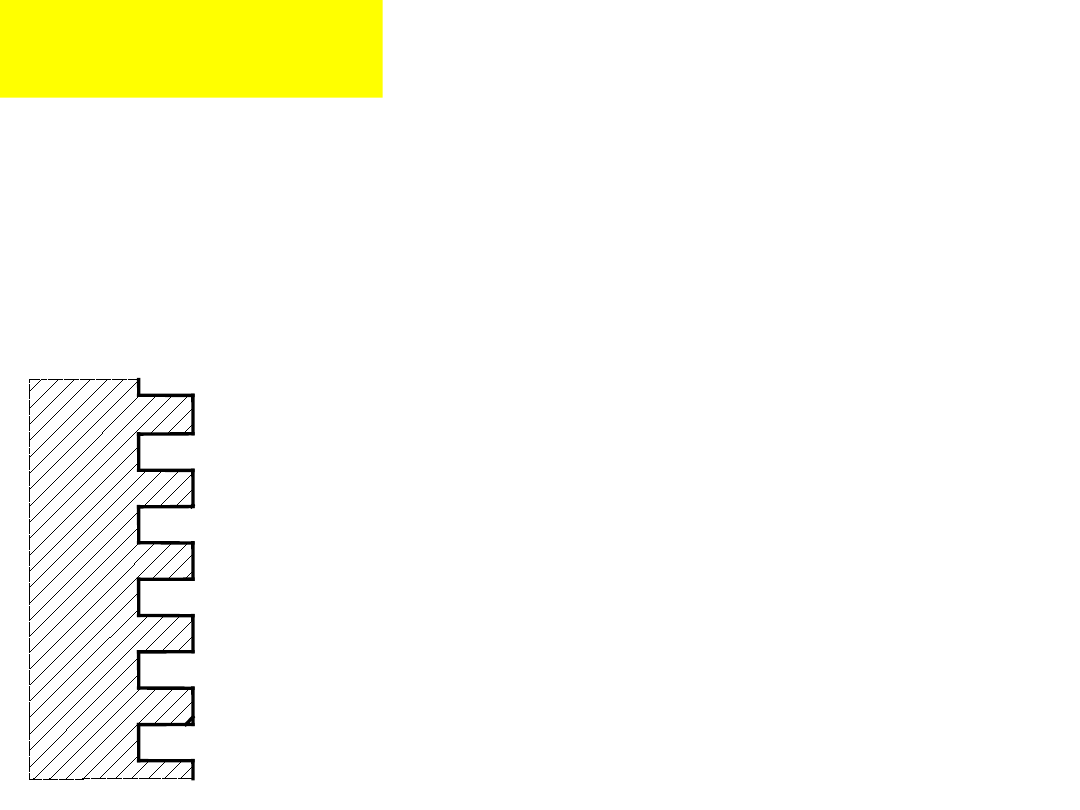
Zarys gwintu prostokątny stosowany jest
w mechanizmach śrubowych do zamiany
ruchu obrotowego na posuwisty w
przypadku, gdy wymagana jest duża
dokładność posuwu, np. napędu suportu
w tokarkach.
Gwint prostokątny ze
względu na trudności
wykonawcze i zmniejszoną
wytrzymałość, w porównaniu
do trapezowego, jest rzadko
stosowany.
Połączenia
śrubowe
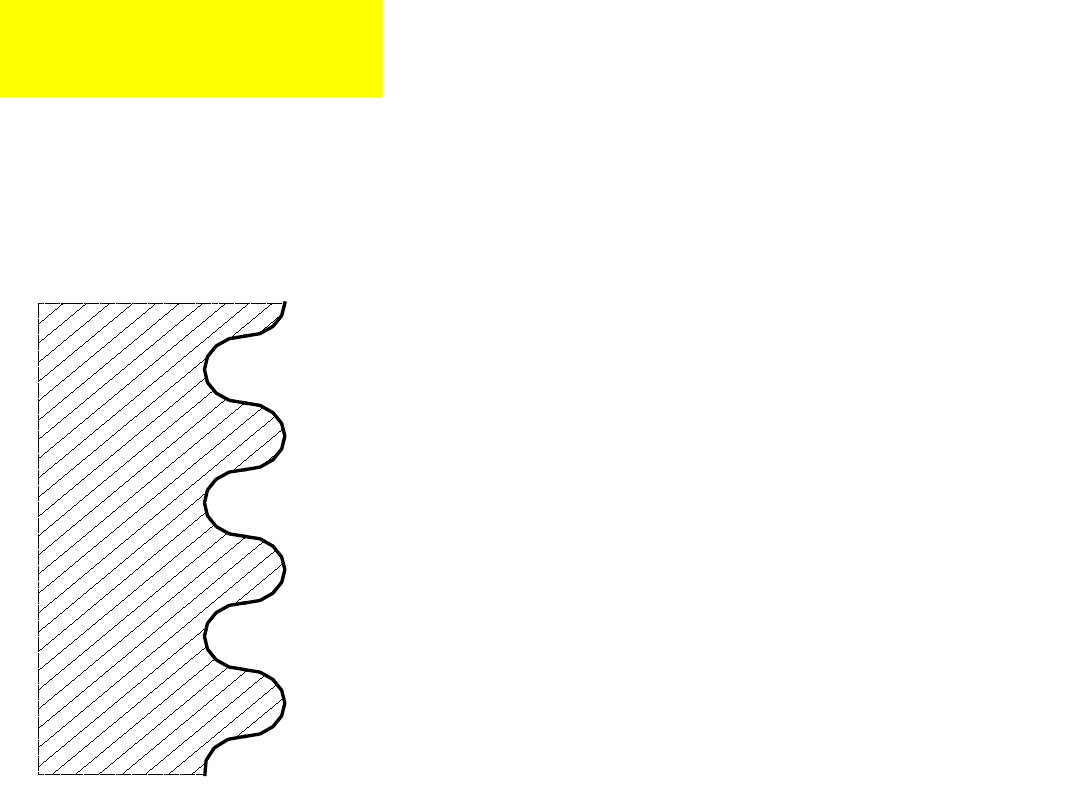
Zarys okrągły stosowany
jest w urządzeniach
poddanych obciążeniom
dynamicznym, np. złącza
wagonów kolejowych.
Połączenia
śrubowe
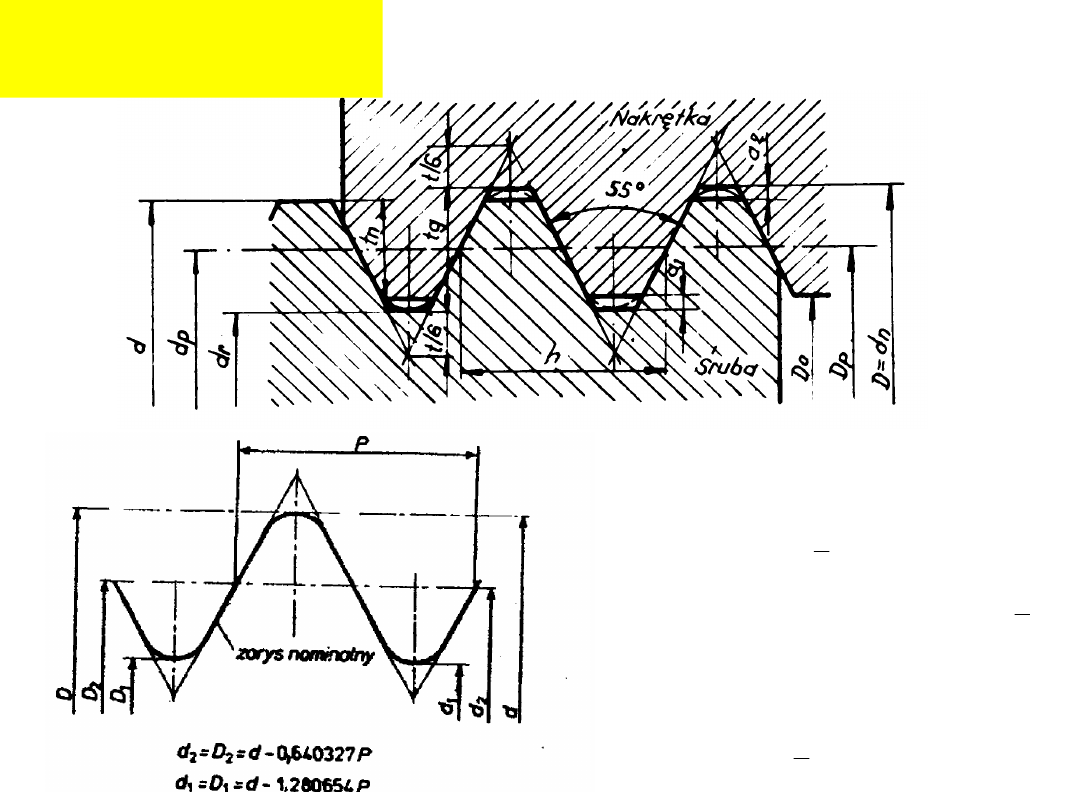
Gwinty
metryczne:
Przykład oznaczenia:
3(P1)LH
M64
8.8
-
70
25
,
1
M12
Śruba:
Połączenia
śrubowe
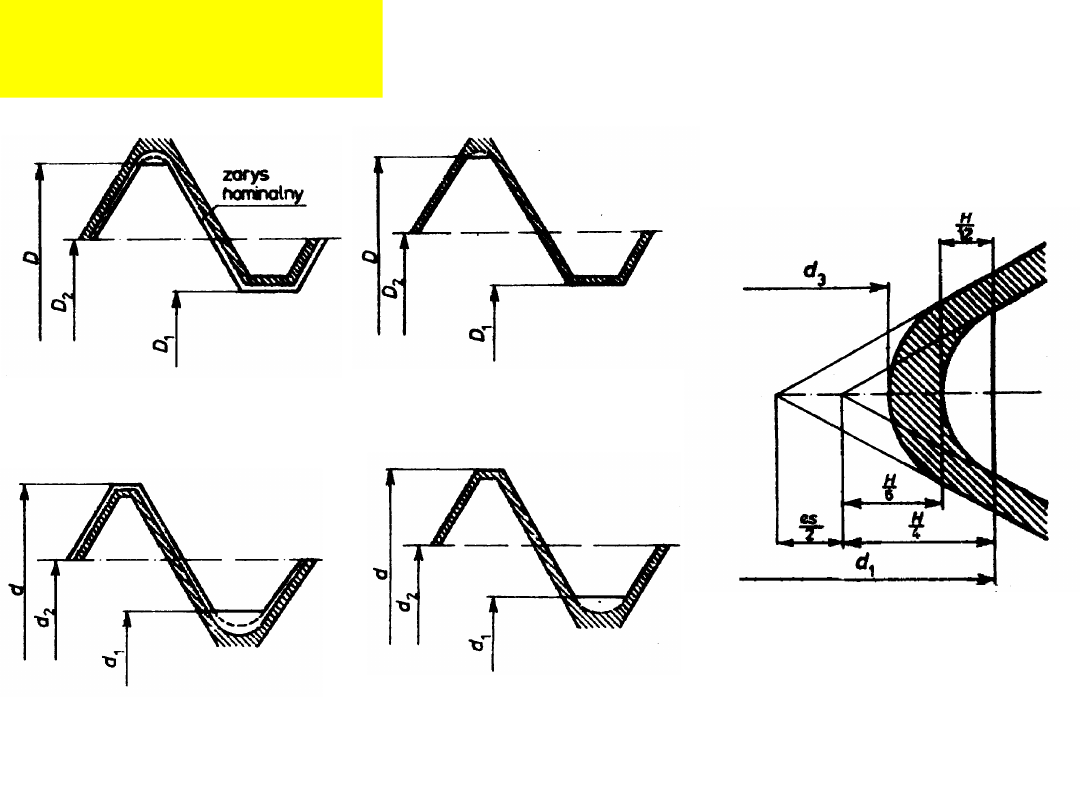
Pola tolerancji
(przykłady):
Nakrętka, pole G Nakrętka, pole H
Śruba, pola d,e,f,g Śruba, pole h
Minimalna
średnica
rdzenia śruby
Połączenia
śrubowe
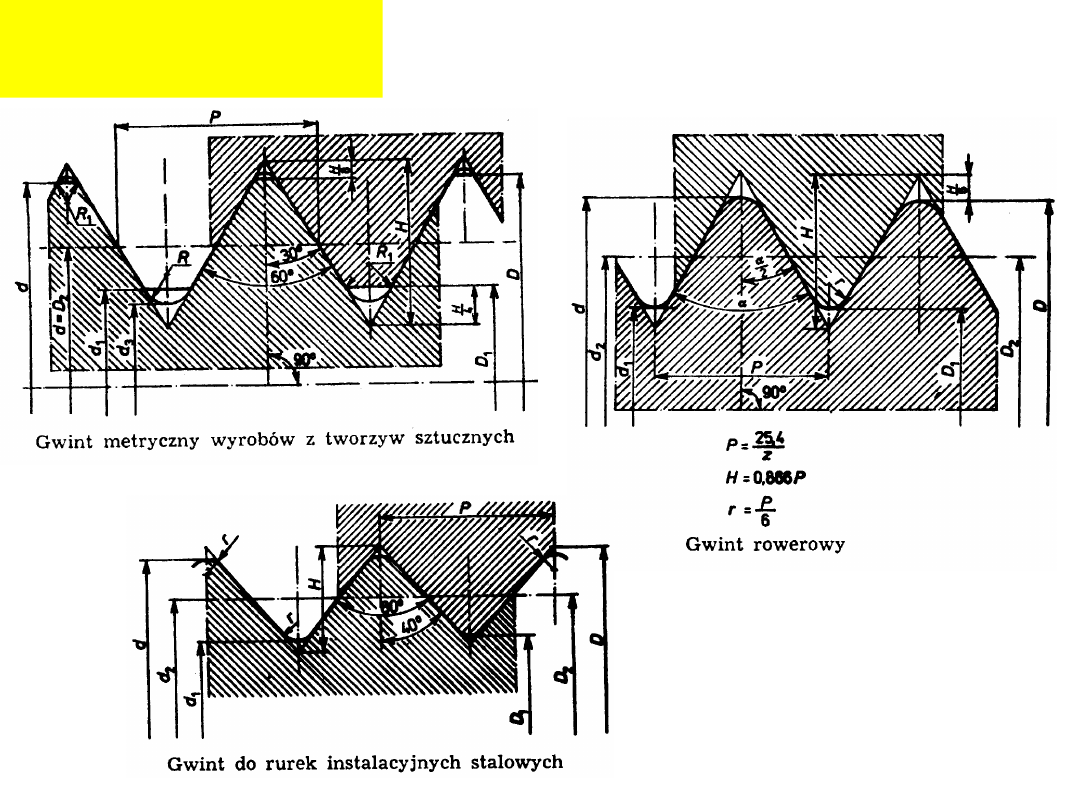
Gwinty
metryczne:
Przykład oznaczenia:
1
M4
Przykład oznaczenia:
28,2
Rw
Przykład oznaczenia:
P16
Połączenia
śrubowe
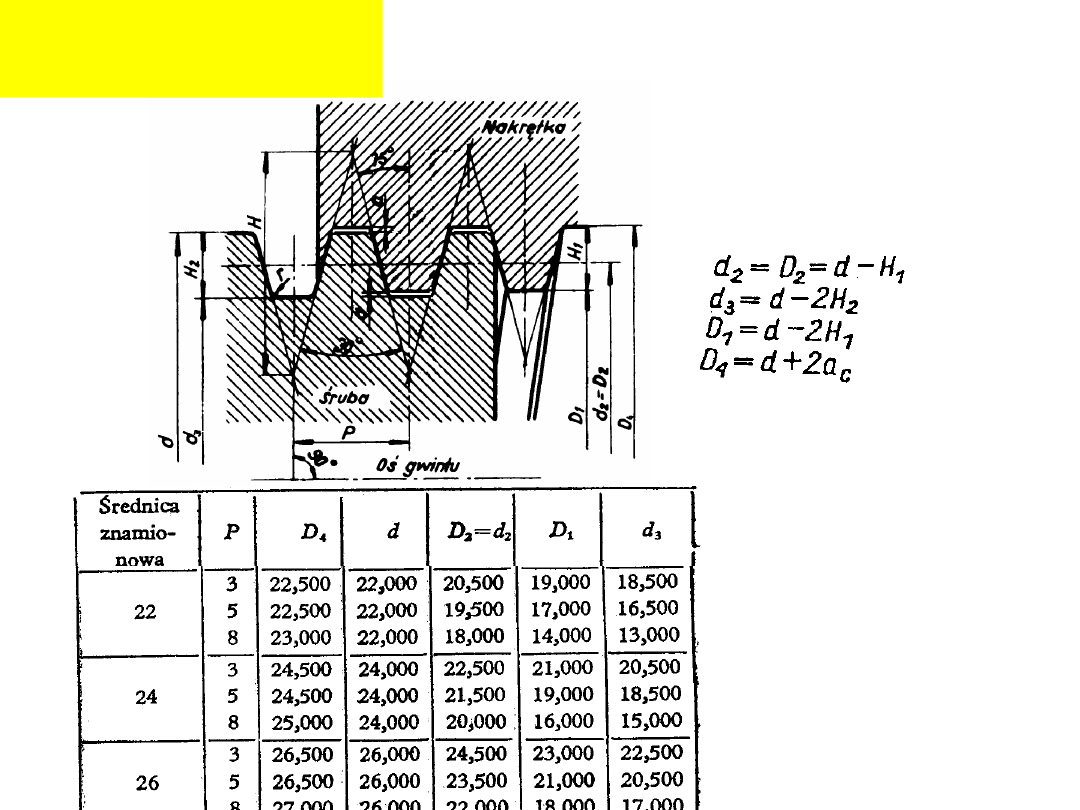
Gwinty calowe:
Przykłady oznaczenia
:
"
4
3
Gwint drobnozwojny:
"
6
1
W60
Gwint zwykły:
Gwint rurowy walcowy:
2
1
G1
Połączenia
śrubowe
Gwinty trapezowe
symetryczne:
Przykład oznaczenia:
LH
6
Tr48
Trapezowe
wiertnicze:
TrW, TrG, TrP;
Optyka
(wielokrotny, =60)
Połączenia
śrubowe
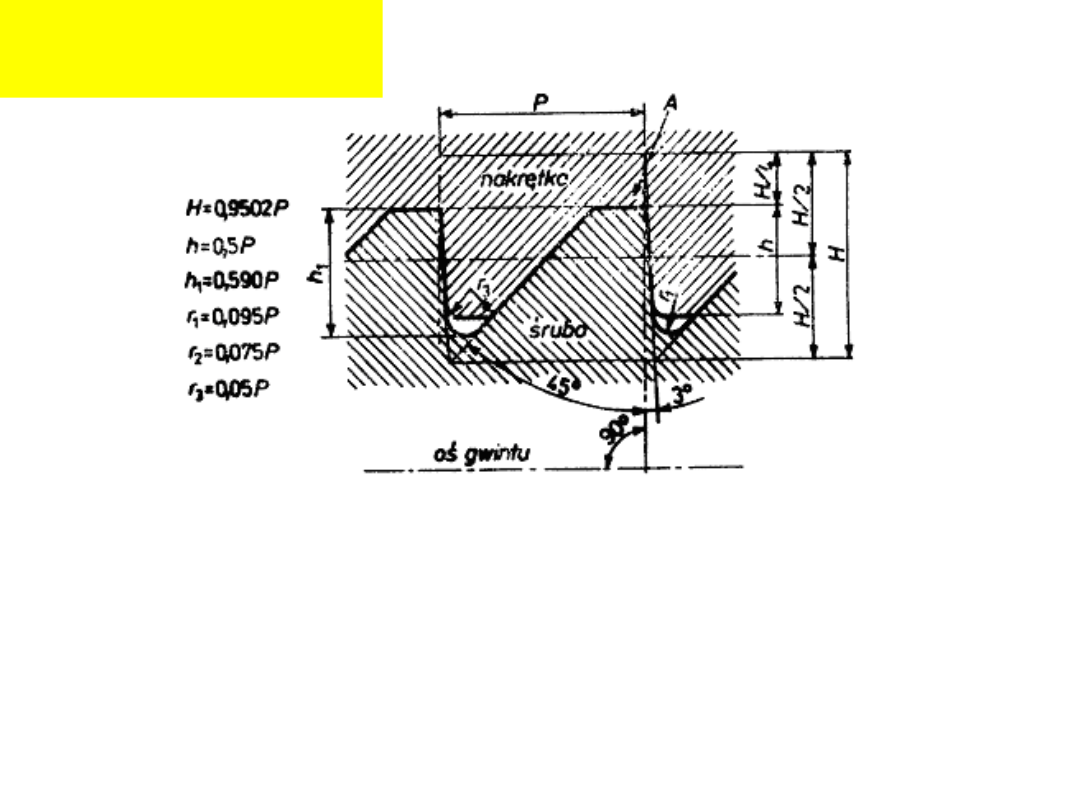
Gwinty trapezowe
niesymetryczne:
Przykłady oznaczeń
:
20(P10)
S80
Złącze gwintowe:
LH
20(P10)
S80
8
20
S45
Połączenia
śrubowe
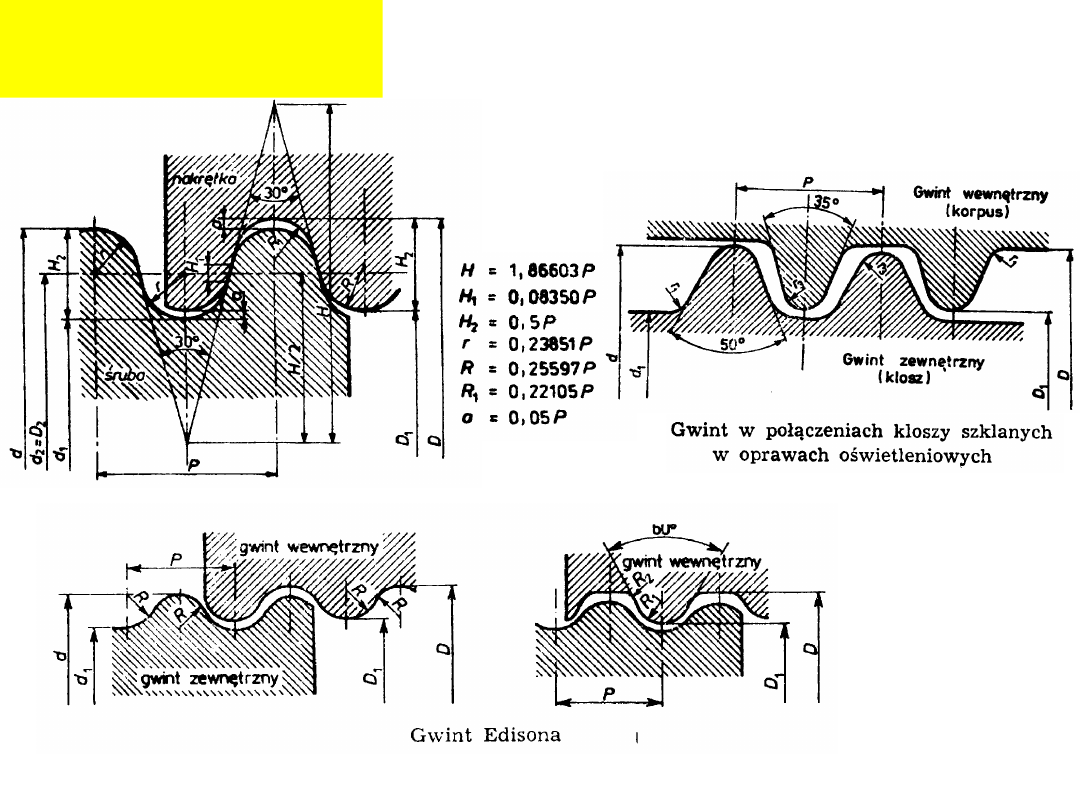
Gwinty okrągłe:
Przykład oznaczenia:
Rd40
Przykład oznaczenia:
E14/N
Przykład oznaczenia:
A85
Połączenia
śrubowe
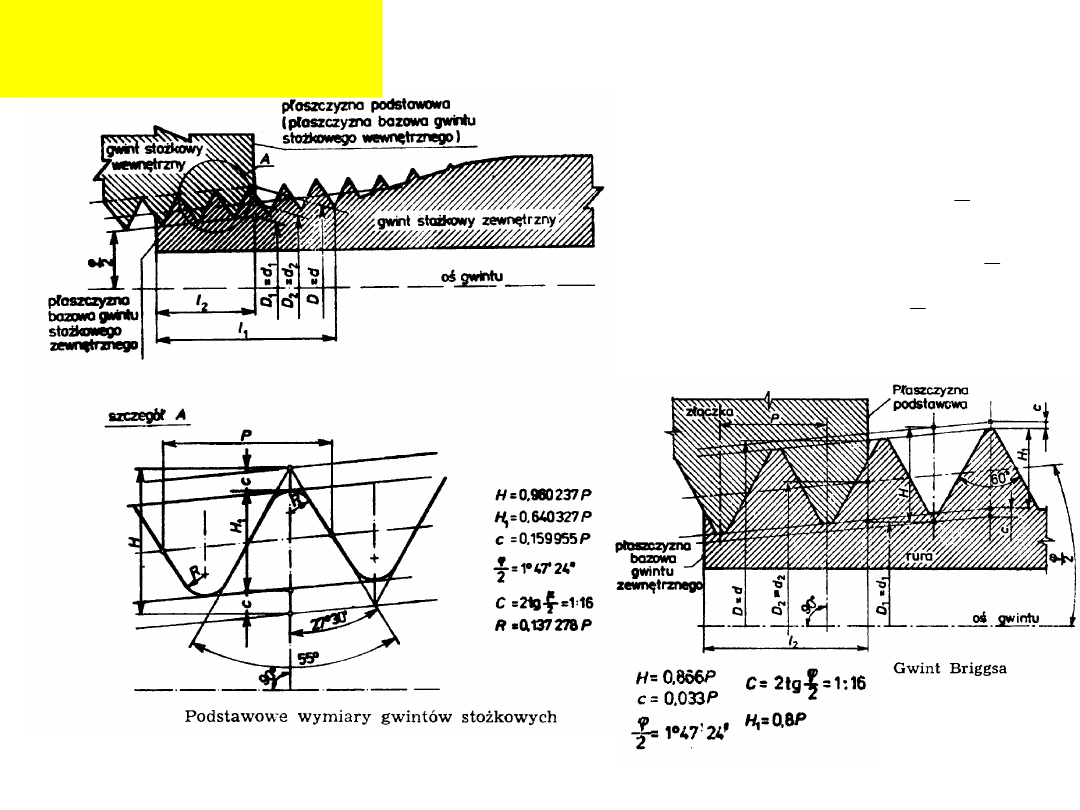
Gwinty stożkowe:
Przykłady oznaczenia
:
2
1
R1
Gwint wewnętrzny lewy:
LH
1
Rc
2
1
Gwint zewnętrzny:
Gwint Briggsa:
2
1
St.B
Gwint stożkowy
1
M6
Połączenia
śrubowe
Gwinty toczne:
Połączenia
śrubowe
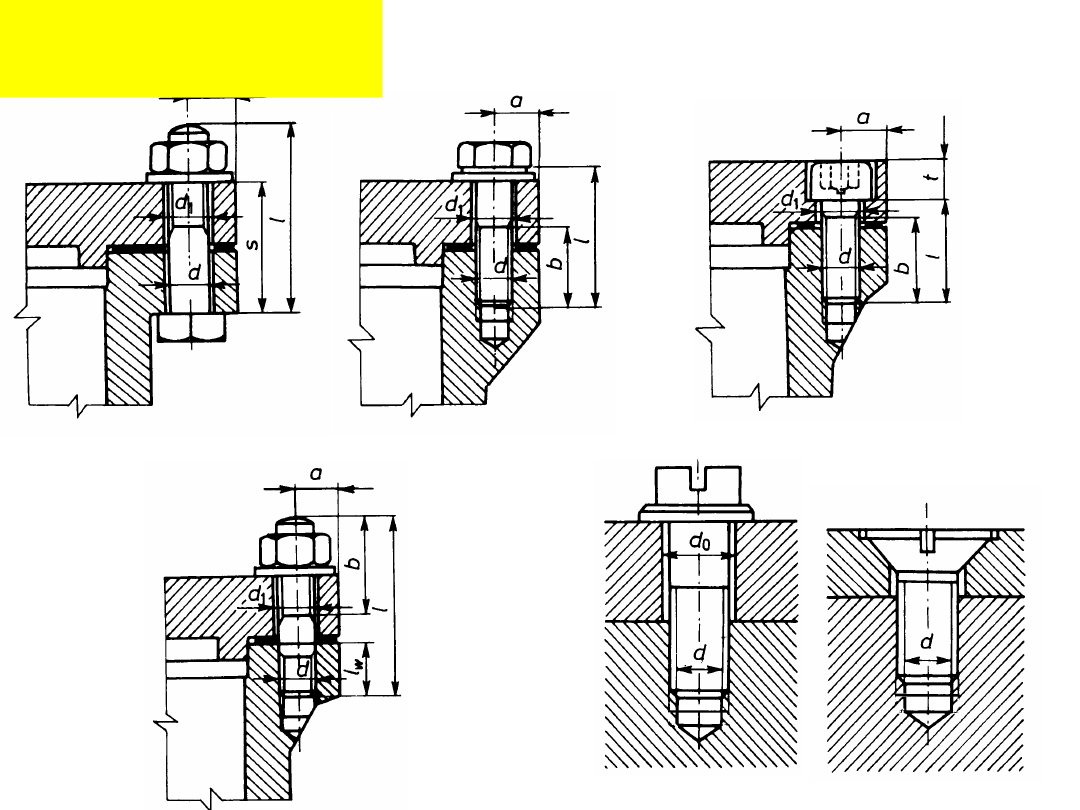
Śruba
„szpilk
a”
wkręty
Rodzaje połączeń
śrubowych:
Śruba z nakrętką
Połączenia
śrubowe
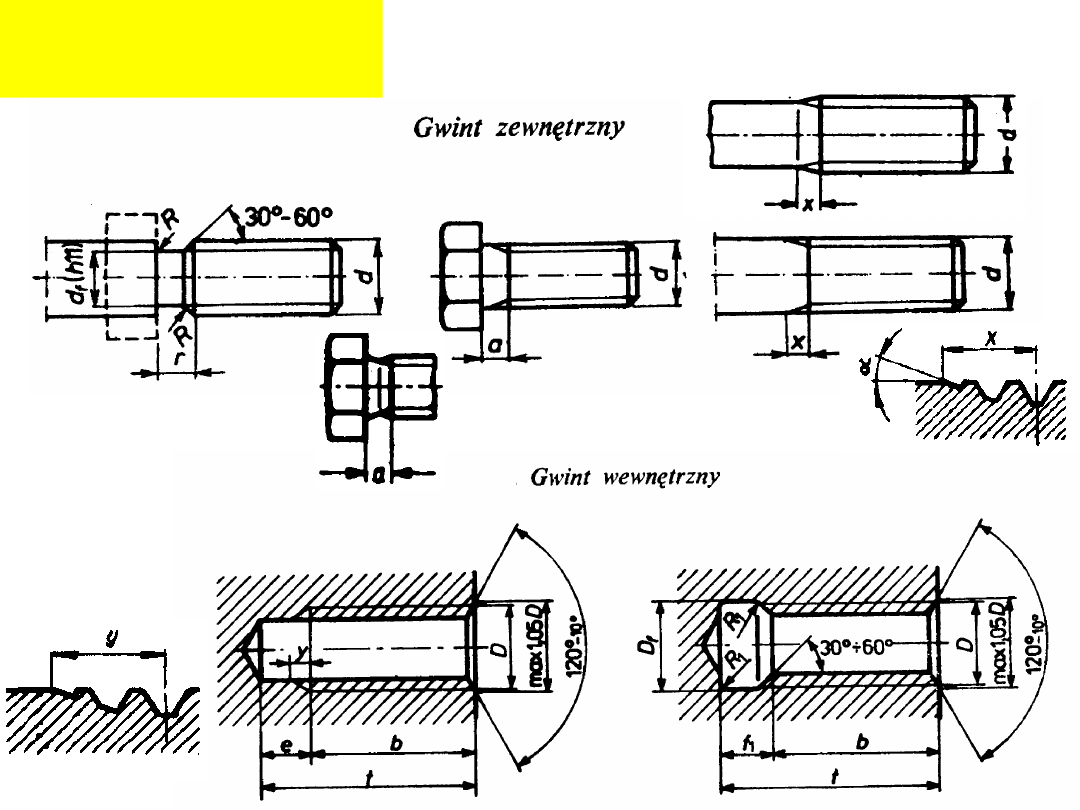
Szczegóły wykonania
gwintów:
Połączenia
śrubowe
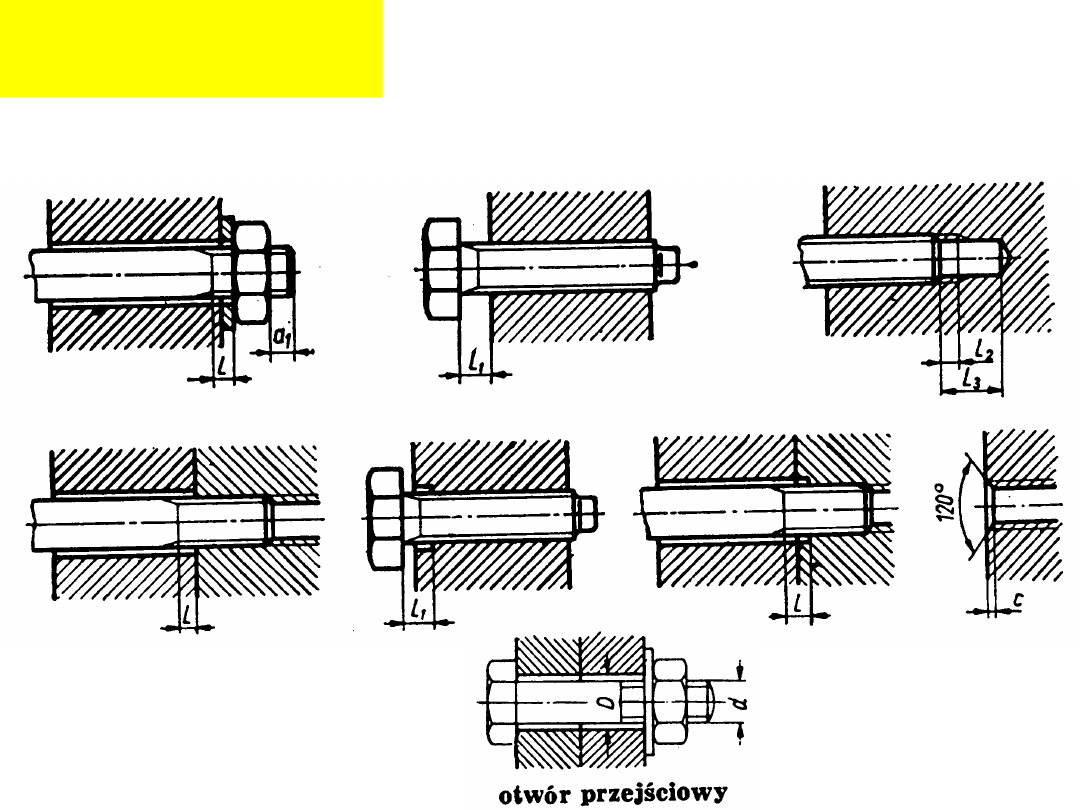
Nadmiar długości
gwintów
i głębokości
otworów:
Połączenia
śrubowe
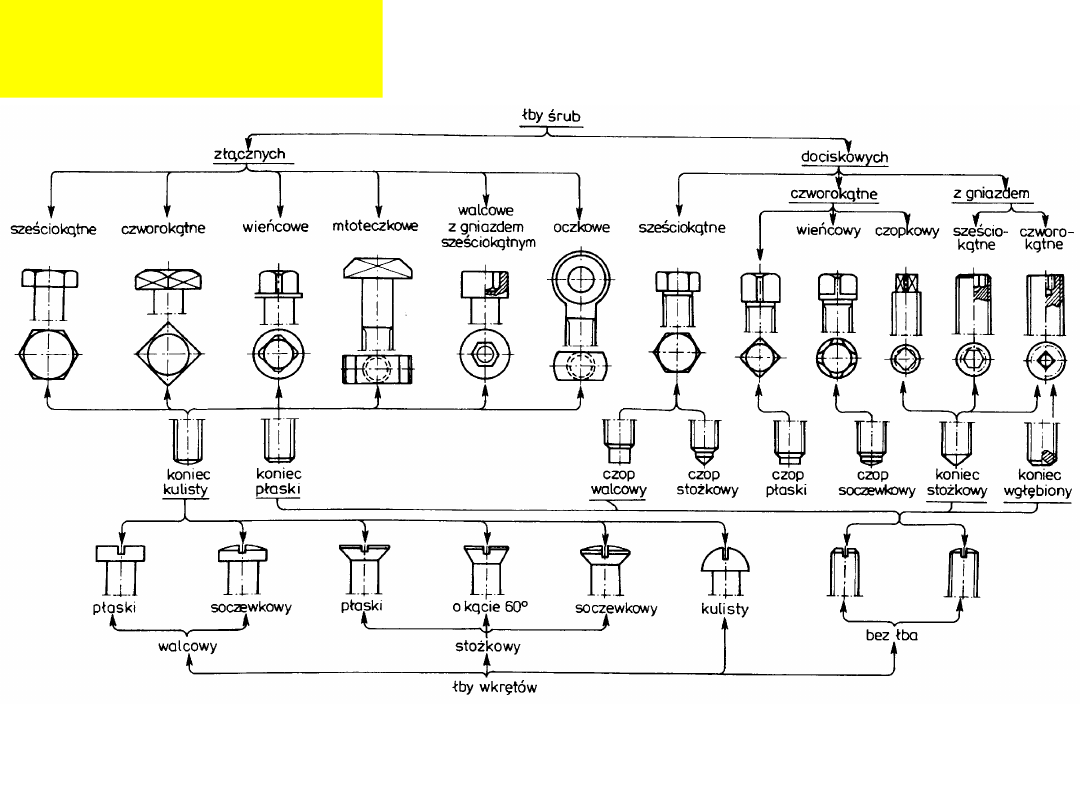
Rodzaje śrub i
wkrętów:
Połączenia
śrubowe
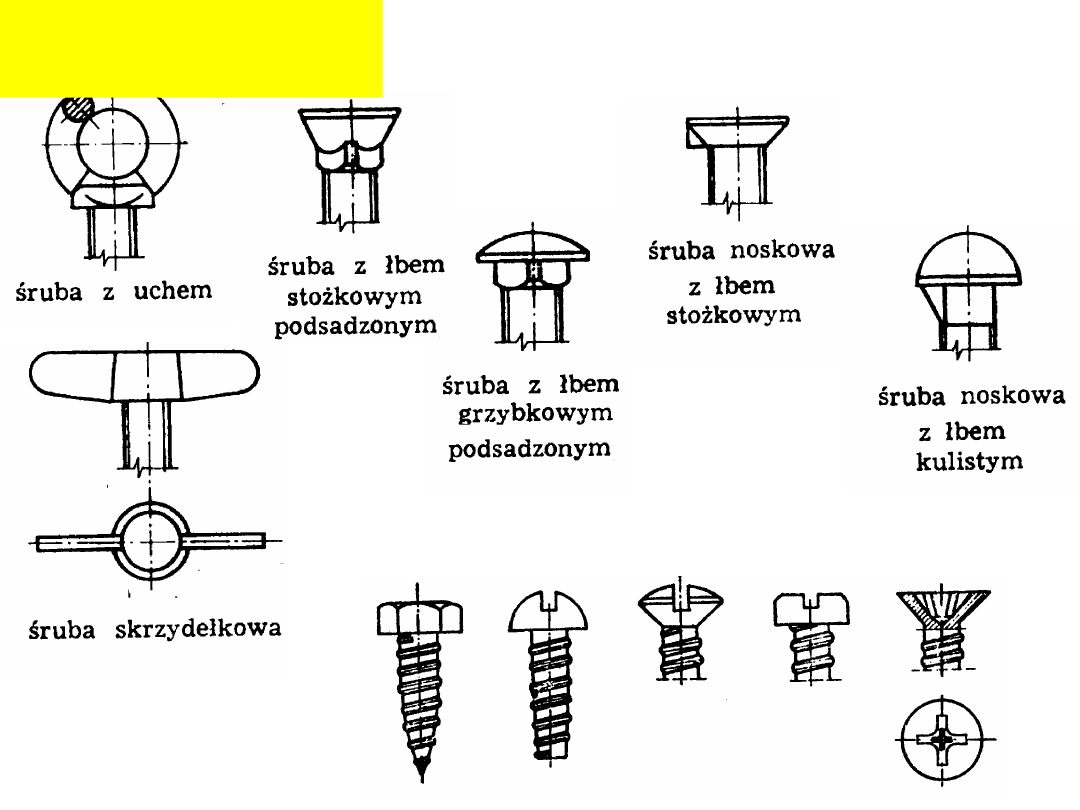
Inne śruby:
Wkręty
samogwintujące:
Połączenia
śrubowe
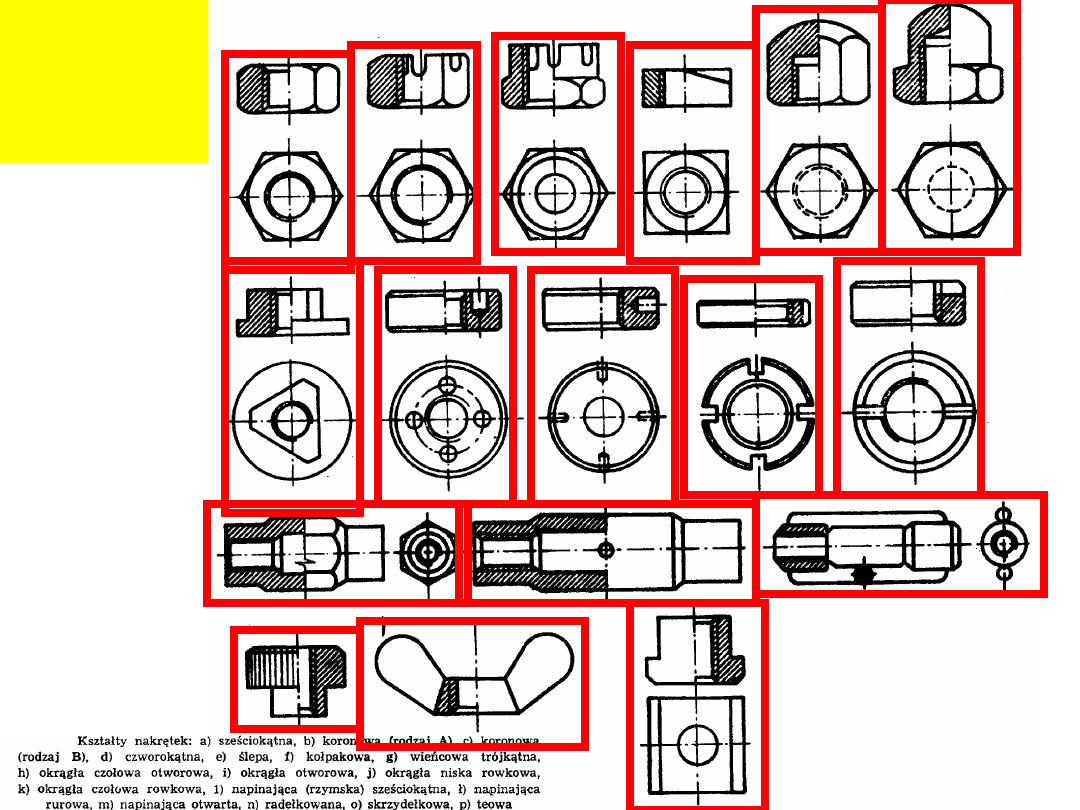
K
sz
ta
łt
y
n
a
k
rę
te
k
:
Połączen
ia
śrubowe
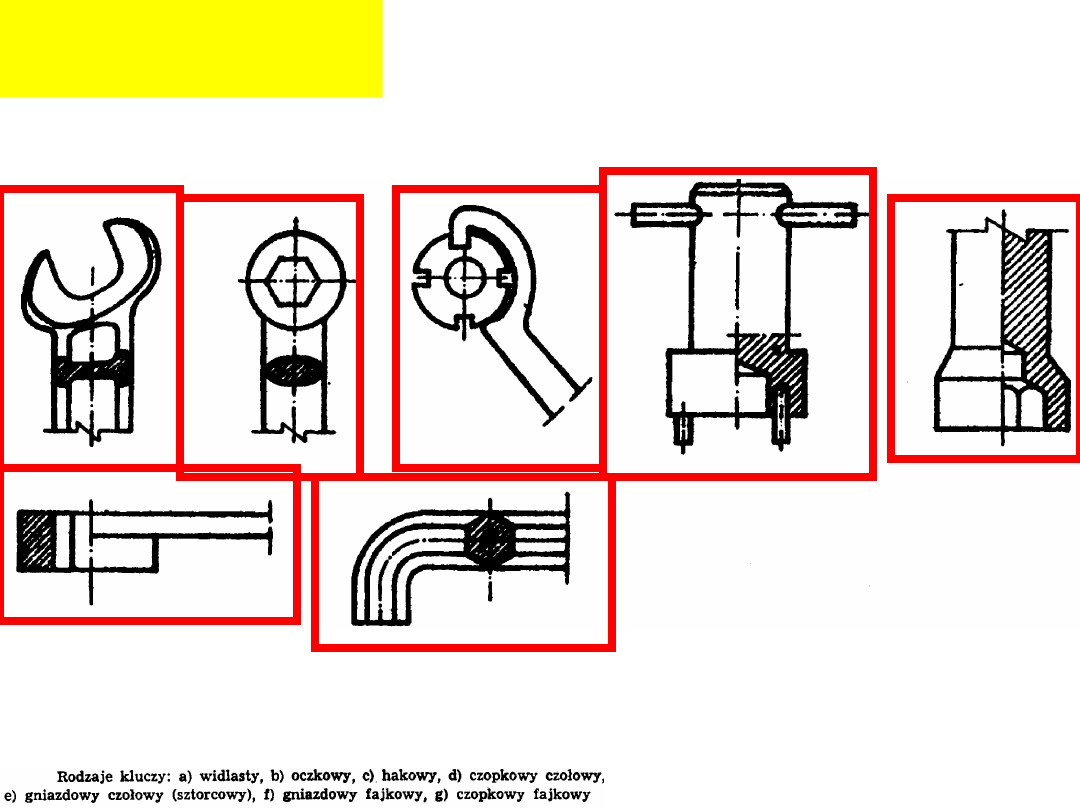
Rodzaje kluczy:
Połączenia
śrubowe
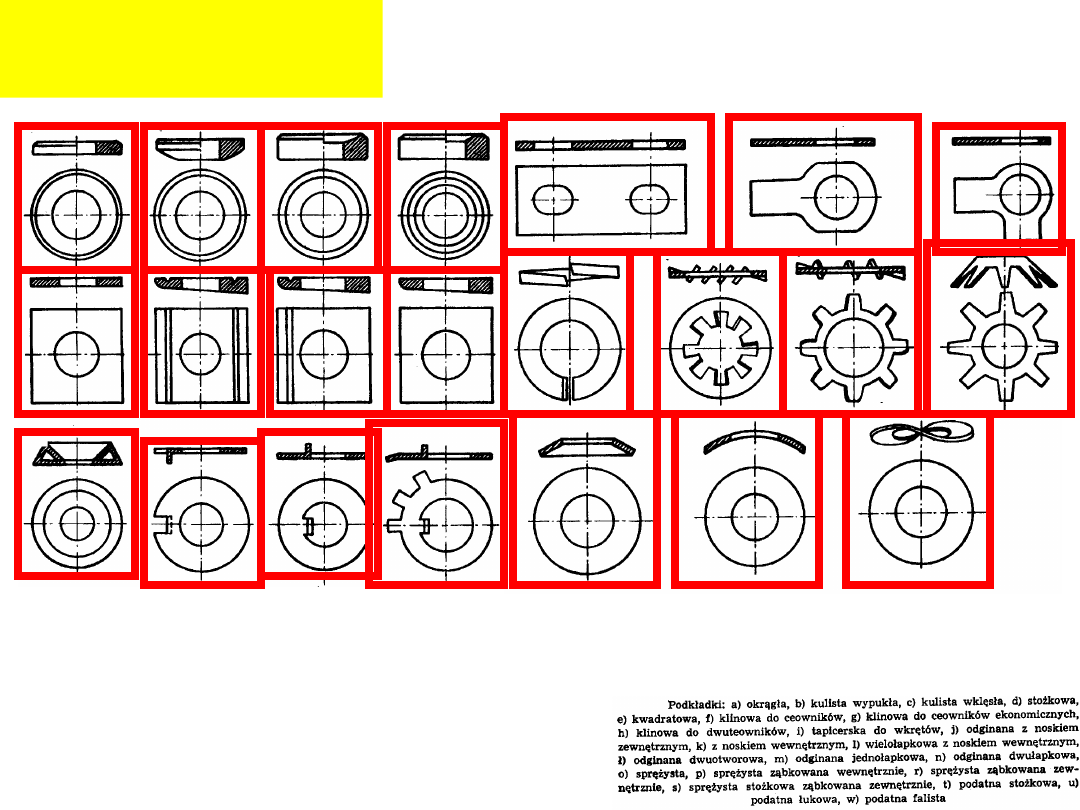
Rodzaje
podkładek:
Połączenia
śrubowe
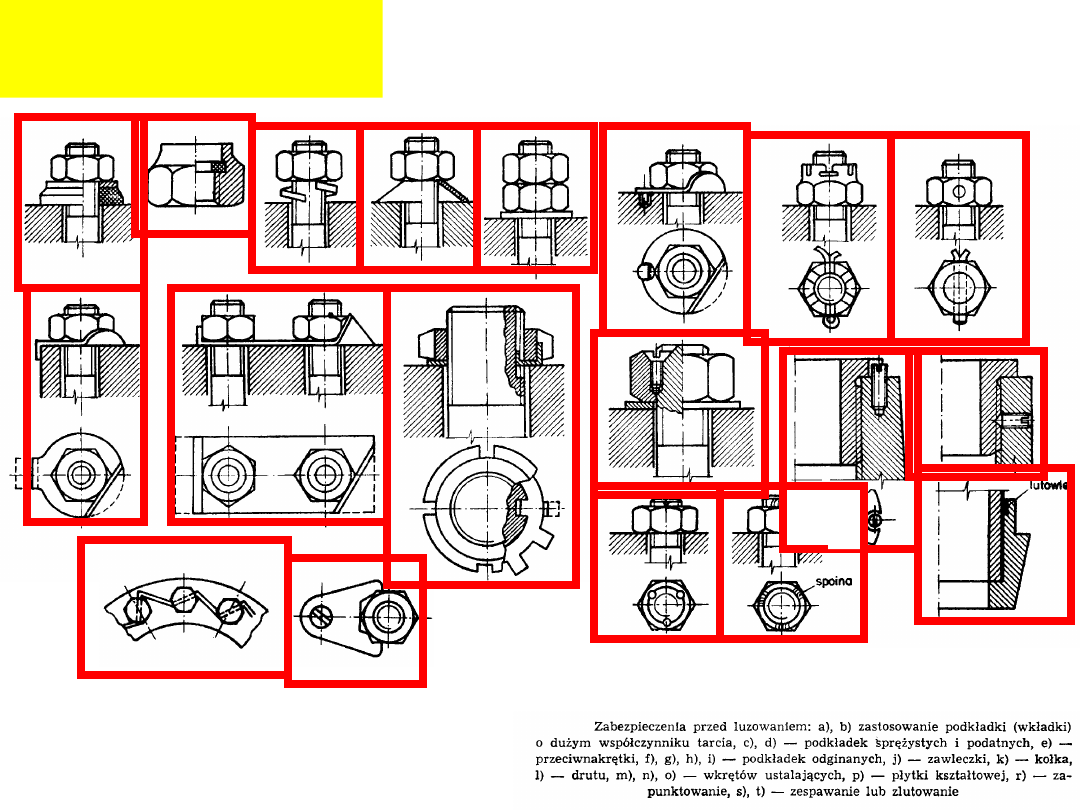
Rodzaje
zabezpieczeń:
Połączenia
śrubowe
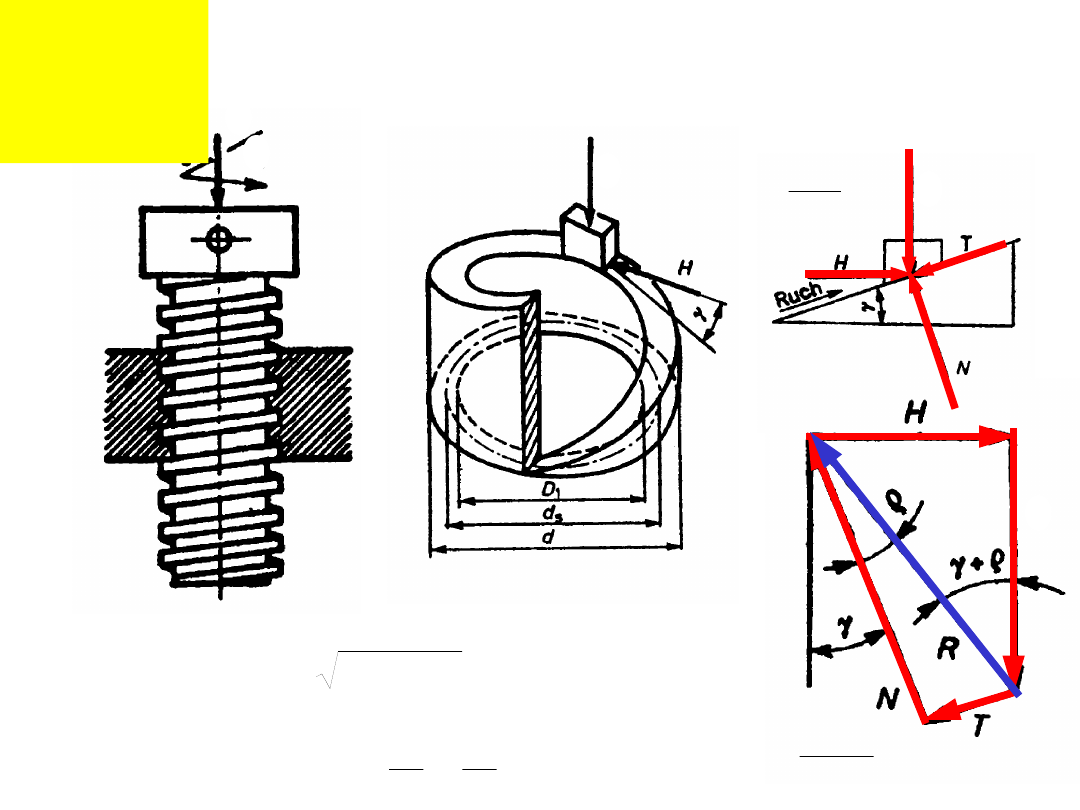
Rozkład sił na gwincie
(dokręcanie):
s
d
h
arctg
tg
F
d
d
H
M
s
s
s
2
2
tg
N
N
T
tg
F
H
T
N
R
2
2
F
F
F
F
2
1
D
d
d
s
Połączen
ia
śrubowe
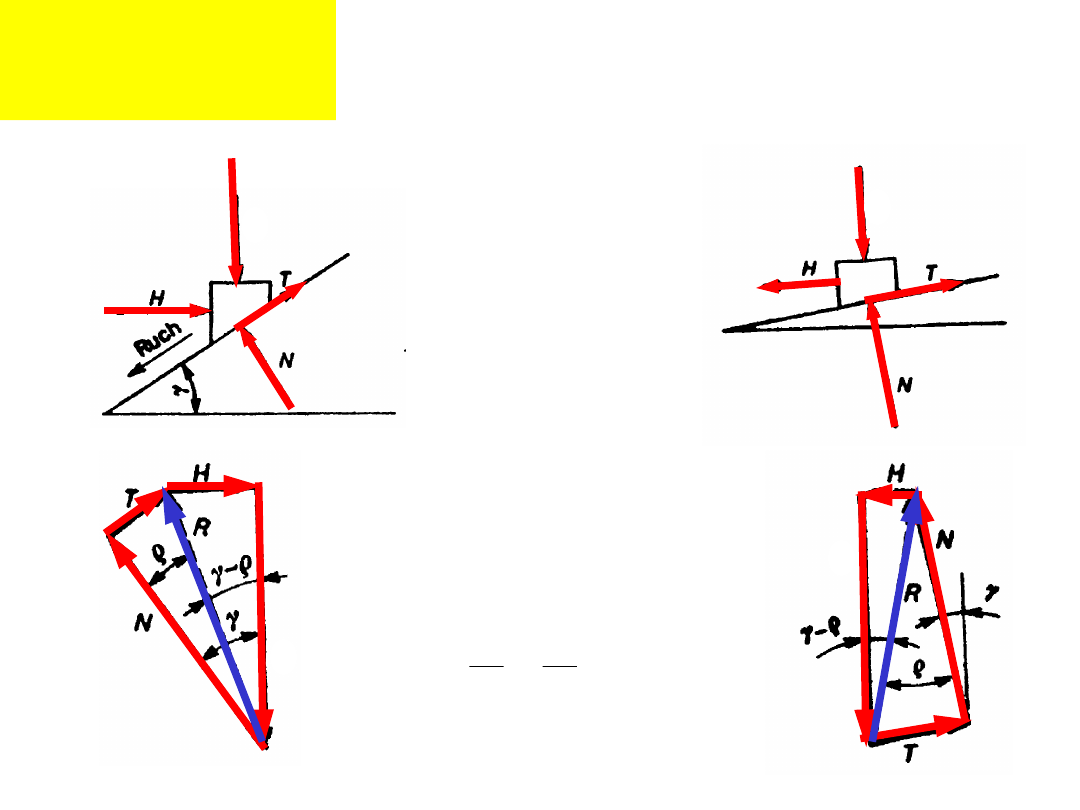
Rozkład sił na gwincie
(odkręcanie):
tg
F
d
d
H
M
s
s
s
2
2
tg
F
H
owny
niesamoham
Gwint
)
(
y
samohamown
Gwint
)
(
F
F
F
F
Połączenia
śrubowe
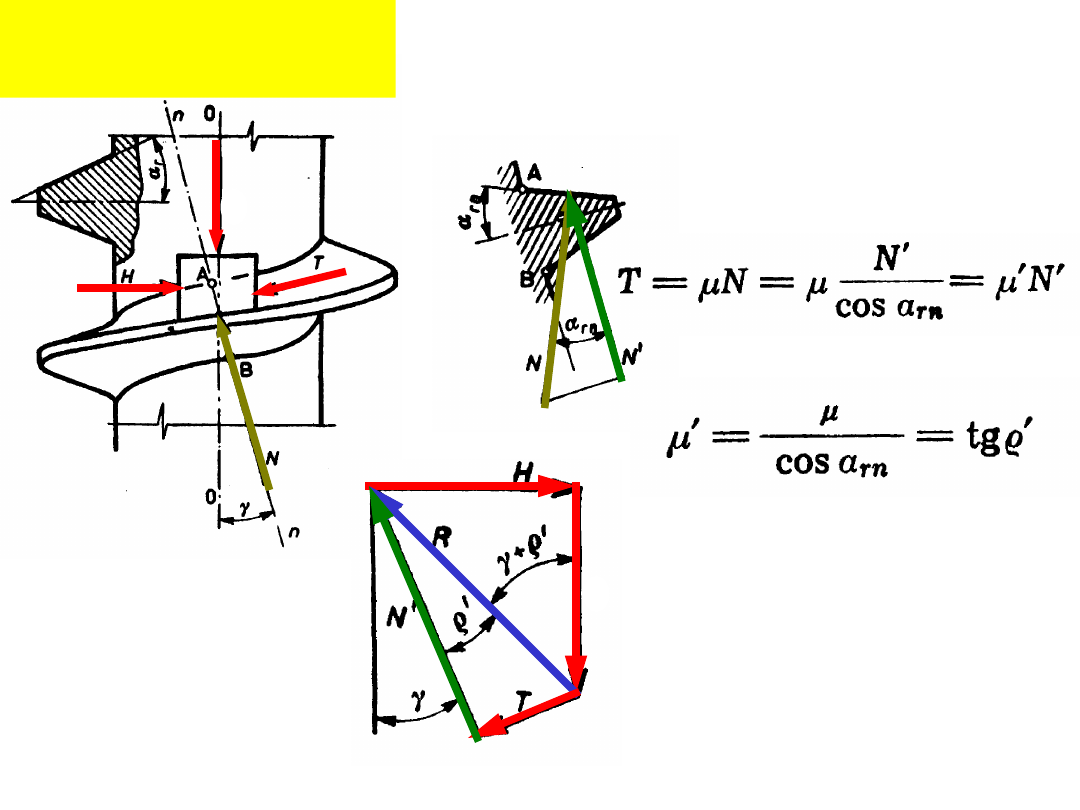
Rozkład sił na
gwincie:
F
F
'
tg
F
H
'
tg
F
H
Połączenia
śrubowe
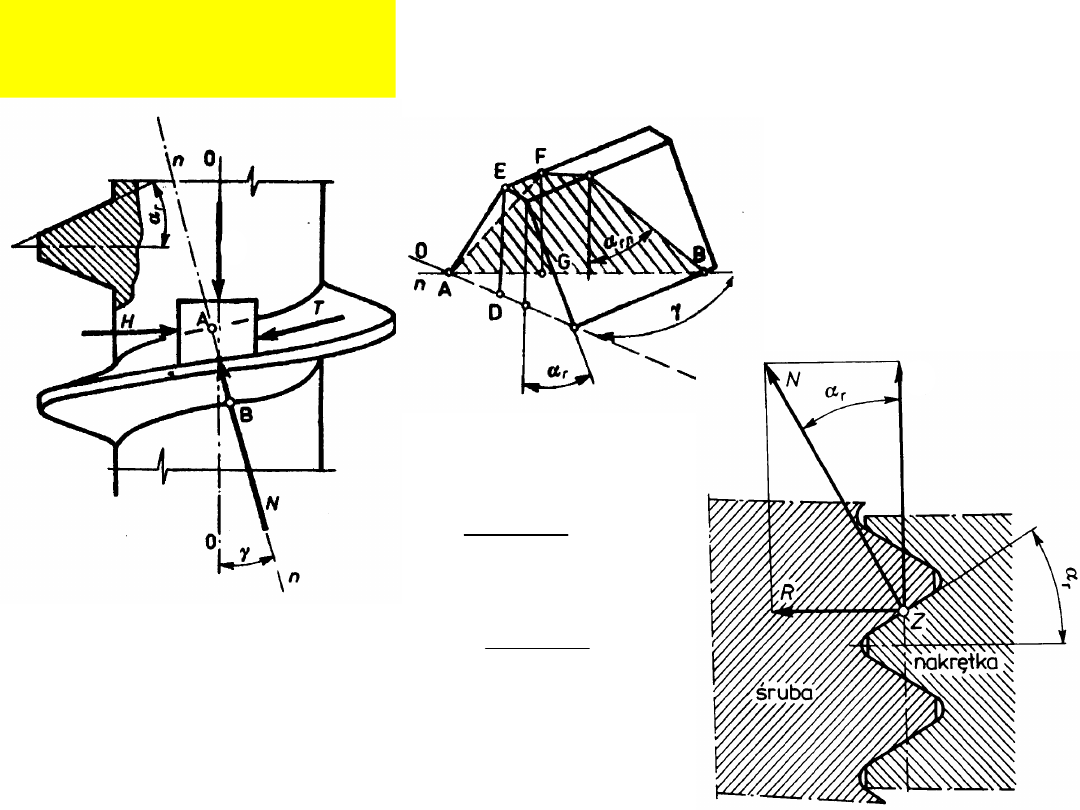
Rozkład sił na
gwincie:
cos
r
r
n
tg
tg
r
r
r
r
n
n
tg
tg
1
cos
'
tg
'
cos
cos
F
F
F
N
T
F
N
r
r
F
F
Połączenia
śrubowe
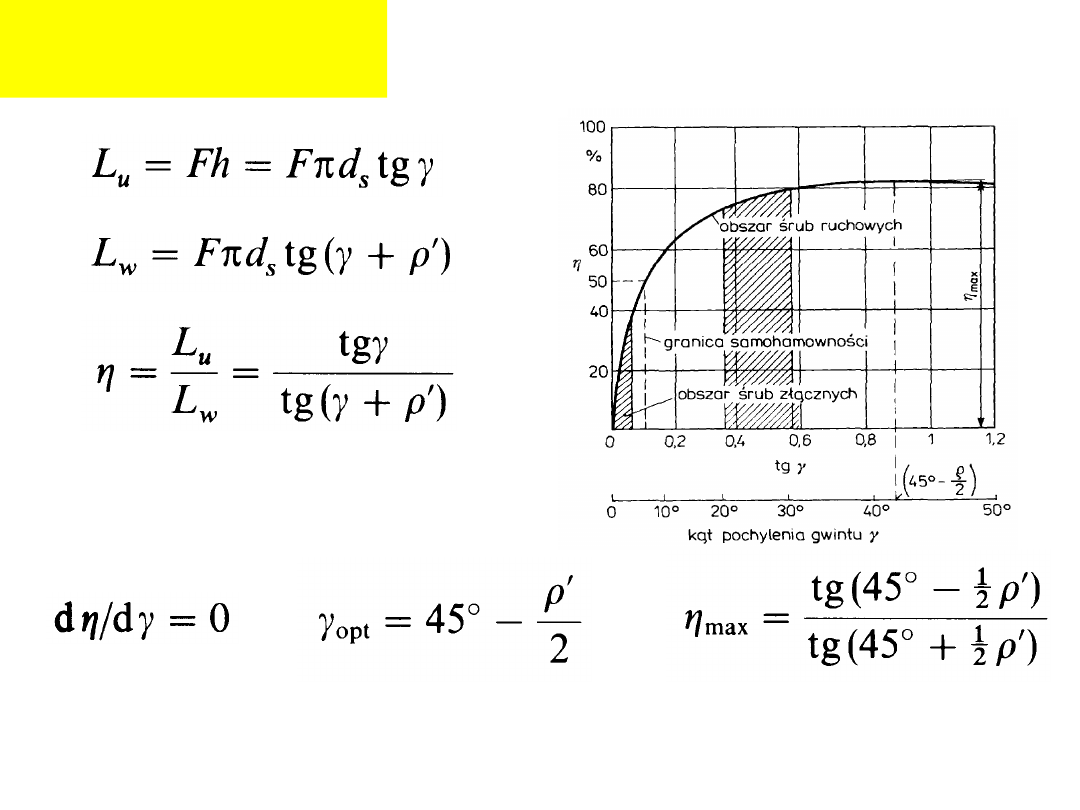
Sprawność mechanizmu
śrubowego:
'
y
samohamown
Gwint
Połączenia
śrubowe
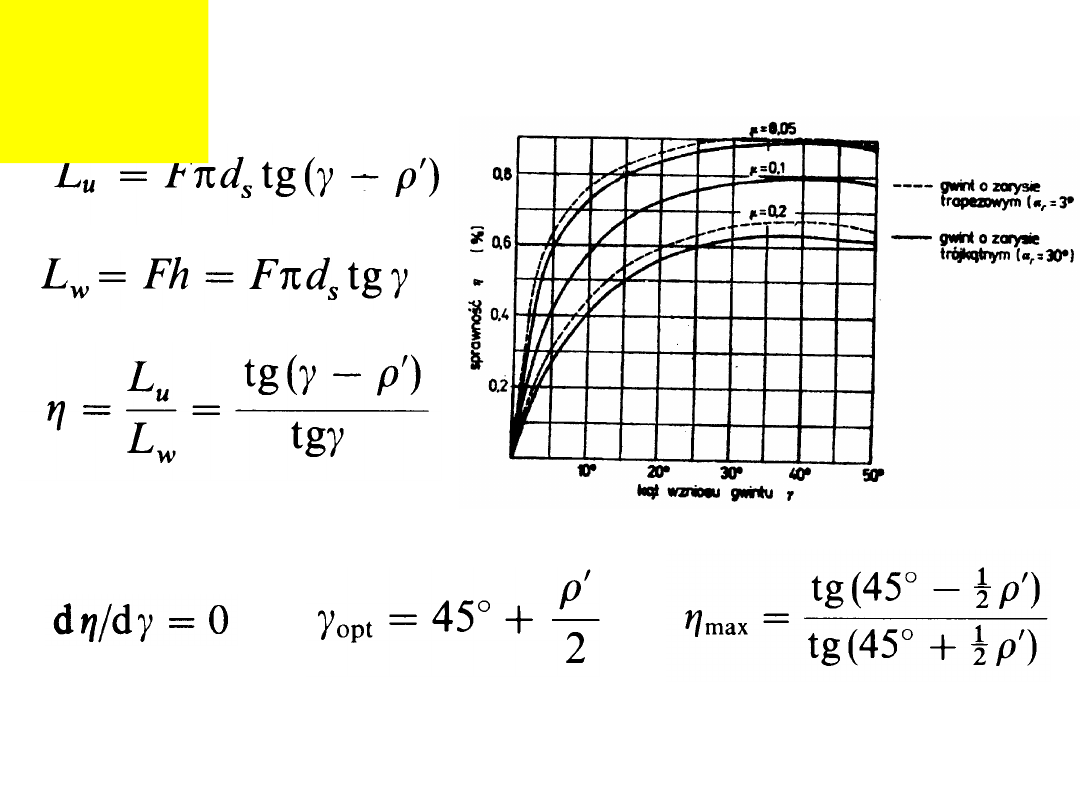
Sprawność mechanizmu
śrubowego:
'
owny
niesamoham
Gwint
Połączen
ia
śrubowe
Naciski równomierne:
Połączen
ia
śrubowe
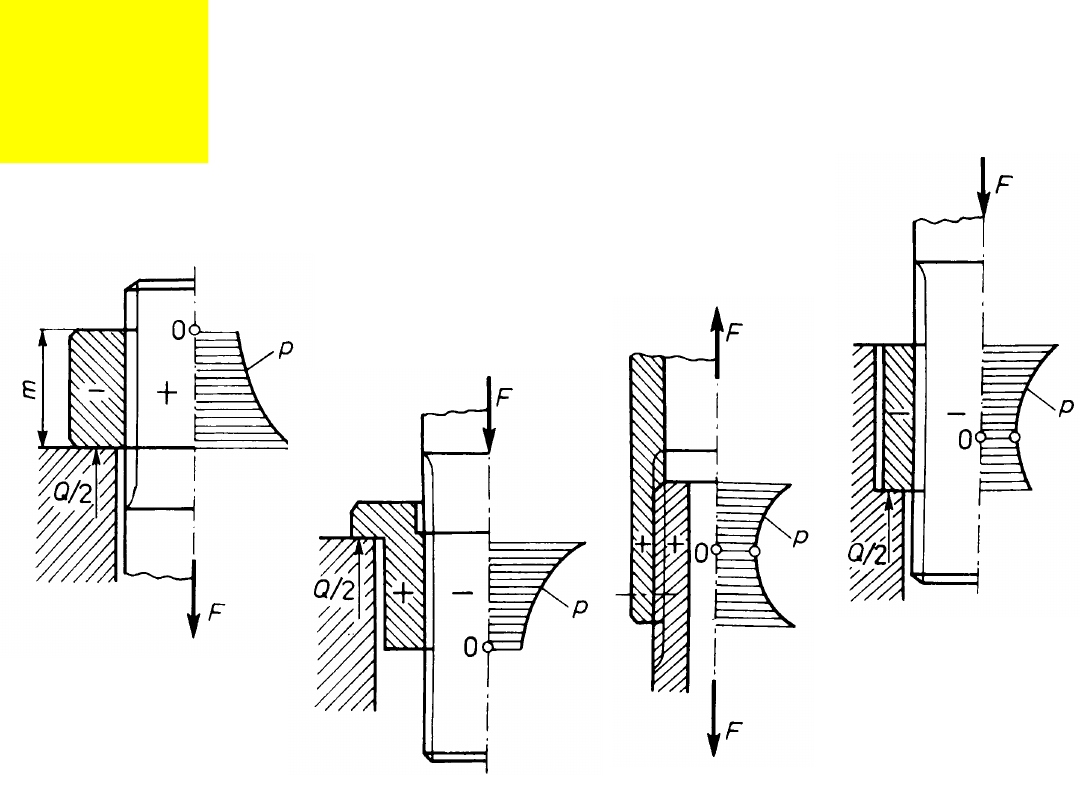
Rozkład nacisków
wzdłuż osi gwintu.
Połączen
ia
śrubowe
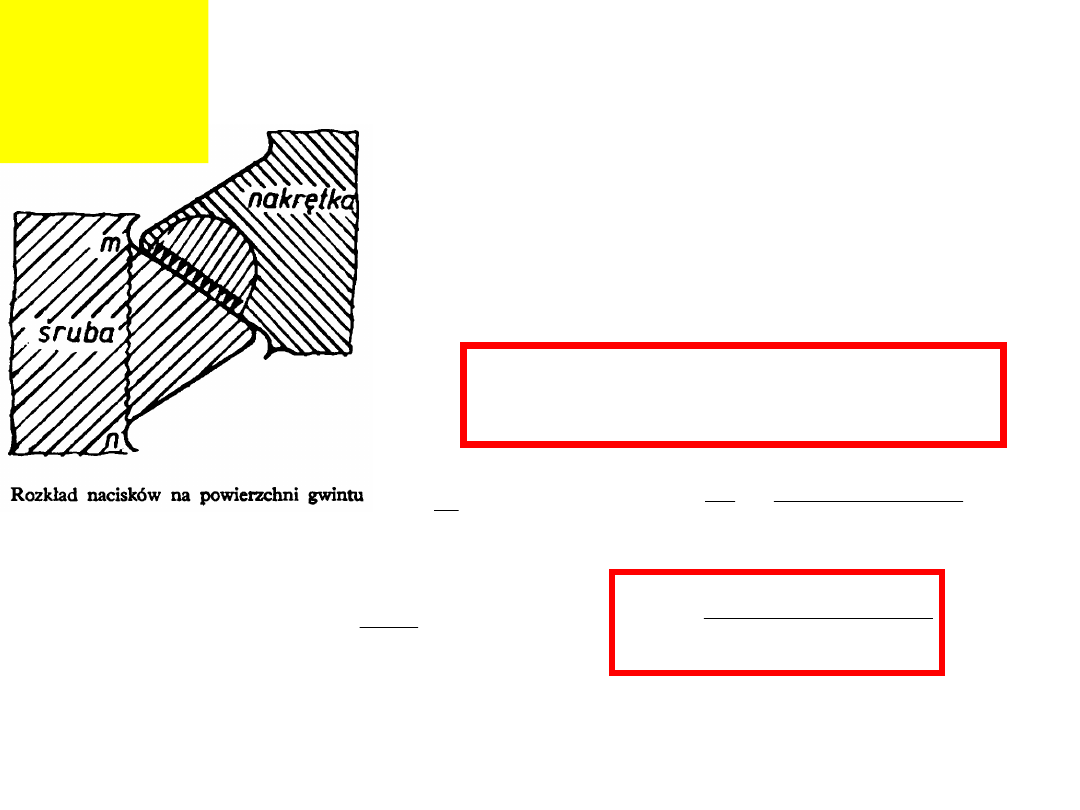
Obliczenia wytrzymałościowe.
Nitka gwintu – wysokość
nakrętki.
Możliwe zniszczenie wskutek
przekroczenia:
• naprężeń gnących w przekroju
m-n;
• naprężeń ścinających w
przekroju m-n;
• nacisków powierzchniowych na
powierzchniach
współpracujących.
dop
p
i
D
d
F
s
F
p
2
1
2
4
2
1
2
4
D
d
s
P
z
H
i
n
dop
n
p
z
D
d
FP
H
2
1
2
4
Połączen
ia
śrubowe
Jeśli gwint jest dostatecznie wytrzymały na naciski, to
wystarczająca jest jego wytrzymałość na inne rodzaje
zniszczenia ( ścinanie, zginanie etc.)
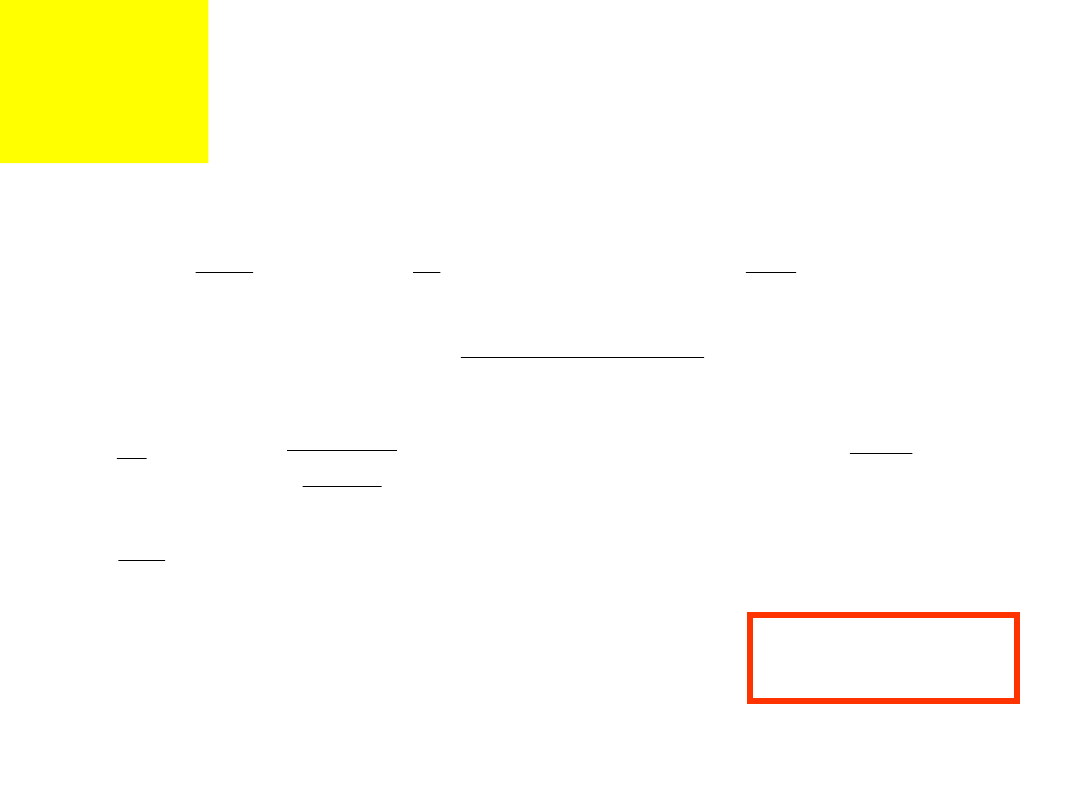
Obliczenia wytrzymałościowe.
Znormalizowana wysokość
nakrętki.
Połączen
ia
śrubowe
Wyrzymałość gwintu na naciski powinna być większa od
wytrzymałości rdzenia śruby na rozerwanie.
)
(
5
,
0
4
4
0
2
0
2
2
D
d
d
P
H
p
D
d
i
p
k
d
F
S
Z
n
dop
dop
r
r
)
(
4
0
2
D
d
d
p
P
d
k
H
s
dop
Z
r
r
n
;
88
,
0
d
d
S
r
;
54
,
1
2
D
d
P
0
Z
d
8
,
0
d
r
d
27
,
0
p
k
H
dop
r
n
5
,
2
p
k
dop
r
d
67
,
0
H
n
d
H
n
48
,
0
d
H
n
8
,
0
S
n
g
H
3
Jeśli:
Jeśli:
Podobnie dla
ścinania:
Normalne nakrętki dla śrub
złącznych:
Normalne nakrętki dla gwintów rurowych (g
S
- grubość
ścianki rury):
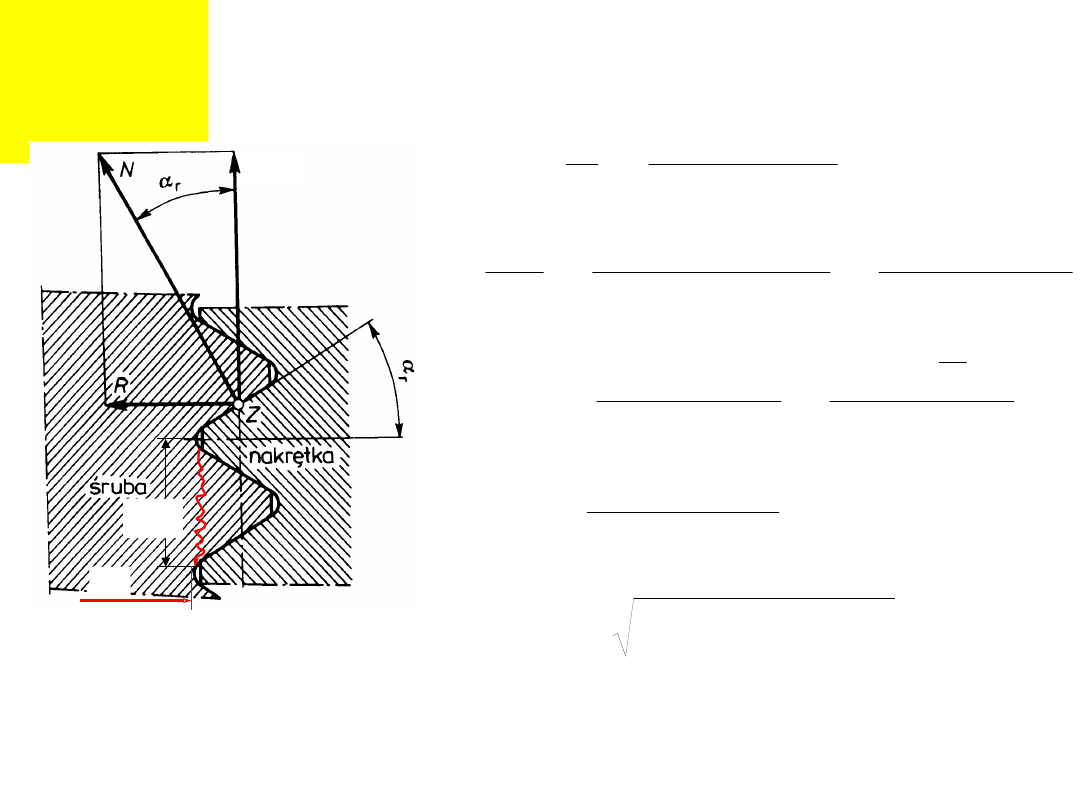
Obliczenia wytrzymałościowe
dowolnego gwintu (nienormalizowanego)
Połączen
ia
śrubowe
h
s
d
r
F
dop
p
D
d
i
F
A
F
p
)
(
4
2
0
2
2
2
3
6
/
5
,
0
S
r
r
S
S
r
r
S
X
g
g
h
d
i
d
d
F
h
d
i
d
d
F
W
M
S
r
S
r
c
h
d
i
Ftg
h
d
i
R
2
S
r
t
h
d
i
F
)
(
3
2
2
gj
g
t
c
g
Z
k
k
Wytrzymałość gwintu znormalizowanego dla tego samego
materiału oraz średnicy d nie zależy od podziałki gwintu P
Z
, a tylko
od jego kształtu i wysokości nakrętki H
n
. Gwinty zwykłe i
drobozwojne o tej samej średnicy d śruby są jednakowo
wytrzymałe
.
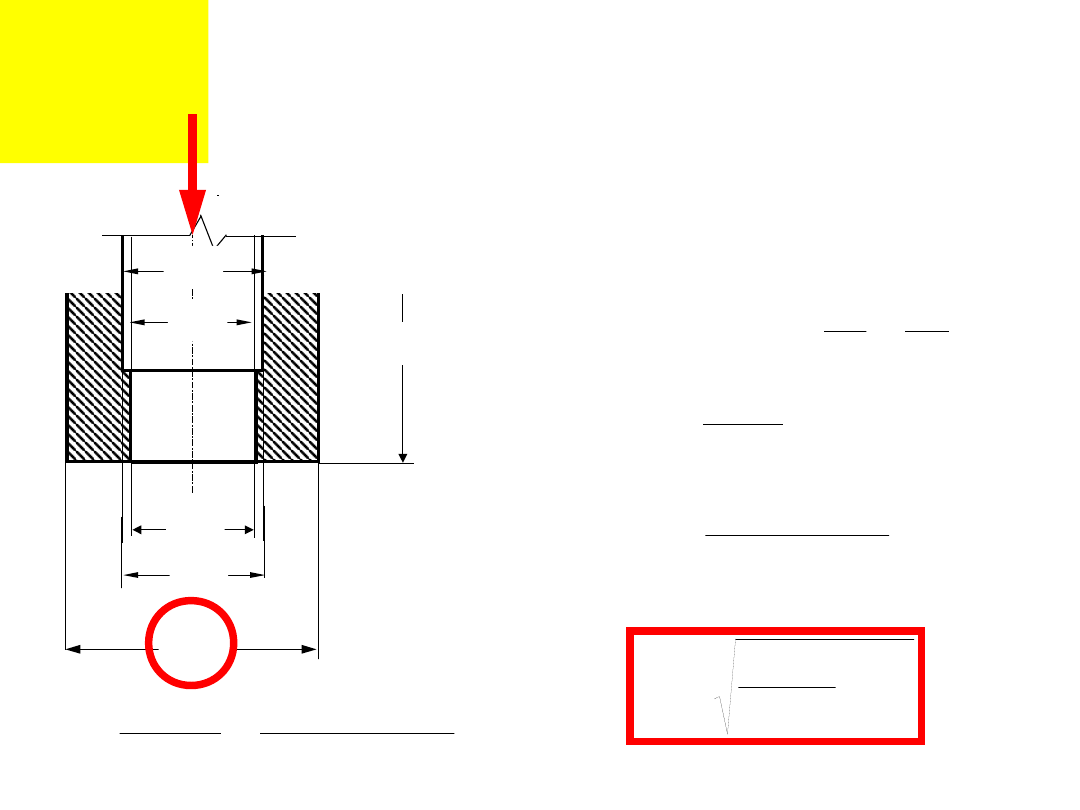
Obliczenia wytrzymałościowe.
Zewnętrzna średnica nakrętki- z równych
odkształceń
śruby i nakrętki.
E
n
n
ś
ś
n
ś
E
E
2
1
4
d
F
ś
2
2
4
D
D
F
z
n
n
z
ś
E
D
D
F
E
d
F
2
2
2
1
4
4
2
2
1
D
E
E
d
D
n
ś
z
Połączen
ia
śrubowe
d
1
D
Z
F
d
D
D
0
d
1
d
H
n
Nakrętki nieznormalizowane
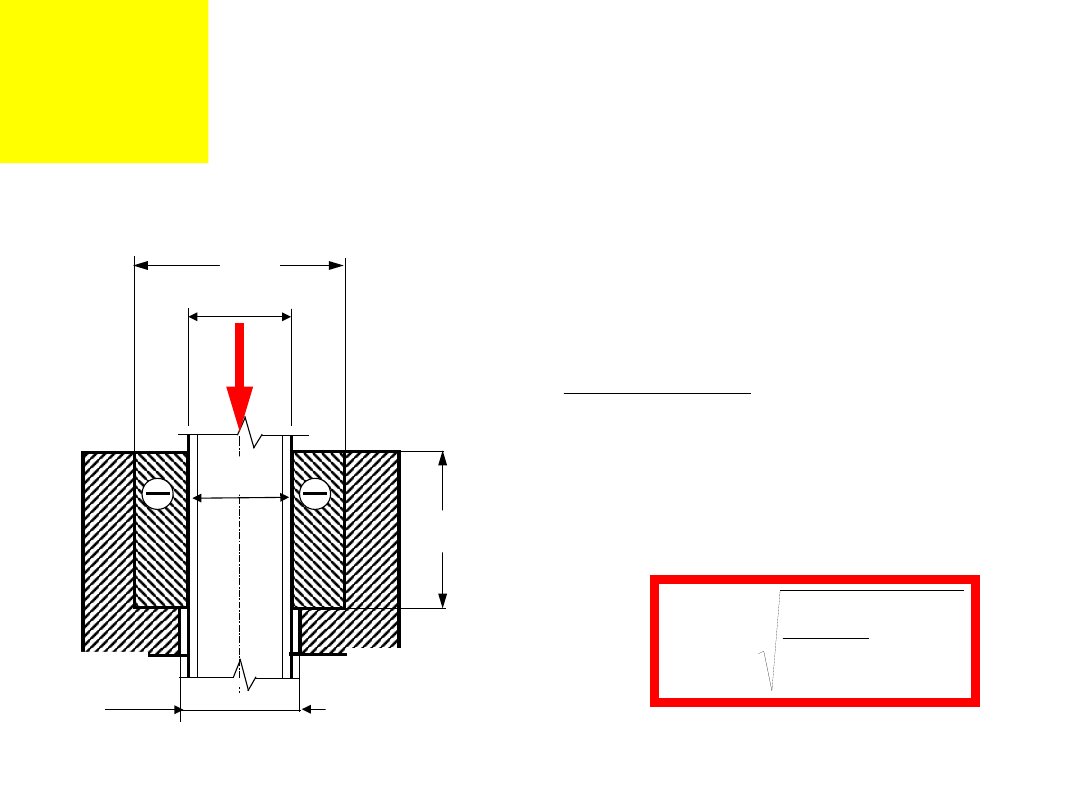
Obliczenia wytrzymałościowe.
Zewnętrzna średnica nakrętki
z warunku na nacisk powierzchniowy na
czołowej powierzchni oporowej nakrętki
Połączen
ia
śrubowe
D
Z
D
d
D
W
F
H
n
cj
c
dop
W
Z
k
k
,
p
D
D
F
p
8
0
4
2
2
2
4
W
dop
Z
D
p
F
D
Nakrętki nieznormalizowane
Zależnie od przypadku
naciski dopuszczalne
statyczne lub ruchowe
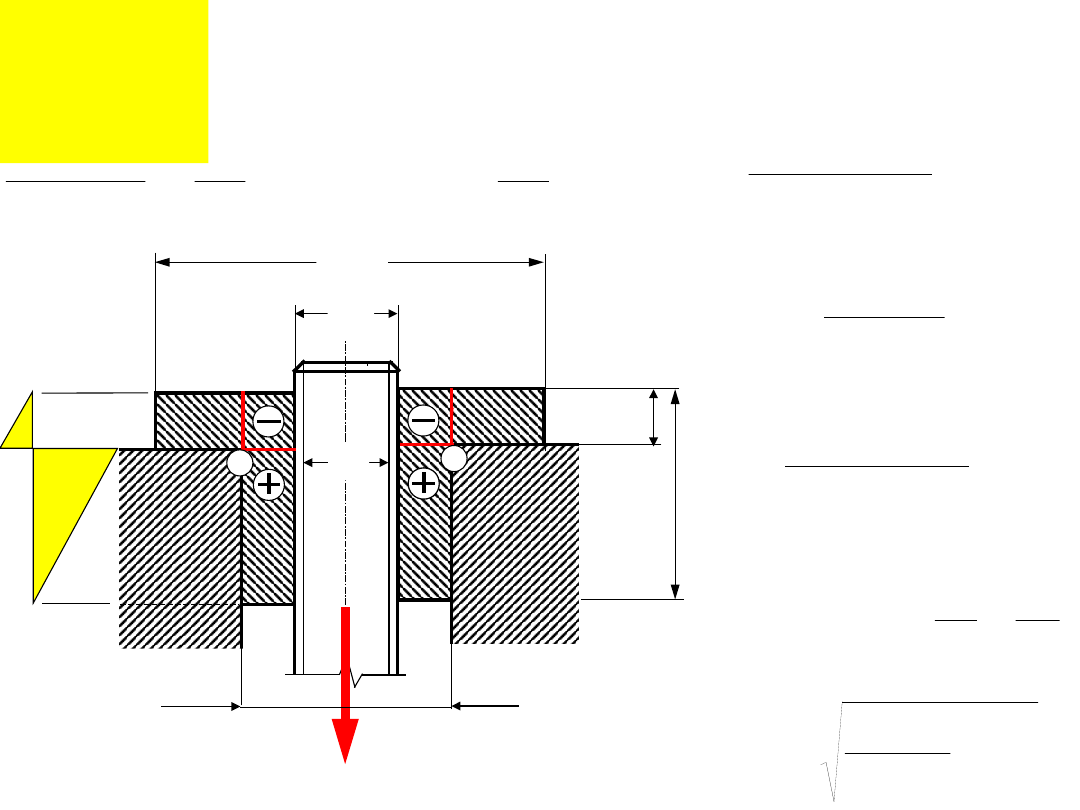
Obliczenia wytrzymałościowe
.
Nakrętka nieznormalizowana z kołnierzem
n
n
ś
ś
n
ś
E
E
2
2
1
D
E
E
d
D
n
ś
W
Połączen
ia
śrubowe
D
Z
D
d
D
W
F
H
k
F
X
H
n
y
x
x
y
n
k
x
n
k
n
x
H
H
F
F
H
F
H
H
F
1
rj
r
W
x
r
k
k
D
D
F
2
2
4
tj
t
k
W
t
k
k
H
D
F
dop
W
Z
r
p
D
D
F
p
2
2
4
(3.
)
(1.
)
(4.
)
(2.
)
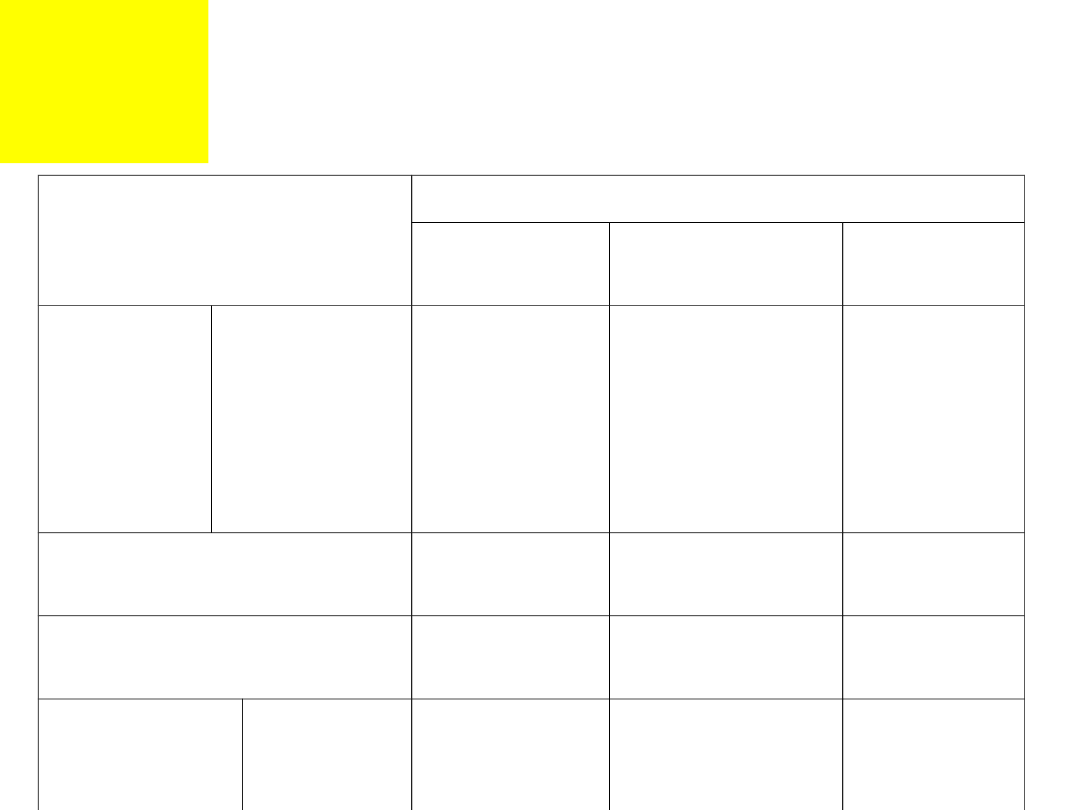
Gwinty.
Naciski dopuszczalne
[MPa]:
Połączen
ia
śrubowe
Materiał
Połączenie
spoczynko
we
półruchowe
ruchowe
Żeliwo
maszyno
we
EN-GJL-
150
EN-GJL-
200
EN-GJL-
250
1215
1620
20 25
810
1013
1316
45
57
68
Staliwo 200-400,
230-450
2530
1620
810
Stal E295, E335,
E360
3240
2227
1114
Mosiądz
Brąz
Spiż
Miękki
Twardy
2428
3240
1519
2227
810
1114
Stopy
lekkie
Miękkie
Twarde
6 8
12 16
W połączeniach spoczynkowych p 0,4k
gj
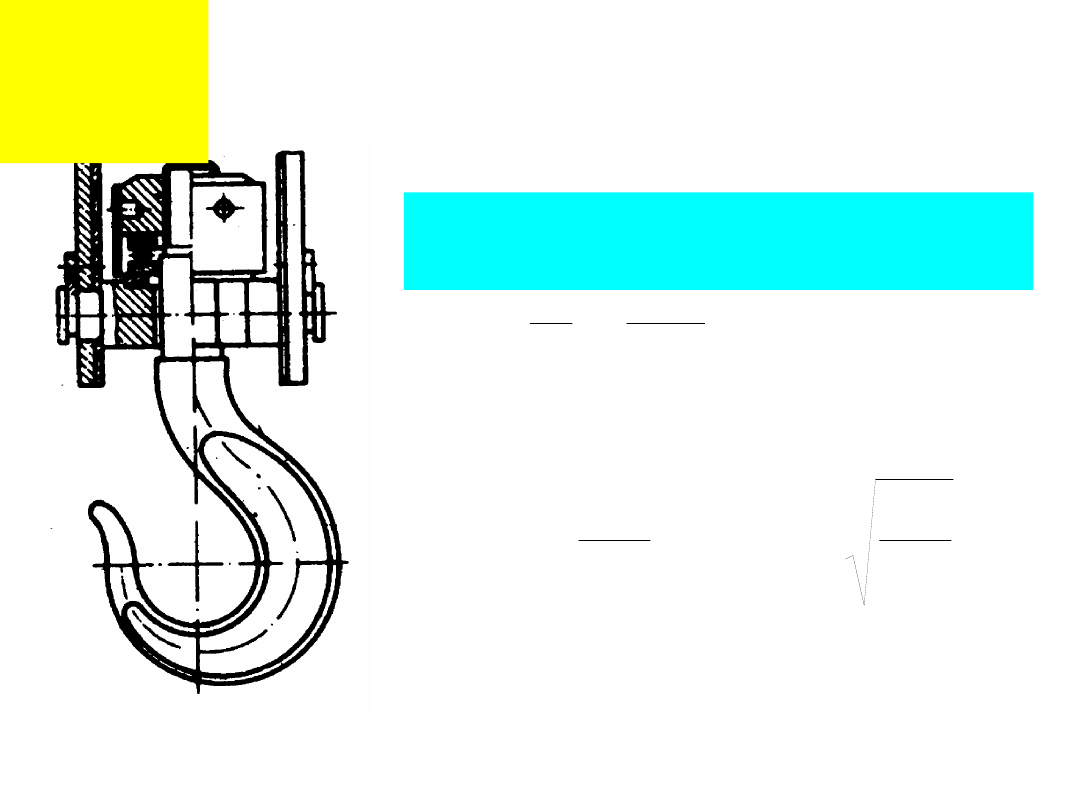
Obliczenia
wytrzymałościowe.
j
r
r
r
r
k
k
d
F
s
F
lub
2
3
4
r
r
k
F
d
k
F
d
4
4
3
2
3
Połączen
ia
śrubowe
I przypadek obciążenia śruby
(1a)
k
r
=Q
r
/x
Q
-obciążenia statyczne,
x
Q
=1,3 ...2,5
k
rj
=Z
rj
/x
Z
- obciążenie tętniące ,x
Z
=
2,5...5
Rdzeń śruby- złącze samohamowne skręcane
swobodnie i obciążone po skręceniu siłą
rozciągającą
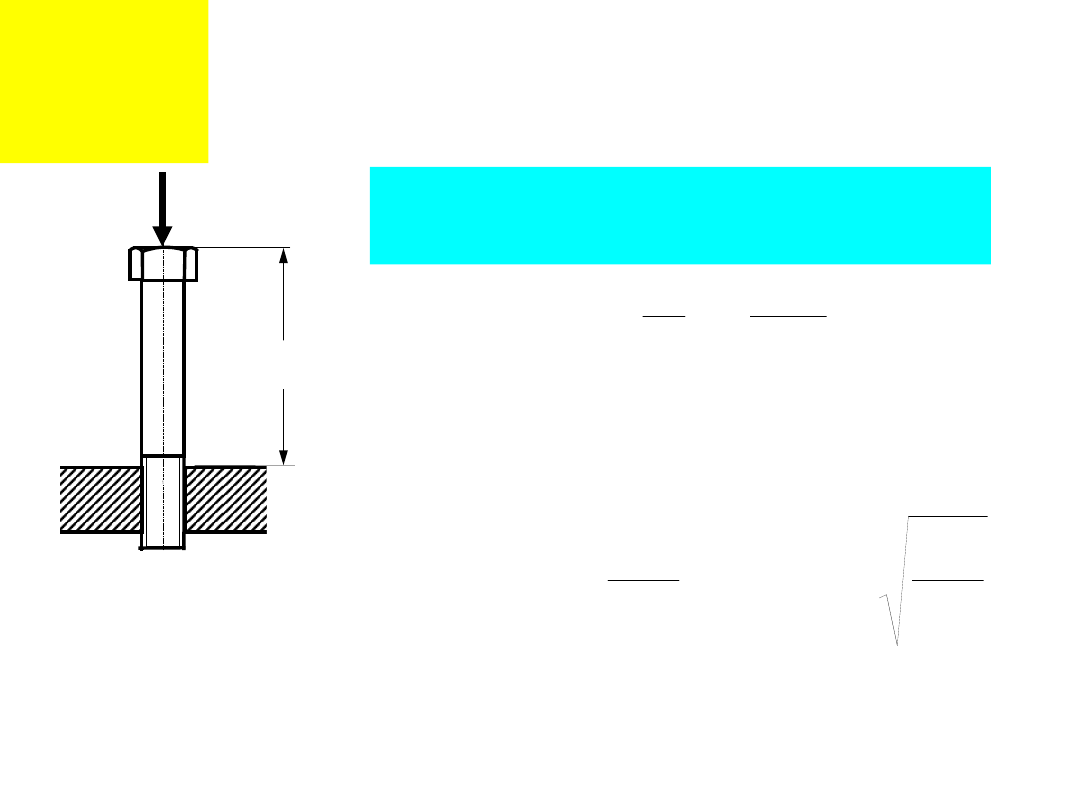
Obliczenia
wytrzymałościowe.
4
2
3
c
r
c
k
d
F
s
F
c
c
k
F
d
k
F
d
4
4
3
2
3
Połączen
ia
śrubowe
I przypadek obciążenia śruby
(1b)
Rdzeń śruby- złącze samohamowne skręcane
swobodnie i obciążone po skręceniu siłą
ściskającą
L
F
L
(1,25 ...2,5)d
3
10 ... 15
Obliczenia wytrzymałościowe.
Rdzeń śruby rozciąganej i
skręcanej.
2
3
4
d
F
s
F
r
r
16
'
2
3
3
d
tg
F
d
W
M
s
o
s
s
3
3
'
8
d
tg
F
d
s
3
2
3
'
2
4
d
tg
d
d
F
s
2
2
3
s
r
z
2
3
2
3
'
2
3
1
4
d
tg
d
d
F
s
2
3
2
2
'
12
1
d
tg
d
s
r
17
.
1
'
12
1
2
3
2
2
d
tg
d
s
j
r
r
z
r
z
k
k
lub
;
17
.
1
Gwint
metryczny,
= 0.1
j
r
r
r
k
k
lub
85
.
0
r
k
F
d
17
.
1
4
2
3
r
k
F
d
22
.
1
3
Połączen
ia
śrubowe
II przypadek obciążenia śruby
(2a)
r
r
r
k
.
k
F
,
d
815
0
25
1
3
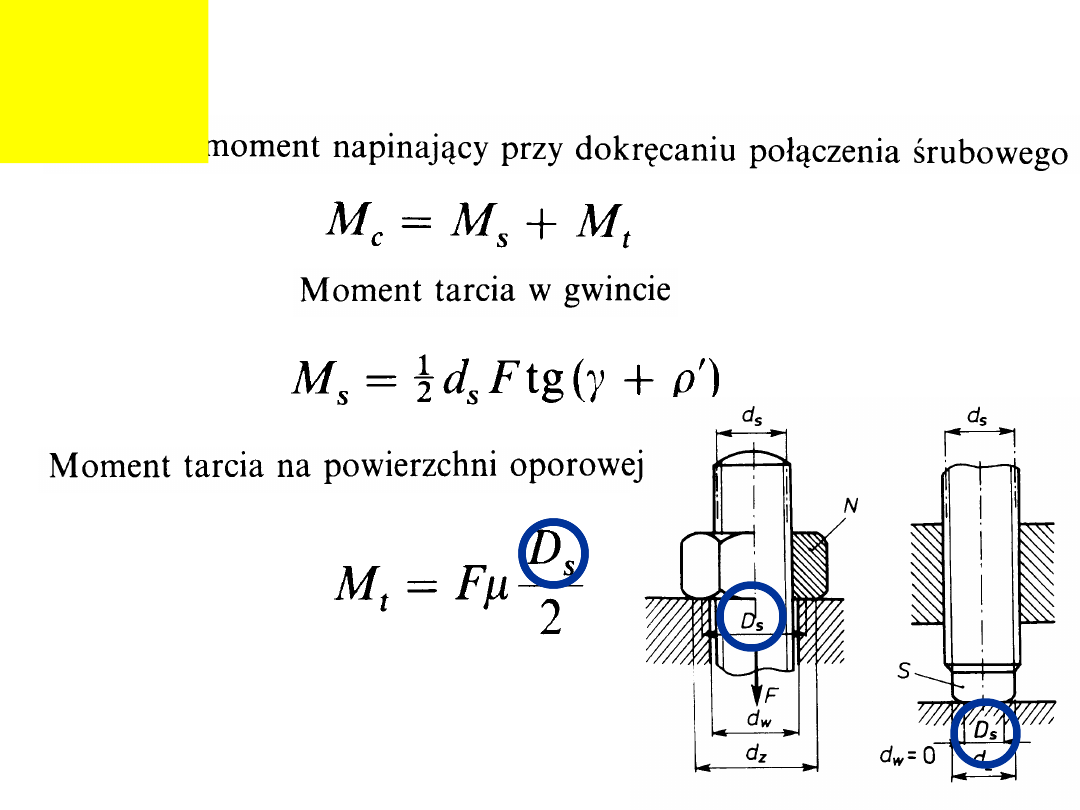
Moment przy dokręcaniu
śruby:
Połączen
ia
śrubowe
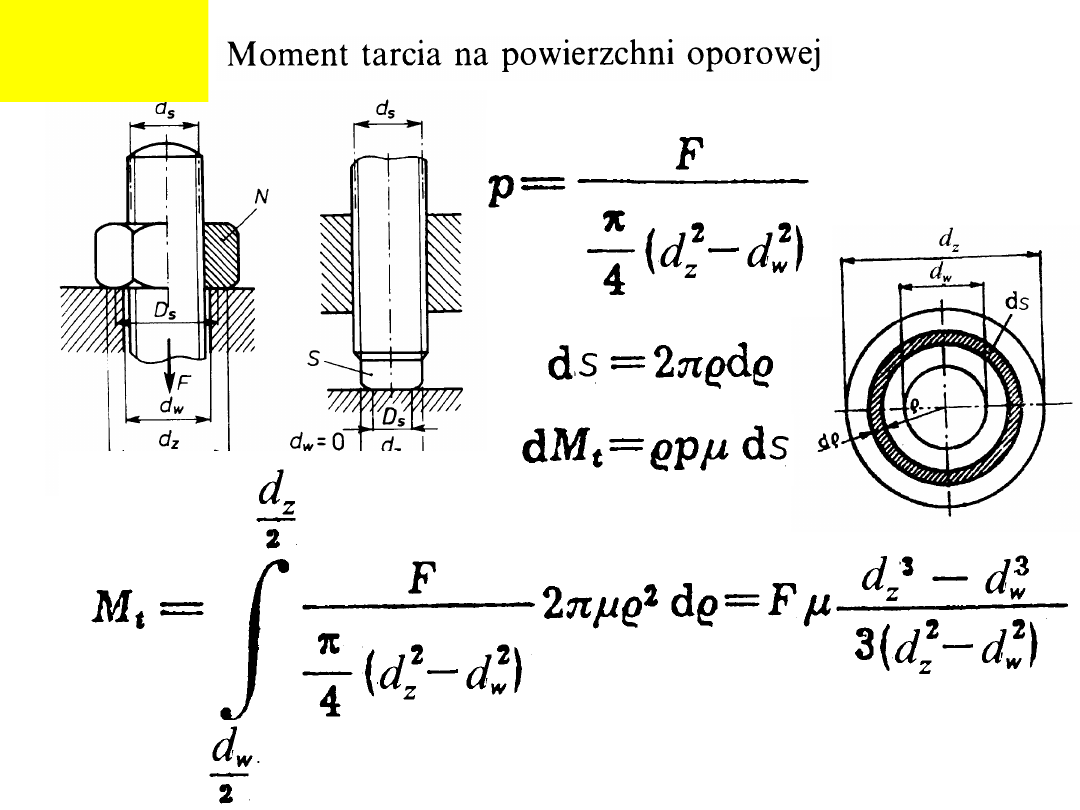
Połączenia
śrubowe
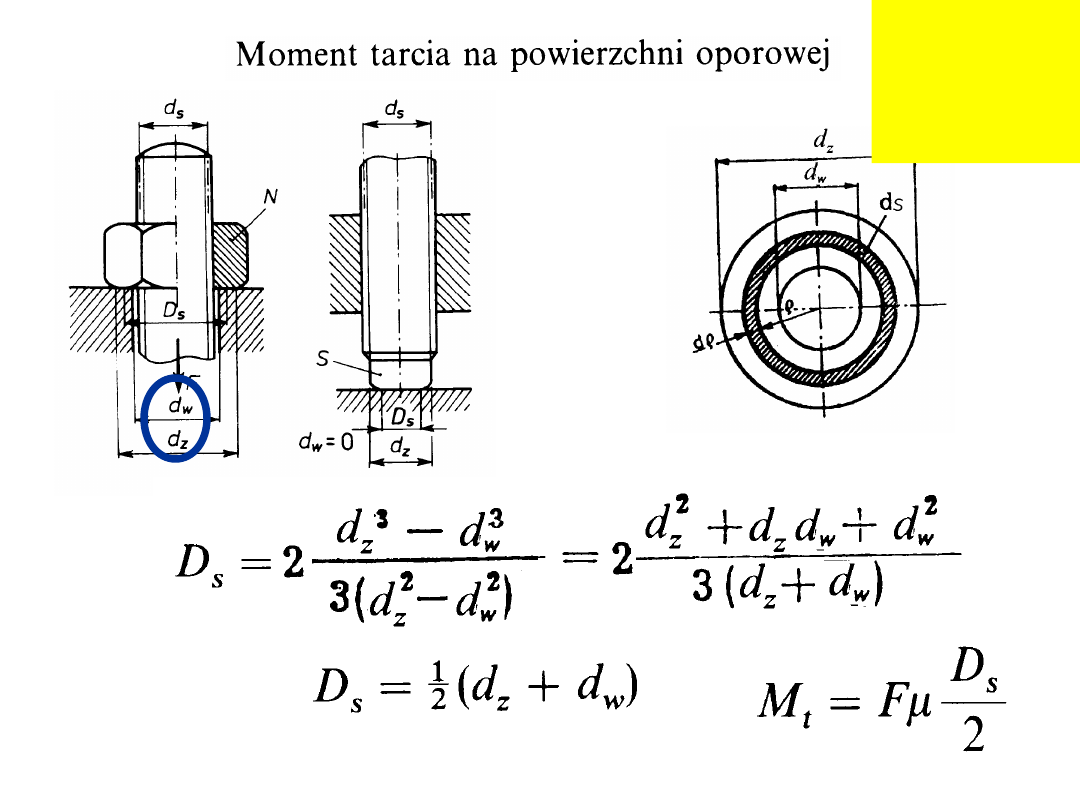
Często rozstaw klucza i średnica otworu
Połączen
ia
śrubowe
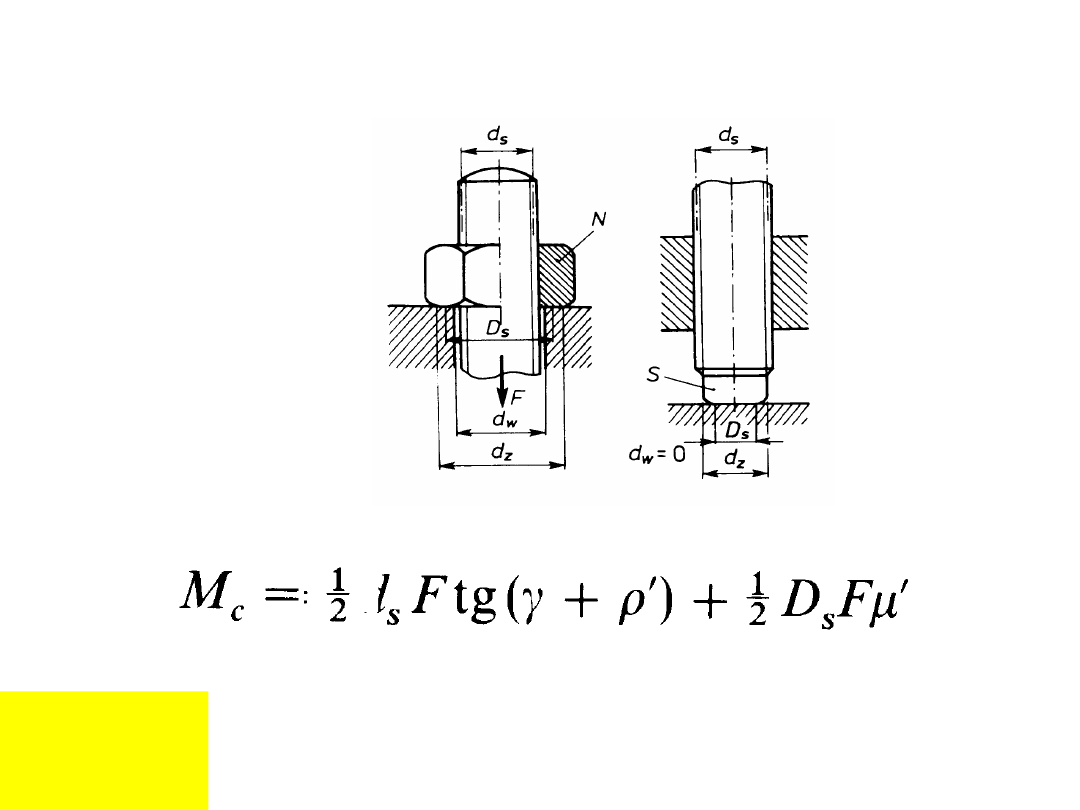
Moment przy dokręcaniu śruby:
Połączen
ia
śrubowe
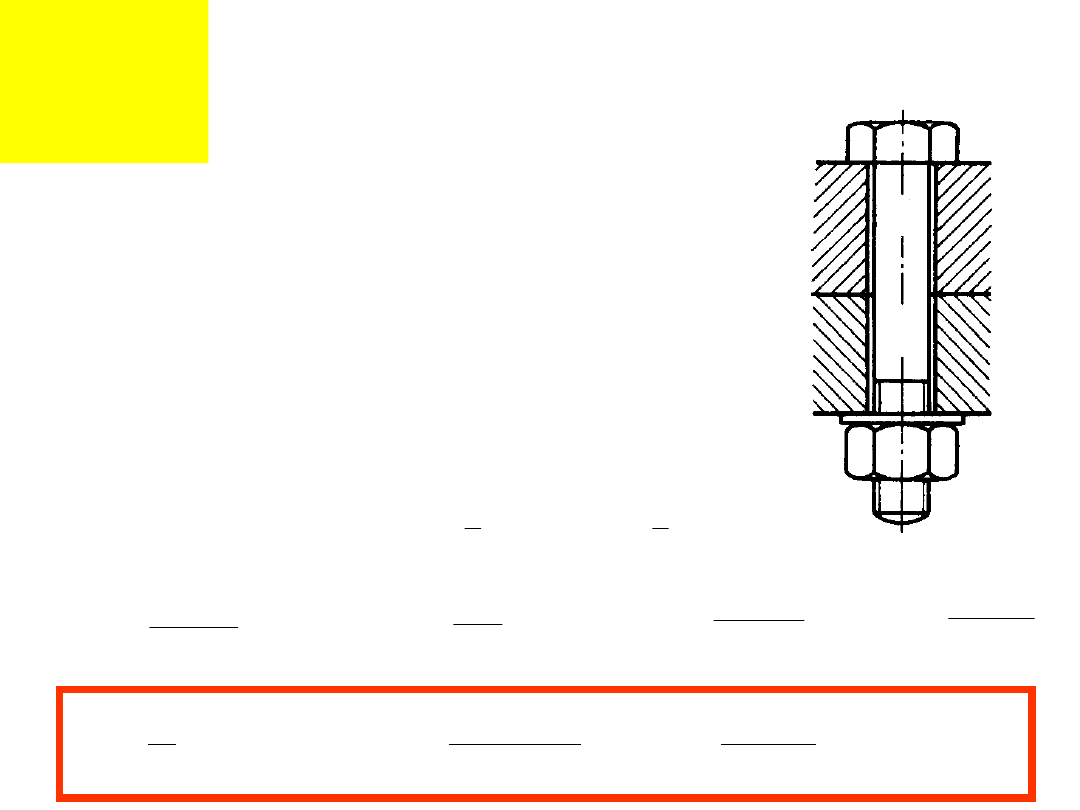
Przykład 1:
Obliczyć moment dokręcania nakrętki
zapewniający docisk
łączonych elementów siłą F. Śruba ma gwint
metryczny.
Podstawowe dane :
- średnica nominalna (zewnętrzna) śruby d,
- średnica wewnętrzna gwintu nakrętki D
1
,
- skok gwintu H,
-
współczynnik
tarcia
między
wszystkimi
elementami
współpracującymi µ,
- średnica zewnętrzna łba śruby S,
- średnica wewnętrzna podkładki = średnica otworu
d
0
,
- średnica zewnętrzna podkładki D
Z
,
s
s
c
D
d
F
M
2
1
'
tg
2
1
s
d
H
arctg
2
1
D
d
d
s
cos30
arctg
'
2
0
S
d
D
s
S
d
D
d
H
D
d
F
M
c
0
1
1
30
cos
4
arctg
2
arctg
tg
Połączen
ia
śrubowe
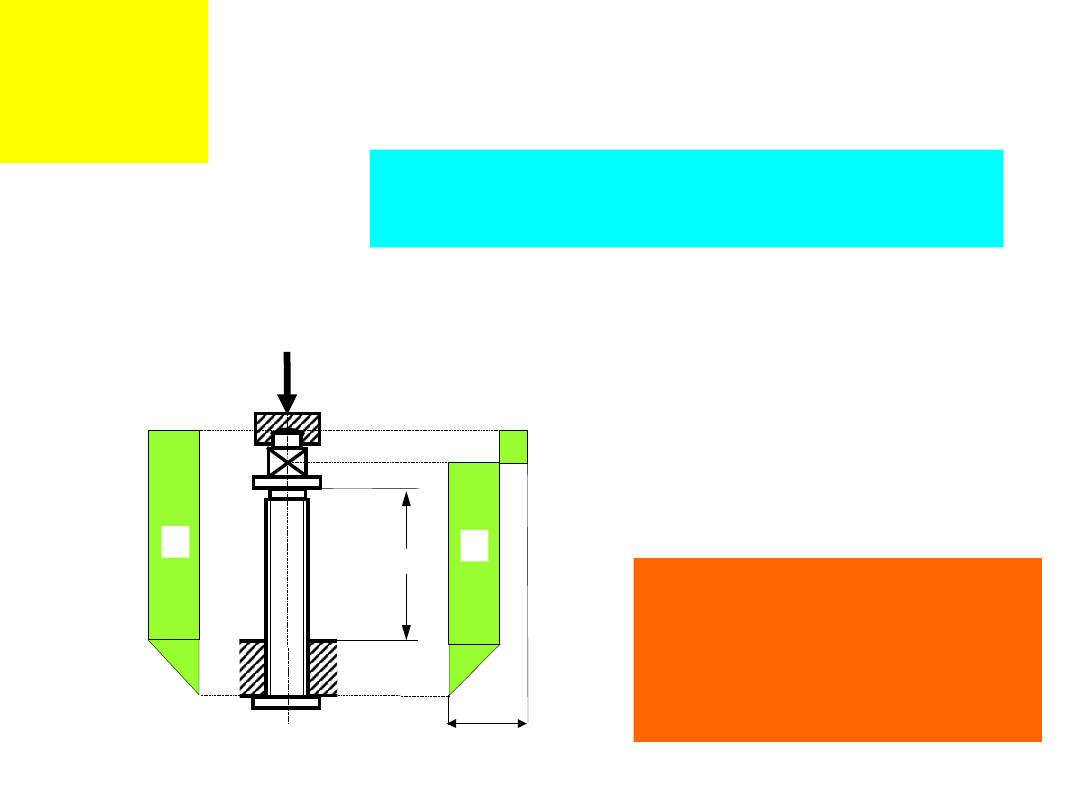
Połączen
ia
śrubowe
Obliczenia wytrzymałościowe.
Rdzeń śruby ściskanej i
skręcanej.
II przypadek obciążenia śruby
(2b)
Długie śruby pracujące pod obciążeniem ściskającym
oblicza się na wyboczenie i sprawdza się w nich złożony
stan naprężeń.
M
t
c
cj
Z
k
k
l
F
M
C
M
S
F
Wyboczen
ie
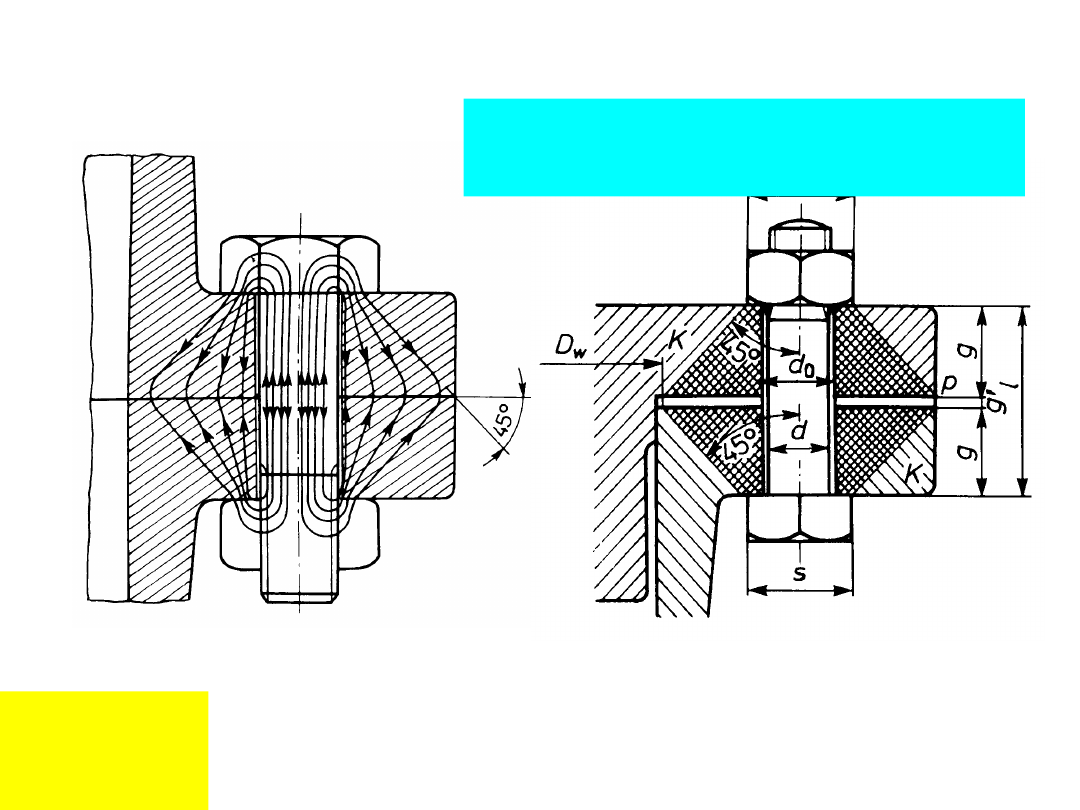
Złącze śrubowe z napięciem
wstępnym:
Schematyczny przebieg sił
Strefy działania
sił zewnętrznych
Połączen
ia
śrubowe
III przypadek obciążenia
śruby
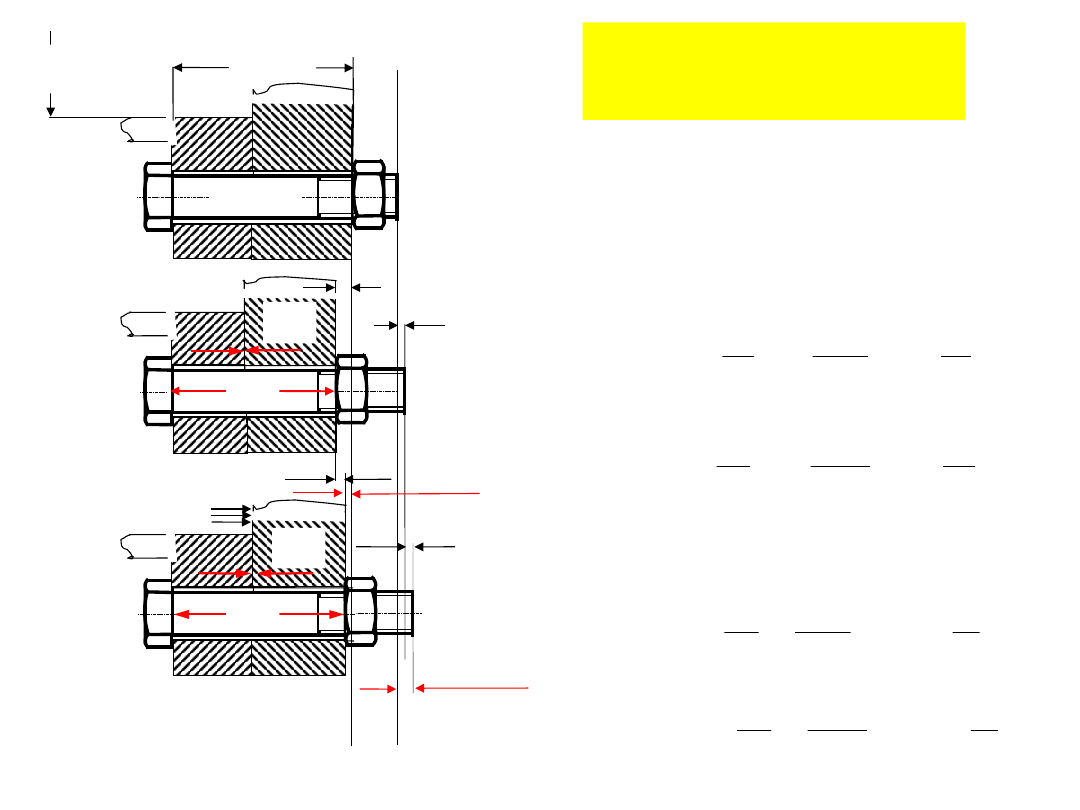
O
k
l
s
l
k
Q
w
=0
Q
w
D
C
p=
0
p=
0
p>
0
Q
w
Q
z
Q
w
w
w
p
w
-
p
p
w
+
p
O
s
O
s
O
k
Połączenia
śrubowe
Śruba napięta wstępnie siłą
Q
w
potem
obciążona siłą
Q
p
. Całkowite obciążenie
śruby
Q
zależy od jej odkształceń własnych
oraz elementów ściskanych, ale
nie jest
sumą Q
w
+ Q
p
.
m
C
Q
E
F
l
Q
l
E
l
s
w
s
s
s
w
s
s
r
s
s
w
1
m
C
Q
E
F
l
Q
l
E
l
k
w
k
k
k
w
k
k
c
k
k
w
1
m
N
C
l
E
F
Q
s
s
s
s
w
w
tg
m
N
C
l
E
F
Q
k
k
k
k
w
w
tg
Wydłużenie:
Skrócenie:
Sztywności śruby oraz elementów
ściskanych
Złącze kołnierzy
cylindra
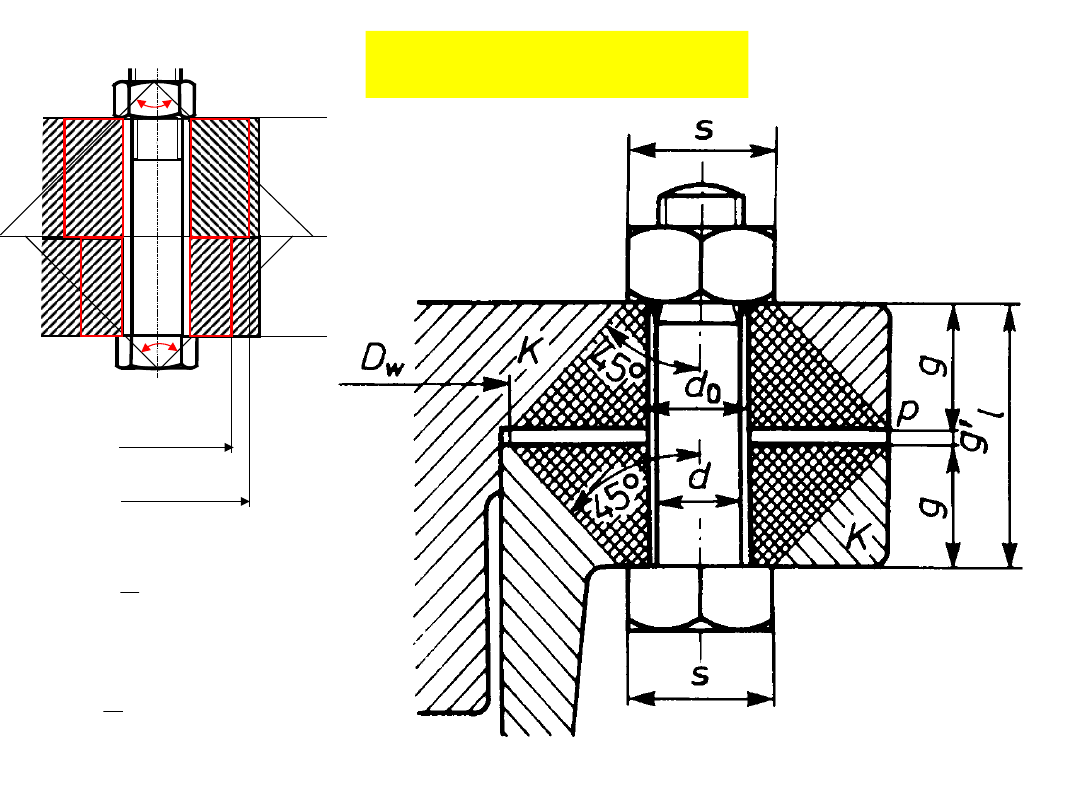
Połączenia
śrubowe
Sztywność dla śruby o zmiennym
przekroju:
– „stożki wpływu ”-
walce zastępcze (powierzchnie
przekrojów F
ki
są równe powierzchniom
przekrojów „stożków wpływu”)
90
0
90
0
D
2z
D
1z
l
1z
l
2z
i
i
i
s
s
F
l
E
C
1
1
i
ki
ki
i
k
F
E
l
C
1
F
i
– przekroje poszczególnych odcinków
trzpienia w m
2
l
i
– długość tych odcinków w m
E
s
– moduł Younga materiału śruby w
N/m
2
l
i
– długość walców zastępczych w
m
E
ki
– moduł Younga materiału
kołnierza
Sztywność
kołnierzy
2
0
2
2
,
1
4
d
g
s
F
k
2
0
2
2
4
d
g
s
F
ku
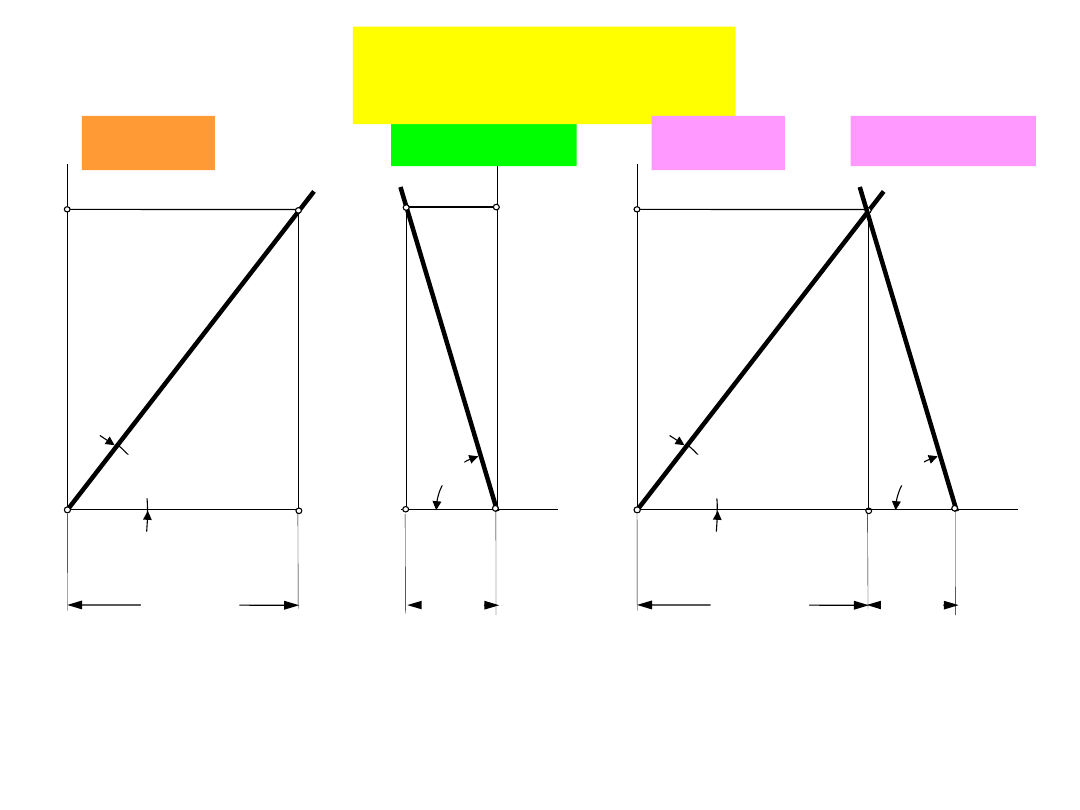
w
O
k
II
m
KOŁNIERZ
Połączenia
śrubowe
w
I
N
Q
w
O
s
ŚRUBA
w
I
N
Q
w
O
s
ŚRUBA
w
O
k
II
m
KOŁNIERZ
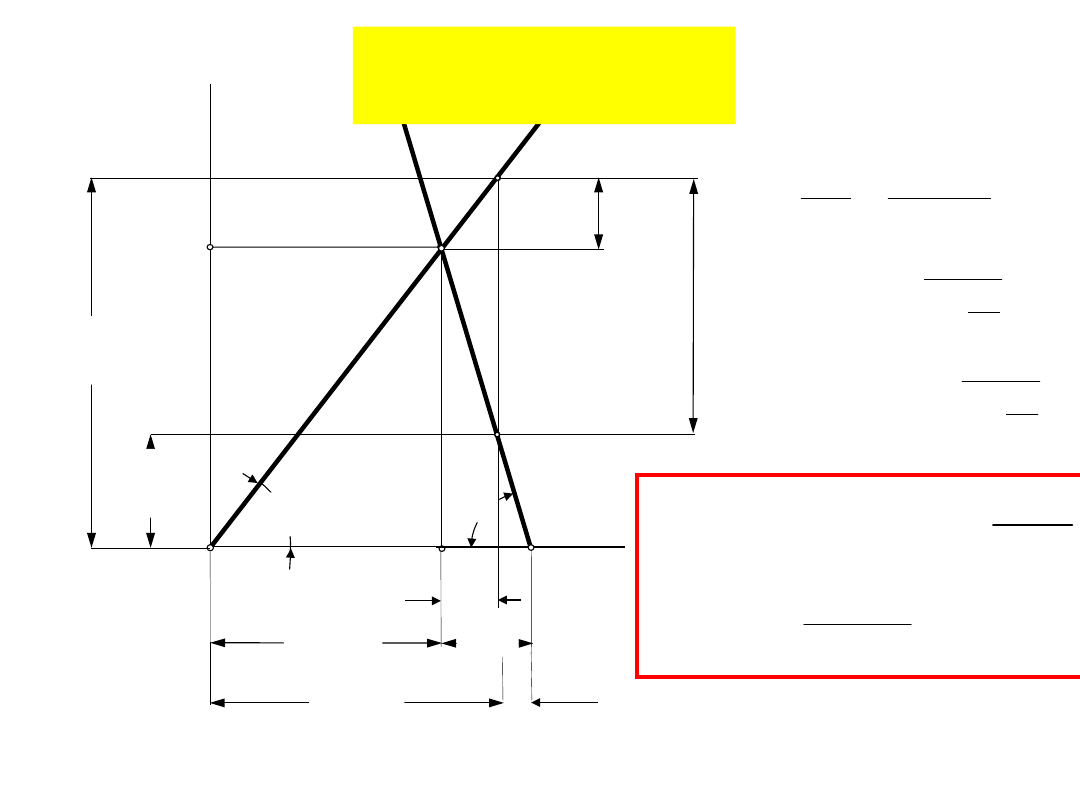
Uwaga! Jeśli podziałka sił wynosi np. 1[mm]=a [N], zaś odkształceń 1
[mm]=b [N], to:
tg =C
s
b/a oraz tg = C
k
b/a
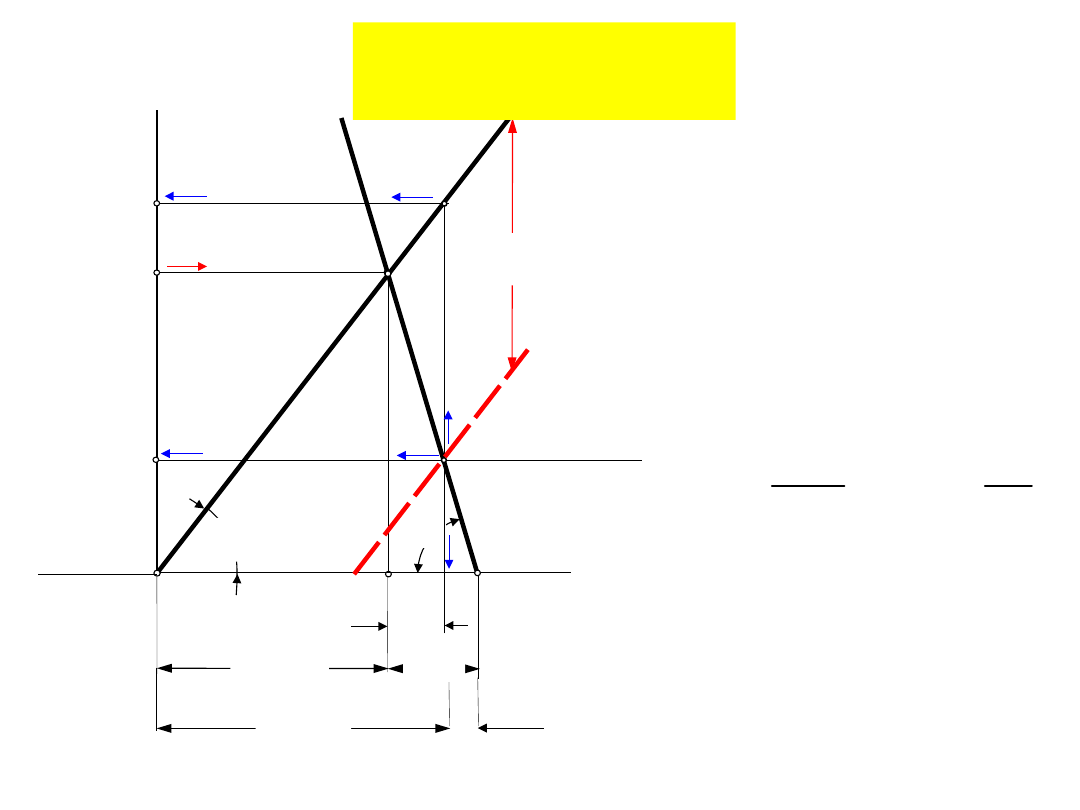
w
I
N
Q
w
O
s
w
O
k
II
m
Q
Q
Z
w
+
P
P
w
-
P
Q
P
Połączenia
śrubowe
Wyznaczanie
obciążenia śruby Q dla
znanego napięcia
wstępnego Q
w
oraz
obciążenia
zewnętrznego Q
p
n
P
Q
D
p
P
p
P
C
p
4
2
P
p
- siła działająca na
pokrywę złącza
cylindra
n – liczba śrub
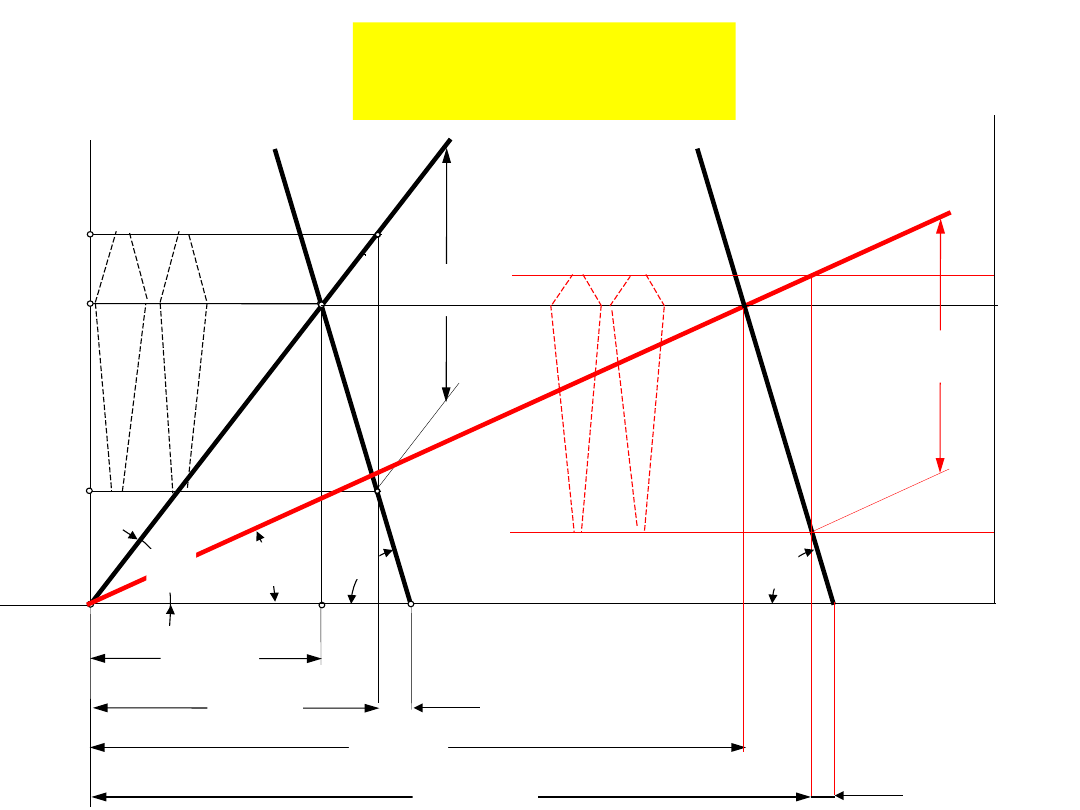
w
I
N
Q
w
O
s
O
k
II
m
Q
Q
Z
w
-
P
Q
P
Q
P
*
*
w
w
+
P
w
*
w
*
+
P
*
I
II
Q
*
Q
Z
*
Q
w
*
w
+
P
w
*
-
P
*
Połączenia
śrubowe
Wpływ zmiany sztywności śruby na siły występującej
w złączu
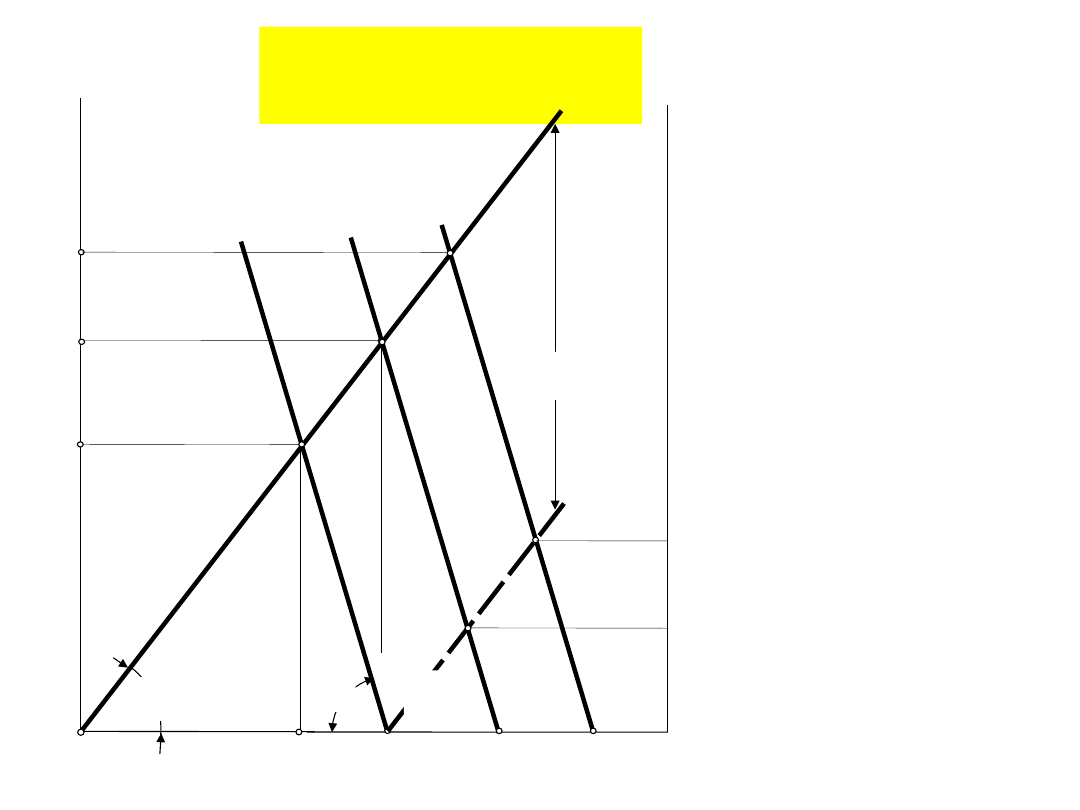
Połączenia
śrubowe
I
N
Q
w3
O
s
II
m
O
k2
2
O
k1
O
k
3
Q
p
Q
w2
Q
w2
Q
w1
N
Q
z3
=0
Q
z
2
Q
z
1
Wpływ napięcia
wstępnego Q
w
na
zacisk resztkowy Q
z
przy danych
sztywnościach C
s
i C
k
i
jednakowej sile
zewnętrznej Q
p.
Warunek szczelności:
ciśnienie
uszczelniające
wywołane przez Q
z:
:
p
u
=(1,5 ...2)p
Stąd zacisk
resztkowy:
Q
z
=p
u
F
u
F
u
- powierzchnia
uszczelki.
Gdy działają tylko
obciążenia (np. śruby
łożyskowe)
Q
z
= (0,2 ...0,6)Q
w
w
I
N
Q
w
O
s
w
O
k
II
m
Q
Q
P
Q
Z
w
+
P
P
w
-
P
Q
P
Połączenia
śrubowe
p
w
Q
Q
Q
tg
tg
p
p
p
Q
Q
Q
s
k
P
p
C
C
Q
Q
1
1
s
k
P
w
C
C
Q
Q
Q
1
1
tg
tg
tg
Q
Q
Q
c
c
c
Q
Q
Q
Q
Q
Q
p
z
w
k
s
k
p
z
p
p
z
w
Obliczenia
analityczne
Wyznaczanie sił w złączu za
pomocą wspólnego
wykresu
Połączen
ia
śrubowe
Uwagi o uzyskiwaniu właściwego
napięcia wstępnego. Dokręcanie ręczne
m
s
s
W
w
D
d
Q
M
'
tg
5
,
0
Długość przeciętna klucza L=10
d ... 16 d
( dla M6... M56)
Siła ręki P
k
= 100 ...400 N P
k
=10d
Współczynnik tarcia na śrubie
= 0,1
2
160
16
10
d
d
d
L
P
M
k
c
m
m
s
r
r
z
d
d
tg
d
d
d
'
d
d
4
d
160
2
1,17
/4
Q
1,17
17
,
1
2
r
2
w
0
2
2400
m
MN
d
Dla śrub złącznych d
r
60 mm
]
[
5
15
,
1
mm
wk
Q
d
r
r
Dla śrub złącznych d
r
> 60 mm
r
r
wk
Q
d
25
,
1
w - współczynnik
poprawności
wykonania gwintu;
w =1,00 - ś.
dokładne
w = 0,75 - ś.
zwykłe
w = 0,50 - ś.
zgrubne
Q = Q
Z
+ Q
P
-
całkowite
obciążenie śruby
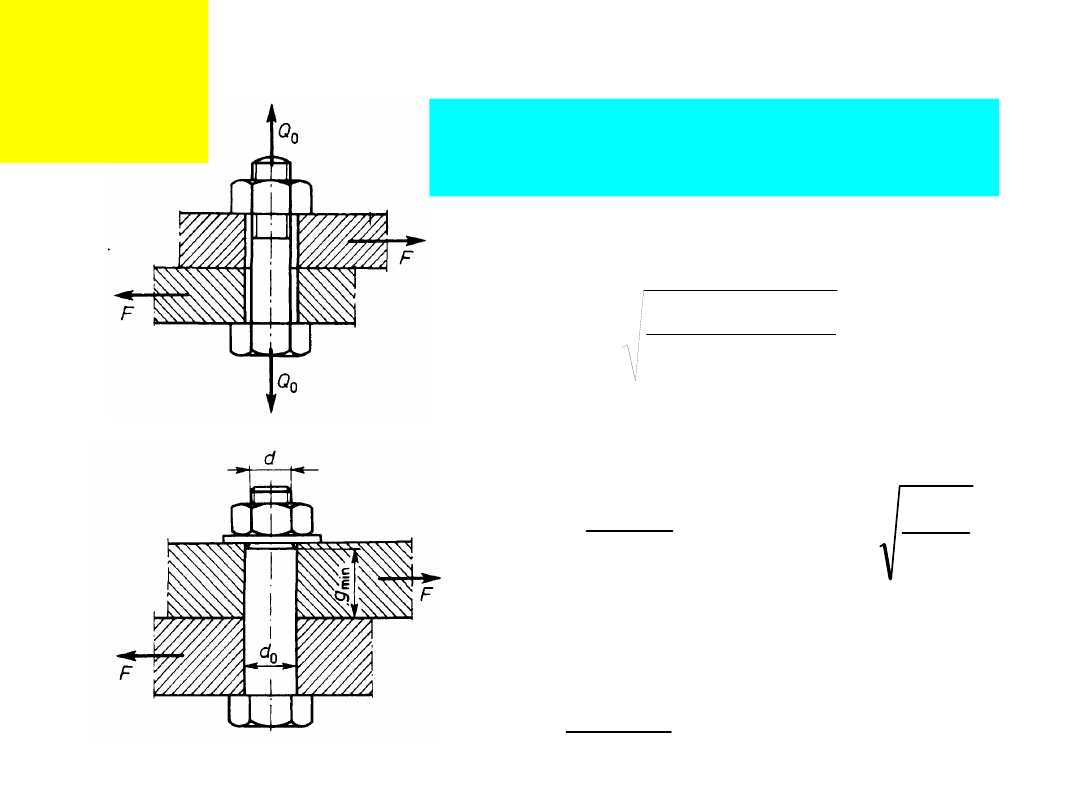
Przenoszenie siły
poprzecznej:
Tarcie,
śruby złączne
Ścinanie,
śruby
pasowane
F
Q
T
0
r
k
m
F
d
85
.
0
4
3
m – liczba powierzchni styku
t
nk
F
d
4
0
t
k
nd
F
2
0
4
dop
p
d
g
F
p
0
min
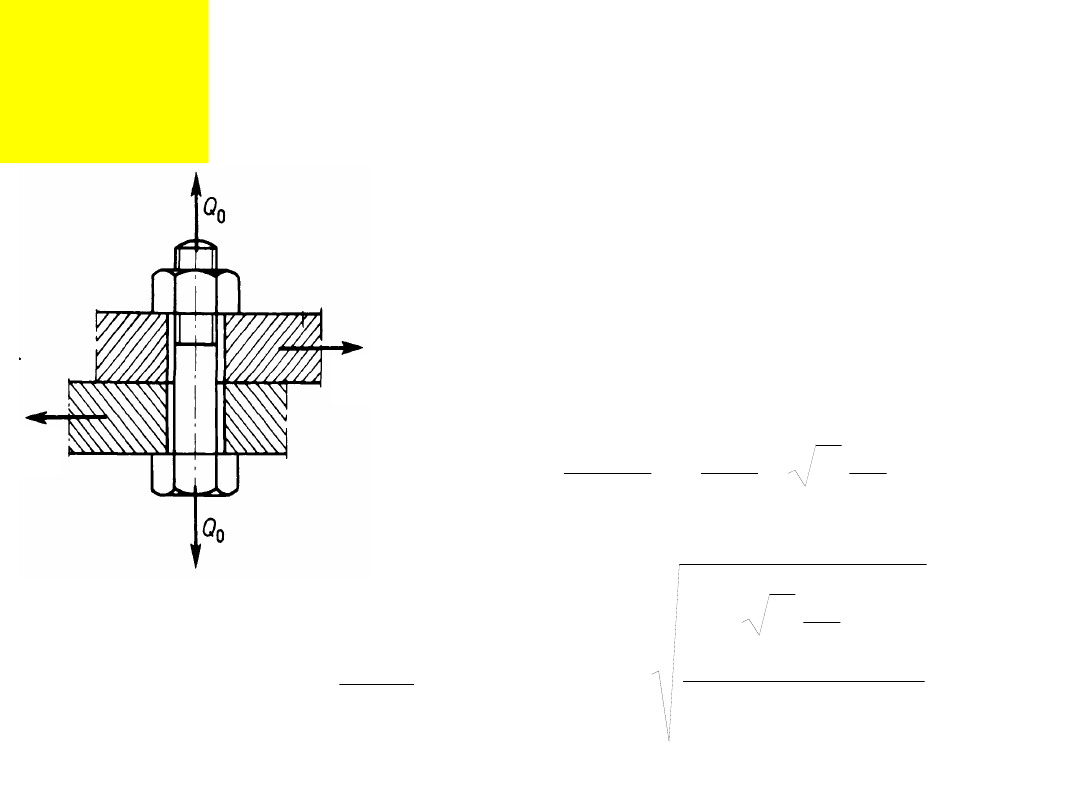
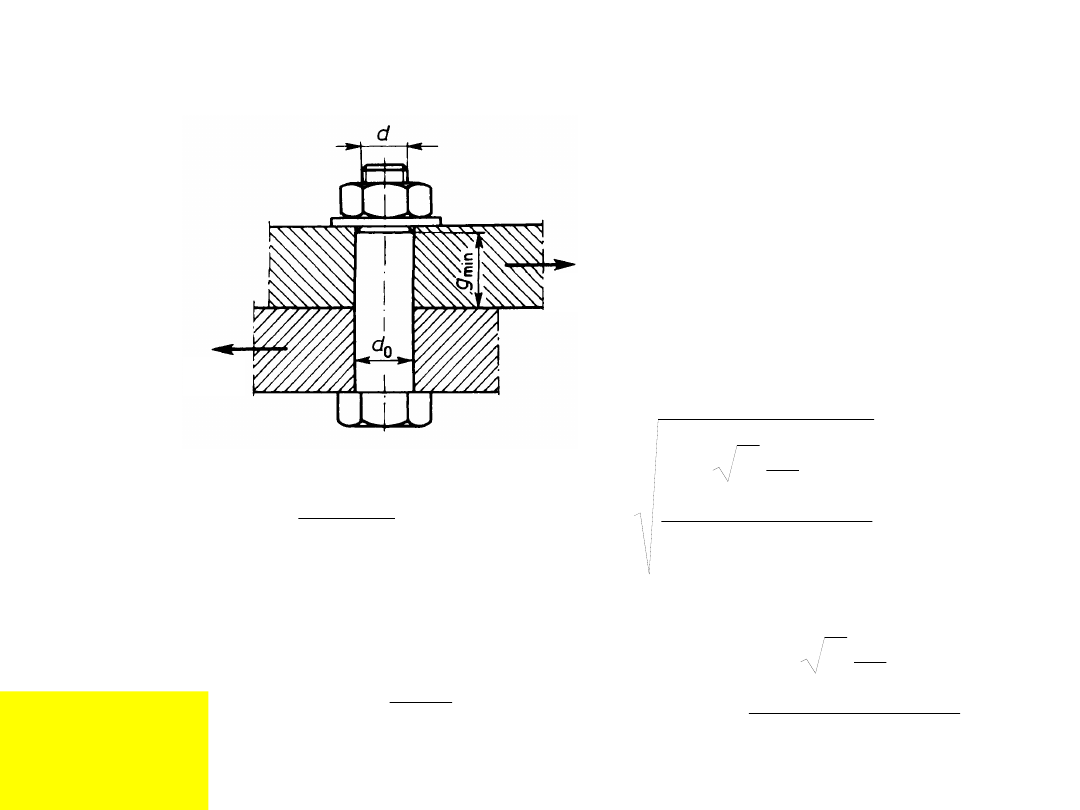
IV przypadek obciążenia
śruby
Połączen
ia
śrubowe
n – liczba przekrojów
ścinanych
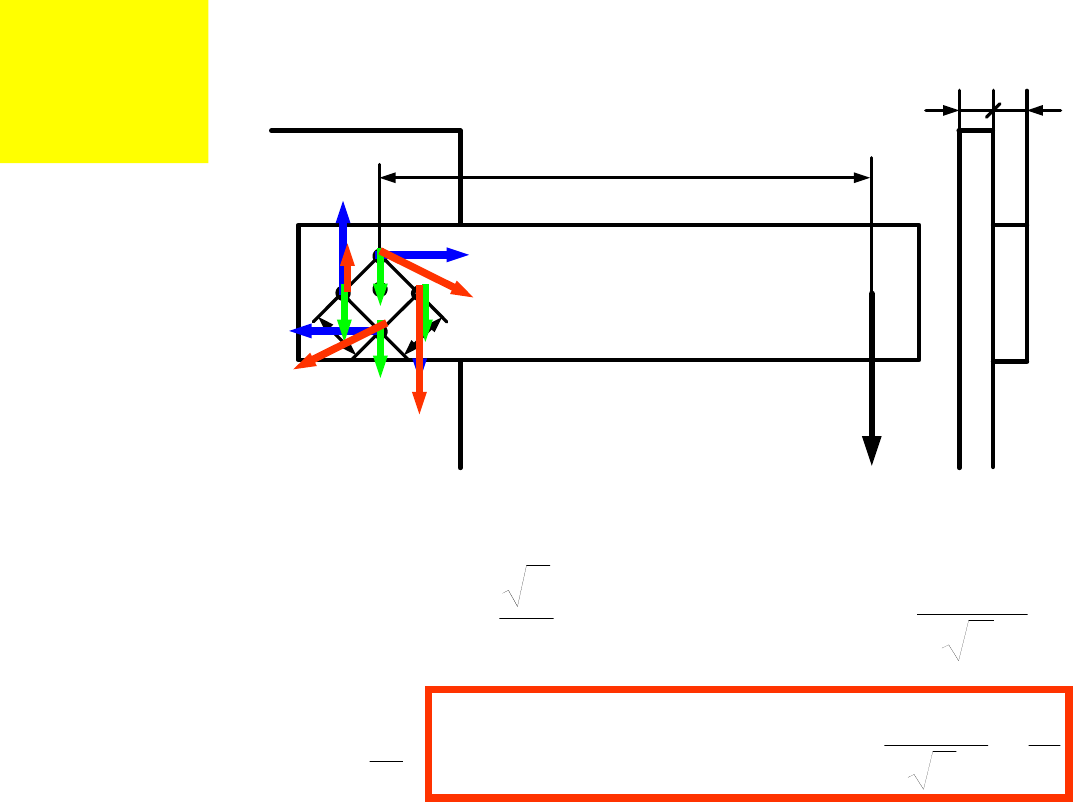
Przykład 2:
Dobrać średnice
śrub mocujących
wspornik jak na
rysunku
zakładając,
że będą to śruby:
a) złączne;
b) pasowane.
1. Obciążenie złącza
względem środka
ciężkości O wszystkich
przekrojów śrub (zasada
skrętnika):
L
P
a
R
L
P
M
g
O
2
2
4
4
P
R
P
F
t
y
L
P
a
g
g
a
O
R
g
R
t
R
a
PL
R
g
2
2
4
2
2
max
max
P
a
PL
R
R
R
R
t
g
Połączen
ia
śrubowe
Przykład 2- c.d. Śruby
złączne:
max
0
R
Q
T
r
k
a
L
P
d
85
.
0
1
2
3
max
R
max
R
1
2
4
max
0
a
L
P
R
Q
2
3
0
4
85
.
0
d
Q
k
r
Połączen
ia
śrubowe
Przykład 2 -c.d. Śruby
pasowane:
t
k
d
R
2
0
max
4
dop
p
gd
F
p
0
4
max
R
max
R
dop
p
g
a
L
P
d
1
2
0
t
k
a
L
P
d
1
2
0
Połączen
ia
śrubowe
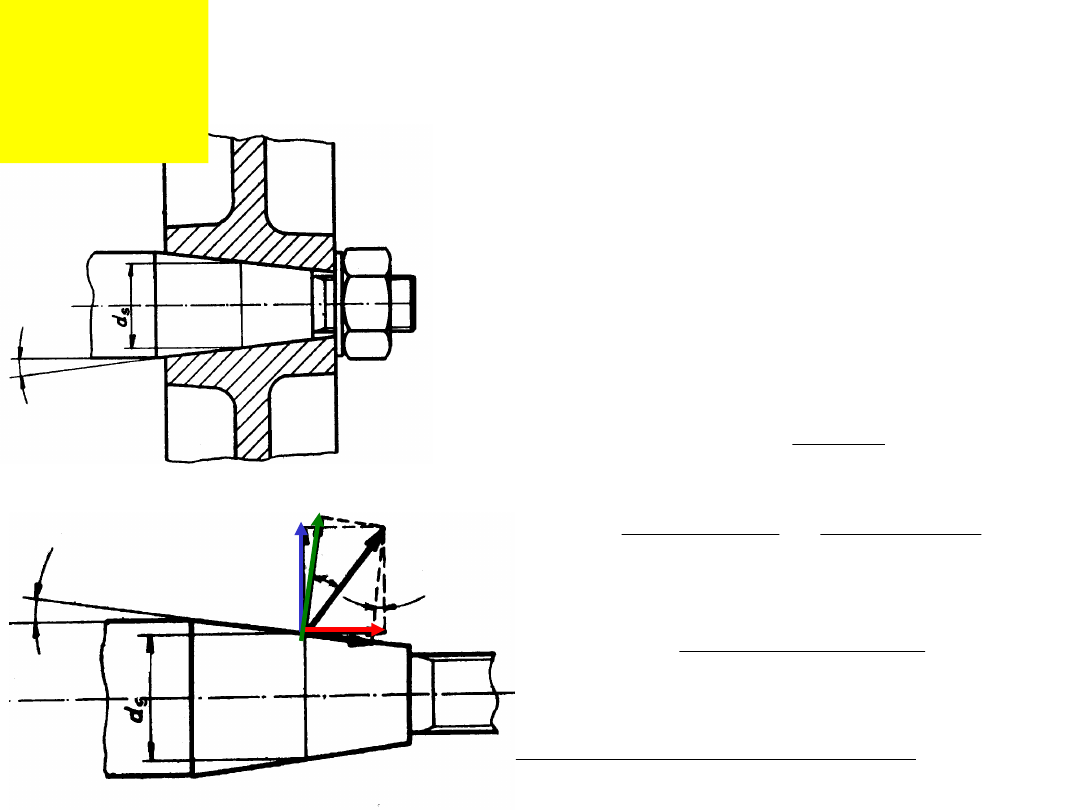
θ
Przykład 3:
Obliczyć moment dokręcenia nakrętki M24
gwarantujący
przeniesienie momentu 300 Nm przy średniej
średnicy stożka
40 mm i kącie nachylenia 3º. Pozostałe dane:
współczynnik
tarcia μ = 0.1; średnia średnica oparcia nakrętki
o podkładkę
d
m
= 32 mm; skok gwintu M24 h = 3 mm,
średnica robocza d
2
= 22.05 mm.
arctg
)
1
.
0
(
1
.
0
71
.
5
Rozkład sił:
P
N
P
w1
S
R
1
s
s
N
d
kM
R
P
2
cos
1
)
cos(
)
sin(
1
1
S
P
R
w
cos(
sin
)
)
(
2
1
s
s
w
d
kM
P
kN
0
.
32
)
71
.
5
cos(
04
.
0
1
.
0
)
71
.
5
3
sin(
300
4
.
1
2
Połączen
ia
śrubowe

Przykład 3– c.d:
Moment dokręcania nakrętki:
m
w
t
s
c
d
d
P
M
M
M
2
1
'
2
1
2
1
tg
59
.
6
'
)
30
cos(
1
.
0
arctg
'
)
cos(
)
'
tg(
2
arctg
tg(
05
.
22
3
)
2
d
h
43
.
2
Nm
tg
2
.
107
1
.
0
32
2
1
02
.
9
05
.
22
2
1
32
c
M
Połączen
ia
śrubowe

Połączen
ia
śrubowe
Uwagi o obliczaniu innych połączeń
śrubowych w których występuje większa
liczba śrub
•Złącze obciążone w płaszczyźnie styku momentem
skręcającym M
s
- śruby rozmieszczone dowolnie
]
/
[
max
max
m
N
const
r
Q
r
Q
T
i
T
i
Założenia:
]
/
[
2
max
max
m
N
r
r
Q
r
Q
M
i
i
T
i
i
T
S
i
]
/
[
2
max
max
m
N
r
r
M
Q
i
i
S
T
np. śruby pasowane
]
/
[
4
2
2
max
m
N
k
d
Q
t
T
]
/
[
2
max
m
N
p
gd
Q
p
dop
T
oraz
oraz
Połączen
ia
śrubowe
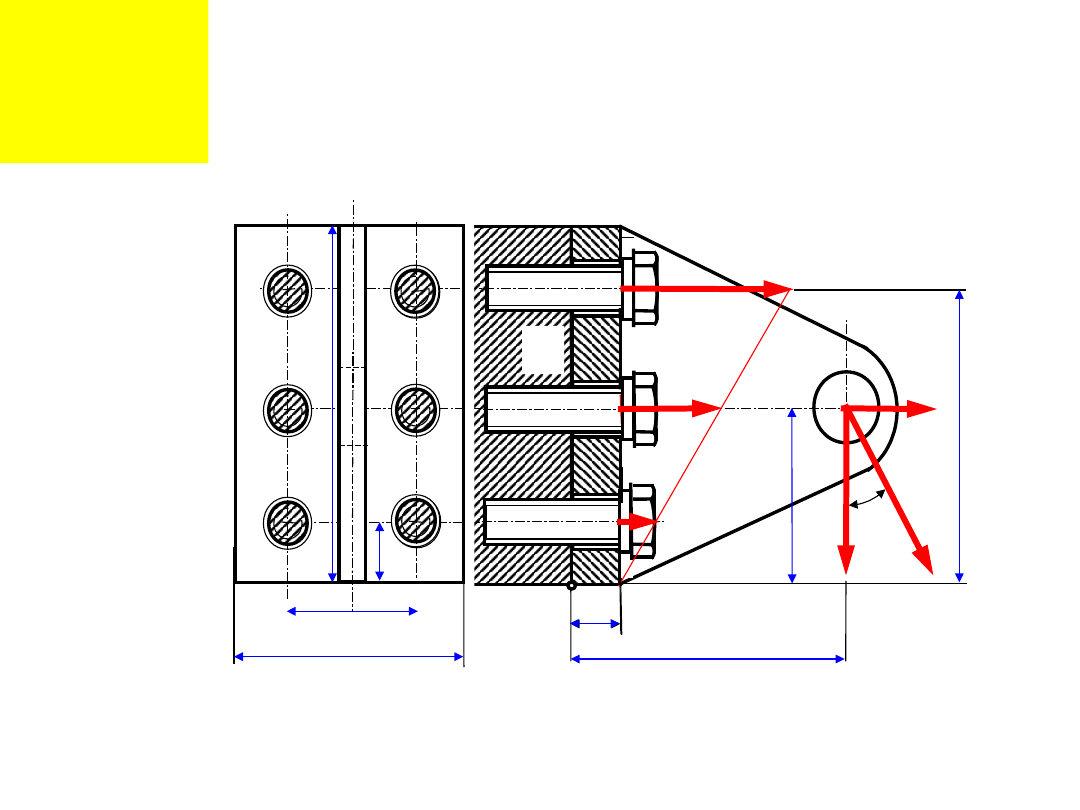
• Złącze obciążone momentem gnącym M
g
oraz siłą
styczną
P
Q ,
i siłą normalną P
N
-działającymi w
płaszczyźnie symetrii powierzchni styku
g
P
P
N
P
T
e
a
Q
M3pł
Q
M2pł
Q
M1pł
i=
3
i=
2
0
j=1
j=2
i=
1
b
L
1
L
L
2
L
3
Dane:
P[N],[
0
], {e, a, b, g, L, L
1
, L
2
, L
3
}[mm], {n, =
m
}[-], k
r
[MPa]
Obliczyć:
d
r
[mm] oraz M
C
[Nm]
Przykład 4:

Połączen
ia
śrubowe
Przykład 4– c.d:
]
[
cos
N
P
P
T
]
[
cos
Nm
e
P
e
P
M
T
g
]
/
[
...
3
3
2
2
1
1
m
N
const
l
Q
l
Q
l
Q
l
Q
i
Mi
pł
M
pł
M
pł
M
]
[
2
max
max
Nm
l
l
Q
l
Q
M
i
i
M
i
i
Mi
g
]
[
2
3
3
max
N
l
l
M
Q
Q
i
i
g
pł
M
pł
M
]
[
max
3
max
3
N
j
Q
Q
pł
M
M
]
[
3
2
max
3
2
N
l
l
Q
Q
M
M
]
[
2
1
2
1
N
l
l
Q
Q
M
M
]
[
sin
N
n
P
n
P
Q
N
Ni
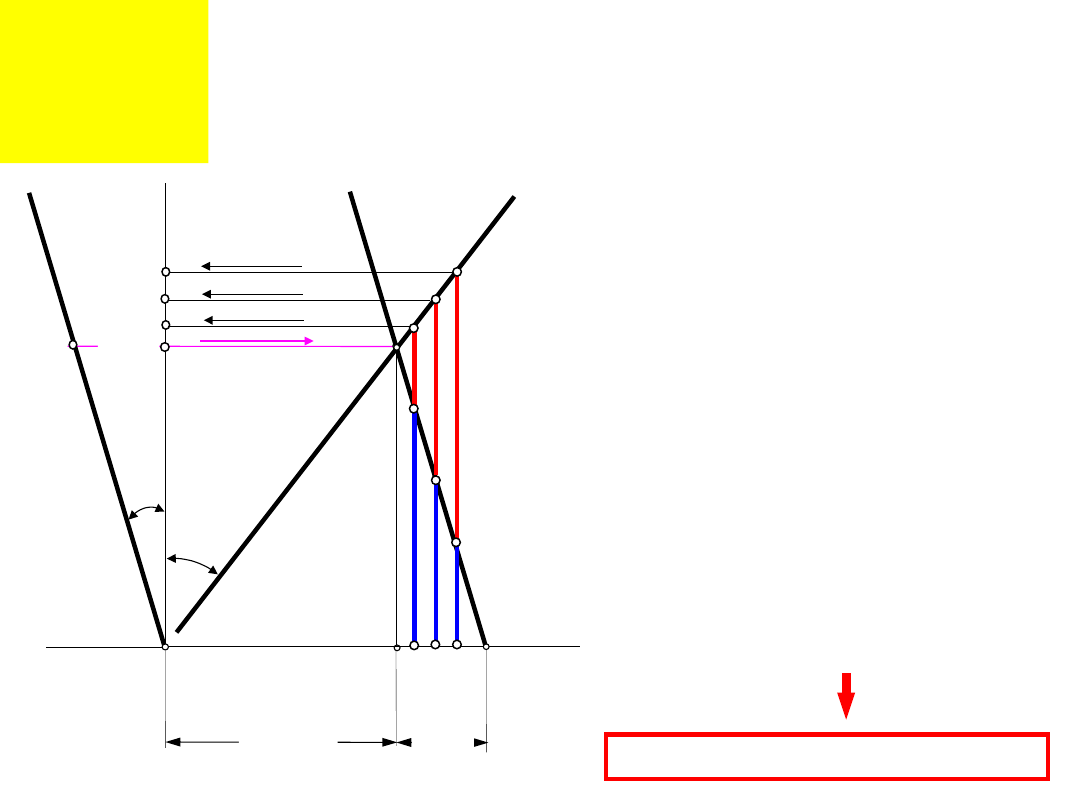
Moment gnący
M
g
Siły pochodzące od momentu gnącego M
g
są proporcjonalne do
odległości od osi 0-0
Siła działająca w płaszczyźnie odległej o l
max
= l
3
od osi 0-0
Siły pochodzące od momentu gnącego przenoszone
przez jedną śrubę
Siły w śrubach wywołane siłą normalną P
N
Połączen
ia
śrubowe
Przykład 4– c.d:
w
Q
w
O
s
w
O
k
Q
1
Q
Z
1
Q
P3
c
r
Q
Z
2
Q
Z
3
Q
P2
Q
P1
Q
2
Q
3
1
1
1
N
M
P
Q
Q
Q
2
2
2
N
M
P
Q
Q
Q
3
3
3
N
M
P
Q
Q
Q
2
2
2
Z
P
Q
Q
Q
3
3
3
Z
P
Q
Q
Q
T
śr
Z
P
n
Q
T
n
i
Zi
P
Q
T
1
T
Z
Z
Z
P
Q
Q
Q
j
T
3
2
1
max
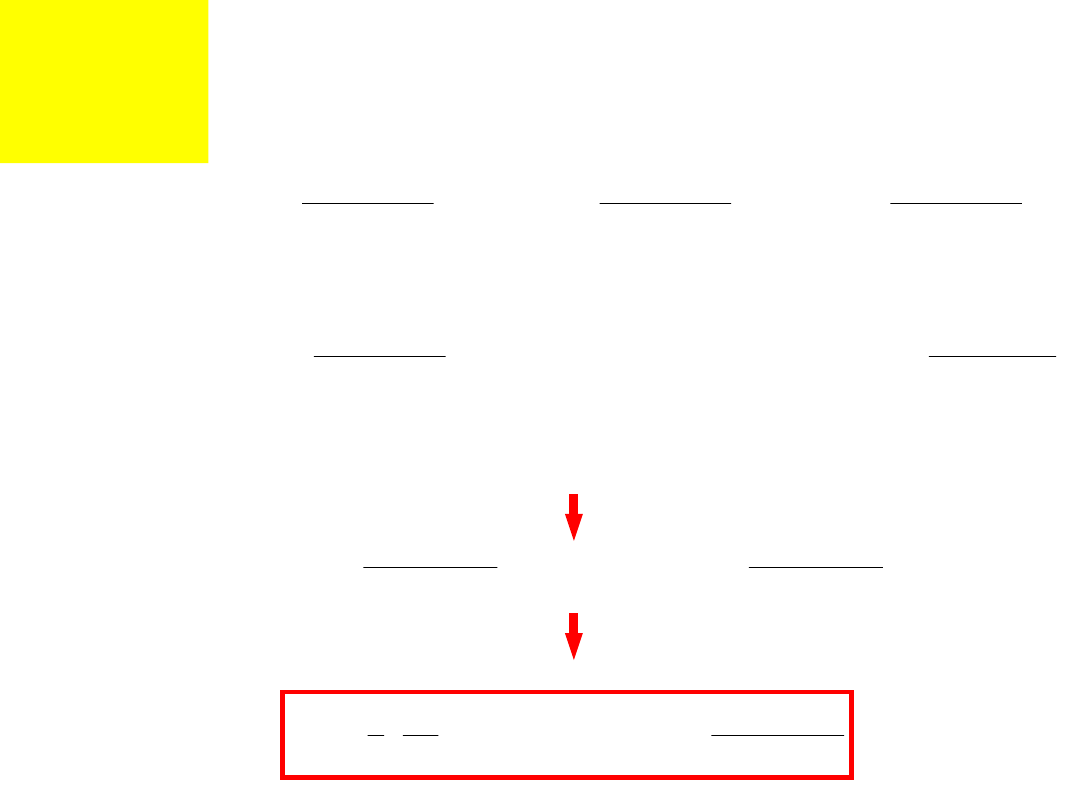
Największe zewnętrzne obciążenia
śrub
Całkowite obciążenia śrub
Warunek przeniesienia obciążenia siły P
T
tarciem
1
1
1
Z
P
Q
Q
Q
Q
Zśr
– średni zacisk resztkowy
wszystkich śrub
Połączen
ia
śrubowe
Przykład 4– c.d:
c
r
r
P
Z
c
r
r
P
Z
c
r
r
P
Z
W
tg
tg
tg
Q
Q
tg
tg
tg
Q
Q
tg
tg
tg
Q
Q
Q
3
3
2
12
1
1
c
r
r
P
P
Z
Z
tg
tg
tg
Q
Q
Q
Q
1
3
3
1
c
r
r
P
P
Z
Z
tg
tg
tg
Q
Q
Q
Q
2
3
3
2
T
Z
c
r
r
P
P
Z
c
r
r
P
P
Z
P
Q
tg
tg
tg
Q
Q
Q
tg
tg
tg
Q
Q
Q
3
2
3
3
1
3
3
2
c
r
r
P
P
P
T
Z
tg
tg
tg
Q
Q
Q
P
Q
2
1
3
3
2
2
3
1
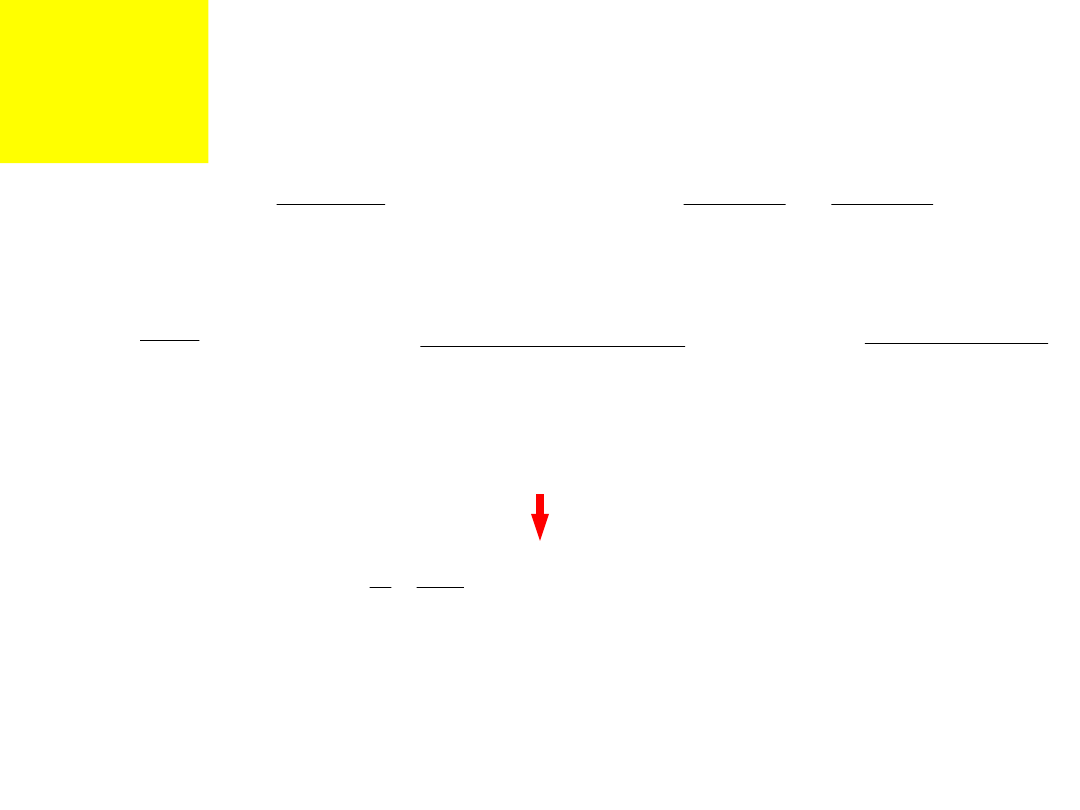
Dla wspólnego napięcia wstępnego (patrz rysunek)
Wyznaczamy zacisk Q
Z3
z równań:
oraz
i podstawiamy do:
T
Z
Z
Z
P
Q
Q
Q
j
T
3
2
1
max
Połączen
ia
śrubowe
Przykład 4– c.d:
r
p
r
A
E
g
g
tg
u
p
k
c
A
E
g
A
E
g
tg
4
2
r
r
d
A
4
2
0
2
d
g
D
A
p
k
4
2
0
2
p
p
p
d
D
A
0
c
tg
2
1
3
3
2
2
3
1
P
P
P
T
Z
Q
Q
Q
P
Q
3
3
3
Z
P
Q
Q
Q
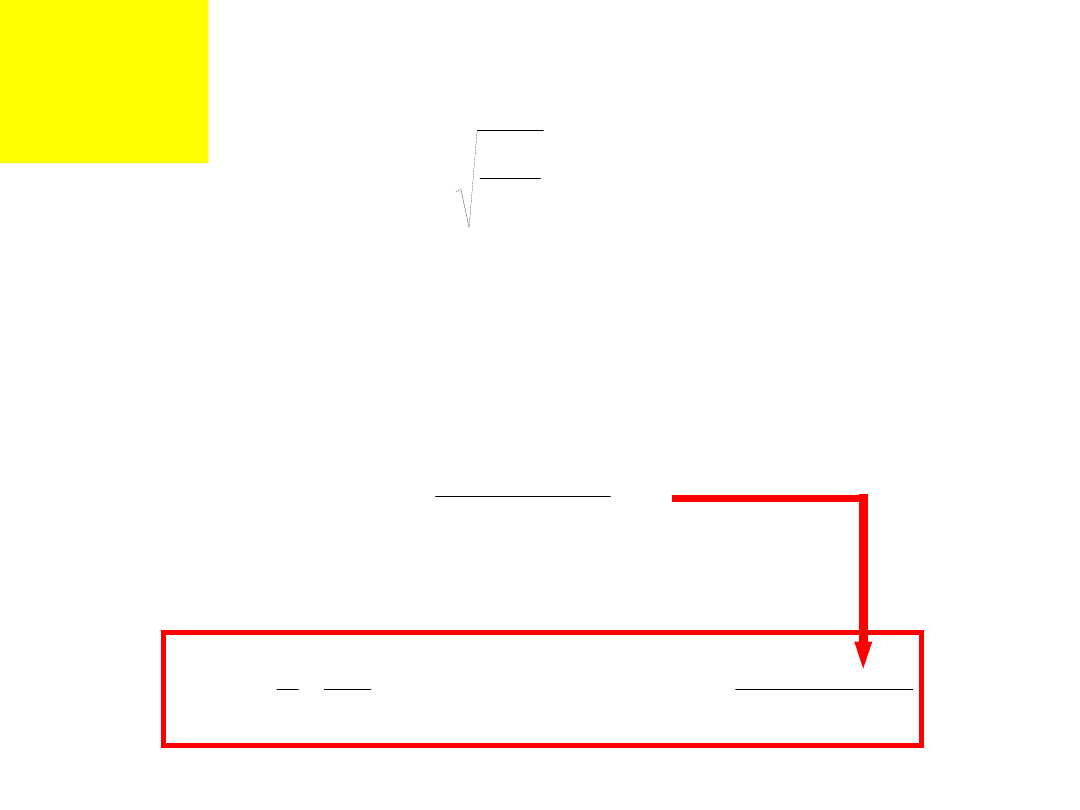
Zakładamy wstępnie, że części ściskane są
nieodkształcalne tzn.
Całkowite obciążenie śruby 3:
Połączen
ia
śrubowe
Przykład 4– c.d:
]
[
5
15
,
1
mm
wk
Q
d
r
r
1.Dobieramy z normy gwint M...., odczytujemy
d
9
=(d+D
0
)/2, d
r
, S. 2.Dobieramy podkładkę (np.
sprężystą), odczytujemy D
p
, g
p
.
3.Za pomocą wzorów na A
r
, A
k
, A
p
oraz pozostałych
danych gwintu śruby i podkładki obliczamy:
c
r
r
tg
tg
tg
c
r
r
P
P
P
T
Z
tg
tg
tg
Q
Q
Q
P
Q
2
1
3
3
2
2
3
1
Średnica rdzenia śruby:
w=1
Rzeczywiste napięcie resztkowe śruby 3:

Moment dokręcenia zapewniający przeniesienia
obciążenia zewnętrznego
( )
Połączen
ia
śrubowe
Przykład 4– c.d:
s
d
h
tg
0
30
cos
'
tg
m
m
s
W
t
s
C
D
tg
d
Q
M
M
M
'
5
,
0
c
r
r
P
Z
W
tg
tg
tg
Q
Q
Q
3
3
3
3
3
Z
P
Q
Q
Q
Rzeczywiste napięcie całkowite śruby 3:
Rzeczywiste napięcie wstępne
T
śr
Z
P
n
Q
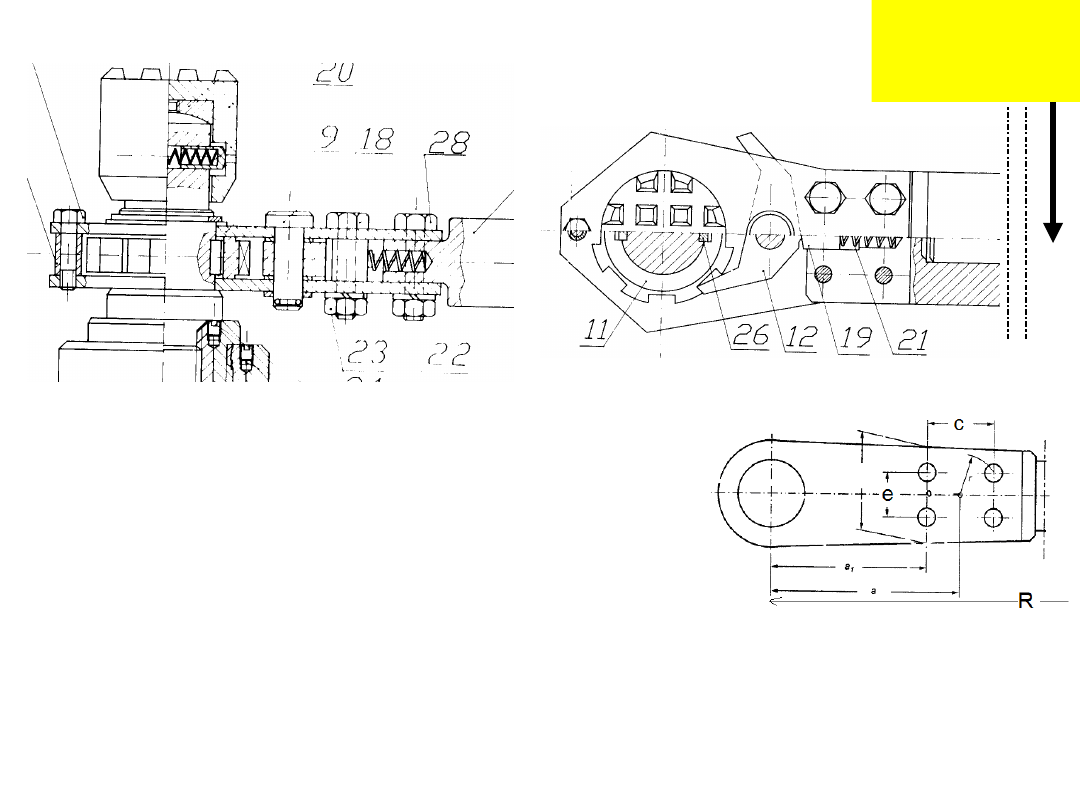
Przykład 5
Połączenia
śrubowe
Dobrać śruby złączne mechanizmu
napędowego podnośnika (połączenie drąga z
mechanizmem zapadkowym) oraz określić
moment dokręcenia nakrętek.
Dane: siłą ręki P=200 [N], R=800 [mm], c=e=40 [mm],
a
1
=100 [mm],
g
= =0.1 – wsp. tarcia na pow. gwintu,
p
=0.15 – na pozostałych powierzchniach, mat. śruby k
r
=160
[MPa], w=1 .
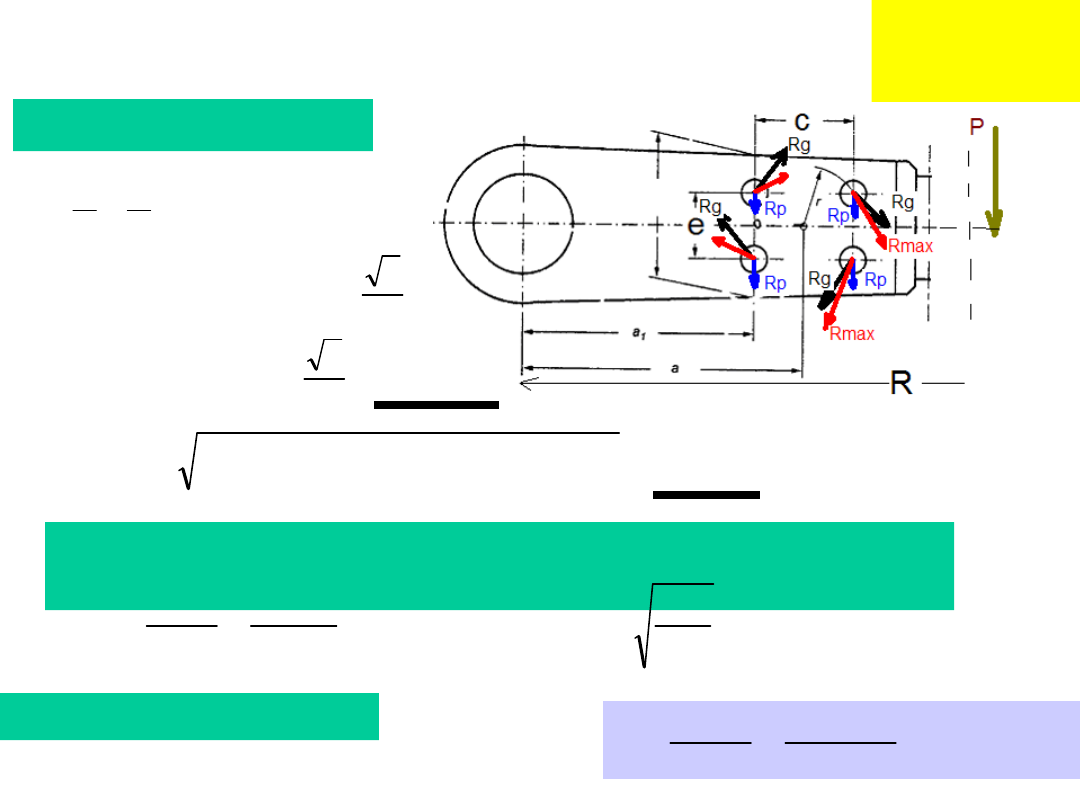
Połączenia
śrubowe
Przykład 5 cd.
Wyznaczenie obc. R
max
]
[
1202
)
2
2
4
/(
)
2
/
(
;
2
2
),
2
/
(
4
];
[
50
4
1
1
N
c
c
a
R
P
R
c
r
c
a
R
P
r
R
N
P
n
P
R
g
g
p
]
[
1238
)
,
cos(
2
2
2
max
N
R
R
R
R
R
R
R
g
p
g
p
g
p
Siła osiowa w śrubie z warunku przeniesienia R
max
siłami
tarcia
]
[
34
.
6
25
.
1
];
[
4126
15
.
0
2
1238
max
mm
wk
F
d
N
m
R
F
r
r
p
Dobór gwintu: M8x1,25;
]
[
466
.
6
mm
d
r
]
[
188
.
7
2
mm
d
]
[
647
.
6
1
mm
D
]
[
3235
.
7
2
647
.
6
8
2
1
mm
D
d
d
s
Przykład 5 cd.
Połączenia
śrubowe
]
[
1
.
10
2
;
12
,
2
.
8
0
0
mm
D
d
D
D
d
m
Podkładka
m
m
s
t
s
C
D
tg
d
F
M
M
M
'
5
,
0
s
d
h
tg
11547
,
0
30
cos
'
0
tg
0
11
.
3
3235
.
7
25
.
1
arctg
0
6
.
6
'
]
[
7
.
5
]
[
7
.
5710
]
15
.
0
1
.
10
1711
.
0
3235
.
7
[
4126
5
.
0
Nm
Nmm
M
C
Całkowity moment dokręcenia nakrętki śruby najbardziej obciążonej
Przykład innego rozwiązania
konstrukcyjnego (2 śruby):
Połączen
ia
śrubowe
Obliczenia wytrzymałościowe.
Śruby pracujące na zginanie
V przypadek obciążenia
śruby
Są to śruby zastosowane w konstrukcji w funkcji
podobnej do tej, jaką pełnią sworznie. Są one
obliczane na zginanie oraz ścinanie
Połączeni
a
kształtow
e
Sworzni
e
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
- Slide 50
- Slide 51
- Slide 52
- Slide 53
- Slide 54
- Slide 55
- Slide 56
- Slide 57
- Slide 58
- Slide 59
- Slide 60
- Slide 61
- Slide 62
- Slide 63
- Slide 64
- Slide 65
- Slide 66
- Slide 67
- Slide 68
- Slide 69
- Slide 70
- Slide 71
- Slide 72
- Slide 73
- Slide 74
- Slide 75
- Slide 76
- Slide 77
- Slide 78
- Slide 79
- Slide 80
- Slide 81
Wyszukiwarka
Podobne podstrony:
Połączenia gwintowe js
Połączenia gwintowe
materiały egzamin, 14.Połączenia gwintowe, Połączenia gwintowe (śrubowe)
Połączenia gwintowe, Mechanika, PKM
Połączenia gwintowe przerobione
polaczenia gwintowe
POŁĄCZENIA GWINTOWE I ŚRUBOWE
Połączenia gwintowe
Polaczenia gwintowen
Połączenia gwintowe sciaga
polaczenia gwintowe i srubowe
Połączenia gwintowe (2)
więcej podobnych podstron