11.06.21
1
Podstawy geometrii
wykreślnej
Zapis konstrukcji

11.06.21
Zapis konstrukcji
2
Tematyka zajęć
Podstawowe konstrukcje geometryczne:
Podział odcinka na równe części
Wykreślanie i dzielenie kątów
Podział okręgu na równe części
Wieloboki foremne
Proste styczne do okręgów
Okrąg i łuk styczny
Podstawowe krzywe płaskie
Zaawansowane konstrukcje geometryczne
Krzywe płaskie
Krzywe cykliczne
Literatura

11.06.21
Podstawowe konstrukcje geometryczne
3
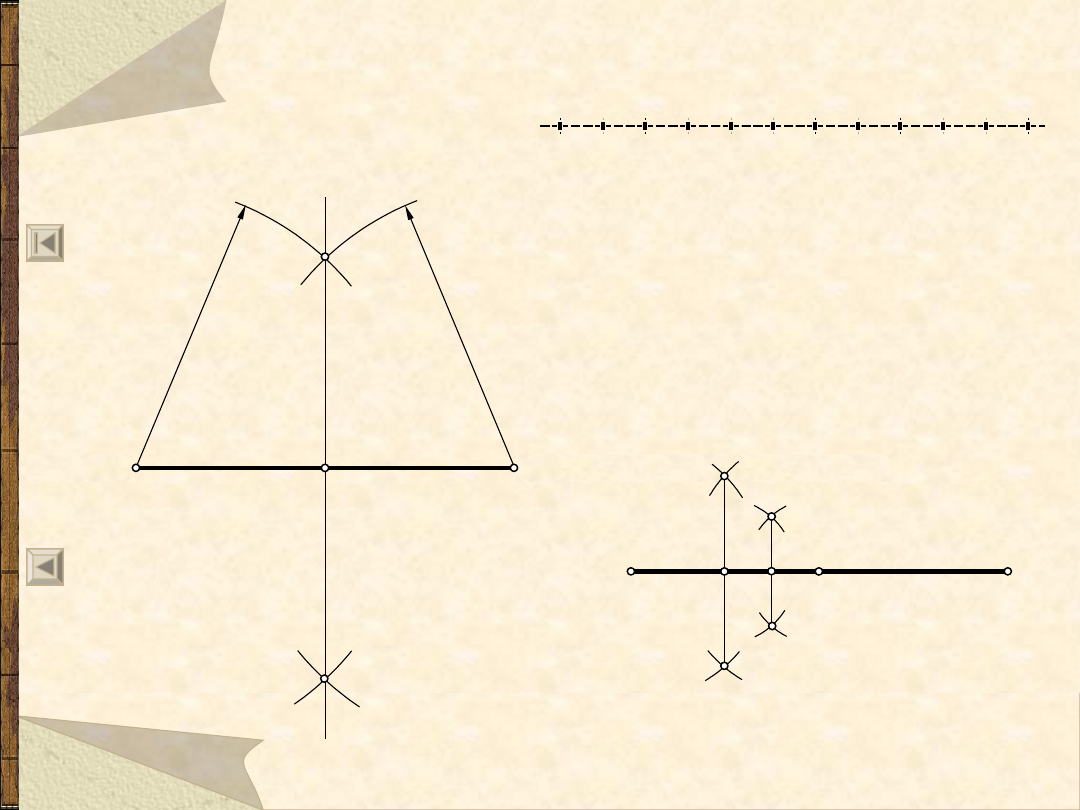
Podział odcinka na równe części
Podział odcinka na 2, 4, 8 ... części
Podział odcinka na dowolną liczbę równych części
11.06.21
Podział odcinka na równe części
4
r
Podział odcinka na 2, 4, 8 ... części
A
E
r
A
E
H
G
F
B
C
D
B
A, B, C, ... – punkt
r – promień łuku, okręgu
AB, CD, ... – odcinek prostej
3:5
np.
Podział odcinka w stosunku 3:5
11.06.21
Podział odcinka na równe części
5
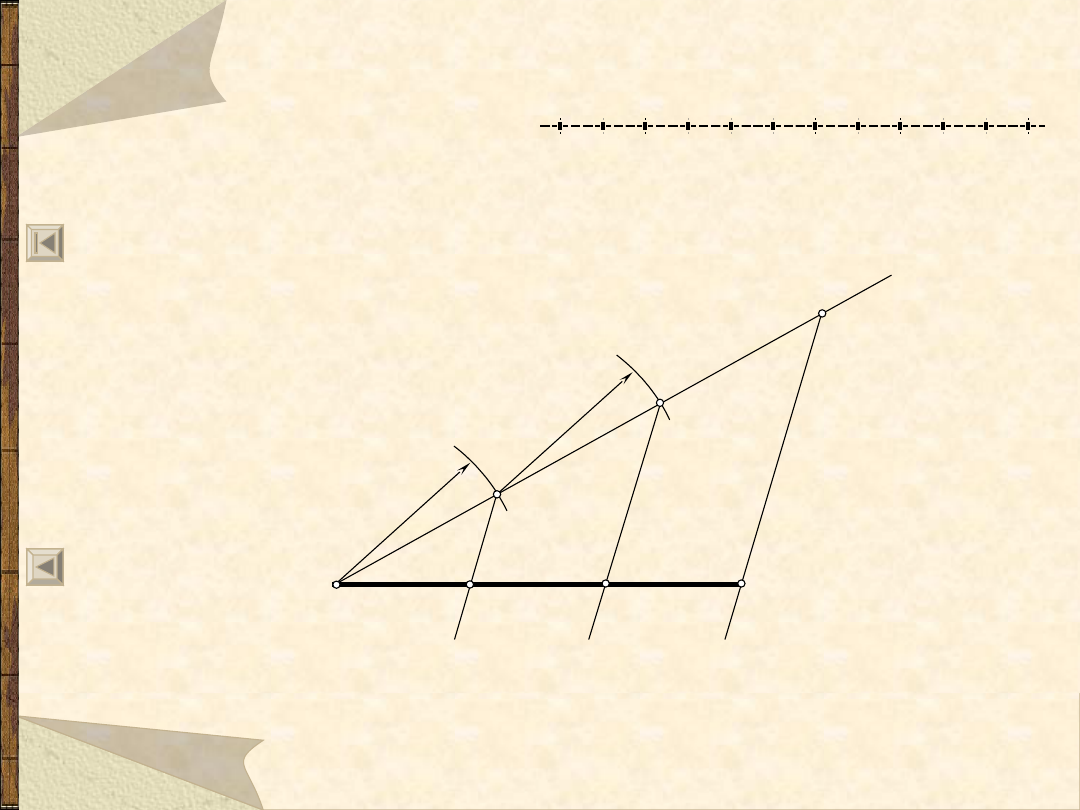
Podział odcinka
na dowolną liczbę części
r
a
r
A
B
E
D
C
F
G
a, b, c, ... – prosta, półprosta, łuk, okrąg, krzywa ...

11.06.21
Podstawowe konstrukcje geometryczne
6
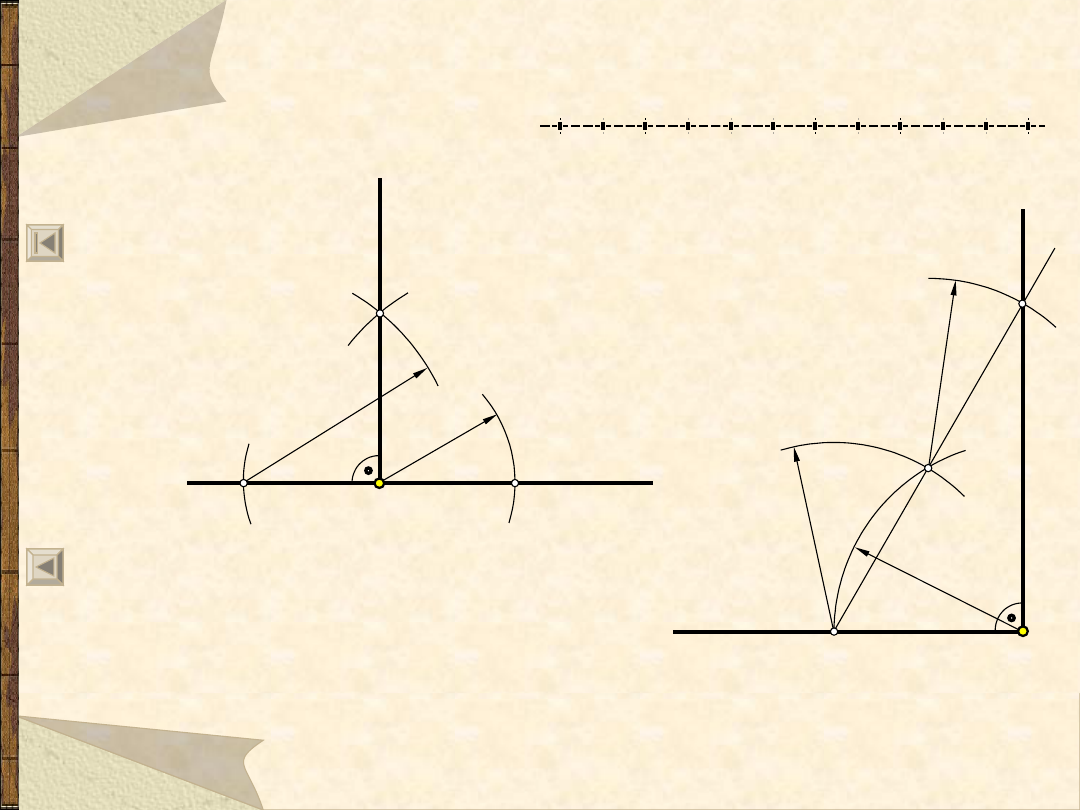
Wykreślanie i dzielenie kątów
Kąt prosty - proste prostopadłe
Dwusieczna kąta – wykreślanie kąta 45º
Kąty n
x
30º i wykreślanie kąta 15º
Dwusieczna kąta bez widocznego wierzchołka
Sieczna, przechodząca przez punkt A, w kącie bez
widocznego wierzchołka
11.06.21
Wykreślanie i dzielenie kątów
7
Proste prostopadłe
a
b
r
2
D
B
C
r
1
a
b
D
A
r
1
r
1
r
1
C
A
B
11.06.21
Wykreślanie i dzielenie kątów
8
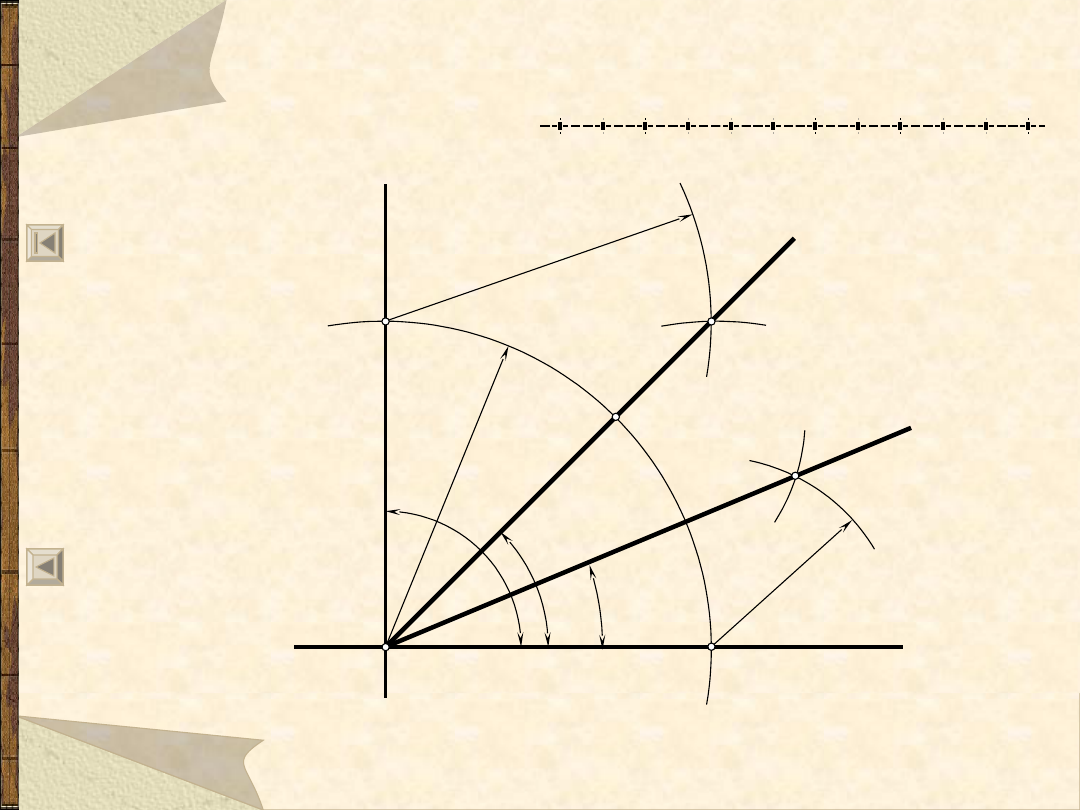
Dwusieczna kąta – wykreślanie kąta 45º
a
b
r
1
r
r
2
d
c
22,5
°
45°
90°
A
C
B
E
F
D
11.06.21
Wykreślanie i dzielenie kątów
9
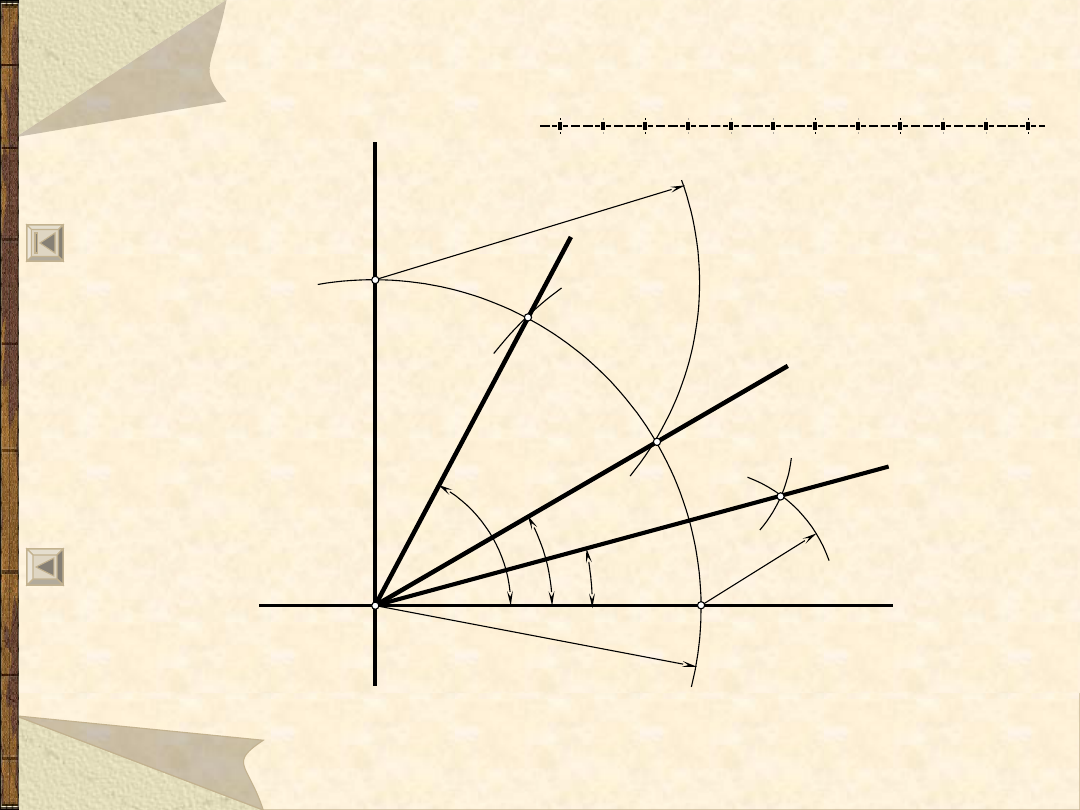
Kąty n
x
30º i wykreślanie kąta 15º
c
a
r
1
d
b
15
°
30
°
60
°
C
E
r
1
r
2
A
D
B
e
F
11.06.21
Wykreślanie i dzielenie kątów
10
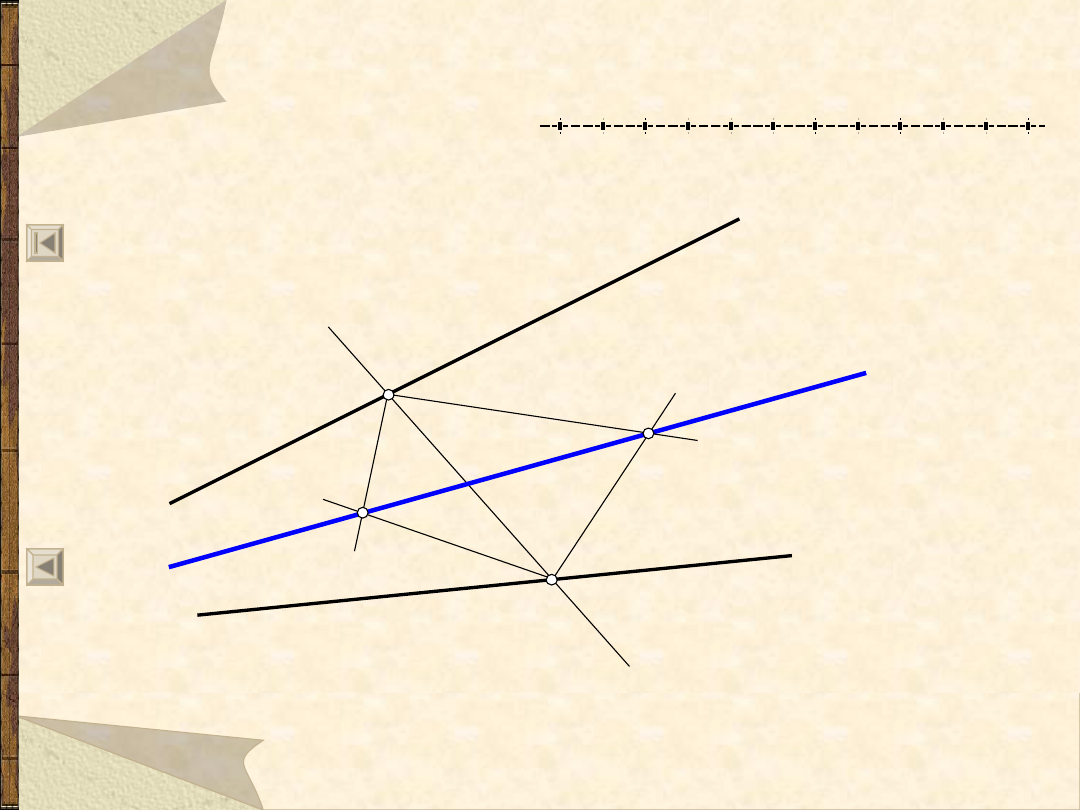
Dwusieczna kąta bez widocznego
wierzchołka
A
B
C
a
D
c
b
d
11.06.21
Wykreślanie i dzielenie kątów
11
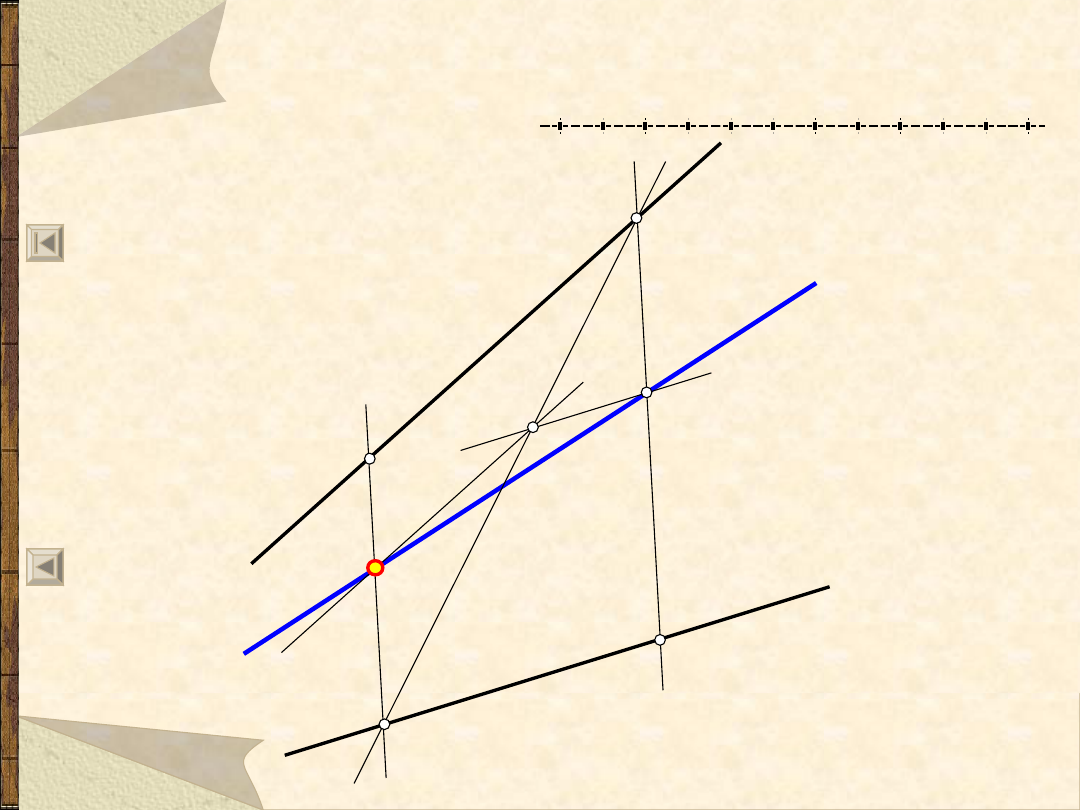
Sieczna, przechodząca przez punkt A, w
kącie bez widocznego wierzchołka
A
a
c
b
k
C
D
B
G
F
E
d
g
f
e

11.06.21
Podstawowe konstrukcje geometryczne
12
Podział okręgu na równe części
Podział okręgu na 4 równe części
Podział okręgu na 8 równych części
Podział okręgu na 3 równe części
Podział okręgu na 6 równych części
Podział okręgu na 12 równych części
11.06.21
Podział okręgu na równe części
13
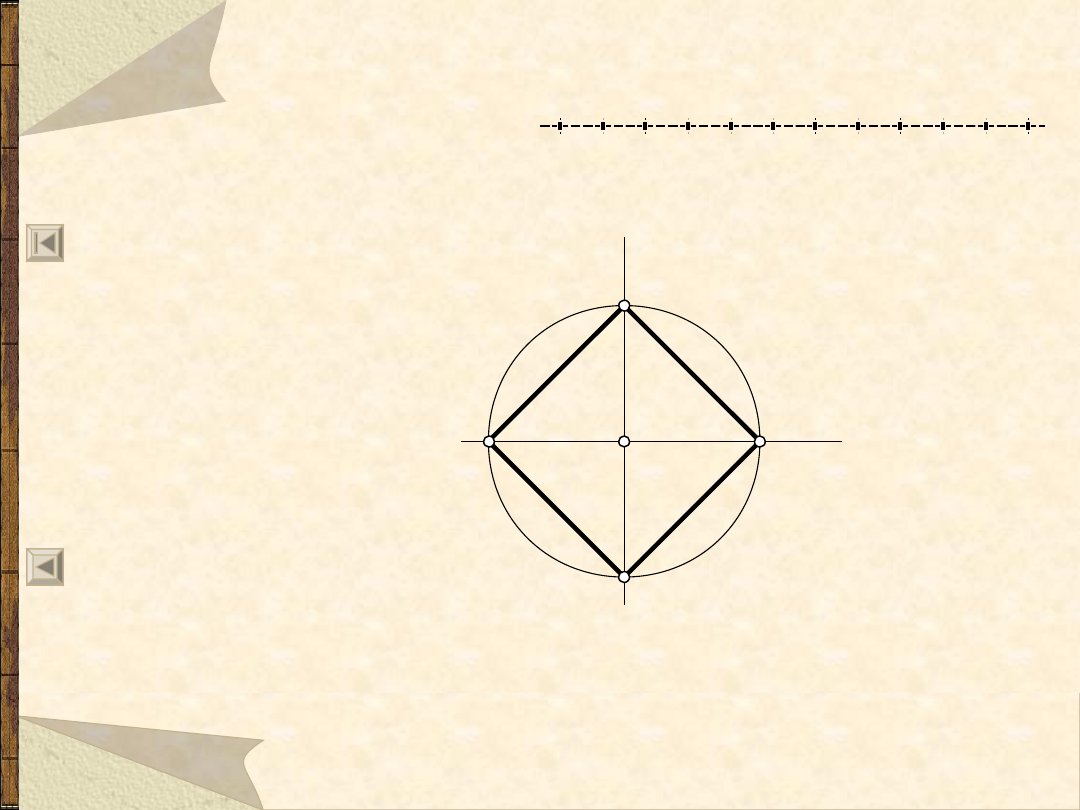
Podział okręgu na 4 równe części
a
b
3
1
2
4
0
11.06.21
Podział okręgu na równe części
14
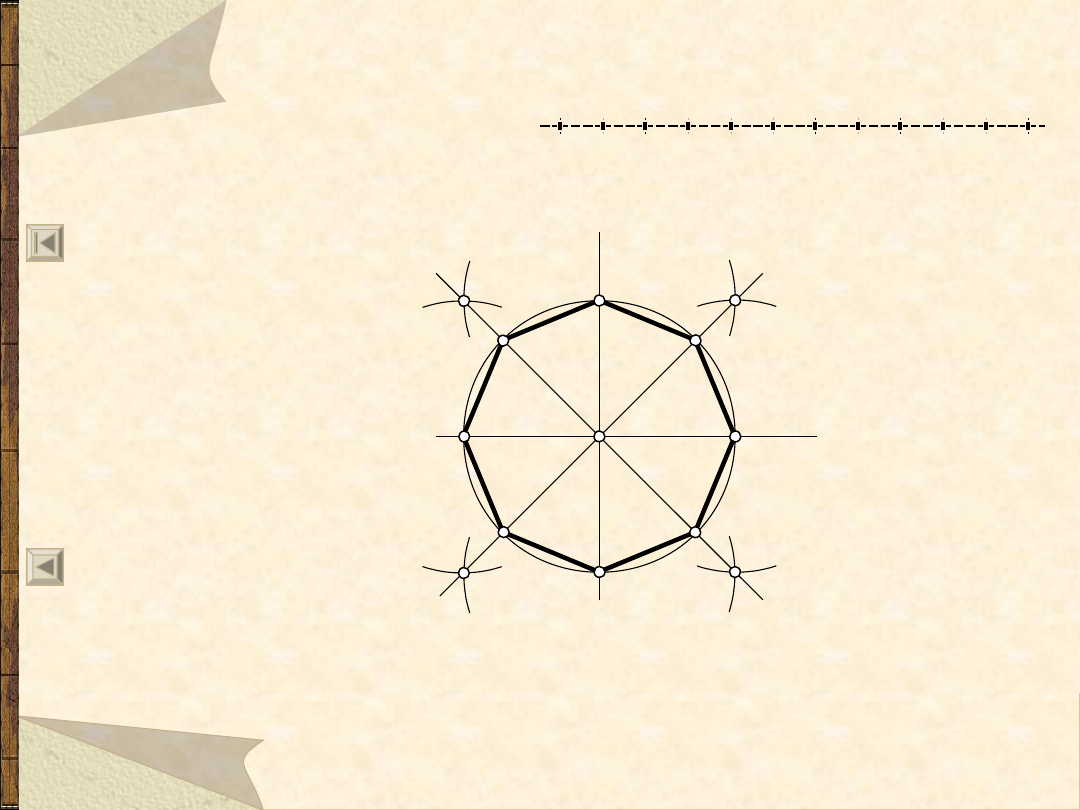
Podział okręgu na 8 równych części
a
b
3
7
6
8
2
1
4
5
0
11.06.21
Podział okręgu na równe części
15
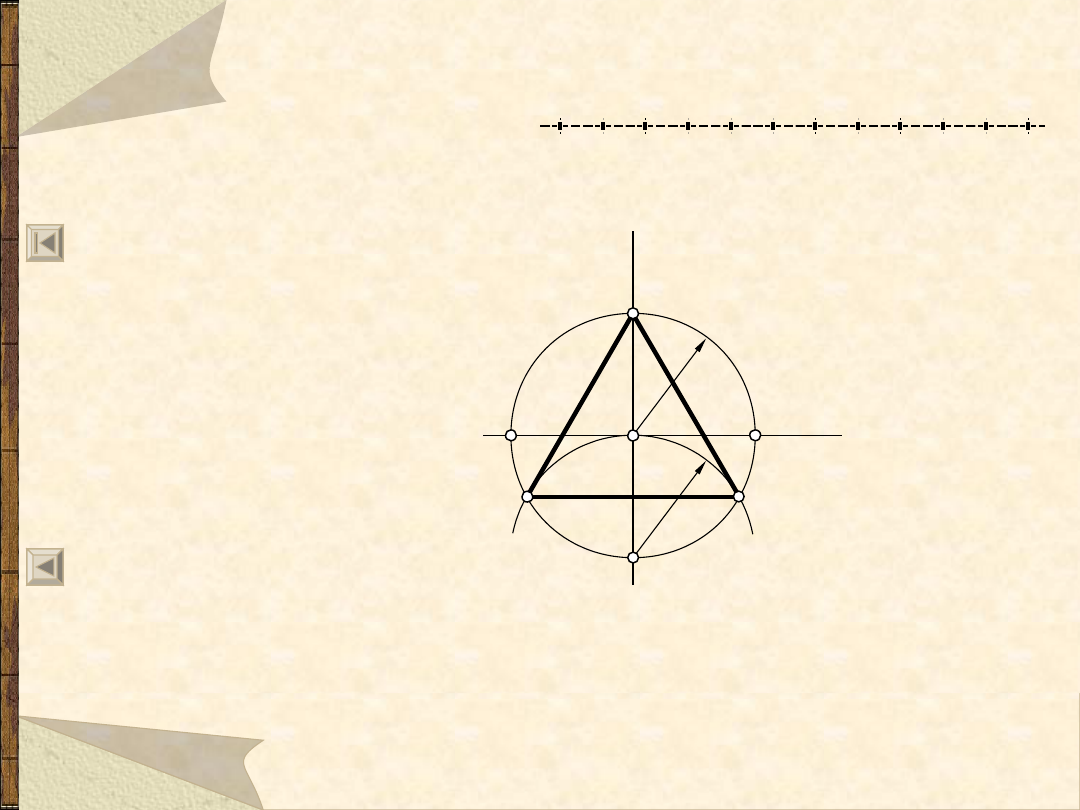
Podział okręgu na 3 równe części
a
2
3
1
b
r
r
B
C
D
0
A
11.06.21
Podział okręgu na równe części
16
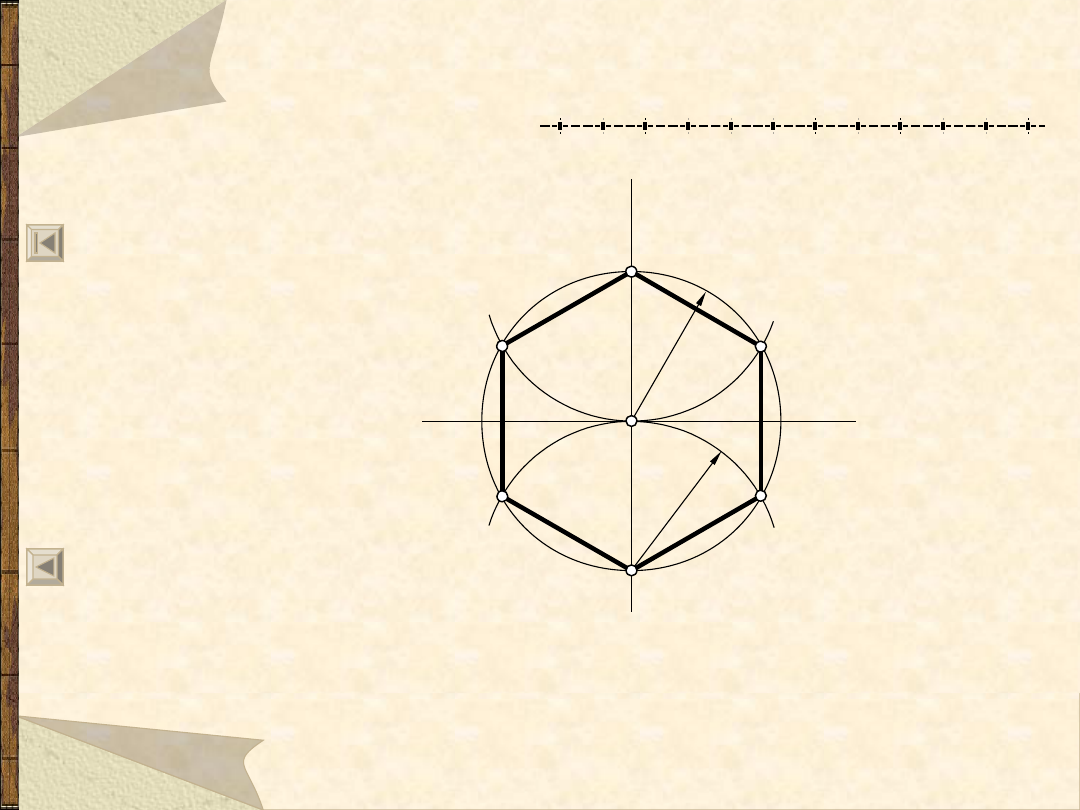
Podział okręgu na 6 równych części
a
b
r
r
2
3
1
A
B
0
4
5
6
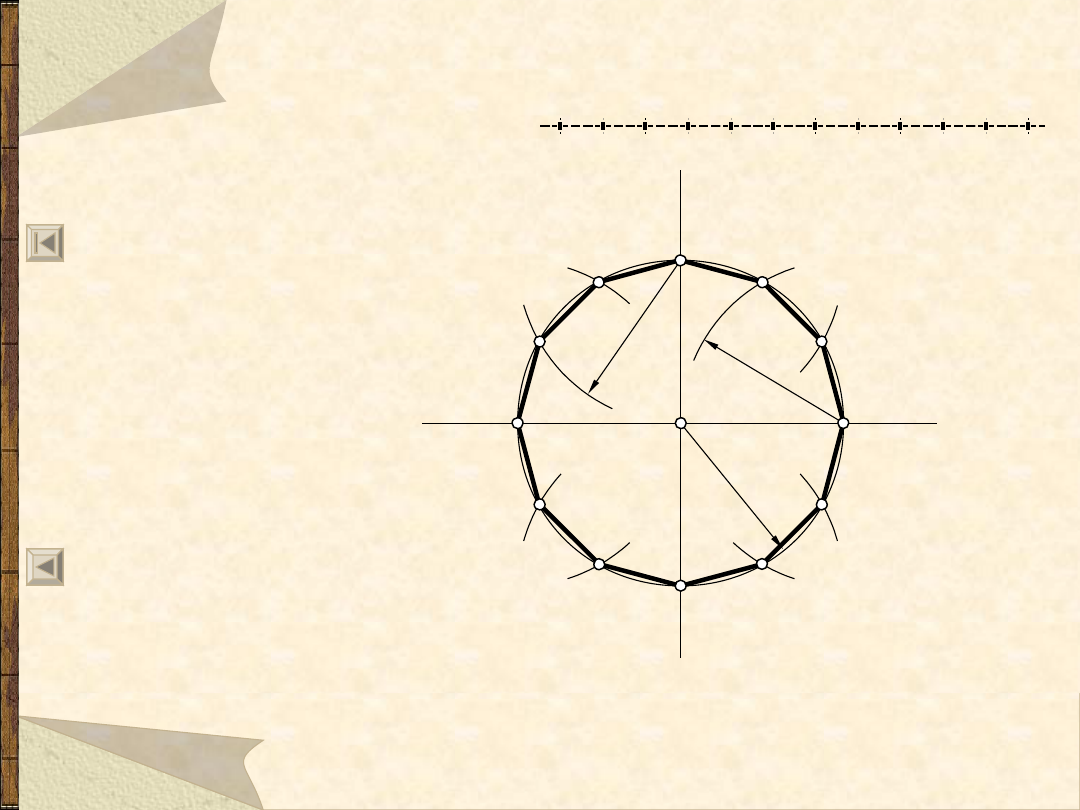
11.06.21
Podział okręgu na równe części
17
Podział okręgu na 12 równych części
1
2
8
1
1
a
3
2
1
b
9
6
r
r
r
7
1
0
5
4
B
C
D
A
0

11.06.21
Podstawowe konstrukcje geometryczne
18
Wieloboki foremne
5-bok foremny
7-bok foremny
Wielobok foremny – metoda ogólna 1
Wielobok foremny – metoda ogólna 2
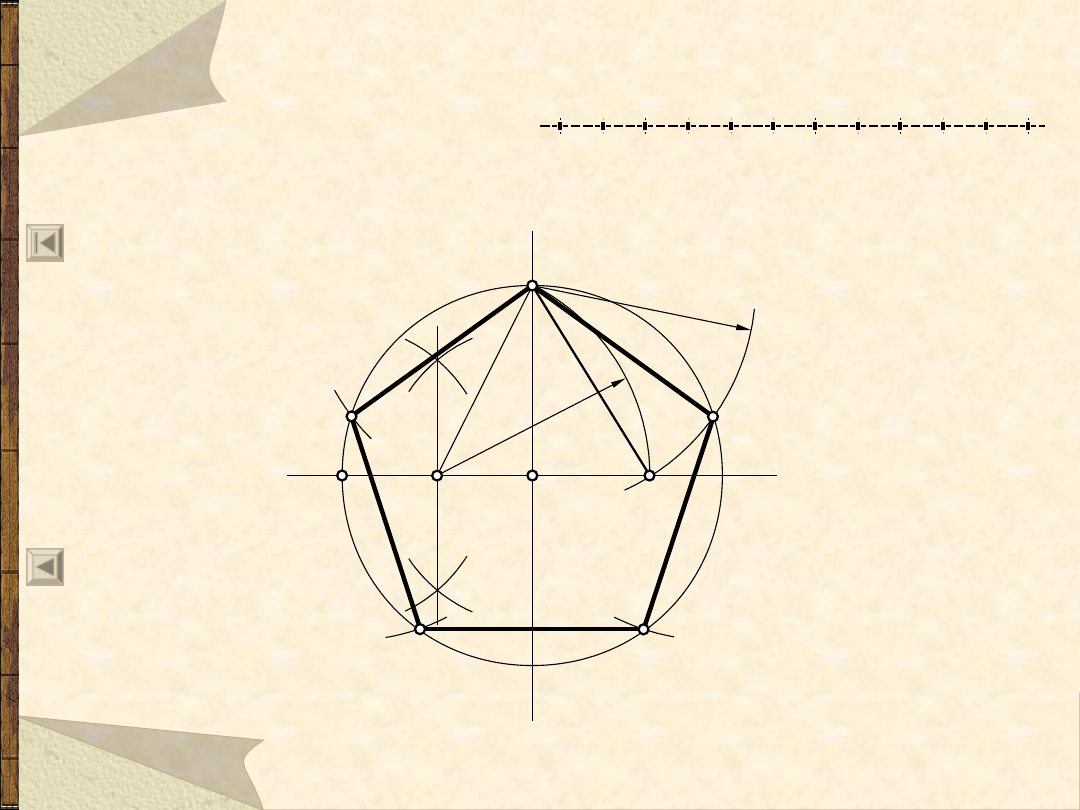
11.06.21
Wieloboki foremne
19
Pięciobok foremny
5
2
1
r
1
r
2
B
D
A
0
C
4
3
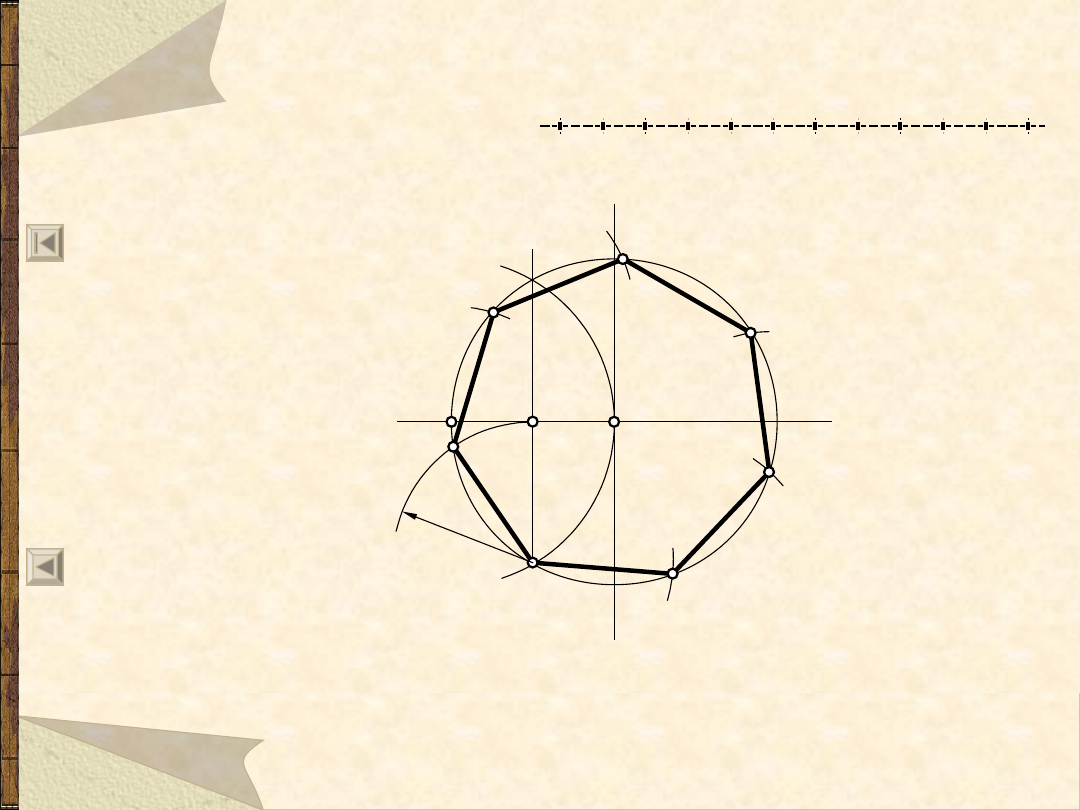
11.06.21
Wieloboki foremne
20
Siedmiobok foremny
1
5
7
C
A
0
2
B
6
3
4
r
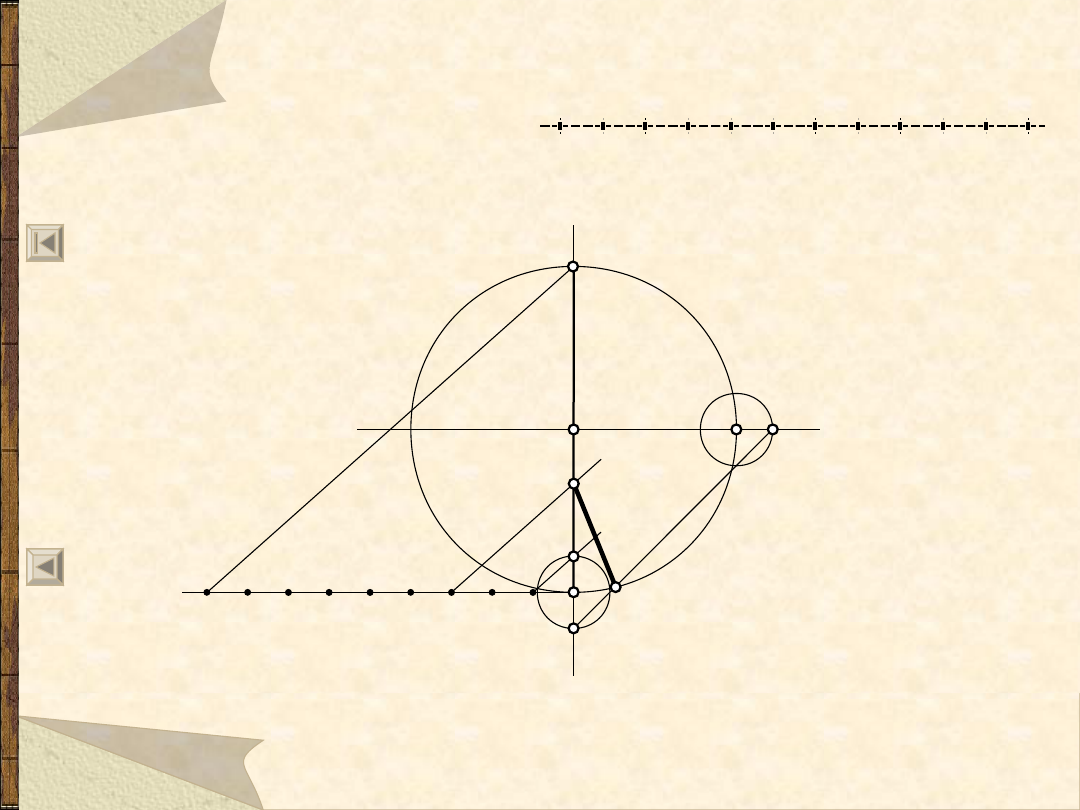
11.06.21
Wieloboki foremne
21
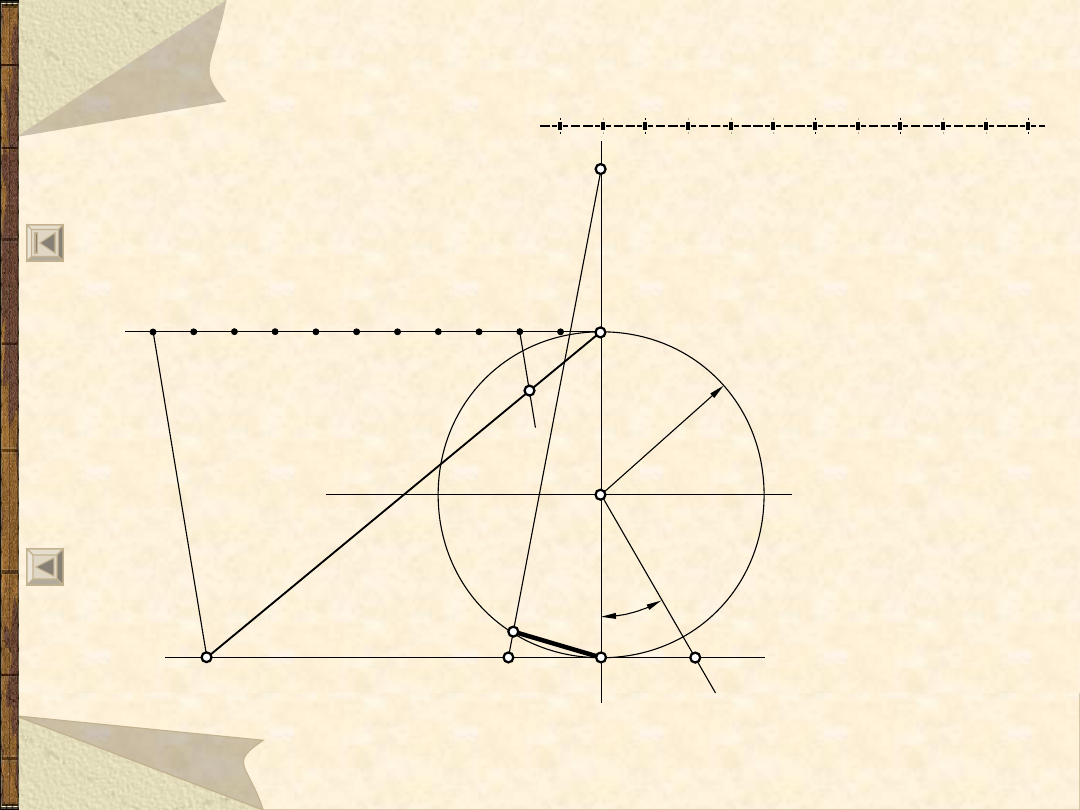
Wielobok foremny (9) – metoda ogólna 1
9
3 2 1
B
E
F
D
A
0
C
1
’
3
’
A1’ =
1/n
x
AC
A3’ =
3/n
x
AC
11.06.21
Wieloboki foremne
22
Wielobok foremny (11) – metoda ogólna 2
r
30
º
1
1
3 2 1
B
H
F
A
G
0
D
E
C
BC = 3r
DG = r
DE =
2/n
x
CD
AF = DE

11.06.21
Podstawowe konstrukcje geometryczne
23
Proste styczne do okręgów
Styczna do okręgu w punkcie A
Styczna do okręgu przechodząca przez punkt A
Styczna do dwóch okręgów – 1
Styczna do dwóch okręgów – 2
11.06.21
Proste styczne do okręgów
24
Styczna do okręgu w punkcie A
a
b
0
B
A
11.06.21
Proste styczne do okręgów
25
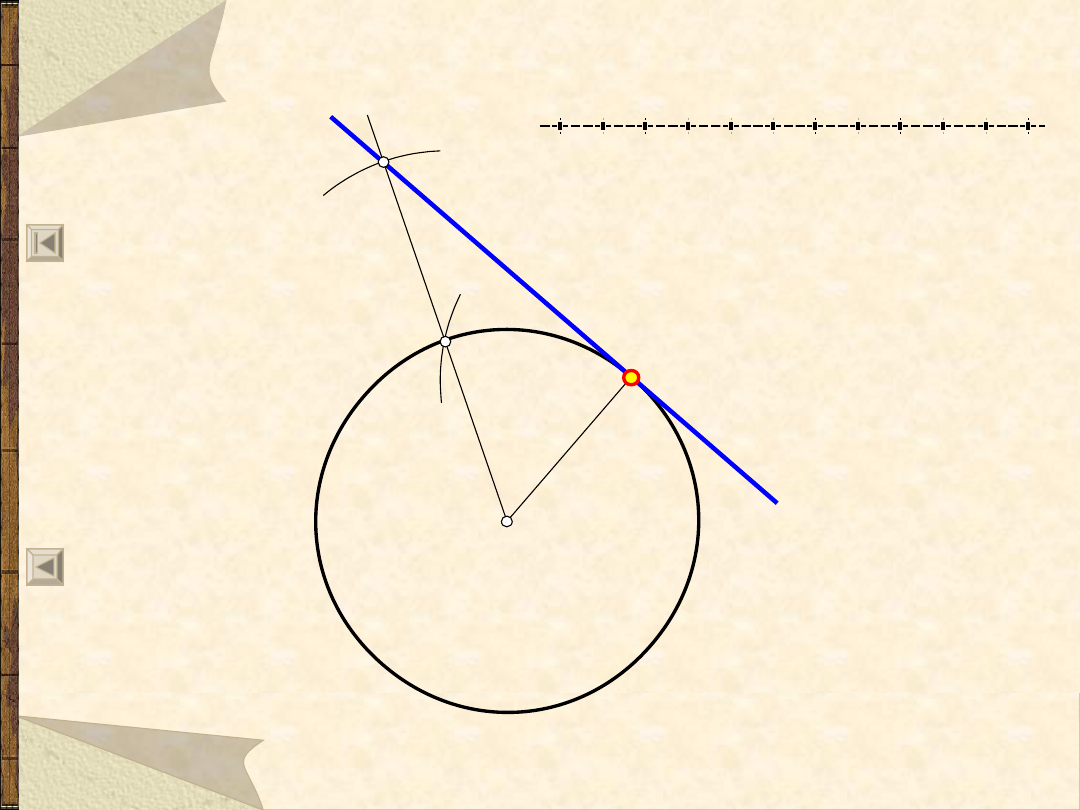
Styczna do okręgu przechodząca
przez punkt A
b
a
c
d
A
B
O
C
11.06.21
Proste styczne do okręgów
26
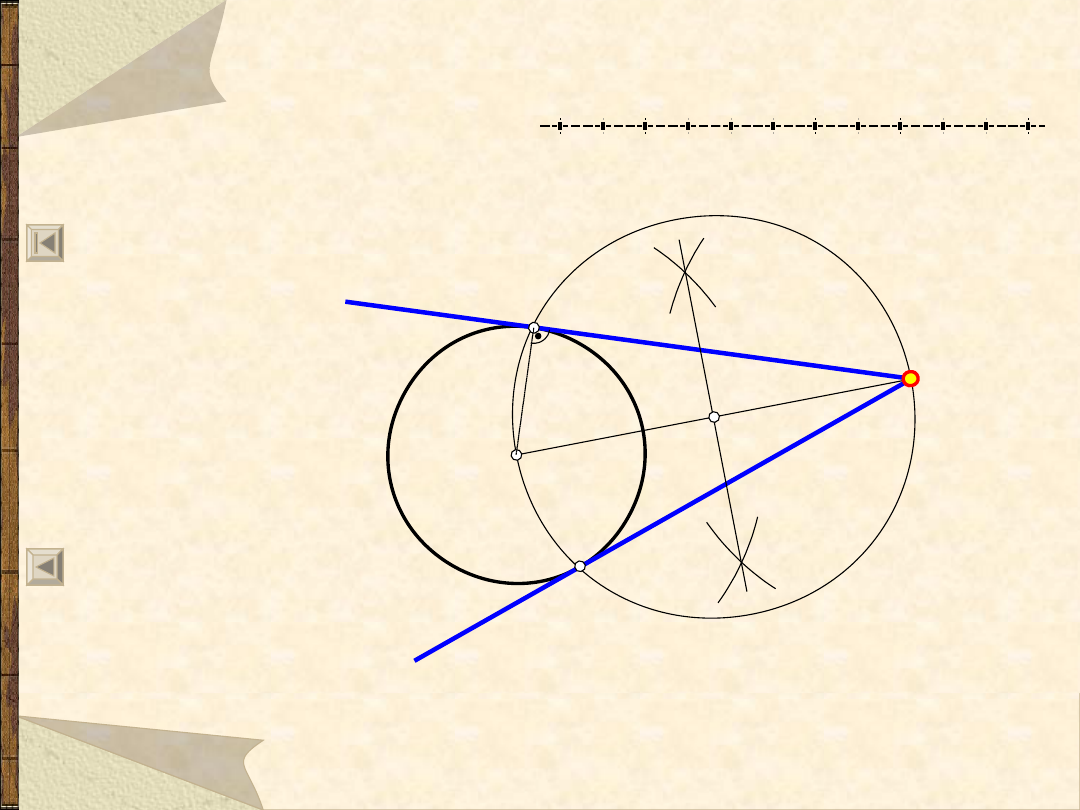
Styczna do dwóch okręgów – 1
c
d
b
a
R
1
R
2
R
1
- R
2
C
B
A
0
1
0
2
11.06.21
Proste styczne do okręgów
27
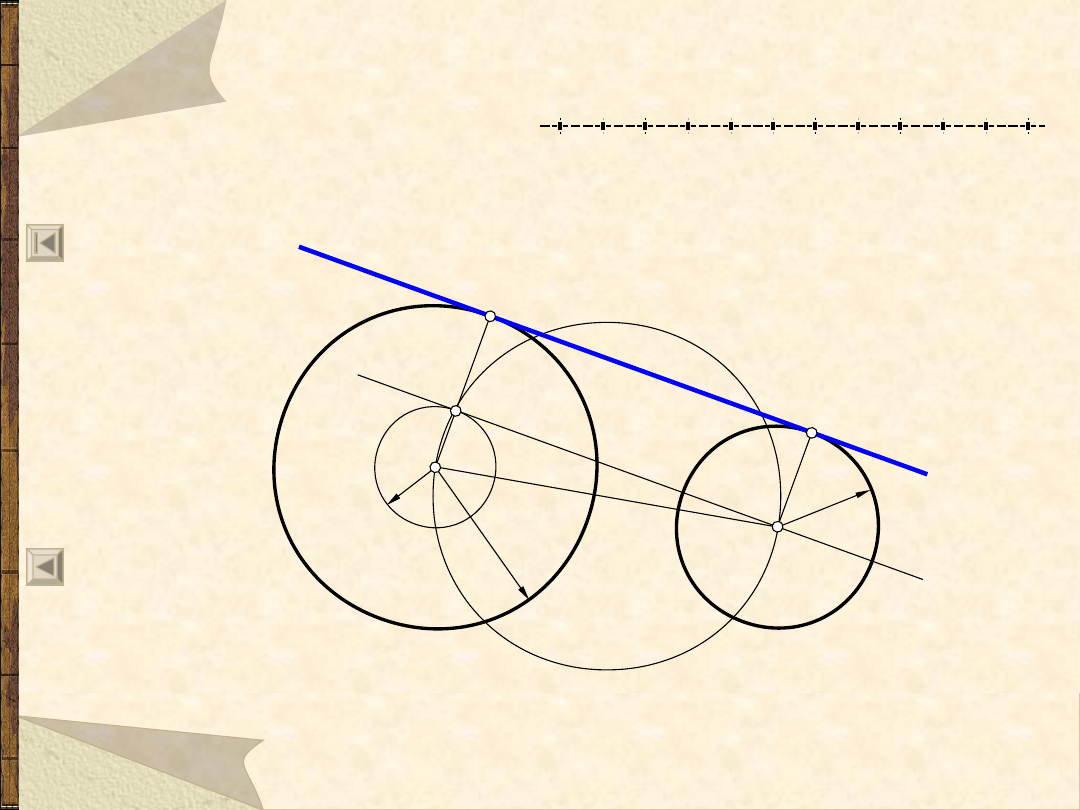
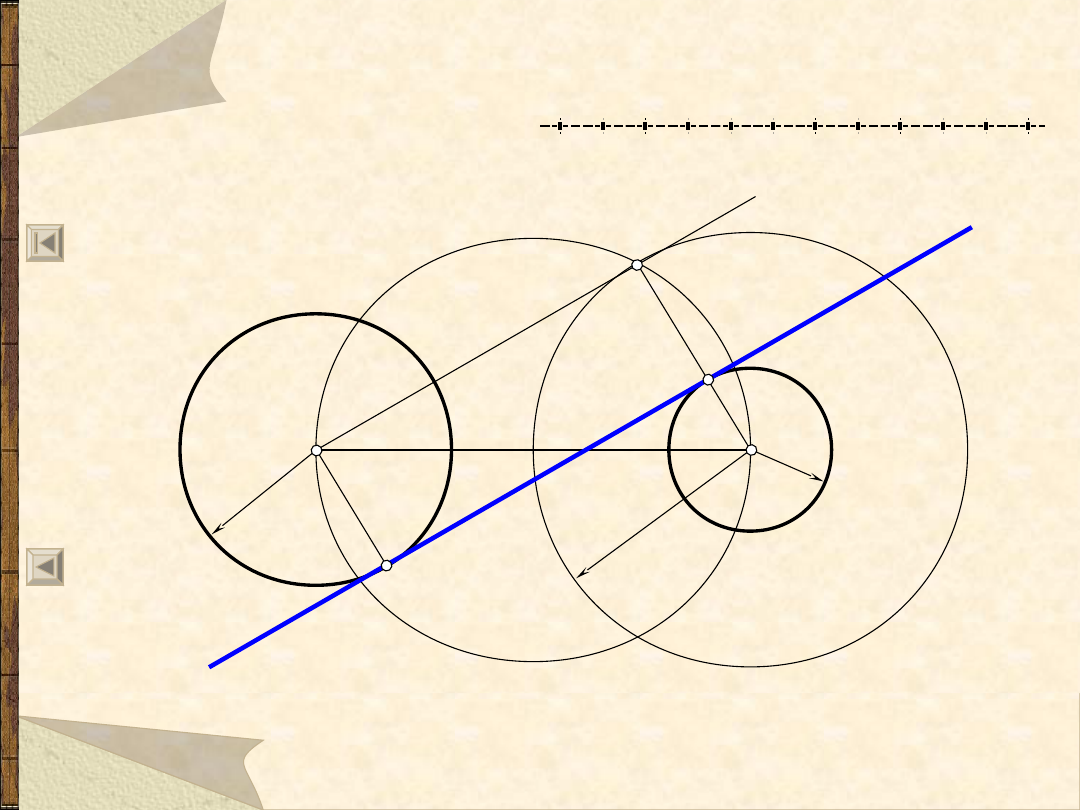
Styczna do dwóch okręgów – 2
a
b
d
c
A
e
R
R+
r
r
0
1
B
C
0
2

11.06.21
Podstawowe konstrukcje geometryczne
28
Łuk (okrąg) styczny do ...
... prostej i przechodzący przez punkt A
... dwóch prostych przecinających się
...
prostej w punkcie A i do drugiej prostej
... trzech prostych
... łuku w punkcie A
... okręgu i prostej, zewnętrznie
... okręgu i prostej w punkcie A, wewnętrznie
... okręgu i prostej w punkcie A, zewnętrznie
... okręgu w punkcie A i do prostej
... okręgu w punkcie A i do okręgu
Dwa łuki styczne do dwóch prostych równoległych
i wzajemnie w punkcie A
11.06.21
Okręgi i łuki styczne do ...
29
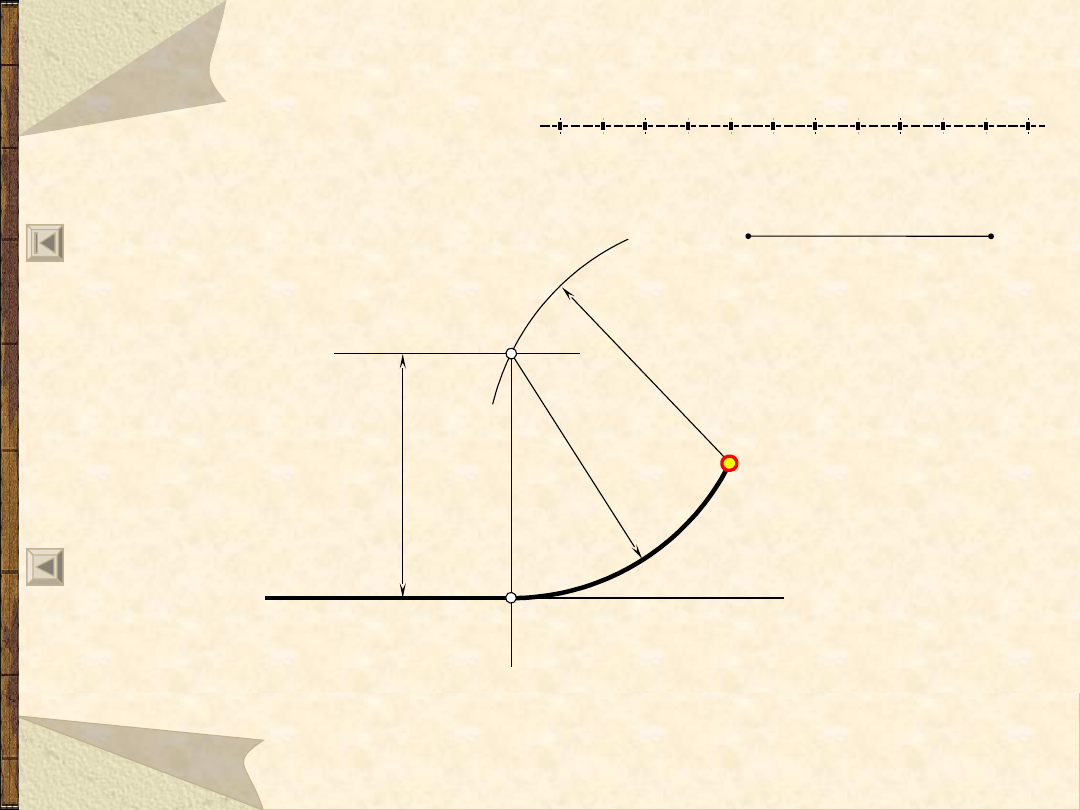
Łuk styczny do prostej
i przechodzący przez punkt A
b
d
c
a
r
r
r
e
r =
B
C
A
11.06.21
Okręgi i łuki styczne do ...
30
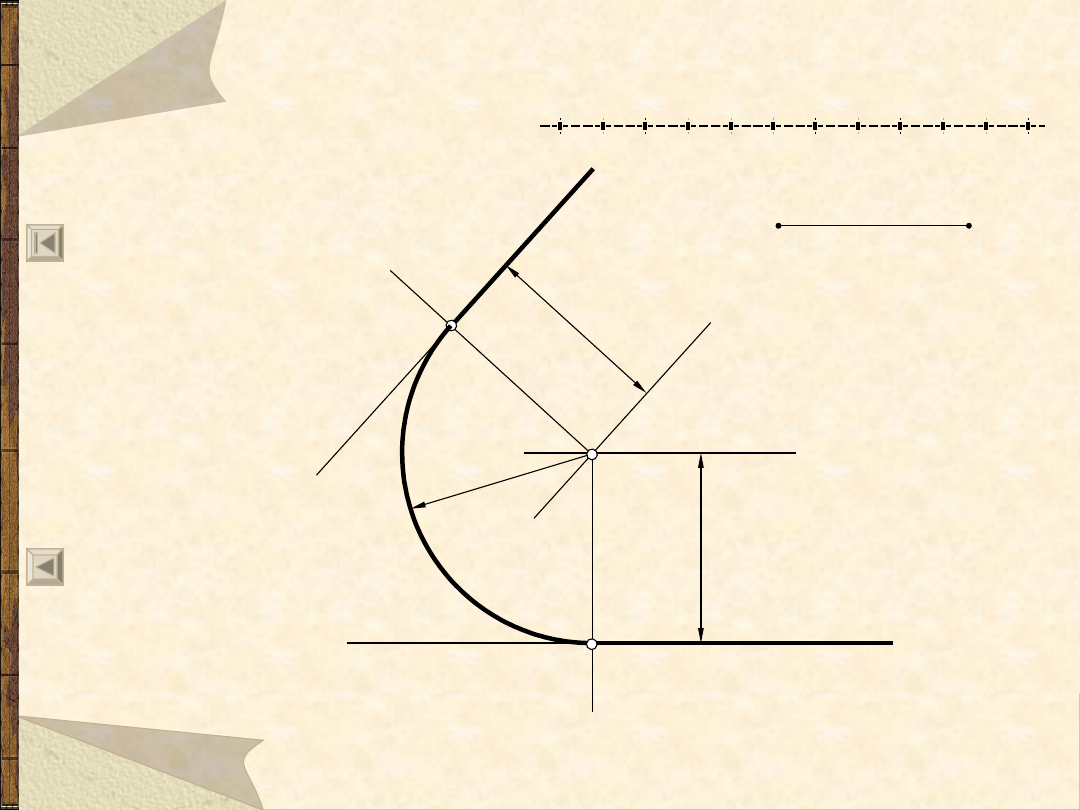
Łuk styczny do dwóch prostych
przecinających się
a
c
b
d
r
r
r
C
A
e
r =
B
11.06.21
Okręgi i łuki styczne do ...
31
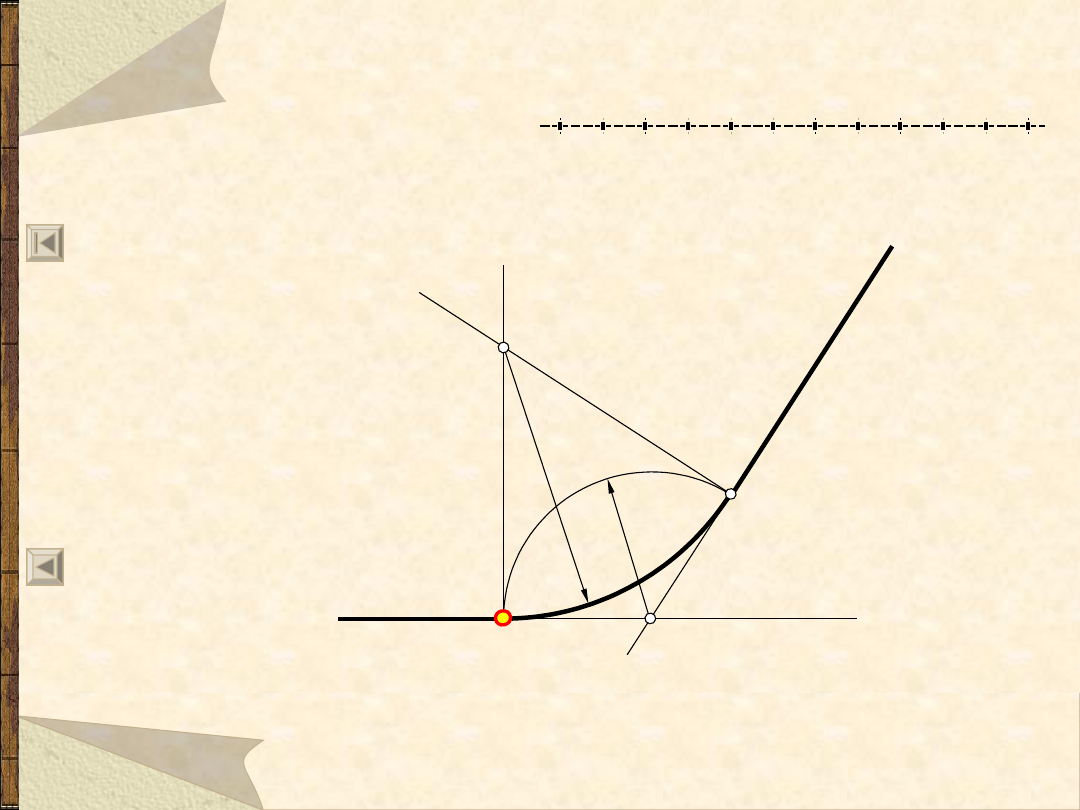
Łuk styczny do prostej w punkcie A
i do drugiej prostej
a
d
c
b
r
1
r
2
D
A
C
B
11.06.21
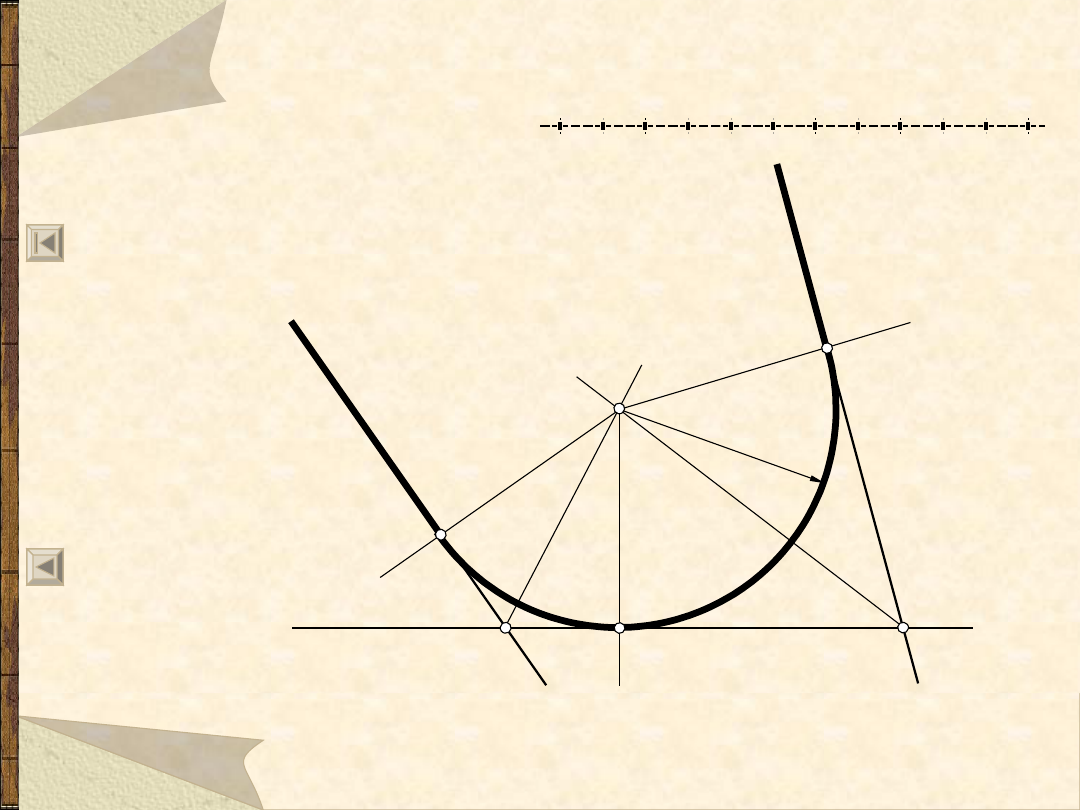
Okręgi i łuki styczne do ...
32
Łuk styczny do trzech prostych
b
c
a
e
d
r
f
D
C
A
B
11.06.21
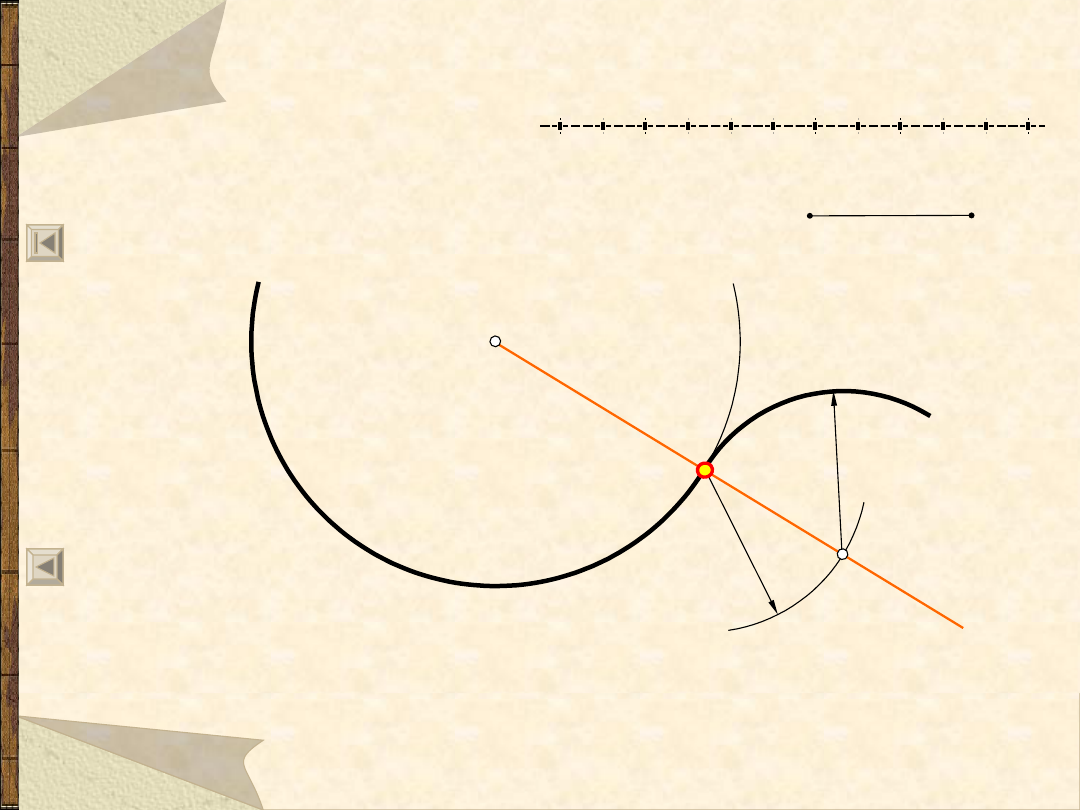
Okręgi i łuki styczne do ...
33
Łuk styczny do łuku w punkcie A
a
c
b
r
r
B
0
A
r =
11.06.21
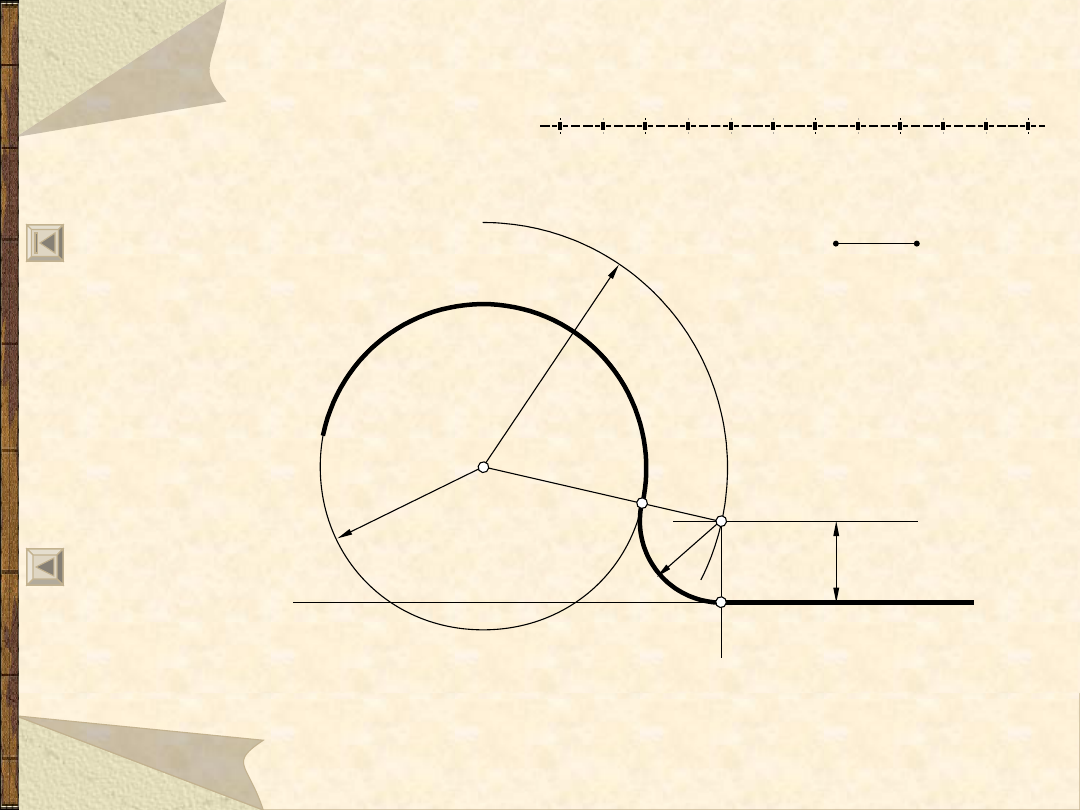
Okręgi i łuki styczne do ...
34
Łuk styczny do okręgu i prostej,
zewnętrznie
a
d
b
c
R
e
r
r
R+
r
B
A
C
r =
0
11.06.21
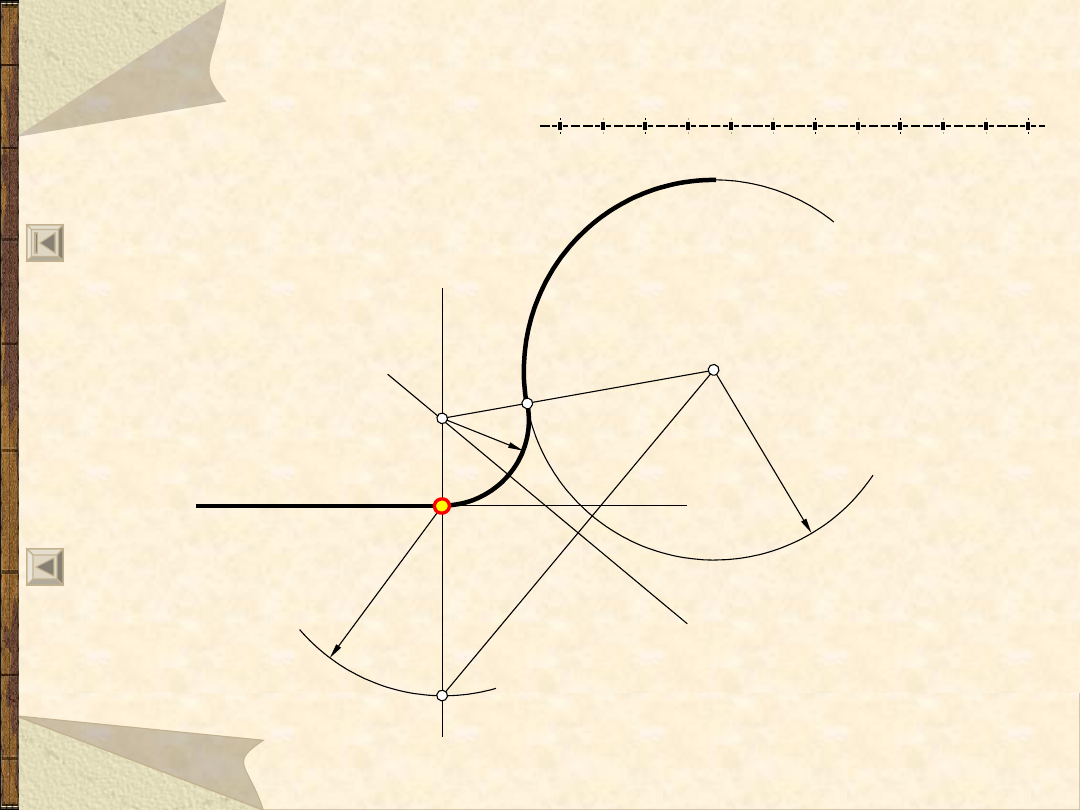
Okręgi i łuki styczne do ...
35
Łuk styczny do okręgu i prostej w
punkcie A, wewnętrznie
b
a
c
d
D
R
r
R
B
A
C
0
11.06.21
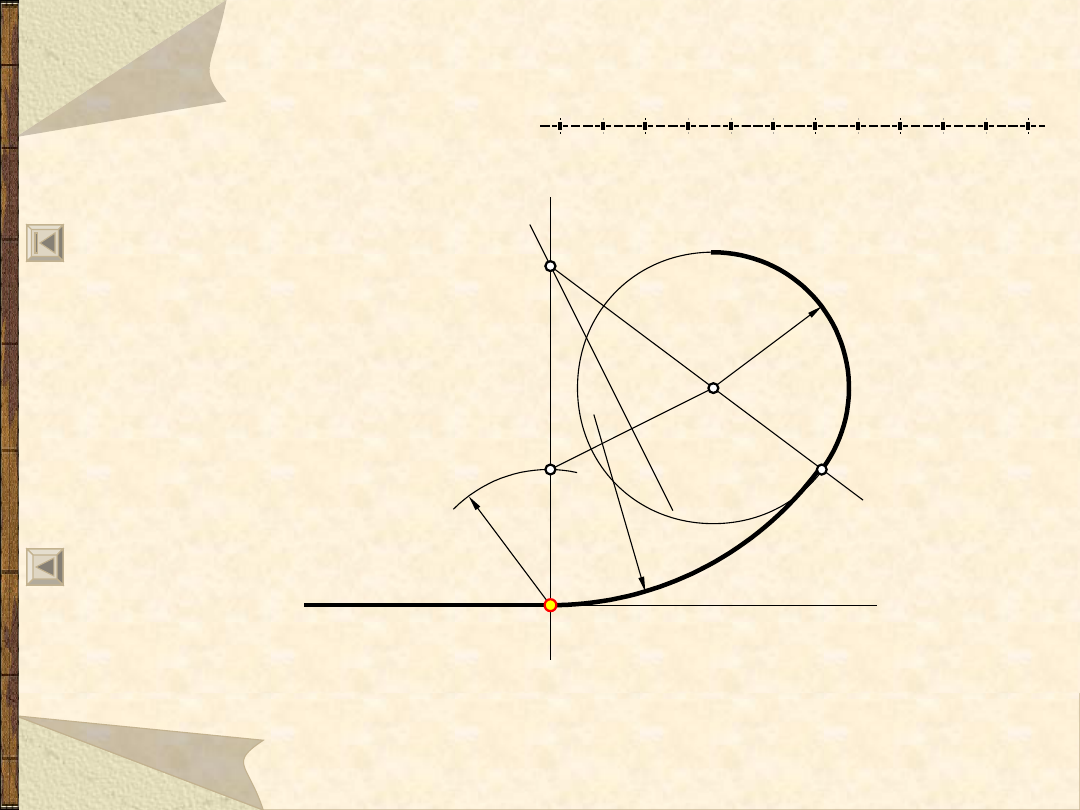
Okręgi i łuki styczne do ...
36
Łuk styczny do okręgu i prostej w
punkcie A, zewnętrznie
b
c
a
d
r
e
R
r
A
0
1
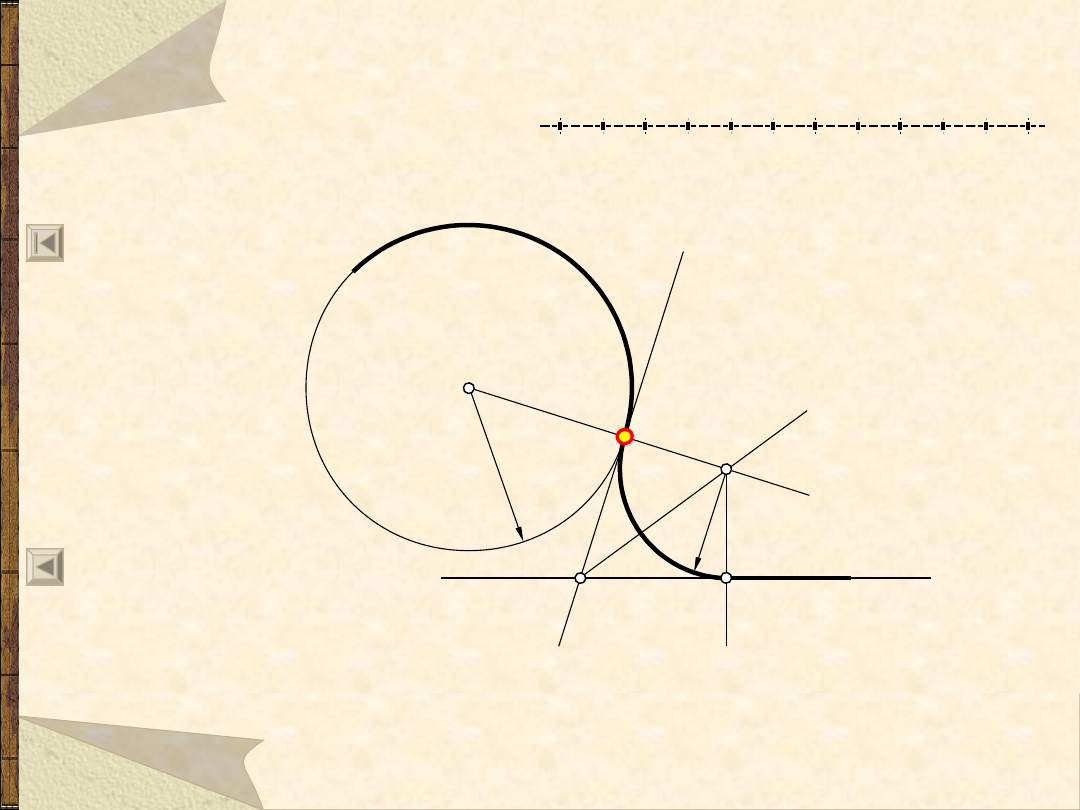
CA = CD = R
C
B
D
11.06.21
Okręgi i łuki styczne do ...
37
Łuk styczny do okręgu w punkcie A
i do prostej
a
b
c
d
e
r
R
B
A
C
D
0
11.06.21
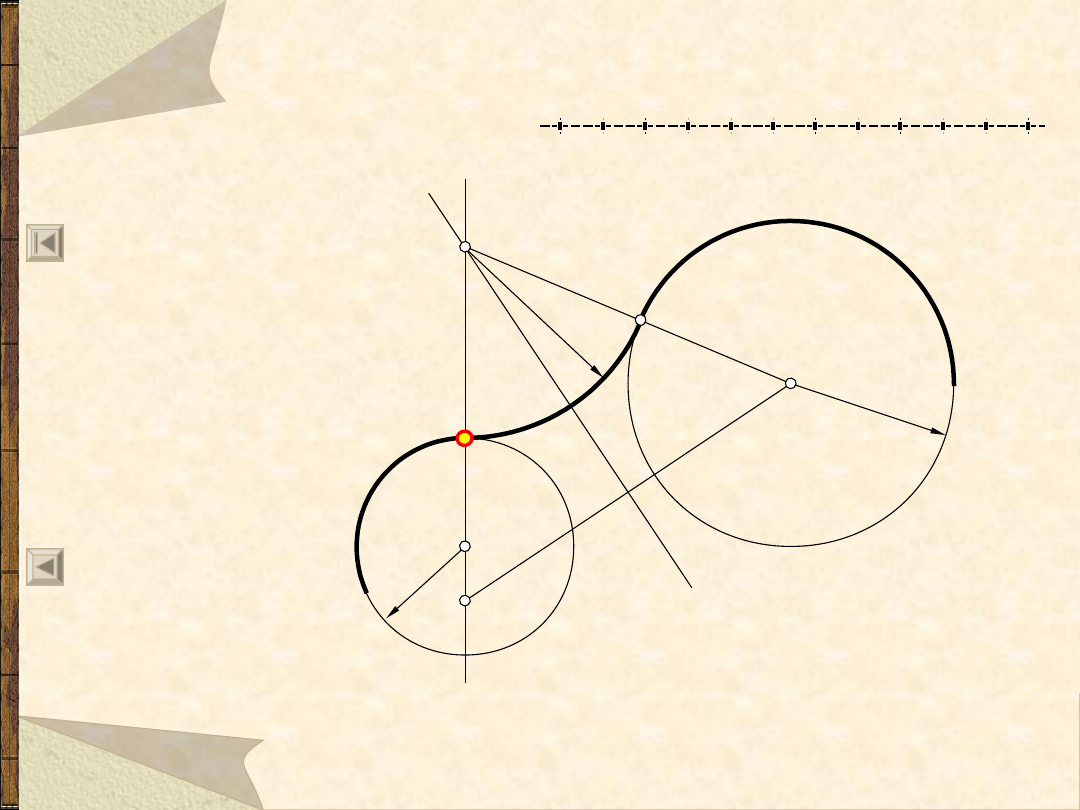
Okręgi i łuki styczne do ...
38
Łuk styczny do okręgu w punkcie A
i do okręgu
a
b
c
R
1
d
R
2
r
B
A
0
2
C
0
1
D
AB = R
2
AC = CD = r
11.06.21
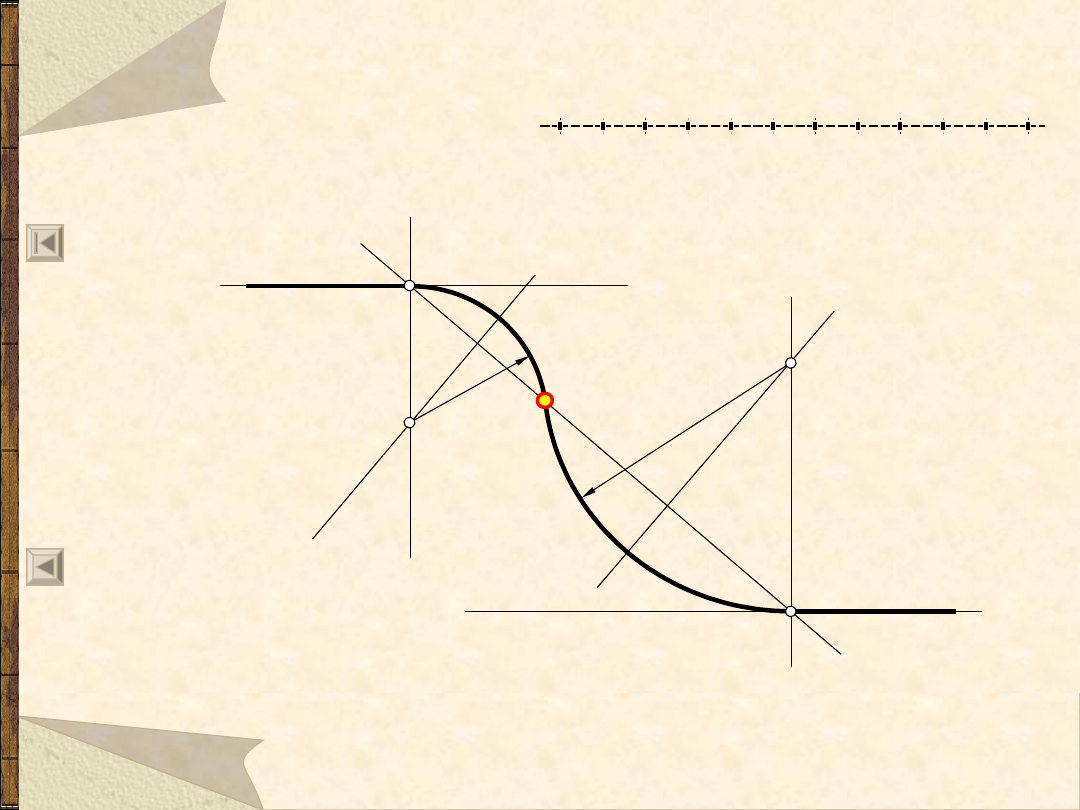
Okręgi i łuki styczne do ...
39
Dwa łuki styczne do dwóch prostych
równoległych i wzajemnie w punkcie A
a
b
d
e
f
g
c
r
2
r
1
A
B
C
0
2
0
1

11.06.21
Podstawowe konstrukcje geometryczne
40
Podstawowe krzywe płaskie
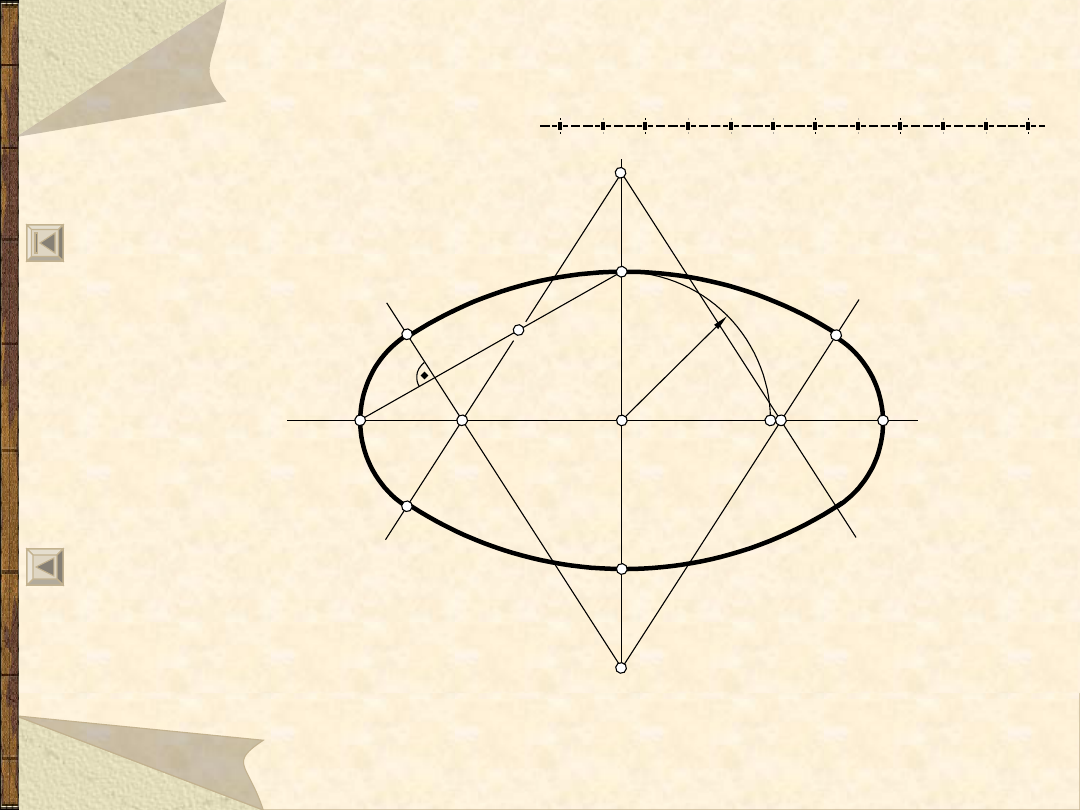
Owal – 1
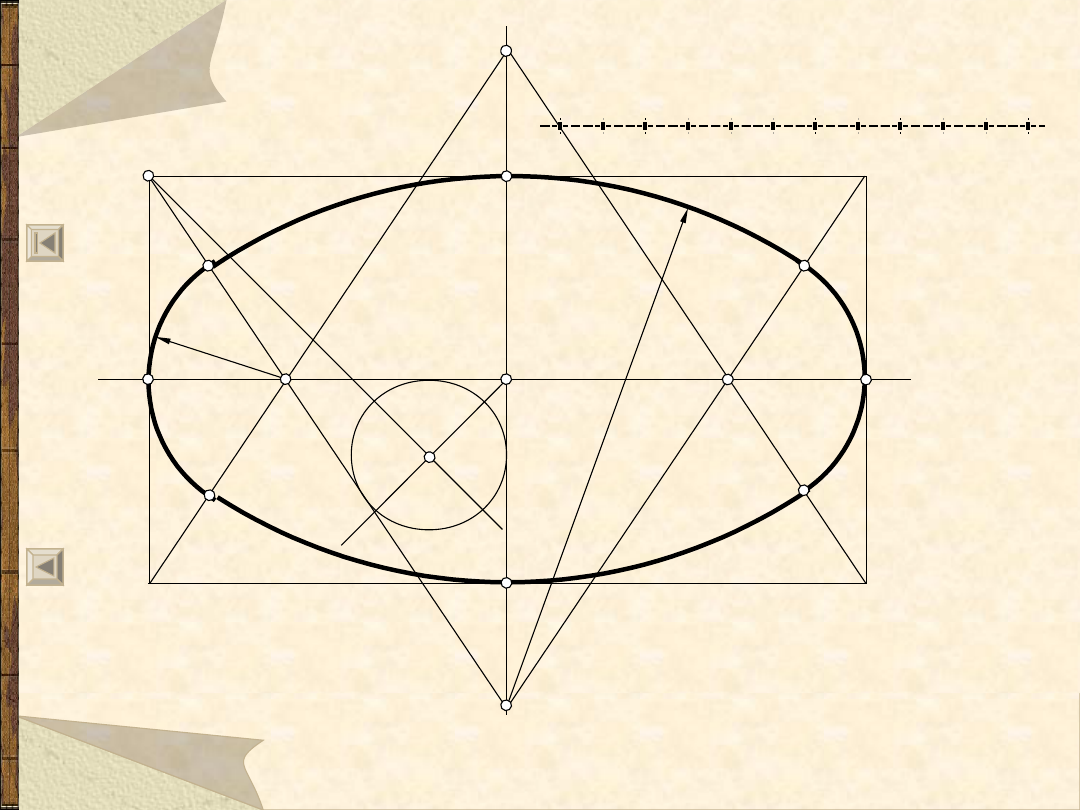
Owal – 2
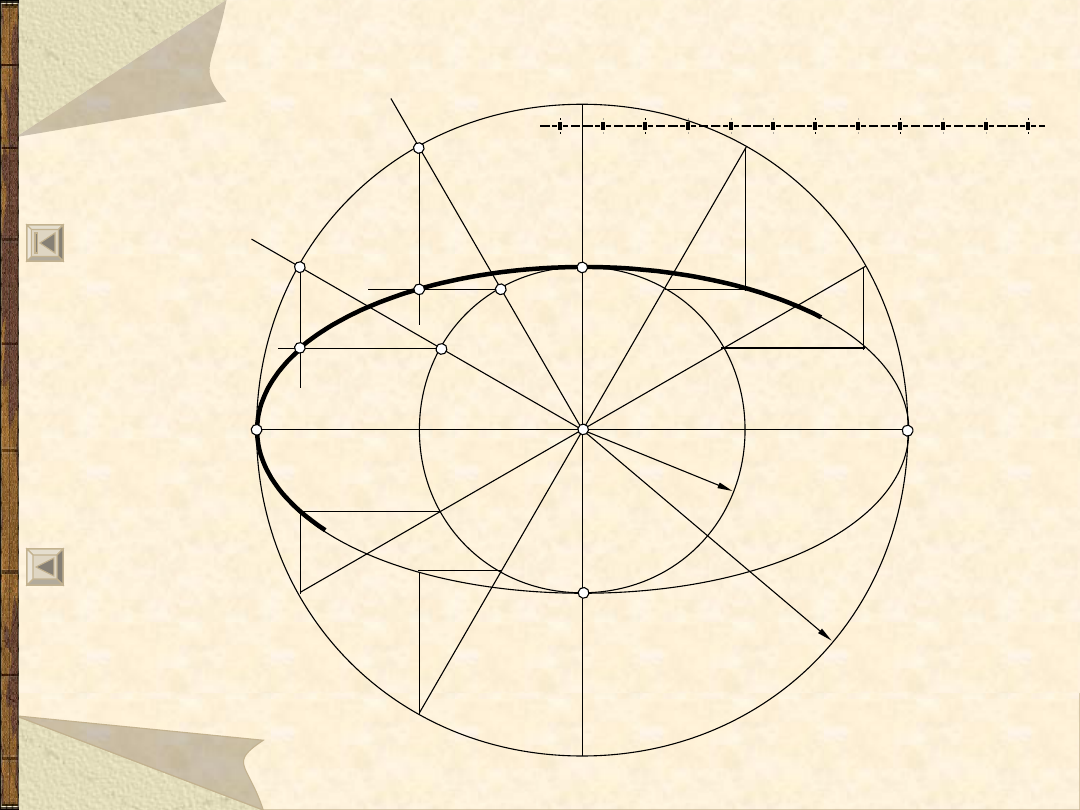
Elipsa – 1
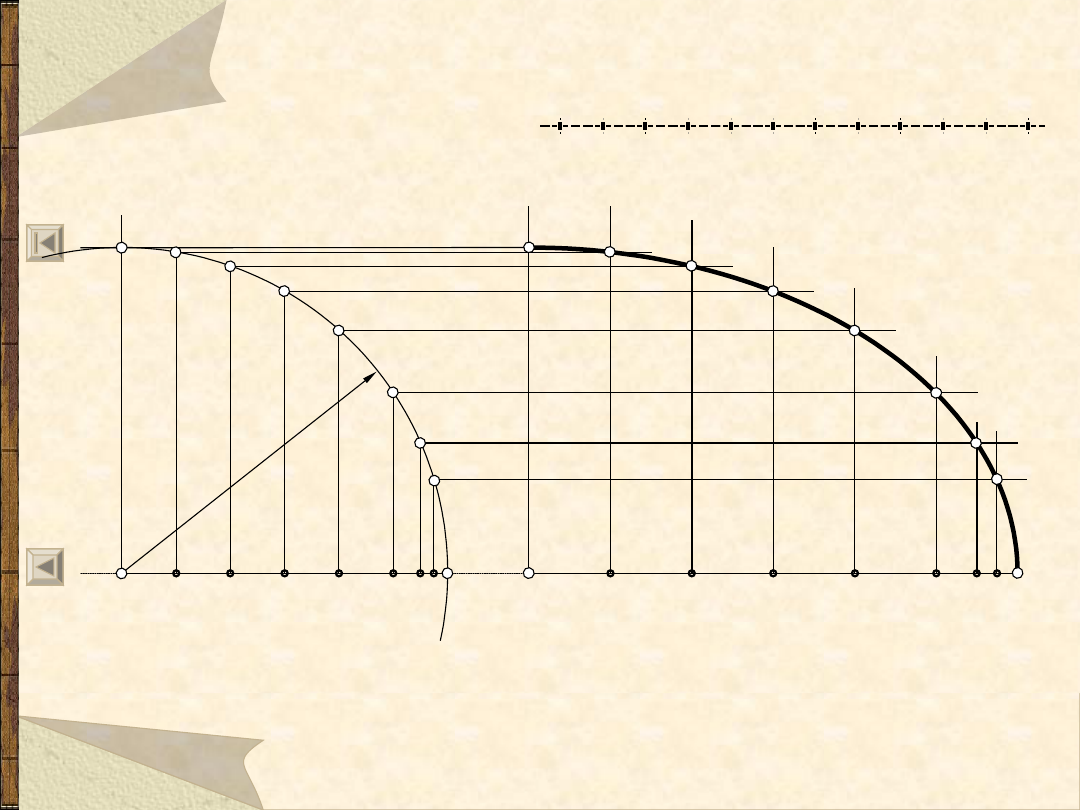
Elipsa – 2
11.06.21
Podstawowe krzywe płaskie
41
Owal – 1
b
a
d
c
r
e
DF = EB
0
C
B
E
F
0
1
0
2
0
3
0
4
A
D
11.06.21
Podstawowe krzywe płaskie
42
R
2
R
1
f
Owal – 2
b
a
C
0
0
2
0
1
e
d
c
F
E
A
B
0
3
0
4
D
11.06.21
Podstawowe krzywe płaskie
43
Elipsa – 1
b
a
R
1
R
2
F
E
F
1
E
1
F
2
E
2
B
C
A
0
D
11.06.21
Podstawowe krzywe płaskie
44
Elipsa – 2
r
A
0
2
B
0
1
D’
A’
H’
G’
F’
E’
E
F
G
H
D
1
5
4
3
2
1’
5’
4’
3’
2’
B’

11.06.21
Zaawansowane konstrukcje geometryczne
45
Krzywe płaskie
Owal w izometrii prostokątnej
Elipsa o osiach sprzężonych
Łuk z cięciwy i strzałki ugięcia
Parabola z wierzch. w punkcie W, przez punkt A – 1
Parabola z wierzch. w punkcie W, przez punkt A – 2
Parabola styczna do dwu prostych w punktach A i B
Hiperbola równoboczna z asymptotami i punktem A
Spirala Archimedesa o skoku H
Spirala Archimedesa o skoku H – uproszczenie
Ewolwenta
11.06.21
Podstawowe krzywe płaskie
46
5
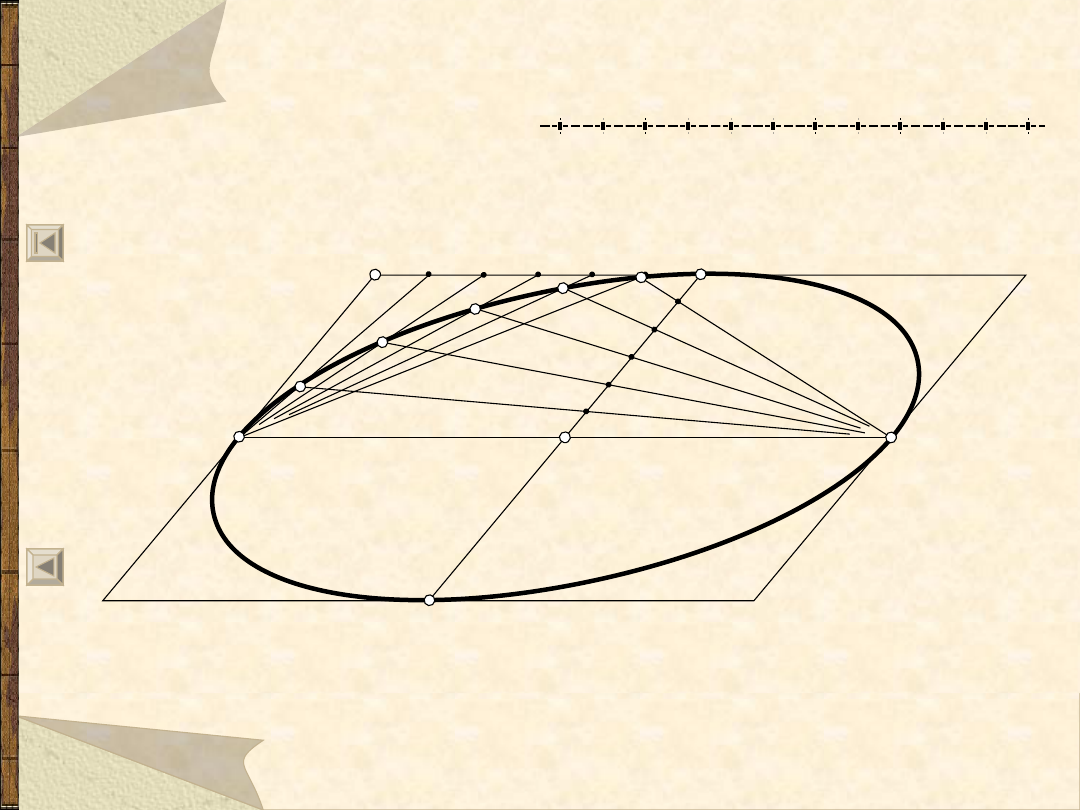
Elipsa o osiach sprzężonych
G
E
F
C
0
B
D
A
H
1
’
2
’
2
1
3
’
5
’
3
4
4
’
11.06.21
Podstawowe krzywe płaskie
47
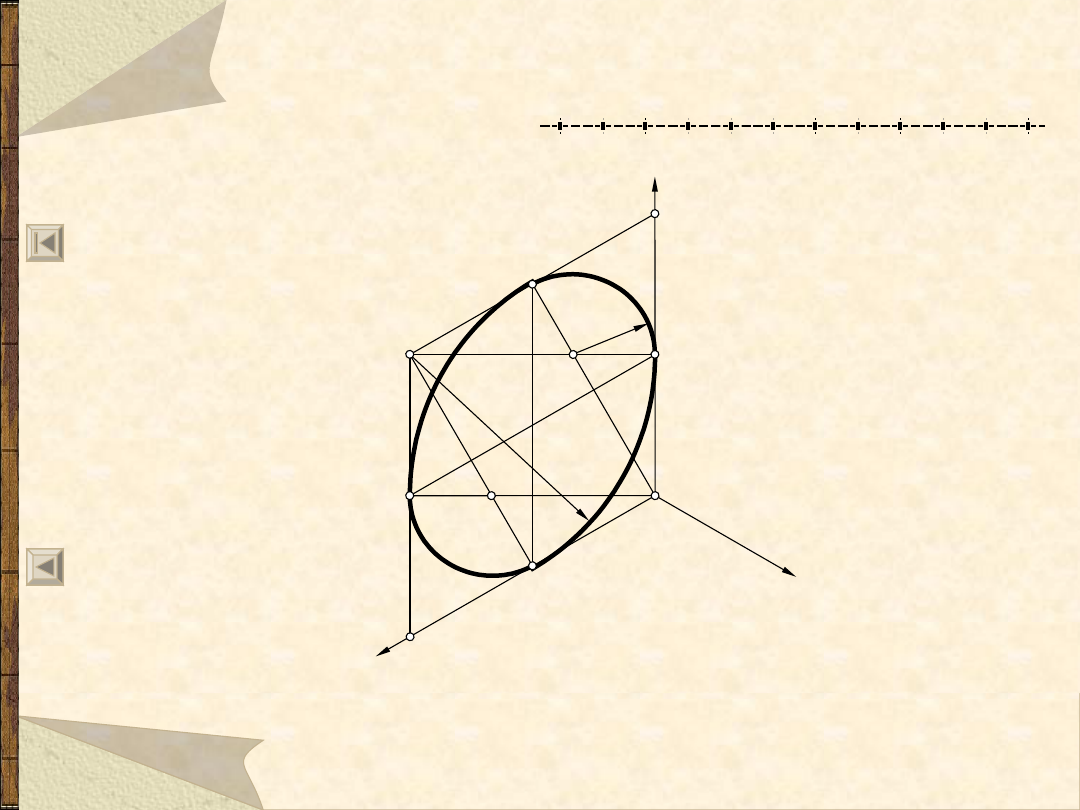
Owal w izometrii prostokątnej
z
x
y
r
1
r
2
F
D
A
0
B
H
G
E
J
C
11.06.21
Podstawowe krzywe płaskie
48
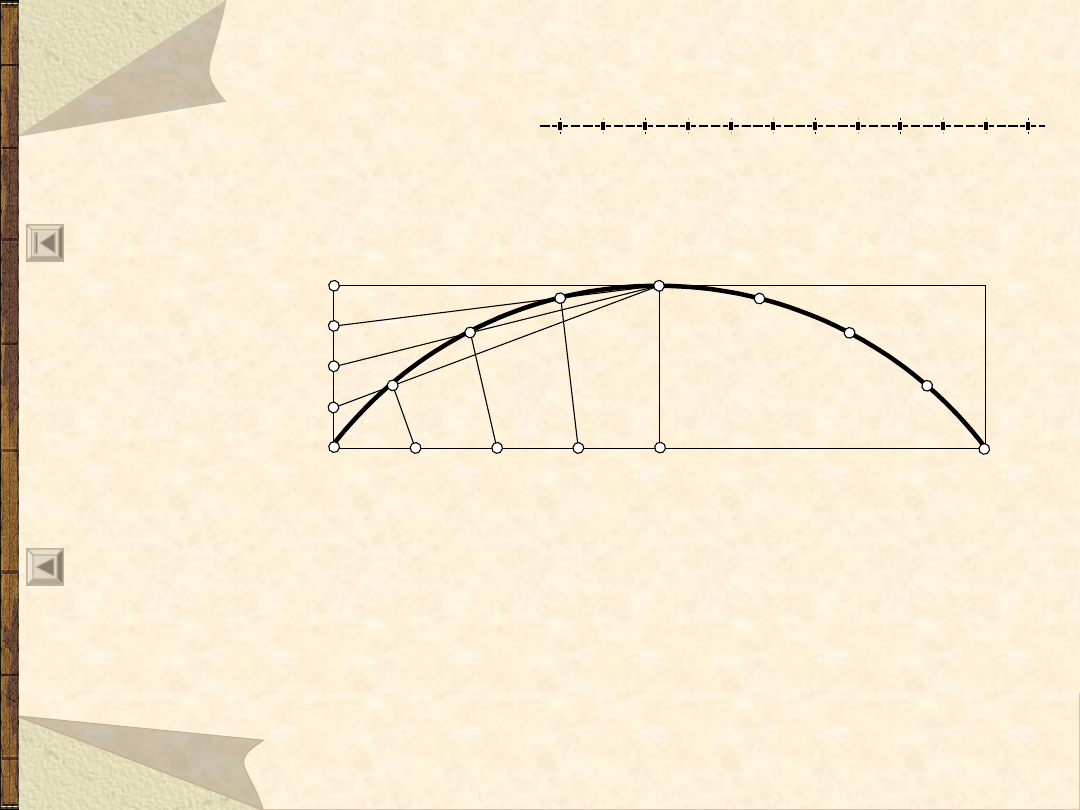
Łuk z cięciwy i strzałki ugięcia
H
f
B
A
2’
3’
1’
3
C
2
1
G
F
D
E
11.06.21
Podstawowe krzywe płaskie
49
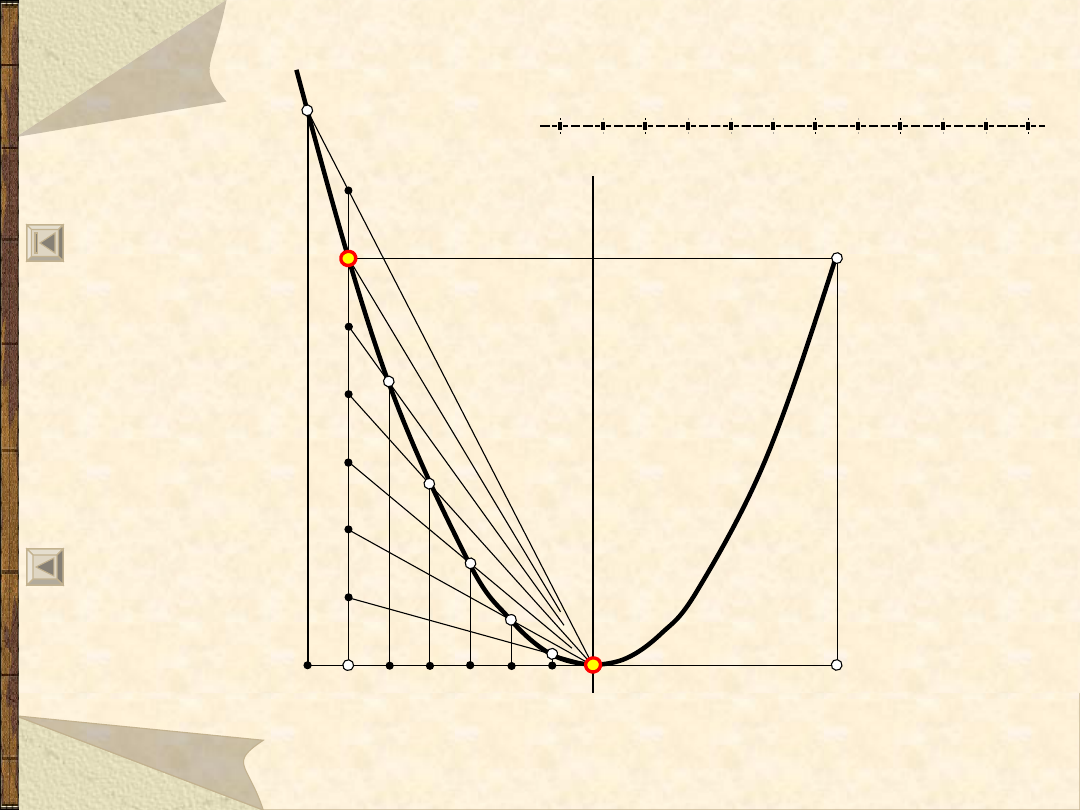
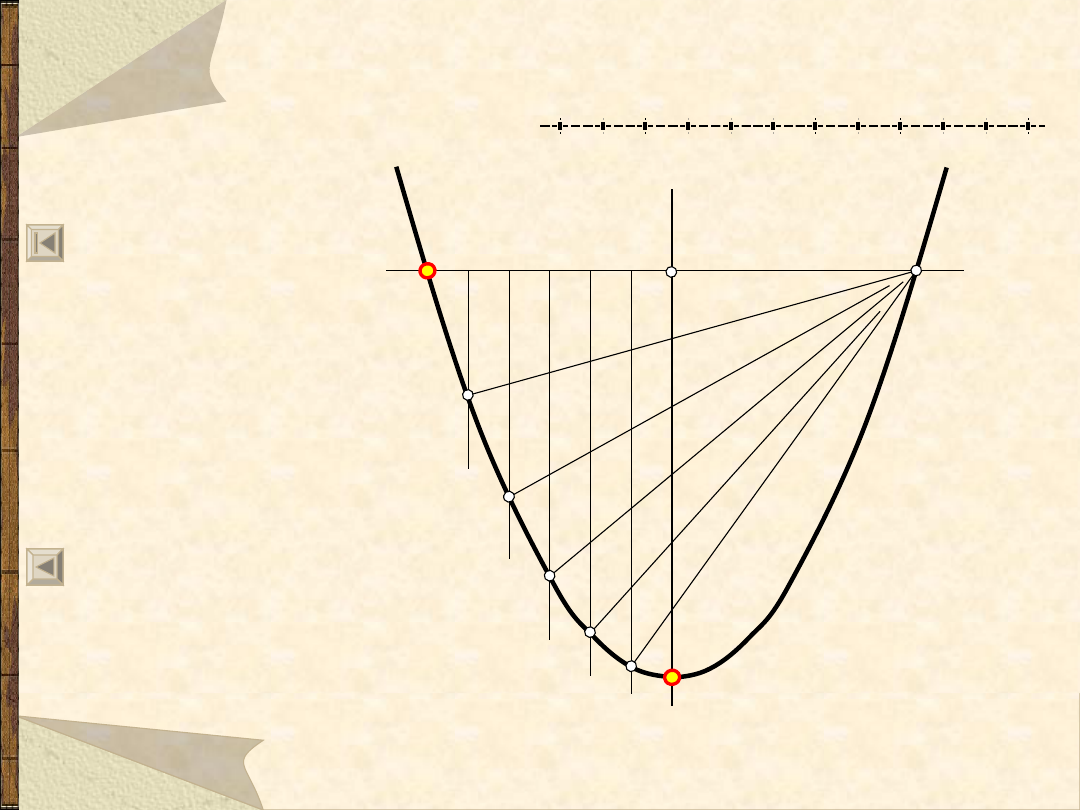
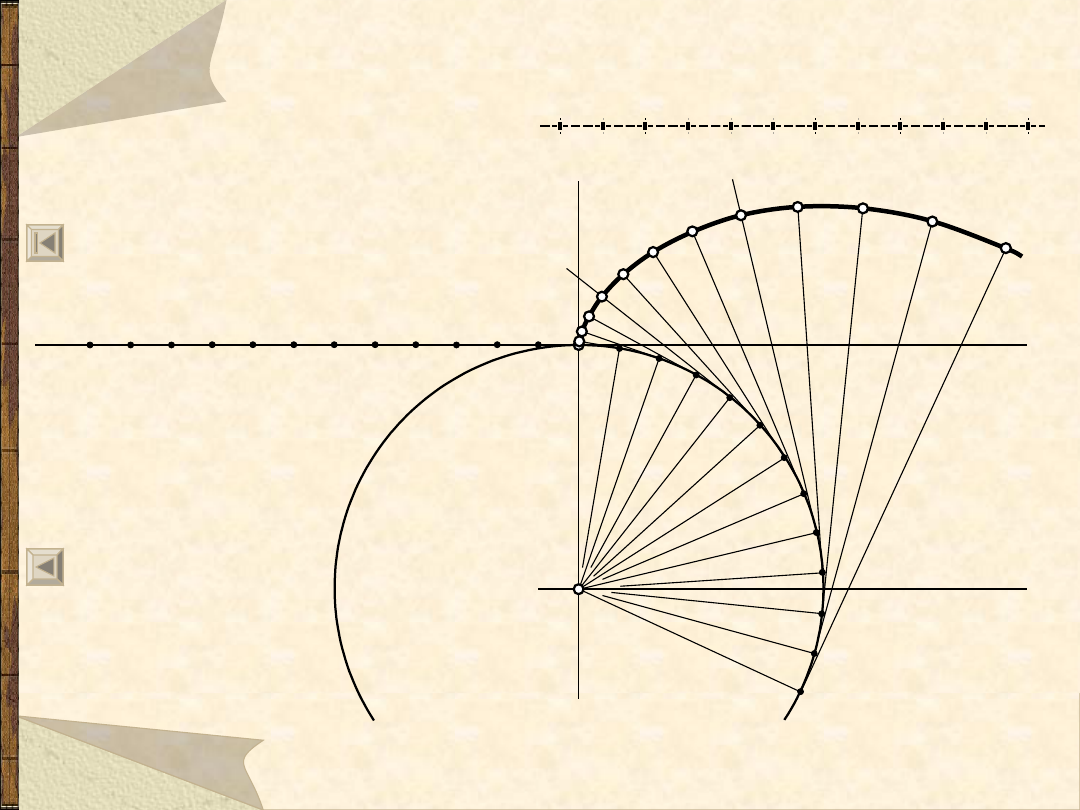
Parabola z wierzch. w punkcie W,
przechodząca przez punkt A – 1
D
B
A
w
C
5
’
4
’
3
’
2
’
1
’
7
’
7
3 2 1
5 4
11.06.21
Podstawowe krzywe płaskie
50
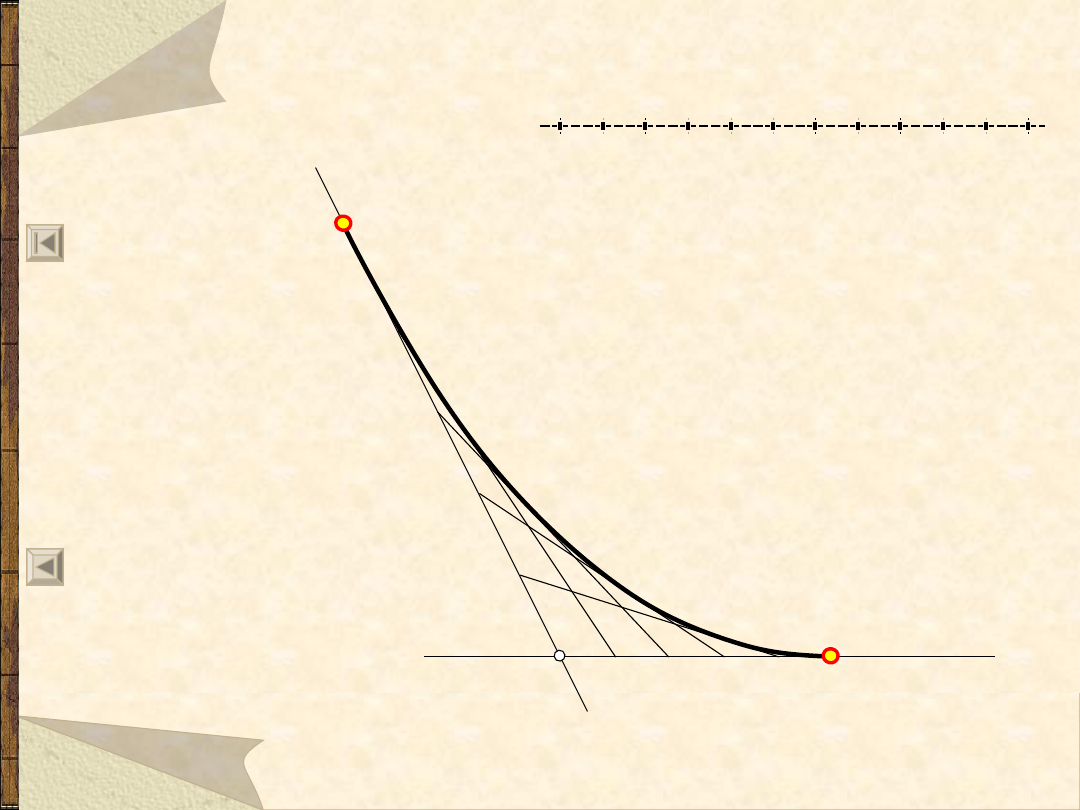
Parabola z wierzch. w punkcie W,
przechodząca przez punkt A – 2
A
w
5 4 3 2 1
4
’
2
’
1
’
5
’
3
’
C
B
11.06.21
Podstawowe krzywe płaskie
51
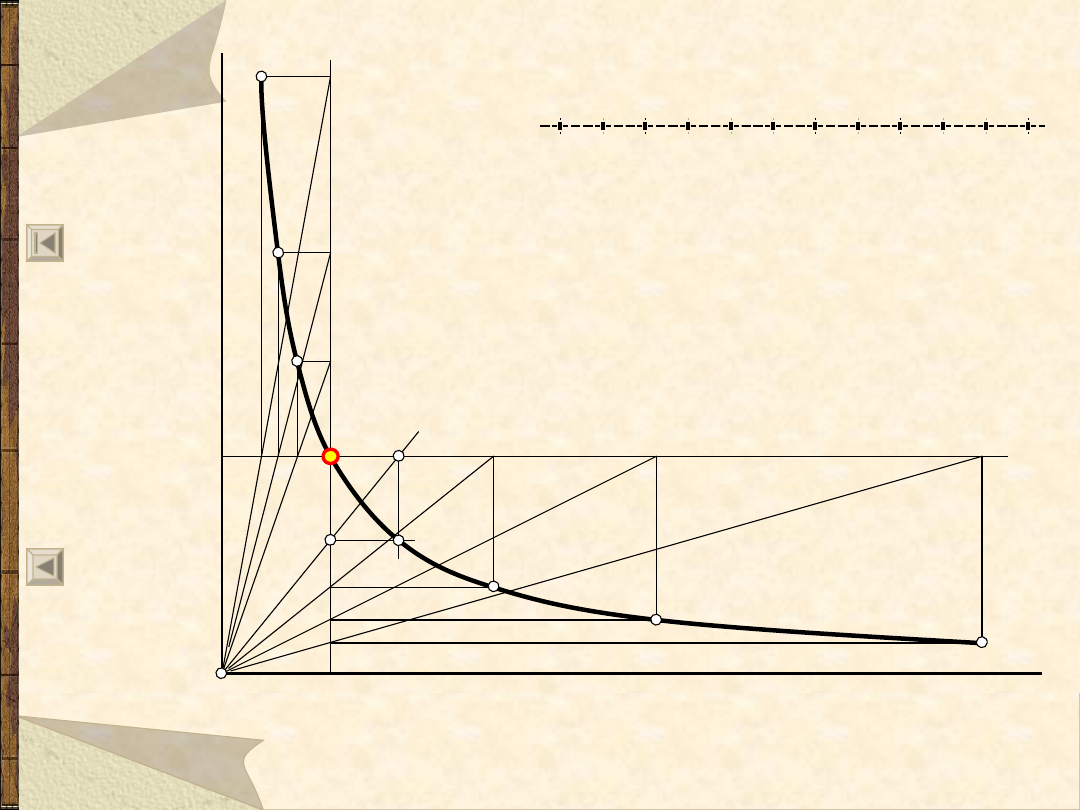
Parabola styczna do dwu prostych
w punktach A i B
4
1
2
3
1
2
3
4
a
b
C
B
A
11.06.21
Podstawowe krzywe płaskie
52
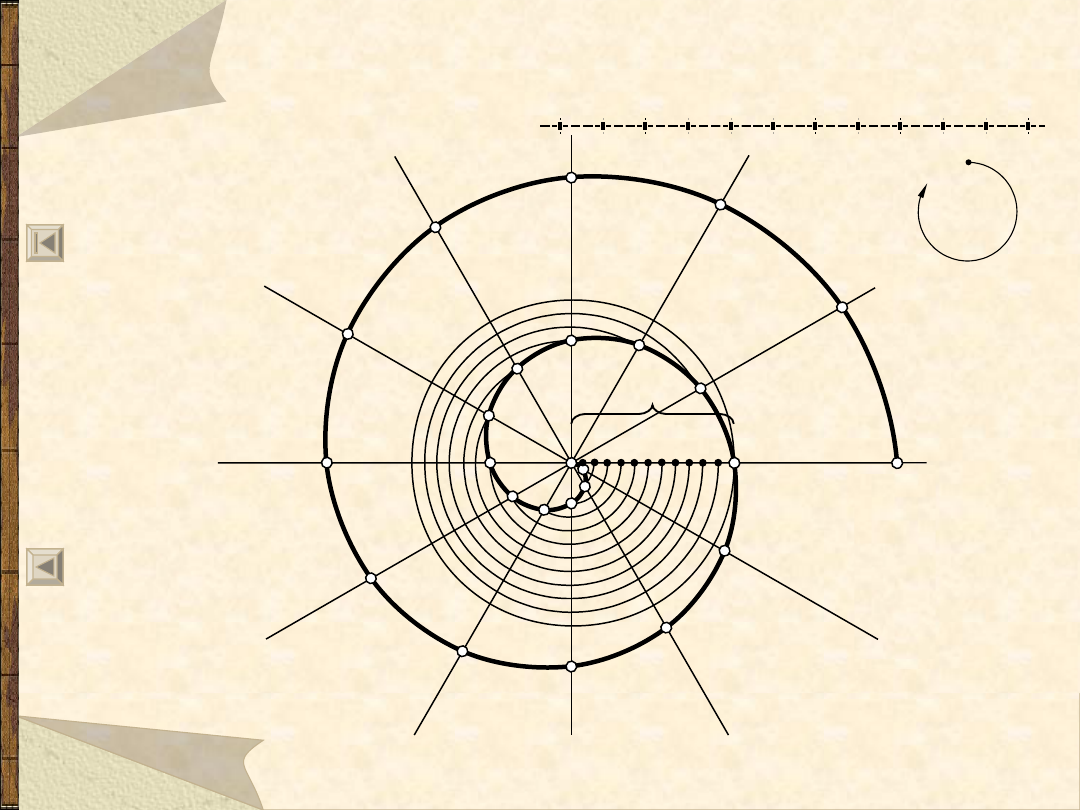
Hiperbola równoboczna,
gdy dane są asymptoty i punkt A
d
b
a
C
E
c
B
D
A
11.06.21
Krzywe płaskie
53
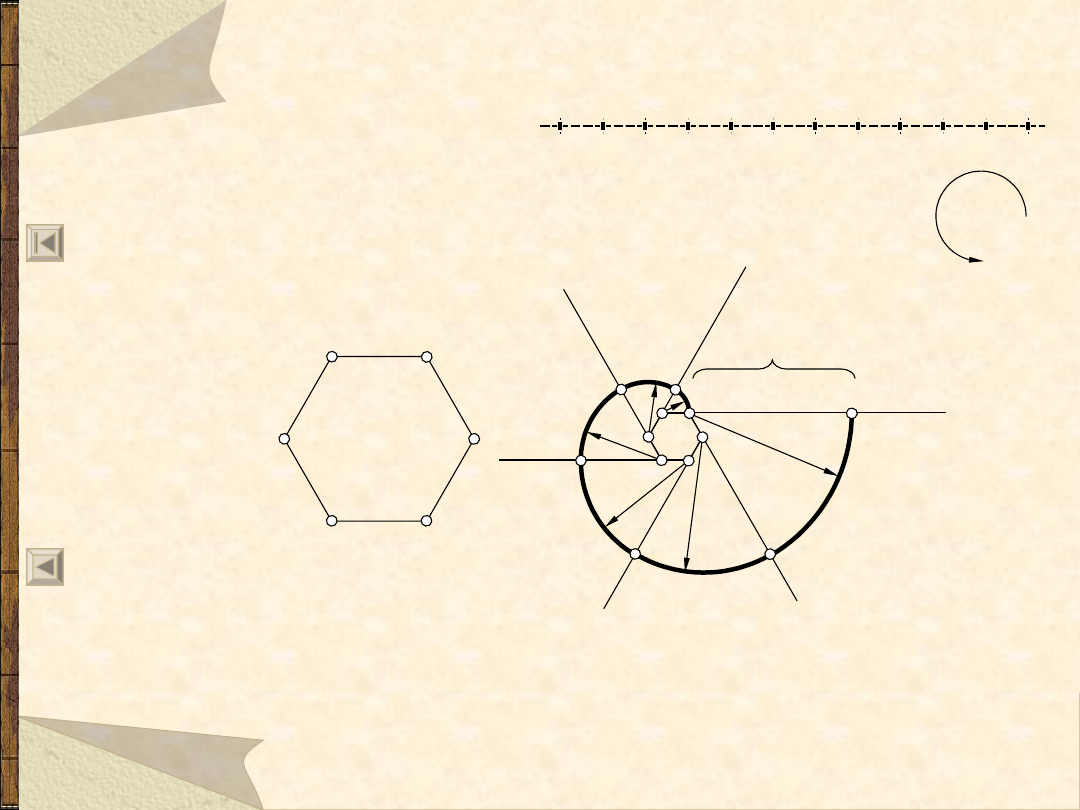
Spirala Archimedesa o skoku H
0
1’
2’
5’
6’
7’
8’
9’
10
’
11
’
12
’
3 6
12
9
3’
4’
h
11.06.21
Krzywe płaskie
54
Spirala Archimedesa o skoku H
(wersja uproszczona)
A
1
F
E
D
A
B
C
A
1
H
r
F
f
e
d
c
b
a
h
B
1
C
1
D
1
r
C
r
D
r
E
E
1
F
1
11.06.21
Krzywe płaskie
55
Ewolwenta
a
6
4
1
2
2
1
0
8
6
’
4
’
2
’
10
’
12
’
8
’
12
”
10
”
8
”
6
”
4
”
2
”
b
O
A

11.06.21
Zaawansowane konstrukcje geometryczne
56
Krzywe cykliczne
Sinusoida
Cykloida
Krzywe cykliczne – pochodne cykloidy
Epicykloida
Hipocykloida
Trochoida
inne warianty trochoidy
Linia śrubowa
11.06.21
Krzywe cykliczne
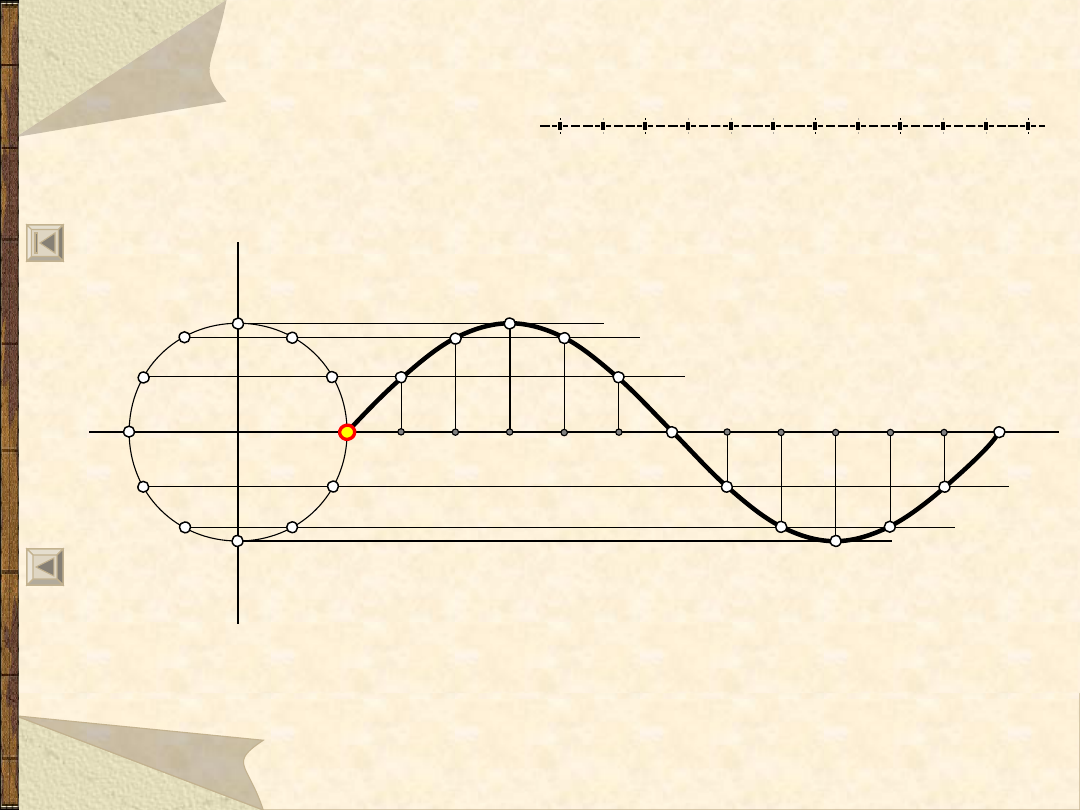
57
Sinusoida
5
6
7
1
2
3
4
A
0°
90
°
180
°
270
°
360
°
1’
3’
6’ 7’
2’
12’
10’
8’
4’
11’
9’
5’
9
10
8
1
1
11.06.21
Krzywe cykliczne
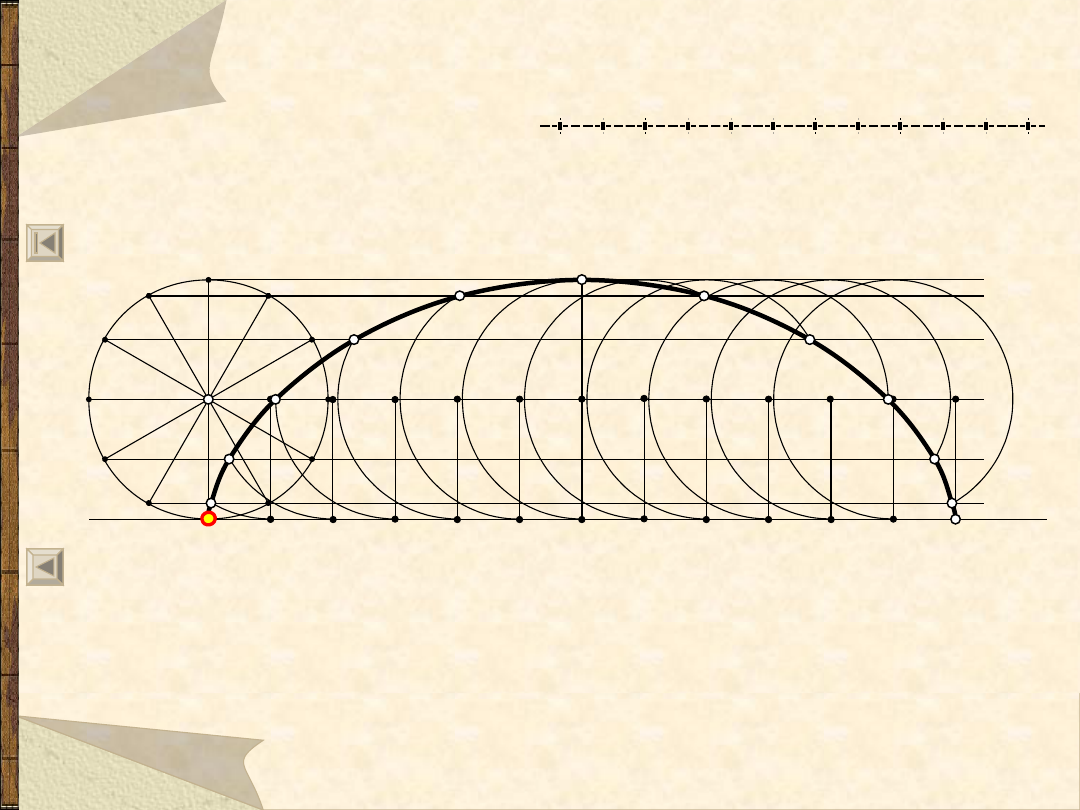
58
Cykloida
7
b
a
1’
7
’
5
’
6
’
4
’
3
’
2
’
8
’
9
’
10’
11
’
12
’
6
5
4
3
2
1
8
9
10
11
12
0
3
0
1
0
2
0
4
0
5
0
6
0
7
0
8
0
9
0
1
0
0
1
1
0
1
2
A
11.06.21
Zapis konstrukcji
59
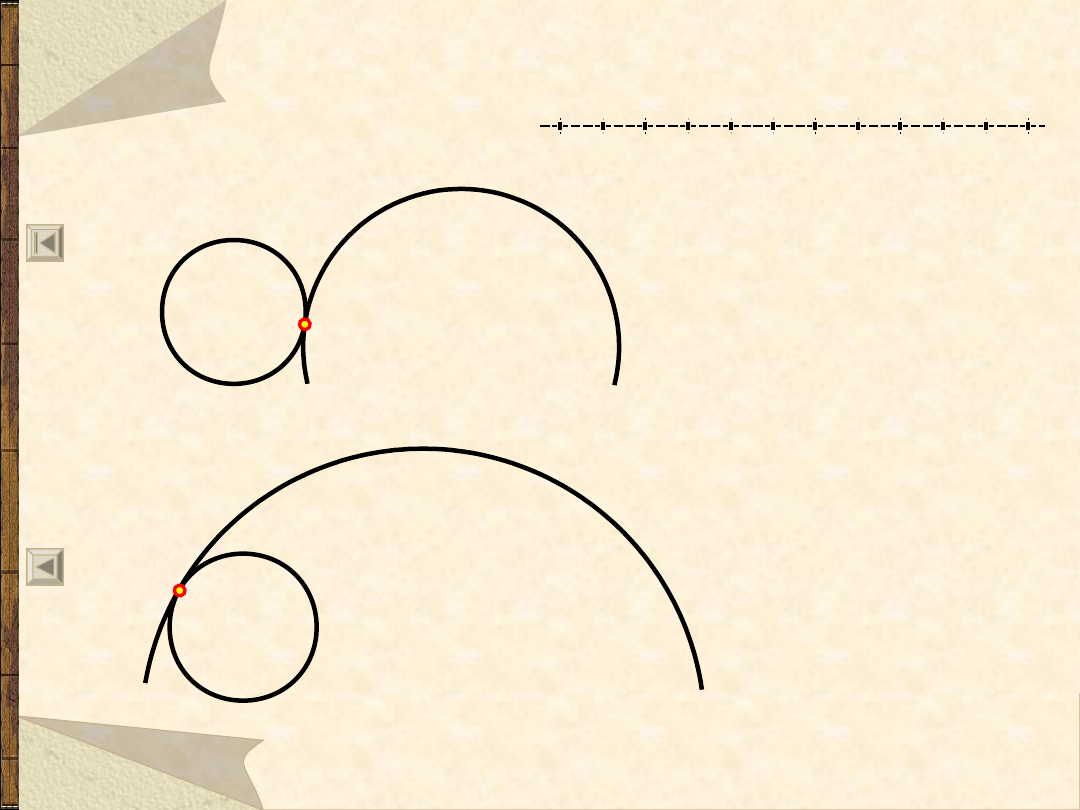
Krzywe cykliczne – pochodne cykloidy
a
b
a
b
Elementy wyjściowe:
a – element odtaczany
b – bieżnia
A – punkt rysujący
krzywą
epicykloida
hipocykloida
A
A
11.06.21
Krzywe cykliczne
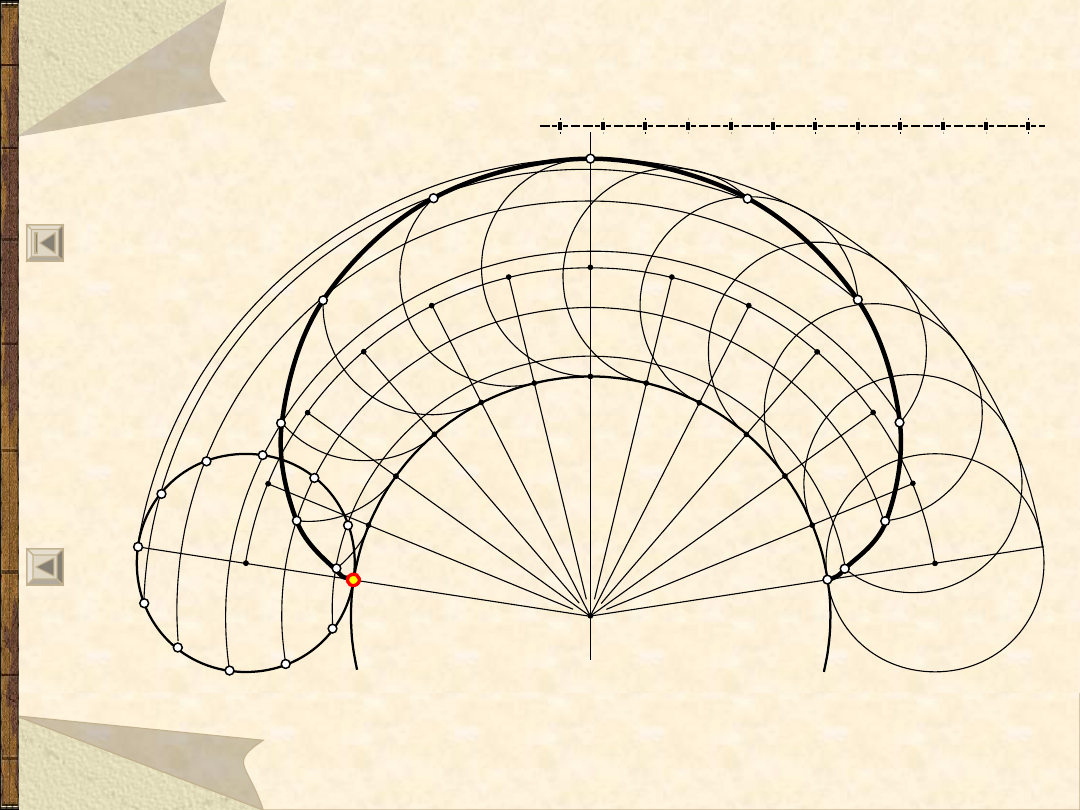
60
Epicykloida
0
1
b
a
1
’
2’
7’
5’
6’
4’
3
’
8
’
0
11
0
12
0
1
0
0
9
0
8
0
7
0
6
0
5
0
4
0
3
0
2
0
0
7
6
8
9
1
0
5
4
3
2
1
9’
10
’
11
’
12’
A
11
1
2
11.06.21
Krzywe cykliczne
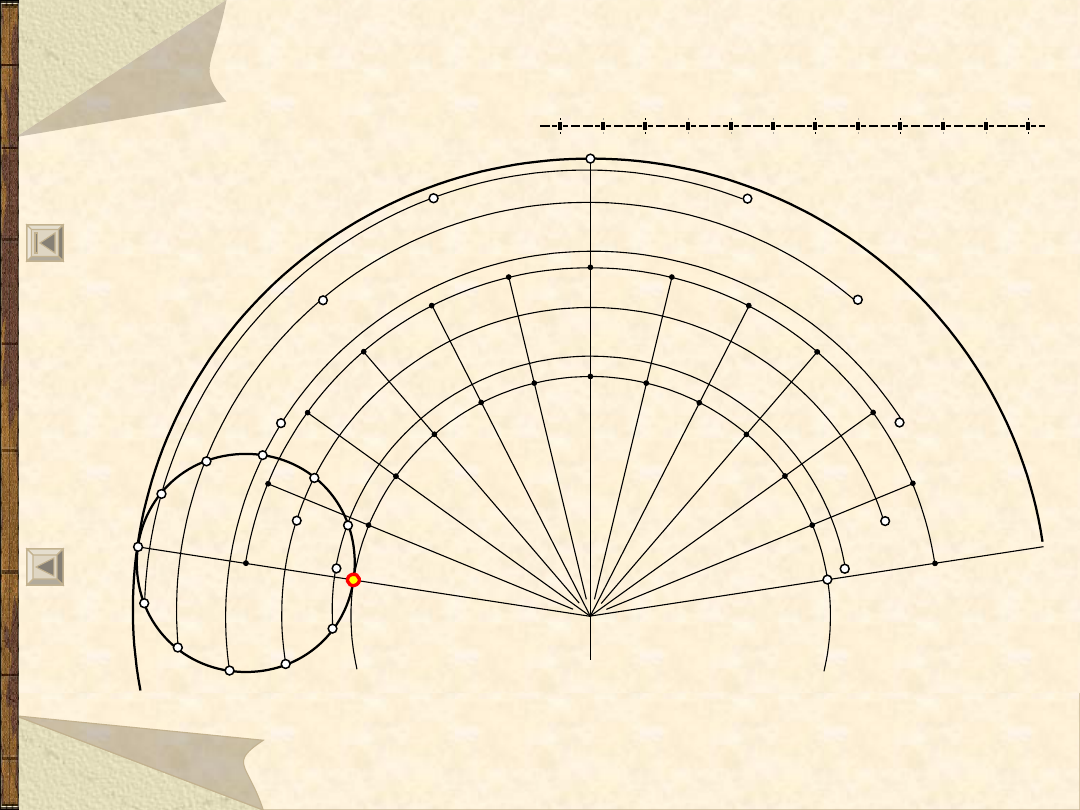
61
Hipocykloida
7
0
1
0
a
b
0
2
1
’
7’
5’
6’
4’
3
’
2’
8
’
9’
10
’
11
’
12’
0
9
0
8
0
7
0
6
0
5
0
4
0
3
0
1
0
11
0
12
6
5
4
3
2
1
8
9
1
0
11
1
2
0
0
A
11.06.21
Krzywe cykliczne
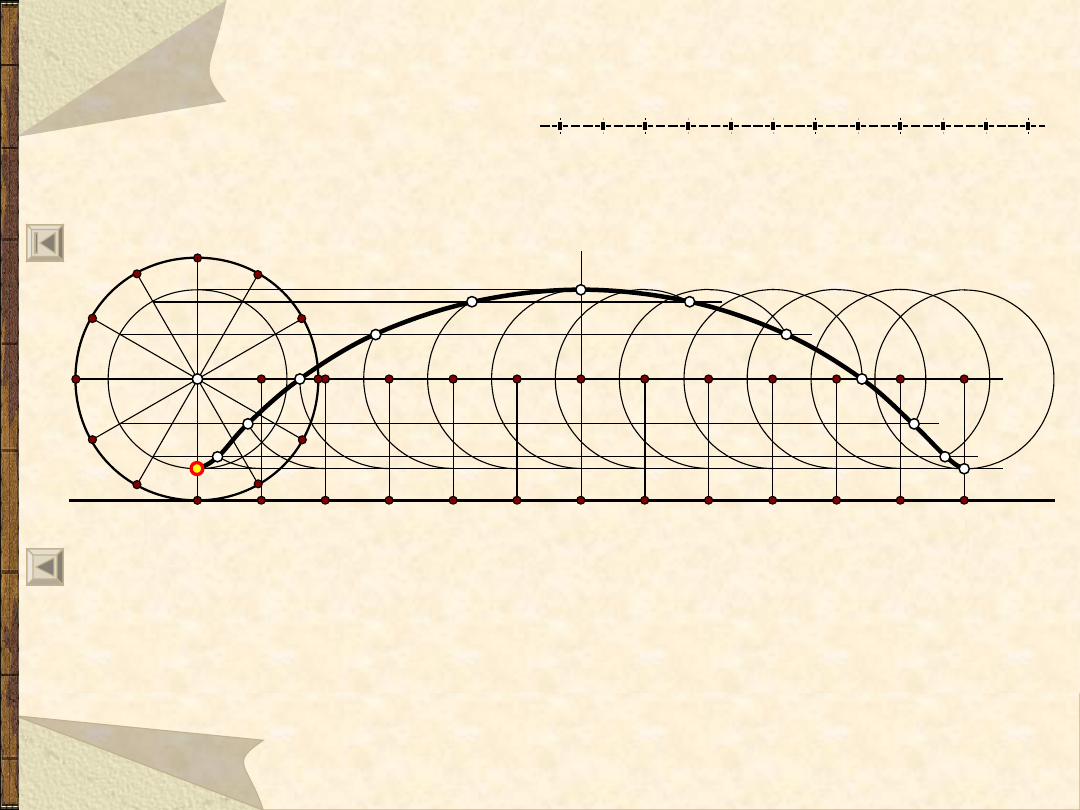
62
Trochoida
b
1
’
7
’
5
’
6
’
4
’
3
’
2
’
8
’
9
’
10’ 11
’
12
’
0
1
0
0
2
0
9
0
8
0
7
0
6
0
5
0
4
0
3
0
1
0
1
1
0
1
2
7
6
5
1
1
1
2
8
9
10
1
0
0
4
2
3
A
a
11.06.21
Zapis konstrukcji
63
inne warianty trochoidy
a
b
a
b
Elementy wyjściowe:
a – element odtaczany
b – bieżnia
A – punkt rysujący
krzywą
A
A

11.06.21
Zaawansowane konstrukcje geometryczne
64
Linia śrubowa ...
... na walcu
... na stożku

11.06.21
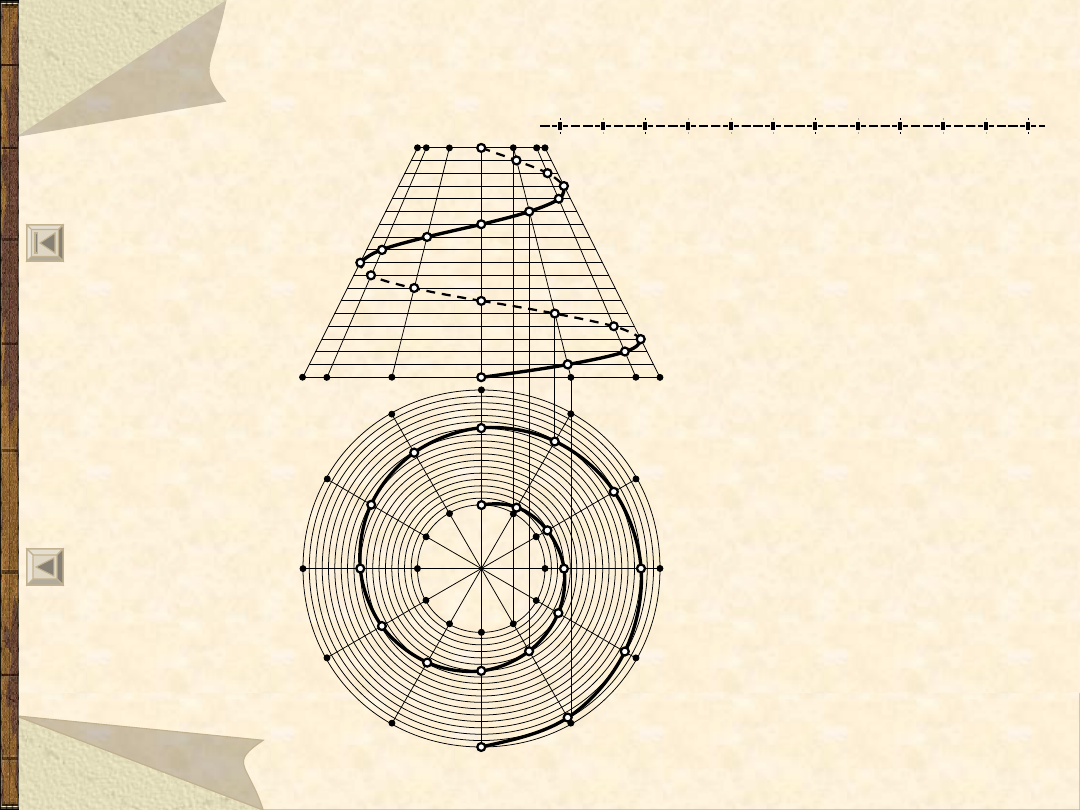
Linia śrubowa
65
... na walcu
11.06.21
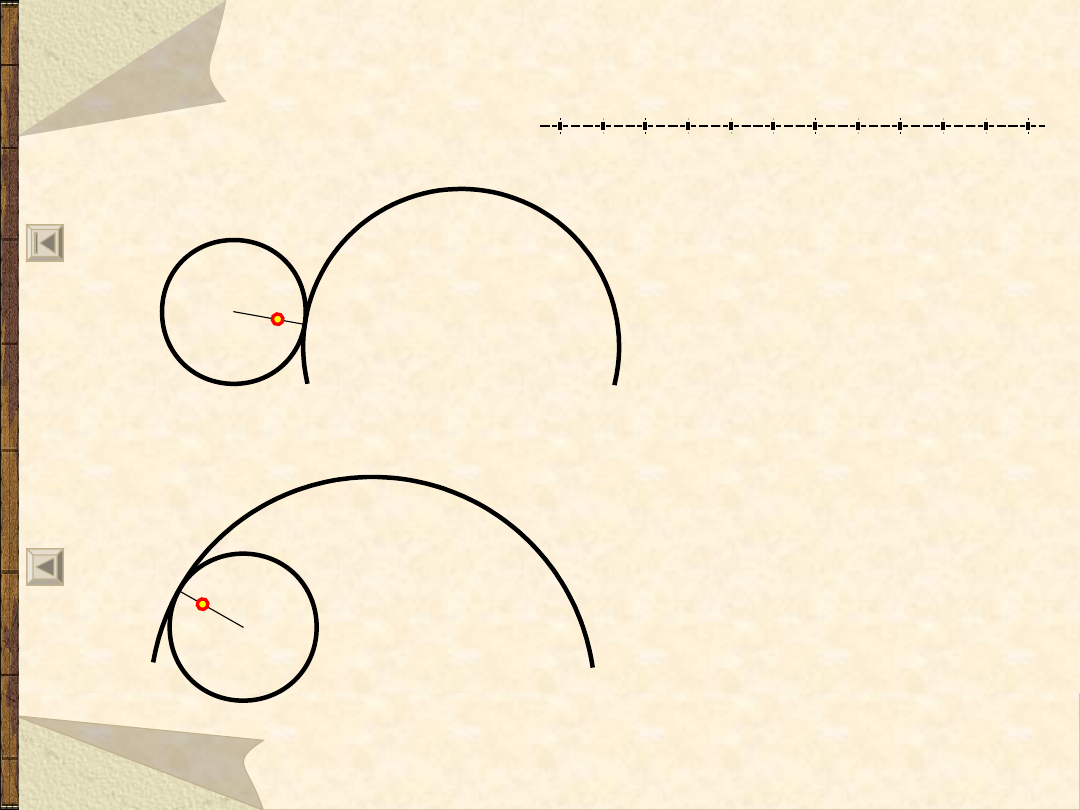
Linia śrubowa
66
... na stożku
7
1
’
7
’
5
’
6
’ 4
’
3
’
2
’
8
’
9
’
10
’
11
’
12
’
6
5
4
3
2
1
8
9
10
1
1
1
2
1
’
5
’
3
’
7
’
6
’ 4
’2
’

11.06.21
Zapis konstrukcji
67
Literatura
T. Dobrza
T. Dobrza
ńs
ńs
ki,
ki,
„Rysunek techniczny maszynowy”
„Rysunek techniczny maszynowy”
,
,
WNT 2005
WNT 2005
E. F. Otto,
E. F. Otto,
„Podr
„Podr
ę
ę
cznik geometrii wykre
cznik geometrii wykre
ś
ś
lnej”
lnej”
, PWN 1975
, PWN 1975
J. Waligórski,
J. Waligórski,
„Geometria wykre
„Geometria wykre
ś
ś
lna dla in
lna dla in
ż
ż
ynierów i
ynierów i
techników”,
techników”,
WSiP 1967
WSiP 1967
T. Buksi
T. Buksi
ń
ń
ski A. Szpecht,
ski A. Szpecht,
„Rysunek techniczny”
„Rysunek techniczny”
, WSiP 1961
, WSiP 1961
J. Rogowski, „Podstawowe konstrukcje geometryczne w
rzutach Monge’a”, PWN 1993
L. Giełdowski, „Rzutowanie prostokątne, widoki. Ćwiczenia
i zadania rysunkowe z rozwiązaniami” WSiP 1998
T. Rachwał, „Ćwiczenia z geometrii wykreślnej” t.1, WSiP
1987
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
- Slide 50
- Slide 51
- Slide 52
- Slide 53
- Slide 54
- Slide 55
- Slide 56
- Slide 57
- Slide 58
- Slide 59
- Slide 60
- Slide 61
- Slide 62
- Slide 63
- Slide 64
- Slide 65
- Slide 66
- Slide 67
Wyszukiwarka
Podobne podstrony:
03 Podstawy geometrii wykre lnej
03 Podstawy geometrii wykreślnej
03 PODSTAWY GENETYKI
Co to jest teoria względności podstawy geometryczne
03 PO Geometria 2013id 4609 Nieznany (2)
Java 03 Podstawowe typy danych
03 Podstawowy funkcjonowania sieci informatycznejid 4248
03 Podstawowe ideeid 4439 Nieznany (2)
03 Podstawowe Zabiegi Resuscytacyjne (BLS)
03 podstawy RBDid 4615 ppt
Wyklad 03 Podstawowe zasady etyczne
03. Podstawy programowania, Materiały z progów
03 Podstawy?mografii
03 Podstawy prawne w przed
więcej podobnych podstron