STAN GRANICZNY 

NOŚNOŚCI

według PN-EN 1992-1-1

Zasady obliczania w stanie SGN

Umowny podział:
• M

Ed

   N

Ed

   - 

naprężenia normalne

 - zginanie,

                     mimośrodowe ściskanie lub rozciąganie 

• V

Ed

    T

Ed

  - 

naprężenia styczne

 – ścinanie, przebicie,

                   skręcanie, rozwarstwienie 

Wyjątki:
Płyty, tarcze – uwzględnia się też   M

xy

  przy obliczaniu pola 

przekroju 

                    zbrojenia w kierunku x i y 

Przebicie      – uwzględnia się wpływ   M

Edx

 i   M

Edy

   na naprężenia 

                    styczne     

Obliczanie przekroju

obciążonego momentem zginającym i 

siłą podłużną

Wyróżniamy trzy stany obciążenia 

przekroju (fazy pracy):

• Faza   I – przed zarysowaniem
• Faza  II – po zarysowaniu
• Faza III – zniszczenie –  

stan SGN (ULS)

 

FAZA III – zniszczenie

Zniszczenie  

zmiażdżenie betonu w strefie 

ściskanej

W zależności od stopnia zbrojenia     

                  

   

dochodzi 
do tego:

- 

pośrednio

, na skutek przyrostu odkształcenia po

             uplastycznieniu rozciąganego zbrojenia,

- 

bezpośrednio

, na skutek osiągnięcia granicznych

             odkształceń skrajnego włókna strefy ściskanej 
przekroju;
             zbrojenie rozciągane nie osiąga stanu 
uplastycznienia.

c

s

A

A





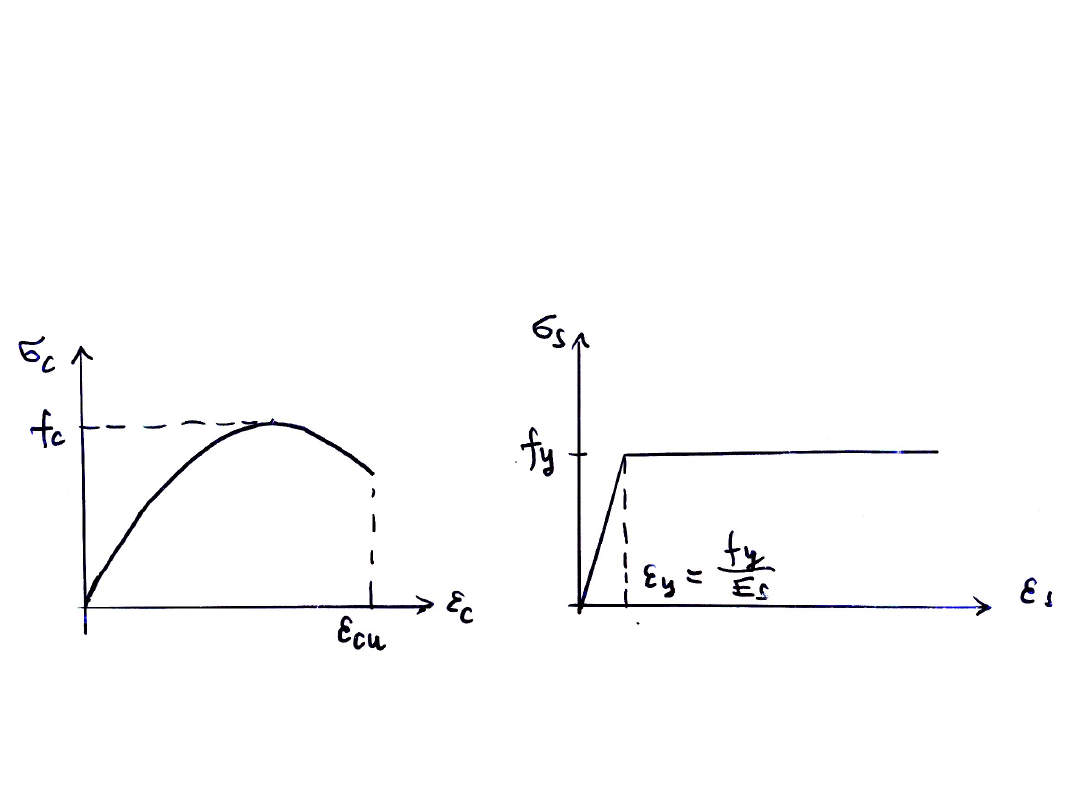
Mechanizmy zniszczenia przy zginaniu

Umowne zależności σ – ε

       

beton w strefie ściskanej           zbrojenie

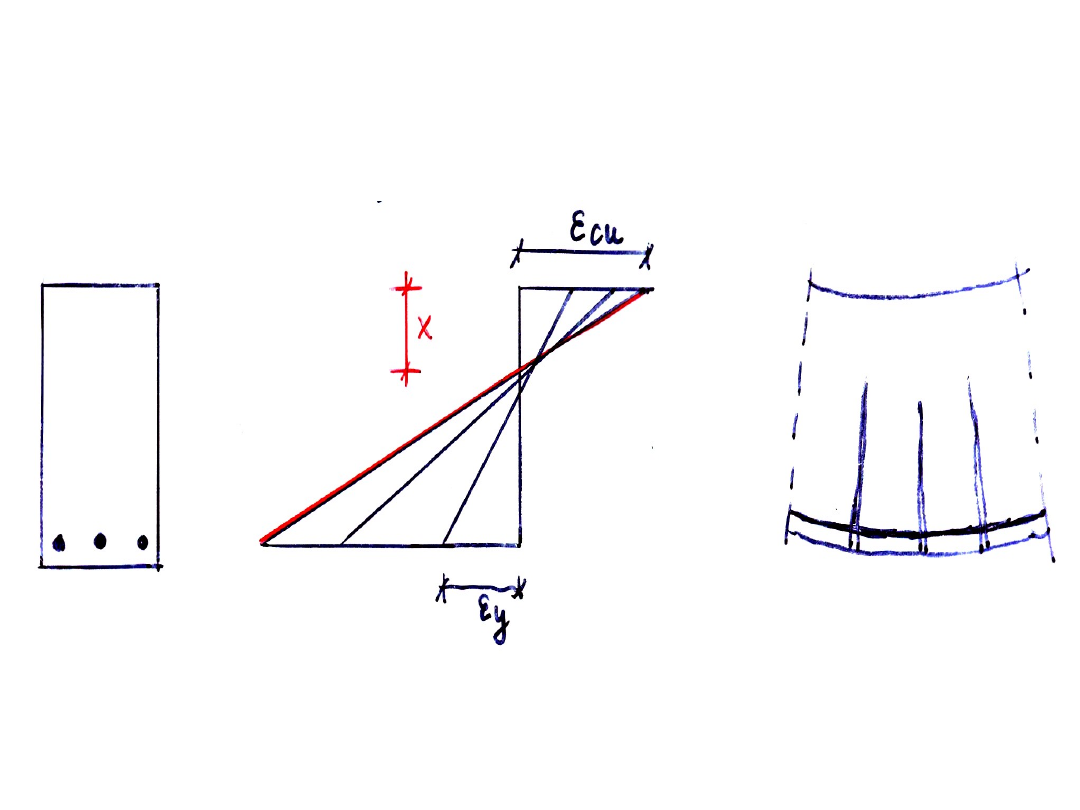
Zniszczenie pośrednie ρ < ρ

lim

Obserwujemy: - 

wyraźny przyrost ugięcia

                         - 

poszerzanie się i wydłużanie 

rys

                                 

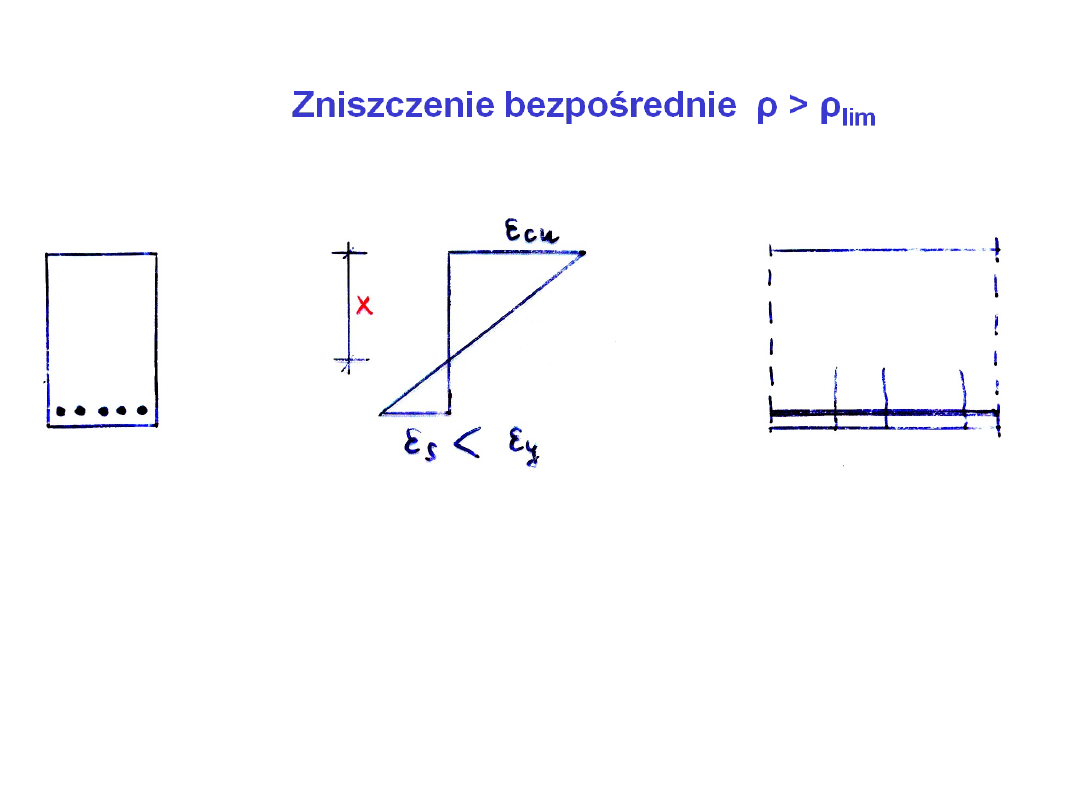
Obserwujemy niewielkie ugięcie i niewielkie 
zarysowanie. Zbrojenie nie osiąga granicy 
plastyczności.

Zniszczenie ma charakter gwałtowny! 

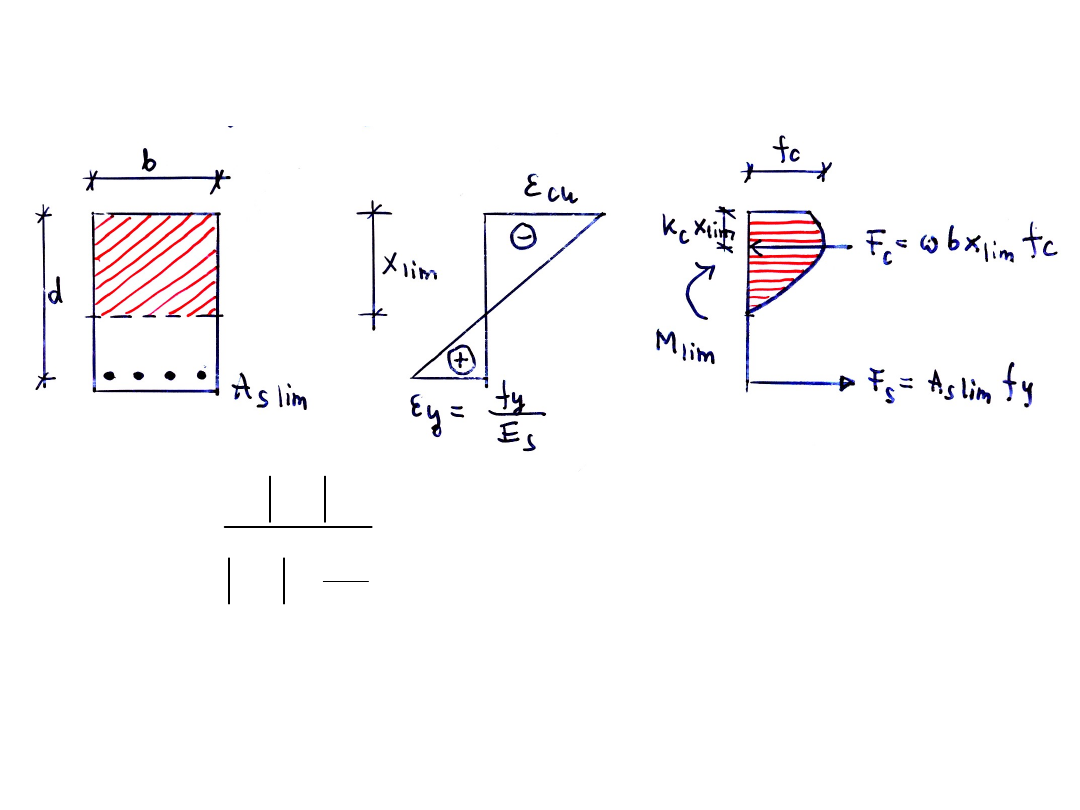
Stan graniczny  ρ = ρ

lim

d

E

f

x

s

y

cu

cu

lim













lim

c

c

lim

lim

x

k

d

f

bx

M







Wyznaczmy   ρ

lim

  przy następujących danych

:

5

,

3

cu





‰

MPa

400

f

y



MPa

200000

E

s



0

,

2

y





‰

d

636

,

0

d

0

,

2

5

,

3

5

,

3

x

lim







4

,

0

k

c



8

,

0





c

2

c

lim

f

bd

379

,

0

f

)

d

636

,

0

4

,

0

d

(

d

636

,

0

b

8

,

0

M











 

Przyjmujemy

 i obliczamy

        

Załóżmy dodatkowo

y

c

lim

lim

,

s

f

f

bx

A





lim

lim

d

x





y

c

lim

lim

s

lim

f

f

bd

A









MPa

40

f

c



051

,

0

400

40

636

,

0

8

,

0

lim











 

Z warunku równowagi sił

 

wobec czego

Załóżmy, że zwiększamy zbrojenie o 50 %

cu

cu

s

1

x

x

d



















lim

5

,

1 





s

s

y

c

lim

c

E

f

f

bx

5

,

1

bxf









200000

0035

,

0

1

400

1

636

,

0

5

,

1



















703

,

0







c

2

f

bd

404

,

0

M

066

,

1

379

,

0

404

,

0



           ξ = x/d

Obliczamy odkształcenie stali

 

Z warunku równowagi sił

 

obliczamy

  ξ oraz M

Przyrost nośności nie jest adekwatny do stopnia zwiększenia 
zbrojenia 

!

Uwaga!

Jeżeli przekrój jest zbrojony tylko w strefie 
rozciąganej, 
a stopień zbrojenia

ρ   ≥  ρ

lim 

           (x ≥ x

lim

)

to taki przekrój nie ma zdolności do 
plastycznych odkształceń!

Można dozbroić strefę ściskaną tak, aby 
zmniejszyć wysokość strefy ściskanej do 
wielkości 

x < x

lim

dzięki czemu przekrój uzyska zdolność do 
plastycznych odkształceń w fazie zniszczenia 

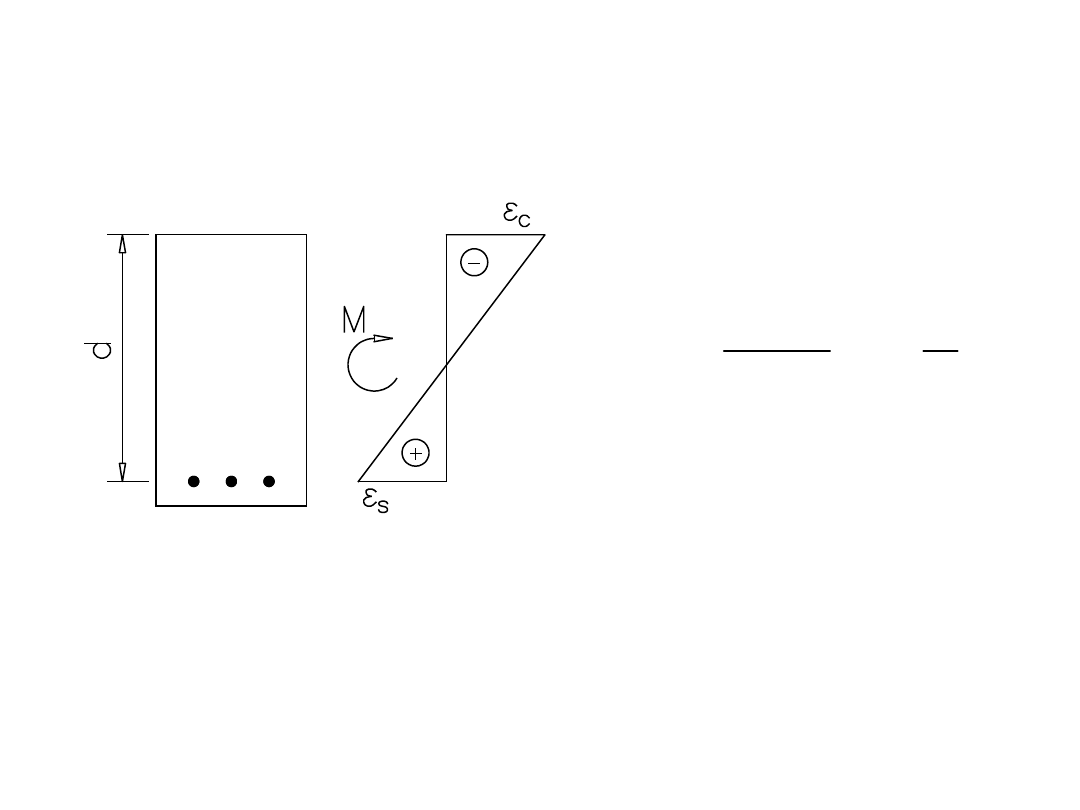
Krzywizna  przekroju zginanego



















m

1

d

c

s

Krzywizna graniczna zostaje osiągnięta przy ε

c

 = ε

cu 

   

Odkształcenia graniczne zbrojenia są znacznie większe niż 
odkształcenia betonu ε

cu

, więc nie decydują o κ

lim

  

 

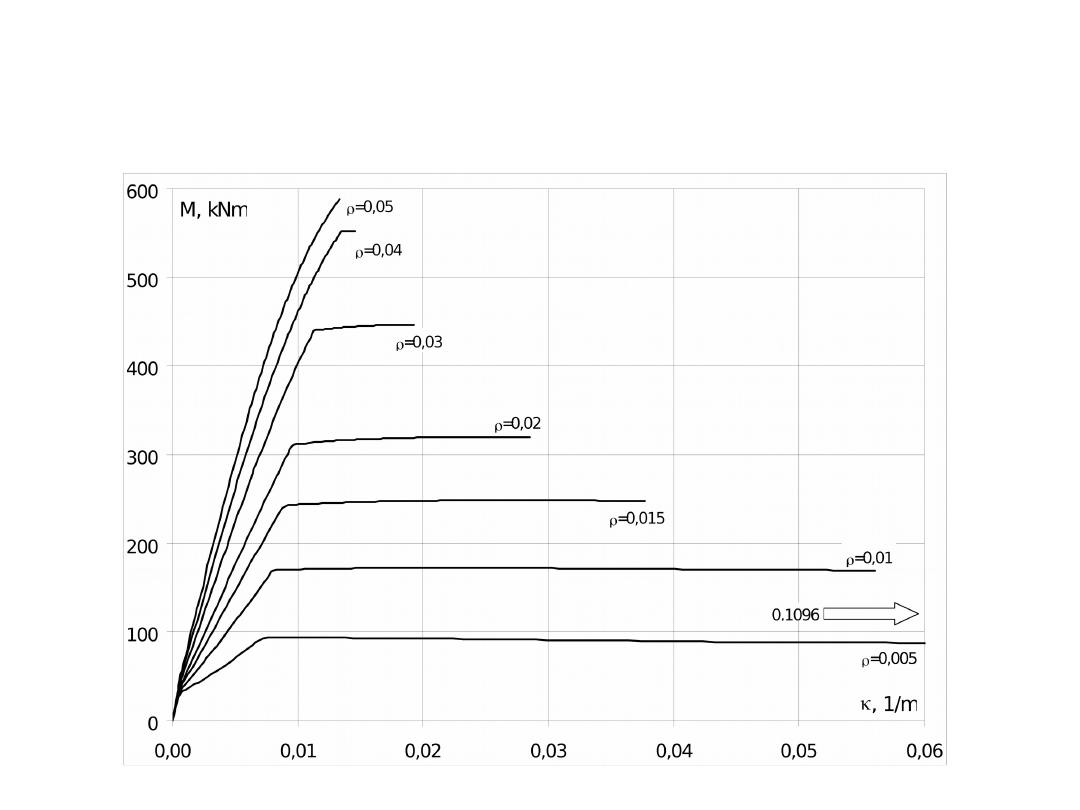
Schematyczne zależności M – κ  (moment – krzywizna)

 przy różnych stopniach zbrojenia podłużnego (tylko w strefie
 rozciąganej)

Przekrój prostokątny
Beton C30/37
Stal  o f

yk

 = 500MPa 

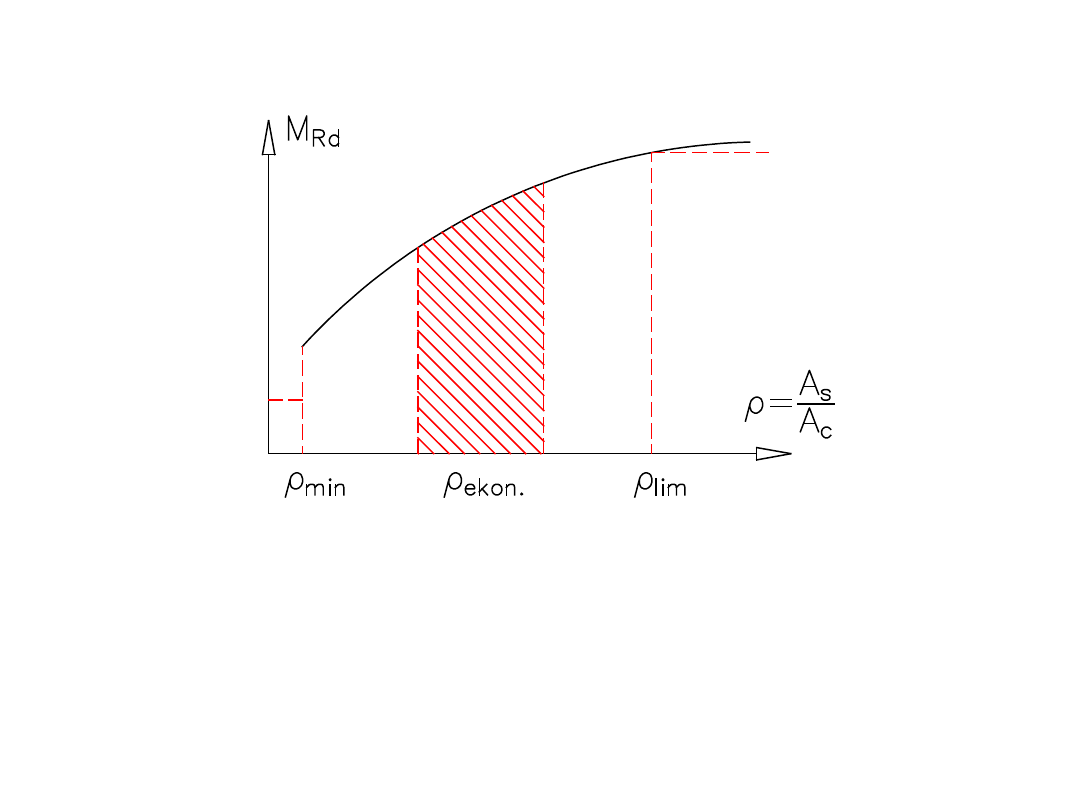
ρ

min

 

– z warunku, aby po zarysowaniu zbrojenie mogło 

przenieść
        tę siłę, którą przed zarysowaniem przenosiła strefa 
        rozciągana (beton + zbrojenie)

ρ

lim 

 

– jak poprzednio

 

Zmienność momentu w funkcji stopnia zbrojenia przekroju 

Projektowanie

Częściowe współczynniki materiałowe

Sytuacja 

obliczeniow

a

Beton



c

Stal 

zbrojeniow

a 



s

SGN – stała i 

przejściowa

1,40  PN

1,50  EN

1,15

Wyjątkowa – 

bez pożaru

1,20

1,00

Wyjątkowa – 

pożar

1,00

1,00

SGU

1,00

1,00

ZAŁOŻENIA OBLICZENIOWE

-    

płaskie przekroje pozostają nadal płaskie,

-    odkształcenie zbrojenia z przyczepnością 
jest 
     takie samo jak otaczającego betonu
 

-    wytrzymałość betonu na rozciąganie pomija 
się
 

-    naprężenia ściskające w betonie ustala się 
na
     podstawie związku σ - ε podanego w PN-EN
 

-    naprężenia w stali zbrojeniowej ustala się na
     podstawie obliczeniowych wykresów wg PN-
EN 

-    

przy ocenie naprężeń w cięgnach 

sprężających 
     uwzględnia się początkowe odkształcenie w 
tych
     cięgnach. 

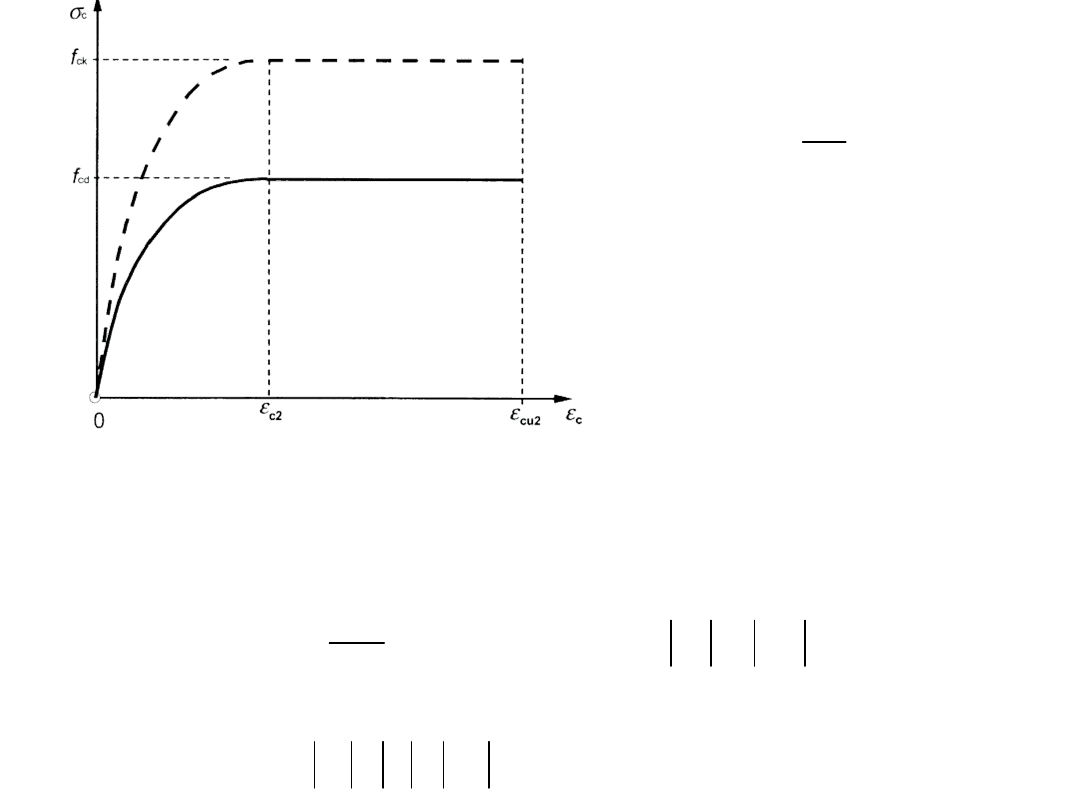
Rys. 3.3: Wykres paraboliczno–prostokątny  przy ściskaniu

f

ck

  ≤ 50MPa     

ε

c2

 = 2,00‰     ε

cu2

=3,50‰        n 

= 2

c2

c

n

 

c2

c

cd

c

ε

ε

0

  

jeżeli

       

ε

ε

-

1

-

1

f

σ

































cu2

c

c2

cd

c

ε

ε

ε

jeżeli

f

σ







PN

4

,

1

EN

5

,

1

zalecane

0

,

1

f

f

c

c

cc

c

ck

cc

cd



















Model betonu (1)

Jeżeli f

ck

  ≥ 50MPa     

ε

c2

 = 2,0 + 0,085 (f

ck

 – 50)

0,53

           [‰]     

ε

cu2

= 2,6 + 35 [0,01 (90 – f

ck

)]

4

         [‰]     

   

n = 1,4 + 23,4 [0,01 (90 – f

ck

)]

4

Przykładowo  przy  f

ck

 = 90MPa  (C90/105)     

ε

c2

 = 2,6‰     

ε

cu2

= 2,6‰        

n = 1,4

Oznacza to, że betonom o wysokiej 
wytrzymałości przypisuje się mniejszą 
zdolność do odkształcania !

Model betonu (1)

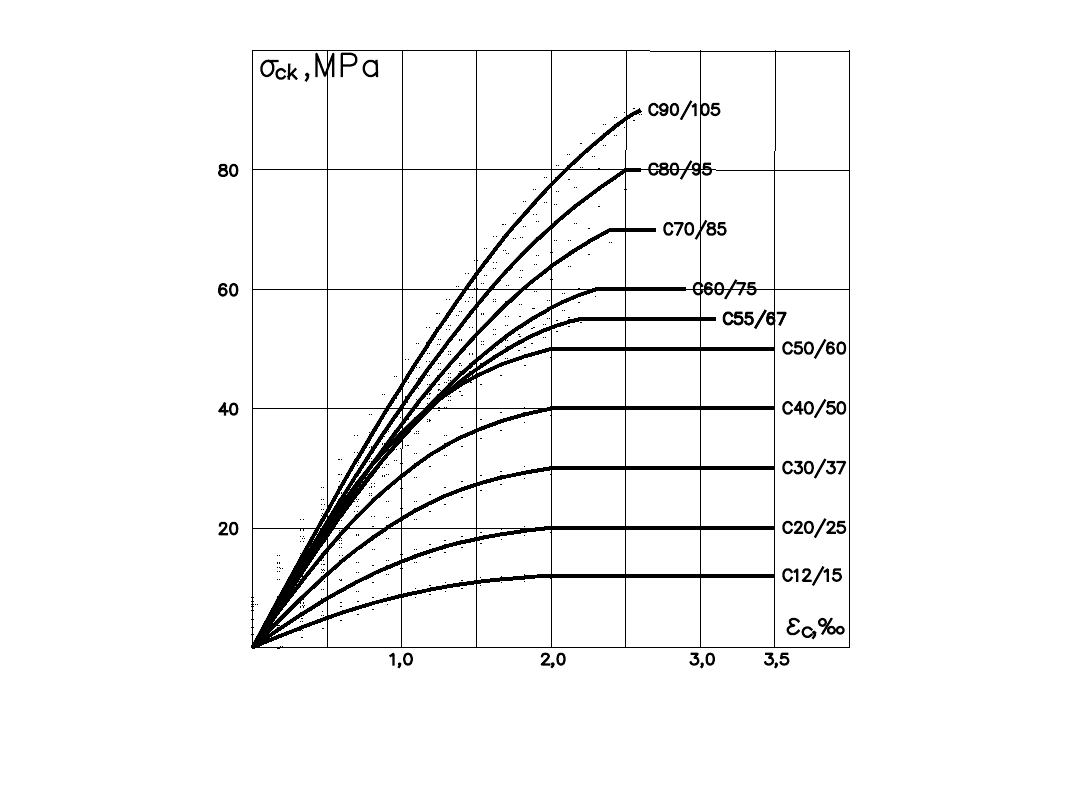
Obliczeniowe charakterystyki w zależności od klasy betonu

Model betonu (1)

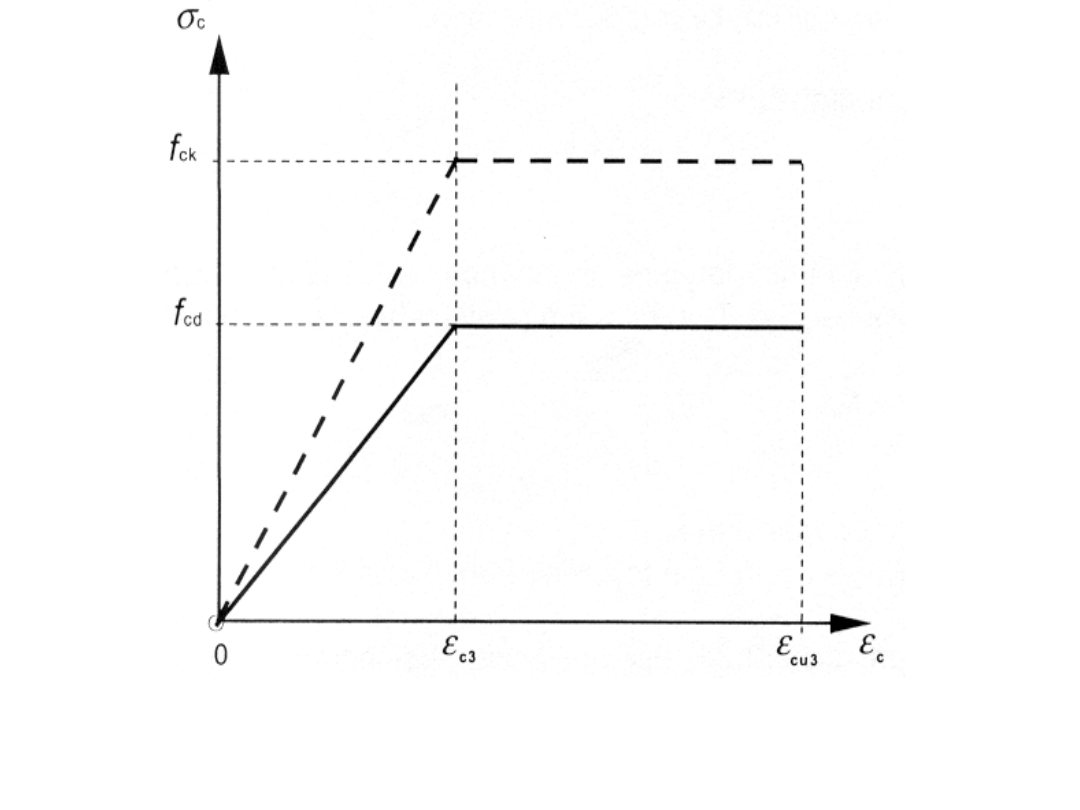
Rysunek 3.4: Bilinearna zależność naprężenie-
odkształcenie 

f

ck

  ≤ 50MPa          

ε

c3

 = 1,75‰     

ε

cu3

=3,50‰

Model betonu (2)

Jeżeli f

ck

  ≥ 50MPa     

ε

c2

 = 2,0 + 0,085 (f

ck

 – 50)

0,53

           [‰]     

ε

cu2

= 2,6 + 35 [0,01 (90 – f

ck

)]

4

         [‰]     

   

n = 1,4 + 23,4 [0,01 (90 – f

ck

)]

4

Przykładowo  przy  f

ck

 = 90MPa  (C90/105)     

ε

c2

 = 2,6‰     

ε

cu2

= 2,6‰        

n = 1,4

Oznacza to, że betonom o wysokiej 
wytrzymałości przypisuje się mniejszą 
zdolność do odkształcania !

Model betonu (2)

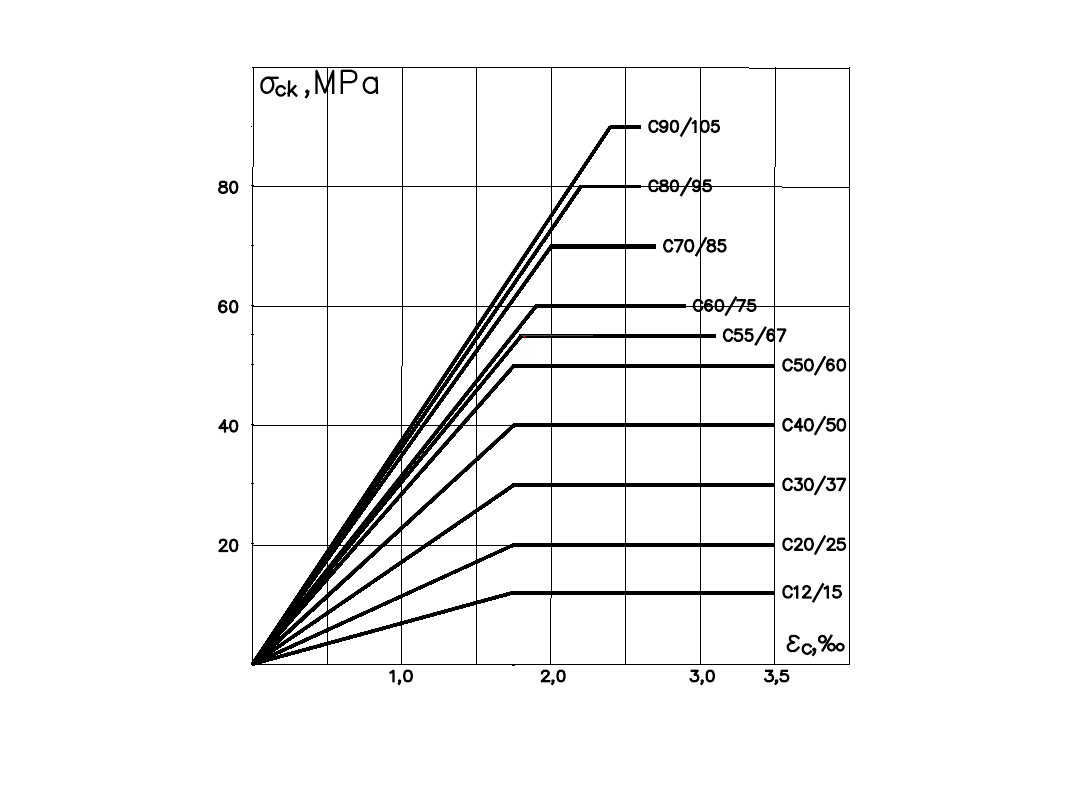
Obliczeniowe charakterystyki w zależności od 

klasy betonu

Model betonu (2)

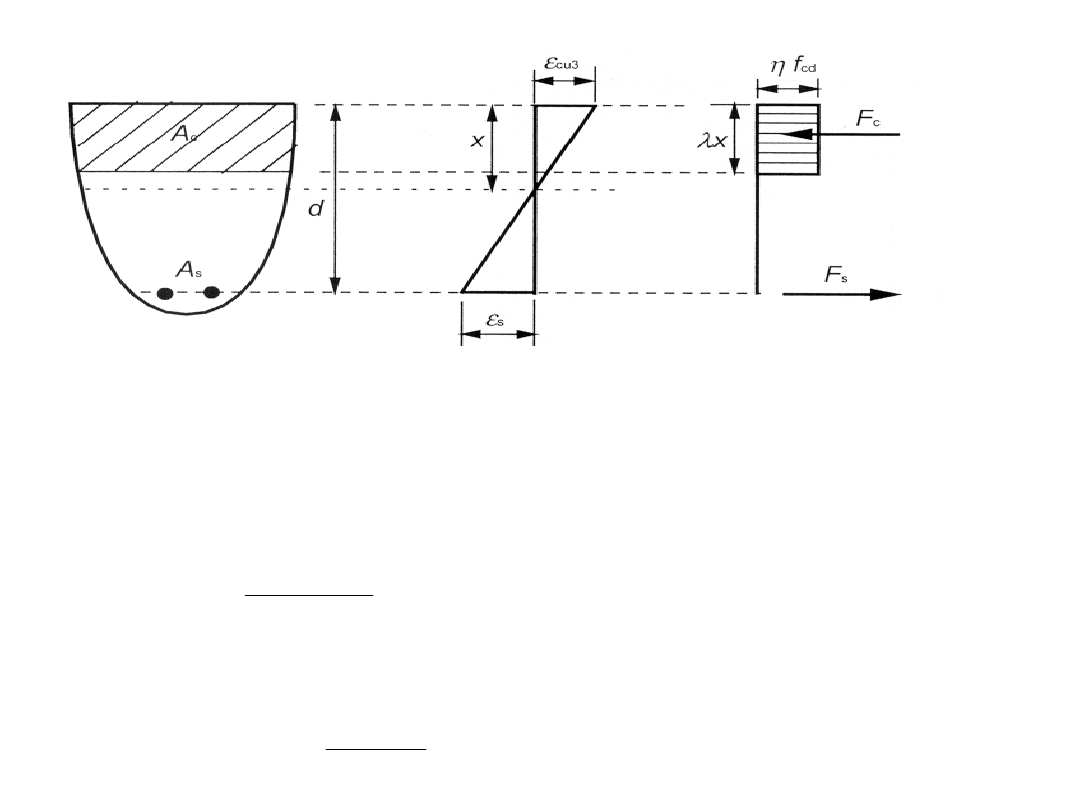
Rysunek 3.5: Prostokątny rozkład naprężeń 

50MPa

f

      

dla

   

          

          

0,8

λ

ck





MPa

90

f

50

      

dla

         

400

50)

(f

-

0,8

λ

ck

ck









MPa

50

f

       

dla

      

          

          

1,0

η

ck





MPa

90

f

50

       

dla

      

          

200

50

f

-

1,0

 

η

ck

ck









f

ck

  ≤ 50MPa         

ε

c3

 = 1,75‰         

ε

cu3

=3,50‰

Model betonu (3)

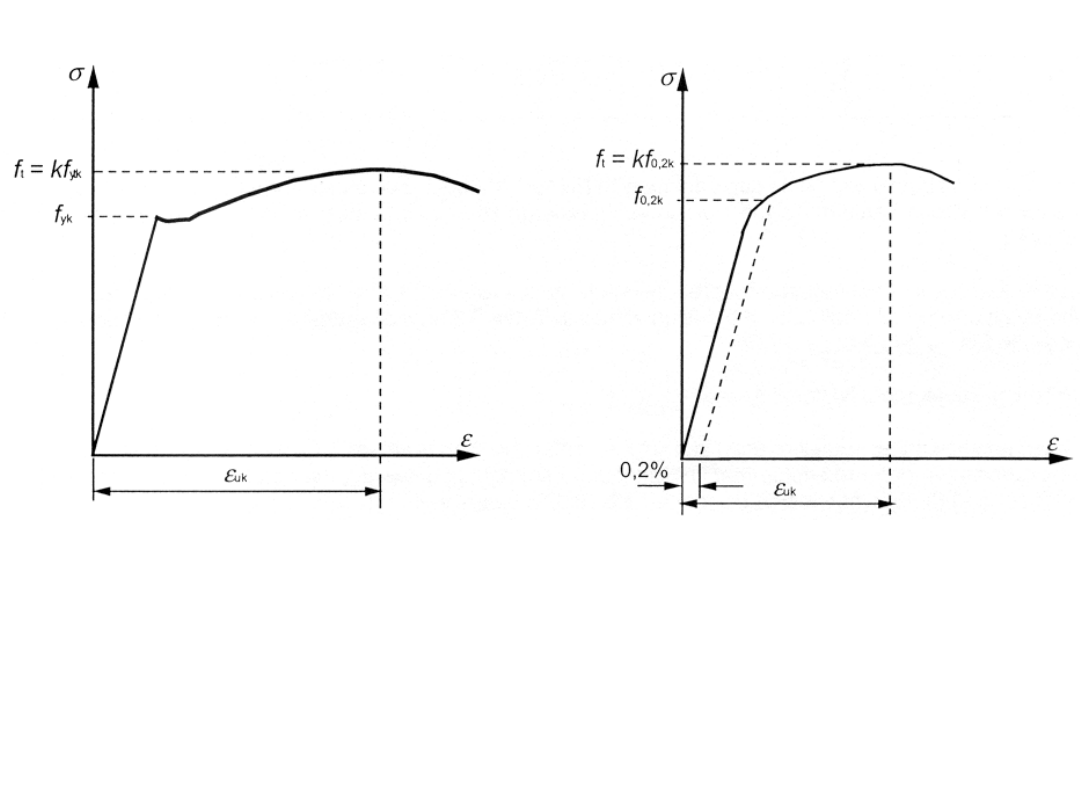
Stal walcowana na gorąco

Stal walcowana 

na zimno 

Wykresy naprężenie-odkształcenie typowej 
stali zbrojeniowej 
(wartości  bezwzględne pokazane są dla 
naprężeń rozciągających i odkształceń)

Model stali

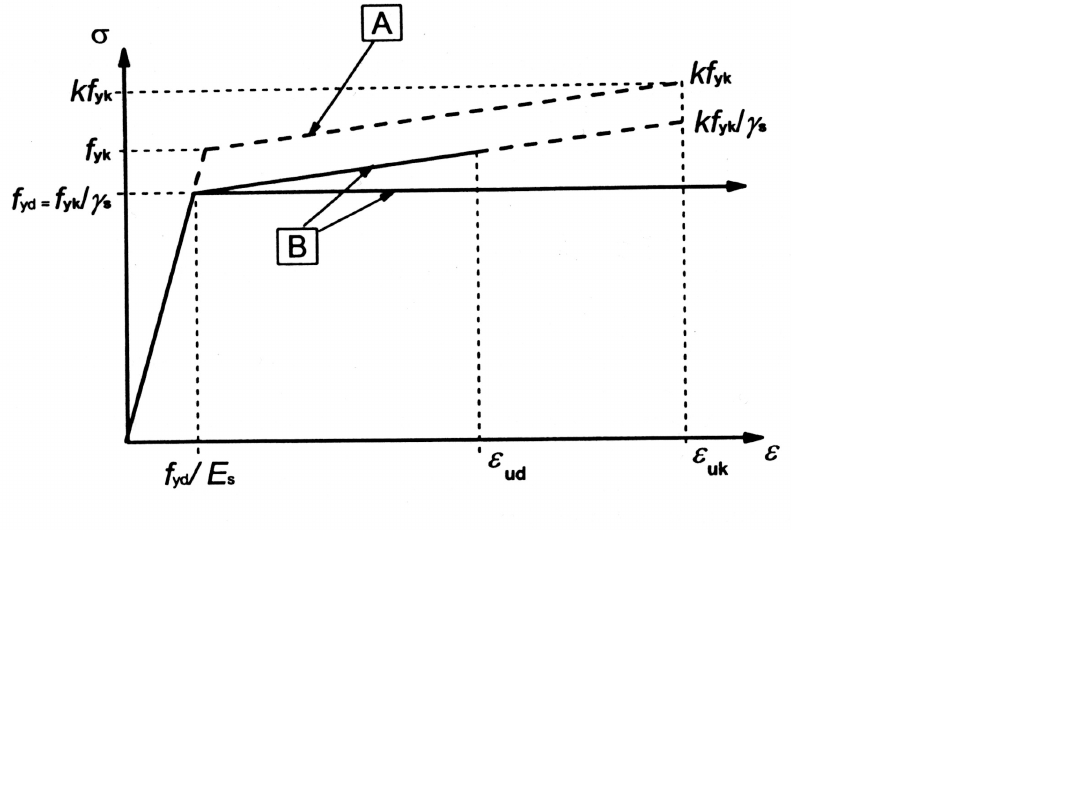
k = (f

t

/f

y

)

k

 

A  Idealizowany

B  Obliczeniowy

Rysunek 3.8. Idealizowany i obliczeniowy wykres б - ε 
stali zbrojeniowej (dla ściskania lub rozciągania)

Ograniczenie ε

ud

 obowiązuje przy wykresie z pochyloną 

górną gałęzią

Wartość zalecana ε

ud

 = 0,9ε

uk

 

Model stali
pasywnej

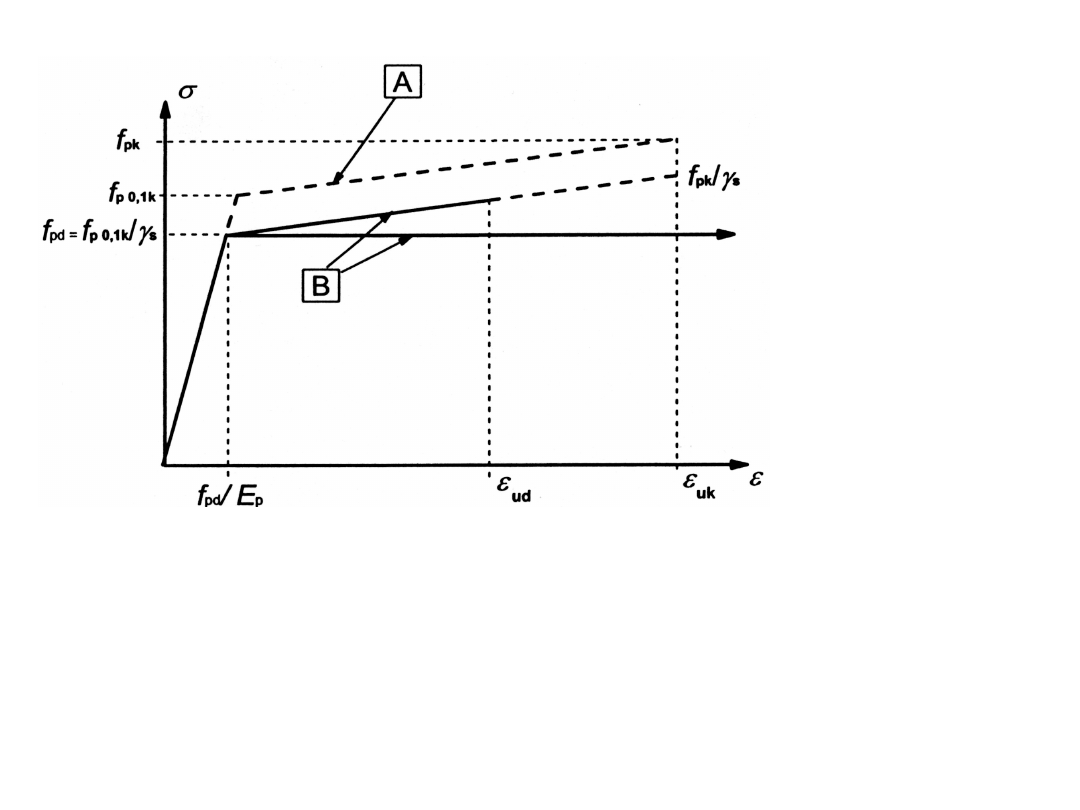
A Idealizowany

B Obliczeniowy

Rysunek 3.10. Idealizowany (A) i obliczeniowy (B) 
wykres naprężenie –odkształcenie  stali sprężającej 
( przedstawiono wartości bezwzględne naprężenia 
rozciągającego i odkształcenia)

 

f

p0,1k

 /f

pk

  = 0,9           ε

ud

 = 0,9 ε

uk

        (ε

ud

 = 0,02)

Model stali
sprężającej

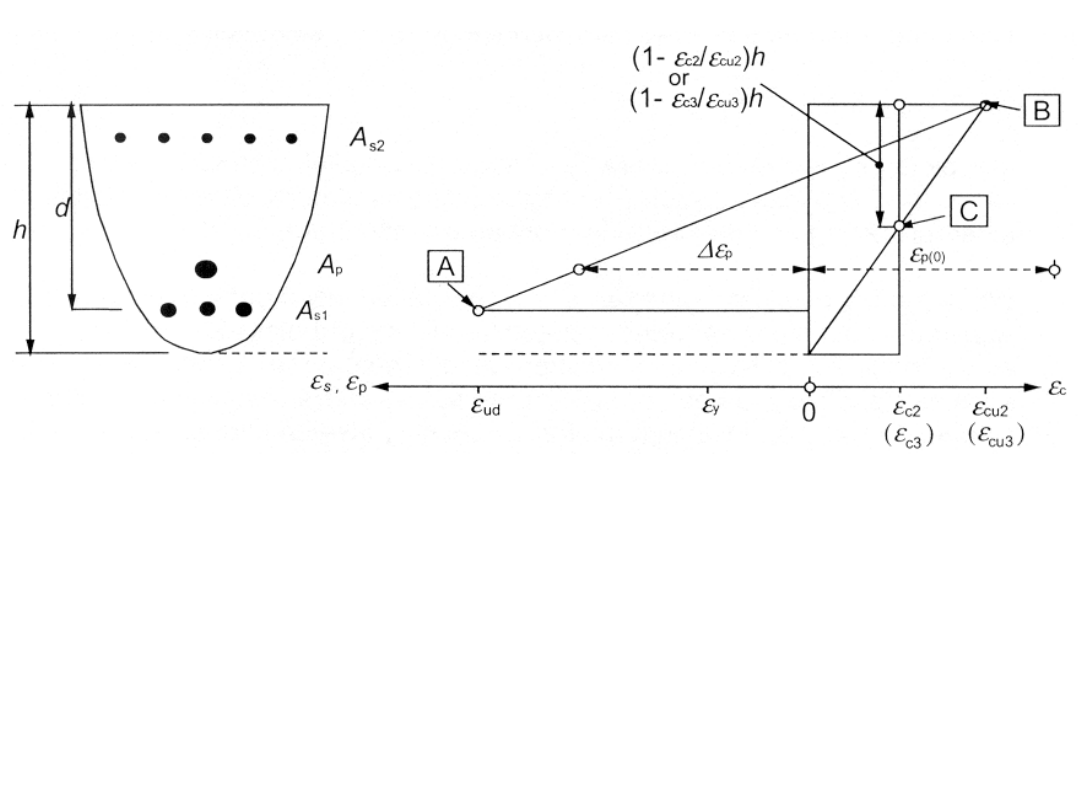
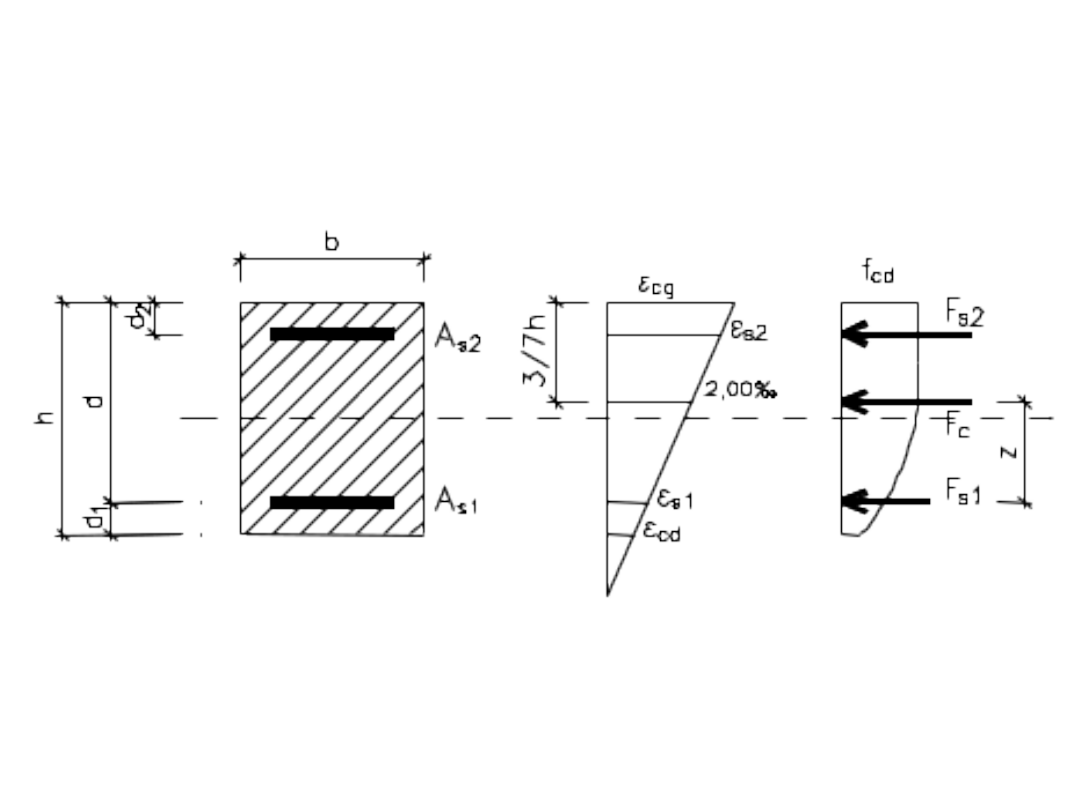
Rys. 6.1: Możliwe rozkłady odkształceń w 
stanie
                granicznym nośności 

 

A  – graniczne wydłużenie stali zbrojeniowej

 B  -  graniczne skrócenie betonu
 C  – graniczne odkształcenia betonu przy 
ściskaniu
         osiowym

Odkztałcenia

 

Możemy rozważać:

- wymiarowanie
  

szukamy pola przekroju zbrojenia A

s1

 i A

s2

, takiego,

aby E

d

 ≤ R

d 

 (M

Ed

 lub M

Ed

 i N

Ed

)

        

ograniczenia: 

        - możemy uwzględnić tylko dwa poziomy zbrojenia 
przekroju;
        - w wielu przypadkach potrzebna będzie iteracja

-

 sprawdzenie nośności za pomocą krzywej 

interakcji
   

przyjmujemy pola przekroju zbrojenia A

s1

 i A

s2

 (a także A

s3

, A

s4

 

itd.), 
   określamy nośność przekroju i sprawdzamy, czy E

d

 ≤ R

d

; 

jeżeli tak nie jest, to korygujemy A

s

 i ponawiamy obliczenia

         

korzyści:

         - nie jest potrzebna iteracja
         - możemy uwzględniać wiele poziomów zbrojenia
         - możemy łatwo sprawdzać, czy przekrój przenosi 
różne kombinacje  M

Ed 

 i  N

Ed

 

   

Tablice pomocnicze – 

beton o f

ck

 ≤ 50 MPa

Za pomocą współczynników podanych w tabelach można 
określić następujące przekrojowe wielkości:

wysokość strefy ściskanej

x=d

ramię sił wewnętrznych

z=d

wypadkową bryły naprężenia w betonie

F

c

=bdf

cd

moment tej wypadkowej względem 
osi zbrojenia rozciąganego

M

cs

=

cs

bd

2

f

cd

oraz odkształcenia skrajnych włókien przekroju i 
odkształcenia zbrojenia ściskanego i 
rozciąganego.

W obliczeniach wykorzystuje się dwa warunki 
równowagi:

                 - sił wewnętrznych
                 - momentów tych sił

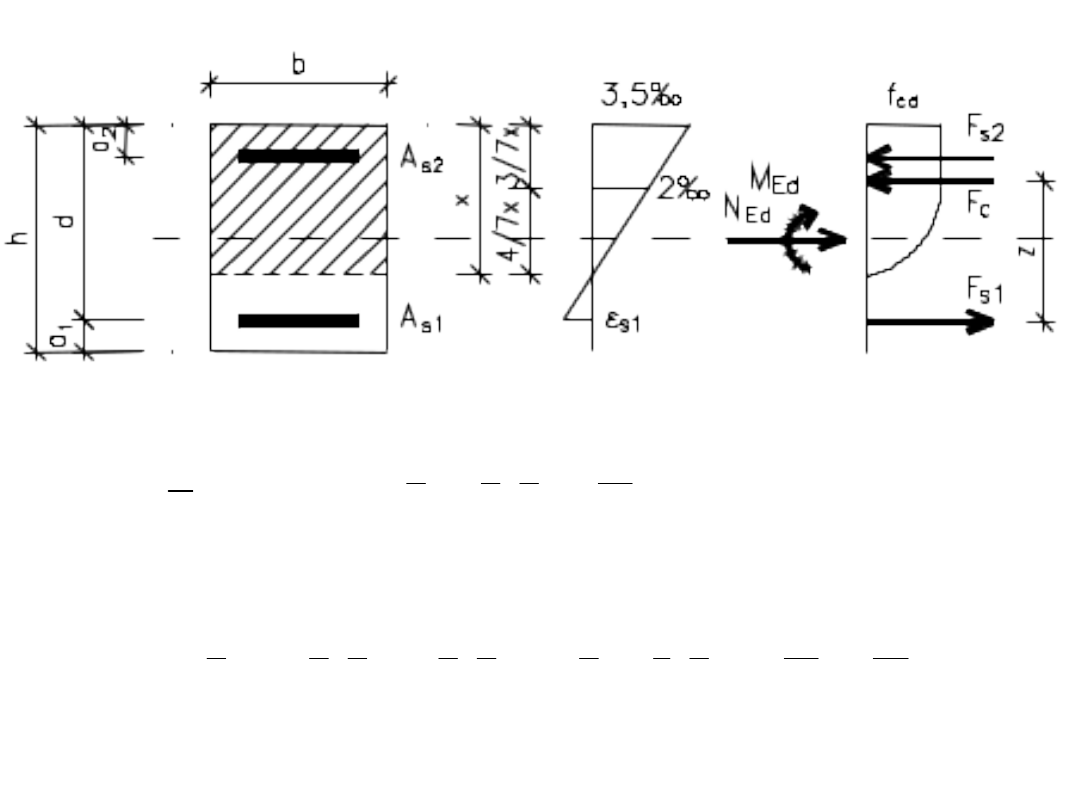
TABLICE POMOCNICZE  - Beton do C50/60

Wypadkowa bryły naprężenia ściskającego

















21

17

7

4

3

2

7

3

cd

c

bdf

F





d

x





Moment siły w betonie względem osi A

s1

2

cs

98

33

21

17

7

4

8

3

7

3

1

7

4

3

2

7

3

2

1

1

7

3





























































cd

2

cs

cs

f

bd

M





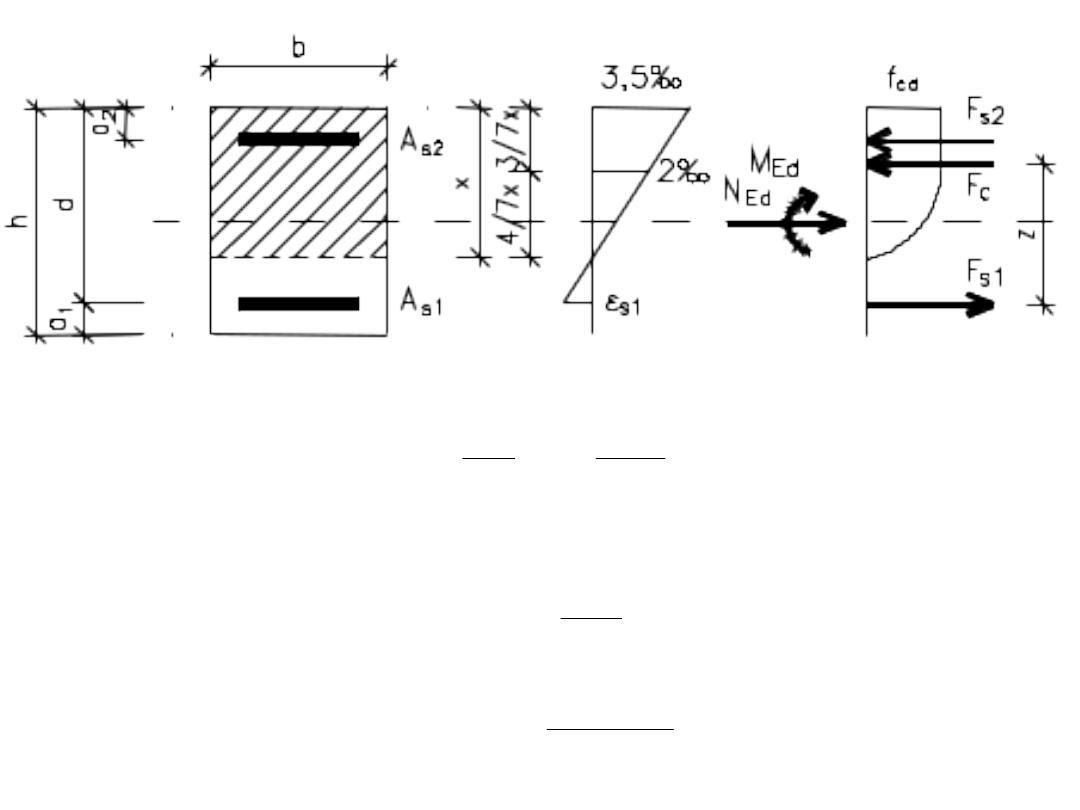
Ramię sił wewnętrznych















1666

693

1

cs

d

z 



Odkształcenia zbrojenia













1

5

,

3

1

s











d

/

a

5

,

3

2

2

s

Beton do C50/60, cały przekrój ściskany, x > h

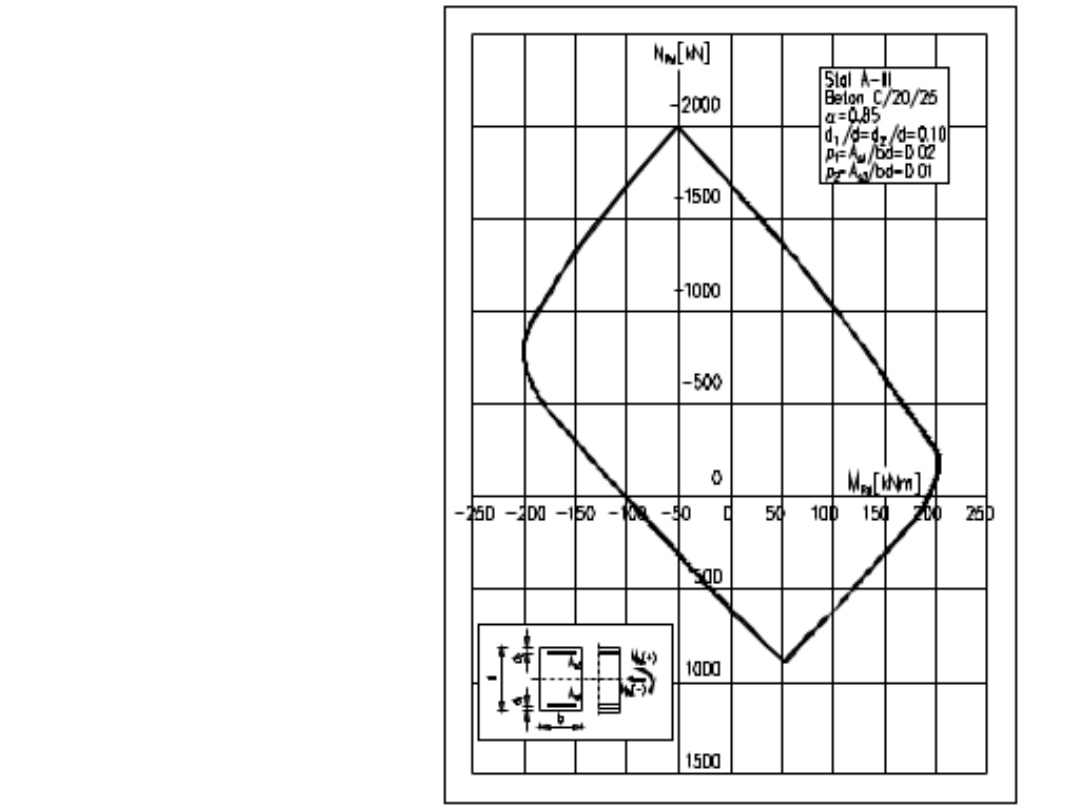
Przykładow
a
krzywa 
interakcji

Przekrój zbrojony 
niesymetrycznie

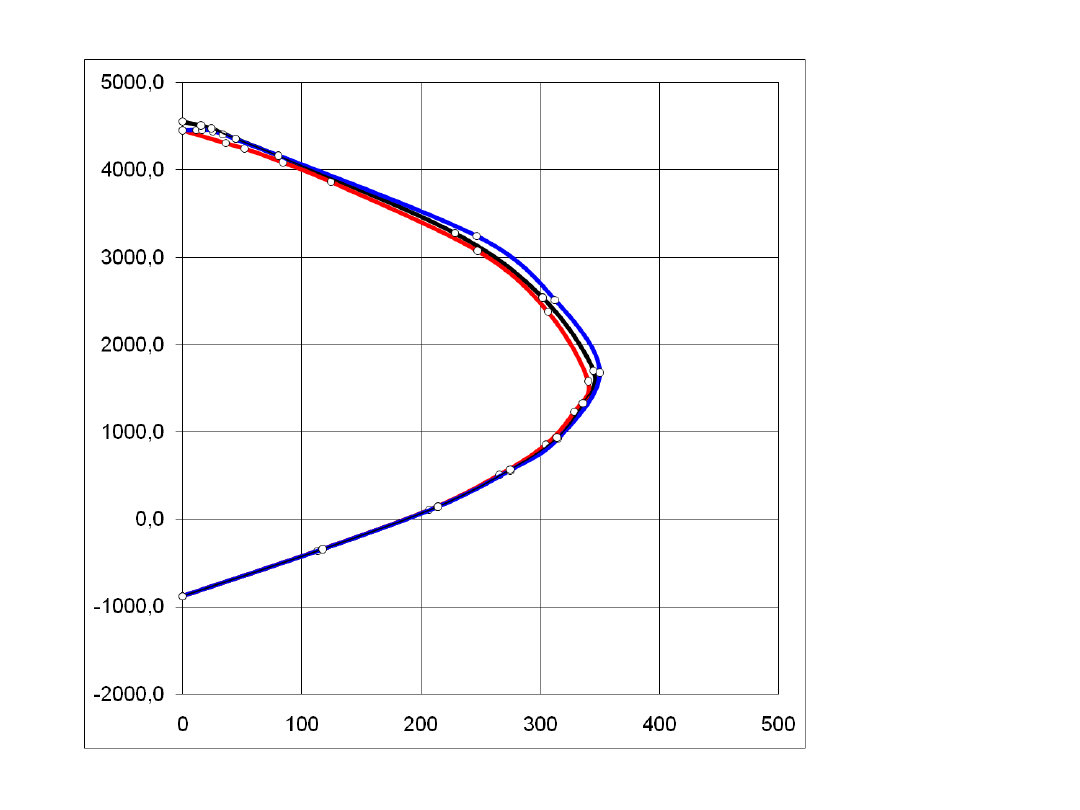
Przykładowe 
krzywe
interakcji

Przekrój zbrojony 
symetrycznie

Modele betonu:

Paraboliczno
-prostokątny

Dwuliniowy

Prostokątny