MASOWY MOMENT

BEZWŁADNOŚCI

WALCA

KATARZYNA KRUK gr 29-CR-A2

DARIUSZ KATANA gr 29-CR-A2

.

 

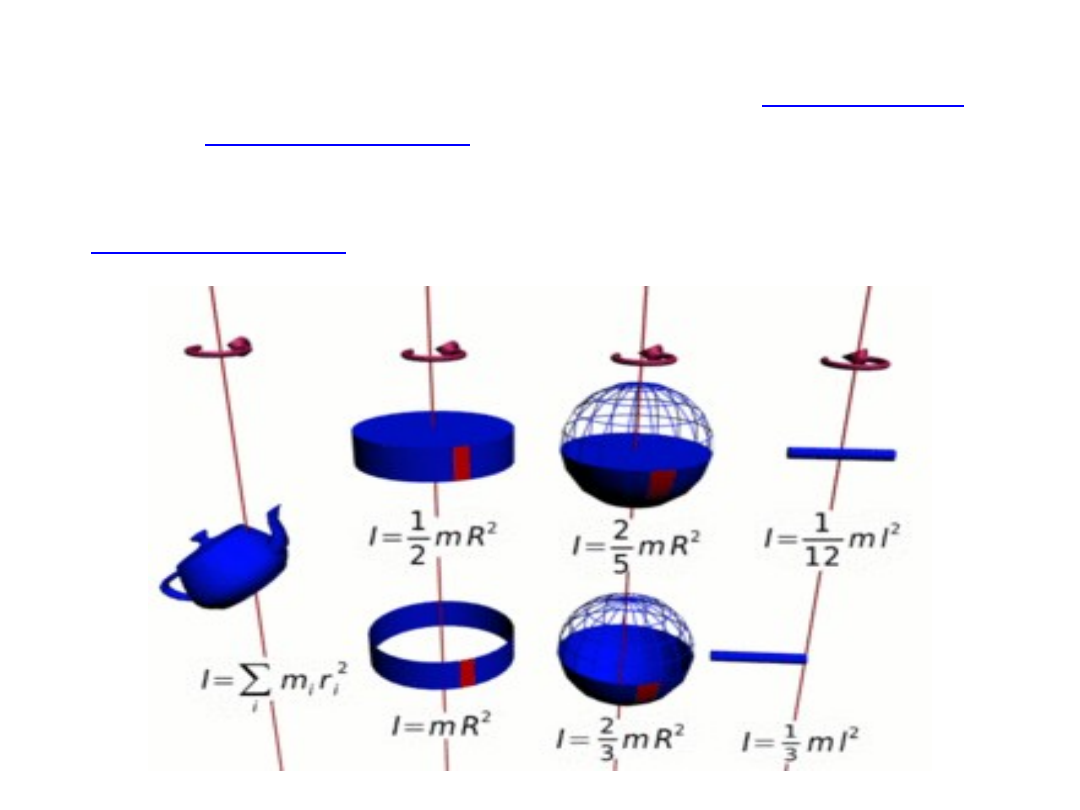
Moment bezwładności

to miara

bezwładności

ciała w

ruchu obrotowym

względem określonej, ustalonej osi

obrotu. Im większy moment, tym trudniej zmienić ruch
obrotowy ciała, np. rozkręcić dane ciało lub zmniejszyć jego

prędkość kątową

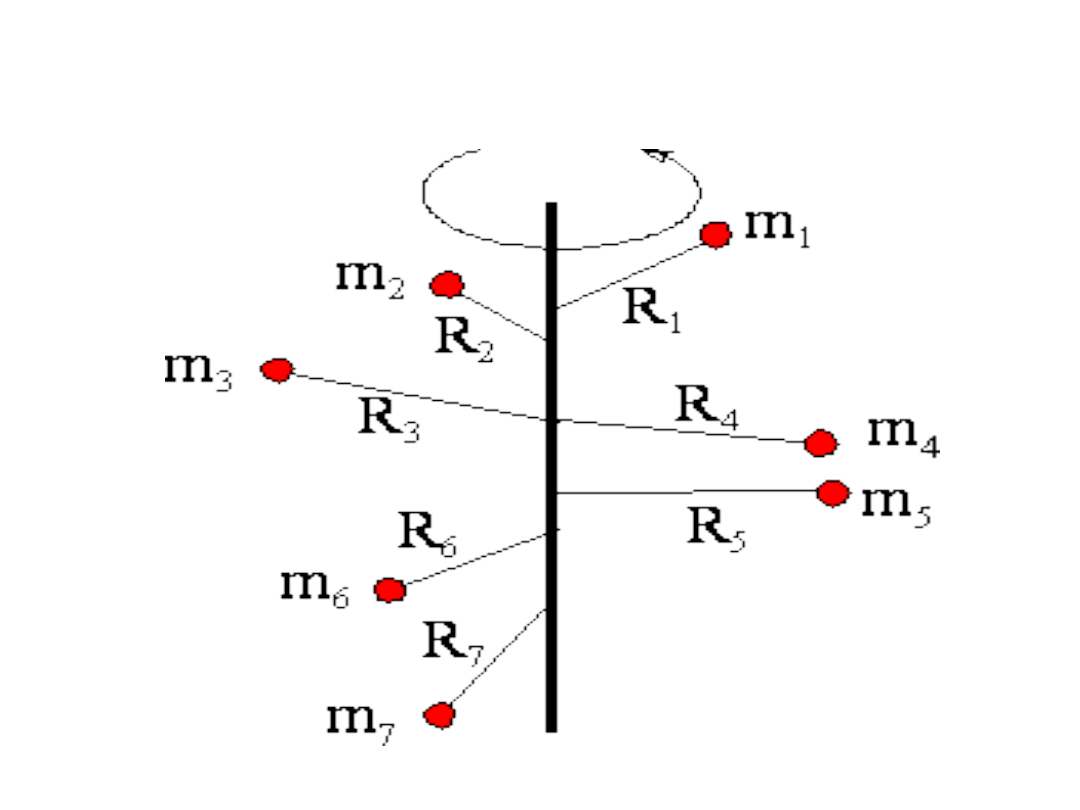
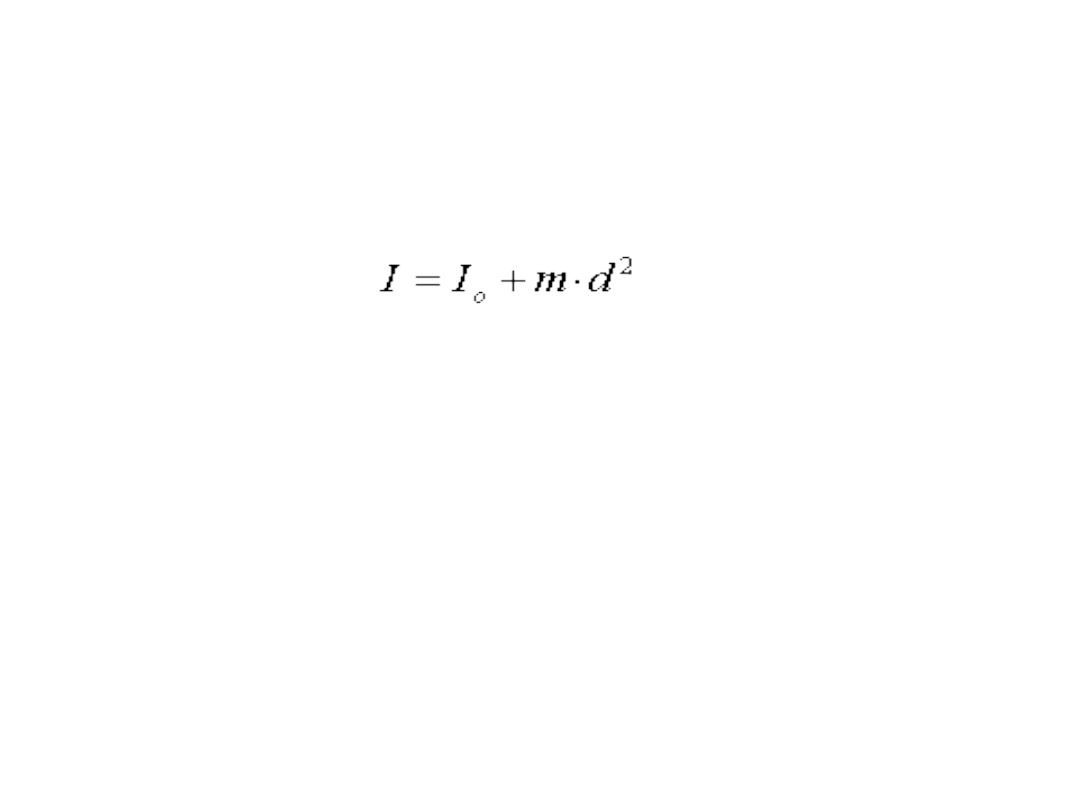
Twierdzenie Steinera

Twierdzenie to mówi, że jeśli znamy moment
bezwładności I

o

danego ciała względem pewnej osi

przechodzącej przez środek masy tego ciała to aby
obliczyć moment bezwładności I względem dowolnej
innej osi równoległej do niej należy do momentu I

o

dodać iloczyn masy ciała i kwadratu odległości d
między tymi osiami czyli md

2

:

  

W ruchu obrotowym bryły sztywnej jej kształt jest w

zasadzie bez znaczenia, gdyż jej ruch jest określony przez
jej osie bezwładności. Każdej bryle, niezależnie od tego, jak
nieregularny jest jej kształt i niejednorodna gęstość,
odpowiada elipsoida bezwładności. Na ogół, jest to
elipsoida trójosiowa, a jej osie noszą nazwę głównych osi
bezwładności. Długość każdej z tych osi jest proporcjonalna
do momentu bezwładności względem tej osi. 

Głównymi osiami bezwładności nazywamy trzy osie
przechodzące przez środek masy C i mające takie
kierunki, że:
  I - moment bezwładności względem tej osi jest
największy;
 II - prostopadła do osi I i taka, względem której moment
bezwładności ciała jest mniejsza
III - prostopadła do obu osi I. i II.

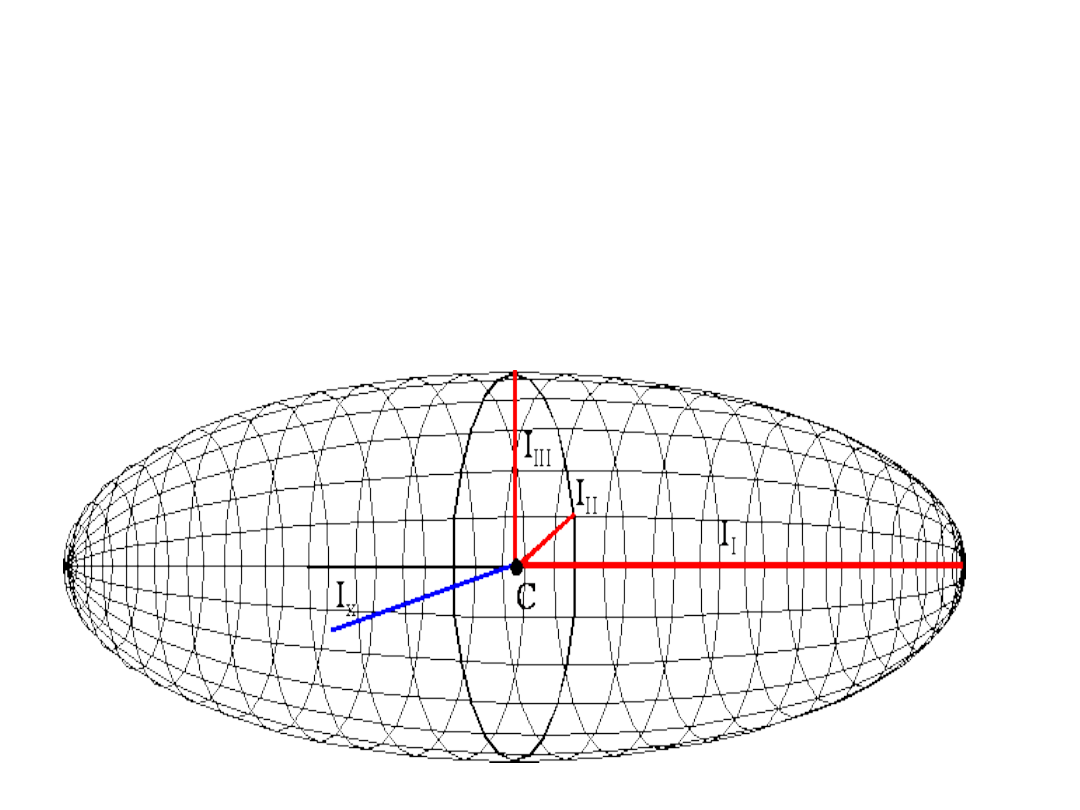
            Obrót bryły sztywnej wokół dowolnej osi przechodzącej przez
środek masy można zawsze rozłożyć na trzy równoczesne obroty wokół
głównych osi bezwładności. Taki rozkład nie jest możliwy dla jakichkolwiek
innych trzech osi prostopadłych względem siebie. Najprostszymi
rodzajami ruchu bryły sztywnej jest ruch obrotowy względem jednej z
głównych osi bezwładności. Ruch taki jest stabilny tylko wtedy, gdy
odbywa się wokół osi, dla której moment bezwładności jest największy.
Ruch wokół osi II., dla której moment bezwładności jest najmniejszy, jest
także stabilny, ale wtedy najmniejsze zaburzenie ruchu powoduje, że
pojawia się para sił odśrodkowych, która stara się doprowadzić do obrotu
wokół osi I. ciała. Ruch wokół osi III. jest zawsze niestabilny

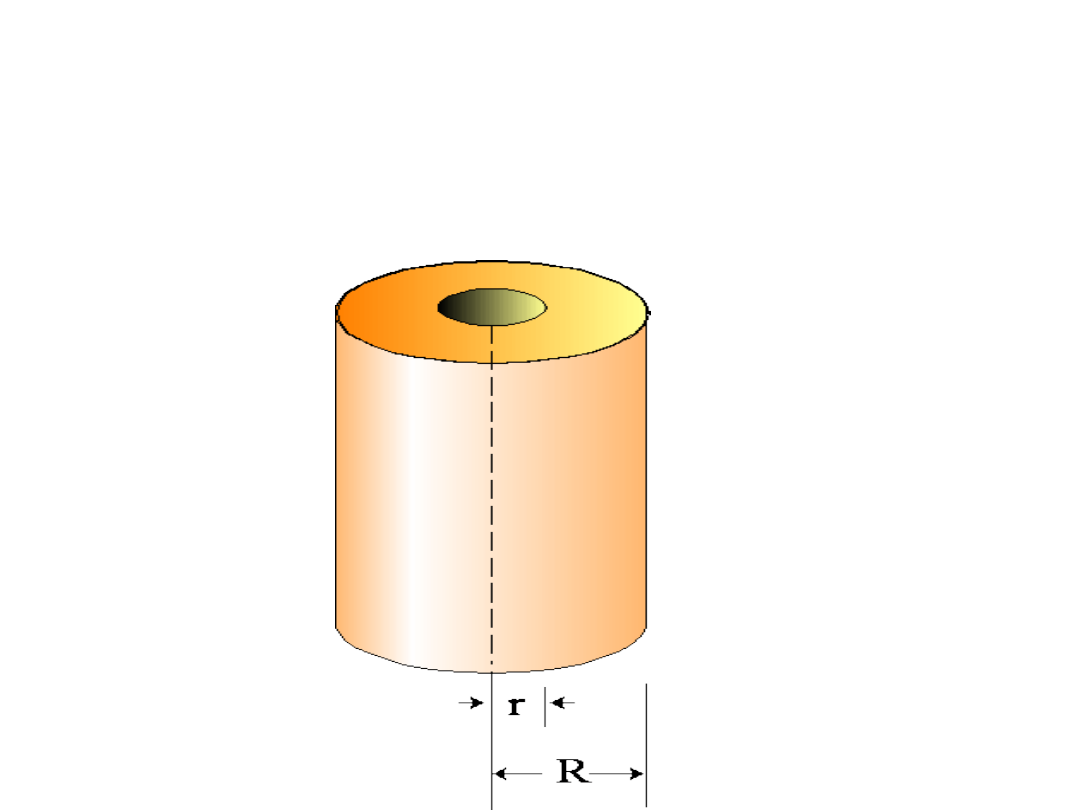
walec o masie M i o promieniu wewnętrznym r, a
zewnętrznym R

:

MOMENT BEZWŁADNOŚCI WALCA

WZGLĘDEM DOWOLNEJ OSI

 
 

 
 

 
 

 
 

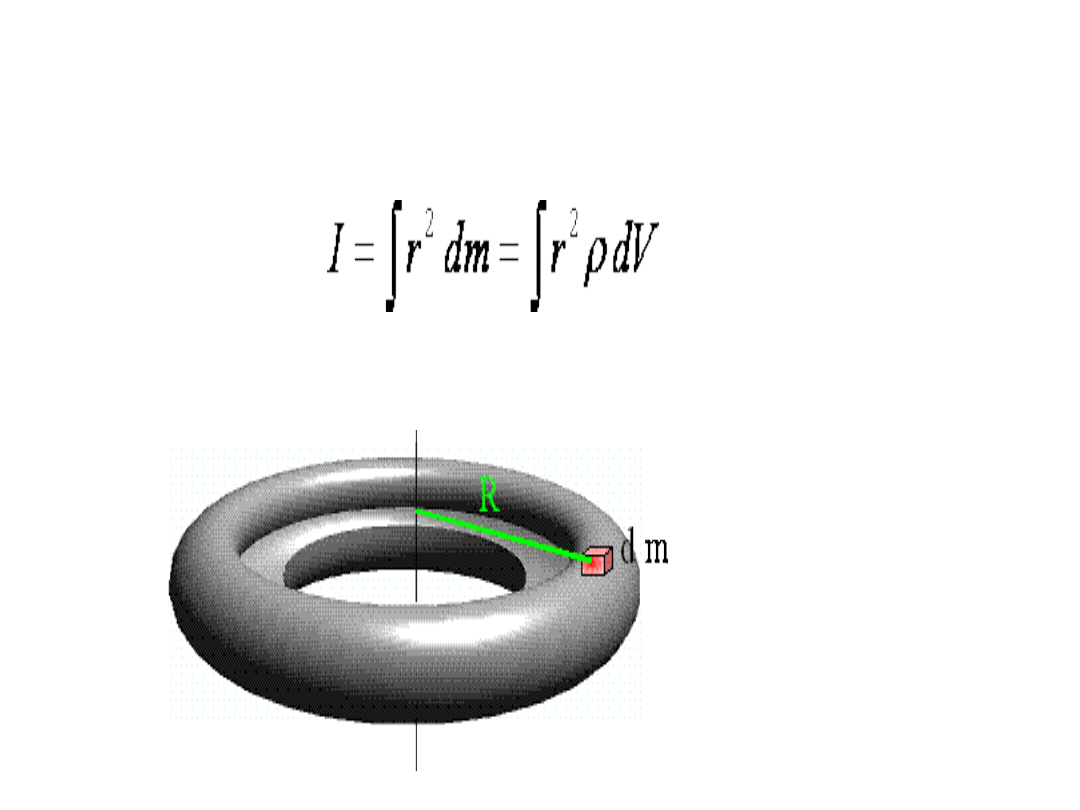
Jeżeli masa m jest rozłożona w sposób ciągły w objętości V, to
moment

bezwładności

ciała

względem

dowolnej

osi

(przechodzącej przez objętość ciała lub poza nią) obliczamy na
podstawie ogólnego równania:
 
 

gdzie r jest odległością elementu masy dm od osi obrotu, ρ -
lokalną gęstością ciała, zaś dV - objętością zajmowaną przez
element masy dm.

 
 

dV – przyrost
objętość
p – gęstość
dm – przyrost
masy

 
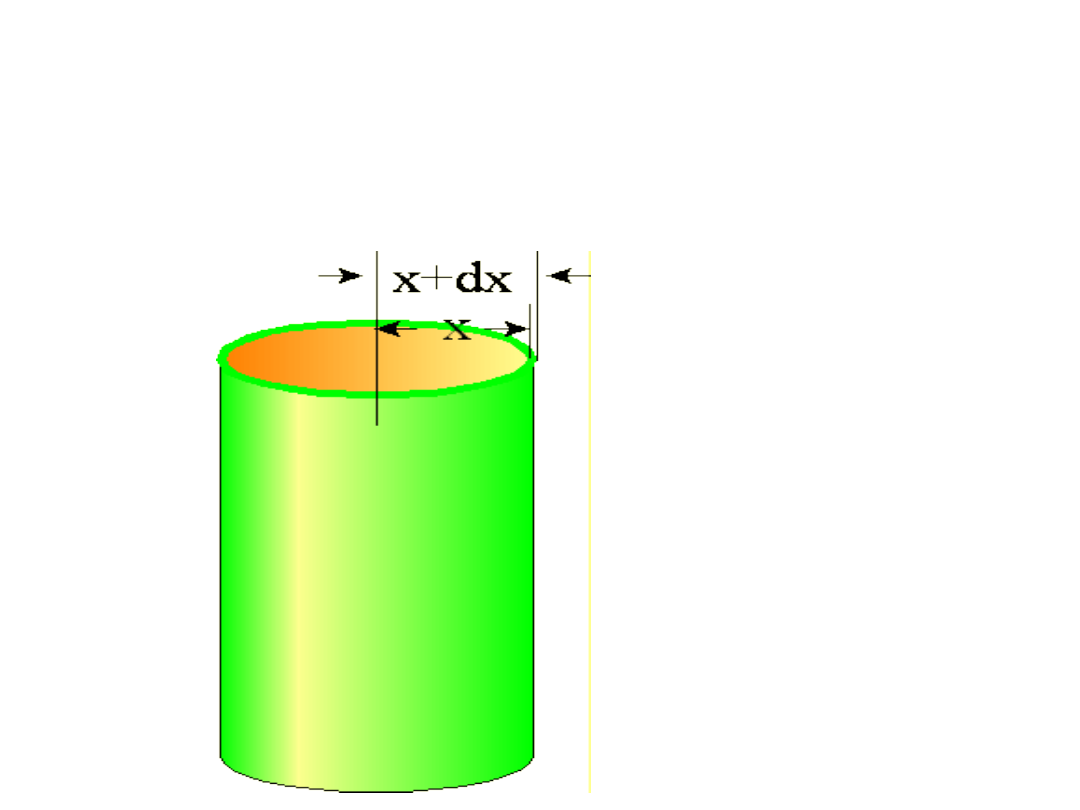
Jeżeli moment bezwładności liczymy względem osi walca, to
standardowo dzielimy go na nieskończenie cienkie cylindry o
grubości dx i masie dm.

dx - przyrost
grubości
dm - przyrost masy

MOMENT BEZWŁADNOŚCI WALCA WZGLĘDEM OSI

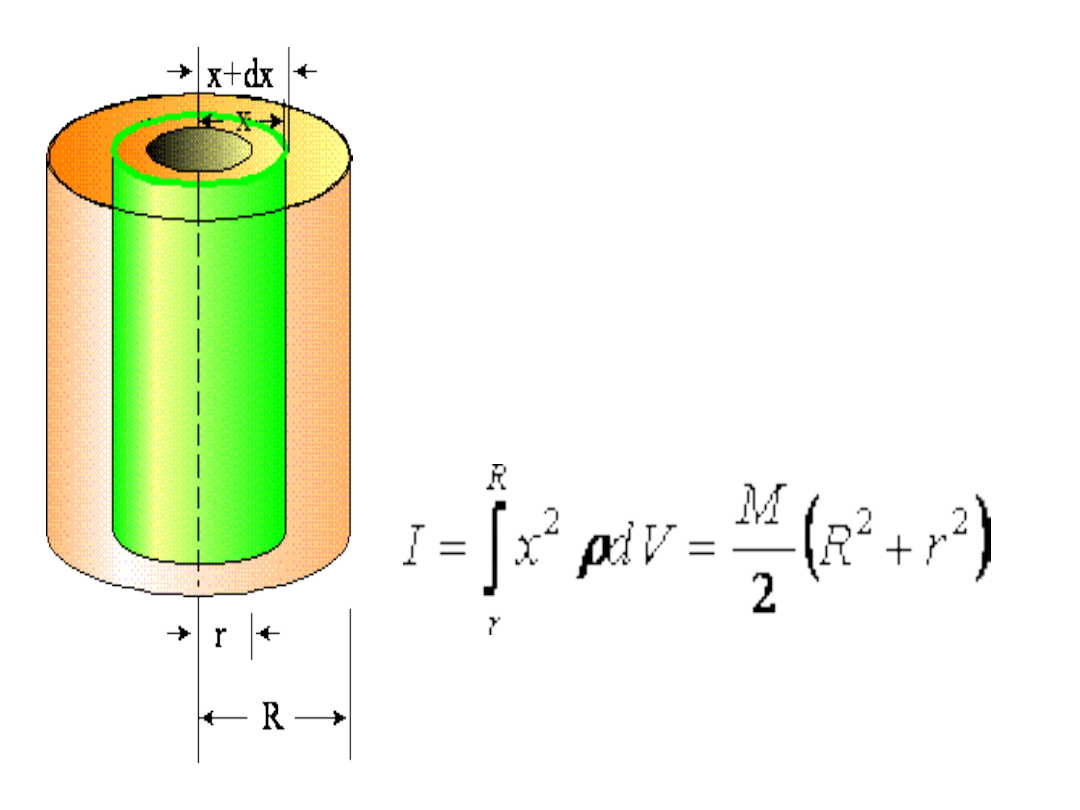
Moment bezwładności takiego
cienkiego cylindra wynosi dI = x

2

dm

Moment bezwładności całego walca
wyniesie

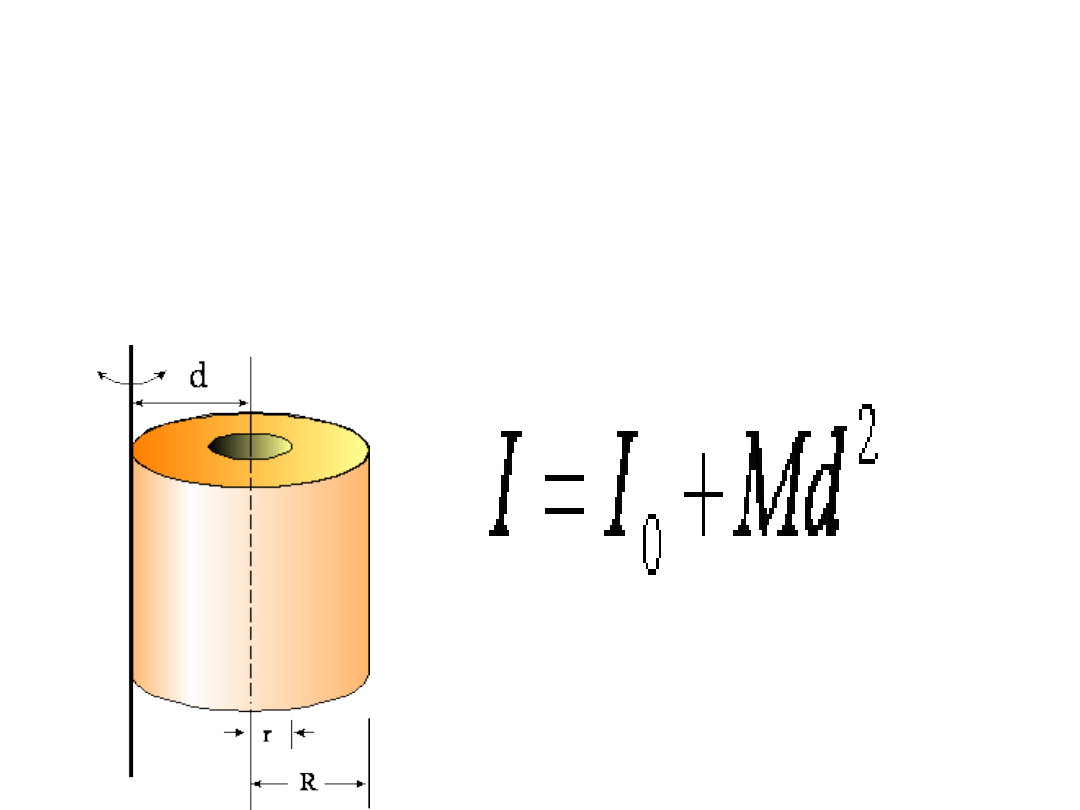
 Jeżeli ta nowa oś jest równoległa do osi przechodzącej przez
środek masy i jest od niej oddalona o odległość d, to wtedy
możemy zastosować twierdzenie o osiach równoległych (tzw.
twierdzenie Steinera):
Moment bezwładności bryły o masie M liczony względem osi
przechodzącej przez jej środek masy wynosi I

0

, to moment

bezwładności I liczony względem innej osi równoległej do
poprzedniej i oddalonej od niej o d jest równy

TWIEDZENIE O OSIACH

RÓWNOLEGŁYCH

I

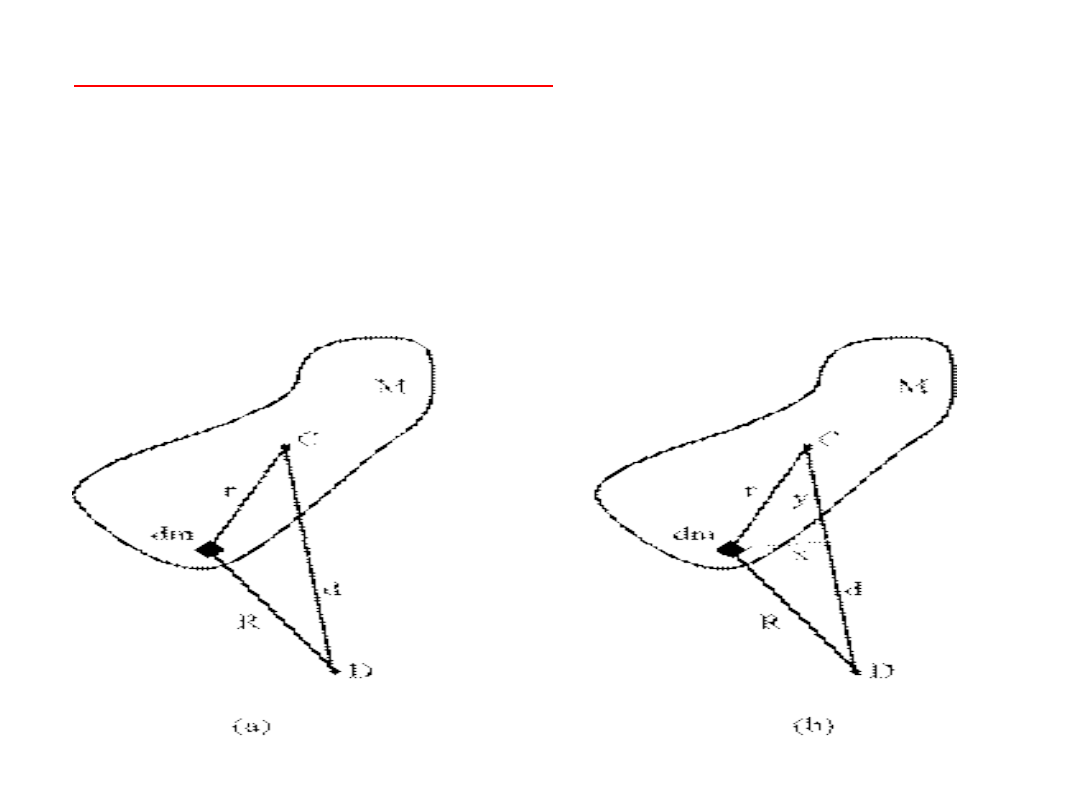
Dowód twierdzenia Steinera

. Wybierzmy płaską płytkę o

masie M (każdą bryłę trójwymiarową możemy pociąć na stos
takich „talarków”). Oś obrotu przechodzi przez środek masy C
i jest prostopadła do płaszczyzny płytki. Moment bezwładności
płytki względem tej osi oznaczymy przez I

0

. Szukamy

momentu bezwładności I względem osi przechodzącej przez
punkt D i równoległej do osi przechodzącej przez środek masy
(punkt C). Odległość między oboma osiami wynosi d.

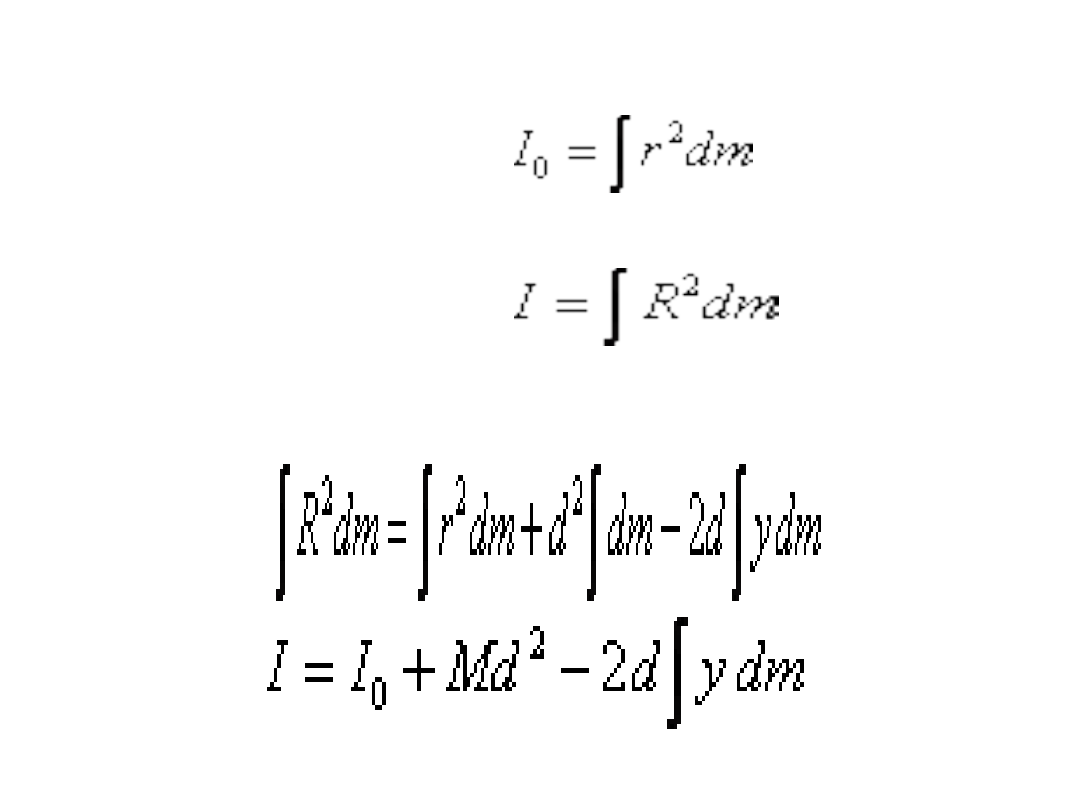
Celem jest znalezienie momentu bezwładności I płytki względem
osi przechodzącej przez D

 

Wybieramy w otoczeniu dowolnego punktu na płytce element
masy dm. Przy oznaczeniach, jak na rysunku, moment
bezwładności I

0

względem osi przechodzącej przez C wyniesie

 
Po pomnożeniu obu stron równania przez dm i po scałkowaniu po
całej powierzchni płytki otrzymujemy

czyli

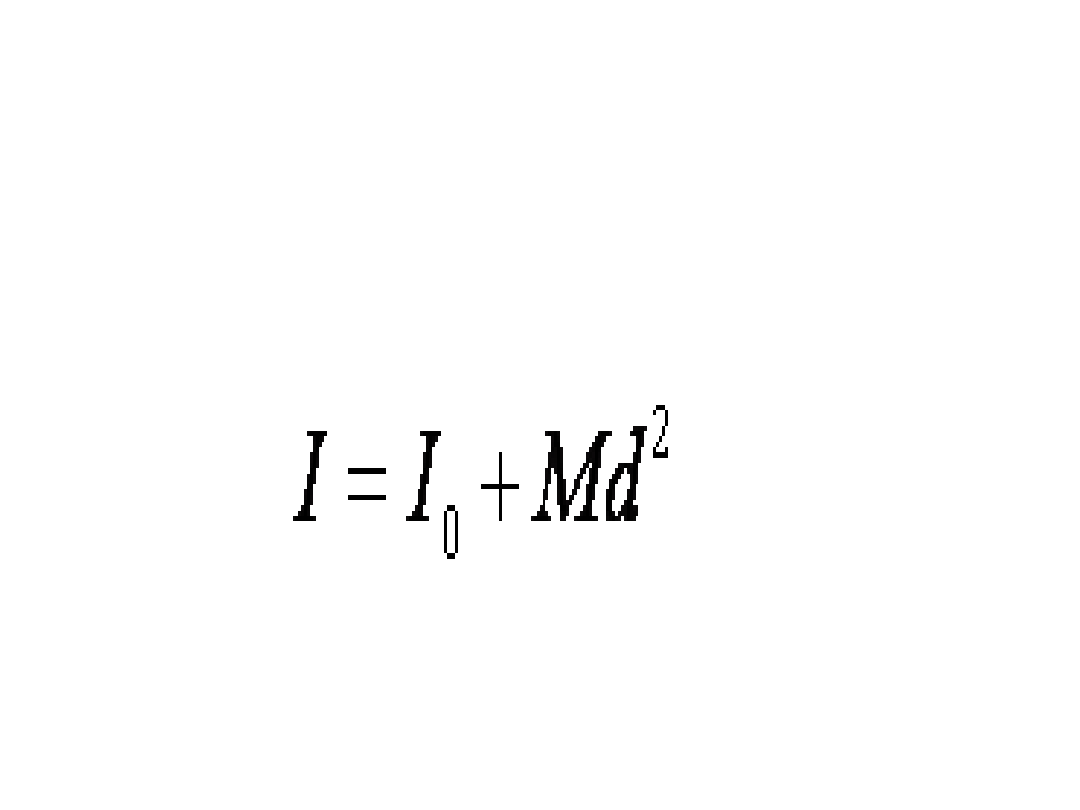
Należy zauważyć, że odległość y jest mierzona od środka
masy, a całka  jest tożsama z całką, jaka występuje we
wzorze na współrzędną środka masy. Jej wartość musi
wynosić zero, ponieważ określa ona odległość środka masy od
tego samego środka masy. Inaczej mówiąc, ponieważ
odległość y jest mierzona od środka masy C to każdy iloczyn
(y dm) jest równoważony przez iloczyn ( –y dm) o przeciwnym
znaku. Zatem, z powodu zerowania się całki , otrzymaliśmy
szukaną zależność