Metody analizy w demografii

Metoda w nauce to kanon postępowania w celu realizacji 

procesu poznawczego, czyli uzyskania wiedzy naukowej – 
zakłada istnienie w danej nauce uniwersalnych procedur 
badania naukowego.

Jego cechą jest systematyczność i stabilność badania 

naukowego.

Podstawowym instrumentem analizy demograficznej jest 

zbiór technik statystycznych.

Analiza demograficzna to sposób statystycznego opisu i 

wnioskowania o zjawiskach ludnościowych na gruncie 
demografii.

Typowa procedura w demografii to opis statystyczny

Procedura badania

1. Cel badania → pytania badawcze i hipotezy
2. Wybór miernika badanego zjawiska
3. Obserwację tego zjawiska i pomiar
4. Identyfikacja cech strukturalnych zjawiska
5. Porównania między różnymi zbiorowościami

Poziom zjawiska przedstawia się w ujęciu absolutnym jak i 

względnym

Ujecie względne uzyskuje się za pomocą miar natężenia 

zwanych współczynnikami

Definicja przedmiotu analizy demograficznej

- stan w danym punkcie czasu lub w okresie
- dynamika, czyli zmiany w czasie

Analiza przestrzenna, dynamiki i czasowo-przestrzenna

Parametry opisowe i konstrukcje teoretyczne

Parametry opisowe – wskaźniki i współczynniki

Konstrukcje teoretyczne – modele i np. tablice 

wymieralności

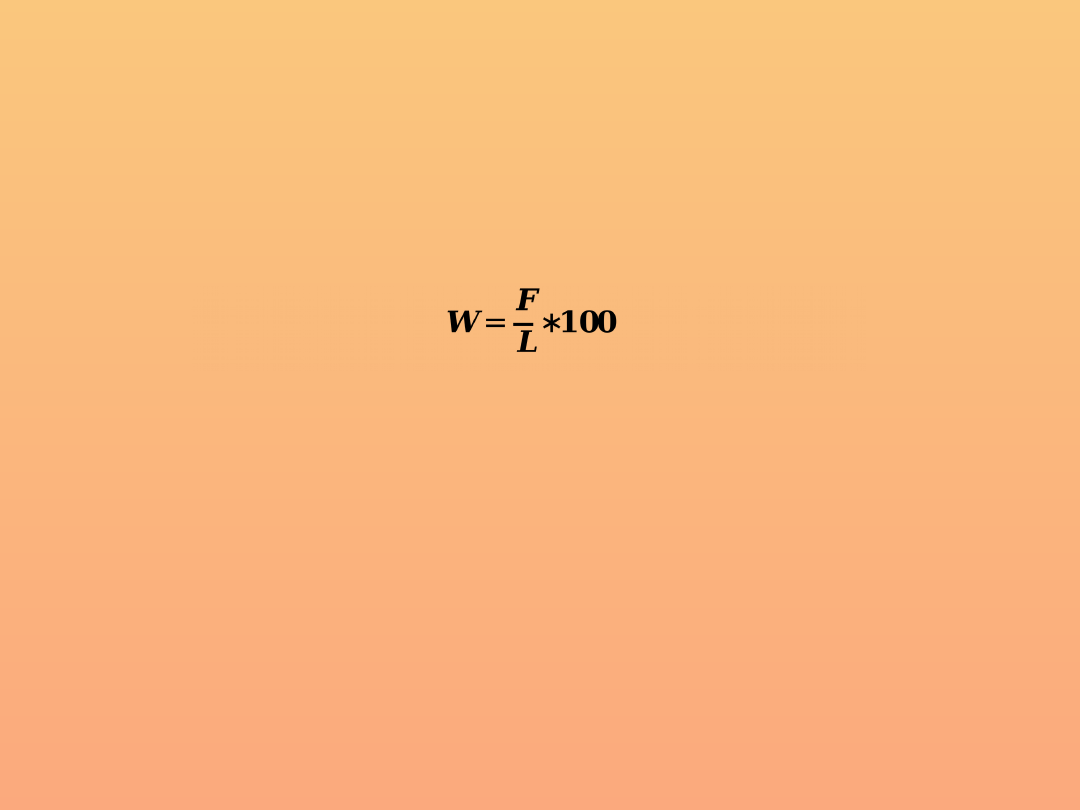
Zasady 

budowy 

podstawowych 

współczynników 

demograficznych

Współczynnik  demograficzny  to  miernik  natężenia  – 

stosunek  liczby  interesujących  nas  faktów  (F)  do  liczby 
określającej  wielkość  badanej  zbiorowości  statystycznej 
(L)

Współczynniki surowe i standaryzowane

Średni stan ludności z roku lub stan ludności ze środka roku

Wyznaczenie  wielkości  współczynnika  w  stosunku  rocznym 

na podstawie informacji z okresów będących częścią roku

Współczynniki demograficzne ogólne i cząstkowe

Współczynniki ogólny – np. współczynnik rodności, czyli 

stosunek liczby urodzeń do liczby ludności w badanym 
okresie

Współczynniki cząstkowy – ze względu na płeć czy wiek

Inny przykład – współczynnik płodności, czyli liczba urodzeń 

w stosunku do liczby kobiet w wieku rozrodczym (15 – 49 
lat)

Cząstkowe współczynniki płodności – ze względu na wiek 

(okresy pięcioletnie)

Wyznaczając współczynniki cząstkowe  należy pamiętać, że 

kryteria grupowania powinny być zasadne

Współczynniki wyodrębnione ze względu na stopień 

„narażenia” na ryzyko doznania określonego zdarzenia: 
pierwszej i drugiej kategorii

Współczynnik  drugiej  kategorii  to  stosunek  zdarzeń 

demograficznych  do  populacji  zasobów  demograficznych 
biorących  i  nie  biorących  udziału  w  generowaniu  tych 
zdarzeń.

Przykład:  liczba  urodzeń  w  danym  roku  w  odniesieniu  do 

liczby ludności ogółem lub liczby kobiet.

Współczynnik  pierwszej  kategorii  to  stosunek  zdarzeń 

demograficznych  do  populacji  zasobów  demograficznych 
biorących udział w generowaniu tych zdarzeń.

Przykład:  liczba  urodzeń  w  danym  roku  podzielona  przez 

liczbę kobiet w wieku reprodukcyjnym w tym roku.

Współczynniki 

zgonów 

obliczane 

są 

wyłącznie 

jako 

współczynniki 

pierwszej 

kategorii. 

W 

mianowniku 

występują tylko osoby żyjące (wszyscy są „wystawieni” na 
ryzyko śmierci).

Dlaczego korzystamy ze współczynników?

• Stanowią  syntetyczne  mierniki  podstawowych 

procesów demograficznej

• Umożliwiają ocenę rzeczywistej skali zjawiska (w 

odniesieniu do zasobów demograficznych)

• Umożliwiają porównania w czasie i przestrzeni

• W  niektórych  przypadkach  ich  dekompozycja 

niesie  informacje  na  temat  mechanizmów  zmian 
wartości współczynników

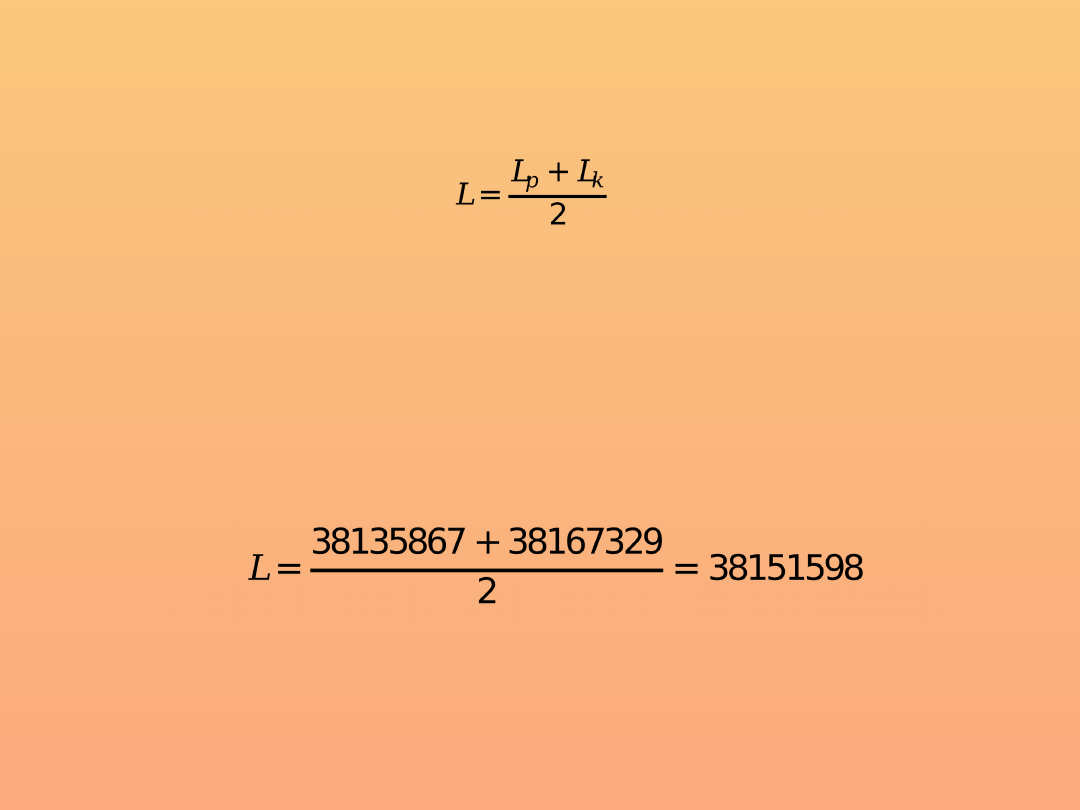
Średni stan ludności – średnia arytmetyczna stanu liczebnego 

ludności z początku i końca badanego okresu

Przykład:

Na 31.12.2008 r. liczba ludności w Polsce wyniosła 

38.135.876 osób, a na 31.12.2009 r. 38.167.329. W 
związku z tym średnia liczba ludności w 2009 r. wyniosła:

Standaryzacja współczynników demograficznych

Porównania zjawiska w czasie lub przestrzeni

Problem 

– 

na 

poziom 

ogólnych 

współczynników 

demograficznych  wpływa  struktura  ludności  wg  wieku 
oraz  natężenie  badanych  procesów  w  poszczególnych 
grupach wieku

Trzy sytuacje:

1. Różne  struktury  ludności  wg  wieku  i  różne  poziomy 

zjawisk w poszczególnych grupach wieku

2. Takie same struktury ludności wg wieku i różne natężenie 

zjawiska w poszczególnych klasach wieku

3. Różne  struktury  ludności  wg  wieku  i  takie  samo 

natężenie zjawiska w poszczególnych grupach wieku

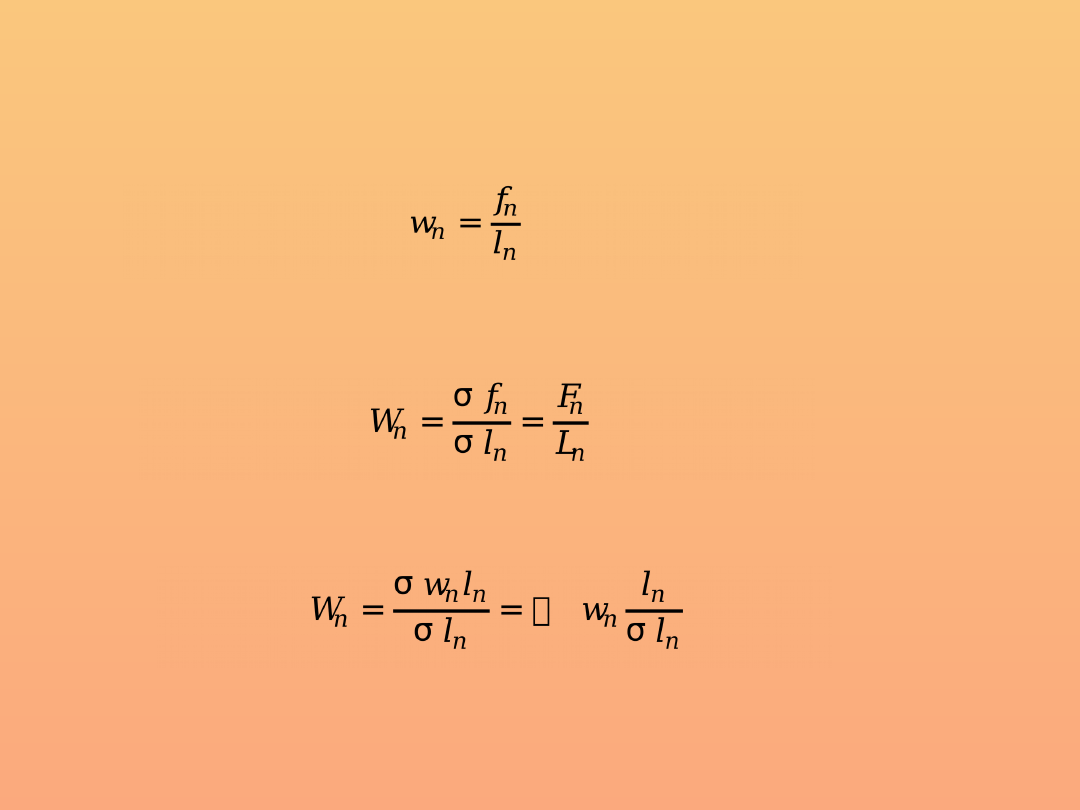
Rozwiązanie to standaryzacja współczynników 

demograficznych

Oznaczenia

w

n

 – współczynnik cząstkowy (dla okresu n lub obszaru n)

W

n

 – współczynnik ogólny (dla okresu n lub obszaru n)

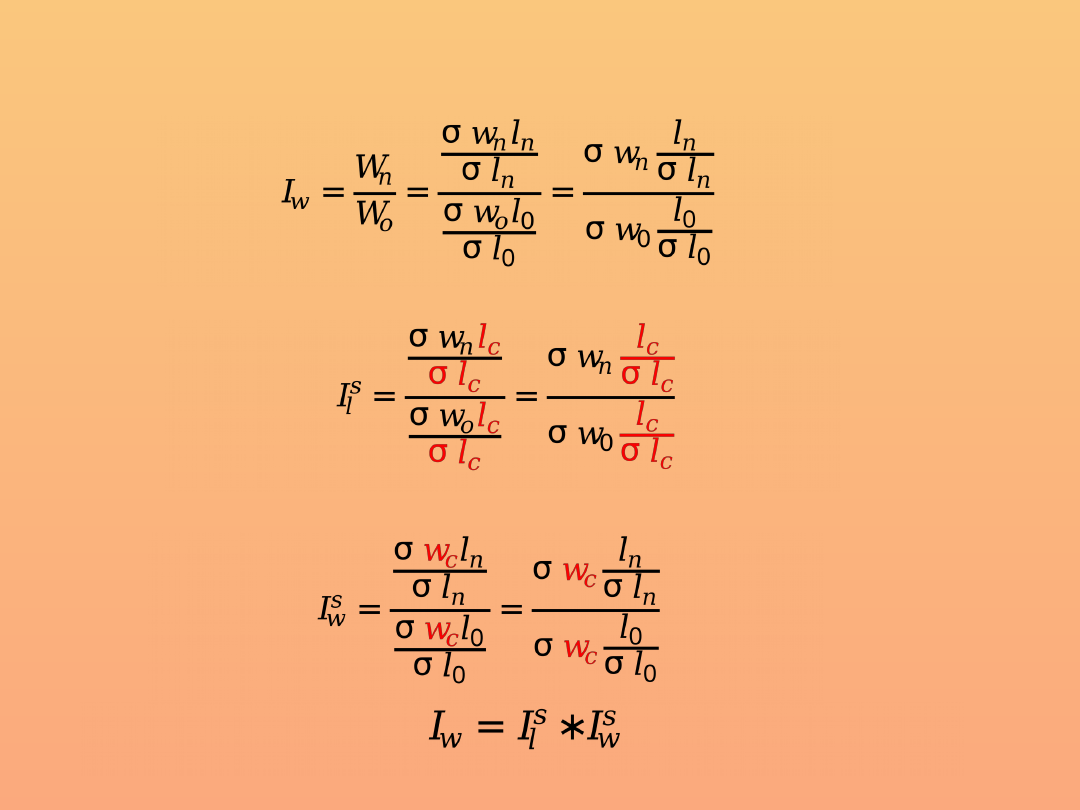
Dynamika ogólnego współczynnika

 Standaryzacja – ustalenie struktury ludności

Standaryzacja – ustalenie poziomu natężenie zjawiska

Przykład
Dynamika płodności w latach 1931/32 (okres 0) i 1955/56 

(okres n)

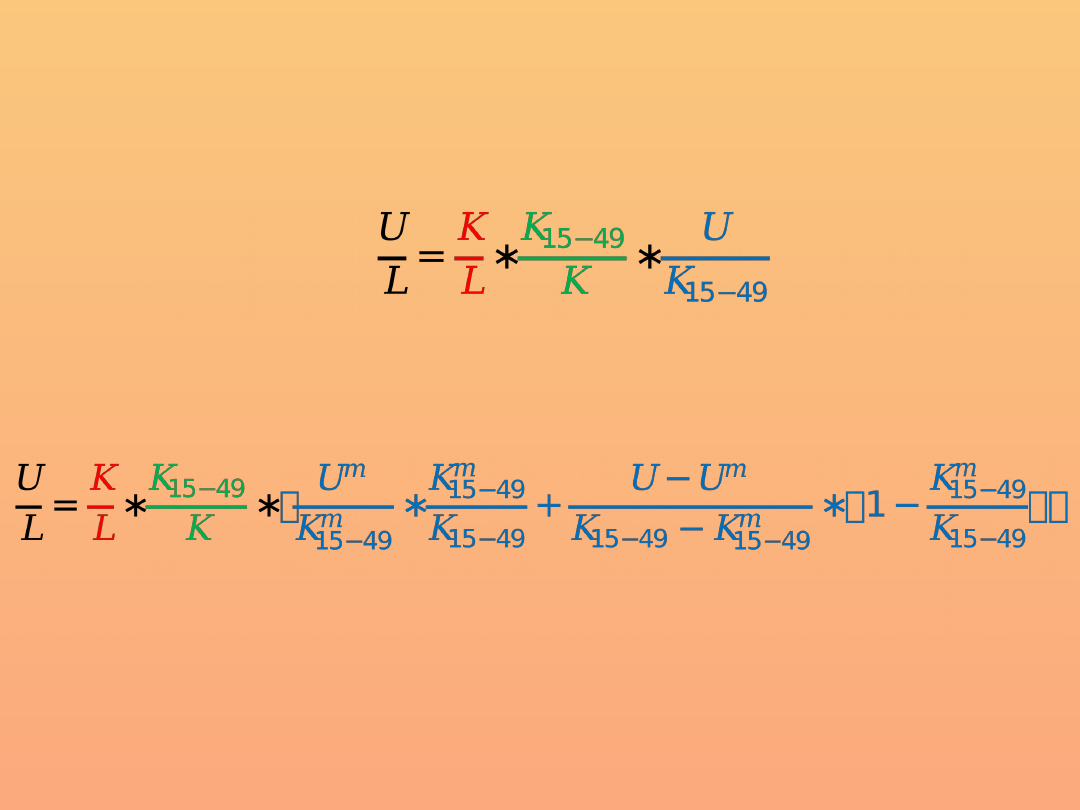
Inna forma standaryzacji współczynników

Współczynnik urodzeń można zapisać następująco:

lub następująco:

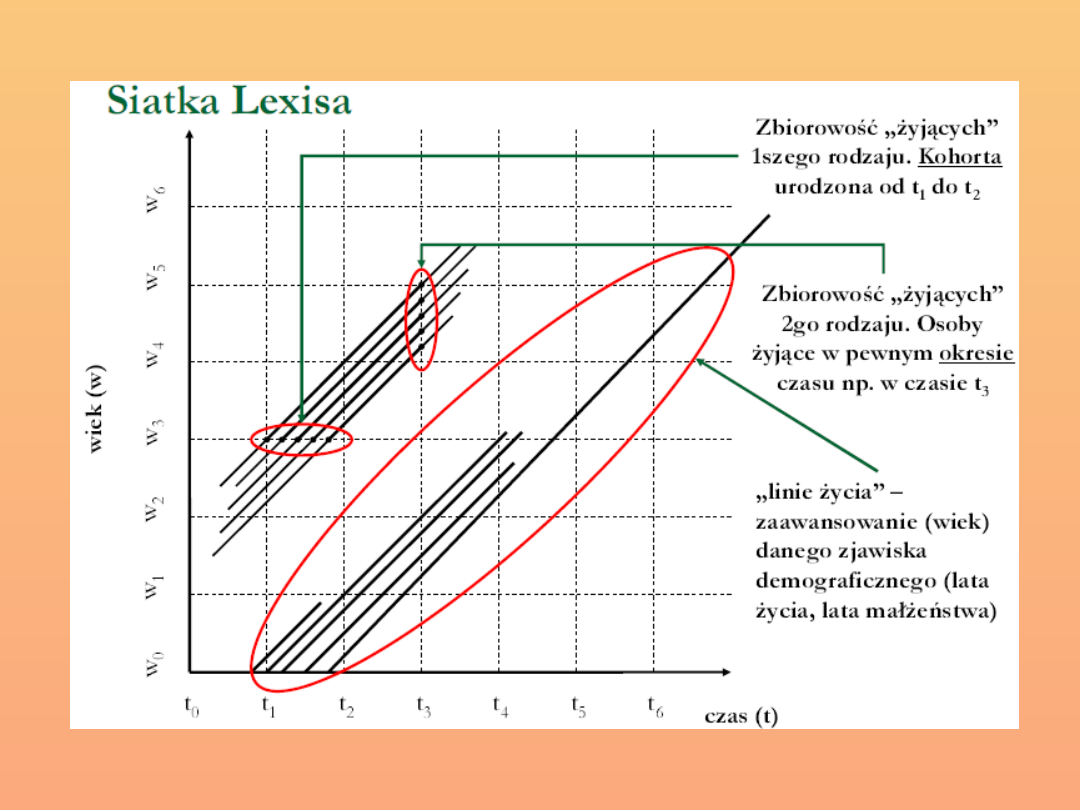
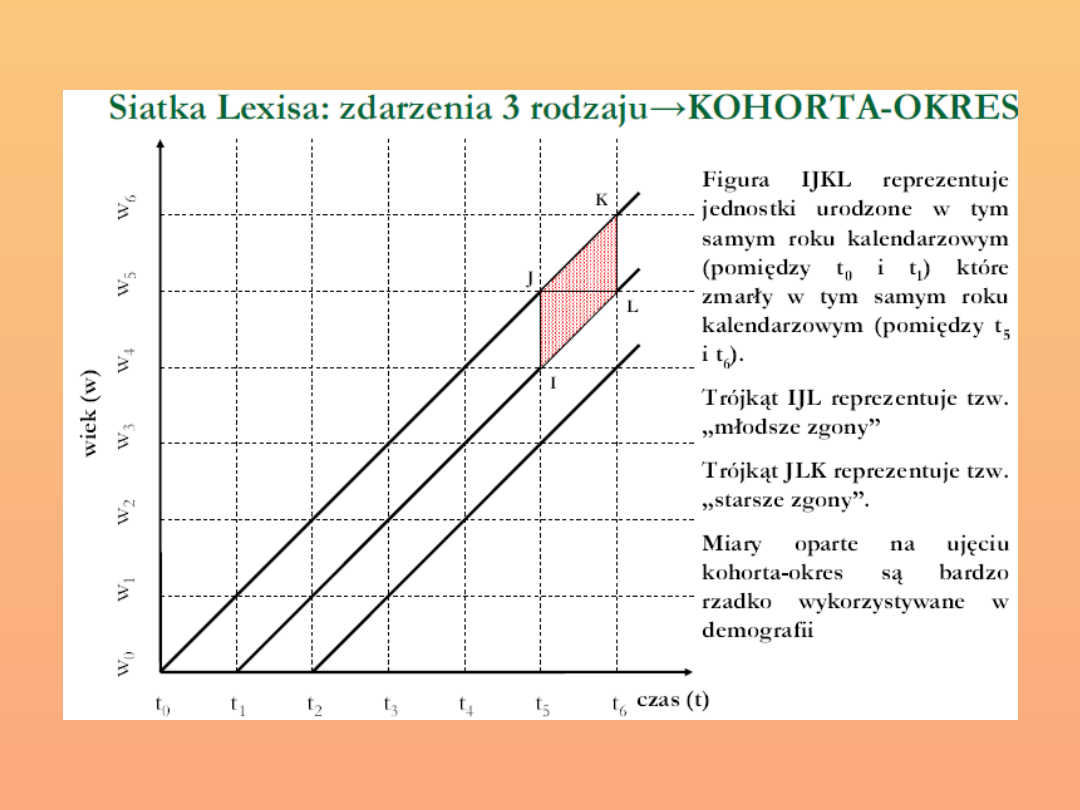
Siatka 

demograficzna 

(siatka 

Lexisa) 

– 

służy 

do 

jednoczesnego wyznaczania daty urodzenia, daty zgonu i 
wieku poszczególnych osób

Jest ona ważnym narzędziem analizy kohortowej (wzdłużnej) 

polegającej na śledzeniu zmian zachodzących w czasie w 
wybranych  zbiorowościach  ludzi  (ze  względu  na  rok 
urodzenia 

lub 

wiek) 

oraz 

analizy 

przekrojowej 

(poprzecznej), gdzie grupuje się ludzi według okresów, lat 
kalendarzowych.

Oś X – to oś czasu;  Oś Y to oś wieku

Linie poziome to linie wieku;  Linie pionowe to linie 

obserwacji

Linie skośne (przekątne powstałych kwadratów) to linie życia 

–  obrazują  długość  życia  poszczególnych  jednostek 
badanej zbiorowości od momentu urodzenia do momentu 
zgonu 

Zbiorowości zasobów:

Zasoby  I  rodzaju  –  osoby,  które  dożyły  wieku  x  ukończonych 

lat  –  kohorty  (osoby  urodzone  w  określonym  okresie  np. 
roku)

Zasoby II rodzaju – osoby żyjące w pewnym momencie czasu 

– grupy osób według roku kalendarzowego

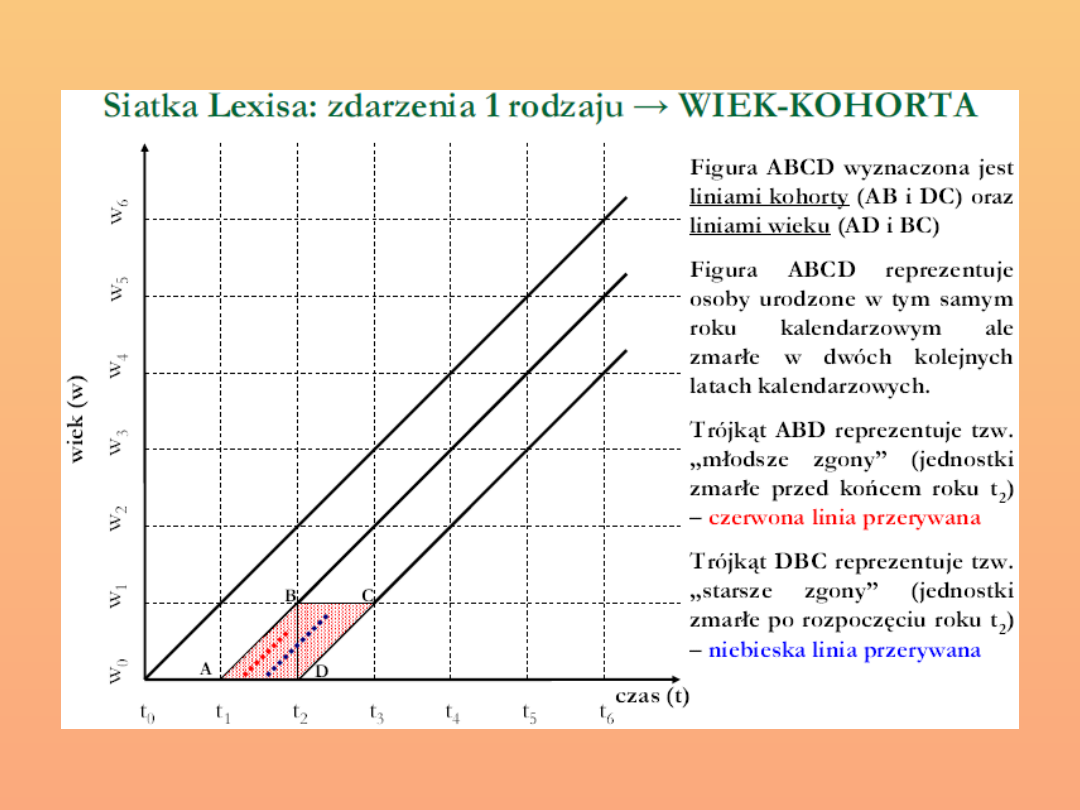
Zbiorowość zdarzeń:

Zdarzenia,  które  zaszły  dla  kohorty  urodzonej  w  danym  roku 

kalendarzowym  (np.  proporcja  kobiet,  które  urodziły 
dziecko)

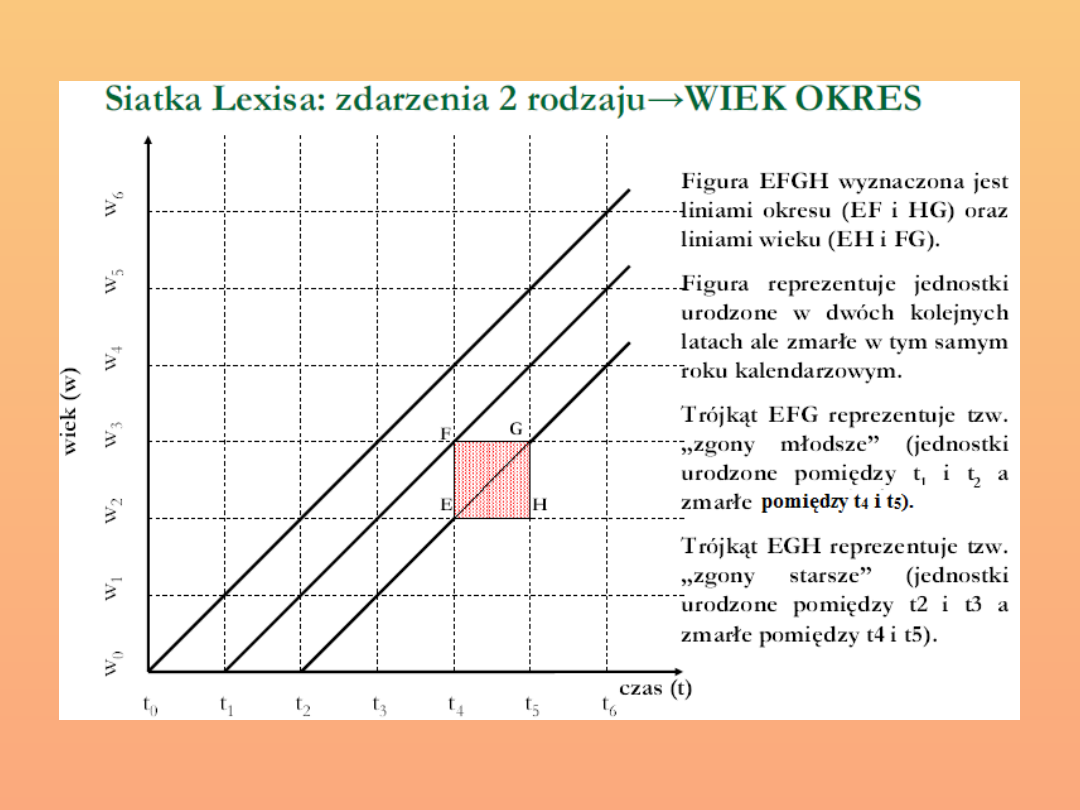
Zdarzenia,  które  zaistniały  w  określonym  okresie,  np.  roku 

kalendarzowym  (dla  wszystkich  żyjących  w  danym  roku 
kalendarzowym  i  wystawionych  na  ryzyko  zaistnienia 
zdarzenia).

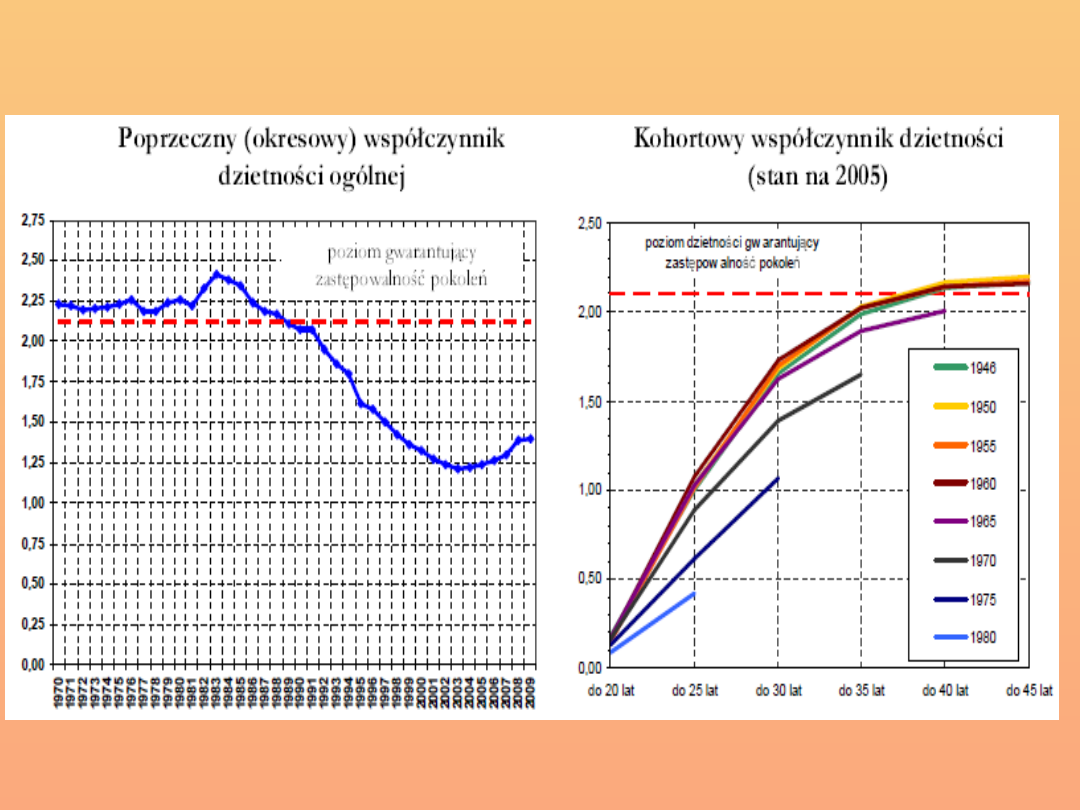
Współczynniki okresowe:
• Powszechnie stosowane
• Łatwe do obliczenia na podstawie danych z 

roczników

• Informują 

syntetycznie 

o 

zjawiskach 

demograficznych  w  danym  roku  kalendarzowym 
i latach wcześniejszych

• Miary hipotetyczne

Współczynniki kohortowe:
• Trudniejsze do obliczenia niż miary okresowe
• Opisują 

faktyczne 

zachowania 

kohort 

urodzonych w kolejnych latach kalendarzowych

• Trudniej  uzyskać  informacje  o  bieżących 

wydarzeniach