Przetworniki / czujniki

pomiarowe

PRZETWORNIKI ELEKTRYCZNE

 

Tor przetwarzania (łańcuch pomiarowy) - ciąg elementów
funkcjonalnych przekazujących informacje, znajdujących się między
obiektem a urządzeniem odbiorczym (wskaźnikiem, sterownikiem).

 

W zależności od charakteru zmian sygnałów pomiarowych rozróżnia
się przetwarzanie: 1)  wielkości - zmianie ulega wielkość
zawierająca informację:

- ze

zmianą rodzaju energii (np. z mechanicznej na elektryczną)

- bez zmiany rodzaju energii (np. zmiana napięcia na prąd

elektr.)

2) wartości (skali) - zmianie ulega wartość cechy

tego samego sygnału (np.

zmiana amplitudy, szerokości

impulsu, itp.)

3) informacji - zmianie ulega cecha

sygnału (np. z analogowego na dyskretny)

x

y

X

Y

Symbol graficzny przetwornika pomiarowego

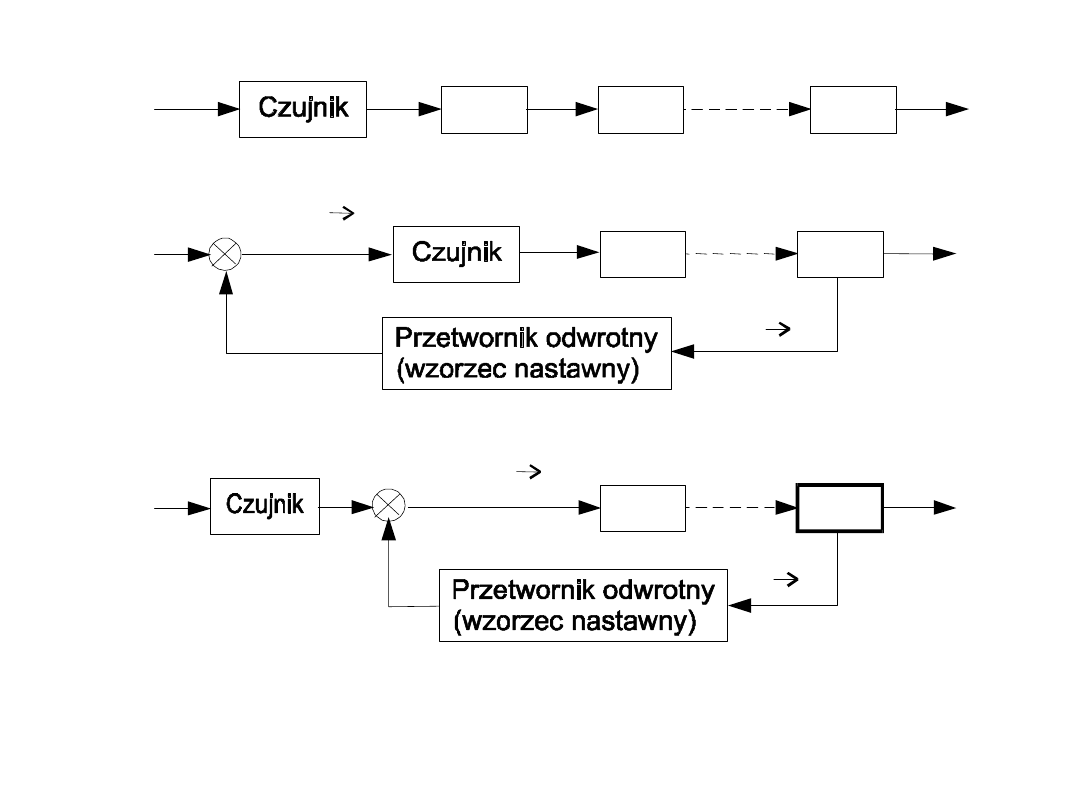
Schematy strukturalne torów przetwarzania: a.) w układzie
otwartym, b.) w układzie zamkniętym typu kompensacyjnego, c.) w
układzie zamkniętym typu komparacyjnego.

x`

x

P

1

P

n

x`-

0

x`

wz

x`

wz

y

0

y`

P

1

P

2

P

n

x

x

1

x

2

x

n

y

a)

x

P

1

P

n

x -

0

x

wz

x

wz

y

0

y`

b)

c)

Czujniki pomiarowe

Podział czujników:

 

a)   w zależności od źródła energii
-         generacyjne (termoelektr., fotoel., elktrodyn., elektrochem., itp.)
-         parametryczne (zmiana param. RLC)

 

b)  w zależności od charakteru sygnału wyjściowego
-         analogowe (zwykle proporcjonalne)
-         cyfrowe (w tym kodowe, dwustanowe t.j. termostaty, wył. krańcowe,

itp.)

c) w zależności od mierzonego

d) w zależności od wykorzystywa-

parametru

wanego zjawiska

-         temperatury

- indukcyjnościowe

-         ciśnienia

- pojemnościowe

-         przemieszczeń

- rezystancyjne

-         prędkości (obrotowej)

- termo(foto)elektryczne

-         natężenia pola

- piezoelektryczne

-         promieniowania

- optyczne

-         przepływu

- ultradźwiękowe

-         stężenia roztworów (pH)

- elektrochemiczne

-         itp.

-   itp.

e) wg innych kryteriów jak np.: szczelności (IP), odporności środowiskowej

(np. do kwasu, bentonitu,...), warunków mechanicznych pracy
(drgania, wibracje, udary,...), kosztów (zakupu, eksploatacji,
serwisu,..), i in.

Czujnik pomiarowy –

zamienia mierzoną wartość wielkości fizycznej na

łatwy do

obróbki i przesyłu sygnał elektryczny

Parametry statyczne czujnika:

Zakres pomiarowy – określony przez

gdy

to zakres =

W zakresie pomiarowym czujnik powinien utrzymać parametry (błędy)
deklarowane
przez producenta. W zakresie stosowania czujnik powinien działać bez
trwałego
uszkodzenia (ale może mieć zwiększone błędy).

Czułość – nachylenie charakterystyki) w punkcie pracy

Dla przetwornika liniowego:

Stała pomiarowa –

dla charakterystyki liniowej

gdzie: stała przetwarzania

C = 1/S

min

max

X

X



0

min



X

max

X

dX

X

dF

dX

dY

S

)

(





X

S

Y





Y

C

Y

S

X









1

Selektywność

–

zdolność „rozróżniania” wielkości mierzonej od podobnych

do niej
wielkości wpływających (np. czujnik metanu jest również czuły na inne
gazy ale w
różnym stopniu).
Można zwiększyć selektywność przez zastosowanie matrycy
czujników
nieselektywnych o różnej czułości na różne wielkości mierzone (i
wpływające).

Liniowość (nieliniowość)

–

stosowane są różne opisy błędu od

nieliniowości
- błąd od nieliniowości musi być znany dla przeprowadzenia linearyzacji
- jeśli błąd od nielin. jest niewielki to traktuje się go często jako błąd
przypadkowy
dla przypadkowej wartości mierzonej.

Powtarzalność

–

określa zakres, w którym mieszczą się charakterystyki

wszystkich
czujników tego samego typu (jeden czujnik można wzorcować lecz dla
wielu tego
samego typu występuje losowość charakterystyki wynikająca np. z
niepowtarzalności
warunków produkcji).

Histereza

–

wynika z różnic działania czujnika przy wzroście i spadku

wielkości
mierzonej (pochodzi od tarcia, luzów mechanicznych, histerezy
magnetycznej, inercji
termicznej, itp.)

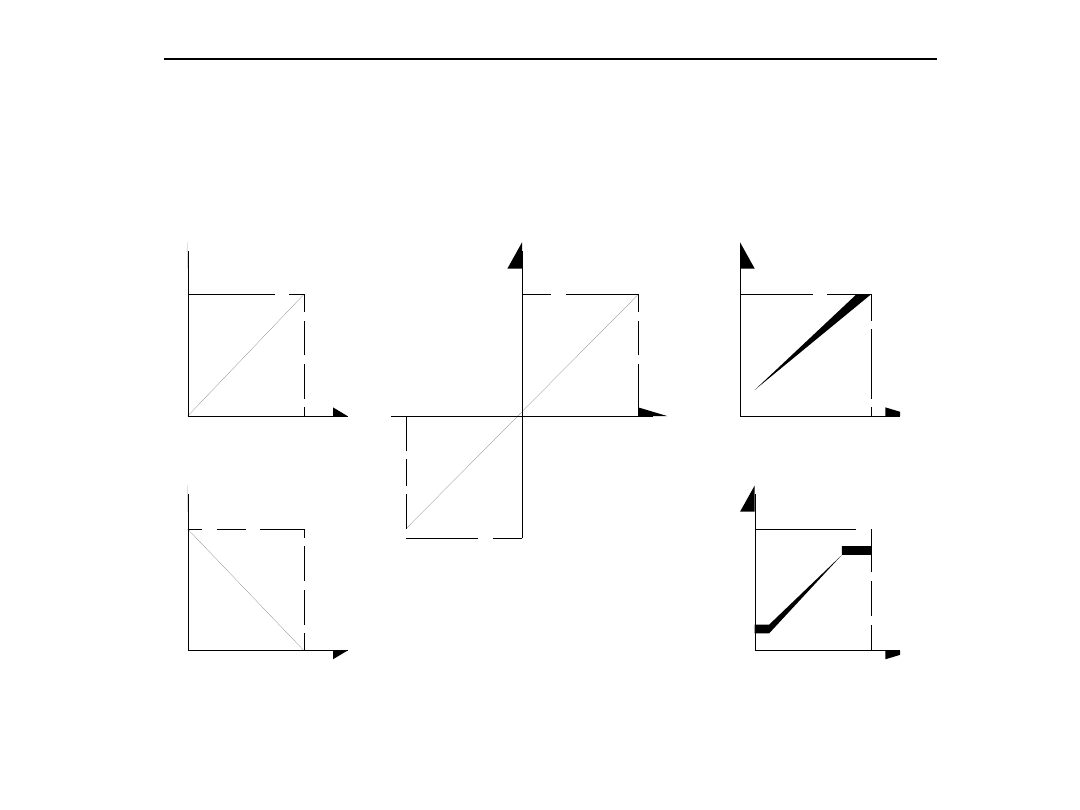
Charakterystyki statyczne przetworników

 

 

Charakterystyka statyczna:

 

 

gdzie: Y - wartość wielkości wyjściowej, X - wartość wielkości wejściowej

2 0

mA

0

Y

X

1 0 0 %

a )

Y

X

1 0 0 %

1 0 V

- 10 V

0 %

b )

2 0

mA

0

Y

X

1 0 0 %

4

c )

0

Y

X

1 0 0 %

1 0 V

d )

2 0

mA

Y

X

1 0 0 %

e )

Typowe charakterystyki przetworników pomiarowych: a.) liniowa

naturalna, b.) liniowa dwubiegunowa, c.) liniowa z przesunięciem, d.)

liniowa zanegowana, e.) liniowa z ograniczeniem sygnału wejściowego

i/lub wyjściowego

)

(X

F

Y 

Zunifikowane sygnały wyjściowe przetworników przemysłowych:

-  prądowe : 0...5mA ; 4...20mA ; 0...20mA ; -5...5mA ;

-20...20mA

-  napięciowe : 0...5V ; 0...10V ; -5...5V ; -10...10V.
- wyjścia 2-stanowe (prądowe lub napięciowe) w w/w

standardach

- wyjścia 2-stanowe przekaźnikowe

 

 

Moc wejściowa możliwie mała  dla wejść prądowych

impedancja Z

wej

mała;

 dla wejść napięciowych impedancja Z

wej

duża.

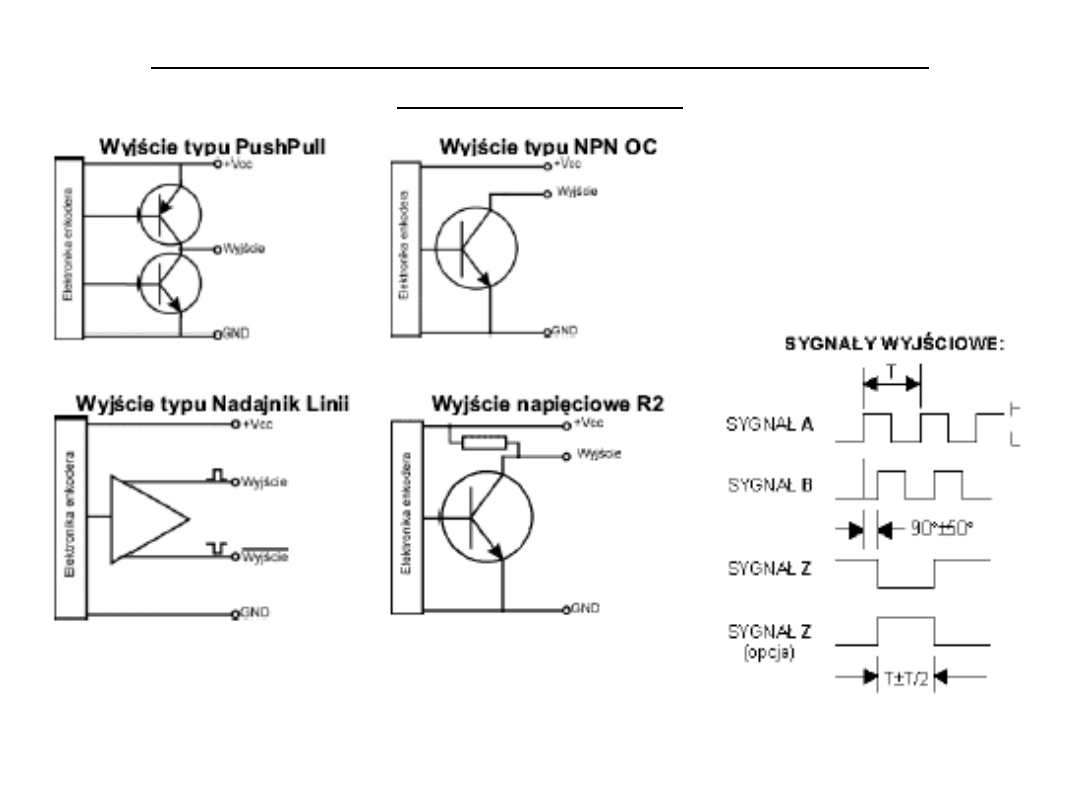
Rodzaje wyjść 2-stanowych pzetworników

przemysłowych

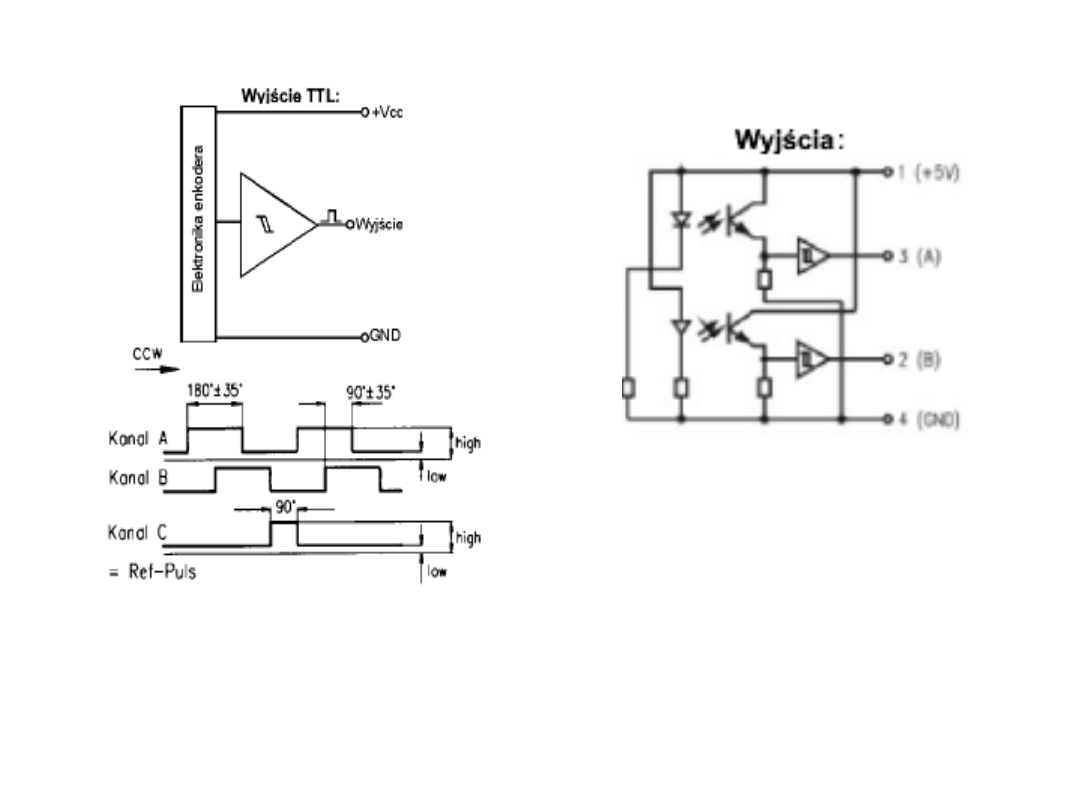
Własności statyczne przetworników

Błąd przetwarzania podawany jako:

- klasa przetwarzania (największa wartość dopuszczalnego

błędu bezwzględnego
odniesiona do zakresu sygnału wejściowego)

- dwie składowe błędu (jedna odniesiona do aktualnej

wartości wielkości
mierzonej, druga do zakresu sygnału wejściowego)

np

.

(0,1

w.m. + 0,05U

N

)

 

Składowe błędu przetwarzania:

- błędy addytywne (bł. zera)
- błędy multiplikatywne (bł. skali)
- błąd nieliniowości
- błąd dyskretyzacji (dla przetw. cyfrowych)
- błąd histerezy

 

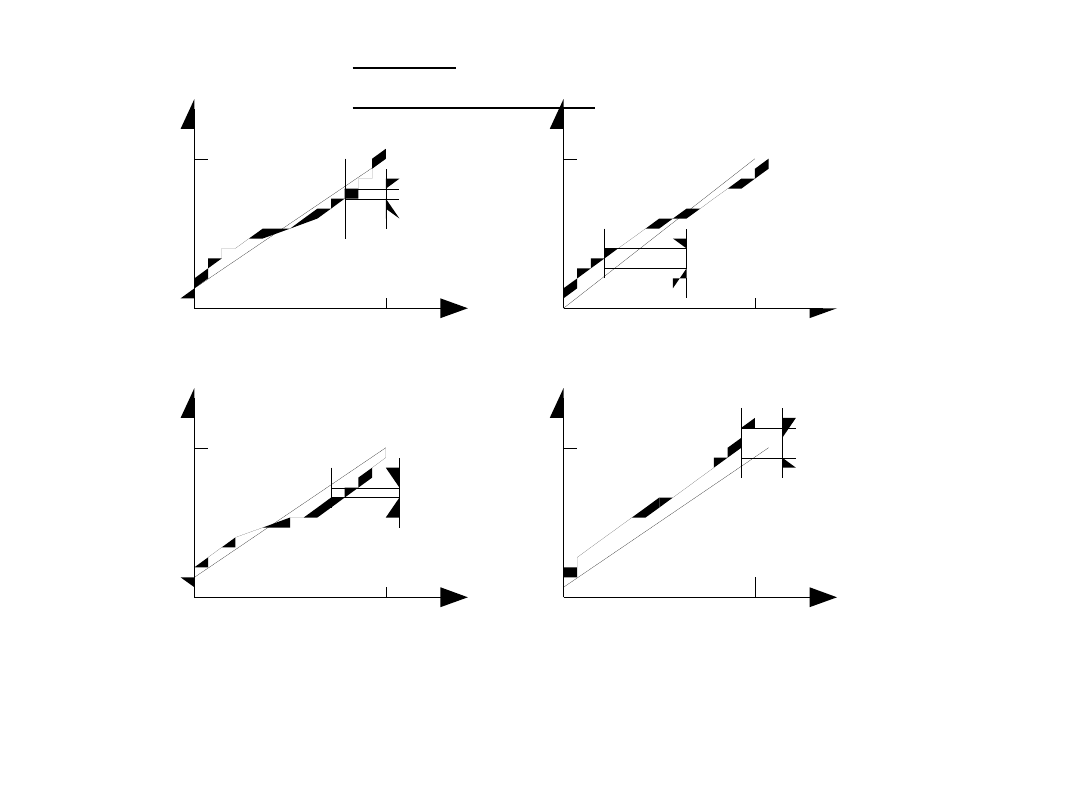
Błąd nieliniowości:

- (różnie opisywany)

0

Y

X

1 0 0 %

1 0 0 %

a )

0

Y

X

1 0 0 %

1 0 0 %

b )

0

Y

X

1 0 0 %

1 0 0 %

c )

0

Y

X

1 0 0 %

1 0 0 %

d )

 lma x

 lma x

 lma x

 lma x

Błędy
nieliniowości

Cztery metody opisu nieliniowości charakterystyki. a.) prosta
najmniejszych kwadratów, b.) prosta najmniejszych kwadratów
przechodząca przez zero, c.) prosta przechodząca przez punkty
końcowe, d.) charakterystyka teoretyczna

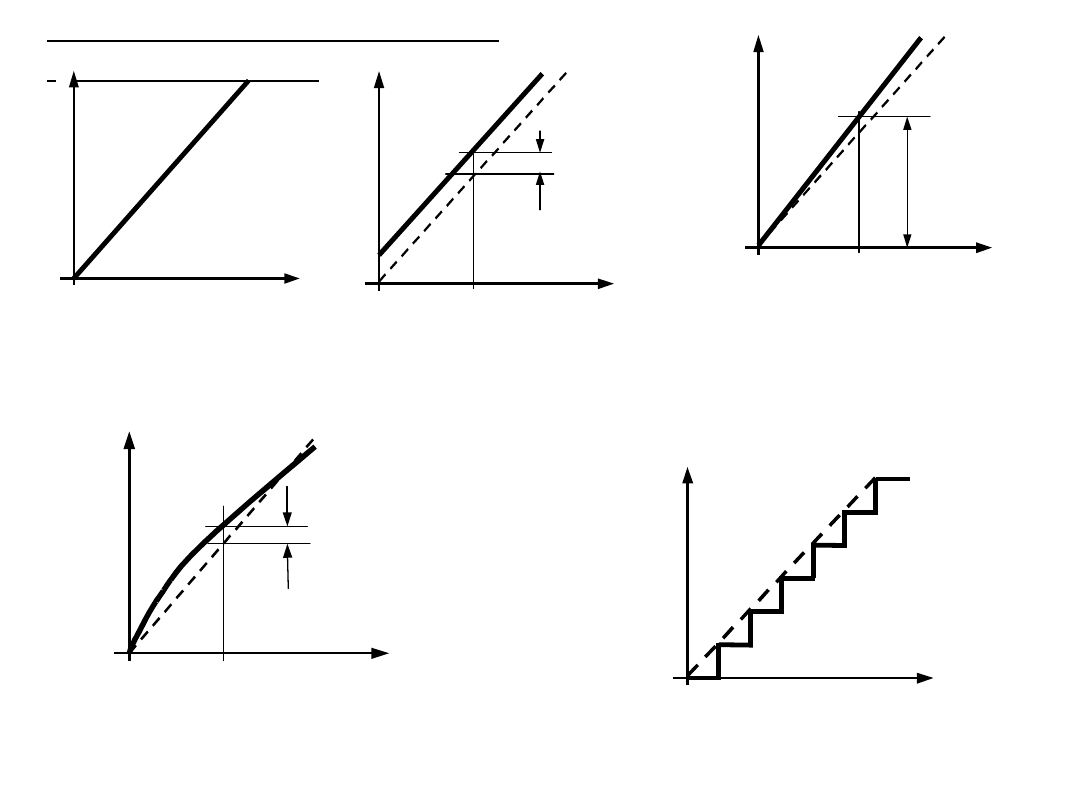
Charakterystyczne błędy
przetworników

n

Y

X

n – charakterystyka

nominalna

Y=SX

X

1

a

n+a

n

Y

X

a - błąd addytywny

(błąd zera)

n+a - ch. z uwzględnieniem

błędu addytywnego

Y=SX+a

X

1

SX

1

(1+

m

)

n+m

n

Y

X



m

- błąd multiplikatywny

(błąd skali)

n+m

- ch. z uwzględnieniem

błędu multiplikatywnego

Y=SX(1+

m

)

X

1



lmax

n+l

n

Y

X



l

- błąd nieliniowości

n+l - ch. z uwzględnieniem

błędu nieliniowości

Y=SX

l

X

n

n+d

n

Y

X



d

- błąd dyskretyzacji

n+d - ch. z uwzględnieniem

błędu dyskretyzacji

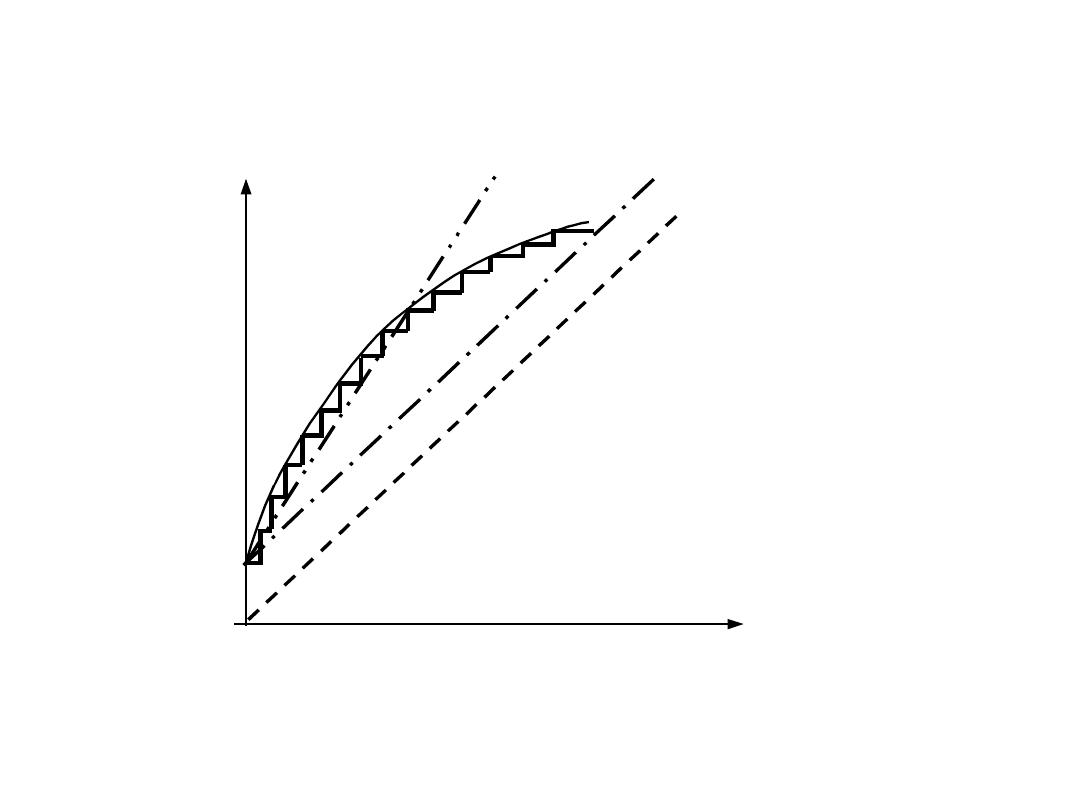
Całkowity błąd przetwarzania i jego

składowe

2

4

Y

X

1 – n charakterystyka

nominalna

2 – n+a

3 – n+a+m

4 – n+a+m+l

5 – n+a+m+l+d

3

5

1

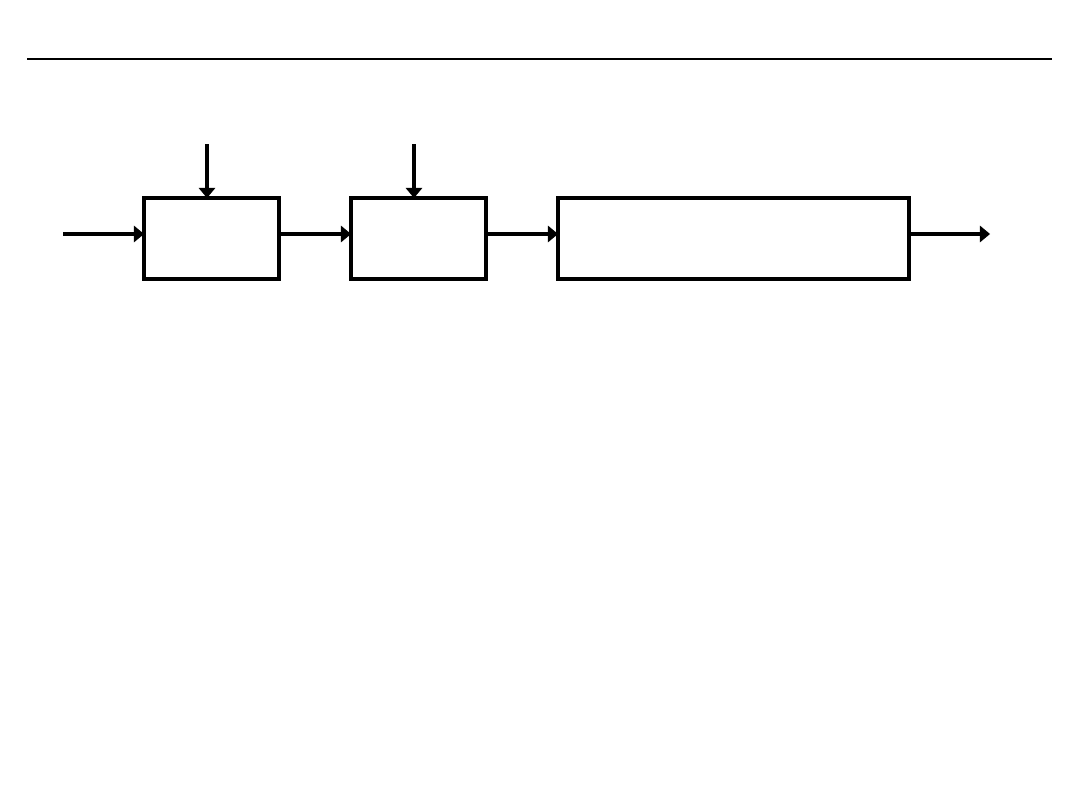
Wpływ czynników zewnętrznych na błędy przetwarzania

Metoda

pomiar

u

Narzędzie
pomiarow

e

Odtwarzanie wartości

mierzonej

(wg modelu, algorytmu, ...)

X

V

Y

Z

Statyczna charakterystykę przetwarzania z uwzględnieniem zewnętrznych
wartości wpływających (temperatura, wartość napięcia zasilania, itp.):

 

gdzie : D

V

, D

Z

– różnice wartości

V

i

Z

od wartości odniesienia (temp.

otoczenia, napięcie zasil., itp.)

...)

,

,

....

,

,

,

(

3

2

1

3

2

1

Z

Z

Z

V

V

V

X

F

Y















 

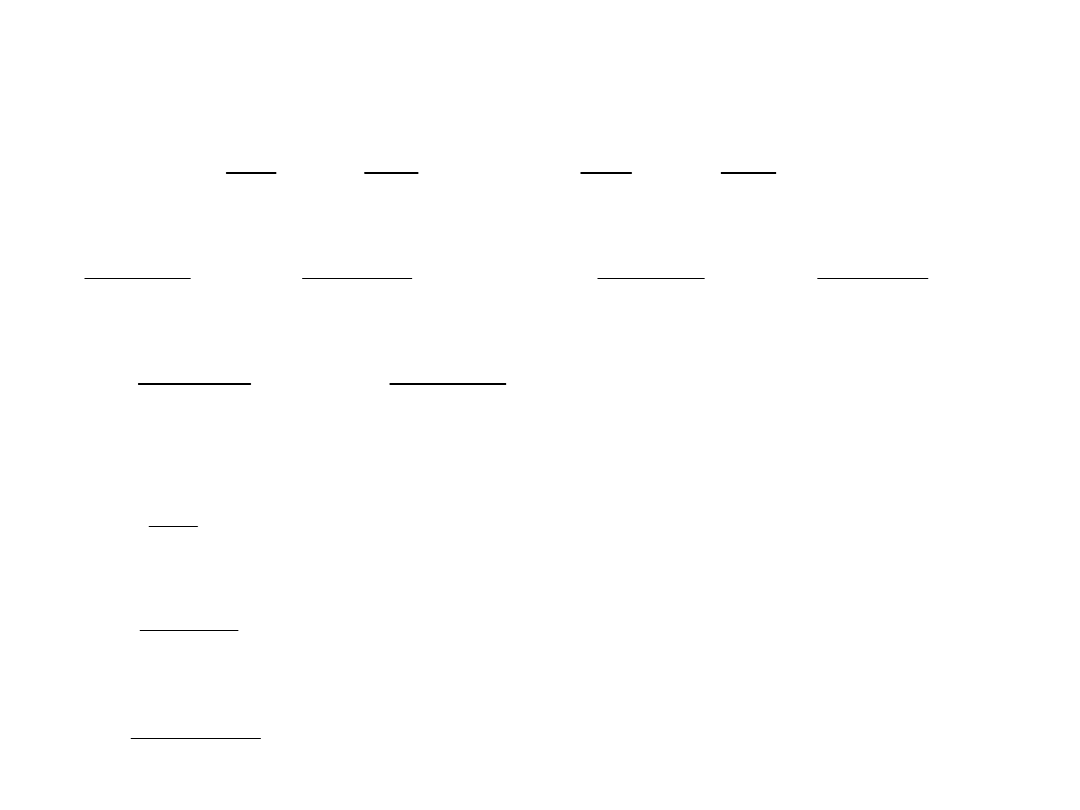
Rozwijając funkcję
w szereg Taylora:

 

 

gdzie :

- wrażliwość na D

V

n

,

zaś

- błąd

addytywny

, zaś

- błąd multiplikatywny

- interakcja

.....

2

2

......

2

2

.....

2

2

....

.....

)

(

1

2

1

2

2

1

1

1

1

2

2

2

2

1

1

2

2

2

2

1

1

2

2

2

1

1

2

2

1

1

























































Z

V

Z

V

F

Z

V

Z

V

F

Z

X

Z

X

F

Z

X

Z

X

F

V

X

V

X

F

V

X

V

X

F

Z

Z

F

Z

Z

F

V

V

F

V

V

F

X

F

Y





















































n

n

W

V

F







...)

,

,

....

,

,

,

(

3

2

1

3

2

1

Z

Z

Z

V

V

V

X

F

Y















n

n

k

V

X

F









2

2

n

n

V

W 



n

n

V

X

k







m

n

m

n

Z

V

Z

V

F

















2

2

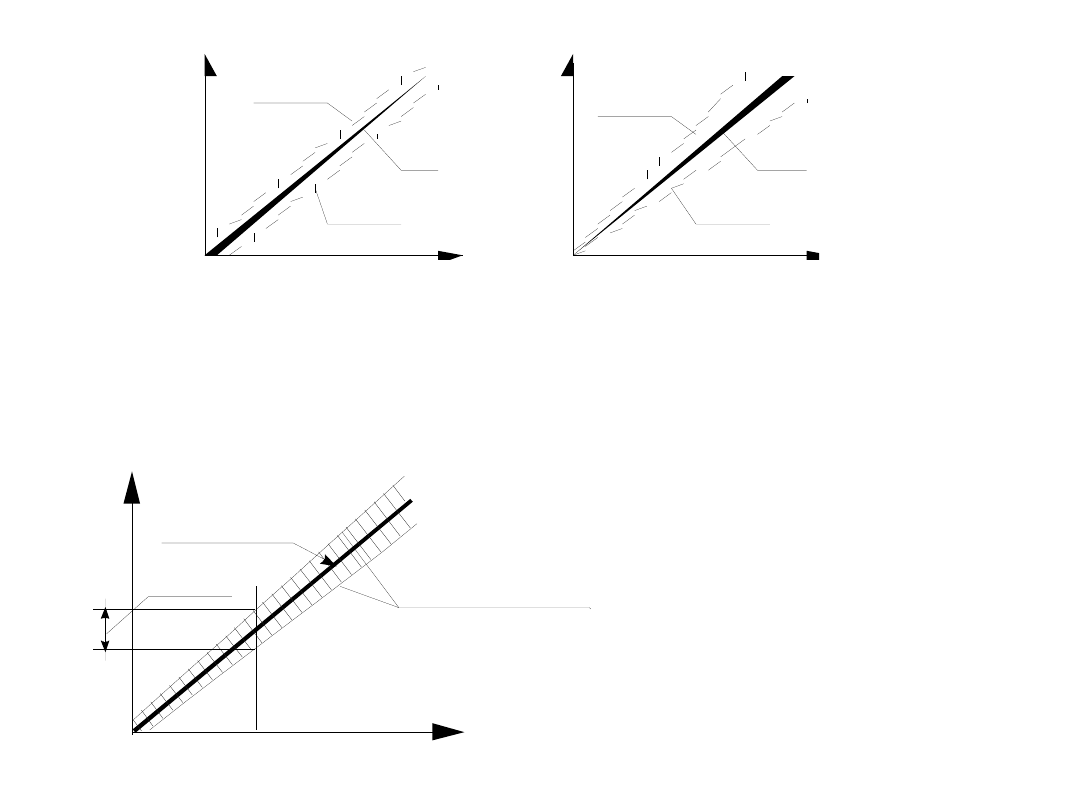
Y

X

a )

Y

X

b )

n







n







n



n



n







n







Przykładowy wpływ temperatury otoczenia na charakterystykę

przetwornika.

a.) przesunięcie zera, b.) zmiana czułości

(np. przez wpływ temperatury

na rezystancję R

w obwodzie a.) kompensacji „0”, b.) wzmocnienia, wzmacniacza

operacyjnego)

Nieokreśloność przetwarzania (powtarzalność
charakterystyki):

0

Y

X

x

1

c h a r a k te r y s ty k a

n o m in a ln a

g r a n ic a o b s z a r u

n ie o k r e lo n o c i

ś

ś

y

y

1





Nieokreśloność przetwarzania dla
danego stanu na wejściu

Eliminacja błędów spowodowanych wielkościami

wpływającymi

1. Zastosowanie lepszych (droższych): metod, materiałów,
podzespołów, ....
(zmniejszenie wrażliwości na wielkości wpływające)
2. Eliminacja błędów przez:

- separację
- kompensację
- korekcję
- autokalibrację
- linearyzację

Separacja

– niedopuszczenie do oddziaływania wielkości wpływających

na

wrażliwe części układu poprzez:

- ekranowanie kabli
- ekwipotencjalizację
- ekranowanie el-magn.
- termostatyzację
- tłumienie drgań i wibracji
- itp.

Kompensacja

(strukturalna eliminacja błędów)

–

wykorzystuje właściwości celowo zrealizowanych struktur torów
pomiarowych,
w których występuje znoszenie się błędów w poszczególnych
elementach
struktury

(Nie ma jednolitej recepty na możliwość skutecznego zastosowania
kompensacji błędów. Wpływa na to wiele czynników – również koszty)

Założenia upraszczające
Omawiane dalej metody kompensacji błędów rozpatrywane są dla
następujących
założeń upraszczających:

- charakterystyka statyczna jest liniowa
- występuje tylko jedna wielkość wpływająca

Z

- wielkość

Z

wywołuje tylko błędy addytywne i multiplikatywne

- elementem poddanym działaniu wielkości wpływającej

Z

jest

czujnik (sytuacja najczęściej występująca w praktyce).

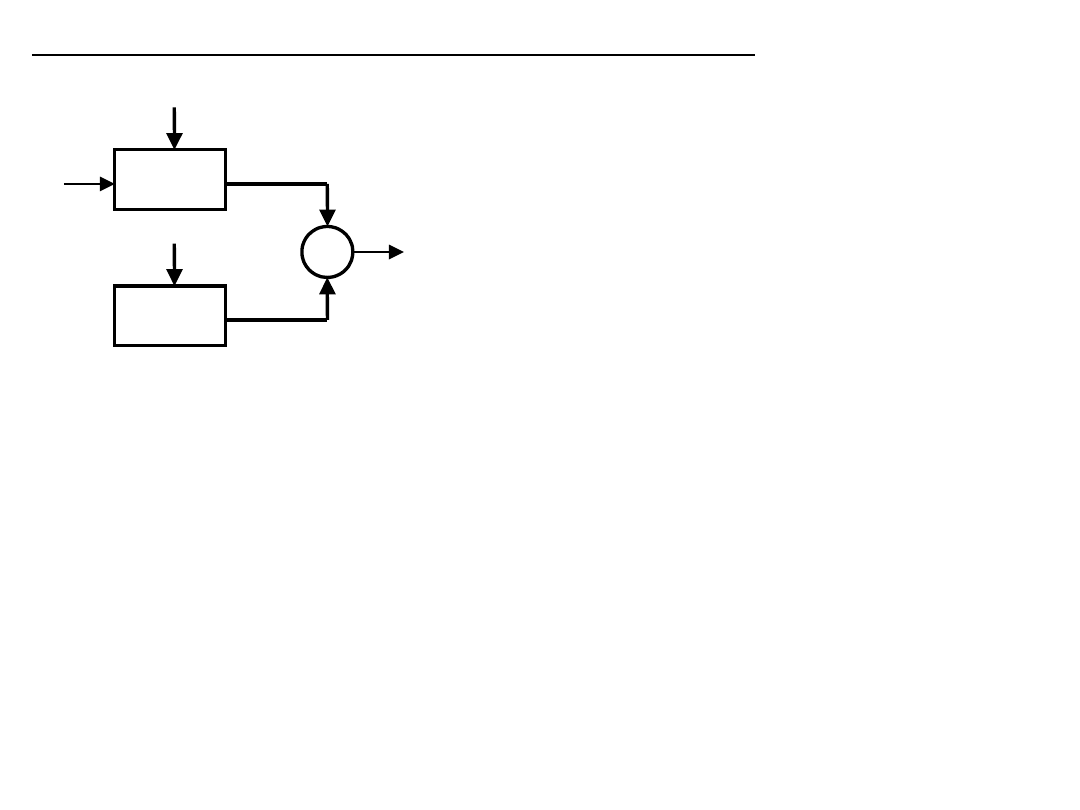
Kompensacja w strukturze równoległej

CZ

KOMP

.

X

Z

Z

Y

1

Y

2

Y

+

_

KOMP. – czujnik, na który nie
działa wielk. wejściowa

X

S

– czułość

W

1

– wrażliwość

k

1

– wsp. multiplikatywny

Dla

W

1

=W

2

eliminacja bł. addytywnych (brak eliminacji bł.

multiplikatywnych

Z

X

k

Z

W

SX

Y











1

1

1

)

0

(bo

2







X

Z

W

Y

K

Z

X

k

Z

W

W

SX

Y

K













1

1

1

)

(

czyli

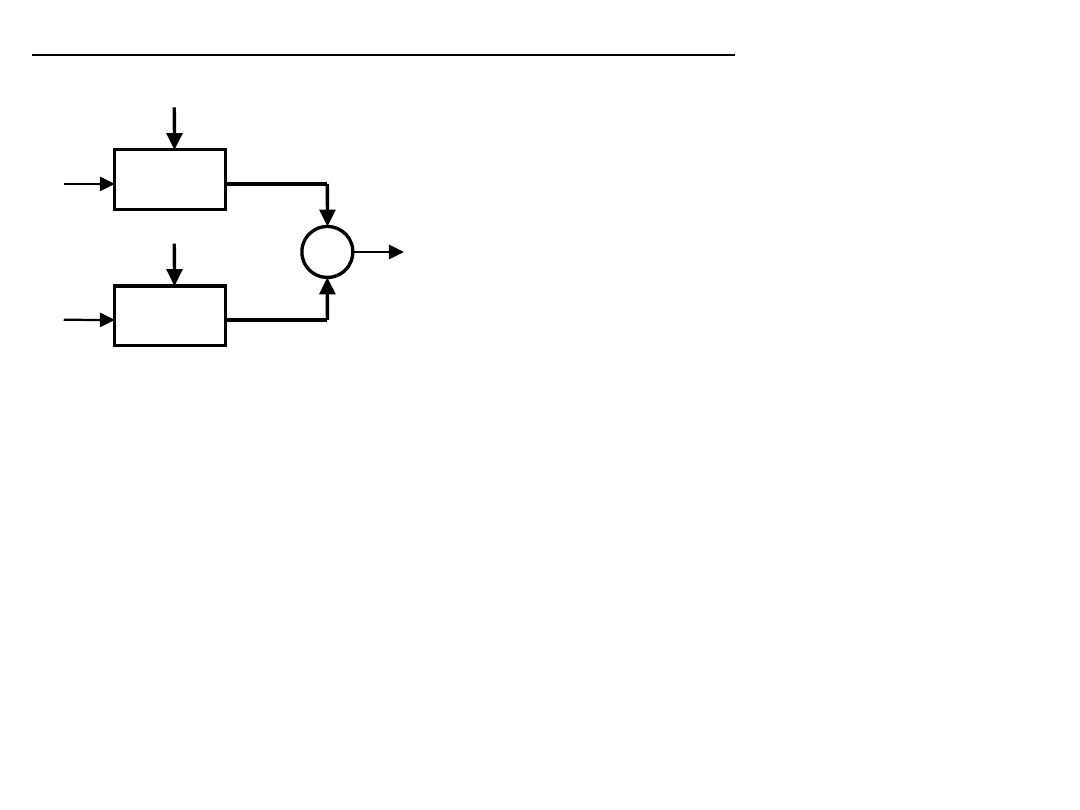
Kompensacja w strukturze różnicowej

- identyczne czujniki 1 i 2

- sygnały identyczne ale o przeciwnych
znakach

(czujniki przemieszczeń –

pojemnościowe
i transformatorowe, czujn. Naprężnooporowe
- nalepione na dwóch stronach belki zginanej,
…. )

– 2 razy większa czułość
– eliminacja bł. addytywnego
– 2 razy większy bł multiplikatywny

CZ 1

CZ 2

+

X

Z

Z

Y

1

Y

2

Y

+

_

-X

Z

kX

Z

W

SX

Y











1

Z

kX

SX

Y







2

2

czyli

Z

kX

Z

W

SX

Y













2

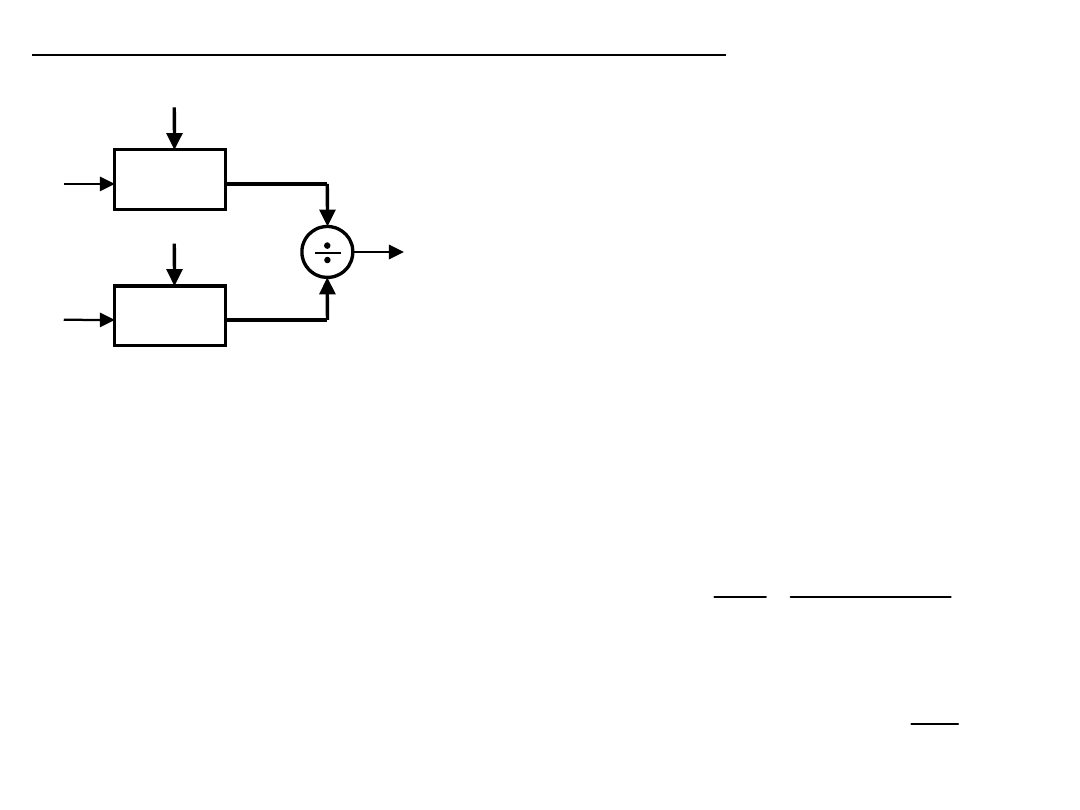
Kompensacja w strukturze ilorazowej

- identyczne czujniki 1 i 2
- X

0

- wielkość stała o tym samym

charakterze

co wielkość wej. X
- realizowane w technice cyfrowej lub
impulso-
wej (bo sygn. analogowe trudno się
dzieli)

CZ 1

CZ 2

X

Z

Z

Y

1

Y

2

Y=Y

1

/

Y

2

X

0

Strukturę można wykorzystać do eliminacji bł. multiplikatywnych dla
małych bł. addytywnych gdyż:

Dla identycznych czujników:

Z

X

k

Z

W

X

S

Y











1

1

1

1

)

(

2

2

1

1

0

2

1

dla

Z

k

S

Z

k

S

X

X

Y

W

W













Z

X

k

W

X

S

Z

X

k

Z

W

X

S

Y



















)

(

0

2

2

0

2

0

2

2

0

2

2

0

2

1

2

1

czyli

i

X

X

Y

k

k

S

S







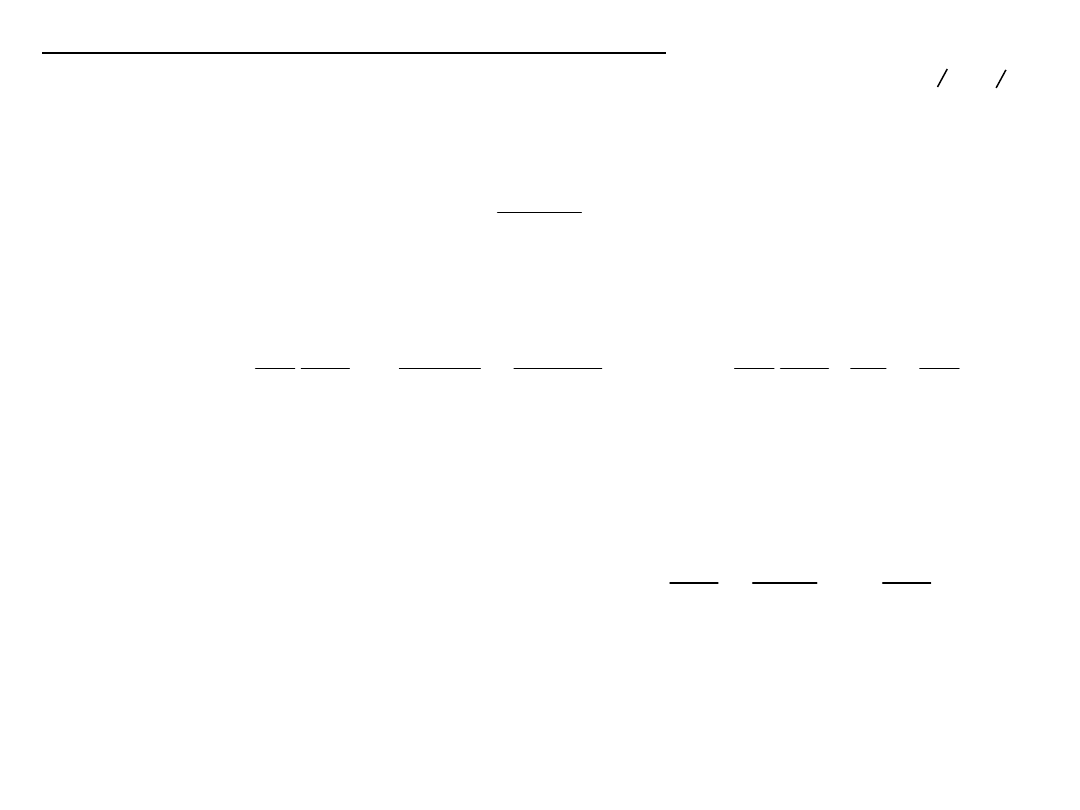
Kompensacja w strukturze ilorazowej c.d. – gdy występują składniki
addytywne

W

1

=

W

2

=

0

Gdy wrażliwości na D

Z

są małe w stosunku do czułości

to wówczas:

Dla identycznych czujników

S

1

=

S

2

=

S

oraz

W

1

=

W

2

=

W

Składowa addytywna nadal występuje i znika jedynie dla

X

=

X

0

Ta metoda nie eliminuje błędów addytywnych, ale bardzo redukuje ich
wartość.

2

2

2

0

2

oraz

S

Z

k

S

X

Z

W









Z

S

k

S

k

X

X

S

S

Z

X

X

S

W

S

X

S

W

X

X

S

S

Y















)

(

)

(

2

2

1

1

0

2

1

2

0

2

2

2

1

0

2

1

0

2

1

Z

X

X

SX

W

X

X

Y









)

(

0

0

0

1

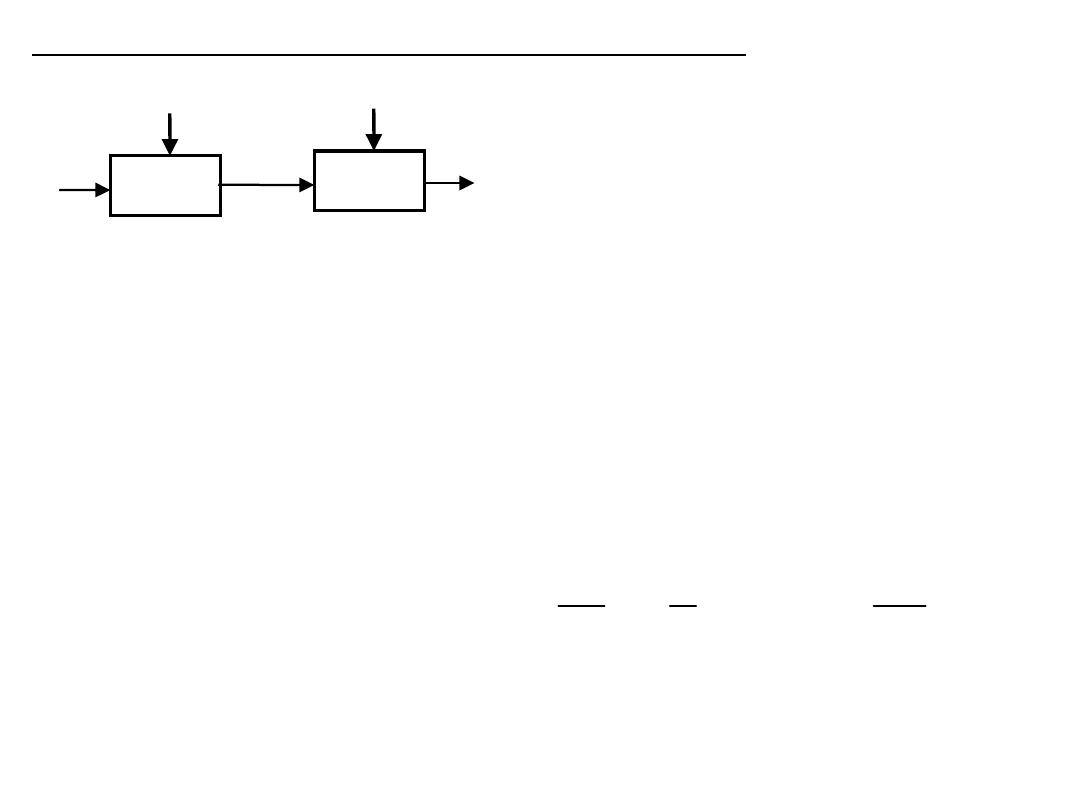
Kompensacja w strukturze szeregowej

- Rzadko wykorzystywana bo

wymaga

rozbudowy części analogowej
układu

- KOMP. nie jest czujnikiem

(realizuje

zupełnie inną funkcję)

kompensują się błędy addytywne i multiplikatywne (b.trudne do
spełnienia).

– met. wykorzystywana raczej rzadko do eliminacji bł.
multiplikatywnych
– trudna do realizacji z uwagi na inną budowę CZ i KOMP.

CZ

KOMP.

X

Z

Z

Y

Y

1

Jedynie przy równoczesnym spełnieniu:

Z

kX

Z

W

SX

Y











1

2

2

Z

kX

k

Z

W

k

Z

kX

S

Z

SX

k

Z

W

S

Z

W

SX

S

Y

K

K

K

K

K

K

K





























Z

Y

k

Z

W

Y

S

Y

K

K

K











1

1

W

S

W

k

S

k

S

K

K

K

K









oraz

Korekcja błędów

- realizowana jest w trzecim bloku układu (bloku odtwarzania wartości
mierzonej

Korekcję przeprowadza się na wartościach numerycznych

N

gdzie:

N

=

aY

Dla jednej wielkości wpływającej

Z

:

Korekcja ma być przeprowadzona wg charakterystyki odwrotnej:

Aby przeprowadzić korekcję należy zmierzyć D

Z

odrębm układem.

Im mniejsze są wartości W

N

i

k

N

tym mniejsza jest wymagana dokładność

pomiaru D

Z

dająca wymagane efekty korekcji.

Korekcję algorytmiczną przeprowadza się:

- metodą tablic przeglądowych
- metodą obliczeniową

Z

X

k

Z

W

X

S

N

N

N

N











)

(

1

Z

N

W

N

Z

k

S

X

N

N











W korekcji

metodą tablic przeglądowych

zapisuje się

uprzednio poprawki wyznaczone w czasie wzorcowania

Poprawka:

- procedura prosta przy występowaniu jedynie bł. addytywnych (mierzy

się

D

Z

,

odczytuje się z tablicy najbliższą wartość

D

Z

i

i wprowadza się poprawkę

z tablicy)
- przy występowaniu bł. multiplikatywnych tablica robi się

wielowarstwowa, zajmuje

więcej pamięci i jest trudna do wyznaczenia (wzorcowanie w b. wielu
punktach)

W korekcji

metodą obliczeniową

oblicza się on-line poprawkę

P

(wg w/w wzoru) i wprowadza się ją do wyniku.

- metoda trudna przy występowaniu wielu wielkości wpływowych z

powodu

komplikowania się zależności

(tablice też gwałtownie rosną)

- dla bardziej złożonych obliczeń stosuje się metody iteracyjne

(met.

kolejnych

przybliżeń)

)

Z

W

Z

k

S

S

Z

k

S

Z

k

N

XS

P

N

N

N

N

N

N

N

N

N























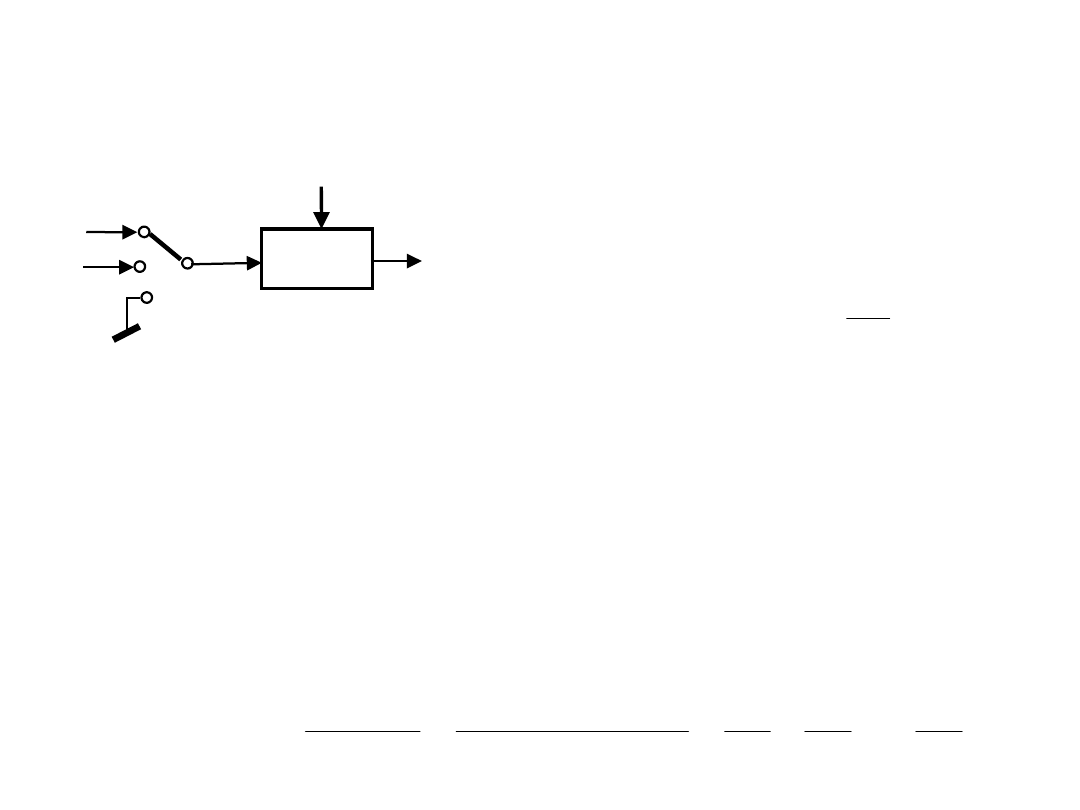
Autokalibracja

- podobnie jak korekcja realizowana jest na wartościach numerycznych

N

W jednostce obliczeniowej wyznacza się:

N

S

Z

1

2

3

X

X

0

- występują błędy addytywne i

multiplikatywne

- błędy są wolnozmienne

- pomiar odbywa się sekwencyjnie
- w pamięci zapisane jest

Wyniki etapowe:

I ostatecznie:

)

0

bo

(

3

3

0

0

2

1



























X

Z

W

N

Z

X

k

Z

W

X

S

N

Z

X

k

Z

W

X

S

N

N

N

N

N

N

N

N

Z

X

k

X

S

N

N

Z

X

k

X

S

N

N

N

N

N

N

















3

1

0

0

3

2

C

X

X

n



0

n

n

N

N

N

N

X

X

C

X

X

C

X

X

Z

X

k

X

S

Z

X

k

X

S

N

N

N

N

N





















0

0

0

0

3

2

3

1

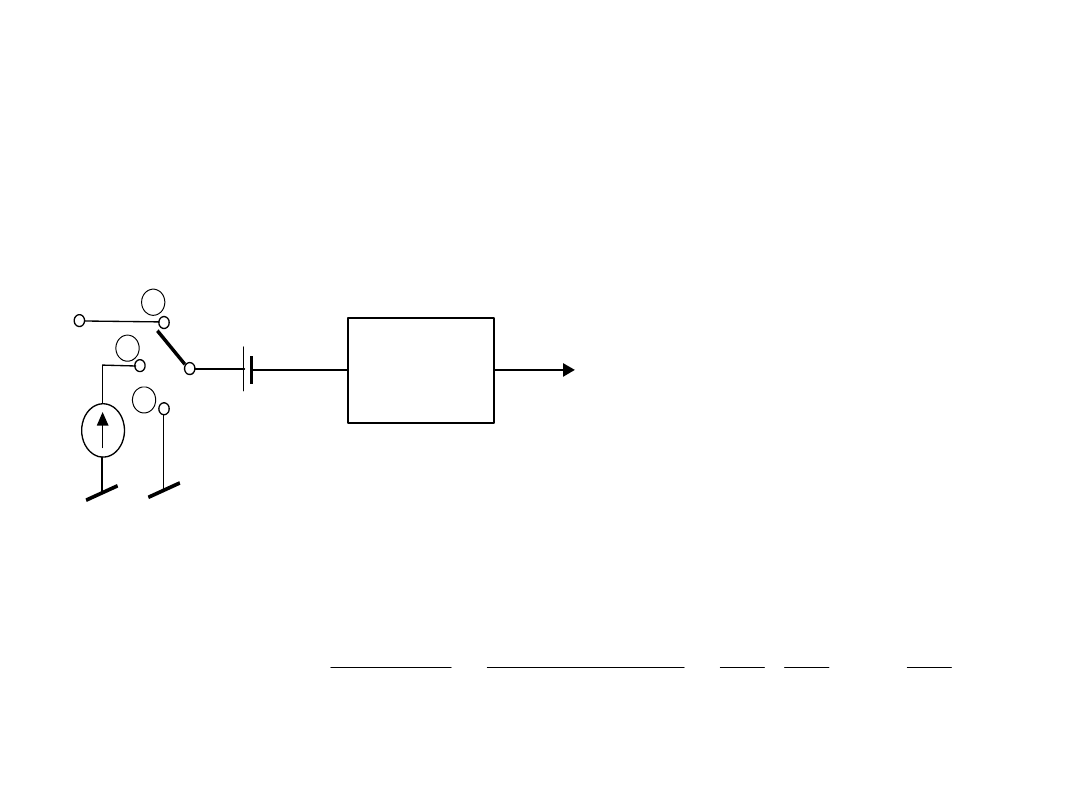
Redukcja błędów przetwarzania na drodze
autokalibracji cyfrowej

Założenia:

• błędy są wolnozmienne

• cały cykl pomiarowy odbywa się w czasie pomijalnym w

stosunku do czasu zmienności błędów

U

x

U

r

E

0

1

2

3

Tor pomiarowy

K

(1

+ )

Wyjście

(N)

Pomiar sekwencyjny:
1)
2)
3)

)

1

(

0

3











K

E

N

Wyznaczanie wyniku na drodze obliczeniowej (w
mikrokontrolerze)

Metoda nie usuwa błędów od nieliniowości (eliminuje bł. addytywne i
multiplikatywne)

)

1

(

)

(

0

1













K

E

U

N

x

)

1

(

)

(

0

2













K

E

U

N

r

)

1

(

3

2













K

U

N

N

r

)

1

(

3

1













K

U

N

N

x

n

x

n

x

r

n

r

x

U

U

C

U

U

U

U

K

U

K

U

N

N

N

N

N





























)

1

(

)

1

(

3

2

3

1





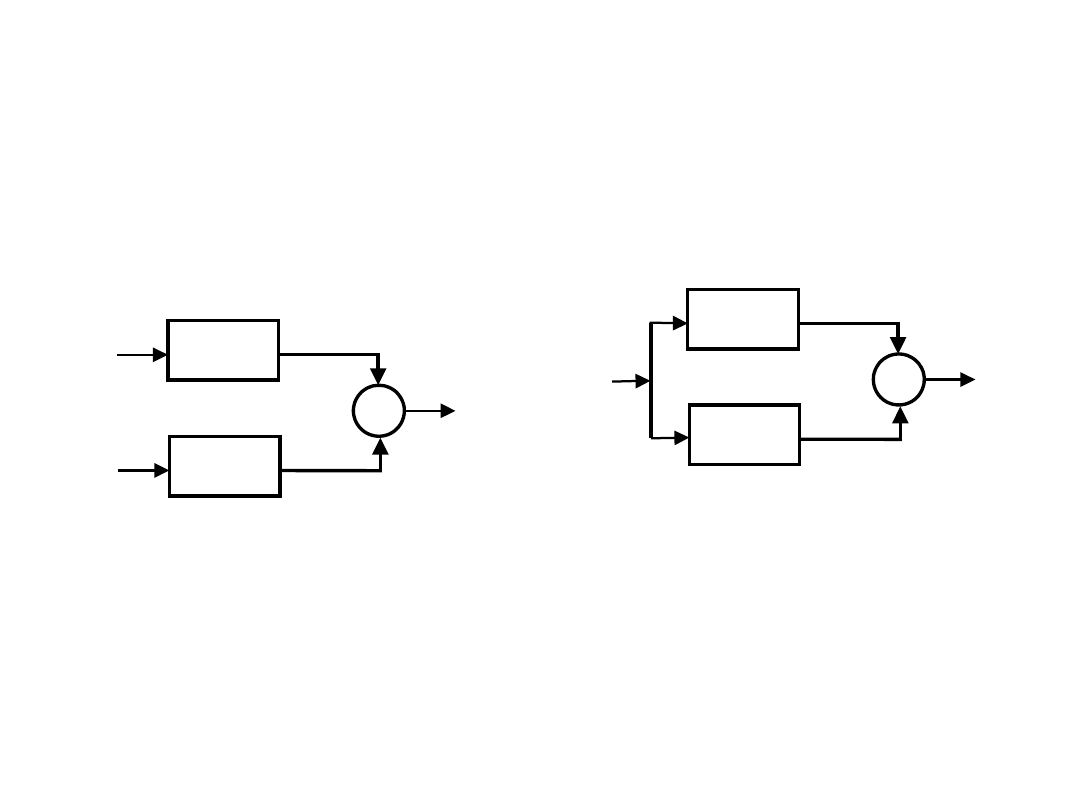
Linearyzacja

Linearyzacja układowa w strukturach otwartych i zamkniętych (typu

kompensacyjnego i komparacyjnego) realizowana rzadko z uwagi na
rozbudowane układy i trudną ich regulację

Linearyzację układową można łatwo zrealizować w strukturach różnicowych
z dwoma identycznymi czujnikami i przeciwnymi sygnałami wejściowymi
oraz z dwoma czujnikami o przeciwnych nieliniowościach.

(np. pojemnościowy,
różnicowy czujnik
przesunięcia)

CZ 1

CZ 2

Y

1

Y

2

Y

+

_

X

W układach tych zmniejszając błąd od nieliniowości zwiększa się
jednocześnie czułość układu i odporność na zakłócenia

CZ 1

CZ 2

+

X

Y

1

Y

2

Y

+

_

-X

(np. dwa tensometry
naklejone na dwóch stronach
zginanej belki)

)

(

)

(

max

2

1

X

X

F

Y

X

F

Y







)

(

)

(

2

1

X

F

X

F

Y

Y

Y











Realizując

linearyzację algorytmiczną

podobnie jak dla korekcji

wprowadza się zapisane w tablicy poprawki wyznaczone w procesie
wzorcowania.
(Nie trzeba mierzyć jak dla korekcji wielkości wpływających ponieważ
nieliniowość charakterystyk jest stała).

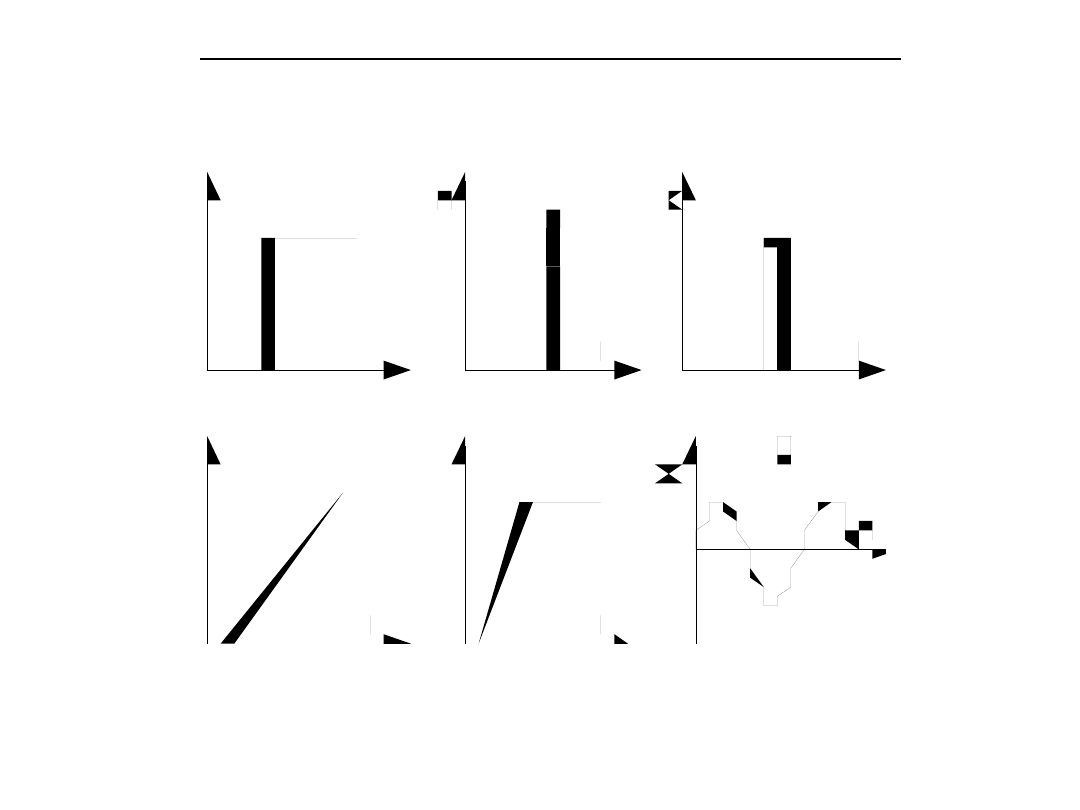
Własności dynamiczne przetworników

 

Typowe sygnały wejściowe do badania własności
dynamicznych przetworników

a )

X

t

c )

X

d )

b )

X

e )

Typowe sygnały wymuszające stosowane do badania własności

dynamicznych przetworników:

a.) skok jednostkowy, b.) impuls idealny (pseudofunkcja Diraca), c.) impuls

rzeczywisty,

d.) sygnał liniowy, e.) sygnał liniowy ograniczony, f.) sygnał sinusoidalny.

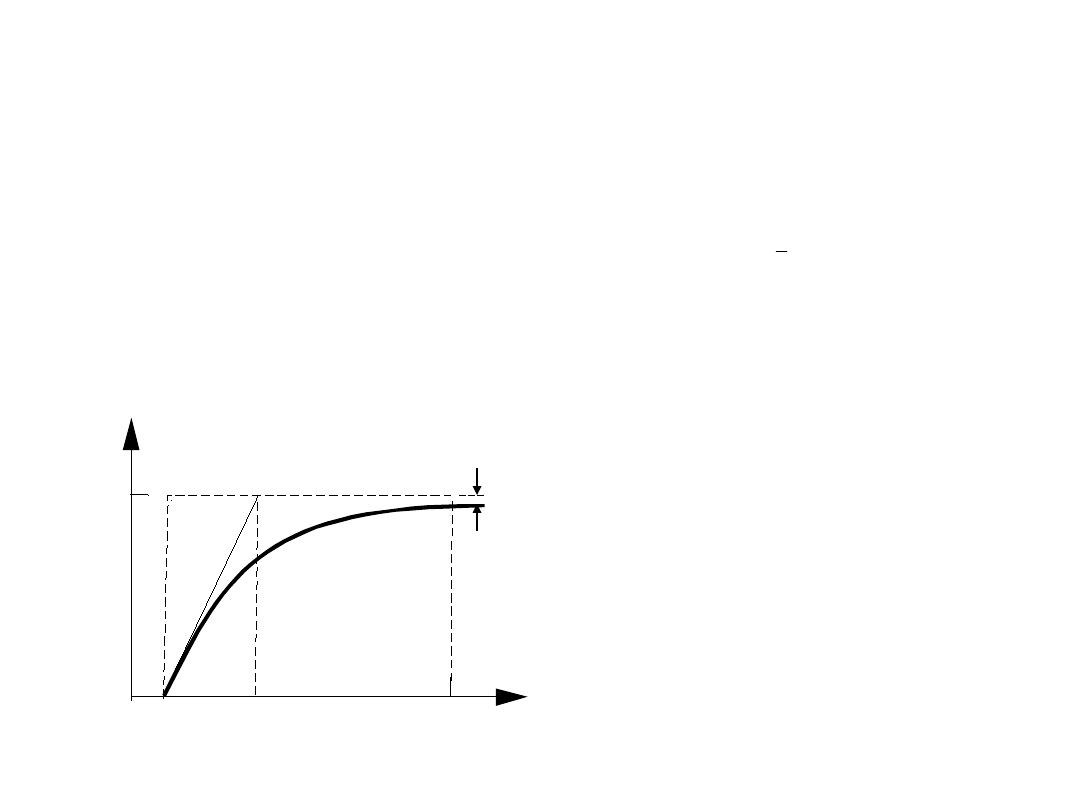
Odpowiedź przetwornika bezinercyjnego:
 

 

gdzie : S - czułość przetwornika (statyczna)

 
Odpowiedź przetwornika z inercją pierwszego rzędu:
 

 

gdzie : A - amplituda skoku jednostkowego

 - stała czasowa przetwornika

Y

t

T

0

t

100

t

0

=

C.A

%

Odpowiedź przetwornika
inercyjnego pierwszego rzędu na
skok jednostkowy.     
( - stała czasowa przetwornika,
T

0

- czas odpowiedzi)

DY

)

(

)

(

t

x

S

t

y





)

1

(

)

(



t

e

A

S

t

y











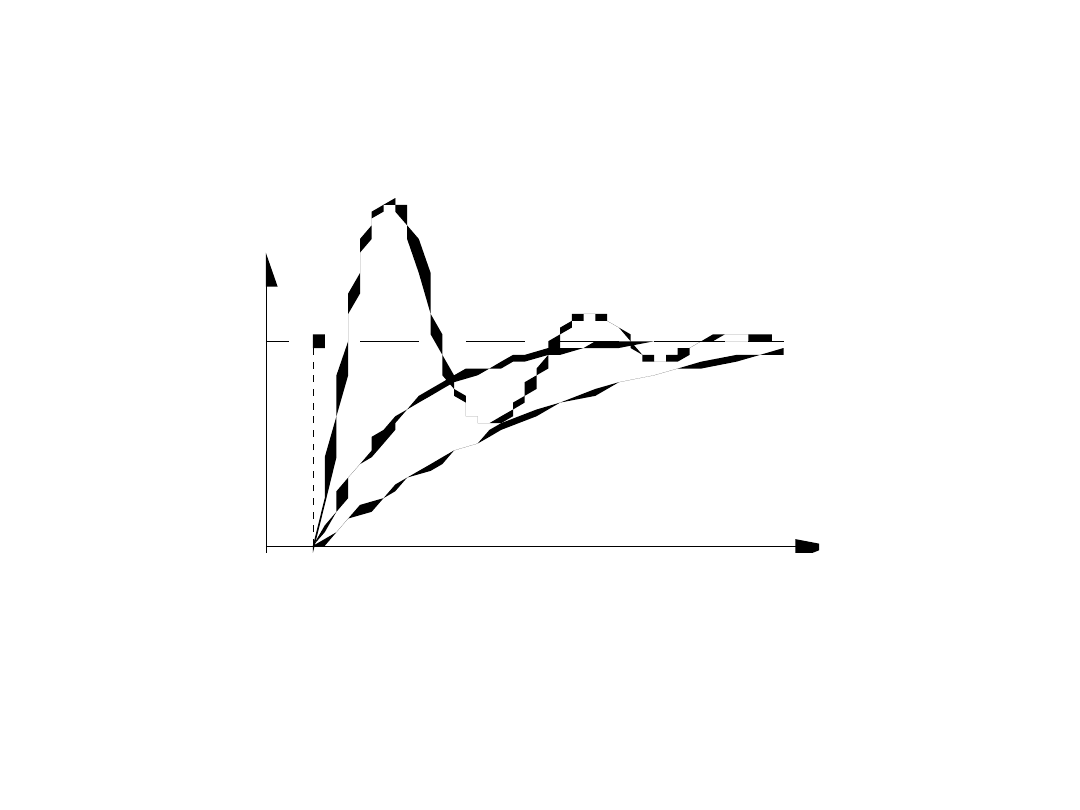
Przetwornik inercyjny drugiego rzędu scharakteryzowany jest

trzema parametrami:

- stałą przetwarzania C (statyczną)
- stopniem tłumienia b (dla b=1 występuje tłumienie krytyczne)
- pulsacją drgań własnych nietłumionych 0

Y

t

1 0 0

%

C A

.

1

2

3

Odpowiedź przetwornika inercyjnego drugiego rzędu na wymuszenie
skokowe: 
 1 - oscylacyjna (niedotłumiona) (b1),  2 - tłumiona krytycznie (b=1),
3 - przetłumiona (b1)

Odpowiedź tłumiona krytycznie i przetłumiona  analogicznie jak dla członu I rzędu.

Parametry charakteryzujące odpowiedź oscylacyjną:

Przeregulowanie - stosunek pierwszego maksymalnego
odchylenia odpowiedzi do jej wartości ustalonej podzielony
przez tą wartość ustaloną.

 

Dekrement tłumienia - jest to stosunek następujących po
sobie maksymalnych odchyleń od wartości ustalonej. Jest on
równy kwadratowi przeregulowania. (Na podstawie określonego
z zarejestrowanej odpowiedzi przeregulowania lub dekrementu
tłumienia można obliczyć stopień tłumienia.).
Czas narastania - jest to czas w jakim wartość sygnału
narasta od chwili początkowej do pierwszego osiągnięcia
wartości ustalonej.
Czas odpowiedzi (uspokojenia) - jest to (jak dla członu I
rzędu) czas, po którym ustala się (z określoną dokładnością)
wartość sygnału.
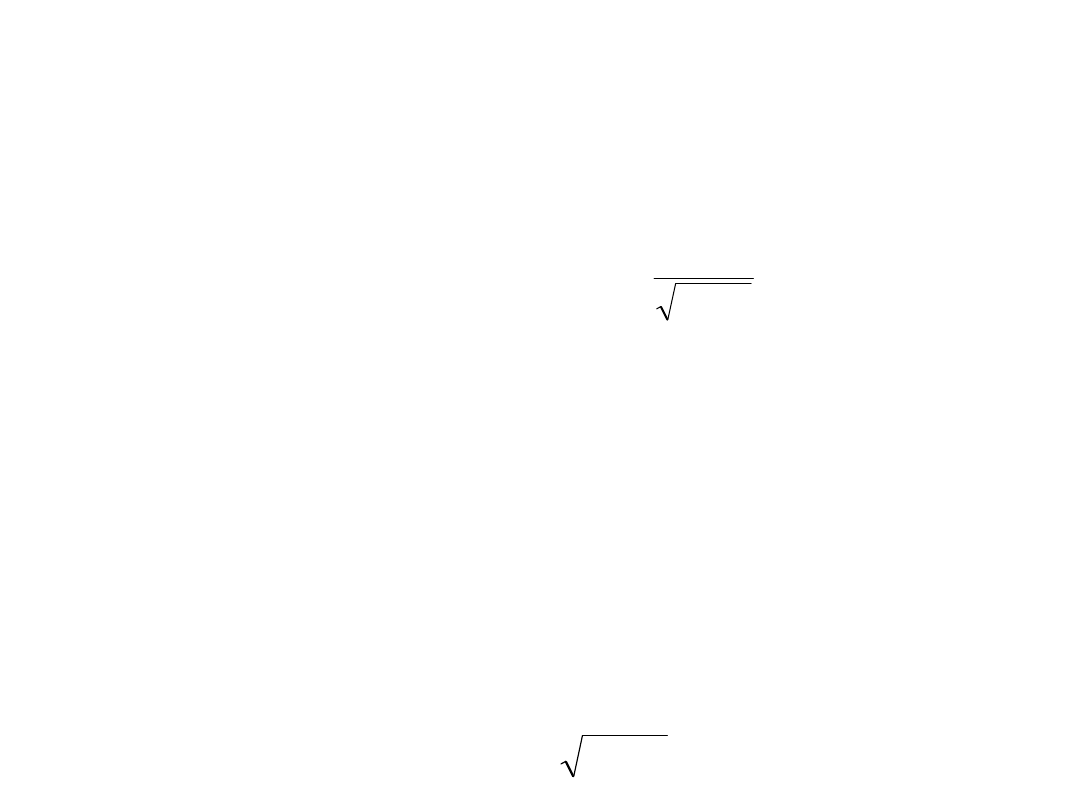
Częstotliwość kątowa oscylacji - zależna od stopnia
tłumienia opisana jest wzorem





















2

1

exp

b

b

wanie

przeregulo



2

0

1 b











Najgorszym przypadkiem teoretycznym

(nie istniejącym w

rzeczywistości)

jest przetwornik drugiego rzędu z zerowym

tłumieniem. Odpowiedź takiego przetwornika na wymuszenie
skokowe miałaby postać drgań niegasnących o pulsacji 

0

.

Przy

testowaniu

przetworników

inercyjnych

sygnałami

sinusoidalnymi występuje tłumienie amplitudy oraz przesunięcie
fazowe odpowiedzi w stosunku do sygnału testowego.

 

Występowanie

w

przetwornikach

inercji

powoduje

dla

nieustalonych w czasie sygnałów wejściowych powstawanie
błędu dynamicznego
 

 
gdzie: y(t)

-

odpowiedź

przetwornika

rzeczywistego

na

wymuszenie sygnałem
testowym,

y

i

(t) - idealny przebieg sygnału wyjściowego

)

(

)

(

)

(

t

y

t

y

t

i







Kryteria całkowe oceny błędu dynamicznego:

 

- liniowe :

- kwadratowe :

 

 

 

Wytwórca zwykle określa pasmo przenoszenia przetwornika

oznaczające zakres częstotliwości sinusoidalnego sygnału wejściowego,

dla którego błąd dynamiczny nie powinien przekraczać wartości błędu

podstawowego określonego dla charakterystyki statycznej przetwornika.





k

t

L

dt

t

t

E

0

)

(

)

(







k

t

K

dt

t

t

E

0

2

)

(

)

(



 

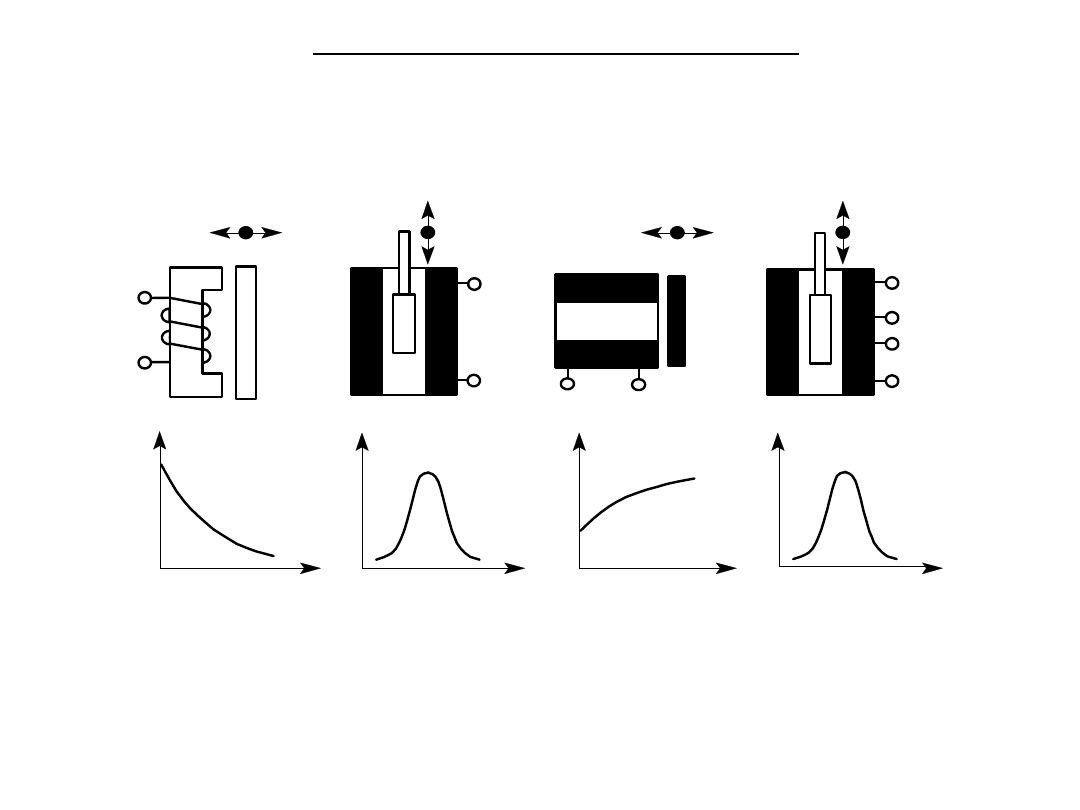
Czujniki indukcyjnościowe

 

Wykorzystują zwykle zmianę L lub M spowodowaną przesunięciem

liniowym

Zasada działania i charakterystyki przetwarzania podstawowych czujników

indukcyjnościowych : a) dławikowego, b) solenoidalnego, c) wiroprądowego,

d) transformatorowego

)

a

x

)

b

x

)

c

x

)

d

x

M

x

L

x

x

L

x

L

 

W czujnikach transformatorowych bezpośrednio U

wyj

= f(x)

 
Czujniki o zmiennej ind. własnej (M) pracują zwykle w układzie mostka
niezrównoważonego

 

 

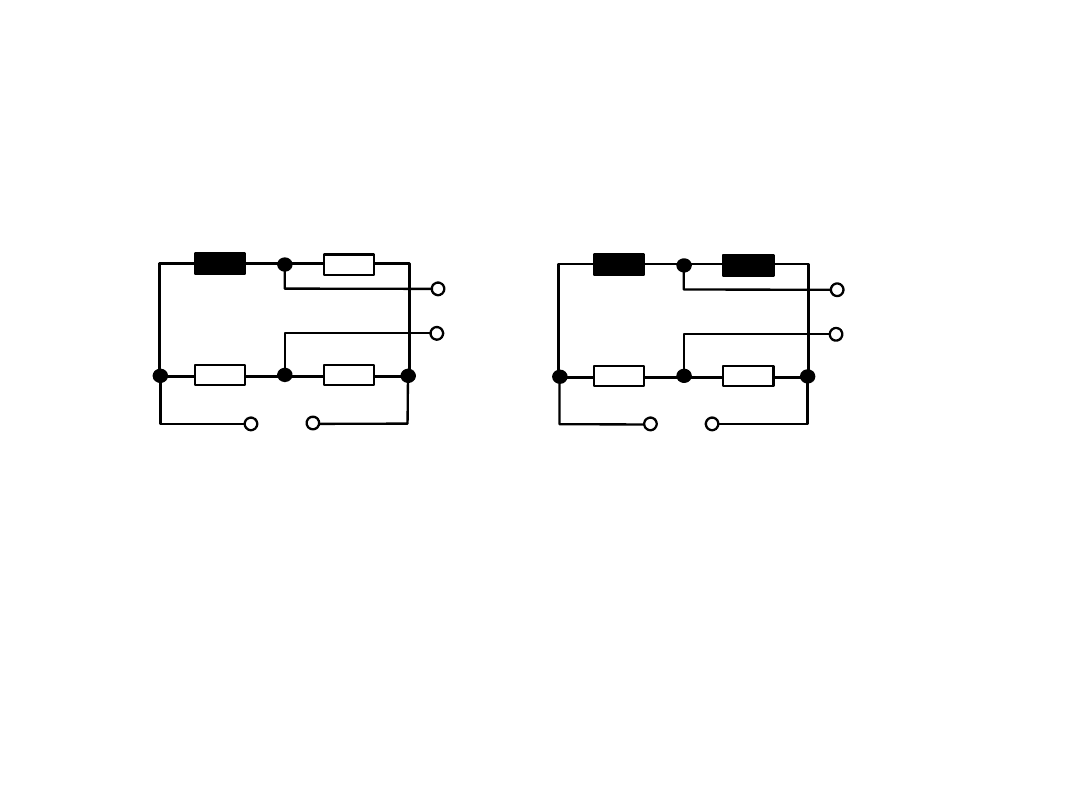
Układ mostka niezrównoważonego : a) z pojedynczym czujnikiem,

b) z dwoma czujnikami w układzie różnicowym.

Dla mostka niezrównoważonego:

 

 

gdzie: U

Z

- napięcie zasilające mostka,

S - współczynnik proporcjonalności (czułość mostka),
Z - względna zmiana impedancji czujnika ( Z = Z / Z ).

)

a

U

z

U

wy

Z

1

Z

2

Z

3

Z

4

)

b

U

z

U

wy

Z

1

Z

2

Z

3

Z

4





4

3

2

1

Z

Z

Z

Z

S

U

U

z

wy





















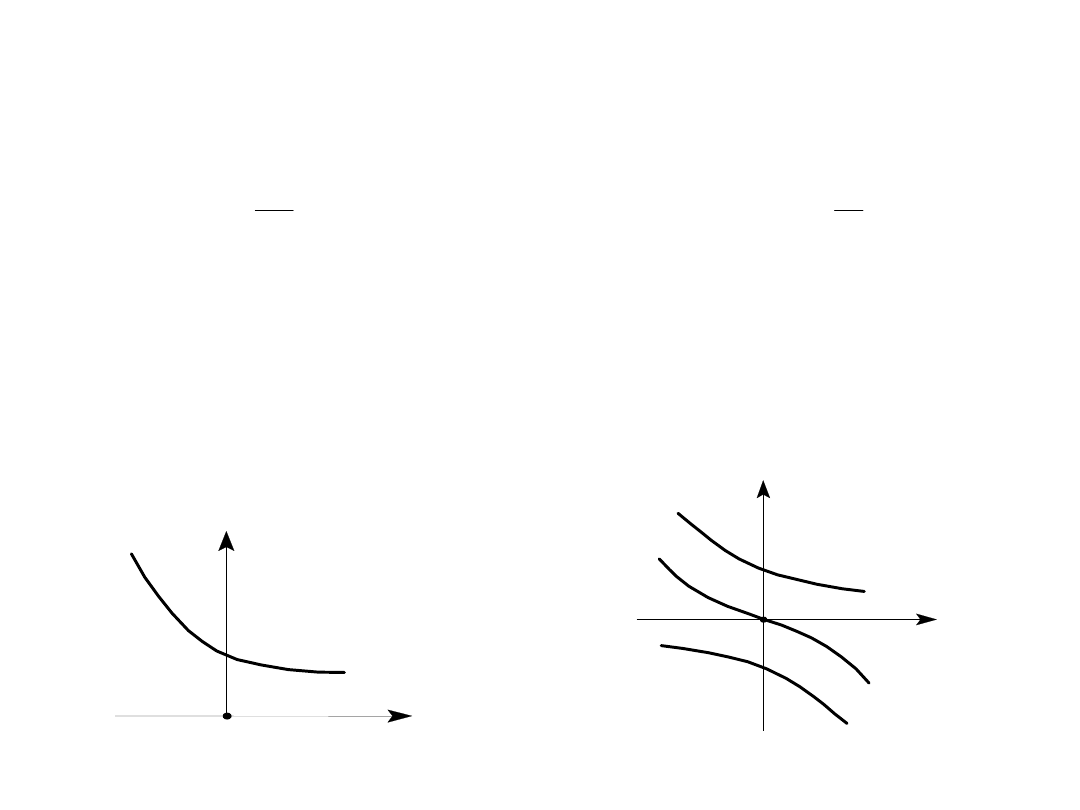
Zasada działania indukcyjnościowego czujnika przesunięcia

liniowego L=f(x) lub L/L=f(x)

 

Pomijając strumień rozproszenia:

 

lub w przybliżeniu:

gdzie:

z

- iczba zwojów cewki,

R



- reluktancja obwodu magnetycznego (oporność magnetyczna),



0

- przenikalność magnetyczna próżni,

l

p

- długość szczeliny,

S

p

- powierzchnia szczeliny.

Charakterystyka przetwarzania czujnika dławikowego : a) pojedynczego,

b) podwójnego w układzie różnicowym.



R

z

L

2



p

p

l

S

z

L

1

0

2











)

a

)

b

L

x

L

1

L

x

2

L

L

1

2

L



Długość szczeliny l

p.

dla przemieszczeń części ruchomej rdzenia o wartość

x

wokół położenia ustalonego l

o

gdzie L

o

=f(x=0):

 

a więc

gdzie

 

Względna zmiana indukcyjności czujnika (L-L

0

)/L

0

:

 

 

 

Napięcie wyjściowe mostka z dwoma czujnikami w ukł. różnicowym:

 





x

l

l

p





0

2

0

0

1

l

x

L

L





0

0

2

0

2

1

l

S

z

L

p











0

0

1

l

l

x

x

L

L































2

2

1

1

L

L

L

L

S

U

U

z

wy

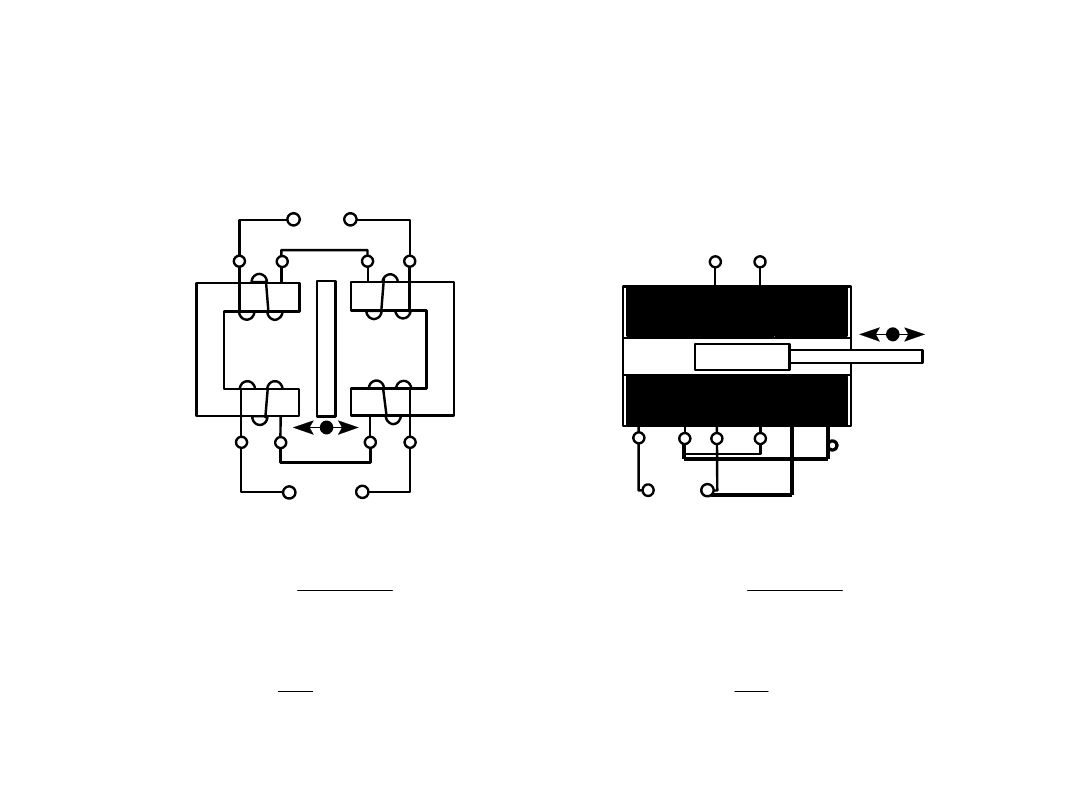
Czujniki transformatorowe

Czujniki transformatorowe - mały błąd nieliniowości (nawet rzędu 0,1%)

- duża czułość
- napięciowy sygnał wyjściowy

Czujniki transformatorowe różnicowe: a) dławikowy, b) solenoidalny.

oraz

gdzie: z

1

, z

2

- liczba zwojów uzwojeń pierwotnych i wtórnych.

2

1

1

1

L

L

L

U

U

z









2

1

2

1

L

L

L

U

U

z











1

1

2

2

U

z

z

U









1

1

2

2

U

z

z

U











)

a

x

U

wy

U

z

1

U 



1

U

2

U

2

U 

)

b

x

U

z

U

wy

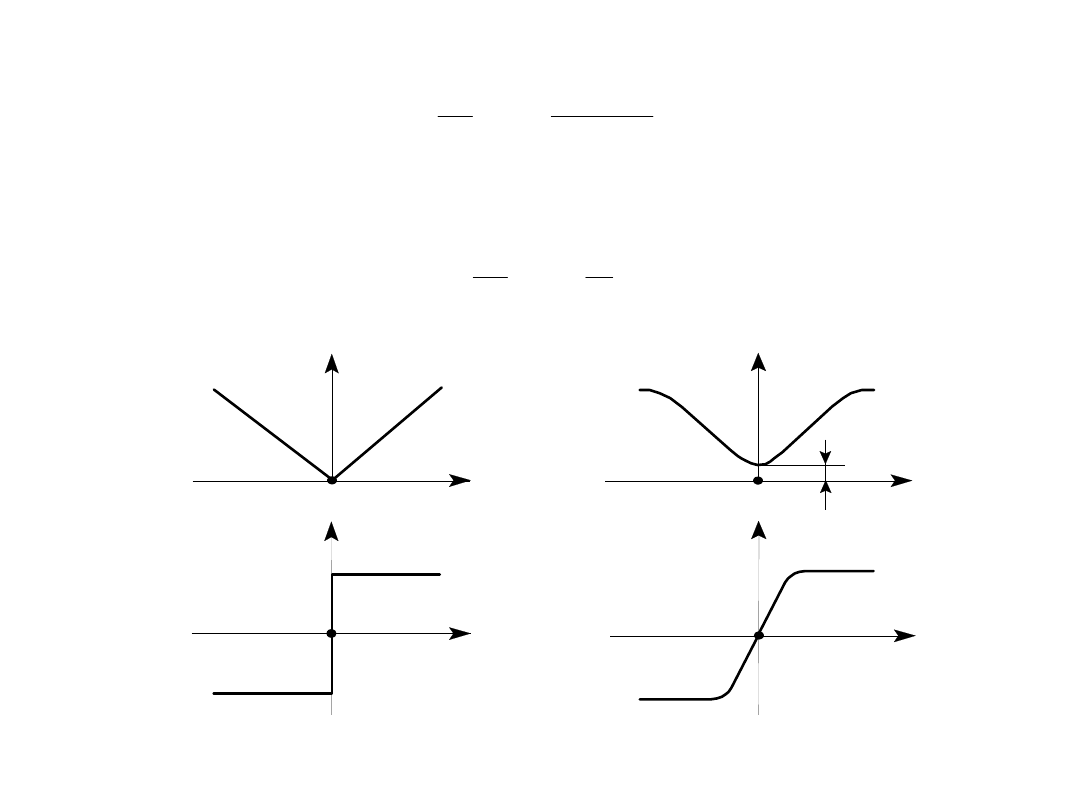
Napięcie wyjściowe czujnika równe różnicy napięć wtórnych wynosi:

 

 

Jeżeli szczelina lewej połówki transformatora jest równa 2(l

0

+ x) , zaś

prawej

2(l

0

- x) :

Charakterystyki przetwarzania transformatorowego czujnika różnicowego:

a) idealne, b) rzeczywiste

2

1

1

2

1

2

L

L

L

L

U

z

z

U

z

wy











0

1

2

l

x

U

z

z

U

z

wy







x

x

x

0

U









wy

U

wy

U

x









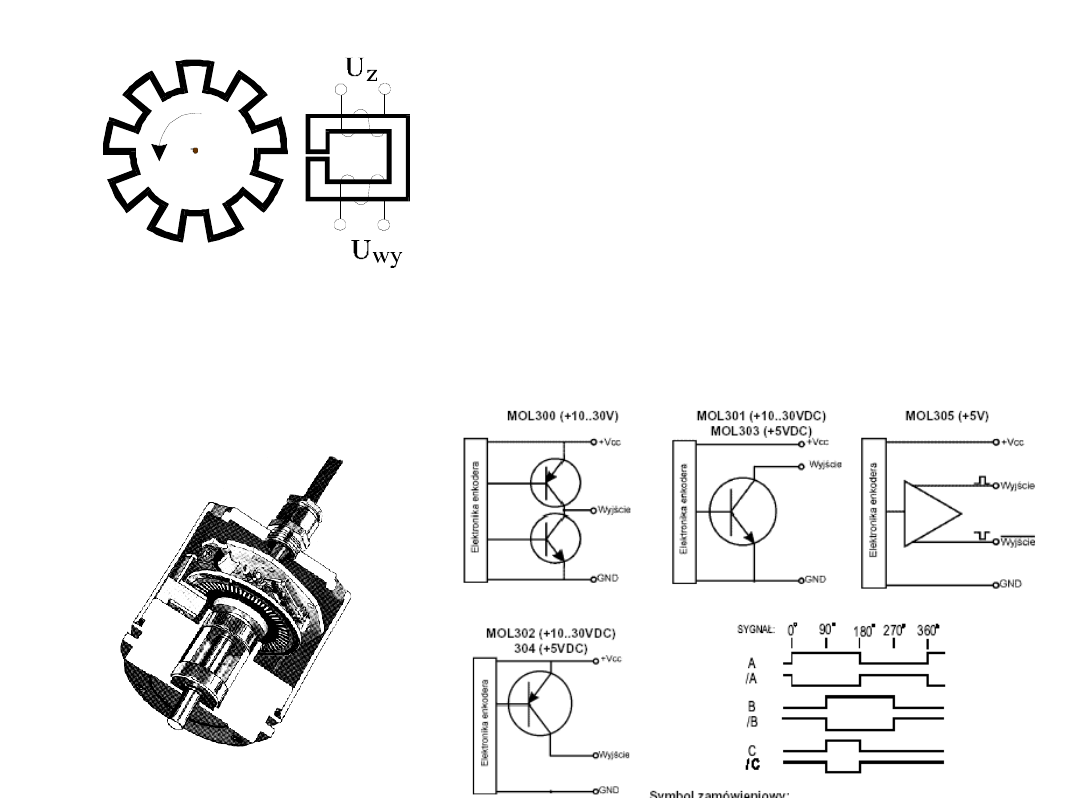
Przykład czujnika indukcyjnego z wyjściem cyfrowym

Indukcyjny czujnik prędkości obrotowej
(kąta obrotu) z wyjściem
dwustanowym

Na podobnej zasadzie działają czujniki optyczne, w których nacięcia
tarczy mogą stanowić przysłony między źródłem i odbiornikiem światła.

 

Stosując dwie tarcze (przesunięte względem siebie) można mierzyć
wartość i kierunek przesunięcia kontowego.

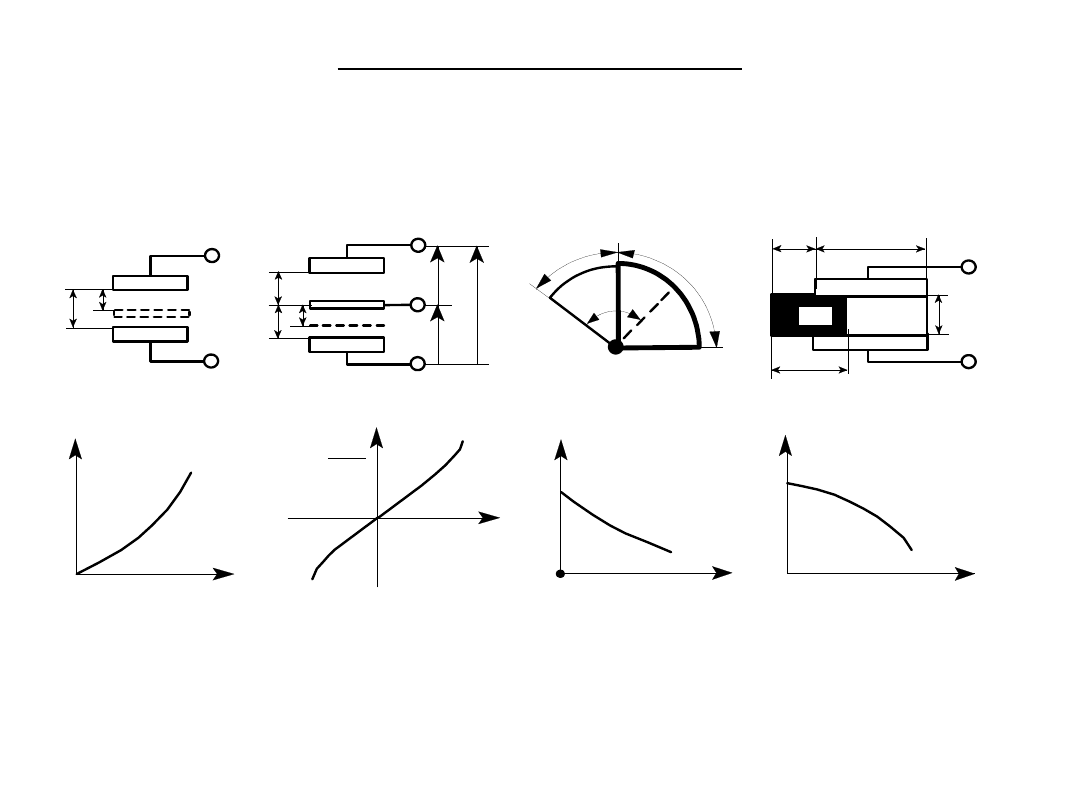
Czujniki pojemnościowe

Podstawowe typy czujników pojemnościowych oraz ich charakterystyki

Zasada działania i charakterystyki przetwarzania czujników pojemnościowych :

a) o zmiennej odległości elektrod, b) różnicowego o zmiennej odległości elektrod,

c) o zmiennej powierzchni czynnej elektrod, d) o zmiennym położeniu dielektryka.

a)

b)

c)

x

d

C

1

U

1

C

2

C

d

d x

2

U

U





0



0

d)

x





x

l

d

l

C

x



C



x



1

C

2

C

x

l

0

C

C

0

C

C

130

o



 
a) Czujnik o zmiennej odległości elektrod - do pomiaru małych
przemieszczeń (warunek: x  d )

 

gdzie: x = x / d - względne przemieszczenie elektrody ruchomej.

 

b) Czujnik różnicowy o zmiennej odległości elektrod –

lepsza czułość i

odporność na zakłócenia zewnętrzne.

 

oraz

 

c) Czujnik o zmiennej powierzchni czynnej elektrod – do pomiaru
przemieszczeń kątowych.
 

d) Czujnik o zmiennym położeniu dielektryka – do pomiaru dużych
przemieszczeń kątowych.

 

gdzie: C

0

- pojemność spoczynkowa (dla x=0),

 , 

X

- przenikalność elektryczna dla powietrza i dielektryka o

zmiennym położeniu.

x

x

C











1

x

x

C

C











1

1

2

1

x

U

U

U

U













1

2

0

0

1









C

C



















x

l

x

C

C





1

1

0

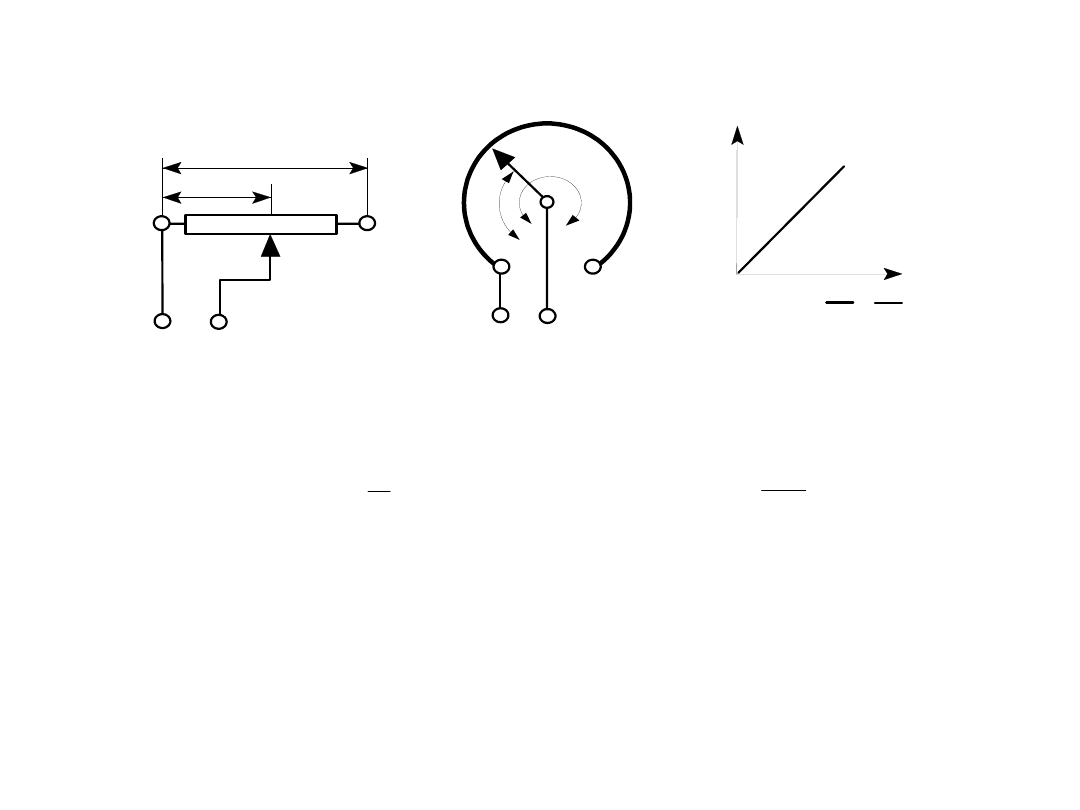
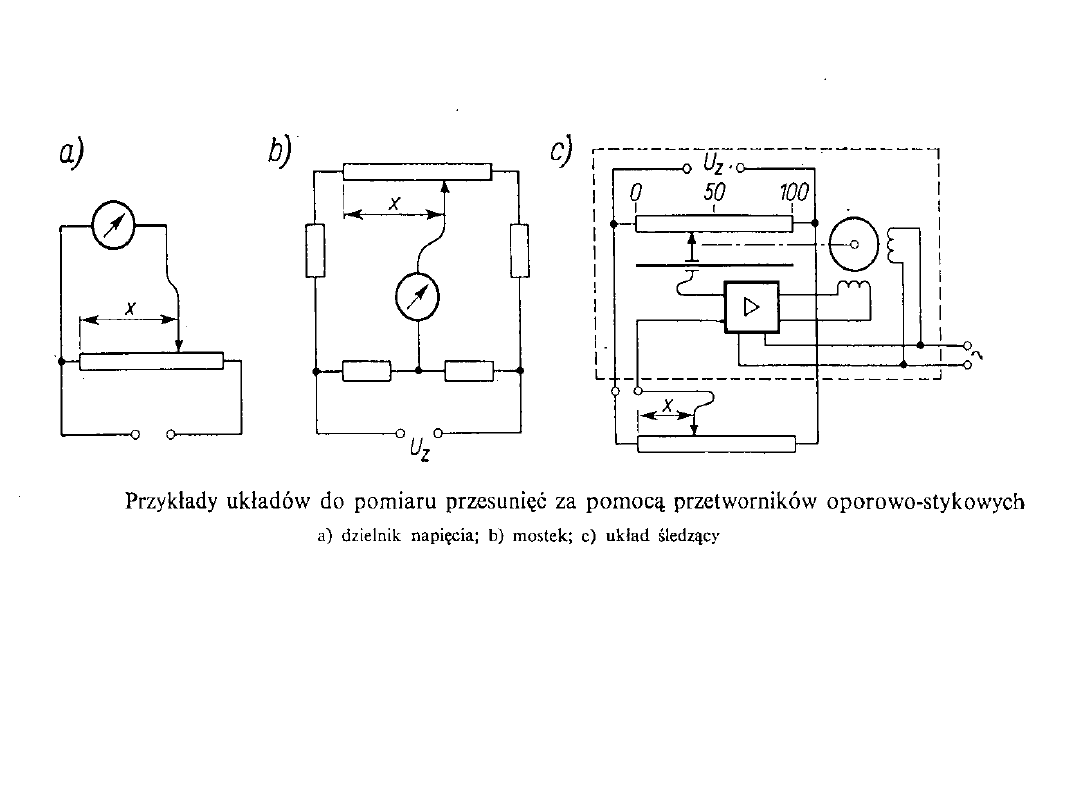
Czujniki rezystancyjne

Czujniki oporowo-stykowe : a) przemieszczenia liniowego,

b)  kąta obrotu, c) charakterystyka przetwarzania czujnika.

lub

Zakresy pomiaru przemieszczeń: liniowych - od kilku mm do ok.
1m, kątowych - do ok. 270.

 

Czujniki tego typu mogą też współpracować z mostkami, w
których obydwie rezystancje czujnika ( R oraz R

n

- R ) włączone

są w sąsiednie gałęzie mostka.

a)

R

x

l



0



)

(





0

R

R

l

x

b)

c)

l

x

R

R

n





n

n

R

R









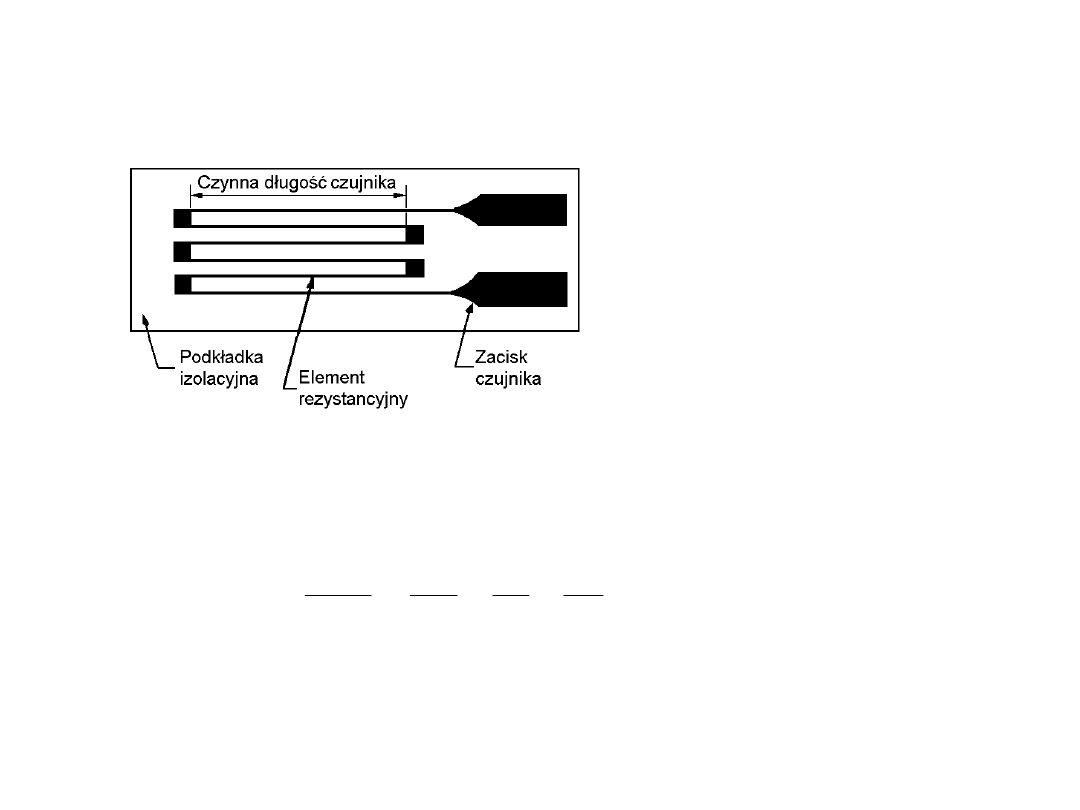
Czujniki naprężno-oporowe (tensometry) (drutowe, foliowe i
półprze-wodnikowe) - wykorzystujące zjawisko zmiany elementu
rezystancyjnego paska pod wpływem naprężenia mechanicznego.
 

Tensometr foliowy

 

Pod wpływem występujących naprężeń rozciągających rezystancja
paska R

T 

= l/s ulega zwiększeniu a jej względny przyrost 

R

wynosi:

gdzie:

 - rezystywność materiału siatki (zwykle konstantanu)

l - całkowita długość czynna elementu rezystancyjnego

s - przekrój elementu rezystancyjnego

s

l

T

T

R

s

s

l

l

R

R





































Względna zmiana przekroju elementu rezystancyjnego s = ab wynosi:
 

 

czyli zmiana rezystancji 

R

:

Czułość tensometru k

T

= 

R

/

l

:

 

Czułość: - dla pasków metalowych - ok.2

- dla pasków półprzewodnikowych - do 200

 

l

s

l

l

b

b

a

a





























2

2















2

1





l

R













2

1







l

l

R

T

k

Rezystancyjny czujnik temperatury -

składa się z drutu

metalowego umieszczonego w obudowie.

gdzie: R

0

- rezystancja czujnika w temperaturze 

0

,

,  - temperaturowe współczynniki rezystancji.

 

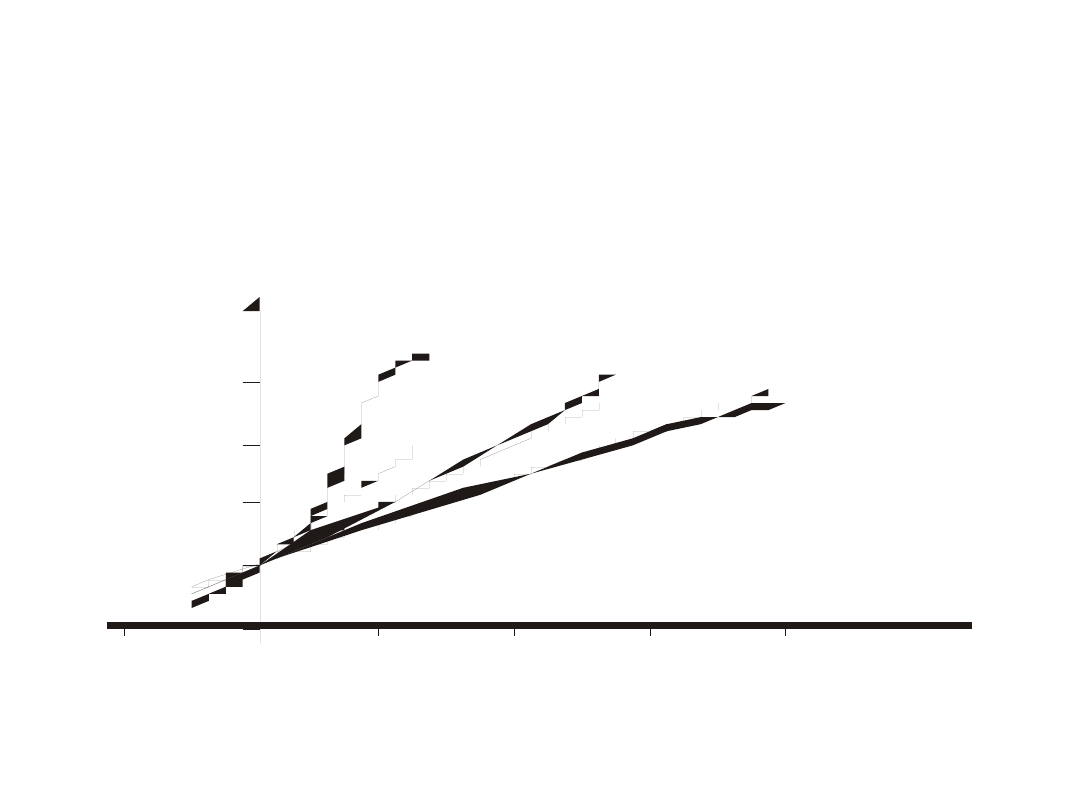
Charakterystyki typowych czujników rezystancyjnych temperatury (metalowych)













2

0

0

0

1





















R

R

-2 0 0

2 0 0

4 0 0

6 0 0

8 0 0



[ d eg ]

1

3

R / R

o

Ni

C u

P t

Półprzewodnikowe czujniki rezystancyjne temperatury termistory -

wykonuje się

je z germanu, krzemu lub tlenków metali.

 

 

gdzie: A,B - stałe materiałowe

T - temperatura bezwzględna

 
 

Rozróżnia się dwa rodzaje termistorów: PTC - z dodatnim

temperaturowym

współczynnikiem rezystancji oraz NTC - ze współczynnikiem ujemnym.

 

Charakterystyki przetwarzania termistorów PTC i NTC.

T

B

e

A

R





1 0 0

2 0 0

3 0 0



[ d e g ]

1 0

1

1 0

3

R

N T C

P T C

]

 

Czujniki piezorezystywne wykorzystujące zależność rezystancji
określonych materiałów od siły ściskającej próbkę materiału stosuje się
często do pomiaru ciśnienia, siły, drgań, itp. (tanie i niezawodne,
liniowość rzędu 0,5 do kilku %).

 

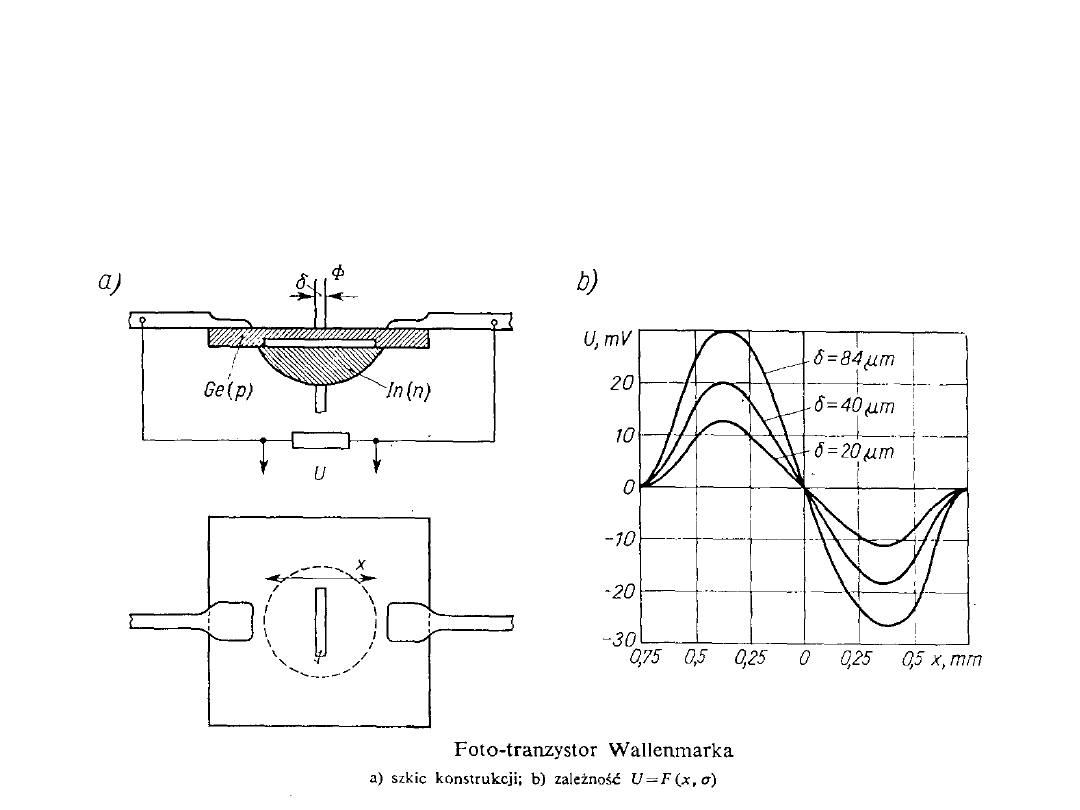
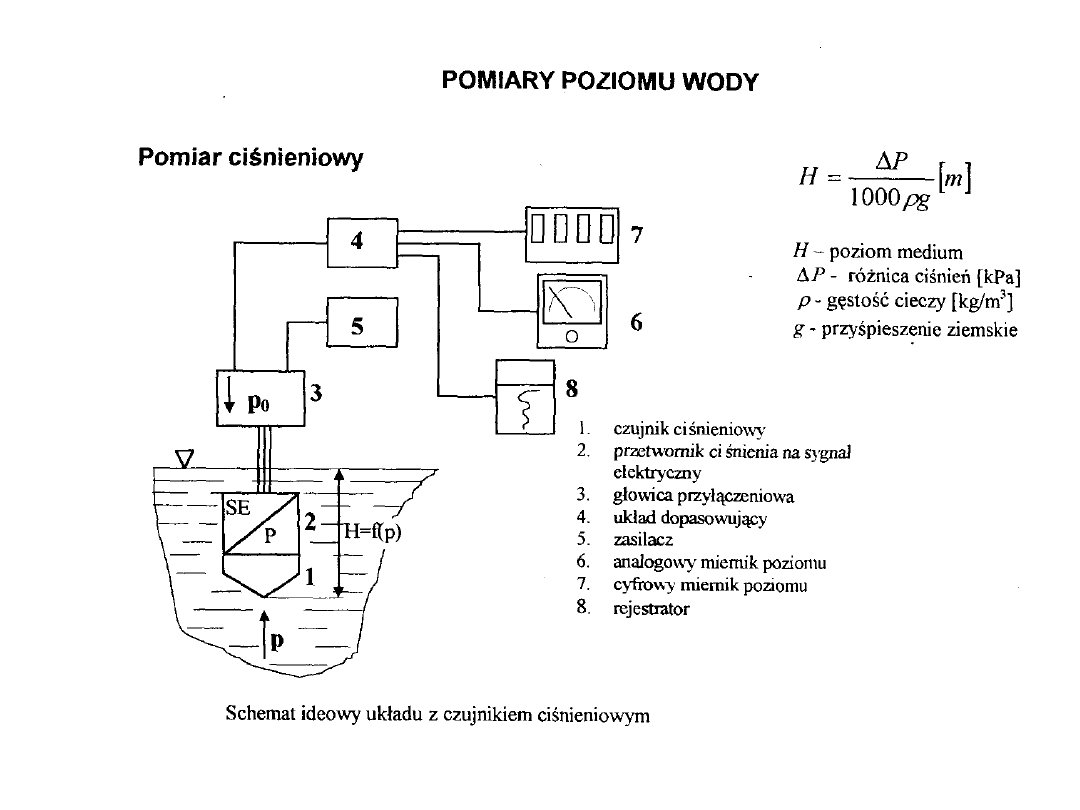
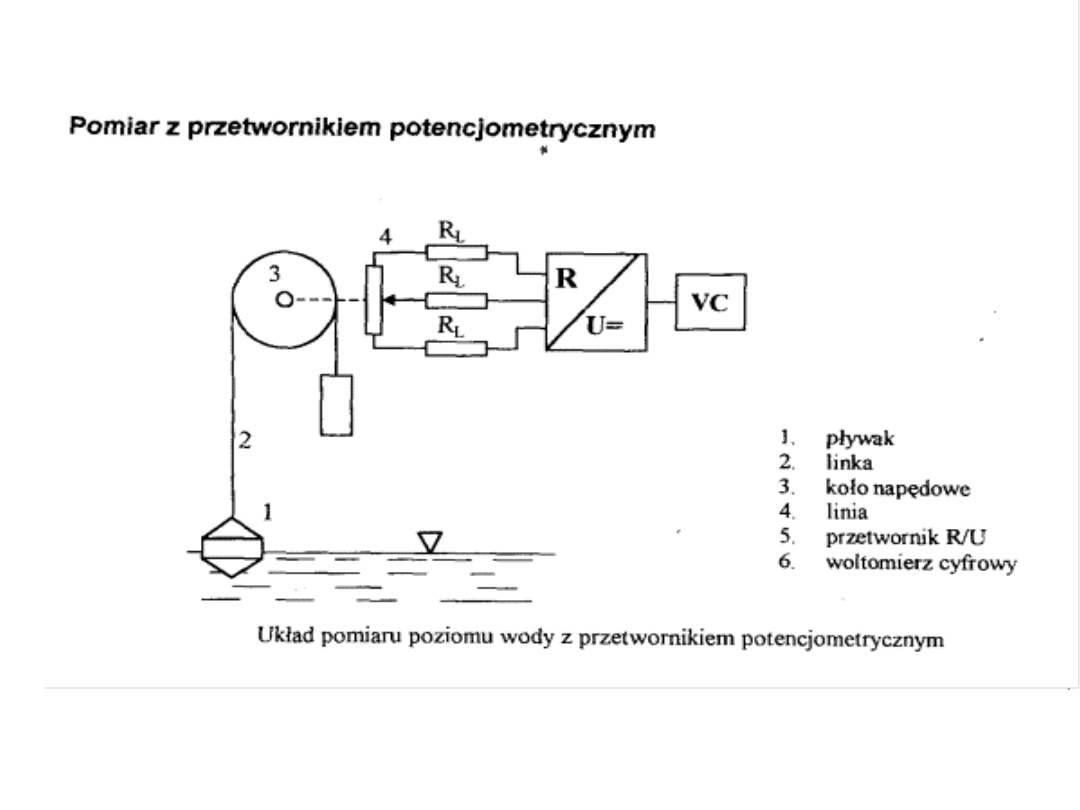
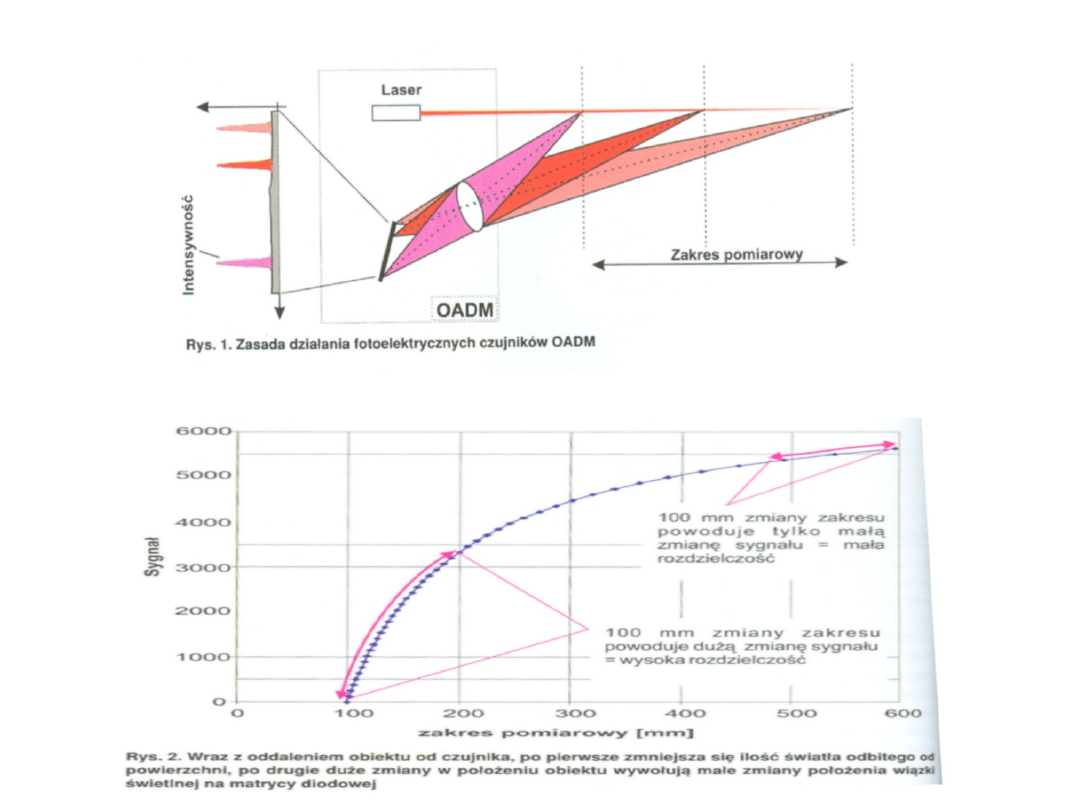
Przykładowy czujnik fotooptyczny

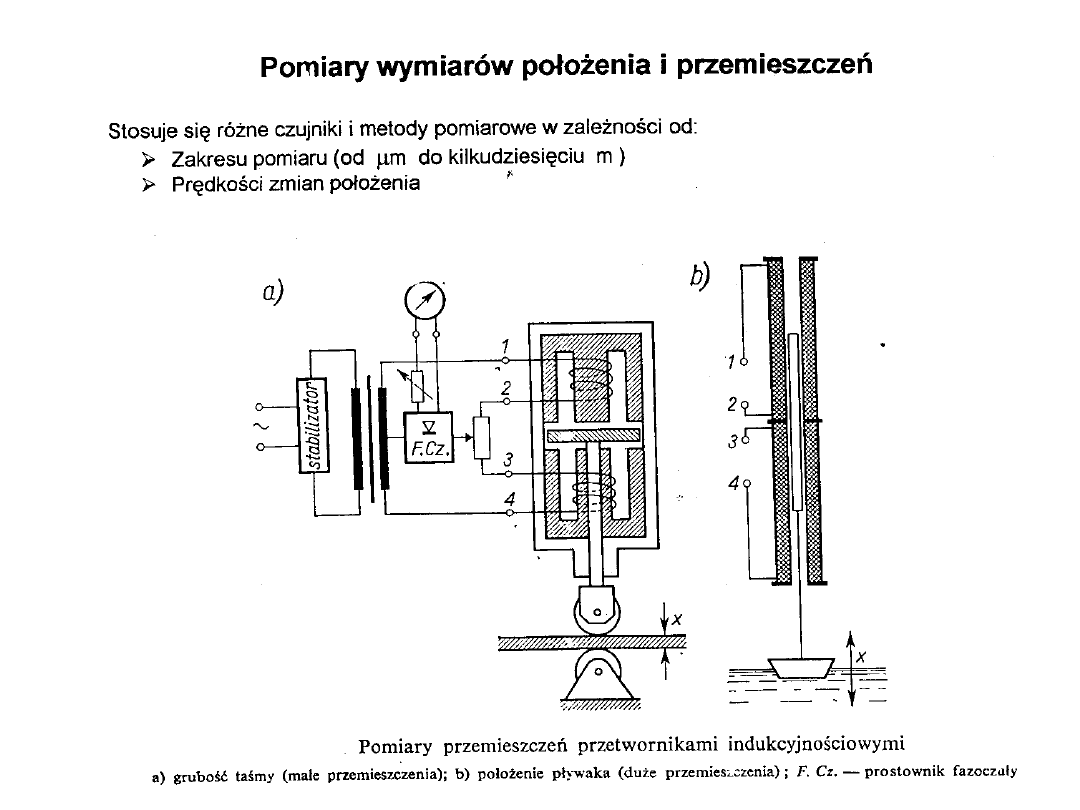
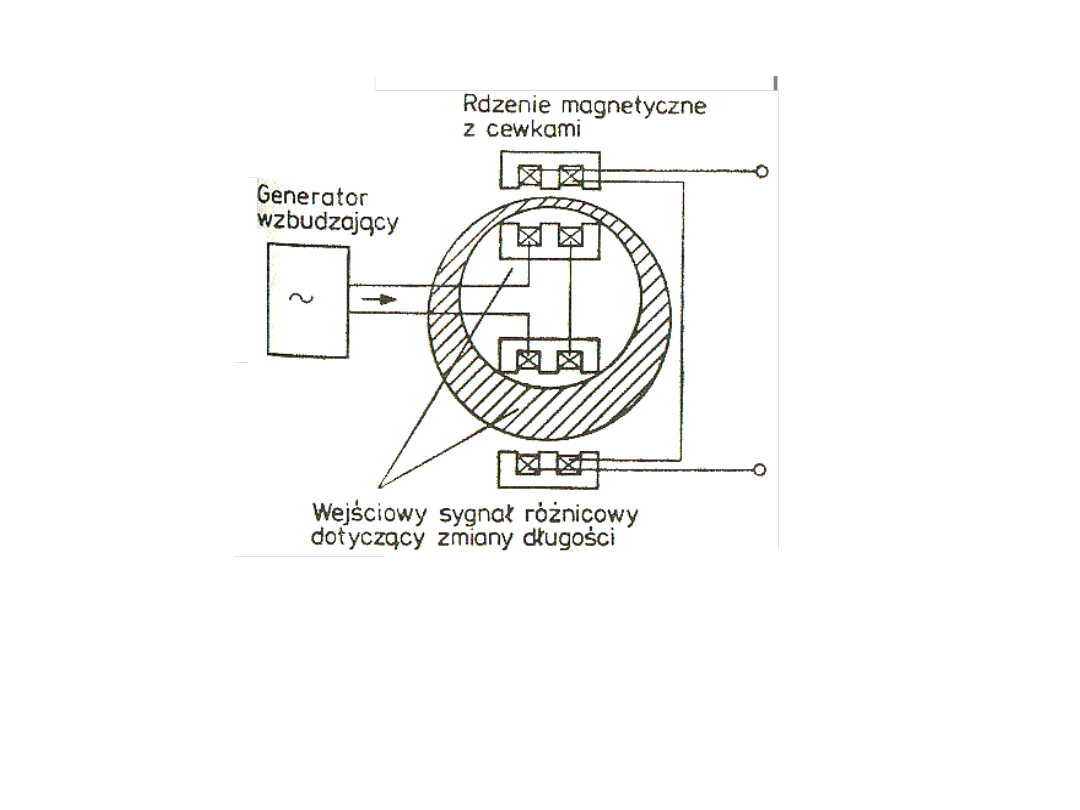
Przetwornik indukcyjny o zmiennej reluktancji

do wyznaczania nierównomierności grubości ścianek

rurociągu

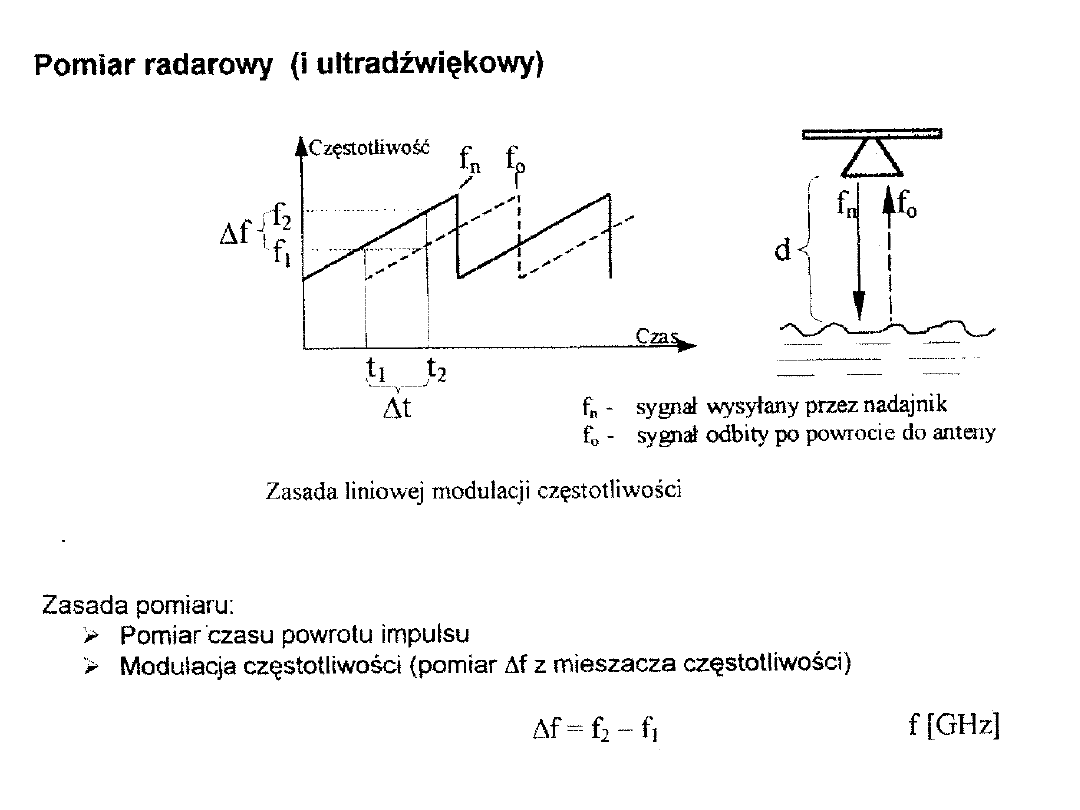
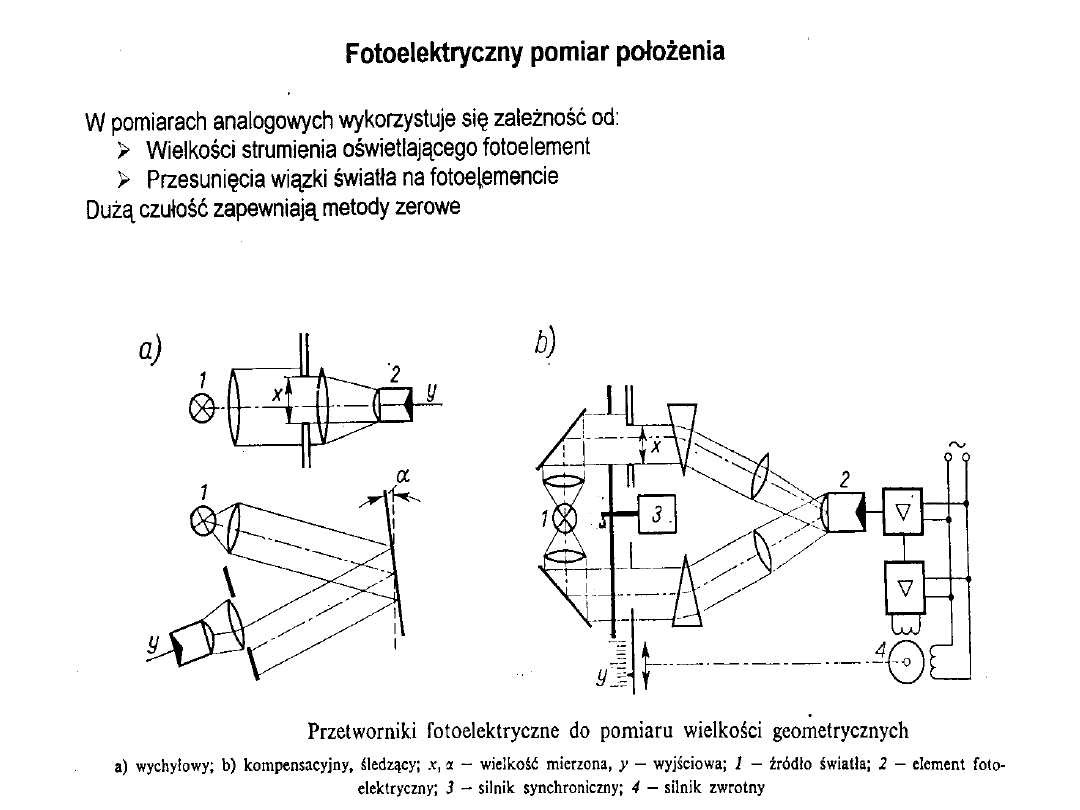
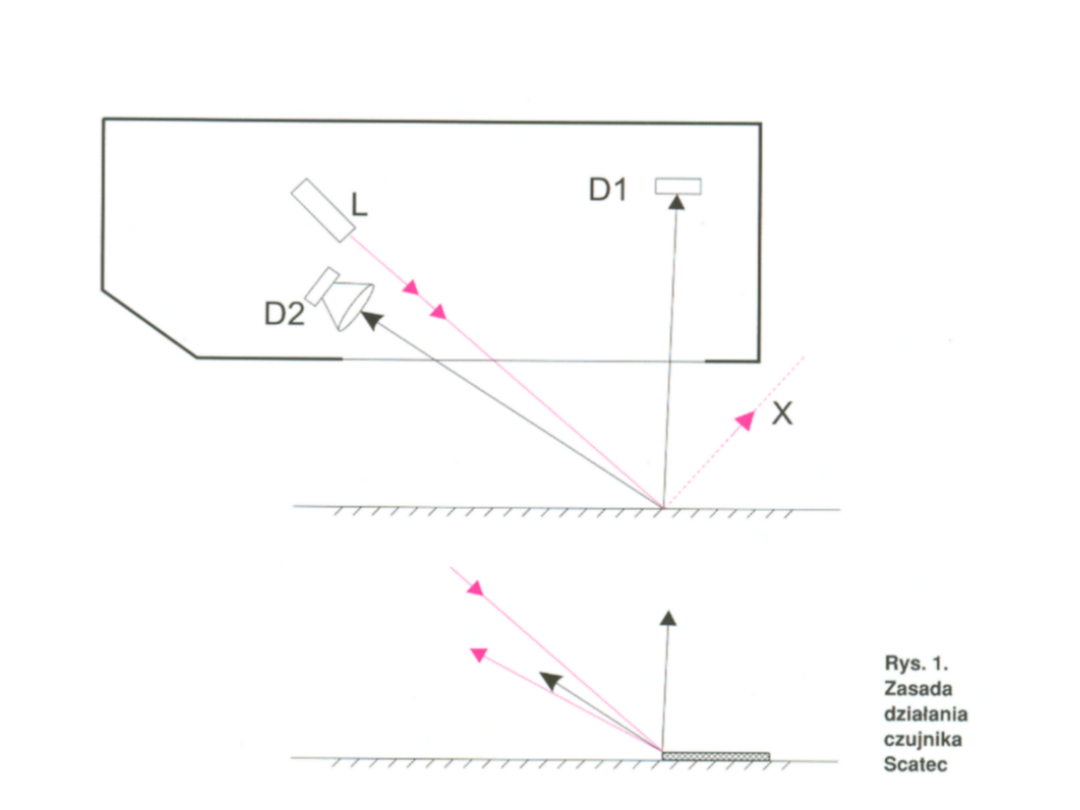
Czujnik do detekcji krawędzi

(np. do zliczania

arkuszy)