Metody modelowania i symulacji

kinematycznej i dynamicznej

przy wykorzystaniu

wspomagania komputerowego

CAD i CAE

Dr inż. Piotr Gospodarczyk

Katedra Maszyn Górniczych Przeróbczych i

Transportowych

B-2 parter Pok. 3

[e-mail]

Pojęcia podstawowe i ich interpretacja

• MODELE I MODELOWANIE
• Model – układ materialny (np. makieta) lub układ abstrakcyjny

(np. .rysunki, opisy słowne, równania matematyczne).

• Model fizyczny (nominalny) – opis procesów w obiekcie

(fizycznych, również eko-nomicznych i społecznych).

• Model matematyczny – zbiór reguł i zależności, na podstawie

których można za pomocą obliczeń przewidzieć przebieg
modelowanego procesu. Modelem matema-tycznym są równania
opisujące proces oraz wszelkie relacje opisujące ograniczenia i
uproszczenia (np. nierówności).

• Modelowanie – całokształt czynności zmierzających do

utworzenia modelu fizycz-nego i matematycznego.

• Model komputerowy – program komputerowy umożliwiający

wprowadzanie para-metrów modelowanego układu i stanu
początkowego, otrzymanie na drodze obliczeniowej przebiegów
czasowych zjawisk i charakterystyk modelowanego układu.

Po co modelować?

• „Dla zabawy”
• Dla prezentacji czegoś
• Dla udowodnienia czegoś
• Dla łatwiejszego zrozumienia „całości”

• Rodzaje modeli i modelowania
• 1. Modelowanie obiektu
• 2. Modelowanie otoczenia
• 3. Modelowanie zjawiska
• model obiektu + model otocznia = model

zjawiska

Różne definicje modeli

• MODEL

szkic, zarys obiektu lub zjawiska wykonany w zmniejszonej
skali
i z materiałów zastępczych, służący eksperymentom
naukowym.

• MODEL
• Uproszczona imitacja (reprezentacja) systemu

rzeczywistego.

• Materialnym lub abstrakcyjnym modelem systemu

empirycznego jest taka abstrakcyjna lub materialna
struktura, pozostająca w relacji podobieństwa do struktury
modelowanego systemu, której badanie może dostarczyć
informacji spełniających cele badania, projektowania lub
doskonalenia tego systemu.

MODEL

• Uproszczona imitacja (reprezentacja) systemu

rzeczywistego.

• Materialnym lub abstrakcyjnym modelem

systemu empirycznego jest taka abstrakcyjna lub
materialna struktura, pozostająca w relacji
podobieństwa do struktury modelowanego
systemu, której badanie może dostarczyć
informacji spełniających cele badania,
projektowania lub doskonalenia tego systemu.

MODELOWANIE

• Próba przedstawienia jakiegoś zjawiska lub

właściwości którą staramy się zrozumieć lub
zbadać, w kategoriach innych zjawisk, które już
rozumiemy.

• Modeluje się nie tylko obiekt lecz najczęściej

zachodzący w tym obiekcie lub realizowany przez
ten obiekt proces.

Modelowanie i symulacje

• MODELOWANIE:

Proces tworzenia modelu obiektu lub zjawiska,
uwzględniający ich rzeczywiste parametry zastosowane w
odpowiedniej skali.

• SYMULACJE KOMPUTEROWE:

Sztuczne odtwarzanie jakiejś sytuacji, zjawiska.

• Eksperyment naukowy umożliwiający obserwację zachowania się

modeli obiektów
lub zjawisk w rzeczywistości wirtualnej, stworzonej za pomocą
programu komputerowego.

• Zaletą symulacji jest to, że eksperyment można wielokrotnie

powtarzać,
zmieniając za każdym razem parametry, oraz obserwować i
analizować
wpływ tych zmian na przebieg zjawiska.
Możemy badać zachowanie jeszcze nie istniejących urządzeń,
modeli,
jak też modeli i zdarzeń historycznych.

Czym jest modelowanie?

• Większość z nas budowała kiedyś lub przynajmniej miała w ręku

modele samochodów, statków, samolotów czy kolei.

• Tego typu modele pozwalają nam znacznie lepiej zrozumieć

budowę oraz zasady działania rzeczywistych układów. Mogliśmy
również zauważyć, że niektóre z tych modeli były bardziej
precyzyjne od innych.

• Materialne modele rzeczywistych obiektów i procesów, którym te

obiekty podlegają, takie jak jazda, lot, ruchy planet, posiadają
swoje naturalne konstrukcyjne ograniczenia.

• Model po prostu charakteryzuje się tym, że oddaje istotne,

chociaż wybrane, właściwości rzeczywistego obiektu, a tym
samym pozwala lepiej zrozumieć jego budowę oraz zasady
funkcjonowania.

• Samo modelowanie nie jest pojęciem jednoznacznym. Zazwyczaj

rozumie się tutaj proces tworzenia komputerowego modelu
jakiegoś obiektu, systemu czy zjawiska w celu zrozumienia jego
struktury oraz mechanizmów funkcjonowania. Mamy zatem
modele obiektów, systemów oraz zjawisk: fizycznych,
chemicznych, biologicznych oraz ekonomicznych.

• Modele konstrukcyjne tworzone przez inżynierów tworzą raczej

odrębną klasę, chociaż można formalnie włączyć je do modeli
fizycznych.

dr inż. Ryszard Myhan

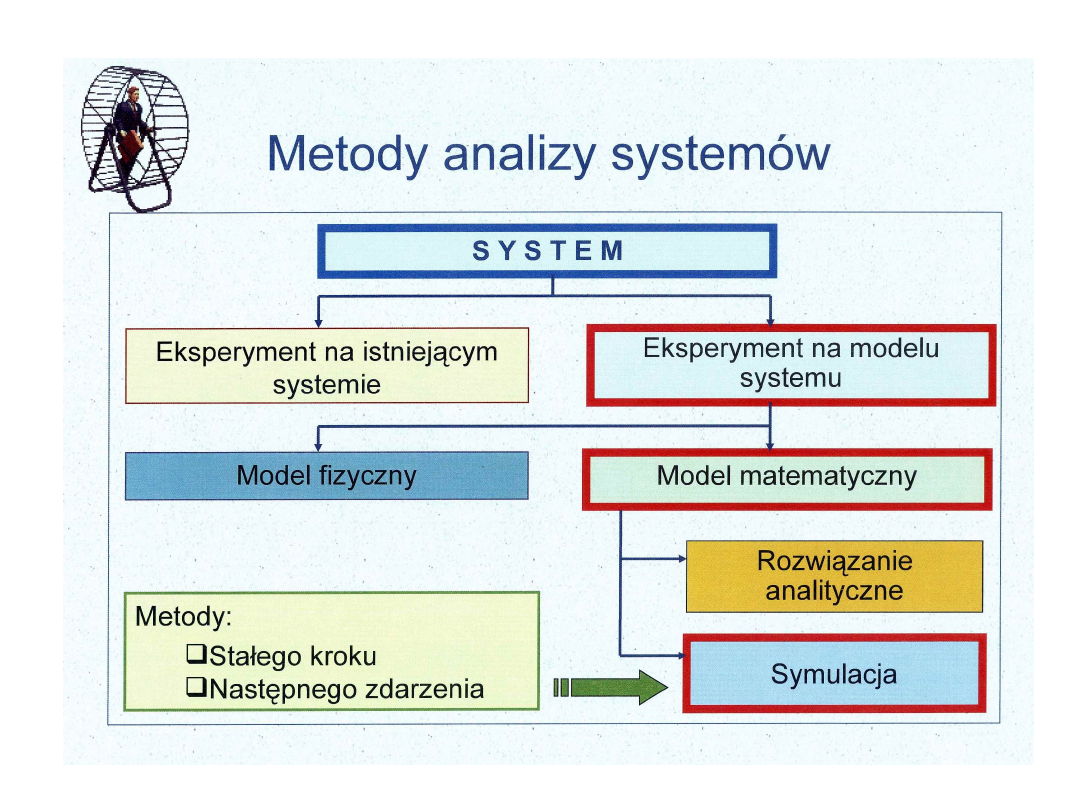
Symulacja komputerowa

• SYMULACJA KOMPUTEROWA – zastosowanie

techniki komputerowej do rozwiązywania
problemów dynamicznych modeli systemów.

• CELEM SYMULACJI KOMPUTEROWEJ jest

odtworzenie przebiegu badanego procesu na
podstawie jego modelu matematycznego za
pomocą techniki komputerowej i badanie wpływu
otoczenia (sygnały wejściowe) oraz
wewnętrznych właściwości obiektu (parametry
procesu) na charakterystyki obiektu.

Zastosowania symulacji:

• Jako metody weryfikacji konstrukcji.
• Jako metody konstruowania.
• Jako metody optymalizacji.
• Symulatory - Trenażery.
• Gry komputerowe.
• Dla określania właściwości obiektów.
• Jako sposobu analizy układów (systemów) lub

procesów złożonych.

• Dla celów prezentacyjnych i poglądowych

animacje komputerowe.

Modele symulacyjne

• Modele bardziej złożonych układów, składających się z wielu

oddziałujących obiektów będziemy nazywali też systemami.

• W przypadku złożonych układów trudno jest budować ich

materialne modele. Znacznie łatwiej i sensowniej jest tworzyć ich
modele komputerowe. Modele takie są w stanie znacznie
dokładniej reprezentować właściwości rzeczywistych układów.
Tworzenie takich modeli jest możliwe od czasu kiedy moc
obliczeniowa komputerów stała się dostatecznie duża, w praktyce
od kilkunastu lat. Mówimy, że modele komputerowe są wirtualne
lub numeryczne. Pomimo tego, że są one wirtualne, cechują się
najczęściej znacznie większą funkcjonalnością niż modele
konwencjonalne. W szczególności model wirtualny, o ile został
zaprojektowany w sposób dostatecznie dokładny, może być
wykorzystany również do symulacji zachowania się obiektów w
warunkach zbliżonych do rzeczywistych.

Modele proste i złożone

• Podział na modele układów prostych i złożonych jest dosyć

umowny. Posługując się przykładami podanymi wyżej moglibyśmy
powiedzieć, że np. samolot jest obiektem prostym, a układ
planetarny układem złożonym. Jednak kiedy zaczynamy
interesować się strukturą wewnętrzną samolotu,
funkcjonowaniem jego silników, oddziaływaniem skrzydeł
samolotu z atmosferą podczas lotu, natychmiast okazuje się, że
samolot staje się układem złożonym, a nawet bardzo złożonym.
Warto tutaj powiedzieć, że współczesne samoloty buduje się
konstruując najpierw ich wirtualne, komputerowe modele.
Pierwszym takim bardzo złożonym, wirtualnym modelem
samolotu był model Boeinga 777, za który firma ta została w roku
1995 uhonorowana prestiżową nagrodą "ComputerWorld-
Smithsonian Award". Stworzone modele, w miarę możliwości,
powinny być ostatecznie weryfikowane i optymalizowane w
warunkach eksperymentalnych. Taką strategię przyjmuje się w
przypadku optymalizacji kształtu samolotów. Końcowe korekty
kształtu i dynamiki opływu powietrza podczas lotu wykonywane
są na podstawie badań modeli samolotu w tunelach
aerodynamicznych.

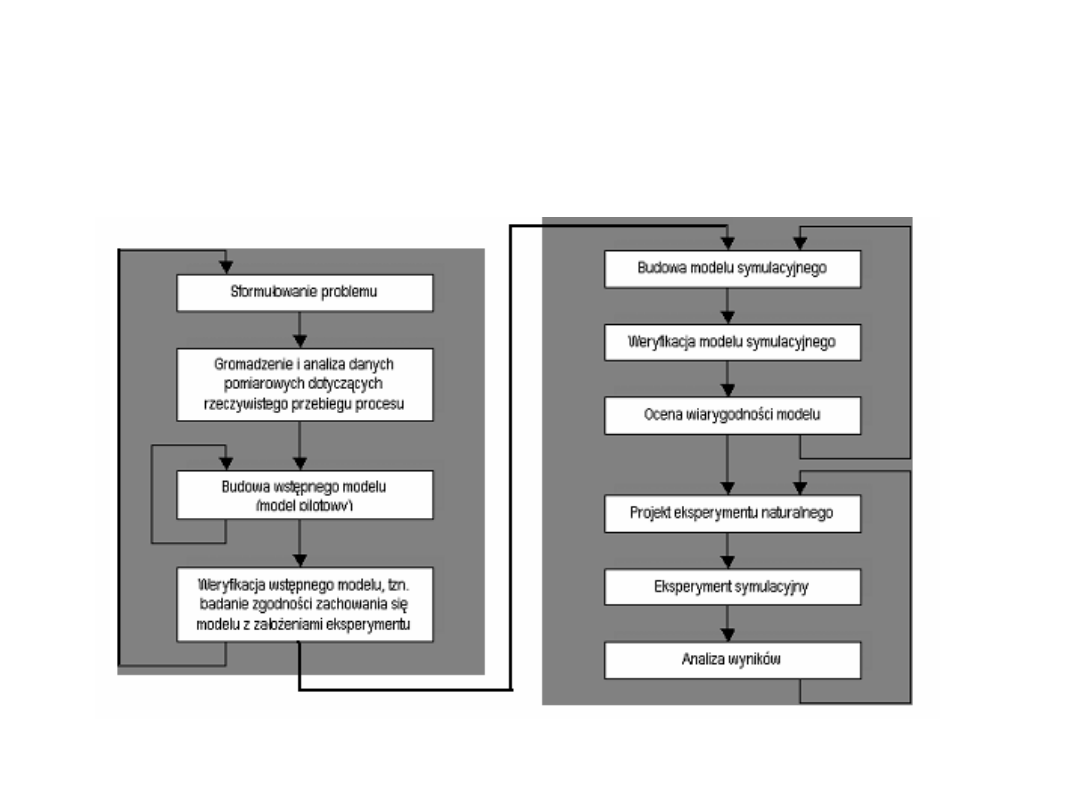
Ogólny schemat postępowania przy tworzeniu

modelu symulacyjnego

Klasyfikacja narzędzi symulacyjnych

• Arkusze kalkulacyjne,
• Programy do wspomagania obliczeń

inżynierskich (MathCAD, Matlab itp.)

• Programy komputerowe do tworzenia modeli

symulacyjnych oraz symulacji (CAD, CAE, CAM),

• Języki symulacyjne,

Modelowanie i symulacja w

projektowaniu

• Struktura to w ogólności zasada organizacji zbioru. Struktura

maszyny to organizacja zbioru jej elementów.

• Maszyny złożone mają strukturę hierarchiczną.
• Projektowanie jest obmyślaniem nowych wytworów i układów lub

wytworów i układów powstających w wyniku przekształcenia
dotychczas istniejących.

• Projektowanie jest działalnością odnoszącą się do wielu dziedzin

życia ludzkiego. Mówimy o projektowaniu wytworów materialnych,
jak maszyny, urządzenia, przedmioty codziennego użytku itp., jak
też układów niematerialnych, np.: systemów organizacji,
systemów finansowania itp. Projektuje się: zakłady przemysłowe,
układy transportowe, tereny leśne, szkoły, szpitale, osiedla,
kombinaty, miasta, zespoły miejskie, sieci transportowe itp.

• Projekt jest abstrakcyjnym obrazem wytworu lub układu, który ma

być wytworzony. Projekt jest rejestrowany w postaci dokumentacji
projektowej.

• Dokumentacja to także model projektowanego obiektu.

Maszyny jako przedmiot badań

symulacyjnych

• Konstruowanie to wg Dietrycha [5] dobieranie cech konstrukcyjnych,

umożliwiających optymalną realizację podstawowego zadania maszyny.

• Jedną z miar zdolności realizacji zadania (funkcji celu) są wskaźniki

jakości.

• Def. 1. Maszyna to zbiór (system) elementów, lub element (maszyna

prosta) połączonych ze sobą w sposób pozwalający na realizację
określonego zadania polegającego na transformacji energii lub informacji.

• Def. 2. Maszyną nazywamy układ materialny, złożony z połączonych ze

sobą ciał wykonujących określony ruch, służący do wykonania pracy
związanej z procesem wytwórczym lub przemianą energii.

• Def. 3. Zgodnie z ustaleniami przyjętymi przez EWG (Dyrektywa Rady z 14

czerwca 1989 r. w sprawie ujednolicenia przepisów prawnych państw
członkowskich dotyczących maszyn — nr. 89/392/EWG) za maszynę
uważa się całość powiązanych ze sobą części lub elementów, z
których przynajmniej jedna jest ruchoma, wraz z odpowiednimi
urządzeniami roboczymi, układami sterowania, zasilania itp., które
są połączone razem w celu określonego zastosowania, w
szczególności do przetwarzania, obrabiania, przemieszczania i
pakowania materiałów.

• Za maszynę uważa się także zespól maszyn, które aby mogły

współpracować, są rozmieszczone i wprawiane w ruch tak, że
działają jako jedna całość.

Maszyny jako przedmiot badań

symulacyjnych

• Określenie maszyny oznacza również wymienny osprzęt zmieniający funkcje

maszyny, wprowadzany na rynek z przeznaczeniem zamontowania do
maszyny lub też do serii różnych maszyn albo przez operatora do ciągnika, o
ile urządzenia te nie stanowią części zamiennych lub narzędzi.

• Maszyny dzieli się zwykle na silniki i maszyny robocze. Silnik jest to maszyna

służąca do zamiany pewnego rodzaju energii na pracę mechaniczną. Maszyna
robocza jest to maszyna, za pomocą której dokonuje się zmiany właściwości
stanu, kształtu lub położenia materiału albo przedmiotu. Maszyny robocze
można podzielić na technologiczne, transportowe i energetyczne.

• Maszyny technologiczne służą do przetwarzania surowców lub półfabrykatów

w gotowy wyrób lub półwyrób. Należą do nich np.: obrabiarki, walcarki,
maszyny górnicze, maszyny do przeróbki materiałów budowlanych i
drogowych, maszyny rolnicze itp.

• Maszyny transportowe służą do zmiany położenia materiałów lub

przedmiotów. Zalicza się do nich: dźwignice, przenośniki, pojazdy
samochodowe i szynowe, statki, samoloty itp.

• Maszyny energetyczne służą do przetwarzania jednej postaci energii na

drugą. Są to: pompy, sprężarki itp.

Tematyka przedmiotu i

podstawowe pojęcia c.d.

• Rodzajem projektowania jest konstruowanie. Termin ten określa

szczegółowe projektowanie maszyn i ich elementów.

• W rzeczywistości konstruowanie i konstrukcja to również pojęcia

znacznie szersze. Stąd też istnieją poglądy, iż pojęcia
konstruowania i projektowania zasadniczo się nie różnią , lub też
przeciwnie, traktują pojęcie projektowania jako szersze
obejmujące swoim zakresem konstruowanie rozumiane jako faza
procesu projektowania związana z syntezą metryczną i
weryfikacją obliczeniową rozwiązania technicznego.

• Konstrukcją nazywamy abstrakcyjny obraz maszyny, ze

wszystkimi jej cechami, powstający w umyśle konstruktora.
Konstruowanie jest procesem tworzenia konstrukcji. Konstrukcja
jest rejestrowana w postaci dokumentacji konstrukcyjnej, w skład
której wchodzą rysunki, obliczenia, opisy itp.

Ogólne i szczegółowe zasady

konstrukcji

• Dwie ogólne zasady konstrukcji

• (sformułowane przez Zbigniewa Osińskiego i Jerzego Wróbla „Teoria

konstrukcji”)

• 1. Konstrukcja powinna spełniać wszystkie podstawowe warunki,

wynikające ze szczegółowych zasad w stopniu równym lub
wyższym od założonego.

• 2. Konstrukcja powinna być optymalna (polioptymalna) w danych

warunkach ze względu na przyjęte kryterium (kryteria)
optymalizacji.

• Konstrukcja, która spełnia pierwszą zasadę, jest konstrukcją dobrą.

Zwykle istnieje zbiór konstrukcji dobrych.

• Konstrukcja spełniająca zasadę drugą jest konstrukcją optymalną

(polioptymalna) ze względy na przyjęte kryterium (kryteria)
optymalizacji. Oczywiście, konstrukcja optymalna należy do zbioru
konstrukcji dobrych.

Szczegółowe zasady konstrukcji

• 1) funkcjonalność,
• 2) niezawodność,
• 3) trwałość,
• 4) sprawność,
• 5) lekkość,
• 6) taniość i dostępność materiałów,
• 7) właściwy układ przenoszenia obciążeń,
• 8) technologiczność,
• 9) łatwość eksploatacji,
• 10) ergonomiczność,
• 11) ochrona środowiska,
• 12) zgodność z obowiązującymi normami i przepisami.

• Uwaga:

Liczba tych zasad nie musi być precyzyjnie określana, można

bowiem ich zbiór rozszerzać zależnie od potrzeby

.

Kryteria oceny konstrukcji

• Według Marka Dietricha – „Podstawy konstrukcji maszyn”

WNT Warszawa

• kryterium bezpieczeństwa,
• kryterium niezawodności,
• kryterium masy,
• kryterium ekonomiki eksploatacji,
• kryterium technologiczności konstrukcji,
• kryterium ergonomii i estetyki,
• kryterium ekologiczne.

• Podstawowe kryterium – kryterium zagregowane – to kryterium

ekonomiczne będące funkcją zysku ze sprzedaży wyrobu tj.
różnicy uzyskanej na rynku ceny i kosztu wytworzenia.

• Cena jest miarą wartości użytkowej wyrobu.
• Z powyższego wynika konieczność racjonalizacji technik

wytwarzania i ich dostosowania do możliwości wykonawcy, jak też
potrzeb rynku.

Fazy procesu projektowania i

konstruowania

• Sformułowanie zadania projektowego,
• Identyfikacja ograniczeń,
• Sformułowanie kryteriów oceny,
• Opracowanie założeń konstrukcyjnych,
• Poszukiwanie koncepcji rozwiązania,
• Wybór koncepcji do dalszego rozwiązania,
• Opracowanie projektu wstępnego,
• Weryfikacja teoretyczna lub eksperymentalna na modelach,
• Projekt techniczny i wykonawczy prototypu,
• Wykonanie prototypu
• Weryfikacja doświadczalna - badania stanowiskowe i

eksploatacyjne,

• Weryfikacja dokumentacji i wdrożenie.

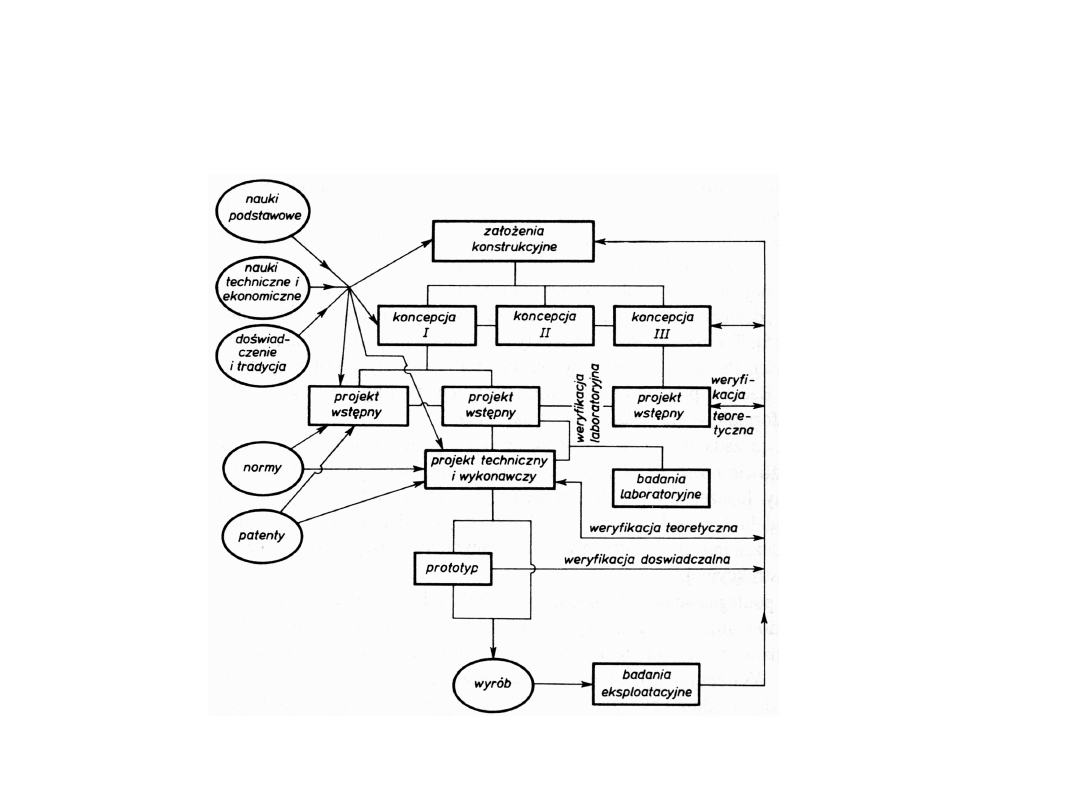
Schemat obrazujący proces

konstruowania

Prototypowanie wirtualne

Charakterystyczne cechy wirtualnego

prototypowania

• Prototypem wirtualnym jest model 3D sparametryzowany pod

względem geometrycznym jak też fizycznym. Model taki,
teoretycznie o dowolnym stopniu złożoności tworzony jest
komputerowo w modelerze CAD (przykładowo AUTODESK
INVENTOR ).

• Docelowo model taki ma być wiernym obrazem rzeczywistego

materialnego obiektu stanowiącego podstawę dla opracowania
dokumentacji konstrukcyjnej rysunkowej w sposób
wspomagany komputerowo, przeprowadzenia badań
symulacyjnych weryfikujących konstrukcję i jej działanie w
określonych warunkach przy wykorzystaniu oprogramowania
CAE w zakresie analiz kinematyki i dynamiki na modelu o
elementach traktowanych jako bryły sztywne, lub bryły
odkształcalne, analiz wytrzymałościowych i modalnych,
opracowaniu i symulacji procesu wytwarzania przy
wykorzystaniu oprogramowania CAM.

• Praktycznie z uwagi na ograniczone możliwości obliczeniowe

dostępnych stacji roboczych także wirtualny model upraszcza
się do modeli stwarzających mniejsze wymagania w stosunku
do posiadanego sprzętu.

Człony mechanizmów

Człon mechanizmu to
element konstrukcyjny o
dowolnym kształcie,
niepodzielny w aspekcie
funkcji jaką spełnia w
układzie kinematycznym.

Człon może być ruchomy bądź
nieruchomy.
Człon nieruchomy nazywa się
podstawą.
Przykłady członów nieruchomych:
- korpusy,
- ramy,
- obudowy.
Przykłady członów ruchomych:
- wały,
- osie,
- dźwignie,
- łączniki przegubowe,
- suwaki o różnych przekrojach,
- krzywki płaskie i przestrzenne,
- koła różnego rodzaju,
- sworznie,
- popychacze,
- zapadki.

Człony mechanizmów

Człon sztywny to element mechanizmu, który w trakcie ruchu
nie zmienia swego kształtu – odległość między dwoma
dowolnymi punktami członu sztywnego pozostaje stała.
Odpowiednikiem w mechanice klasycznej jest ciało sztywne, lub
bryła sztywna.
 
Człony podatne to takie człony, które pod działaniem sił ulegają
odkształceniom.
Można je podzielić na człony o podatności o charakterze
dyskretnym, takie jak sprężyny, resory, membrany itp., oraz
człony o podatności wynikającej z rozpatrywania członu jako
elementu o ciągłym rozkładzie własności sprężystych i
tłumiących (dyssypatywnych).

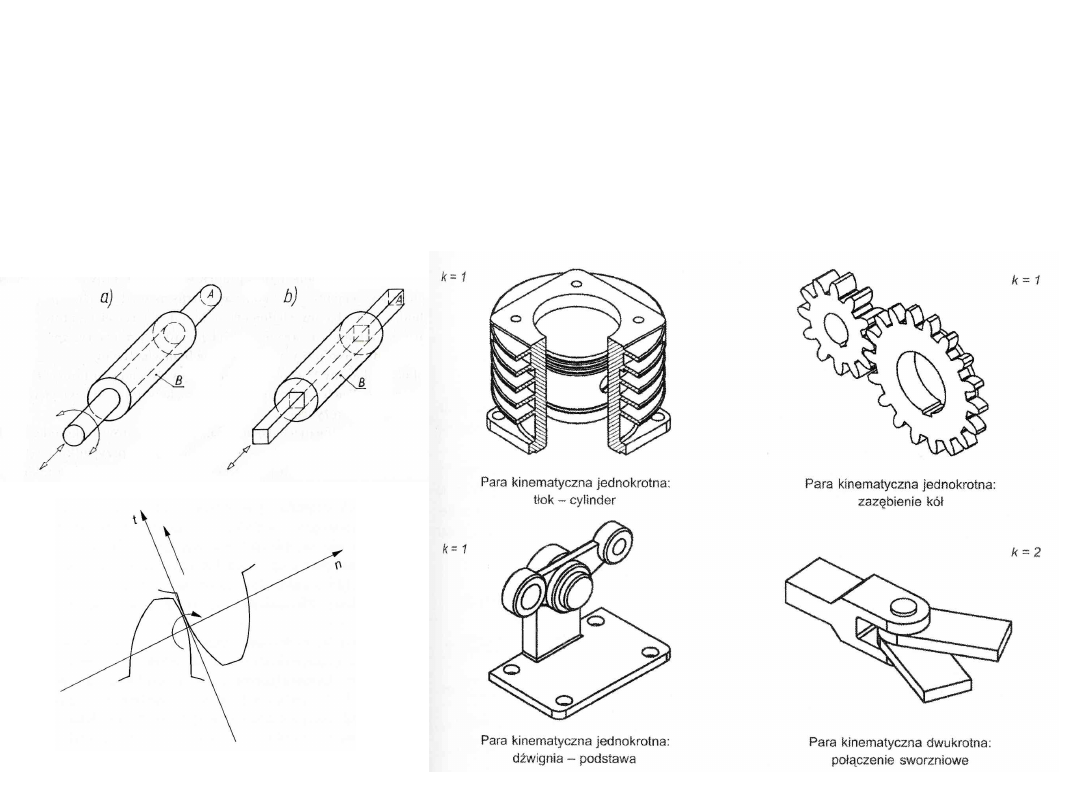
Pary kinematyczne

Para kinematyczna jest to ruchowe połączenie dwóch członów.
Człony stykają się punktowo lub powierzchniowo z możliwością
ruchów względnych, z czym wiąże się utrata pewnej liczby stopni
swobody każdego członu.

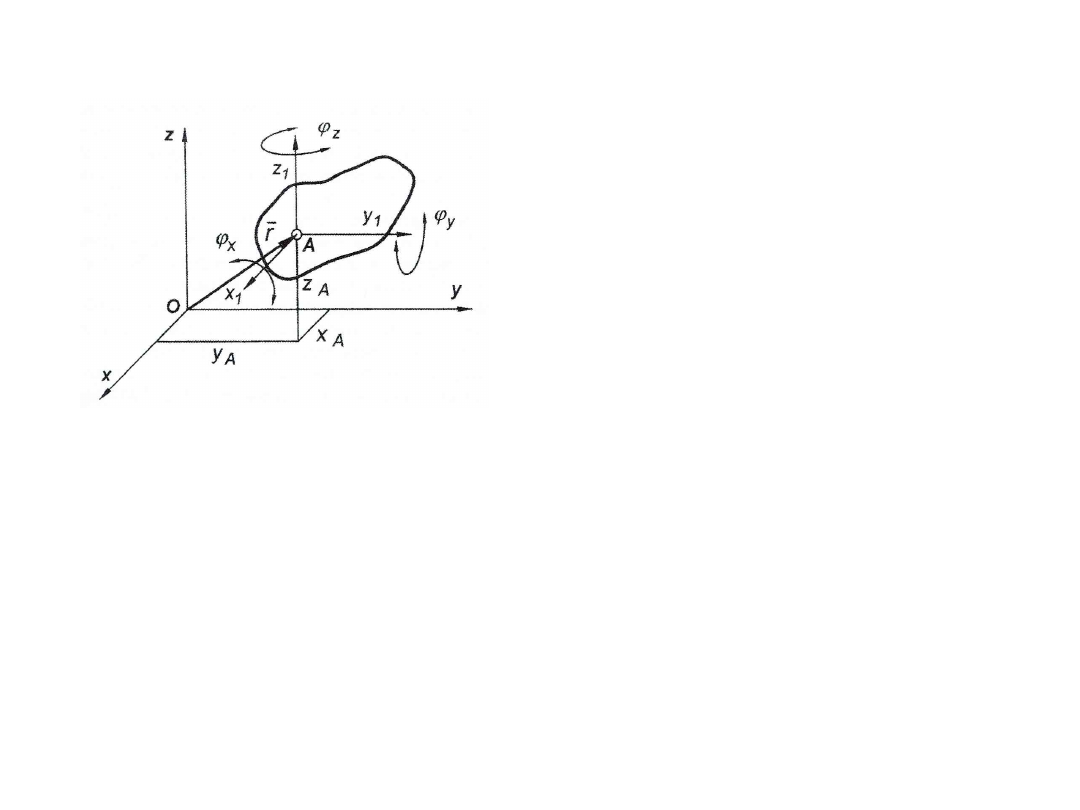
Stopnie swobody i więzy

Więzy podzielić można na holonomiczne tj. takie, które
ograniczają wyłącznie możliwości ruchu członów w przestrzeni i
nie zależą od ich prędkości względnej, oraz aholonomiczne
zależne od prędkości względnej członów, występujące w
przypadku połączeń członów odkształcalnych.
Więzy można też podzielić na jednostronne i dwustronne.
Ponadto więzy mogą być rozpatrywane jako idealne –
beztarciowe, oraz rzeczywiste – tarciowe.
Na liczbie odebranych stopni swobody w ruchu względnym oparto
klasyfikację par kinematycznych.

Liczba stopni swobody to liczba
niezależnych wielkości, których
znajomość jest konieczna do
jednoznacznego określenia
położenia układu (np. mechanizmu)
Pojedynczy nie związany z innymi
człon sztywny ma w przestrzeni 6
stopni swobody.

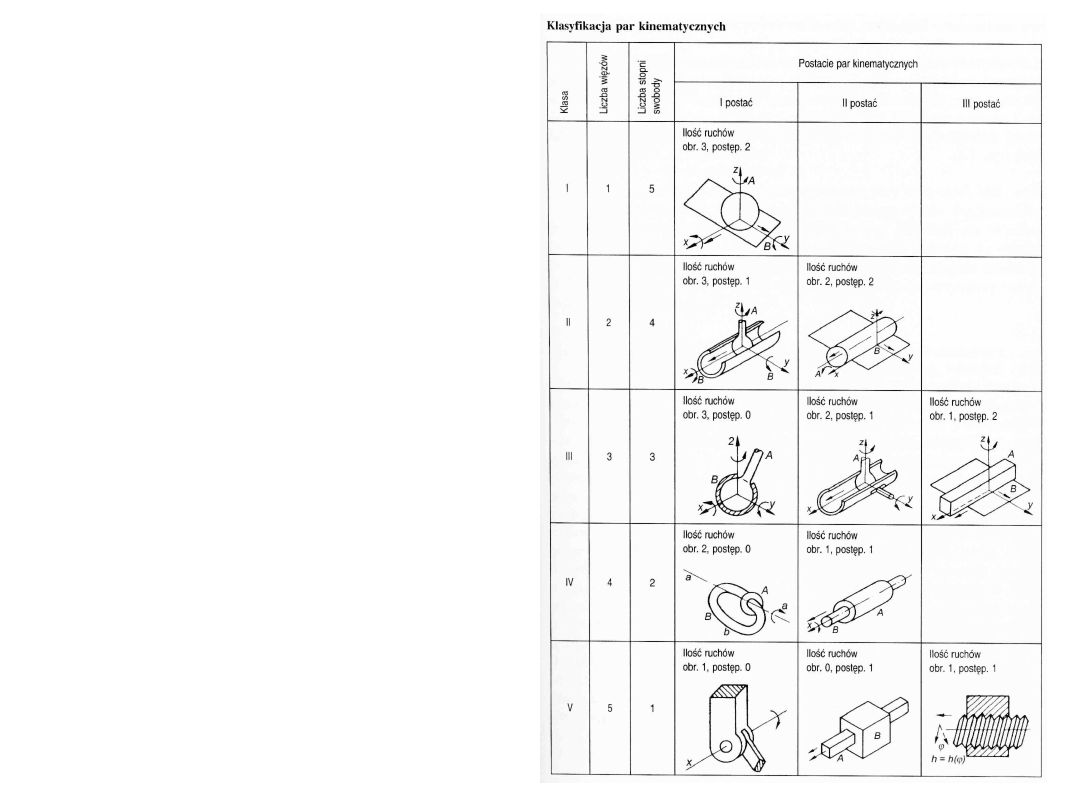
Pary kinematyczne dzieli się
na 5 klas:
para V klasy to para, w której
człon ma jeden stopień swobody
(5 stopni swobody zostało
odjętych),
para IV klasy to para o 2
stopniach swobody odebrane 4
stopnie, itd.,
aż do pary I klasy o pięciu
stopniach swobody, - 1 stopień
swobody odebrany.
Klasę „i” określa się więc z
zależności:

i = 6-s

gdzie: - s – liczba pozostałych
stopni swobody,
Wyróżnia się także pary
kinematyczne jednokrotne
występujące w przypadku
połączenia dwóch członów i
wielokrotne, gdy jednym więzem
połączona jest większa liczba
członów.
krotność pary kinematycznej
oblicza się z zależności:

k = n-1

gdzie: - n – liczba członów
stykających się w jednym węźle.

Definicje obiektu badań symulacyjnych

Innym węższym pojęciem jest łańcuch kinematyczny czyli zbiór
ogniw połączonych ruchowo.

Układ wieloczłonowy jest abstrakcyjnym modelem układu
rzeczywistego budowanym przy upraszczającym założeniu, iż
elementy układu rzeczywistego można traktować jako człony
sztywne lub odkształcalne połączone ze sobą w różny sposób
(połączenia suwliwe, obrotowe lub sferyczne itp.) i poruszające się
pod działaniem sił i momentów zewnętrznych lub wewnętrznych,
skupionych lub rozłożonych, sił kontaktów z tarciem lub bez tarcia
itp.

Mechanizm to łańcuch kinematyczny wykonujący ściśle określony
ruch.
Maszyna to zespół mechanizmów wykonujących żądaną pracę
związaną z procesami technologicznymi lub przemianą energii

Ruchliwość mechanizmu

Liczba stopni swobody względem nieruchomej podstawy,
którą posiada dowolny układ członów (łańcuch kinematyczny), jest
miarą jego ruchliwości
Dowolny ustrój sprężysty, złożony z masowych elementów
odkształcalnych,
posiada nieskończenie wiele stopni swobody a więc jego ruchliwość
jest również nieskończenie wielka.
Dlatego obliczenie ruchliwości dowolnego układu członów,
rozumianego jako
łańcuch kinematyczny mechanizmu, ma sens tylko wtedy, gdy
założymy, że składa się on z członów sztywnych.

Ruchliwością mechanizmu w nazywamy liczbę więzów, które
należałoby na-
rzucić na człony, aby łańcuch kinematyczny mechanizmu był
nieruchomy względem podstawy.
Zatem jest to liczba stopni swobody mechanizmu względem
podstawy.
Ruchliwość w jest równa liczbie niezależnych napędów, które należy
przyłożyć
do łańcucha kinematycznego, aby wykonywał on ściśle określony
ruch, czyli był mechanizmem.

Ruchliwość mechanizmu

Dla dowolnego układu przestrzennego wprowadzimy następujące
oznaczenia:
n - liczba członów ruchomych łańcucha kinematycznego,
6n - liczba stopni swobody przestrzennego układu swobodnego,
i - klasa par występujących w łańcuchu kinematycznym i = 1,2, ..5,
• p

i

- liczba par kinematycznych klasy i-tej,

i *p

i

- liczba odebranych stopni swobody przez p, par kinematycznych

klasy i-tej,

Całkowita liczba odebranych stopni swobody przez wszystkie pary
kinematyczne.

Ostatecznie ruchliwość mechanizmu przestrzennego wyraża się
wzorem:







5

1

i

i

p

i













5

1

6

i

i

p

i

n

w

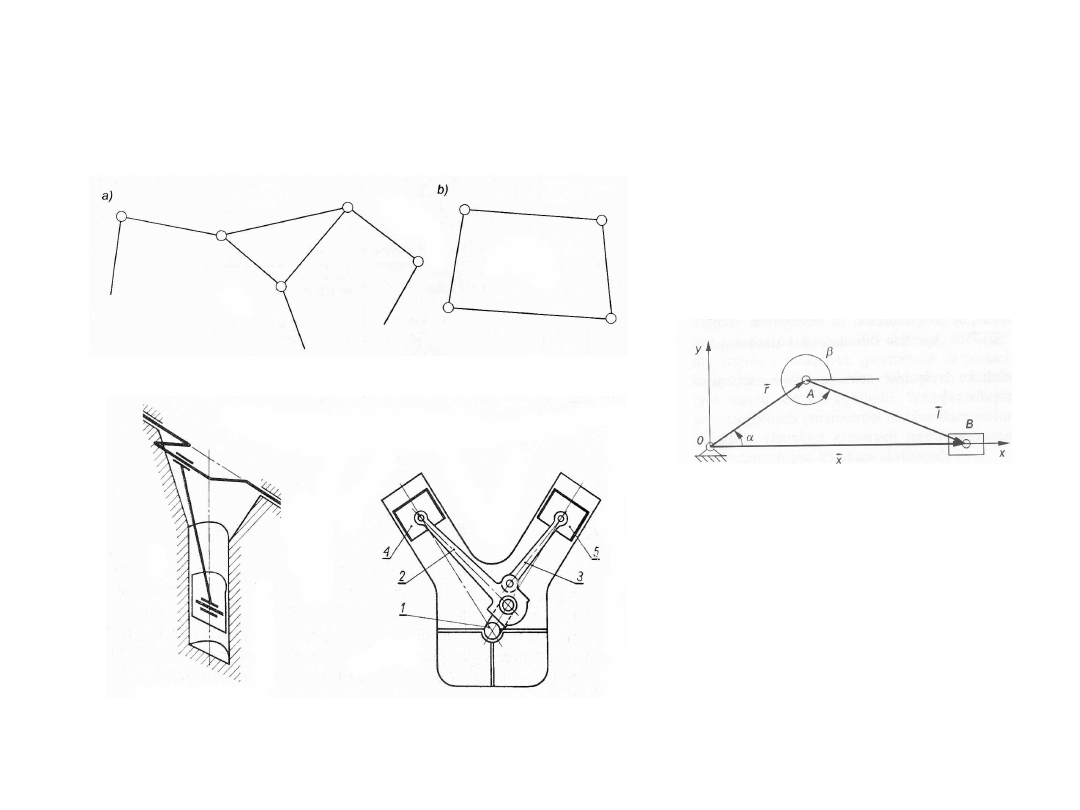
Łańcuchy kinematyczne

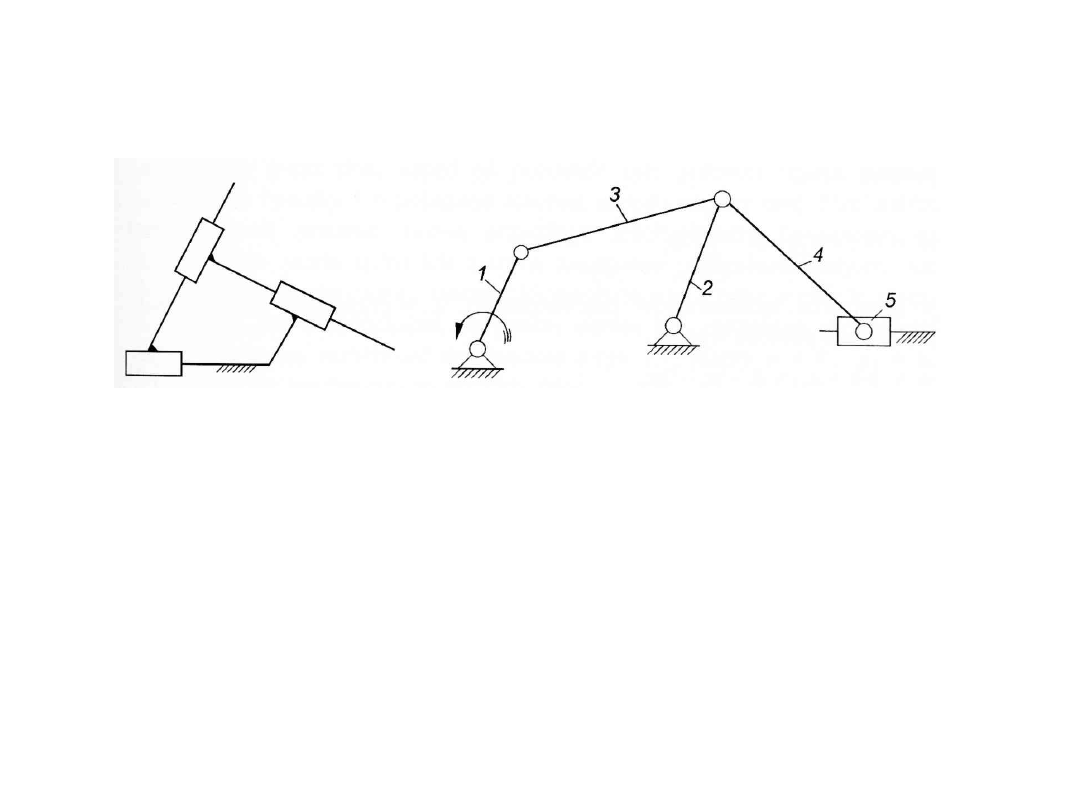
Przykład obliczania ruchliwości

P5(01,31,23,20,24,34,45,50)

w=3*5-0-2*8=-1 (para wielokrotna 324)

Łącząc człon 2 z układem odniesienia otrzymamy:

P5(01,31,20,2,42,45,50)=7

w=3*5-0-2*7=1

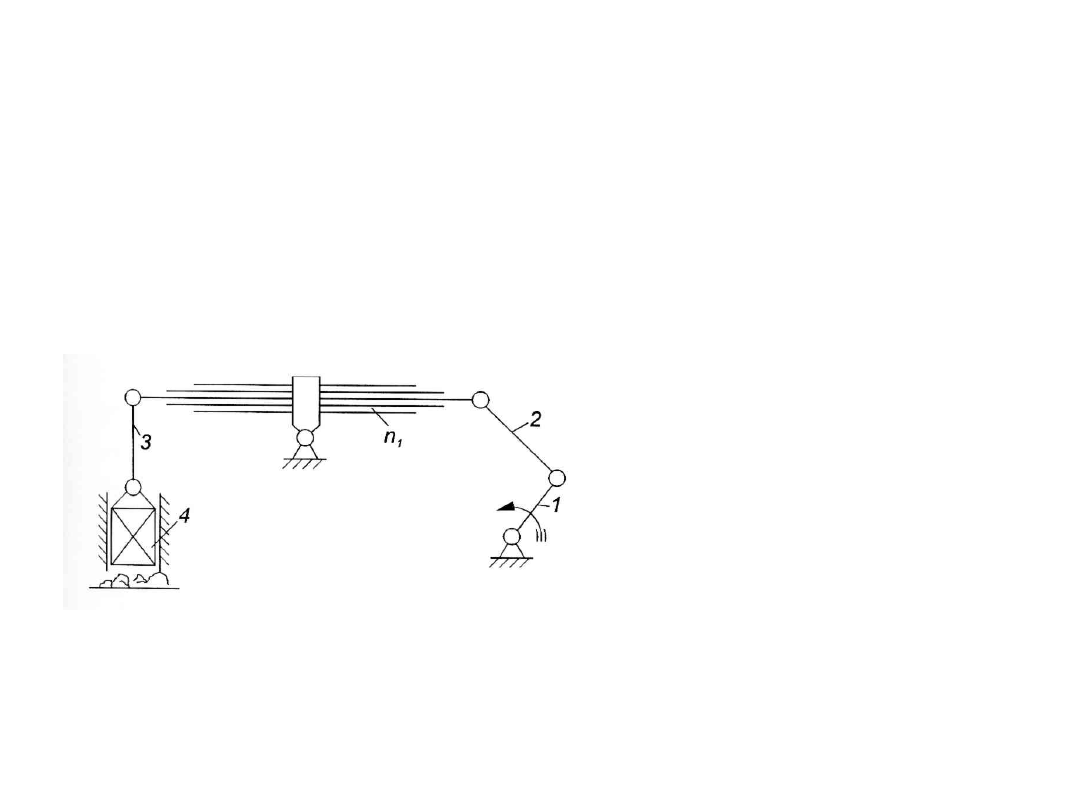
Mechanizmy z członami podatnymi























5

1

1

6

i

i

p

i

n

n

w

gdzie: n1 – liczba członów podatnych,

Δ – liczba dodatkowych stopni swobody wprowadzana przez człon podatny

Δ=1, p4=0, p5=7

W=3*(4+1) + 1-2+7 = 2

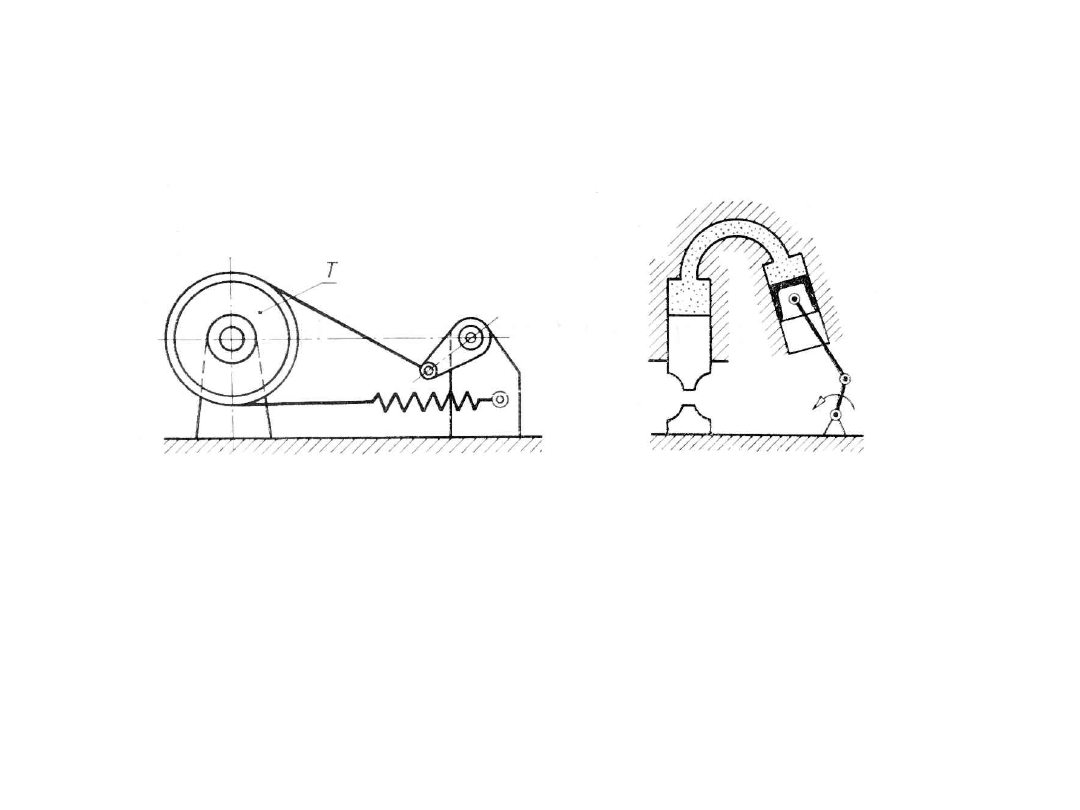
Mechanizmy z członami podatnymi

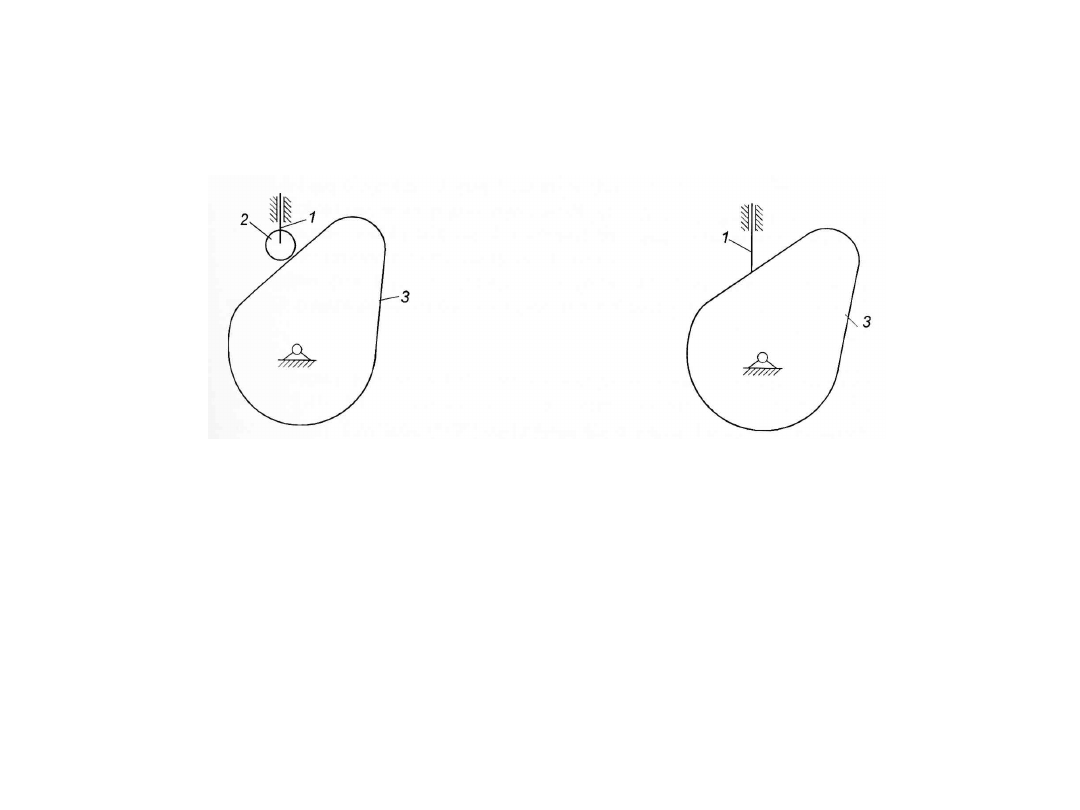
Ruchliwość lokalna

Przykład mechanizmu ze zbędnym stopniem swobody

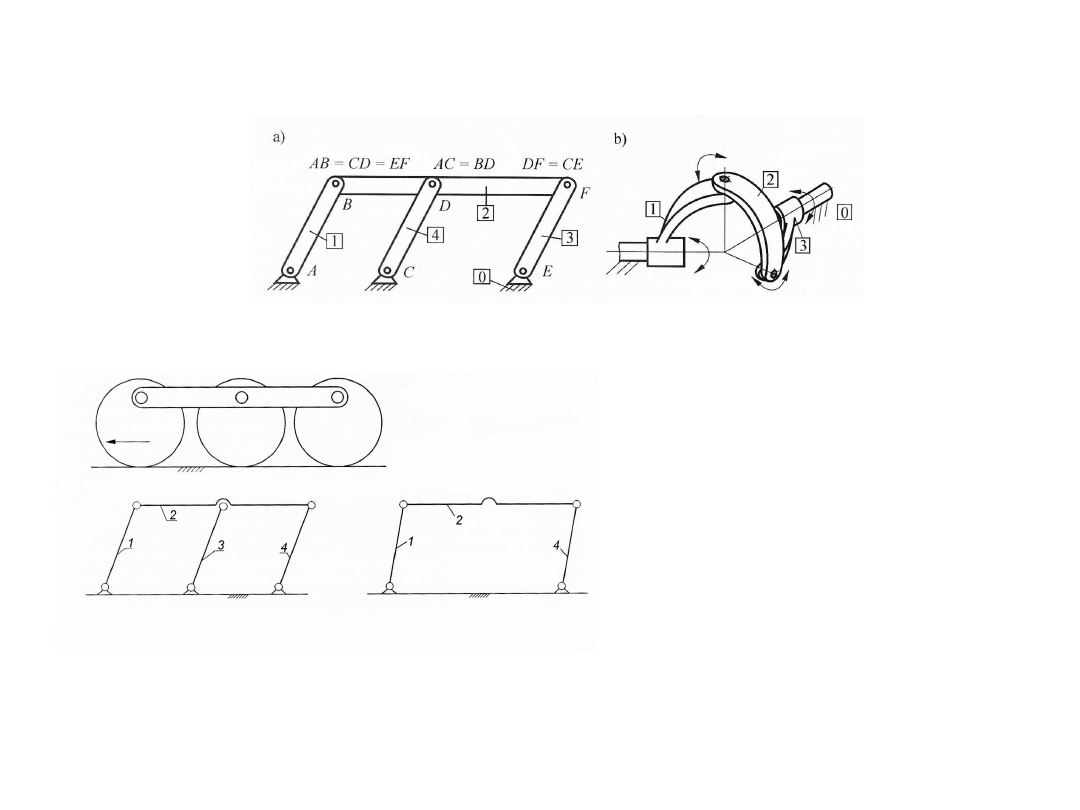
Mechanizmy z członami biernymi (więzy

nadmiarowe)

n=4, p5=6
w=3*4-2*6

n=3 p5=4
w=3*3-2*4=1

Więzy nadmiarowe (bierne)

Więzy bierne są to przesztywnienia występujące w
mechanizmie, uniemożliwiające jego poprawne działanie w
przypadku dużych błędów wykonawczych i montażowych.
Jeżeli liczba więzów biernych jest większa lub równa
jeden, R

b

> 1, to mechanizm ma strukturę

nieracjonalną.
Mówimy, że jest mechanizmem przesztywnionym.

Warunkiem racjonalnej struktury jest, aby liczba więzów
biernych była równa zero, czyli R

b

= 0.

Większość rzeczywistych mechanizmów ma strukturę
nieracjonalną, jednak mogą poprawnie funkcjonować dzięki
bardzo małym błędom wykonania i montażu.
Uzyskanie racjonalnej struktury wiąże się z usunięciem
zbędnych członów oraz z zastosowaniem par kinematycznych o
większej liczbie stopni swobody.
Zamiana par kinematycznych klasy 5 (przegubów walcowych) na
pary klasy 3 (przeguby kuliste) zmniejsza liczbę więzów
biernych.
W praktyce może to być zamiana łożysk tocznych zwykłych na
łożyska wahliwe.

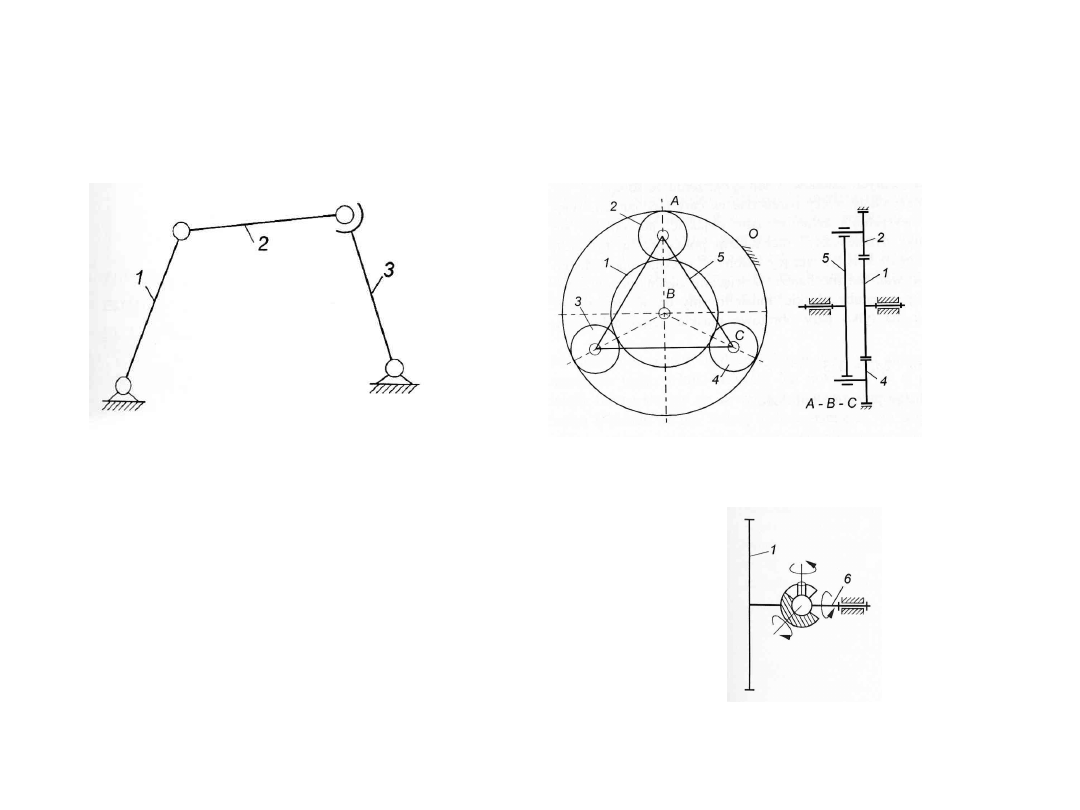
Mechanizmy z członami biernymi

Obliczanie liczby członów
biernych:















5

1

6

i

i

zał

b

p

i

n

w

s

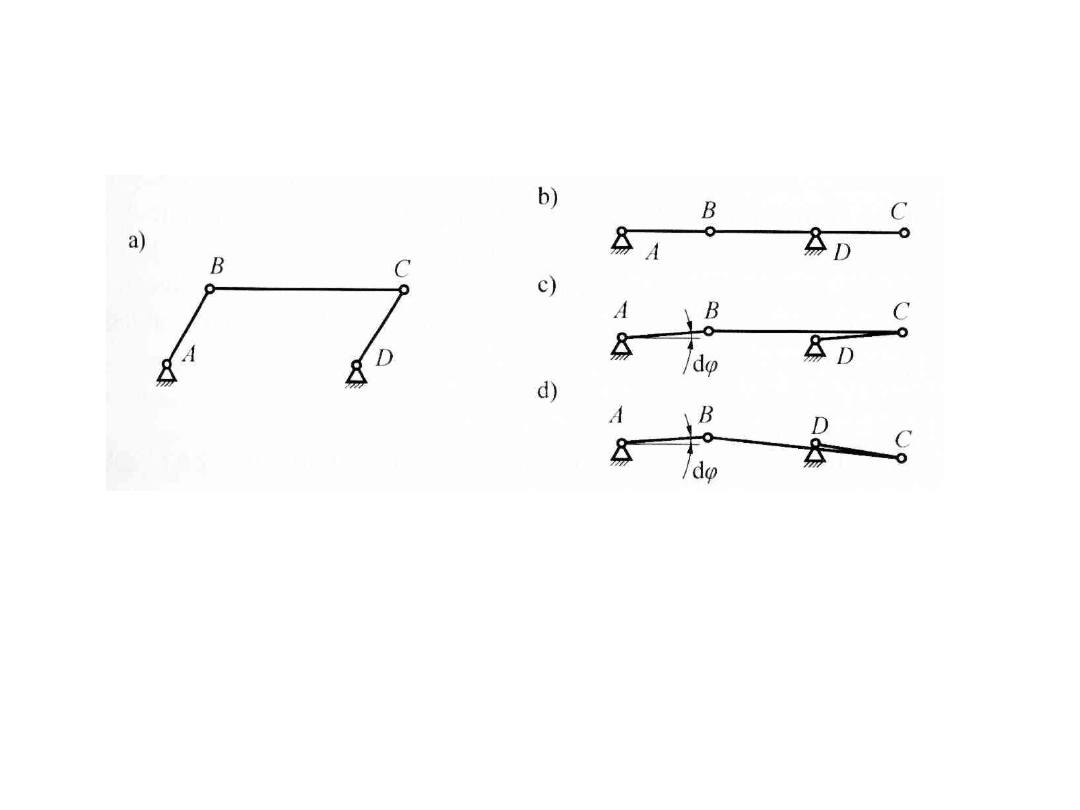
Konfiguracje osobliwe

Są to położenia chwilowe, w których ruch mechanizmu nie
jest jednoznacznie określony (zdeterminowany).

Klasyfikacja strukturalna mechanizmów

Klasyfikacja strukturalna mechanizmów dzieli mechanizmy na klasy
według
kryteriów strukturalnych, tj. według liczby członów, par kinematycznych
oraz
sposobu ich połączenia.
Celem klasyfikacji jest wskazanie zbioru prostych struktur, tzw. grup
strukturalnych, stanowiących podstawę budowy analizowanych łańcuchów
kinematycznych mechanizmów oraz ich metodycznej analizy i syntezy.
Kolejność postępowania przy klasyfikacji strukturalnej mechanizmów
płaskich
jest następująca:
1. Należy sporządzić schemat kinematyczny mechanizmu w postaci

zamkniętego łańcucha kinematycznego.

2. W przypadku występowania w mechanizmie par kinematycznych

wyższych
(klasy 4) należy sporządzić schemat zastępczy, w którym występują
wyłącznie
pary niższe (klasy 5).

3. Obliczyć ruchliwość w tak utworzonego łańcucha kinematycznego.
4. Wybrać człony napędzające w liczbie równej ruchliwości w i oddzielić je

od
łańcucha kinematycznego.

5. Pozostałą część łańcucha podzielić na grupy strukturalne.
6. Określić klasę mechanizmu, która jest równa najwyższej klasie grupy

strukturalnej.

Uwaga. Przy zamianie par wyższych na niższe muszą być spełnione następujące
warunki:

• ruch chwilowy łańcucha musi pozostać niezmieniony;

• ruchliwość łańcucha musi pozostać niezmieniona, dlatego każdą parę klasy 4

należy zastąpić dwiema parami klasy 5, wprowadzając dodatkowy człon łączący
się z nowo utworzonymi parami niższymi.

Grupy strukturalne mechanizmów

Grupa strukturalna jest częścią łańcucha kinematycznego
mechanizmu spełniającą dwa warunki:
1. połączenie ruchowe z podstawą wszystkich członów

zewnętrznych grupy zamienia ją w układ sztywny, tj. układ o
ruchliwości w = 0; (układ o ruchliwości w = 0 jest zawsze
układem statycznie i dynamicznie wyznaczalnym);

2. wyodrębniona część łańcucha kinematycznego spełniająca

warunek 1) nie da się podzielić na prostsze układy (np.
poprzez odłączenie członów) również spełniające ten
warunek.

Grupę strukturalną definiuje się w sposób umowny na
podstawie liczby
członów i par oraz sposobu przyłączenia ich do podstawy.
Definiuje się pojęcie rzędu i klasy grupy.
O klasie grupy decyduje najbardziej rozbudowany wielobok
występujący
w schemacie grupy. Klasa grupy jest równa liczbie boków tego
wieloboku.
Rząd grupy strukturalnej jest określony poprzez liczbę półpar
kinematycznych zewnętrznych, za pomocą których łączy się
grupę z podstawą, aby zamienić
ją w układ sztywny.

Cechy grupy strukturalnej mechanizmu

Połączenie członów zewnętrznych grupy

strukturalnej z podstawą powoduje zamianę
wyodrębnionej część łańcucha kinematycznego
w układ sztywny w

gr

= 0.

Taki układ członów jest statycznie i

dynamicznie wyznaczalny.

Ta ważna cecha grupy strukturalnej jest

szczególnie przydatna w trakcie analizy sił
działających w parach kinematycznych
mechanizmów.

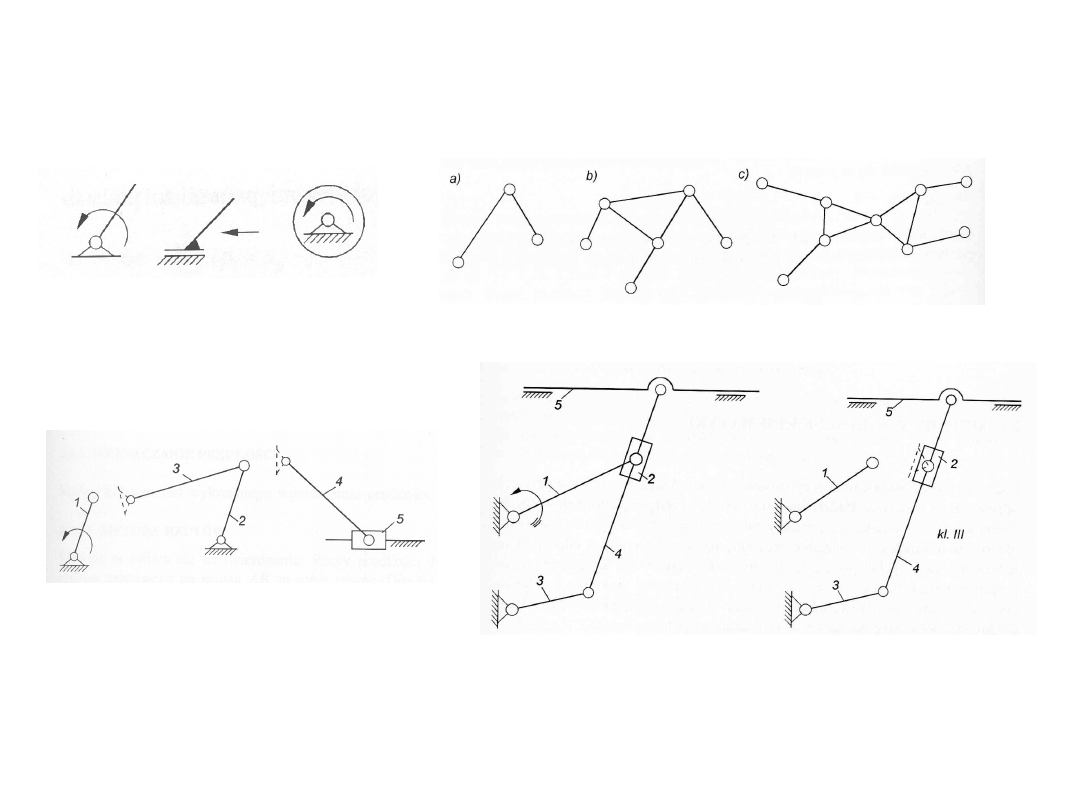
Podział strukturalny mechanizmów

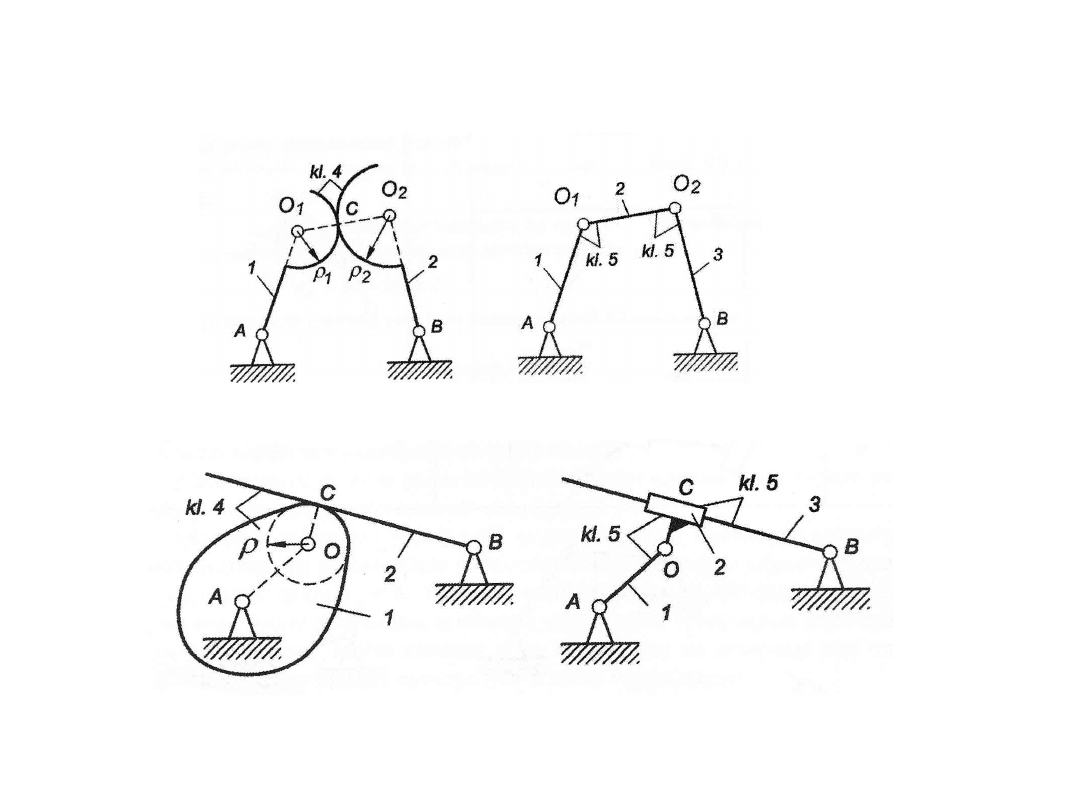
Zastępowanie par klasy 4 na pary klasy 5

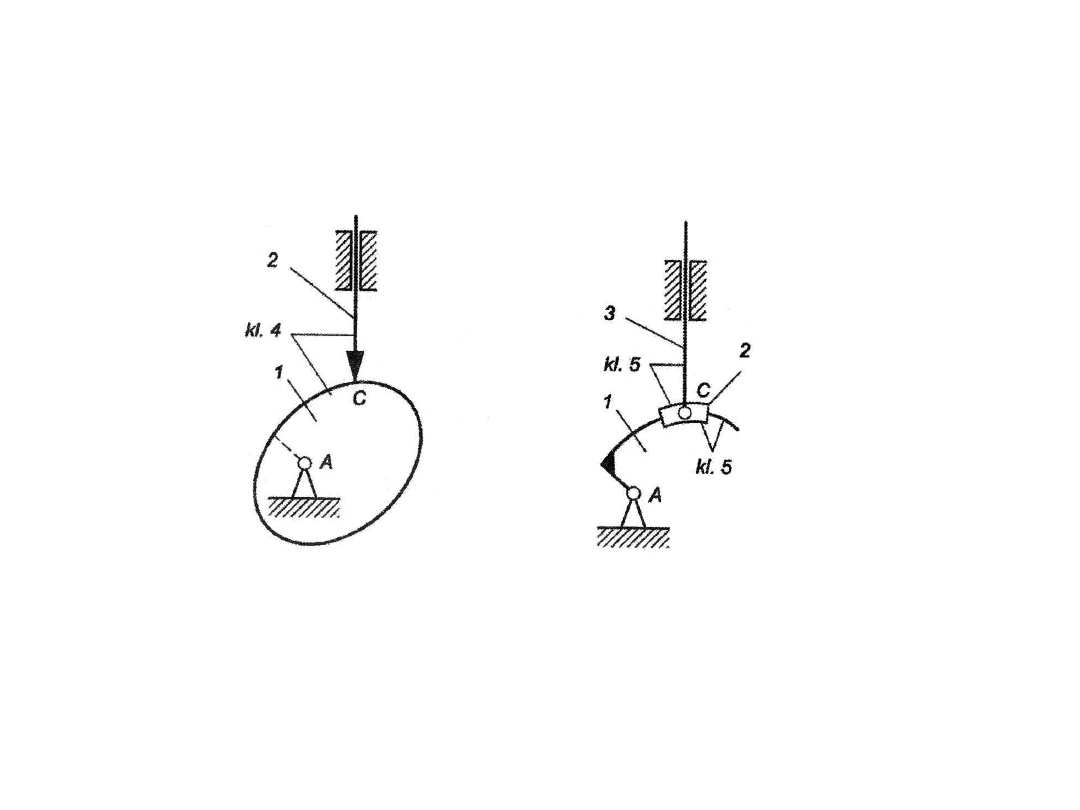
Zastępowanie par klasy 4 na pary klasy 5

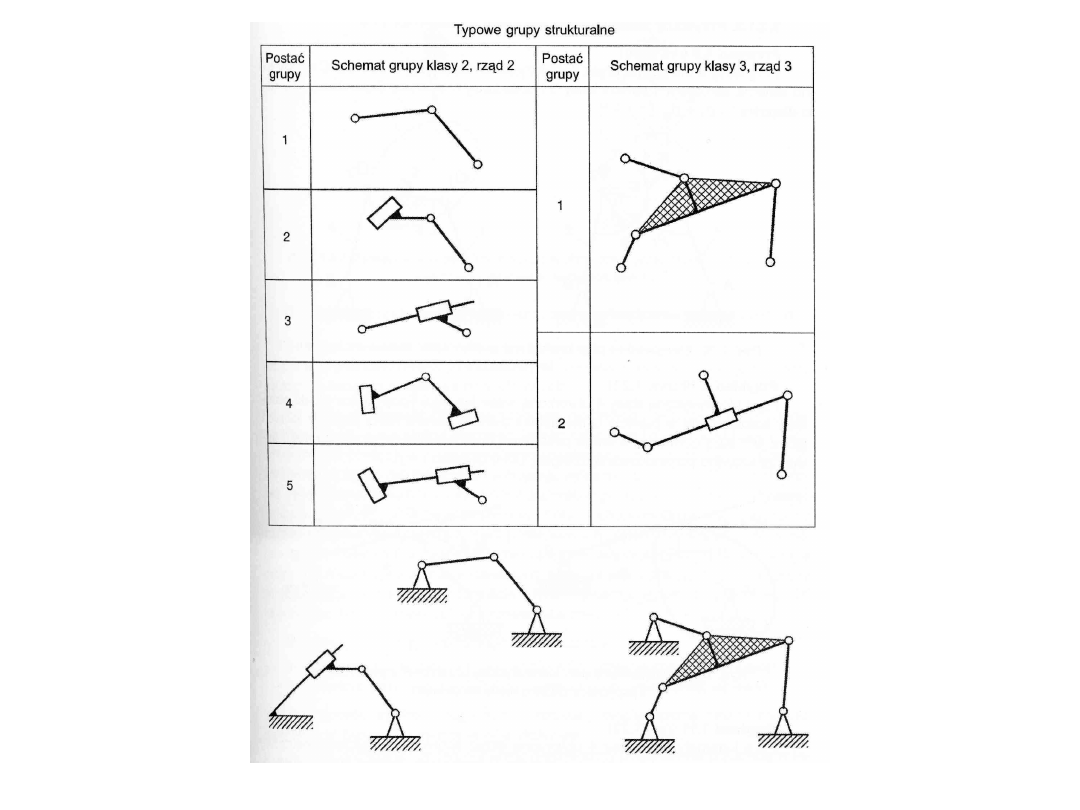
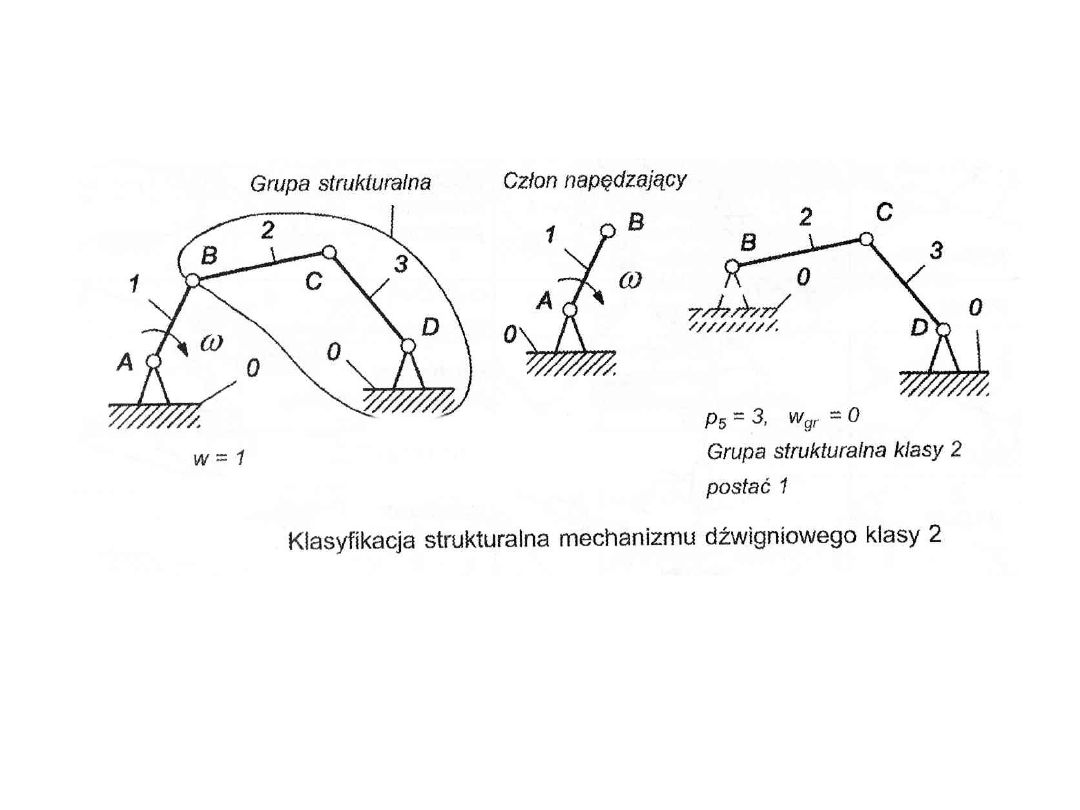
Klasyfikacja strukturalna mechanizmów

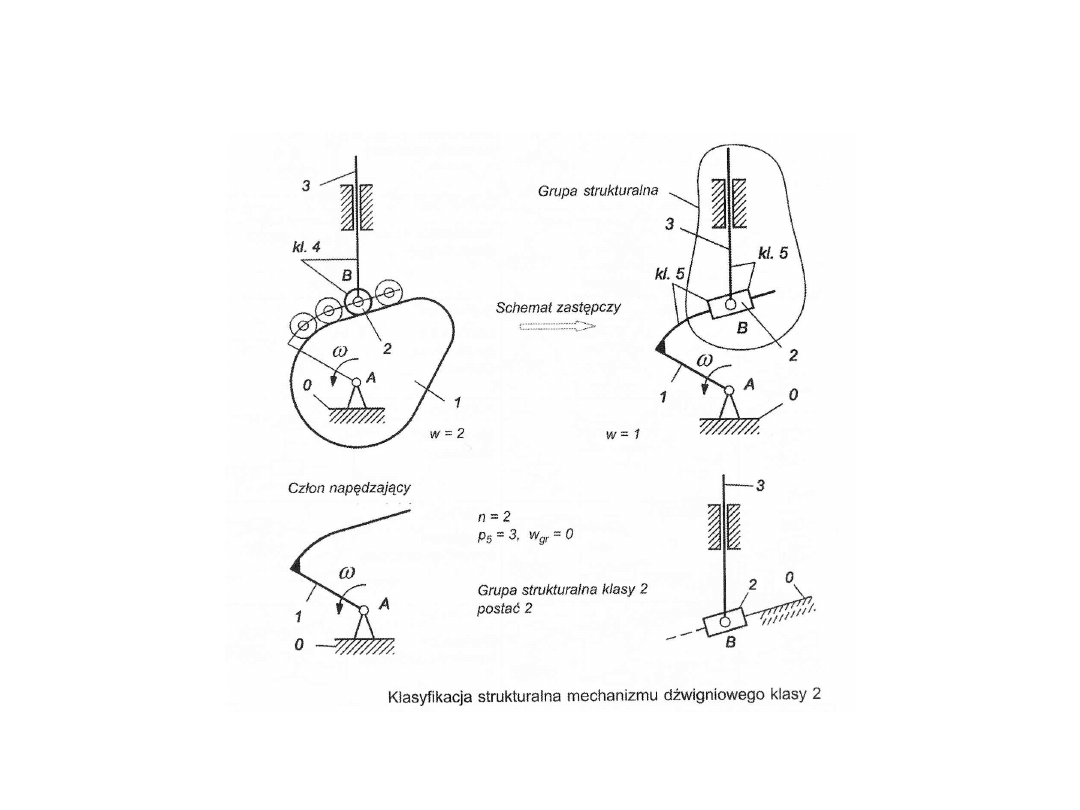
Klasyfikacja strukturalna mechanizmów

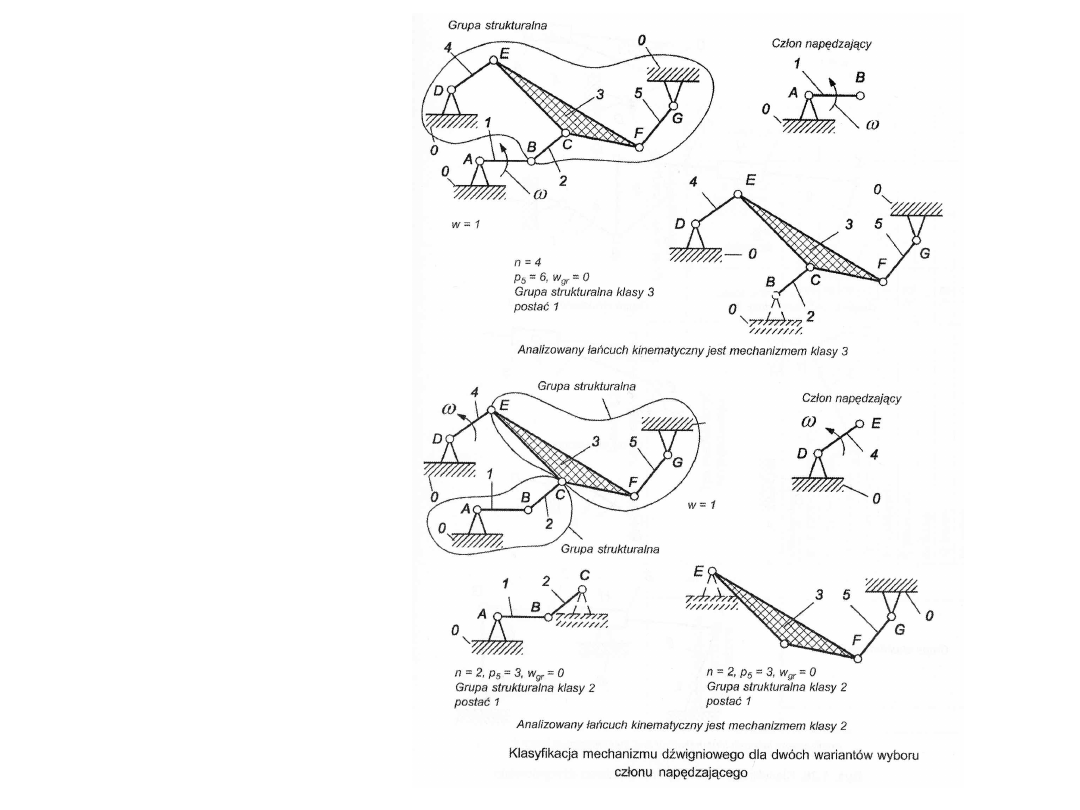
Klasyfikacja

strukturalna

mechanizmów

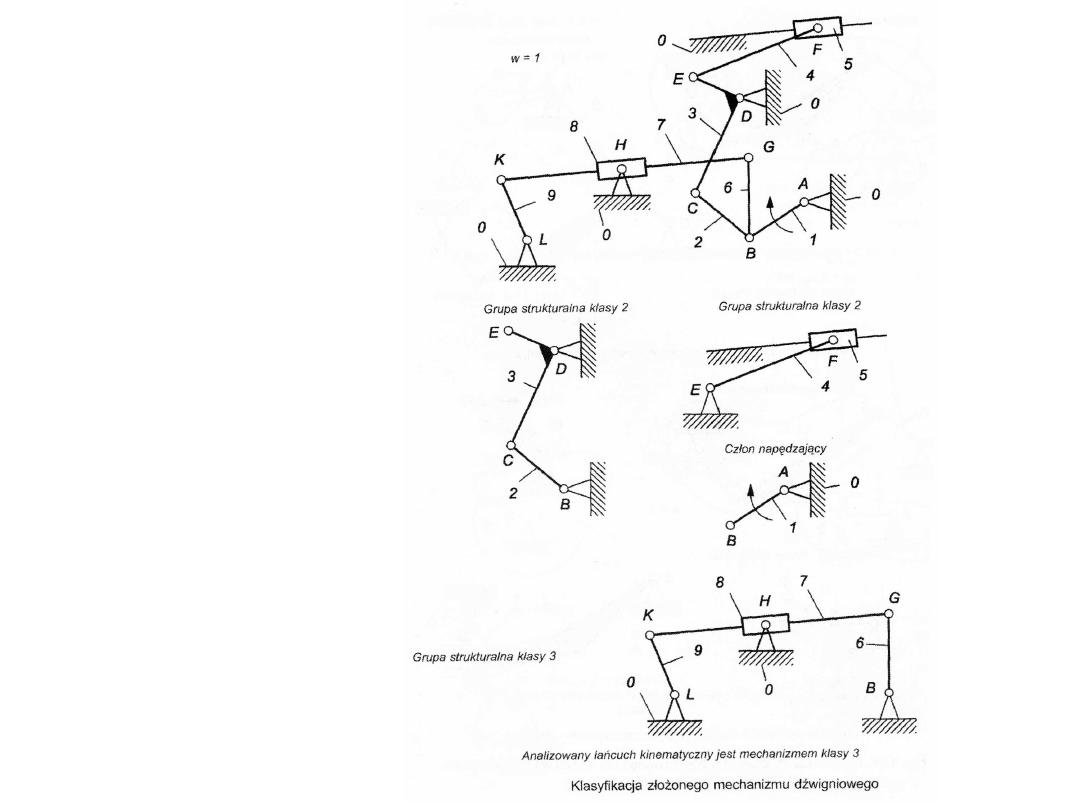
Klasyfikacja

strukturalna

mechanizmó

w

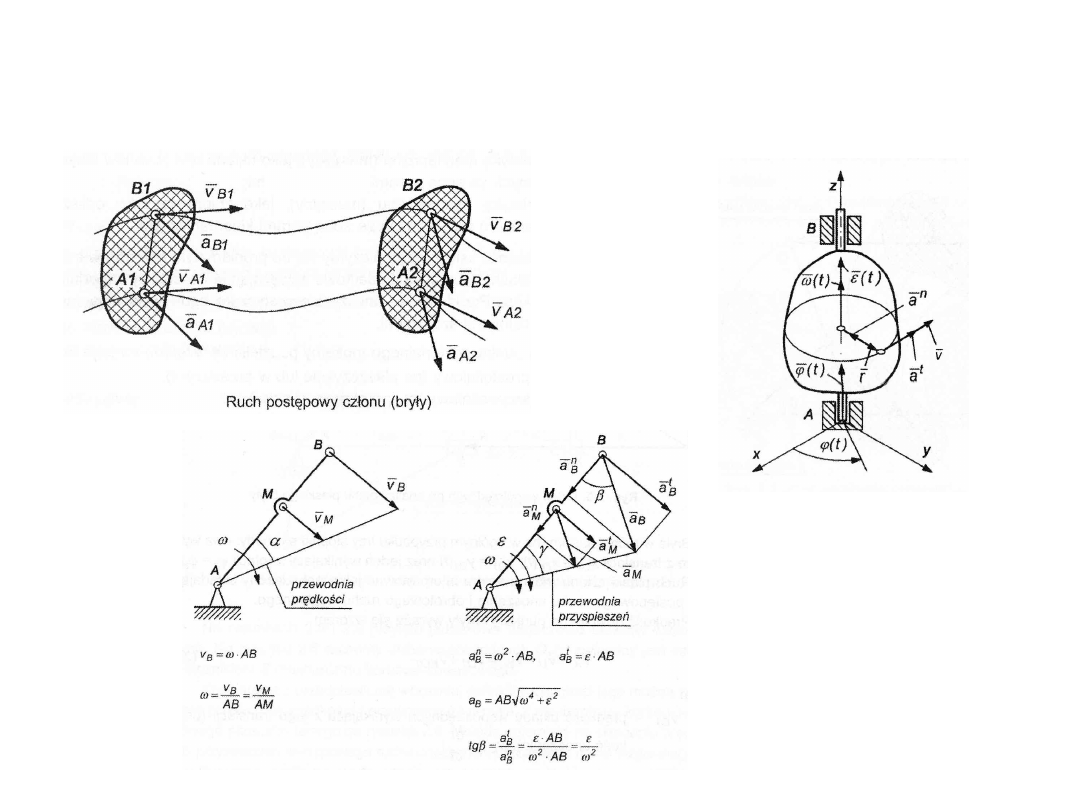
Ruch postępowy i obrotowy jako

podstawowe rodzaje ruchów bryły sztywnej

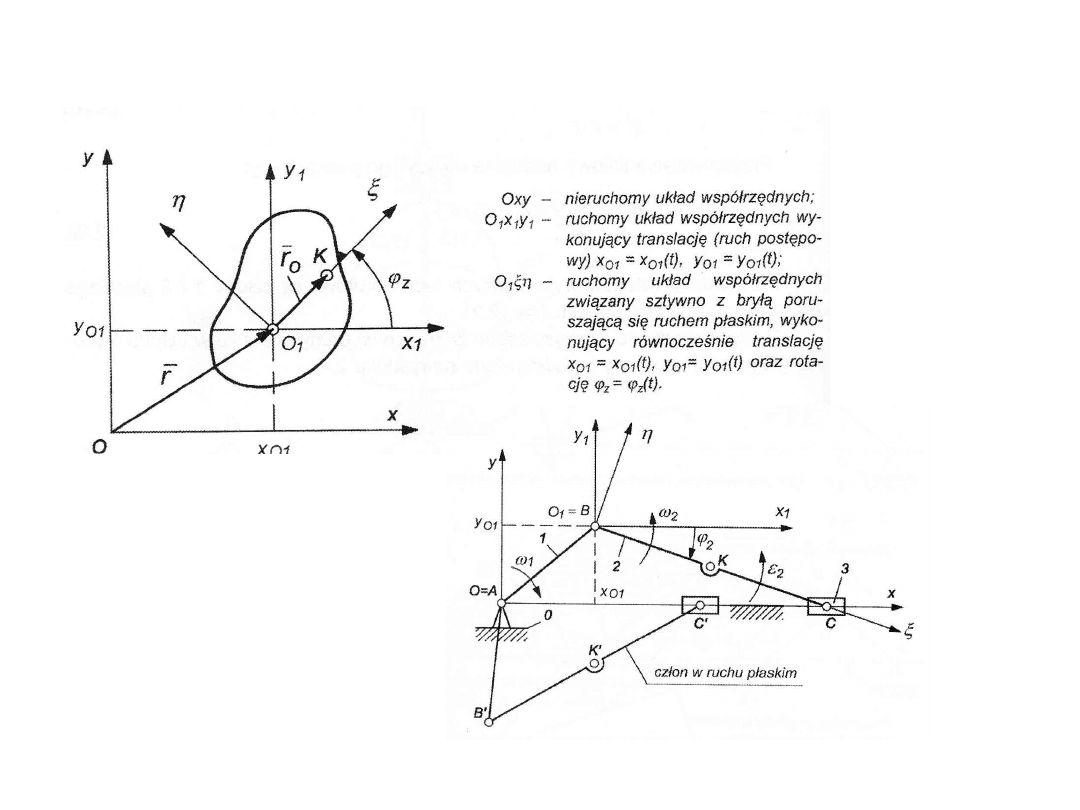
Ruch płaski

Zadania kinematyki mechanizmów

Zadanie o położeniach.
Badanie położenia wybranych punktów członów mechanizmu, w
funkcji st położenia członu napędzającego.

Zadanie o prędkościach.
Badanie prędkości wybranych punktów członów mechanizmu, w
funkcji prędkości członu napędzającego.

Zadanie o przyspieszeniach.
Badanie przyspieszeń wybranych punktów członów mechanizmu,
w funkcji przyspieszeń lub prędkości członu napędzającego.

Równania kinematyki (1)

Wektor współrzędnych uogólnionych q

i

członu swobodnego w

przestrzeni można zapisać w postaci:





T

i

i

i

T

i

i

q







,

,

,

r



Przyjmując oznaczenie:





T

i

i

i

i









,

,



Otrzymuje się:





T

T

i

T

i

i

q



,

r







T

T

n

T

T

q

q

q

q

,.....

,

2

1



Równania kinematyki (2)

Równania więzów par kinematycznych:

Dla przemieszczeń

Dla prędkości

Dla przyspieszeń

Liczba równań skalarnych jest równa

Jeśli równania więzów są niezależne to
liczba stopni swobody UW jest równa
liczbie w obliczonej ze wzoru
strukturalnego

Równania kinematyki (3)

Równania więzów kierujących zależnych od współrzędnych absolutnych i czasu:

W rezultacie kinematykę układu opisuje N nieliniowych
równań algebraicznych o N zmiennych zebranych w wektorze
q:

Metody numeryczne w rozwiązywaniu

równań kinematyki

Metody numeryczne w rozwiązywaniu

równań kinematyki

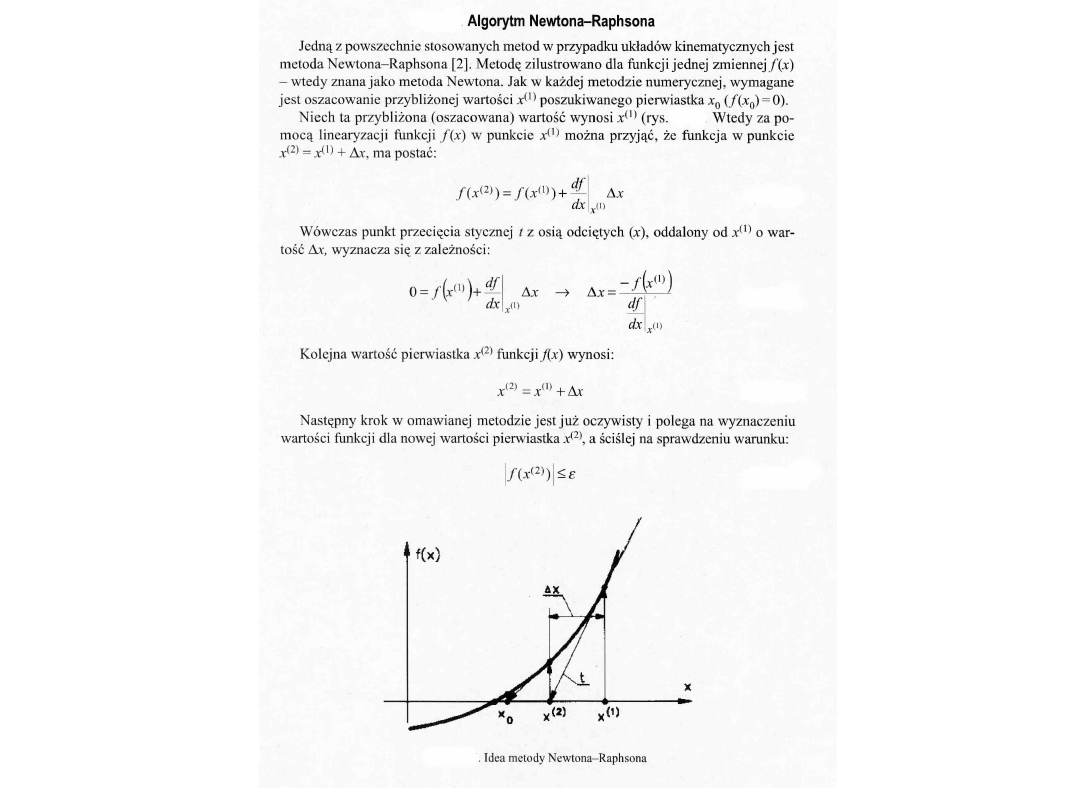
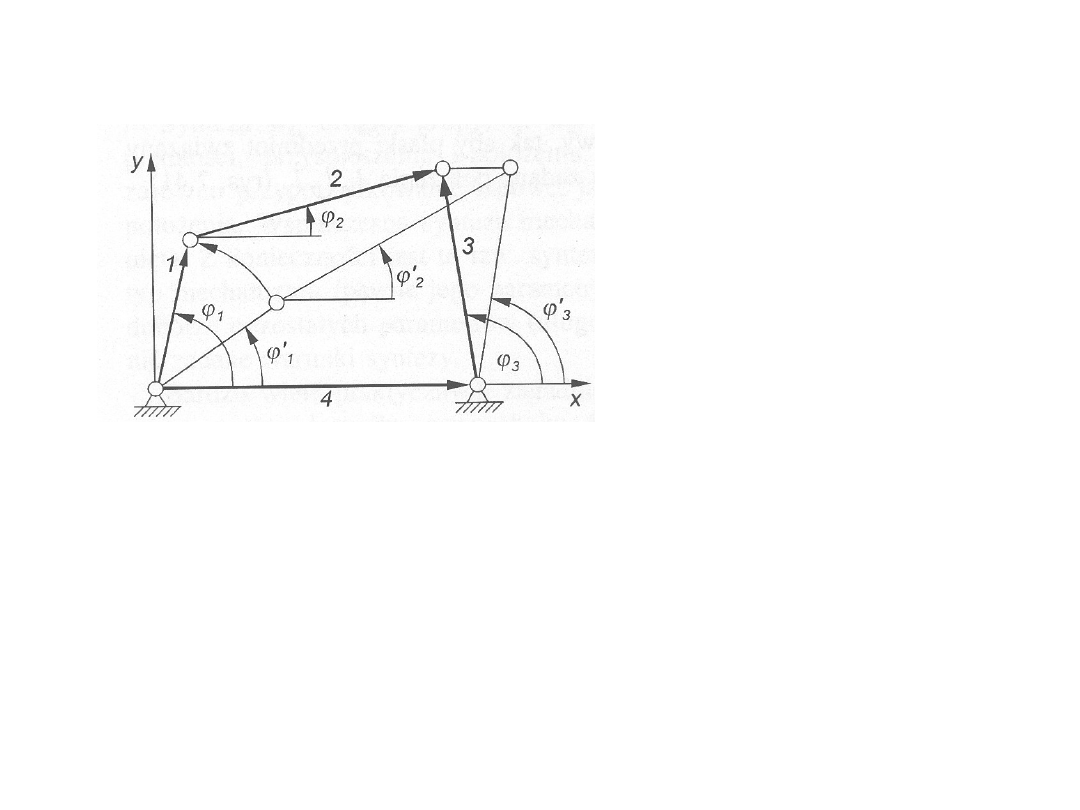
Czworobok przegubowy w zapisie

matematycznym

0

cos

cos

cos

0

cos

cos

cos

0

sin

sin

sin

0

cos

cos

cos

1

3

3

1

2

2

1

1

1

4

1

3

3

1

2

1

1

1

3

3

2

2

1

1

4

3

3

2

2

1

1

2













































































l

l

l

l

l

l

l

l

l

l

l

l

l

l

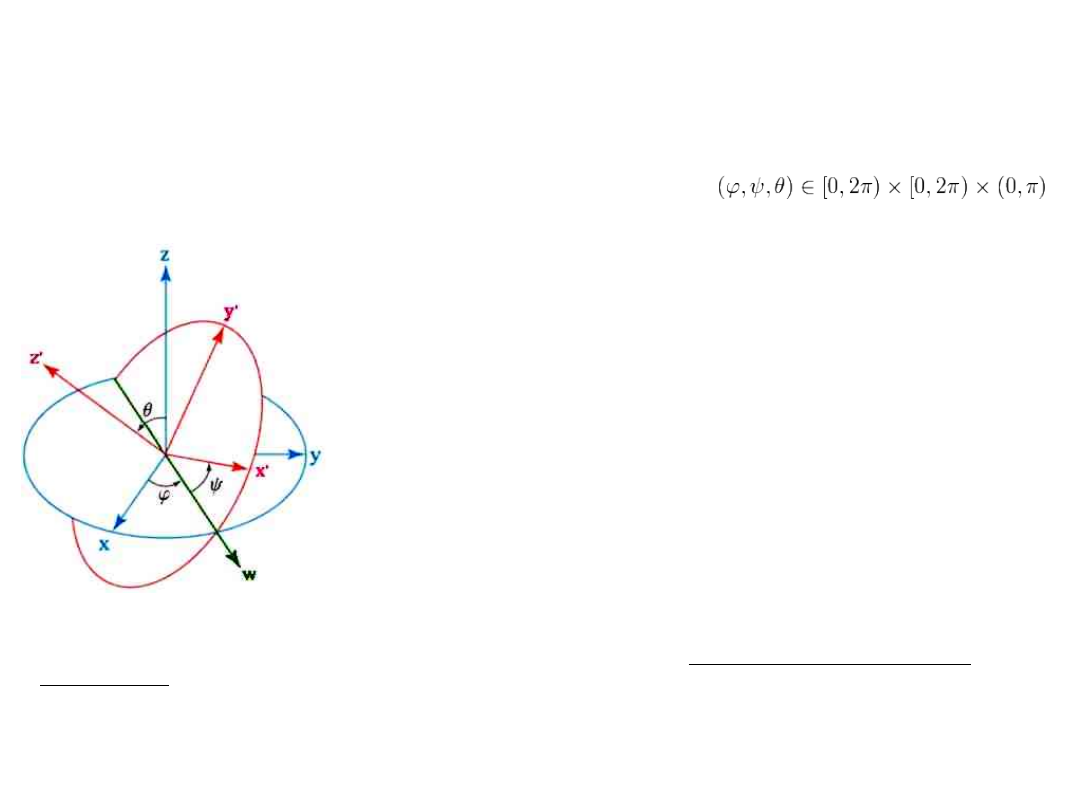
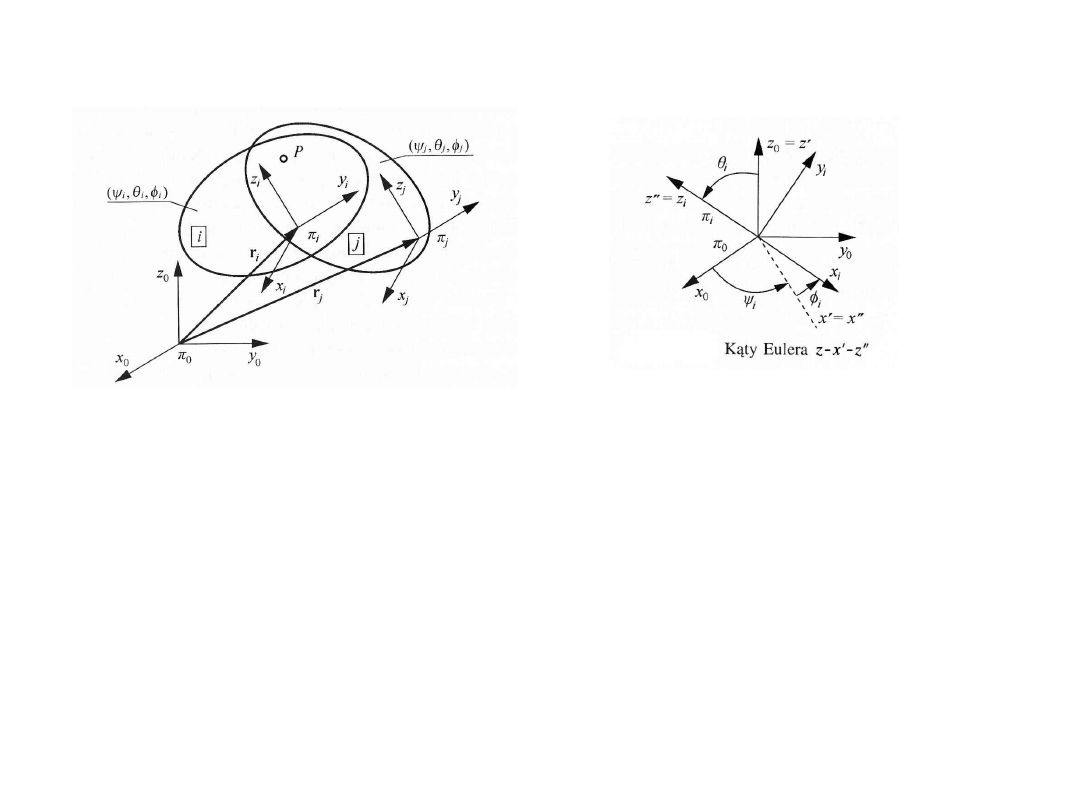
Układ współrzędnych kątowych Eulera (uwagi

dodatkowe)

Dowolnie zorientowany układ współrzędnych Ox'y'z' można otrzymać z danego układu
Oxyz przez złożenie trzech obrotów wokół osi układu. Istnieje kilka takich kombinacji
obrotów , a wybór konkretnej z nich jest arbitralny jednak najszerzej przyjętą konwencją
jest układ kątów Eulera.

Jeśli osie nie pokrywają się nie są równoległe wtedy płaszczyzna
Ozz' jest dobrze określona, a jedynym obrotem, który przekształca
oś z na oś z', jest obrót o odpowiedni kąt wokół linii węzłów w. Linia
węzłów jest prostopadła do obu osi z i z', jest prostą, wzdłuż której
przecinają się płaszczyzny Oxy i Ox'y'.
Układ Oxyz można nałożyć na Ox'y'z', dokonując kolejno
następujących trzech obrotów:
1. obrotu wokół osi z o kąt φ, taki aby oś x pokryła się z linią

węzłów w,

2. obrotu wokół osi x ( = w) o kąt θ , taki aby oś z pokryła się z osią

z‘,

3. obrotu wokół osi z ( = z') o kąt ψ , taki aby oś x pokryła się z osią

x' (y pokryje y').

Wybieramy zwrot zgodny ze zwrotem iloczynu wektorowego
wersorów osi z i z‘ przyjmując go za zwrot osi węzłów. Obrót 2.
będzie więc zawsze obrotem o kąt z zakresu (0,π).
Kąty Eulera (φ,ψ,θ) parametryzują powyższe trzy obroty i
definiujemy je jako:

•ϕ — kąt mierzony od osi x do osi węzłów w w kierunku
wyznaczonym osią z,

•ψ — kąt mierzony od osi węzłów w do osi x' w kierunku
wyznaczonym osią z‘,.

•θ — kąt mierzony od osi z do z' w kierunku wyznaczonym osią
węzłów w,.

Uwaga !
W ten sposób każdemu obrotowi układu współrzędnych w przestrzeni, nie zachowującemu zwrotu ani
kierunku osi z, można wzajemnie jednoznacznie przypisać uporządkowaną trójkę kątów (φ,ψ,θ) . Gdy osie z i
z' są równoległe (identyczne lub o przeciwnych zwrotach), płaszczyzna Ozz' i linia węzłów nie są
jednoznacznie określone; oś z można przekształcić na oś z' w wyniku obrotu (o kąt 0 lub π, zależnie od zwrotu
osi z') wokół dowolnej prostej przechodzącej przez punkt O i leżącej w płaszczyźnie Oxy = Ox'y'. Mamy zatem
θ = 0 lub θ = π, a ustawienie osi x', y' jest jednoznacznie wyznaczone odpowiednio przez sumę lub różnicę
kątów φ i ψ.

Zadania dynamiki

Przedmiotem dynamiki jest badanie relacji zachodzących pomiędzy ruchami
elementów badanego układu fizycznego, a siłami działającymi na te elementy.

Wyróżnić można dwa zasadnicze rodzaje zadań badawczych, a mianowicie:
I.

Dla zadanych kinematycznych równań ruchu układu (mechanizmu) wyznacza
się siły działające w układzie i na układ, które wywołują ruchy określone tymi
równaniami.

II. Dla zadanego układu sił działających na układ (mechanizm) lub w układzie

(mechaniźmie) wyznacza się kinematyczne równania ruchu układu lub jego
elementów.

W zależności od rodzaju badanego układu (modelu układu) wyróżnić można
szereg działów klasycznej dynamiki jak:
1. dynamika punktu materialnego,
2. dynamika układu punktów materialnych,
3. dynamika ciała sztywnego ,
4. dynamika układu ciał sztywnych (maszyna lub mechanizm traktowane jako

układy ciał nieodkształcalnych ,

5. dynamika układu ciał odkształcalnych (maszyna lub mechanizm traktowane

jako układy ciał odkształcalnych ),

6. dynamika ciał o zmiennej masie,
7. Inne działy dynamiki związane z badaniami cząstek elementarnych.

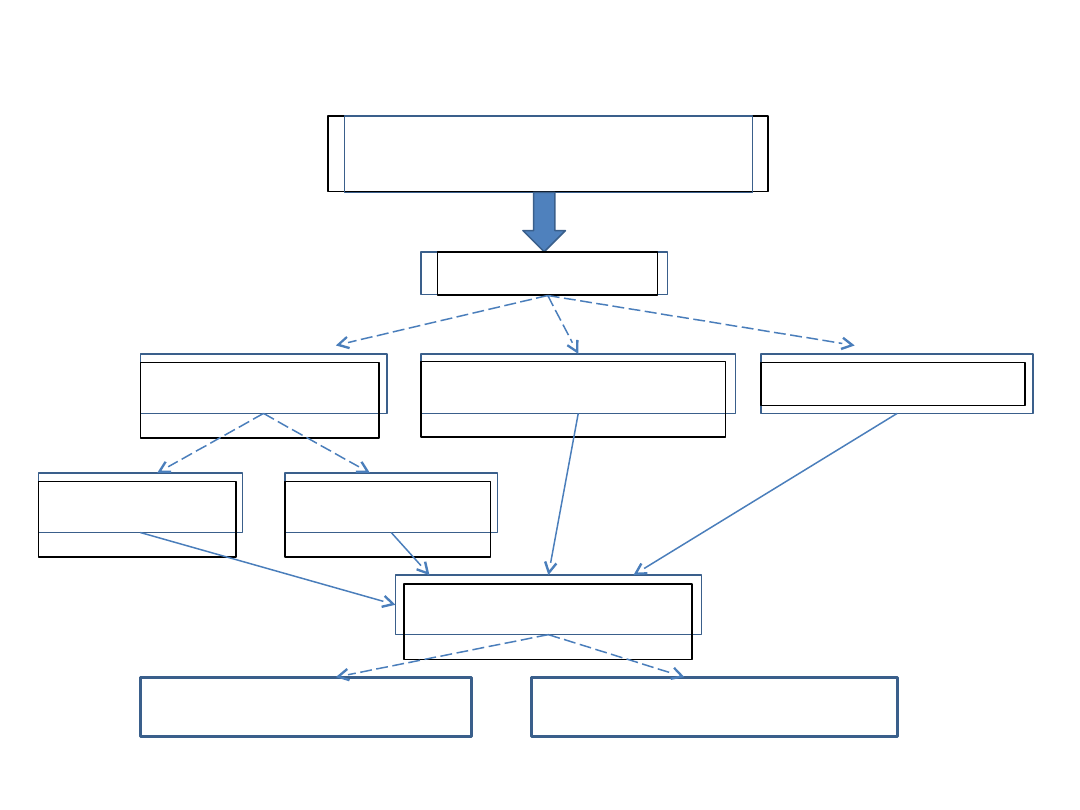
Etapy modelowania i rodzaje modeli dynamicznych

maszyn

Układ materialny (rzeczywisty)

np. maszyna

Model fizyczny

Model

dyskretny

Model ciągły

Zredukowan

y

Wieloczłonow

y

Model dyskretno-

ciągły

Model

matematyczny

Rozwiązanie

analityczne

Rozwiązanie
numeryczne

Siły i ich rodzaje.

• Siła ciężkości G to siła z jaką ziemia przyciąga każde ciało

materialne o masie m.

• G = m*g, gdzie g – przyspieszenie ziemskie wynoszące ok.. 9,81

m/s^2,

• Siły wewnętrzne to siły wzajemnego oddziaływania na siebie ciał

materialnych rozpatrywanego układu.

• Siły zewnętrzne to siły oddziaływania na ciała danego układu

pochodzące od ciał innego ukladu.

• Siły czynne to siły wywołujące ruch ciała swobodnego.
• Siły bierne (reakcje) są wynikiem oddziaływania więzów.
• Ze względu na rodzaj kontaktu ciał materialnych siły można

podzielić na:

– Skupione.
– Rozłożone liniowo (liniowe),
– Rozłożone powierzchniowo (naciski)
– Rozłożone objętościowo (objętościowe)

• W zależności od warunków kontaktu i kierunku działania siły w

stosunku do powierzchni lub linii kontaktu, a w przypadku

kontaktu punktowego stycznej do powierzchni lub linii kontaktu

w punkcie kontaktu siła odziaływania może być rozpatrywana

jako suma składowych normalnej i stycznej

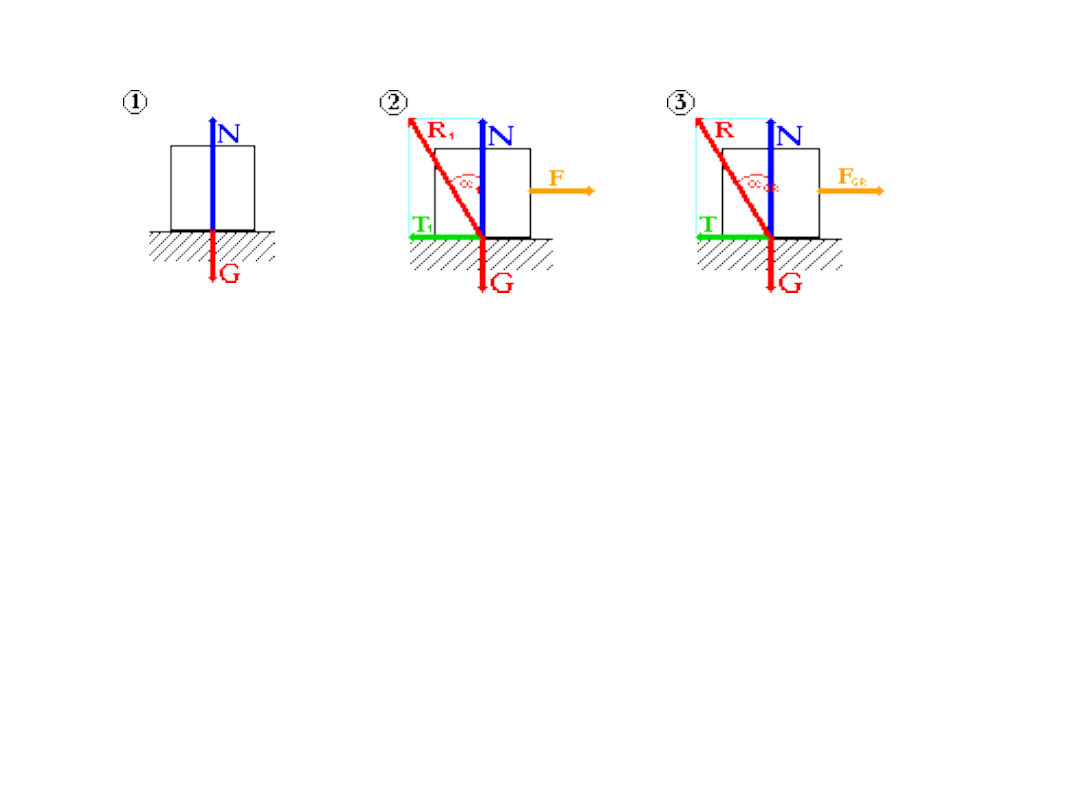
T = N

.

μ

Przypadek trzeci przedstawia tzw. równowagę graniczną. Ciało nie porusza się,
lecz każda minimalnie większa siła od F

gr.

(granicznego) spowoduje ruch.

G - Ciężar ciała (siła czynna), F

1

, F

gr.

- Siły ciągnące (siła czynna), N - Reakcja

normalna.
T

1

, T - Reakcja na siłę ciągnącą, R

1

, R - Reakcje wypadkowe.

α

1

- Kąt między reakcją normalną a wypadkową.

α

gr.

= ρ - Kąt pomiędzy reakcją normalną a wypadkową, w przypadku równowagi

granicznej. Kąt ten zwany jest kątem tarcia.
Współczynnik tarcia ślizgowego zależy od:
- Stanu powierzchni (chropowatości).
- Rodzaju powierzchni (rodzaj materiału).
- Od obecności smaru.
N - Nacisk ciała na powierzchnię.
μ - Współczynnik tarcia, μ

K

- Współczynnik tarcia kinetycznego. μ

K

jest mniejsze

od μ.
Siła tarcia jest wektorem o następujących cechach:
1. Wartość - N * μ, 2. Kierunek - Zgodny z kierunkiem ruchu 3. Zwrot -
Przeciwny niż ruch.

Tarcie Ślizgowe

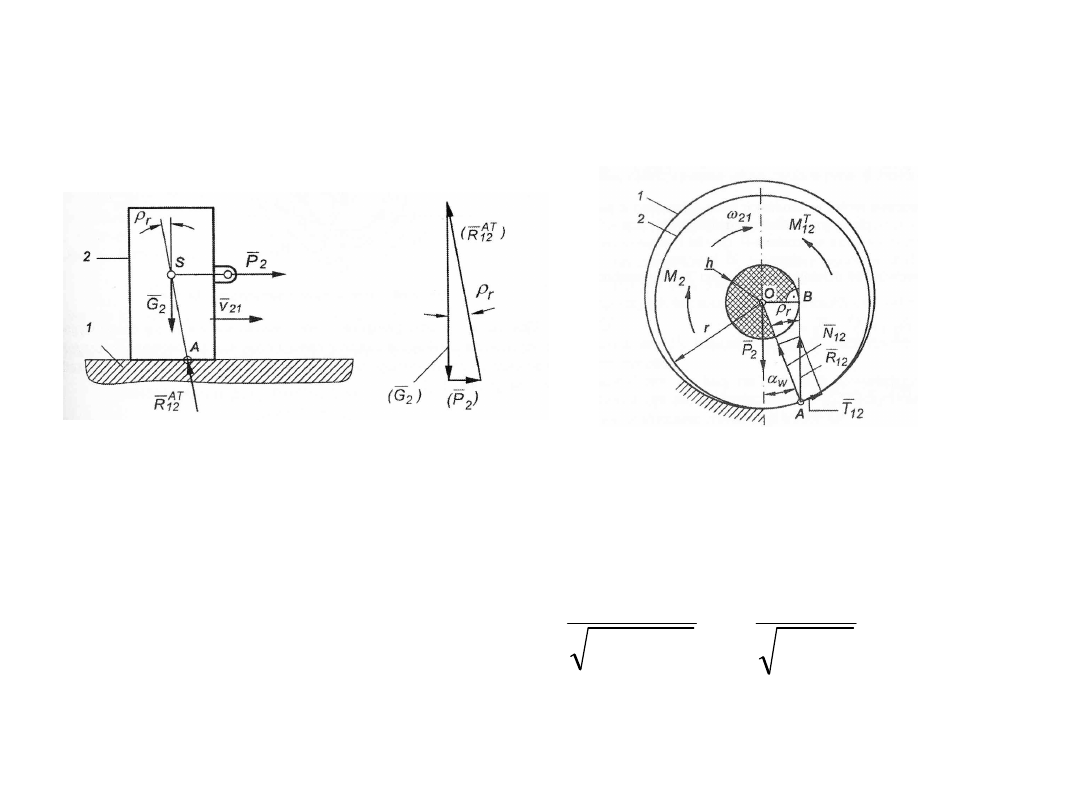
Siły tarcia w parach postępowych i obrotowych













2

2

2

G

tg

G

P

h

R

r

T







12

12

r

r

h



sin





12

2

12

2

12

1

1



























r

r

tg

tg

r

h

r

r

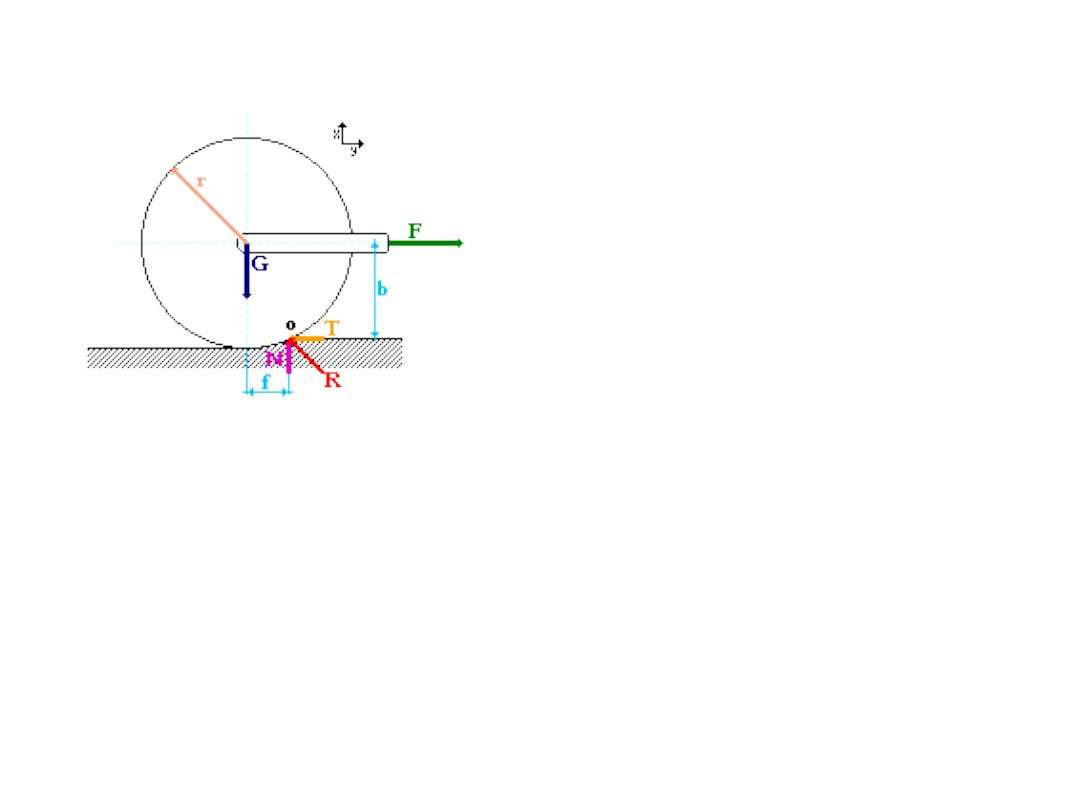
Tarcie toczne

F = f *G/ r

G - Ciężar elementu tocznego.
R - Reakcja podłoża.
N - Składowa normalna reakcji
T - Składowa styczna reakcji.
F - Siła ciągnąca.
r - Promień walca.
b - Odległość między siłą ciągnącą a reakcją styczną.
f - Przesunięcie reakcji normalnej względem ciężaru na skutek odkształcenia powierzchni i
elementu tocznego.
f

[em]

- Współczynnik tarcia toczenia (tocznego). Zależny od rodzaju materiałów walca i podłoża.

Σ F

ix

=0;    F-T = 0;       F=T

Σ F

iy

=0;    -G+N=0;     N=G

Σ M

o

=0;    G

.

f-F

.

b=0;

•

Lepkość (tarcie wewnętrzne) - właściwość płynów i plastycznych ciał stałych
charakteryzująca ich opór wewnętrzny przeciw płynięciu. Lepkością nie jest opór
przeciw płynięciu powstający na granicy płynu i ścianek naczynia. Lepkość jest
jedną z najważniejszych cech płynów (cieczy i gazów).

•

Inne znaczenie słowa "lepkość" odnosi się do "czepności" - terminu stosowanego w
dziedzinie klejów.

•

Zgodnie z laminarnym modelem przepływu lepkość wynika ze zdolności płynu do
przekazywania pędu pomiędzy warstwami poruszającymi się z różnymi
prędkościami.

•

Różnice w prędkościach warstw są charakteryzowane w modelu laminarnym przez
szybkość ścinania. Przekazywanie pędu zachodzi dzięki pojawieniu się na granicy
tych warstw naprężeń ścinających. Wspomniane warstwy są pojęciem
hipotetycznym, w rzeczywistości zmiana prędkości zachodzi w sposób ciągły
(zobacz: gradient), a naprężenia można określić w każdym punkcie płynu. Model
laminarny lepkości zawodzi też przy przepływie turbulentnym, powstającym np. na
granicy płynu i ścianek naczynia. Dla przepływu turbulentnego jak dotąd nie istnieją
dobre modele teoretyczne.

•

Płyn nielepki to płyn o zerowej lepkości (→ nadciekłość).

Tarcie wiskotyczne (1)

Lepkość dynamiczna
Lepkość dynamiczna wyraża stosunek naprężeń ścinających do szybkości ścinania:

Jednostką lepkości dynamicznej w układzie SI jest paskal*sekunda o wymiarze

W układzie CGS jednostką lepkości dynamicznej jest puaz (P). 1 P = 1 dyn/cm

2

= 1 g·cm

−1

·s

−1

, 1 Pa·s = 10 P

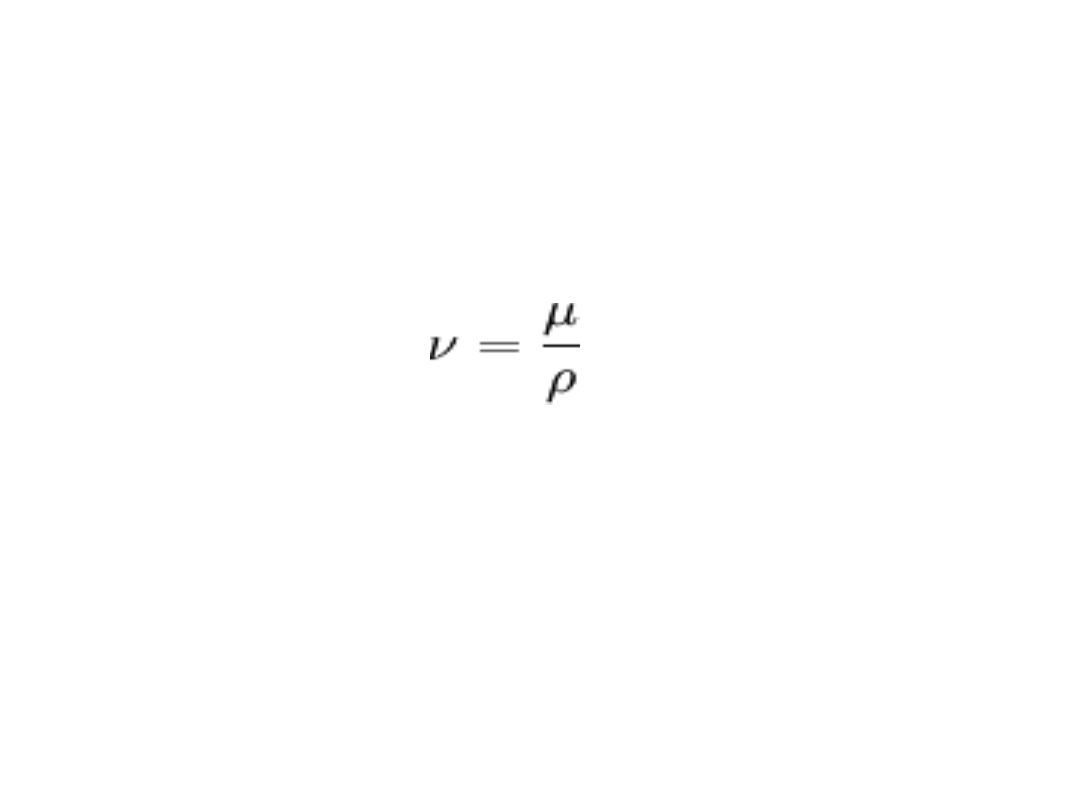
Tarcie wiskotyczne (2)

Lepkość kinematyczna
Lepkość kinematyczna, nazywana też kinetyczną, jest
stosunkiem lepkości dynamicznej do gęstości płynu:

Jednostką lepkości kinematycznej w układzie SI jest:
metr

2

·sekunda

-1

.

W układzie CGS lepkość kinematyczną mierzy się w Stokesach:
1 St=1 cm

2

/{1 s).

Dziedziną nauki zajmującą się badaniami nad lepkością jest
reologia. Pomiary lepkości prowadzi się na wiskozymetrach i
reowiskozymetrach.
Współczynnik lepkości dynamicznej dla rozrzedzonych gazów
doskonałych jest proporcjonalny do pierwiastka z temperatury
(jest to wynikiem ruchu cząsteczek gazów), a nie zależy od
ciśnienia. Dla cieczy współczynnik ten jest odwrotnie
proporcjonalny do temperatury, a rośnie wraz ze wzrostem
ciśnienia (jest to spowodowane oddziaływaniem
międzycząsteczkowym

Siła sprężystości

x

k

F

s







Siła tłumienia

Siła sprężystości to siła generowana przez
element odkształcalny posiadający
własności sprężyste, a więc powrotu do
stanu wyjściowego po ustaniu działania
wywołującego odkształcenie Przykładem
może być sprężyna.

Siła tłumienia wiskotycznego to siła
generowana przez zewnętrzny element
powodujący dyssypację energii. Modele
opisujące działanie tej siły mogą być
różne, najczęściej przyjmuje się model
opisujący tę siłę jako proporcjonalną do
prędkości ruchu.

x

c

F

s









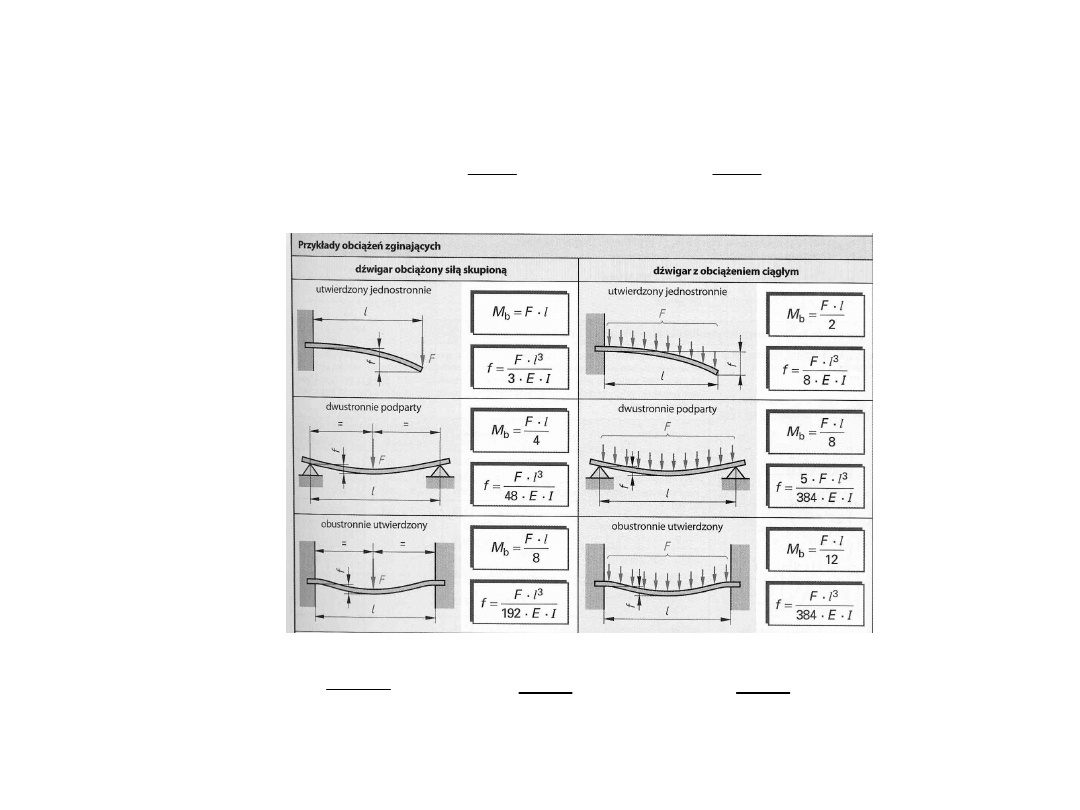
Siła sprężystości

x

k

F

s







Dla skręcania

Dla zginania

Dla rozciągania - ściskania

l

l

A

E

F









l

A

E

k





o

s

I

G

l

M

















l

I

G

M

o

s

l

I

G

k

o

skr





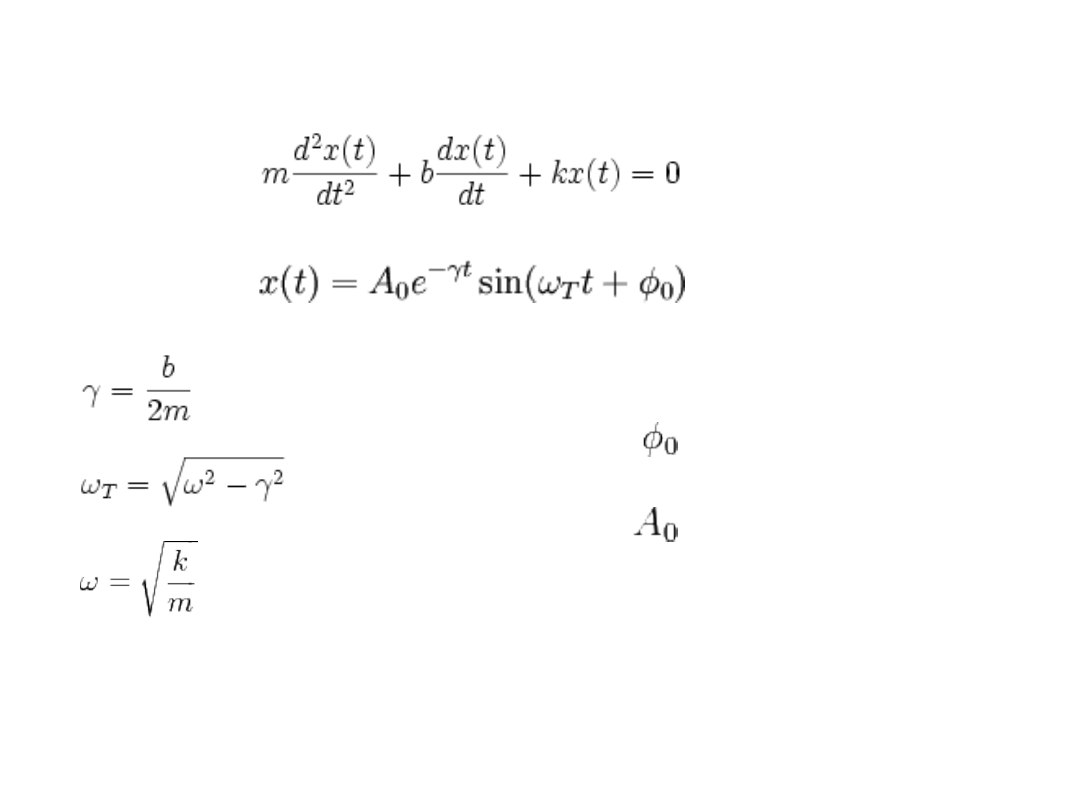
Współczynniki sprężystości i tłumienia

lub

lub

współczynnik tłumienia

częstość drgań tłumionych

częstość drgań swobodnych

faza drgań początkowa

amplituda początkowa

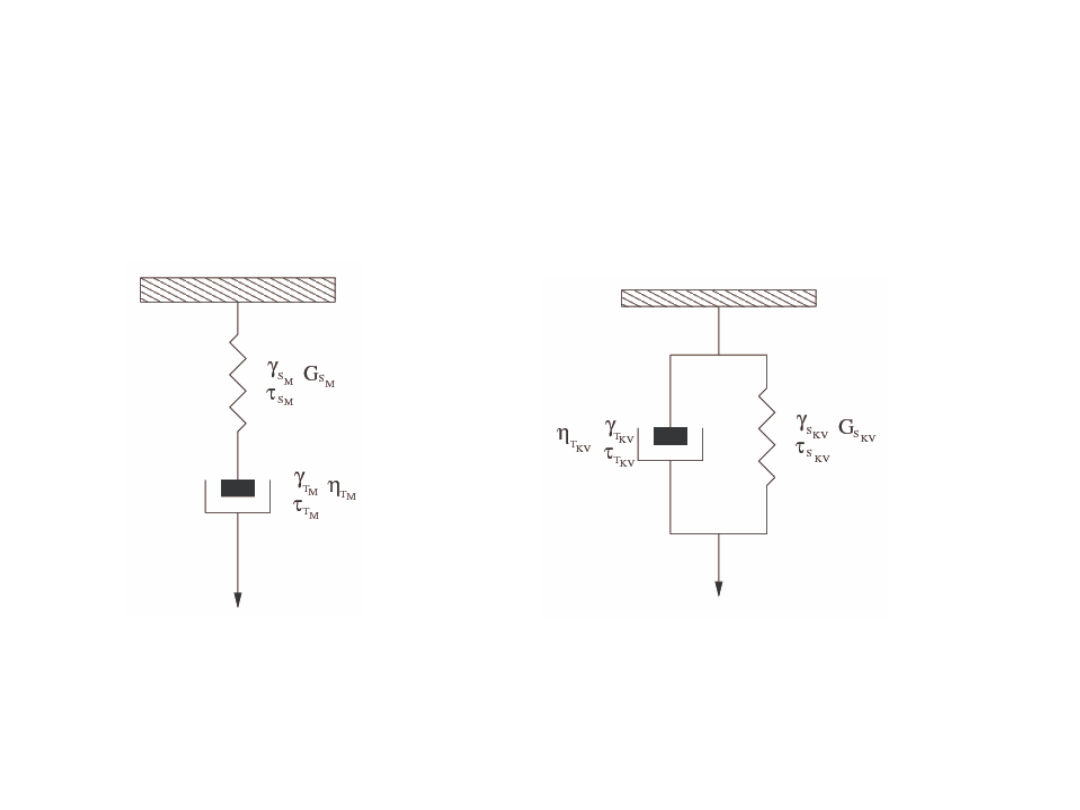
Modele ciał lepkosprężystych

Model Maxwella

Model Kelvina - Voigta

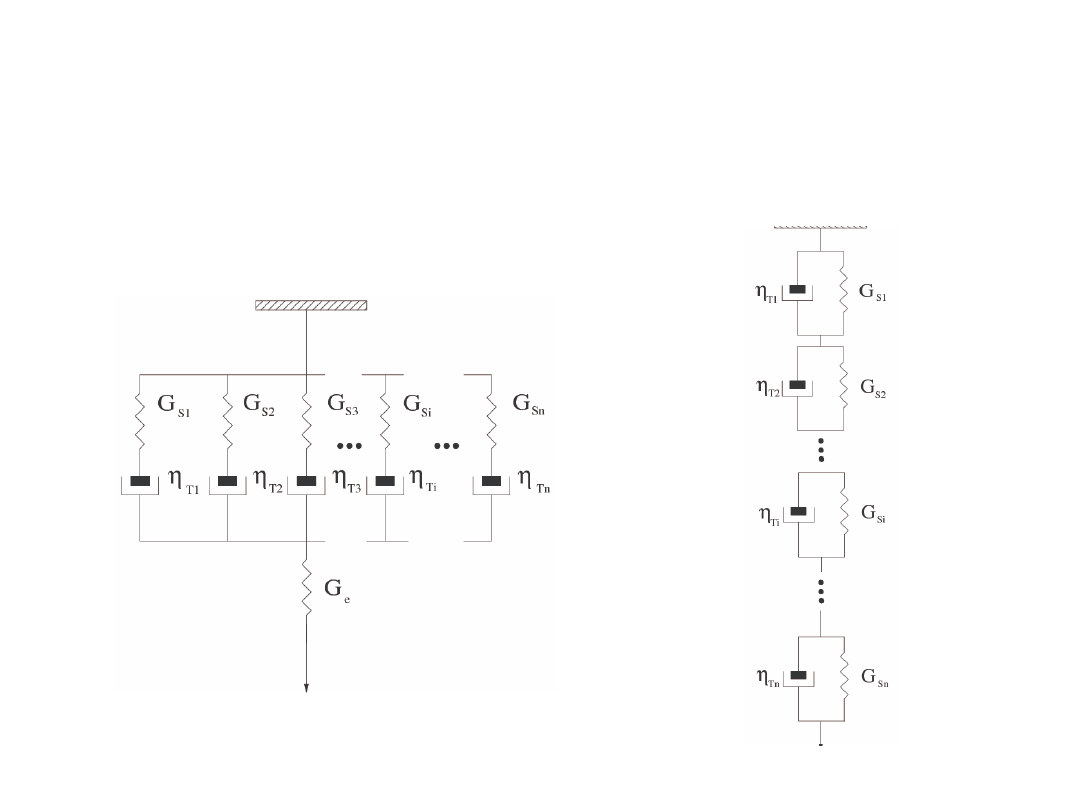
Modele ciał lepkosprężystych

Dyskretny model Maxwella

Dyskretny model Kelvina - Voigta

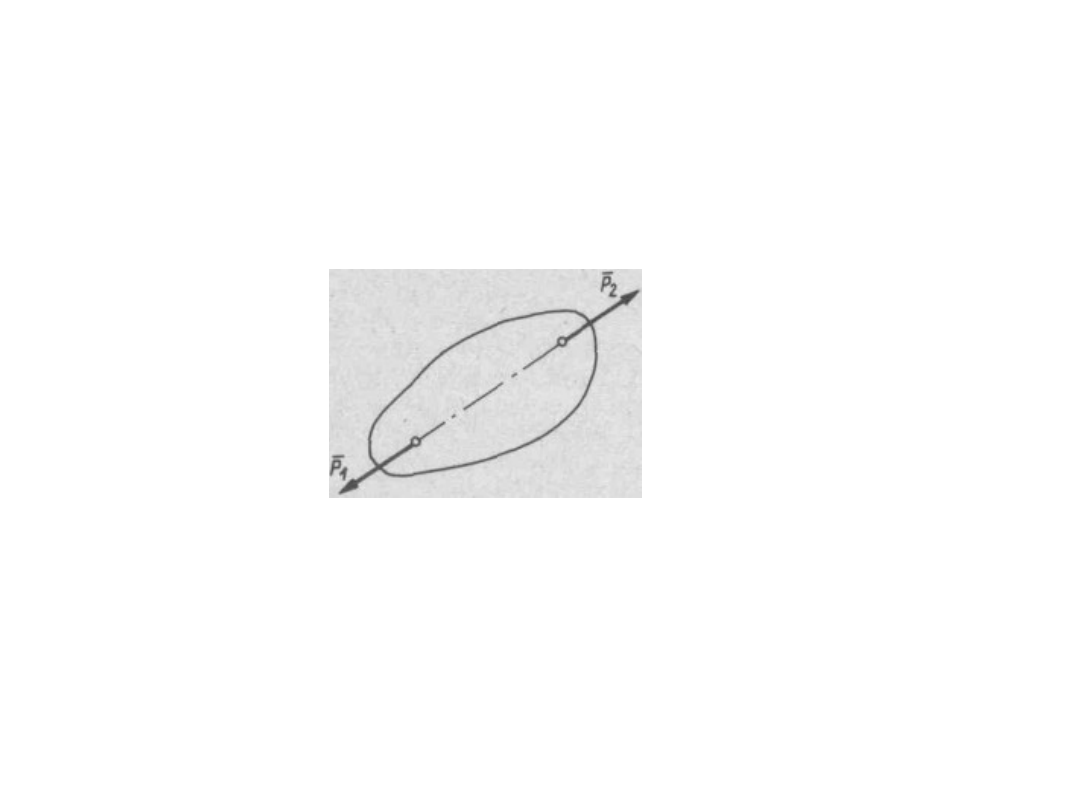
Aksjomaty statyki

• Aksjomat 1. Dwie siły przyłożone do ciała sztywnego

równoważą się wzajemnie, jeżeli mają one jednakowe
wartości (moduły), działają wzdłuż wspólnej linii działania i
mają przeciwne zwroty.

Zgodnie z podanym aksjomatem, aby ciało, na które działa
układ dwóch sił P! i P

2

, było w równowadze muszą te siły działać

wzdłuż jednej prostej i musi zachodzić równość P

1

= - P

2

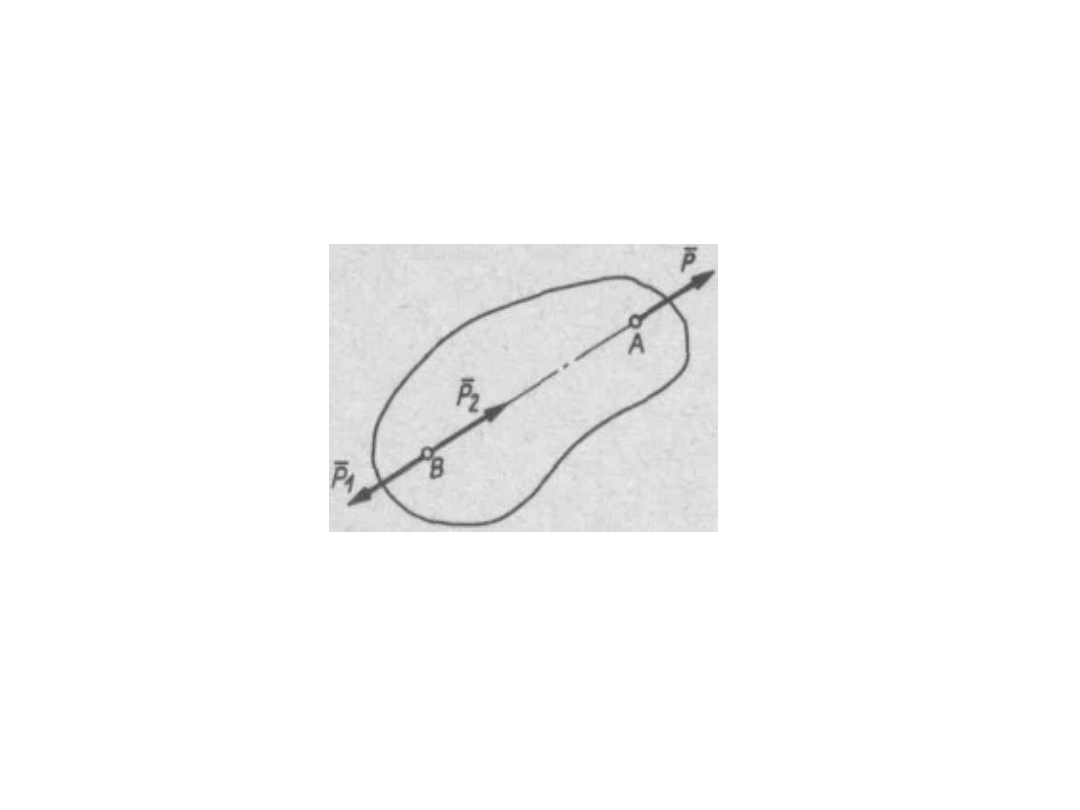
• Aksjomat 2. Jeżeli do działającego na ciało sztywne układu

sił dodamy lub od niego odejmiemy układ równoważny zeru,
to działanie na ciało tego układu sił nie ulegnie zmianie.

Aksjomaty statyki

Jeżeli np. ciało sztywne znajdowało się w równowadze, to równowaga zostanie
zachowana.
Jeżeli więc na ciało sztywne działa przyłożona w punkcie A siła P (rys. 2), to nic
nie zmieni się jeżeli w punkcie B przyłożymy układ sił P

1

i P

2

o linii działania

przechodzącej przez punkt A i B, stanowiący układ zerowy (P

1

= - P

2

). Jeżeli

teraz założymy, że wartości wszystkich trzech sił są jednakowe (P = P

1

= P

2

), to

możemy zgodnie z aksjomatem odjąć od układu równoważny zeru układ (P

1

, P).

Pozostanie wówczas siła P przyłożona w punkcie B. Wyciągamy stąd ważny
wniosek, że działanie siły na ciało sztywne nie ulegnie zmianie, jeżeli punkt
zaczepienia siły przeniesiemy

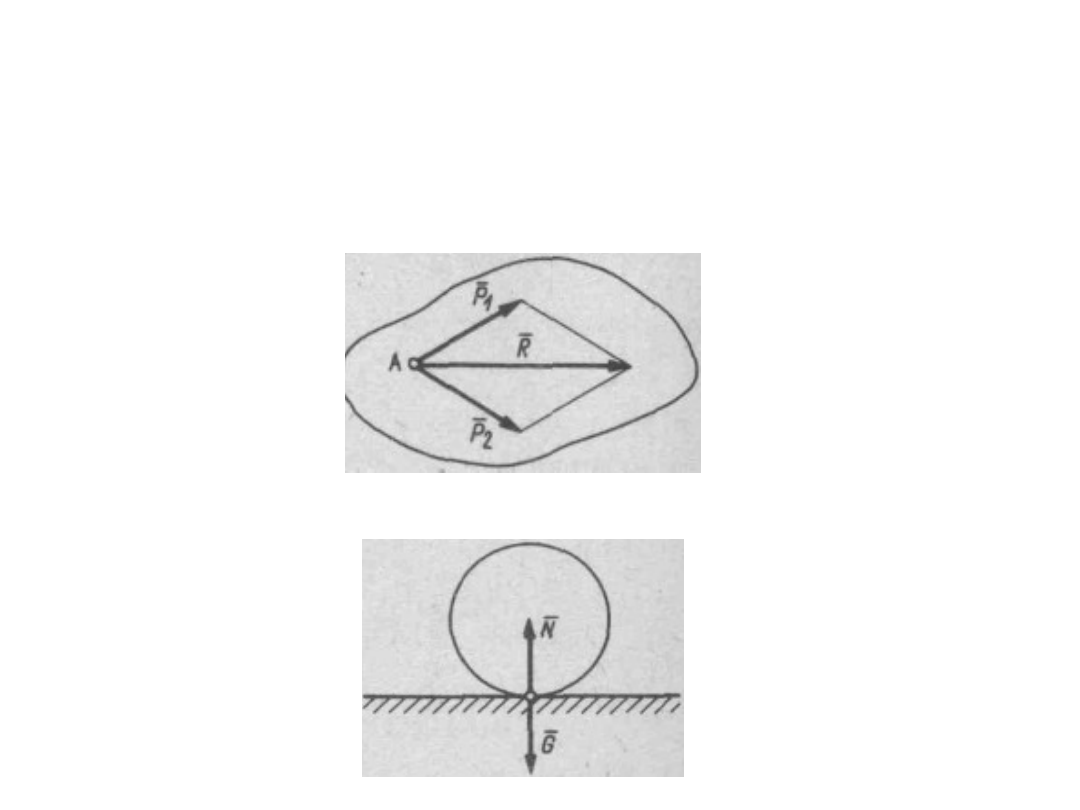
• Aksjomat 3. Wypadkowa dwóch sil przyłożonych w jednym

punkcie jest przyłożona w tymże punkcie i wyraża się
długością przekątnej równoległoboku zbudowanego na tych
siłach (reguła równoległoboku — rys. 3).

Aksjomaty statyki

Aksjomat 4. Wszelkiemu działaniu siły odpowiada równe i
przeciwnie skierowane przeciwdziałanie.

Aksjomaty statyki

Aksjomat 5. Równowaga ciała odkształcalnego nie zostanie
naruszona, jeżeli ciało to stanie się ciałem sztywnym.

Z aksjomatu tego, zwanego również zasadą zesztywnienia, wynika, że
układ sił - pod działaniem którego ciało odkształcalne znajduje się w
równowadze - spełnia te same warunki równowagi, które dotyczą układu sił
działających na ciało sztywne. Należy jednakże pamiętać o tym, że warunki
równowagi dla ciała sztywnego są warunkami koniecznymi, lecz nie zawsze
dostatecznymi dla równowagi ciała odkształcalnego.

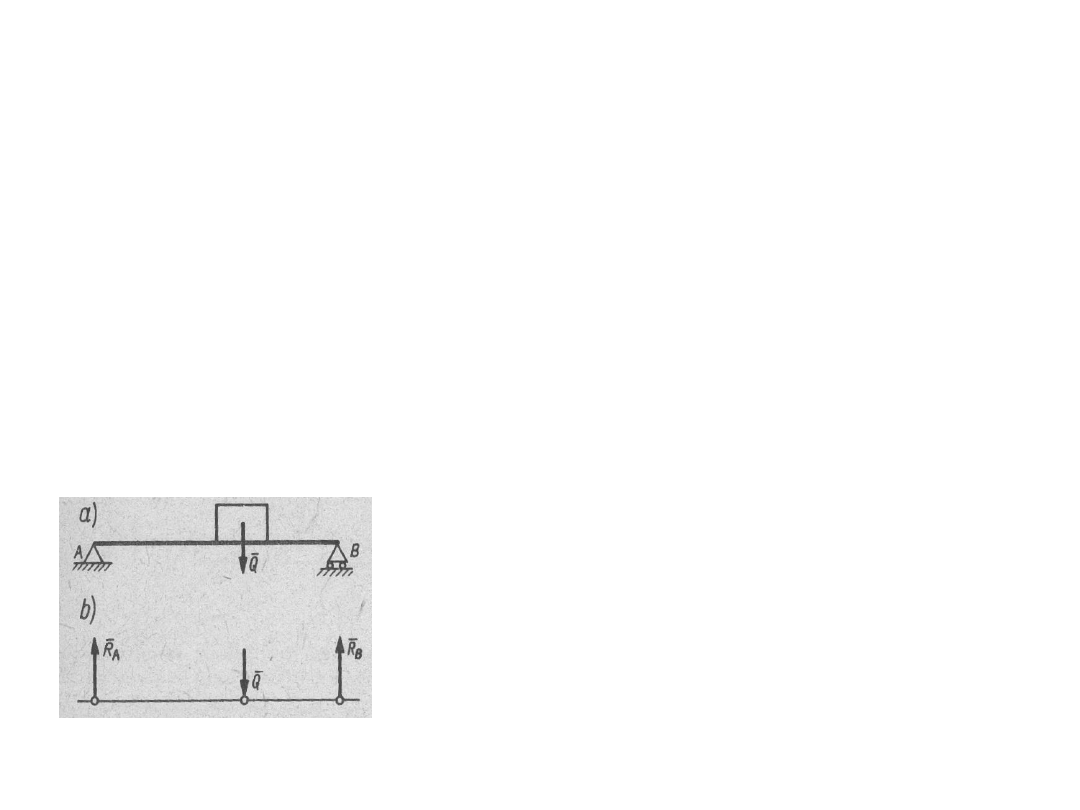
Aksjomat 6. Ciało nieswobodne można zawsze rozpatrywać
jako ciało swobodne, jeżeli myślowo uwolnimy je z więzów,
zastępując ich działanie odpowiednimi reakcjami.

Aksjomat ten umożliwia badanie równowagi ciał
nieswobodnych przez stosowanie warunków
równowagi dotyczących w zasadzie ciał
swobodnych. Spoczywająca na podporach belka
(rys. a) jest ciałem nieswobodnym. Uwalniając ją
myślowo od podpór i wprowadzając reakcje R

A

i

R

B

, pochodzące od podpór w punktach A i B,

rozpatrujemy jej równowagę jako równowagę ciała
swobodnego (rys. b).

Modele o zredukowanej liczbie stopni swobody

Zasada redukcji polega na równoważności energii kinetycznej członu
zredukowanego i sumy energii kinetycznych członów ruchomych
mechanizmu (maszyny)







n

i

i

zr

E

E

1