Podstawowe wiadomości z zakresu modelowania i
symulacji

POJĘCIE MODELU

Model fizyczny może być rozumiany dwojako:

-

jako zminiaturyzowany obiekt

, w którym zachodzą identyczne

zjawiska jak w obiekcie rzeczywistym, poddany badaniom
laboratoryjnym,
-

jako opis zjawisk

w tym obiekcie zrealizowany w oparciu o

równania fizyki (zwane też równaniami fizyki matematycznej)
i może dotyczyć opisu pojedynczego zjawiska lub grupy
zjawisk zachodzących w obiekcie:

- jedno zjawisko –

model prosty

- grupa zjawisk –

model złożony

(ze

sprzężeniami miedzy modelami

prostymi)

Główne

rodzaje modeli

stworzonych w obszarze zagadnień

dotyczących zjawisk w mechanice i budowie maszyn :

-

Model Naviera-Stokesa

(dotyczy przepływu masy fizycznej

(wydatek mierzony w kg/s lub w m

3

/s) parametry przepływu (np.

pola prędkości) w określonych warunkach rzeczywistych,
wymuszonych gradientem ciśnienia)

-

Model Fouriera-Kirchhoffa

(jest związany z przepływem energii

cieplnej (strumień ciepła W/m

2

) – to model wiodący dla wielu ujęć

modelowych zjawisk rzeczywistych, rozwiązujący
parametry przepływu ciepła w warunkach gradientu
temperatury)

-

Model Ficka

(opis przepływu masy w skali atomowej (przepływ

dyfuzyjny))

-

Model Darcy’ego

(przepływu płynów w ośrodkach (szkieletach)

porowatych)

Możliwe

sprzężenia

między modelami:

-

model Naviera-Stokesa

z

modelem Fouriera-Kirchhoffa

(sprzężenie mechaniki płynów z uwzględnieniem zmian lepkości
płynu (wywołanych zmiennością temperatury) i zagadnień
zmienności samej temperatury, oddziałującej na tę lepkość),

-

model Fouriera-Kirchhoffa

z

modelem Ficka

(sprzężenie

przepływu energii z dyfuzyjnym przepływem masy w skali
atomowej),

-

model Fouriera-Kirchhoffa

z

modelem Darcy’ego

(sprzężenie

przepływu energii z przepływem w ośrodkach porowatych).

Kompletnie sformułowany

model matematyczno-fizyczny

musi

zawierać zawsze następujące elementy:

1.

Pojedyncze równanie

lub

układ równań różniczkowych

(w

zależności od wymiarów opisujących przestrzeń: 1D, 2D lub 3D –
jedno, dwu lub trójwymiarowa przestrzeń, D – dimension)

2.

Warunki jednoznaczności

:

-

warunki geometryczne

(geometria zespołu technologicznego:

narzędzia technologiczne + wyrób),
-

parametry fizyczne

(właściwości materiałów składających się na

zespół technologiczny) zestawione w bazy danych. Baza musi się
rodzajowo (co do natury parametrów materiałowych) zgadzać z
modelowanym procesem (tylko te właściwości, które dotyczą
modelowanego procesu),
-

warunki brzegowe

(również umiejscowione w bazie danych) –

dopasowane do klasy i rodzaju modelu. Warunki te uwzględniają
granice w ramach zespołu technologicznego (między narzędziem a
wyrobem) lub granice lokalne w wyrobie (przemiany fazowe).
-

warunki początkowe

(stan wyjściowy).

Zespół technologiczny

–

narzędzia

+

wyrób

(np. forma wtryskowa

+ wypraska, matryca kuzienna-odkuwka, forma-odlew).

Rodzaj modelu

– określa

warunki i naturę fizyczną zjawiska

(zjawisk) jaką zamierza się opisać.

Klasa modelu

– określa

jak dokładnie model odwzorowuje

rzeczywistość

By umożliwić

rozwiązanie modelu fizycznego

(sformułowanego j.w.)

należy go

uprościć

przez:

-

założenie stałych

parametrów fizycznych, warunków brzegowych

oraz warunków początkowych,

-

uproszczenie geometrii modelu

do przestrzeni dwuwymiarowej

(ewentualnie do przestrzeni jednowymiarowej np. poprzez
przyjęcie nieskończonejwysokości).

Istnieje również inna klasyfikacja modeli:

Modele twarde

(

hard modelling

) – opierają się o równania

(różniczkowe) fizyki matematycznej, opisujące zjawiska
występujące w procesie, który modelujemy

Modele miękkie

(

soft modelling

) – opierają się na równaniach i

zależnościach uzyskanych na drodze empirycznej (zwane też są
wprost modelami empirycznymi lub typu „czarna skrzynka”). Mogą
w nich występować parametry identyczne z tymi w modelach
twardych,
lecz powiązane są zależnością uzyskaną z aproksymacji wyników
eksperymentu za pomocą funkcji elementarnych (nie będących
jednak rozwiązaniem modelu opisanego równaniami

TYPY MODELI

ze względu na „kierunek” poszukiwania rozwiązania, na przykładzie

modelu energetycznego (przepływ ciepła):

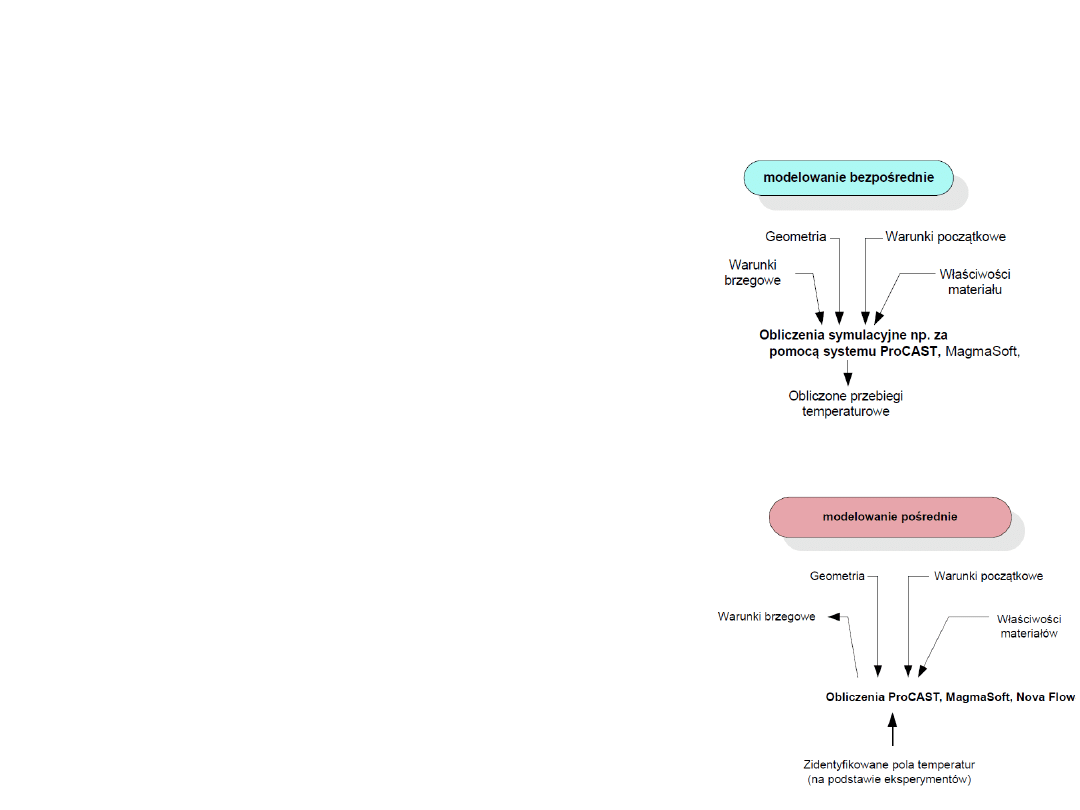
RODZAJE MODELOWANIA

-

modelowanie wprost

(klasyczne),

direct modelling

,

polegające na poszukiwaniu rozwiązania czyli w
tym przypadku – pola temperatury w funkcji
współrzędnych przestrzennych i czasu

-

modelowanie odwrotne

–

inverse modeling

lub

inverse solution

(gdy jakiś z warunków

jednoznaczności nie jest znany i zamierza się
wyznaczyć jego wartość czy zmienność jego
wartości np. z temperaturą lub/i czasem,
korzystając z wyników pochodzących z
eksperymentu: pomierzonych i zarejestrowanych
pól temperatury)

Istnieją dwie główne metody rozwiązywania modeli
sformułowanych w postaci układu równań fizyki matematycznej z
warunkami jednoznaczności :
-

metody analizy matematycznej

-

metody przybliżone

(najczęściej numeryczne)

Metody analizy matematycznej

pozwalają nam klasycznie

rozwiązać model, którego rozwiązaniem jest funkcja ciągła.
Zaletami tej metody jest przejrzystość od strony rachunkowej jak i
merytorycznej, gdyż modele tak sformułowane muszą spełniać
formalnie warunek rozwiązywalności. Natomiast wadą jest
niewystarczająca (szczególnie dla bardziej złożonych technologii i
kształtów) dokładność tego podejścia, ze względu na wymuszone
mocne uproszczenia modelu w stosunku do naszej wiedzy o
procesie rzeczywistym ( warunek rozwiązywalności jest warunkiem
wymuszającym takie uproszczenia)

METODY ROZWIĄZYWANIA MODELI

Metody przybliżone

– zwane są także przybliżonym rozwiązaniem

problemu brzegowego, brzegowo-poczatkowego, co jest skrótowym
hasłem stosowanym przez specjalistów mechaników. Model opisany jest
układem równań różniczkowych cząstkowych (gdy zmienne niezależne
występują dla dwóch domen: przestrzeni i czasu) i warunkami
jednoznaczności.

Metody przybliżone są wykorzystywane w modelowaniu procesów
zachodzących w dowolnym układzie narzędzi technologicznych, m.in.
proces powstawania odlewu w formie, proces wtrysku tworzywa do formy,
proces kucia lub tłoczenia, proces spawania, obróbki cieplnej, itp.

Zastosowanie tej metody do modelowania procesów złożonych, dla
których brak jest najczęściej rozwiązania analitycznego, pozwala na lepsze
przybliżenie do warunków rzeczywistych i sformułowanie a priori
formalnego opisu matematycznego modelu pod kątem numerycznego
algorytmu rozwiązującego, z mniejszą ilością uproszczeń. Uzyskane
rozwiązanie (mimo, że nominalnie pochodzi z rozwiązania uproszczonego)
pozwala wyznaczyć np. pola temperatury w rozważanym układzie,
kinetykę przemian fazowych, pole
stężeń, pole prędkości przepływu płynu, itd., lepiej przybliżających
rzeczywistość.

METODY ROZWIĄZYWANIA MODELI

W sensie matematycznym – problem (model) nieliniowy pojawia się wtedy,
gdy szukana jest pewna funkcja np. T = f (X,t ) (gdzie X jest wektorem
opisującym położenie w przestrzeni, który można zapisać jako funkcję
T = f (x, y, z,t ) ). Jednocześnie od T są uzależnione pewne parametry
procesu, które wchodzą do opisu modelu np. λ = f (T ), c = f (T ).

Rozwiązanie takiego

problemu uwikłanego

jest możliwe

po dyskretyzacji

czasoprzestrzeni

i uruchomieniu obliczeń w pętlach typu for-next. Dla

kolejnych kroków czasowych można założyć, że chwilowo np. λ = const i
jednocześnie, że to λ = f (x) – to wartości przypisane lokalnym adresom
(materiału), a lokalna temperatura odniesienia jest temperaturą
przypisaną poprzedniemu krokowi czasowemu i to dla niej wyznaczane są
wartości λ = const używane do obliczeń w bieżącym kroku czasowym.

Przy takich założeniach problem uwikłania jest rozwiązywalny

DEFINICJA MODELU NIELINIOWEGO

(PROBLEM FUNKCJI UWIKŁANEJ)

Właściwe zainstalowanie i skuteczna eksploatacja systemu
symulacyjnego (zwanego też kodem symulacyjnym), opartego o
pełen sformułowany model, wymaga odpowiedniego ujęcia
procedur identyfikacji parametrów modelowanych zjawisk
cieplnych (parametrów wchodzących w zakres warunków
jednoznaczności) ich

walidacji

.

Końcowe porównanie stanu „obliczonego” ze zidentyfikowanym
doświadczalnie stanem „rzeczywistym”, z ewentualną korektą
modelu, zwane jest jego walidacją (uwiarygodnieniem).
Decyduje to o przydatności i celowości wprowadzenia kodu do
produkcji.
Dopiero wtedy mówić można o przygotowaniu narzędzia
symulacyjnego do optymalizacji procesu w konkretnych warunkach
produkcyjnych.

SCHEMAT ZWIĄZKU PROCEDUR IDENTYFIKACJI

I WALIDACJI MODELU PROCESU KRZEPNIĘCIA

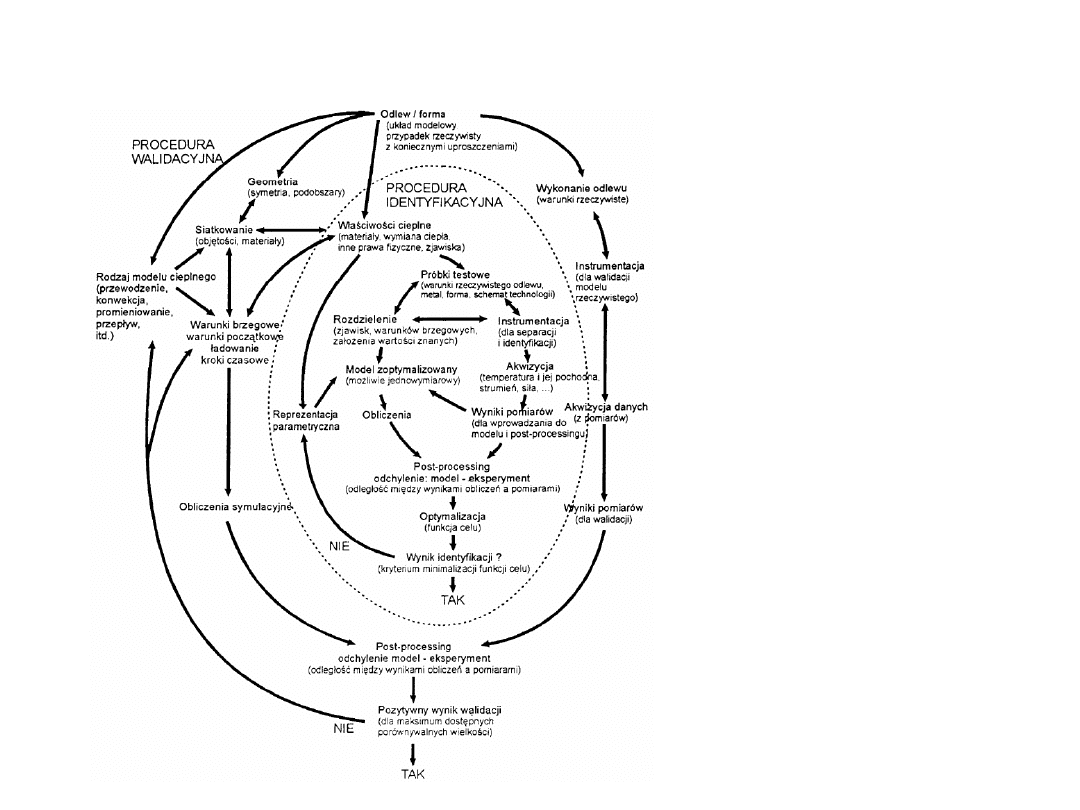
SCHEMAT ZWIĄZKU PROCEDUR IDENTYFIKACJI

I WALIDACJI MODELU PROCESU KRZEPNIĘCIA

Warunkiem bezwzględnie wymaganym,

koniecznym ze względu na różnorodność

materiałów użytych do budowy formy, jest

tzw.

energetyczna walidacja modelu

, czyli

uzyskanie m.in. zgodności rzeczywistych i

obliczonych za pomocą symulacji czasów

krzepnięcia ścian odlewu.

Dopiero taka zgodność upoważnia do

wiarygodnego wnioskowania o przebiegu

poszczególnych etapów krzepnięcia i

zasilania.

WARUNKI JEDNOZNACZNOŚCI – OPIS FORMUŁOWANIA

(NA PRZYKŁADZIE UKŁADU ODLEW-FORMA)

Układ równań różniczkowych opisujących
przepływ ciepła w układzie odlew – forma
uzupełniają

warunki jednoznaczności

:

- warunki geometryczne

- warunki fizyczne

- warunki brzegowe

- warunki początkowe

Warunki geometryczne

– zidentyfikowana geometria obszarów

istniejących w początkowym okresie procesu (forma jako narzędzie
technologiczne i odlew wg koncepcji odlewania) np. układ wlewowy.

Warunki geometryczne wynikają z koncepcji technologii
wytwarzania odlewu lub wlewka i zawierają przede wszystkim:

– kształt formy i wnęki formy,

– rozmieszczenie układu wlewowego, ochładzalników i nadlewów,

– miejsce doprowadzenia metalu do zbiornika układu wlewowego.

WARUNKI JEDNOZNACZNOŚCI – OPIS FORMUŁOWANIA

(NA PRZYKŁADZIE UKŁADU ODLEW-FORMA)

Warunki fizyczne

– każdy z obszarów musi mieć nadane pewne

cechy fizyczne wyrażone parametrami (odpowiednimi
współczynnikami), konieczna jest zatem dostosowana baza danych
Dla opisywanego przykładu warunki fizyczne opisane są przez
następujące współczynniki dla poszczególnych materiałów
biorących udział w modelowanym procesie (współczynniki mogą
być funkcją temperatury):
-

przewodność cieplna

λ

[W/(m·K)],

można stosować tylko do ciał

jednorodnych, w których porowatość p = 0 . Porowatość w
przypadku, gdy p ≠ 0 np. w masach formierskich, stosujemy

λ

zastępcze (substytucyjne) (

λ

sub

)

-

ciepło właściwe c [J/(kg·K)],

-

gęstość  [kg/m

3

]

-

utajone ciepło krzepnięcia (topnienia) L [J/kg]

-

ciepło wydzielane podczas reakcji egzotermicznej w otulinach

[J/kg] (gdy są używane)

WARUNKI JEDNOZNACZNOŚCI – OPIS FORMUŁOWANIA

(NA PRZYKŁADZIE UKŁADU ODLEW-FORMA)

Warunki brzegowe

– definiują wpływ jaki wywierają na siebie poszczególne obszary
(tylko wpływ typu cieplnego, z pominięciem innych oddziaływań
poza tymi, uwzględnionymi w modelu),

– ważna jak i w przypadku baz danych fizycznych jest wiedza na
temat przebiegu zjawisk na granicach obszarów i umiejętność
przypisania im jednego z typowych warunków brzegowych, które
wpływając na przepływ ciepła między obszarami (ciałami) lub
podobszarami tego samego ciała względnie między całościowo
widzianym układem a otoczeniem.

WARUNKI JEDNOZNACZNOŚCI – OPIS FORMUŁOWANIA

(NA PRZYKŁADZIE UKŁADU ODLEW-FORMA)

W teorii procesów cieplnych rozważa się 5 typów warunków
brzegowych:

–

warunek brzegowy I-go rodzaju

– Dirichleta (na wycinku brzegu jest

zadana temperatura)

-

warunek brzegowy II-go rodzaju

– Neumanna (na wycinku brzegu jest

zadany strumień ciepła (jako składowa w kierunku normalnym do brzegu
obszaru) odprowadzany z układu do otoczenia)

-

warunek brzegowe III-go rodzaju

– Newtona (zwany też – Robina).

(na wycinku brzegu jest określony związek między ilością ciepła
doprowadzonego do brzegu przez przewodzenie a ilością ciepła
odprowadzonego do otoczenia. Otoczenie musi charakteryzować się
nieskończoną pojemnością cieplną)

-

warunek brzegowy IV-go rodzaju

, zwany „warunkiem ze szczeliną” (na

styku dwóch obszarów obowiązuje warunek ciągłości strumienia ciepła)

-

warunek STEFANA

(warunek ten opisuje stan cieplny na granicy

rozdziału
ciecz - ciało stałe w przypadku, jeżeli metal krzepnie w stałej temperaturze
(źródło ciepła jest obecne tylko na tym froncie).

WARUNKI JEDNOZNACZNOŚCI – OPIS FORMUŁOWANIA

(NA PRZYKŁADZIE UKŁADU ODLEW-FORMA)

Warunki początkowe

– opisują stan ciała w momencie uznanym

jako start procesu.

Dla

modelu cieplnego

jest to stan opisany jako T = f (X,t ) dla t = 0.

Takie warunki są łatwe do zdefiniowania, kiedy na początku procesu
można założyć stałą temperaturę w całym ciele lub zespole ciał
(układzie) i wtedy mogą być to temperatury stałe, ale zróżnicowane
dla poszczególnych ciał

Ważne jest w przypadku każdego modelowanego procesu, aby mieć
rozpoznanie co do słuszności przyjęcia stałości temperatury, na
podstawie doświadczenia

W przypadku odlewania – warunek początkowy dla modelu
sformułowanego dla okresu krzepnięcia wynika z pola temperatury
obliczonego w okresie zalewania (model Naviera-Stokesa
sprzężonego z modelem Fouriera-Kirchhoffa)

WARUNKI JEDNOZNACZNOŚCI – OPIS FORMUŁOWANIA

(NA PRZYKŁADZIE UKŁADU ODLEW-FORMA)