CHEMIA 1



Kinetyka

◦

Teoria kompleksu aktywnego i zderzeń aktywnych, energia
aktywacji

◦

Katalizatory

Wykład 14

Teoria kompleksu aktywnego

i zderzeń aktywnych, energia

aktywacji

Wprowadzenie

Na przełomie XIX i XX wieku stwierdzono (Van’t Hoff), że

szybkość reakcji chemicznych, przy wzroście temperatury o 10°C
rośnie ok. 2-4 razy

. Reguła Van’t Hoffa spełniona jest dla dużej

grupy reakcji homogenicznych do temperatury ok. 500°C.

Ponieważ ogólne równanie kinetyczne reakcji ma postać:

a stężenia reagentów b. słabo zależą od temperatury, główną
przyczyną zmiany szybkości musi być temperaturowa zależność
stałej szybkości reakcji

k

.

Arrhenius ustalił, że stała szybkości spełnia równanie:

gdzie A i B to dodatnie stałe zależne od reagujących substancji.

Zależność tą można uzasadnić w oparciu o teorię zderzeń
aktywnych.

...

c

c

c

k

v

γ

C

β

B

α
A









T

B

A

lnk





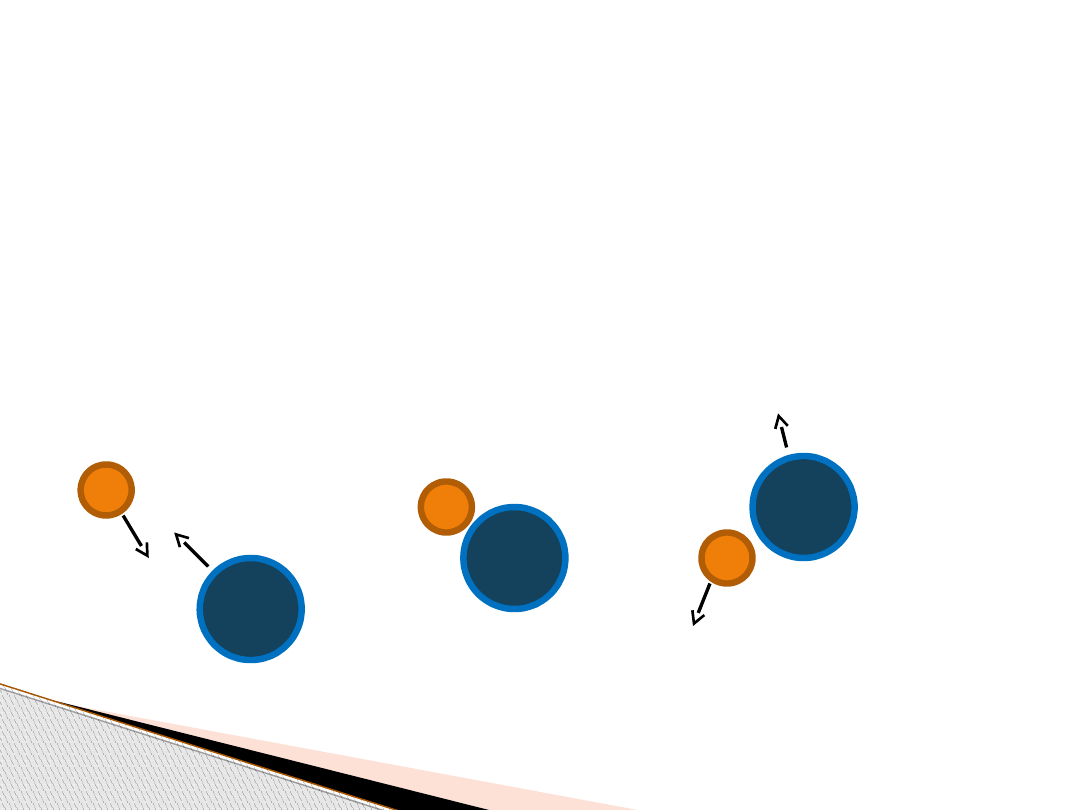
Teoria zderzeń aktywnych

Szybkość reakcji chemicznej powinna być proporcjonalna do
ilości zderzeń pomiędzy cząsteczkami reagujących substratów,
ponieważ atomy (cząsteczki) reagujących substancji muszą
„wejść w kontakt” (zderzyć się).

Nie każde takie zderzenie prowadzić będzie do zajścia reakcji:

zd

*

N

k

v





A

B

A

B

A

B

zderzenie sprężyste, reakcja nie zachodzi

E

A

+ E

B

< E

a

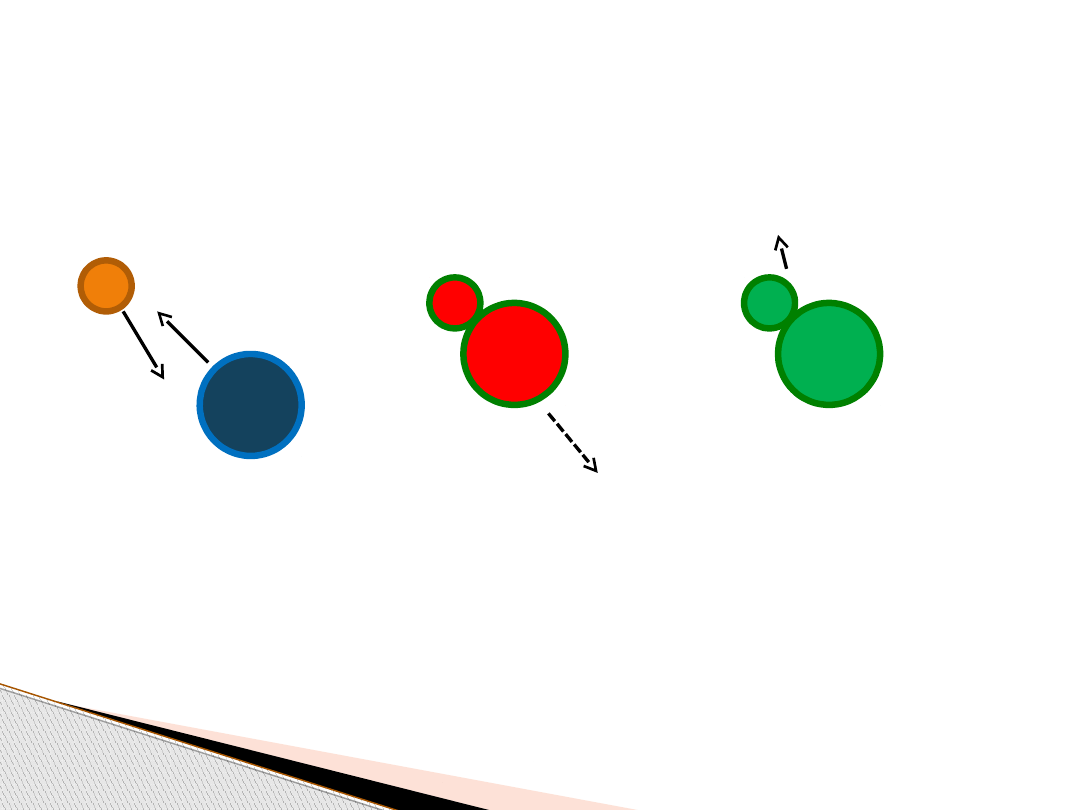
Teoria zderzeń aktywnych

Aby reakcja zaszła, konieczne jest utworzenie kompleksu
aktywnego, czyli zderzenie musi być aktywne.

A

B

zderzenie aktywne, reakcja zachodzi

E

A

+ E

B

≥ E

a

C

kompleks aktywny

wydziela się
nadmiar energii

C = AB

Teoria zderzeń aktywnych

Szybkość reakcji chemicznej będzie wobec tego zależna od ilości
zderzeń aktywnych, przeliczonych na jednostkę objętości,
zachodzących w danym czasie.

Można wykazać, że w mieszaninie gazów A i B liczba zderzeń
pomiędzy

cząsteczkami

A i B dana jest zależnością:

Aby zderzenie było aktywne, zderzające cząstki muszą mieć
wystarczająco wysoką energię (równą lub przekraczającą
wartość E

A

i E

B

). Ilość takich cząstek dana jest zależnością:

zd(akt)

N

k

v







B

A

#

zd

c

c

T

k

N









T

R

E

A

)

E

A(E

A

A

e

N

n









T

R

E

B

)

E

B(E

B

B

e

N

n









Teoria zderzeń aktywnych

Można zatem wyrazić liczbę zderzeń aktywnych zależnością:

Korzystając ze wzorów:

otrzymujemy:

T

R

E

zd

T

R

E

E

zd

T

R

E

T

R

E

zd

zd(akt)

a

B

A

B

A

e

N

k

e

N

k

e

e

N

k

N













































B

A

#

zd

c

c

T

k

N









zd(akt)

N

k

v







T

R

E

B

A

T

R

E

B

A

#

T

R

E

zd

a

a

a

e

c

c

T

k

v

e

c

c

T

k

k

k

e

N

k

k

v























































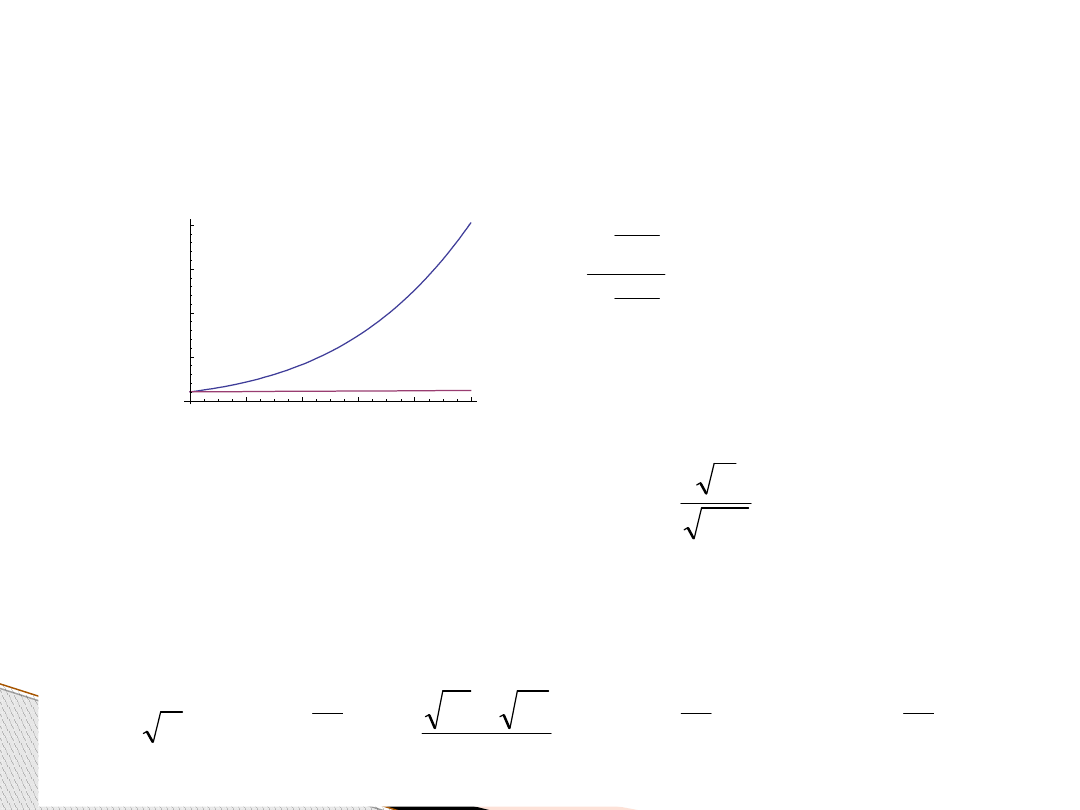
Teoria zderzeń aktywnych

Zmiany temperaturowe związane z czynnikiem eksponencjalnym
są jednak nieporównywalnie większe, w porównaniu do czynnika
T

0,5

.

Można więc zastosować przybliżenie:

3 2 0

3 4 0

3 6 0

3 8 0

4 0 0

5

1 0

1 5

2 0

T [K]

p

rz

y

ro

s

t

c

zy

n

n

ik

a

e

k

s

p

o

n

e

n

c

ja

ln

e

g

o

i

p

ie

rw

ia

s

tk

o

w

e

g

o

00

3

R

30000

T

R

30000

e

e









300

T

T

R

E

B

A

0

T

R

E

B

A

2

1

T

R

E

B

A

a

a

a

e

c

c

k

e

c

c

2

T

T

k

e

c

c

T

k

v















































Teoria zderzeń aktywnych

W ogólnym przypadku, dla reakcji zachodzących w układzie
homogenicznym można stosować wyrażenie na szybkość reakcji:

Stałe w równaniu Arrheniusa wynoszą:

T

R

E

0

γ

C

β

B

α
A

γ

C

β

B

α

A

T

R

E

0

a

a

e

k

k

...

c

c

c

k

...

c

c

c

e

k

v



































T

B

A

lnk





0

lnk

A 

R

E

B

a



Energia aktywacji reakcji

A + B → AB

e

n

e

rg

ia

droga reakcji

energia substratów

energia produktu

energia kompleksu
aktywnego

A + B

(A+B)*

AB = C

E

a

Q

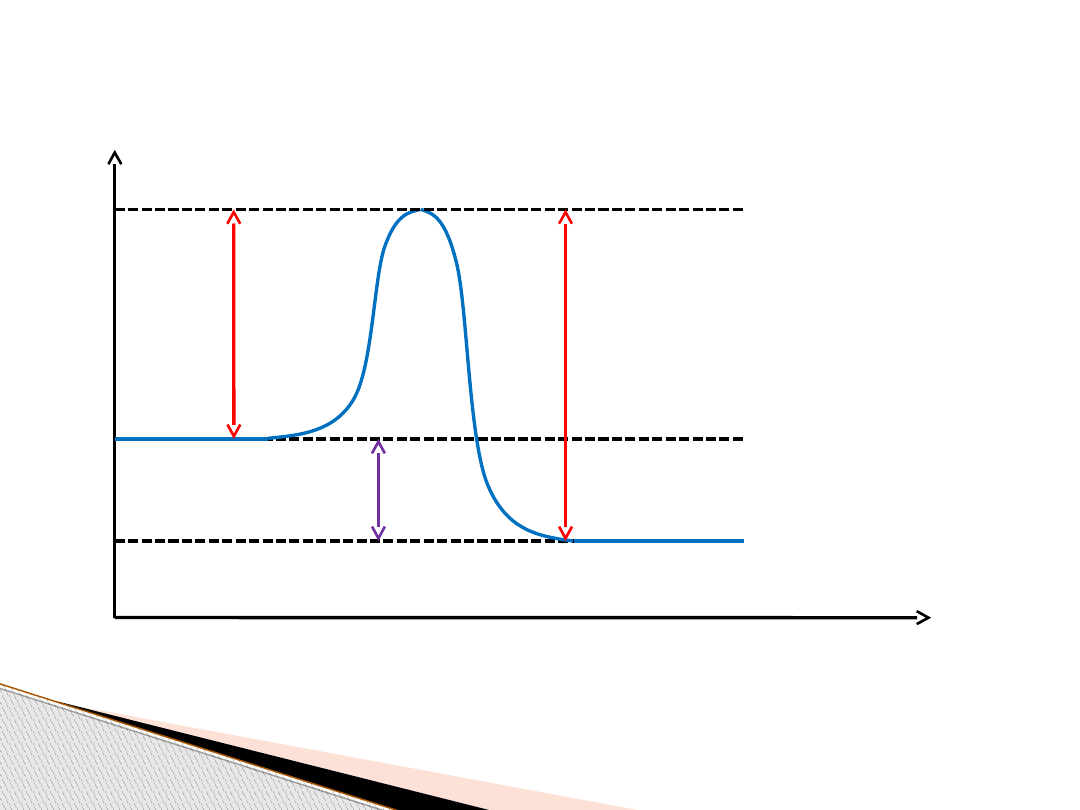
Energia aktywacji w reakcji
odwracalnej

A + B ↔ AB

e

n

e

rg

ia

droga reakcji

energia substratów

energia produktu

energia kompleksu
aktywnego

A + B

(A+B)*

AB = C

E

a L→P

Q

E

a P→L

Q = E

a P→L

– E

a P→L

Kompleks aktywny i teoria stanu
przejściowego

W trakcie zderzenia aktywnego powstaje kompleks aktywny.
Proces tez zachodzi zgodnie z równaniem

A + B → (A+B)*

. Można

zapisać wyrażenie na stałą stężeniową:

Analizując drgania w kompleksie aktywnym, można określić
szybkość zachodzenia reakcji:

[B]

[A]

B)*]

[(A

K







A

B

(A+B)*

Kompleks aktywny i teoria stanu
przejściowego

Średnia częstotliwość drgań w kompleksie aktywnym dana jest
zależnością:

gdzie k – stała Boltzmanna, h – stała Plancka.

Jeśli kompleks aktywny ma wyższą częstotliwość drgań to
częściej przybierze konfigurację umożliwiająca rozpad na
produkty

reakcji.

A

więc

szybkość

reakcji

v

będzie

proporcjonalna do v

śr

. Z drugiej strony, szybkość reakcji będzie

też proporcjonalna do stężenia kompleksów aktywnych, wobec
czego:

Z termodynamiki można wyprowadzić zależność:

h

T

k

v

śr





[A][B]

K

h

T

k

k

B)*]

[(A

v

k

v

$

śr

$



















RT

ΔH

R

ΔS

0

0

e

e

K







Kompleks aktywny i teoria stanu
przejściowego

Otrzymuje się zatem równanie:

ΔH

0

dla kompleksu aktywnego ma więc sens energii aktywacji.

R

ΔS

$

0

t

RT

ΔH

0

t

RT

ΔH

R

ΔS

$

0

0

0

0

e

h

T

k

k

k

[A][B]

e

k

[A][B]

e

e

h

T

k

k

v































Katalizatory

Katalizatory

Energia aktywacji można traktować jako pewną barierę, którą
muszą pokonać cząsteczki substratów aby utworzyć produkty.
Obniżenie tej bariery spowodowało by zwiększenie szybkości
zachodzenia reakcji w danej temperaturze, dla tych samych
wyjściowych stężeń substratów .

Aby to osiągnąć stosuje się tzw. katalizatory.

Kataliza to

zjawisko zmiany szybkości reakcji chemicznych pod wpływem
katalizatorów.

Wyróżniamy

katalizę homogeniczną

: substraty i katalizator

tworzą jedną fazę, oraz

katalizę heterogeniczną

: substraty i

katalizator występują w różnych fazach.

Zapis reakcji homogenicznej z katalizatorem można przedstawić
jako:

A + B + K → (AK)* + B → (AKB)* → AB + K

lub

A + B + K → A + (BK)* → (ABK)* → AB + K

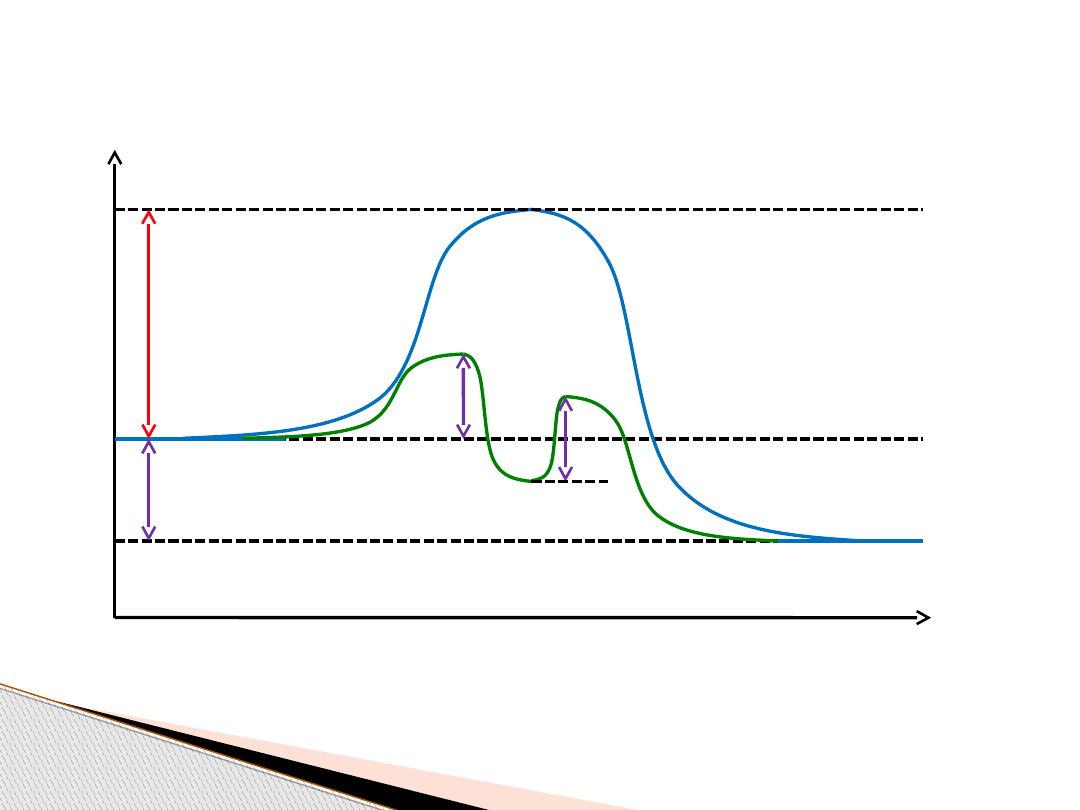
Przykład działania katalizatora:

A + B

+ K → AB + K

e

n

e

rg

ia

droga reakcji

A + B

+ K

(AK)* + B

AB = C

+ K

E

a

Q

E

a

> E

I

a

E

a

> E

II

a

(AK+B)*

E

I

a

E

II

a

AK + B