2. Analogie między elektrycznymi, mechanicznymi, hydraulicznymi i pneumatycznymi elementami układów automatyki.

2.1. Podstawowe równania układów liniowych

Układem liniowym określa się układ złożony z elementów, których charakterystyki statyczne są linią prostą.

Urządzenia regulacji automatycznej realizowane są przy użyciu układów elektrycznych, mechanicznych, pneumatycznych i hydraulicznych.

Elementy wchodzące w skład tych układów podzielić można na następujące trzy rodzaje:

1. elementy rozpraszające energię ( 2.3. )

2. elementy magazynujące energię w postaci kinetycznej ( 2.4. )

3. elementy magazynujące energię w postaci potencjalnej ( 2.5. )

Zakładamy, że rozpatrywane układy liniowe składają się z elementów o stałych parametrach skupionych, niezależnie od wielkości występujących w tych układach. Założenie to w odniesieniu:

1. do układów elektrycznych równoważne jest założeniu, że rezystancje, indukcyjności i pojemności są stałe oraz niezależne od prądu i napięcia,

2. do układów mechanicznych równoważne jest założeniu, że siła tarcia jest proporcjonalna do prędkości w pierwszej potędze (tarcie lepkie) oraz, że układy te składają się z ciał idealnie twardych i sprężyn idealnych o pomijalnej masie,

3. do układów pneumatycznych równoważne jest założeniu, że opór przepływu jest stały, niezależny od przepływu i ciśnienia, gaz zaś jest doskonale sprężysty o stałej wartości współczynnika sprężystości,

4. do układów hydraulicznych równoważne jest założeniu, że ciecze są nieściśliwe, a opór przepływu jest stały, niezależny od przepływu i ciśnienia.

Własności dynamiczne liniowych układów o stałych parametrach skupionych opisują liniowe równania różniczkowo-całkowe o stałych współczynnikach. Różniczkując obie strony tych równań możemy je sprowadzić do odpowiednich liniowych równań różniczkowych o stałych współczynnikach.

Oznaczenia oraz podstawowe zależności opisujące właściwości dynamiczne (tzn. w stanie nieustalonym) elementów podane są w tabelach (załącznik).

Jak wynika z tabeli (załącznik) elementy elektryczne, hydrauliczne i mechaniczne można opisać analogicznymi równaniami matematycznymi. W związku z tym jedne układy można modelować innymi układami, np. układy mechaniczne lub hydrauliczne za pomocą układów elektrycznych.

2.2. Modelowanie układów automatyki.

Modelowanie jest to metoda badania procesów fizycznych, technicznych, blokowych itp. lub rozwiązywanie zagadnień matematycznych przy użyciu modeli tych procesów (zagadnień).

Metoda ta polega na tym, że zamiast badać proces rzeczywisty, bada się model procesu i na podstawie wyników badań wnioskuje się o przebiegu procesu rzeczywistego (rozwiązaniu zagadnienia).

Rozróżniamy modelowanie analogowe i cyfrowe.

Modelowanie cyfrowe można interpretować np. jako program rozwiązywania równań modelu matematycznego i analizy tych rozwiązań za pomocą techniki obliczeniowej (komputera).

W układach automatyki stosuje się przede wszystkim modelowanie analogowe. Przez modelowanie analogowe rozumie się badania przeprowadzane na modelach zbudowanych na zasadzie analogii fizycznych. Należy w takim przypadku znać opis matematyczny modelowanych procesów.

Zalety modelowania analogowego:

• Możliwość odwzorowania badanych procesów w innej, dogodniejszej do pomiaru technice,

• Możliwość zmiany skali czasu, np. przedstawienie wolnozmiennego procesu rzeczywistego za pomocą przebiegających znacznie szybciej procesów w modelu,

• Służy do rozwiązywania zadań „czysto matematycznych”, nie dotyczących żadnych procesów rzeczywistych

Analogia ogólnie oznacza podobieństwo zachodzące pod pewnymi względami między różnymi przedmiotami, zjawiskami lub procesami.

Analogia fizyczna polega na tym, że różnymi zjawiskami fizycznymi rządzą takie same lub podobne prawa i dzięki temu przebieg tych zjawisk może być opisany za pomocą takich samych zależności matematycznych.

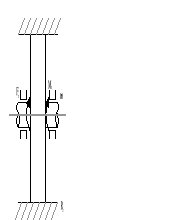
Klasyczny przykład analogii fizycznej dotyczy układów mechanicznego i elektrycznego przedstawionych na rysunkach.

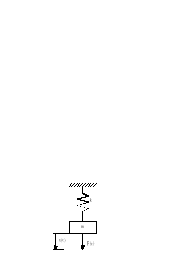
Rys.2.1.Układ analogowy mechaniczny.

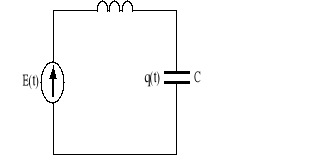
Rys.2.2.Układ analogowy elektryczny.

Układy są opisane równaniami:

(2.1)

(2.2)

Jeżeli po przyjęciu odpowiednich jednostek zajdą równości:

(2.3);(2.4);(2.5)

i równe będą odpowiadające sobie warunki początkowe:

(2.6)

(2.7)

to rozwiązania obu równań będą miały identyczną postać matematyczną:

(2.8)

Można zatem powiedzieć, że w tym przypadku układ elektryczny jest modelem analogowym układu mechanicznego. Stwierdzenie to można odwrócić mówiąc, że układ mechaniczny jest modelem układu elektrycznego.

Analogię elektryczną układu mechanicznego znajduje się tworząc obwód elektryczny, którego równanie różniczkowe ma postać identyczną z równaniem układu mechanicznego.

Przy ustalaniu analogowego obwodu elektrycznego zaleca się następujące postępowanie:

1. wpisuje się równania układu mechanicznego,

2. podstawia się stosowane w obwodzie elektrycznym wielkości elektryczne stałe i zmienne,

3. interpretuje się otrzymane równanie w celu zestawienia analogowego obwodu elektrycznego.

a)

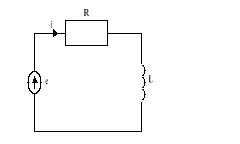
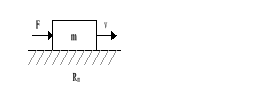
b)

c)

d)

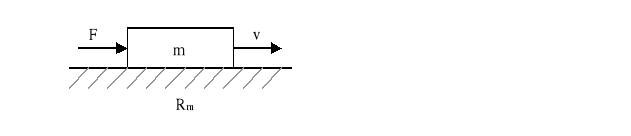
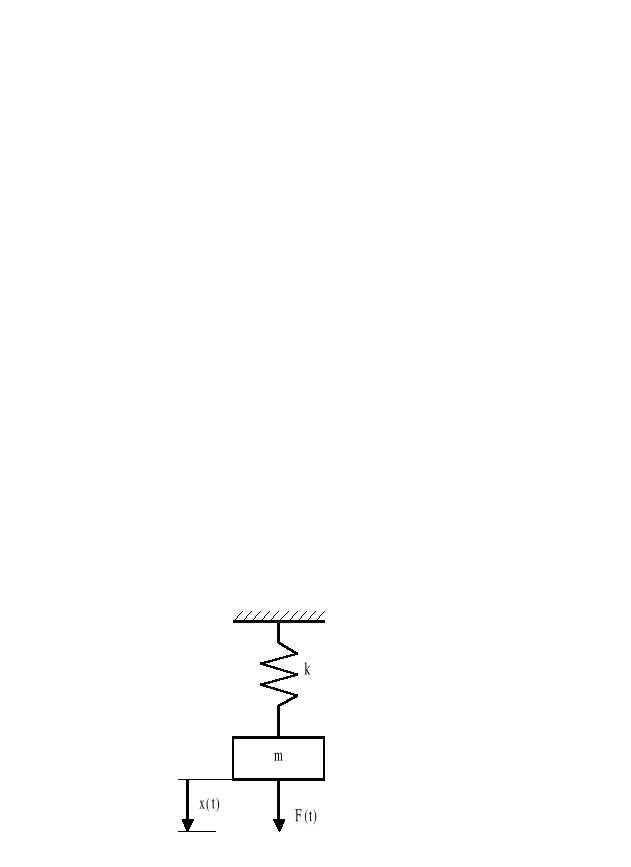
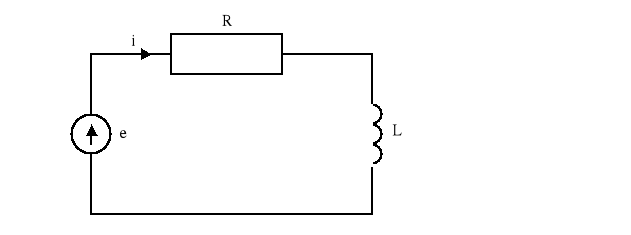
Rys.2.3.Układy analogowe: a)elektryczny, b)mechaniczny, c)mechaniczny, d)hydrauliczny.

Do podstawowych elementów z rysunku 2.3 można napisać ,że:

(2.9)

lub

(2.10)

Dla całości układu elektrycznego:

(2.11)

Układów mechanicznych:

1. tarcia

(2.12)

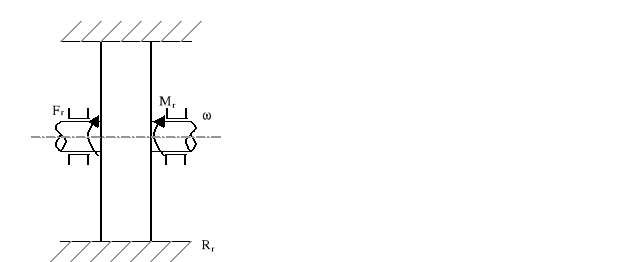
2. ruchu obrotowego

(2.13)

3. przepływu cieczy

(2.14)

Na podstawie przytoczonych wyżej przykładów i Rys.2.3. widzimy w jaki sposób model analogowe może służyć do rozwiązywania zagadnień matematycznych.

Każdy z przedstawionych przykładów może "rozwiązać" równanie różniczkowe pierwszego rzędu:

(2.15)

lub wyższego rzędu:

(2.16)

2.3. Elementy rozpraszające energię

• Opór elektryczny R

(2.17)

u - napięcie, i - prąd

• Opór tarcia R_m w układach mechanicznych o ruchu postępowym

(2.18)

F - siła, v - prędkość w ruchu postępowym

• Opór tarcia R_r w układach mechanicznych w ruchu obrotowym

(2.19)

F_r - siła,
- prędkość w ruchu postępowego

• Opór przepływu R_p w układach pneumatycznych lub hydraulicznych

(2.20)

p₁,p₂ - ciśnienie na wejściu i wyjściu przewodu, i_p - przepływ (w jednostkach objętości na jednostce czasu)

2.4. Elementy magazynujące energię w postaci

kinetycznej.

• Cewka elektryczna o indukcyjności L

(2.21)

L - współczynnik indukcji własnej cewki, t - czas

• Ciało twarde o masie m (układ mechaniczny o ruchu postępowym)

(2.22)

m - masa ciała

• Ciało twarde o momencie bezwładności M

(2.23)

• Bezwładność m_p gazów i cieczy

(2.24)

(2.25)

p₁,p₂ - ciśnienie na wejściu i wyjściu przewodu, i_p - przepływ,

m - całkowita masa substancji (gaz, ciecz) w danym przewodzie, s - przekrój przewodu

2.5. Elementy magazynujące energię w postaci

potencjalnej

• Kondensator o pojemności C

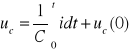
(2.26)

u_c(0) - początkowe napięcie na kondensatorze

• Element sprężysty o sprężystości C_m w układach mechanicznych o ruchu postępowym

(2.26)

x - przesunięcie, jakiego dozna dana sprężyna pod wpływem siły F,

f(0) - początkowa wartość siły w chwili t=0

• Element sprężysty o sprężystości C_r w układach mechanicznych o ruchu obrotowym

(2.27)

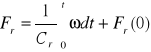
(2.28)

 - kąt skręcania, jakiego dozna sprężyna pod wpływem momentu F_r,

F_r(0) - początkowa wartość momentu obrotowego

• Sprężystość C_p gazu w komorze pneumatycznej

(2.29)

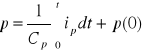
(2.30)

i_p - przepływ, p(0) - wartość ciśnienia w chwili początkowej

• Napełnianie zbiornika cieczą nieściśliwą w układach hydraulicznych

(2.31)

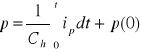
(2.32)

i_p - przepływ, p(0) - wartość ciśnienia w chwili początkowej

Moc idąca na straty w elementach rozpraszających energię określona jest wzorami:

• w układach elektrycznych:

(2.33)

• w układach mechanicznych o ruchu postępowym:

(2.34)

• w układach mechanicznych o ruchu obrotowym:

(2.35)

• w układach pneumatycznych i hydraulicznych:

(2.36)

Elementy magazynujące energię w postaci kinetycznej określone są wzorami:

• w układach elektrycznych:

(2.37)

• w układach mechanicznych o ruchu postępowym:

(2.38)

• w układach mechanicznych o ruchu obrotowym:

(2.39)

• w układach pneumatycznych i hydraulicznych:

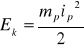
(2.40)

Elementy magazynujące energie w postaci potencjalnej określone są wzorami:

• w układach elektrycznych:

(2.41)

• w układach mechanicznych o ruchu postępowym:

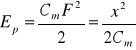
(2.42)

• w układach mechanicznych o ruchu obrotowym:

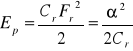
(2.43)

• w układach pneumatycznych:

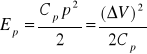
(2.44)

• w układach hydraulicznych:

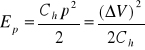
(2.45)

Nowoczesne metody prezentacji wiedzy w dydaktyce automatyki

Str.47

Analogie między układami automatyki

i_p

R_p

p

m_p

---