Politechnika Warszawska

Instytut Mikroelektroniki i Optoelektroniki

Zakład Optoelektroniki

Badanie Parametrów Lasera He-Ne

Instrukcja wykonawcza do ćwiczenia laboratoryjnego

ćwiczenie opracował w ramach

inżynierskiej pracy dyplomowej

Tomasz Kasjaniuk

kierownik pracy - dr inż. Jerzy Kęsik

Warszawa 2001

Spis treści

1. Cel i zakres ćwiczenia 3

2. Schemat i opis elementów układu pomiarowego 4

3. Część wykonawcza ćwiczenia 8

3.1 Określanie poziomu strat własnych rezonatora lasera 8

3.2. Wyznaczenie wartości nienasyconego współczynnika wzmocnienia 9

3.3. Wyznaczenie zależności mocy lasera od strat tłumika. 10

3.4. Określenie optymalnej transmisji zwierciadła 11

3.5. Pomiar parametru nasycenia i obliczenie mocy wyjściowej lasera 12

4. Załącznik nr 1 - justowanie rezonatora lasera 13

5. Załącznik nr 2 - program wspomagania matematycznego MATHCAD 16

1. Cel i zakres ćwiczenia:

Celem ćwiczenia jest pomiar parametrów lasera He-Ne mających zasadniczy wpływ na moc wyjściową i widmo promieniowania lasera. Należą do nich: nienasycony współczynnik wzmocnienia k₀, straty własne rezonatora a_s, parametr nasycenia I_s i optymalna ze względu na maksymalną moc wyjściową wartość transmisji zwierciadeł T_opt.

Przed przystąpieniem do wykonania ćwiczenie należy dokładnie zapoznać się z opracowaniem pt. „LASERY - Podstawy Fizyczne”, zwracając szczególną uwagę na mechanizmy fizyczne prowadzące do uzyskania inwersji obsadzeń, warunki generacji laserowej, efekt nasycenia wzmocnienia. Właściwe zrozumienie tych zjawisk ma silny wpływ na właściwą interpretację otrzymanych w ćwiczeniu wyników pomiarowych.

Ćwiczenie składa się z kolejno po sobie następujących bloków wykonawczych i należy je wykonywać we wskazanej w niniejszej instrukcji kolejności. W każdym bloku wykonawczym następuje porównanie zmierzonych wielkości z obliczonymi teoretycznie. Głównym zadaniem wykonawców ćwiczenia jest właściwa interpretacja otrzymanych wyników - wyjaśnienie przyczyn ewentualnych różnic między wielkościami zmierzonymi i obliczonymi.

Podstawowym, przewidzianym w ćwiczeniu eksperymentem jest pomiar zależności mocy wyjściowej lasera od kalibrowanych strat wprowadzanych do rezonatora przez tłumik optyczny. Staranne wykonanie tej części ćwiczenia ma decydujący wpływ na zgodność wyników doświadczalnych i obliczonych. W tym celu należy przed przystąpieniem do pomiarów wykonać dokładne justowanie rezonatora lasera oraz oczyścić elementy optyczne lasera i tłumika. Niezbędny proces dokładnego justowania rezonatora lasera został opisany w załączniku nr 1, który znajduje się na końcu instrukcji.

Wszystkie przewidziane w programie ćwiczenia obliczenia należy wykonać programem wspomagania matematycznego MATHCAD (załącznik nr 2). Program ten radykalnie ułatwi wykonanie tych dość skomplikowanych i żmudnych obliczeń oraz pozwoli na graficzne przedstawienie zarówno wielkości obliczonych jak i doświadczalnych. Stanowi on jednocześnie sprawozdanie z wykonanego ćwiczenia i zawiera miejsce na sformułowanie wniosków końcowych..

2. Schemat i opis elementów układu pomiarowego:

Podstawowym podzespołem układu pomiarowego (rys. 2.1) jest laser helowo-neonowy pracujący na czerwonej linii widmowej o długości fali 633 nm. Wiązka wyjściowa promieniowania laserowego skierowana jest na analizator widma AW. W tor wiązki wyjściowej można wprowadzić miernik mocy lasera MM, zaś w rezonatorze lasera od strony zwierciadła transmisyjnego można umieścić tłumik optyczny.

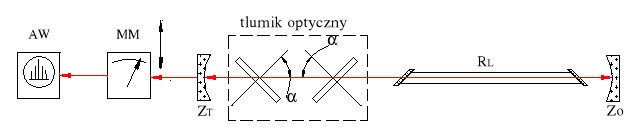
Rys.2.1. Schemat układu pomiarowego wykorzystywanego w ćwiczeniu:
Z₁ - zwierciadło transmisyjne (T=1.5%), Z₂ - zwierciadło całkowicie odbijające (T=0%), MM - miernik mocy, R_L - rura laserowa, AW - analizator widma

Szklana rura laserowa R_L, napełniona mieszaniną helu i neonu i zamknięta jest okienkami Brewstera wykonanymi ze szkła optycznego. Długość kapilary wyładowczej rury wynosi 640 mm, zaś jej średnica wewnętrzna 2,2 mm.

Rezonator lasera tworzą dwa wklęsłe zwierciadła o promieniu krzywizny ok. 2 m., z których jednoZ₀ jest całkowicie odbijające, a drugie Z_T posiada transmisję T=1.5%. Zwierciadła osadzone są w uchwytach, które przy pomocy śrub mikrometrycznych umożliwiają ich precyzyjne ustawienie kątowe. Rura laserowa i uchwyty zwierciadeł są umieszczone na stabilnej mechanicznie ławie optycznej, umożliwiającą zmianę długości rezonatora.

Do rezonatora lasera wprowadzony jest tłumik optyczny, który tworzą dwie płasko-równoległe płytki wykonane z kwarcu topionego, obracane symetrycznie przy pomocy śruby mikrometrycznej (1mm przesuwu śruby odpowiada obrotowi płytek o ok.1,8°). Tłumik ten służy do wprowadzania dodatkowych, kontrolowanych (wg wzorów 2.1 i 2.2) strat do rezonatora lasera.

Zgodnie ze znanymi wzorami Fresnela, współczynnik odbicia R liniowo spolaryzowanego promieniowania laserowego od jednej powierzchni płytki tłumika o współczynniku załamania n ustawionej pod kątem a wynosi:

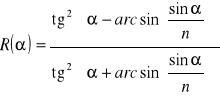
(2.1)

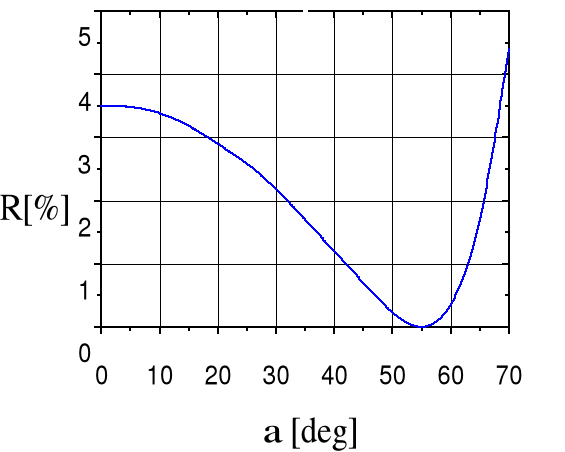
Rys.2.2. Zależność współczynnika odbicia R od kąta a dla n=1.46 (obliczona wg 2.1)

Przy ustawieniu płytek tłumika pod kątem Brewstera (a_B=56^o) straty odbiciowe przyjmują wartość bliską zeru, zaś przy zmianie kątowego ustawienia płytki odpowiednio zwiększają się: Prostopadłemu (a=0) do kierunku osi wiązki laserowej ustawieniu płytki odpowiada R=3.5%, a przy a>a_B. dąży do 100%.

Zależność kąta ustawienia płytek tłumika α od położenia śruby mikrometrycznej dz nie jest ściśle liniowa. Z konstrukcji mechanicznej tłumika wynika:

(2.2)

gdzie: dz₀=15 dz - położenie pokrętła przy którym płytki tłumika ustawione są pod kątem 45⁰

Podstawowym podzespołem analizatora widma promieniowania laserowego (rys.2.3.) jest przestrajany (skaningowy) interferometr Fabry-Perot (IFP). W skład interferometru wchodzą dwa jednakowe zwierciadła o dużych współczynnikach odbicia R, odległe od siebie o wartość D. Jedno ze zwierciadeł interferometru przymocowane jest do elementu piezoelektrycznego Pc z otworem, przez który wiązka laserowa opuszcza interferometr i pada na fotodetektor Fd. Sygnał z fotodetektora jest podawany na wejście oscyloskopu, natomiast grubość piezoelektryka, a więc i długość interferometru D jest cyklicznie liniowo zmieniana (przestrajana) napięciem piłokształtnym podstawy czasu oscyloskopu.

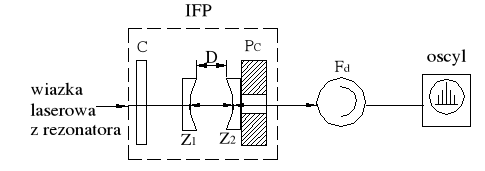
Rys.2.3. Schemat analizatora widma promieniowania lasera: IFP - interferometr Fabry - Perot, Z₁,Z₂ - zwierciadła interferometru , P_c - element piezoceramiczny, F_d - fotodetektor, oscyl - oscyloskop

Widmową charakterystykę transmisji interferometru przedstawioną na tle widma promieniowania lasera, wyjaśniającą zasadę pomiaru pokazano rys. 2.4.

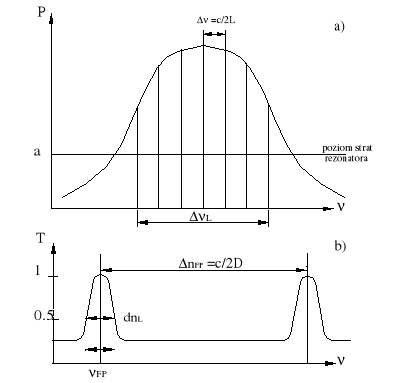
Rys.2.4. Zasada wizualizacji widma lasera przestrajanym interferometrem Fabry-Perot:

a) widmo generowane przez laser

b) zależność transmisji interferometru T od częstotliwości światła laserowego

Widmo częstotliwości rezonansowych interferometru Fabry-Perot (tzn. takich dla których w rezonatorze o długości D mieści się całkowita liczba półfal) składa się (podobnie jak widmo rezonatora lasera). z jednakowo od siebie odległych o wartość Dn_FP = c/2D częstotliwości. Dla tych częstotliwości transmisja interferometru T, niezależnie od wartości R jest równa 1 (przy założeniu bezstratnego rezonatora). Od wartości współczynnika odbicia zwierciadeł R zależy natomiast szerokość pasm transmisyjnych δν_FP zdefiniowana dla T=0.5 w/g zależności:

(2.3)

Interferometr Fabry-Perot działa więc jak cykliczny, wąskopasmowy filtr transmisyjny o rosnącej wraz z R wg (2.3) selektywności.

Bezwzględna wartość częstotliwości rezonansowych interferometru ν_FP jest ściśle związana z długością rezonatora D:

gdzie: m - liczba półfal (2.4)

Amplituda napięcia podstawy czasu jest tak dobrana aby uzyskać przesunięcie pasm transmisyjnych o wartość zbliżoną do Δν_FP (odpowiada to zmianie długości interferometru o λ/2), zaś odległość D w ten sposób aby zakres Δν_FP przekraczał zakres generacji lasera Δν_L (rys.3.4). W ten sposób uzyskujemy liniowe, cykliczne „przemiatanie” wąskiego pasma transmisji interferometru wzdłuż całego widma emitowanego przez laser.

W momentach zgodności położenia pasma z modami generowanymi przez laser na wejściu oscyloskopu pojawia się sygnał proporcjonalny do amplitudy modu. Wykorzystanie podstawy czasu oscyloskopu jako źródła napięcia piłokształtnego zapewnia w efektowny sposób wizualizację widma lasera. Metoda ta daje pełną informację o ilości generowanych modów lasera, wzajemnych relacjach amplitudowych i o względnym odstępie międzymodowym. Nie można jednak tą metodą określić szerokości pojedynczego modu Δν_m ze względu na to, że jest ona dużo mniejsza od szerokości pasma transmisyjnego interferometru dν_FP.

Zasilający element piezoceramiczny sterownik napięcia piłokształtnego pozwala na zmianę obrazu obserwowanego widma lasera:

• zmieniając amplitudę (pokrętło AMPLITUDE) dokonujemy zmiany odstępu międzymodowego widma

• zmieniając poziom napięcia stałego (pokrętło DC LEVEL) przesuwamy poziomo obraz widma

Oba napięcia należy tak dobrać aby obserwowane widmo lasera wypełniało symetrycznie cały ekran oscyloskopu.

3.Część wykonawcza ćwiczenia

3.1 Określanie poziomu strat własnych rezonatora lasera

1. Zestawić układ pomiarowy w/g schematu pokazanego na rys.2.1. (z wyjątkiem tłumika optycznego)

2. Uruchomić laser, analizator widma oraz miernik mocy

3. Ustawić długość rezonatora równą L=100cm uważając, aby nie doprowadzić do zaniku generacji lasera (nie rozjustować rezonatora). W tym celu należy ostrożnie odsuwać zwierciadło transmisyjne obserwując jednocześnie moc lasera. Przy wyraźnym zmniejszeniu mocy należy zatrzymać ruch zwierciadła i dojustowywać rezonator pokrętłami justowniczymi do maksymalnej mocy. Czynność powtarzać aż do osiągnięcia żądanej długości rezonatora.

4. Oczyścić alkoholem metylowym okienka Brewstera oraz w razie potrzeby zwierciadła rezonatora w celu uzyskania maksymalnej mocy lasera.

5. Dojustować przy pomocy pokręteł justowniczych analizator widma tak, aby uzyskany na ekranie obraz widma lasera był najostrzejszy.

6. Dobrać amplitudę napięcia piłokształtnego tak, aby uzyskać wystarczający zakres przestrajania interferometru.

7. Odczytać z ekranu oscyloskopu liczbę modów poosiowych N generowanych przez laser

8. Obliczyć względny poziom strat własnych rezonatora a_W:

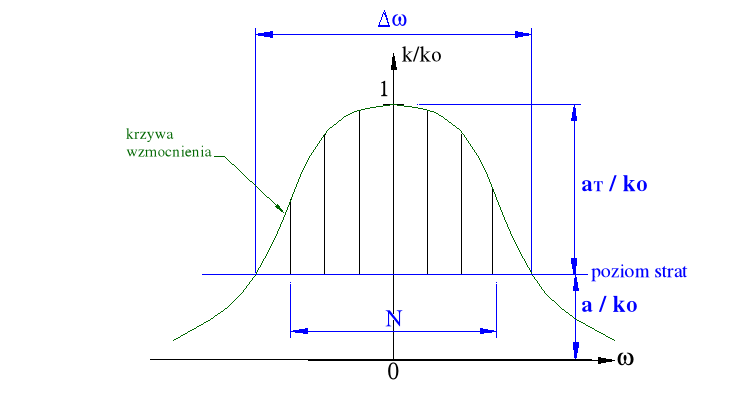
Rys.2.5 . Widmo lasera - zasada określenia poziomu strat i nienasyconego współczynnika wzmocnienia

przybliżony częstotliwościowy zakres generacji lasera Dw:

(2.5)

W celu określenia względnego poziomu strat własnych rezonatora a_W=a/k₀ skorzystać należy z uproszczonego wzoru opisującego kształt krzywej wzmocnienia oraz z progowego warunku generacji:

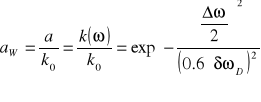
(2.6)

gdzie: Dω - zakres generacji

δω_D - szerokość połówkowa (δω_D = 1500MHz)

k₀ - nienasycony współczynnik wzmocnienia

Podobne pomiary należy przeprowadzić dla lasera z wprowadzonym do rezonatora tłumikiem optycznym:

1. Wprowadzić ostrożnie tłumik do rezonatora lasera

2. Dojustować rezonator do maksymalnej mocy

3. Pokrętłem śruby mikrometrycznej ustawić płytki tłumika pod kątem Brewstera umożliwiającym uzyskanie maksymalnej mocy lasera.

4. Ponownie dojustować rezonator do maksymalnej mocy

5. Oczyścić metanolem płytki tłumika

6. Podobnie jak poprzednio określić względne straty własne rezonatora a_WT

7. Sformułować wnioski

3.2 Wyznaczenie wartości nienasyconego współczynnika wzmocnienia

Pomiar wartości współczynnika wzmocnienia k₀ ośrodka aktywnego lasera polega na wprowadzaniu przy pomocy regulowanego tłumika optycznego znanych strat do wnętrza rezonatora aż do uzyskania zaniku akcji laserowej.

1. W układzie jak poprzednio pokrętłem tłumika doprowadzić do zaniku akcji laserowej.

2. Tuż przed zanikiem generacji dojustować laser

3. Odczytać dwie wielkości położenia tłumika dz_prog1 i dz_prog2 odpowiadające zanikowi generacji przy pochylaniu tłumika w obie strony od kąta Brewstera.

4. Korzystając z obliczonej poprzednio wartości względnego poziomu strat rezonatora a_WT określić bezwzględną wartość nienasyconego współczynnika wzmocnienia k₀:.

• Całkowite straty odbiciowe wprowadzone przez tłumik a_T na jedno przejście wiązki laserowej przez rezonator uwzględniając wyrażenia (1, 2) wynoszą:

(2.7)

• Przyjąć średnią wartość strat progowych tłumika

(2.8)

• Uwzględniając warunki progowe generacji (rys. 2.5):

(2.9)

obliczyć korzystając z (1, 2) wartość k₀

3.3. Wyznaczenie zależności mocy lasera od strat tłumika.

Część doświadczalna

1. W układzie pomiarowym jak poprzednio dokonać pomiaru zależności mocy wyjściowej lasera P_Ld od wartości ustawienia płytek tłumika dz.

2. Ustawienie dz zmieniać co 0.5 mm od wartości progowej dz_prog1 do dz_prog2.

3. Po każdorazowej zmianie ustawienia tłumika dojustować rezonator lasera

4. Wykreślić na jednym wykresie zależność zmierzonej mocy P_Ld(dz) i obliczoną z (2.7) a_T(dz)

• Sformułować wnioski

Część teoretyczna

1. Do teoretycznego wyznaczenia tej zależności posługujemy się wzorami na pracę wielomodową lasera. W takim przypadku nasycenie wzmocnienia uznaje się za jednorodne. Moc wyjściowa lasera ( ) wynosi wtedy
   
   
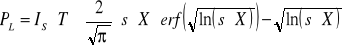
   (2.10 )
   gdzie prametr pobudzenia X jest zależny od położenia tłumika dz :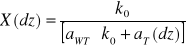
   
   
   ,
   ,

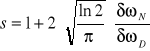
2. Na podstawie zmierzonych wielkości a_WT, i k₀ oraz wyznaczonej z (2.7) a_T(dz), obliczyć i przedstawić graficznie obliczoną zależność zredukowanej do wartości maksymalnej mocy lasera P_Zo od położenia tłumika dz
   :
   
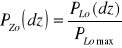
   (2.11)

3. Podobnie jak w p.2 przedstawić na tym samym wykresie doświadczalną zależność zredukowanej do wartości maksymalnej mocy lasera P_Zd od położenia tłumika dz:
   
   
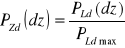
   (2.12)

4. Sformułować wnioski

3.4. Wyznaczanie optymalnej transmisji zwierciadła

Metoda doświadczalna

Doświadczalny dobór optymalnej z punktu widzenia maksymalnej mocy lasera transmisji zwierciadła T_opt pozornie wydaje się łatwy. Wystarczy po prostu kolejno umieszczać w rezonatorze lasera zwierciadła o różnych transmisjach i wybrać najlepsze. Ta pozornie prosta metoda posiada jednak poważne wady:

• jest kosztowna - należy dysponować dużym zbiorem zwierciadeł o różnych transmisjach

• zwierciadła te powinny mieć identyczną jakość optyczną (absorpcja, rozpraszanie itp.)

• kolejna wymiana zwierciadeł wymaga każdorazowego ich starannego czyszczenia i justowania rezonatora --ten proces jest żmudny i pracochłonny

W ćwiczeniu zaproponowano znacznie lepszą metodę wykorzystującą zarówno umieszczony poprzednio w rezonatorze tłumik optyczny jak i wykonane poprzednio pomiary.

Tłumik ten jak wiadomo, wnosi głównie do rezonatora zmienne straty odbiciowe. Można więc zespół tłumik - zwierciadło transmisyjne potraktować jako „zwierciadło zastępcze” o zmiennej, płynnie regulowanej transmisji.

Określenie mocy lasera z takim zwierciadłem zastępczym może się odbywać dwojako:

• przez bezpośredni pomiar sumy mocy wszystkich odbitych od płytek tłumika wiązek promieniowania i wiązki wyjściowej za zwierciadłem. Ta dość żmudna czysto doświadczalna metoda jest jednak obarczona dużym błędem pomiarowym.

• przez proste obliczenie mocy wiązek odbitych i dodanie do niej zmierzonej uprzednio mocy lasera. Ta quasi-doświadczalna metoda będzie dalej stosowana.

Transmisję zwierciadła zastępczego T_Z łatwo jest określić z zależności (wyjaśnić-dlaczego?):

-gdzie R(dz) wg formuł (1,2 ) (2.13)

zaś całkowitą moc lasera P_Cd należy określić z wyrażenia (wyjaśnić):

gdzie P_Ld moc wyjściowa lasera (2.14)

Metoda teoretyczna

Korzystając z teoretycznego wyrażenia na moc lasera ( )

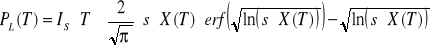
(2.15)

gdzie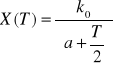

Obliczyć miejsca zerowe pierwszej pochodnej wg:


(2.16)

Wykonanie ćwiczenia

1. Obliczyć i wykreślić doświadczalną zależność całkowitej mocy lasera P_Cd od położenia tłumika dz.

2. Obliczyć i wykreślić doświadczalną zależność całkowitej mocy lasera P_Cd od transmisji zwierciadła zastępczego T_Z.

3. Odczytać z wykresu doświadczalną wartość transmisji optymalnej T_{opt d}

4. Obliczyć z wyrażenia (2.15) teoretyczną wartość transmisji optymalnej T_{opt t} - porównać z wartością doświadczalną

5. Podobnie obliczyć teoretyczną wartość transmisji optymalnej przy bez strat wprowadzanych przez tłumik - porównać z rzeczywistą wartością transmisji zwierciadła T

6. Sformułować wnioski

3.5. Pomiar parametru nasycenia i obliczenie mocy wyjściowej lasera

Parametr nasycenia I_S ma decydujący wpływ na moc wyjściowa lasera (2.10). Chociaż nasycenie wzmocnienia w laserze He-Ne ma charakter bardzo zbliżony do niejednorodnego to jednak przy jego wielomodowej pracy cały obszar krzywej wzmocnienia powyżej poziomu strat ulega jednorodnemu obniżeniu. Tak więc ilościowe zmniejszenie wzmocnienia jest zbliżone do jednorodnego wg zależności:

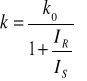
(2.17)

gdzie w warunkach generacji laserowej natężenie promieniowania przechodzącego przez ośrodek aktywny jest oczywiście równe natężeniu promieniowania I_R w rezonatorze lasera:

wyjaśnić wzór (2.18)

W warunkach generacji laserowej efekt nasycenia powoduje zmniejszenie wartości wzmocnienia k do poziomu strat rezonatora a. Stąd z wyrażeń ( i ) można określić wartość I_S:

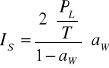
wyjaśnić wzór (2.19)

gdzie a_w - poziom strat względnych rezonatora

Wykonanie ćwiczenia

1. Wyjąć tłumik z rezonatora lasera

2. Starannie wyjustować rezonator i odczytać rzeczywistą wartość mocy wyjściowej lasera P_L

3. Obliczyć korzystając z wyznaczonej uprzednio wartości a_w wartość parametru nasycenia I_S

4. Obliczyć ( wg ) i wykreślić zależność mocy wyjściowej lasera P_L od położenia tłumika dz

5. Porównać obliczoną zależność ze zmierzoną w p.

6. Sformułować wnioski

Załącznik nr 1

4. JUSTOWANIE REZONATORA LASERA

Do uzyskania generacji promieniowania laserowego konieczne jest precyzyjne ustawienie zwierciadeł stanowiących rezonator optyczny. Winne one być ustawione:

• prostopadle do osi kapilary wyładowczej aby umożliwić bezstratne przejście przez nią wiązki laserowej

• równolegle do siebie z dokładnością rzędu ułamka minuty kątowej w celu stworzenia rezonatora Fabry-Perot.

Przeprowadzenie powyższych czynności nazywamy justowaniem rezonatora lasera.

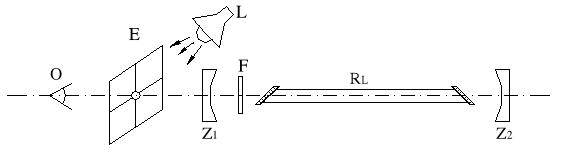
Rys.2.6. Zgrubne justowanie rezonatora lasera: O - oko obserwatora, E - ekran z krzyżem justowniczym, L - lampa oświetlająca, Z₁,Z₂ - zwierciadła, R_L - rura laserowa, F - filtr

Proces justowania rezonatora lasera He-Ne przeprowadzamy w trzech etapach:

Etap pierwszy polega na zgrubnym ustawieniu obu zwierciadeł prostopadle do osi kapilary wyładowczej. W tym celu obserwujemy obraz wyładowania jarzeniowego w kapilarze od strony justowanego zwierciadła poprzez mały otwór w ekranie pomocniczym E umieszczony w środku krzyża justowniczego (rys.3.6). Oko obserwatora powinno być umieszczone dokładnie na osi kapilary. Wtedy świecąca plazma wyładowania jarzeniowego objawi się w postaci jasnej plamki umieszczonej koncentrycznie w kapilarze.

Jednocześnie obserwujemy obraz (oświetlony pomocniczym źródłem światła L) krzyża justowniczego odbitego od powierzchni zwierciadła Z₁. Pokrętłami justowniczym ustawiamy zwierciadło tak, aby obraz krzyża znalazł położenie koncentryczne względem kapilary (rys.3.7). W celu zabezpieczenia oka przed przypadkową generacją lasera należy wprowadzić do rezonatora filtr ochronny F.

Procedurę powyższą powtarzamy dla drugiego zwierciadła Z₂.

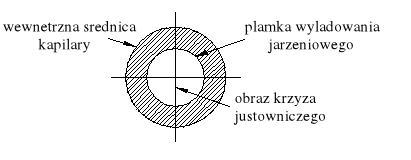
Rys.2.7. Prawidłowy obraz wyładowania jarzeniowego w procesie zgrubnego justowania rezonatora

Przeprowadzona w poprzednim etapie zgrubna procedura justowania jest stosunkowo mało dokładna i z reguły nie wystarcza do uzyskania akcji laserowej. Umożliwia ona jednak na przystąpienie do drugiego etapu, etapu dokładnego justowania. Polega ono, podobnie jak poprzednio na obserwacji wyładowania jarzeniowego od strony jednego ze zwierciadeł (np. Z₁ ), ale przy pomocy lunetki justowniczej (rys.3.8). Ostrość widzenia lunetki ustawiamy w pobliżu zwierciadła Z₂. Wtedy, pod warunkiem zgrubnego (w etapie I) ustawienia zwierciadła Z₂ zaobserwujemy wewnątrz kapilary jasną plamkę, której położenie zależy od ustawienia zwierciadła Z₂. Pokrętłami justowniczym zwierciadła Z₂ należy umieścić te plamkę w położeniu koncentrycznym względem kapilary.

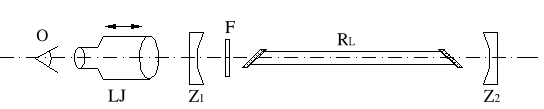
Rys.2.8. Dokładne justowanie rezonatora lasera przy pomocy lunetki justowniczej LJ

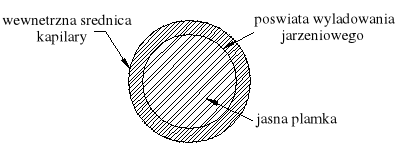
Rys.2.9. Prawidłowy obraz wyładowania jarzeniowego w procesie dokładnego justowania rezonatora

Procedurę powyższą powtarzamy ustawiając lunetkę od strony zwierciadła Z₂, a regulując położenie zwierciadła Z₁. Po usunięciu filtru z rezonatora powinna nastąpić generacja laserowa. Pokrętłami justowniczymi dowolnego zwierciadła doprowadzamy do uzyskania maksymalnej mocy wyjściowej lasera.

Justowanie przeprowadzone w etapie 2 doprowadziło do dokładnie równoległego ustawienia obu zwierciadeł rezonatora i umożliwiło generację laserową. Jednak nie oznacza to, że oś optyczna rezonatora jest zgodna z osią kapilary wyładowczej. Generacja laserowa jest możliwa również wtedy, gdy położenie tych osi różni się od siebie (rys.3.10) chociaż moc promieniowania laserowego będzie w tym przypadku mniejsza.

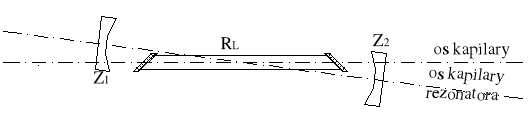
Rys.2.10. Justowanie zgodności przebiegu osi optycznej rezonatora względem osi kapilary wyładowczej lasera

W celu doprowadzenia do zgodności obu osi i uzyskania maksymalnej mocy lasera należy wykonać następujące czynności (etap trzeci):

• zmontować układ zgodnie z rys.3.11

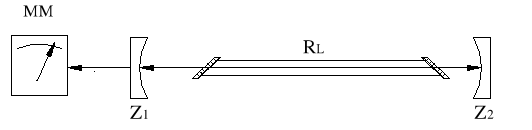
Rys.2.11. Schemat pomiarowy: Z₁ -zwierciadło transmisyjne (T=1.5%), Z₂ - zwierciadło całkowicie odbijające (T=0), MM - miernik mocy, R_L - rura laserowa

• jednym z pokręteł justowniczych dowolnego zwierciadła rozjustować rezonator aż do progu generacji

• analogicznym pokrętłem drugiego zwierciadła doprowadzić do maksymalnej mocy lasera i zmierzyć tę moc

• powtarzać powyższą czynność aż do uzyskania maksymalnej mocy lasera

• procedurę powtórzyć w drugiej (prostopadłej) płaszczyźnie

• oczyścić powierzchnie okienek Brewstera i zaobserwować ewentualne zmiany mocy lasera, wynikające z zanieczyszczeń okienek.

1. Literatura

1. W.W.Rigrod „Journal of Appl. Phys.” Vol. 34, nr 9, september (1963).

2. Adam Kujawski,Paweł Szczepański „Lasery podstawy fizyczne”.

3. Herman Klejman „Lasery”.

4. Franciszek Kaczmarek „Wstęp do fizyki laserów”.

5. Franciszek Kaczmarek „Podstawy działania laserów”.

6. W.F.Kitaeva, A.I.Odincov „Usp. Fiz. Nauk” vol. 99, nr 3, (1969)

7. R.L.Fork, C.K.N.Patel „Phys. Rev.” Vol. 129, nr 6, march (1963)

5

---