Pracownia Zakładu Fizyki Technicznej Politechniki Lubelskiej

Nazwisko i imię							Wydział ZiM 3,5 Grupa
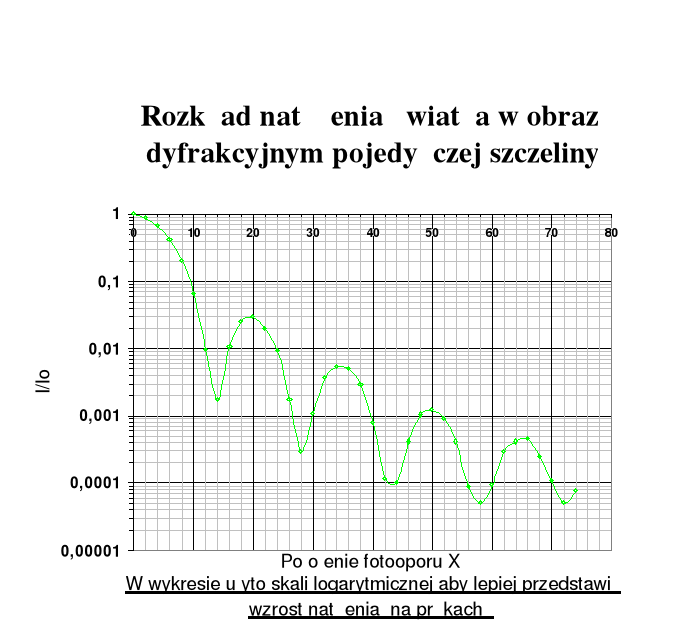
Data 10,11,98 wyk. ćwicz		Numer ćwicz 7,1			Temat Pomiar rozkładu energii promieniowania w widmie dyfrakcyjnym światła pojedynczej szczeliny i szerokości tej szczeliny
Zaliczenie		Ocena	Data		Podpis

Zestawienie wyników w tabeli:

Lp	Natężenie prądu I zależne od natężenia światła [μA]	X położenie fotooporu na ekranie	I/Io Io- natężenie prądu dla X=0
	480	0	1
	420	2	0,875
	320	4	0,6666
	200	6	0,4166
	98	8	0,2041
	32	10	0,0666
	4,6	12	0,0095
	0,82	14	0,0017
	5,2	16	0,0108
	12	18	0,025
	14	20	0,0291
	9,4	22	0,0195
	4,4	24	0,0092
	0,82	26	0,0017
	0,14	28	0,000291
	0,54	30	0,0011
	1,8	32	0,0037
	2,6	34	0,0054
	2,4	36	0,005
	1,4	38	0,00291
	0,38	40	0,0007916
	0,056	42	0,000116
	0,048	44	0,0001
	0,20	46	0,000416
	0,50	48	0,00104
	0,58	50	0,0012
	0,44	52	0,000916
	0,20	54	0,000416
	0,042	56	0,0000875
	0,024	58	0,00005
	0,044	60	0,00009166
	0,14	62	0,0002916
	0,20	64	0,000416
	0,22	66	0,0004583
	0,12	68	0,00025
	0,052	70	0,0001083
	0,024	72	0,00005
	0,036	74	0,000075

Podstawy teoretyczne:

Laser użyty w ćwiczeniu jest laserem helowo - neonowym. Głównymi elementami tego lasera są:

• rura wyładowcza

• rezonator optyczny (złożony z dwóch zwierciadeł)

• zasilacz

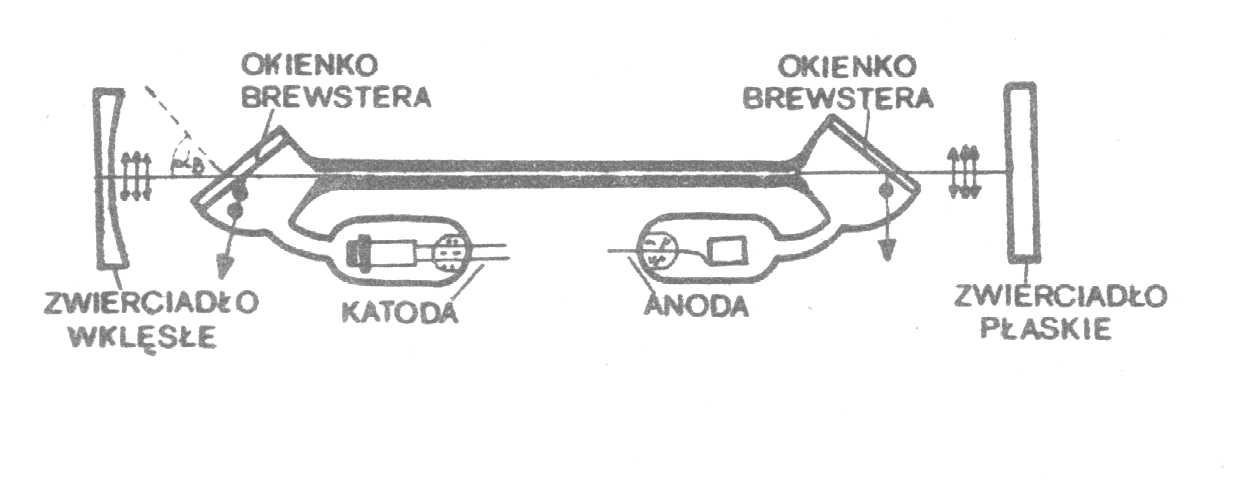
Rura wyładowcza wykonana jest w postaci kapilary o długości 600 mm i średnicy 2 mm ze szkła laboratoryjnego . W skład zespołu rury wyładowczej wchodzą bańka katodowa i anodowa., które stanowią osłonę dla elektrod rury wyładowczej. Katoda wykonana jest w postaci cylindra z blachy aluminiowej. Anoda jest wolframowa. Rura wyładowcza zamocowana jest na wspornikach. Kapilarę na końcu zamykają dwa okienka szklane ustawione pod kątem Brewstera. Rura znajduje się między zwierciadłami. Jedno jest sferyczne wklęsłe i odbija w całości promieniowanie drugie jest płaskie o 1,5% przepuszczalności. Źródłem zasilania jest zasilacz o natężeniu 10mA przy napięciu 1,7 kV.

Elektrony z elektrod zderzają się z atomami helu a te z kolei pobudzają atomy neonu. W wyniku pompowania elektrycznego uzyskujemy wiązkę o długości fali λ = 0,6328μm

Światło laserowe wyróżnia się od światła ze źródeł klasycznych:

1. bardzo małą rozbieżnością wiązki

2. duże natężenie światła

3. dużo większa monochromatyczność

4. wysoki stopień spójności

5. może być całkowicie spolaryzowane

Dyfrakcja fali płaskiej na pojedynczej szczelinie

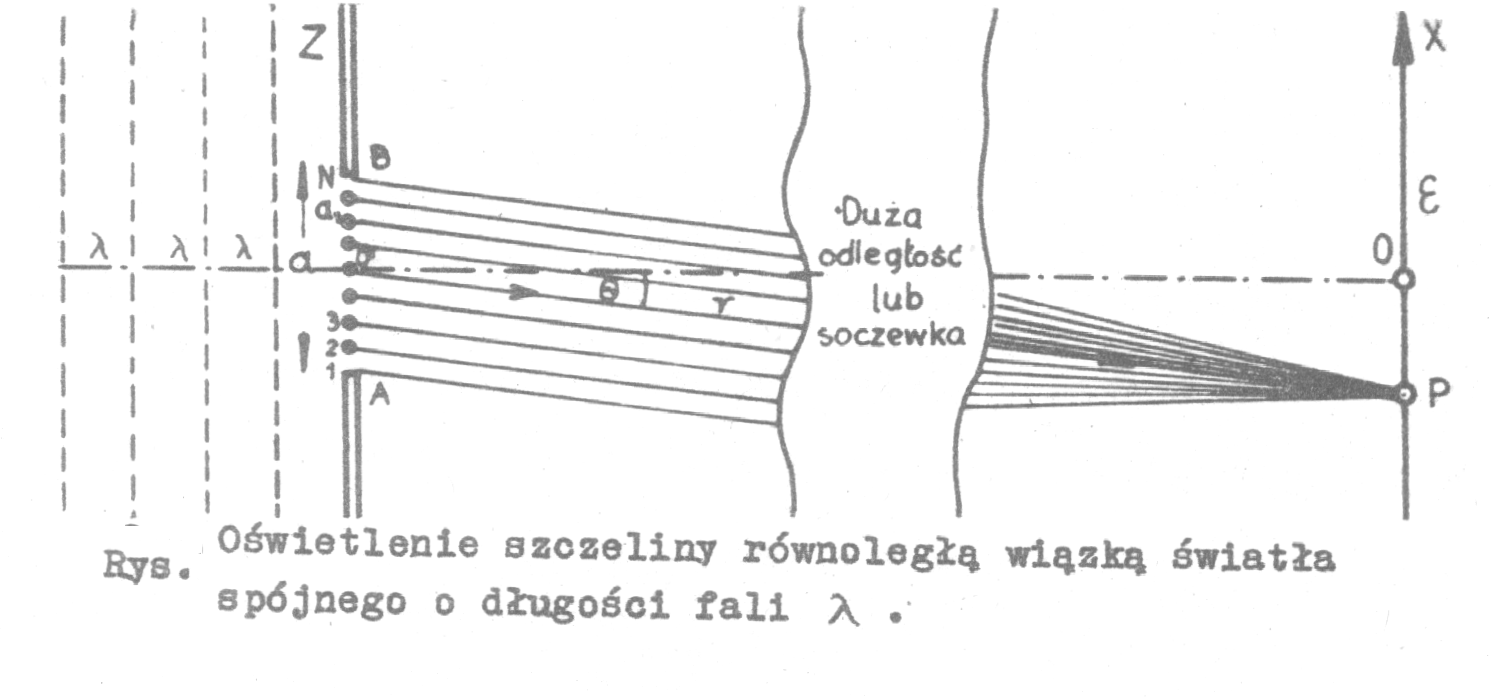
Weźmy pod uwagę monochromatyczną falę płaską padającą na szczelinę o szerokości AB = a w zasłonie (Rys.)

Aby opisać obraz dyfrakcyjny jaki powstanie na odległym ekranie E (tworzącym płaszczyznę xy) należy zgodnie z zasadą Huygensa - Fresnela podzielić całą szczelinę na N (bardzo wąskich) równoległych do osi y szczelin. Każda taka szczelina może być uważana za prostolinijne źródło światła spójnego. W wyniku superpozycji fali pochodzącej od N takich źródeł otrzymamy na ekranie obraz dyfrakcyjny całej szczeliny symetryczny względem osi y. Można więc ograniczyć się przy badaniu rozkładu natężenia światła tylko do osi x.

Oznaczając szerokość szczeliny przez , otrzymujemy, że szerokość całej szczeliny

a = N *a₁

Obraz dyfrakcyjny otrzymany w wyniku ugięcia światła monochromatycznego spójnego na pojedynczej szczelinie pokazany jest na rysunku:

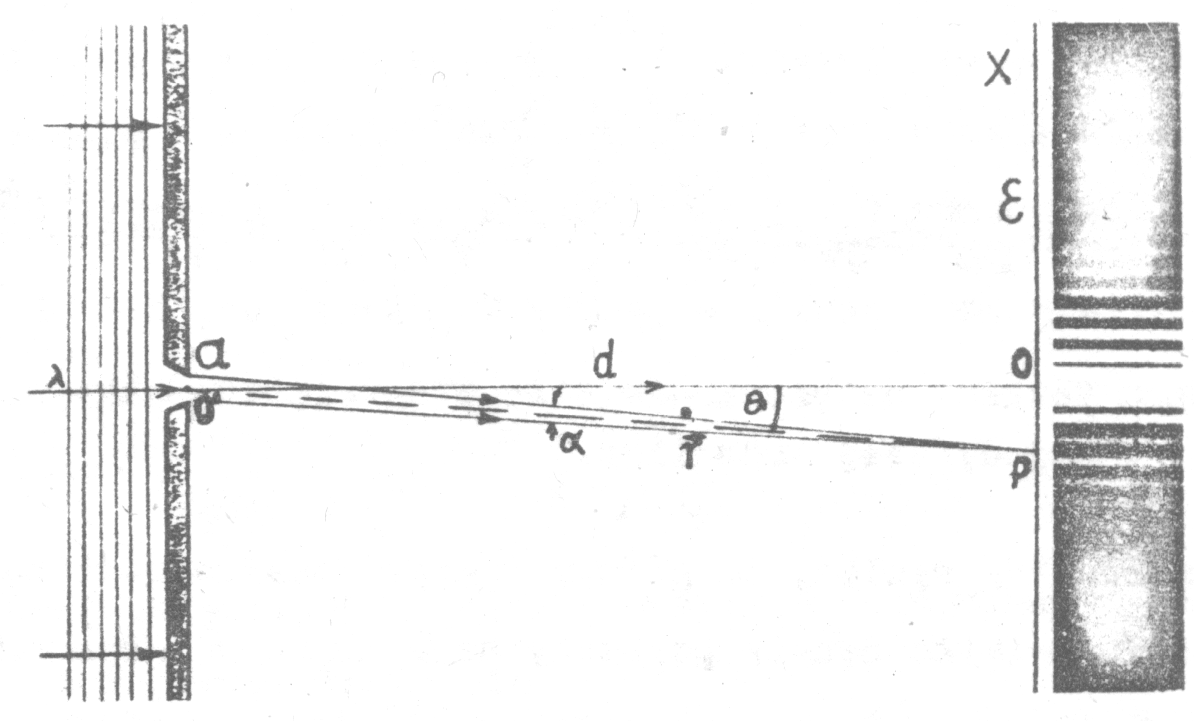
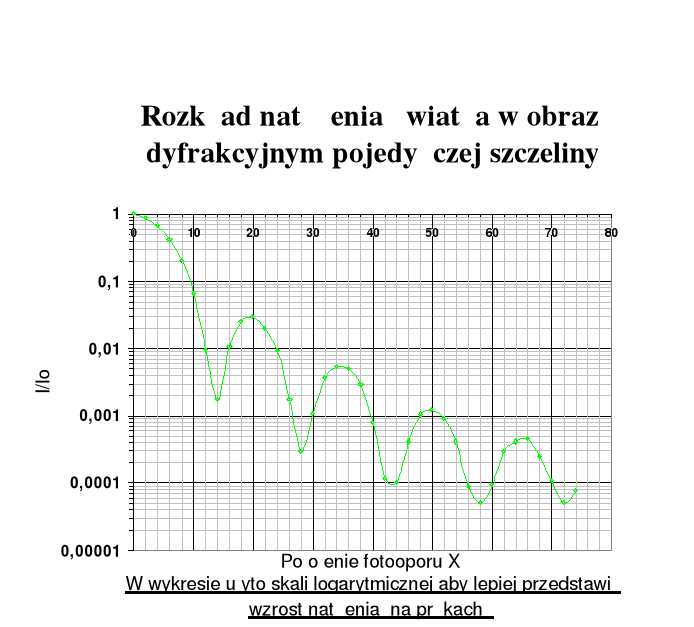
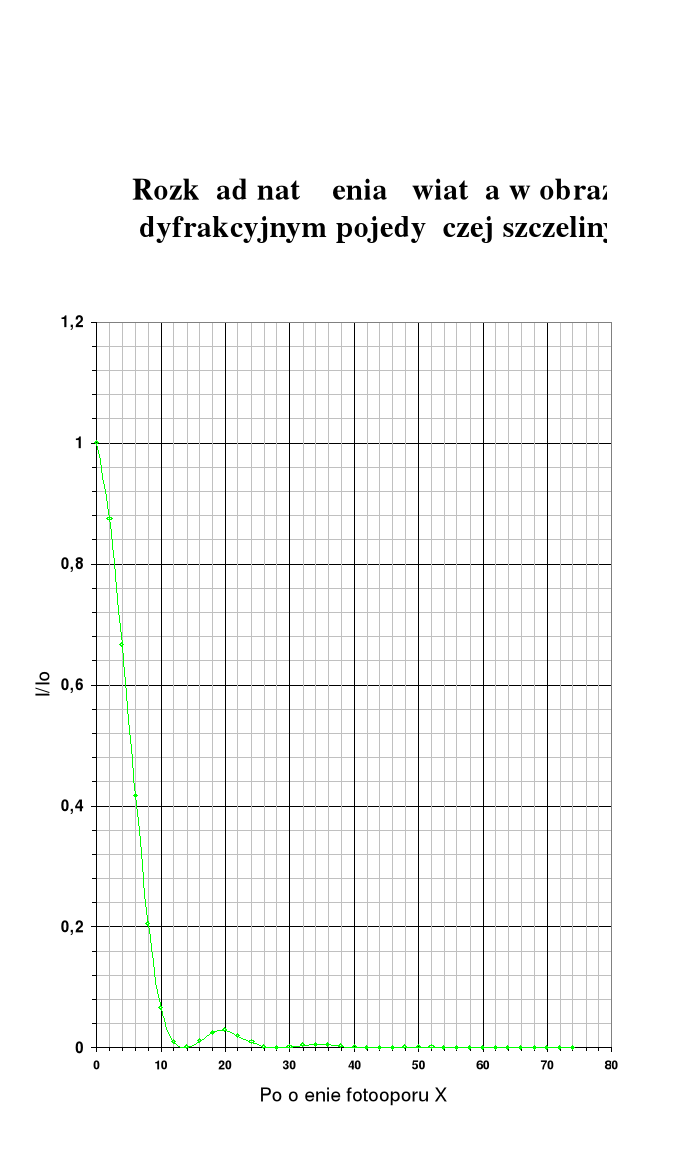
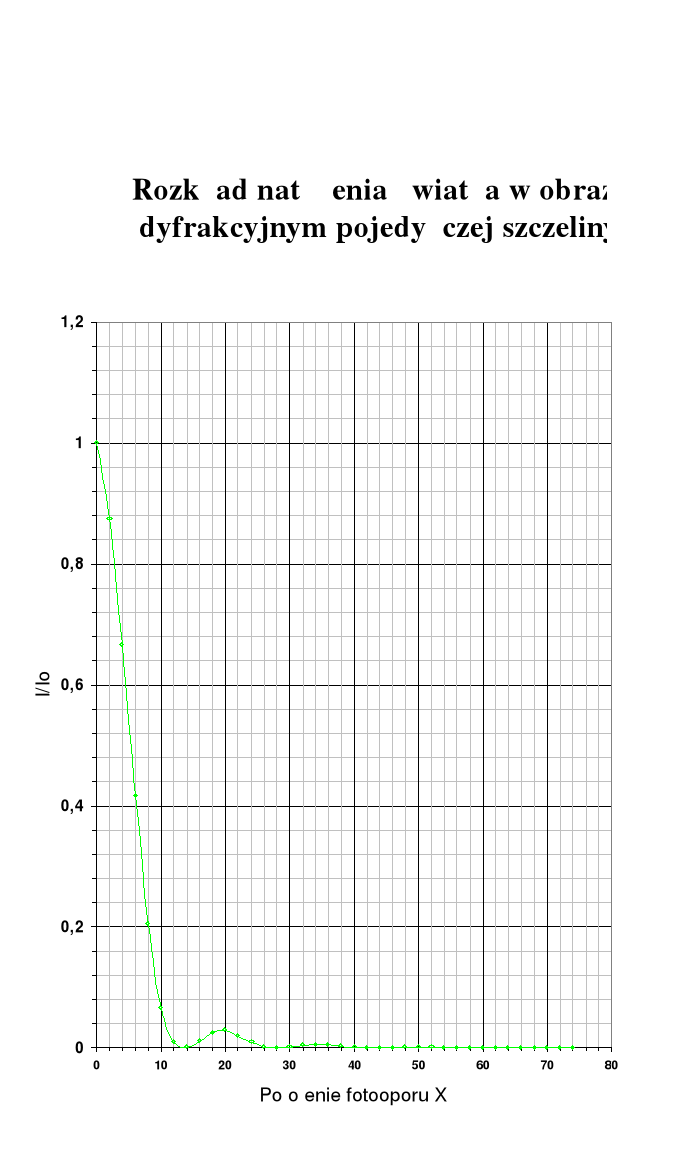
Natomiast rozkład amplitudy a natężenia światła w poszczególnych punktach ekranu przedstawia wykres:

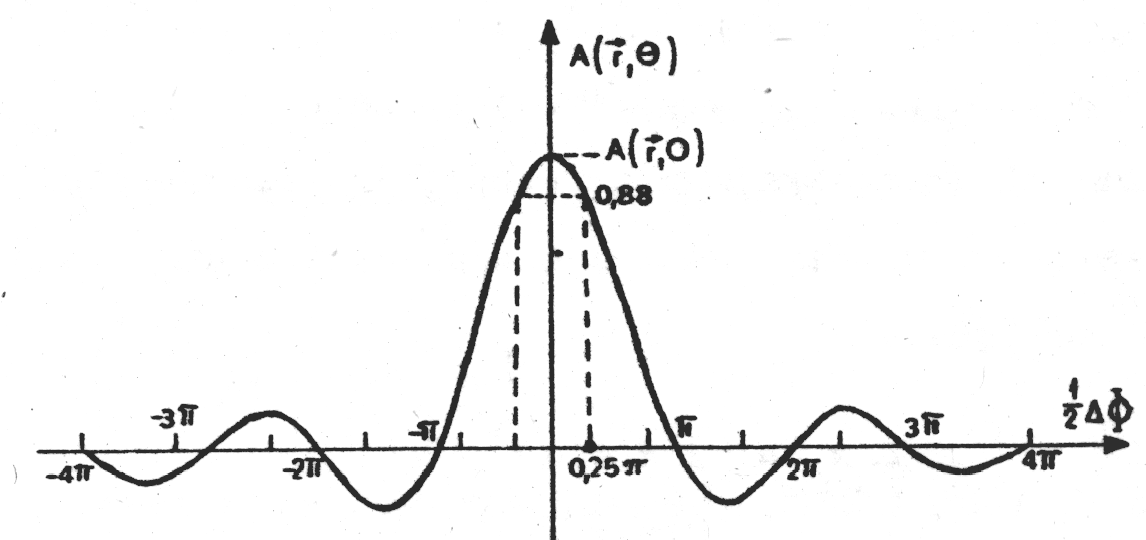
Opracowanie wyników:

Odległość szczeliny od ekranu wynosi d = 0,90m.

Długość fali lasera λ = 0,6328μm.

Ze wzoru

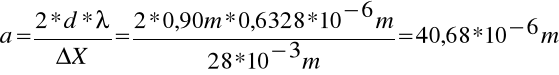
mierzymy szerokość szczeliny a.

Dyskusja błędu metodą różniczkową:

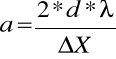
Logarytmując powyższe równanie otrzymujemy

ln a = ln 2 + ln d + ln λ -ln ∆X

różniczkuje powyższy zapis i biorąc pod uwagę, że d=const i λ=const otrzymuje:

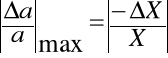
∆X=10^-3m

X=28*10^-3m

Wyliczam bezwzględny błąd maksymalny

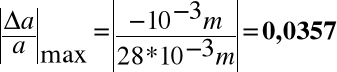
Względny błąd maksymalny wynosi:

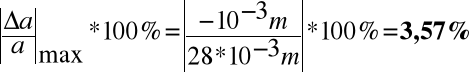
Oba wykresy są symetryczne względem oy

1

1

---