Politechnika Świętokrzyska
Wydział Mechatroniki i Budowy Maszyn
Przedmiot: Mechanika doświadczalna
Ćw. Nr 10 Temat: Pomiar parametrów dynamicznej odporności na pękanie przy pomocy instrumentowego młota spadowego .
Wykonał: Łukasz Skiba	Grupa: 302	Data: 14.1.2009	Prowadzący: dr inż. Lis Zbigniew	Ocena:

1. Cel ćwiczenia.

Celem ćwiczenia jest wyznaczenie parametrów dynamicznej odporności na pękanie oraz poznanie stanowiska badawczego do badań dynamiczne odporności na pękanie.

2. Wstęp teoretyczny.

Pomiar dynamicznej wartości całki Jic dla metody jednej próbki.

Całka J opisywać zachowanie się materiałów sprężysto-plastycznych zawierających szczelinę. Całka J jest niezmiennicza od konturu całkowania . Dla ciął plastycznych całka J jest różnicą pomiędzy energiami potencjalnymi dwóch prawie identycznych , obciążonych elementów różniących się jedynie długością szczeliny da .Ta pozornie błaha w definicji całki J dla ciała nieliniowo sprężystego i plastycznego ma istotne znaczenie . W przypadku obciążenia z dużymi prędkościami , całka J przestaje być całką niezmienniczą od drogi całkowania ze względu na fakt oddziaływania wierzchołka pęknięcia z wielokrotnie odbitą falą sprężystą od powierzchni próbki .Nie traci jednak sensu fizycznego definicja całki J jako różnica energii potencjalnych dwóch obciążonych próbek różniących się jedynie o długość szczeliny da .Prawdziwy zatem jest wzór :

η-parametr określający kształt próbki,

b_o-początkowa długość nie pękniętego odcinka próbki ,

B_N-efektywna grubość próbki.

Krytyczną wartość całki można by bez problemu obliczyć pod warunkiem , że będzie znane pole A pod krzywą F-s w momencie inicjacji wzrostu szczeliny . Metody wyznaczania wartości całki J można podzielić ze względu na ilość użytych próbek :

metoda zmian podatności ( metoda jednej próbki ),

metoda zatrzymanego bijaka ( metoda wielu próbek ).

Udarność jest to energia potrzebna na złamanie próbki.

Po wyzwoleniu sygnału na przygotowaną próbkę spada młot łamiąc ją. Wynik jest zapamiętywany przez oscyloskop.

Powszechnie zakłada się że własności mechaniczne metali nie zależą od prędkości odkształcenia . W rzeczywistości jednak własności te są zależne od prędkości odkształcenia , chociaż dla metali w dość szerokim zakresie małych prędkości odkształcenia wpływ ten jest pomijalnie mały . Zakres ten oczywiście umowny i jest on różny dla różnych metali , ale orientacyjnie można powiedzieć , że przy prędkościach odkształcenia rzędu dε/dt<10³ s^-1 ich wpływ na własności np. plastyczne można pominąć. Przy większych prędkościach odkształcenia ich wpływ na zachowanie się metali ma charakter zarówno ilościowy i jakościowy i nie może być pominięty przy formułowaniu związków fizycznych .

Maksymalny zakres prędkości odkształcenia dε/dt , stosowany w badaniach doświadczalnych metali , zawiera się w wielu rzędach dziesiętnych mierzonych w s^-1 .Jako statyczną krzywą umocnienia przyjmuje się zazwyczaj krzywą otrzymaną przy prędkościach rzędu 10^-4 s^-1.

W widmie prędkości odkształcenia wyróżnia się następujące zakresy :

dε/dt<10^-4 s^-1 - zakres ten odpowiada prędkości pełzania metali ,

10^-4 s^-1 <dε/dt<10^-2 s^-1 - zakres normalnych prób statycznych przeprowadzanych na standardowych maszynach wytrzymałościowych , pozwalających na stałe prędkości odkształcenia,

10^-2 s^-1 <dε/dt<10² s^-1 - zakres ten jest zakresem prób quasi-statycznych dokonywanych przy pomocy takich urządzeń jak młoty spadowe , rotacyjne , maszyny pneumatyczne ,

10² s^-1 <dε/dt<10⁴ s^-1 - zakres prób przy dużych prędkościach odkształcenia, , badania doświadczalne przeprowadza się na ściskanie lub skręcanie próbek , jak również na rozciąganie ,

dε/dt>10⁴ s^-1 - zakres ten nazywany jest zakresem bardzo dużych prędkości odkształcenia , prędkości te uzyskuje się przy pomocy generacji fal uderzeniowych .

Konstrukcje mechaniczne , budowlane są często poddawane obciążeniom z dużymi prędkościami . Bezwładność materiału powoduje ,że w obciążanym dynamicznie elemencie generowane są dodatkowe obciążenia , których zmiana jest na ogół rozbieżna w fazie z zewnętrznym wymuszeniem . Propagujące fale sprężyste i drgania próbki powodują złożony stan naprężeń . Odpowiedz materiału w wierzchołku szczeliny na zewnętrzne obciążenia , czyli współczynnik intensywności naprężeń K₁ , nie jest już liniową funkcją przemieszczenia punktu przyłożenia siły . Jest to funkcja oscylująca wokół statycznej wartości , przy czym amplituda zmienia się w czasie . Sytuacja taka powoduje ,że zachowanie się sprężystej próbki dynamicznie obciążonej zależy od wielu parametrów : masy bijaka, prędkości uderzenia , podatności maszyny .

Metoda wielu próbek .

Polega na wykreśleniu „dynamicznej” krzywej J-R. W tym celu wykonuje się kilka identycznych próbek z zainicjowaną szczeliną zmęczeniowa. Próbki te obciąża się na młocie spadowym wyposażonym w sztywny zderzak . Rolą zderzaka jest zatrzymanie bijaka młota w taki sposób , aby za każdym razem otrzymać inny przyrost długości szczeliny . Oznacza to , że próbka pozostaje nie złamana a część energii kinetycznej bijaka młota zostaje przejęta przez sztywne uderzenie bijaka w zamocowane ograniczniki .Za każdym razem rejestruje się P(t) i kreśli wykres P-s. Można więc określić powierzchnię A dla każdego przyrostu szczeliny da. Długość szczeliny mierzy się po próbie ( po dołamaniu próbki ) na mikroskopie warsztatowym .Następnie wykreśla się wykres J-R ze wszystkimi ograniczeniami jak w przypadku wyznaczania całki J dla metod statycznych . Przeciążcie się linii regresji z linią stępienia określa nam wartość J_1d.

3. Wykresy

Przebieg zadany

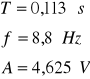
Wykres siły i przemieszczenia w funkcji czasu - próba działania urządzenia

Wykres siły i przemieszczenia dla badanej próbki w funkcji czasu

Wykres siły w funkcji przemieszczenia, do wyznaczenia energii

Energia wynosi: A = 29,059 [J]

Wyniki badań do metody wielu próbek

Lp	Grupa	B	W	a		A	da	J
1	pon10JD1	10	10	3,049	6,851	15,739	0,849	0,459	459,466
2	pon10J_D2	10	10	3,244	6,756	14,661	0,664	0,434	434,014
3	pon13	9,97	9,91	3,04	6,87	16,369	0,883	0,478	477,970
4	pon15_2	10	10	2,59	7,41	22,807	0,523	0,616	615,574
5	wt8_3	10	10	2,681	7,319	29,091	1,296	0,795	794,945
6	wt_13	10	10	2,48	7,52	25,313	0,792	0,673	673,218
7	wt 15	9,93	9,9	2,46	7,44	29,806	1	0,807	806,885
8	wt_17	9,9	10	2,073	7,927	30,713	0,534	0,783	782,723
9	sr_08	10,04	10,01	2,4547	7,5553	29,059	0,7793	0,766	766,170
10	sr_09	10	9,98	2,45	7,53	30,101	1,05	0,799	799,495

Gdzie:

Parametry
dobieramy z tabeli.

Re [MPa]	350
E [MPa]	205000
Rm [MPa]	550

J=500 [kN/m]

, warunek niespełniony

Zatem J =500 [kN/m] nie możemy uznać jako J_ID

4. Wnioski.

W doświadczeniu zapoznaliśmy się z zasadą pomiaru wartości amplitudy drgań przy pomocy oscyloskopu cyfrowego. Metody dynamicznych badań wytrzymałościowych są niezwykle szybkie i bardzo precyzyjne, jednak aparatura wymaga bardzo dokładnego przygotowania i ustawienia parametrów początkowych. Otrzymane dane trzeba w odpowiedni sposób przekalibrować, gdyż na oscyloskopie otrzymujemy mierzone wartości w V w przebiegu czasowym, a nam potrzebne jest siła wyrażona w [kN] i przemieszczenie wyrażone w [mm].

Wartość całki została wyznaczona na podstawie danych zebranych podczas przeprowadzania doświadczenia. Zebranie wyniki otrzymanych przez poszczególne grupy laboratoryjne pozwoliły na zestawienie i przeprowadzenie analizy metodą wielu próbek. W naszym przypadku wartość całki J wyniosła 500 [N/mm]. Lecz nie można ją przyjąć za stałą materiałową, gdyż nie został spełniony warunek płaskiego stanu odkształcenia.

---