Temat:

WYZNACZANIE PROMIENI KRZYWIZNY SOCZEWKI I DŁUGOŚCI FALI ŚWIETLNEJ ZA POMOCĄ PIERŚCIENI NEWTONA

1. Cel ćwiczenia:

Poznanie zjawiska interferencji w klinie optycznym ( tzw. prążki równej grubości ) oraz praktyczne zastosowanie go do celów pomiarowych.

2. Wprowadzenie:

Doświadczenie opiera się na zjawisku załamania i częściowego odbicia światła przy przejściu wiązki światła przez granicę dwóch ośrodków o różnych współczynnikach załamania. Jeżeli dwie powierzchnie graniczne tworzą klin , to wiązki odbite od nich wzajemnie ze sobą interferują . Za przykład może posłużyć powietrzny klin interferencyjny utworzony pomiędzy dwiema wewnętrznymi powierzchniami P₁ i P₂ płaskorównoleglych płytek szklanych. Fale odbite nakładają się we wszystkich punktach powierzchni P₁. Amplitudę zinterferowanej fali określa różnica dróg optycznych promieni padających -
. Przy założeniu że kąt klina jest bardzo mały , a równoległa wiązka światła monochromatycznego pada na powierzchnię klina prostopadle , możemy obliczyć różnicę dróg optycznych między interferującymi promieniami. Określa to zależność :

gdzie h jest grubością klina w danym miejscu . W miejscach gdzie
wynosi :

k = 0 , 1 , 2 ,.... n

nastąpi wygaszenie światła na skutek interferencji , a dla

k=0, 1 ,2,.... n

nastąpi wzmocnienie światła. W klinie o płaskich powierzchniach , zaobserwujemy więc na przemian jasne i ciemne prążki. Tak zwany prążek zerowy (k=0) powstaje w miejscu styku obu powierzchni , czyli na krawędzi klina. Pierwszy (k=1) na wysokości
itd.

W klinie takim odległość wzajemna prążków jest jednakowa i jej wielkość zależy od wielkości kąta klina. Można to wykorzystać do pomiaru kąta. Jeżeli nastąpiłaby deformacja prostoliniowego przebiegu prążka , to świadczy to o odstępstwie od płaskości powierzchni. Jeżeli jedną z nich przyjmiemy za wzorcową , czyli idealnie płaską , to z uzyskanego obrazu można wnioskować o wielkości odchyłki od płaskości powierzchni P₂ i dzięki temu można ją zlokalizować.

Prążki interferencyjne najłatwiej jest zaobserwować umieszczając na płaskiej płytce szklanej wypukło-sferyczną soczewkę. Powstaje wówczas między powierzchnią płytki , a powierzchnią soczewki klin powietrzny o zmieniającym się kącie. Prążki powstające w takim klinie mają kształt kolisty. Nazywamy je prążkami Newtona. W miejscu styku soczewki i płytki powstaje ciemny (zerowy ) prążek, natomiast kolejne prążki coraz bardziej się zagęszczają , aż przestaną być zauważalne.

3. Spis przyrządów :

1. mikroskop z przyrządem odczytowym o klasie 0.01

2. zestaw soczewek

3. źródło światła z zasilaczem

4. filtry monochromatyczne IF 650 i IF 575

4. Przebieg ćwiczenia :

Prążki Newtona można wykorzystać do wyznaczania promienia krzywizny soczewki (R). Trzeba w tym celu znać długość fali
użytego światła oraz zmierzyć promień (r) dowolnego k-tego ciemnego prążka. Promień krzywizny soczewki oblicza się ze wzoru na promień czaszy sferycznej o promieniu podstawy (r) i wysokości (h) :

lub dla r>>h

Wysokość czaszy (h) odpowiadającą k-temu ciemnemu prążkowi obliczamy ze wzoru :

Ostatecznie otrzymujemy zależność :

Znając więc długość fali
oraz promień k-tego prążka kołowego (r) można wyznaczyć promień krzywizny soczewki. Do obserwacji używa się przyrządu jak na rysunku :

t - stolik mikroskopu

P - płytka płasko - równoległa

L_O - badana soczewka

ob - obiektyw mikroskopu

Z - zwierciadło półprzepuszczalne

L1 - soczewka kondensatora

ok - okular mikroskopu

F - filtr

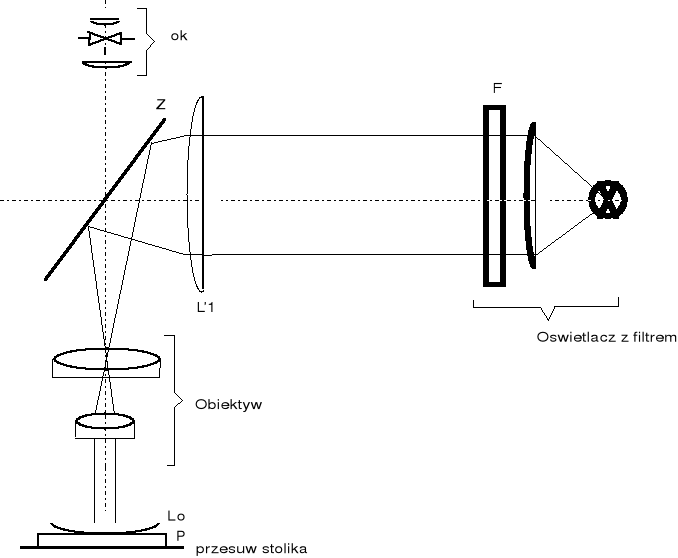
Jest to mikroskop , na którego stoliku umieszcza się płytkę P i mierzoną soczewkę L_O . Poprzez obiektyw są one oświetlane równoległą wiązką światła monochromatycznego z oświetlacza, odbitego od zwierciadła półprzepuszczalnego Z umieszczonego nad obiektywem mikroskopu. w okularze znajduje się krzyż celowniczy, który ustawia się na wybrany obraz prążka. Ustawienie takie umożliwia przesuwny stolik mikroskopu , którego przesunięcie jest mierzone poprzez czujnik zegarowy. Dokładność tego wskaźnika 10^-5 m. Należy dokonać pomiaru promienia wybranego prążka, poprzez odczytanie wskaźników przesunięcia lewostronnego i prawostronnego - ( a^L ) i ( a^P ). Opisuje to zależność :

Dzięki znajomości długości fali świetlnej , możemy obliczyć promień krzywizny soczewki. Mając już obliczony promień możemy odwrócić przebieg doświadczenia i po przekształceniu wzoru na promień obliczyć nieznaną długość fali świetlnej, wydzielonej z wiązki światła białego poprzez założenie na oświetlacz filtra interferencyjnego.

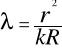
5. Tablice wyników pomiarów :

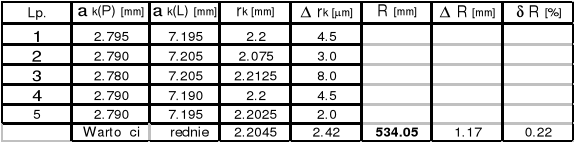
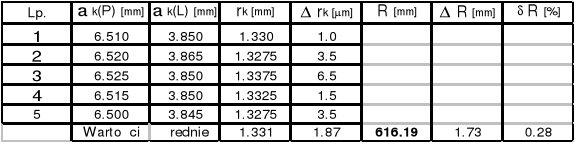
Zad.1

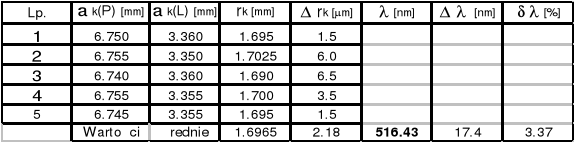
Soczewka Nr 1 IF = 650 (
= 650*10^-9 [m] )

k = 14

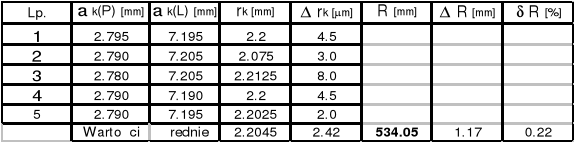
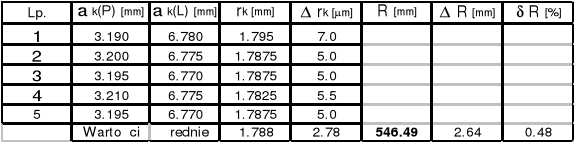
k = 9

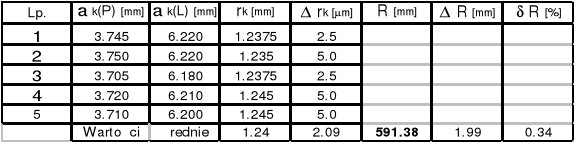
k = 4

Promień soczewki Nr 1 R = ( 557,31
17.41 )*10^-3 [m]

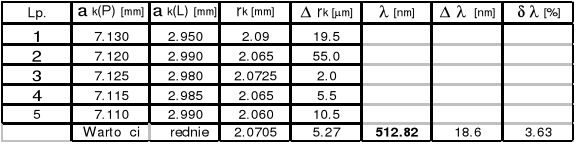
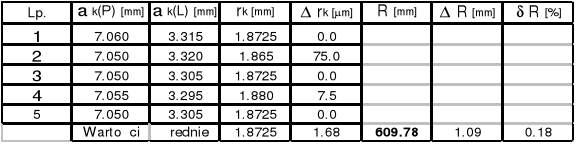
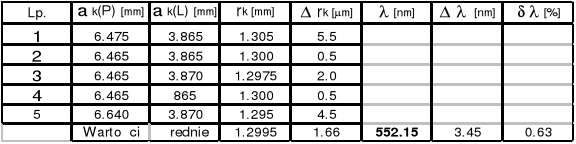
Zad.2

Soczewka Nr 1 R = ( 557,31
17.41 )*10^-3 [m]

k = 15

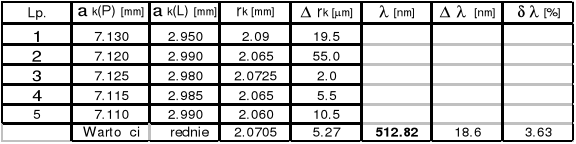
k = 10

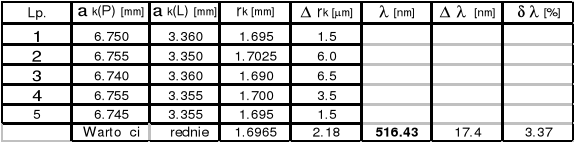
k = 5

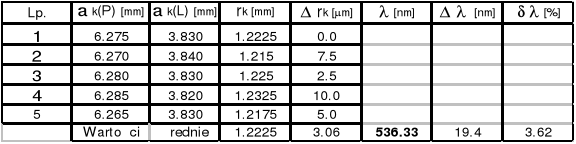
Długość fali Nr 1
= ( 521,86
7.31 )*10^-9 [m]

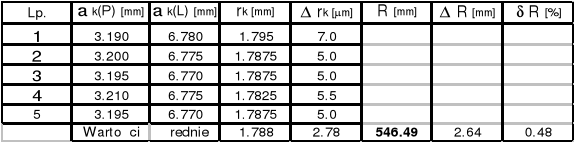
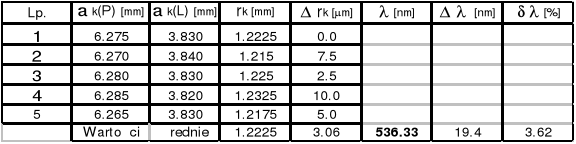
Zad.3

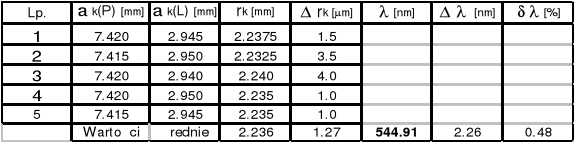
Soczewka Nr 2 IF = 575 (
= 575*10^-9 [m]

k = 15

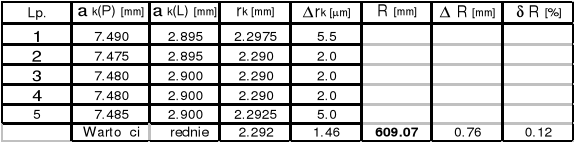
k = 10

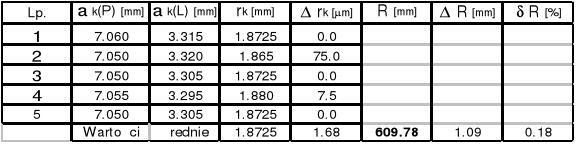
k = 5

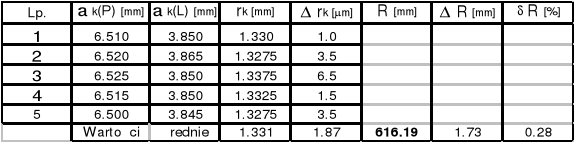
Promień soczewki Nr 2 R = ( 611,68
2.26 )*10^-3 [m]

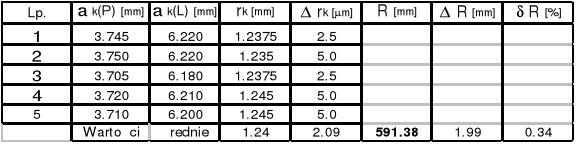
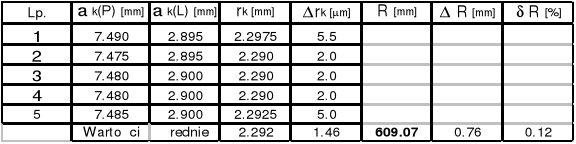
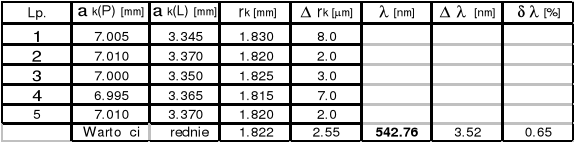
Zad.4

Soczewka Nr 2 R = ( 611,68
2.26 )*10^-3 [m]

k = 15

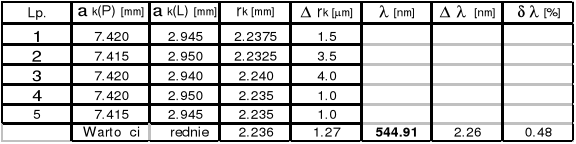
k = 10

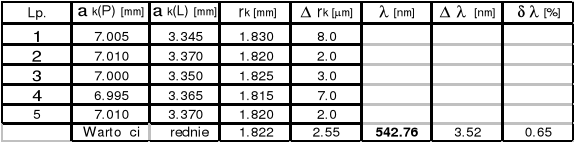
k = 5

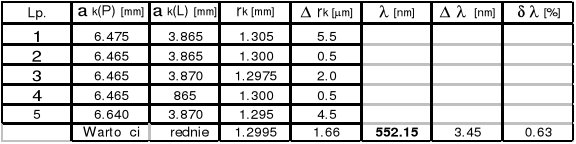
Długość fali Nr 2
= ( 546,61
2.52 )*10^-9 [m]

6. Przykładowe obliczenia:

a^l_{k ,} a^p_k - wskazania czujnika w mm

1. Do Zad. 1 i Zad.3

r_k =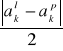

=

=

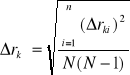
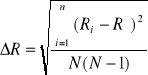
Np.

r_k =
[mm]

r_kśr =
= 2.2045 [mm]

= 0.0045 [mm]

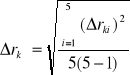
= 2.42*10^-3 [mm] = 2.42 [
m]

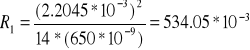
[mm]

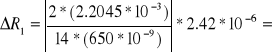
1.17*10^-3 [m] = 1.17 [mm]

= 0.22 [%]

=
=
[m] = 557.31[mm]

=
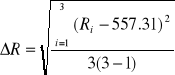
[m] = 17.41 [mm]

a^l_{k ,} a^p_k - wskazania czujnika w mm

2. Do Zad. 2 i Zad. 4

r_k =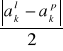

=

=

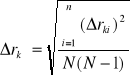
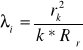
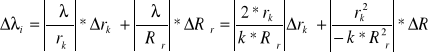
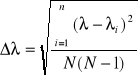
Np.

r_k =
[mm]

r_kśr =
= 2.0705 [mm]

= 0.0195 [mm]

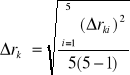
= 2.18*10^-3 [mm] = 2.42 [
m]

= 512.82*10^-9 [m] = 512.82 [nm]

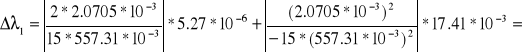
5.04*10^-9 [m] =

= 5.04 [nm]

= 3.63 [%]

=
=
[m] = 521.86 [nm]

= 7.31*10^-9 [m] = 7.31 [nm]

7. Wnioski i dyskusja błędów:

Dokonaliśmy pomiarów odległości oddalenia k-tego prążka od jego środka w stronę lewą i prawą. Do pomiarów tych służył mikroskop z przyrządem odczytowym o klasie 0.01 mm. Na podstawie zmierzonych wielkości można było dokonać obliczeń : k-tego promienia prążka r_k , by następnie obliczyć promień soczewki R ( Zad.1 i 3 ) i znając R obliczyć długość fali świetlnej padającej na soczewkę
( Zad. 2 i 4 ). Aby otrzymać najbardziej dokładne wyniki szukanych wielkości , zastosowaliśmy po 5 pomiarów dla 3 różnych prążków przy każdej soczewce osobno. Otrzymane wielkości szukane R i
wynoszą :

Dla soczewki nr 1 : R = ( 557.31
17.41 )*10^-3 m
= ( 521.86
7.31 )*10^-9 m
Dla soczewki nr 2 : R = ( 611.68
2.26 )*10^-3 m
= ( 546.61
2.52 )*10^-9 m

Pomiar nieznanej długości światła wskazuje na wartość dla światła zielono-żółtego , co jest zgodne z tym co obserwowaliśmy na ćwiczeniu. Na wartość R ma wpływ błędu
r_k , który należało uwzględnić przy obliczeniach , a na wartość
ma wpływ błąd
r_k oraz błąd
R obliczony wcześniej. Błędy

i
R liczone były metodą różniczki zupełnej. Wartości błędów względnych wielkości
i R zawierają się w przedziale ( 0.12%
3.63% ) wartości obliczonej. Z tego wynika , że zmierzone i obliczone wartości są dokładne oraz błędy bezwzględne są rzędu 10^-2 mniejsze od wielkości
i R. Na poprawę dokładności pomiaru mogło by wpłynąć zwiększenie liczby pomiarów oraz staranne przygotowanie materiałów badanych i przyrządów oraz wyeliminowanie błędu spowodowanego ustawieniem punktu na wybranym k-tym prążku , które dokonywane było przez ćwiczącego obserwacją prążków w mikroskopie „na oko”.

1

9

---