Nr ćwicz. 305	Data: 28.05. 2009	Agnieszka Kamińska Marta Dębska	Wydział Technologii Chemicznej	Semestr: I I	Grupa 3
prowadzący: dr A. Skibiński			Przygotowanie:	Wykonanie:	Ocena ostat.:

Temat: Wyznaczanie długości fali świetlnej za pomocą pierścieni Newtona.

Kołowe pierścienie interferencyjne, zwane pierścieniami Newtona, powstają, gdy równoległa wiązka światła pada na układ złożony z dokładnie płaskiej płyty szklanej oraz leżącej na niej soczewki o promieniu krzywizny R (rys. obok).

Między soczewką i płytą znajduje się warstwa powietrza o grubości d wzrastającej wraz ze wzrostem odległości od osi układu.

Obraz interferencyjny powstaje w wyniku nałożenia promieni odbitych od dolnej powierzchni soczewki i od górnej powierzchni płyty.

Różnica dróg geometrycznych obu promieni wynosi 2d. Dla obliczenia dróg optycznych przyjmujemy, że współczynnik załamania powietrza jest równy jedności, a także uwzględniamy fakt, że odbiciu od ośrodka gęstszego towarzyszy zmiana fazy o
, czemu odpowiada dodatkowa różnica dróg
.

Biorąc powyższe pod uwagę możemy napisać warunek powstania jasnego pierścienia interferencyjnego:

(1)

Na podstawie rysunku możemy wyrazić grubość warstwy powietrznej przez promień pierścienia interferencyjnego a:

(2)

Jeżeli a/R<<1, to można powyższe wyrażenie przedstawić w postaci

(3)

Łącząc powyższe równanie z równaniem (1) otrzymamy

(4)

Otrzymane równanie określa promienie jasnych prążków interferencyjnych.

W miejscu zetknięcia się soczewki z płytą tworzy się bardzo cienka warstwa powietrza, o grubości wielokrotnie mniejszej od długości fali. Różnica dróg optycznych powstająca między promieniami w tym punkcie jest skutkiem jedynie straty połowy długości fali przy odbiciu od płyty. W rezultacie wynosi ona
- w środku obrazu interferencyjnego obserwujemy ciemne pole.

Jeżeli układ oświetlamy światłem białym, powstają barwne pierścienie, które przy wyższych rzędach m zachodzą na siebie.

Analiza wyników:

Rząd prązka	al [m]	ap [m]	am [m]	R [m]	∆ R [m]
1	0,02022	0,01991	0,000155	0,0816	3,65E-10
2	0,020555	0,01991	0,000485	0,266	3,81E-10
3	0,028	0,019585	0,000713	0,345	3,36E-10
4	0,0299	0,019375	0,00091	0,402	3,06E-10
5	0,021155	0,01917	0,001053	0,418	2,76E-10
6	0,02135	0,01905	0,001255	0,486	2,69E-10
7	0,02149	0,01884	0,001393	0,506	2,52E-10
8	0,021605	0,018705	0,001523	0,525	2,39E-10
9	0,021735	0,01856	0,001643	0,539	2,28E-10
10	0,02186	0,01854	0,001758	0,552	2,18E-10
11	0,021935	0,018345	0,001853	0,555	2,08E-10
12	0,021985	0,01823	0,001915	0,541	1,96E-10
13	0,02206	0,018115	0,002015	0,551	1,90E-10
14	0,02213	0,01803	0,002103	0,556	1,83E-10
15	0,02219	0,17925	0,002175	0,554	1,77E-10
16	0,022245	0,01784	0,00223	0,545	1,69E-10
17	0,022285	0,017785	0,00226	0,526	1,61E-10
18	0,02233	0,017765	0,00231	0,518	1,55E-10
19	0,022375	0,01771	0,002355	0,509	1,50E-10
20	0,02241	0,017665	0,002405	0,504	1,45E-10
21	0,022455	0,01760	0,002455	0,499	1,41E-10
22	0,02250	0,017545	0,002503	0,495	1,37E-10
23	0,02255	0,017495	0,002553	0,492	1,34E-10
24	0,022595	0,017445	0,00259	0,485	1,30E-10
25	0,02263	0,017415	0,00264	0,483	1,27E-10
26	0,02265	0,01735	0,002665	0,473	1,23E-10
27	0,022695	0,01732	0,002703	0,468	1,20E-10
28	0,02275	0,01729	0,00276	0,470	1,18E-10
29	0,022795	0,01719	0,002803	0,468	1,16E-10

λ=5,89E-07

a_r - współczynnik nachylenia (λR) otrzymany za pomocą regresji liniowej

a_r= 2,83E-07 Δa_r=6,27E-09

R=a_r/λ R= 4,81E-01m

Błąd wyznaczenia promienia pierścienia:

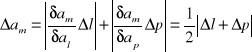
=10 [
]

gdzie
(dokładność odczytu ze śruby mikrometrycznej).

Błąd popełniany przy wyznaczaniu promienia pierścienia obliczamy ze wzoru:

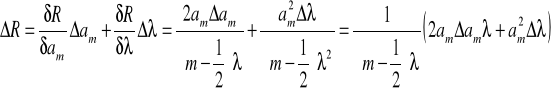
Błąd promienia krzywizny soczewki:

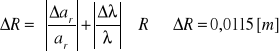
Wynik końcowy:

R=(0,481±0,016)m

Wnioski:

Podczas wykonywania ćwiczenia zmierzono wartości 29 pierścieni. Dalsze pomiary nie były możliwe, ponieważ pierścienie nie były już dobrze widoczne. Otrzymana w wyniku doświadczenia wartość promienia soczewki znacznie różni się od wartośći takbicowej (0,9m), co mogło spowodować niedokładność oka ludzkiego oraz to, że podczas wykonywania ćwiczenia pierścienie Newtona zlewały się ze sobą, co powodowało problemy z ich policzeniem.

Podczas wykonywania obliczeń zauważono, że promienie pierścieni wpierw rosną, a następnie maleją. Może to być wynikiem tego, iż soczewka nie jest płaska, o czym świadczy wyznaczony promień krzywizny.

---