311[10] O1 02 Posługiwanie się jednostkami miar, skalą oraz współrzędnymi geodyzejnymi

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

MINISTERSTWO EDUKACJI

NARODOWEJ

Grzegorz Korzela

Posługiwanie się jednostkami miar, skalą
oraz współrzędnymi geodezyjnymi 311[10].O1.02

Poradnik dla ucznia

Wydawca

Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy
Radom 2007

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Recenzenci:
dr inż. Barbara Gąsowska
mgr inż. Wanda Brześcińska

Opracowanie redakcyjne:
mgr inż. Grzegorz Korzela

Konsultacja:
mgr Małgorzata Sienna

Poradnik stanowi obudowę dydaktyczną programu jednostki modułowej 311.[10].O1.02
„Posługiwanie się jednostkami miar, skalą oraz współrzędnymi geodezyjnymi”, zawartego
w modułowym programie nauczania dla zawodu technik geodeta.

Wydawca

Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy, Radom 2007

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

SPIS TREŚCI

Wprowadzenie

Wymagania wstępne

Cele kształcenia

Materiał nauczania

4.1.

Definicja, historia, zadania geodezji oraz podstawowe informacje

o układzie współrzędnych prostokątnych, mapie i skali

4.1.1.

Materiał nauczania

4.1.2. Pytania sprawdzające

4.1.3. Ćwiczenia

4.1.4. Sprawdzian postępów

4.2.

Jednostki miar stosowane w geodezji

4.2.1. Materiał nauczania

4.2.2.

Pytania sprawdzające

4.2.3.

Ćwiczenia

4.2.4.

Sprawdzian postępów

4.3.

Posługiwanie się współrzędnymi do rozwiązywania podstawowych zadań

geodezyjnych

4.3.1

Materiał nauczania

4.3.2

Pytania sprawdzające

4.3.3

Ćwiczenia

4.3.4

Sprawdzian postępów

22
22
24

25
25
34
35
39

Sprawdzian osiągnięć

6. Literatura

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

1. WPROWADZENIE

Poradnik będzie Ci pomocny w przyswajaniu wiedzy o historii geodezji, jej działach,

znaczeniu dla gospodarki narodowej oraz w rozwiązywaniu podstawowych zadań z rachunku
współrzędnych.

W poradniku znajdziesz:

−

wymagania wstępne – wykaz umiejętności, jakie powinieneś mieć już ukształtowane,
abyś bez problemów mógł korzystać z poradnika,

−

cele kształcenia – wykaz umiejętności, jakie ukształtujesz podczas pracy z poradnikiem,

−

materiał nauczania – wiadomości teoretyczne niezbędne do opanowania treści jednostki
modułowej,

−

zestaw pytań, abyś mógł sprawdzić, czy już opanowałeś określone treści,

−

ćwiczenia, które pomogą Ci zweryfikować wiadomości teoretyczne oraz ukształtować
umiejętności praktyczne,

−

sprawdzian postępów,

−

sprawdzian osiągnięć, przykładowy zestaw zadań; zaliczenie testu potwierdzi
ukształtowanie umiejętności całej jednostki modułowej,

−

literaturę.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Schemat układu jednostek modułowych

311[10].O1.01

Przestrzeganie przepisów

bezpieczeństwa i higieny

pracy, ochrony

przeciwpożarowej

oraz ochrony środowiska

311[10].O1.02

Posługiwanie się jednostkami

miar, skalą oraz

współrzędnymi geodezyjnymi

311[10].O1

Podstawy geodezji

i kartografii

311[10].O1.03

Posługiwanie się mapami

stosowanymi w geodezji

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

2. WYMAGANIA WSTĘPNE

Przystępując do realizacji programu jednostki modułowej, powinieneś umieć:

−

korzystać z różnych źródeł informacji,

−

obsługiwać komputer,

−

charakteryzować układ współrzędnych prostokątnych,

−

przestrzegać zasad bezpieczeństwa i higieny pracy,

−

uczestniczyć w dyskusji.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

3. CELE KSZTAŁCENIA

W wyniku realizacji programu jednostki modułowej powinieneś, umieć:

–

określić rolę geodezji w gospodarce,

–

przedstawić rys historyczny geodezji,

–

scharakteryzować poszczególne działy geodezji,

–

posłużyć się jednostkami miar stosowanymi w geodezji,

–

obliczyć azymut kierunku ze współrzędnych,

–

obliczyć długość odcinka ze współrzędnych,

–

obliczyć współrzędne punktu na prostej,

–

obliczyć wartość kąta ze współrzędnych,

–

określić wartość kąta w różnych jednostkach,

–

odczytać współrzędne punktu z mapy,

–

odszukać na mapie punkt o określonych współrzędnych,

–

posłużyć się podziałką poprzeczną,

–

zastosować do obliczeń geodezyjnych technikę komputerową,

–

scharakteryzować graficzne zobrazowanie rzeźby,

–

obliczyć powierzchnię figury ze współrzędnych

–

skontrolować poprawność obliczeń geodezyjnych.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4. MATERIAŁ NAUCZANIA

4.1.

Definicja, historia, zadania geodezji oraz podstawowe
informacje o układzie współrzędnych prostokątnych, mapie
i skali

4.1.1. Materiał nauczania

Geodezja – nazwa wprowadzona przez Arystotelesa, pochodzi z języka greckiego geo –

Ziemia, daiso – będę dzielił, a więc dosłownie oznacza podział ziemi, czyli pomiar i podział
posiadłości – nieruchomości, co i w obecnych czasach stanowi jedno z ważnych zadań
geodezji.

Geodezja jest jedną z nauk o Ziemi a zarazem działem techniki. Zajmuje się pomiarami

obiektów na powierzchni ziemi oraz pomiarami Ziemi jako planety. Pomiary geodezyjne
określają wymiary, kształt i wzajemne położenie w przestrzeni obiektów (naturalnych
i sztucznych) znajdujących się na powierzchni ziemi a także kształt i wymiary Ziemi jako
planety. Praktyczne zadania geodezji obejmują pomiary topograficzne przydatne do
sporządzania map, pomiary gruntów oraz pomiary obiektów inżynierskich związane z ich
budową a także późniejszą eksploatacją. Podstawy teoretyczne geodezji opierają się na takich
naukach jak: matematyka, fizyka, astronomia, geografia, mechanika i inne.
Rys historyczny geodezji [2]

Początki geodezji sięgają 3–5 tysięcy lat przed naszą erą, kiedy to wykonywane były

pomiary katastralne. Z czasów najodleglejszych zachowały się do dzisiaj tylko nieliczne ślady
działalności "geodezyjnej". Są to malowidła ścienne w tureckiej Anatolii, niewielkie
fragmenty glinianych tablic katastralnych w Mezopotamii, zapisy na papirusie czy też
średniowieczne kopie starożytnych map. Im bliżej czasów współczesnych, tym więcej mamy
przekazów historycznych i dowodów, mówiących nie tylko o roli i znaczeniu geodezji, ale
i kolejnych etapach jej rozwoju. Za niezwykle ważne w rozwoju geodezji uważa się
wyznaczenie wymiarów Ziemi przez Eratostenesa z Cyreny (III w. p.n.e.). Ten grecki
astronom i matematyk porównał obserwacje Słońca w dwóch odległych punktach (Asuan
i Aleksandria) leżących w przybliżeniu na tym samym południku. Dokonał on pomiaru kąta
padania promienia słonecznego w Aleksandrii, w momencie, gdy w Asuanie słońce świeciło
w zenicie. Określając odległość między tymi miastami na podstawie czasu przejścia
karawany, uczony obliczył promień kuli ziemskiej: R~6300 km.
Początki geodezji w Polsce [3]

Najwcześniejsze wzmianki o mierniczych na ziemiach polskich pochodzą z XII i XIII

wieku. Wykonujących pomiary nazywano wtedy żerdnikami królewskimi, bo też posługiwali
się tak prostymi narzędziami, jak żerdź i sznur, za pomocą których mierzyli grunty i tyczyli
nowe miasta. Budowę tych ostatnich zaczynano od wytyczenia rynku, z reguły prostokątnego
do prowadzenia handlu, potem siatki ulic i parceli budowlanych.

W średniowieczu znana była, również w Polsce, instytucja Podkomorzego. Na dworze

pierwszych Piastów kontrolowali oni zarządzanie dobrami królewskimi i byli zastępcami
wojewodów. Jednym z ich obowiązków było rozstrzyganie sporów granicznych. W połowie
XV wieku Podkomorzy był już dobrze zakorzenioną, szlachecką instytucją samorządową, swą
funkcję sprawował praktycznie dożywotnio. Podkomorzy rozstrzygał spory graniczne, potrafił
oszacować wartość nieruchomości, a z czasem – sklasyfikować grunty.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

W XVI wieku ukazały się pierwsze podręczniki geodezji w języku polskim, jak

chociażby „Geometria to jest miernicka nauka...” Stanisława Grzepskiego z 1566 r. Rozwijało
się szkolnictwo. Na Akademii Krakowskiej dzięki inicjatywie kanonika Jana Brożka w 1631
r. utworzono katedrę geodezji. Jej nieliczni adepci nosili – jak na królewską uczelnię przystało
– tytuł geometry królewskiego. Zaczęły się pojawiać przyrządy miernicze, wynaleziono
lunetę, podziałkę transwersalną (używana jest do dnia dzisiejszego – zostanie omówiona
w rozdziale następnym), a matematyka dostarczała już narzędzi do rozwiązywania coraz
bardziej skomplikowanych zadań.

W XVIII wieku za panowania Stanisława Augusta Poniatowskiego, spopularyzowano

instytucję Geometry Jego Królewskiej Mości. Przywilej uzyskiwało się z rąk królewskich
i wymagane były referencje lub poparcie zaufanych króla. Kandydaci na geometrów
królewskich nie musieli legitymować się szlacheckim pochodzeniem, nie byli też przypisani
do pracy na terenie określonego powiatu, a obszarem ich działania było całe państwo.
W końcu XVIII wieku liczbę wszystkich parających się zawodem geometry (mierniczego)
można szacować na około 400.

Rozbiory Polski i utrata niepodległości pozostawiły, niestety, na dwa wieki sprawy

polskiego miernictwa w rękach trzech państw: Austrii, Prus i Rosji. Dwa pierwsze,
dysponujące sprawną administracją, stosowały na podporządkowanych terenach swoje
regulacje prawne. Z kolei w zaborze rosyjskim utrzymano, co prawda, instytucję
Podkomorzego, ale zlikwidowano wolny zawód. Wyjątkiem był okres Księstwa
Warszawskiego. Aby zostać geometrą II klasy, należało legitymować się odpowiednią
praktyką i zdać egzamin przed komisją departamentową. Następnie po rocznej praktyce
i zaliczeniu egzaminu u Najwyższej Komisji Egzaminacyjnej można było zdobyć stopień
wyższy – geometry klasy I. Tytuły takie uzyskało 70 geometrów, a część z nich stanowili byli
geometrzy JKM Stanisława Augusta. Po upadku Księstwa Warszawskiego, przez ponad sto
lat, polskich mierniczych egzaminowali Austriacy, Niemcy i Rosjanie, a we wszystkich trzech
zaborach zostali oni wprzęgnięci w obce struktury państwowe.

Po odzyskaniu niepodległości w 1918 r. dostaliśmy w spadku nie tylko niespójne

jednostki miar, osnowy, mapy, systemy hipoteczne i instrukcje, ale też mierniczych
o przeróżnych tytułach i zróżnicowanych umiejętnościach. Potrzeby gospodarcze młodego
państwa wymagały szybkiego ujednolicenia odziedziczonych po zaborcach regulacji
prawnych, także tych dotyczących naszego zawodu. W 1925 r. wprowadzono ustawą tytuł
Mierniczego Przysięgłego. Aby nim zostać, należało mieć: obywatelstwo polskie,
wykształcenie miernicze wyższe lub średnie i odpowiednio 2- lub 5-letnią praktykę
zawodową. Trzeba było również zaliczyć egzamin przed jedną z dwóch państwowych komisji
egzaminacyjnych, z których pierwsza zbierała się we Lwowie, a druga w Warszawie (sesje
odbywały się dwa razy do roku, na wiosnę i jesienią). Mierniczy przysięgły był wyłącznym
wykonawcą wszelkich prac pomiarowych, które nie były zastrzeżone dla służb państwowych.
Plan czy mapa opatrzone pieczęcią mierniczego były dokumentem urzędowym.

Okres międzywojenny przyniósł dużo zmian. Uregulowano lub stworzono od podstaw

wiele przepisów pomiarowych, dla potrzeb katastru zastosowano na szeroką skalę zdjęcia
lotnicze, scalono prawie 5,5 mln ha gruntów, w większych miastach powstały samorządowe
jednostki geodezyjne. Według różnych szacunków w 1939 r. zarejestrowanych było w kraju
1200-1500 mierniczych przysięgłych, z których 20% miało tytuł inżyniera, pozostali
legitymowali się średnim wykształceniem. W administracji i szkolnictwie pracowało dalsze
750 osób (około 60% z nich miało wyższe wykształcenie). Do tego można doliczyć 1800 osób
personelu pomocniczego. Razem daje to blisko 4 tysiące osób. Taki był stan liczebny
środowiska geodezyjnego u progu II wojny światowej.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Po II wojnie światowej nowe ludowe państwo wzięło sprawy zawodowe geodetów

w swoje ręce. Według artykułu 1. dekretu Polskiego Komitetu Wyzwolenia Narodowego
z 7 października 1944 r. do realizacji reformy rolnej mobilizacji podlegały wszystkie „siły
miernicze” (wraz z przyrządami pomiarowymi), które nie ukończyły 60-tego roku życia.
„Siłami mierniczymi” byli: inżynierowie mierniczy, mierniczy przysięgli, mierniczy,
praktykanci i absolwenci szkół mierniczych. Kto nie podporządkował się mobilizacji,
ryzykował 2 lata więzienia, a dodatkowo utratę prawa wykonywania zawodu na 5 lat.
W kolejnym dekrecie Krajowej Rady Narodowej z 30.03.1945 r., został ustanowiony Główny
Urząd Pomiarów Kraju. Wzorcem dla nowopowstałego urzędu był moskiewski Wyższy
Urząd Geodezyjny, utworzony dekretem Rady Komisarzy Ludowych, podpisanym przez
samego Włodzimierza I. Lenina. Jedną z głównych bolączek geodezji w 1945 r. były
zniszczone i niekompletne archiwa geodezyjne, oraz brak sprzętu pomiarowego. Teodolity
i niwelatory rozszabrowano lub zniszczono. Wiele materiałów i map wywieziono w głąb
Niemiec. Po kilku latach starań zdołano odzyskać tylko około 20 ton tej dokumentacji.
Ocalałe i odzyskane materiały przejęły archiwa geodezyjne zorganizowane przez Główny
Urząd Pomiarów Kraju. Już od 1947 r., czyli w czasie akcji ich porządkowania, zaczął
funkcjonować przepis o obowiązku rejestrowania pomiarów i oddawania ich wyników do tych
archiwów (przepis w dużej mierze aktualny do dzisiaj).

Wraz z odbudową kraju ruszyły pierwsze prace geodezyjne. Były one związane przede

wszystkim z delimitacją granic kraju, przygotowaniem dokumentacji geodezyjnej dla akcji
osiedleńczej na Ziemiach Zachodnich i Północnych, pomiarami na potrzeby reformy rolnej,
katastrem i odbudową gospodarki. Prace geodezyjne miały wykonywać przedsiębiorstwa
państwowe, bowiem dyskryminacyjna polityka podatkowa państwa doprowadziła w 1950 r.
do prawie całkowitej likwidacji sektora prywatnego. Było to bowiem sprzeczne
z obowiązującą już pod koniec lat 40. linią upaństwowienia gospodarki. Ostatnie biura
mierniczych przysięgłych zamknięto w 1953 r. Prace geodezyjne związane z odbudową kraju
prowadziły przedsiębiorstwa państwowe, niejednokrotnie z liczną załogą, dochodzącą do
1000 pracowników i więcej (nawet 1500 osób), które miały monopol na takie prace. Ponieważ
firmy te nie mogły wykonywać niewielkich prac dla zwykłego obywatela, w 1983 r.
umożliwiono wykonywanie tych prac geodetom posiadającym uprawnienia zawodowe.
Określono siedem zakresów, w których można było nadawać takie uprawnienia w dziedzinie
geodezji i kartografii oraz wybrano specjalną komisję do egzaminowania. Od 1 stycznia
1989 r. zaczęła obowiązywać ustawa o działalności gospodarczej, fundament życia
gospodarczego w nowej Polsce i podstawa wolnego rynku.
W nowy ustrój wkroczyło 6964 geodetów mających uprawnienia zawodowe. Teraz każdy
mógł, bez żadnych przeszkód, założyć własną prywatną firmę. Od tego czasu nadano
uprawnienia ponad 17 tysiącom ludzi.

Zadania geodezji w gospodarce

Znaczenie geodezji w gospodarce jest ogromne. Do najważniejszych można zaliczyć:

1. Określanie kształtu i wymiarów Ziemi, jako planety.
2. Opisywanie powierzchni Ziemi poprzez określenie przestrzennego rozmieszczenia

obiektów naturalnych i sztucznych oraz rzeźby terenu. Najpowszechniejszym materiałem
wynikowym tego procesu jest mapa w różnych skalach (począwszy od 1:500), zarówno
tradycyjna jak i cyfrowa realizowana w technologii informatycznej.

3. Budowanie katastru tj. systemu informacji o nieruchomościach (gruntach, budynkach

i lokalach) dla potrzeb ksiąg wieczystych i podatków. W skład tych informacji wchodzi
min.: sposób użytkowania, stan prawny, klasyfikacja gleboznawcza, wartość rynkowa.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4. Wytyczanie (realizacja) w terenie projektów budowli (budynków, dróg,zakładów

przemysłowych, mostów, kolei itp.) oraz kontrola ich funkcjonowania (pomiary
odkształceń i przemieszczeń).

Sporządzanie i gromadzenie dokumentacji geodezyjnej zawierającej opis podziemnej
infrastruktury technicznej (kanalizacja, wodociągi, energetyka, telekomunikacja, gaz itp.),
opis złóż mineralnych i wyrobisk górniczych oraz archiwizacja tej dokumentacji w celach
użytkowych i udostępnianie jej zainteresowanym osobom i instytucjom.

Przekształcanie struktury powierzchniowej gruntów (scalenia i wymiany gruntów).

Monitorowanie środowiska i przestrzennego zagospodarowania kraju.

Dostarczanie danych do Systemu Informacji Przestrzennej (SIP), które określają
lokalizację oraz cechy jakościowe i ilościowe opisywanych obiektów.

Jak można się zorientować z powyższego zestawienia rola geodezji w codziennym życiu
obywatela, gminy – miasta oraz całego kraju jest nieoceniona.

Podział geodezji

Geodezja dzieli się na szereg działów zajmujących się określonym zakresem zadań.

Można wyróżnić następujące działy: [1]
1. Geodezja ogólna nazywana dawniej geodezją niższą lub miernictwem – zajmuje się

pomiarami na małych obszarach, które można odnieść do płaszczyzny bez uwzględnienia
krzywizny Ziemi.

2. Geodezja wyższa – zajmuje się badaniem kształtu oraz wymiarów Ziemi i pomiarami na

dużych obszarach z uwzględnieniem jej krzywizny.

3. Kartografia zajmuje się podstawami matematycznymi przedstawienia zakrzywionej

powierzchni Ziemi na płaszczyźnie rysunku mapy, poprzez tzw. odwzorowania
kartograficzne oraz technikami sporządzania i reprodukcji map.

Topografia zajmuje się sporządzaniem map w skalach średnich 1:10 000, 1:50 000,
1: 100 000, w oparciu o opracowania wielkoskalowe lub odrębną technikę pomiarową.

Fotogrametria zajmuje się wykonywaniem i wykorzystaniem zdjęć naziemnych,
lotniczych i satelitarnych do potrzeb pomiarowych. W oparciu o te zdjęcia mogą być
wykonywane mapy, plany oraz badania zjawisk zachodzących na powierzchni Ziemi.
Fotogrametria stosowana do celów sporządzania map średnioskalowych nosi nazwę
fotogrametrii topograficznej lub fototopografii.

Instrumentoznawstwo geodezyjne zajmuje się konstrukcją, badaniem, użytkowaniem
i konserwacją przyrządów geodezyjnych.

Rachunek wyrównawczy zajmuje się metodami obliczeń geodezyjnych, wyrównania
wyników pomiarów i szukaniem ich najbardziej prawdopodobnych wartości liczbowych
wielkości mierzonych.

Geodezja gospodarcza, to geodezja stosowana w różnych dziedzinach gospodarki.
Wyróżniamy zatem geodezję: inżynieryjno – przemysłową, rolną, leśną, górniczą, i inne.

Astronomia geodezyjna zajmuje się określaniem położenia punktów na powierzchni
Ziemi za pomocą astronomicznych obserwacji ciał niebieskich.
Polska jest jednym z nielicznych krajów, w których słowa „geodezja” używa się do

określenia dziedziny wiedzy i techniki związanej z pomiarami na małych obszarach (geodezja
ogólna). W większości krajów Europy zachodniej termin „geodezja” zarezerwowany jest
wyłącznie dla nauki zajmującej się pomiarami na dużych obszarach i całej Ziemi. Zadania
zarezerwowane dla geodezji ogólnej określane są tam mianem miernictwa.

Podstawowymi czynnościami technika geodety jest przeprowadzanie pomiarów

w terenie, wykonywanie obliczeń, rysunków i szkiców a w oparciu o nie, sporządzanie map
do różnych celów. Te czynności wykonują geodeci będący pracownikami jednostek

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

wykonawstwa geodezyjnego, urzędów administracji rządowej lub samorządowej. Geodeta
zajmuje się również prowadzeniem spraw dotyczących gospodarki gruntami lub
gromadzeniem i archiwizacją dokumentacji geodezyjnej – w przypadku pracy w Ośrodku
Dokumentacji Geodezyjnej i Kartograficznej.

Powierzchnia odniesienia

Ziemia jest nieregularną bryłą, której w matematyczny sposób nie da się opisać, dlatego

wyniki pomiarów i obliczeń geodezyjnych muszą być określane na regularnej powierzchni
dającej się opisać równaniami matematycznymi. Powierzchnia ta musi być zbliżona kształtem
do fizycznej powierzchni Ziemi. Powierzchnię, na którą rzutuje się pomierzone w terenie
punkty, nazywamy powierzchnią odniesienia. W zależności od wielkości obszaru
podlegającego pomiarowi powierzchnię odniesienia może stanowić: płaszczyzna, kula lub
elipsoida obrotowa. Elipsoida obrotowa spłaszczona powstaje poprzez obrót elipsy wokół osi
małej.
Układy współrzędnych

Układ współrzędnych jest to zespół obiektów geometrycznych względem, których określa

się jednoznacznie położenie punktu lub zbioru punktów. Przy dwuwymiarowym układzie
współrzędnych, który występuje na płaszczyźnie, określenie położenia punktu wymaga
podania dwóch liczb, w układzie trójwymiarowym natomiast – trzech liczb. Na płaszczyźnie
i w przestrzeni stosuje się różne typy współrzędnych prostokątnych (kartezjańskich), ponadto
na płaszczyźnie biegunowy układ współrzędnych. Na powierzchniach odniesienia używane są
układy współrzędnych krzywoliniowych (sferycznych lub elipsoidalnych), do których
zaliczamy współrzędne geograficzne.
Na przestrzeni lat, w Polsce stosowane były różne państwowe układy współrzędnych
prostokątnych [2]. Różnice między nimi polegają m. in. na przyjętej powierzchni odniesienia
– elipsoidzie obrotowej. W Polsce, podobnie jak w innych państwach byłego Układu
Warszawskiego, obowiązywała od roku 1952 elipsoida Krassowskiego, z punktem
przyłożenia do geoidy w Pułkowie koło Sankt Petersburga. Kształt Ziemi najlepiej wyraża
geoida - bryła powstała w wyniku przedłużenia średniej powierzchni mórz i oceanów w stanie
spoczynku pod lądami i nad depresjami. Ze względu na niejednolity rozkład mas wewnątrz
Ziemi, bryła ta jest nieregularna. Bryłą regularną, która najbardziej zbliżona jest do kształtu
Ziemi jest elipsoida obrotowa. Wielu uczonych wykonało pomiary, których celem było
ustalenie dokładnych wymiarów elipsoidy ziemskiej. Od nazwisk tych uczonych przyjęto
nazwy elipsoid. Znane są elipsoidy Bessela, Clarka, Hayforda oraz wymieniona wyżej
elipsoida Krassowskiego.

Układ współrzędnych geograficznych – geodezyjnych jest jednym z układów, który

składa się na jednolity dla całego kraju, państwowy system odniesień przestrzennych.
Stosowanie jednolitych układów współrzędnych dla całego kraju wynika z zasady ciągłości
i porównywalności wyników pomiarów oraz powstałej w ich rezultacie dokumentacji
sporządzanej przez różnych wykonawców, która jest gromadzona w państwowym zasobie
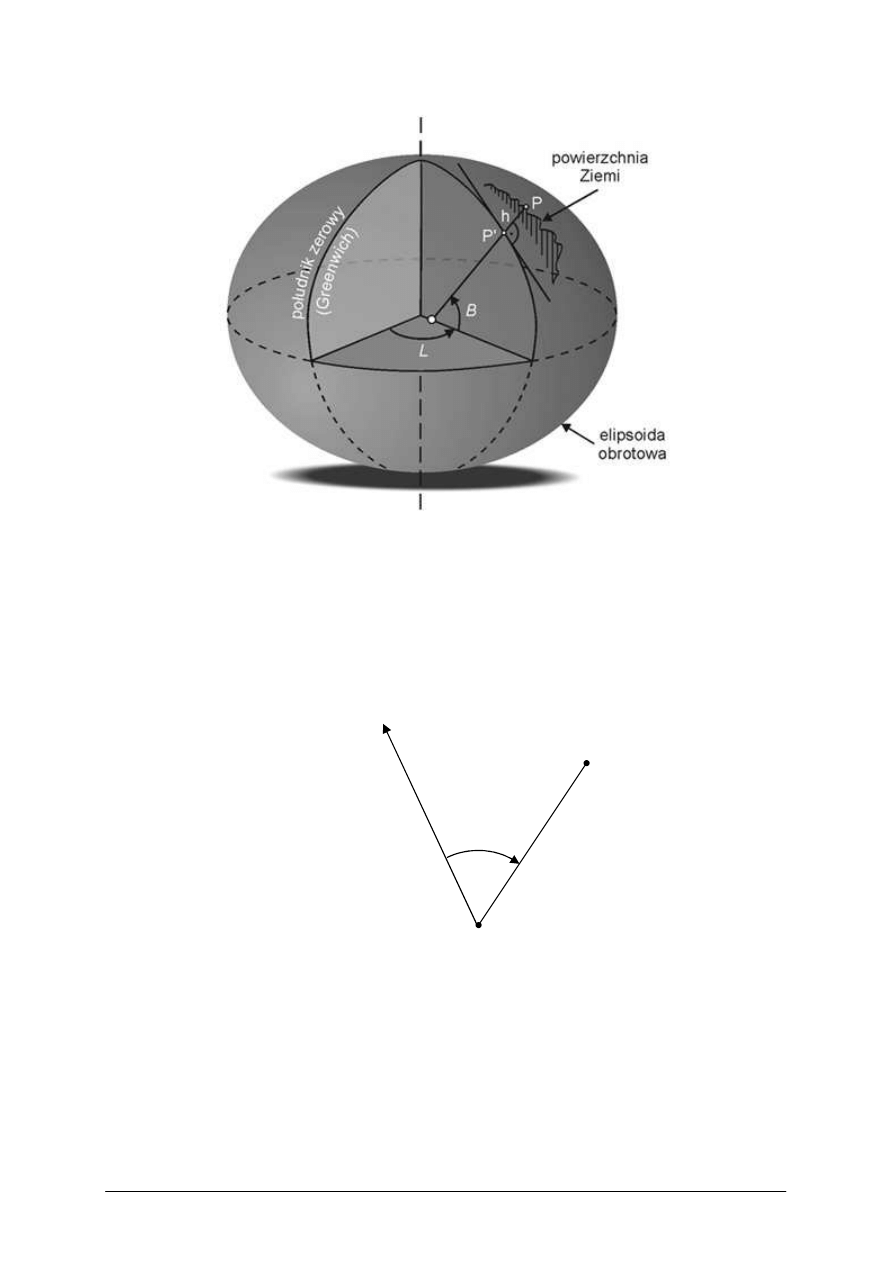
geodezyjnym i kartograficznym. Układ ten określa położenie punktu leżącego na elipsoidzie
za pomocą dwóch wielkości: szerokości oraz długości geograficznej geodezyjnej. Szerokość
geograficzna geodezyjna B jest to kąt zawarty pomiędzy normalną (prostopadłą) do elipsoidy
w danym punkcie a płaszczyzną równika. Długość geograficzna geodezyjna L jest to kąt
dwuścienny, zawarty pomiędzy półpłaszczyzną południka zerowego a płaszczyzną południka
przechodzącego przez dany punkt. Płaszczyznę południka na elipsoidzie wyznaczają: oś
obrotu elipsoidy i normalna do elipsoidy w danym punkcie.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 1. Układ współrzędnych geograficznych – geodezyjnych [4]

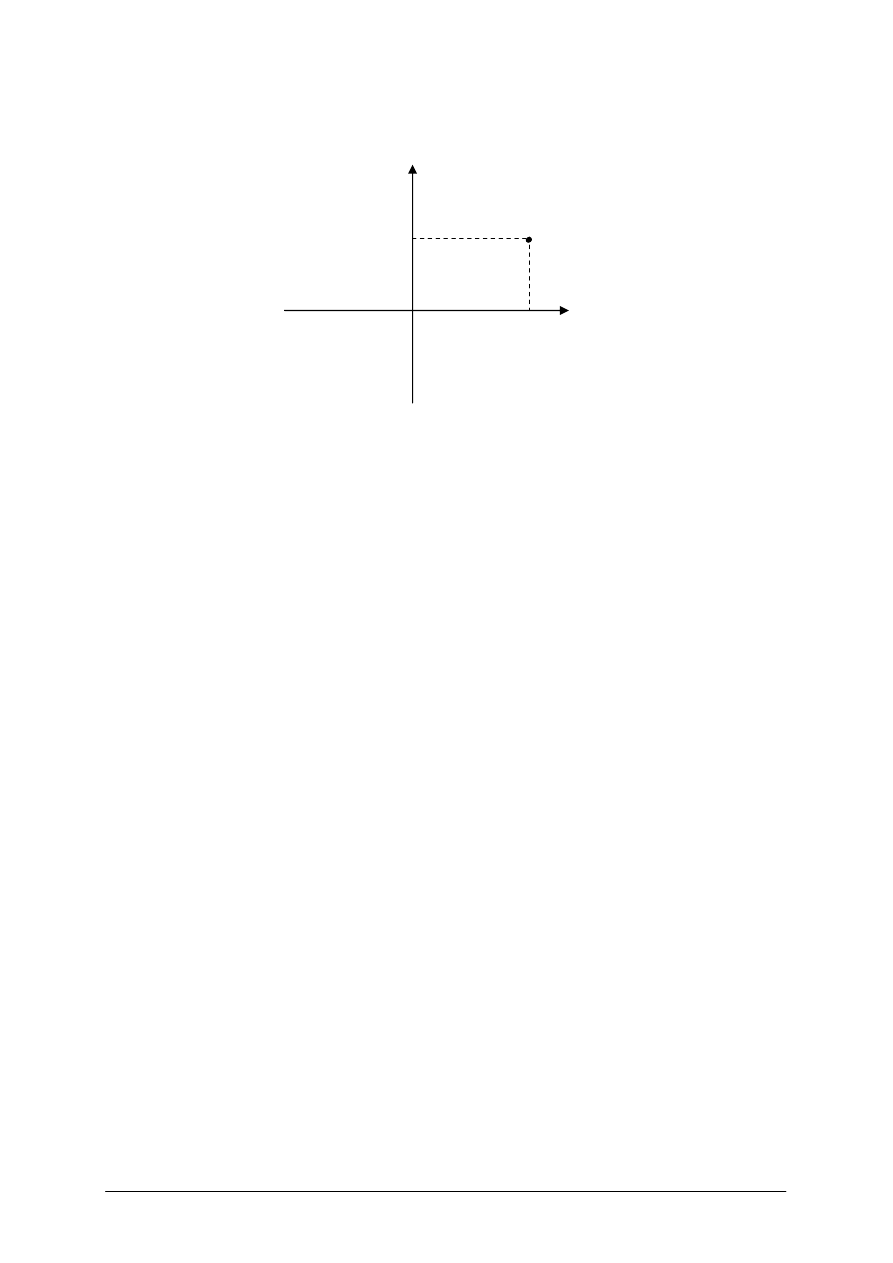
Układ współrzędnych biegunowych określa punkt B – początek układu, czyli biegun

i wychodząca z niego półprosta Z nazywana osią biegunową (Rys. 2). Współrzędnymi
biegunowymi danego punktu P są: promień wodzący „r”, czyli długość od bieguna do punktu
P oraz kąt kierunkowy α zawarty pomiędzy osią biegunową a promieniem wodzącym
mierzony od osi zgodnie z ruchem wskazówek zegara. W przypadku, gdy oś Z pokrywa się
z kierunkiem południka i kieruje się na północ, kąt kierunkowy α jest zarazem azymutem
odcinka BP – czyli α = A

BP.

Rys. 2. Układ współrzędnych biegunowych [opracowanie własne]

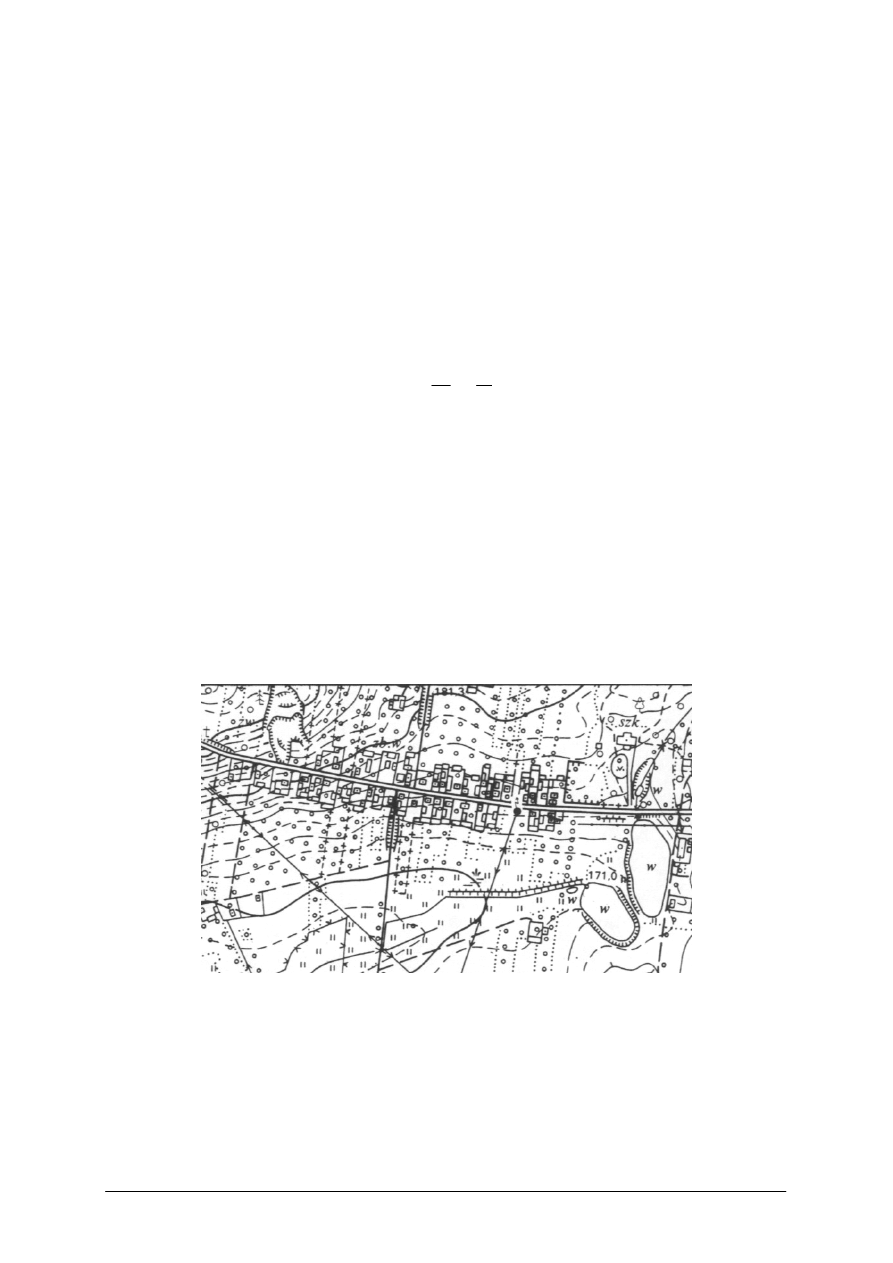
Układ współrzędnych prostokątnych płaskich stosowany w geodezji różni się od

układu matematycznego usytuowaniem osi układu X i Y oraz kierunkiem liczenia kątów.
Kierunek liczenia kątów w układzie geodezyjnym jest zgodny z kierunkiem ruchu wskazówek
zegara (Rys. nr 3). Dla niewielkiego obszaru kierunek osi X można uznać za zgodny
z kierunkiem południka przechodzącego przez środek obszaru. Położenie punktu P wyrażane
jest za pomocą współrzędnych X

i Y

(lub x i y).

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 3. Geodezyjny układ współrzędnych prostokątnych [opracowanie własne]

Do połowy lat 60 – tych, obowiązywał w Polsce układ współrzędnych zwany „1942”. Układ
ten powstał w wyniku zastosowania odwzorowania Gaussa – Krőgera na elipsoidzie
Krassowskiego.

Od końca lat 60-tych w służbie cywilnej zaczęto wprowadzać nowy, pięciostrefowy układ

współrzędnych prostokątnych, zwany skrótowo układem „1965”. W tym układzie
opracowano mapę zasadniczą kraju.

Od początku lat 90-tych podjęto prace, mające na celu włączenie obszaru Polski do

europejskiego systemu odniesień przestrzennych ETRS (European Terrestial Reference
System), będącego częścią światowego systemu ITRS (International Terrestial Reference
System). Wszystkie obliczenia wykonano już na nowej elipsoidzie, zwanej w skrócie GRS-80
(nazwa pełna:„Geodetic Reference System 1980”).

Zarówno dla poziomych sieci pomiarowych jak i dla opracowań kartograficznych

przyjęto dwa nowe układy współrzędnych prostokątnych:
1.

układ nazywany skrótowo „1992”, stanowiący podstawę do wykonywania nowych map
urzędowych w skalach 1:10 000 i mniejszych.

układ nazywany skrótowo „2000”, stosowany do opracowań map w skalach dużych oraz
dla osnów geodezyjnych. Układ ten wprowadzono w Polsce do 2000r. Układ „1965”
może być wykorzystywany tylko do końca 2009 r.

Poza wymienionymi wyżej państwowymi układami współrzędnych prostokątnych na

terenach niektórych miast wprowadzono lokalne układy współrzędnych. Przykładem takiego
układu jest układ współrzędnych nazywany skrótowo „ŁAM” (Łódzka Aglomeracja Miejska),
obejmujący dawniej miasto Łódź i okoliczne miejscowości, a obecnie funkcjonujący jedynie
na terenie samego miasta.

Mapa to rzut prostokątny powierzchni Ziemi na płaszczyznę, wykonany w określonym

zmniejszeniu, czyli w skali, w przyjętym układzie odniesienia.

Mapy służą człowiekowi już od kilku tysięcy lat, a najstarsze pochodzą ze starożytnego

Egiptu i Babilonii (ok. 3 tys. lat p.n.e.).

Przy tworzeniu map dla niewielkich obszarów (o powierzchni nieprzekraczającej

750 km

), fizyczną powierzchnię mierzonego terenu przenosi się na płaszczyznę mapy

przyjmując odpowiednią skalę, stosując odpowiednie znaki umowne oddające, wybraną treść.
Przy wykonywaniu map bez uwzględnienia krzywizny Ziemi stosuje się układ współrzędnych
prostokątnych.

P (X

)

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Przy przedstawianiu większych obszarów niż 750 km

, występuje trudność związana

z przedstawieniem zakrzywionej powierzchni Ziemi na płaszczyźnie mapy. Trudność ta
polega na tym, że fizyczna powierzchnia Ziemi, zbliżona kształtem do powierzchni kuli lub
elipsoidy obrotowej, nie daje się rozwinąć na płaszczyznę bez zniekształceń liniowych,
kątowych a także zniekształceń pól powierzchni. Matematycznie określony sposób
przeniesienia punktów znajdujących się na powierzchni odniesienia na płaszczyznę rysunku
mapy, nazywany jest odwzorowaniem kartograficznym. Odwzorowanie w sposób
jednoznaczny ustala zależności pomiędzy współrzędnymi geograficznymi punktu (φ, γ) na
kuli lub elipsoidzie obrotowej, a współrzędnymi prostokątnymi (X,Y), rzutu tego punktu na
płaszczyznę.

Skalą mapy nazywamy stosunek długości odcinka na mapie do rzutu poziomego jego

długości w terenie. Skalę możemy wyrazić wzorem:

Gdzie: M – mianownik skali.

d – długość odcinka na mapie.

D – długość rzutu poziomego tego odcinka w terenie.

Skala mapy jest, zatem ułamkiem, którego licznik jest równy jedności, a mianownik jest
liczbą, wskazującą stopień zmniejszenia rysunku w porównaniu do obrazu terenu.

Spośród kilku skal ta jest mniejsza, która ma większy mianownik. Skale duże stosowane

są dla zobrazowania terenów o dużym zagęszczeniu szczegółów terenowych (naziemnych
i podziemnych) – takich jak tereny zurbanizowane. Dla terenów miejskich mapa zasadnicza
wykonywana jest zwykle w skali 1:500 lub 1:1000, dla zurbanizowanych obszarów wiejskich
w skali 1:1000 i 1:2000, a dla terenów o mniejszym zagęszczeniu obiektów terenowych np.
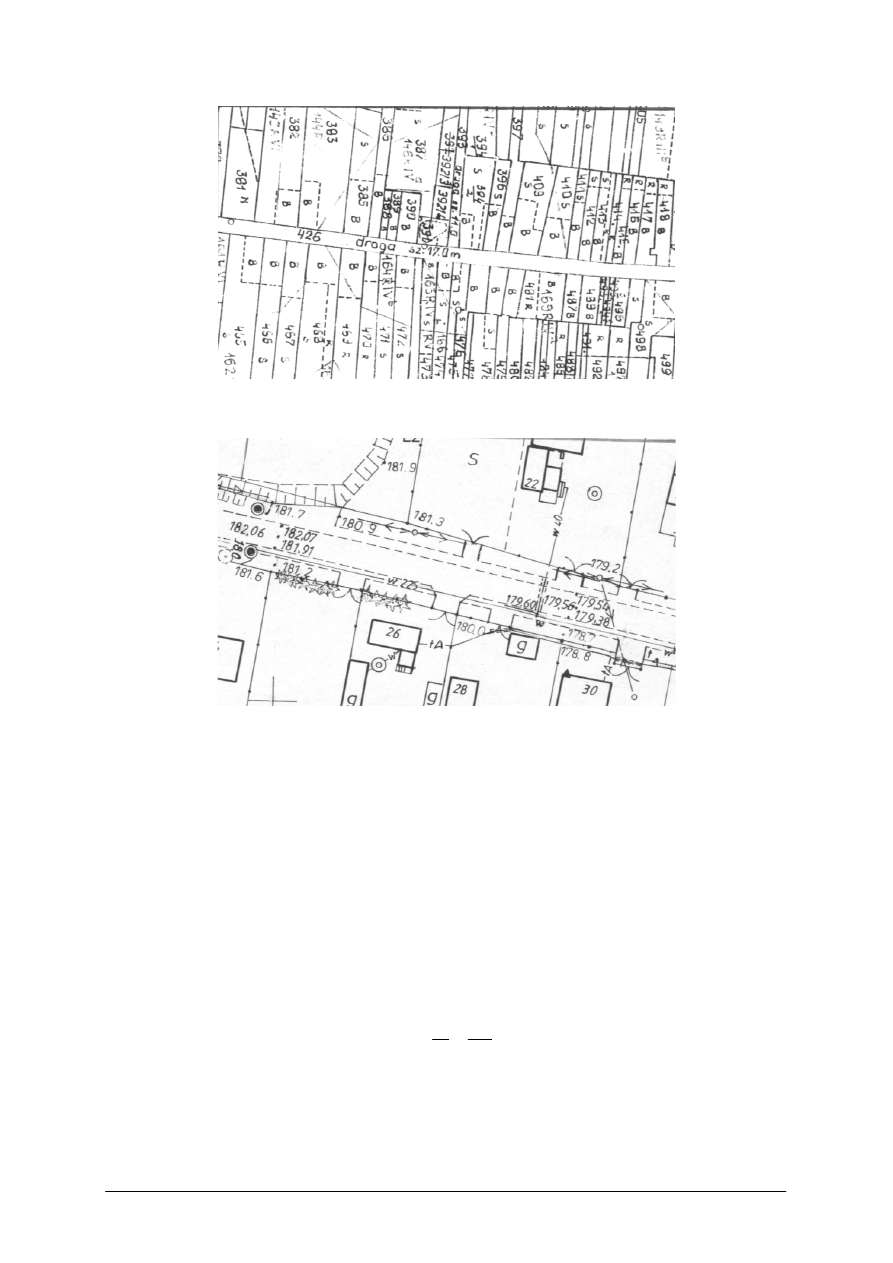
terenów leśnych w skali 1:5000. Poniżej przedstawiono fragmenty map o różnych skalach
obrazujących ten sam teren (Rys. 4).

Mapa topograficzna w skali 1:10 000

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Mapa ewidencji gruntów i budynków w skali 1:5000

Mapa zasadnicza w skali 1:1000

Rys. 4. Mapy w różnych skalach [opracowanie własne]

Mapy archiwalne, które jeszcze można spotkać np. w księgach wieczystych i archiwach

mogą mieć skale: 1:2880 i 1:4200. Taka wielkość mianownika skali wynika z jednostek
długości stosowanych w zaborze austriackim i rosyjskim.

Oko człowieka jest zdolne ocenić wielkość liniową z dokładnością do 0,1 mm. Długość

terenową, odpowiadającą tej wielkości, nazywamy dokładnością danej skali. Np. dla skali
1:5000 będzie to 0,5 m.

W trakcie korzystania z map obrazujących ten sam obszar, a wykonanych w różnych

skalach, może zaistnieć potrzeba przeniesienia określonego odcinka d

w skali 1: M

na mapę

w skali 1: M

. Aby odłożyć odpowiednią odległość d

na mapie w skali 1: M

należy

przekształcić zależność:

Na podstawie powyższej zależności można również określić nieznaną skalę mapy.

Aby wykonać to zadanie musimy dysponować mapą o znanej skali na ten sam teren. W celu
określenia nieznanej skali mapy musimy zidentyfikować na obydwu mapach odcinki oparte na

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

tych samych punktach i zmierzyć ich długości z największą możliwą dokładnością.
Na podstawie wzoru:

obliczamy nieznany mianownik skali mapy.

Graficzne przedstawienie skali to podziałka. Podziałka wykorzystywana jest do mierzenia

oraz odkładania odległości na mapie. W powszechnym stosowaniu rozróżnia się podziałki
liniowe i poprzeczne – inaczej nazywane transwersalnymi.

Podziałka liniowa podobna jest do linijki z podziałem centymetrowym, ale jej podział

opisany jest odległościami terenowymi.

Podziałka poprzeczna ma kształt liniału, zwykle wykonanego z mosiądzu, o długości ok.

25 cm i szerokości 4 cm, z wytrawionymi liniami pionowymi, poziomymi i ukośnymi.
Określenie odległości pomierzonej cyrklem – odmierzaczem na mapie, polega na przyłożeniu
jego ostrzy do odpowiednich linii pionowych i ukośnych podziałki i odczytaniu odległości
terenowej.

Jak opisano w początkowej części rozdziału, dla niedużych obszarów, wykonuje się mapy

z wykorzystaniem układu współrzędnych prostokątnych płaskich. Prowadząc linie równoległe
do osi X i Y otrzymamy siatkę kwadratów, która ułatwia odszukanie na mapie punktu
o znanych współrzędnych, odczytanie współrzędnych konkretnego punktu lub wniesienie na
mapę punktu o zadanych współrzędnych. Siatka kwadratów przedstawiana jest na mapie
w postaci krzyży, umiejscowionych w punktach przecięcia się prostych równoległych do osi X
i Y. Krzyże te rozmieszczone są w stałej odległości 10 cm od siebie, co odpowiada
(w zależności od skali mapy) odcinkom o długości 50 m, 100 m, 200 m lub 500 m w terenie.

Używając podziałki transwersalnej, cyrkla – odmierzacza oraz ekierek, można,

wykorzystując siatkę kwadratów, wykonać następujące zadania:

−

odszukać punkt o znanych współrzędnych,

−

skartować, czyli wnieść na mapę punkt o znanych współrzędnych,

−

odczytać współrzędne wybranych punktów obrysu konkretnego obiektu zobrazowanego
na mapie.

Aby wykonać te zadania należy ustalić kwadrat siatki, dla którego współrzędne naroży

będą zbliżone do współrzędnych interesującego nas punktu. Następnie konieczne jest
odłożenie lub określenie różnicy współrzędnych między liniami siatki kwadratów a szukanym
punktem.
Graficzne przedstawienie rzeźby terenu na mapie

Rzeźba terenu – czyli jego pionowe ukształtowanie (naturalne lub sztuczne), jest

przedstawiane na mapie za pomocą znaków umownych, opisu wysokości charakterystycznych
punktów terenowych oraz warstwic.

Znaki umowne są graficznym obrazem obiektów znajdujących się na powierzchni ziemi,

których nie można przedstawić w skali mapy. Obiektami mającymi znaczenie dla opisania
ukształtowania terenu będą np. skarpy, wąwozy.

Punkty charakterystyczne dla danego obszaru takie jak: szczyty wyróżniających się

wzniesień, najwyższe punkty działów wodnych i przełęczy, najniższe punkty dolin,
wąwozów, parowów, sztucznych zagłębień, rowów, oraz punkty na osiach dróg urządzonych,
uzupełnia się opisem wysokości tych punktów nad poziomem odniesienia.

Warstwice są to linie na mapie, łączące punkty o tej samej wysokości względem

przyjętego poziomu odniesienia. Obrazami warstwic na mapie są ślady przecięcia
powierzchni terenu płaszczyznami poziomymi równoodległymi od siebie. Odległość pionowa
między warstwicami nazywana jest cięciem warstwicowym. Wielkość cięcia warstwicowego

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

uzależniona jest od ukształtowania terenu (wielkości nachylenia terenowego) oraz skali mapy.
Wartości cięcia warstwicowego dla różnych skal mapy zasadniczej podano w tabeli nr 1.

Tabela 1. Cięcie warstwicowe dla mapy zasadniczej [1, s. 176]

Skala mapy
zasadniczej

Zasadnicze cięcie

warstwicowe

1:500

0,5 m

1:1000

1,0 m

1:2000
1:5000

2,5 lub 5,0 m

W przypadku gdy opracowywany teren jest równinny, z małym nachyleniem terenu, dla

lepszego zobrazowania rzeźby terenu można zastosować tzw. warstwice pomocnicze, których
cięcie warstwicowe wynosi połowę cięcia zasadniczego podanego w tabeli nr 1, a w razie
potrzeby także warstwice uzupełniające, o cięciu równym 1/4 cięcia. Charakterystyczną
wartością liczbową każdej warstwicy jest wysokość płaszczyzny tnącej nad poziomem
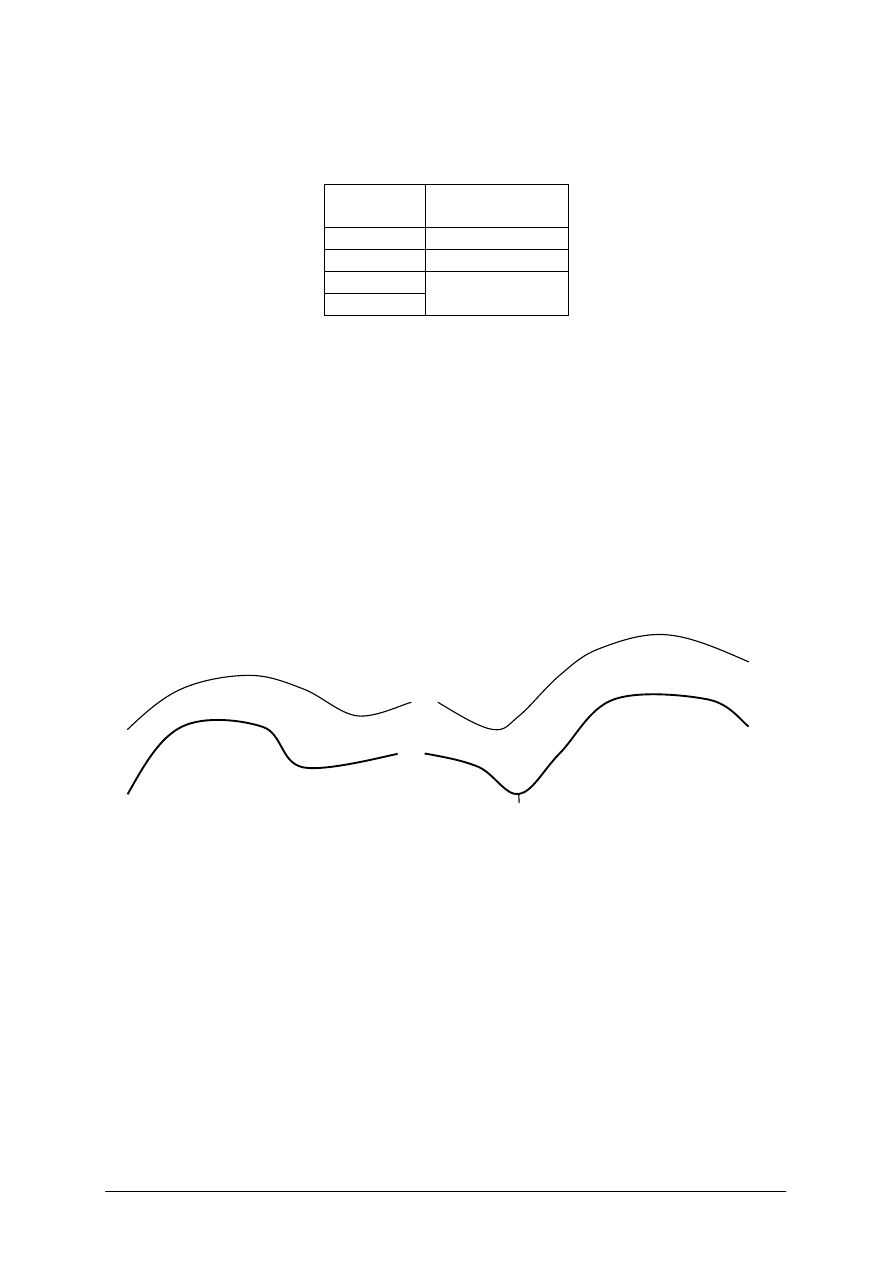
odniesienia, określana jako cecha warstwicy. Opis cechy warstwicy umieszcza się w luce
powstałej w wyniku przerwania ciągłości warstwicy (Rys. 5). Liczba, stanowiąca cechę
warstwicy, jest zapisana w taki sposób, że jej podstawa wskazuje kierunek spadku terenu a jej
wartość stanowi całkowitą wielokrotność cięcia warstwicowego. Na mapach możemy spotkać
się z opisem tylko warstwic „pogrubionych”, czyli posiadających cechy stanowiące
wielokrotność 5m. Dodatkowym elementem, uzupełniającym rysunek warstwic, są wskaźniki
spadu, czyli krótkie kreski przylegające do linii warstwic, pozwalające odróżnić formy
wypukłe od wklęsłych oraz określić na mapie kierunki spadku terenu w zakolach warstwic.

Rys. 5. Opis warstwicy [opracowanie własne]

4.1.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

Jakimi cechami charakteryzuje się geodezyjny układ współrzędnych prostokątnych
płaskich?

Jakimi cechami charakteryzuje się mapa?

Jaką zależność określa skala mapy?

Jaka się nazywa graficzna postać skali mapy?

W jaki sposób zobrazowany jest układ współrzędnych prostokątnych na mapie?

Jakimi narzędziami można odczytywać i odszukiwać współrzędne na mapie?

W jaki sposób przedstawiana jest rzeźba terenu na mapie?

195

196

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.1.3. Ćwiczenia

Ćwiczenie 1

Określ odległość rzeczywistą między punktami wskazanymi na mapie przez nauczyciela.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

odszukać w materiale nauczania zależności dotyczące skali mapy,

pomierzyć zadany odcinek cyrklem – odmierzaczem,

ustalić używając podziałki liniowej lub poprzecznej terenową długość odcinka.

Wyposażenie stanowiska pracy:

−

wycinek mapy o znanej skali,

−

cyrkiel – odmierzacz,

−

podziałka liniowa lub transwersalna,

−

papier formatu A4.

Ćwiczenie 2

Odłóż na kartce papieru zadane przez nauczyciela odległości w skali: 1:250, 1:500,

1:1000, 1: 2000.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

odszukać w materiale nauczania zależności dotyczące skali mapy,

odłożyć zadane odległości za pomocą cyrkla – odmierzacza i podziałki liniowej lub
transwersalnej.

Wyposażenie stanowiska pracy:

−

cyrkiel – odmierzacz,

−

podziałka liniowa lub transwersalna,

−

papier formatu A4.

Ćwiczenie 3

Na mapie o nieznanej skali 1:M

oraz na mapie w skali 1: 5000 zidentyfikowano

i pomierzono długość tego samego odcinka terenowego otrzymując wyniki: d

= 23.1 mm,

=19.4 mm. Na podstawie pomierzonych długości ustal mianownik skali – M

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

odszukać w materiale nauczania potrzebne wzory,

wykonać obliczenie,

opisać uzyskany wynik.

Wyposażenie stanowiska pracy:

−

papier formatu A4,

−

kalkulator.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Ćwiczenie 4

Odszukaj na mapie punkty o podanych przez nauczyciela współrzędnych.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

odszukać w materiale nauczania zależności dotyczące skali mapy,

ustalić kwadraty, w których umiejscowione są zadane punkty,

wykorzystać dwie ekierki do skonstruowania linii równoległych do osi X i Y,

wykorzystać podziałkę poprzeczną do właściwego określenia usytuowania punktów.

Wyposażenie stanowiska pracy:

−

mapa o znanej skali,

−

cyrkiel – odmierzacz,

−

dwie ekierki

−

podziałka transwersalna,

−

poradnik dla ucznia.

Ćwiczenie 5

Odczytaj współrzędne punktów wskazanych na mapie przez nauczyciela.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

odszukać w materiale nauczania zależności dotyczące skali mapy,

ustalić współrzędne naroży kwadratów, w których znajdują się zadane punkty,

wykorzystać dwie ekierki do skonstruowania linii równoległych do osi X i Y,

wykorzystać podziałkę transwersalną do odczytania współrzędnych.

Wyposażenie stanowiska pracy:

−

mapa o znanej skali,

−

cyrkiel – odmierzacz,

−

dwie ekierki,

−

podziałka transwersalna.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.1.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

zdefiniować pojęcie geodezja?

przedstawić rys historyczny geodezji?

scharakteryzować poszczególne działy geodezji?

podać główne zadania geodezji w gospodarce?

wymienić rodzaje układów współrzędnych stosowanych w geodezji?

scharakteryzować geodezyjny układ współrzędnych prostokątnych?

scharakteryzować pojęcie skali mapy?

posłużyć się podziałką transwersalną?

odczytać współrzędne punktu na mapie?

10)

znaleźć na mapie punkt o zadanych współrzędnych?

11)

scharakteryzować graficzne zobrazowanie rzeźby terenu?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.2.

Jednostki miar stosowane w geodezji

4.2.1. Materiał nauczania

Miary długości

Podstawową jednostką długości stosowaną w geodezji jest metr. Jest to w przybliżeniu,

długość jednej dziesięciomilionowej (10

-7

) części ćwiartki południka ziemskiego.

W metrach wyrażone są takie wielkości jak:

−

długości odcinków,

−

wysokości (rzędne) punktów nad poziomem morza,

−

współrzędne prostokątne płaskie.

Pochodnymi jednostkami długości a wykorzystywanymi w geodezji są:

−

milimetr (mm) – używany w dokumentacjach projektowych do zwymiarowania
elementów oraz w podziale na łatach niwelacyjnych do niwelacji precyzyjnej
1 mm = 0,001 m.

−

kilometr (km) – stosowany przy wyrównywaniu sieci geodezyjnych poziomych
i wysokościowych, jako wartość określająca wielkość tych sieci oraz na mapach
i w dokumentacji związanej z drogami, 1km = 1000 m = 1 000 000 mm.

Dawne miary stosowane w Polsce:
1 pręt = 7,5 łokcia = 15 stóp = 4,32 m
1 łokieć = 0,576 m
1 cal = 0,024 m
1 klafter (sążeń wiedeński) = 6 stóp = 1,8965 m – dawna miara austriacka
1sążeń = 7 stóp = 2,1336 m – dawna miara rosyjska
1 stopa pruska lub reńska = 0.3139 m
1 krok = 3 stopy = 0.9417 m

Miary kątowe

Najstarszą miarą kątową, liczącą ponad 5000 lat, jest miara sześćdziesiętna, nazywana

stopniową [1]. Podział stopniowy powstał przez podzielenie kąta pełnego na 360 części
(stopni). Dalszy podział odbywa się w systemie sześćdziesiętnym, tj. jeden stopień dzieli się
na sześćdziesiąt minut (') a minuta z kolei na sześćdziesiąt sekund (").

1° =

360

część kąta pełnego

1' =

1" =

Zapis kąta w podziale stopniowym podaje się wpisując kolejno stopnie, minuty i sekundy

np.150°02'09"

Niewygoda wynikająca z konieczności przeliczania minut i sekund na części dziesiętne

stopnia, wymusiła wprowadzenie dziesiętnej miary kątowej. Jednostka tej miary kata
nazywana jest gradem. Jeden grad (

)powstaje przez podział kąta prostego na 100 części, lub

podziału kąta pełnego na 400 części. Dalszy podział powstaje przez podzielenie 1 grada na
100 części – centygradów (

), i przez podział 1 centygrada na 100 decymiligradów (

400

część kąta pełnego

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

100

Zapis kąta w gradach można wykonać w dwóch postaciach: grady-centygrady-decymiligrady
lub tylko w gradach, np.: 155

lub 155,7796

Zamiana (przeliczanie) miar kątowych

Wiedząc, że 90° = 100

można określić zależności między jednostkami.

1° =

=1,1111(1)

oraz 1

= 0,9°

Wzory na przeliczenie kątów wyrażonych w różnych miarach można, więc napisać w postaci:

stopnie → grady :

α°

grady → stopnie

α° =

9 .

gdzie: α° - kąt wyrażony w stopniach,

g -

kąt wyrażony w gradach.

Przy zamianie stopni na grady lub odwrotnie – gradów na stopnie, należy na wstępie

wyrazić przeliczany kąt w jednostkach „najgrubszych” (stopnie, grady) a następnie
zastosować odpowiedni współczynnik zamiany.

4.2.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

Jakie miary długości stosowane są w geodezji?

Jakie są zależności pomiędzy miarami długości?

Jakie miary kątowe stosowane są w geodezji?

Jaki jest podział kąta pełnego na stopnie i grady?

Jaką postać mają zależności niezbędne przy przeliczaniu miar kątowych?

4.2.3. Ćwiczenia

Ćwiczenie 1

Zamień podane długości na metry.

11235 km,

21352 mm,

0,534 km,

161 mm,

1,010 km,

1010 mm.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

przypomnieć sobie zależności pomiędzy miarami długości,

przeliczyć podane długości na metry, korzystając z odpowiednich zależności.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Wyposażenie stanowiska pracy:

−

papier formatu A4,

−

kalkulator.

Ćwiczenie 2

Wykonaj sumowanie i odejmowanie kątów wyrażonych w tych samych jednostkach.

100°10'20" + 181°01'02",

269°59'57" + 359°58'57,

269°59'57" - 100°10'20",

311

+399

222

- 99

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

wyrazić kąty w jednolitych jednostkach,np. w stopniach lub w sekundach dla kątów
podanych w mierze stopniowej lub w gradach lub decymiligradach – dla kątów podanych
w mierze gradowej,

wykonać sumowanie lub odejmowanie kątów,

wyrazić ponownie kąty w stopniach – minutach – sekundach, lub gradach – centygradach
– decymiligradach,

sprawdzić czy otrzymane wyniki nie przekraczają wartości kata pełnego. Jeżeli tak, to
należy je zredukować o wartość kąta pełnego.

Wyposażenie stanowiska pracy:

−

papier formatu A4,

−

kalkulator.

Ćwiczenie 3

Zamień wartości kątów wyrażone w stopniach na grady:

100°10'20",

181°01'02",

269°59'57",

359°58'57,

0°01'01".

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

odszukać w materiale nauczania zależności między jednostkami miar kątowych,

zamienić minuty i sekundy na części stopnia,

przeliczyć wartości kątów na grady, stosując odpowiednie zależności.

Wyposażenie stanowiska pracy:

−

papier formatu A4,

−

kalkulator.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Ćwiczenie 4

Wyrażone w gradach miary kątowe, zamień na stopnie.

a) 99

222

311

399

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

odszukać w materiale nauczania zależności między jednostkami miar kątowych,

zamienić centygrady i decymiligrady na części grada,

przeliczyć wartości kątów na stopnie, stosując odpowiednie zależności,

wyrazić otrzymany wynik w stopniach, minutach i sekundach.

Wyposażenie stanowiska pracy:

−

papier formatu A4,

−

kalkulator.

4.2.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

podać miary długości stosowane w geodezji?

przeliczyć miary długości stosowane w geodezji?

scharakteryzować podział stopniowy i gradowy?

scharakteryzować sposób zapisu kąta w stopniach i w gradach?

przeliczyć stopnie na grady i odwrotnie?

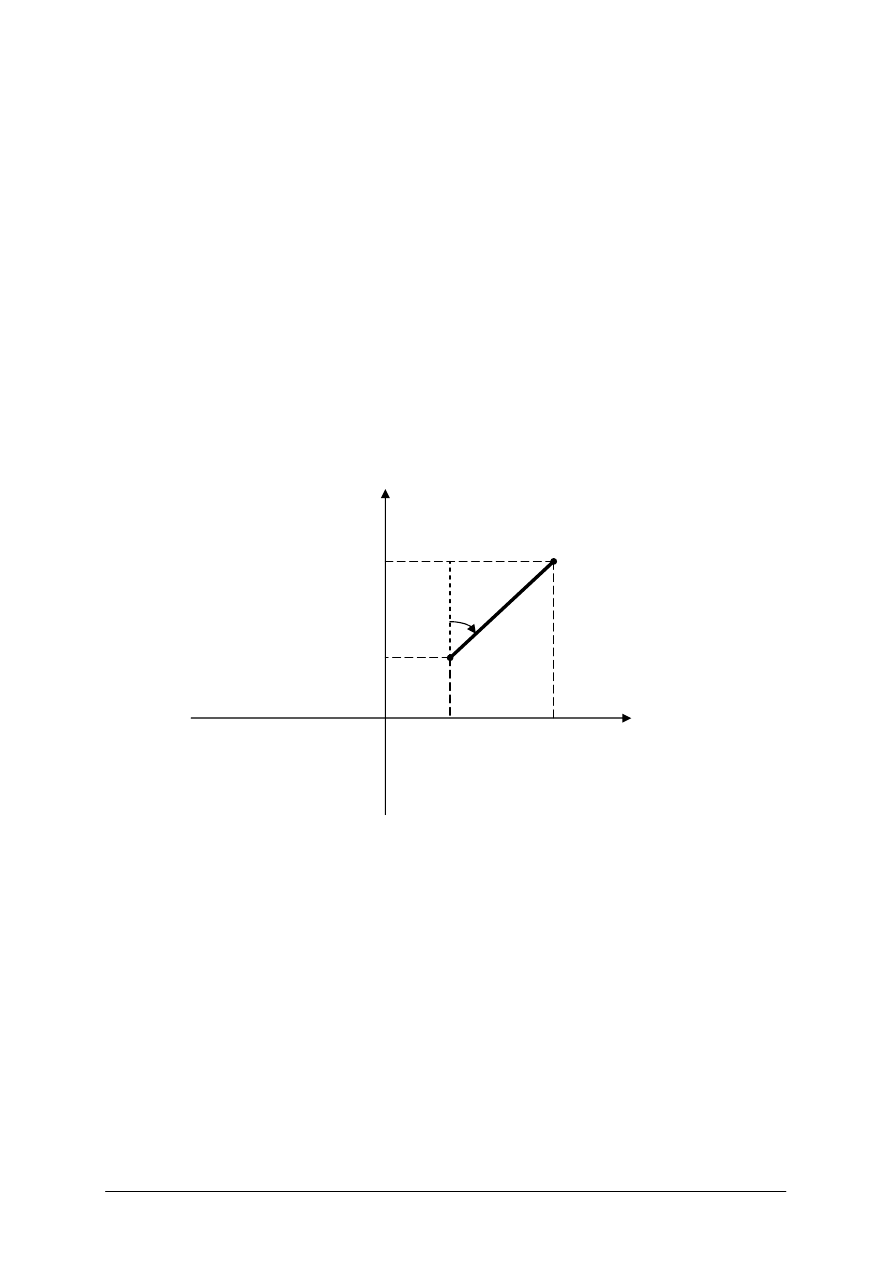
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.3.

Posługiwanie

się

współrzędnymi

rozwiązywania

podstawowych zadań geodezyjnych

4.3.1. Materiał nauczania

Azymut odcinka

Azymutem A

odcinka AB, jest kąt zawarty pomiędzy kierunkiem południka

przechodzącego przez punkt A, a odcinkiem AB, liczony zgodnie z ruchem wskazówek
zegara od kierunku południka. Azymut może przybierać wartości od 0° do 360° (0

– 400

)

Rys. 6. Jeżeli punktem wyjściowym dla określenia azymutu jest punkt B, wówczas
prowadzimy z niego kierunek północy i wyprowadzamy w prawo kąt pomiędzy linią północy
a bokiem BA. Otrzymamy wówczas azymut boku odwrotnego BA (azymut odwrotny),
oznaczany symbolem A

, który różni się od azymutu boku wyjściowego o wartość kąta

półpełnego - 180° (200

). Możemy to zapisać wzorem: A

= A

± 180° (lub 200

). Znak

„plus” we wzorze dotyczy azymutów wyjściowych do 180° (lub 200

), znak „minus”

wprowadzany jest gdy azymut wyjściowy przekracza 180° (lub 200

Rys. 6. Azymut odcinka, przyrosty współrzędnych [1, s. 85]

Ponieważ południk może być określany różnymi sposobami, w związku, z czym

wyróżnia się kierunki południków: geograficznego, topograficznego i magnetycznego.

Południk geograficzny jest to linia na powierzchni kuli ziemskiej, łącząca bieguny

geograficzne Ziemi.

Południk topograficzny jest obrazem na mapie południka geograficznego przechodzącego

przez określony punkt na mapie. Na mapach w dużych skalach opracowanych w prostokątnym
układzie współrzędnych, kierunek osi 0X pokrywa się z kierunkiem południka
topograficznego, przechodzącego przez środek obszaru przedstawionego na mapie. Przyjmuje
się, że na mapach wielkoskalowych południki topograficzne są do siebie równoległe
i równoległe do osi 0X układu współrzędnych prostokątnych.

∆Y

∆X

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Południk magnetyczny, to linia na powierzchni Ziemi, łącząca bieguny magnetyczne

Ziemi. Kierunek południka magnetycznego jest wyznaczany przez igłę magnetyczną busoli.
W zależności od przyjętego kierunku odniesienia, wyróżnia się azymuty: geograficzny,
topograficzny i magnetyczny. Ponieważ kierunki południków geograficznego, magnetycznego
i topograficznego nie pokrywają się, w związku, z tym azymuty odcinka, mającego swój,
początek w danym punkcie, będą się różniły o wartości kątowe:

−

azymut geograficzny i magnetyczny o kąt deklinacji magnetycznej „δ”– (jest to kąt
zawarty pomiędzy południkiem geograficznym Ng i magnetycznym Nm. Azymut
geograficzny Ag obliczamy sumując azymut magnetyczny i deklinację magnetyczną:
Ag = Am + δ,

−

azymut geograficzny i topograficzny o kąt zbieżności południków „γ”– (jest to kąt
zawarty pomiędzy południkiem geograficznym Ng i topograficznym Nt). Azymut
geograficzny Ag obliczamy sumując azymut topograficzny i kąt zbieżność południków:
Ag = At + γ. (Rys. 7)

Rys. 7. Zależność między azymutem geograficznym, topograficznym i magnetycznym [1, s. 84]

Zgodnie z rys. nr 6, wzór na obliczenie azymutu topograficznego ma postać:

tgA

∆Y

∆

gdzie:
tgA

– tangens azymutu odcinka AB,

∆X

– różnica (przyrost) współrzędnych na odcinku AB wzdłuż osi X: ∆X

= X

– X

∆Y

– różnica (przyrost) współrzędnych na odcinku AB wzdłuż osi Y: ∆Y

= Y

– Y

Jak opisano wcześniej wartości azymutu przybierają wielkości od 0° do 360° (0

-400

a na podstawie podanego wzoru nie jesteśmy w stanie określić wartości kąta A

W celu jednoznacznego określenia tej wartości wprowadzono pojęcie czwartaka. Czwartak
„φ” jest to kąt ostry, zawarty pomiędzy linią osi X a danym odcinkiem AB obliczony na
podstawie podanego wyżej wzoru. Zależności pomiędzy czwartakiem, a azymutem
przedstawia tabela nr 2.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Tabela 2. Zależność pomiędzy czwartakiem a azymutem [1, s. 86]

Znaki

Numer ćwiartki

azymutu

∆X

cos A

∆Y

sin A

Zależność pomiędzy
azymutem „A”
i czwartakiem „φ”

A =

–

A = 200

III

–

A = 200

–

A = 400

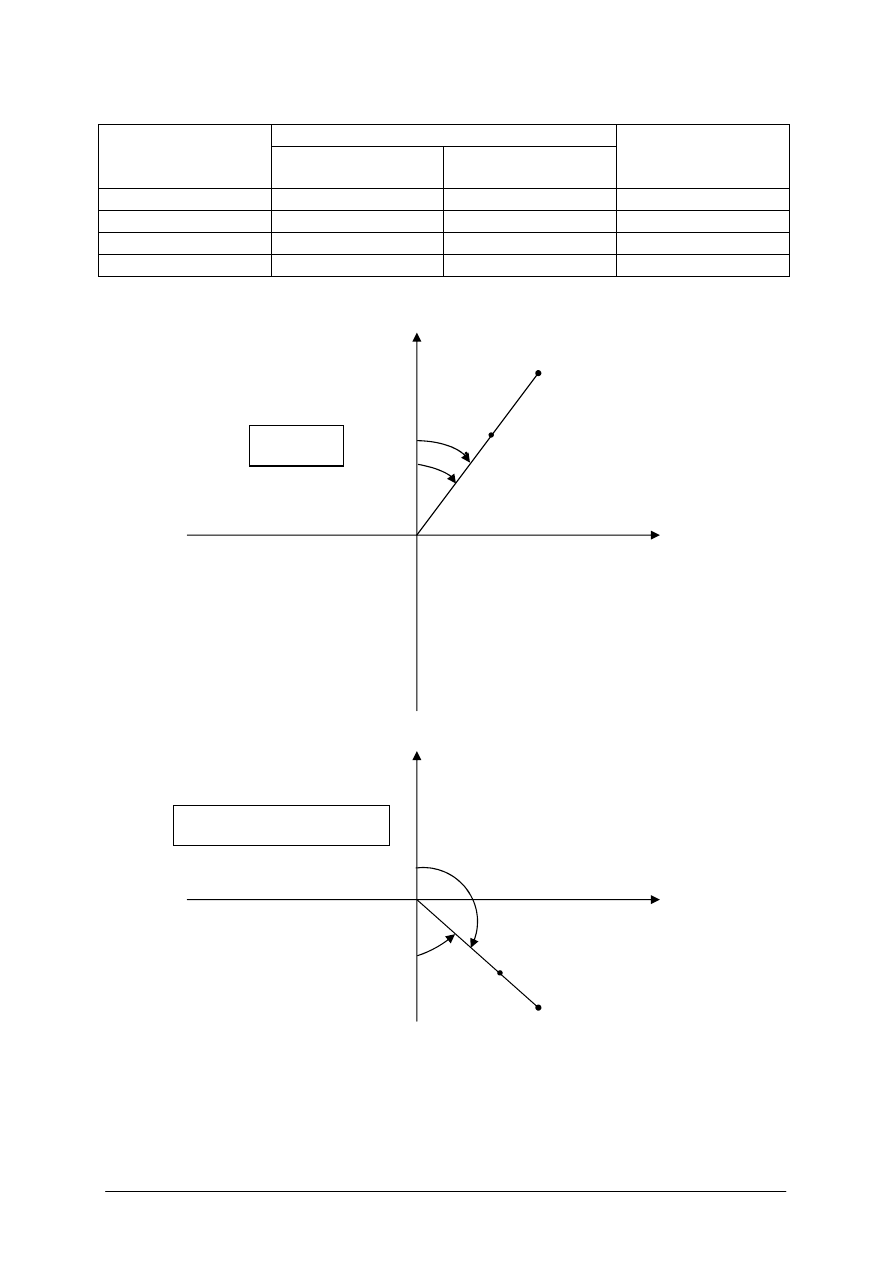
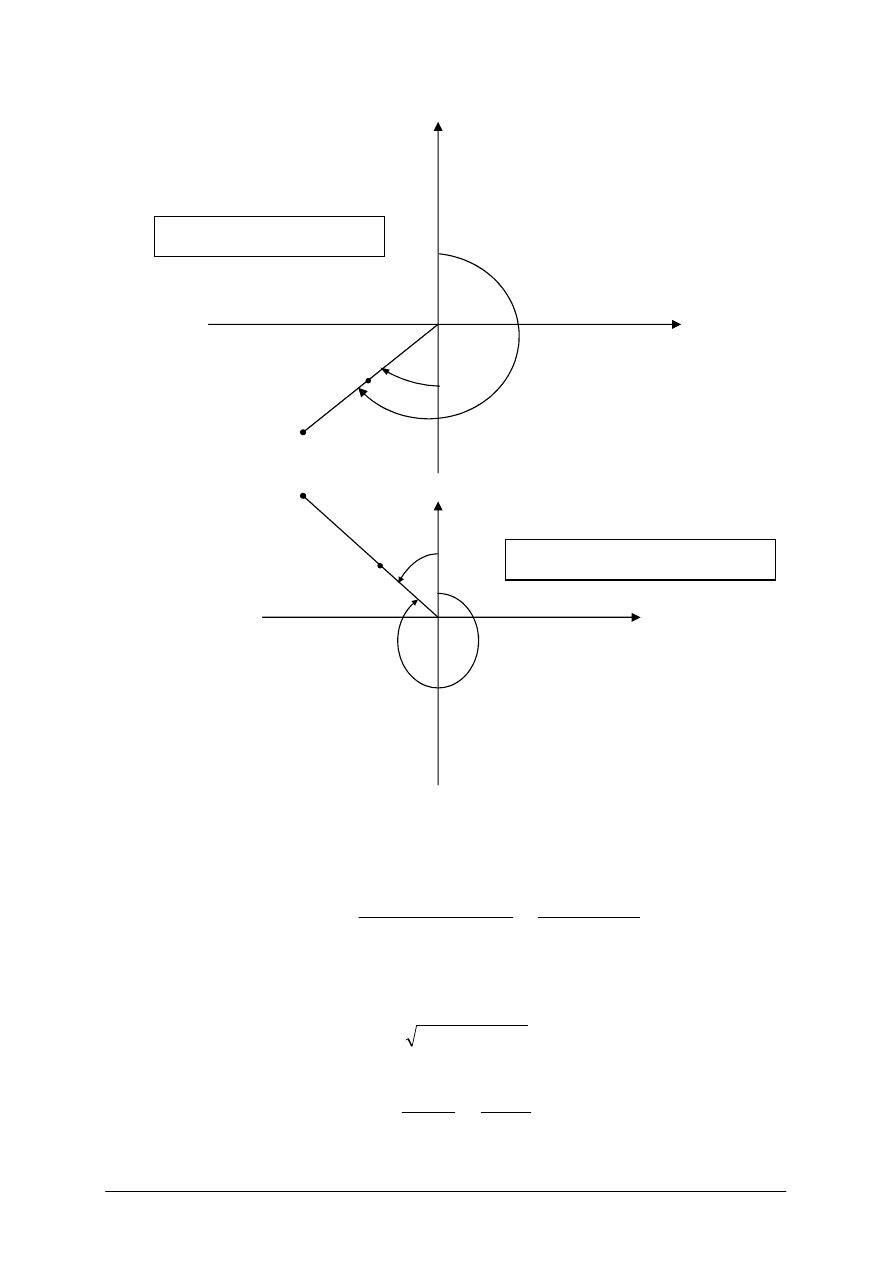
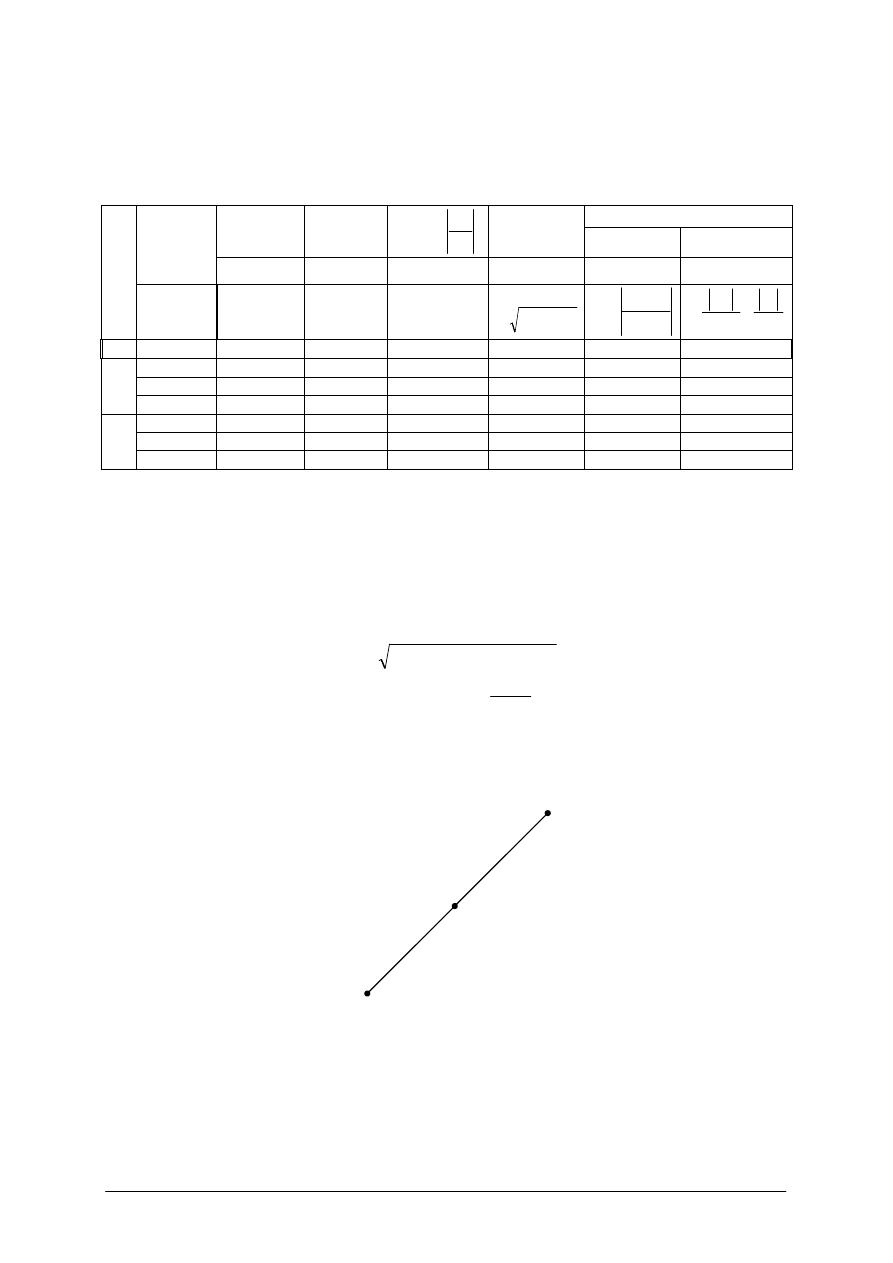
Układ ćwiartek i czwartaków przedstawia Rys. nr 8. (a,b,c,d)

II ćwiartka

= 200

(180°) - φ

I ćwiartka

= φ

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 8. Zależności pomiędzy azymutem i czwartakiem [2, s. 85]

Obliczenia kontrolne azymutu odcinka polegają obliczeniu azymutu powiększonego o kąt 45°
(50

tg(A

+45°) =

)

(

∆

−

∆

Obliczenie odległości ze współrzędnych

Wzór na obliczenie długości odcinka AB ze współrzędnych ma postać:

∆

Dla kontroli poprawności obliczeń można stosować wzór:

cosA

∆

sinA

∆

III ćwiartka

IV ćwiartka

= 200

(180°) + φ

= 400

(360°) - φ

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

W praktyce geodezyjnej stosuje się formę tabelarycznego zestawienia danych do

obliczeń, wyników oraz obliczeń kontrolnych. Przykład takich obliczeń przedstawia tabela
nr 3.

Tabela 3. Obliczenie azymutu i długości ze współrzędnych [1, s. 87]

Kontrola

∆

cos

∆x + ∆y

Oznaczenie

punktów:

końcowy B

początkowy -

Czwartak φ

sin

∆x - ∆y

A+45° (50

)

Lp.

Oznaczenie

zwrotu

boku: A→B

∆X

∆Y

Azymut A

Odległość

∆

tgΨ=

∆

cos

∆

sin

∆

2 708,63

4 541,15

0,364 483 9

0,939 537 4

-980,29

89,1

4 251,14

3 978,93

10,9

0,342 446 2

-2 104,73

227

A - B

-1 542,51

+562,22

177

1 641,776

0,465 7557

1 641,776

3 978,93

12 561,78

0,804 230 1

0,779 258 4

+144,21

6°11'33,8"

+562,22

13 154,20

38°48'26,2"

0,626 702 8

+1 329,05

6°11'33,8"

C - D

+736,63

-592,42

321°11'33,8"

945,296

0,108 506 1

945,296

Obliczenie współrzędnych punktu końcowego, gdy znany jest azymut i długość odcinka

Jeżeli znane są współrzędne punktu A (X

) – początku odcinka, azymut linii AB oraz

jej długość d

(Rys. 6) aby obliczyć współrzędne punktu B – końca odcinka, stosujemy

wzory:

= X

+ ∆X

= X

+ d

AB.

cosA

= Y

+ ∆Y

= Y

+ d

sinA

Obliczenia kontrolne:

)

(

oraz A

= arc tg

∆

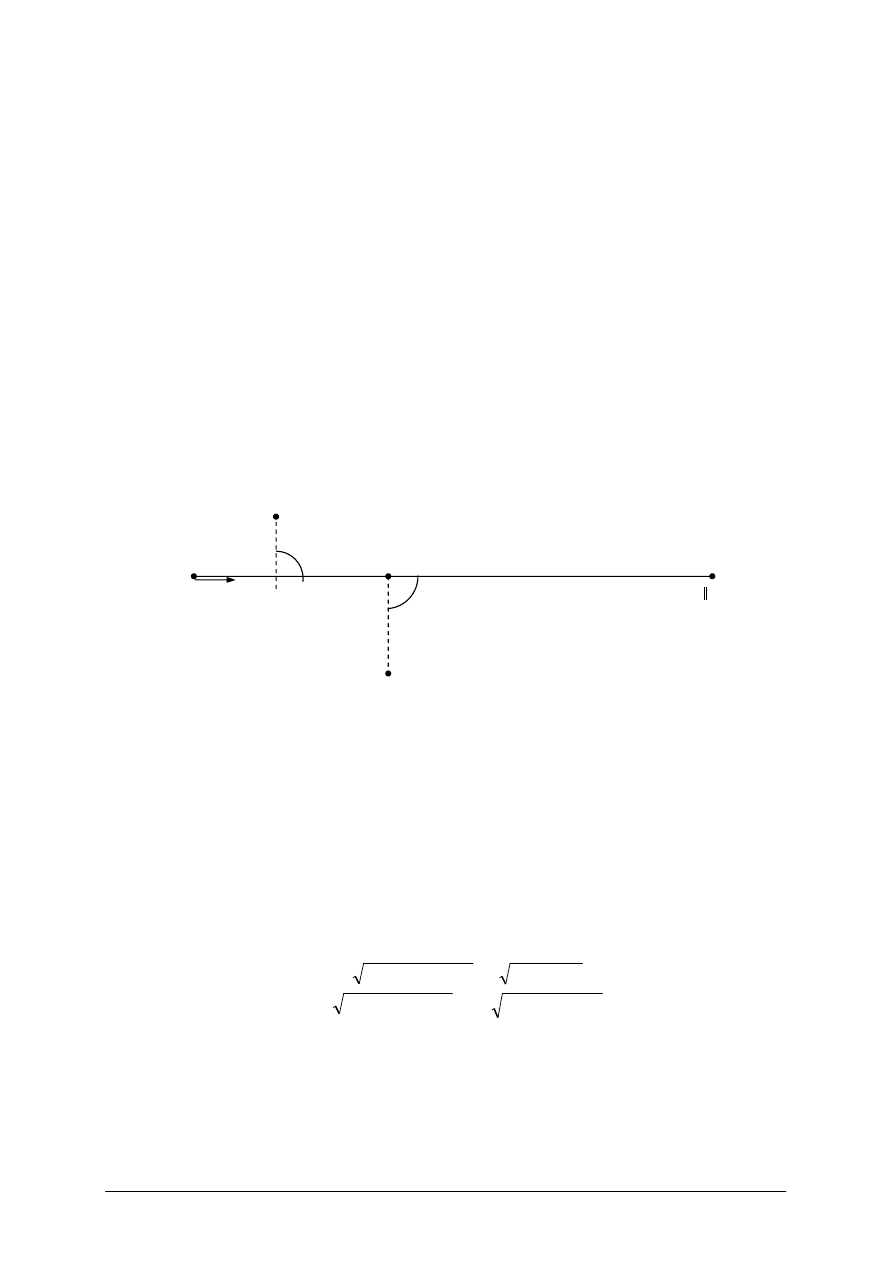
Obliczenie współrzędnych punktu na prostej

Aby obliczyć współrzędną punktu P położonego na prostej wyznaczonej przez punkty A

i B o znanych współrzędnych (Rys. nr 9),

Rys. 9. Punkt na prostej AB [opracowanie własne]

należy posłużyć się wzorem:

= X

+ d

cosA

= Y

+ d

sinA

A(X

)

B(X

, Y

)

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Jako obliczenie kontrolne można obliczyć odległości: d

AP,

oraz d

AB,

ze współrzędnych

a następnie sprawdzić czy spełniona jest równość:

= d

AP,

+ d

lub obliczyć azymut A

i sprawdzić czy A

= A

Obliczenie współrzędnych punktu na domiarze prostokątnym

Jedną z metod pomiaru położenia obiektów terenowych jest metoda rzędnych i odciętych

nazywana również metodą domiarów prostokątnych. Metoda ta wykorzystuje odcinek – linię
pomiarową - oparty na punktach o znanych współrzędnych, do zrzutowania na nią szczegółów
terenowych i polega na określeniu ich rzędnej i odciętej.
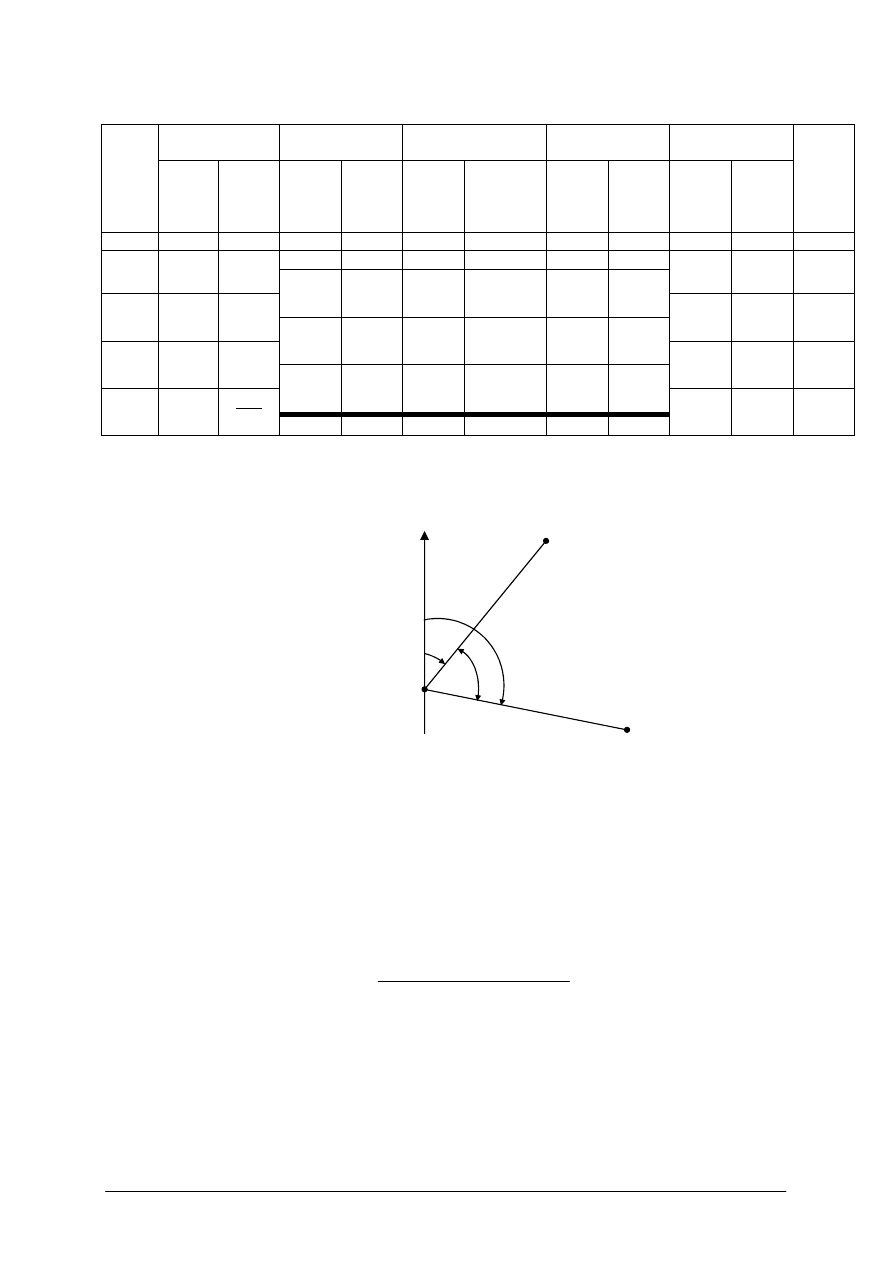
Zgodnie z Rys. 10, odciętą nazywamy odcinek „d” a rzędną - prostopadły do linii AB odcinek
„h”. Przy obliczaniu współrzędnych punktów pomierzonych metodą domiarów prostokątnych,
rzędnym nadaje się różne znaki w zależności od tego, po której stronie linii AB znajduje się
mierzony punkt. Jeżeli punkt P znajduje się po prawej stronie linii, to rzędna otrzymuje znak
plus (+), a jeżeli po lewej stronie – znak minus (-). Podana zasada jest słuszna przy założeniu,
że linia pomiarowa jest tak zorientowana, że w punkcie A jest jej początek a w punkcie
B – koniec.

Rys. 10. Rzędna i odcięta punktów P i R [opracowanie własne]

Do obliczenia współrzędnych punktu P służą wzory:

= X

+ d cosA

– h sinA

= Y

+ d sinA

+ h cosA

Obliczenia kontrolne możemy wykonać dwoma sposobami:

Ponownie określić współrzędne szukanego punktu, po zmianie kierunku obliczeń na
odwrotny (od B do A). Wymaga to przeliczenia wartości odciętych i zmiany znaku
rzędnych.

Obliczyć odległość AP i BP ze współrzędnych oraz z danych terenowych:

∆

)

W przypadku obliczania współrzędnych wielu punktów rzutowanych na tę samą prostą,

wskazane i wygodne jest wykonywanie obliczeń w formie tabelarycznej. Przykładową tabelę
przedstawiono poniżej.

)

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Tabela 4. Obliczenie współrzędnych punktów na domiarze prostokątnym [1, s. 91]

Domiary

prostokątne

Przyrosty

domiarów

Bok osnowy

Przyrosty

współrzędnych

Współrzędne

punktów

Oznacze

nie

punktó

Odcięta

Rzędna

odciętej

∆l

rzędnej

∆h

∆x

∆y

AB ob.l

-f

dmax

Współczynnik

Kierunkowe

cosA

sinA

∆x=

∆lcosA-

∆hsinA

∆y=

∆lsinA-

∆hcosA

Oznacze-

nie

punktów

0,00

4950,12

7251,84

+47,93

-22,47

+14,32

-186,89

+0,0763978

-0,9970657

-18,75

-49,49

47,93

-22,47

4931,37

7202,35

+30,19

+46,41

187,44

+48,59

-26,55

78,12

+23,94

4979,96

7175,80

0,00

62,94

-23,94

+0,06
±0,13

-15,52

-110,85

187,50

SUMY

187,44

0,00

+14,32

-186,89

4964,44

7064,95

Obliczenie kąta ze współrzędnych

Jeżeli dane są trzy punkty o znanych współrzędnych to można na ich podstawie obliczyć

kąt zawarty pomiędzy odcinkami opartymi na tych punktach.

Rys. 11. Zależności między wartością kąta a azymutami jego ramion [1, s. 92]

Na podstawie Rys. 11, możemy stwierdzić, że kąt β zawarty pomiędzy odcinkami CL

i CP równy jest różnicy azymutów kierunków, które są jego ramionami.

β = A

- A

Możliwe jest również obliczenie kąta ze współrzędnych na podstawie wzoru:

tgβ =

∆

•

Wykorzystując ten wzór należy zwrócić uwagę na znaki licznika i mianownika w celu

ustalenia ćwiartki i prawidłowego obliczenia wartości funkcji arc tg.

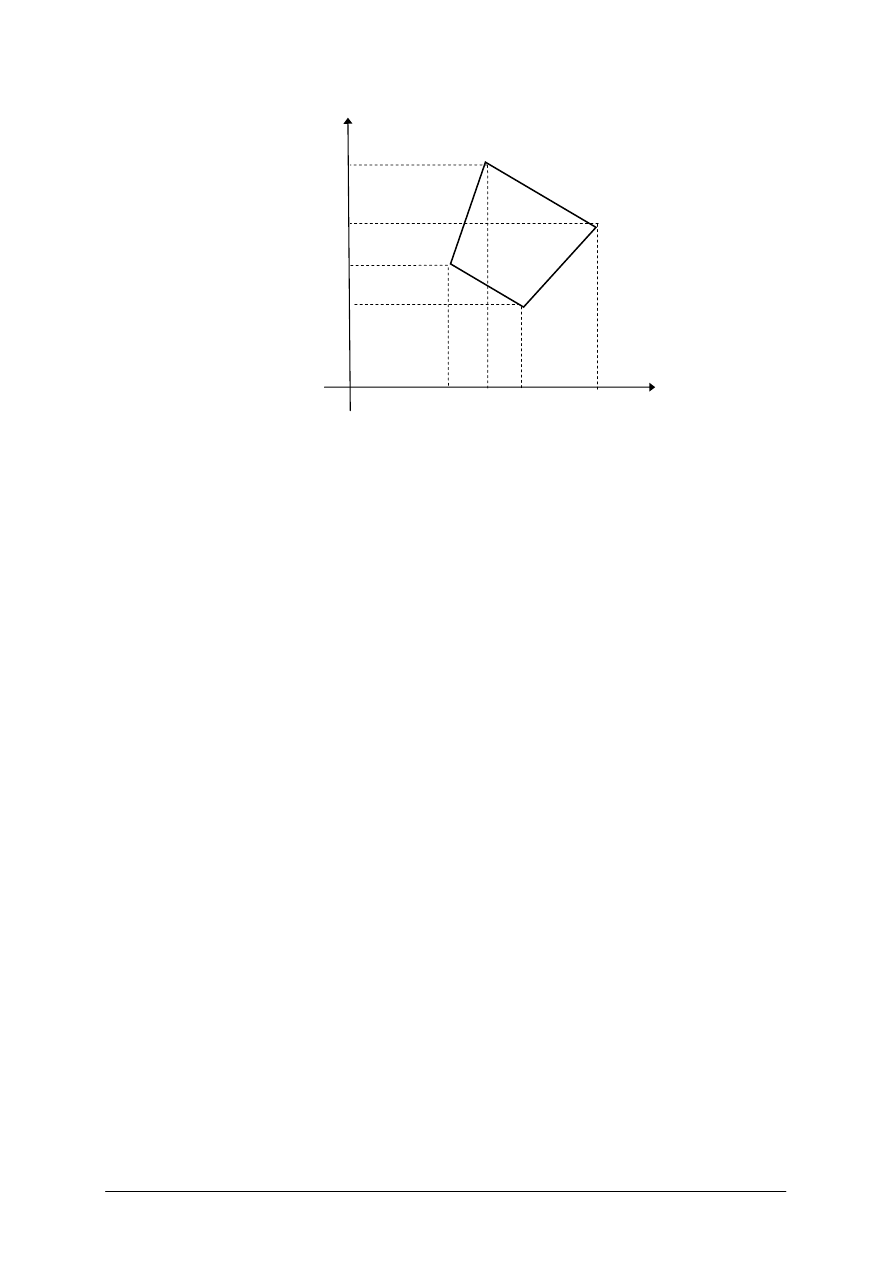
Obliczenie pola powierzchni figury ze współrzędnych

Powierzchnię czworoboku 1,2,3,4 przedstawionego na Rys. 12 możemy przedstawić jako

kombinację powierzchni trapezów.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 12. Powierzchnia wieloboku jako kombinacja powierzchni trapezów [1, s. 115]

Są to trapezy o podstawach równoległych do osi X lub o podstawach równoległych do osi

Y. Pole wieloboku można rozpatrywać jako sumę pól trapezów zawierających fragmenty
wieloboku, pomniejszoną o pola trapezów znajdujących się na zewnątrz wieloboku.
Rozpatrując trapezy o podstawach równoległych do osi X, możemy napisać:

2P = (X

+ X

)(Y

– Y

) – (X

+ X

)(Y

– Y

) – (X

+ X

)(Y

– Y

) + (X

+ X

)(Y

– Y

)

Analogicznie rozpatrując trapezy o podstawach równoległych do osi Y możemy napisać:

2P = (Y

+ Y

)(X

– X

) + (Y

+ Y

)(X

– X

) – (Y

+ Y

)(X

– X

) – (Y

+ Y

)(X

– X

)

Po odpowiednich przekształceniach i uogólnieniu oznaczeń otrzymamy wzory:

2P =

∑

i 1

)

)(Y

(

-2P =

)

)(X

(

∑

Wzory te noszą nazwę wzorów trapezowych.

Po wymnożeniu wyrażeń w nawiasach oraz dokonaniu redukcji wyrazów i uogólnieniu,

otrzymamy wzory:

2P =

∑

i 1

-2P =

∑

Podczas ustalania kierunku wzrostu wskaźnika „

i” dla obliczeń poszczególnych

iloczynów należy pamiętać, że kierunek ten powinien biec zgodnie z ruchem wskazówek
zegara, tj. (w prawo). W przypadku niezachowania tej zasady otrzymamy na podstawie
pierwszego wzoru pole ujemne a na podstawie drugiego pole dodatnie.

Kontrolę obliczenia różnic Y

i+1

– Y

i-1

oraz X

i+1

– X

i-1

stanowi warunek, że suma tych

różnic równa się zero (wielobok zamknięty):

∑

i 1

)

(

)

(

∑

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Kontrolą jest również dwukrotne obliczenie tej samej powierzchni ze wzorów 2P oraz -

2P. Otrzymane wartości powinny być takie same.

Obliczenia pośrednie różnic współrzędnych, a zwłaszcza iloczynów wchodzących

w skład sumy, nie muszą być zapisywane, lecz rejestrowane w pamięci kalkulatora.

Przy obliczaniu pola powierzchni korzystne jest utworzenie tabeli z punktami ułożonymi

po obwodzie figury zgodnie z ruchem wskazówek zegara, w postaci: nr punktu, współrzędna
X, współrzędna Y. Dla ułatwienia wyszukiwania z tabeli właściwych wartości współrzędnych,
potrzebnych do utworzenia każdego iloczynu, wygodne jest korzystanie z szablonów
z wyciętymi okienkami, przedstawionych poniżej.

Współrzędnymi prostokątnymi, które mogą być wykorzystane do obliczania pól wyżej

wymienionymi wzorami mogą być zarówno współrzędne geodezyjne X i Y jak i domiary
prostokątne z metody ortogonalnej: odcięte jako współrzędne X i rzędne jako współrzędne Y.

Należy przy tym pamiętać o właściwych znakach odciętych i rzędnych. Ujemna

współrzędna X występuje tylko, wtedy, gdy pomierzony punkt obrysu figury znajduje się na
przedłużeniu linii pomiarowej, przed jej punktem początkowym. Ujemna współrzędna Y
występuje wtedy, gdy pomierzony punkt obrysu figury znajduje po lewej stronie linii
pomiarowej.

Przykład: na rys. nr 13 przedstawiono pomiar działki wykonany metodą domiarów

prostokątnych.

Rys. 13. Pomiar działki metodą domiarów prostokątnych [2, s. 114]

Sposób obliczenia powierzchni działki zestawiono w tabeli nr 5.

Tabela 5. Obliczenie pola działki wg. danych pokazanych na rys. 13 [2, s. 116]

Współrzędne

punktów

Iloczyny

pkt

i+1

-Y

i-1

i+1

-X

i-1

i+1

- Y

i-1

) Y

i+1

-X

i-1

)

Pole obiektu

+15,40

+13,40

+19,60

-21,50

-31,10

+16,10

-589,96

-346,15

+31,50

-16,70

+30,70

+30,40

+967,05

-507,68

+50,00

+9,20

+30,10

-16,10

+1505,00

-148,12

+15,40

+13,40

-30,70

-30,40

-472,78

-407,36

+19,60

-21,50

Σ=0,00

2p=+1409,31 -2p=-1409,31

704,66m

i-1

i+1

i-1

i+1

działka 245/2

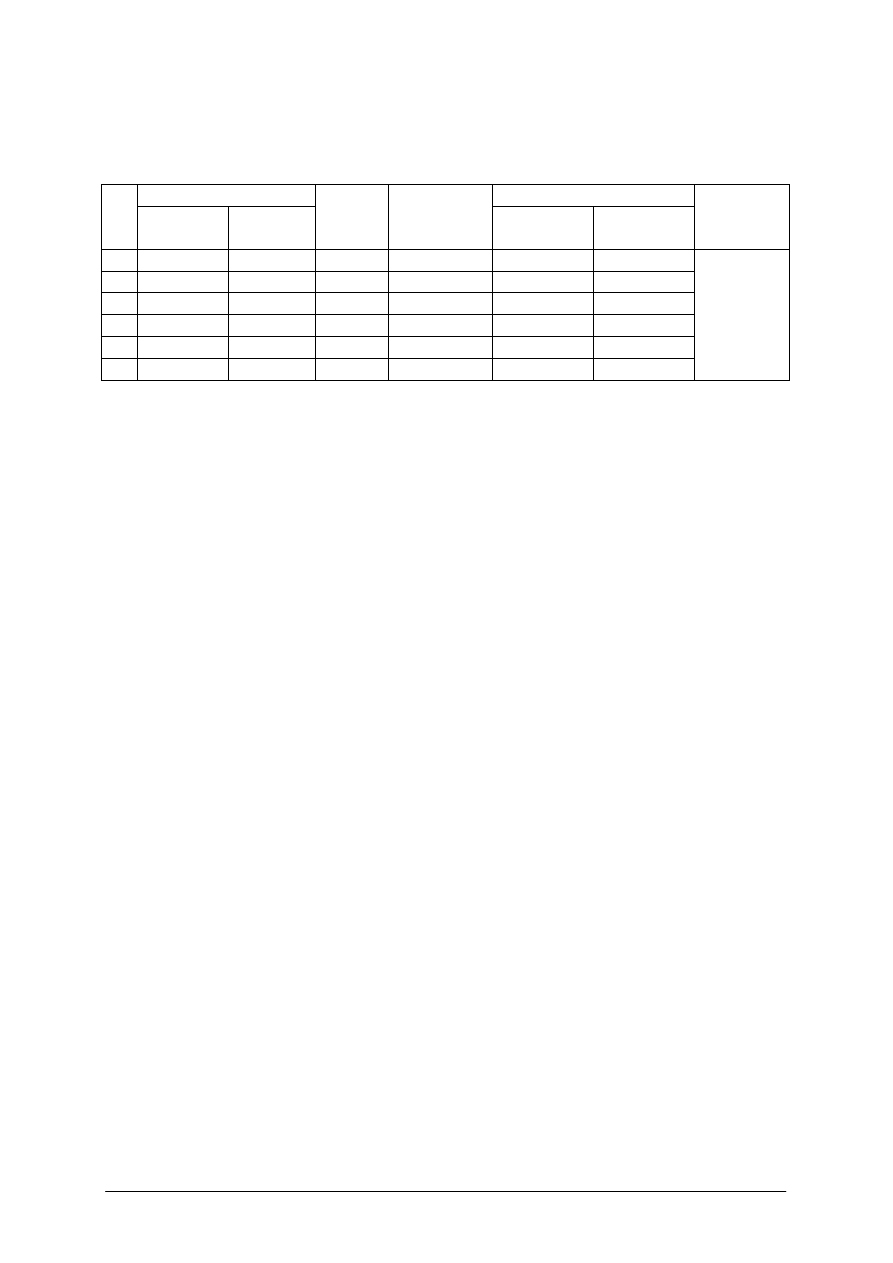
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Sposób obliczenia powierzchni działki na podstawie znanych współrzędnych zestawiono

w tabeli nr 6.

Tabela 6. Obliczenie pola działki wg. danych współrzędnych [opracowanie własne]

Współrzędne punktów

Iloczyny

Pkt

i+1

-Y

i+1

-X

i-1

i+1

- Y

i-1

)

i+1

-X

i-1

)

Pole

obiektu

136,89

623,31

121,60

778,25

+153,80

-27,67

18702,08

-21534,18

109,22

777,11

-156,10

+2,91

-17049,24

2261,39

124,51

622,15

-153,80

+27,67

-19149,64

17214,89

136,89

623,31

+156,10

-2,91

21368,53

-1813,83

121,60

778,25

Σ=0,00

2P=3871,73

-2P=-3871,73

1935,86m

Zastosowanie do obliczeń geodezyjnych programów obliczeniowych

Wszystkie podane powyżej zadania z rachunku współrzędnych można wykonać

z wykorzystaniem komputera i zainstalowanych na nim programów obliczeniowych. Spośród
popularnych programów obliczeniowych, wykorzystywanych przez geodetów, można
wymienić następujące: Geo89, C-geo, Geonet, WinKalk, GeoMap. W różnych programach te
zadania mogą być nieco inaczej nazywane, niemniej, jednak jeżeli szukamy w programie
sposobu obliczenia współrzędnych punktu na prostej lub punktu pomierzonego metodą
rzędnych i odciętych, to szukamy obliczeń lub pomiarów wykonanych metodą domiarów
prostokątnych. Jeżeli mamy obliczyć współrzędną punktu, gdy dany jest punkt zaczepienia,
azymut i długość odcinka, to szukamy obliczeń metodą biegunową, nazywaną również
w programie WinKalk tachimetrią. Obliczenie odległości, azymutu, pola powierzchni ze
współrzędnych też nie będzie trudnym zadaniem, ponieważ rozwijając zakładki w zadaniach
obliczeniowych, znajdziemy interesujące nas zadanie obliczeniowe. W przypadku obliczania
azymutu lub kąta ze współrzędnych, nie musimy ustalać w której ćwiartce znajdują się
szukane wielkości i podstawiać do obliczeń czwartaki, ponieważ program obliczeniowy zrobi
to za nas i poda nam prawidłową wielkość.

Niezależnie od tego, jaki program obliczeniowy zastosujemy, przed wykonaniem

obliczeń musimy założyć obiekt, nadając mu nazwę (najlepiej kojarzącą się nam z konkretną
pracą geodezyjną), wprowadzić do tego obiektu dane, takie jak numery i współrzędne
punktów. Zapisanie tych danych pozwoli nam wielokrotnie powracać do tego obiektu, a przy
wykonywaniu obliczeń operować numerami punktów, co przyśpieszy wykonanie pracy.

W trakcie pracy możemy wykonać (w celach kontrolnych) edycję rysunku obliczonej

konstrukcji. Po wykonaniu obliczeń, w zależności od zastosowanego programu, możemy
wykonywać wydruki raportów obliczeniowych, które będą zawierały dane, przyjęte do
obliczeń oraz wyniki.

4.3.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1. Jakie układy współrzędnych są stosowane w geodezji?
2.

Jak zorientowany jest geodezyjny układ współrzędnych prostokątnych płaskich?

Co to jest czwartak?

Przy jakich obliczeniach stosowany jest czwartak?

Jakie są rodzaje azymutów?

Na jakich zasadach nadaje się odciętym znak (+) lub (–), przy obliczaniu współrzędnych
punktu na domiarze prostokątnym?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Z jakich zależności korzysta się przy obliczaniu azymutu i długości ze współrzędnych?

Jakie wzory stosuje się przy obliczaniu pola powierzchni ze współrzędnych?

Jakie czynności należy wykonać, aby wykonać obliczenia geodezyjne przy pomocy
komputerowego programu obliczeniowego?

4.3.3. Ćwiczenia

Ćwiczenie 1

Odcinek AB oparty jest na punktach o znanych współrzędnych X

= 5000.00,

= 5000.00, X

= 4842.77, Y

= 5118.17. W oparciu o podane wartości współrzędnych

oblicz azymut odcinka AB wyrażony w gradach oraz długość tego odcinka.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

odszukać w materiale nauczania potrzebne wzory,

obliczyć przyrosty współrzędnych,

ustalić ćwiartkę azymutu,

obliczyć szukane wielkości,

wykonać obliczenia kontrolne.

Wyposażenie stanowiska pracy:

−

papier formatu A4,

−

kalkulator inżynierski.

Ćwiczenie 2

Znany jest odcinek AC o długości 123,45 m, zaczepiony w punkcie A o współrzędnych:

= 5000.00, Y

= 5000.00, zorientowany azymutem A

= 311

. Na podstawie

podanych danych oblicz współrzędne końca odcinka – punktu C.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

odszukać w materiale nauczania potrzebne wzory,

obliczyć przyrosty współrzędnych,

obliczyć szukane wartości,

wykonać obliczenia kontrolne.

Wyposażenie stanowiska pracy:

−

papier formatu A4,

−

kalkulator inżynierski.

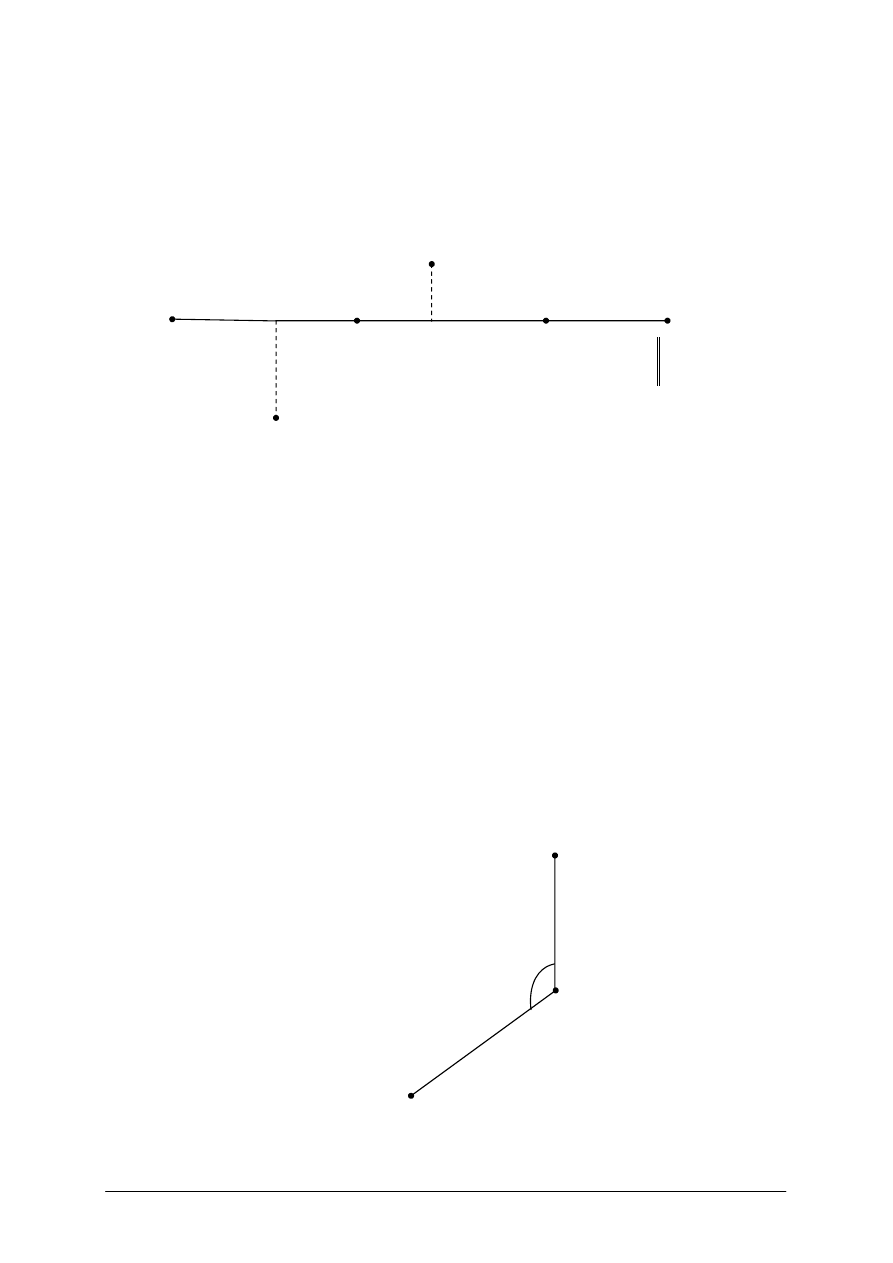
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Ćwiczenie 3

Na rysunku przedstawiono punkty pomierzone na prostej oraz metodą domiarów

prostokątnych. Oblicz współrzędne punktów 1,2,3,4.Jako współrzędne punktów A i B
przyjmij wartości: X

= 5000.00, Y

= 5000.00, X

= 4842.77, Y

= 5118.17. Obliczenia

wykonaj w formie tabelarycznej.

Rysunek do ćwiczenia 3

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

odszukać w materiale nauczania potrzebne wzory,

ułożyć tabelę do obliczeń współrzędnych punktów na domiarach prostokątnych,

określić współczynniki kierunkowe,

określić znaki dla domiarów,

obliczyć współrzędne pomierzonych punktów,

wykonać obliczenia kontrolne.

Wyposażenie stanowiska pracy:

−

papier formatu A4,

−

kalkulator inżynierski.

Ćwiczenie 4

Odcinki LC i CP zaczepione są we wspólnym punkcie C (Rys.). Znając współrzędne

punktów LCP oblicz kąt α (wyrażony w gradach), zawarty między odcinkiem CL i CP. Dane
współrzędne punktów:
Punkt L:

X = 4325.00,

Y = 6467.00

Punkt C:

X = 4416.00,

Y = 6560.00

Punkt P:

X = 4444.00,

Y = 6560.00

Rysunek do ćwiczenia 4

↑

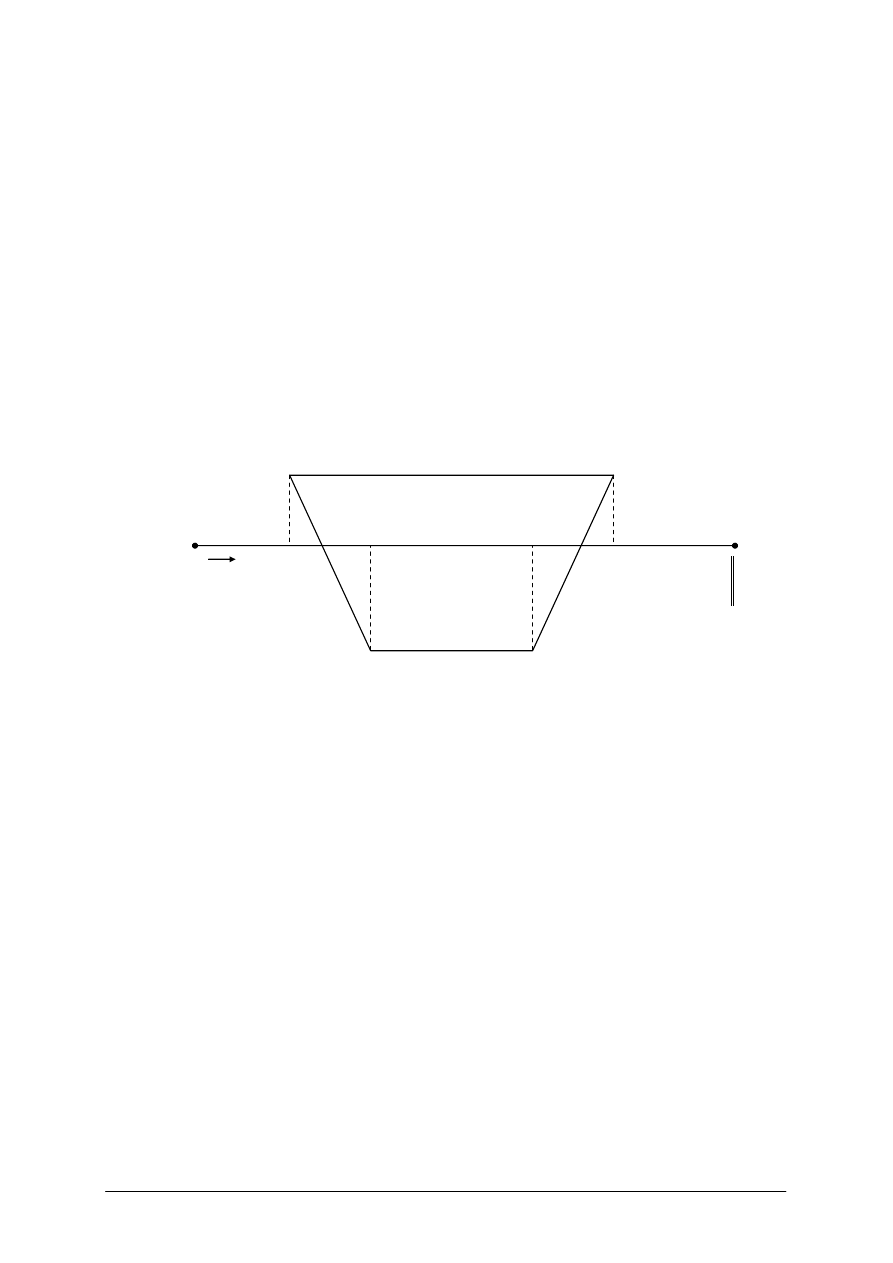
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) odszukać w materiale nauczania potrzebne wzory,
2) obliczyć azymuty ramion kąta,
5)

obliczyć kąt z różnicy azymutów,

wykonać jako kontrolę obliczenie kąta ze współrzędnych wg. odpowiedniego wzoru
kontrolnego, zwracając uwagę na znak licznika i mianownika.

Wyposażenie stanowiska pracy:

−

papier formatu A4,

−

kalkulator inżynierski.

Ćwiczenie 5

Wykorzystując miary z pomiaru metodą domiarów prostokątnych oblicz powierzchnię

figury ograniczonej punktami1, 2, 3, 4.

Rysunek do ćwiczenia nr 5

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

odszukać w materiale nauczania potrzebne wzory,

ułożyć tabelę do obliczenia pola powierzchni na podstawie rzędnych i odciętych,

określić znaki domiarów ,

przyjąć odcięte i rzędne jako współrzędne punktów do obliczenia powierzchni figury,

obliczyć powierzchnię figury 1,2,3,4,

wykonać obliczenia kontrolne.

Wyposażenie stanowiska pracy:

−

papier formatu A4,

−

kalkulator.

..6

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Ćwiczenie 6

Znane są współrzędne punktów granicznych działki.

punktu

153.42

608.99

138.51

606.87

124.51

622.15

109.22

777.11

136.45

779.62

W podanym wykazie punkty ułożone są kolejno po obwodnicy, zgodnie z ruchem

wskazówek zegara. Na podstawie podanych wartości współrzędnych oblicz powierzchnię
działki.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

odszukać w materiale nauczania potrzebne wzory,

wykonać szablon, przydatny do obliczenia powierzchni ze współrzędnych,

obliczyć pole powierzchni działki wykorzystując wykonany szablon,

wykonać obliczenia kontrolne.

Wyposażenie stanowiska pracy:

−

papier formatu A4,

−

kalkulator.

Ćwiczenie 7

Wykorzystując komputer i dostępny program do obliczeń geodezyjnych, wykonaj zadania

opisane w ćwiczeniach 1 - 6, przyjmując te same dane.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

przestrzegać zasad bezpieczeństwa koniecznych przy pracy z komputerem,

odszukać odpowiednie zadanie w programie obliczeniowym,

wprowadzić konieczne dane do wykonania obliczeń,

ustawić o ile to konieczne odpowiednie jednostki w programie,

wykonać niezbędne obliczenia,

porównać uzyskane wyniki z obliczonymi bez pomocy komputera.

Wyposażenie stanowiska pracy:

–

papier formatu A4,

–

komputer,

–

program do obliczeń geodezyjnych zainstalowany na komputerze.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.3.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

zdefiniować pojęcie azymutu kierunku?

zdefiniować pojęcie czwartaka?

obliczyć azymut kierunku ze współrzędnych?

obliczyć długość odcinka ze współrzędnych?

obliczyć współrzędną punktu na prostej i na domiarze prostokątnym?

obliczyć wartość kąta ze współrzędnych?

obliczyć pole powierzchni figury ze współrzędnych?

wykonać

obliczenia

zakresu

rachunku

współrzędnych,

wykorzystując oprogramowanie komputerowe?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

SPRAWDZIAN OSIĄGNIĘĆ

INSTRUKCJA DLA UCZNIA

Przeczytaj uważnie instrukcję.

Podpisz imieniem i nazwiskiem kartę odpowiedzi.

Zapoznaj się z zestawem zadań testowych.

Test zawiera dwadzieścia trzy zadania. Do każdego zadania dołączone są cztery
możliwości odpowiedzi. Tylko jedna jest prawidłowa.

Udzielaj odpowiedzi na załączonej karcie odpowiedzi stawiając w odpowiedniej rubryce
znak „X”. W przypadku pomyłki należy błędną odpowiedź zaznaczyć kółkiem a
następnie ponownie zakreślić odpowiedź prawidłową.

Zadania wymagają stosunkowo prostych obliczeń, które powinieneś wykonać przed
wskazaniem poprawnego wyniku.

Pracuj samodzielnie, bo tylko wtedy będziesz miał satysfakcję z wykonanego zadania.

Jeżeli udzielanie odpowiedzi będzie sprawiało Ci trudność, wtedy odłóż jego rozwiązanie
na później i wróć do niego, gdy zostanie Ci wolny czas.

Po zakończeniu testu podnieś rękę i zaczekaj aż nauczyciel odbierze od Ciebie pracę.

10.

Na rozwiązanie testu masz 80 minut.

Powodzenia!

ZESTAW ZADAŃ TESTOWYCH

1. Geodezja jako nauka zajmuje się

budową wnętrza Ziemi.

określeniem wymiarów i kształtu Ziemi.

budową geologiczną Ziemi.

badaniem jądra Ziemi.

Jako jeden z pierwszych pomiary i obliczenia kształtu Ziemi wykonywał

Tales z Miletu.

Pitagoras.

Erastostenes.

Galileusz.

Układ współrzędnych geodezyjnych różni się od układu współrzędnych matematycznych
a)

położeniem osi X i Y oraz kierunkiem liczenia kątów.

promieniem wodzącym i kierunkiem liczenia kątów.

kierunkiem osi pionowej, która jest zgodna z kierunkiem południka magnetycznego.

oznaczeniem osi: H i Z.

Podział gradowy polega na podziale kąta pełnego na
a)

100 części.

360 części.

400 części.

1000 części.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Kąt wyrażony w mierze stopniowej wynosi: 259°16'25". Ten sam kąt wyrażony w gradach
ma wielkość
a)

288

289

295

Kąt wyrażony w mierze gradowej ma wielkość 135

. Ten sam kąt wyrażony

w mierze stopniowej ma wielkość
a)

121°58'34".

164°56'24".

125°13'26".

121°48'14".

Skala mapy oznacza
a)

wielkość arkusza, na którym wykreślona jest mapa.

wielkość terenu objętego mapą.

stosunek długości odcinka na mapie do długości rzutu poziomego tego odcinka
w terenie.

odległość pionową między warstwicami.

Podziałka poprzeczna (transwersalna) jest stosowana do
a)

pomiaru i odkładania odległości na mapie.

podziału odcinka na równe części.

sprawdzania prawidłowości naniesienia podziału na taśmach geodezyjnych.

nanoszenia siatki kwadratów na mapach.

Na mapie o nieznanej skali 1:M

oraz na mapie w skali 1:5000 zidentyfikowano

i pomierzono ten sam odcinek terenowy, otrzymując wynik: d

= 46,2 mm, i d

38,8 mm. Nieznany mianownik skali - M

1000.

2000.

2880.

4199.

10.

Ta terenach byłego zaboru rosyjskiego można się spotkać ze skalą mapy
a)

1:2000.

1:2880.

1:4200.

1:5000.

11.

Na mapie w skali 1:500 pomierzono odcinek o długości 125.3 mm. W terenie odpowiada
mu odcinek o długości
a)

62.65 m.

105.30 m.

125.30 m.

626.50 m.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

12.

Odcinek łączący dwa punkty geodezyjnej sieci pomiarowej o znanych współrzędnych ma
długość: 201.60 m. Po naniesieniu tych punktów na mapę w skali 1:2000, ten sam odcinek
będzie miał na mapie długość
a)

100.8 mm.

151.1 mm.

201.6 mm.

403.2 mm.

13 Dany jest odcinek oparty na punktach A i B o znanych współrzędnych: X

= 100.00,

= 100.00, XB= 50.00, Y

= 50,00. Prawidłowa wartość azymutu odcinka AB wyrażona

w gradach to
a)

150

250

350

14. Dany jest odcinek oparty na punktach A i B o znanych współrzędnych: X

= 100.00,

= 100.00, XB= 50.00, Y

= 50,00, prawidłowa długość odcinka AB to

50.71 m.

70.07 m.

70,71 m.

107.71 m.

15. Od punktu A o współrzędnych X

= 100.00, Y

= 100.00, odmierzono odcinek o długości

110.00 m i azymucie: 335

. Współrzędne końca odcinka będą miały wartość

X = 107.47, Y = 56.21.

X = 160.00, Y = 150.00.

X = 160.00, Y = 56.21.

X = 107.47, Y = 6.21.

16. Na odcinek oparty na punktach A i B o znanych współrzędnych: X

= 100.00,

= 100.00, XB= 50.00, Y

= 50,00, wtyczono punkt D w odległości 50.00 m od punktu

A. Prawidłowa wartość współrzędnych punktu D to
a)

X = 54.64, Y = 136.56.

X = 64.64, Y = 64.64.

X = 34.34, Y = 36.36.

X = 164.64, Y = 136.35.

17. Podczas obliczania współrzędnych punktów pomierzonych metodą domiarów

prostokątnych, odcięte pomierzonych punktów przyjmuje się ze znakiem (-), w przypadku,
gdy punkt znajduje się
a)

na prawo od prostej.

na lewo od prostej.

na przedłużeniu prostej, za punktem końcowym.

na przedłużenie prostej, przed punktem początkowym.

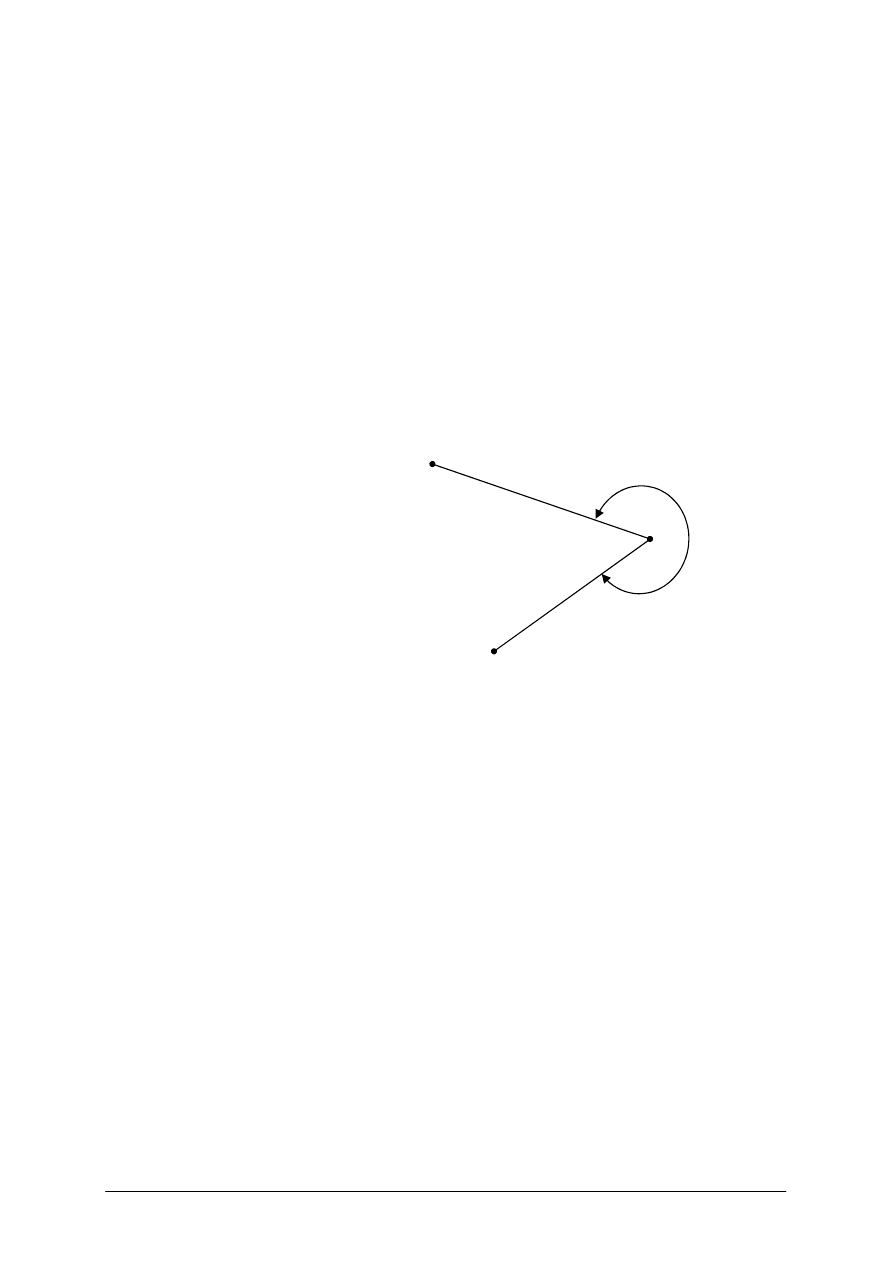
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

18. Na linię pomiarową poprowadzoną przez punkty A i B o znanych współrzędnych:

= 100.00, Y

= 100.00, XB= 50.00, Y

= 50,00, zrzutowano punkt E, otrzymując

wartości: odcięta d = 25.00 m, rzędna h = -15.00 m. Przyjmując, że odcinek jest
zorientowany A→B oraz podane dane, właściwe współrzędne punktu E to

X = 93.93, Y = 128.28.

X = 71.72, Y = 107.07.

X = 71.72, Y = 92.93.

X = 100.00,Y = 135.36.

19. Czwartakiem nazywamy

azymut kierunku znajdującego się w IV ćwiartce.

kąt zawarty pomiędzy południkiem magnetycznym i geograficznym.

kąt zawarty pomiędzy południkiem geograficznym i topograficznym.

kąt ostry zawarty pomiędzy osią X a danym kierunkiem.

20. Znane są odcinki LF i FP zaczepione we wspólnym punkcie F.(Rys.) Współrzędne

punktów mają wartości:

L: X = 200.00, Y = 100.00

F: X = 150.00, Y = 150.00

P: X = 100.00, Y = 100.00.

Rysunek do zadania nr 20

Przyjmując oznaczenia zgodne z rysunkiem oraz podane wartości współrzędnych, kąt

wyrażony w gradach będzie miał wartość

275

300

335

350

21. Warstwica jest to linia

oddzielająca warstwy gleby na profilu glebowym.

łącząca na mapie punkty o tym samym azymucie.

łącząca punkty na mapie o tej samej wysokości względem przyjętego poziomu
odniesienia.

łącząca punkty na mapie o tej samej wartości współrzędnej X lub Y.

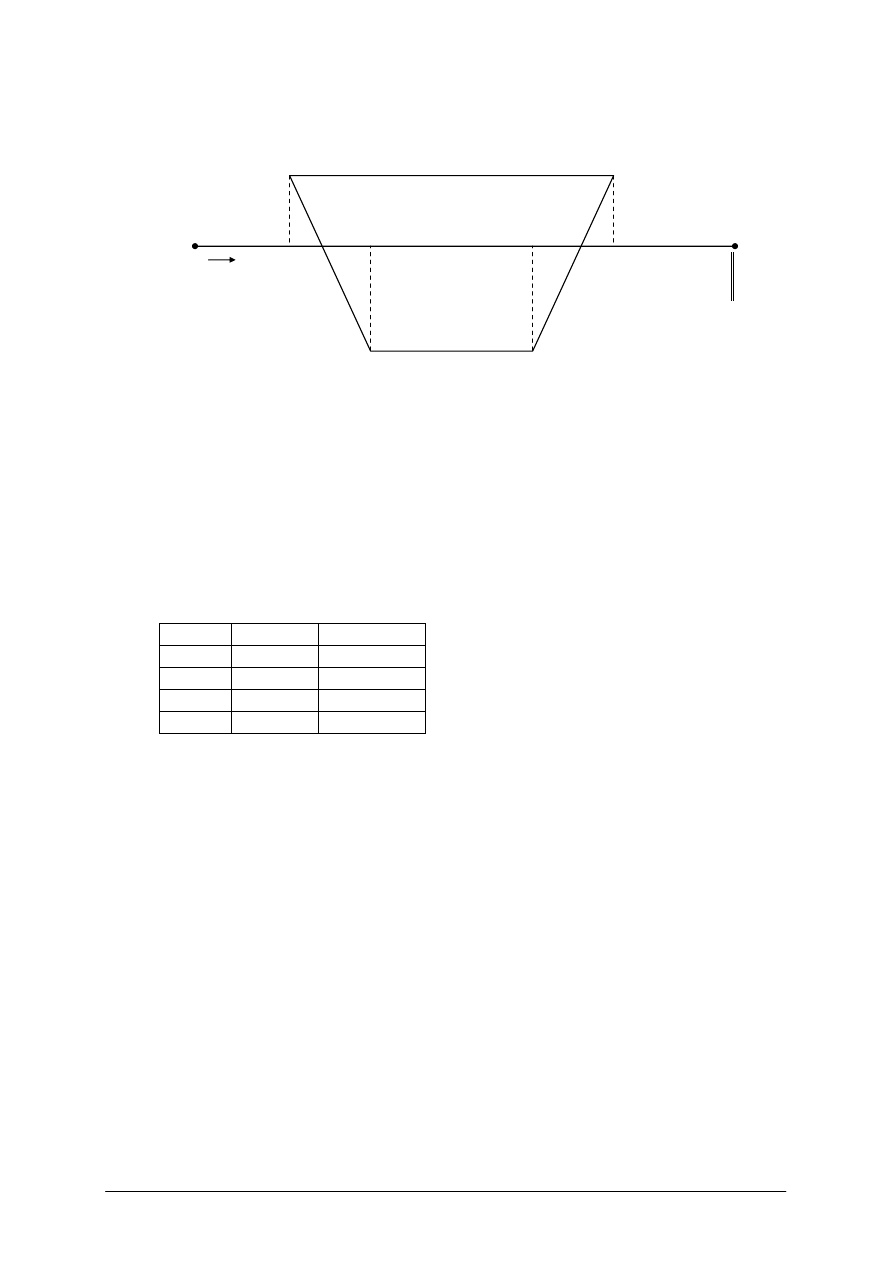
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

22. Metodą domiarów prostokątnych pomierzono punkty graniczne działki przedstawionej na

rysunku.

Rysunek do zadania 22

Pole powierzchni pomierzonej w ten sposób działki ma wartość

3100 m

3110 m

3112 m

3118 m

23.

Pomierzono położenie i obliczono współrzędne punktów granicznych działki. Punkty
położone na obwodnicy działki mają wartości współrzędnych:

136,89

623,31

121,60

778,25

109,22

777,11

124,51

622,15

Przyjmując, że punkty ułożone są po obwodnicy działki zgodnie z kierunkiem ruchu

wskazówek zegara, pole powierzeni działki ma wartość

1926 m

1936 m

1946 m

1956 m

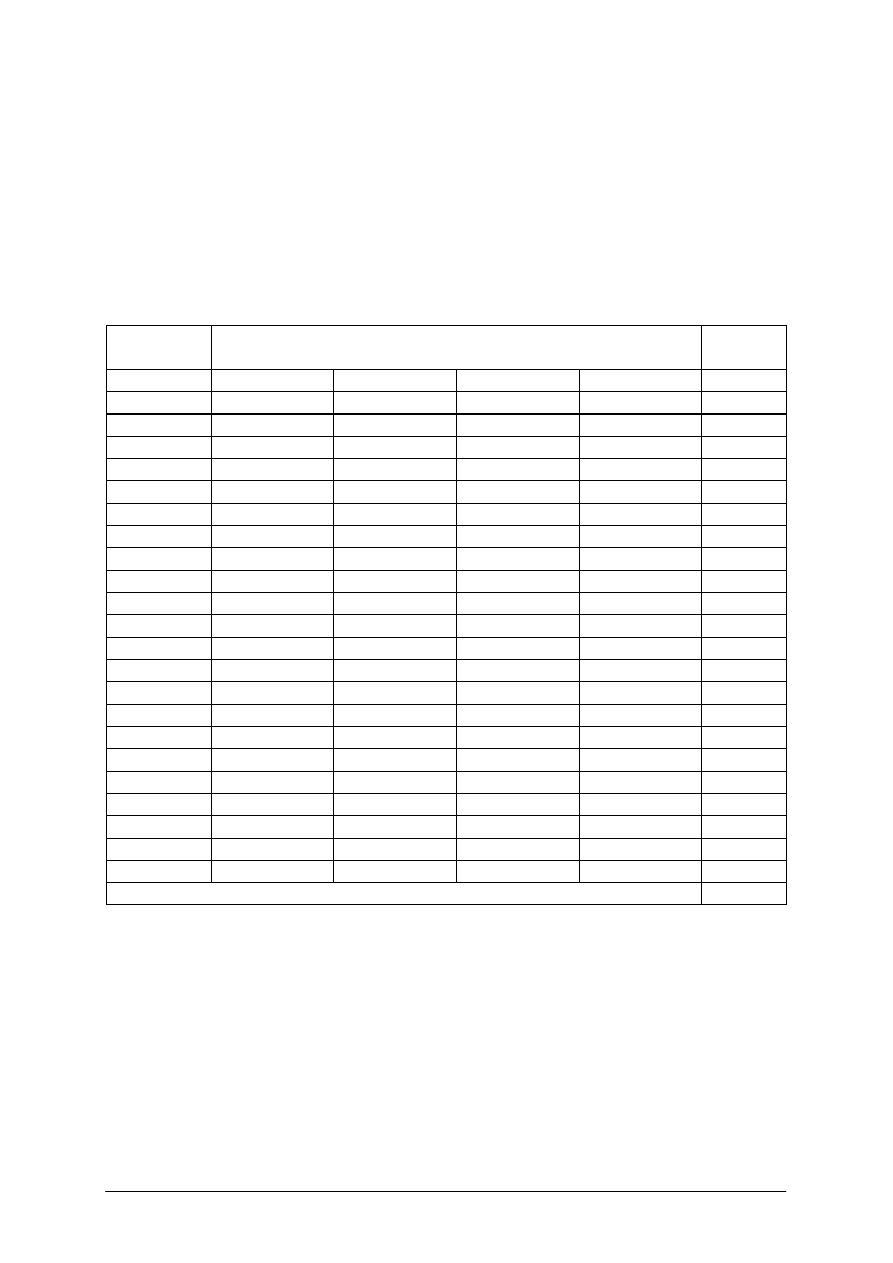
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

KARTA ODPOWIEDZI

Imię i nazwisko:..........................................................................................

Posługiwanie

się

jednostkami

miar,

skalą

oraz

współrzędnymi

geodezyjnymi

Zakreśl poprawną odpowiedź.

zadania

Odpowiedź

Punkty

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

Razem:

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

LITERATURA

Jagielski A.: Geodezja I, Wydawnictwo P.W. „Stabil” Kraków 2002

Przywara J.: www.geoforum /geodezja/ od katastru do

Przywara J.: www.geoforum /geodezja/w Polsce

Szeliga K.: www.geoforum /geodezja/ wprowadzenie do geodezji

Ząbek J.: Geodezja I, Oficyna, Wydawnicza Politechniki Warszawskiej, Warszawa 2003

Ząbek J.: Ćwiczenia z geodezji I, Państwowe Wydawnictwo Naukowe 1984