1. Źródła pola

Pole grawitacyjne

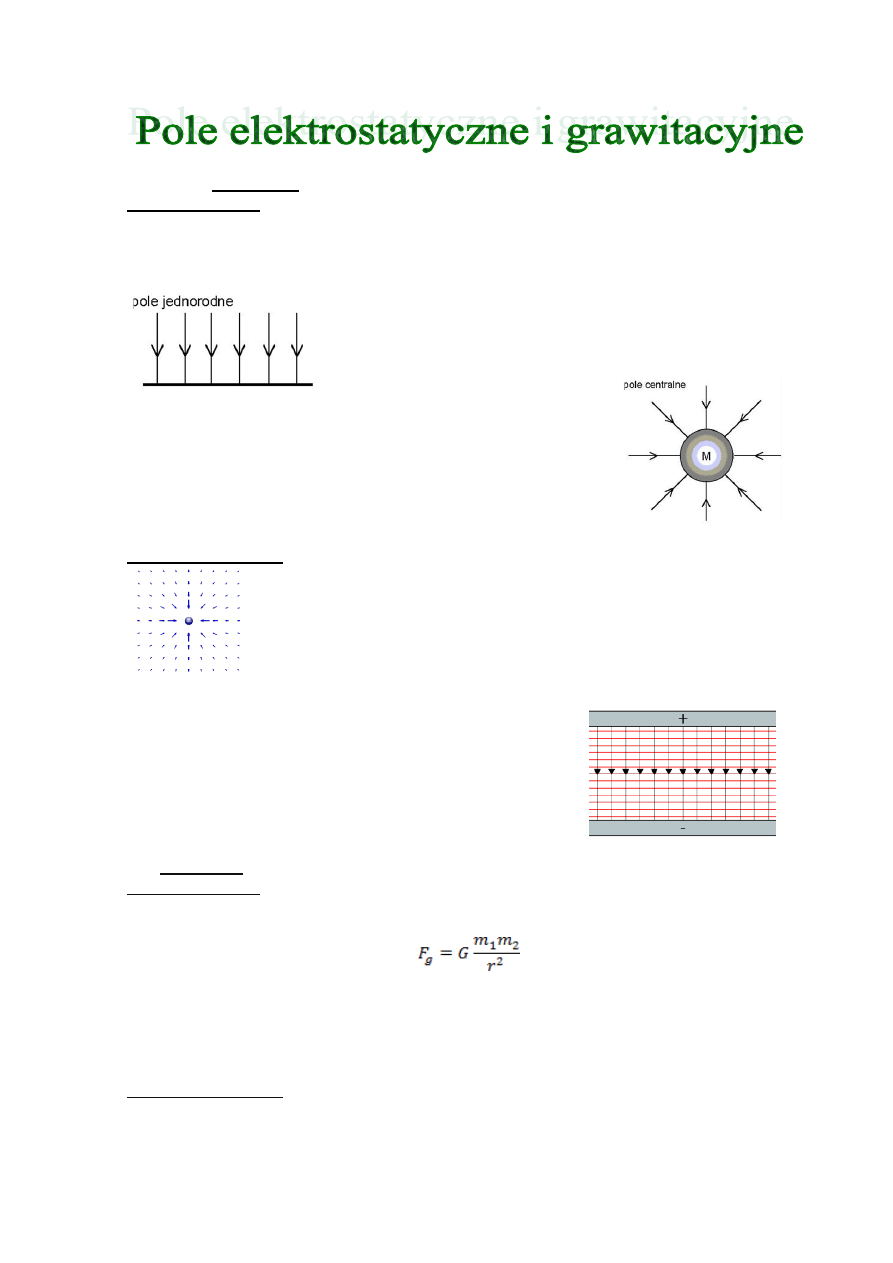
Źródłem pola grawitacyjnego jest obiekt posiadający masę. W zależności od warunków

zagadnienia rozpatruje się pole grawitacyjne jako pole jednorodne lub jako pole centralne.

Dla niezbyt dużych wysokości i niezbyt dużych odległości (znacznie mniejszych od

promienia Ziemi) można przyjąć, że pole grawitacyjne Ziemi,
w rozpatrywanym obszarze, jest jednorodnym polem o
kierunku pionowym i zwrocie w dół. Wówczas za poziom
odniesienia można przyjąć dowolny punkt. Wszystkie punkty
na tej samej wysokości mają energię
równą zero, powierzchnię tę nazywa

się powierzchnią Ziemi.

Dla dużych wysokości i dużych odległości (większych od

promienia Ziemi) można przyjąć, że pole grawitacyjne Ziemi , jest
centralnym polem o kierunku i zwrocie do środka obiektu. Za
poziom

odniesienia

najwygodniej

jest

wówczas

przyjąć

nieskończoność, gdzie siła oddziaływania wynosi 0.

Pole elektrostatyczne

Źródłem pola elektrostatycznego (elektrycznego) są ładunki

elektryczne, naładowane dodatnio (+) lub ujemnie (-). W zależności od
warunków zagadnienia rozpatruje się pole elektrostatyczne jako pole

jednorodne lub jako pole centralne.

Pole elektrostatyczne jest polem centralnym, gdy w polu o ładunku

dodatnim linie zbiegają się do centrum, w polu o ładunku ujemnym linie

te maja przeciwny zwrot. Obrazuje to rysunek po  lewej
stronie.

Natomiast pole elektryczne może też być polem

jednorodnym, jest to rodzaj oddziaływania na odległość. Linie
w tym polu są równoległe a ich zwrot jest zawsze skierowany od
ładunku naładowanego dodatnio (+) do ładunku naładowanego
ujemnie (-) (tak jak na rysunku).

2.

Siła w polu

Pole grawitacyjne

W polu grawitacyjnym działają tylko siły przyciągania grawitacyjnego i są one słabe w

porównaniu do przyciągania elektrostatycznego.

gdzie:
F

g

- siła grawitacji;

G- stała grawitacyjna;
m

1

i m

2

– masy ciał przyciąganych przez siebie;

r-

odległość od środka masy źródła pola grawitacyjnego(m

1

) do przyciąganego obiektu (m

2

)

Pole elektrostatyczne

W polu elektrycznym występują siły przyciągania (przy ładunkach różnoimiennych (+ i

-)) oraz odpychania (przy ładunkach jednoimiennych (+ i + lub - i -)) i są one silne.

Prawo Columba:

;

gdzie:
F

e

- siła elektrostatyczna

k- stała oddziaływania elektrostatycznego
q

1

i q

2

- ładunki

r – odległość między ładunkami

3. Wielkości opisujące pole

Pole grawitacyjne

Pole grawitacyjne opisuje się poprzez:

 podanie natężenia pola grawitacyjnego γ, czyli siły F działającej na masę

jednostkową m:

Pole elektrostatyczne

Pole elektrostatyczne opisuje się poprzez:



podanie natężenia pola elektrycznego (i niekiedy samo jest nazywane krótko

polem elektrycznym). Jest to pole wektorowe

, zdefiniowane w danym

punkcie pola jako stosunek siły

wywieranej przez pole na ładunek próbny q

umieszczony w tym punkcie do wartości tegoż ładunku q:

 podanie potencjału pola elektrycznego. Potencjał jest polem skalarnym ,

zdefiniowane w każdym punkcie pola elektrycznego jako stosunek energii
potencjalnej E

p

ładunku próbnego q umieszczonego w tym punkcie, do wartości

tegoż ładunku q:

 poprzez podanie energii pola elektrostatycznego. Energia jest równa pracy

potrzebnej do ułożenia układu ładunków wytwarzających dane pole elektryczne,
można więc stwierdzić, że energia potencjalna układu ładunków jest
równoważna energii w wytworzonym przez nie polu elektrycznym. Gęstość
energii pola elektrycznego (energia zawarta w jednostce objętości) wyraża się
przez:

gdzie:

- przenikalność elektryczna próżni,

- natężenia pola elektrycznego

4. Praca i energia

Pole grawitacyjne
Pole jednorodne- praca

Pracę w polu jednorodnym obliczamy ze
wzoru:

W

z

=

r

gdzie: W

z

– praca siły zewnętrznej.

Praca siły grawitacji W

g

= –W

z

.

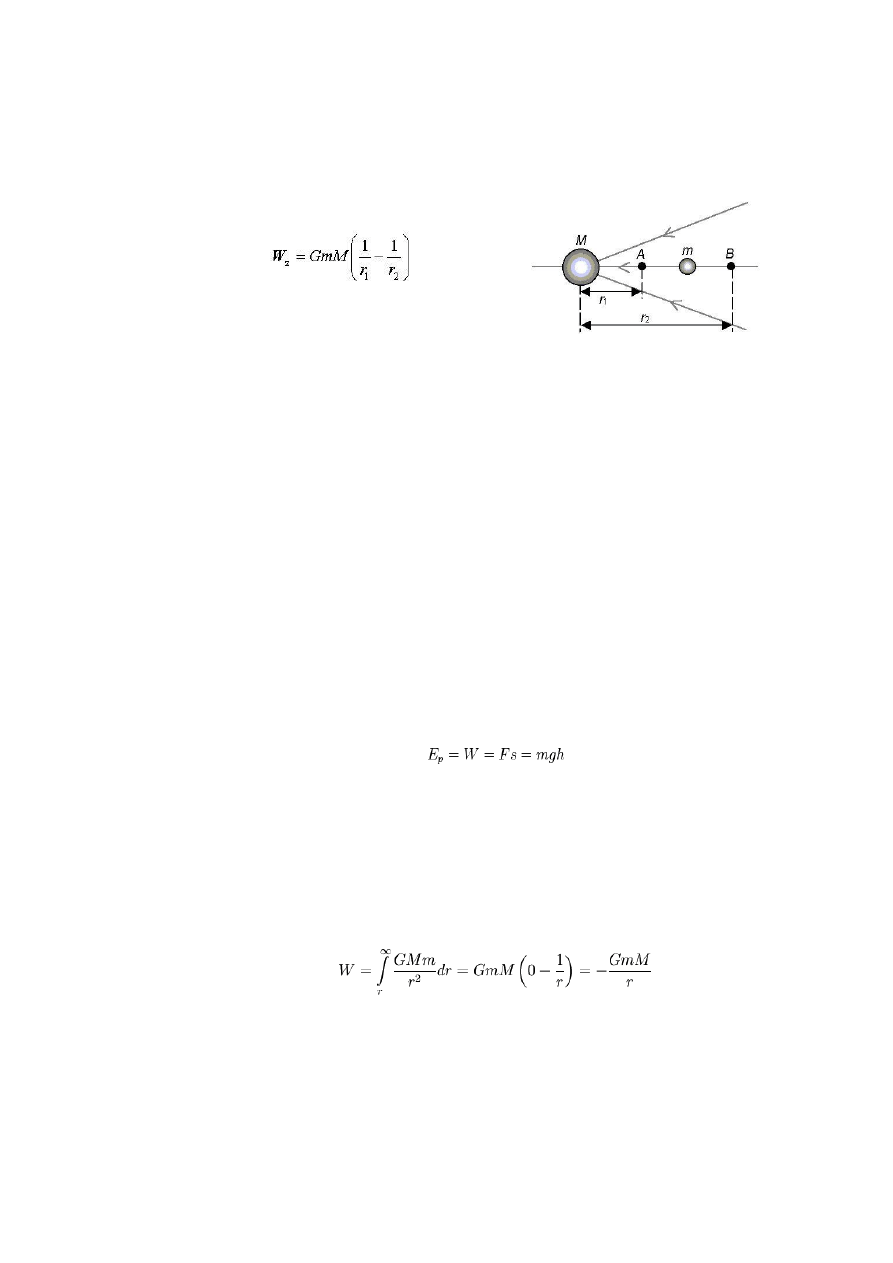
Praca wykonana przez siłę zewnętrzną na drodze AB równa jest pracy

wykonanej przez tę siłę na drodze AC (praca zależy tylko od przemieszczenia

ciała mierzonego wzdłuż linii pola).

Pole centralne - praca

Pracę w polu centralnym obliczamy ze
wzoru:

Praca w polu centralnym, podobnie jak w
polu jednorodnym, nie zależy od drogi, a
jedynie od przemieszczenia mierzonego wzdłuż linii pola. Dzięki tej własności
pole grawitacyjne jest polem zachowawczym.

Ogólny wzór na pracę w polu grawitacyjnym przy przemieszczaniu ciała o masie

m między punktami A i B pola grawitacyjnego:

W = m (V

B

– V

A

)

Pole jednorodne – energia

Dla niezbyt dużych wysokości i niezbyt dużych odległości (znacznie mniejszych
od promienia Ziemi) można przyjąć, że pole grawitacyjne Ziemi, w
rozpatrywanym obszarze, jest jednorodnym polem o kierunku pionowym i
zwrocie w dół. Wówczas za poziom odniesienia można przyjąć dowolny punkt.
Wszystkie punkty na tej samej wysokości mają energię równą zero,
powierzchnię tę nazywa się powierzchnią Ziemi. Przyrost energii potencjalnej
grawitacji ciała jest równy pracy siły zewnętrznej, wykonanej przy jego
podnoszeniu na wysokość h.
Energia potencjalna grawitacji ciała o masie m umieszczonego na wysokość h
nad poziom odniesienia (poziom ziemi) jest równa iloczynowi masy,
przyspieszenia ziemskiego g i wysokości

Pole centralne – energia

W zagadnieniach, w których trzeba rozpatrywać zmiany energii grawitacyjnej w
skali porównywalnej do odległości od źródeł grawitacji (np. w lotach
kosmicznych, oddziaływaniach międzyplanetarnych), trzeba uwzględnić
niejednorodność pola grawitacyjnego. Za poziom odniesienia najwygodniej jest
wówczas przyjąć nieskończoność, gdzie siła oddziaływania wynosi 0.
Wyrażenie na pracę potrzebną do przeniesienia obiektu z pewnego punktu
odległego o r od środka masy M do nieskończoności można wyznaczyć
obliczając całkę

gdzie:
r – odległość od środka masy źródła pola grawitacyjnego do przyciąganego obiektu [m],
G – stała grawitacyjna [N·m²·kg

–2

],

M – masa źródła pola grawitacyjnego [kg],
m – masa przenoszonego ciała [kg].

Za poziom odniesienia przyjęta została nieskończoność, z czego wynika, że w
nieskończoności energia potencjalna jest równa zero. Zatem w położeniu
początkowym energia potencjalna, która rośnie w trakcie przenoszenia, ma
wartość

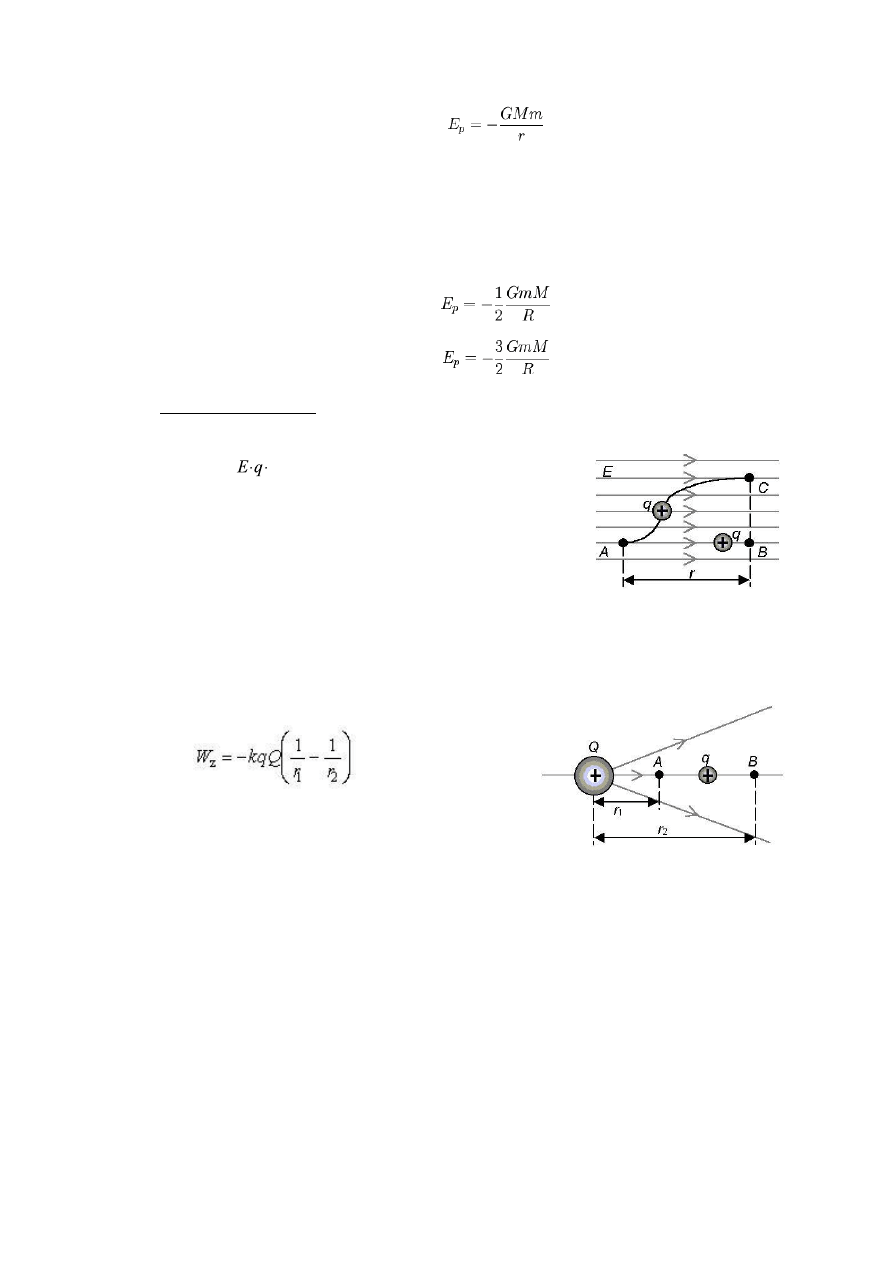
Wzór ten jest prawdziwy dla sytuacji, gdy źródłem pola grawitacyjnego jest
masa punktowa. Pozostaje prawdziwy również dla kuli o symetrycznym
rozkładzie masy, ale tylko na zewnątrz tej kuli.
Dla ciała znajdującego się w jednorodnej kuli siła grawitacji zależy tylko od
masy zawartej w części kuli od środka do danego ciała. W tej sytuacji,
przyjmując że na powierzchni kuli energia jest równa 0, energia potencjalna
osiąga w środku wartość:

A względem nieskończoności:

Pole elektrostatyczne

Pole jednorodne - praca

Pracę w polu jednorodnym obliczamy ze wzoru:
W

Z

= –

r

gdzie: W

z

– praca siły zewnętrznej.

Praca siły pola W

g

= –W

z

.

Praca wykonana przez siłę zewnętrzną na drodze AB
jest równa pracy wykonanej przez tę siłę na drodze
AC (praca zależy tylko od wartości przemieszczenia ładunku q wzdłuż linii pola, a
nie zależy od długości toru).

Pole centralne – praca
Pracę w polu centralnym obliczamy ze wzoru:

Praca w polu centralnym, podobnie jak w
polu jednorodnym, nie zależy od drogi, a
jedynie od wartości przemieszczenia ładunku q, mierzonego wzdłuż linii pola.
Pole elektrostatyczne jest polem zachowawczym

Ogólny wzór na pracę w polu elektrostatycznym przy przemieszczaniu ładunku

q między punktami A i B pola elektrostatycznego:

W = q (V

B

– V

A

)

Napięcie elektryczne U to różnica potencjałów pomiędzy dwoma punktami pola

elektrycznego:

U = V

B

– V

A

Pracę w polu elektrycznym można więc obliczać ze wzoru:

W = qU

Energia w polu elektrostatycznym
Energię potencjalna w polu elektrostatycznym obliczamy ze wzoru:

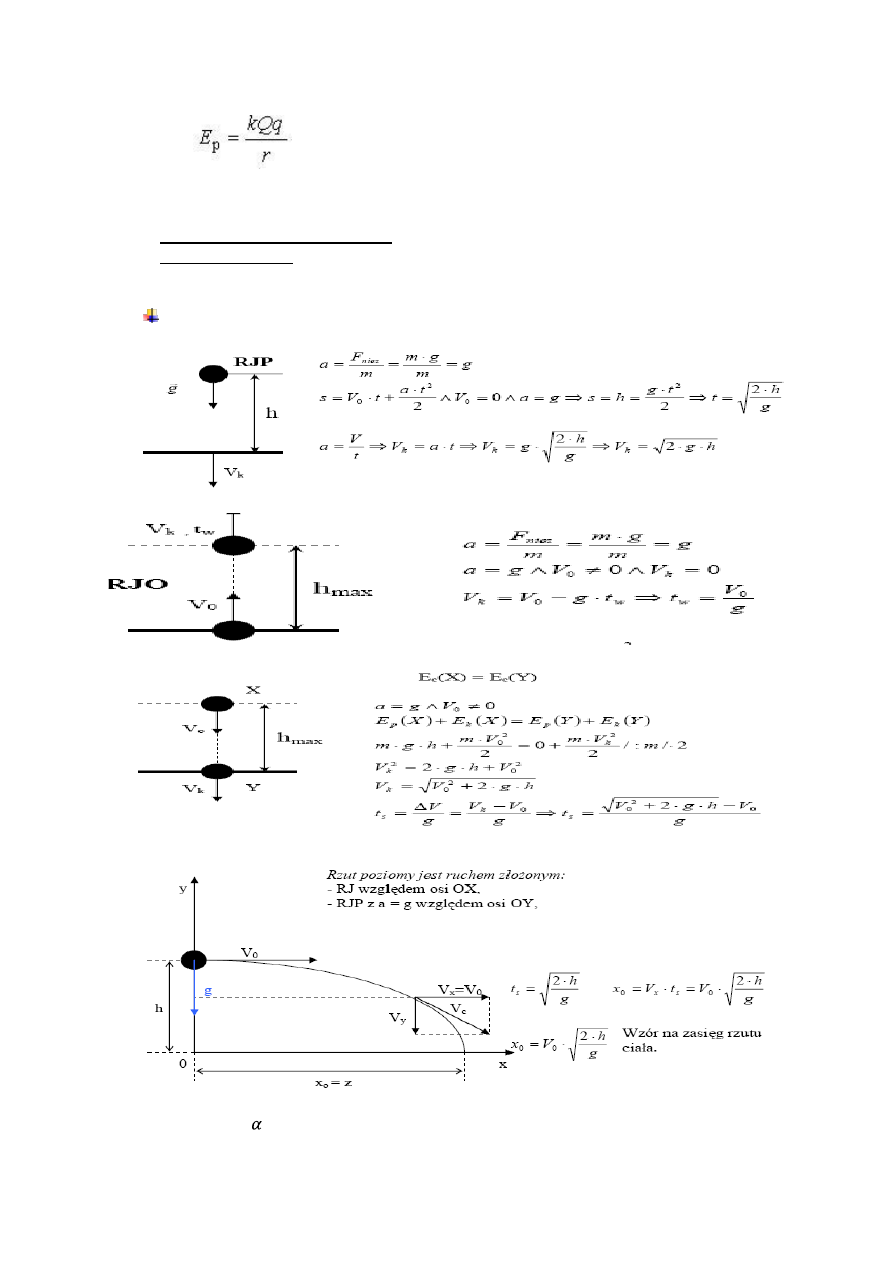
gdzie: r – odległość ładunku q od ładunku źródłowego Q.
Jeżeli ładunki q i Q są jednoimienne, to E

p

> 0; dla ładunków różnoimiennych E

p

< 0

5. Ruch masy lub ładunku w polu

Pole grawitacyjne

W polu grawitacyjnym występuje ruch niejednostajnie przyspieszony (przy
uwzględnieniu oporu ośrodka).

Ruch ciał w polu grawitacyjnym:

 Spadanie swobodne

 Rzut pionowy do góry

 Rzut pionowy w dół

 Rzut poziomy – ruch następujący po nadaniu ciału prędkości początkowej V

0

w

kierunku poziomym

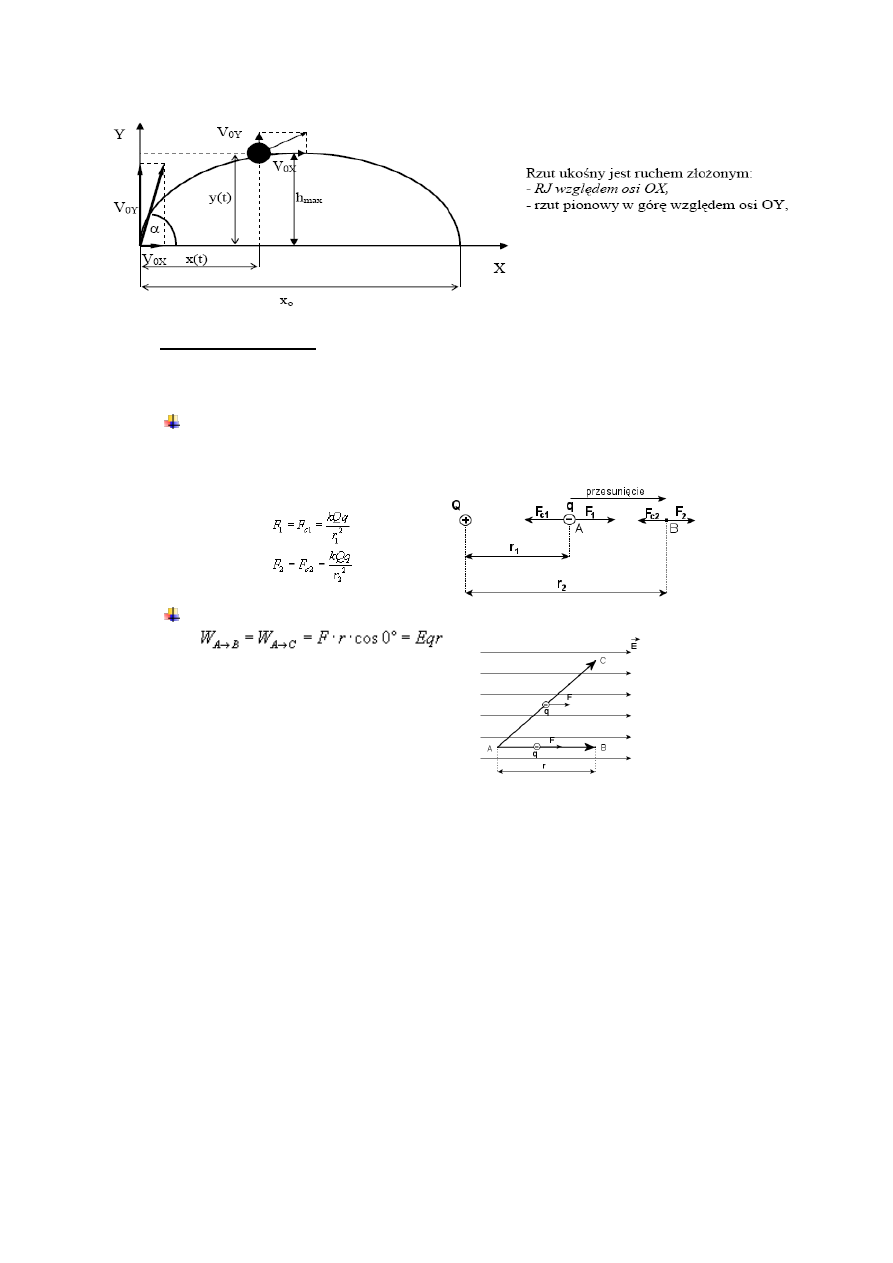
 Rzut ukośny – ruch następujący po nadaniu ciału prędkości początkowej V

0

pod

kątem do poziomu.

Pole elektrostatyczne

W polu elektrostatycznym występuje ruch jednostajnie lub niejednostajnie
przyspieszony. Ładunek w polu elektrycznym porusza się równolegle do linii
pola.

Ruch w polu elektrostatycznym centralnym

Ruch ładunku q jest jednostajny, działające na niego siły, tj. coulombowska i
zewnętrzna (wykonująca pracę) – muszą się równoważyć (zgodnie z pierwszą zasadą
dynamiki):

Ruch w polu elektrostatycznym jednorodnym