F1-49

Przykład syntezy.

Dana jest tablica stanów

x

2

x

1

x

0

k

P

k

(X)

f(X)

S

k

(X)

0 0 0 0 P

0

= x

2

'x

1

'x

0

'

1

S

0

= x

2

+ x

1

+ x

0

0 0 1 1 P

1

= x

2

'x

1

'x

0

0

S

1

= x

2

+ x

1

+ x

0

'

0 1 0 2 P

2

= x

2

'x

1

x

0

'

0

S

2

= x

2

+ x

1

' + x

0

0 1 1 3 P

3

= x

2

'x

1

x

0

0

S

3

= x

2

+ x

1

' + x

0

'

1 0 0 4 P

4

= x

2

x

1

'x

0

'

1

S

4

= x

2

' + x

1

+ x

0

1 0 1 5 P

5

= x

2

x

1

'x

0

1

S

5

= x

2

' + x

1

+ x

0

'

1 1 0 6 P

6

= x

2

x

1

x

0

'

0

S

6

= x

2

' + x

1

' + x

0

1 1 1 7 P

7

= x

2

x

1

x

0

1

S

7

= x

2

' + x

1

' + x

0

'

Określić zbiór T

3

i kanoniczną formę sumacyjną, obliczyć wskaźnik złożoności Z.

Wykonać minimalizację formy, obliczyć wskaźnik złożoności Z

m

i narysować schemat

logiczny układu. Określić równoważną formę iloczynową i narysować odpowiedni
schemat logiczny.

• Zbiór T

3

zawiera wszystkie liczby k, dla których f(X) = 1, czyli T

3

= {0,4,5,7}.

• f = x

2

'x

1

'x

0

' + x

2

x

1

'x

0

' + x

2

x

1

'x

0

+ x

2

x

1

x

0

. Z = 4 + 4·3 = 16.

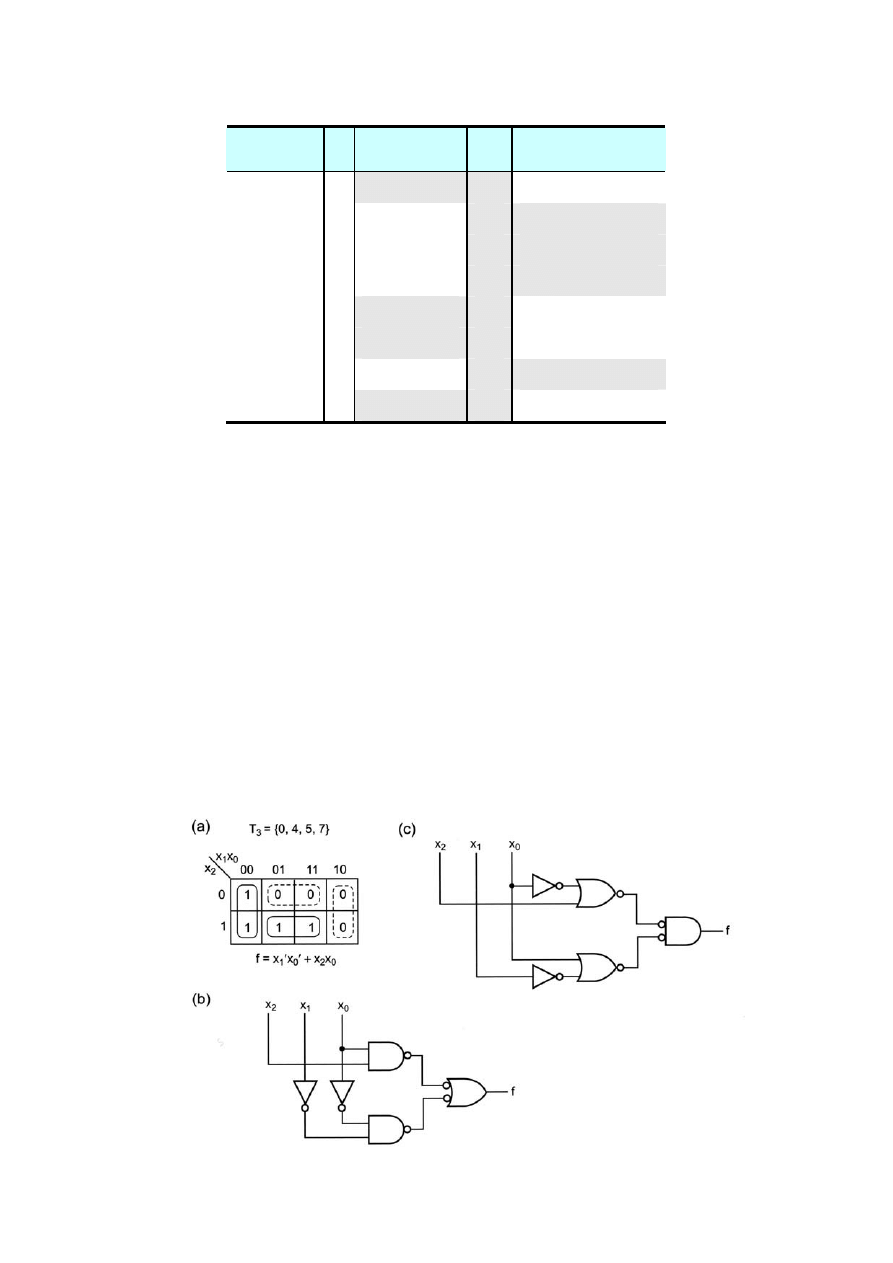
• Minimalizację wykonujemy na siatce Karnaugh (rys. a) i po sklejeniu jedynek

otrzymujemy f = x

1

'x

0

' + x

2

x

0

. Z

m

= 2 + 4 = 6.

• Tworzymy schemat logiczny (rys. b).
• F

3

= N

3

– T

3

= {1,2,3,6}

• f = (x

2

+ x

1

+ x

0

')(x

2

+ x

1

' + x

0

)( x

2

+ x

1

' + x

0

')( x

2

' + x

1

' + x

0

). Z = 16.

• Wykonujemy minimalizację na siatce Karnaugh, sklejając zera.
• Otrzymujemy f ' = x

2

'x

0

+ x

1

x

0

' więc f = (x

2

+ x

0

'

)(x

1

' + x

0

). Z

m

= 6.

• Tworzymy schemat logiczny (rys. c).

© J. Kalisz, WAT, 2008