MECHANIK NR 1/2008

41

* Dr hab. inż. Jerzy Z. Sobolewski – Wydział Samochodów

i Maszyn Roboczych Politechniki Warszawskiej

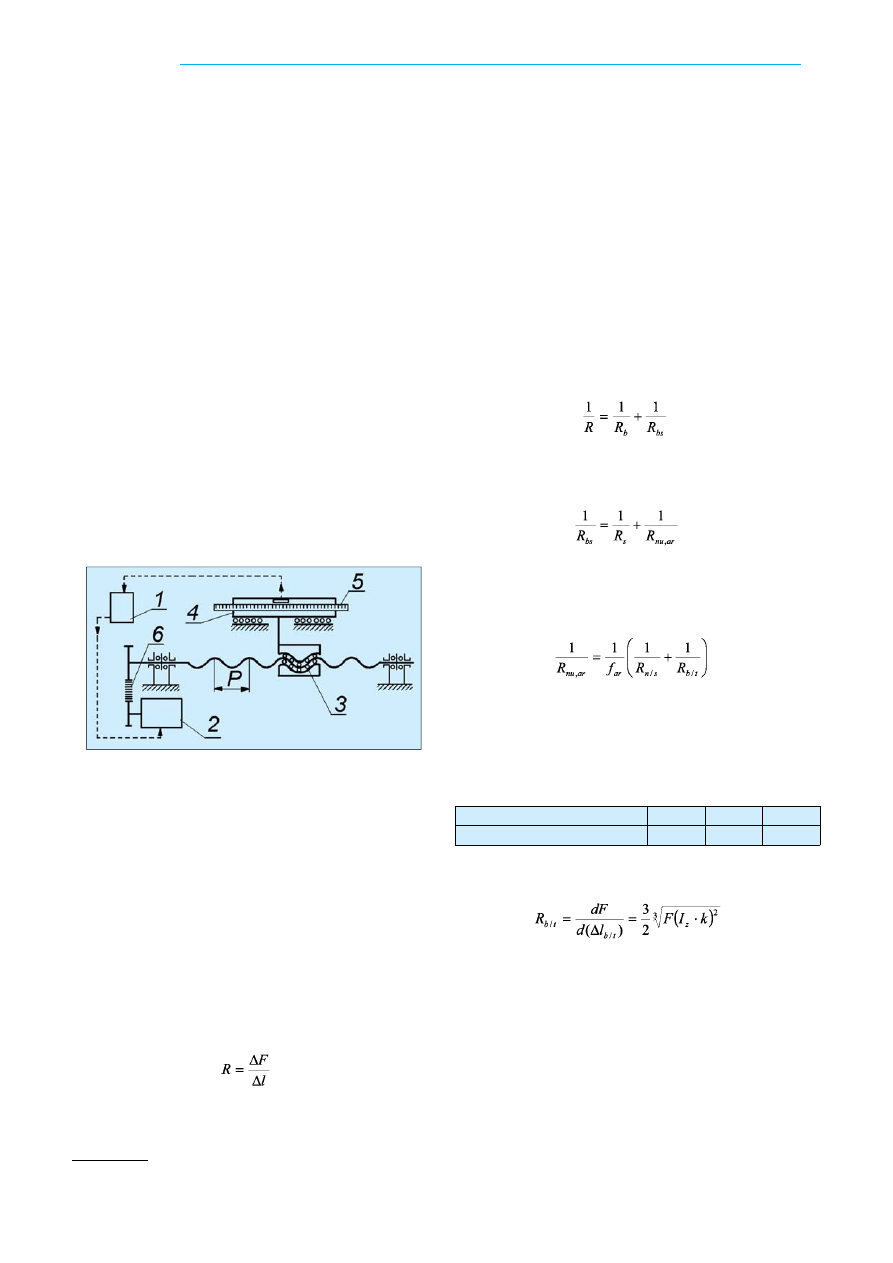
Rys. 1. Przykład zastosowania przekładni śrubowej tocznej w ob-
rabiarkach sterowanych numerycznie [1]: 1 – serwokontroler, 2 – ser-
womotor, 3 – przekładnia śrubowa kulkowa, 4 – stół, 5 - liniowy
pomiar położenia, 6 – pasek klinowy

TABLICA I. Współczynnik dokładności wykonania

f

ar

[6]

Klasa dokładności wg ISO

0,1

3

5

Współczynnik f

ar

0,6

0,55

0,5

Sztywność serwonapędów z gwintem kulkowym

JERZY Z. SOBOLEWSKI *

Opisano nową metodę obliczania sztywności osiowej
przekładni z gwintem kulkowym.

Napędy z gwintem kulkowym, zwane także przekład-

niami śrubowymi kulkowymi, charakteryzuje duża sztyw-
ność, duża precyzja i łatwość kontroli ruchu. Ze względu
na te zalety są one powszechnie stosowane w obrabiar-
kach sterowanych numerycznie (OSN), centrach obrób-
kowych do napędu suportów (rys. 1), z jednoczesnym
pomiarem położenia, i w członach napędowych (przegu-
bowo-teleskopowych) wykorzystywanych w urządzeniach
z kinematyką równoległą [1, 3]. Wysoka sprawność, osią-
gająca nawet 98%, skłania konstruktorów do stosowania
tych napędów w różnych urządzeniach: prasach i pod-
nośnikach, manipulatorach i robotach przemysłowych,
urządzeniach pomiarowych, serwomechanizmach ukła-
dów kierowniczych pojazdów, napędach lotniczych ukła-
dów sterowania itp.

Rys. 1 przedstawia przykład konstrukcji napędu OSN.

Przekładnie śrubowe kulkowe są wprzęgnięte w łańcuch
kinematyczny i służą do pomiaru przemieszczenia stołu
obrabiarki. Podczas projektowania serwonapędów, zwła-
szcza w OSN, należy przestrzegać kilku podstawowych
kryteriów konstrukcyjnych. Najważniejsze z nich to:

a) kryterium częstotliwości rezonansowej,
b) kryterium strefy nieczułości napędu,
c) kryterium stateczności (wyboczenie śruby tocznej).

Obliczenie sztywności zespołu napędzającego.

W kryteriach a) i b) istotną rolę odgrywa wskaźnik sztyw-
ności statycznej wzdłużnej serwonapędu, który jest zdefi-
niowany następująco:

(1)

gdzie:
∆F – przyrost siły działającej na zespół napędzany, N,

∆l – przemieszczenie zespołu napędzanego, µm.

Odkształcenie

∆l jest sumą odkształceń śruby ∆l

s

, kor-

pusu nakrętki i rdzenia śruby w obszarze wypełnionym
kulkami

∆l

n/s

, łożyskowania śruby

∆l

b

, zamocowania na-

krętki

∆l

m

, oraz odkształcenia węzła kulkowego

∆l

b/t

, które

wynika z hertzowskiego odkształcenia kulek i bieżni śruby
oraz nakrętki pod wpływem sił osiowych F działających
na układ.

Sztywność zespołu oblicza się [6]:

(2)

gdzie: R

b

– sztywność łożyskowania, R

bs

– sztywność

całkowita napędu ze śrubą toczną.

Sztywność całkowitą można znaleźć [6]:

(3)

gdzie: R

s

– sztywność trzpienia śruby, R

nu,ar

– sztywność

nakrętki wypełnionej kulkami; ar – uwzględnienie wpływu
dokładności wykonania.

Sztywność nakrętki R

nu,ar

oblicza się z [6]:

(4)

gdzie: R

n/s

– sztywność cylindra nakrętki, R

b/t

– sztywność

obszaru styku kulek z bieżniami śruby i nakrętki, f

ar

–

współczynnik uwzględniający dokładność wykonania we-
dług norm ISO [6] (tabl. I).

Sztywność obszaru styku oblicza się z zależności [6]:

(5)

gdzie: k – współczynnik sztywności jednego zwoju [N/

µm

3/2

],

I

z

– liczba zwojów wypełniona kulkami.

Ocena wpływu odchyłek wykonania na sztyw-

ność przekładni.

Badania [2, 4] wykazały, że współczyn-

nik dokładności wykonania nie uwzględnia w stopniu
wystarczającym wpływu odchyłek wykonania na sztyw-
ność obszaru styku kulek z bieżniami (rys. 2). Wykonano
model matematyczny zależności odkształceń kontakto-
wych w

i

od wymiarów i odchyłek wykonania bieżni śruby

i nakrętki [5]. Odkształcenie w

i

traktowane jako wymiar

jest funkcją wymiarów konstrukcyjnych, z których każdy
ma pewną tolerancję wykonania. Jest on wymiarem za-
leżnym w łańcuchu wymiarowym. Odkształcenie to jest
wartością przypadkową dla i-tej kulki. Zbudowano pro-

42

MECHANIK NR 1/2008

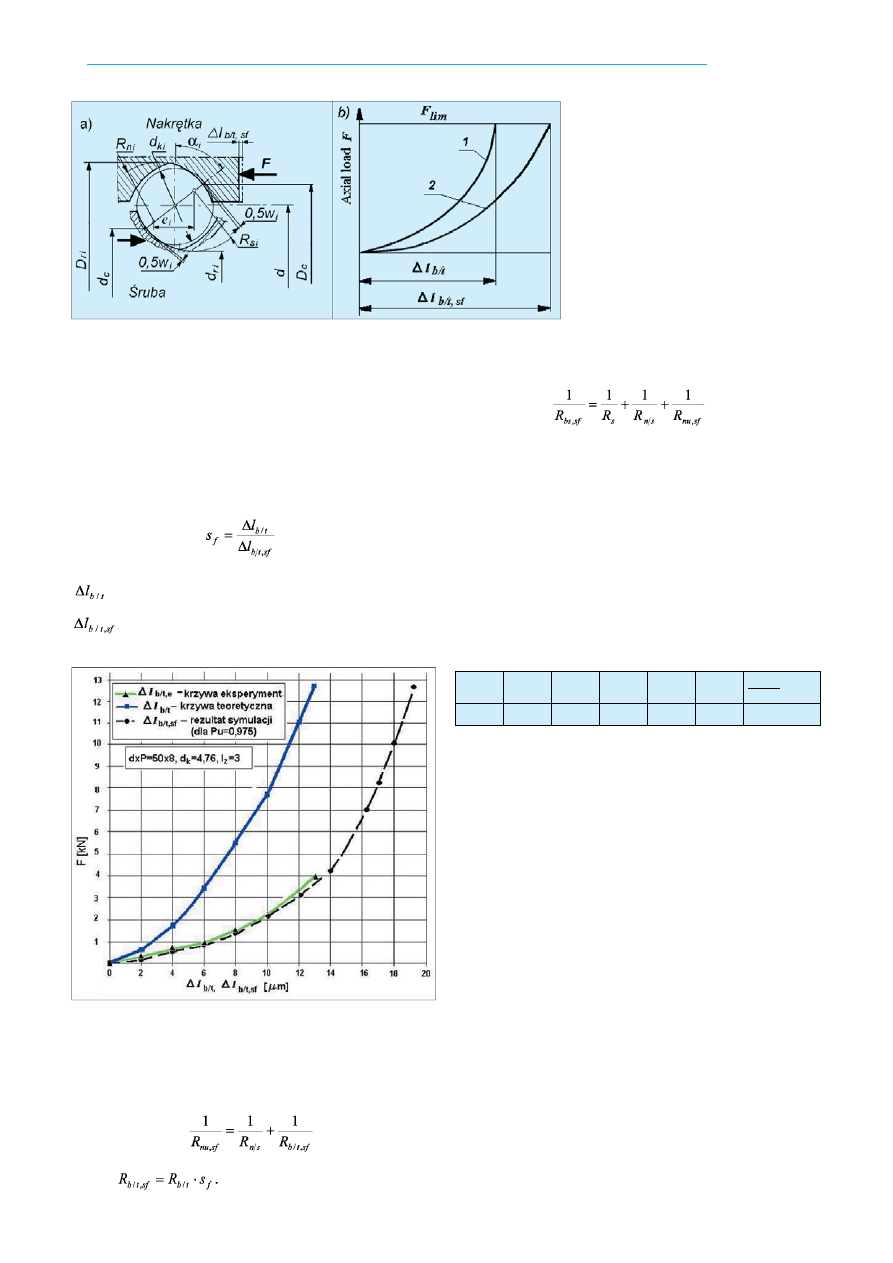
Rys. 2. a) Parametry geometryczne gwintu
kulkowego (dla i-tej kulki): d – średnica
nominalna, R

s,n

– promień łuku zarysu bie-

żni gwintu śruby (indeks s) i nakrętki (in-
deks n), d

k

– średnica kulki,

α

– kąt działa-

nia, k

s,n

– współrzędne punktów zaczepie-

nia promieni R

s,n

,

∆

l

k/b.sf

– odkształcenie

węzła kulkowego uwzględniające odchyłki
wykonania, w

i

– odkształcenie kontaktowe

i-tej kulki, b) odkształcenia węzła kulkowe-
go

Rys. 3. Pomierzone odkształcenie węzła kulkowego

∆

l

b/t,e

, odkształ-

cenie teoretyczne

∆

l

b/t

i rezultaty symulacji komputerowej

∆

l

b/t,sf

(dla poziomu ufności Pu = 0,975)

TABLICA II. Porównanie wyników obliczeń sztywności dla

f

ar

= 0,55

i s

f

= 0,7

R

b/t

wg (5)

R

nu,ar

wg (4)

R

bs

wg (3)

R

b/t,sf

wg (7)

R

nu,sf

wg (7)

R

bs,sf

wg (8)

R

nu, ar

· 100%

R

nu,sf

936

820

339

655

596

404

137%

gram symulacyjny NAK1 liczący odkształcenia teoretycz-
ne i odkształcenia uwzględniające odchyłki wykonania.

Przeprowadzone badania symulacyjne wykazały dla

tych samych wartości siły F, że rzeczywiste odkształcenia
są o wiele większe od teoretycznych (rys. 3). Przeprowa-
dzone pomiary przekładni rzeczywistych potwierdziły za-
sadność rozważań teoretycznych. W celu oceny wpływu
odchyłek wykonania sztywności nakrętki wprowadzono
współczynnik dokładności geometrycznej, który został
zdefiniowany następująco [2]:

(6)

gdzie:

– teoretyczne odkształcenie hertzowskie obszaru

styku,

– odkształcenie

rzeczywiste

lub

symulowane

(rys. 2).

Sztywność nakrętki rzeczywistej można teraz obliczyć

z następującego równania:

(7)

gdzie:

Analogicznie do (3) sztywność całkowitą przekładni

rzeczywistej R

bs,sf

można znaleźć z równania:

(8)

W tabl. II pokazano wyniki obliczeń sztywności dla

przekładni o następujących wymiarach: średnica d = 50,
skok P = 8, średnica kulki d

k

= 4,76, liczba zwojów wy-

pełnionych kulkami I

z

= 3 (łączna liczba kulek w obie-

gu n

k

= 85), promienie zarysu bieżni śruby i nakrętki

R

n,s

= 2,48. Tolerancje maszynowe (odpowiadające 3 kla-

sie dokładności wykonania wg ISO) są następujące: tole-
rancja rdzenia śruby T

dr

= 0,01, rdzenia nakrętki T

dr

= 0,01,

promieni śruby i nakrętki T

Rs,n

= 0,02, tolerancja skoku

śruby T

Ps

= 0,005, skoku nakrętki T

Pn

= 0,004. Przyjęto

długość śruby l = 1000 i łożyskowanie dwustronne.

Dla siły zewnętrznej F = 0,45C

a

= 12551 [N] wartość

współczynnika dokładności geometrycznej wg (6) s

f

= 0,7,

natomiast wartość współczynnika dokładności wykonania
wg ISO f

ar

= 0,55. Wyliczenie wszystkich składników szty-

wności podano w [4].

Tak duża różnica obliczeń sztywności wymaga dal-

szych badań w celu oceny zasadności stosowania norm
ISO.

Dobór przekładni do napędów posuwów OSN.

Dalsza droga obliczeń zależy od warunków wytrzymałoś-
ciowych i od przyjętego w obrabiarce układu pomiaru
położenia. Najczęściej stosowane są dwa podstawowe
rodzaje pomiaru [1]: a) z pośrednim pomiarem położenia,
b) z bezpośrednim pomiarem położenia stołu za pomocą
liniowego układu pomiarowego (rys. 1).

Średnica śruby kulkowej jest wyliczana z warunków

wytrzymałościowych i jest wielkością podstawową do ob-
liczeń systemu doboru serwonapędu. Dopuszczalna siła
osiowa (siła skrawania) działająca na śrubę nie może
przekroczyć maksymalnej siły wyboczeniowej (warunek
Eulera). Siła ta zależy od średnicy śruby, jej długości
i typu łożyskowania.

Dla pośredniego systemu pomiaru głównym kryterium

doboru śrub kulkowych jest odpowiednia sztywność na-
pędu a dla bezpośredniego – średnicę śruby dobiera się
z warunku częstotliwości rezonansowej zespołu stół –
śruba.

MECHANIK NR 1/2008

43

Rezonans osiowy oblicza się z następującej zależności

[1]:

(9)

gdzie: m

s

– masa stołu, m

po

– masa przedmiotu ob-

rabianego, f

cr

– wartość kryterialna częstotliwości drgań

własnych układu mechanicznego serwonapędu (zależy
od częstotliwości rezonansowej napędu).

Kryterium rezonansu jest jednym z najważniejszych

kryteriów projektowania serwonapędów.

Maksymalna prędkość kątowa śruby powinna być zna-

cznie mniejsza od prędkości krytycznej, przy której mogą
wystąpić rezonansowe drgania poprzeczne, co ostatecz-
nie prowadzi do następującego warunku na średnicę
śruby [4]:

(10)

gdzie: l

s

– długość śruby.

Dla obu typów pomiaru pozycjonowania niezbędne jest

wyznaczenie kryterium strefy nieczułości napędu S

n

[1]:

(11)

gdzie: T – siła tarcia napędzanego zespołu (siła tarcia
w prowadnicach),
(S

n

)

cr

– wartość kryterialna, wynikająca z dokładności

pozycjonowania

Dla obrabiarek średniodokładnych (S

n

)

cr

= 10

µm, a dla

dokładnych (S

n

)

cr

= 1

µm [1].

Sztywność osiowa jest głównym czynnikiem określenia

jakości układu napędowego, wpływa bowiem na dokład-
ność pozycjonowania. Badania wykazały, że znaczna
część odkształceń systemu jest powodowana przez od-
kształcenia hertzowskie na styku bieżnia śruby – kulki
– bieżnia nakrętki. Odkształcenia te ulegają znacznemu
zwiększeniu na skutek odchyłek wykonania gwintu kul-
kowego. Zaproponowany współczynnik dokładności geo-
metrycznej jest głównym kryterium oceny jakości wykona-
nia gwintu kulkowego. Z przeprowadzonej analizy ob-
liczeń sztywności wynika duża różnica między metodą
obliczania sztywności układu zalecanego przez ISO i me-
todą zaproponowaną. Nowa metoda obliczeń jest bar-
dziej dokładna i umożliwia przy tym symulacyjne badanie
sztywności przekładni śrubowych kulkowych we wstępnej
fazie projektu technicznego.

LITERATURA

1. J. KOSMOL: Serwonapędy obrabiarek sterowanych numerycznie.

WNT Warszawa 1998.

2. J. MAŁKIŃSKI: Ocena jakości wykonania przekładni śrubowych

kulkowych. Rozprawa doktorska. Oficyna Wydawnicza Politech-
niki Warszawskiej Warszawa 2006.

3. K. E. OCZOŚ, E. WEISS: Kinematyki równoległe w budowie

obrabiarek, robotów i manipulatorów (część I). Mechanik 5-6
(2002), 323

÷ 333.

4. J. Z. SOBOLEWSKI: Criteria of Ball Screws Selection for CNC

Machines. Journal of Machine Engineering, Vol. 7, 1, 2007,
Wrocław 2007, 42

÷ 50.

5. J. Z. SOBOLEWSKI: Symulacyjne badanie właściwości przekładni

śrubowych kulkowych. Mechanik 10 (2002), 678

÷ 681.

6. ISO/DIS 3408-4:1992 Ball screws – Part 4: Static axial rigidity.